Mask-Guided Teacher–Student Learning for Open-Vocabulary Object Detection in Remote Sensing Images

Highlights

What are the main findings?

• A selective masking strategy enables direct utilization of partially annotated data, eliminating strict data separation requirements and improving annotation efficiency.
• Dynamic frequency class weighting based on information theory automatically balances class distributions.

What is the implication of the main finding?

• The approach eliminates the need for strict data separation and complex preprocessing, providing a more practical and data-efficient solution compared to large-scale pretraining methods.
• The dynamic frequency class weighting mechanism can be integrated into other openvocabulary frameworks to address class imbalance issues, offering broad applicability.

Abstract

Open-vocabulary object detection in remote sensing aims to detect novel categories not seen during training, which is crucial for practical aerial image analysis applications. While some approaches accomplish this task through large-scale data construction, such methods incur substantial annotation and computational costs. In contrast, we focus on efficient utilization of limited datasets. However, existing methods such as CastDet struggle with inefficient data utilization and class imbalance issues in pseudo-label generation for novel categories. We propose an enhanced open-vocabulary detection framework that addresses these limitations through two key innovations. First, we introduce a selective masking strategy that enables direct utilization of partially annotated images by masking base category regions in teacher model inputs. This approach eliminates the need for strict data separation and significantly improves data efficiency. Second, we develop a dynamic frequency-based class weighting that automatically adjusts category weights based on real-time pseudo-label statistics to mitigate class imbalance issues. Our approach integrates these components into a student–teacher learning framework with RemoteCLIP for novel category classification. Comprehensive experiments demonstrate significant improvements on both datasets: on VisDroneZSD, we achieve 42.7% overall mAP and 41.4% harmonic mean, substantially outperforming existing methods. On DIOR dataset, our method achieves 63.7% overall mAP with 49.5% harmonic mean. Our framework achieves more balanced performance between base and novel categories, providing a practical and data-efficient solution for open-vocabulary aerial object detection.

1. Introduction

Remote sensing object detection (RSOD) aims to determine whether objects of interest exist in given remote sensing images and return the category and location of each predicted object. Here, “objects” refer to discrete, man-made structures such as aircraft, vehicles, and ships, as opposed to unstructured scene elements like terrain, sky, and vegetation [1]. As a fundamental task in remote sensing image interpretation, remote sensing object detection has undergone significant evolution from traditional methods to deep learning approaches over the past two decades. Initially inspired by successful natural image detection methods, many studies have applied these frameworks (such as Faster R-CNN [2], YOLO [3], and SSD [4]) to remote sensing object detection, achieving breakthroughs. Based on the characteristics of geospatial objects in remote sensing images, many methods specifically designed for remote sensing images have emerged in recent years [5,6]. For example, ROI-Transformer [7], R3Det [8], and RSDet++ [9] for rotated object detection; CA-CNN [10], ASPP [11], and RFB [12] for mining remote sensing-related context information; and edge-enhanced GAN [13] and YOLO-DCTI [14] for small object detection. However, these methods operate under closed-set assumptions and require extensive manual annotations for new categories.

Open-vocabulary object detection (OVD [15]) aims to locate and identify new categories not annotated in the dataset by leveraging base categories and linguistic vocabulary knowledge, i.e., large-scale language models or vocabulary data, which are of significant importance in remote sensing image analysis. With the proliferation of drone technology and advances in satellite image acquisition capabilities, the diversity of observable targets in aerial images far exceeds the limited categories covered by existing annotated datasets [16,17]. Traditional closed-set detection methods require collecting and annotating large amounts of training data for each new category, which is particularly expensive and time-consuming in the remote sensing domain. Therefore, developing open-vocabulary detection techniques that can detect additional categories using limited annotated data is of great value for advancing practical applications of aerial image interpretation. First in natural images, OVR-CNN [18] introduced the first method for OVD. In recent years, due to the rapid development of large-scale language models in the remote sensing field, models such as RemoteCLIP [19] and GeoRSCLIP [20] have obtained rich semantic understanding capabilities through pre-training on large-scale remote sensing image–text pairs, providing strong foundational support for remote sensing open-vocabulary tasks. Remote sensing open-vocabulary detection is an emerging research direction that has gained attention only recently.

Unlike natural image OVD, which has been extensively studied with numerous established methods, specialized approaches for remote sensing scenarios are still limited. In this nascent field, CastDet [21] proposed the first CLIP-activated student–teacher open-vocabulary detection framework specifically for aerial images in ECCV 2024. The core contribution of CastDet lies in integrating RemoteCLIP as an external teacher into a student–teacher learning mechanism, effectively leveraging the rich knowledge of pre-trained vision–language models for novel category discovery. This design significantly improves the detection performance of novel categories in aerial images. LAE-DINO [22] defines the task as “locating anything on Earth,” constructing the first large-scale remote sensing object detection dataset LAE-1M, and proposing a foundation model with dynamic vocabulary construction and vision-guided text prompt learning. OpenRSD [23] proposes a general open prompt detection framework supporting multi-modal prompts, integrating alignment heads and fusion heads to balance speed and accuracy, and adopting a multi-stage training pipeline to enhance generalization capabilities. This method constructs a large-scale dataset ORSD+, containing 470k images and 200 categories.

However, large-scale pre-training methods (such as LAE-DINO and OpenRSD) require constructing large-scale datasets, which results in extremely high data collection and training costs, making them difficult to implement in resource-constrained practical application scenarios. Unlike their pursuit of more data, we focus more on how to make good use of limited datasets. CastDet is precisely based on this setting, but its data filtering constraints prevent images containing mixed categories from being fully utilized. Specifically, these methods require strict separation of annotated base categories data and completely unlabeled data during training. When base categories and novel categories coexist in the same image, this constraint becomes problematic because the presence of novel targets makes the entire image unusable for supervised training of base categories, requiring the removal of all annotations from the image for unsupervised learning. This design stems from the strict assumptions of traditional semi-supervised learning but appears overly conservative in open-vocabulary scenarios, resulting in an enormous waste of annotation resources. This limitation significantly introduces considerable annotation overhead in practical application scenarios. When facing potentially increasing novel categories, strict inspection and re-partitioning of annotated datasets are required.

Furthermore, severe class imbalance problems are often encountered when generating pseudo-labels for novel categories. The inherent difficulty of detecting rare or small targets in aerial images exacerbates this problem, resulting in training bias and poor performance on certain categories. CastDet adopts a static weighting scheme that cannot adapt to the dynamic distribution of pseudo-labels during training and changes in datasets.

To address these limitations, we propose an enhanced open-vocabulary detection framework that supports one-step training with partially annotated data. The main contributions of this work are summarized as follows:

• Selective masking strategy: We propose a selective masking strategy that enables direct utilization of images containing both base and novel categories, relaxing the strict data separation constraints of existing methods and achieving more flexible dataset utilization.
• Dynamic frequency-based class weighting: We propose a dynamic weighting mechanism based on pseudo-label queue frequency, which automatically adjusts category weights by monitoring pseudo-label category distribution to alleviate class imbalance issues in pseudo-labels.
• We conduct comprehensive experiments on aerial open-vocabulary detection baselines VisDroneZSD and DIOR, demonstrating significant improvements over existing methods.

2. Methods

2.1. Problem Formulation

Given a detection dataset containing only annotations of base categories, $D_{\mathrm{labeled}}={\left\{(I_i,y_i)\right\}}_{i=1}^N$, where N denotes the total number of images in the dataset, $I_i\in {\mathbb{R}}^{H\times W\times 3}$ represents the input image, and $y_i={\left\{(b_{i,k},c_{i,k})\right\}}_{k=1}^{K_i}$ represents the corresponding annotations with $K_i$ being the number of objects in the i-th image. Each annotation includes bounding box coordinates $b_{i,k}\in {\mathbb{R}}^4$ and category labels $c_{i,k}\in {\mathcal{C}}_{\mathrm{base}}$, where ${\mathcal{C}}_{\mathrm{base}}$ denotes the set of base categories with available annotations during training.

Existing methods require strict separation of labeled and unlabeled data. The dataset must be traversed first, and if an image contains targets of novel categories ${\mathcal{C}}_{\mathrm{novel}}$, the entire image must be assigned to the unlabeled dataset, thus discarding the base categories ${\mathcal{C}}_{\mathrm{base}}$ annotations in that image. In contrast, our approach aims to fully utilize partially annotated images. For images containing both base categories ${\mathcal{C}}_{\mathrm{base}}$ and novel categories ${\mathcal{C}}_{\mathrm{novel}}$, we no longer need to assign them completely as unlabeled data but can instead directly train a detector that can simultaneously detect both category types.

Our goal is to train a detector capable of detecting objects from the complete category set ${\mathcal{C}}_{\mathrm{test}}={\mathcal{C}}_{\mathrm{base}}\cup {\mathcal{C}}_{\mathrm{novel}}$ during inference, where ${\mathcal{C}}_{\mathrm{test}}$ represents the union of base and novel categories that the model should recognize at test time. Therefore, the key challenge lies in how to effectively discover and learn novel categories while maintaining supervised learning performance on base categories.

2.2. Overall Framework

We propose a mask-guided teacher–student framework for open-vocabulary object detection. The core idea is to achieve functional decoupling through differentiated data input strategies, enabling an image containing both base and novel categories to simultaneously serve supervised learning and pseudo-label generation. As shown in Figure 1, our framework contains four components: a data processing module, a teacher model, a dynamic label queue, and a student model.

The data processing module handles input preparation with two parallel pathways. For the teacher branch, we first apply weak augmentation to the original images. Subsequently, our selective masking strategy masks base category regions, forcing the teacher model to focus on potential novel category objects. For the student branch, we apply strong augmentation directly to the complete images to improve model robustness and generalization capability during training.

The teacher model operates on selectively masked images where base category regions are removed through our selective masking strategy, forcing the model to focus on discovering novel category objects. The teacher branch employs Faster R-CNN for object localization, generating high-quality region proposals that are subsequently classified using RemoteCLIP’s powerful vision–language capabilities. This design leverages the rich semantic knowledge from large-scale remote sensing image–text pre-training to achieve robust novel category identification.

The dynamic label queue serves as the central coordination module that manages both novel category pseudo-labels generated by the teacher model and base category ground-truth annotations from the original dataset. This queue continuously tracks category frequency statistics and implements our information-theoretic dynamic weighting mechanism to address class imbalance issues. The queue performs label merging operations, combining reliable pseudo-labels with ground-truth annotations to create comprehensive supervision signals for the student model.

The student model receives complete unmasked images along with the merged supervision signals from the dynamic queue. Using the same Faster R-CNN architecture as the teacher, the student model trains on both base and novel categories simultaneously through our weighted supervision learning approach. The teacher model parameters are updated through an exponential moving average (EMA) from the student model, ensuring consistent learning progress and stability.

This design eliminates the need for prior data separation and directly utilizes original annotated data containing multiple categories for end-to-end training, significantly improving data utilization efficiency and simplifying actual deployment workflows. The entire training process is completed through a single-stage weighted supervision approach, avoiding complex multi-stage training and loss balancing issues between different learning paradigms.

2.3. Selective Masking Strategy

As illustrated in Figure 2, to achieve one-step training, we design a selective masking strategy to process data. For image $I_i$, we extract all the base categories’ bounding boxes from their annotations $y_i={\left\{(b_{i,k},c_{i,k})\right\}}_{k=1}^{K_i}$:

$${\mathcal{B}}_{\mathrm{base}}^{\left(i\right)}=\{b_{i,k}\mid c_{i,k}\in {\mathcal{C}}_{\mathrm{base}},k=1,\dots ,K_i\}$$

(1)

Based on the extracted bounding box set, we construct a binary mask matrix, written as follows:

$$M_{\mathrm{base}}^{\left(i\right)}(u,v)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}\exists b\in {\mathcal{B}}_{\mathrm{base}}^{\left(i\right)}\mathrm{such}\mathrm{that}(u,v)\in b\hfill \\ 1\hfill & \mathrm{otherwise}\hfill \end{array}\right.,$$

(2)

where $(u,v)$ represents pixel coordinates in the image.

For images input to the teacher model, we mask the base category regions, calculated as follows:

$$I_{\mathrm{teacher}}^{\left(i\right)}=I_i\odot M_{\mathrm{base}}^{\left(i\right)}+f_{\mathrm{mask}}\odot (1-M_{\mathrm{base}}^{\left(i\right)}),$$

(3)

where $I_i\odot M_{\mathrm{base}}^{\left(i\right)}$ represents preserving original pixel values of non-base category regions, and $f_{\mathrm{mask}}\odot (1-M_{\mathrm{base}}^{\left(i\right)})$ represents applying mask function $f_{\mathrm{mask}}$ to base category regions.

The mask function can adopt strategies such as Gaussian blur $\mathrm{GaussianBlur}\left(I\right)$ or zero padding 0. Here, we adopt zero padding. Zero padding provides complete information suppression, which is theoretically superior to other masking strategies for our objective. Theoretically, the advantage of zero padding lies in reducing the information entropy of masked regions to zero, completely blocking the visual information propagation of base categories. In contrast, while Gaussian blur reduces information clarity, it still preserves low-frequency information (such as shape contours), and this residual information may be exploited by the strong fitting capability of deep networks, thereby weakening the masking effect. Meanwhile, zero padding provides deterministic background suppression, avoiding the random interference that noise injection may bring, ensuring that the teacher model learns genuine novel category features rather than possible noise patterns.

Theoretically, selective masking addresses the fundamental challenge in open-vocabulary detection: how to prevent the model from being dominated by well-represented categories while encouraging exploration of under-represented ones. The selective masking strategy directly impacts the behavior of the Region Proposal Network (RPN) in Faster R-CNN. Without masking, the RPN generates proposals with a strong bias toward base categories, as these regions produce higher objectness scores. By masking base category regions, we eliminate these high-confidence proposals and force the RPN to generate proposals from regions that might contain novel categories. This redistribution of proposal generation increases the likelihood of discovering novel category objects that would otherwise be overshadowed by dominant base category responses.Through this masking strategy, base category regions are “hidden” in images received by the teacher model, forcing it to focus on discovering and localizing potential novel category targets, while the student model still receives the complete image $I_i$ for training.

2.4. Pseudo-Label Generation and Quality Control

The quality of pseudo-labels directly affects the learning effectiveness of the student model. Therefore, after the teacher model receives masked images, we adopt a complete pseudo-label generation and quality control mechanism to ensure that only reliable predictions are used as supervision signals.

Teacher model pseudo-label generation. The teacher model receives masked images where base category regions have been selectively masked out, forcing it to focus on potential novel category objects. The process begins with feature extraction using the backbone network, followed by the Region Proposal Network (RPN), which generates an initial set of object proposals. These proposals represent potential object locations but lack category-specific information.

To refine the localization accuracy, we employ an iterative optimization strategy where the predicted bounding boxes undergo multiple rounds of regression refinement. In each iteration t, the current bounding boxes ${\widehat{b}}_i^{\left(t\right)}$ (where $i=1,2,\dots ,N$ indexes the proposals) are first converted to ROI format, then fed through the ROI pooling layer to extract fixed-size feature representations $f_i^{\left(t\right)}$. The regression head processes these features to predict coordinate refinement offsets ${\mathrm{\Delta }}_i^{\left(t\right)}$:

$${\mathrm{\Delta }}_i^{\left(t\right)}=\mathrm{BBoxHead}\left(f_i^{\left(t\right)}\right)$$

(4)

The refined bounding boxes are obtained by decoding the current coordinates with the predicted offsets:

$${\widehat{b}}_i^{(t+1)}=\mathrm{BBoxDecode}({\widehat{b}}_i^{\left(t\right)},{\mathrm{\Delta }}_i^{\left(t\right)}),$$

(5)

where $\mathrm{BBoxDecode}(·,·)$ transforms the regression deltas into absolute coordinates based on the current bounding box positions. This iterative refinement process continues for a predetermined number of steps, progressively improving the spatial accuracy of the bounding box predictions.

Once high-quality bounding box proposals, ${\left\{{\widehat{b}}_i\right\}}_{i=1}^K$, are obtained, the critical step of category classification begins. We crop the corresponding image regions based on the refined bounding boxes and resize them to the input resolution required by RemoteCLIP (typically 224 × 224 pixels). These cropped regions, ${\left\{x_i\right\}}_{i=1}^K$, are then fed into the visual encoder of RemoteCLIP, which extracts rich semantic features:

$$v_i=\mathrm{VisualEncoder}\left(x_i\right)\in {\mathbb{R}}^{d_v}$$

(6)

For the textual component, we construct category descriptions using a predefined template “a photo of [category]” for each target category, including both base and novel categories. These textual descriptions are processed through RemoteCLIP’s text encoder:

$$t_j=\mathrm{TextEncoder}\left({\mathrm{template}}_j\right)\in {\mathbb{R}}^{d_t},$$

(7)

where ${\mathrm{template}}_j$ represents the text template for category j.

The classification process involves computing similarity scores between the L2-normalized visual and text embeddings, scaled by a learnable temperature parameter:

$$s_{ij}={\displaystyle \frac{v_i^T·t_j}{\tau \parallel v_i{\parallel }_2·{\parallel t_j\parallel }_2}},$$

(8)

where ${\displaystyle \frac{1}{\tau }}$ corresponds to the clip logit scale parameter in the implementation. The final classification probabilities are obtained by applying a softmax function over these similarity scores:

$$p_{ij}={\displaystyle \frac{exp\left(s_{ij}\right)}{{\sum }_{k=1}^{\left|\mathcal{C}\right|}exp\left(s_{ik}\right)}},$$

(9)

where $p_{ij}$ represents the probability that the i-th cropped region belongs to category j. The predicted category label for each region is determined by the following:

$${\widehat{c}}_i=arg\underset{j}{max}{p}_{ij}$$

(10)

This integration of RemoteCLIP enables our framework to leverage the rich semantic knowledge acquired from large-scale remote sensing image–text pairs, providing robust classification capabilities for both base and novel categories without requiring additional training on the target dataset.

Multi-Layer Quality Control Mechanism. We adopt a three-layer progressive filtering strategy to ensure pseudo-label quality:

First step: Non-maximum suppression. NMS processing is applied to candidate boxes of the same category to eliminate duplicate detections while removing redundancy without mistakenly deleting adjacent targets.

Second step: Geometric constraint filtering based on physical characteristics and statistical patterns of targets in aerial images. To avoid mistaking large background areas as targets, we apply a geometric constraint to filter obviously oversized detection boxes. Based on empirical analysis of target size distributions in aerial imagery, we set a maximum bounding box area threshold of 400,000 pixels (approximately equivalent to a 632 × 632 pixel square).

Third step: Overlap detection. Calculate IoU between pseudo-labels and ground-truth annotations, removing pseudo-labels with overlap exceeding 0.5 to avoid conflicts with already annotated base categories.

2.5. Dynamic Frequency-Based Class Weighting

To address imbalance issues among novel categories, commonly used methods establish higher static weights for few-shot samples, but this approach cannot adapt to dynamic changes in pseudo-label distribution during training and changes across different datasets. In the classic Class-Balanced Loss paper, weights can be defined by counting effective sample numbers:

$$w_i={\displaystyle \frac{1-\beta }{1-{\beta }^{n_{c_i}}}},$$

(11)

where $\beta$ is a hyperparameter controlling the re-weighting strength and $n_{c_i}$ represents the number of samples for category $c_i$.

However, CB Loss is based on fixed training sample statistics, assuming that the number of samples for each category is determined at the beginning of training. In our method, samples of novel categories are actually dynamically generated pseudo-labels, whose quantity and quality continuously change as teacher model capabilities improve. Static effective sample number formulas cannot capture this dynamic evolution process. Therefore, we propose a weight adjustment mechanism based on dynamic label queue frequency, which can automatically adjust loss weights according to real-time category frequency statistics in the pseudo-label queue, ensuring all rare novel categories receive adequate learning opportunities.

Long-Term and Short-Term Frequency Statistics. We maintain a pseudo-label queue to track category distribution and combine long-term and short-term statistical information. The design philosophy of combining long-term and short-term statistics is that long-term statistics reflect overall data distribution, providing a stable baseline, while short-term statistics reflect recent detection trends and can respond promptly to distribution changes. The specific frequency calculation formula is written as follows:

$$f_{c_i}=0.5·f_{\mathrm{queue},c_i}+0.5·f_{\mathrm{recent},c_i},$$

(12)

where $f_{\mathrm{queue},c_i}={\displaystyle \frac{N_{\mathrm{queue},c_i}}{N_{\mathrm{queue},\mathrm{total}}}}$ represents the long-term frequency of category $c_i$ in the entire queue, and $f_{\mathrm{recent},c_i}={\displaystyle \frac{N_{\mathrm{recent},c_i}}{N_{\mathrm{recent},\mathrm{total}}}}$ represents the short-term frequency of category $c_i$ in the most recent 500 updates.

This design effectively prevents overfitting: pure short-term statistics might lead to excessive weight adjustment on local batches, while adding long-term statistics provides a global perspective, avoiding dramatic weight changes due to short-term fluctuations while still being able to respond promptly to real distribution shifts.

Adaptive Weight Calculation. Inspired by Shannon’s information theory, we believe that rare categories carry a higher information value in imbalanced pseudo-label distributions. According to information theory principles, the self-information of category $c_i$ is defined as follows:

$$I\left(c_i\right)=-logp\left(c_i\right)=-log{f}_{c_i}$$

(13)

Self-information measures the “information content” obtained when observing this event. Rare events contain more information and should therefore receive more attention in training. Based on this principle, we use self-information as the theoretical foundation for weight adjustment, ensuring the model allocates more learning resources to rare categories with high information content. We design the training weight for each novel category as follows:

$$w_{c_i}^{\mathrm{raw}}\left(t\right)=1+\mu ·I\left(c_i\right)=1+\mu ·(-log(f_{c_i}+ϵ)),$$

(14)

where $\mu$ is the information intensity coefficient controlling the influence of self-information on weights. $ϵ={\displaystyle \frac{1}{N_{\mathrm{queue},\mathrm{total}}}}$ is a smoothing term preventing numerical issues caused by zero frequency. The base weight 1 ensures all novel categories have weights no lower than base categories.

Smooth Weight Updates. To ensure stability in weight updates and avoid training shocks caused by sudden weight changes, we adopt exponential moving average for weight updates:

$$W_{c_i}\left(t\right)=\alpha ·W_{c_i}(t-1)+(1-\alpha )·w_{c_i}^{\mathrm{raw}}\left(t\right),$$

(15)

where $\alpha$ is the smoothing coefficient and t represents the update step.

The exponential moving average update mechanism ensures training stability by smoothing weight fluctuations. The smoothing parameter provides a balance between responsiveness to distribution changes and stability against noise in pseudo-label generation.

The advantage of an exponential moving average over directly using the latest predicted values is that it assigns higher weights to recent data while retaining historical trend information, making gradient descent smoother. We update weights every fixed number of iterations (e.g., 100), which can respond to distribution changes promptly while avoiding computational overhead from overly frequent updates.

2.6. Training with Merged Labels and Weighted Loss

The final training stage integrates high-quality pseudo-labels with ground-truth annotations to train the student model. Novel category pseudo-labels that pass quality control are merged with base category ground truth to create comprehensive supervision signals. For image $I_i$, the merged annotation is calculated as follows:

$$y_i^{\mathrm{merged}}={\left\{(b_{i,k}^{\mathrm{base}},c_{i,k}^{\mathrm{base}})\right\}}_{k=1}^{K_i^{\mathrm{base}}}\cup {\left\{(b_{i,j}^{\mathrm{novel}},c_{i,j}^{\mathrm{novel}})\right\}}_{j=1}^{K_i^{\mathrm{novel}}},$$

(16)

where the former represents original base category ground-truth annotations (confidence set to 1.0), and the latter represents filtered novel category pseudo-labels (maintaining original confidence).

After merging ground-truth annotations with high-quality pseudo-labels, the student model is trained using supervised learning with dynamic class weighting. Our loss function integrates multiple components to handle both learning on base categories and novel categories simultaneously:

$$\mathcal{L}={\mathcal{L}}_{\mathrm{rpn}}+{\mathcal{L}}_{\mathrm{reg}}+{\mathcal{L}}_{\mathrm{cls}}^{\mathrm{weighted}}$$

(17)

RPN Loss. The Region Proposal Network (RPN) loss adopts the standard formulation for object proposal generation. In our framework, RPN performs binary classification (foreground vs. background) rather than multi-class classification, with both classification and regression components:

$${\mathcal{L}}_{\mathrm{rpn}}={\displaystyle \frac{1}{N_{\mathrm{rpn}}}}\sum _i{\mathcal{L}}_{\mathrm{cls}}^{\mathrm{rpn}}(p_i,p_i^{*})+\lambda {\displaystyle \frac{1}{N_{\mathrm{reg}}}}\sum _i{p}_i^{*}{\mathcal{L}}_{\mathrm{reg}}^{\mathrm{rpn}}(t_i,t_i^{*}),$$

(18)

where $p_i$ is the predicted probability of anchor i being an object (foreground), $p_i^{*}$ is the binary ground-truth label (1 for positive, 0 for negative), $t_i$ represents the predicted bounding box regression parameters, $t_i^{*}$ denotes the ground-truth regression targets, $N_{\mathrm{rpn}}$ and $N_{\mathrm{reg}}$ are normalization terms, and $\lambda$ is the balance weight between classification and regression loss. Importantly, all ground-truth labels are set to binary (foreground/background) for RPN training, regardless of their original categories.

Regression Loss. The regression loss operates on the ROI head level, applying Smooth L1 loss to the sampled proposals after RPN processing:

$${\mathcal{L}}_{\mathrm{reg}}={\displaystyle \frac{1}{N_{\mathrm{roi}}}}\sum _{i=1}^{N_{\mathrm{roi}}}{\mathcal{L}}_{\mathrm{smooth}\text{-}\mathrm{L}1}({\widehat{b}}_i,b_i^{*}),$$

(19)

where $N_{\mathrm{roi}}$ is the number of ROI samples (both positive and negative), ${\widehat{b}}_i$ represents the predicted bounding box refinement parameters from the ROI head, and $b_i^{*}$ denotes the corresponding regression targets. This loss refines the initial proposals from RPN to achieve more precise object localization. The Smooth L1 loss is defined as follows:

$${\mathcal{L}}_{\mathrm{smooth}\text{-}\mathrm{L}1}\left(x\right)=\left\{\begin{array}{cc}0.5x^2\hfill & \mathrm{if}\left|x\right|<1\hfill \\ \left|x\right|-0.5\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(20)

This loss function is less sensitive to outliers compared to L2 loss while maintaining differentiability, making it particularly suitable for bounding box regression tasks.

Weighted Classification Loss. To address the inherent class imbalance in pseudo-label generation, we introduce a dynamically weighted classification loss:

$${\mathcal{L}}_{\mathrm{cls}}^{\mathrm{weighted}}={\displaystyle \frac{1}{N_b}}\sum _{i=1}^{N_b}{W}_{c_i}·{\mathcal{L}}_{\mathrm{cls}}({\widehat{s}}_i,c_i),$$

(21)

where $N_b$ is the total number of samples in a batch, ${\widehat{s}}_i$ represents the predicted class scores, $c_i$ is the ground-truth class label, and $W_{c_i}$ is the dynamic weight corresponding to category $c_i$. The base classification loss ${\mathcal{L}}_{\mathrm{cls}}$ employs standard cross-entropy:

$${\mathcal{L}}_{\mathrm{cls}}({\widehat{s}}_i,c_i)=-log\left({\displaystyle \frac{exp\left({\widehat{s}}_{i,c_i}\right)}{{\sum }_{k=1}^{K}exp\left({\widehat{s}}_{i,k}\right)}}\right),$$

(22)

where K is the total number of classes including background.

The category-specific weights are computed based on our proposed information-theoretic approach, updated periodically according to pseudo-label queue frequency statistics as described in Section 2.5:

$$W_{c_i}=\left\{\begin{array}{cc}1.0\hfill & \mathrm{if}{c}_i\in {\mathcal{C}}_{\mathrm{base}}\hfill \\ W_{c_i}\left(t\right)\hfill & \mathrm{if}{c}_i\in {\mathcal{C}}_{\mathrm{novel}}\hfill \end{array}\right.,$$

(23)

where ${\mathcal{C}}_{\mathrm{base}}$ and ${\mathcal{C}}_{\mathrm{novel}}$ represent base and novel category sets, respectively, and $W_i\left(t\right)$ is the time-dependent dynamic weight that increases for rare categories to ensure balanced learning.

Our weighted supervision design offers the following key advantages: (1) Simplicity: Unlike traditional semi-supervised methods that require careful balancing between multiple loss branches (e.g., supervised loss, consistency loss, and pseudo-label loss), our approach integrates all supervision signals into a single coherent framework, eliminating the need for manual loss weight tuning between different branches. (2) Adaptivity: The dynamic weighting mechanism automatically adjusts to the evolving class distribution during training, ensuring that rare novel categories receive adequate attention without requiring prior knowledge of class frequencies. (3) Robustness: By maintaining standard loss formulations with principled information-theoretic weighting, our approach preserves training stability while effectively addressing class imbalance issues that commonly affect pseudo-label-based learning.

3. Materials and Experimental Settings

3.1. Dataset Introduction

We conduct main experimental evaluations on the DIOR and VisDroneZSD datasets. DIOR is a large-scale benchmark dataset for optical remote sensing image object detection, with each image having a resolution of 800 × 800 pixels. The dataset contains 23,463 images and 192,472 instances, covering 20 object categories. Similar to VisDroneZSD, we have set the same 16 basic categories and 4 new categories. We use the test set of 11,738 images for evaluation.

VisDroneZSD is a subset of the DIOR dataset, following the settings of the VisDrone2023 zero-shot object detection challenge. It includes 16 base categories and 4 novel categories, where novel categories are airport, basketball court, ground track field, and windmill. It contains 8730 images for training and 3337 images for testing. The training set contains only base category annotations without any novel category labels, following the standard open-vocabulary detection setting. The test set includes 10,554 base category instances and 7693 novel category instances, totaling 18,247 instances.

3.2. Comparative Methods

To verify the effectiveness of the our proposed method, the following state-of-the-art methods are selected:

• VILD [24] distills knowledge from a pre-trained open-vocabulary image classification model (teacher) into a two-stage detector (student). VILD uses the teacher model to encode category texts and image regions of object proposals, then trains a student detector whose region embeddings are aligned with text and image embeddings inferred by the teacher.
• GLIP [25] unifies object detection and phrase grounding for pre-training, enabling learning from both detection and grounding data. The method leverages 27M grounding data, including 3M human-annotated and 24M web-crawled image–text pairs.
• OV-DETR [26] is the first end-to-end Transformer-based open-vocabulary detector based on DETR architecture. OV-DETR formulates the learning objective as binary matching between input queries (class name or exemplar image) and corresponding objects, enabling detection of any object given its class name or an exemplar image.
• Detic [27] expands the vocabulary of detectors to tens of thousands of concepts by simply training the classifiers of a detector on image classification data. Unlike prior work, Detic does not need complex assignment schemes and is compatible with various detection architectures, achieving state-of-the-art results on the open-vocabulary LVIS benchmark.
• GroundingDINO [28] combines the Transformer-based detector DINO with grounded pre-training to detect arbitrary objects with human inputs such as category names or referring expressions.
• YOLO-World [29] enhances YOLO with open-vocabulary detection capabilities through vision–language modeling and pre-training on large-scale datasets. The method proposes Re-Parameterizable Vision–Language Path Aggregation Network (RepVL-PAN) and demonstrates superior efficiency for real-time applications.
• CastDet is the first open-vocabulary object detection framework designed for aerial images. The method employs a CLIP-activated student–teacher learning mechanism to detect objects without annotations.

3.3. Evaluation Metrics

To comprehensively evaluate the performance of our proposed open-vocabulary detection framework, we adopt standard object detection metrics with specific adaptations for the open-vocabulary setting. Our evaluation focuses on Precision (P), Recall (R), Mean Average Precision (mAP), and class-specific performance metrics for base and novel categories.

(1) Precision measures the accuracy of positive predictions, defined as the fraction of correct detections among all predictions:

$$P={\displaystyle \frac{TP}{TP+FP}},$$

(24)

where $TP$ represents true positive detections and $FP$ represents false positive detections.

(2) Recall quantifies the model’s ability to identify all relevant objects, calculated as the fraction of ground-truth objects that are successfully detected:

$$R={\displaystyle \frac{TP}{TP+FN}},$$

(25)

where $FN$ denotes false negative detections (ground-truth objects that were missed by the model).

(3) Average Precision (AP) summarizes the precision–recall trade-off by computing the area under the precision–recall curve:

$$\mathrm{AP}={\int }_0^{1}P·\mathrm{RdR},$$

(26)

where P is the precision as a function of recall R.

(4) Mean Average Precision (mAP) provides an overall performance measure by averaging AP across all categories:

$$mAP={\displaystyle \frac{1}{\left|C\right|}}\sum _{c\in C}AP,$$

(27)

where C represents the set of all object categories and $\left|C\right|$ is the total number of categories. In our experiments, mAP is computed at an IoU threshold of 0.5.

(5) Base categories performance (mA${\mathrm{P}}_{base}$) specifically evaluates the detection performance on categories with available training annotations:

$$mA{P}_{base}={\displaystyle \frac{1}{|{\mathcal{C}}_{base}|}}\sum _{c\in {\mathcal{C}}_{base}}AP,$$

(28)

where ${\mathcal{C}}_{base}$ denotes the set of base categories with ground-truth annotations during training.

(6) Novel category performance (mA${\mathrm{P}}_{novel}$) measures the model’s open-vocabulary capability by evaluating performance on categories without training annotations:

$$mA{P}_{novel}={\displaystyle \frac{1}{|{\mathcal{C}}_{novel}|}}\sum _{c\in {\mathcal{C}}_{novel}}AP,$$

(29)

where ${\mathcal{C}}_{novel}$ represents the set of novel categories that are only encountered during testing.

(7) Harmonic mean (HM) provides a balanced evaluation of both base and novel category performance by computing the harmonic mean of mA${\mathrm{P}}_{base}$ and mA${\mathrm{P}}_{novel}$:

$$HM={\displaystyle \frac{2\times mA{P}_{base}\times mA{P}_{novel}}{mA{P}_{base}+mA{P}_{novel}}}$$

(30)

The HM metric is particularly valuable in open-vocabulary detection, as it penalizes approaches that achieve high performance on one category type at the expense of the other, ensuring a comprehensive assessment of the model’s ability to handle both seen and unseen object categories.

mA${\mathrm{P}}_{base}$, mA${\mathrm{P}}_{novel}$, and HM are crucial for open-vocabulary evaluation, as they allow us to assess whether the proposed method maintains strong performance on known categories while effectively generalizing to unseen ones.

3.4. Implementation Details

Our method is implemented based on the MMDetection framework, using PyTorch version 1.10.0, with training and testing scripts in Python 3.8. We adopt Faster R-CNN as the detector backbone network, using ResNet-50 as the feature extractor. The model is initialized using pre-trained RemoteCLIP, and RemoteCLIP is frozen during the training process. Batch size is 8, trained on a single NVIDIA A100 GPU (40 GB VRAM, NVIDIA Corporation, Sunnyvale, CA, USA). The optimizer uses SGD with a learning rate of 0.01, a momentum of 0.9, and a weight decay of 0.0001.

In the selective masking strategy, base category regions are masked using zero padding. The dynamic weight update interval is set to 100 iterations, and the smoothing coefficient $\alpha$ is set to 0.8. Long-term statistics of the pseudo-label queue are based on all accumulated pseudo-label data in the queue; the short-term statistics window is set to the most recent 500 updates.

Considering that the teacher model has weak foreground-background separation capability in the early training stages, directly using low-quality pseudo-labels would introduce noise and affect the student model’s learning effectiveness. Specifically, the model is trained for a total of 40,000 iterations, with the first 30,000 iterations not using pseudo-labels generated by the teacher model. The first 30,000 iterations allow the model to focus on learning basic object detection capabilities, including foreground-background discrimination, object proposal generation, and other fundamental skills. In the early stages, the teacher model’s pseudo-label quality is poor, and introducing pseudo-labels too early would generate numerous incorrect pseudo-labels due to insufficient teacher model capability, thereby interfering with the student model’s learning process. Based on training experience from previous related work and loss analysis, basic object detection fundamentally converges at around 30,000 iterations. The 10,000 iterations of semi-supervised learning provide sufficient learning opportunities for novel categories, which also reference previous semi-supervised learning training methods.

4. Result and Discussion

4.1. Comparison with SOTA Methods

We compare our proposed method with several state-of-the-art approaches in the open-vocabulary detection field, including VILD, GLIP, OV-DETR, Detic, GroundingDINO, YOLO-World, and CastDet. As shown in

Table 1. Comparison of our model with other methods on VisDroneZSD.

Method	mAP	mA${\mathbf{P}}_{\mathbf{base}}$	mA${\mathbf{P}}_{\mathbf{novel}}$	HM
VILD	25.6	28.5	14.2	19.0
GLIP	33.8	41.0	5.4	9.5
OV-DETR	28.7	30.8	20.6	24.7
Detic	16.8	19.8	4.8	7.7
GroundingDINO	33.0	40.5	3.3	6.1
YOLO-World	32.9	39.1	8.5	13.9
CastDet	35.2	33.6	41.5	37.1
Ours	42.7	43.5	39.5	41.4

, our method achieves significant performance improvements on the VisDroneZSD dataset. Specifically, our approach achieves 42.7% overall mAP, 43.5% base categories mAP, and 39.5% novel category mAP, with a harmonic mean of 41.4%.

Notably, our method demonstrates superior performance across all evaluation metrics compared to baseline methods. The 39.5% mA${\mathrm{P}}_{novel}$ represents a substantial improvement over methods like VILD (14.2%) and GLIP (5.4%), showing relative improvements of 178.2% and 631.5%, respectively. This indicates that our enhanced framework with RemoteCLIP, selective masking strategy, and dynamic frequency weighting significantly improves the model’s ability to detect novel categories in aerial imagery.

Compared to the original CastDet baseline (41.5% mA${\mathrm{P}}_{novel}$), our student model achieves competitive performance while maintaining better overall balance as reflected in the harmonic mean metric. The HM score of 41.4% demonstrates that our approach effectively balances performance between base and novel categories, avoiding the common trade-off where improvements in novel category detection come at the cost of base categories performance.

Extended experiments on the DIOR dataset (

Table 2. Comparison of our model with other methods on DIOR.

Method	mAP	mA${\mathbf{P}}_{\mathbf{base}}$	mA${\mathbf{P}}_{\mathbf{novel}}$	HM
VILD	45.7	53.5	14.2	22.4
GLIP	56.0	69.1	3.6	6.9
OV-DETR	54.0	62.6	19.9	30.2
Detic	36.9	45.3	3.5	6.5
GroundingDINO	57.3	70.8	3.2	6.2
YOLO-World	57.7	70.2	8.0	14.4
CastDet	56.9	61.0	40.3	48.5
Ours	63.7	70.1	38.2	49.5

) further validate the generalization capability of our method. Our approach achieves 63.7% overall mAP, 70.1% base categories mAP, and 38.2% novel category mAP, with a harmonic mean of 49.5%. Our method outperforms all baseline approaches in terms of overall mAP and harmonic mean performance.

Specifically, our method shows substantial improvements over existing open-vocabulary detection methods on the DIOR dataset. Compared to VILD, which achieves the most competitive overall performance among traditional methods with 45.7% mAP, our approach delivers a significant 39.4% relative improvement in overall mAP (from 45.7% to 63.7%). More impressively, for novel category detection, our method achieves 38.2% mA${\mathrm{P}}_{novel}$ compared to VILD’s 14.2%, representing a remarkable 169.0% relative improvement. The harmonic mean metric shows an even more dramatic enhancement, improving from 22.4% to 49.5% (a 120.9% relative improvement), demonstrating the balanced performance gains across both base and novel categories.

When compared to more recent methods, like GLIP and GroundingDINO, our approach demonstrates superior novel category detection capabilities. GLIP achieves 56.0% overall mAP but only 3.6% mA${\mathrm{P}}_{novel}$, while our method improves the overall mAP by 13.8% and achieves a massive 961.1% relative improvement in novel category detection. Similarly, GroundingDINO, despite achieving the highest base categories performance (70.8% mA${\mathrm{P}}_{base}$), performs poorly on novel categories (3.2% mA${\mathrm{P}}_{novel}$). Our method maintains a competitive base categories performance (70.1% mA${\mathrm{P}}_{base}$) while achieving 38.2% mA${\mathrm{P}}_{novel}$, resulting in a substantially higher harmonic mean (49.5% vs. 6.2%).

Compared to the original CastDet baseline, our enhanced framework shows consistent improvements across all metrics. We achieve 11.9% relative improvement in overall mAP (from 56.9% to 63.7%) and 14.9% improvement in base categories mAP (from 61.0% to 70.1%). Although CastDet demonstrates strong novel category performance (40.3% mA${\mathrm{P}}_{novel}$), this is achieved by selecting images containing novel categories for unsupervised training, which requires extensive dataset preprocessing and strict data separation. In contrast, our method eliminates the need for such dataset filtering and can directly utilize partially annotated data without prior separation while still maintaining competitive novel category performance (38.2% mA${\mathrm{P}}_{novel}$) and significantly improving the overall balance, as reflected in the harmonic mean improvement from 48.5% to 49.5%. The notable improvement in base categories performance can be attributed to our ability to simultaneously train on both base and novel categories within the same images, eliminating the data waste inherent in CastDet. Specifically, for CastDet, when an image contains novel category objects, the entire image must be used for unsupervised learning, resulting in the loss of valuable base category annotations.

4.2. Ablation Study

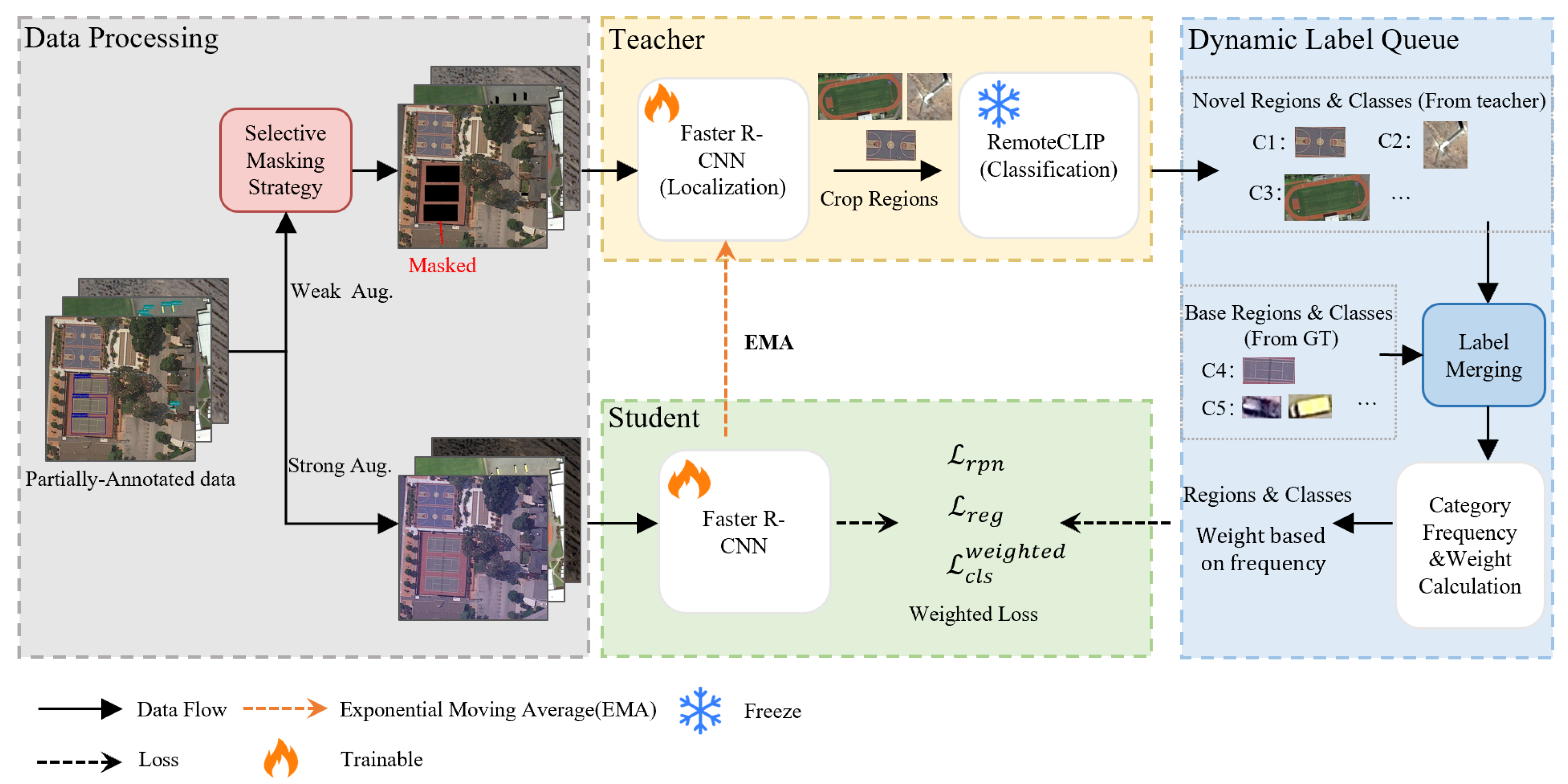
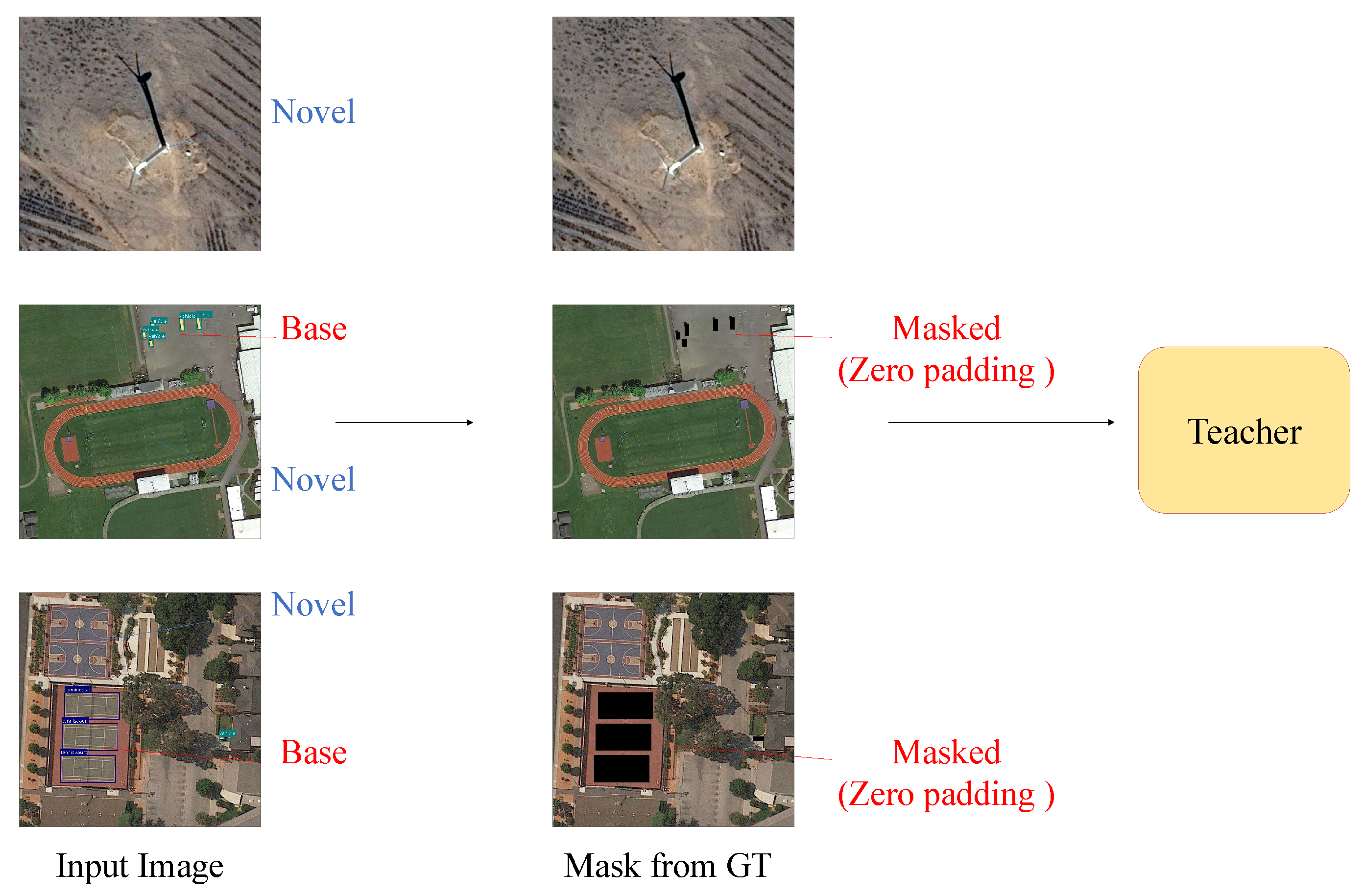
To validate the effectiveness of our proposed components, we conduct comprehensive ablation studies focusing on the key innovations of our framework.

4.2.1. Effectiveness of Selective Masking Strategy

Table 3. Ablation study of different masking strategies on VisDroneZSD.

Masking Strategy	mAP	mA${\mathbf{P}}_{\mathbf{base}}$	mA${\mathbf{P}}_{\mathbf{novel}}$	HM
No Masking	37.6	39.4	30.5	34.4
Gaussian Blur	40.3	41.1	37.1	39.0
Zero Padding	42.7	43.5	39.5	41.4

demonstrates the results of the ablation study, comparing different masking strategies. Without any masking strategy, the student model achieves an overall mAP of 37.6%, a base categories mAP of 39.4%, a novel category mAP of 30.5%, and a harmonic mean of 34.4%. The Gaussian blur masking strategy shows improvement with an overall mAP of 40.3%, a base categories mAP of 41.1%, a novel category mAP of 37.1%, and a harmonic mean of 39.0%. Our proposed zero padding masking strategy achieves the best performance with an overall mAP of 42.7%, a base categories mAP of 43.5%, a novel category mAP of 39.5%, and a harmonic mean of 41.4%.

The progressive improvements demonstrate the effectiveness of different masking approaches. Compared to non-masking, zero padding achieves a relative improvement of 13.6% in overall mAP, 10.4% in base categories detection, and a substantial improvement of 29.5% in the detection of novel categories. More importantly, zero padding outperforms Gaussian blur with a 5.96% relative improvement in overall mAP and a 6.47% improvement in novel category detection, validating our theoretical analysis regarding complete information suppression.

These results confirm that by completely masking base category regions through zero padding, the teacher model more effectively focuses on discovering novel category targets. The generated high-quality pseudo-labels, when merged with accurate ground-truth annotations of base categories, provide more complete and consistent supervision signals for the student model. The superior performance of zero padding over Gaussian blur validates our information-theoretic approach, demonstrating that complete information suppression is more effective than partial information degradation for novel category discovery.

4.2.2. Effectiveness of Queue-Based Dynamic Frequency Weighting

Table 4. Ablation study of dynamic frequency weighting on VisDroneZSD.

Method	mAP	mA${\mathbf{P}}_{\mathbf{base}}$	mA${\mathbf{P}}_{\mathbf{novel}}$	HM
Static Weight	37.1	41.8	18.3	25.4
CB Loss	39.2	41.7	29.1	34.3
Ours	42.7	43.5	39.5	41.4

presents a comprehensive comparison of different weighting strategies applied to address class imbalance in novel category detection. The results clearly demonstrate the progressive improvement achieved by more sophisticated weighting mechanisms.

When employing static weights where all categories are assigned uniform importance (w = 1.0), the model achieves modest performance with 37.1% overall mAP and only 18.3% mA${\mathrm{P}}_{novel}$. The integration of Class-Balanced Loss, which adjusts weights based on effective sample numbers computed from the dynamic label queue, provides notable improvement, achieving 39.2% overall mAP and 29.1% mA${\mathrm{P}}_{novel}$. However, our proposed dynamic frequency weighting mechanism yields the most significant performance gains, reaching 42.7% overall mAP and 39.5% mA${\mathrm{P}}_{novel}$.

The quantitative analysis reveals several key insights. Compared to static weighting, our dynamic approach delivers a substantial 21.2 percentage point improvement in novel category detection (from 18.3% to 39.5%), representing a remarkable 115.8% relative enhancement. Even when benchmarked against the established CB Loss method, our information-theoretic weighting strategy maintains a significant edge with 10.4 percentage points improvement in mA${\mathrm{P}}_{novel}$ (from 29.1% to 39.5%) and 3.5 percentage points improvement in overall mAP. The harmonic mean shows consistent improvement from 25.4% (static) to 34.3% (CB Loss) to 41.4% (ours), demonstrating better balanced performance across base and novel categories.

Table 5. Novel category performance on VisDroneZSD.

Method	Airport		Basketball Court		Ground Track Field		Windmill
	AP	Recall	AP	Recall	AP	Recall	AP	Recall
Static Weight	0.0	0.0	39.0	79.4	34.2	55.2	0.0	0.0
CB Loss	24.8	45.5	45.1	79.1	37.5	55.6	9.1	3.3
Ours	38.5	69.1	65.1	79.7	41.1	56.3	13.2	18.1

provides detailed per-category analysis, revealing both the effectiveness and limitations of dynamic weighting for addressing class imbalance issues. The results are particularly striking for the most challenging rare categories. For airport detection, our method achieves 38.5% AP with 69.1% recall, compared to complete failure (0.0% AP and recall) with static weighting. The basketball court and ground track field also show consistent improvements across all methods, with our approach achieving the best performance (65.1% AP and 41.1% AP, respectively).

However, the analysis also reveals persistent challenges in extremely rare categories. Windmill detection, which represents the most severe class imbalance challenge, shows limited improvement with our method achieving only 13.2% AP and 18.1% recall. While this represents a significant improvement over static weighting (complete failure) and CB Loss, the recall rate remains substantially lower compared to other novel categories.

To understand the root causes of this performance gap, we conducted detailed quality analysis of pseudo-labels across novel categories. We sampled 300 instances from each novel category during VisDroneZSD training to analyze confidence scores. The results reveal that the windmill has an average confidence of only 42.2%, while the basketball court achieves 78.1%, corresponding with the confidence patterns shown in Figure 3. Additionally, statistical analysis of the VisDroneZSD test set shows that windmill targets have an average size of only 2807 pixels, compared to the basketball court at 18,327 pixels and the ground track field at 54,760 pixels, with the windmill being nearly 20 times smaller than the ground track field.

We believe the fundamental causes are attributed to the following: Small object problem—windmill targets are significantly smaller than other categories, leading to insufficient feature extraction and limited model recognition capability on small-scale targets. Since standard geometric bounding boxes are used, the actual pixels occupied by windmills are far smaller than the statistical results, as they are mostly composed of linear structures, further exacerbating the difficulty for RPN extraction.

Based on these findings, we propose specific improvement directions for future research: integrating small object detection enhancement modules, such as multi-scale feature fusion and specialized feature extractors for small targets, and introducing context-aware mechanisms that leverage geographic and environmental context information to assist small target identification.

Figure 3 provides a qualitative visualization of the effectiveness of different weighting strategies on novel category detection. The results corroborate the quantitative findings presented in Table 4 and Table 5, demonstrating clear visual improvements across all categories.

As shown in the figure, the static weighting approach (row a) fails completely to detect the most challenging categories, airport and windmill, producing no detection results for these rare object types. This complete failure corresponds to the 0 AP values reported in Table 5 for these categories. Furthermore, the static weighting method suffers from numerous false positives in basketball court and ground track field detection, indicating poor discrimination capability. The CB Loss method (row b) shows improved performance compared to static weighting, successfully detecting some instances of airport and windmill categories, but still exhibits suboptimal localization accuracy and confidence scores.

In contrast, our proposed dynamic frequency weighting method (row c) achieves the most accurate detection results with precise bounding box localization and minimal false negatives. Notably, the windmill category shows significant confidence score improvements compared to CB Loss, demonstrating the effectiveness of our information-theoretic weighting approach in addressing severe class imbalance. The visual results confirm the quantitative analysis, showing that our method not only improves detection recall for rare categories but also enhances overall detection precision across all novel object types.

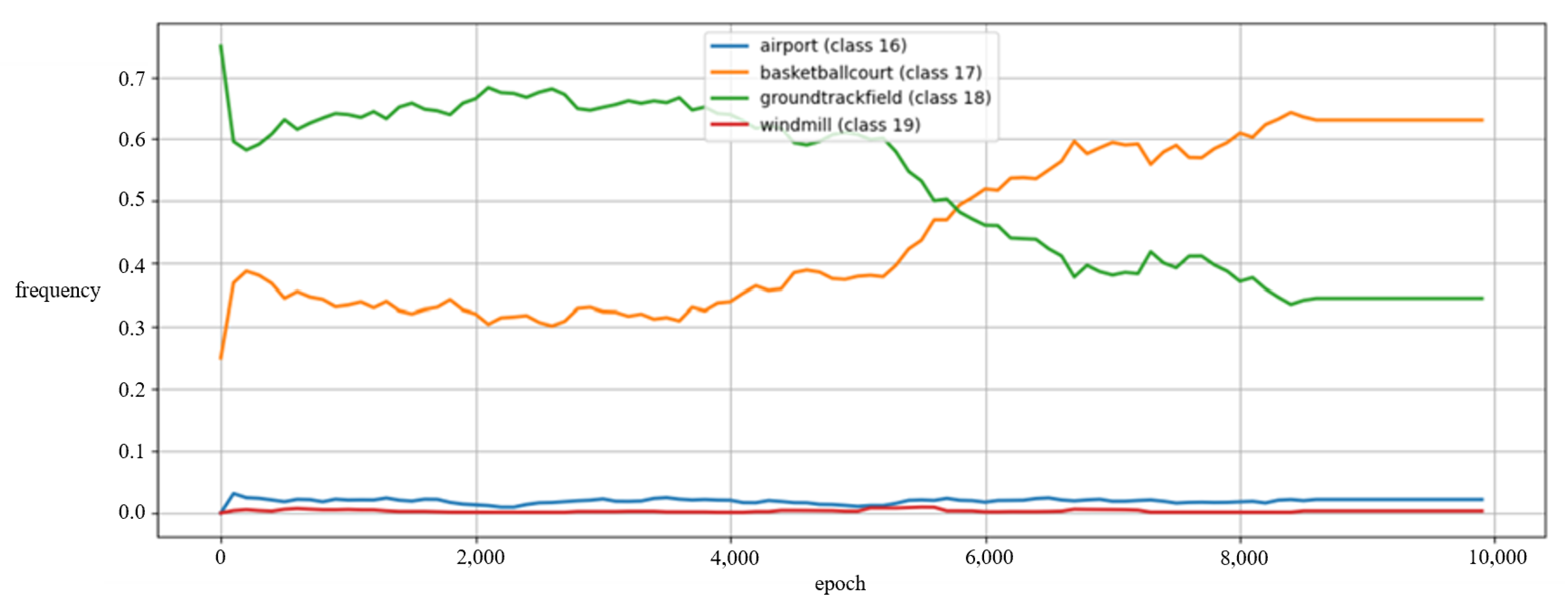
Figure 4 illustrates the frequency evolution of each novel category in the pseudo-label queue during the training process, clearly revealing the dynamic characteristics of the class imbalance problem. The horizontal axis represents the training epochs during the pseudo-label introduction phase. The following key observations can be made from the figure: The ground track field dominates in the early training stage with a frequency as high as 0.75, but gradually decreases to 0.35 as training progresses. The basketball court exhibits the opposite trend, rising from an initial frequency of 0.25 to 0.65, ultimately becoming the most frequently detected category. Meanwhile, the airport and windmill categories maintain frequencies close to 0 throughout the entire training process, demonstrating severe scarcity.

This dynamic change in frequency distribution fully validates the necessity of our proposed dynamic weight adjustment mechanism. Traditional static weighting schemes cannot adapt to such time-varying category distributions, nor can they accommodate the variations of rare categories across different datasets. Our method, by real-time monitoring of frequency changes and correspondingly adjusting weights, can provide higher learning weights for rare categories (such as airport and windmill), ensuring that the model is not dominated by frequent categories. This effectively improves the detection performance of these difficult categories, which also explains why we observe performance improvements from the dynamic weighting mechanism in the ablation experiments shown in Table 4.

4.2.3. Parameter Sensitivity Analysis

Impact of the information intensity coefficient: To investigate the impact of the information intensity coefficient $\mu$ on our dynamic weighting mechanism, we conduct a comprehensive sensitivity analysis, as shown in

Table 6. Parameter sensitivity analysis of the information intensity coefficient $\mu$ on VisDroneZSD.

$\mathit{\mu }$	mAP	mA${\mathbf{P}}_{\mathbf{base}}$	mA${\mathbf{P}}_{\mathbf{novel}}$	HM
0	37.1	41.8	18.3	25.4
2	41.1	43.2	32.6	37.2
4	42.7	43.5	39.5	41.4
8	41.9	43.3	36.3	39.5
16	37.2	39.9	26.5	31.8

. The coefficient $\mu$ controls the influence of self-information on the weight calculation, where $\mu =0$ indicates that novel category weights are uniformly set to 1.0 (equivalent to no dynamic adjustment).

The experimental results reveal a clear pattern in performance variation across different $\mu$ values. When $\mu =0$, representing the absence of dynamic weight adjustment, the model achieves baseline performance with 37.1% overall mAP and 18.3% mA${\mathrm{P}}_{novel}$. As $\mu$ increases to 2, substantial improvements are observed across all metrics, with mA${\mathrm{P}}_{novel}$ rising to 32.6% (78.1% relative improvement) and the harmonic mean increasing from 25.4% to 37.2%.

The optimal performance is achieved at $\mu =4$, where the model reaches peak performance with 42.7% overall mAP, 39.5% mA${\mathrm{P}}_{novel}$, and 41.4% harmonic mean. This optimal value demonstrates that moderate weight adjustment based on self-information provides the best balance between emphasizing rare categories and maintaining training stability. The substantial improvement from $\mu =0$ to $\mu =4$ (115.8% relative improvement in mA${\mathrm{P}}_{novel}$) validates the effectiveness of our information-theoretic approach.

However, further increasing $\mu$ to 8 and 16 leads to performance degradation, with mA${\mathrm{P}}_{novel}$ dropping to 36.3% and 26.5%, respectively. When $\mu$ is too small, the weight adjustment is insufficient to address the severe class imbalance, resulting in continued dominance by frequent categories. Conversely, when $\mu$ is too large, excessive weight adjustment leads to training instability and reduced overall performance, as the loss becomes dominated by potentially noisy pseudo-labels from rare categories. The performance decline at $\mu =16$ (26.5% mA${\mathrm{P}}_{novel}$) demonstrates that overly aggressive weighting can be counterproductive. These findings confirm that $\mu =4$ provides the optimal trade-off between addressing class imbalance and maintaining robust training dynamics.

The analysis provides valuable insights for practitioners implementing our dynamic frequency weighting mechanism. The results demonstrate that selecting an appropriately moderate value of $\mu$ (around 4) is sufficient to achieve substantial performance improvements without requiring extensive hyperparameter tuning. Importantly, the findings suggest that pursuing excessively large $\mu$ values is not only unnecessary but also potentially detrimental to model performance. This robustness to parameter selection makes our method practically applicable across different datasets and scenarios, as users can expect reliable improvements by choosing $\mu$ values in the moderate range (2–4) rather than engaging in aggressive parameter optimization.

Impact of the Weight Update Interval:

Table 7. Parameter sensitivity analysis of the weight update interval on VisDroneZSD.

Weight Update Interval	Training Time/iter	mAP	mA${\mathbf{P}}_{\mathbf{base}}$	mA${\mathbf{P}}_{\mathbf{novel}}$	HM
25	0.878s	42.4	43.2	39.4	41.2
50	0.872s	42.5	43.1	40.1	41.5
100	0.865s	42.7	43.5	39.5	41.4
500	0.860s	41.9	43.3	36.3	39.5

presents the impact of different weight update intervals on both model performance and computational efficiency. The update interval determines how frequently the dynamic weights are recalculated based on the current dynamic label queue statistics, balancing between responsiveness to distribution changes and computational overhead.

The experimental results demonstrate that moderate update frequencies yield optimal performance. With an update interval of 50–100 iterations, the model achieves peak performance, with the 50-iteration interval reaching 40.1% mA${\mathrm{P}}_{novel}$ and 41.5% harmonic mean, while the 100-iteration interval achieves 42.7% overall mAP. These frequencies provide an effective balance between timely response to class distribution changes and training stability.

When the update interval is too frequent (25 iterations), although the model responds quickly to distribution changes, the performance shows slight degradation (39.4% mA${\mathrm{P}}_{novel}$), potentially due to weight fluctuations that introduce training instability. Conversely, when the update interval is too sparse (500 iterations), significant performance deterioration occurs, with mA${\mathrm{P}}_{novel}$ dropping to 36.3% and the harmonic mean declining to 39.5%. This demonstrates that infrequent updates fail to adequately respond to class distribution changes and cannot fully exploit the advantages of dynamic adjustment, resulting in limited improvement for novel categories.

An important practical consideration is the computational overhead introduced by the dynamic weighting mechanism. The training time analysis reveals that the weight update frequency has minimal impact on computational cost, with per-iteration training times ranging from 0.860 s to 0.878 s across all tested intervals. The difference between the most frequent (25 iterations) and least frequent (500 iterations) update schedules is merely 0.018 s per iteration. For a typical training scenario of 10,000 iterations, this translates to approximately 3 min additional training time, which is negligible considering the substantial performance improvements achieved. This analysis confirms that our dynamic weighting mechanism introduces minimal computational burden while providing significant performance gains, making it highly practical for real-world applications.

Impact of the Smoothing Coefficient:

Table 8. Parameter sensitivity analysis of the smoothing coefficient $\alpha$ on VisDroneZSD.

$\mathit{\alpha }$	mAP	mA${\mathbf{P}}_{\mathbf{base}}$	mA${\mathbf{P}}_{\mathbf{novel}}$	HM
0	40.1	40.8	37.3	39.0
0.5	41.6	42.2	39.2	40.6
0.8	42.7	43.5	39.5	41.4
0.95	39.1	40.5	33.5	36.7

presents the impact of different smoothing coefficient values on the stability and responsiveness of our dynamic weighting mechanism. The parameter sensitivity analysis for the smoothing coefficient $\alpha$ reveals the importance of our dynamic loss weighting mechanism. The results demonstrate a clear inverted-U-shaped performance curve across different $\alpha$ values.

When $\alpha =0$ (no smoothing), the model achieves moderate performance with 40.1% overall mAP and 37.3% mA${\mathrm{P}}_{\mathrm{novel}}$. This setting allows weights to change drastically based on immediate results, leading to training instability and suboptimal convergence. The relatively poor performance indicates that excessive responsiveness to short-term fluctuations harms the learning process.

As $\alpha$ increases to 0.5, performance improves significantly to 41.6% overall mAP and 39.2% mA${\mathrm{P}}_{\mathrm{novel}}$, demonstrating that moderate smoothing helps stabilize the training process while maintaining reasonable adaptability to distribution changes.

The optimal performance is achieved at $\alpha =0.8$, reaching 42.7% overall mAP and 39.5% mA${\mathrm{P}}_{\mathrm{novel}}$. This value provides an effective balance between maintaining historical weight information and adapting to recent distribution changes, ensuring stable convergence while preserving sufficient responsiveness to evolving pseudo-label statistics.

When $\alpha$ becomes too large (0.95), performance degrades significantly to 39.1% overall mAP and 33.5% mA${\mathrm{P}}_{\mathrm{novel}}$. This excessive smoothing makes the weighting mechanism overly conservative, failing to adapt promptly to changing class distributions and essentially approaching static weighting behavior. The substantial performance drop confirms that insufficient responsiveness limits the effectiveness of our dynamic adjustment strategy.

Impact of the Short-Term Frequency Window Size:

Table 9. Parameter sensitivity analysis of the short-term frequency window size on VisDroneZSD.

Window Size	mAP	mA${\mathbf{P}}_{\mathbf{base}}$	mA${\mathbf{P}}_{\mathbf{novel}}$	HM
50	41.7	42.7	37.8	40.1
300	42.2	42.9	39.6	41.2
500	42.7	43.5	39.5	41.4
5000	40.5	41.8	35.2	38.2

presents the impact of different short-term frequency window sizes on model performance. The results demonstrate a clear performance pattern that validates our choice of window size for the dynamic loss weighting mechanism.

When the window size is too small (about 50 updates), the model achieves suboptimal performance with 41.7% overall mAP and 37.8% mA${\mathrm{P}}_{\mathrm{novel}}$. This reduced performance indicates that overly small windows make the frequency statistics too sensitive to short-term fluctuations, leading to unstable weight adjustments that can negatively impact training.

The window size of 300 updates shows improved performance compared to 50, achieving 42.2% overall mAP and 39.6% mA${\mathrm{P}}_{\mathrm{novel}}$. It is already similar to the best outcome.

Our chosen window size of 500 updates achieves the best overall performance with 42.7% overall mAP. This configuration effectively balances short-term adaptability with sufficient stability to avoid noise interference, confirming the appropriateness of our parameter selection.

When the window becomes excessively large (5000 updates), performance degrades significantly to 40.5% overall mAP and 35.2% mA${\mathrm{P}}_{\mathrm{novel}}$. This substantial decline indicates that overly large windows reduce the mechanism’s responsiveness to recent distribution changes, losing the benefits of dynamic adaptation.

5. Conclusions

We present a one-step training open-vocabulary detection framework that supports partially annotated data, effectively addressing key challenges faced by existing methods in aerial image open-vocabulary detection, including complex data filtering processes, low data utilization efficiency, and novel category imbalance issues. Our main contributions encompass the following three aspects:

First, we propose a selective masking strategy and label merging mechanism that eliminates the constraint of strict data separation required by existing methods. This approach no longer necessitates pre-partitioning images containing novel categories, significantly improving data utilization efficiency. Second, we design a frequency-based dynamic weighting mechanism built upon a dynamic pseudo-label queue. Through long-term and short-term frequency statistics combined with exponential moving average updates, this mechanism adaptively addresses imbalance issues among novel categories, ensuring that rare categories receive adequate learning attention. Finally, we develop a single-stage weighted supervision approach that avoids complex multi-stage training and loss-balancing problems between different learning paradigms, achieving end-to-end optimization.

Compared to existing frameworks, our approach offers a distinct technical route for open-vocabulary remote sensing detection. While LAE-DINO focuses on dynamic vocabulary construction through massive pre-training, our method addresses vocabulary expansion through intelligent utilization of existing limited annotations. OpenRSD’s multi-modal prompt framework requires careful prompt engineering and supports various input modalities. Our method offers a more automated approach that adapts to data distribution without manual prompt tuning, making it more suitable for scenarios with limited domain expertise. Importantly, our dynamic weighted loss could be integrated into other frameworks when facing class imbalance issues.

Despite achieving significant progress, our method still has some limitations. For instance, generating high-quality pseudo-labels for certain novel categories remains challenging, which exacerbates class imbalance issues. Future research directions include improving pseudo-label generation quality, incorporating small object detection enhancement modules, and using context-aware detection mechanisms that leverage geographic and environmental information to address the unique challenges of aerial image interpretation and enhance the overall performance of open-vocabulary detection in remote sensing imagery.