Highlights
What are the main findings?
- The integrated multiscale approach improves the performance of FE source parametric optimization, providing more reliable solutions while drastically reducing the computing time.
- Unconstrained and constrained modeling approaches identify an overpressurized oblate-like source at ~3 km b.s.l. embedded in a heterogeneous crust for unrest at Campi Flegrei caldera that occurred during 2019–2022.
What is the implication of the main findings?
- The integrated multiscale approach makes FE parametric optimization a viable and efficient tool for modelling more accurate and realistic volcanic scenarios.
- The improved performance of the proposed modeling workflow enables a more reliable evaluation of the volcanic hazard, supporting the monitoring networks in risk mitigation tasks.
Abstract
Parametric optimization/inversion of Interferometric Synthetic Aperture Radar (InSAR) measurements enables the modeling of the volcanic deformation source by considering the approximation of the analytic formulations or by defining refined scenarios within a Finite Element (FE) framework. However, the geodetic data modeling can lead to ambiguous solutions when constraints are unavailable, turning out to be time-consuming. In this work, we use an integrated multiscale approach for retrieving the geometric parameters of volcanic deformation sources and then constraining a Monte Carlo optimization of FE parametric modeling. This approach allows for contemplating more physically complex scenarios and more robust statistical solutions, and significantly decreasing computing time. We propose the Campi Flegrei caldera (CFc) case study, considering the 2019–2022 uplift phenomenon observed using Sentinel-1 satellite images. The workflow firstly consists of applying the Multiridge and ScalFun methods, and Total Horizontal Derivative (THD) technique to determine the position and horizontal sizes of the deformation source. We then perform two independent cycles of parametric FE optimization by keeping (I) all the parameters unconstrained and (II) constraining the source geometric parameters. The results show that the innovative application of the integrated multiscale approach improves the performance of the FE parametric optimization in proposing a reliable interpretation of volcanic deformations, revealing that (II) yields statistically more reliable solutions than (I) in an extraordinary tenfold reduction in computing time. Finally, the retrieved solution at CFc is an oblate-like source at approximately 3 km b.s.l. embedded in a heterogeneous crust.
1. Introduction
Geodetic data modeling is a commonly adopted strategy for understanding the evolution of physical processes deforming the Earth’s surface and interior, often supported by geodetic strain analysis [1,2]. This allows the characterization of the displacement source in terms of the physical/geometrical parameters starting from the observed ground deformation field [3,4,5,6,7,8]. The latter is now characterized by adequate spatial and temporal resolutions at any area on the Earth due to the advances in satellite Synthetic Aperture Radar Interferometry (InSAR) [9,10,11,12,13,14].
Parametric optimization and tomographic inversion are the most used and fastest strategies to characterize deformation sources from the related ground deformation field through analytic models or aggregates of them. Unfortunately, these models are based on simplified shapes embedded in homogeneous media [15,16,17,18], which is often limited as an approximation for volcanic contexts since mechanical heterogeneities can differently amplify the deformation field than the homogeneity condition [19,20,21]. However, these strategies may also provide unreliable results if valid constraints are not assumed, leading to ambiguous solutions [22,23,24,25]. Parametric optimization and tomographic inversions can also be implemented in a Finite Element (FE) model, which provides greater versatility, especially in modeling heterogeneous half-spaces and complex geometries [26,27]. However, a great concern is the time-consuming nature of the FE model as it requires the discretization of the investigated domain using refined meshes, in whose nodes the differential equations are solved [28]. This unfavorably makes the FE model an impractical strategy when many models must be computed to adequately explore the variability range of the unknowns [29].
Multiscale methods and boundary analysis techniques belong to a different category of modeling strategies, able to provide unambiguous information on source geometrical parameters, such as the location, the shape, and the extent [30,31,32]. While several works have highlighted the advantages and limitations of these methods to analyze the potential field data, such as Multiridge [33], ScalFun [34], Total Horizontal Derivative (THD) [35], and the ground deformation field in volcanic regions [36], their integration with classical geodetic modeling approaches has not yet been explored.
This work aims to refine the FE optimization procedure for geodetic modeling to provide more reliable and representative solutions for volcanic contexts, while keeping the computing time affordable. We investigate the combined use of multiscale methods and boundary analysis techniques with optimization/inversion procedures for deriving the physical and geometric parameters of deformation sources. The proposed methodology consists of first applying Multiridge, ScalFun methods, and THD technique to the InSAR-derived ground deformation field (i.e., the integrated multiscale approach described in [36]). In this way, we may retrieve the depth, the horizontal position and the horizontal extent of the field sources. This information is then used as constraints in the framework of FE physically based parametric optimization to provide a comprehensive model of the source parameters. We expect that the integrated multiscale approach will contribute to achieving more reliable solutions from FE parametric optimization procedures, while reducing the computational costs. Consequently, FE becomes a viable strategy for modeling more realistic volcanic scenarios. To accomplish this, after the application of the integrated multiscale approach, we perform two different rounds of optimization: in the first, (I) we search for the best-fit solution by optimizing all the source parameters starting from likely variability ranges; in the second, (II) we constrain some of the source geometric parameters using the integrated multiscale approach-derived information. The statistical analysis of the best-fit solutions and the explored models in both FE optimization procedures highlights the advantages and limitations of the proposed modeling strategy.
As a case study, we test this workflow on the Campi Flegrei caldera (CFc) ground deformation pattern derived from the InSAR technique. CFc (Figure 1a) is an active volcanic area well-known for the bradyseism phenomenon, where the interaction of magmatic and hydrothermal fluids causes intense seismicity, degassing, anomalous thermal patterns, and uplift and subsidence processes in a densely populated region [37,38,39,40,41,42,43,44,45,46,47]. Since 2005, CFc has been experiencing an uplift with different rates over time, for which several authors have provided various solutions using different modeling approaches. For example, studying deformations during 2009–2013, Trasatti et al. [48] provided a North dipping mixed-mode dislocation source at ~5 km depth in an elastic heterogeneous medium using FE and Neighbourhood Algorithm (NA); Amoruso et al. [49] found a thin quasi-horizontal ∼4 km deep source embedded in an elastic and homogeneous medium using Adaptive Simulating Annealing (ASA) and NA, while D’Auria et al. [50] proposed a ~3 km depth sill-like intrusion through two-steps optimization workflows considering the Nelder-Mead simplex algorithm and Akaike Information Criterion; Castaldo et al. [26] suggested a three-axis oblate spheroid ~3 km deep mostly elongated in the NE–SW direction using FE modeling. Likewise, for more recent unrests until 2022, Amoruso and Crescentini [51] retrieved the inflation of both 3–4 and ∼8 km deep reservoirs using Empirical Orthogonal Function (EOF) analysis; Astort et al. [52] found a 3.9 km deep E-W elongated spheroid in an elastic heterogenous medium through FE modeling, while Tizzani et al. [42] used a tomographic approach to propose a distributed geometrically irregular source extending from 2 to 4 km to even 1–0.5 km of depth below the Solfatara hydrothermal system, where a reservoir of pressurized hydrothermal fluids has also been imaged at the same depth in Barone et al. [44]. CFc thus proves to be a suitable site for highlighting the role of constraints derived from the integrated multiscale approach in improving FE optimization of model parameters for volcanic deformation sources using InSAR measurements.
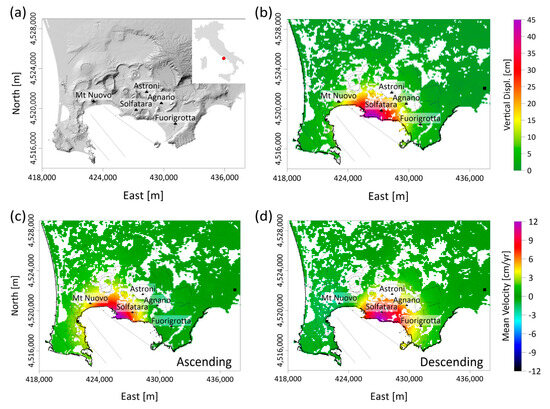
Figure 1.
Study area and DInSAR Sentinel 1–A data. (a) Morpho-structural map of Campi Flegrei caldera redrawn from [44] with an inset of the Italian country. (b) Cumulative vertical deformation map. Mean velocity maps of the projected deformation along (c) ascending and (d) descending orbits. Datasets refer to the January 2019–July 2022 interval. The black square is the reference point.
2. Materials and Methods
In this section, we first describe the InSAR-derived deformation dataset (Figure 1b–d). Then, we outline the integrated multiscale approach. Finally, we discuss the FE model setup and the applied optimization procedures.
2.1. InSAR Data at CFc from 2019 to 2022
We apply the well-established Small Baseline Subset (SBAS) approach [53], which belongs to the class of Differential SAR interferometric (DInSAR) techniques [54,55,56], to retrieve the radar Line Of Sight (LOS)-projected ground deformation time series and the related velocity maps, which are computed to a referenced (stable) pixel. SBAS employs a straightforward pixel-by-pixel combination of a selected set of multi-looked, unwrapped DInSAR interferograms generated from SAR data pairs with short spatial and temporal baselines. In particular, for our investigation, we utilized the set of SAR images acquired through the Interferometric Wide (IW) mode during the analyzed January 2019–July 2022 time interval from the Sentinel–1 (S–1A/B) SAR sensors, considering those acquired along ascending (Path 44, 355 images) and descending (Path 124, 355 images) orbits. Starting from these data, we identified and generated a sequence of short baseline interferograms considering a maximum temporal baseline of 96 days. The interferograms were unwrapped [57] and inverted, adopting the SBAS strategy. The referenced point for the DInSAR products is in the center of Naples city (437,175 m E, 4,521,791 m N). Precise orbital information (https://s1qc.asf.alaska.edu/aux_poeorb/ (accessed on 1 September 2024)) and the NASA Shuttle Radar Topography Mission (SRTM) Version 3.0 Global one arc sec (SRTMGL1) data (https://dwtkns.com/srtm30m/ (accessed on 1 September 2024)) of the study area were used to reconstruct the topographic profile of the terrain and flatten the interferograms. Subsequently, the ascending and descending LOS-projected ground deformation products were geocoded; then, they were combined over the set of coherent points in common to both SAR datasets, to discriminate between the LOS-projected measurements and the maps (and relevant time series) of the vertical and East–West ground deformation components. Note that there is a time lag of one day between the ascending and descending flight tracks, making their combination feasible assuming a quasi-synchronous approximation. The coherent and well-processed points were preliminarily identified by computing the temporal coherence [57], which accounts for decorrelation noise and phase unwrapping mistakes, and imposing a threshold of 0.7 for the determination of the final group of high-coherent points.
The mean velocity maps of the projected deformation along the ascending (Figure 1c) and descending (Figure 1d) orbits describe a deforming CFc portion approaching the satellite along the LOS direction with maximum of about 12 cm/yr as mean rate during the January 2019–July 2022 time interval; the mean velocity maps of both the E-W and vertical components, and the time series of the vertical deformation at the maximum vertical rate, are reported in Figure S1 of the Supplementary Information. The cumulative vertical deformation (Figure 1b) shows that CFc has experienced an uplift phase with 46 cm maximum deformation near Pozzuoli harbor for the same period.
2.2. Integrated Multiscale Approach
The considered integrated multiscale approach contemplates the multiscale imaging methods, the Multiridge and ScalFun, integrated with the boundary analysis, as the THD technique.
Multiridge and ScalFun provide the location and the morphological features of sources of potential field [58,59], including the ground deformation in volcanic environments [4,36,60,61]. These methods are generally used in tandem, providing for the same field anomaly an unambiguous estimate of the depth and the horizontal position (by Multiridge) of the field source and an indication of its type through the evaluation of the Structural Index (N) parameter (by ScalFun).
Multiridge is based on analyzing the lines joining the zeros of the field or of its derivatives at different scales (i.e., the ridges). It consists of the following procedures:
- (i)
- Data interpolation on a regular grid and transformation from an uneven measurement surface (topographical surface) to a flat one, since the Multiridge is based on a level-to-level algorithm. The output of this transformation is a numerically processed dataset that could have been measured in the case of a constant distance between the source and measurement surface. This is performed using a draped-to-flat upward continuation filter [62], which employs the Continuous Wavelet Transform (CWT) applied to the ground deformation data to relocate it onto the constant reduction level, as proposed and validated in [60].
- (ii)
- Forming a 3D multiscale dataset using upward continuation to a set of altitudes (or scales) to compute deformations at different distances from the investigated source. This is performed through the Fast Fourier Transform (FFT)-based algorithm.
- (iii)
- Identification of the zeros of the vertical (Multiridge subset I) and horizontal (Multiridge subset II) derivatives of the 3D deformation field at a set of scales. Horizontal derivatives are computed using finite difference relationships, while vertical ones are evaluated with an FFT-based algorithm, as proposed and validated for the ground deformation field in [61].
- (iv)
- Ridge definition through linear regression of the single Multiridge subsets. Each defined ridge is characterized by the intercept and slope coefficient, and the determination coefficient, in order to quantify how well ridges predict the subsets.
- (v)
- Estimating the ridges’ intersections, representing the position (East-North position, depth) of the source. This is performed by solving the linear system with the considered ridge equations. The retrieved intersections are then physically validated using the ScalFun method [36], as explained below.
- (vi)
- Retrieving the bounds solutions for each ridge, considering the best-fit linear regression errors within the 95% confidence interval on the estimates of the intercept and slope parameters.
ScalFun is instead based on analyzing the scaling function of one of the components of the ground deformation field, or any p-order derivatives, at the Multiridge subset II:
where , is the considered set of scales, is the source depth estimated by the Multiridge method through ridges intersection; for ideal sources, 1, 0, −1, −2 is the integer homogeneity degree of the field, which leads to the structural index 0, 1, 2, 3 since for ground deformation field [36]:
Specifically, when , Equation (1) becomes:
It follows that by plotting the variation of versus , is retrieved as the intercept parameter (i.e., condition) of the function and, in turn, is evaluated with Equation (2). Evaluating for each Multiridge intersection allows the characterization of the morphological attributes of the latter. For example, when the estimated of the intersection matches with the deformation source center, the ScalFun applied to the field component () provides , that means , while, for the second-order vertical derivative () of the same component, we have , which again corresponds to and . It is worth noting that and conditions are physically inadmissible for ground deformation field analysis. In this case, Multiridge intersections are considered spurious and discarded from the analysis.
THD belongs to the boundary analysis methods, which are edge detection techniques for constraining the horizontal extent of multipolar field sources [36,63,64,65,66]. In the case of the ground deformation field, the technique consists of computing the horizontal gradient of the vertical component ():
and analyzing the distribution of since its maxima occur at projection on the measurement surface of the greatest variations in the subsurface physical property, which are the source horizontal boundaries. We specify that THD results deteriorate as the source sharpness and/or size-to-depth ratio decrease, generally leading to an overestimation of the source extent [36,63]. To avoid misinterpretation, THD is here used to fix the upper search bound of the source horizontal size during the constrained parametric optimization procedure (II). We finally specify that Equation (4) is computed using finite difference formulas.
2.3. FE Modeling and Parametric Optimization Procedure
To set the 3D Finite Element (FE) model, we use the COMSOL Multiphysics software v6.0 package and the related Structural Mechanics module, which allows integration of constraints [67].
We follow [26] and set isothermal conditions in a linearly elastic and heterogeneous medium, by considering the elastic parameters variation derived from [68], which intrinsically includes the main large-scale discontinuity systems. We do not involve the effects of multiphase fluids or viscoelastic rheology since our model does not contemplate any time-dependent study. The modeled 3D domain (Figure 2) includes the CFc topography and extends for about 22 km × 16 km along the East and North directions, respectively, to a depth of 8 km b.s.l.; the domain extent is set according to the available model input parameters and InSAR data distribution. A border strip was also added to mitigate numerical boundary effects. We discretized the FE volume into 203,500 mesh tetrahedral elements, with denser sampling in the source region and at the CFc topography. We used a quadratic shape function to size the elements from 200 to 800 m. The reliability of the adopted mesh is confirmed through convergence tests by considering variations less than 1 cm on the reproduced ground deformation field as the convergence threshold. We applied the free surface condition to the upper bound of the domain, while the lower one is fixed, and the lateral ones are characterized by the roller condition. We also considered the lithostatic stress, which has an atmospheric value at the surface and then increases with depth in accordance with the derived density model [69,70]; further information about the modeled heterogeneous medium is reported in Figure S2 of the Supplementary Information. A hydrostatic load (ΔP) is applied to a 3-axis spheroidal filled source of deformation, taking into account its internal body force. This choice makes it possible to model different types of sources (sill-, dyke-, and pipe-like) with good approximation and to consider the ΔP as the required pressure change to overcome the lithostatic stress, so as to deform the upper FE domain.
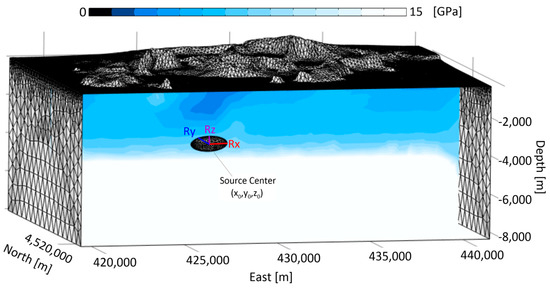
Figure 2.
FE model setting. Three-dimensional FE model developed by considering the heterogeneous distribution of rock density and elastic parameters (Young’s modulus and Poisson’s coefficient), topography, and discretizing the volumes through a tetrahedral mesh. The reported section describes the Young modulus distribution; the starting source is a 3-axis spheroidal body having its center in (, , ) with semi-axes , , .
We estimate the best-fit deformation source parameters using an optimization procedure based on the Monte Carlo method. For the first unconstrained optimization (I), we search for 9 source parameters: the 3 semi-axes (, , ), the center position (, , ), the orientation (Dip and Strike), ΔP. For the second constrained optimization (II), the parameters decrease to 6 as the center position is constrained by Multiridge and ScalFun, while the variability ranges of and are dictated by THD maxima. In both (I) and (II), we evaluate the best-fit solution by minimizing the sum of the Root Mean Square Error (RMSE) between the observed ascending and descending LOS mean velocity maps in 90,270 and 103,340 pixels, respectively, and the modeled field during the considered January 2019–July 2022 time interval; we achieve the best-fit solution fixing the threshold of the RMSE objective function search at 0.7 cm/yr.
3. Results
We first propose the results of the integrated multiscale approach to the vertical deformations. Then, we show the findings revealed by performing both the (I) unconstrained and (II) constrained FE parametric optimizations.
3.1. Retrieval of Source Geometric Parameters from the Integrated Multiscale Approach
We apply the integrated multiscale approach to the January 2019–July 2022 cumulative vertical deformation. We start from InSAR pixels (i.e., Figure 1b) and calculate a regular grid using a natural neighbor interpolator and a sampling step of 100 m along both directions, which is a coherent value also smoothing the InSAR dataset. We then extend the grid around the investigated area using an extrapolation method based on the smooth extension of order 1 to circumvent aliasing from circular convolution [25,71]; this operation allows avoiding artifacts at the spatial boundary of the dataset. We then use draped-to-flat continuation to estimate the vertical deformation to a +0.5 km scale. Finally, we compute the 3D multiscale dataset up to +4.5 km scale with 100 m sampling step by considering the second-order vertical derivative () of the processed vertical deformation.
We show the Multiridge results by considering five profiles. All profiles start in the area of maximum deformation and extend along the North-West (1 in Figure 3a), North/North-West (2 in Figure 3a), North (3 in Figure 3a), North/North-East (4 in Figure 3a), and North-East (5 in Figure 3a) directions. We identify the Multiridge Subset I (red dots in Figure 3a) and II (blue dots in Figure 3a) only in the areas covered by InSAR pixels by excluding the subsets related to no data regions (i.e., the sea). We apply the linear regression to each subset in order to retrieve the ridges (gray lines in Figure 3a) and study their intersection. Specifically, all the intersections occur in a 300 × 300 × 300 m3 region with a mean coordinate of 426,350 m E (±150 m), 4,519,350 m N (±150 m), and −3100 m b.s.l. (±150 m) mean depth (black dashed lines in Figure 3a). We then apply the ScalFun method to the Multiridge Subset II and study the intercept of the function (blue dots in Figure S3), by retrieving corresponding to and since . The estimated indicates that the Multiridge solutions are relative to the deformation source centers. The obtained solutions (i.e., ridges intersection) for each profile with their uncertainties and evaluations are reported in Table S1 of the Supplementary Materials.
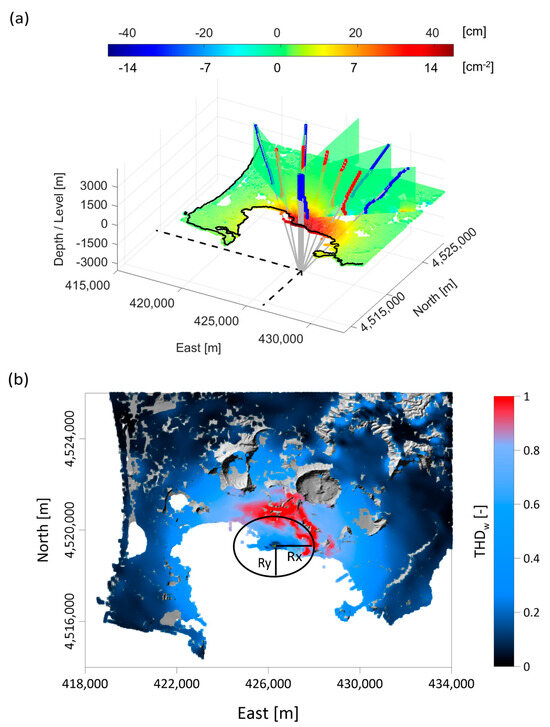
Figure 3.
Retrieval of geometric constraints: (a) 3D view of Multiridge analysis applied to 5 profiles extended along the NW-SE (1), N/NW-S/SE (2), N-S (3), N/NE-S/SW (4) and NE/SW (5) directions; red and blue dots are the Multiridge Subset I and II, respectively; gray lines are the ridges; black dashed lines indicates the mean value of the ridges intersections. (b) Normalized map, where black lines represent the result interpretation by supposing the presence of a 3-axial spheroidal deformation source located as revealed by Multiridge solution.
We finally apply the THD technique to the vertical deformation component at +0.5 km flat scale and analyze the maxima distribution of the normalized function (Figure 3b). By supposing the presence of a 3-axial spheroidal deformation source located as revealed by the Multiridge solutions, THD suggests that and are extended to no more than 1200 m and 1000 m, respectively (Figure 3b).
3.2. Unconstrained Parametric Optimization Procedure (I)
We perform the optimization procedure considering the variability ranges of all nine parameters of the deformation sources as previously applied in [26]. The parameters of the best-fit solution and the explored range are reported in Table 1. The best-fit solution has been searched after ~21,000 iterations, and it consists of an oblate-like spheroid, located beneath Pozzuoli harbor at a depth of −3100 m b.s.l., N/NW–S/SE (−16°) oriented and almost horizontal (3° west-dipping). The necessary ΔP to overcome the lithostatic stress and instantaneously deform the crust is equal to −6.2 MPa.

Table 1.
Unconstrained parametric optimization procedure (I): parameter search bounds.
The unimodal Gaussian curve (blue continuous line in Figure 4) does not fit well with the distribution of the model parameters investigated during the optimization (blue bars in Figure 4). Indeed, the distributions of some modeled parameters (i.e., , , , Dip, Strike and ΔP) have more than one modal value (i.e., Figure 4b,d,e,g–i) and/or have different maximum values (i.e., , , , , Dip, Strike and ΔP) with respect to the related Gaussian envelope (i.e., Figure 4a,b,e,f,g–i). Furthermore, the parameters of the best-fit solution (blue dashed lines in Figure 4) align with the modal values of the modeled parameter distributions and with the maxima of the Gaussian distributions only in a few cases of , Dip (Figure 4c,g), and , , ΔP (Figure 4c,e,i) parameters, respectively.
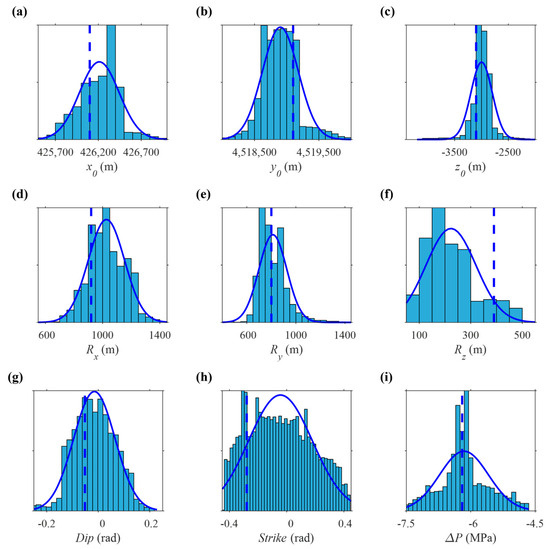
Figure 4.
Unconstrained optimization (I). Source parameters distribution (blue bars) of the investigated 21,000 models during the unconstrained Monte Carlo process: (a–c) East, North, and depth of source center (x0, y0, z0) in 33N UTM coordinates, (d–f) Semi-axes of spheroidal source (Rx, Ry, Rz) in meters, (g) Dip angle in radians, (h) Strike angle in radians, and (i) source overpressure (ΔP) in MPa. Blue lines are the related Gaussian envelopes, while blue dashed lines stand for the best-fit solution parameters.
This solution yields 0.66 cm/yr RMSE between the observed and cumulative best-fit modeled ascending and descending LOS-projected deformation. The residual maps (Figure 5) indicate a maximum deviation of approximately 1.5 cm/yr to the East of the Solfatara hydrothermal system and nearby Mt. Nuovo, for both the ascending and descending ones.
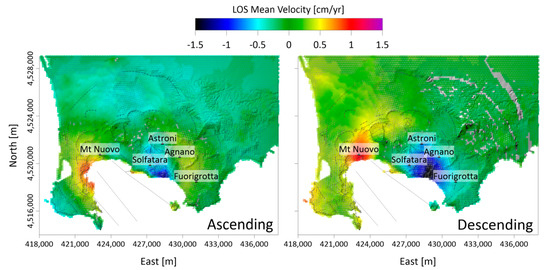
Figure 5.
Unconstrained optimization (I): residuals analysis. Residuals between the observed and best-fit modeled LOS-projected ascending (left) and descending (right) deformations. The morpho-structural map is redrawn from [44].
3.3. Constrained Parametric Optimization Procedure (II)
We optimize only six parameters of the deformation source, constraining the position and the range of variability of its horizontal size based on the results of the integrated multiscale approach (Figure 3). The parameters of the best-fit solution and the related explored range are reported in Table 2. The best-fit solution has been searched after ~2600 iterations, and it still is an oblate-like spheroid with −3100 m b.s.l. depth, N/NW–S/SE (−25°) oriented and almost horizontal (4° west-dipping). The necessary ΔP to overcome the lithostatic stress and instantaneously deform the crust is equal to −5.8 MPa. The distributions of the investigated model parameters (red bars in Figure 6) fit with the related unimodal Gaussian envelopes (red continuous lines in Figure 6). We also observe a good match among the best-fit solution parameters (red dashed lines in Figure 6), the modal value of the modeled parameter distributions, and the Gaussian envelope maxima.

Table 2.
Constrained parametric optimization procedure (II): parameter search bounds.
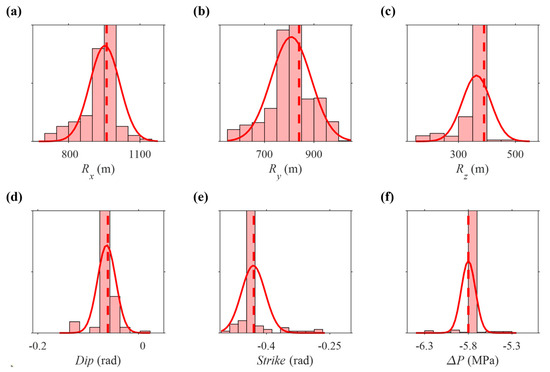
Figure 6.
Constrained optimization (II). Source parameters distribution (red bars) of the investigated 2600 models during the constrained Monte Carlo process: (a–c) Semi-axes of spheroidal source (Rx, Ry, Rz) in meters, (d) Dip angle in radians, (e) Strike angle in radians, and (f) source overpressure (ΔP) in MPa. Red lines are the related Gaussian envelopes, while red dashed lines stand for the best-fit solution parameters.
This solution yields 0.64 cm/yr RMSE between the observed and the cumulative modeled ascending and descending LOS-projected deformation. The maps of residuals (Figure 7) show maximum deviation less than 0.7 cm/yr, especially at the East of the Solfatara hydrothermal system for the ascending case and at Mt. Nuovo for the descending one.
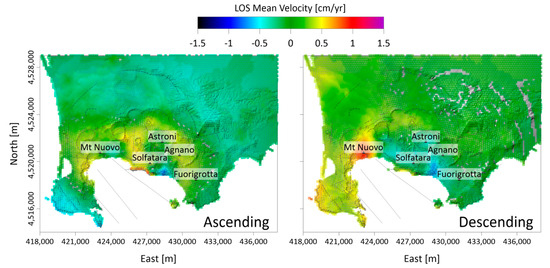
Figure 7.
Constrained optimization (II): residual analysis. Residuals between the observed and best-fit modeled LOS-projected ascending (left) and descending (right) deformations. The morpho-structural map is redrawn from [44].
4. Discussion
The proposed workflow, innovatively combining an integrated multiscale approach with the FE optimization, turned out to be an efficient strategy for retrieving more significant and reliable solutions. The integrated multiscale approach provides constraints for the FE optimization procedure, including the source depth, horizontal position, and size, thereby enabling a comprehensive characterization of both the physical and geometric source parameters embedded in heterogeneous media. To show the advantages and limitations of this workflow, we applied it to the test-site of CFc by performing FE parametric optimizations as (I) unconstrained and (II) constrained from an integrated multiscale approach.
The adopted integrated multiscale approach consisted of Multiridge and ScalFun methods and THD techniques. We applied Multiridge and ScalFun methods for studying ridges intersections with and to detect the depth and the horizontal position of the deformation source center. CFc is a particular case of applying multiscale methods, as the Multiridge method is generally used to study complete and well-sampled field anomalies. This is not the case of the InSAR-derived deformation pattern at CFc, as the anomalous field is not sampled in its seaward portion (Figure 1). To avoid the analysis of ridges at interpolated and extrapolated data regions, we only selected ridges at the emerged part of CFc. Although this could be a limitation, especially for determining the horizontal position of the source, we overcame this by identifying the region where the ridges’ intersections extracted from 5 profiles occur (Figure 3a). Specifically, the small size of the intersection region (i.e., 300 × 300 × 300 m3) provided reliability to the obtained Multiridge solution ( m E, m N, m b.s.l.), characterized by an uncertainty of barely ±150 m. The ScalFun results were also consistent, characterizing the Multridge solutions of each analyzed profile with (Figure S3). This suggests the proposed estimate of the deformation source location is related to its center. Finally, we applied the THD technique and analyzed the maxima of . The choice of modeling a 3-axial spheroidal deformation source located at the Multiridge intersection could allow us to associate maxima to the m and m case (Figure 3b). This would be true in the case of sources with sharp edges along the vertical direction [35], and, therefore, we considered the evaluated and as an overestimation (i.e., upper bound during optimization) of the source horizontal size. Although the integrated multiscale approach was already validated in several previous studies [4,36,60,61,63], uncertainty related to Multiridge and ScalFun methods may increase in the case of significant rheological crustal complexity in the embedding medium and of strongly non-hydrostatic sources, as well as THD when deforming bodies are really small or very deep. It is therefore hardly advisable to use the integrated multiscale approach for the detection of parameters defining the fault plane rupture. Moreover, the use of the integrated multiscale approach is also not recommended for data with poor spatial sampling and coverage, as is the case with Global Navigation Satellite System (GNSS).
The chosen optimization procedure is based on the Monte Carlo method, belonging to the class of derivative-free solvers. Its use allowed for the prevention of limitations of the gradient-based methods. Indeed, although several solvers, such as Levenberg–Marquardt, and others, potentially guarantee a fast convergence progressively reducing the search space toward a local or global optimum through deterministic and guided algorithms, the Monte Carlo method relies on random sampling of parameter space, making it valuable for global exploration and statistical robustness. However, it is significantly less efficient in converging rapidly to an optimal solution. It is worth specifying that the choice of the Monte Carlo solver allowed evaluating the efficiency of the integrated multiscale approach in an optimization framework that is as unbiased as possible. This proposed strategy could obviously also be implemented using different optimization methods.
The performance of both the (I) unconstrained and (II) constrained FE optimization allows discussing the role of the integrated multiscale approach within the framework of FE parametric optimization. Both (I) and (II) led to similar source model scenarios (Table 3) based on the presence of an oblate-like spheroid, −3100 m b.s.l. at Pozzuoli harbor. The main differences are related to source orientation (Strike), changing from −16° to −25° (N/NW–S/SE oriented) in (I) and (II), respectively, and its horizontal position (less than 300 m). Minor differences instead occur for the source size (less than 50 m) and its overpressure variation (0.4 MPa). However, the number of necessary iterations to reach the RMSE threshold (Figure 8) and, consequently, the computation time is extraordinarily different: while (I) takes 20.8 days to estimate the best-fit solution, the latter is derived from (II) in only 2.3 calculation days. It follows that the use of an integrated multiscale approach makes the FE optimization more feasible, drastically reducing the computing time and allowing for source model solution with slightly lower RMSE (Figure 8). The comparison between (I) and (II) also enables some argumentations about the choice of the best-fit solutions. Indeed, although the use of the integrated multiscale approach in (II) led to a solution with comparable RMSE with respect to (I), i.e., 0.64 vs. 0.66 cm/yr, respectively, the analysis of the residuals (Figure 5 and Figure 7) and the investigated parameters distributions (Figure 4 and Figure 6) highlight different findings.

Table 3.
Source model solutions from (I) and (II) procedures.
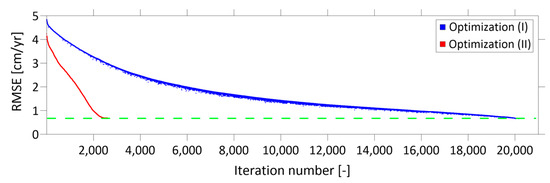
Figure 8.
RMSE analysis. Iteration number versus RMSE during (I) unconstrained (blue continuous line) and (II) constrained (red continuous line) optimization procedures. The green dashed line stands for the RMSE threshold value (0.7 cm/yr).
The (I) residuals maps (Figure 5) show a worse distribution of the differences between data and model than (II) (Figure 7), even pointing out larger deviations of 1.5 cm/yr to the East of Solfatara crater and nearby Mt. Nuovo. This makes the (II)-derived solution more representative of the observed data than (I). Although they are alternatives and equivalent in terms of RMSE, the (II)-derived solution would lead to a different assessment of any other secondary source than (I)-one. This is also the case with faults and structures that modulate the ground deformations and can definitely contribute to potentially reducing the observed residuals, especially nearby Mt. Nuovo and Solfatara. For (I), the source depth is the only parameter for which the modeled distribution fits well with a unimodal Gaussian envelope (Figure 4), whose maximum matches with the best-fit parameter. It follows that the best-fit solution is not statistically so robust, suggesting the need for further iterations. Instead, in (II) (Figure 6), we observe a good statistical robustness of the modeled parameters distribution, retrieving a best-fit solution with more reliability in all its estimated parameters than (I). These ultimately prove the validity of the integrated multiscale approach for retrieving more reliable solutions with FE optimization.
Our results show that the 2019–2022 unrest at CFc is caused by overpressure within an oblate-like spheroid at −3100 m b.s.l. and embedded in a heterogeneous crust in its elastic parameters. This finding is consistent with published works on geodetic data, as for [51], although the EOF analysis revealed a second deeper source, or as for [42], albeit the tomographic approach identified a shallower part of the source in the eastern Solfatara hydrothermal system. Compatibility of our results is also observed with [52], although our approach prevents us from discriminating about the nature of the deformation source. We specify that our work is not designed to propose a definitive interpretation of the sources of the unrest at CFc but to introduce a more feasible source model employing the constraints of the integrated multiscale approach with the versatility of FE optimization. Indeed, the proposed solution, while statistically sound, could be improved considering a complex medium rheology and fault systems effectively modulating the deformation field. Further developments will indeed aim to integrate the proposed approach with other boundary analysis techniques and potential function analyses to overcome these issues.
5. Conclusions
The innovative combined use of the integrated multiscale approach with the FE source parametric optimization turned out to be an effective strategy for the geodetic modeling of InSAR measurements in volcanic contexts.
Compared to standard FE parametric optimization, our workflow provided a more reliable solution of the physical/geometric model of the geodetic source in a tenfold shorter time, providing a better distribution of the residuals with respect to the observed data.
The proposed application to the 2019–2022 unrest at CFc led to the identification of an over-pressurized triaxial oblate-like spheroid embedded in a heterogeneous medium located at ~3.1 km below Pozzuoli’s harbor and with a horizontal extent from 1700 to 2000 m.
All the results confirmed the need to refine the existing geodetic modeling strategies with further investigations in order to gain greater reliability for monitoring tasks.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs17183237/s1. Table S1: Multiridge and ScalFun results for each considered profile; Figure S1: 2019–2022.65 DInSAR Sentinel 1-A data; Figure S2: FE model parameters; Figure S3: ScalFun results.
Author Contributions
Conceptualization, A.B., R.C. and P.T.; methodology, A.B. and R.C.; validation, A.B. and R.C.; investigation, A.B. and R.C.; data curation, A.P.; writing—review and editing, A.B., M.F., R.C., P.T. and A.P.; visualization, A.B. and R.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Processed InSAR data are available by contacting the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, Y.; Zhao, D.; Shan, X. Asymmetric Interseismic Strain across the Western Altyn Tagh Fault from InSAR. Remote Sens. 2022, 14, 2112. [Google Scholar] [CrossRef]
- Salmanian, M.; Rastbood, A.; Hossainali, M.M. Evaluating interseismic deformation patterns in the North Tabriz Fault (Iran) using enhanced fitting of velocity field and analysis of surface deformation. J. Asian Earth Sci. 2025, 277, 106376. [Google Scholar] [CrossRef]
- Li, K.; Li, Y.; Tapponnier, P.; Xu, X.; Li, D.; He, Z. Joint InSAR and Field constraints on Faulting during the mw 6.4, July 23, 2020, Nima/Rongma Earthquake in Central Tibet. JGR Solid Earth 2021, 126, e2021JB022212. [Google Scholar] [CrossRef]
- Barone, A.; Fedi, M.; Pepe, S.; Solaro, G.; Tizzani, P.; Castaldo, R. Modeling the deformation sources in volcanic environments through Multi-scale Analysis of DInSAR measurements. Front. Earth Sci. 2022, 10, 859479. [Google Scholar] [CrossRef]
- Eiden, E.; MacQueen, P.; Henderson, S.; Pritchard, M. Multiple spatial and temporal scales of deformation from geodetic monitoring point to active transcrustal magma system at Uturuncu volcano, Bolivia. Geosphere 2023, 19, 370–382. [Google Scholar] [CrossRef]
- Liu, F.; Elliott, J.R.; Ebmeier, S.K.; Craig, T.J.; Hooper, A.; Novoa Lizama, C.; Delgado, F. First Onset of Unrest Captured at Socompa: A Recent Geodetic Survey at Central Andean Volcanoes in Northern Chile. Geophys. Res. Lett. 2023, 50, e2022GL102480. [Google Scholar] [CrossRef]
- Famiglietti, N.A.; Miele, P.; Defilippi, M.; Cantone, A.; Riccardi, P.; Tessari, G.; Vicari, A. Landslide Mapping in Calitri (Southern Italy) Using New Multi-Temporal InSAR Algorithms Based on Permanent and Distributed Scatterers. Remote Sens. 2024, 16, 1610. [Google Scholar] [CrossRef]
- Zhao, R.; Du, S.; Zheng, M.; Guo, Q.; Wang, L.; Wang, T.; Guo, X.; Fernández, J. Advances and Future Directions in Monitoring and Predicting Secondary Surface Subsidence in Abandoned Mines. Remote Sens. 2025, 17, 379. [Google Scholar] [CrossRef]
- Klees, R.; Massonnet, D. Deformation measurements using SAR interferometry: Potential and limitations. Geol. Mijnbouw. 1998, 77, 161–176. [Google Scholar] [CrossRef]
- Vasco, D.W.; Wicks, C.; Karasaki, K.; Marques, O. Geodetic imaging: Reservoir monitoring using satellite interferometry. Geoph. J. Int. 2002, 149, 555–571. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar] [CrossRef]
- Pepe, A.; Calò, F. A Review of Interferometric Synthetic Aperture RADAR (InSAR) Multi-Track Approaches for the Retrieval of Earth’s Surface Displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D. Sentinel-1 Big Data Processing with P-SBAS InSAR in the Geohazards Exploitation Platform: An Experiment on Coastal Land Subsidence and Landslides in Italy. Remote Sens. 2021, 13, 885. [Google Scholar] [CrossRef]
- Kim, J.; Jung, H.S.; Lu, Z. Ground surface displacement measurement from SAR imagery using deep learning. Remote. Sens. Environ. 2025, 318, 114577. [Google Scholar] [CrossRef]
- Battaglia, M.; Cervelli, P.F.; Murray, J.R. dMODELS: A MATLAB software package for modeling crustal deformation near active faults and volcanic centers. J. Volcanol. Geotherm. Res. 2013, 254, 1–4. [Google Scholar] [CrossRef]
- Bagnardi, M.; Hooper, A. Inversion of surface deformation data for rapid estimates of source parameters and uncertainties: A Bayesian approach. Geochem. Geophys. Geosystems 2018, 19, 2194–2211. [Google Scholar] [CrossRef]
- Camacho, A.G.; Fernández, J.; Cannavò, F. PAF: A software tool to estimate free-geometry extended bodies of anomalous pressure from surface deformation data. Comput. Geosci. 2018, 111, 235–243. [Google Scholar] [CrossRef]
- Camacho, A.G.; Fernández, J. Modeling 3D Free-geometry Volumetric Sources Associated to Geological and Anthropogenic Hazards from Space and Terrestrial Geodetic Data. Remote. Sens. 2019, 11, 2042. [Google Scholar] [CrossRef]
- De Natale, G.; Petrazzuoli, S.M.; Pingue, F. The effect of collapse structures on ground deformations in calderas. Geophys. Res. Lett. 1997, 24, 1555–1558. [Google Scholar] [CrossRef]
- Masterlark, T. Magma intrusion and deformation predictions: Sensitivities to the Mogi assumptions. J. Geophys. Res. 2007, 112, B6. [Google Scholar] [CrossRef]
- Manconi, A.; Walter, T.R.; Manzo, M.; Zeni, G.; Tizzani, P.; Sansosti, E.; Lanari, R. On the effects of 3-D mechanical heterogeneities at Campi Flegrei caldera, southern Italy. J. Geophys. Res. Solid Earth 2010, 115, B8. [Google Scholar] [CrossRef]
- Grandin, R.; Klein, E.; Métois, M.; Vigny, C. Three-dimensional displacement field of the 2015 Mw8.3 Illapel earthquake (Chile) from across- and along-track Sentinel-1 TOPS interferometry. Geophys. Res. Lett. 2016, 43, 2552–2561. [Google Scholar] [CrossRef]
- Delgado, F.; Grandin, R. Dynamics of episodic magma injection and migration at Yellowstone caldera: Revisiting the 2004–2009 episode of caldera uplift with INSAR and GPS data. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022341. [Google Scholar] [CrossRef]
- Cui, Y.; Ma, Z.; Aoki, Y.; Liu, J.; Yue, D.; Hu, J.; Zhou, C.; Li, Z. Refining slip distribution in moderate earthquakes using Sentinel-1 burst overlap interferometry: A case study over 2020 May 15 Mw 6.5 Monte Cristo Range Earthquake. Geophys. J. Int. 2022, 229, 472–486. [Google Scholar] [CrossRef]
- Barone, A.; Fedi, M.; Pepe, A.; Mastro, P.; Tizzani, P.; Castaldo, R. Inferring 3D displacement time series through InSAR measurements and potential field theory in volcanic areas. Sci. Rep. 2025, 15, 4719. [Google Scholar] [CrossRef] [PubMed]
- Castaldo, R.; Tizzani, P.; Solaro, G. Inflating Source Imaging and Stress/Strain Field Analysis at Campi Flegrei Caldera: The 2009–2013 Unrest Episode. Remote Sens. 2021, 13, 2298. [Google Scholar] [CrossRef]
- Przeor, M.; D’Auria, L.; Pepe, S.; Tizzani, P.; Barone, A.; Vitale, A.; Pérez, N.M.; Castaldo, R. Independent component analysis and finite element modelling of the 2004–2005 ground deformation in Tenerife (Canary Islands). Front. Earth Sci. 2024, 12, 2024. [Google Scholar] [CrossRef]
- Charco, M.; Galán del Sastre, P. Efficient inversion of three-dimensional finite element models of volcano deformation. Geophys. J. Int. 2014, 196, 1441–1454. [Google Scholar] [CrossRef][Green Version]
- Hickey, J.; Gottsmann, J. Benchmarking and developing numerical Finite Element models of volcanic deformation. J. Volcanol. Geotherm. Res. 2014, 280, 126–130. [Google Scholar] [CrossRef]
- Milano, M.; Fedi, M.; Fairhead, J.D. The deep crust beneath the Trans-European Suture Zone from a multiscale magnetic model. J. Geophys. Res. Solid Earth 2016, 121, 6276–6292. [Google Scholar] [CrossRef]
- Milano, M.; Fedi, M. Surface Gravity Response of CO2 Storage in the Johansen Deep Reservoir. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5922014. [Google Scholar] [CrossRef]
- Abbas, M.A.; Speranza, L.; Fedi, M.; Garcea, B.; Bianco, L. Magnetic data modelling of salt domes in Eastern Mediterranean, offshore Egypt. Acta Geophys. 2024, 72, 1293–1303. [Google Scholar] [CrossRef]
- Fedi, M.; Florio, G.; Quarta, T.A.M. Multiridge analysis of potential fields: Geometric method and reduced Euler deconvolution. Geophysics 2009, 74, L53–L65. [Google Scholar] [CrossRef]
- Fedi, M.; Florio, G. SCALFUN: 3D analysis of potential field scaling function to determine independently or simultaneously Structural Index and depth to source. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2006. [Google Scholar] [CrossRef]
- Blakely, J.R. Potential Theory in Gravity and Magnetic Applications, Revised ed.; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Barone, A.; Pepe, A.; Tizzani, P.; Fedi, M.; Castaldo, R. New advances of the Multiscale Approach for the analyses of InSAR Ground measurements: The Yellowstone caldera case-study. Remote Sens. 2022, 14, 5328. [Google Scholar] [CrossRef]
- Carlino, S.; Mirabile, M.; Troise, C.; Sacchi, M.; Zeni, L.; Minardo, A.; Caccavale, M.; Darányi, V.; De Natale, G. Distributed-Temperature-Sensing Using Optical Methods: A First Application in the Offshore Area of Campi Flegrei Caldera (Southern Italy) for Volcano Monitoring. Remote Sens. 2016, 8, 674. [Google Scholar] [CrossRef]
- Petrillo, Z.; Tripaldi, S.; Mangiacapra, A.; Scippacercola, S.; Caliro, S.; Chiodini, G. Principal component analysis on twenty years (2000–2020) of geochemical and geophysical observations at Campi Flegrei active caldera. Sci. Rep. 2023, 13, 18445. [Google Scholar] [CrossRef]
- Marotta, E.; Peluso, R.; Avino, R.; Avvisati, G.; Bellucci Sessa, E.; Belviso, P.; Caputo, T.; Carandente, A.; Cirillo, F.; Pescione, R.A. Clusterisation and Temporal Trends of Heat Flux by UAS Thermal Camera. Remote Sens. 2024, 16, 1102. [Google Scholar] [CrossRef]
- Danesi, S.; Pino, N.A.; Carlino, S.; Kilburn, C.R.J. Evolution in unrest processes at Campi Flegrei caldera as inferred from local seismicity. Earth Planet. Sci. Lett. 2024, 626, 118530. [Google Scholar] [CrossRef]
- Giacomuzzi, G.; Chiarabba, C.; Bianco, F.; De Gori, P.; Piana Agostinetti, N. Tracking transient changes in the plumbing system at Campi Flegrei Caldera. Earth Planet. Sci. Lett. 2024, 637, 118744. [Google Scholar] [CrossRef]
- Tizzani, P.; Fernández, J.; Vitale, A.; Escayo, J.; Barone, A.; Castaldo, R.; Pepe, S.; De Novellis, V.; Solaro, G.; Pepe, A.; et al. 4D imaging of the volcano feeding system beneath the urban area of the Campi Flegrei caldera. Remote Sens. Environ. 2024, 315, 114480. [Google Scholar] [CrossRef]
- Mercogliano, F.; Barone, A.; D’Auria, L.; Castaldo, R.; Silvestri, M.; Bellucci Sessa, E.; Caputo, T.; Stroppiana, D.; Caliro, S.; Minopoli, C.; et al. Thermal Patterns at the Campi Flegrei Caldera Inferred from Satellite Data and Independent Component Analysis. Remote Sens. 2024, 16, 4615. [Google Scholar] [CrossRef]
- Barone, A.; Gola, G.; Caliro, S.; Chiodini, G.; Tizzani, P.; Castaldo, R. Long-term thermo-fluid dynamic modeling of Solfatara hydrothermal system, Campi Flegrei caldera. J. Volcanol. Geotherm. Res. 2025, 459, 108277. [Google Scholar] [CrossRef]
- Giacomuzzi, G.; Fonzetti, R.; Govoni, A.; De Gori, P.; Chiarabba, C. Causal processes of shallow and deep seismicity at Campi Flegrei caldera. Commun. Earth Environ. 2025, 6, 70. [Google Scholar] [CrossRef]
- Patanè, D.; Barberi, G.; Martino, C. Seismic Images of Pressurized Sources and Fluid Migration Driving Uplift at the Campi Flegrei Caldera During 2020–2024. GeoHazards 2025, 6, 19. [Google Scholar] [CrossRef]
- Convertito, V.; Godano, C.; Petrillo, G.; Tramelli, A. Insights from b value analysis of Campi Flegrei unrests. Sci. Rep. 2025, 15, 14974. [Google Scholar] [CrossRef] [PubMed]
- Trasatti, E.; Polcari, M.; Bonafede, M.; Stramondo, S. Geodetic constraints to the source mechanism of the 2011–2013 unrest at Campi Flegrei (Italy) caldera. Geophys. Res. Lett. 2015, 42, 3847–3854. [Google Scholar] [CrossRef]
- Amoruso, A.; Crescentini, L.; Sabbetta, I.; De Martino, P.; Obrizzo, F.; Tammaro, U. Clues to the cause of the 2011–2013 Campi Flegrei caldera unrest, Italy, from continuous GPS data. Geophys. Res. Lett. 2014, 41, 3081–3088. [Google Scholar] [CrossRef]
- D’Auria, L.; Pepe, S.; Castaldo, R.; Giudicepietro, F.; Macedonio, G.; Ricciolino, P.; Tizzani, P.; Casu, F.; Lanari, R.; Manzo, M.; et al. Magma injection beneath the urban area of Naples: A new mechanism for the 2012–2013 volcanic unrest at Campi Flegrei caldera. Sci. Rep. 2015, 5, 13100. [Google Scholar] [CrossRef] [PubMed]
- Amoruso, A.; Crescentini, L. Clues of Ongoing Deep Magma Inflation at Campi Flegrei Caldera (Italy) from Empirical Orthogonal Function Analysis of SAR Data. Remote Sens. 2022, 14, 5698. [Google Scholar] [CrossRef]
- Astort, A.; Trasatti, E.; Caricchi, L.; Polcari, M.; De Martino, P.; Acocella, V.; Di Vito, M.A. Tracking the 2007–2023 magma-driven unrest at Campi Flegrei caldera (Italy). Commun. Earth Environ. 2024, 5, 506. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential interferometry. J. Geophys. Res. Solid Earth 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R. Synthetic aperture radar interferometry. IEEE Proc. 2000, 88, 333–376. [Google Scholar] [CrossRef]
- Pepe, A.; Lanari, R. On the extension of the minimum cost flow algorithm for phase unwrapping of multitemporal differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2374–2383. [Google Scholar] [CrossRef]
- Florio, G.; Fedi, M. Multiridge Euler deconvolution. Geophys. Prospect. 2014, 62, 333–351. [Google Scholar] [CrossRef]
- Ferrara, G.; Ferraccioli, F.; Fedi, M. Potential fields as a tool to characterize the inaccessible areas of the earth: The case of Pine Island–Ellsworth Mountains area, West Antarctica. Lead. Edge 2024, 43, 218–226. [Google Scholar] [CrossRef]
- Castaldo, R.; Barone, A.; Fedi, M.; Tizzani, P. Multiridge Method for studying ground-deformation sources: Application to volcanic environments. Sci. Rep. 2018, 8, 13420. [Google Scholar] [CrossRef]
- Barone, A.; Fedi, M.; Tizzani, P.; Castaldo, R. Multiscale Analysis of DInSAR measurements for Multi-source Investigation at Uturuncu Volcano (Bolivia). Remote Sens. 2019, 11, 703. [Google Scholar] [CrossRef]
- Ridsdill-Smith, T.A.; Dentith, M.C. The wavelet transform in aeromagnetic processing. Geophysics 1999, 64, 1003–1013. [Google Scholar] [CrossRef]
- Pepe, S.; De Siena, L.; Barone, A.; Castaldo, R.; D’Auria, L.; Manzo, M.; Casu, F.; Fedi, M.; Lanari, R.; Bianco, F.; et al. Volcanic structures investigation through SAR and seismic interferometric methods: The 2011–2013 Campi Flegrei unrest episode. Remote Sens. Environ. 2019, 234, 111440. [Google Scholar] [CrossRef]
- Florio, G.; Fedi, M.; Cella, F.; Rapolla, A. The Campanian Plain and Phlegrean Fields: Structural setting from potential field data. J. Volcanol. Geotherm. Res. 1999, 91, 361–379. [Google Scholar] [CrossRef]
- Paoletti, V.; Fedi, M.; Florio, G. Magnetic Structure of the Ischia volcanic island, Southern Italy. Ann. Geophys. 2017, 60, GM674. [Google Scholar] [CrossRef]
- Gola, G.; Barone, A.; Castaldo, R.; Chiodini, G.; D’Auria, L.; García-Hernández, R.; Pepe, S.; Solaro, G.; Tizzani, P. A Novel Multidisciplinary Approach for the Thermo-Rheological Study of Volcanic Areas: The Case Study of Long Valley Caldera. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020331. [Google Scholar] [CrossRef]
- Fagan, M. Finite Element Analysis. Theory and Practice; Longman Pub Group: New York, NY, USA; Wiley: Hoboken, NJ, USA, 1992; 344p, ISBN 0470218177. [Google Scholar]
- Chiarabba, C.; Moretti, M. An insight into the unrest phenomena at the Campi Flegrei caldera from Vp and Vp/Vs tomography. Terra Nova 2006, 18, 373–379. [Google Scholar] [CrossRef]
- Wang, Z. Dynamic versus static elastic properties of reservoir rocks. In Seismic and Acoustic Velocities in Reservoir Rocks; Society of Exploration Geophysicists: Tusla, OK, USA, 2000; pp. 531–539. ISBN 0931830001, 9780931830006. [Google Scholar]
- Brocher, T.M. Empirical relations between elastic wavespeeds and density in the Earth’s crust. Bull. Seismol. Soc. Am. 2005, 95, 2081–2092. [Google Scholar] [CrossRef]
- Fedi, M.; Florio, G.; Cascone, L. Multiscale analysis of potential fields by a ridge consistency criterion: The reconstruction of the Bishop basement. Geophys. J. Int. 2012, 188, 103–114. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).