Closed and Structural Optimization for 3D Line Segment Extraction in Building Point Clouds

Highlights

What are the main findings?

• A closed and topology-aware line optimization framework integrates graph-cut contour extraction with structural constraints, ensuring continuous and complete building contours.
• Geometric regularization with adjacency, collinearity, and orthogonality constraints improves line accuracy and reduces redundant segments in both indoor and outdoor datasets.

What are the implications of the main findings?

• The proposed method enhances the reliability of 3D building contour representation, offering more accurate primitives for structural modeling.
• Length-weighted completeness and redundancy metrics, together with BIM-based ground truth, provide a comprehensive evaluation protocol for future line extraction studies.

Abstract

The extraction of architectural structural line features can simplify the 3D spatial representation of built environments, reduce the storage and processing burden of large-scale point clouds, and provide essential geometric primitives for downstream modeling tasks. However, existing 3D line extraction methods suffer from incomplete and fragmented contours, with missing or misaligned intersections. To overcome these limitations, this study proposes a patch-level framework for 3D line extraction and structural optimization from building point clouds. The proposed method first partitions point clouds into planar patches and establishes local image planes for each patch, enabling a structured 2D representation of unstructured 3D data. Then, graph-cut segmentation is proposed to extract compact boundary contours, which are vectorized into closed lines and back-projected into 3D space to form the initial line segments. To improve geometric consistency, regularized geometric constraints, including adjacency, collinearity, and orthogonality constraints, are further designed to merge homogeneous segments, refine topology, and strengthen structural outlines. Finally, we evaluated the approach on three indoor building environments and four outdoor scenes, and experimental results show that it reduces noise and redundancy while significantly improving the completeness, closure, and alignment of 3D line features in various complex architectural structures.

1. Introduction

With the rapid development of LiDAR sensor and 3D reconstruction technology, acquiring large-scale and high-density point clouds has become a fundamental approach for digitally representing real-world environments [1]. Due to their high accuracy and realistic spatial representation, point clouds are widely used in various domains such as digital twin construction [2,3,4], infrastructure management [5], Building Information Modeling [6], and cultural heritage preservation [7]. However, the inherently massive, unstructured, and redundant characteristics of point clouds, especially in the representation of geometrically simple or repetitive architectural features, result in substantial data redundancy, which not only increases storage but also hinders the efficiency of downstream modeling and semantic analysis tasks [8,9,10,11].

Currently, many studies have focused on extracting structurally meaningful geometric primitives from raw point clouds to simplify spatial representation and reduce redundancy [12,13,14]. These primitives are typically classified into shape-based elements (e.g., lines, planes, and volumes) and structure-based elements (e.g., edges and skeletons). Among them, line features provide a concise and informative representation of describing the geometric outlines of objects, with low dimensionality and a parametric form that allows direct expression through endpoint coordinates and direction vectors. As such, line features serve as a crucial bridge between raw point clouds and structured geometric modeling [15]. Nevertheless, current line extraction methods often suffer from issues such as fragmentation, discontinuity, and angular deviation, which is primarily caused by variations in point cloud density as well as occlusions and noise arising from data acquisition. In addition, existing approaches [16,17,18,19] are still largely confined to edge-detection-based strategies, which are effective for highlighting boundary cues but insufficient for directly deriving line segments or parametric line representations. This leads to a lack of robust structural descriptors that can directly support geometry-based modeling. Moreover, most line segment extraction methods [20,21,22,23] tend to treat each line segment independently, without explicitly considering their topological associations such as adjacency, connectivity, and intersection relationships. This simplification often results in incomplete contours, misaligned corners, and deviations at structural junctions, thereby restricting the integrity and applicability of extracted features in large-scale architectural environments. Although several topology-aware methods [24,25,26,27,28] have been developed, they are primarily oriented toward capturing the global spatial layout of structures, and often fail to preserve the finer geometric details of local contours, resulting in a gap between large-scale organization and precise structural representation. These limitations compromise the integrity and precision of extracted geometric features and restrict their application in high-level modeling tasks. Therefore, overcoming these limitations is essential for achieving reliable and high-quality extraction of structural line features from building point clouds.

To address these common limitations in 3D line segment extraction, including incomplete contours, discontinuities, and missing intersections, this study proposes a patch-level 3D line extraction and optimization framework specifically designed for building point clouds. The method begins by segmenting the input point clouds into planar patches. Depending on these patches, the method systematically analyzes the spatial relationships and typical structural deficiencies of line features in complex scenes. Then, a graph-cut-based optimization strategy is employed at the patch level to enhance the completeness and closure of 2D contours extracted from image-projected patches. These refined contours are then vectorized and back-projected into 3D space. To further improve the structural consistency and geometric accuracy of the extracted lines, a constraint-guided 3D optimization procedure is introduced, including the adjacency and collinearity constraints to merge redundant line segments, as well as the orthogonality constraint to correct angular deviations and improve alignment among intersecting structures. The proposed framework enhances the quality and reliability of geometric line primitives derived from unstructured point clouds, facilitating more accurate and efficient geometric modeling in downstream applications such as building information modeling and architectural reconstruction. The main contributions of this work can be summarized as follows:

• Closed and Topology-Aware Line Optimization: Unlike existing edge-detection-based methods that treat segments independently, our framework integrates graph-cut contour extraction with topology-guided constraints, ensuring closed and structurally consistent line features.
• Geometric Regularization through Structural Constraints: Adjacency, collinearity, and orthogonality constraints are introduced to merge redundant lines, enforce closure, and correct angular deviations, thereby improving both geometric accuracy and structural fidelity.
• Length-weighted Evaluation Metrics: We design quantitative metrics (completeness and redundancy) for indoor datasets with BIM-derived ground truth and introduce qualitative comparisons for outdoor scenes using robust edge-extraction references, providing a balanced validation across diverse scenarios.

2. Related Works

In recent years, the extraction of line features from 3D point clouds has emerged as a crucial area of research for architectural contour reconstruction. Depending on the underlying data structures employed, existing approaches can be broadly categorized into three types: point-based methods, space-based methods, and patch-based methods. Each type offers distinct advantages in terms of accuracy, robustness, and structural preservation, rendering them well-suited for diverse application scenarios.

2.1. Point-Based Methods for 3D Line Extraction

Point-based 3D line extraction methods normally regard discrete points as basic units and design regional geometric descriptors to identify edge points representing line features. The most common approach is to derive local geometric characteristics, such as planarity, scattering, linearity, curvature and normal vectors [16,29], from the eigenvalues of covariance matrices constructed using the K-nearest neighbor searching. Depending on these descriptors, the vector deflection angle [30] and vector distributions [17] are subsequently introduced to calculate angular deviations between neighboring vectors to identify boundary points. However, such methods require eigen-decomposition and clustering for each point, resulting in high computational cost and limited scalability for large-scale point clouds.

To address this, several studies [18,19,31] focus on constructing spatial gradients and structural tensors by evaluating confidence differences between a point and its neighbors. Nevertheless, these methods are sensitive to noise and outliers, which can lead to false or missed detections. Thus, the concept of geometric center displacement in point neighborhoods [21,22] are proposed to avoid the overhead of local decomposition for feature detection, but they require multiple manually tuned parameters and may mistakenly identify fine surface textures as edges when thresholds are too strict, thereby resulting in unnecessary redundancy.

To reduce manual parameter tuning, hypothesis-and-selection strategies based on geometric model fitting have been introduced, in which a global energy function is defined and minimized to extract the optimal set of line segments. For example, initial model parameters can be generated through random sampling, followed by graph-based α-expansion algorithms to perform energy minimization [32]. Energy functions that integrate internal smoothness and external boundary alignment terms [33] have also been employed to iteratively adjust contour boundaries toward actual point cloud edges. A Bayesian point-edge collaborative framework called PEco is designed and embedded into an expectation-maximization algorithm for iterative edge inference. These optimization methods are flexible and robust but remain susceptible to local optima.

To address these limitations, recent studies [34,35,36,37,38] have applied deep learning techniques that formulate edge detection as a supervised classification task, where trained networks leverage high-dimensional features to classify points into corners, edges, or non-structural regions. GMcGAN [34], a GAN framework where the generator predicts edge parameters and the discriminator evaluates contour authenticity, is proposed to enhance output quality through adversarial training. Additionally, other studies improve classification accuracy by enriching input features with eigen-based [35] or multi-scale descriptors [38]. These deep learning approaches are constrained by the availability of extensive, high-quality annotated datasets, and the annotation process is often time-consuming, labor-intensive, and susceptible to errors.

2.2. Space-Based Methods for 3D Line Extraction

Given that point-based line feature extraction methods are often sensitive to point cloud quality, space-based approaches leveraged spatial partitioning and planar intersections to construct idealized wireframe representations from a global structural modeling perspective. These methods are effective in mitigating the impact of point cloud holes on large-scale structural profile extraction. Under the Manhattan-world assumption, such approaches typically begin by identifying potential structural planes and partitioning the 3D space accordingly. A global energy function [24,25,39] is then constructed to select the optimal set of intersecting configurations for line segment formation. However, when dealing with complex architectural scenes involving a large number of planes, the number of intersection candidates increases exponentially, which dramatically raises the computational complexity of pairwise energy optimization. To address this issue, several studies transform the 3D spatial partitioning problem into a 2D domain by combining planar graphs with geometric extrusion. Optimization algorithms such as integer programming [27,40,41] or Markov Random Fields [28] are then employed to extract optimal polygonal structures.

An alternative approach, typically applied in structured indoor environments, involves projecting point clouds onto a horizontal plane to generate grayscale images, segmenting spatial regions using image morphological processing, and extracting boundary lines. Building on this, the topological layout of indoor spaces has been further integrated into room-level floorplan extraction. A hybrid integer programming (MIP) [42] combined deep learning-based recognition of geometric primitives to construct semantically consistent space layout. Similarly, topological connectivity between subspaces [43] is inferred from door detection results obtained via deep learning, thus guiding cell-based partitioning and spatial topology reconstruction. Although these space-based methods demonstrate strong modeling capabilities in large-scale building scenarios and are particularly suitable for extracting LOD0–LOD3 building contours, they rely heavily on the accurate detection of planar structures. Consequently, they are prone to falling into local optima when dealing with complex or irregular structures, which limits their ability to represent finer-grained structure details.

2.3. Patch-Based Methods for 3D Line Extraction

Patch-based methods for 3D line feature extraction circumvent explicit modeling of spatial topological relationships among intersecting planes. Instead, they generate local planar patches by clustering points with similar planar characteristics, typically based on normal direction or point-to-plane distance thresholds. Structural lines are then reconstructed by extracting the boundaries of these patches. To segment patches from point clouds, clustering, such as random sample consensus (RANSAC), supervoxel-based segmentation, and region growing techniques, are frequently adopted. Among them, RANSAC-based approaches [44,45] are widely used for their robustness to noise, but they often require numerous iterations to achieve precise model fitting and are computationally inefficient when applied to large-scale point clouds. Supervoxel segmentation methods [46,47,48] simplify point clouds by dividing them into smaller and more regular clusters, which improves feature consistency and processing efficiency, though at the cost of potentially losing geometric details. Region growing techniques [20,23] expand from initial seed points to cluster homogeneous points into planar regions. However, they are highly sensitive to the choice of seed points and are prone to over-segmentation or under-segmentation, particularly in areas with ambiguous boundaries. Once the patch structure is established, the alpha shape algorithm [46] is used to detect boundary points and delineate patch contours. However, its sensitivity to sampling density often leads to inaccurate or incomplete boundary shapes in sparse regions.

To mitigate the impact of uneven point density on boundary extraction, many approaches project 3D patches onto local image planes to generate grayscale representations, enabling the application of classical image processing techniques for edge detection. Common methods include the Sobel operator [49], Canny edge detector [50], and Hough Transform [51]. The Hough Transform maps image-space points to curves in parameter space to identify line features. Methods like MCMLSD [52] employed probabilistic Hough Transform with Markov chain modeling and dynamic programming to extract line segments via maximum a posteriori (MAP) estimation, but they are computationally expensive and slow. To address this, a convolutional neural network operating in Hough space, called HT-IHT [53], is proposed to directly predict line parameters. While this method improves automation, it remains dependent on high-quality annotated datasets. The Canny edge detection algorithm performs edge extraction through Gaussian smoothing, gradient computation, non-maximum suppression, and dual-threshold edge linking. Inspired by this, the Line Segment Detector (LSD) [54] accelerated line extraction using image gradients and integral images, while introducing geometric consistency constraints to improve detection accuracy. The Fast Line Detector (FLD) [55] enhanced the robustness of line extraction by employing the Mean Standard-Deviation Line Descriptor (MSLD) to represent local structural features. CannyLines [56] combined edge point clustering and splitting with least-squares line fitting to efficiently extract long straight segments.

However, line fitting processes inevitably suffer from direction deviations, discontinuities, and missing intersections. To overcome these limitations, the Modified Random Step Clustering (M-RSC) method [57] refines incomplete line segments by classifying feature points as curve or linear types and enforcing geometric constraints. The split-and-merge method [58] generates closed contours with low complexity using semantic probability maps and image gradients, but its performance strongly depends on the accuracy of the input semantic labels.

3. Methods

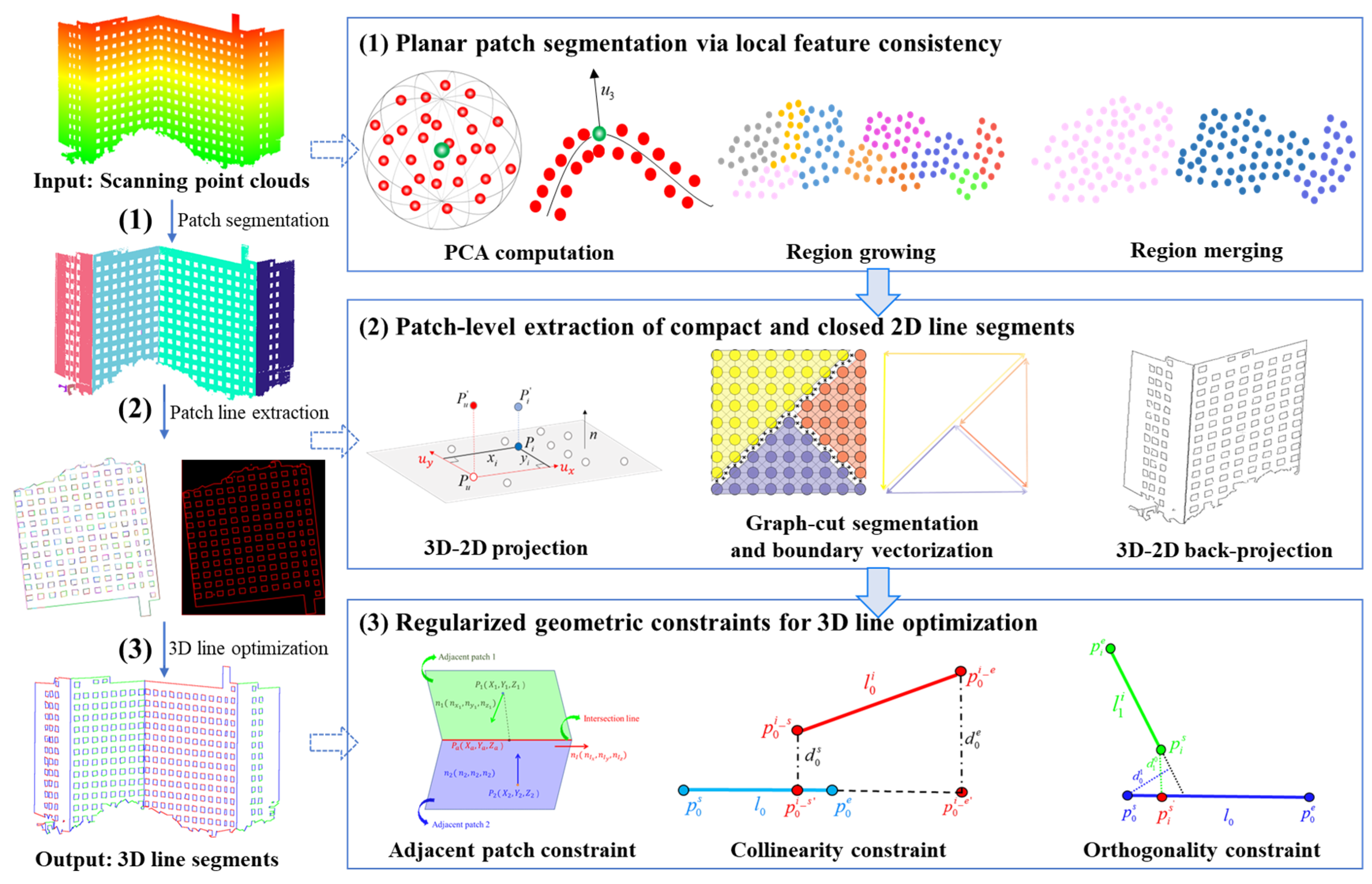
The proposed approach takes scanning point clouds of building structures as input and it outputs parameterized 3D line segments to characterize the outline of buildings. Figure 1 shows the pipeline of the proposed method, which consists of three main stages:

(1) Planar patch segmentation. It first performs region growing and merging on scanning point clouds via local geometry features to generate an initial set of planar patches which serve as fundamental geometric units for subsequent processing.

(2) Patch line extraction. For each planar patch, a 3D-to-2D projection is then performed to construct a local image coordinate system and generate a grayscale image. Depending on this projection, a graph-cut segmentation algorithm is applied to extract clear and salient patch boundaries, effectively separating the patch region from the background. These boundaries are then vectorized into a compact and closed polygonal line set using a contour-following vectorization method, followed by the 3D-2D back-projection for generation of an initial set of structured 3D line features.

(3) 3D line optimization. Considering the spatial regularity of building structures, a geometric regularization process is applied to optimize the initial 3D line segments by introducing adjacency, collinearity, and orthogonality constraints. These constraints jointly improve structural coherence by correcting angular deviations between adjacent patches, merging collinear segments to reduce redundancy, and refining orthogonal relationships to enhance closure and directional accuracy. Through these operations, the refined 3D line segments exhibit better continuity, completeness, and directional accuracy, providing a more coherent and reliable geometric representation.

3.1. Planar Patch Segmentation

3.1.1. Region Growing

To achieve geometric region clustering for point clouds, we first implement principal component analysis (PCA) [59] to compute geometric features and provide clustering constraints for region growing. Specifically, KD-trees are constructed for neighborhood indexing, followed by the computation of the covariance matrix for each point’s neighborhood. The PCA algorithm is then applied to derive the eigenvalues $e_1$, $e_2$ and $e_3$ ($e_1\ge e_2\ge e_3$), and their corresponding eigenvectors $u_1$, $u_2$ and $u_3$, characterizing the geometric properties of the point neighborhood. The eigenvector $u_3$ associated with the smallest eigenvalue $e_3$ represents the normal vector $n_e$ of the local neighborhood of the point, while the neighborhood curvature $c_e$ is defined as

$$c_e={\displaystyle \frac{e_3}{e_1+e_2+e_3}}$$

(1)

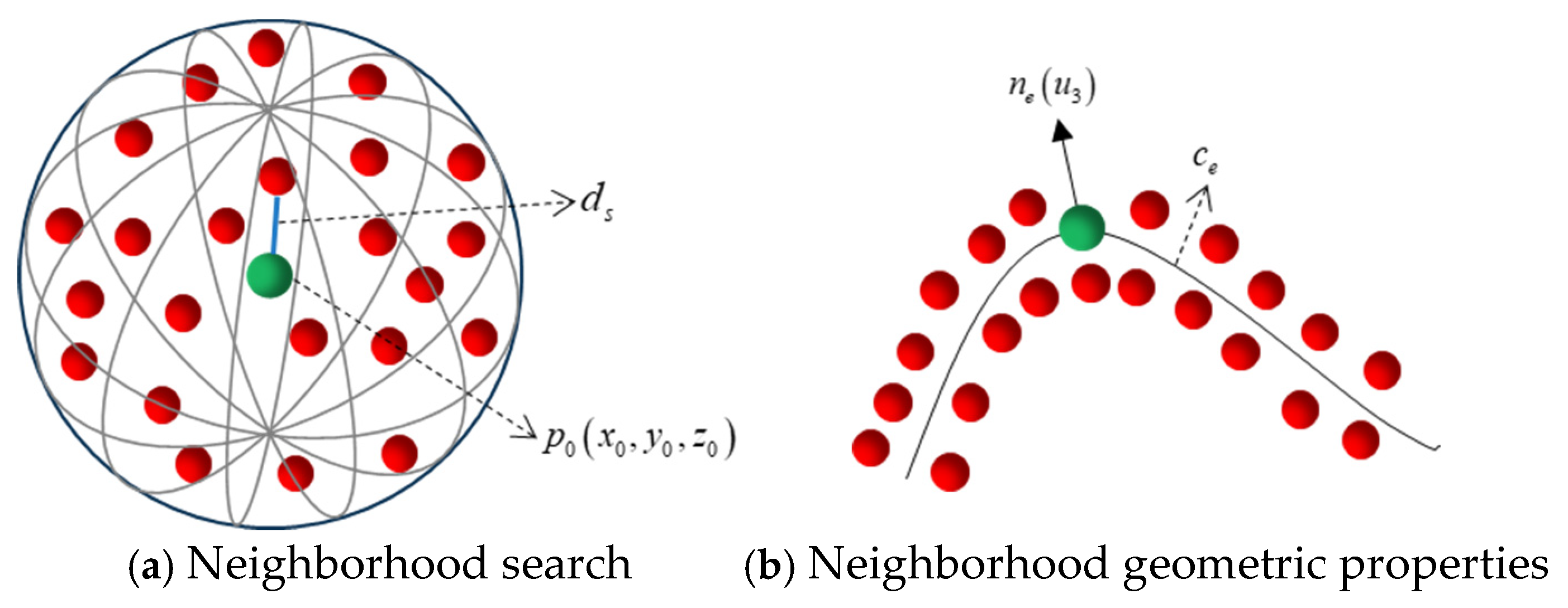
To ensure the region-growing algorithm adapts to point clouds of varying scales, a distance scale parameter $d_s$ is defined as the distance between a point and its third nearest neighbor, typically represented by the Euclidean distance in meters. As illustrated in Figure 2, for example, let $p_0\left(x_0,y_0,z_0\right)$ denote a reference point, and $p_0^3\left(x_0^3,y_0^3,z_0^3\right)$ its third nearest neighbor in the KNN search neighborhood. Then $d_s$ can be explicitly formulated as:

$$d_s={‖p_0-p_0^3‖}_2=\sqrt{{\left(x_0-x_0^3\right)}^2+{\left(y_0-y_0^3\right)}^2+{\left(z_0-z_0^3\right)}^2}$$

(2)

This $d_s$ provides a locally adaptive scale for the neighborhood, serving as a normalization factor for similarity thresholds in the region-growing process and ensuring that the algorithm remains robust across point clouds with varying densities and scales. Drawing on these neighborhood geometric properties, the geometry-based region growing algorithm for point clouds consists of five steps:

(1) Geometric feature calculation and sorting: For each point $p_i\in P_t$, compute the geometric features for each point, including curvature $c_i$, normal vector $n_i$, and the distance scale parameter $d_s^i$. The points are then sorted in ascending order by $c_i$, thus generating a sorted point cloud list $P_C$.

(2) Seed point selection and region growing: To enhance the computational efficiency of region growing, a traversal list $P_Q$ is constructed using 90% sorted point clouds $P_C$, from which seed points are selected to determine the region-growing conditions. Initially, the point with the smallest curvature is chosen as the initial seed point $p_s^0$. The geometric relationship between this seed point $p_s^0$ and its neighboring points $p_j^0$ is then assessed through three clustering conditions: (1) Determine if the directional deviation of the normal vectors between $p_s^0$ and $p_j^0$ satisfies Equation (2); (2) Determine if the orthogonal distance between the normal directions of $p_s^0$ and $p_j^0$ satisfies Equation (3); (3) Determine if the spatial distance between $p_s^0$ and $p_j^0$ falls within the distance threshold specified by Equation (4). Points that satisfy all three conditions are added to the current seed list $S_i$ and the temporary clustering region $R_i$.

$${\cos }^{-1}\left(n_s^i\cdot n_j^i\right)<{\theta }_n$$

(3)

$$\left|n_s^i\cdot \stackrel{\rightharpoonup }{P_s^i{P}_j^i}\right|<d_{ortho}$$

(4)

$$\left|\stackrel{\rightharpoonup }{P_s^i{P}_j^i}\right|<d_{proj}$$

(5)

where ${\theta }_n$ denotes the angle between the normal vectors of $p_s^0$ and $p_j^0$, serving to constrain the angular deviation between the seed point and candidate points, $d_{ortho}$ defines the orthogonal distance from the candidate point to the neighborhood plane along the normal direction of the seed point, with a value set to $d_s^i$, and $d_{proj}$ is set to $50d_s^i$ adaptively determining the distance threshold between the seed point and candidate points.

(3) Cluster region set generation: Select the next seed point from $S_i$ in sequence, and repeat step (2) until no seed points can find any points in $P_t$ that meet the clustering conditions for the current clustering region $R_i$.

(4) Homogeneity clustering evaluation: Count the number of points in the temporary clustering region $R_i$. If it exceeds 30, the $R_i$ is added to the clustering region set $R_c$; otherwise, it is deemed too sparse and its points are reinserted into $P_t$ for further growth.

(5) Repeat step (2), (3), and (4) until the traversal of $P_Q$ is finished.

The pseudocode for the geometry-based region growing algorithm for point clouds is as follows (Algorithm 1):

Algorithm 1: Geometry-based region growing for point clouds

Input: $P_t=\left\{p_0,p_1,\mathrm{\dots },p_i\right\}$

Output: Set of clustering regions $R_c=\left\{R_0,R_1\dots ,R_n\right\},R_n=\left\{{\displaystyle \sum _0^m}{P}_m\right\}$

1:  For each point $p_i\in P_t$, compute its curvature $c_i$, normal vector $n_i$ and point distance scale $d_s$

2:  Sort $P_t$ in ascending order by $c_i$ and select 90% of sorted points as the traversal list $P_Q$

3:  For each $p_i$ in $P_Q$ do

4:        Treat $p_i$ as a seed and add it to the seed list $S\leftarrow p_i$

5:        Establish an index query for $P_t$: $E_i$

6:        While $E_i\ne \varnothing$ do

7:                Retrieve all neighboring points $P_j^i$ of $p_i$

8:                For each $p_j^i$ in $P_j^i$ do

9:                          If ${\cos }^{-1}\left(n_s^i\cdot n_j^i\right)\ge {\theta }_n$ then

10:                                Continue

11:                        If $\left|n_s^i\cdot \stackrel{\rightharpoonup }{P_s^i{P}_j^i}\right|\ge d_{ortho}$ then

12:                                Continue

13:                        If $\left|\stackrel{\rightharpoonup }{P_s^i{P}_j^i}\right|\ge d_{proj}$ then

14:                                Continue

15:                        Add $p_j^i$ to the seed list $S_i$ and temporary clustering region $R_i$: $p_j^i\to S_i$, $p_j^i\to R_i$

16:                        Remove $p_j^i$ from the query list: $E_i\backslash p_j^i$

17:        If the number of points in $R_i$ exceeds 30 then

18:                Add the temporary region $R_i$: to the clustering region set $R_c$: $R_i\to R_c$

19:        Else

20:                Reinsert the points of $R_i$ into the query list $E_i$: $R_i\to E_i$

3.1.2. Region Merging

While the initial clustering regions exhibit local homogeneity, large-scale planar structures like walls are often divided into multiple clusters, necessitating further merging to reduce redundant boundaries. To achieve this, we first compute geometric properties of each clustering region and identify adjacent clustering regions by detecting spatially neighboring points across clusters. By applying angle and distance constraints, homogeneous clusters are then merged to form cohesive planar regions. Consequently, the neighborhood geometry-based region merging algorithm is divided into five steps, as outlined below:

(1) Computation of geometric properties for clustering regions: For each clustering region $R_i\in R_c$, compute its geometric features, including curvature $c_{R_i}$, normal vector $n_{R_i}$, and the distance scale parameter $d_{R_s}^i$.

(2) Neighboring Cluster Identification: For points within each clustering region $R_i$, its neighboring points are examined to determine if they belong to other clustering regions. If found, the neighboring region ID is recorded in the adjacency list ${\prod }_i$ and overlapping points are stored in $P_{{\prod }_i}$. After traversing all points, we further refine ${\prod }_i$ by eliminating weak adjacencies with insufficient overlap support (less than three shared points).

(3) Clustering region merging: Similarly to the region growing process, we calculate the directional angle between it and its adjacent clustering regions in ${\prod }_i$, as well as the distance from the centroid of neighboring cluster regions along the normal vector of the current cluster region to its own centroid, to compute the angular and orthogonal deviation metrics for merging decisions:

$${\cos }^{-1}\left(n_{R_i}\cdot n_{R_a^{ij}}\right)<{\theta }_{p_{-}n}$$

(6)

$$\left|n_{R_i}\cdot \overrightarrow{P_{R_i}{P}_{R_a^{ij}}}\right|<d_{p\_ortho}$$

(7)

If both conditions are met, the neighboring clustering region $R_{{\pi }_i}$ is added to the temporary planar region list $R_{\mathrm{temp}}$.

(4) Homogeneity clustering evaluation: If the number of points in the merged planar cluster $R_{\mathrm{temp}}$ exceeds 100, it is considered successfully merged and added to the patch set $R_p$.

(5) Repeat steps (3) and (4) until all elements in the clustering region list $R_c$ have been processed.

The pseudocode for the geometry-based region merging algorithm for point clouds is as follows (Algorithm 2):

Algorithm 2: Region merging of point clouds via neighborhood geometry

Input: Set of clustering regions $R_c=\left\{R_0,R_1\dots ,R_n\right\},R_n=\left\{{\displaystyle \sum _0^m}{P}_m\right\}$

Output: Set of patches $R_p=\left\{R_{c0},R_{c1}\dots ,R_{cm}\right\},R_{cm}=\left\{{\displaystyle \sum _0^n}{R}_n\right\}$

1:  For each clustering region $R_i$, compute its curvature $c_{R_i}$, normal vector $n_{R_i}$ and point distance scale $d_{R_s}^i$

2:  Assign a cluster region ID to each point in $P_t$: $L=l_0,l_1,\mathrm{\dots },l_t$

3:  For each $R_i$ in $R_c$ do

4:         Retrieve all points within $R_i$: $R_n=\left\{{\displaystyle \sum _0^m}{p}_m\right\}$

5:         For each $p_m$ in $R_n$ do

6:                  Find all neighboring points $p_m^a=\left\{p_m^0,p_m^1,\dots ,p_m^a\right\}$ of $P_m^a$

7:                  For each $p_m^a$ in $P_m^a$ do

8:                          If $p_m^a$ belongs to other cluster regions then

9:                                    Add the cluster ID of $p_m^a$ to the adjacency list ${\prod }_i$ of $R_i$

10:                                    Record $p_m^a$ to overlapping point list $P_{{\prod }_i}$

11:         For each $\pi$ in ${\prod }_i$ do

12:                  Count the overlapping points $N_a$ with the current region $R_i$

13:                  If the point number of $N_a$ less than 3 then

14:                           Remove the adjacent cluster ID from the adjacency list: ${\prod }_i\backslash \pi$

15:  For each $R_i$ in $R_c$ do

16:         Initialize a temporary list of planar regions: $R_{\mathrm{temp}}\to R_i$

17:         For each ${\pi }_i$ in ${\prod }_i$ do

18:                  Compute the normal vector deviation: ${\mathrm{A}}_i={\cos }^{-1}\left(n_{R^i}\cdot n_{R_a^{ij}}\right)$

19:                  Compute the vertical distance deviation: $D_i=\left|n_{R^i}\cdot \overrightarrow{P_{R^i}{P}_{R_{{\pi }_i}}}\right|$

20:                  If $A_i<{\theta }_n$ and $D_i<d_{p\_ortho}$ then

21:                           Add the corresponding region of ${\pi }_i$ to the temporary list: $R_{\mathrm{temp}}\to R_{{\pi }_i}$

22:         Count the number of points $N_t$ in $R_{\mathrm{temp}}$

23:         If $N_t$ exceeds 100 then

24:                  $R_{\mathrm{temp}}\to R_p$

3.2. Patch Line Extraction

To extract 3D lines from patches, we first project point clouds within each patch onto its corresponding fitted plane for image generation. Then, a 2D line extraction method combining graph-cut and edge vectorization algorithm is employed to obtain high-precision 2D edge features, ensuring the completeness of the extracted lines while effectively reducing boundary complexity.

3.2.1. 3D-2D Projection for Image Generation

With points in the patch projected onto a fitted plane, its corresponding plane coordinate system is established and the image is generated for contour extraction and 2D line segment fitting. According to the centroid $P_o\left(x_o,y_o,z_o\right)={\displaystyle \frac{{\displaystyle \sum _0^m}{P}_m\left(x_m,y_m,y_m\right)}{m}}$ and normal vector $n$ of the point cloud within the patch, the plane on which the patch lies can be formulated as follows:

$$n\cdot {\left(x-x_0,y-y_0,z-z_0\right)}^T=0$$

(8)

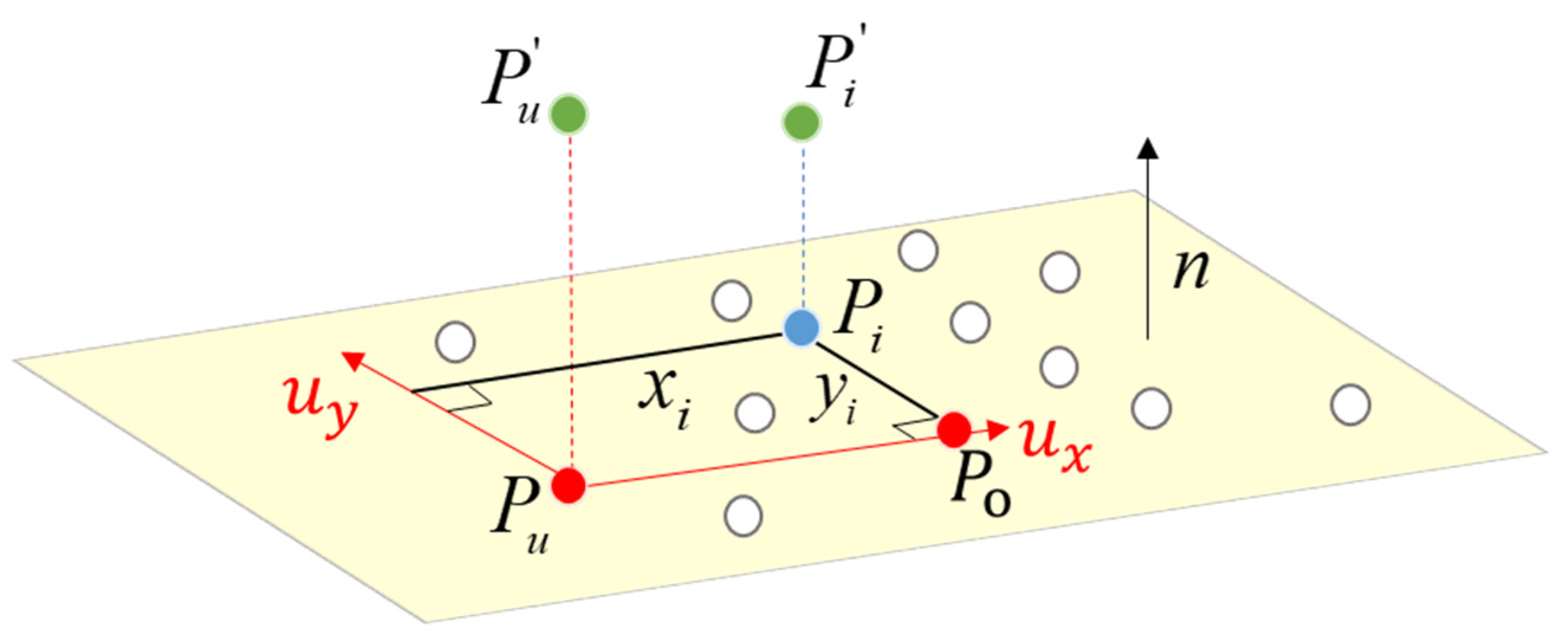
As shown in Figure 3, we assume a point $P_u^{\prime }$ within the patch is projected along the normal vector $n$ onto the fitted plane. The unit direction vector $u_x$ from patch centroid $P_o$ to projected point $P_u$ is treated as the x-axis, while another unit direction vector $u_y=u_x\otimes n$, obtained by the cross production of $u_x$ and $n$, is defined as the y-axis, thereby establishing the fitted plane coordinate system. Under this coordinate system, the projected coordinates of all points $P_i^{\prime }\in P^{\prime }$ within the patch on the fitted plane can be expressed as:

$$\left\{\begin{array}{l}\begin{array}{l}{x}_i=\left(\stackrel{\rightharpoonup }{P_o{P}_i^{\prime }}-\stackrel{\rightharpoonup }{P_i{P}_i^{\prime }}\right)\cdot u_x\hfill \\ y_i=\left(\stackrel{\rightharpoonup }{P_o{P}_i^{\prime }}-\stackrel{\rightharpoonup }{P_i{P}_i^{\prime }}\right)\cdot u_y\hfill \end{array}\\ \stackrel{\rightharpoonup }{P_i{P}_i^{\prime }}=\left(\stackrel{\rightharpoonup }{P_o{P}_i^{\prime }}\cdot n\right)\cdot n\end{array}\right.$$

(9)

With the distance scale $d_s$ of the points in the patch treated as the image resolution, a projected image is generated for 2D contour extraction, and its width and height are computed by the distance scale $d_s$ and the range of the projected point cloud:

$$\left\{\begin{array}{c}w=Int\left(x_{\max }-x_{\min }\right)/d_s+d_{dilate}\\ h=Int\left(y_{\max }-y_{\min }\right)/d_s+d_{dilate}\end{array}\right.$$

(10)

where $d_{dilate}$ represents the number of expansion pixels extending beyond the boundary of the projected point cloud range, and the pixel coordinate $\left(u_i,v_i\right)$ corresponding to the projected point in the image can be formulated as:

$$\left\{\begin{array}{l}{u}_i={\displaystyle \frac{x_i-x_{\min }}{d_s}}\hfill \\ v_i={\displaystyle \frac{y_i-y_{\min }}{d_s}}\hfill \end{array}\right.$$

(11)

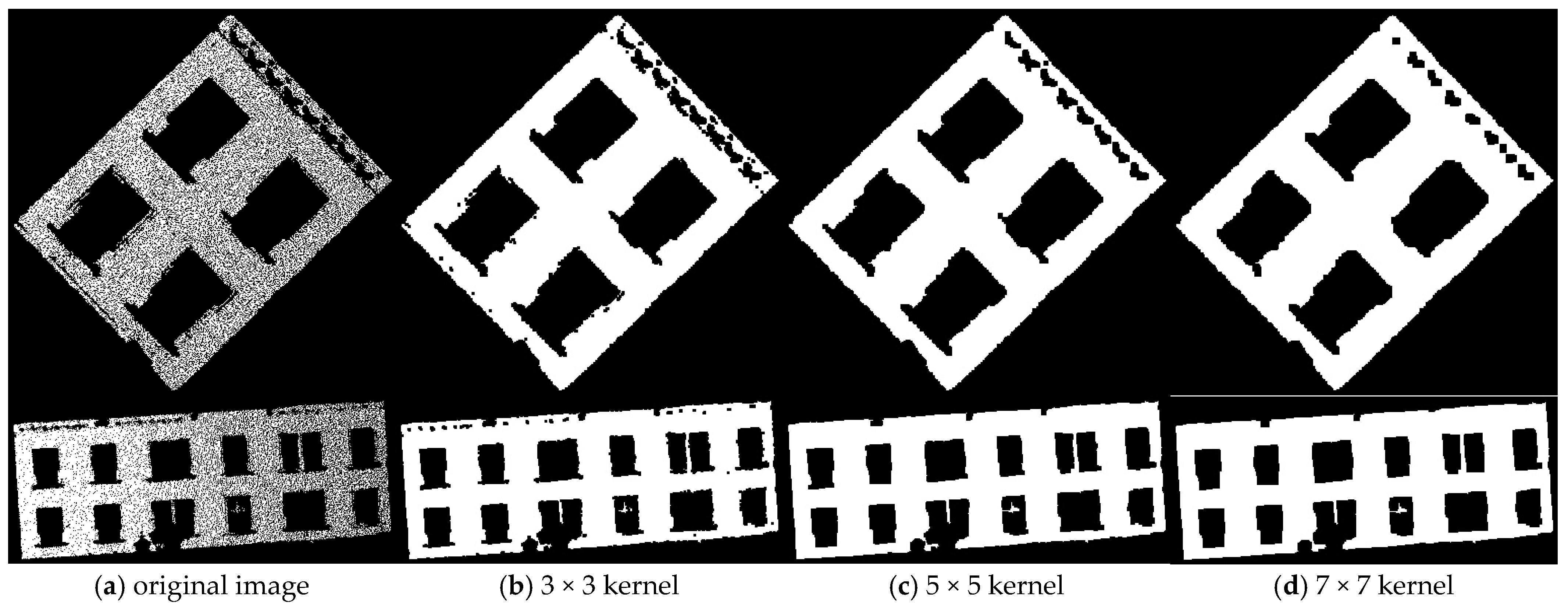
In the grayscale image, the gray values of pixels corresponding to the projected point cloud are set to 255, with all other regions set to 0. As shown in Figure 4a, due to the inherent sparsity of point clouds, there are small holes within the patch, potentially generating unnecessary contours or causing jagged edges along the boundaries, which can adversely affect subsequent 2D line fitting. To mitigate these impacts, the morphological closing processing is implemented through sequential dilation and erosion operations to fill small gaps and smooth contour edges. Specifically, the dilation operation uses a $k\times k$ convolution kernel to expand the bright regions of the image, effectively filling small salt-and-pepper noise within the highlighted areas. On the other hand, the erosion operation erodes the bright parts of the image and then reestablishes the original boundary.

In practice, increasing the size of the convolutional kernel tends to remove more internal salt-and-pepper noise, but this comes at the cost of blurring the image edges and potentially degrading critical boundary details, as illustrated in Figure 4b–d. To reduce the offset error, a $3\times 3$ convolutional kernel is applied for image preprocessing. The kernel is defined in the projected image coordinate system rather than in a fixed 3D metric space, and the physical size of each pixel is estimated adaptively by computing the 90th percentile of the point distance scales within each patch and scaling it by a factor of 0.75. This adaptive strategy ensures consistency between the kernel size and the local geometric scale of the point cloud patches.

3.2.2. Graph-Cut Method for Image Segmentation

In the graph-cut segmentation algorithm, the image is discretized as an undirected graph $G=\left(V,E\right)$, where each node $v_i$ corresponds to a pixel in the vertices set $V=\left(v_1,v_2,\mathrm{\dots },v_n\right)$, and the edge set $E$ defines the connectivity between nodes. The connectivity can be described with the 8-neighborhood relationship and the edge weights describing connectivity between two neighbors can be formulated as follows:

$$w\left(u,v\right)={\displaystyle \frac{‖\left(x_u,y_u\right)-\left(x_v,y_v\right)‖}{\sigma }}$$

(12)

where $\left(x_u,y_u\right)$ and $\left(x_v,y_v\right)$ represent the coordinates of pixels $u$ and $v$, respectively, and $\sigma$ is a smoothing factor that controls the decay rate of edge weights with respect to pixel distance. ${‖·‖}_2$ denotes the Euclidean distance used to compute weights based on spatial proximity in image grids, which ensures pixels with greater spatial distance maintain lower connectivity, thereby effectively reducing boundary redundancy.

Then, the cut-pursuit approach formulates an energy minimization function for region segmentation over the constructed weighted graph:

$$x^{*}=\arg \underset{x\in {\mathsf{\Omega }}_V}{\min }\left({\displaystyle \sum _{v\in V}f\left(y_v,x_v\right)}+{\displaystyle \sum _{\left(u,v\right)\in E}w\left(u,v\right){‖x_u-x_v‖}_0}\right)$$

(13)

where the loss function $f\left(y_v,x_v\right)$ measures the differences between the pixel label $x_v$ and the ground truth label $y_v$. The $l_0$ pseudo-norm ${‖x_u-x_v‖}_0$ represents the label differences between adjacent pixels, defined as:

$${‖x_u-x_v‖}_0=\left\{\begin{array}{l}0, \mathrm{if} x_u = x_v \\ 1, \mathrm{otherwise}\end{array}\right.$$

(14)

To promote consistency among adjacent pixels while accounting for discrepancies between predicted and actual labels, the loss function is formulated as a weighted sum of squared differences and smoothed Kullback–Leibler divergence (i.e., cross-entropy):

$$f\left(y_v,x_v\right)=w{\left(f\right)}_v\left[{\displaystyle \sum _{d\in D}m{\left(f\right)}_d{\left(x_{v,d}-y_{v,d}\right)}^2+\lambda {\displaystyle \sum _{d\in D}m{\left(f\right)}_{d}KL\left(p_d\left|\right|q_d\right)}}\right]$$

(15)

where $m{\left(f\right)}_d$ are weights on point coordinates and $\lambda$ balances the contributions between the squared difference term and the KL divergence term. The probability terms in the KL component are defined as the predicted label distribution $p_d$ and the prior distribution $q_d$, where $q_d$ is modeled as a smoothed categorical distribution to avoid overconfidence in class assignments. The squared differences focus on minimizing label discrepancies, while the KL divergence term $KL\left(p_d\left|\right|q_d\right)={\displaystyle {\sum }_d{p}_d\log \left(\frac{p_d}{q_d}\right)}$ promotes a smoother label distribution, thereby achieving a balance between accuracy and smoothness.

The cut-pursuit method iteratively solves the energy minimization problem, i.e., $\arg \underset{\xi \in {\mathsf{\Omega }}_V}{\min }F\left(x\right)$, to obtain constant connected components, which correspond to the optimal partitions of the vertices set $V$ in image graph $G=\left(V,E\right)$. The termination of the procedure is jointly governed by two hyperparameters, the maximum number of iterations fixed at 10 and the convergence tolerance threshold set to 0.01, which together constitute the stopping criterion. The workflow of the graph-cut segmentation is illustrated in Figure 5.

3.2.3. 2D/3D Line Segment Extraction

Once the image has been segmented, the widely used Potrace algorithm [60] is employed to obtain compact and closed boundary lines. This polygon-based tracing method initially creates a binary bitmap containing boundaries information, and then converts the boundaries of homogeneous regions into initial paths through contour tracing and path segmentation operations. Each of these paths are subsequently smoothed and simplified to generate vectorized paths, primarily consisting of sequences of straight lines or cubic Bézier curves to delineate the desired 2D contour lines with fixed endpoints.

With the pixel coordinates $\left(u_i,v_i\right)$ of endpoints of extracted 2D line segments, the 2D-3D back-projection is applied to calculate their corresponding 3D coordinates:

$$\left\{\begin{array}{l}\begin{array}{l}{P}_i=P_o+v_{x_i}+v_{y_i}\\ v_{x_i}=\left(\left(u_i-d_{dilate}\right)\cdot d_s+x_{\min }\right)\cdot u_x\end{array}\hfill \\ v_{y_i}=\left(\left(v_i-d_{dilate}\right)\cdot d_s+y_{\min }\right)\cdot u_y\hfill \end{array}\right.$$

(16)

where $\left(v_{x_i},v_{y_i}\right)$ denotes its coordinates under the local coordinate system of the fitted plane and $P_i$ is its corresponding 3D coordinates.

3.3. Three-Dimensional Line Optimization

3.3.1. Adjacent Patch Constraint

Due to the errors caused by 2D line segment fitting in the image, the same line segment extracted from the contours of different patches may appear as two disjoint 3D line segments when back-projected into 3D space. Therefore, this study proposes a patch-based optimization algorithm leveraging intersecting line constraints from adjacent patches, with the goal of refining the extracted line segments with patch planarity.

(1) Establishment of the contour information list for each patch: Traverse through each patch $P_a^i={\displaystyle \sum _{i=0}^t}{p}_a^i$, store contour points and their associated patch IDs in the mapping list ${\Gamma }_i$.

(2) Adjacent patch search for contour points: For extracted contour points, a spherical neighborhood with radius $5D_{scale}$ is established to search for neighboring contour points labeled with other patches. If more than two contour points share the same patch label, the corresponding patch label is recorded in the adjacent patch information list ${\Gamma }_i$.

(3) Patch intersection matrix $M_{\mathrm{intersect}}\in R^{C\times C}$ construction: For each patch ${\Gamma }_i$, traverse its adjacency information list ${\Gamma }_i$ and compute the intersection angle ${\alpha }_I$ between the direction vectors $n_I$ of ${\Gamma }_i$ and its neighboring patches, as formulated as follows:

$${\alpha }_I=\arccos \left({\displaystyle \frac{n_m\cdot n_a}{‖n_m‖‖n_a‖}}\right)$$

(17)

$$n_I\left(n_{x_I},n_{y_I},n_{z_I}\right)=n_m\left(n_{x_m},n_{y_m},n_{z_m}\right)\times n_a\left(n_{x_a},n_{y_a},n_{z_a}\right)$$

(18)

If ${\alpha }_I$ exceeds the threshold angle ${\alpha }_{adj}$, the two patches are considered to be effectively intersecting, and the corresponding intersection line ID is recorded in the elements $M_{ij}$ and $M_{ji}$ of the patch intersection adjacency matrix $M_{\mathrm{intersect}}$. Here, ${\alpha }_{adj}$ is defined as the adjacency angle threshold, which filters out intersections between nearly parallel patches. This prevents the generation of redundant or invalid intersection lines and ensures that only geometrically meaningful constraints are retained for subsequent Patch optimization.

(4) Construction of intersection line equations for adjacent patches: Depending on the point clouds within two adjacent patches, the intersection line structure is established, as shown in Figure 6. The intersection line structure is defined by the point $P_a$ on the line and the direction vector $n_I$ constructed between two adjacent patches $\left(R_{a_1},R_{a_2}\right)$, where the direction vector $n_I$ is derived from the cross product of the normal vectors of the two adjacent patches, as formulated as follows:

$$n_I=n_{a_1}\times n_{a_2}$$

(19)

And the point $P_a$ on the intersection line is determined as the midpoint between the projected points from each patch along the intersection direction. Let $P_1\in R_{a_1}$, $P_2\in R_{a_2}$, and $P_a$ can be formulated as follows:

$$\left\{\begin{array}{l}{P}_a={\left|P_1,P_2,n_I\right|}^{-1}\cdot \left|P_1,P_2,P_3\right|\\ P_1=P_{a_1}\cdot n_{a_1},P_2=P_{a_2}\cdot n_{a_2},P_3=P_a\cdot n_I\end{array}\right.$$

(20)

(5) Patch optimization using intersection lines: For each intersection line, we identify the adjacent patches and search within their line segment sets to find line segments collinear to the intersection line by evaluating their distance and direction. Specifically, Equation (19) represents the vector angle between the direction vector of the intersection line and that of a line segment within the corresponding patch, while Equation (20) defines the orthogonal distance between the projections of the two endpoints of the line segment onto the intersection line.

$${\cos }^{-1}\left(v_{L_I}\cdot v_{L_R}\right)<{\theta }_I$$

(21)

$$\left\{\begin{array}{l}\overrightarrow{P_{L_R^0}{P}_{L_I}}-\left|v_{L_I}\cdot \overrightarrow{P_{L_R^0}{P}_{L_I}}\right|\cdot v_{L_I}<d_I\hfill \\ \overrightarrow{P_{L_R^1}{P}_{L_I}}-\left|v_{L_I}\cdot \overrightarrow{P_{L_R^1}{P}_{L_I}}\right|\cdot v_{L_I}<d_I\hfill \end{array}\right.$$

(22)

For line segments within a patch that satisfy both constraints, their direction vectors are aligned with that of the intersection line, thereby optimizing the line segments leveraging the planar properties of patches.

3.3.2. Structural Collinearity Constraint

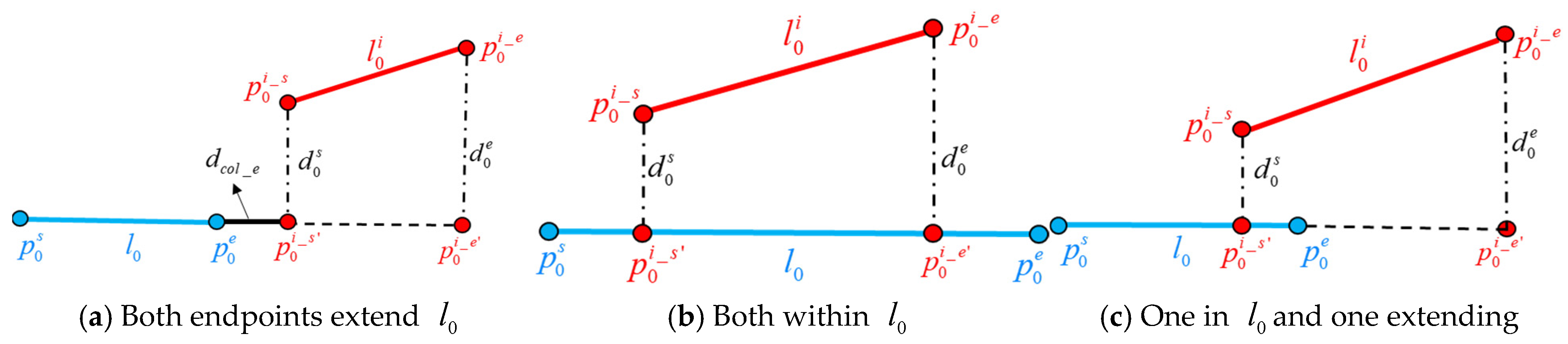
The aforementioned line segment optimization algorithm is focused on boundary line refinement for lines associated with adjacent patches. However, discontinuity and non-collinearity still occur in the extraction of some non-intersecting line segments. To address this, a 3D line segment optimization method utilizing structural collinearity is proposed, with the specific steps detailed below:

(1) The line segments from all patches are sorted in descending order of length to aggregate a three-dimensional line segment set $L_{col}$, which records the direction vector, endpoint coordinates, and length information of each segment.

(2) By traversing $L_{col}$, starting with the first segment $l_0$, the directional angle between $l_0$ and the remaining segments is calculated. We define $L_0=\left\{l_0^0,l_0^1,\dots ,l_0^i\right\}$ as the collinearity candidate set. If the angle is smaller than the collinearity threshold ${\vartheta }_{col }$, the line segment is added to $L_0$.

(3) Traverse the line segments in $L_0$, project the two endpoints of $l_0^i$, i.e., $p_0^{i\_s}$ and $p_0^{i\_e}$, onto the $l_0$ to obtain the projection points $p_0^{i\_s\prime }$ and $p_0^{i\_e\prime }$, and calculate the corresponding projection distances $d_0^s$ and $d_0^e$ to evaluate their alignment. If both projection distances are smaller than the collinearity distance threshold $d_{col}$, $l_0^i$ and $l_0$ are considered to belong to the same contour and entail merging operation.

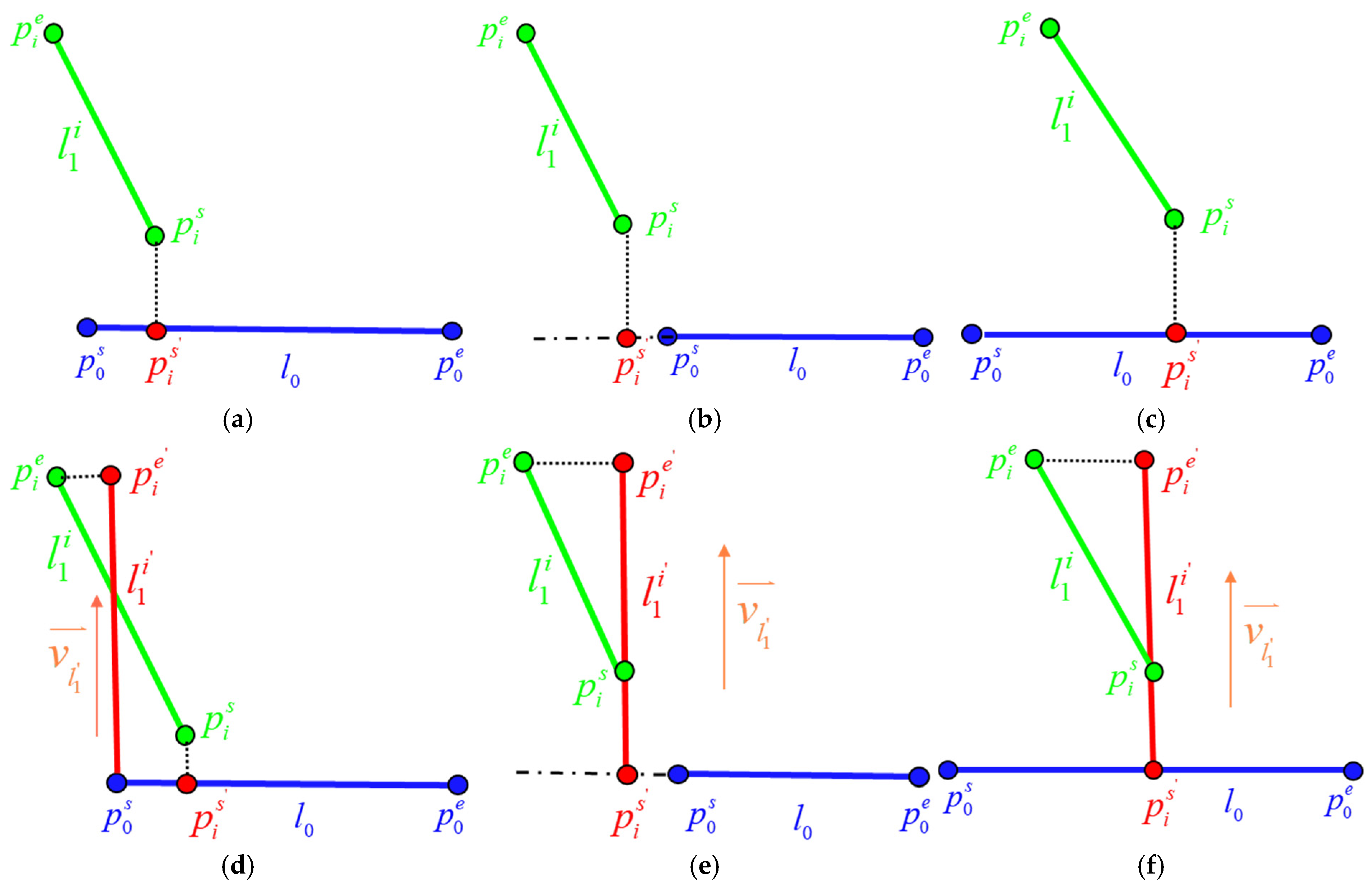
(4) The endpoints of the merged line segment are determined by position relationship between the projected endpoints of $l_0^i$ and the endpoints of $l_0$. As illustrated in Figure 7, this relationship can generally be classified into three types:

(1) The first type of relative positional relationship occurs when both projected endpoints lie on the extension of $l_0$, which can result in two scenarios: the endpoints being on the extensions on opposite sides of $l_0$ or on the same side of the extension of one endpoint. Due to the sorting order by length, projected points cannot fall on opposite extensions in practice. Therefore, only the case where the projected points lie on the same side of the extension of one endpoint is considered. Generally, the relative position of projected points is determined by the direction vectors between the projected point and the endpoints of $l_0$, with the angle being 0° when the projected point lies on the extension of $l_0$ and 180° when it lies within $l_0$, which can be formulated as follows:

$$\left\{\begin{array}{l}{T}_s=\left(\overrightarrow{P_0^s{P}_0^{i\_s^{\prime }}}\cdot \overrightarrow{P_0^e{P}_0^{i\_s^{\prime }}}>0\right)\hfill \\ T_e=\left(\overrightarrow{P_0^s{P}_0^{i\_e^{\prime }}}\cdot \overrightarrow{P_0^e{P}_0^{i\_e^{\prime }}}>0\right)\hfill \end{array}\right.$$

(23)

$T_s$ and $T_e$ represent the relative position identifiers of the projected points, where 1 indicates that the point lies on the extension, and 0 indicates that the point lies within the segment. When both $T_s$ and $T_e$ are 1, further evaluation is performed to check if the distance between $l_0$ and the projected segment $l_0^{i\prime }$ is smaller than the collinearity extension distance threshold $d_{col\_e}$. If this condition is met, the endpoints of the longest line segment among the four endpoints are selected as the endpoints of the collinearly optimized line segment.

(2) The second type of relative positional relationship occurs when both endpoints lie within $l_0$, as shown in Figure 7b. In this case, $l_0^i$ is merged into $l_0$, and the endpoints of $l_0$ are retained.

(3) The third type of relative positional relationship occurs when one projected endpoint lies on the extension of $l_0$, and the other lies within $l_0$, as shown in Figure 7c. In this case, the collinearly optimized segment is formed by using the projected point $p_0^{i\_s\prime }$ on the extension of $l_0$ and the other endpoint $p_0^s$ of $l_0$ as the new endpoints, denoted as $\stackrel{\rightharpoonup }{P_1^{s\prime }{P}_0^s}$.

(4) Repeat steps (2) and (3) until $L_{col}$ is empty.

3.3.3. Structural Orthogonality Constraint

For line segment pairs exhibiting spatial orthogonality, a structural orthogonality constraint is applied to achieve angle correction and contour closure. The optimization algorithm assumes that longer segments are more reliably extracted, and in a pair of line segments that satisfy the orthogonality condition, the longer segment serves as the reference, with the shorter one adjusted to preserve orthogonality.

(1) Similarly, the line segments optimized for collinearity are recalculated for their lengths and sorted by length to form a new orthogonal line segment list $L_{ortho}$, with direction vector, endpoint coordinates, and length information recorded.

(2) Traverse the line segment list $L_{ortho}$, starting with the first segment $l_0$ as an example. For each remaining segment in $L_{ortho}$, calculate the angle between the direction vector of $l_0$ and each of the remaining segments in $L_{ortho}$. If the angle is greater than the orthogonality angle threshold ${\vartheta }_{ortho}$ and smaller than 90°, add the segment to the candidate list of collinear segments $L_1=\left\{l_1^0,l_1^1,\mathrm{\dots },l_1^i\right\}$.

(3) Traverse $L_1$ and calculate the orthogonal distance between the line segments. For example, as shown in the relative position of the line segments in Figure 8, $d_1^0$ represents the orthogonal distance from the closest endpoint of $l_1^i$ to $l_0$, while $d_0^1$ represents the orthogonal distance from the closest endpoint of $l_0$ to $l_1^i$.

Figure 9 illustrates the relative position relationships of the line segments before and after optimization while $d_1^0$ satisfies the orthogonality distance threshold condition, i.e., $d_1^0<d_{s-ortho}$:

(1) $d_0^1<d_{s-ortho}$ and the projected point of $l_1^i$ within $l_0$. As shown in Figure 9a, since $l_0$ is the main reference line, the endpoint $p_0^s$ of $l_0$ closest to $l_1^i$, is taken as one endpoint of optimized line. At the same time, the direction vector of $l_1^i$ is rotated within the plane spanned by the direction vectors of $l_1^i$ and $l_0$, such that the optimized line segment $l_1^{i^{\prime }}$ satisfies the orthogonality constraint with respect to $l_0$. The resulting line segment $l_1^{i^{\prime }}$ (Figure 9d) can be expressed in parametric form as follows:

$$\left\{\begin{array}{l}{l}_1^{i^{\prime }}:{\displaystyle \frac{X-X_{l_1^{i^{\prime }}}}{v_x^{\prime }}}={\displaystyle \frac{Y-Y_{l_1^{i^{\prime }}}}{v_y^{\prime }}}={\displaystyle \frac{Z-Z_{l_1^{i^{\prime }}}}{v_z^{\prime }}}\\ \stackrel{\rightharpoonup }{v_{l_1^{i^{\prime }}}}\left(v_x^{\prime },v_y^{\prime },v_z^{\prime }\right)=\left(\stackrel{\rightharpoonup }{v_0}\times \stackrel{\rightharpoonup }{v_1}\right)\times \stackrel{\rightharpoonup }{v_0}\\ P_1^{\prime }\left(X_{l_1^{i^{\prime }}},Y_{l_1^{i^{\prime }}},Z_{l_1^{i^{\prime }}}\right)=P_0-P_1\cdot \stackrel{\rightharpoonup }{v_0}\end{array}\right.$$

(24)

where $\stackrel{\rightharpoonup }{v_{l_1^{\prime }}}$ represents the direction vector of the optimized line segment $l_1^{i^{\prime }}$, is one endpoint of it. The line equation is then derived in point-vector form, and by calculating the projection of the other endpoint of the original $d_1^0<d_{s-ortho} \&\&d_0^1<d_{s-ortho}$ onto $d_1^0<d_{s-ortho} \&\&d_0^1<d_{s-ortho}$, the spatial coordinates of both endpoints of $d_1^0<d_{s-ortho} \&\&d_0^1<d_{s-ortho}$ can be obtained.

(2) $d_0^1<d_{s-ortho}$ and the projected point of $l_1^i$ on the extension of $l_0$. By replacing the corresponding endpoint of $d_1^0<d_{s-ortho} \&\&d_0^1<d_{s-ortho}$ with its projection point, the direction vector of the optimized line segment $d_1^0<d_{s-ortho} \&\&d_0^1<d_{s-ortho}$ can be derived using the same calculation as for $\stackrel{\rightharpoonup }{v_{l_1^{\prime }}}$ in step (1). Additionally, $l_0$ is also optimized by replacing the closest endpoint with that of $d_1^0<d_{s-ortho} \&\&d_0^1<d_{s-ortho}$, achieving the closure of the two orthogonal line segments within $d_{s-ortho}$, as shown in Figure 9b,e.

(3) $d_0^1>d_{s-ortho}$ and the projected point of $l_1^i$ within $l_0$. This situation applies when the length of the main reference line $l_0$ is much greater than that of $d_1^0<d_{s-ortho} \&\&d_0^1<d_{s-ortho}$, and the nearest endpoint of $d_1^0<d_{s-ortho} \&\&d_0^1<d_{s-ortho}$ is far from both endpoints of $l_0$. In this case, only $l_1^i$ performs line optimization, including both segment closure and direction orthogonality optimization, as shown in Figure 9c,f.

(4) Repeat step (2) and (3) until $L_{ortho}$ is empty.

3.4. Evaluation Metrics and Parameters Configuration

To quantitatively evaluate 3D line extraction, earlier studies [61,62] adopted precision and recall to estimate the likelihood that an extracted segment belongs to a ground truth segment. Precision is defined as the proportion of points on the extracted segments that lie within a predefined distance threshold from any ground truth segment. Recall is defined as the proportion of points on the ground truth segments that lie within the same threshold from any extracted segment. However, these two metrics are evaluated based on the total length of predicted or ground truth segments, which primarily provide an overall assessment but do not account for the actual lengths of the extracted segments.

To achieve a more fine-grained and intuitive accuracy metric, this study further refines the precision metric at the level of individual line segments. Specifically, each extracted segment is projected onto the corresponding ground truth segment, and the ratio of the overlapping length is used to quantify the matching accuracy. This design enables a more localized and quantitative assessment of the extraction quality. 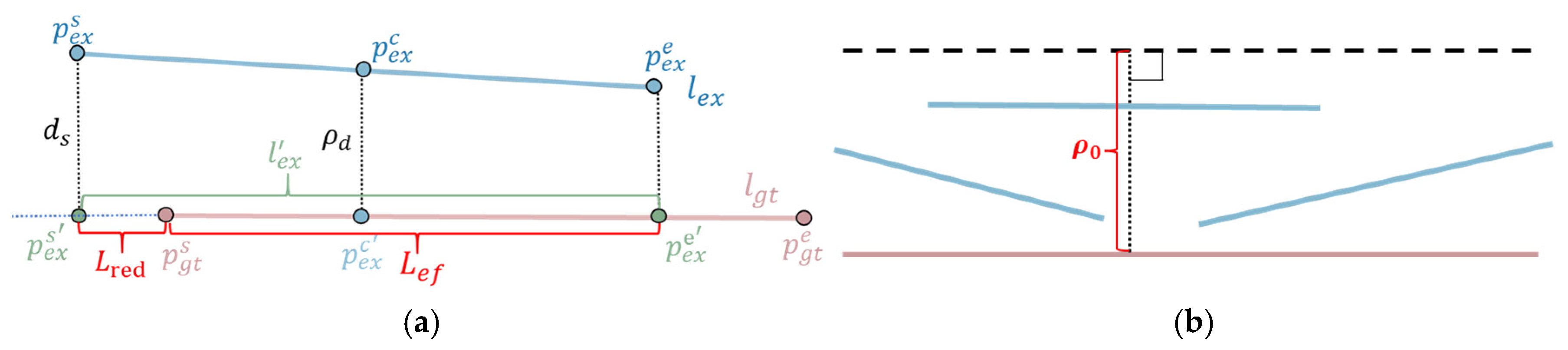The relative geometric overlap between each extracted and ground truth segment is illustrated in Figure 10a: the manually delineated segment (red) served as ground truth is compared with the automatically extracted line segment (blue), and three indicators are computed to describe their coincidence.

(1) Average distance ${\rho }_d$: The mean of the orthogonal distances from both endpoints of one line segment to the other line segment:

$${\rho }_d={\displaystyle \frac{d_1^s+d_1^e}{2}}$$

(25)

(2) The effective length $L_{ef}$ is defined as the length of the projected part of the extracted segment $l_{ex}$ onto the corresponding ground truth segment $l_{gt}$, where the average distance between them is below a predefined threshold. This is computed by projecting the endpoints of $l_{ex}$ onto $l_{gt}$, and calculating the geometric Boolean intersection between the resulting projected segment $l_{ex}^{\prime }$ and $l_{gt}$:

$$L_{ef}=l_{gt}\cap l_{ex}^{\prime }$$

(26)

(3) The redundant length $L_{red}$, representing the non-overlapping portion of the projected segment, is computed as the difference between the total projected length $l_{ex}^{\prime }$ and the valid (overlapping) length $L_{ef}$:

$$L_{\mathrm{red}}=l_{ex}^{\prime }-L_{ef}$$

(27)

According to the definitions of effective length and redundant length, this study introduces two accuracy metrics, completeness and redundancy, to evaluate the similarity between the extracted line segments and the ground truth line segments. Specifically, completeness measures the proportion of the total effective length of the projected parts of all extracted line segments to their corresponding actual segments relative to the total length of all ground truth segments. redundancy, in contrast, is defined as the ratio of the total redundant length of all extracted segments to the total ground truth length, as formulated as follows:

$$completeness= {\displaystyle \frac{{\displaystyle \sum _{i=0}^n}\left(L_{GT}^i\cap {\displaystyle \sum _{j=0}^t}{L}_{DT}^{ij}\right)}{{\displaystyle \sum _{i=0}^n}{L}_{GT}^i}}$$

(28)

$$redundancy={\displaystyle \frac{{\displaystyle \sum _{i=0}^m}\left({\displaystyle \sum _{j=0}^t}{L}_{DT}^{ij}-\left(L_{GT}^i\cap {\displaystyle \sum _{j=0}^t}{L}_{DT}^{ij}\right)\right)}{{\displaystyle \sum _{i=0}^n}{L}_{GT}^i}}$$

(29)

where $L_{GT}^i$ denotes a ground truth line segment, and ${\displaystyle \sum _{j=0}^t}{L}_{DT}^{ij}$ refers to the set of extracted line segments associated with $L_{GT}^i$. It is worth noting that the number of extracted line segments often exceeds the number of ground truth segments, which may result in a redundancy value greater than 1. In general, a larger total effective length indicates higher completeness, while a smaller total redundant length corresponds to lower redundancy, both of which reflect improved performance in 3D line segment extraction.

Due to limitations in data quality and extraction accuracy, a single ground truth segment may be fragmented into multiple discontinuous extracted segments, as shown in Figure 10b. Therefore, when computing completeness and redundancy, it is necessary to consider this one-to-many correspondence. The evaluation procedure can be summarized as follows:

(1) Assignment of extracted segments to ground truth segments: All ground truth segments are first assigned unique identifiers. Each extracted segment is then compared to all ground truth segments by calculating the minimum average distance. If this distance is smaller than a predefined threshold ${\rho }_0$, the corresponding ground truth segment is added to the candidate list of extracted segments. The segment in the candidate list with the smallest average distance is assigned as the corresponding ground truth, and its label is attached to the extracted segment. If no ground truth segment satisfies the threshold, the extracted segment is considered redundant and added to the redundancy list.

(2) Collection of candidate sets for each ground truth segment: Using the assignments from Step (1), a candidate list of extracted segments is collected for every ground truth segment. The segments in each list are sorted in descending order of length.

(3) Calculation of effective and redundant lengths: For each ground truth segment, its sorted candidate list is traversed to compute the projection of each extracted segment onto the ground truth segment. Geometric Boolean operations are then used to calculate the effective and redundant lengths. The cumulative effective length and cumulative redundant length for the ground truth segment are obtained by summing the results over all corresponding extracted segments.

(4) Calculation of completeness and redundancy: The overall completeness is measured by the ratio of the total effective length to the total length of all ground truth segments. Similarly, the overall redundancy is defined as the ratio of the total redundant length (including both matched and unmatched extracted segments) to the total ground truth length.

Furthermore, considering that most edge extraction algorithms employ recall and precision as the primary metrics for evaluating extraction performance, where the confusion matrix can be quantitatively derived from the edge point sets to calculate F1-scores. this study extends the definition to line segment extraction. To avoid the influence of edge point sampling resolution, recall is defined as the ratio between the total length of ground truth line segments successfully matched and the total length of all ground truth line segments. Precision is defined as the ratio between the total length of successfully matched extracted line segments and the total length of all extracted line segments.

$$Precision={\displaystyle \frac{{\displaystyle \sum _{i=0}^m}{L}_{matched}^{DT\_i}}{{\displaystyle \sum _{i=0}^n}{L}_{DT}^i}}$$

(30)

$$Recall={\displaystyle \frac{{\displaystyle \sum _{i=0}^m}{L}_{matched}^{GT\_i}}{{\displaystyle \sum _{i=0}^n}{L}_{GT}^i}}$$

(31)

Based on these two metrics, a length-weighted F1-score is calculated to cross-validate the effectiveness of our proposed completeness and redundancy, which is formulated as follows:

$$F1= {\displaystyle \frac{2\cdot Precision\cdot Recall}{Precision+Recall}}$$

(32)

4. Experiments and Analysis

We evaluate the effectiveness of the proposed method through experiments in both indoor and outdoor environments, focusing on 2D line extraction and structural constraints for 3D line regularization. Quantitative evaluations were subsequently performed using accuracy metrics that account for the lengths of the extracted line segments in indoor environments. Additionally, the method was applied to outdoor scenes to demonstrate its generalization to large-scale and complex building structures.

4.1. Dataset Deployment

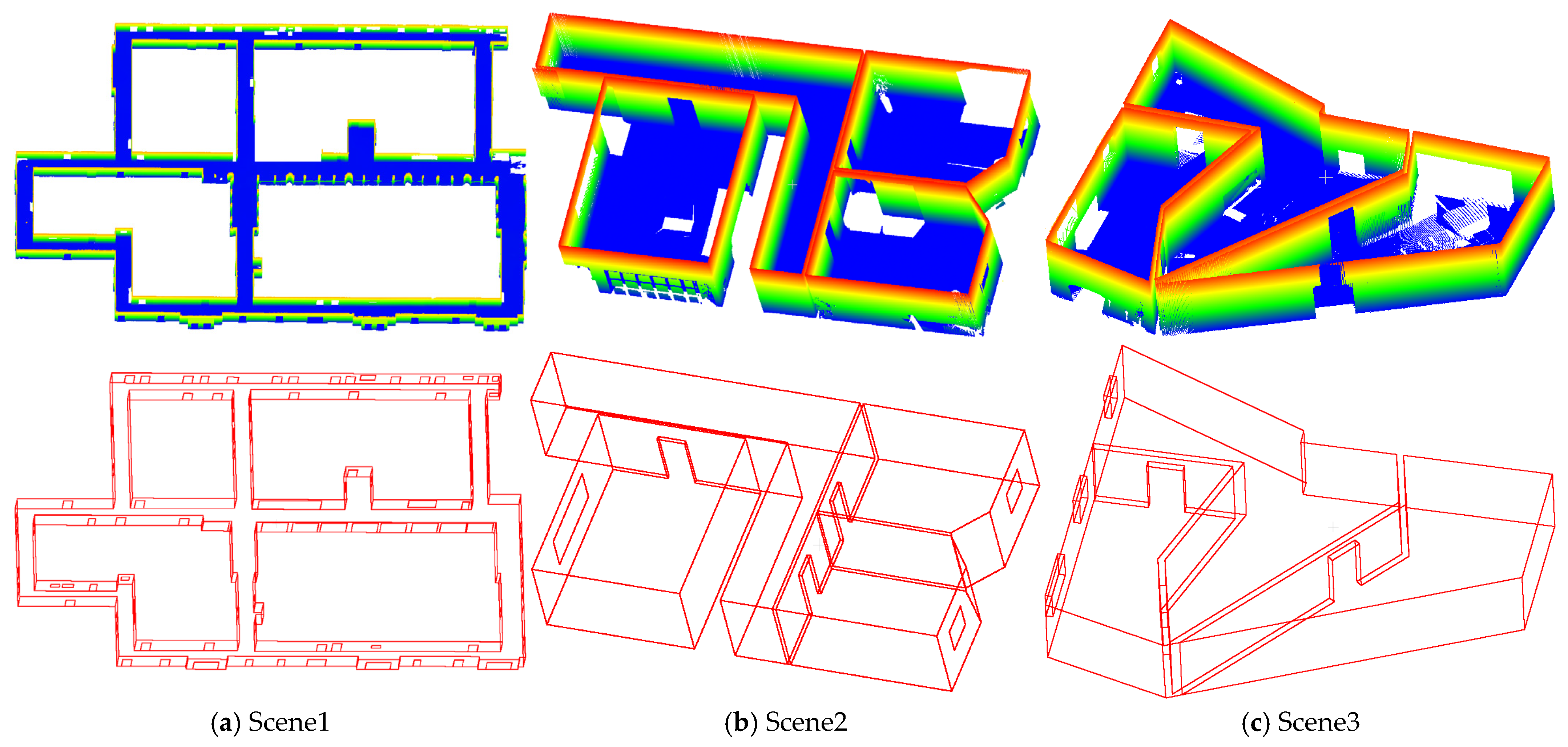
To quantitatively analyze line feature extraction, three indoor scenes were selected from the S3DIS [63] and ETH-UZH benchmarks, from which BIM models were reconstructed and their corresponding line segment sets were manually delineated and subsequently regarded as ground truth segments for evaluation, as summarized in

Table 1. Information of three indoor scenes (point clouds, BIMs and line segments).

Data Benchmark	Scene Name	Number of Points	Extracted Line Amount	Total Segment Length (m)
S3DIS	Scene1	1,402,988	595	1723.31
ETH-UZH	Scene2	1,919,351	225	252.21
	Scene3	3,861,241	231	397.67

and illustrated in Figure 11.

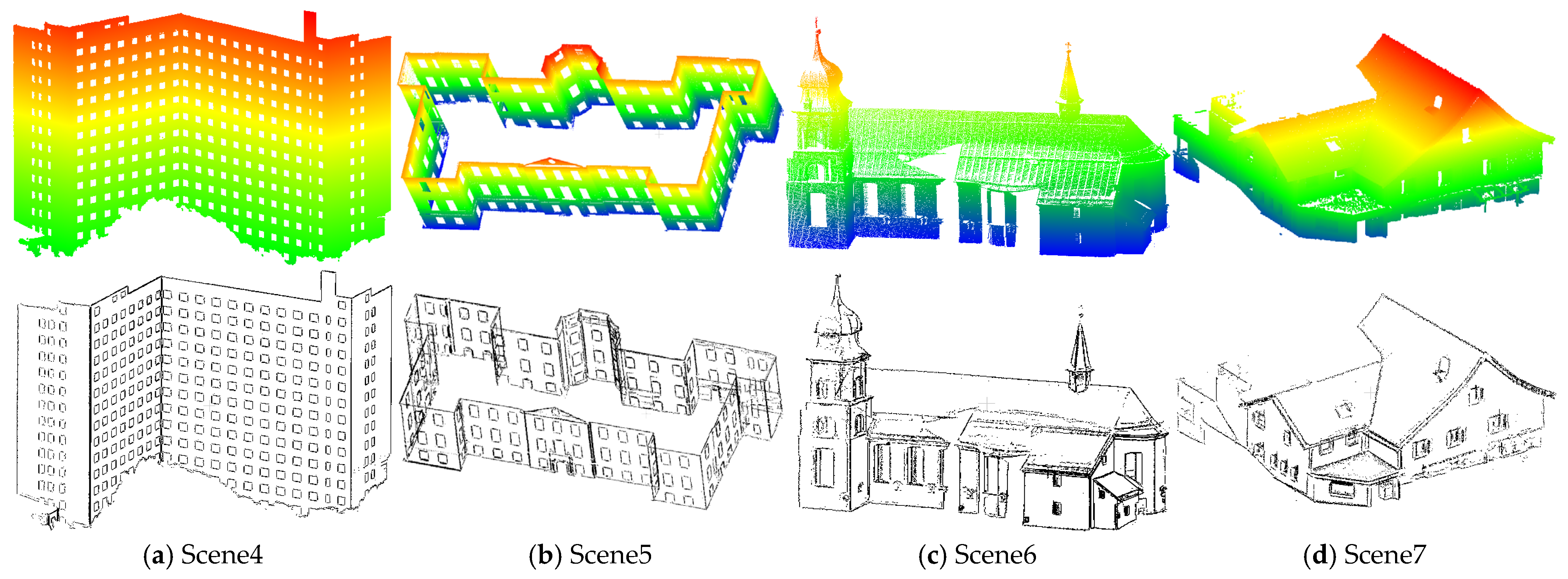
To further validate the applicability of the proposed method in outdoor environments, we applied it to four scenes with building façades, including Scene4 acquired using a Leica P50 terrestrial laser scanner, Scenes5 and Scene6 from the Semantic3D [64] benchmark, and Scene7 from the Oxford-Spires [65] benchmark, as shown in Figure 12. Compared to indoor environments, the large scale and frequent occlusions in outdoor scenes often result in more severe data incompleteness, and the manual extraction of line features in such complex scenes is highly time-consuming and labor-intensive. Given these challenges, we adopt point edges extracted using a gradient-based edge detector [66] as the reference ground truth and conduct comparative experiments on outdoor scenes, with the primary emphasis placed on the qualitative analysis of different methods.

4.2. Quantitative Analysis

To comprehensively evaluate the effectiveness and applicability of the proposed method, we conduct experiments focusing on three aspects: patch segmentation, patch-level line extraction, and 3D line extraction and optimization. Specifically, in the patch segmentation stage, five parameters are involved: ${\theta }_n$, $d_{ortho}$, $d_{proj}$, ${\theta }_{p\_n}$ and $d_{p\_ortho}$. Among these, $d_{ortho}$, $d_{proj}$ and $d_{p\_ortho}$ are adaptively adjusted according to the point density scale $d_s$, enabling the method to accommodate different scene resolutions, and the selection of parameters ${\theta }_n$ and ${\theta }_{p\_n}$. In patch-level line extraction stage, its effectiveness primarily depends on the quality of grayscale images and 2D edge detection performance. During the 3D line optimization stage, we consider three sets of parameters: adjacency parameters (${\theta }_I$ and $d_I$), collinearity parameters (${\vartheta }_{col }$, $d_{col}$ and $d_{col\_e}$) and orthogonality parameters (${\vartheta }_{ortho}$ and $d_{s-ortho}$).

In the quantitative experiments, we set $d_{col\_e}$ to 0.25 m and analyze completeness and redundancy by varying one parameter at a time while keeping others constant. The line distance threshold ${\rho }_0$ for accuracy evaluation is set to 0.35 m. Furthermore, we gradually increase ${\rho }_0$ from 0.15 m to 0.5 m, which produces completeness and redundancy curves as functions of ${\rho }_0$. We then calculate the average completeness (AComp, in %) and average redundancy (ARed, in %) over this range to comprehensively assess overall quality. Finally, with the optimal parameter combination, we conduct comparative experiments with existing methods and extend to outdoor scenes to verify its applicability and generalizability in qualitative experiments.

4.2.1. Comparative Analysis of Different 2D Line Extraction Methods

Prior to 2D line segment extraction, patch segmentation is performed to define the fundamental processing units. The number and quality of the resulting patches are primarily influenced by the angular threshold applied during the region’s growing and merging processes. To investigate its impact, we tested four angle thresholds (5°, 10°, 15°, and 20°) and evaluated their influence on patch structure and subsequent line extraction performance.

Table 2. Patch segmentation results under different angle thresholds.

Angle (°)	Metrics	Scene1	Scene2	Scene3	Angle (°)	Metrics (%)	Scene1	Scene2	Scene3
5	Drop rate (%)	14.32	4.96	3.03	15	Drop rate (%)	7.24	4.24	2.61
	Cluster amount	236	56	50		Cluster amount	316	56	45
10	Drop rate (%)	9.06	4.58	2.79	20	Drop rate (%)	6.24	3.99	2.50
	Cluster amount	301	56	45		Cluster amount	338	57	45

presents patch segmentation results under different angle thresholds. The Scene2 and Scene3 feature clear and simple planar structures, making them less sensitive to variations in the angular threshold during region growing and merging. In contrast, the large-scale Scene1, which contains numerous and diverse planar structures, is more susceptible to the effects of angle constraints. When the threshold is set too low, over-segmentation tends to occur during region growing, resulting in multiple fragmented point cloud clusters. In the subsequent merging stage, clusters containing very few points are often identified as noise and discarded, which leads to the loss of important structural information and fewer patches available for subsequent line extraction. Conversely, a higher threshold reduces cluster loss but tends to produce fragmented patches and raises the risk of erroneously merging patches from different planes, which may cause structural boundaries to be missed during 2D line extraction. Hence, a threshold of 15° achieves the best trade-off between patch integrity and noise suppression, yielding the most complete and accurate extraction of valid line segments, as shown in Figure 13.

Then, we perform a 3D-to-2D spatial projection to establish a local image coordinate system for each patch. Specifically, the physical size of each pixel in the projection is not fixed but estimated in a robust and adaptive manner. We compute the 90th percentile of the distance scale parameter among points within a patch and scale it by a factor of 0.75 to define the representative pixel size. Consequently, the kernel size corresponds to this adaptive pixel resolution for each patch rather than a uniform metric size across the entire point clouds. To further quantify the variations across different scenarios, we computed the mean and standard deviation of the representative pixel size in meters for all patches within each scene, as presented in

Table 3. Mean ± standard deviation of representative pixel size per scene (m).

Scene ID	Scene1	Scene2	Scene3	Scene4	Scene5	Scene6	Scene7
Mean pixel size (m)	0.035	0.014	0.015	0.051	0.05	0.037	0.04
Std pixel size (m)	0.002	0.003	0.004	0.019	0.014	0.02	0.016

. The results indicate a clear distinction between indoor and outdoor datasets. For indoor scenes (Scene1–3), the representative pixel sizes remain relatively small and consistent, ranging from 0.014 ± 0.003 m to 0.035 ± 0.002 m. This stability is attributed to the compact spatial extent and the presence of regular and simple planar structures in indoor environments. In contrast, outdoor scenes (Scene4–7) exhibit larger pixel sizes and higher variability, with values spanning from 0.037 ± 0.020 m to 0.051 ± 0.019 m. The increased pixel size reflects the broader coverage of outdoor areas and their diverse geometric compositions, including irregular or large-scale structural elements. These findings demonstrate that the adaptive projection strategy effectively preserves local resolution consistency across heterogeneous indoor and outdoor scenarios, while ensuring the geometric fidelity required for robust line extraction.

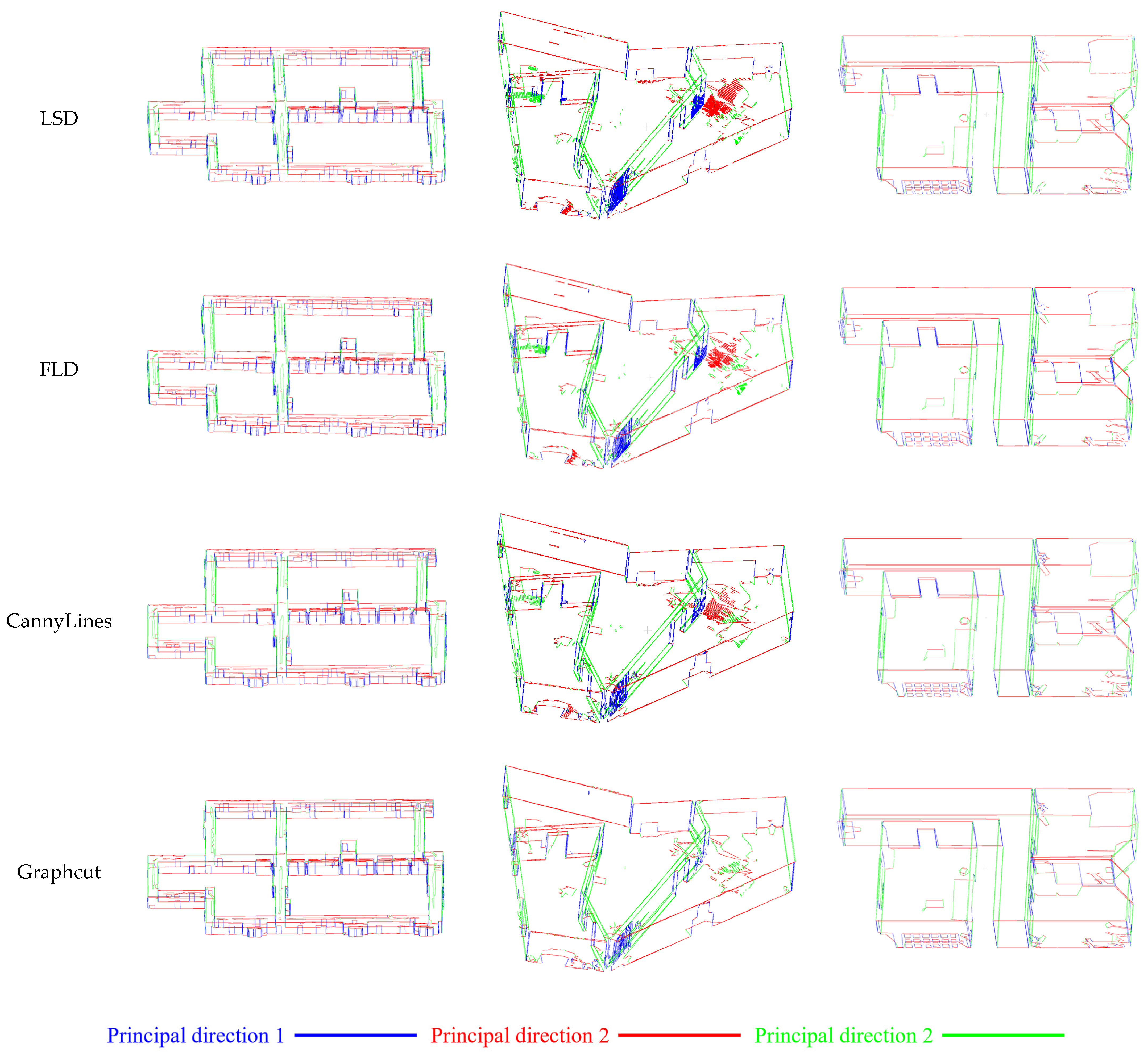
To evaluate their extraction performance, several commonly used 2D line extraction methods are compared, including LSD [54], FLD [55], CannyLines [56], and Graph-cut algorithm adopted in this study. As shown in

Table 4. Evaluation metrics of extracted 3D line segments in different 2D line detection algorithms.

Scene Name	Algorithm	Amount of Line Segments	Completeness (%)	Redundancy (%)
Scene1	LSD	3367	81.8	127.2
	FLD	2515	82.5	128.5
	CannyLines	1838	84.9	132.5
	Graph-cut (Ours)	2330	86.2	163.8
Scene2	LSD	859	84.9	119.5
	FLD	615	84.5	122.7
	CannyLines	584	85.7	131.4
	Graph-cut (Ours)	820	86.9	182.2
Scene3	LSD	2206	87.8	184.9
	FLD	1744	88.6	169.6
	CannyLines	1303	91.0	207.9
	Graph-cut (Ours)	2498	90.9	317.5

and Figure 14, the LSD and FLD algorithms generate numerous line segments but exhibit low completeness and high redundancy. This is primarily due to the fragmentation of single structural lines into multiple segments. In contrast, the CannyLines algorithm extracts fewer segments and achieves quite improvements in accuracy, indicating better line continuity. However, some disconnections, especially among orthogonal lines, are still observed. The Graph-cut algorithm further enhances the continuity and closure of 2D segments by explicitly optimizing segment connectivity.

Moreover, sparse linear point distributions may lead to spurious line detections. Our proposed method, which emphasizes the integrity of closed structural lines, demonstrates enhanced robustness against density variations introduced by linear scanning. This advantage is further reflected in the reconstructed 3D scenes obtained by reprojecting the extracted 2D lines, as shown in Figure 15. The extracted line segments are rendered in red, blue and green according to the three principal directions of all building point clouds derived from PCA algorithm.

4.2.2. Comparative Analysis of Structural Geometry Regularization Parameters

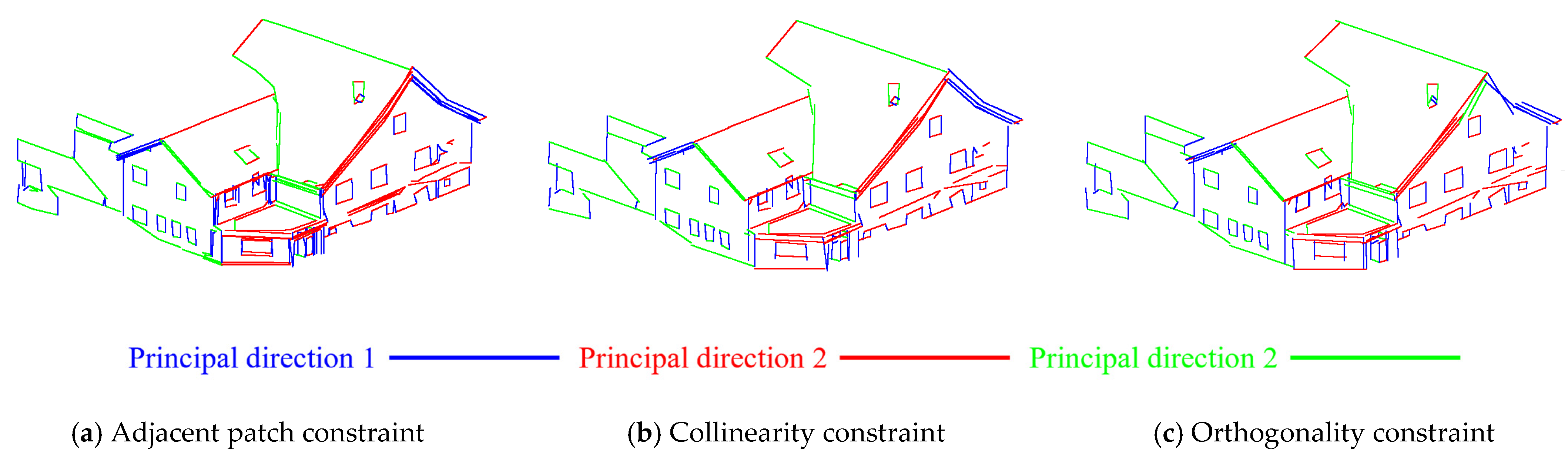
To optimize the extraction under architectural structural constraints, we progressively determine the parameters for adjacent patch constraint, collinearity constraint, and orthogonality constraint. The adjacent patch constraint leverages the intersection lines between patches on different planes to correct contour deviations introduced by 2D line extraction errors, effectively reducing angular deviations in the resulting 3D lines. 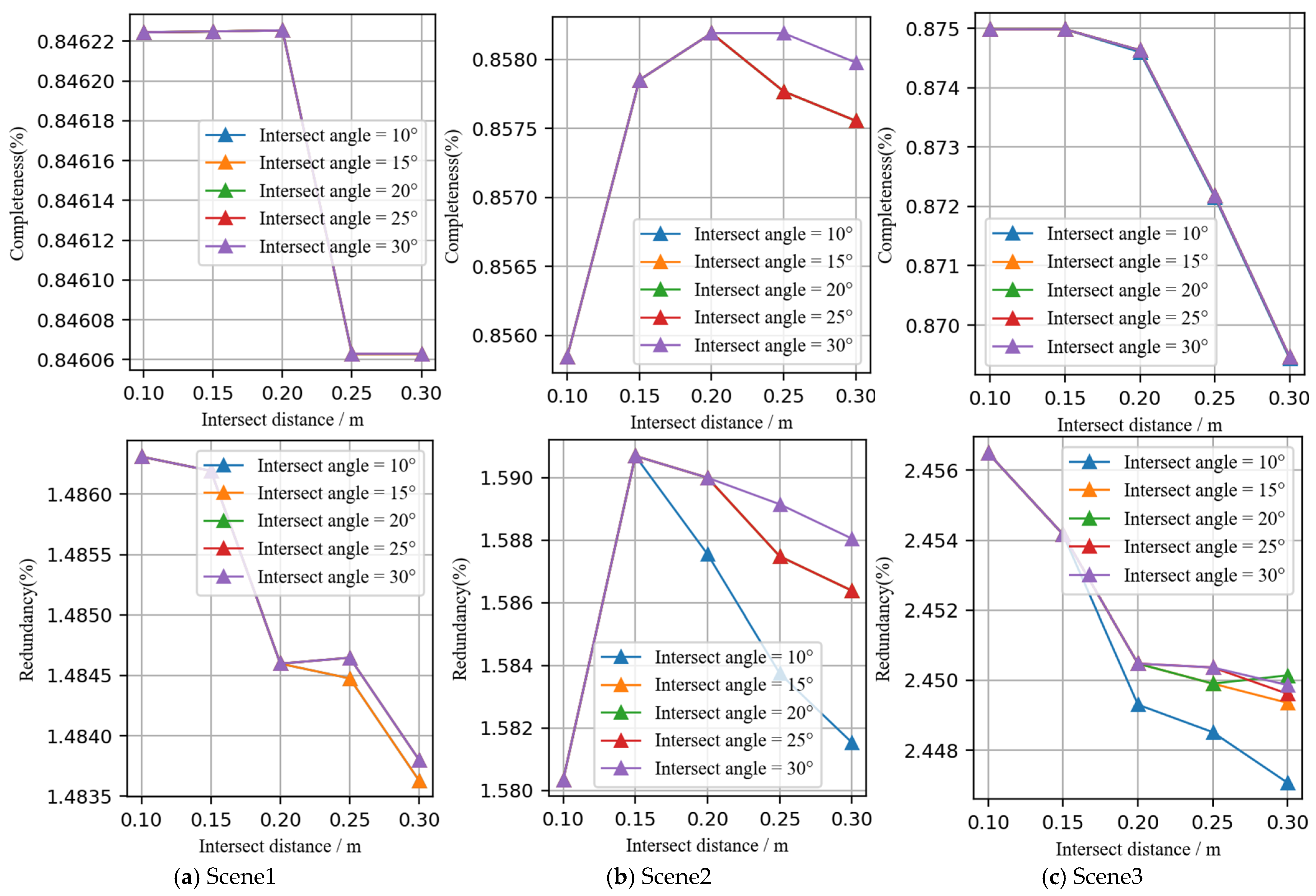Figure 16 illustrates the completeness and redundancy curves under varying angle thresholds and distance thresholds for the adjacent patch constraint. As the distance threshold $d_I$ increases, both Scene1 and Scene2 achieve peak completeness at a distance threshold of 0.2 m. Beyond this point, completeness tends to decline across all three scenes. This drop may be attributed to distant line segments being incorrectly adjusted to align with adjacent patch intersection lines, thereby distorting their actual directions. On the other hand, the angle threshold ${\theta }_I$ has no significant impact on completeness, but a lower redundancy is consistently observed when ${\theta }_I={10}^{°}$. To ensure high completeness and low redundancy, we select $d_I$ = 0.2 m, ${\theta }_I$ = 10°, as the optimal values for the adjacent patch constraint in subsequent collinearity parameter analysis.

Similarly, Figure 17 presents the completeness and redundancy curves under different collinearity angle thresholds (10°, 20°, 30°, and 40°), with respect to the collinearity distance threshold $d_{col}$. Due to the patch-based line extraction strategy adopted in this study, a single geometric line in 3D space may correspond to multiple line segments associated with different patches. As a result, after applying the collinearity constraint, these collinear segments are merged, significantly reducing redundancy to below 0.8. Moreover, since the collinear patch contours have already been corrected during the adjacent patch constraint stage and all three test scenes exhibit strong architectural directional regularity, the collinearity constraint causes no substantial changes to line segments within patches. However, as the distance threshold increases, particularly beyond the typical wall thickness between adjacent rooms in Scenes2 and Scene3, it becomes possible for line segments representing two different yet collinear walls to be mistakenly merged into a single segment. This results in a decrease in both the total number and length of extracted lines, leading to a drop in completeness and redundancy. To ensure high completeness and low redundancy, the parameter combination yielding the best performance ($d_{col}=0.1 \mathrm{m}, {\vartheta }_{col }={40}^{°}$) is selected for subsequent orthogonality constraint analysis.

As shown in Figure 18, in the orthogonality constraint experiment, the large-scale Scene1, which contains numerous structural holes, achieved the highest completeness at $d_{s-ortho}=0.3 \mathrm{m}$ through line extension and closure operations to compensate for missing intersections of orthogonal segments. In contrast, the smaller-scale Scene2 and Scene3, featuring more complete architectural structures in the scanned point clouds, achieved maximum completeness when $d_{s-ortho}=0.1 \mathrm{m}$. However, as the distance threshold increases, all three scenes exhibit higher redundancy because the provided ground truth segment sets include only major structural elements such as ceilings, floors, walls, doors, and windows, whereas additional lines extracted along the edges of holes are not part of the reference data and thus contribute to redundancy. As for the angle threshold, Scene1 and Scene2 exhibited minimal sensitivity, whereas Scene3 with multiple non-orthogonal structures exhibited decreased completeness and increased redundancy under overly strict orthogonality corrections due to deviations from actual boundaries. Therefore, we set the orthogonality angle threshold to ${\vartheta }_{ortho}={80}^{°}$, and select $d_{s-ortho}=0.3 \mathrm{m}$ for the large-scale Scene1 and $d_{s-ortho}= 0.1 \mathrm{m}$ for Scene2 and Scene3.

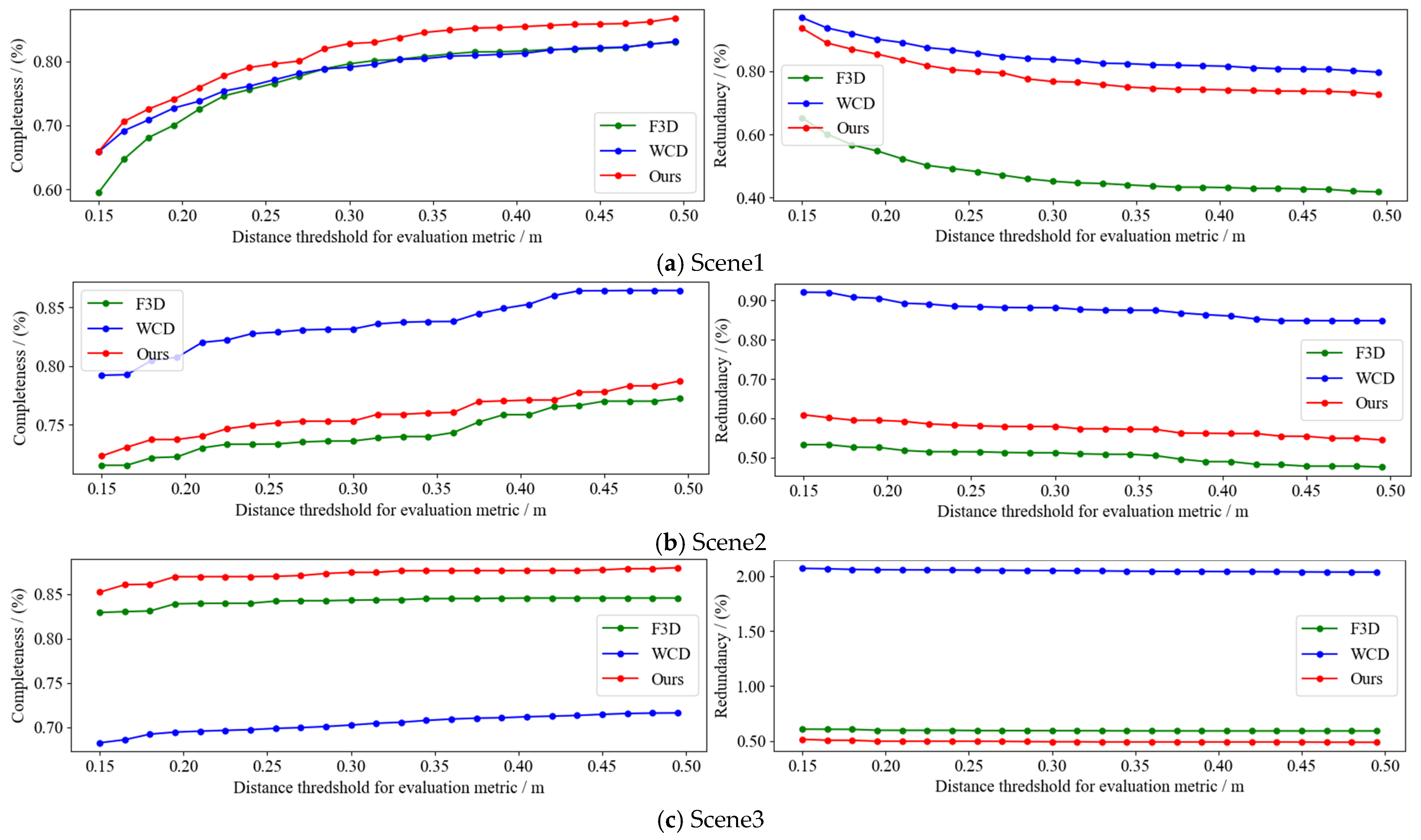
Depending on the optimal parameters derived from the above comparative experiments, we further evaluate our proposed method in comparison with two other approaches: the Fast 3D Line Segment Detector (F3D) [20] and the Weighted Centroid Displacement method (WCD) [22]. The F3D method is open-source and uses the CannyLines [56] algorithm for 2D line extraction, while our method adopts graph-cut segmentation followed by edge vectorization. Since the WCD method is not publicly available, we reimplemented its weighted centroid displacement scheme for edge detection and applied least-squares line fitting to each group of clustered points. By varying the line segment distance threshold ${\rho }_0$ for accuracy assessment from 0.15 m to 0.5 m, Figure 19 illustrates the variation curves of completeness and redundancy, and

Table 5. Statistical results of extracted segments.

Scene Name	Method	Extracted Line Segments		ACom (%)	ARed (%)
		Amount	Length (m)
Scene1	F3D	768	2150.90	77.6	47.21
	WCD	2024	2805.93	78.24	84.58
	Ours	1130	2749.02	81.37	78.15
Scene2	F3D	269	314.89	74.44	50.42
	WCD	925	432.01	83.65	87.64
	Ours	259	336.05	75.90	57.34
Scene3	F3D	362	571.16	84.17	59.46
	WCD	2273	1094.97	70.41	204.94
	Ours	343	543.53	87.28	49.40

presents the quantitative evaluation metrics, including the number and total length of extracted segments, as well as the average completeness (ACom) and redundancy (ARed). With the increase in distance thresholds, our method consistently outperforms the other two approaches in Scene1 and Scene3, achieving average completeness values of 81.37% and 87.28%, respectively, while maintaining relatively low redundancy. However, in Scene2, both the completeness and redundancy metrics are inferior to those of the WCD method.

Furthermore, the length-weighted F1-scores of completeness and redundancy are calculated, where the F1-score of completeness is derived from the precision and recall defined in Equations (30) and (31), while the F1-score of redundancy is obtained in an opposite manner by considering the mismatched extracted line segments and the ground truth segments. The F1-score curves for completeness and redundancy versus the distance threshold are presented in Figure 20. By comparing Figure 19 and Figure 20, it can be observed that the trend of the length-weighted F1-score curve is consistent with the curves of completeness and redundancy defined in this study. This consistency not only demonstrates the reliability of the precision metric designed in this work, but also further validates that our method is effective in improving extraction accuracy.

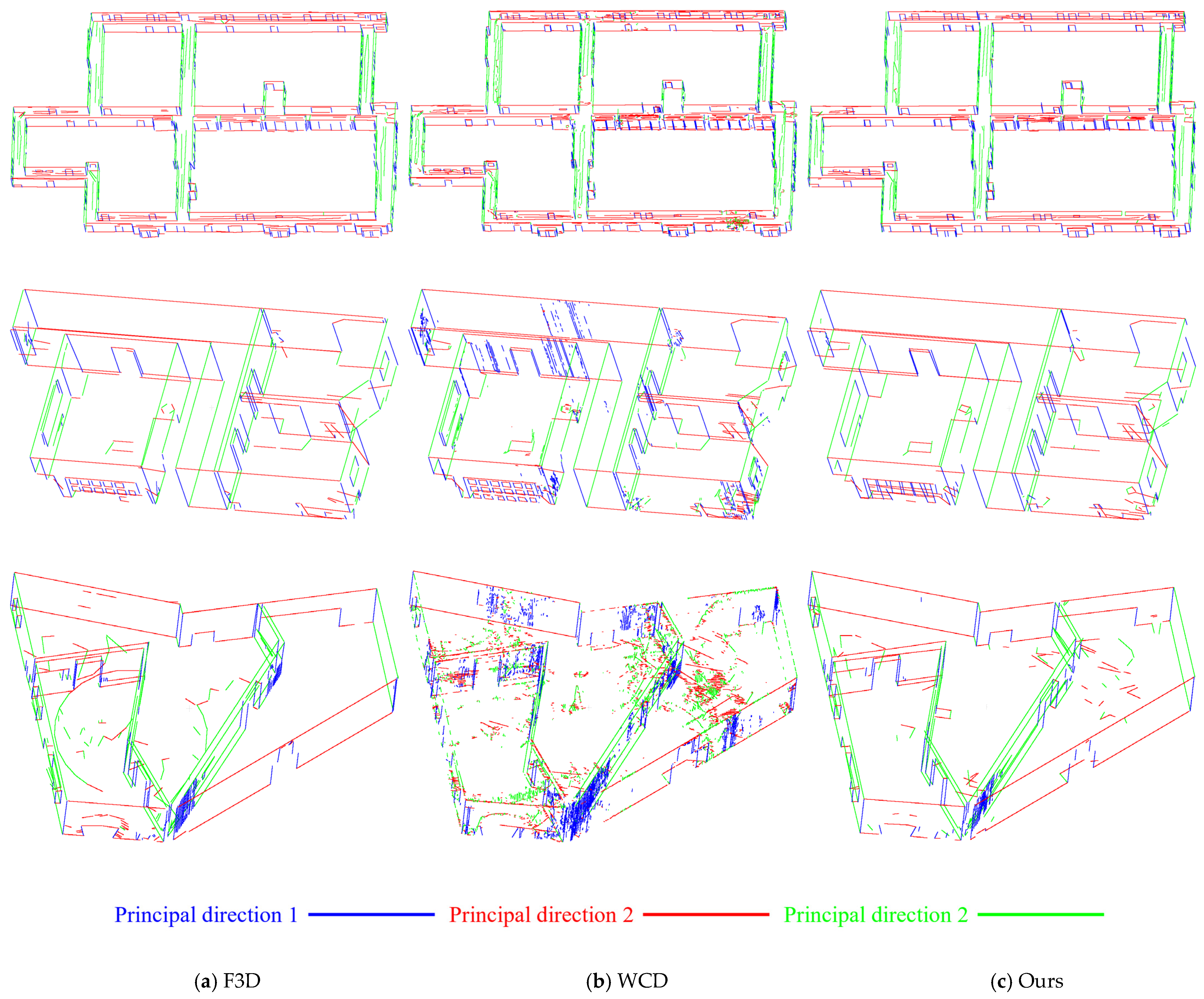
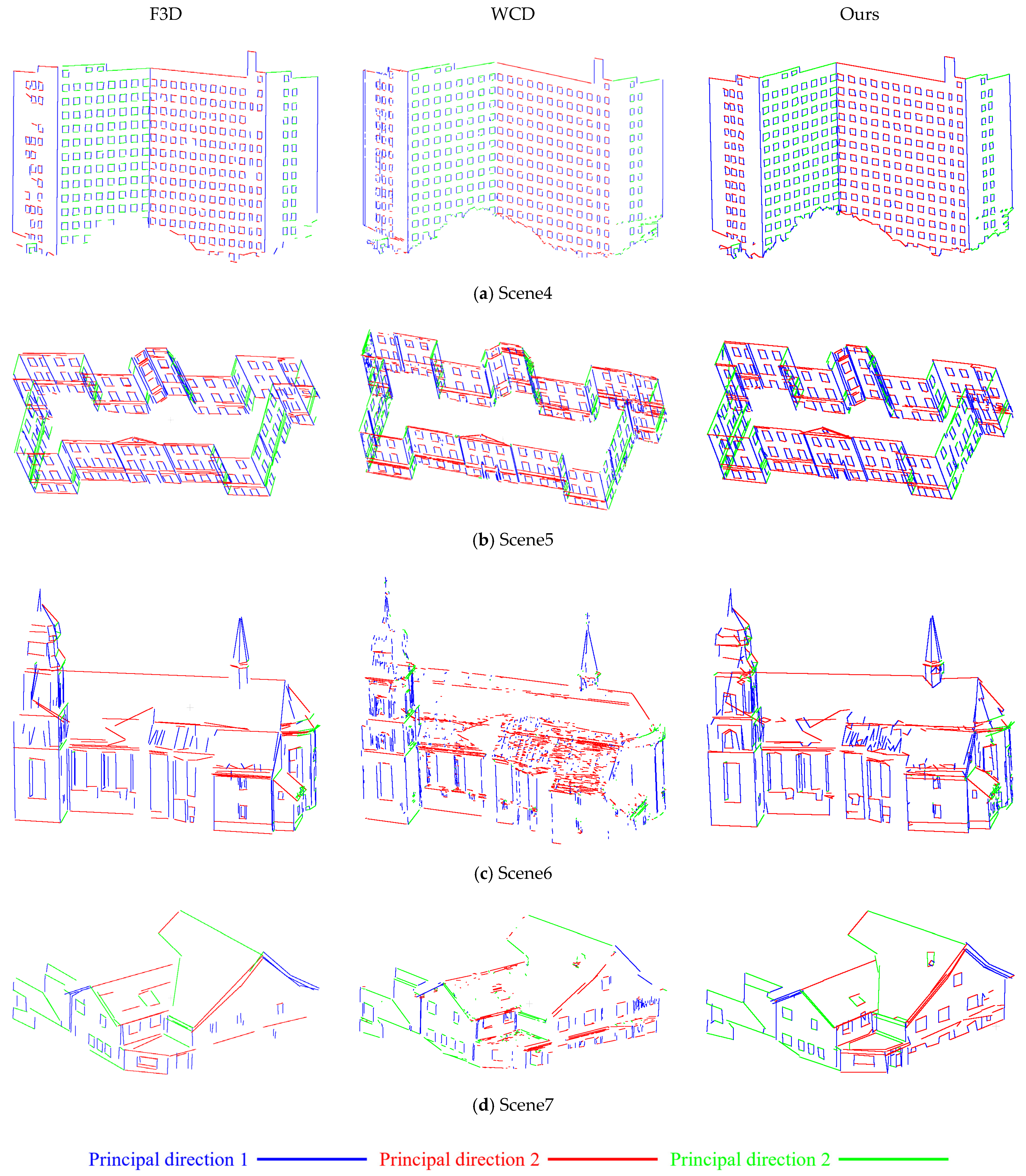
Figure 21 presents the visualization results. We can see that the performance of WCD is heavily influenced by the choice of neighborhood size. With the neighborhood size set to 25, the method tends to extract numerous non-salient edge points in regions with uneven density or varying sparsity, indicating that its edge detection is highly sensitive to parameter settings. Although certain line segments accurately describe the building contours, the WCD method tends to produce fragmented results, with the number of segments reaching as high as 925, thereby notably increasing redundancy. In contrast, our method extracted only 1130, 259, and 343 line segments in three scenes, achieving higher total length and completeness with significantly fewer segments. Moreover, the line segments extracted by F3D and WCD appear irregular and lack clear orthogonality, especially in regions characterized by prominent orthogonal structures. This limitation stems from the 2D line fitting strategy in F3D, which relies solely on least-squares optimization for individual edge segments and does not account for projection errors from 2D to 3D space. Similarly, WCD directly extracts edge points and fits 3D line segments via least-squares without structural regularization. Both methods fail to merge intersecting lines that share common endpoints, leading to evident geometric gaps and discontinuities.

In contrast, our method explicitly enforces line closure and endpoint alignment during the 2D extraction phase, significantly enhancing the geometric consistency of the resulting line segments. This improvement in geometric consistency is especially pronounced in structured regions, such as door frames and wall corners. Compared to Scene1, Scene2 and Scene3 feature cleaner and more regular architectural geometries with fewer noisy or fragmented lines, enabling more evident and reliable improvements in line closure and orthogonality.

4.3. Qualitative Analysis

We further extend the line segment extraction to four outdoor building façade scenes and conduct a qualitative comparison among F3D, WCD and our method. Given that outdoor scenes are generally larger in scale than indoor scenes, an angle threshold of 20° was selected for region growing and merging to ensure local planarity and reduce over-segmentation that may cause redundant line segments. Figure 22 presents the extraction results under each of the three geometric constraints in Scene7. Because the roof structure is not strictly orthogonal, applying the orthogonality constraint incorrectly alters the actual roof structure. Specifically, the two roof planes generate three dominant directions without being mutually orthogonal. As a result, the longer beam line segment (green) is regarded as the reference, which causes the eave line segments (both red and blue) to be miscorrected toward an angle orthogonal to the other two dominant directions. In this case, the collinearity constraint proves more suitable and is therefore adopted as the final constraint for comparison.

In this case, the collinearity constraint proves more suitable and is therefore adopted as the final constraint for comparison.

We can see from the visualization results in Figure 23 that our method demonstrates superior capability in extracting closed polygonal structures, with particularly notable improvements in the delineation of windows. In Scene4 and Scene5 (Figure 23a,b), building facade profiles are more complete, and all window frame outlines are accurately captured, with enhanced closure at intersection points. In Scene6 and Scene7 (Figure 23c,d), the WCD method, which relies on a fixed number of neighboring points, still shows limited robustness due to uneven point density and higher noise levels. The F3D method, although incorporating structural heuristics to filter out line segments in each patch that do not exhibit orthogonal relationships, tends to miss several window outlines. In contrast, our approach achieves more complete line extraction across various components, including walls, windows, and roofs.

5. Discussion

Despite these promising results, the method still exhibits several limitations. Firstly, missing data and holes in the original point clouds may result in non-structural information being mistakenly extracted when excessive closure is pursued, leading to increased redundancy. Secondly, the constraint thresholds within the optimization framework currently rely on empirical parameter tuning, which may restrict both scalability and generalizability. From the experiments, we observed that the values of these parameters are closely related to the regularity of scene structures, data completeness, and point density. The experiments indicate that these parameter values are influenced by the structural regularity, completeness, and density of the scene, yet it is not feasible to achieve global optimality by adjusting a single variable. This limitation may be alleviated by constructing scale-normalized point clouds or by integrating topological relation recognition into deep learning models, which would require both geometric and topological semantics to be jointly extracted for automated identification. Future work will focus on developing adaptive algorithms for constraint parameter selection, while further exploring how factors such as scale, structural regularity, and data completeness influence the performance of these algorithms, with the goal of improving their generalizability and automation.

Thirdly, while the quantitative evaluation in this study has primarily relied on BIM-assisted ground truth for indoor scenes, the absence of manually extracted reference data for outdoor environments remains a limitation. Outdoor point clouds present higher structural heterogeneity, occlusions, and noise, making the manual delineation of line segments substantially more challenging. As part of future research, we plan to manually extract line segments from several representative outdoor scenes and incorporate them into quantitative analyses to enhance the generalization of the method. This approach will allow a more comprehensive assessment across diverse environments and provide robust reference data for validating extraction accuracy. Furthermore, the availability of high-quality outdoor ground truth will support adaptive refinement experiments, where geometric constraint parameters can be dynamically adjusted according to the structural complexity of different scenes. With improved generalizability and reliability, the framework is expected to be more applicable to large-scale real-world scenarios, and it may also benefit tasks such as mesh simplification.

6. Conclusions

To efficiently and accurately extract structural contours of buildings, this study takes 3D point cloud data of planar-assembled building structures as input and utilizes segmented planar patches as the fundamental units for line extraction. For each patch, a local image coordinate system is established, enabling the application of mature image segmentation algorithms to distinguish between point cloud regions and background, followed by a vector-tracing algorithm to obtain compact and closed polygons as well as a set of 2D line segments. To verify the effectiveness of our adopted graph-cut method for patch segmentation and line segment extraction, experiments were conducted on four indoor building scenes with representative structural features, and comparisons were made with several widely used 2D line detection methods. The results demonstrate that our proposed method significantly improves continuity and completeness by compensating for broken or fragmented segments, thereby enhancing the closure of polygonal structures.

Nevertheless, due to errors introduced in 2D line detection and limitations in point cloud quality, the reconstructed 3D line segments obtained through 2D-to-3D back-projection still exhibit discontinuities, omissions, and angular deviations, particularly along non-patch boundaries. To address these issues, the spatial relationships between collinear and orthogonal segments were analyzed. Combined with building structural characteristics, three geometric regularization constraints, namely adjacent patch constraint, collinearity constraint, and orthogonality constraint, are designed to merge homogeneous segments, refine the topological continuity contours, and improve structural outlines. To quantitatively assess the effectiveness of the proposed method, two evaluation metrics, namely completeness and redundancy, were introduced to analyze its optimization performance under different constraint parameters. The results validate its accuracy, applicability, and generalizability. Furthermore, it was extended to four outdoor scenes for qualitative evaluation, and the experimental results demonstrate that it also performs well in façade structures, where most window contours are extracted as complete, closed, and orthogonal lines.