Quantifying the Relationship Between the FPAR and Vegetation Index in Marsh Wetlands Using a 3D Radiative Transfer Model and Satellite Observations
Abstract
Highlights
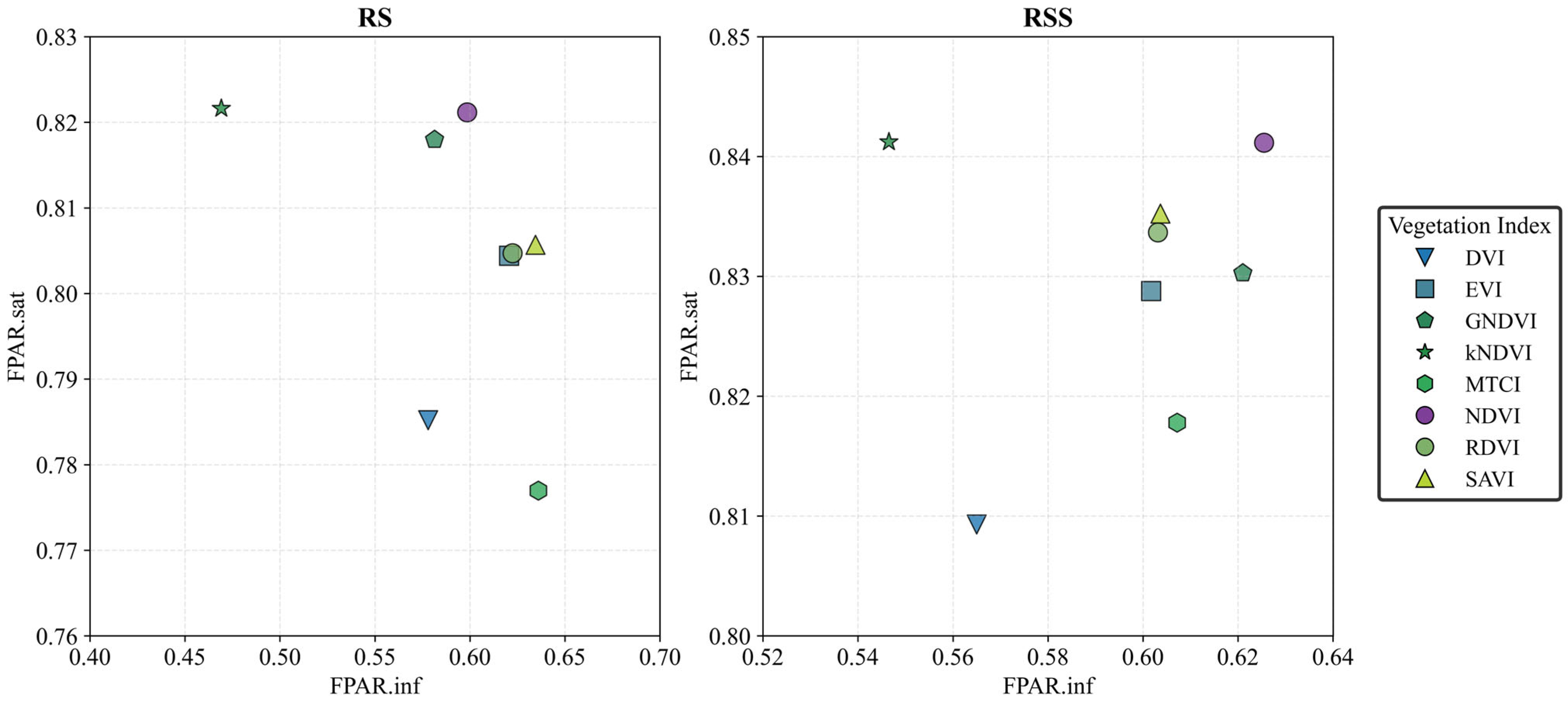
- The study quantified the relationship between FPAR and nine vegetation indices (VIs) in marsh wetlands, identifying saturation thresholds: FPAR.inf (saturation onset) ranged from 0.423 to 0.762 (mean = 0.597), while FPAR.sup (saturation point) ranged from 0.786 to 0.921 (mean = 0.857).
- The NDVI demonstrated the highest predictive accuracy for FPAR before saturation, whereas the EVI was found to be the most effective VI for estimating FPAR after the saturation point occurred.
- The established saturation thresholds provide critical benchmarks for remote sensing monitoring, indicating that different vegetation indices must be selected for accurate FPAR estimation depending on whether the vegetation is below or above its saturation point.
- This finding enhances the precision of carbon flux and productivity assessments in wetland ecosystems, which is vital for improving climate change modeling and informing effective ecosystem management strategies.
Abstract
1. Introduction
2. Materials
2.1. Study Area
2.2. Sample Setting
2.3. Field Survey
2.4. Remote Sensing Data and Other Auxiliary Data
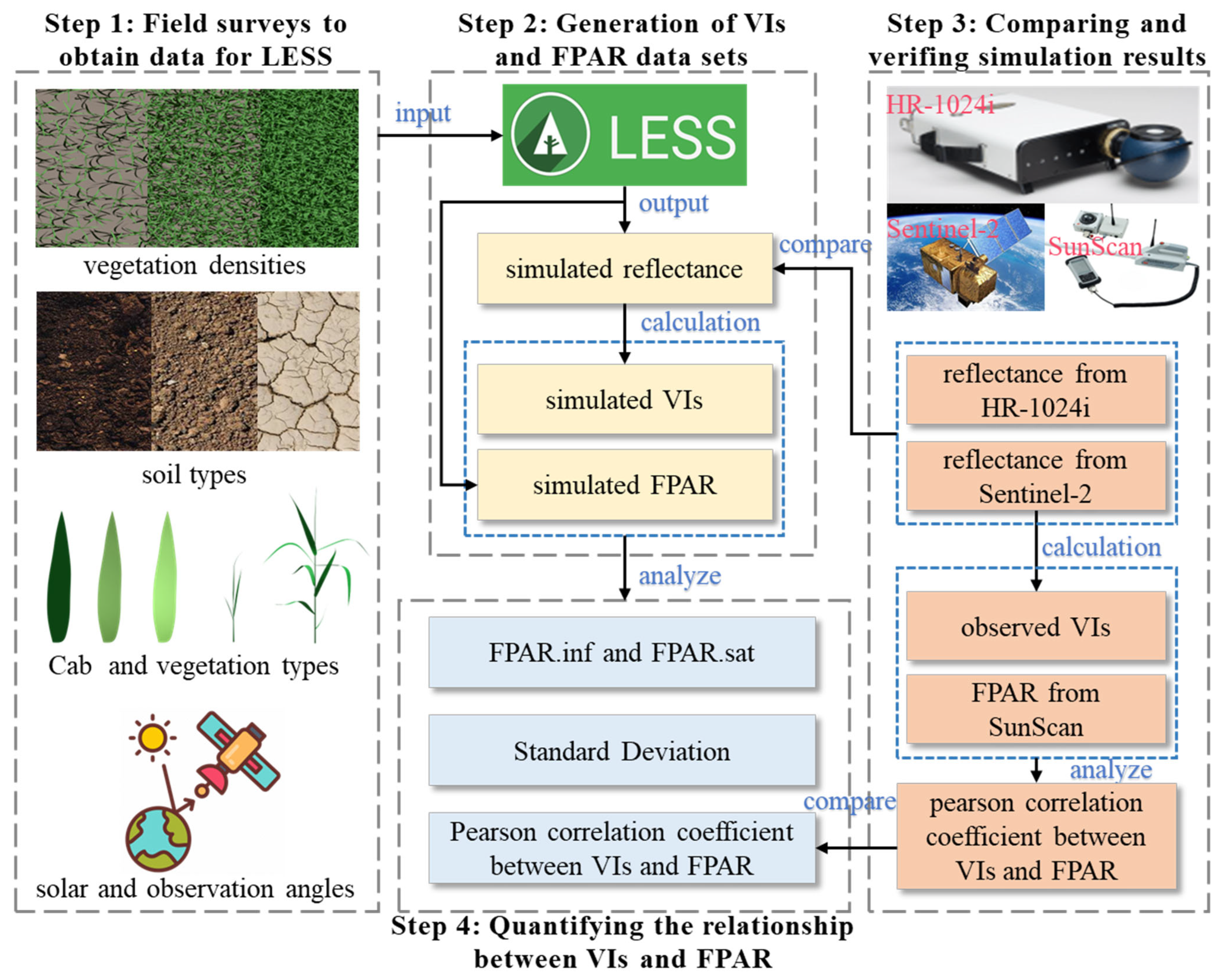
3. Methods
3.1. Basic Principles of LESS
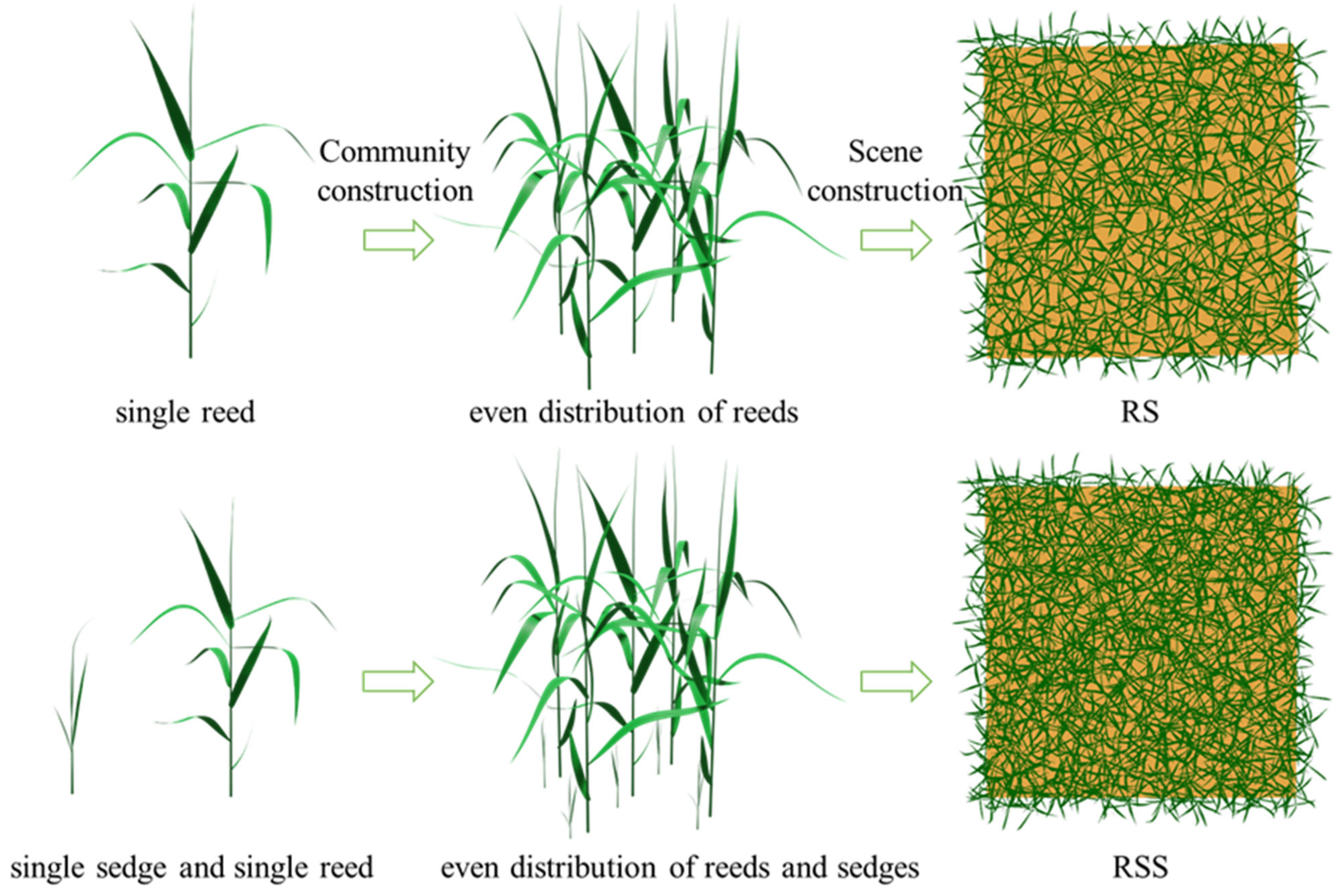
3.2. Reed Marsh Scene Construction
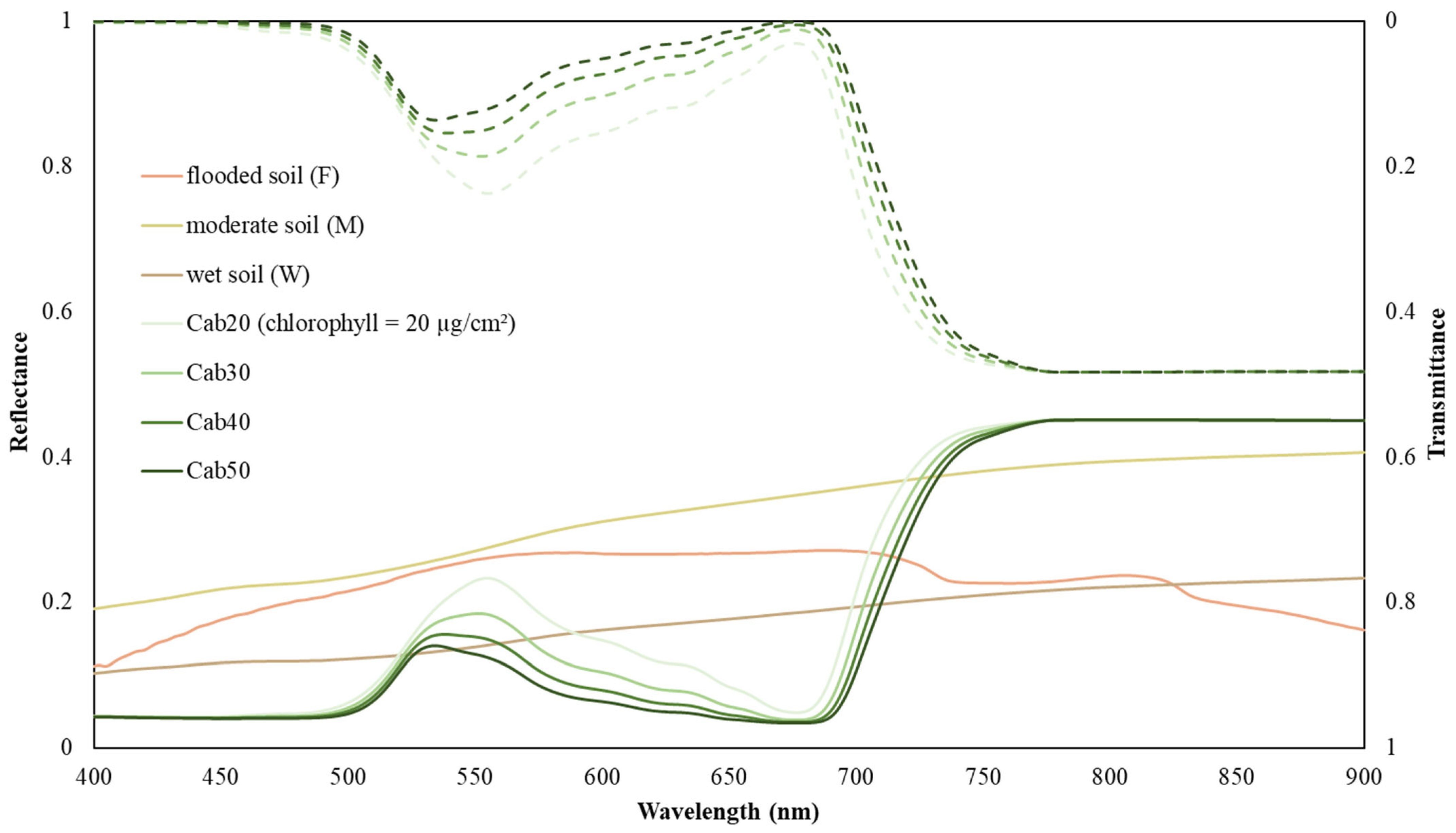
3.2.1. Simulation of Leaf Spectrum
3.2.2. Modeling of a Single Plant
3.2.3. Modeling of the Reed Marsh Scene
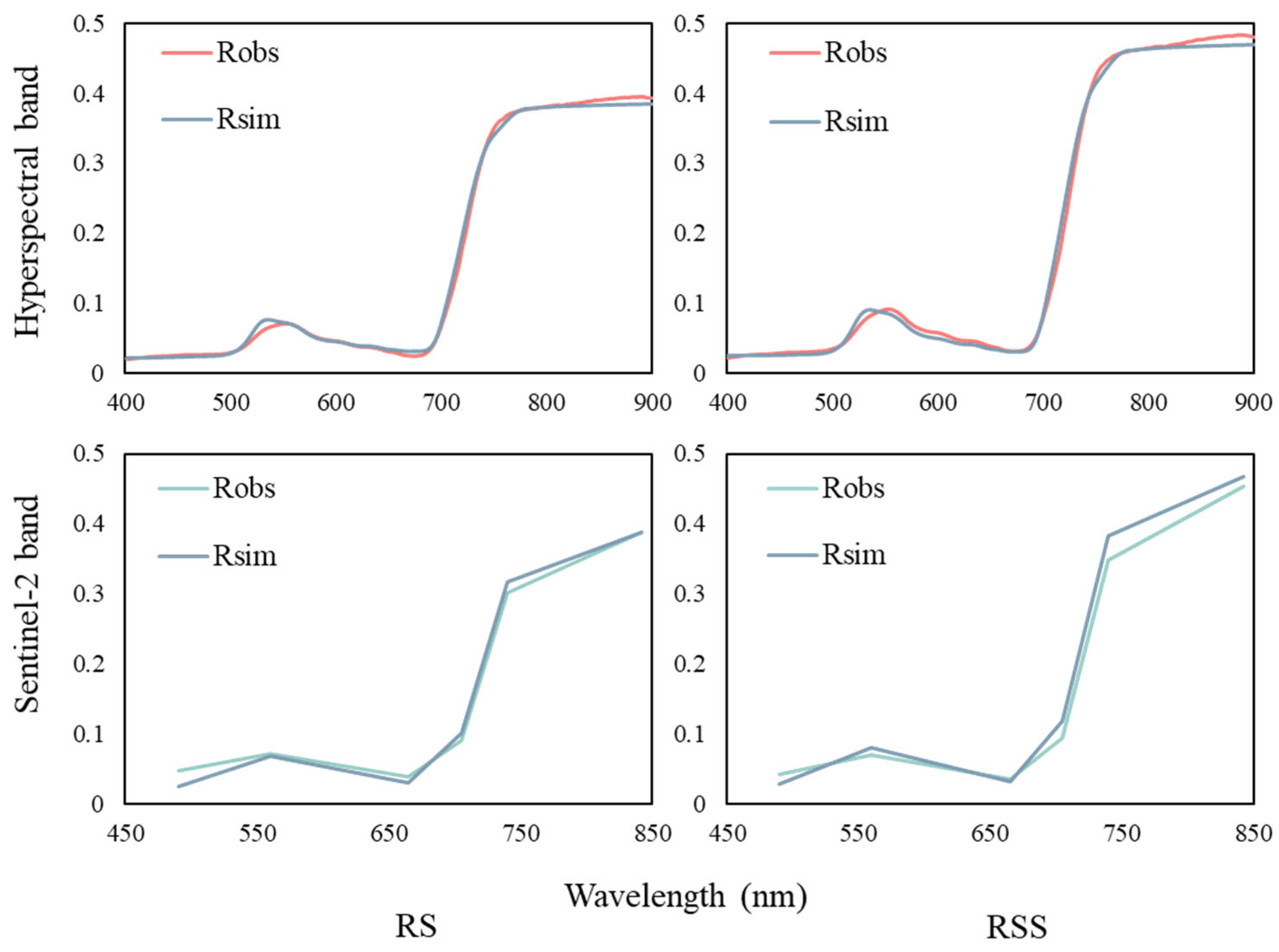
3.3. Verification of the Simulation Accuracy of Reed Marsh Canopy Reflectance
3.4. VIs Calculation
3.5. Quantifying the Relationship Between VIs and the FPAR
4. Results
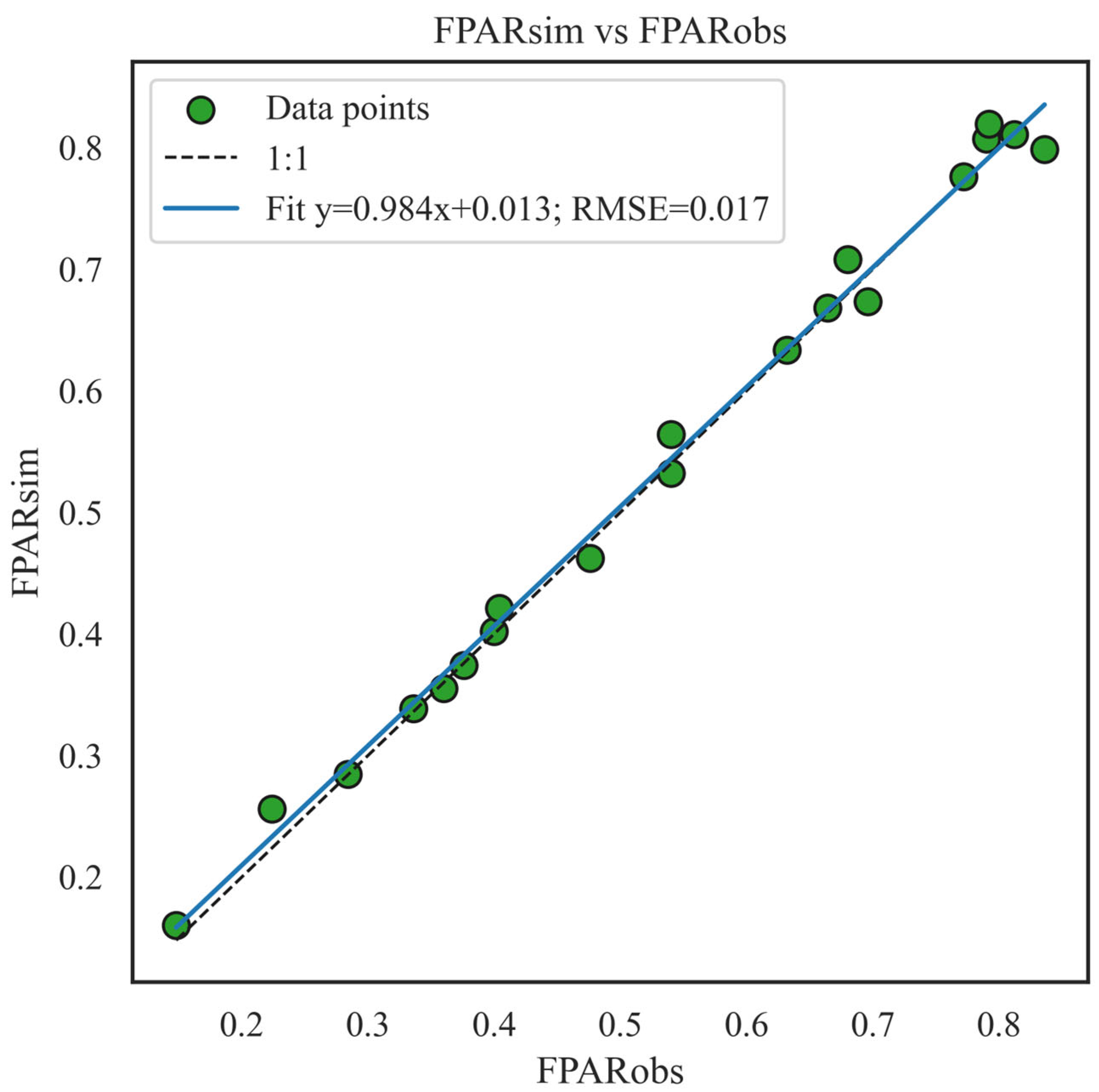
4.1. Canopy Spectrum and the FPAR Simulation Accuracy of LESS
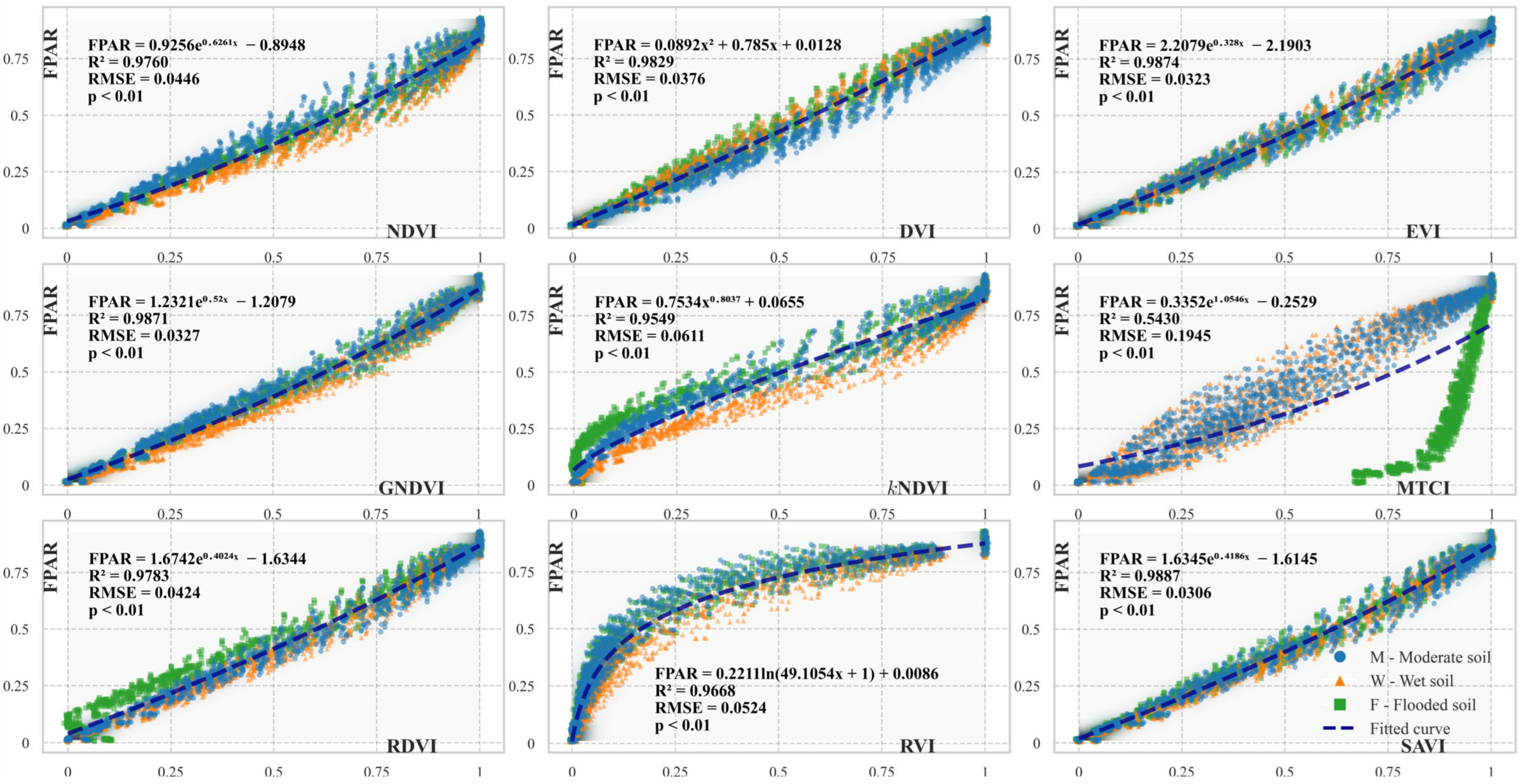
4.2. Correlation Between VIs and FPAR
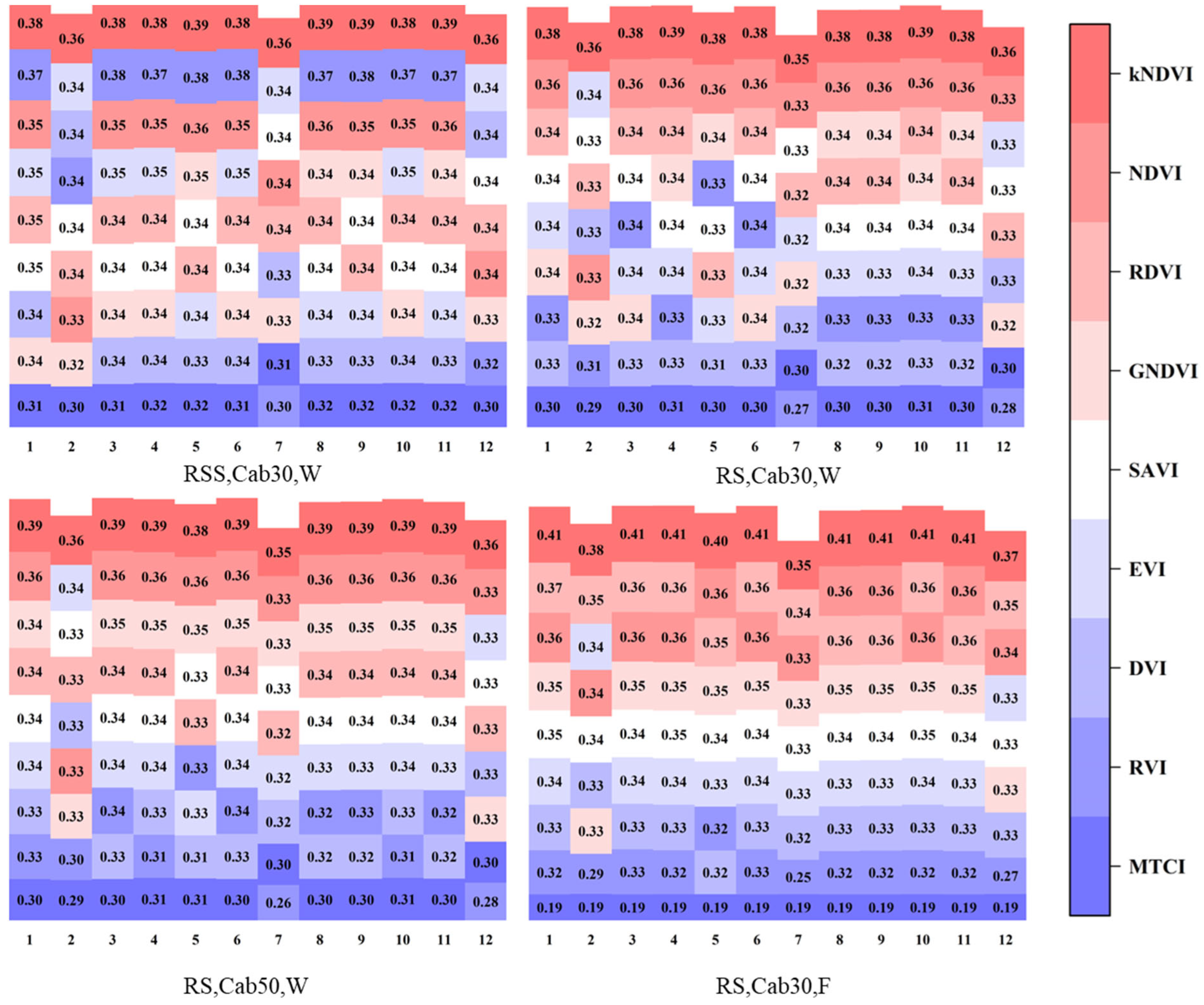
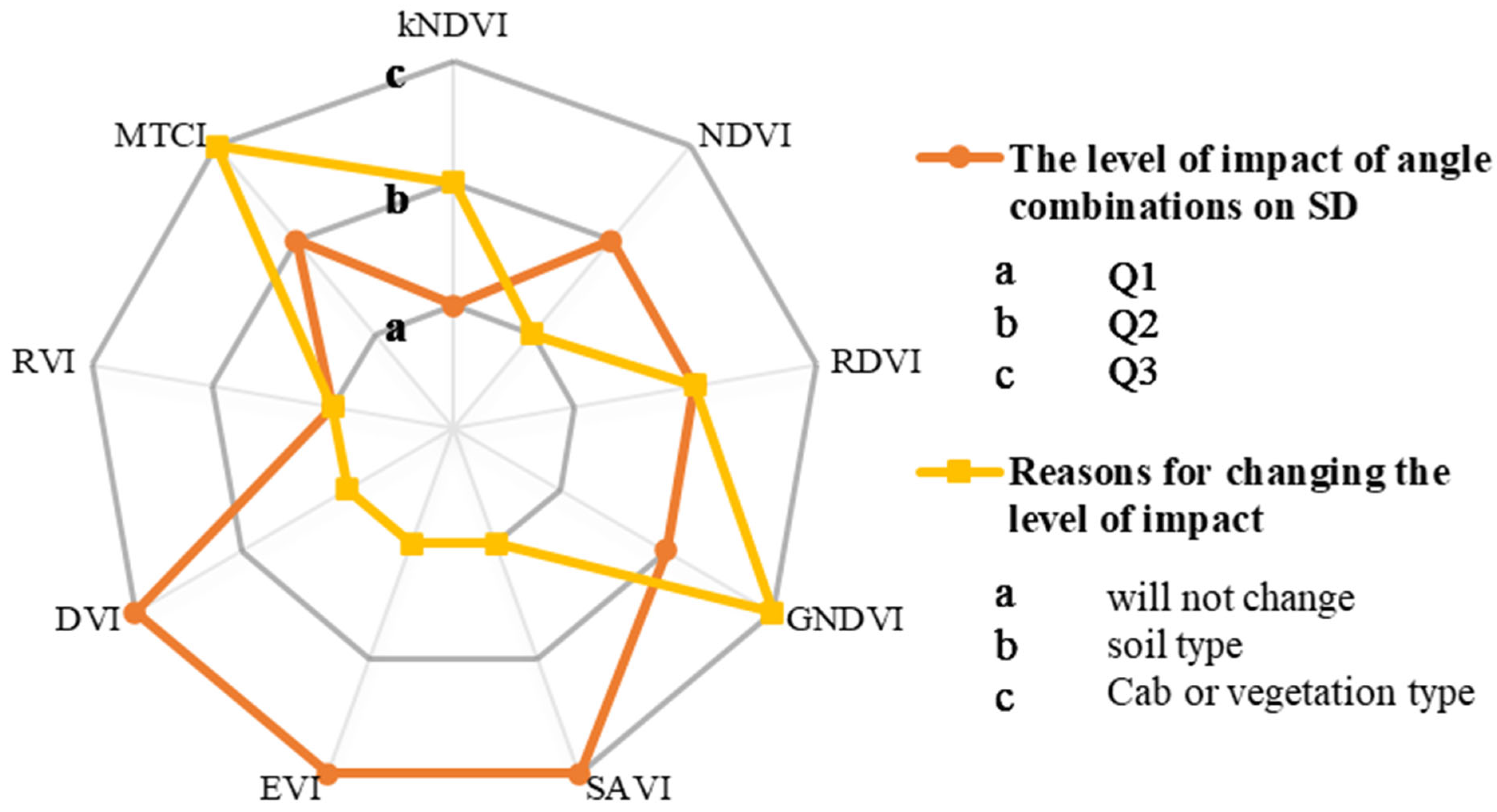
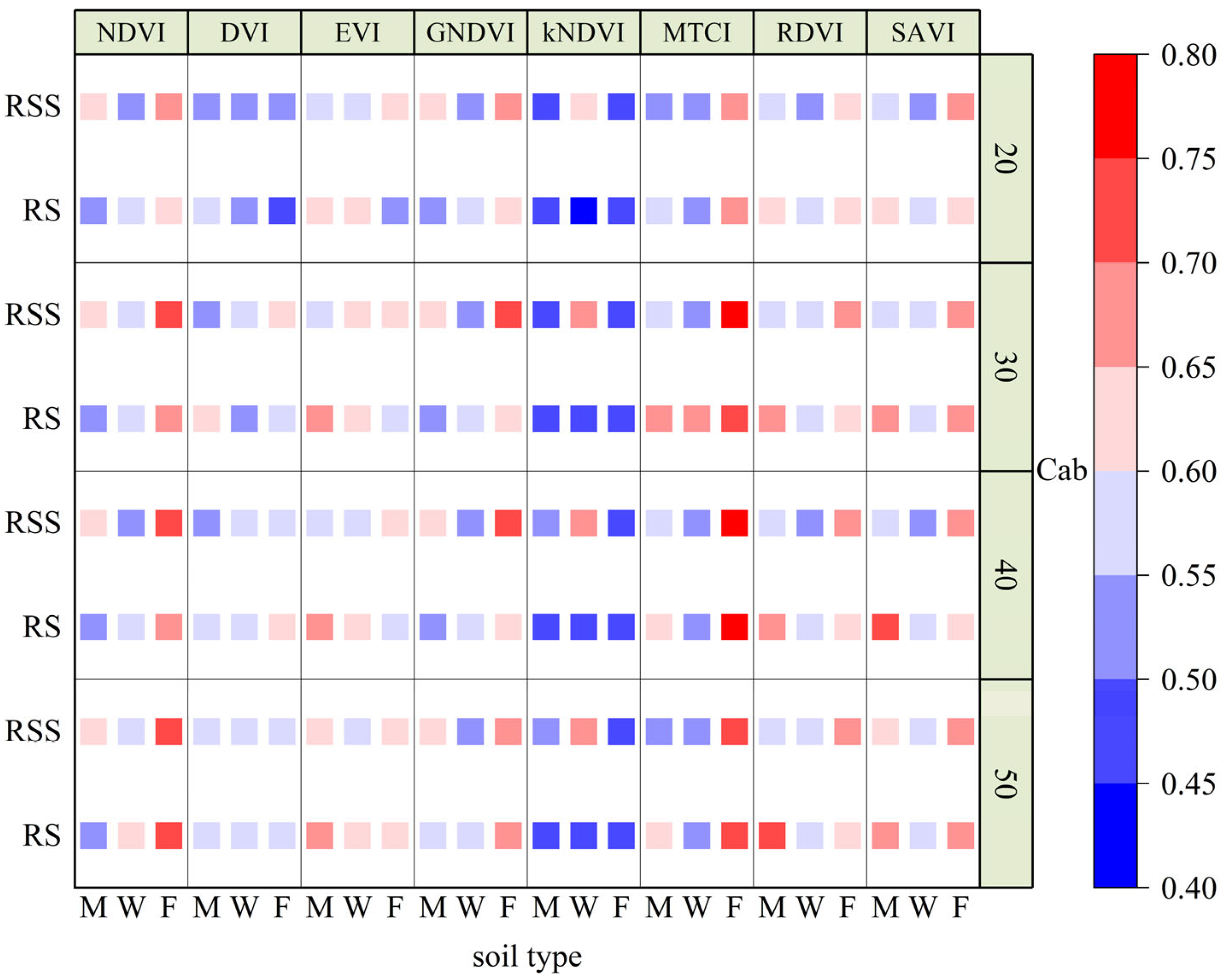
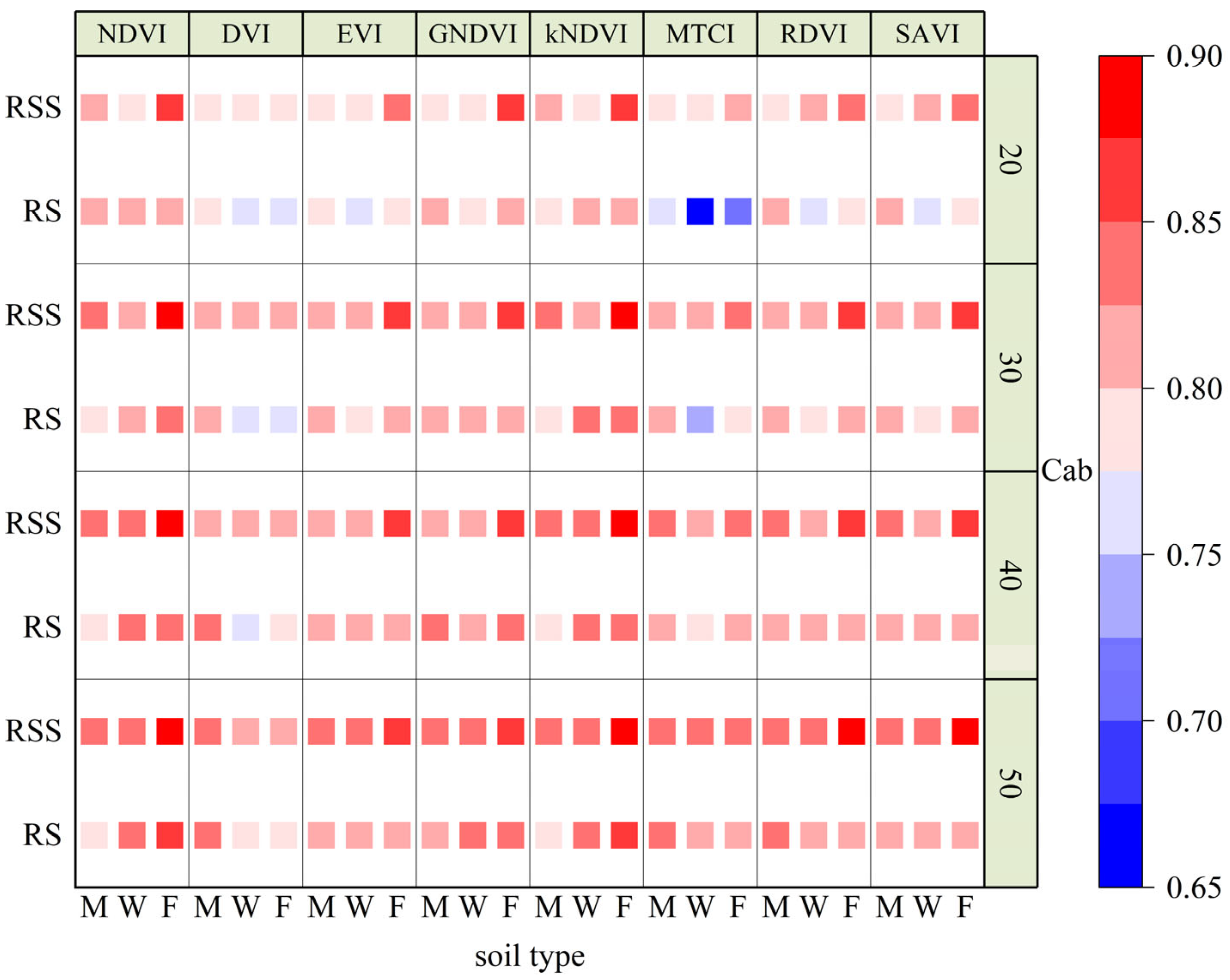
4.3. Sensitivity of VIs to Scene Conditions
4.4. FPAR-Estimated Saturation Inflection Point (FPAR.inf) and Critical Point (FPAR.sat) Analysis
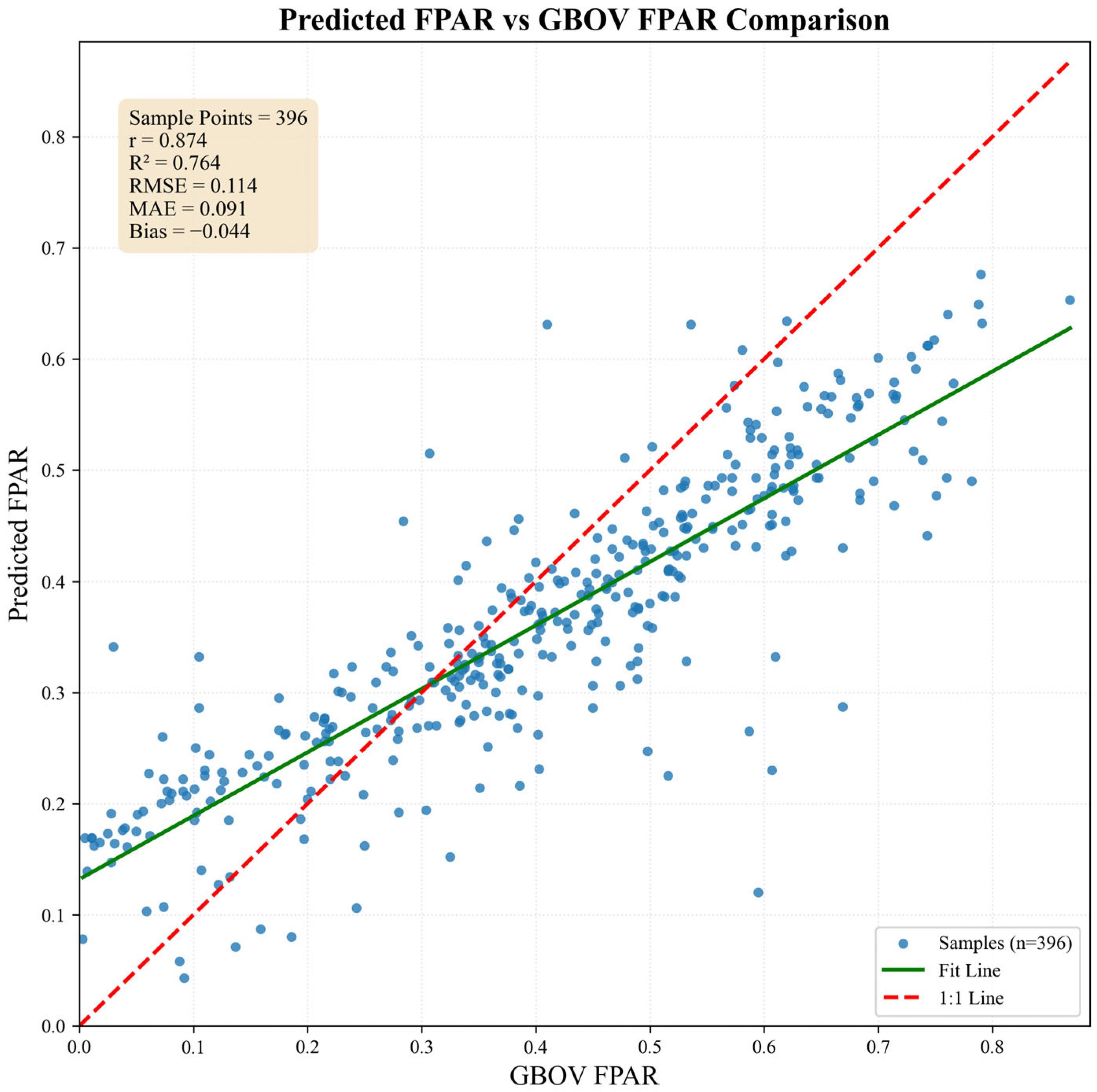
4.5. Model Transferability and Cross-Ecosystem Validation
5. Discussion
5.1. Factors Affecting the Relationship Between VIs and FPAR
5.2. Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VI | Vegetation indices |
| FPAR | Fraction of absorbed photosynthetically active radiation |
| FPAR.inf | the saturation inflection points |
| FPAR.sat | the saturation critical points |
| Cab | chlorophyll content |
| NPP | Net primary productivity |
| LUE | light use efficiency |
| RSS | reed and sedge mixed-growth |
| RS | reed monoculture |
| F | Flooded soil |
| M | Moderate soil |
| W | Wet soil |
| SZA | solar zenith angle |
| SAA | solar azimuth angle |
| VZA | observation zenith angle |
| VAA | observation azimuth angle |
| PAR | photosynthetically active radiation |
| RMSE | The root mean square error |
| d | the index of agreement |
| B | Sentinel-2 Band 2 |
| G | Sentinel-2 Band 3 |
| R | Sentinel-2 Band 4 |
| RE1 | Sentinel-2 Band 5 |
| RE2 | Sentinel-2 Band 6 |
| NIR | Sentinel-2 Band 8 |
| R2 | determination coefficients |
| SD | standard deviation |
| Rsim | the reflectance simulated by LESS |
| Robs | The reflectance observed by the HR-1024i and Sentinel-2 |
| Q1 | strong: SD range > 0.040 |
| Q2 | medium: 0.020–0.040 |
| Q3 | weak: 0–0.020 |
| NDVIobs | the observed NDVI calculated from the reflectance of sample plots measured by Sentinel-2 |
| GNDVIobs | the observed GNDVI calculated from the reflectance of sample plots measured by Sentinel-2 |
| NDVIsim | the simulated NDVI calculated from the reflectance of sample plots simulated by LESS |
| GNDVIsim | the simulated GNDVI calculated from the reflectance of sample plots simulated by LESS |
References
- An, X.; Jin, W.; Zhang, H.; Liu, Y.; Zhang, M. Analysis of long-term wetland variations in China using land use/land cover dataset derived from Landsat images. Ecol. Indic. 2022, 145, 109689. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, H.; Yao, B.; Lin, H.; An, X.; Liu, Y. Spatiotemporal changes of wetlands in China during 2000–2015 using Landsat imagery. J. Hydrol. 2023, 621, 129590. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, J.; Gong, Y. Valuing wetland ecosystem services based on benefit transfer: A meta-analysis of China wetland studies. J. Clean. Prod. 2020, 276, 122988. [Google Scholar] [CrossRef]
- Xu, X.; Chen, M.; Yang, G.; Jiang, B.; Zhang, J. Wetland ecosystem services research: A critical review. Glob. Ecol. Conserv. 2020, 22, e01027. [Google Scholar] [CrossRef]
- Li, L.; Xu, H.; Zhang, Q.; Zhan, Z.; Liang, X.; Xing, J. Estimation methods of wetland carbon sink and factors influencing wetland carbon cycle: A review. Carbon Res. 2024, 3, 50. [Google Scholar] [CrossRef]
- Schuster, L.; Taillardat, P.; Macreadie, P.I.; Malerba, M.E. Freshwater wetland restoration and conservation are long-term natural climate solutions. Sci. Total Environ. 2024, 922, 171218. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, N.; Lin, H.; Liu, Y.; Zhang, H. Quantitative estimation of the factors impacting spatiotemporal variation in NPP in the Dongting Lake wetlands using Landsat time series data for the last two decades. Ecol. Indic. 2022, 135, 108544. [Google Scholar] [CrossRef]
- Forrester, D.I.; Plaga, B.N.E.; Bauhus, J. The Effects of Tree Size, Stand Density, and Tree-Species Mixing on Stand Level and Tree Level Light Absorption and Light-Use Efficiency: A Review. Curr. For. Rep. 2025, 11, 15. [Google Scholar] [CrossRef]
- Dong, D.; Zhang, R.; Guo, W.; Gong, D.; Zhao, Z.; Zhou, Y.; Xu, Y.; Fujioka, Y. Assessing Spatiotemporal Dynamics of Net Primary Productivity in Shandong Province, China (2001–2020) Using the CASA Model and Google Earth Engine: Trends, Patterns, and Driving Factors. Remote Sens. 2025, 17, 488. [Google Scholar] [CrossRef]
- Wang, Y.; Li, R.; Hu, J.; Fu, Y.; Duan, J.; Cheng, Y. Daily estimation of gross primary production under all sky using a light use efficiency model coupled with satellite passive microwave measurements. Remote Sens. Environ. 2021, 267, 112721. [Google Scholar] [CrossRef]
- Wei, X.; Yang, J.; Luo, P.; Lin, L.; Lin, K.; Guan, J. Assessment of the variation and influencing factors of vegetation NPP and carbon sink capacity under different natural conditions. Ecol. Indic. 2022, 138, 108834. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, Z.; Wang, C.; Wang, H.; Ma, C. Quantitative estimation of net primary productivity by an improved tCASA model using Landsat time series data: A case study of Central Plains, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 10403–10418. [Google Scholar] [CrossRef]
- Jin, X.; Lou, Y.; Zhang, P.; Tang, H.; Zhang, Q.; Smith, P. Allometric equations for estimating above- and below-ground biomass of reed (Phragmites australis) marshes. J. Plant Ecol. 2025, 18, rtae113. [Google Scholar] [CrossRef]
- Leolini, L.; Bregaglio, S.; Ginaldi, F.; Costafreda-Aumedes, S.; Di Gennaro, S.; Matese, A.; Maselli, F.; Caruso, G.; Palai, G.; Bajocco, S. Use of remote sensing-derived fPAR data in a grapevine simulation model for estimating vine biomass accumulation and yield variability at sub-field level. Precis. Agric. 2023, 24, 705–726. [Google Scholar] [CrossRef]
- Liang, S.; Ma, W.; Sui, X.; Wang, M.; Li, H. An Assessment of Relations between Vegetation Green FPAR and Vegetation Indices through a Radiative Transfer Model. Plants 2023, 12, 1927. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Pourreza, A.; Cheung, K.H.; Zuniga-Ramirez, G.; Lampinen, B.D.; Shackel, K.A. Estimation of fractional photosynthetically active radiation from a canopy 3D model; case study: Almond yield prediction. Front. Plant Sci. 2021, 12, 715361. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, K.; Jiang, J.; Liu, Q.; Wu, J.; Guo, C.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; et al. Remotely assessing FIPAR of different vertical layers in field wheat. Field Crops Res. 2023, 297, 108932. [Google Scholar] [CrossRef]
- Zhu, W.; Zhiying, X.; Cenliang, Z.; Zhoutao, Z.; Kun, Q.; Dailiang, P.; Fu, Y.H. Remote sensing of terrestrial gross primary productivity: A review of advances in theoretical foundation, key parameters and methods. GISci. Remote Sens. 2024, 61, 2318846. [Google Scholar] [CrossRef]
- Pei, Y.; Dong, J.; Zhang, Y.; Yuan, W.; Doughty, R.; Yang, J.; Zhou, D.; Zhang, L.; Xiao, X. Evolution of light use efficiency models: Improvement, uncertainties, and implications. Agric. For. Meteorol. 2022, 317, 108905. [Google Scholar] [CrossRef]
- Li, A.; Song, K.; Chen, S.; Mu, Y.; Xu, Z.; Zeng, Q. Mapping African wetlands for 2020 using multiple spectral, geo-ecological features and Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 2022, 193, 252–268. [Google Scholar] [CrossRef]
- Fu, Y.; Tan, X.; Yao, Y.; Wang, L.; Shan, Y.; Yang, Y.; Jing, Z. Uncovering optimal vegetation indices for estimating wetland plant species diversity. Ecol. Indic. 2024, 166, 112367. [Google Scholar] [CrossRef]
- Fang, P.; Yan, N.; Wei, P.; Zhao, Y.; Zhang, X. Aboveground Biomass Mapping of Crops Supported by Improved CASA Model and Sentinel-2 Multispectral Imagery. Remote Sens. 2021, 13, 2755. [Google Scholar] [CrossRef]
- Epiphanio, J.N.; Huete, A.R. Dependence of NDVI and SAVI on sun/sensor geometry and its effect on fAPAR relationships in Alfalfa. Remote Sens. Environ. 1995, 51, 351–360. [Google Scholar] [CrossRef]
- Fernandes, R.; Brown, L.; Canisius, F.; Dash, J.; He, L.; Hong, G.; Huang, L.; Le, N.Q.; MacDougall, C.; Meier, C.; et al. Validation of Simplified Level 2 Prototype Processor Sentinel-2 fraction of canopy cover, fraction of absorbed photosynthetically active radiation and leaf area index products over North American forests. Remote Sens. Environ. 2023, 293, 113600. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Y.; Yin, T.; Wang, C.; Lauret, N.; Regaieg, O.; Xi, X.; Gastellu-Etchegorry, J.P. Comprehensive LiDAR simulation with efficient physically-based DART-Lux model (I): Theory, novelty, and consistency validation. Remote Sens. Environ. 2022, 272, 112952. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.; Running, S.W. Estimation of global leaf area index and absorbed par using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar] [CrossRef]
- Zhao, W.; Wu, J.; Shen, Q.; Liu, L.; Lin, J.; Yang, J. Estimation of the net primary productivity of winter wheat based on the near-infrared radiance of vegetation. Sci. Total Environ. 2022, 838, 156090. [Google Scholar] [CrossRef] [PubMed]
- Qi, S.; Chen, S.; Long, X.; An, X.; Zhang, M. Quantitative contribution of climate change and anthropological activities to vegetation carbon storage in the Dongting Lake basin in the last two decades. Adv. Space Res. 2023, 71, 845–868. [Google Scholar] [CrossRef]
- Long, X.; Lin, H.; An, X.; Chen, S.; Qi, S.; Zhang, M. Evaluation and analysis of ecosystem service value based on land use/cover change in Dongting Lake wetland. Ecol. Indic. 2022, 136, 108619. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K.; Wellburn, A.R. Determinations of total carotenoids and chlorophylls a and b of leaf extracts in different solvents. Biochem. Soc. Trans. 1983, 11, 591–592. [Google Scholar] [CrossRef]
- Long, X.; Li, X.; Lin, H.; Zhang, M. Mapping the vegetation distribution and dynamics of a wetland using adaptive-stacking and Google Earth Engine based on multi-source remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102453. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Yin, T.; Yan, G.; Gastellu-Etchegorry, J.-P.; Li, L.; Zhang, W.; Mu, X.; Norford, L.K. LESS: LargE-Scale remote sensing data and image simulation framework over heterogeneous 3D scenes. Remote Sens. Environ. 2019, 221, 695–706. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Jiang, J.; Huang, H. 3D radiative transfer modeling of structurally complex forest canopies through a lightweight boundary-based description of leaf clusters. Remote Sens. Environ. 2022, 283, 113301. [Google Scholar]
- Qi, J.; Jiang, J.; Zhou, K.; Xie, D.; Huang, H. Fast and accurate simulation of canopy reflectance under wavelength-dependent optical properties using a semi-empirical 3D radiative transfer model. J. Remote Sens. 2023, 3, 0017. [Google Scholar]
- Zhao, X.; Qi, J.; Xu, H.; Yu, Z.; Yuan, L.; Chen, Y.; Huang, H. Evaluating the potential of airborne hyperspectral LiDAR for assessing forest insects and diseases with 3D Radiative Transfer Modeling. Remote Sens. Environ. 2023, 297, 113759. [Google Scholar]
- Zhao, X.; Qi, J.; Yu, Z.; Yuan, L.; Huang, H. Fine-scale quantification of absorbed photosynthetically active radiation (APAR) in plantation forests with 3D radiative transfer modeling and LiDAR data. Plant Phenomics 2024, 6, 0166. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Zhong, R.; Yan, K.; Ma, X.; Chen, X.; Pu, J.; Gao, S.; Qi, J.; Yin, G.; Myneni, R.B. Evaluating the saturation effect of vegetation indices in forests using 3D radiative transfer simulations and satellite observations. Remote Sens. Environ. 2023, 295, 113665. [Google Scholar] [CrossRef]
- Villa, P.; Dalla Vecchia, A.; Piaser, E.; Bolpagni, R. Assessing PROSPECT performance on aquatic plant leaves. Remote Sens. Environ. 2024, 301, 113926. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Signature Analysis of Leaf Reflectance Spectra: Algorithm Development for Remote Sensing of Chlorophyll. J. Plant Physiol. 1996, 148, 494–500. [Google Scholar] [CrossRef]
- Gitelson, A.; Viña, A.; Inoue, Y.; Arkebauer, T.; Schlemmer, M.; Schepers, J. Uncertainty in the evaluation of photosynthetic canopy traits using the green leaf area index. Agric. For. Meteorol. 2022, 320, 108955. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Tan, P.; Fang, T.; Xiao, J.; Zhao, P.; Quan, L. Single image tree modeling. ACM Trans. Graph. TOG 2008, 27, 108. [Google Scholar]
- Godin, C.; Costes, E.; Sinoquet, H. A method for describing plant architecture which integrates topology and geometry. Ann. Bot. 1999, 84, 343–357. [Google Scholar] [CrossRef]
- Willmott, C.J. On the Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Zhen, Z.; Chen, S.; Yin, T.; Gastellu-Etchegorry, J.-P. Globally quantitative analysis of the impact of atmosphere and spectral response function on 2-band enhanced vegetation index (EVI2) over Sentinel-2 and Landsat-8. ISPRS J. Photogramm. Remote Sens. 2023, 205, 206–226. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Campos-Taberner, M.; Moreno-Martínez, Á.; Walther, S.; Duveiller, G.; Cescatti, A.; Mahecha, M.D.; Muñoz-Marí, J.; García-Haro, F.J.; Guanter, L.; et al. A unified vegetation index for quantifying the terrestrial biosphere. Sci. Adv. 2021, 7, eabc7447. [Google Scholar] [CrossRef] [PubMed]
- Roujean, J.-L.; Breon, F.-M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Liu, H.Q.; Huete, A. A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Qian, B.; Ye, H.; Huang, W.; Xie, Q.; Pan, Y.; Xing, N.; Ren, Y.; Guo, A.; Jiao, Q.; Lan, Y. A sentinel-2-based triangular vegetation index for chlorophyll content estimation. Agric. For. Meteorol. 2022, 322, 109000. [Google Scholar] [CrossRef]
- Bai, G.; Dash, J.; Brown, L.; Meier, C.; Lerebourg, C.; Ronco, E.; Lamquin, N.; Bruniquel, V.; Clerici, M.; Gobron, N. Gbov (ground-based observation for validation): A copernicus service for validation of vegetation land products. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 4592–4594. [Google Scholar]
- Hase, N.; Doktor, D.; Rebmann, C.; Dechant, B.; Mollenhauer, H.; Cuntz, M. Identifying the main drivers of the seasonal decline of near-infrared reflectance of a temperate deciduous forest. Agric. For. Meteorol. 2022, 313, 108746. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, Y.; Feng, H.; Chen, R.; Bian, M.; Ma, Y.; Yue, J.; Yang, G. Estimating potato above-ground biomass based on vegetation indices and texture features constructed from sensitive bands of UAV hyperspectral imagery. Comput. Electron. Agric. 2024, 220, 108918. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Mutanga, O.; Masenyama, A.; Sibanda, M. Spectral saturation in the remote sensing of high-density vegetation traits: A systematic review of progress, challenges, and prospects. ISPRS J. Photogramm. Remote Sens. 2023, 198, 297–309. [Google Scholar]
- Lv, Z.; Meng, R.; Man, J.; Zeng, L.; Wang, M.; Xu, B.; Gao, R.; Sun, R.; Zhao, F. Modeling of winter wheat fAPAR by integrating Unmanned Aircraft Vehicle-based optical, structural and thermal measurement. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102407. [Google Scholar] [CrossRef]
- Xu, L.; Shi, S.; Gong, W.; Chen, B.; Sun, J.; Xu, Q.; Bi, S. Mapping 3D plant chlorophyll distribution from hyperspectral LiDAR by a leaf-canopy radiative transfer model. Int. J. Appl. Earth Obs. Geoinf. 2024, 127, 103649. [Google Scholar]
- Gu, Y.; Wang, Y.; Wu, Y.; Warner, T.A.; Guo, T.; Ai, H.; Zheng, H.; Cheng, T.; Zhu, Y.; Cao, W.; et al. Novel 3D photosynthetic traits derived from the fusion of UAV LiDAR point cloud and multispectral imagery in wheat. Remote Sens. Environ. 2024, 311, 114244. [Google Scholar] [CrossRef]




| Categories | Variables | Values |
|---|---|---|
| Canopy | Plant type | Reed/sedge |
| Reed density (plants/m2) | 0–62 | |
| Competitive proportions | 1:1/pure reed | |
| Leaf | Cab (µg/cm2) | 20–50 for reed; 30 for sedge |
| N | 1.5 for reed and sedge | |
| Carotenoids (µg/cm2) | 8 for reed; 0.7 for sedge | |
| Water thickness (cm) | 0.012 for reed; 0.03 for sedge | |
| Dry matter (g/cm2) | 0.007 for reed; 0.008 for sedge | |
| Environment | Soil type | W/M/F |
| SZA:SAA (°) | 45:90/10:130/30:270 | |
| VZA:VAA (°) | 0:0/45:90/10:130/30:270 | |
| Terrain size (m) | 10 × 10 (Match the pixel size of Sentinel-2 image) | |
| Sensor | Type | Photon tracing |
| Spectral bands (nm) | 400–900 | |
| Illumination resolution | 0.001 | |
| Products | bidirectional reflectance factor (BRF)/FPAR |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, A.; Duan, X.; Jin, W.; Zhang, M. Quantifying the Relationship Between the FPAR and Vegetation Index in Marsh Wetlands Using a 3D Radiative Transfer Model and Satellite Observations. Remote Sens. 2025, 17, 3223. https://doi.org/10.3390/rs17183223
Zhong A, Duan X, Jin W, Zhang M. Quantifying the Relationship Between the FPAR and Vegetation Index in Marsh Wetlands Using a 3D Radiative Transfer Model and Satellite Observations. Remote Sensing. 2025; 17(18):3223. https://doi.org/10.3390/rs17183223
Chicago/Turabian StyleZhong, Anhao, Xiangyuan Duan, Wenping Jin, and Meng Zhang. 2025. "Quantifying the Relationship Between the FPAR and Vegetation Index in Marsh Wetlands Using a 3D Radiative Transfer Model and Satellite Observations" Remote Sensing 17, no. 18: 3223. https://doi.org/10.3390/rs17183223
APA StyleZhong, A., Duan, X., Jin, W., & Zhang, M. (2025). Quantifying the Relationship Between the FPAR and Vegetation Index in Marsh Wetlands Using a 3D Radiative Transfer Model and Satellite Observations. Remote Sensing, 17(18), 3223. https://doi.org/10.3390/rs17183223







