LEO Augmentation Effect on BDS Precise Positioning in High-Latitude Maritime Regions

Highlights

What are the main findings?

• The polar-orbiting LEO constellation increased the average number of visible BDS satellites by 70.2% in high-latitude maritime regions and reduced BDS PPP convergence time from 45.3 min to under 1 min (a 97% improvement), while enhancing three-dimensional positioning accuracy by 54.7% to 0.039 m.
• Incorporation of LEO signals increased the fixed solution success rate of short-baseline BDS RTK from 96.5% to 100%, achieving horizontal and vertical positioning accuracies of 1.1 cm (31.5% enhancement) and 6.4 cm (12.3% enhancement), respectively.

What is the implication of the main finding?

• Utilizing real shipborne BDS data from the Southern Hemisphere’s high-latitude waters, this study empirically demonstrates the enhancement effect of polar-orbiting LEO constellations on GNSS-challenged polar maritime areas, providing a real-time centimeter-level navigation solution to support polar shipping and marine resource exploration.
• The research reveals the differential impacts of LEO constellation types (polar versus medium-inclination orbits) and satellite quantities on BDS precise positioning performance in high-latitude regions, thereby providing critical insights for optimizing orbital configurations of LEO constellations in high-latitude and polar areas.

Abstract

The economic and strategic value of high-latitude maritime regions is increasingly significant, yet traditional Global Navigation Satellite Systems remain constrained by unfavorable geometric configurations and slow convergence speeds at high latitudes, failing to meet the growing demand for real-time centimeter-level high-precision positioning in these areas. Benefiting from their rapid motion and superior coverage over high-latitude zones, Low Earth Orbit (LEO) satellites offer an effective means to enhance positioning performance in such regions. This paper uses the real BDS data collected by an unmanned surface vessel in the high-latitude waters of the Southern Hemisphere, jointly simulates polar and medium-inclination LEO constellations, and systematically assess the enhancement effects of LEO augmentation on Precise Point Positioning (PPP) and Real-Time Kinematic (RTK) techniques. The results demonstrate that the polar-orbiting constellation markedly improves the observation environment, increasing the number of visible satellites by 70.2% and reducing the Position Dilution of Precision from 2.4 to 1.7, whereas the medium-inclination orbit constellation offered negligible improvement due to insufficient visibility. The rapid geometric change brought by LEO constellations is the core key to achieving fast convergence. Incorporating LEO observations drastically shortened the BDS PPP convergence time from 45.3 min to under 1 min, achieving a reduction of over 97%. Simultaneously, it improved the three-dimensional Root Mean Square accuracy by 54.7%, from 0.086 m to 0.039 m. Convergence within one minute was consistently achieved when at least 5.4 LEO satellites were included in the solution. Moreover, the addition of LEO signals increased the fixed solution rate of short-baseline RTK from 96.5% to 100%, while improving horizontal and vertical accuracy by 31.5% and 12.3%, respectively. This study confirms that LEO constellations, especially those in polar orbits, can substantially enhance BDS precise positioning performance in high-latitude maritime environments, thereby providing critical technical support for related navigation applications.

1. Introduction

The marine environment is characterized by high complexity and uniqueness. Its vast spatial coverage, dynamically changing hydro-meteorological conditions (e.g., waves, ocean currents, typhoons), and the absence of stable landmarks pose significant challenges to conventional positioning methods [1]. Satellite navigation technology has become the predominant solution for maritime positioning due to its extensive coverage, high accuracy, and strong real-time capability. In recent years, the high-latitude maritime regions have witnessed a surge in economic and strategic importance—such as shipping route development, resource exploration, and military deployment—which has generated an unprecedented demand for high-precision positioning capabilities from satellite navigation systems.

To meet the positioning requirements in high-latitude maritime regions, various satellite navigation technologies have been widely employed. Satellite-Based Augmentation Systems (SBAS), such as the United States’ WAAS and Europe’s EGNOS, enhance positioning accuracy and reliability in mid- and low-latitude areas by providing differential corrections and integrity information. However, their service performance significantly degrades in high-latitude marginal zones, resulting in limited availability [2]. Precise Point Positioning (PPP) technology utilizes precise orbit and clock products to achieve global decimeter- to centimeter-level positioning with a single receiver. Nevertheless, its extended initial convergence time—typically exceeding 30 min—restricts its effectiveness in real-time dynamic applications [3]. Real-Time Kinematic (RTK) technology, which processes observation differences between a reference station and a rover station, can rapidly achieve centimeter-level accuracy over short distances (usually <20 km). Yet, its performance heavily relies on stable and reliable data links as well as reference station infrastructure, making deployment and maintenance in open seas and high-latitude regions extremely costly [4,5].

Although the BeiDou-3 Global Navigation Satellite System (BDS-3) has significantly enhanced coverage in high-latitude regions through its unique hybrid constellation design (GEO + IGSO + MEO), and multi-system (GPS, GLONASS, Galileo, BDS) integrated positioning has become a common strategy to improve positioning performance [6,7], these approaches still fail to fundamentally overcome the inherent limitations of traditional Global Navigation Satellite Systems (GNSS) due to their medium- and high-earth orbits. In high-latitude areas, the number of visible satellites remains relatively low, and the satellite geometry—reflected by a high Position Dilution of Precision (PDOP)—is often poor, resulting in insufficient positioning accuracy, availability, and reliability [8]. This bottleneck directly restricts the execution of critical missions such as safe navigation in ice-infested waters, precise deployment of resource exploration equipment, and marine scientific monitoring. The lack of robust positioning capabilities poses significant risks to operational safety and economic efficiency in these regions.

The rapid development of Low Earth Orbit (LEO) satellite constellations offers new opportunities to address the aforementioned challenges. Due to their low orbital altitudes (typically 500–1500 km), LEO satellites exhibit strong signal received power on the ground. Their high orbital velocity enables rapid geometric changes relative to terrestrial users, which is particularly beneficial for enhancing coverage in high-latitude regions and accelerating ambiguity resolution in precise positioning [9]. With the large-scale deployment of communication constellations (e.g., Starlink, OneWeb, Iridium NEXT) and national projects (e.g., China SatNet), the use of signals from these non-traditional constellations for navigation augmentation has become a research hotspot [10,11,12]. Current research primarily focuses on utilizing LEO broadcast navigation signals or simulated data to evaluate their potential in enhancing GNSS positioning performance, especially in improving PPP convergence speed. Li et al. [13] demonstrated that LEO augmentation can reduce PPP float solution convergence time from 30 min to just a few minutes, and even under one minute under favorable conditions. Li et al. [14] indicated that incorporating 60–288 LEO satellites reduced the PPP-AR initial fixation time from 7.1 min to 0.7–4.8 min while improving positioning accuracy by 60–90%. Specifically, with 288 LEO satellites, triple-frequency PPP-AR achieved initial fixation in merely 55.2 s, representing over a 20% improvement in both convergence speed and accuracy. Gao et al. [15] showed that 150 LEO satellites assisting BDS could achieve global PPP with a convergence time of approximately 1 min, attaining horizontal and vertical accuracies of 5 cm and 10 cm, respectively, with some stations experiencing a 20-fold improvement in convergence speed. Deng et al. [16] further confirmed that with 192 LEO satellites, BDS PPP-RTK could converge within about 10 s even with a station spacing of 500 km. Hong et al. [17] demonstrated through simulations that 180 LEO satellites could improve single-system PPP convergence by over 90% and significantly enhance fixed solution performance and success rate. Gao et al. [18] based on real measured data, showed that even adding only 1–2 LEO satellites could reduce multi-system PPP convergence time by more than 50% and improve accuracy by 10–20%.

LEO constellations offer unique advantages in improving satellite geometry, accelerating convergence speed, and enhancing signal strength [19,20], demonstrating significant potential for positioning applications in high-latitude regions. However, current research in this field still exhibits certain limitations. Most studies are conducted under ideal static land-based conditions or use static receivers to simulate kinematic scenarios. Consequently, the validity of their findings in the highly dynamic and complex environments characteristic of high-latitude waters remains to be verified. Moreover, there is a lack of systematic research on LEO-enhanced GNSS technology for precise positioning in these regions. In light of this context, this study utilizes, for the first time, genuine BDS observation data collected in high-latitude waters, combined with data from two typical types of LEO constellations (polar and inclined orbits). It focuses on investigating the enhancement effects of different LEO orbital constellations and numbers of LEO satellites on the precise positioning performance of BDS in high-latitude areas. The study first introduces the positioning model for LEO-enhanced BDS PPP and RTK, followed by a detailed elaboration of the data processing strategies employed in the experiments. The analysis then focuses on the impacts of different LEO constellation types, the number of LEO satellites, and the rapid geometric changes in the satellite constellation on the kinematic precise positioning performance of BDS in high-latitude marine environments. Finally, the results are discussed in depth, and conclusions are drawn, aiming to provide valuable insights for future research and applications in related fields.

2. Methodology

The fundamental observation equations for the pseudorange and carrier phase observations of GNSS can be expressed as [21]:

$$\left\{\begin{array}{c}{P}_{r,j}^{s,sys}={\rho }_r^{s,sys}+{c(dt}_r^{sys}-{dt}^{s,sys})+c(d_{r,j}^{sys}-d_j^{s,sys})+I_{r,j}^{s,sys}+T_r^{s,sys}+e_{r,j}^{s,sys}\\ L_{r,j}^{s,sys}={\rho }_r^{s,sys}+c({dt}_r^{sys}-{dt}^{s,sys})+{\lambda }_j^{sys}\left(b_{r,j}^{sys}-b_j^{s,sys}\right)+{\lambda }_j^{sys}{N}_{r,j}^{s,sys}-I_{r,j}^{s,sys}+T_r^{s,sys}+{\epsilon }_{r,j}^{s,sys}\end{array}\right.$$

(1)

where the superscripts $s$ and $sys$ denote a specific satellite and the satellite system, respectively, while the subscripts $r$ and $j$ represent the receiver and the carrier frequency, respectively. The term ${\rho }_r^{s,sys}$ represents the geometric distance between the satellite and the receiver antenna phase centers at the signal transmission and reception times. $d{t}^{s,sys}$ and $d{t}_r^{sys}$ denote the satellite and receiver clock errors, respectively; $d_{r,j}^{sys}$ and $d_j^{s,sys}$ represent the receiver and satellite code biases, respectively; $b_{r,j}^{sys}$ and $b_j^{s,sys}$ are the uncalibrated phase delays associated with the receiver and satellite, respectively; $N_{r,j}^{s,sys}$ is the integer ambiguity; ${\lambda }_j^{sys}$ denotes the wavelength; $I_{r,j}^{s,sys}$ represents the ionospheric delay on the signal path with frequency $j$; $T_r^{s,sys}$ is the frequency-independent tropospheric delay; $e_{r,j}^{s,sys}$ and ${\epsilon }_{r,j}^{s,sys}$ denote the measurement noise and multipath errors in the pseudorange and carrier phase observations, respectively. Errors such as antenna phase wind-up, antenna phase center variations, Earth rotation corrections, relativistic delays, and tidal loading effects can be corrected through models and are therefore not explicitly included in the equation.

2.1. LEO-Augmented BDS PPP Model

In PPP, the dual-frequency ionosphere-free combination observation model is typically employed to eliminate ionospheric effects [18]. The pseudorange and carrier phase observation equations for the ionosphere-free combination can be expressed as [22,23,24]:

$$\left\{\begin{array}{c}{ P}_{r,IF}^{s,sys}={\rho }_r^{s,sys}+c{\overline{dt}}_r^{sys}-c{\overline{dt}}^{s,sys}+M_{w,r}^{s,sys}{d}_{w,r}+e_{r,IF}^{s,sys}\\ L_{r,IF}^{s,sys} ={\rho }_r^{s,sys}+c{\overline{dt}}_r^{sys}-c{\overline{dt}}^{s,sys}+{\overline{N}}_{r,IF}^{s,sys}+M_{w,r}^{s,sys}{d}_{w,r}+{\epsilon }_{r,IF}^{s,sys}\end{array}\right.$$

(2)

with

$$\left\{\begin{array}{c}c{\overline{dt}}_r^{sys}=c{dt}_r^{sys}+d_{r,IF}^{sys}\\ c{\overline{dt}}^{s,sys}=cd{t}^{s,sys}+d_{IF}^{s,sys}\\ {\overline{N}}_{r,IF}^{s,sys}=N_{r,IF}^{s,sys}+b_{r,IF}^{sys}-b_{IF}^{s,sys}-d_{r,IF}^{sys}+d_{IF}^{s,sys}\end{array}\right.$$

(3)

where ${ P}_{r,IF}^{s,sys}$ and $L_{r,IF}^{s,sys}$ denote the ionosphere-free combinations of pseudorange and carrier-phase observations, respectively. The terms $d_{r,IF}^{sys}$and $d_{IF}^{s,sys}$ represent the ionosphere-free pseudorange hardware delays of the receiver and the satellite, whereas $b_{r,IF}^{sys}$and $b_{IF}^{s,sys}$ are the corresponding ionosphere-free carrier-phase delays. The parameter $N_{r,IF}^{s,sys}$ signifies the integer ambiguity of the ionosphere-free combination. The zenith wet delay of the troposphere is given by $d_{w,r}$ and its associated mapping function is denoted by $M_{w,r}^{s,sys}$. All remaining symbols retain the definitions specified in Equation (1).

In LEO-augmented PPP, the observations from LEO satellites must be processed jointly with those from GNSS satellites, effectively treating the LEO constellation as an independent satellite navigation system. In this study, simulated LEO observations are combined with real BDS measurements for experimental validation. The simulated LEO observations at the receiver already incorporate the principal modeled error sources, namely satellite clock offsets, solid-Earth and ocean-tidal displacements, relativistic effects, and carrier-phase wind-up. The pseudorange noise and carrier-phase noise were set to 0.5 m and 0.003 m, respectively. The frequencies of the first and second frequency bands for LEO, denoted as L1 and L2, were configured at 1575.42 MHz and 1227.6 MHz, respectively. Consequently, the ionosphere-free pseudorange and carrier-phase observation equations for the combined LEO-BDS constellation can be expressed as:

$$\left\{\begin{array}{c}{ P}_{r,IF}^{s,C}={\rho }_r^{s, C}+c{\overline{dt}}_r^C-c{\overline{dt}}^{s,C}+M_{w,r}^{s,C}{d}_{w,r}+e_{r,IF}^{s,C}\\ L_{r,IF}^{s,C} ={\rho }_r^{s, C}+c{\overline{dt}}_r^C-c{\overline{dt}}^{s,C}+{\overline{N}}_{r,IF}^{s, C}+M_{w,r}^{s,C}{d}_{w,r}+{\epsilon }_{r,IF}^{s, C}\\ { P}_{r,IF}^{s,L}={\rho }_r^{s, L}+c{\overline{dt}}_r^L-c{\overline{dt}}^{s,L}+e_{r,IF}^{s,L}\\ L_{r,IF}^{s,L} ={\rho }_r^{s, L}+c{\overline{dt}}_r^L-c{\overline{dt}}^{s,L}+{\overline{N}}_{r,IF}^{s, L}+{\epsilon }_{r,IF}^{s, L}\end{array}\right.$$

(4)

In the equation, the symbols $C$ and $L$ denote BDS and LEO, respectively. All remaining symbols retain the definitions given in Equations (1) and (2).

2.2. LEO-Augmented BDS RTK Model

For short baselines, if the effects of atmospheric delay errors are neglected, the functional model of GNSS RTK positioning can be expressed as [25,26]:

$$\left\{\begin{array}{c}{P}_{rb,j}^{kl,sys}=P_{rb,j}^{k,sys}-P_{rb,j}^{l,sys}={\rho }_{rb}^{kl,sys}+e_{rb,j}^{kl,sys}\\ L_{rb,j}^{kl,sys}=L_{rb,j}^{kl,sys}-L_{rb,j}^{kl,sys}={\rho }_{rb}^{kl,sys}+{\lambda }_j^{sys}{N}_{rb,j}^{kl,sys}+{\epsilon }_{rb,j}^{kl,sys}\end{array}\right.$$

(5)

where $P_{rb,j}^{kl,sys}$ and $L_{rb,j}^{kl,sys}$ denote the inter-satellite and inter-station double-difference observations of pseudorange and carrier phase, respectively; the superscripts $k$ and $l$ refer to the satellites, while the subscripts $r$ and $b$ designate the rover and base stations. The term $N_{rb,j}^{kl,sys}$ represents the corresponding double-difference integer ambiguity. All other symbols retain the definitions specified in Equation (1).

Similarly, in LEO-augmented RTK, the joint processing of LEO satellite observation data and GNSS satellite observation data requires treating the LEO constellation as an independent satellite navigation system. Therefore, the short-baseline RTK observation equation for the LEO-augmented BDS combined system can be expressed as:

$$\left\{\begin{array}{c}{P}_{rb,j}^{kl,C}={\rho }_{rb}^{kl,C}+e_{rb,j}^{kl,C}\\ L_{rb,j}^{kl,C}={\rho }_{rb}^{kl,C}+{\lambda }_j^{sys}{N}_{rb,j}^{kl,C}+{\epsilon }_{rb,j}^{kl,C}\\ P_{rb,j}^{kl,L}={\rho }_{rb}^{kl,L}+e_{rb,j}^{kl,L}\\ L_{rb,j}^{kl,L}={\rho }_{rb}^{kl,L}+{\lambda }_j^{sys}{N}_{rb,j}^{kl,L}+{\epsilon }_{rb,j}^{kl,L}\end{array}\right.$$

(6)

In this equation, $C$ and $L$ represent BDS and LEO, respectively. The definitions of all other symbols remain consistent with Equations (1) and (5).

2.3. Data Processing Methods

The experimental strategy employed in this study is detailed in

Table 1. Data processing strategy for PPP and RTK.

Parameters	Processing Settings
	PPP Float Solution	RTK Solution (Short Baseline)
Observations	BDS: B1I/B3I, LEO: L1/L2	BDS: B1I/B3I, LEO: L1/L2
Sampling rate	1s	1s
Elevation cutoff	10°	10°
Observation weight	Elevation dependent weight	Elevation dependent weight
Satellite orbit and clock	BDS: WUM precise products, LEO: simulated products	BDS: WUM * precise products, LEO: simulated products
Ionosphere delay	First-order eliminated with IF combination	Eliminated by double-difference
Satellite PCOs/PCVs	Igs14.atx	Eliminated by double-difference
Phase wind-up	Model correct [27]	Model correct [27]
Tidal displacements	IERS 2010 [28]	IERS 2010 [28]
Earth rotation effect, Relativistic effect, Troposphere dry delay	IERS 2010 [28]	Eliminated by double-difference
Estimator	Kalman filtering	Kalman filtering
Troposphere wet delay	Estimation,	Eliminated by double-difference
Phase ambiguities	Estimation, Constant, Float	Estimation, Constant, Fix, LAMBDA
Receiver clock	Estimation, White noise	Eliminated by double-difference
Station coordinate	Estimation, Epoch-wise kinematic mode	Estimation, Epoch-wise kinematic mode

* WUM: Wuhan University Multi-GNSS Analysis Center.

. Self-developed software was utilized for PPP and RTK solutions using the collected data.

This study employs a dual-frequency ionosphere-free (IF) PPP model to process dual-frequency observations from BDS and LEO. The data sampling interval is set to one second, the elevation cutoff is fixed at 10°, and observations are weighted by elevation angle. BDS precise orbit and clock products are provided by the GNSS Research Center of Wuhan University, whereas LEO precise orbits and clocks are derived from simulation. First-order ionospheric delay is eliminated through the dual-frequency ionosphere-free linear combination; satellite phase-center offsets and variations (PCO/PCV) are corrected using antenna phase–center models. Tropospheric dry delay, Earth-rotation effects, relativistic effects, phase wind-up, and solid-Earth and ocean-tidal displacements are corrected with the corresponding physical models. A Kalman filter is adopted as the estimator, treating zenith wet delay, float ambiguities, receiver coordinates, and receiver clock offsets as unknown parameters to be estimated jointly.

Building on the PPP configuration, short-baseline RTK processing is performed with the same Kalman-filter estimator using dual-frequency observations from both BDS and the simulated LEO constellation at rover and base stations. Identical data settings are employed: a 1 s sampling rate, a 10° elevation cutoff, and elevation-dependent weighting. BDS precise products from Wuhan University and the simulated LEO precise products are again utilized. Under short-baseline conditions, the inter-satellite and inter-station double-difference observations effectively eliminate satellite PCO/PCV biases, receiver clock offsets, Earth-rotation effects, and relativistic effects. Provided that temporal and spatial variations in the atmospheric delay are negligible, ionospheric and tropospheric delays are likewise canceled in the double-difference. Non-common errors such as phase wind-up and tidal displacements cannot be fully removed by double-difference and are therefore corrected with the appropriate models. Float ambiguity estimates are propagated via the Kalman filter and subsequently fixed using the LAMBDA method.

3. Experimental Analysis

The experimental data were collected in the calm waters of the high-latitude region in the Southern Hemisphere using a USV equipped with a self-developed device and an Applanix POS MV system. The data acquisition period spanned from 07:00 to 10:00 on 28 January 2023, with a sampling rate of 1 s. A power splitter was used to connect the antenna to both the self-developed device and the POS MV system, ensuring identical observation conditions. The Applanix POS MV, developed by Trimble Inc., Westminster, CO, USA, is a high-precision maritime positioning and orientation system capable of achieving centimeter-level positioning accuracy. It is internationally recognized as a benchmark for high-performance navigation systems and demonstrates exceptional RTK performance, with horizontal and vertical positioning accuracies of 1 cm and 1.5 cm, respectively.

Given the intrinsic difficulty of establishing a ground-truth position in maritime environments, the evaluation adopted in this study follows the widely accepted practice of using an external reference derived from post-processed Inertial Explorer (IE) solutions. Specifically, raw measurements collected by the POS MV system were imported into IE, which generated RTK solutions subsequently treated as the ground truth for assessing positioning performance.

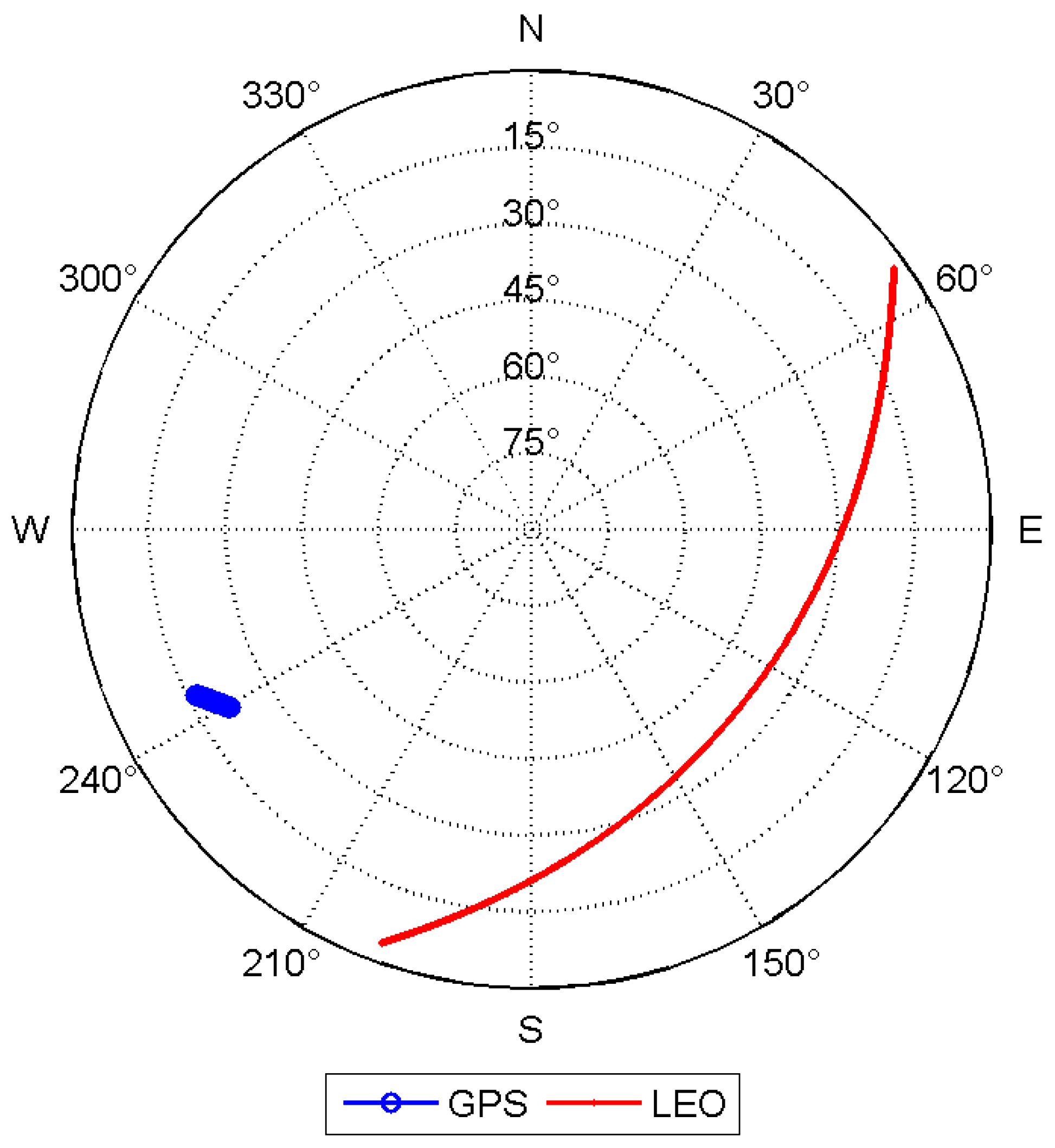
3.1. Observation Condition

The experiment simulated a total of 160 LEO satellites, which were divided into two constellations based on their orbital characteristics. The first constellation consisted of 70 polar-orbiting satellites with an inclination of 90°, uniformly distributed across 6 orbital planes. The second constellation comprised 90 satellites in inclined orbits with an inclination of 60°, deployed across 10 orbital planes. The simulated LEO satellite data were generated using software developed through secondary development based on the Panda platform. Due to the distinct orbital configurations of the two constellations, their satellite visibility characteristics over high-latitude regions differed significantly. Hereafter, the polar-orbit constellation and the inclined-orbit constellation are referred to as LEO-L and LEO-M, respectively.

To analyze the number of visible satellites and the spatial geometry distribution over the station during the observation period under BDS-only, BDS augmented with the polar-orbiting constellation (BDS/LEO-L), and BDS augmented with the medium-inclination constellation (BDS/LEO-M), Figure 1 illustrates the variations in the number of visible satellites and PDOP values under a cutoff elevation angle of 10°.

As can be seen from Figure 1, with BDS alone, the station consistently observes approximately ten satellites. After adding LEO-L, rapid fluctuations occur: the satellite count oscillates between 10 and 23, and the PDOP drops markedly, remaining below 2.0 for most of the session. In contrast, the addition of LEO-M yields far smaller changes in both satellite number and PDOP relative to standalone BDS, particularly during the latter half of the observation period; indeed, for a 10° elevation cutoff, the station records zero LEO-M satellites after mid-session.

To provide a more intuitive assessment of satellite visibility and PDOP during the observation period,

Table 2. Statistical values of visible satellites and PDOP for BDS, BDS/LEO-L, and BDS/LEO-M (10° cutoff).

System	Satellite Number			PDOP
	Max	Min	Mean	Max	Min	Mean
BDS	13	8	10.4	4.9	1.6	2.4
BDS/LEO-L	23	10	17.7	3.4	1.2	1.7
BDS/LEO-M	13	8	10.5	4.9	1.6	2.3

summarizes the maximum, minimum, and mean values of the number of visible satellites and PDOP for the station under BDS-only, BDS/LEO-L, and BDS/LEO-M configurations at a 10° elevation cutoff.

Table 2 indicates that, with a 10° elevation cutoff:

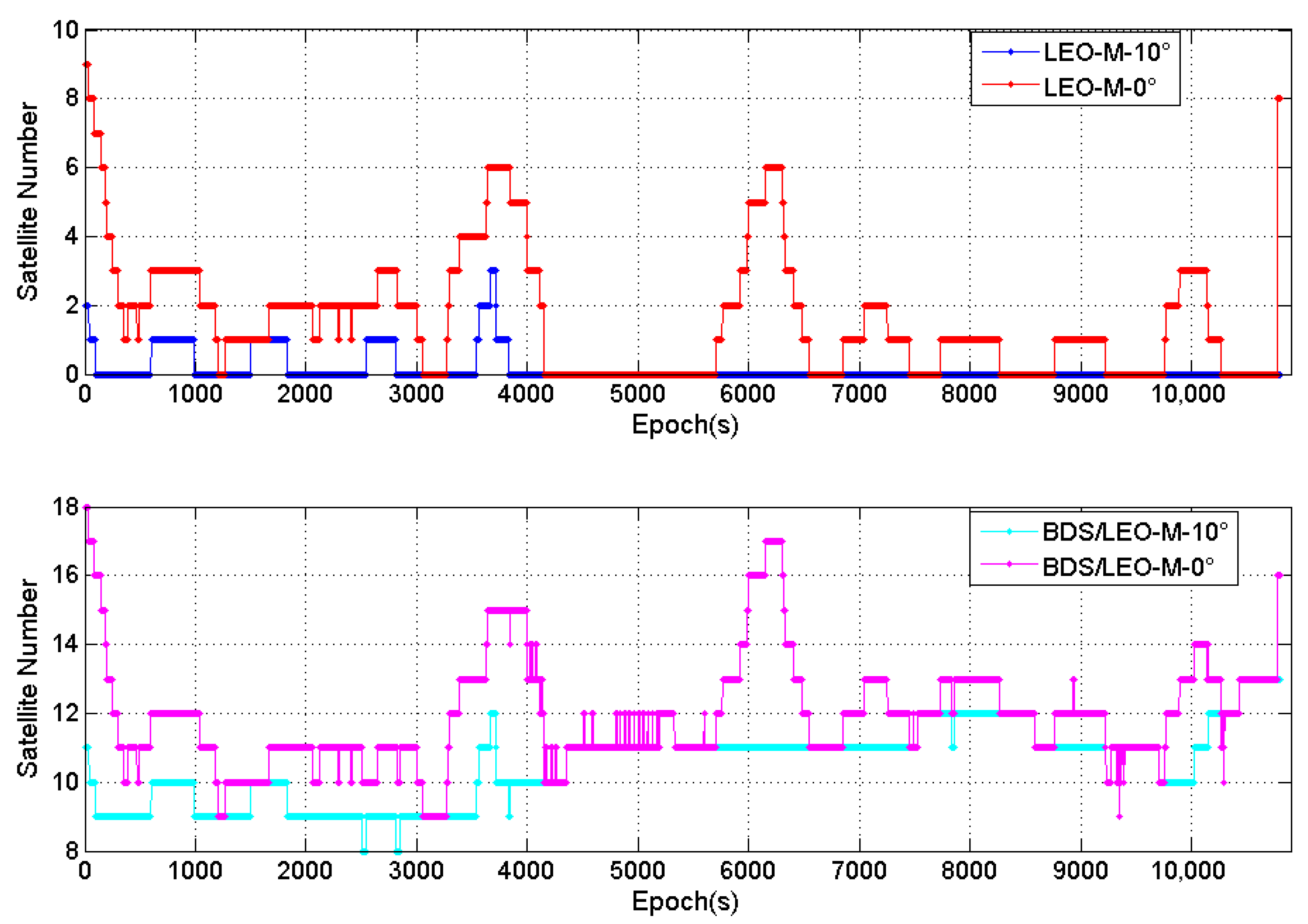
• Compared to BDS alone, BDS/LEO-L shows an average increase of 7.3 in the number of visible satellites. The integration of LEO effectively enhances the number of satellites visible to the station. The maximum PDOP decreases from 4.9 to 3.4, while the average PDOP improves from 2.4 to 1.7. The high orbital inclination of the polar-orbiting satellites significantly enhances observation conditions in high-latitude regions.
• The maximum and minimum PDOP values for BDS/LEO-M and BDS are identical, with the average PDOP showing a marginal improvement of 0.1. During the observation period, the average number of visible satellites increased by only 0.1.

To investigate the visibility of the LEO mid-inclination constellation at high latitudes, Figure 2 presents the number of LEO-M and BDS/LEO-M satellites tracked by the station with no elevation cutoff and with a 10° elevation cutoff, and

Table 3. Statistical summary of visible LEO-M and BDS/LEO-M satellites (No cutoff vs. 10° cutoff).

Term	LEO-M-10°	LEO-M-0°	BDS/LEO-M-10°	BDS/LEO-M-0°
max	3	9	13	18
min	0	0	8	9
mean	0.2	1.6	10.5	11.9

provides a detailed statistical summary of these results.

As illustrated in Figure 2 and Table 3, during the observation period, the maximum number of LEO-M satellites observed by the station was 9, the minimum was 0, with an average of 1.6. When the elevation cutoff angle was increased to 10°, the maximum number dropped to only 3, and the average was merely 0.2. For the BDS/LEO-M combination, when the elevation cutoff was set to 10°, the average number of observed satellites decreased from 11.9 to 10.5, a trend consistent with the change observed in LEO-M alone.

As can also be observed from Figure 2, the station was not able to continuously track LEO-M satellites. The visibility percentage is defined as (number of epochs with LEO-M observations/total number of epochs) × 100%. The statistical results of the visibility percentage for LEO-M are presented in Figure 3.

Statistical analysis shows that with a 0° elevation cutoff, the visibility percentage of LEO-M satellites during the observation period was 63.1%. When the elevation cutoff was raised to 10°, the visibility percentage was only 12.8%. Consequently, the number of effective LEO-M satellites observable from the high-latitude station is extremely limited. This result demonstrates that the design of a LEO polar constellation is more capable of significantly improving the satellite geometry in high-latitude regions.

3.2. LEO-Augmented BDS PPP

LEO satellites, characterized by low altitudes and high orbital velocities, offer distinctive advantages in improving satellite geometry, accelerating convergence, and enhancing signal strength. Consequently, investigating how LEO constellation type and satellite count influence BDS PPP performance in high-latitude maritime regions is of considerable practical significance. The following analysis separately addresses two research aspects: the influence of LEO constellation type on BDS PPP performance in high-latitude maritime regions, and the influence of LEO satellite count on this performance.

3.2.1. Impact of LEO Constellation Type on BDS PPP in High-Latitude Maritime Regions

To investigate the impact of LEO constellation type on BDS PPP performance in high-latitude maritime areas, the PPP processing strategy described in Chapter 3 was applied to four distinct scenarios: (i) BDS-only, (ii) BDS augmented with the full LEO constellation, (iii) BDS combined with the LEO-L polar-orbit constellation, and (iv) BDS combined with the LEO-M mid-inclination constellation. The corresponding error time series are presented in Figure 4.

As observed in Figure 4, compared to the BDS-only and BDS/LEO-M PPP solutions, the BDS/LEO and BDS/LEO-L combinations exhibit significantly faster convergence in all East-North-Up (ENU) directions, particularly in the Up component. Convergence is considered achieved when the planar and vertical positioning errors simultaneously fall below 0.2 m and remain under this threshold for the subsequent 5 min. Figure 5 presents a statistical comparison of the convergence time and positioning accuracy in the East (E), North (N), and Up (U) directions for the four satellite constellation configurations: BDS-only, BDS/LEO, BDS/LEO-L, and BDS/LEO-M. The corresponding convergence times and positioning accuracy values for these configurations are further summarized in

Table 4. Statistical results of PPP convergence time, STD, and RMS for BDS and BDS/LEO (10° cutoff).

System	Convergence Time (min)	STD 1 (m)				RMS 2 (m)
		E	N	U	3D	E	N	U	3D
BDS	45.32	0.016	0.014	0.078	0.081	0.017	0.017	0.082	0.086
BDS/LEO	0.93	0.013	0.008	0.028	0.032	0.014	0.008	0.036	0.039
BDS/LEO-L	0.95	0.013	0.008	0.029	0.032	0.015	0.008	0.036	0.039
BDS/LEO-M	45.32	0.016	0.014	0.078	0.081	0.017	0.017	0.082	0.086

¹ STD: Standard Deviation. ² RMS: Root Mean Square.

.

Based on the statistical data, the following observations can be made:

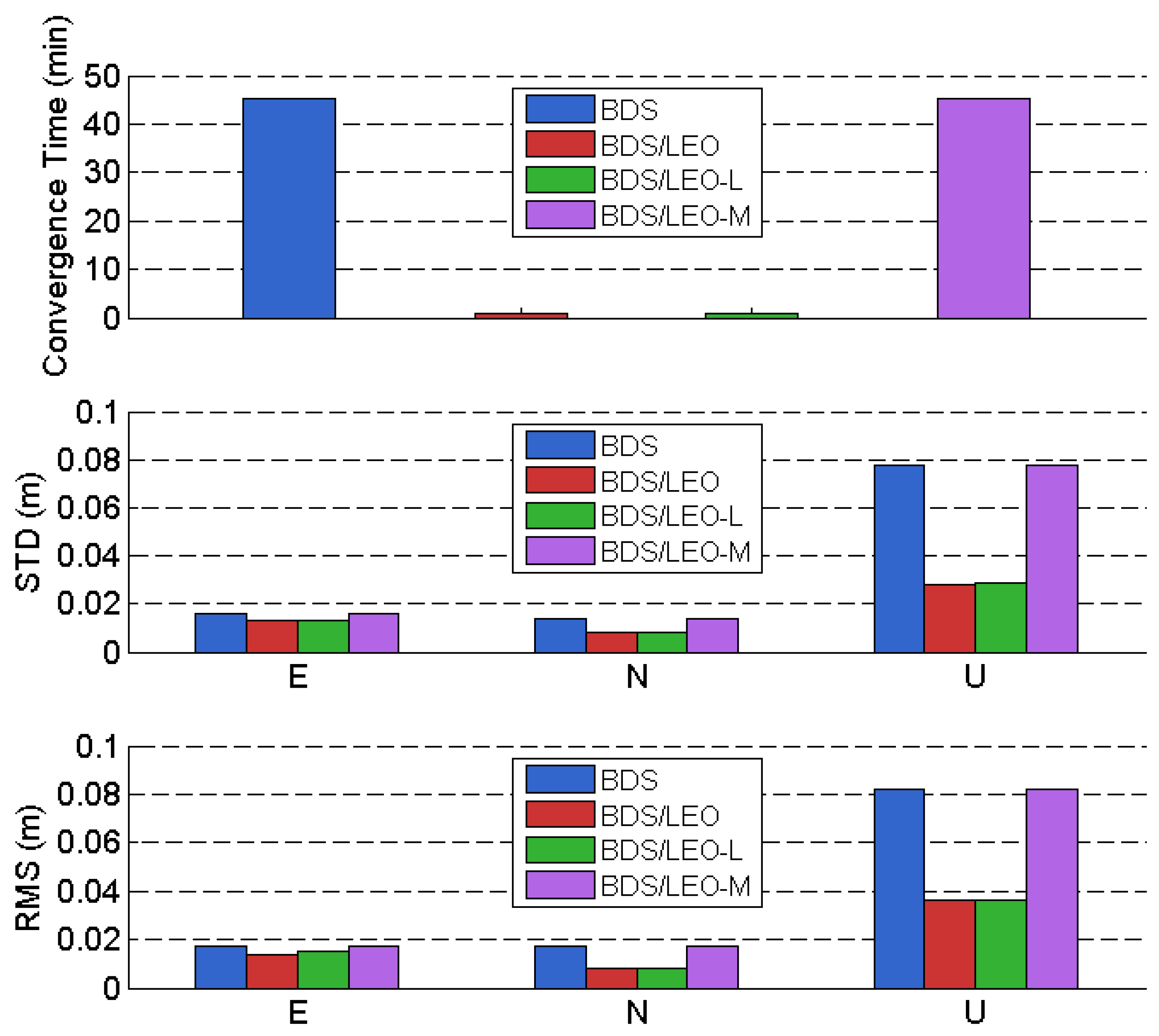
• In the high-latitude maritime regions of the Southern Hemisphere, BDS alone demonstrates centimeter-level dynamic PPP capability. The convergence time for BDS PPP is approximately 45 min. The Standard Deviations (STD) in the E, N, and U directions are 0.016 m, 0.014 m, and 0.078 m, respectively, while the corresponding Root Mean Square (RMS) values are 0.017 m, 0.017 m, and 0.082 m.
• The integration of LEO satellites significantly shortens the BDS PPP convergence time and effectively enhances positioning accuracy. The convergence time for BDS/LEO is approximately 1 min. The STD values in the E, N, and U directions are 0.013 m, 0.008 m, and 0.028 m, respectively, with RMS values of 0.014 m, 0.008 m, and 0.036 m. The 3D positioning accuracy, represented by STD and RMS, is 0.032 m and 0.039 m, respectively. Compared to BDS-only PPP, the convergence time is improved by 97.8%, while the STD and RMS are enhanced by 60.5% and 54.7%, respectively.
• LEO polar-orbiting satellites play a crucial role in improving PPP performance in high-latitude regions. The convergence time for BDS/LEO-L is 0.95 min, with 3D positioning accuracy (STD and RMS) of 0.032 m and 0.039 m, respectively. In contrast, the convergence time for BDS/LEO-M is 45.3 min, with 3D STD and RMS of 0.081 m and 0.086 m, respectively. Compared to the standalone BDS PPP, the addition of LEO polar-orbiting satellites drastically improves the convergence speed by 98.0%. However, the incorporation of LEO-M does not reduce the PPP convergence time or enhance positioning accuracy. As concluded in the analysis of LEO-M visibility conditions in Section 3.1, under a 10° elevation cutoff, the average number of observable LEO-M satellites in the experimental high-latitude area of the Southern Hemisphere is merely 0.2. Consequently, medium-inclination orbit satellites provide no substantial benefit for PPP performance in high-latitude regions.

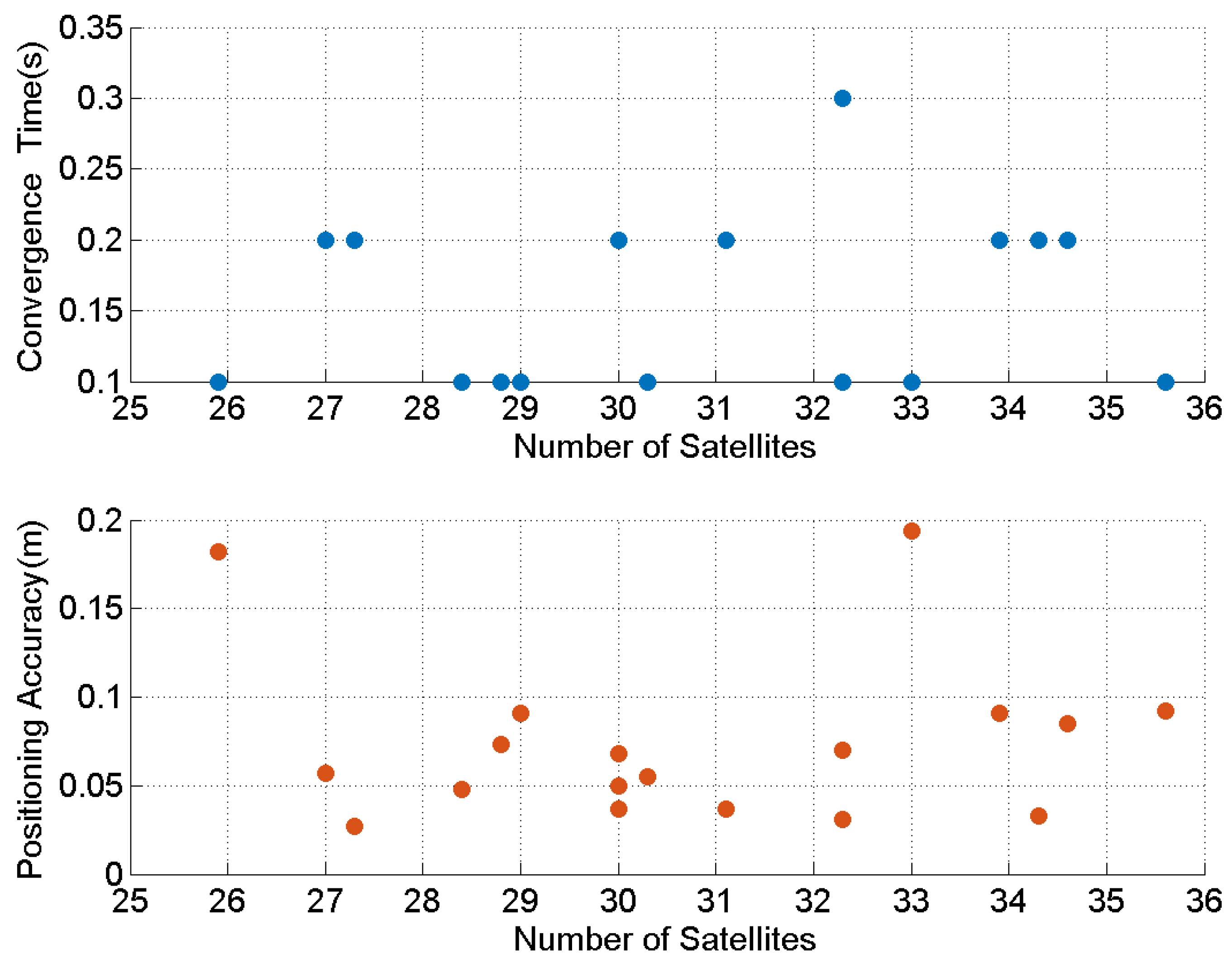
3.2.2. Impact of LEO Satellite Count on BDS PPP in High-Latitude Maritime Regions

Due to the low orbital altitude and high operational velocity of LEO satellites, the constellation geometry observed from a station changes rapidly over short time intervals. The enhancement effect of LEO on GNSS is contingent upon both the number of visible satellites and their geometric distribution. To investigate the impact of the number of LEO satellites on BDS PPP performance, this section analyzes the LEO satellite count and the corresponding PPP performance metrics aggregated in ten-minute intervals. The observation data from the station were divided into 18 consecutive ten-minute segments. Figure 6 illustrates the variation in the number of visible satellites for both BDS-only and BDS/LEO configurations throughout the observation period. The upper subplot shows the number of observed BDS and BDS/LEO satellites, while the lower subplot presents the maximum, minimum, and average number of BDS/LEO satellites within each ten-minute segment across the 18 intervals. The term “Group” in the figures refers to the grouping of data at every ten-minute interval.

As illustrated in Figure 6, the inclusion of LEO satellites induces pronounced short-term fluctuations in the number of tracked satellites. Across the 18 analyzed epochs, the observed LEO satellite count varied between 4.3 and 9.8, with the average satellite counts being 9.0, 7.7, 9.4, 9.4, 4.3, 7.1, 9.5, 5.5, 8.6, 6.6, 5.3, 9.2, 7.4, 9.4, 6.8, 4.5, 9.8, and 7.7, respectively.

To investigate the impact of LEO satellite quantity on BDS PPP performance, PPP solutions were computed for both BDS-only and BDS/LEO configurations at 10 min intervals. Figure 7 and Figure 8 present the error series of these PPP solutions along with the corresponding parameters and number of satellites used in the solution for each respective time epoch.

As evidenced in Figure 7 and Figure 8, the number of satellites utilized in the BDS-only PPP solution is notably lower compared to the BDS/LEO PPP scenario. While the BDS-only system fails to converge within a 10 min window, the BDS/LEO integration achieves rapid convergence consistently across all observed intervals. To examine the impact of LEO satellite quantity on BDS PPP convergence time and positioning accuracy in high-latitude regions, Figure 9 provides a statistical overview of the average number of LEO satellites included in the solution during the initial two minutes of convergence, along with the associated convergence time and accuracy metrics. These results are further detailed in

Table 5. Statistical summary of convergence time, RMS, and number of LEO satellites used in BDS/LEO PPP at 10 min intervals.

Group	Convergence Time (min)	RMS-3D (m)	LEO Sat Number
1	0.9	0.056	7.2
2	0.1	0.049	10.7
3	0.6	0.042	7.8
4	0.3	0.049	10.8
5	0.7	0.079	6.0
6	1.6	0.216	3.4
7	0.8	0.112	13.0
8	0.3	0.098	6.8
9	0.6	0.109	5.4
10	0.3	0.158	10.5
11	4.0	0.240	2.5
12	0.3	0.113	10.0
13	0.3	0.194	6.8
14	0.4	0.102	8.9
15	0.4	0.157	9.4
16	Failed	/	4.0
17	0.4	0.173	9.7
18	0.5	0.186	5.5

.

Figure 9 and Table 5 jointly demonstrate that the incorporation of LEO satellites markedly improves convergence time. With the exception of the sixteenth data set, all remaining seventeen sets converged within 10 min; furthermore, 83.3% (15 of 18) achieved convergence in less than 1 min. For the sixth data set, the convergence time and three-dimensional positioning accuracy are 1.6 min and 0.216 m, respectively, corresponding to 3.4 LEO satellites in the solution. The 11th data set exhibited a convergence time of 4.0 min and a three-dimensional positioning accuracy of 0.240 m. Despite having only 2.5 LEO satellites participating in the solution, it still demonstrated a significant improvement effect on PPP. The remaining fifteen data sets all attained convergence times and positioning accuracies better than 1 min and 0.200 m, supported by more than 5.4 LEO satellites.

To provide a more intuitive visualization of how variations in the number of LEO satellites influence convergence time and positioning accuracy for BDS PPP in high-latitude regions, Figure 10 presents scatter plots correlating the number of LEO satellites employed in the solution with both convergence time and positioning accuracy for the seventeen qualifying data sets.

Analysis of the results in Figure 10 reveals a significant negative correlation between the number of participating LEO satellites and both the PPP convergence time and positioning accuracy. This indicates that increasing the number of LEO satellites can effectively accelerate PPP convergence and improve positioning performance, although the improvement does not follow a simple linear trend.

In cases with a limited number of LEO satellites (e.g., 2 to 5), each additional satellite leads to a pronounced reduction in convergence time. However, as the number of LEO satellites increases beyond 5, the rate of improvement gradually decreases, indicating that the system approaches a performance saturation point. It is noteworthy that even when fewer than 4 LEO satellites are involved in the solution, their accelerating effect on the convergence process remains highly pronounced. Compared to medium and high Earth orbit GNSS satellites, the LEO constellation demonstrates a more substantial enhancement in the convergence speed of PPP.

In terms of positioning accuracy, the BDS/LEO PPP solution consistently achieves an accuracy within 0.2 m when more than 5 LEO satellites are included. Unlike the convergence time, however, positioning accuracy is influenced not only by the number of satellites but also by other factors such as satellite geometry and observation quality. Importantly, when the number of participating LEO satellites exceeds 5.4, the BDS/LEO PPP convergence time can be optimized to within 1 min. This threshold offers valuable insight for optimizing the configuration of LEO-augmented systems.

As demonstrated in Section 3.2.1, polar-orbiting LEO constellations provide a pronounced augmentation effect at high latitudes. To further quantify how the size of the LEO constellation (i.e., the number of LEO satellites) impacts BDS PPP performance, the constellation is expanded to 180 and 288 polar-orbiting satellites. Consistent with the previous experiment, a combined LEO/BDS PPP solution is computed every 10 min. Hereafter, the 180-satellite and 288-satellite augmented solutions are abbreviated as BDS/LEO-180 and BDS/LEO-288, respectively.

Table 6. Convergence time, RMS, and number of LEO satellites used in the PPP solution at 10-Minute intervals for BDS/LEO-180 and BDS/LEO-288.

Group	Convergence Time (min)		RMS-3D (m)		LEO Sat Number
	LEO-180	LEO-288	LEO-180	LEO-288	LEO-180	LEO-288
1	0.4	0.2	0.034	0.027	18.1	28.4
2	0.5	0.2	0.034	0.033	20.3	33.6
3	0.2	0.1	0.041	0.031	19.2	31.9
4	0.2	0.2	0.035	0.037	19.0	31.6
5	0.3	0.2	0.045	0.037	18.4	30.0
6	0.4	0.2	0.093	0.050	17.1	29.1
7	0.1	0.2	0.054	0.068	19.6	30.1
8	0.3	0.2	0.116	0.085	21.0	34.4
9	0.2	0.1	0.055	0.055	21.9	29.5
10	0.2	0.2	0.083	0.057	16.3	27.5
11	0.3	0.1	0.074	0.048	19.8	28.9
12	0.3	0.3	0.092	0.070	20.5	32.1
13	0.1	0.2	0.042	0.091	21.4	34.0
14	0.3	0.1	0.101	0.194	19.1	32.6
15	0.2	0.1	0.106	0.073	17.9	28.1
16	0.2	0.1	0.067	0.182	16.0	26.0
17	0.1	0.1	0.104	0.091	18.2	29.7
18	0.3	0.1	0.082	0.092	20.8	34.7

and Figure 11 summarize the positioning accuracy of PPP for BDS/LEO-180 and BDS/LEO-288 and the average number of LEO satellites contributing to the solution during the minute immediately preceding convergence.

As shown in Table 6 and Figure 11, the LEO-288 constellation demonstrates a clear advantage in overall performance compared to the LEO-180 constellation, along with a significant increase in the number of available satellites. When using the 180-satellite polar-orbiting constellation, the number of LEO satellites involved in the solution ranges between 16 and 22, with the convergence time consistently within 0.5 min and positioning accuracy maintained below 0.12 m. In contrast, with the 288-satellite polar constellation, the number of LEO satellites used in the solution ranges from 26 to 35. The convergence time is within 0.2 min or less for 17 out of 18 data sets, with only one instance at 0.3 min. Positioning accuracy remains below 0.2 m, with the majority of results stabilized below 0.1 m. In terms of convergence time, LEO-288 requires an average of only 0.16 min, which is 38.5% faster than the 0.26 min required by LEO-180. Regarding positioning accuracy, both constellations perform similarly: LEO-180 achieves an average 3D-RMS of 0.071 m, while LEO-288 reaches 0.077 m, indicating a minor difference and meeting the requirement for centimeter-level high-precision positioning. In visible satellite count, LEO-288 shows a notable advantage, with an average of 30.8 visible satellites, an increase of 60.4% compared to the 19.2 satellites observed with LEO-180. This provides the system with greater observational redundancy. The expansion of the constellation size increases the number of satellites visible to the user, effectively enhancing the overall performance of the navigation system, particularly in convergence speed and system availability.

Therefore, increasing the size of the LEO constellation can further enhance the PPP performance of BDS in high-latitude regions. For the 160-satellite hybrid constellation (70 polar-orbiting + 90 inclined-orbiting satellites), the 180-satellite polar-orbiting constellation, and the 288-satellite polar-orbiting constellation, the average convergence times for BDS-augmented PPP in high-latitude maritime areas are 0.47 min, 0.26 min, and 0.16 min, respectively, while the corresponding 3D positioning accuracies are 0.071 m, 0.077 m, and 0.118 m. Note that the positioning statistics for the 160-satellite hybrid constellation only include epochs where more than five LEO satellites are tracked prior to convergence, as the positioning performance reaches a stable state under this condition. Different constellation designs can meet diverse application requirements. Although the enhancement effect of LEO improves with an increase in satellite quantity, the degree of improvement is not substantial.

We further analyzed the relationship between the number of visible satellites and the enhancement effect provided by LEO. Figure 12 and Figure 13 present scatter plots illustrating the correlation between the number of LEO satellites involved in the solution and both the convergence time and positioning accuracy for the 18 sets of BDS/LEO PPP results under the 180- satellite and 288-satellite LEO constellations, respectively.

It is evident that under both constellation configurations, the number of LEO satellites involved in the solution shows no significant correlation with either PPP convergence time or positioning accuracy. This indicates that once the number of satellites reaches a certain threshold, the enhancement performance of LEO tends to stabilize. With reference to Figure 10, Figure 12 and Figure 13, when more than five LEO satellites are used in the solution, the BDS/LEO PPP convergence time is less than 1 min, and the three-dimensional positioning accuracy is better than 0.2 m. When the number exceeds eight satellites, the convergence time can be further reduced to within 0.5 min, and the positioning accuracy improves to 0.1 m. Although additional increases in satellite count lead to further improvements in enhancement performance, the gains are not substantial. While expanding the constellation size can improve enhancement performance, it also raises deployment costs. Practical applications should therefore consider specific scenario requirements and cost-effectiveness in the design of LEO constellations. The experimental results provide comprehensive reference data regarding the service performance of LEO-augmented BDS in high-latitude regions.

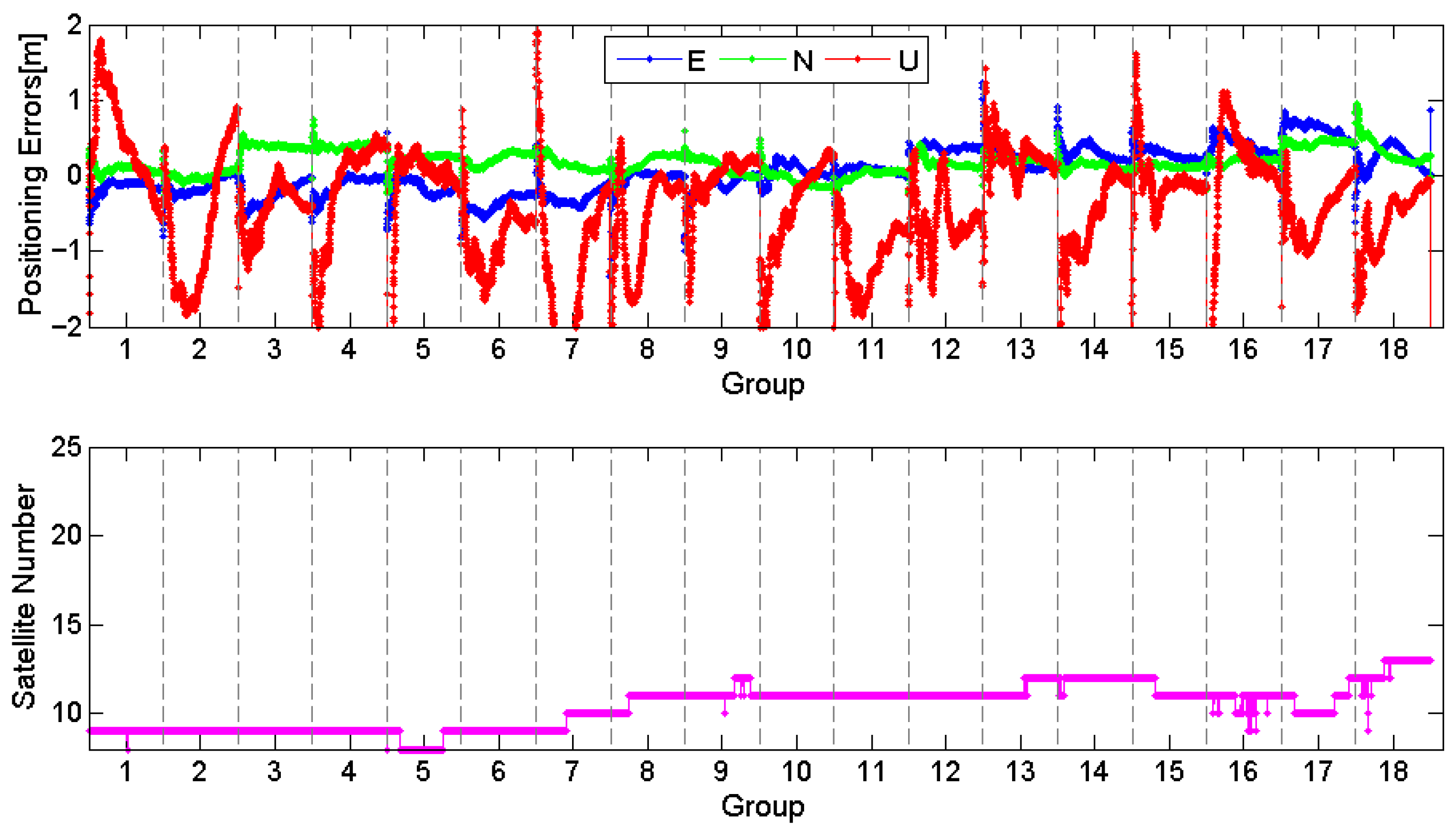
3.2.3. Impact of LEO Rapid Geometry Variations on BDS PPP Convergence in High-Latitude Maritime Regions

The rapid motion of LEO satellites results in continuously changing observation geometry, which effectively reduces the correlation among observation equations. To further investigate the contribution of fast-changing LEO geometry to the convergence performance of precise positioning, this study compares and analyzes the enhancement effects of GPS and LEO constellations on the convergence speed of BDS PPP.

Figure 14 illustrates the sky trajectories of GPS and LEO satellites over a 15 min period. Compared to GPS satellites, LEO satellites, due to their lower orbital altitude and higher velocity, exhibit significantly longer sky trajectories within the same time interval. This indicates that LEO constellations can provide more dynamic geometric diversity. Such rapid geometric variation effectively reduces the temporal correlation among observation equations, improves parameter estimability, and fundamentally alleviates the slow convergence of carrier-phase ambiguity parameters. This offers a new avenue for achieving rapid precise positioning.

To quantitatively evaluate the improvement in convergence performance brought by the LEO constellation, PPP resolution experiments were conducted using BDS/GPS and BDS/LEO combinations, respectively. The statistical results are presented in

Table 7. Convergence time of BDS/GPS and BDS/LEO PPP.

System	Convergence Time (s)
BDS/GPS	56
BDS/LEO	729

. As shown in the table, the average convergence time for BDS/GPS PPP is 729 s (approximately 12.15 min), while that for BDS/LEO PPP is only 56 s, representing an approximately 13-fold acceleration in convergence speed.

Figure 15 illustrates the positioning error sequences and the number of satellites used in the solution for the GPS/BDS and LEO/BDS combinations during the first 30 min of the observation period. Subplots 1 through 3 show the positioning error sequences in the East, North, and Up directions, respectively. Subplot 4 displays the variation in the number of GPS and LEO satellites participating in the PPP solution, with the time at which the BDS/LEO augmented combination achieved convergence marked on the horizontal axis.

As clearly evidenced by the error sequences, the integration of the LEO constellation significantly accelerates the convergence process in all three directions (East, North, and Up), with the most pronounced improvement observed in the Up direction. Analysis of Subplot 4 reveals that although the number of visible satellites provided by the GPS system was not lower than that of the LEO satellites prior to convergence of the LEO-augmented BDS solution, the BDS/LEO combination achieved convergence in only 56 s, whereas the BDS/GPS combination required 12.15 min to meet the convergence criterion. This comparative result strongly validates that the rapidly changing geometry of LEO satellites effectively reduces the correlation among observation equations, thereby substantially enhancing the convergence speed of PPP.

3.3. LEO-Augmented BDS RTK

The trajectory of the USV is shown in Figure 16. Marker 1 indicates the starting position of the observation, and Marker 2 denotes the location of the static reference station. The baseline distance between them varies from 0.9 km to 1.7 km.

To evaluate the enhancement effect of LEO on BDS RTK positioning, the RTK processing strategy introduced in Chapter 3 was applied to both BDS-only and BDS/LEO full-constellation scenarios. Figure 17 present scatter plots of the horizontal and vertical positioning errors for BDS-only RTK and LEO-augmented BDS/LEO RTK.

Figure 17 reveals that the inclusion of LEO satellites reduces the fluctuation of positioning errors in the East, North, and Up directions, thereby improving overall positioning accuracy. To quantitatively assess the impact of LEO augmentation on the performance of single-BDS short-baseline RTK positioning in high-latitude regions, the fixed solution rates and positioning accuracy for both BDS-only and BDS/LEO RTK were statistically evaluated, as summarized in

Table 8. Fix rate and positioning accuracy for BDS and BDS/LEO RTK solutions.

System	Fix Rate (%)	E (m)	N (m)	2D (m)	U (m)	3D (m)
BDS	96.50	0.015	0.007	0.016	0.071	0.073
BDS/LEO	100.00	0.009	0.006	0.011	0.063	0.064

.

The statistical results indicate that:

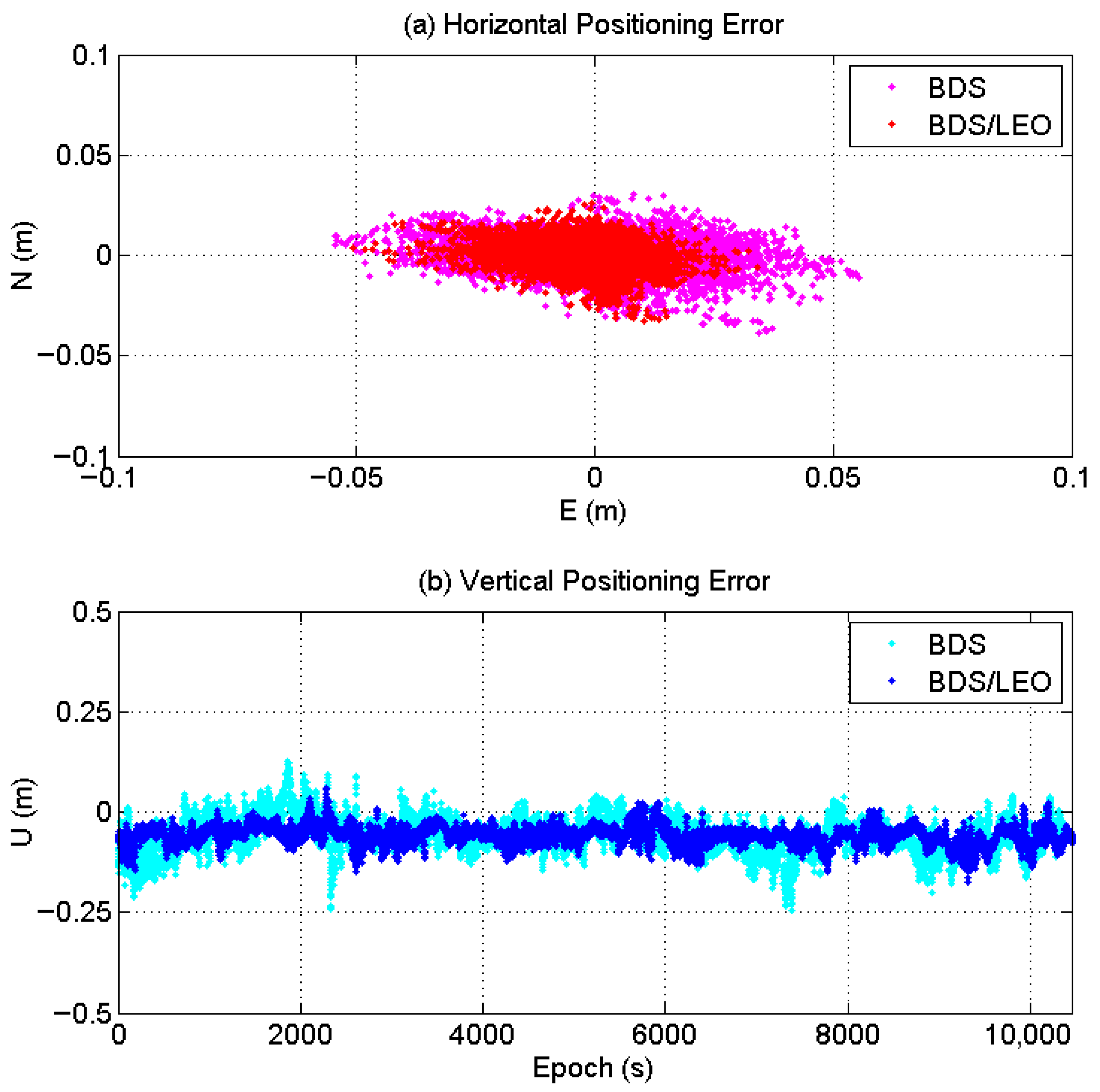
• In the high-latitude maritime regions of the Southern Hemisphere, the BDS short-baseline RTK achieves three-dimensional positioning accuracy at the sub-meter level, with a fix rate reaching 96.5%. The positioning accuracies in the E, N, and U directions are 0.015 m, 0.007 m, and 0.071 m, respectively, while the horizontal and vertical positioning accuracies are 0.016 m and 0.073 m, respectively.
• The integration of LEO satellites significantly enhances the fix rate of BDS RTK and also improves positioning accuracy to some extent. For BDS/LEO, the positioning accuracies in the E, N, and U directions are 0.009 m, 0.006 m, and 0.063 m, respectively, with corresponding horizontal and vertical accuracies of 0.011 m and 0.064 m. Compared to standalone BDS, the addition of LEO improves the RTK fix rate from 96.5% to 100%, while enhancing horizontal and vertical positioning accuracy by 31.5% and 12.3%, respectively.

4. Discussion

This study systematically evaluated the impact of LEO constellation augmentation on the performance of BDS PPP and RTK positioning in the high-latitude maritime regions of the Southern Hemisphere. The following aspects are discussed respectively.

First, the type of LEO constellation is a critical factor determining the level of performance enhancement. Experimental results demonstrate that the polar-orbiting constellation played a decisive role in improving PPP performance at high latitudes, while the medium-inclination orbit constellation contributed almost no improvement. The fundamental reason for this disparity lies in satellite visibility and geometric distribution. As shown in Section 3.1 (Observation Conditions), under a 10-degree cutoff elevation angle, the average number of visible LEO-M satellites was only 0.2, with a visibility percentage as low as 12.8%, which is insufficient to form stable and effective observations. This results from the geometric distribution characteristics of medium-inclination orbit satellites in high-latitude regions, whose orbital paths struggle to provide consistent coverage over these areas. In contrast, the design of polar-orbiting satellites enables frequent passes over the Arctic and Antarctic regions, significantly improving the satellite geometry (as evidenced by a notable reduction in PDOP values) in high-latitude areas. This enhancement provides the necessary conditions for rapid ambiguity resolution and fast convergence of positioning solutions. Therefore, in designing future LEO constellations for navigation augmentation targeting polar or high-latitude regions, priority should be given to configurations that include a substantial number of polar-orbiting or high-inclination satellites.

Secondly, the number of LEO satellites exert a complex influence on PPP performance. As detailed in Section 3.2.2 (Impact of LEO Satellite Count on BDS PPP in High-Latitude Maritime Regions), the number of LEO satellites involved in the solution exhibits an overall negative correlation with both convergence time and positioning accuracy. PPP convergence within one minute was consistently achieved when more than 5.4 LEO satellites were available. However, this relationship is not strictly linear or uniformly proportional. For instance, the positioning accuracy in Group 7 (13 satellites, accuracy 0.112 m) was lower than that in Groups 2 and 4 (approximately 10.7 satellites, accuracy 0.049 m), indicating that factors such as satellite geometry (PDOP) and observation quality are equally critical. If the spatial geometry cannot be optimized simultaneously, the benefits of merely increasing the number of satellites will be diminished. Furthermore, the failure in the solution of Group 16 (with only 4 LEO satellites) underscores the importance of maintaining a sufficient number of visible LEO satellites to ensure service reliability and continuity. Nevertheless, even a small number of LEO satellites (2–5) can significantly accelerate convergence, highlighting the effectiveness of LEO-augmented systems. When the number of LEO satellites exceeds eight, the performance improvement gradually saturates with further increases in satellite count. Comparative experiments of different constellation size show that although the 288-satellite polar orbit constellation has 60% more visible satellites than the 180-satellite configuration, the difference in positioning accuracy is only 0.006 m, and the average convergence time is reduced from 0.26 min to 0.16 min, an improvement that is not significant. This indicates that once a certain number of satellites is reached, the precision positioning performance of BDS stabilizes. The above conclusions provide important guidance for the constellation design and optimization strategies of future LEO augmentation systems.

Furthermore, the rapidly changing geometry of LEO satellites is the key factor behind their ability to enhance PPP convergence speed. As demonstrated in the experiment described in Section 3.2.3, a comparison of the convergence times between BDS/GPS PPP and BDS/LEO PPP shows that, even when the number of visible satellites is similar, the BDS/LEO PPP convergence occurs significantly faster than that of BDS/GPS PPP. This result confirms that the rapid variation in sky trajectories caused by the low orbital altitude and high velocity of LEO satellites effectively reduces the correlation between observation equations across epochs and significantly improves parameter estimability.

Finally, regarding the RTK results, the integration of LEO satellites increased the fixed solution rate from 96.5% to 100%, demonstrating a significant improvement. In short-baseline RTK, most error sources—such as ionospheric and tropospheric delays, as well as orbital errors—can be effectively eliminated through double-differencing. The primary performance bottleneck in such scenarios often lies in the ambiguity resolution success rate. Successful ambiguity fixing heavily depends on satellite geometry, as well as the quantity and quality of observations. Therefore, the improvement in PDOP and the increase in the number of visible satellites brought by LEO constellations enhance the model strength for ambiguity resolution, thereby improving the reliability and success rate of fixed solutions. Even in short-baseline scenarios where most errors are substantially mitigated, LEO augmentation further improves positioning accuracy and stability by strengthening the geometric configuration. Future research could explore the potential of LEO augmentation in medium- and long-baseline RTK applications, particularly in scenarios where atmospheric errors are difficult to fully eliminate through differential techniques.

Currently, the precise orbits and clock offsets of LEO satellites used in this study are simulated products. If actual LEO communication or navigation satellites are employed, errors in orbit determination, clock estimation, and differences in signal systems may directly affect the positioning model. Furthermore, limited by the observation conditions, the data collection period spanned only three hours, which is insufficient to capture variations due to solar activity, sea states, or seasonal changes in satellite geometry. Future work should involve long-term data collection to validate the robustness of the findings under diverse environmental and orbital conditions.

5. Conclusions

Benefiting from unique advantages such as rapid motion, high orbital inclination, and strong received signal power, LEO constellations demonstrate significant potential for enhancing positioning performance in high-latitude maritime regions. Based on real observational data collected from the high-latitude waters of the Southern Hemisphere, this study thoroughly investigates the enhancement effects of LEO satellites on the performance of BDS PPP and RTK techniques. Through systematic data processing and analysis, the following main conclusions are drawn:

• LEO significantly improves the observation conditions in high-latitude regions: Under a 10-degree cutoff elevation angle, the integration of the polar-orbiting LEO constellation increases the average number of visible satellites from 10.4 to 17.7—an improvement of approximately 70.2%—while the average PDOP value improves from 2.4 to 1.7. This markedly enhances the geometry of the satellite constellation. In contrast, the medium-inclination orbit LEO constellation contributed minimally in the experimental area due to its inherent orbital characteristics.
• LEO substantially enhances BDS PPP performance: The incorporation of the full LEO constellation reduced the convergence time of BDS PPP from 45.3 min to less than 1 min—an improvement of over 97%. The three-dimensional positioning accuracy (RMS) improved from 0.086 m to 0.039 m, representing an enhancement of 54.7%. This performance improvement is primarily attributable to the polar-orbiting LEO satellites, whereas the medium-inclination LEO satellites, due to their insufficient visibility, contributed no observable enhancement.
• The number of LEO satellites is a critical factor influencing PPP performance: Segmented PPP experiments demonstrate a negative correlation between the number of LEO satellites involved in the solution and both convergence speed and positioning accuracy. When the average number of LEO satellites during the first two minutes of the convergence phase exceeds 5.4, PPP convergence can be achieved within one minute with positioning accuracy better than 0.2 m. When the number of satellites used in the solution exceeds eight, the convergence time is shortened to within 0.5 min, and positioning accuracy can be improved to 0.1 m. Although further increasing the number of satellites continues to enhance positioning performance, the resulting improvement is not substantial.
• Accelerated convergence via rapid geometric changes from LEO: Under comparable numbers of visible satellites, the BDS/LEO combined PPP achieves convergence in approximately 56 s, significantly faster than the BDS/GPS combination, which requires about 12.15 min. This result directly validates that the rapidly changing sky trajectories of LEO satellites, resulting from their low orbital altitude and high velocity, effectively reduce the correlation among observation equations, thereby enabling rapid (minute-level) convergence
• LEO effectively enhances BDS RTK performance: In short-baseline (<1.7 km) RTK processing, the integration of LEO satellites increased the ambiguity fixed rate from 96.5% to 100%, achieving a fixed solution throughout the entire observation period. Meanwhile, the horizontal positioning accuracy improved from 0.016 m to 0.011 m (a 31.5% enhancement), and the vertical positioning accuracy improved from 0.073 m to 0.064 m (a 12.3% improvement), significantly boosting both the reliability and precision of positioning.

In summary, this study confirms that LEO augmentation constellations—particularly those in polar orbits—constitute an effective solution to positioning challenges in high-latitude and other GNSS-vulnerable regions. By increasing the number of available satellites and providing rapidly varying geometric diversity, LEO enhancements significantly improve satellite geometry configuration, substantially reduce PPP convergence time, and enhance both the fixed rate and accuracy of RTK positioning. The findings provide clear recommendations for constellation configuration to support high-precision navigation of unmanned maritime systems in high-latitude areas. By integrating polar-orbiting LEO satellites with BDS, it is possible to achieve minute-level PPP convergence and centimeter-level accuracy with continuous fixed solutions in short-baseline RTK, offering direct engineering benefits for polar shipping, marine scientific research, and resource exploration.