Driving Factors of Hala Lake Water Storage Changes from 2011 to 2023
Abstract
Highlights
- The lake area, water level, and LWSC of Hala Lake exhibited three stages of synchronous expansion from 2011 to 2023.
- Lake surface precipitation and precipitation-caused runoff contributed the majority to the LWSC, with the latter being the key factor driving the formation of its three stages.
- The study provides a practical and replicable blueprint for researching hydrological changes in alpine lakes and their responses to climate change.
- The findings of this research offer useful insights for government agencies in the rational development and utilization of water resources.
Abstract
1. Introduction
2. Data and Methods
2.1. Study Area
2.2. Data
2.2.1. Landsat Satellite Imagery
2.2.2. Satellite Altimetry
2.2.3. Hydrological and Climatic Data
2.3. Methods
2.3.1. Extraction of the Lake Area
2.3.2. Calculation of the Lake Level
2.3.3. Estimation of Lake Water Storage Changes
2.3.4. Estimation of Glacier Meltwater
2.3.5. Simulation of Lake Water Storage Changes
2.4. Uncertainty Assessment
2.4.1. Uncertainty of Lake Water Storage Change
2.4.2. Uncertainty of Glacier Meltwater
2.4.3. Uncertainty of Estimated Hydrological and Climatic Contributions
3. Results
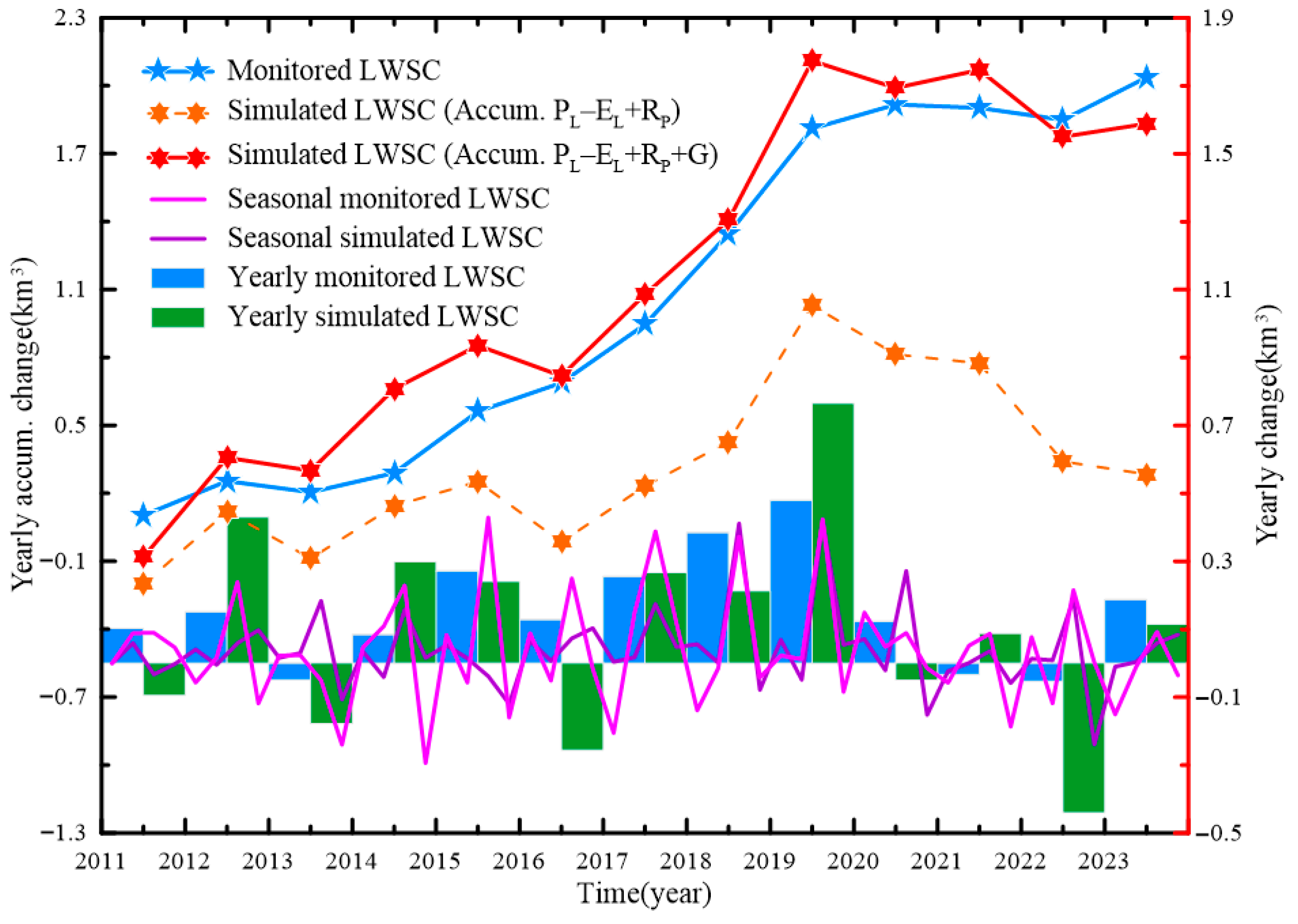
3.1. Changes in Hala Lake Area, Lake Level, and Lake Water Storage
3.2. Simulation of Hala Lake Water Balance
3.2.1. Hala Lake Water Storage Changes Response to Climate Change
3.2.2. Simulation of Glacier Melting
3.3. Water Balance of Hala Lake
4. Discussion
4.1. Comparison with Previous Studies
4.2. Other Factors Introducing Uncertainty
4.3. Perspective of the Hala Lake Water Balance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Complementing the Evaporation Data
| Area | Fitting Methods | Equation |
|---|---|---|
| Lake | Proportional factor method | |
| Seventh-degree polynomial | ||
| Exponential function | ||
| Land | Proportional factor method | |
| Seventh-degree polynomial | ||
| Exponential function |
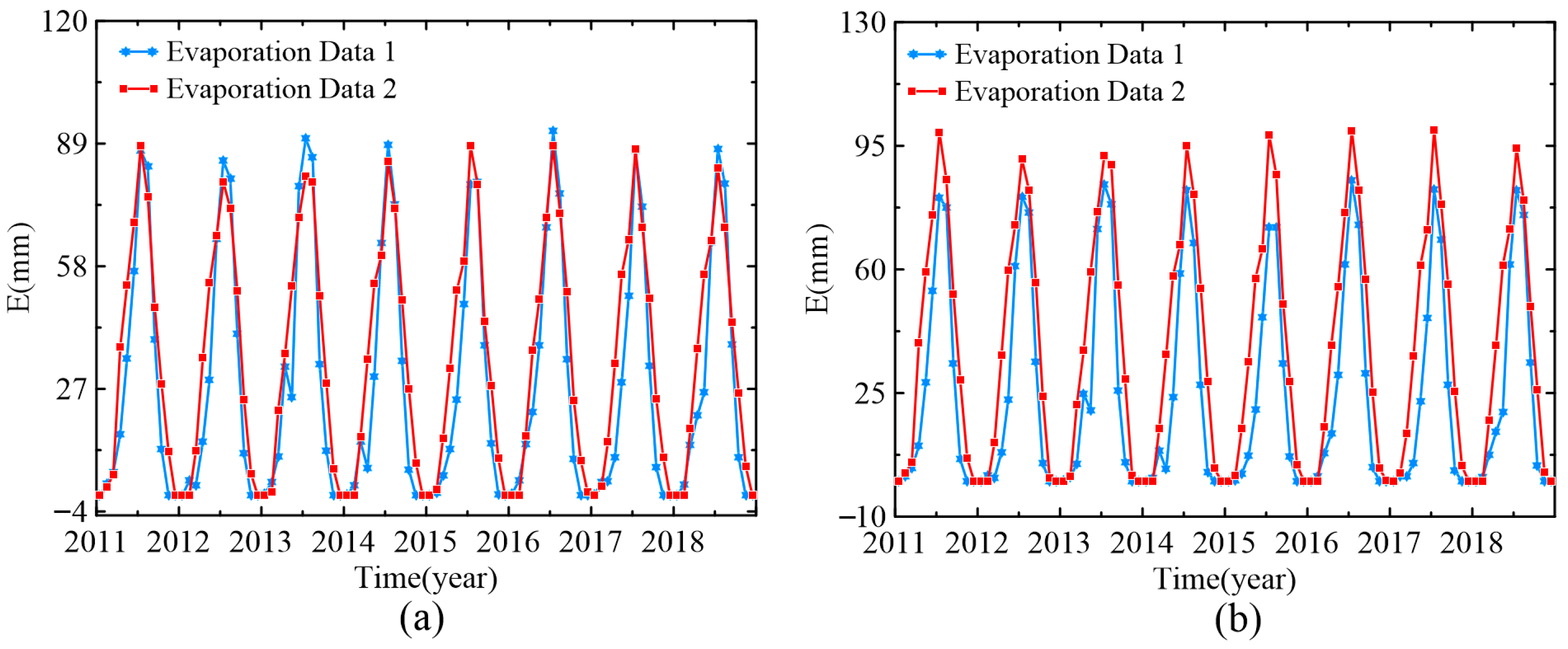

| Stage | Areas Concerned | Proportional Factor Method (r/RMSE) | Seven-Degree Polynomial (r/RMSE) | Exponential Function (r/RMSE) |
|---|---|---|---|---|
| 2015–2018 | Lake | 0.990/4.611 | 0.989/4.566 | 0.975/6.806 |
| Land | 0.991/4.110 | 0.991/3.985 | 0.973/6.687 | |
| 2016–2018 | Lake | 0.992/3.864 | 0.990/4.437 | 0.976/7.247 |
| Land | 0.993/3.856 | 0.992/3.644 | 0.975/6.979 | |
| 2017–2018 | Lake | 0.991/4.071 | 0.993/4.096 | 0.991/4.846 |
| Land | 0.992/3.781 | 0.993/3.497 | 0.989/5.039 |
Appendix A.2. Pearson’s Correlation Coefficient (r)
Appendix A.3. Root Mean Square Error (RMSE) and Coefficient of Determination (R2)
Appendix A.4. Supplementing the Missing Monthly Lake Areas and Levels
| Time | Formula | R2 | RMSE |
|---|---|---|---|
| January 2011–August 2011 | 0.96092 | 0.36502 | |
| August 2011–August 2012 | 0.95213 | 0.52535 | |
| August 2012–May 2013 | 0.93976 | 0.37027 | |
| January 2013–December 2013 | 0.84195 | 0.56017 | |
| October 2013–September 2014 | 0.93942 | 0.32695 | |
| April 2014–April 2015 | 0.80862 | 0.63627 | |
| April 2015–July 2016 | 0.92848 | 0.76709 | |
| December 2015–November 2016 | 0.88478 | 0.829 | |
| November 2016–August 2017 | 0.94315 | 0.58407 | |
| May 2017–May 2018 | 0.90091 | 0.8469 | |
| May 2018–February 2019 | 0.97653 | 0.85701 | |
| February 2019–April 2020 | 0.97834 | 0.87676 | |
| April 2020–January 2021 | 0.96699 | 0.24712 | |
| January 2021–June 2022 | 0.99304 | 0.18264 | |
| June 2022–January 2023 | 0.95184 | 0.57042 | |
| January 2023–December 2023 | 0.9669 | 0.34917 |
| Satellite Mission | Time | Formula | R2 | RMSE |
|---|---|---|---|---|
| CryoSat–2 | January 2011–January 2012 | 0.77033 | 0.06981 | |
| February 2012–January 2013 | 0.41925 | 0.10762 | ||
| January 2013–September 2013 | 0.83136 | 0.02836 | ||
| September 2013–February 2014 | 0.16347 | 0.13088 | ||
| February 2014–July 2014 | 0.97593 | 0.03783 | ||
| July 2014–April 2015 | 0.88133 | 0.06762 | ||
| May 2015–December 2015 | 0.86518 | 0.08123 | ||
| December 2015–August 2016 | 0.52787 | 0.09532 | ||
| August 2016–March 2017 | 0. 97372 | 0.01561 | ||
| March 2017–August 2017 | 0.84256 | 0.10563 | ||
| August 2017–February 2018 | 0.6195 | 0.06853 | ||
| April 2018–November 2018 | 0.89539 | 0.08445 | ||
| November 2018–July 2019 | 0.95437 | 0.05678 | ||
| July 2019–November 2019 | 0.99999 | 0.00043 | ||
| November 2019–May 2020 | 0.87489 | 0.08814 | ||
| May 2020–December 2020 | 0.91756 | 0.03545 | ||
| December 2020–July 2021 | 0.99999 | 0.00005 | ||
| July 2021–March 2022 | 0.88567 | 0.05877 | ||
| October 2021–September 2022 | 0.95146 | 0.04179 | ||
| October 2022–September 2023 | 0.96248 | 0.02657 | ||
| May 2023–December 2023 | 0.99999 | 0.00001 | ||
| ICESat–2 | October 2018–March 2019 | 0.99996 | 0.0003 | |
| December 2018–September 2019 | 0.97898 | 0.04487 | ||
| September 2019–September 2020 | 0.99089 | 0.00791 | ||
| September 2020–July 2021 | 0.87672 | 0.02995 | ||
| July 2021–April 2022 | 0.84827 | 0.0398 | ||
| December 2021–July 2022 | 0.51813 | 0.04604 | ||
| June 2022–January 2023 | 0.8878 | 0.03431 | ||
| January 2023–December 2023 | 0.82109 | 0.04359 |
| Model | Name | Formula | R2 | RMSE |
|---|---|---|---|---|
| Polynomial functions | First-degree polynomial | 0.98568 | 1.65424 | |
| Second-degree polynomial | 0.98614 | 1.62744 | ||
| Third-degree polynomial | 0.98703 | 1.57446 | ||
| Fourth-degree polynomial | 0.98764 | 1.53703 | ||
| Fifth-degree polynomial | 0.98814 | 1.50537 | ||
| Sixth-degree polynomial | 0.98812 | 1.50655 | ||
| Seventh-degree polynomial | 0.98840 | 1.48846 | ||
| Eighth-degree polynomial | 0.97805 | 2.04792 | ||
| Ninth-degree polynomial | 0.98355 | 1.77295 | ||
| Exponential functions | Single exponential model | 0.9859 | 1.6576 | |
| Binomial exponential model | 0.9859 | 1.6741 | ||
| Power functions | Single power model | 0.98589 | 1.6577 | |
| Binomial power model | 0.98589 | 1.6659 |
| Model | Name | Formula | R2 | RMSE |
|---|---|---|---|---|
| Polynomial functions | First-degree polynomial | 0.97911 | 0.17436 | |
| Second-degree polynomial | 0.98034 | 0.16917 | ||
| Third-degree polynomial | .442 | 0.98043 | 0.16878 | |
| Fourth-degree polynomial | 0.98146 | 0.16429 | ||
| Fifth-degree polynomial | 0.98217 | 0.1611 | ||
| Sixth-degree polynomial | 0.98364 | 0.15433 | ||
| Seventh-degree polynomial | 0.98375 | 0.15380 | ||
| Eighth-degree polynomial | 0.9837 | 0.15404 | ||
| Ninth-degree polynomial | 0.984 | 0.15259 | ||
| Exponential functions | Single exponential model | 0.97911 | 0.17552 | |
| Binomial exponential model | 0.97911 | 0.17667 | ||
| Power functions | Single power model | 0.9795 | 0.17384 | |
| Binomial power model | 0.98031 | 0.17094 |
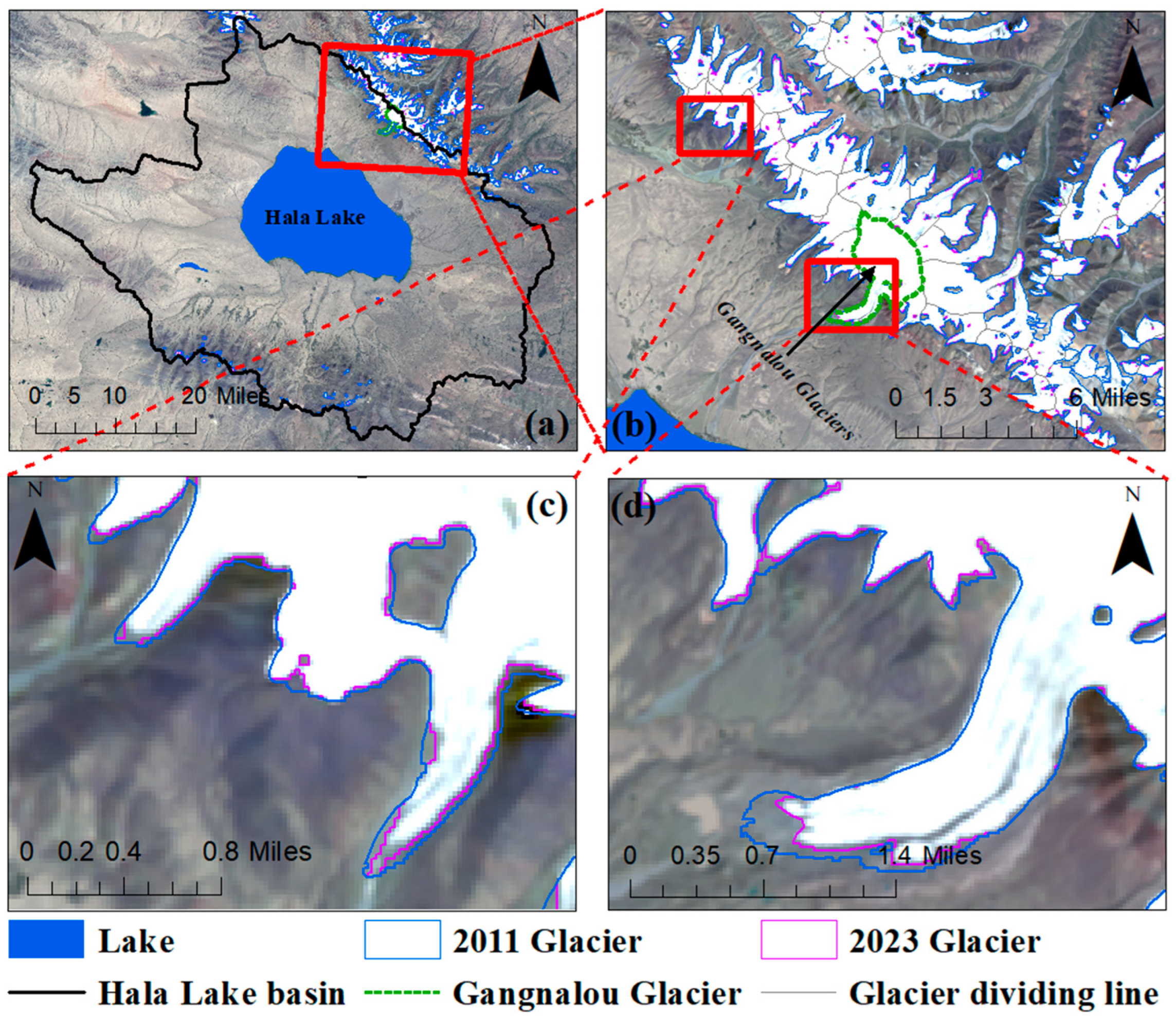
Appendix A.5. Exhibition of Glacier Melting Cases
References
- Zhao, S. A new scheme for comprehensive physical regionalization in China. Acta Geogr. Sin. 1983, 38, 1–10. [Google Scholar]
- Liu, X.; Chen, B. Climatic warming in the Tibetan Plateau during recent decades. Int. J. Climatol. 2000, 20, 1729–1742. [Google Scholar] [CrossRef]
- Zhang, G.; Luo, W.; Chen, W.; Zheng, G. A robust but variable lake expansion on the Tibetan Plateau. Sci. Bull. 2019, 64, 1306–1309. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Chen, W.; Zheng, G.; Shum, C.K.; Yang, K.; Piao, S.; Sheng, Y.; Yi, S.; Li, J.; et al. Regional differences of lake evolution across China during 1960s–2015 and its natural and anthropogenic causes. Remote Sens. Environ. 2019, 221, 386–404. [Google Scholar] [CrossRef]
- Jin, Z.; You, Q.; Wu, F.; Sun, B.; Cai, Z. Changes of climate and climate extremes in the three-rivers headwaters’ region over the Tibetan plateau during the past 60 years. Trans. Atmos. Sci. 2020, 43, 1042–1055. [Google Scholar]
- Zhu, L.; Zhang, G.; Yang, R.; Liu, C.; Yang, K.; Qiao, B.; Han, B. Lake variations on Tibetan Plateau of recent 40 years and future changing tendency. Bull. Chin. Acad. Sci. 2019, 34, 1254–1263. [Google Scholar] [CrossRef]
- Yao, T. Glacial fluctuations and its impacts on lakes in the southern Tibetan Plateau. Chin. Sci. Bull. 2010, 55, 2071. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, W.; Xie, H. Tibetan Plateau’s Lake Level and Volume Changes from NASA’s ICESat/ICESat-2 and Landsat Missions. Geophys. Res. Lett. 2019, 46, 13107–13118. [Google Scholar] [CrossRef]
- Yang, R.; Zhu, L.; Wang, J.; Ju, J.; Ma, Q.; Turner, F.; Guo, Y. Spatiotemporal variations in volume of closed lakes on the Tibetan Plateau and their climatic responses from 1976 to 2013. Clim. Chang. 2017, 140, 621–633. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Q.; Li, Y.; Li, H.; Li, J. Area, lake-level and volume variations of typical lakes on the Tibetan Plateau and their response to climate change, 1972–2019. Geo-Spat. Inf. Sci. 2021, 24, 458–473. [Google Scholar] [CrossRef]
- Sun, K.; Chen, J.; Lhakpa, D.; He, H.; Duan, Z. Estimating the lake storage capacity on the Tibetan Plateau using satellite altimetry and imagery data: A comparative analysis of water volume change methods. J. Mt. Sci. 2025, 22, 1388–1404. [Google Scholar] [CrossRef]
- Luo, S.; Song, C.; Zhan, P.; Liu, K.; Chen, T.; Li, W.; Ke, L. Refined estimation of lake water level and storage changes on the Tibetan Plateau from ICESat/ICESat-2. Catena 2021, 200, 105177. [Google Scholar] [CrossRef]
- Chen, J.; Gao, J.; Wang, Y.; Jin, L. Estimation of Water Volume Changes in Typical Alpine Lakes on the Tibetan Plateau by Combining Sentinel-3 Radar Altimetry Data and Optical Images. Mt. Res. 2023, 41, 926–940. [Google Scholar]
- Zheng, J.; Ke, C.; Shao, Z.; Lie, F. Monitoring changes in the water volume of Hulun Lake by integrating satellite altimetry data and Landsat images between 1992 and 2010. J. Appl. Remote Sens. 2016, 10, 016029. [Google Scholar] [CrossRef]
- Yang, X.; Wang, N.; Chen, A.; He, J.; Hua, T.; Qie, Y. Changes in area and water volume of the Aral Sea in the arid Central Asia over the period of 1960–2018 and their causes. Catena 2020, 191, 104566. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, A. Natural situation and vegetation types of Lake Hala in Qinghai province. Grassl. China 1984, 2, 27–31. [Google Scholar]
- Li, D.; Cui, B.; Wang, Y.; Xiao, B.; Jiang, B. Glacier extent changes and possible causes in the Hala Lake Basin of Qinghai–Tibet Plateau. J. Mt. Sci. 2019, 16, 1571–1583. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, Y.; Wuennemann, B.; Biskaborn, B.K.; Yin, H.; Xia, F.; Zhou, L.; Diekmann, B. Linkages between Quaternary climate change and sedimentary processes in Hala Lake, northern Tibetan Plateau, China. J. Asian Earth Sci. 2015, 107, 140–150. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, J.; Zhang, C.; Chen, F. Environmental changes during the past 800 years recorded in lake sediments from Hala Lake on the Northern Tibetan Plateau. Quat. Sci. 2007, 27, 100–107. [Google Scholar]
- Yan, D.; Wuennemann, B. Late Quaternary water depth changes in Hala Lake, northeastern Tibetan Plateau, derived from ostracod assemblages and sediment properties in multiple sediment records. Quat. Sci. Rev. 2014, 95, 95–114. [Google Scholar] [CrossRef]
- He, M.; Fang, H.; Zhu, Y.; Sun, Z.; Hu, X.; Zhang, P.; Wang, X.; Pei, F.; Qiu, G.; Du, B.; et al. A study of geological structural features of Hala Lake Depression in Qilian Mountain and reservoir-forming conditions of natural gas hydrate. Geol. China 2020, 47, 173–187. [Google Scholar]
- Li, D.; Zhang, R.; Cui, B.; Zhao, Y.; Wang, Y.; Jiang, B. Response of lake dynamics to climate change in the Hala Lake basin of Tibetan Plateau from 1986 to 2015. J. Nat. Resour. 2021, 36, 501–512. [Google Scholar] [CrossRef]
- Wang, R.; Liu, B.; Huang, B. Analysis of Dynamic Change and Causes of the Area of Hala Lake from 1986 to 2019. Pearl River. 2021, 42, 20–25+33. [Google Scholar]
- Wu, H.; Yang, M.; Yang, C.; Li, Y. Effect of glacier mass loss on water level fluctuation of lake in Hala Lake basin. J. Water Resour. Water Eng. 2016, 27, 13–20. [Google Scholar]
- Jiang, Z.; Wang, J.; Cai, X.; Zhao, J.; Zhang, H.; Zhang, Y.; Wang, C. Hydrological Characteristics Change of Hala Lake and Its Response to Climate Change, 1987–2018. Remote Sens. 2022, 14, 2886. [Google Scholar] [CrossRef]
- Guo, L.; Li, J.; Charrier, L.; Dehecq, A.; Beraud, L.; Li, Z.; Li, X.; Zhu, J.; Li, L.; Wang, Y. Surging Processes and Mechanisms at Small Glaciers in the Qilian Mountains, Northwestern China, Revealed by Long-Term, Temporally Dense Remote Sensing Observations. J. Geophys. Res. Earth Surf. 2025, 130, e2024JF008157. [Google Scholar] [CrossRef]
- Jiang, L.; Nielsen, K.; Andersen, O.B.; Bauer-Gottwein, P. Monitoring recent lake level variations on the Tibetan Plateau using CryoSat-2 SARIn mode data. J. Hydrol. 2017, 544, 109–124. [Google Scholar] [CrossRef]
- Labroue, S.; Boy, F.; Picot, N.; Urvoy, M.; Ablain, M. First quality assessment of the Cryosat-2 altimetric system over ocean. Adv. Space Res. 2012, 50, 1030–1045. [Google Scholar] [CrossRef]
- Siegfried, M.R.; Fricker, H.A.; Roberts, M.; Scambos, T.A.; Tulaczyk, S. A decade of West Antarctic subglacial lake interactions from combined ICESat and CryoSat-2altimetry. Geophys. Res. Lett. 2014, 41, 891–898. [Google Scholar] [CrossRef]
- Wei, X.; Li, F.; Zhang, S.; Hao, W. CryoSat-2 satellite altimetry and its application. Chin. J. Polar Res. 2015, 27, 446–453. [Google Scholar]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Femenias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Jiang, L.; Nielsen, K.; Dinardo, S.; Andersen, O.B.; Bauer-Gottwein, P. Evaluation of Sentinel-3 SRAL SAR altimetry over Chinese rivers. Remote Sens. Environ. 2020, 237, 111546. [Google Scholar] [CrossRef]
- Parrish, C.E.; Magruder, L.A.; Neuenschwander, A.L.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinski, M. Validation of ICESat-2 ATLAS Bathymetry and Analysis of ATLAS’s Bathymetric Mapping Performance. Remote Sens. 2019, 11, 1634. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, G.; Yi, S.; Chen, W. Seasonal trends and cycles of lake–level variations over the Tibetan Plateau using multi-sensor altimetry data. J. Hydrol. 2022, 604, 127251. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Cretaux, J.F.; Abarca-del-Rio, R.; Berge-Nguyen, M.; Arsen, A.; Drolon, V.; Clos, G.; Maisongrande, P. Lake Volume Monitoring from Space. Surv. Geophys. 2016, 37, 269–305. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Liu, W.; Li, Z. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
- Wang, L.; Han, S.; Tian, F.; Li, K.; Li, Y.; Tudaji, M.; Cao, X.; Nan, Y.; Cui, T.; Zheng, X.; et al. The Evaporation on the Tibetan Plateau Stops Increasing in the Recent Two Decades. J. Geophys. Res.-Atmos. 2022, 127, e2022JD037377. [Google Scholar] [CrossRef]
- Ding, Y.; Peng, S. Spatiotemporal change and attribution of potential evapotranspiration over China from 1901 to 2100. Theor. Appl. Climatol. 2021, 145, 79–94. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Du, Z.; Li, W.; Zhou, D.; Tian, L.; Ling, F.; Wang, H.; Gui, Y.; Sun, B. Analysis of Landsat-8 OLI imagery for land surface water mapping. Remote Sens. Lett. 2014, 5, 672–681. [Google Scholar] [CrossRef]
- Wang, X.; Xie, S.; Du, J. Water index formulation and its effectiveness research on the complicated surface water surroundings. Natl. Remote Sens. Bull. 2018, 22, 360–372. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Ma, W.; Bai, L.; Ma, W.; Hu, W.; Xie, Z.; Su, R.; Wang, B.; Ma, Y. Interannual and Monthly Variability of Typical Inland Lakes on the Tibetan Plateau Located in Three Different Climatic Zones. Remote Sens. 2022, 14, 5015. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Guo, M.; Bao, A.; Hu, R.; Zhao, S. Time-series analysis of Sayram Lake area changes during 1989–2014. Arid Land Geogr. 2016, 39, 851–860. [Google Scholar]
- Munyaneza, O.; Wali, U.G.; Uhlenbrook, S.; Maskey, S.; Mlotha, M.J. Water level monitoring using radar remote sensing data: Application to Lake Kivu, central Africa. Phys. Chem. Earth 2009, 34, 722–728. [Google Scholar] [CrossRef]
- Cai, X.; Gan, W.; Ji, W.; Zhao, X.; Wang, X.; Chen, X. Optimizing Remote Sensing-Based Level–Area Modeling of Large Lake Wetlands: Case Study of Poyang Lake. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 471–479. [Google Scholar] [CrossRef]
- Ling, F.; Cai, X.; Li, W.; Xiao, F.; Li, X.; Du, Y. Monitoring river discharge with remotely sensed imagery using river island area as an indicator. J. Appl. Remote Sens. 2012, 6, 063564. [Google Scholar] [CrossRef]
- Zhu, W.; Jia, S.; Lv, A. Monitoring the Fluctuation of Lake Qinghai Using Multi–Source Remote Sensing Data. Remote Sens. 2014, 6, 10457–10482. [Google Scholar] [CrossRef]
- Chen, P.; An, Z.; Xue, H.; Yao, Y.; Yang, X.; Wang, R.; Wang, Z. INPPTR: An improved retracking algorithm for inland water levels estimation using Cryosat-2 SARin data. J. Hydrol. 2022, 613, 128439. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Li, J.; Hua, C.; Yang, Y.; Guan, X. Bayesian Block Structure Sparse Based T–S Fuzzy Modeling for Dynamic Prediction of Hot Metal Silicon Content in the Blast Furnace. IEEE Trans. Ind. Electron. 2018, 65, 4933–4942. [Google Scholar] [CrossRef]
- Yuan, C.; Gong, P.; Bai, Y. Performance Assessment of ICESat-2 Laser Altimeter Data for Water–Level Measurement over Lakes and Reservoirs in China. Remote Sens. 2020, 12, 770. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Y.; Cao, L.; Hu, J.; Liu, S. A review on the research of remote sensing monitoring of lake changes and quantitative estimation of lake water balance in Qinghai–Tibet Plateau. J. Glaciol. Geocryol. 2022, 44, 1203–1215. [Google Scholar]
- Taube, C.M. Three methods for computing the volume of a lake. In Manual of Fisheries Survey Methods II: With Periodic Updates; Schneider, J.C., Ed.; Michigan Department of Natural Resources: Ann Arbor, MI, USA, 2000; Volume 25, pp. 175–179. [Google Scholar]
- Qiao, B.; Zhu, L. Differences and cause analysis of changes in lakes of different supply types in the north-western Tibetan Plateau. Hydrol. Process. 2017, 31, 2752–2763. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. Development of methods for mapping global snow cover using moderate resolution imaging spectroradiometer data. Remote Sens. Environ. 1995, 54, 127–140. [Google Scholar] [CrossRef]
- Liu, S.; Sun, W.; Shen, Y.; Li, G. Glacier changes since the Little Ice Age maximum in the western Qilian Shan, northwest China, and consequences of glacier runoff for water supply. J. Glaciol. 2003, 49, 117–124. [Google Scholar] [CrossRef]
- Adler, J.; Parmryd, I. Quantifying Colocalization by Correlation: The Pearson Correlation Coefficient is Superior to the Mander’s Overlap Coefficient. Cytom. Part A 2010, 77, 733–742. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Yao, X.; Guo, W.; Xu, J.; Shangguan, D.; Wei, J.; Bao, W.; Wu, L. The contemporary glaciers in China based on the Second Chinese Glacier Inventory. Acta Geogr. Sin. 2015, 70, 3–16. [Google Scholar]
- Bianduo; Bianbaciren; Li, L.; Wang, W.; Zhaxiyangzong. The response of lake change to climate fluctuation in north Qinghai–Tibet Plateau in last 30 years. J. Geog. Sci. 2009, 19, 131–142. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, K. The cause of rapid lake expansion in the Tibetan Plateau: Climate wetting or warming? WIREs Water 2017, 4, e1236. [Google Scholar] [CrossRef]
- Mao, D.; Wang, Z.; Yang, H.; Li, H.; Thompson, J.R.; Li, L.; Song, K.; Chen, B.; Gao, H.; Wu, J. Impacts of Climate Change on Tibetan Lakes: Patterns and Processes. Remote Sens. 2018, 10, 358. [Google Scholar] [CrossRef]
- Chen, R.; Duan, K.; Shang, W.; Shi, P.; Meng, Y.; Zhang, Z. Increase in seasonal precipitation over the Tibetan Plateau in the 21st century projected using CMIP6 models. Atmos. Res. 2022, 277, 106306. [Google Scholar] [CrossRef]
- Qiu, H.; Zhou, T.; Zou, L.; Jiang, J.; Chen, X.; Hu, S. Future changes in precipitation and water availability over the Tibetan Plateau projected by CMIP6 models constrained by climate sensitivity. Atmos. Ocean. Sci. Lett. 2024, 17, 100537. [Google Scholar] [CrossRef]
- Wang, K.; Song, X.; Lu, F.; Yu, S.; Zhou, Y.; Sun, J. CMIP6 Simulation-Based Daily Surface Air Temperature and Precipitation Projections over the Qinghai-Tibetan Plateau in the 21st Century. Atmosphere 2024, 15, 434. [Google Scholar] [CrossRef]
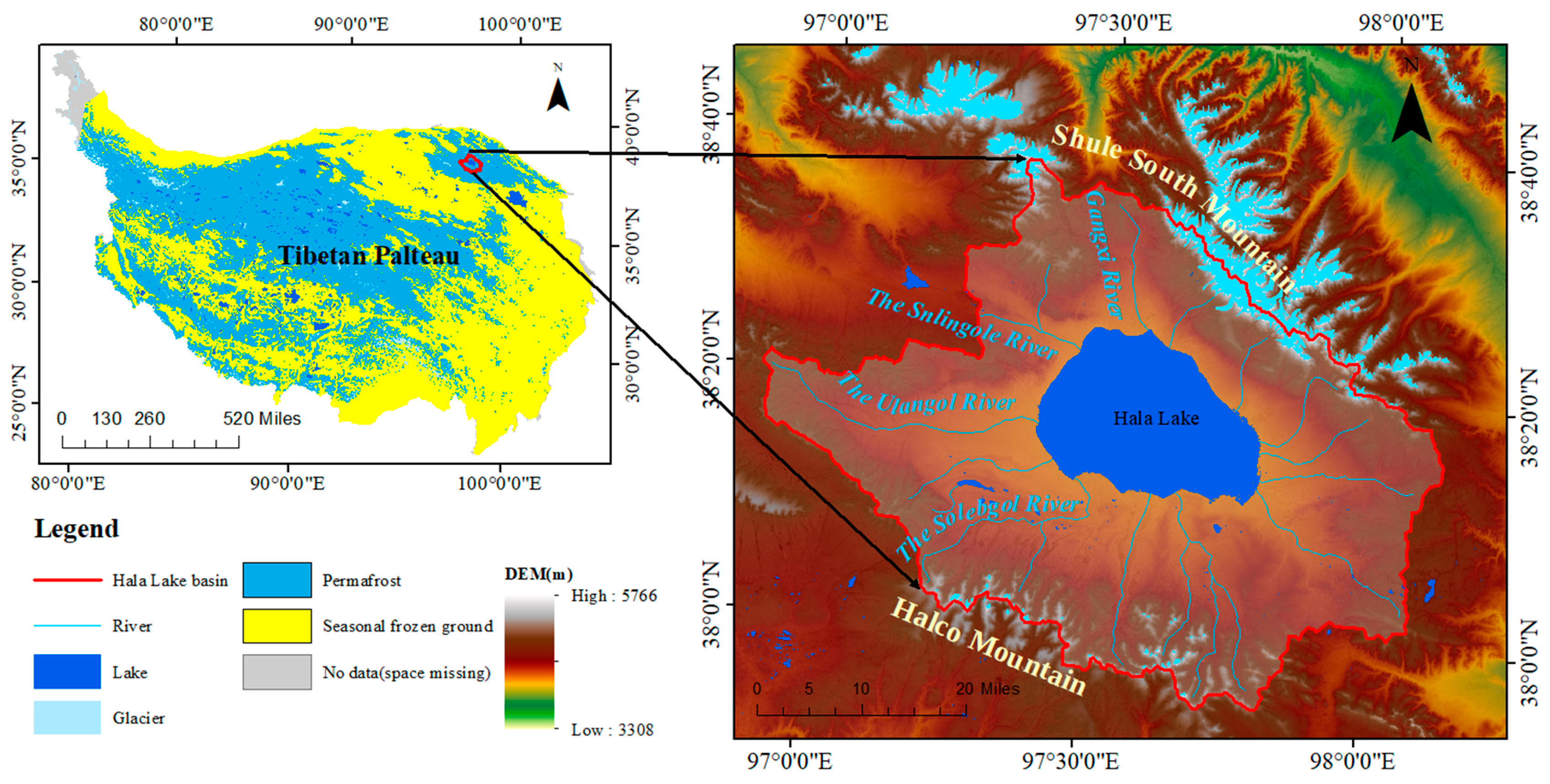



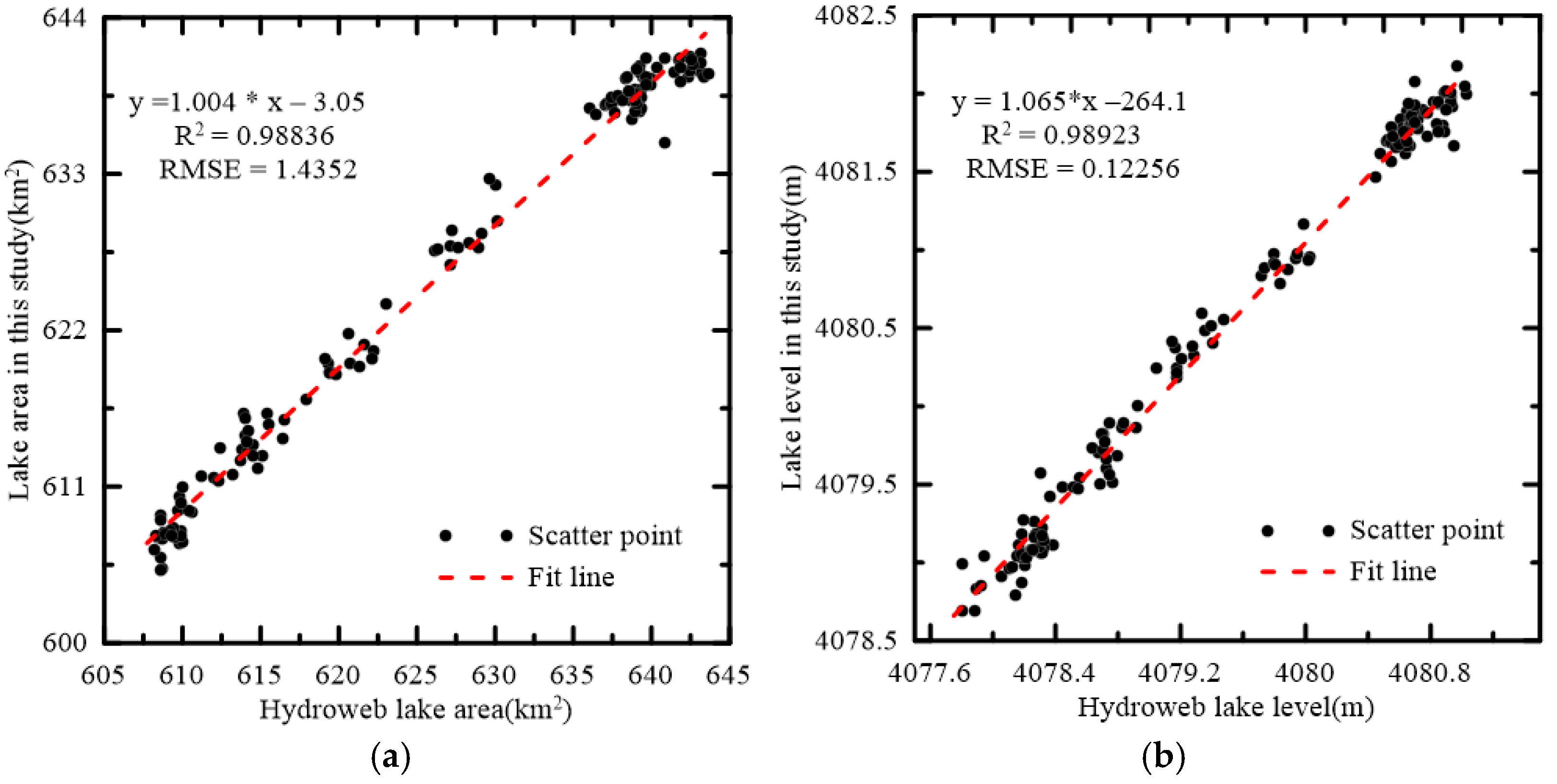
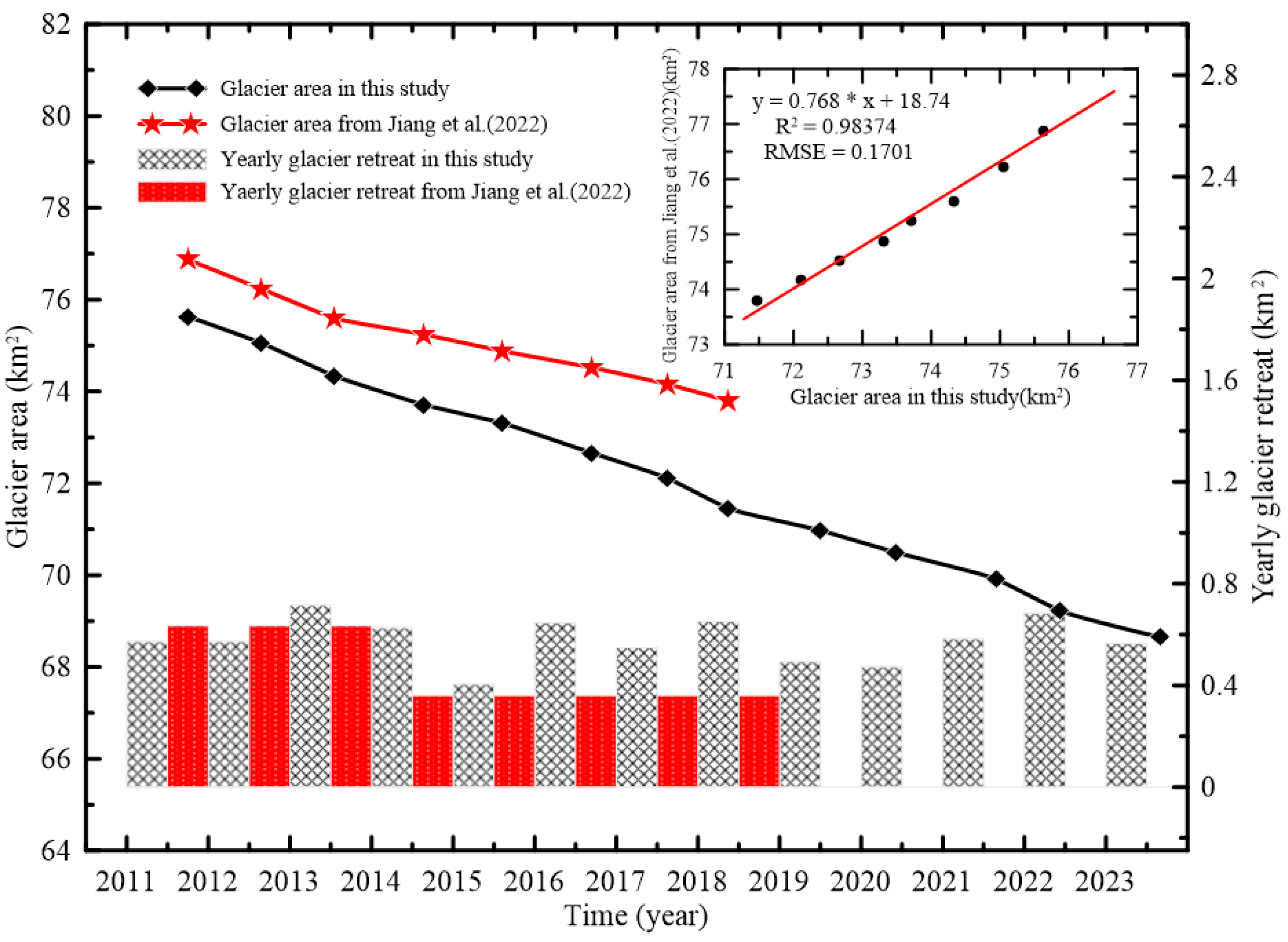
| Mission | Sensor | Launch Time | Repetition Period (Day) | Spatial Resolution(m) | Number of Images (Scene) |
|---|---|---|---|---|---|
| Landsat 5 | TM | August 1984 | 16 | 30 | 3 |
| Landsat 7 | ETM+ | April 1999 | 16 | 30 | 31 |
| Landsat 8 | OLI/TIRS | February 2013 | 16 | 30 | 58 |
| Landsat 9 | OLI–2/TIRS–2 | September 2021 | 16 | 30 | 13 |
| Water Balance Components | Mean Yearly Contributions (km3) | |||||
|---|---|---|---|---|---|---|
| 2011–2014 | 2015–2019 | 2020–2023 | 2011–2023 | |||
| Recharge | 0.026 | 0.028 | 0.020 | 0.015 | 51.00% | |
| 0.218 | 0.210 | 0.131 | 0.112 | 40.96% | ||
| 0.015 | 0.035 | 0.018 | 0.015 | 8.04% | ||
| Water loss | 0.011 | 0.013 | 0.014 | 0.007 | 59.37% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Xiang, L.; Wang, H.; Steffen, H.; Deng, F.; Chen, Z.; Li, G.; Nong, A.; Guo, J.; Xiao, X. Driving Factors of Hala Lake Water Storage Changes from 2011 to 2023. Remote Sens. 2025, 17, 3184. https://doi.org/10.3390/rs17183184
Hu K, Xiang L, Wang H, Steffen H, Deng F, Chen Z, Li G, Nong A, Guo J, Xiao X. Driving Factors of Hala Lake Water Storage Changes from 2011 to 2023. Remote Sensing. 2025; 17(18):3184. https://doi.org/10.3390/rs17183184
Chicago/Turabian StyleHu, Keyu, Longwei Xiang, Hansheng Wang, Holger Steffen, Fan Deng, Zugang Chen, Guoqing Li, Aile Nong, Jingjing Guo, and Xu Xiao. 2025. "Driving Factors of Hala Lake Water Storage Changes from 2011 to 2023" Remote Sensing 17, no. 18: 3184. https://doi.org/10.3390/rs17183184
APA StyleHu, K., Xiang, L., Wang, H., Steffen, H., Deng, F., Chen, Z., Li, G., Nong, A., Guo, J., & Xiao, X. (2025). Driving Factors of Hala Lake Water Storage Changes from 2011 to 2023. Remote Sensing, 17(18), 3184. https://doi.org/10.3390/rs17183184









