Evaluation of Tropospheric Delays over China from the High-Resolution Pangu-Weather Model at Multiple Forecast Scales
Abstract
Highlights
- The Pangu-Weather model outperforms the traditional GFS product at both lead times, especially in the climatically and topographically complex regions of Southern China.
- The Pangu-Weather model based on artificial intelligence deep learning algorithms exhibits a lower error accumulation trend, maintaining more stable accuracy over longer forecast periods.
- The Pangu-Weather model shows significant potential for applications in real-time GNSS positioning and meteorological monitoring.
Abstract
1. Introduction
2. Data Description
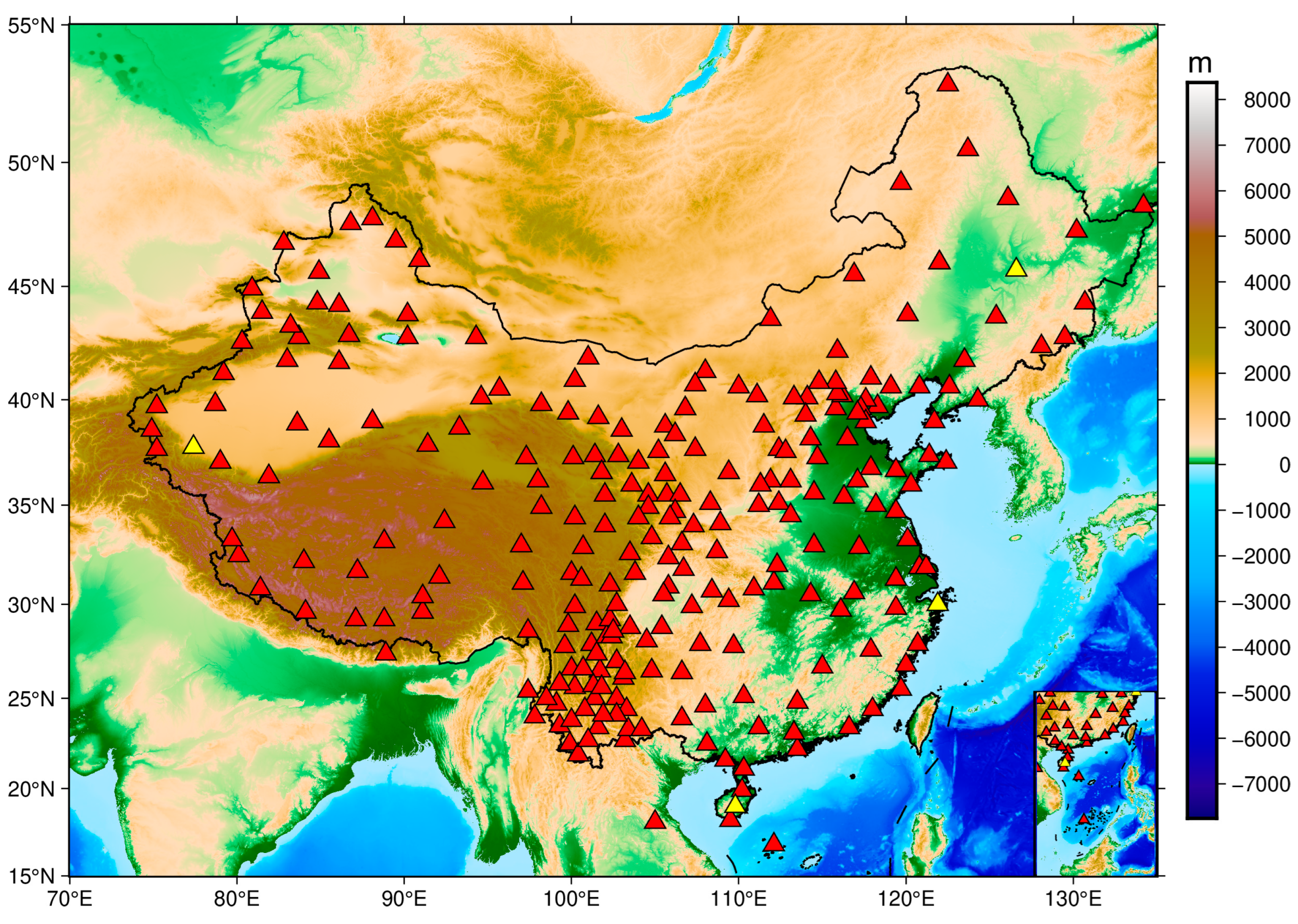
2.1. GNSS Tropospheric Delays
2.2. Pangu-Weather Model
2.3. GFS Forecast Grids
3. Methodology
4. Results and Discussion
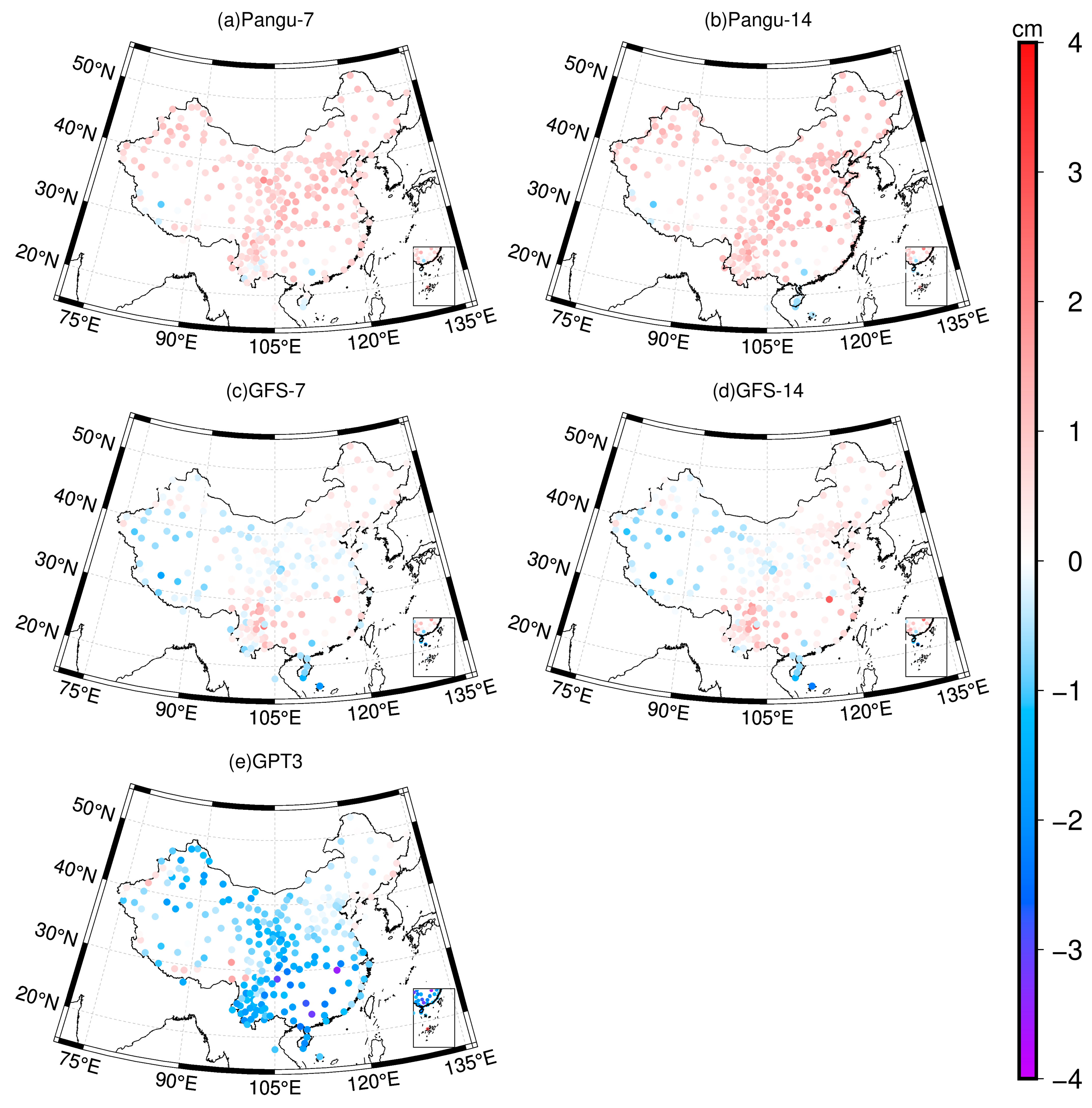
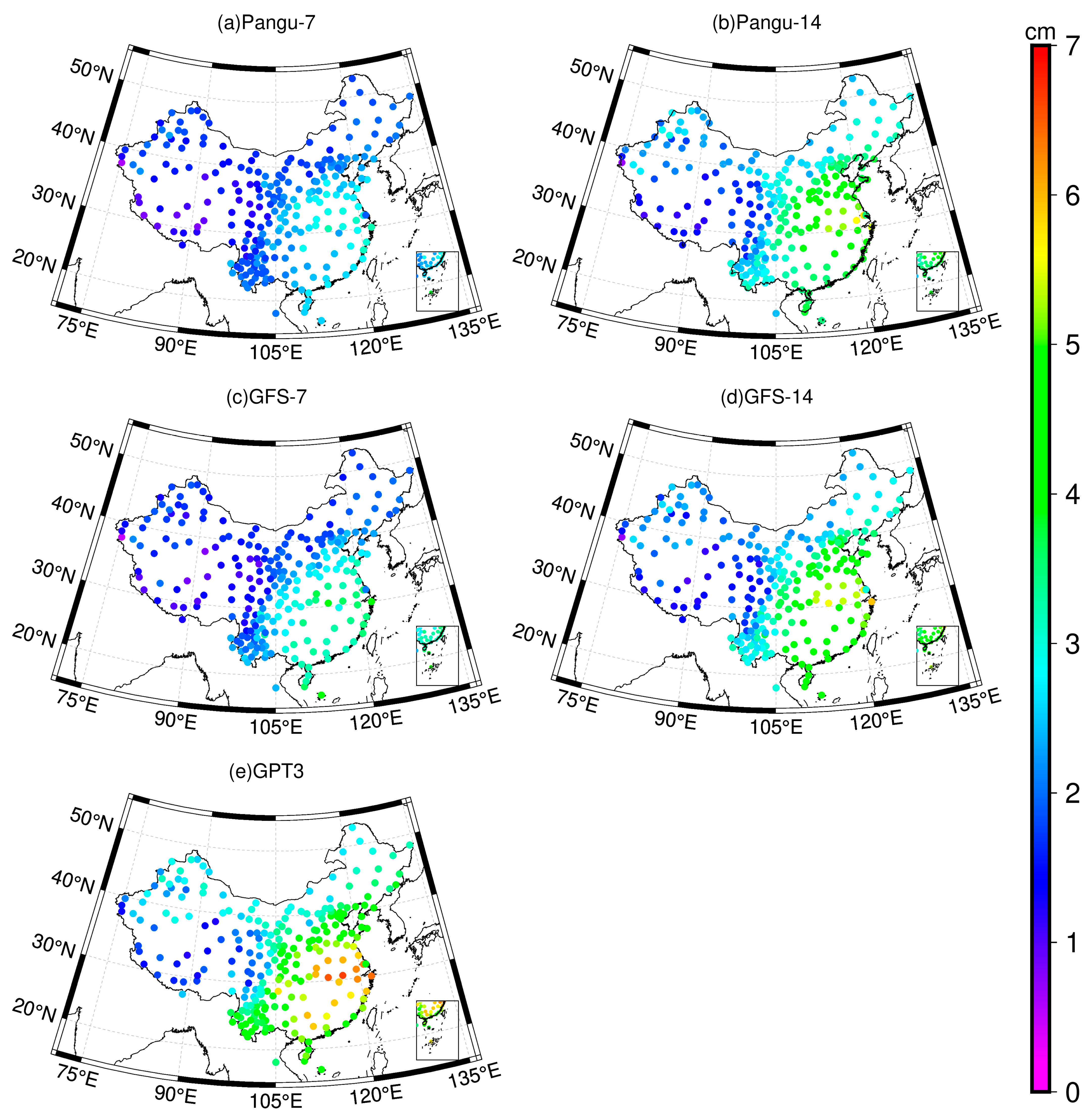
4.1. Accuracy Analysis of Spatial Distribution
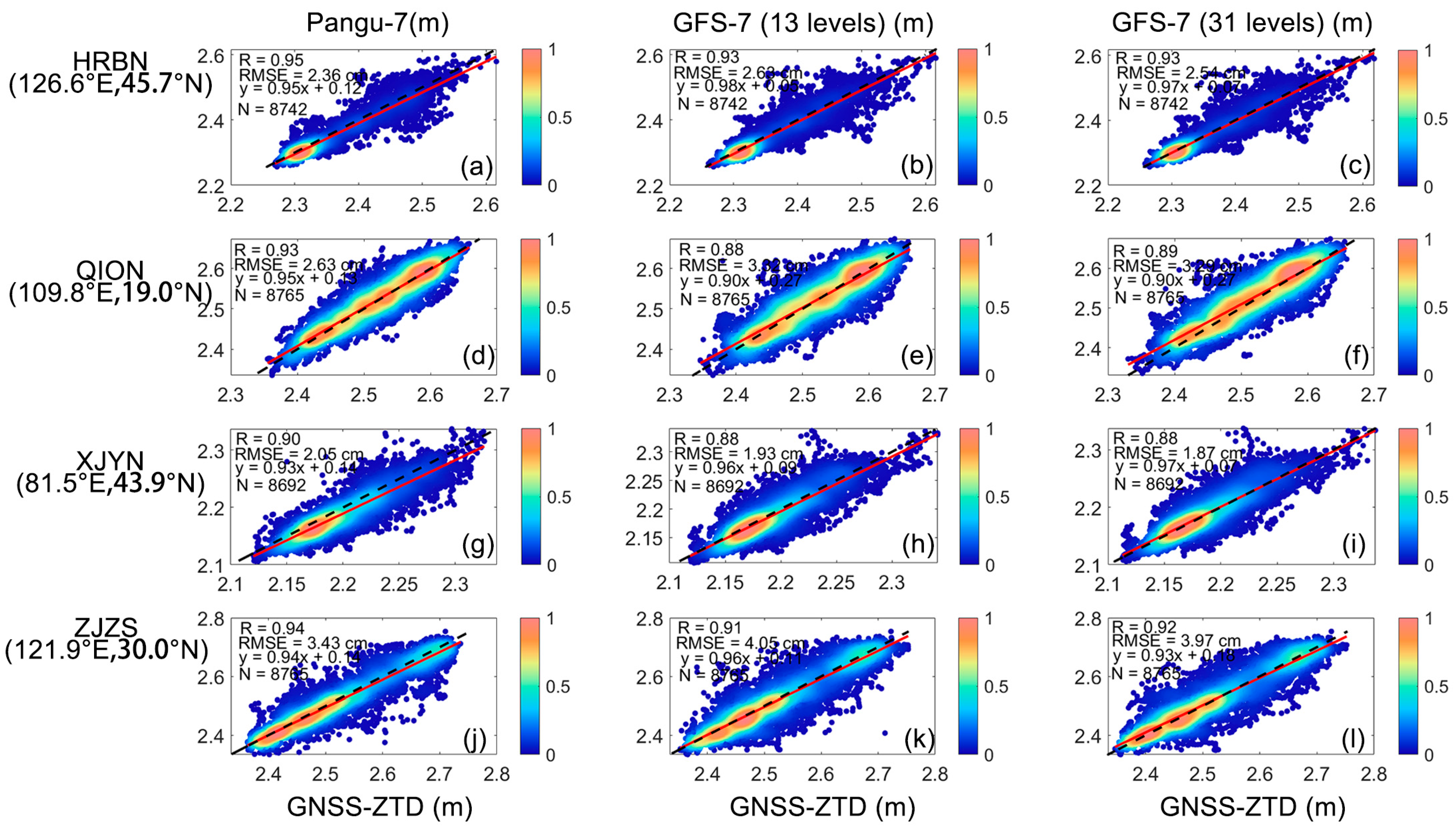
4.2. Accuracy Analysis of Density Scatter for Four Randomly Selected Stations
4.3. Accuracy Analysis of Different Latitude Belts and Different Height Ranges
4.4. Accuracy Analysis of Different Months
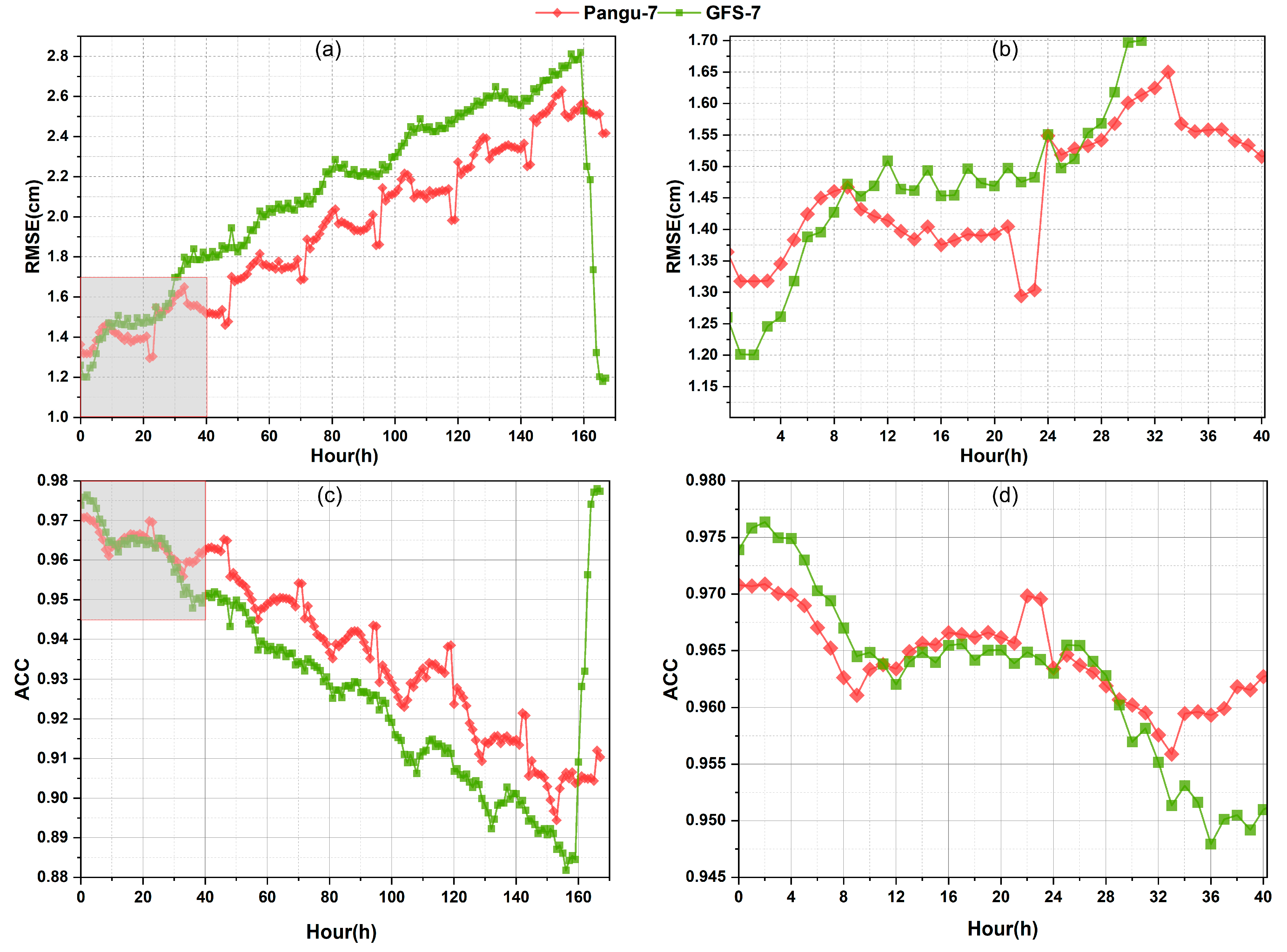
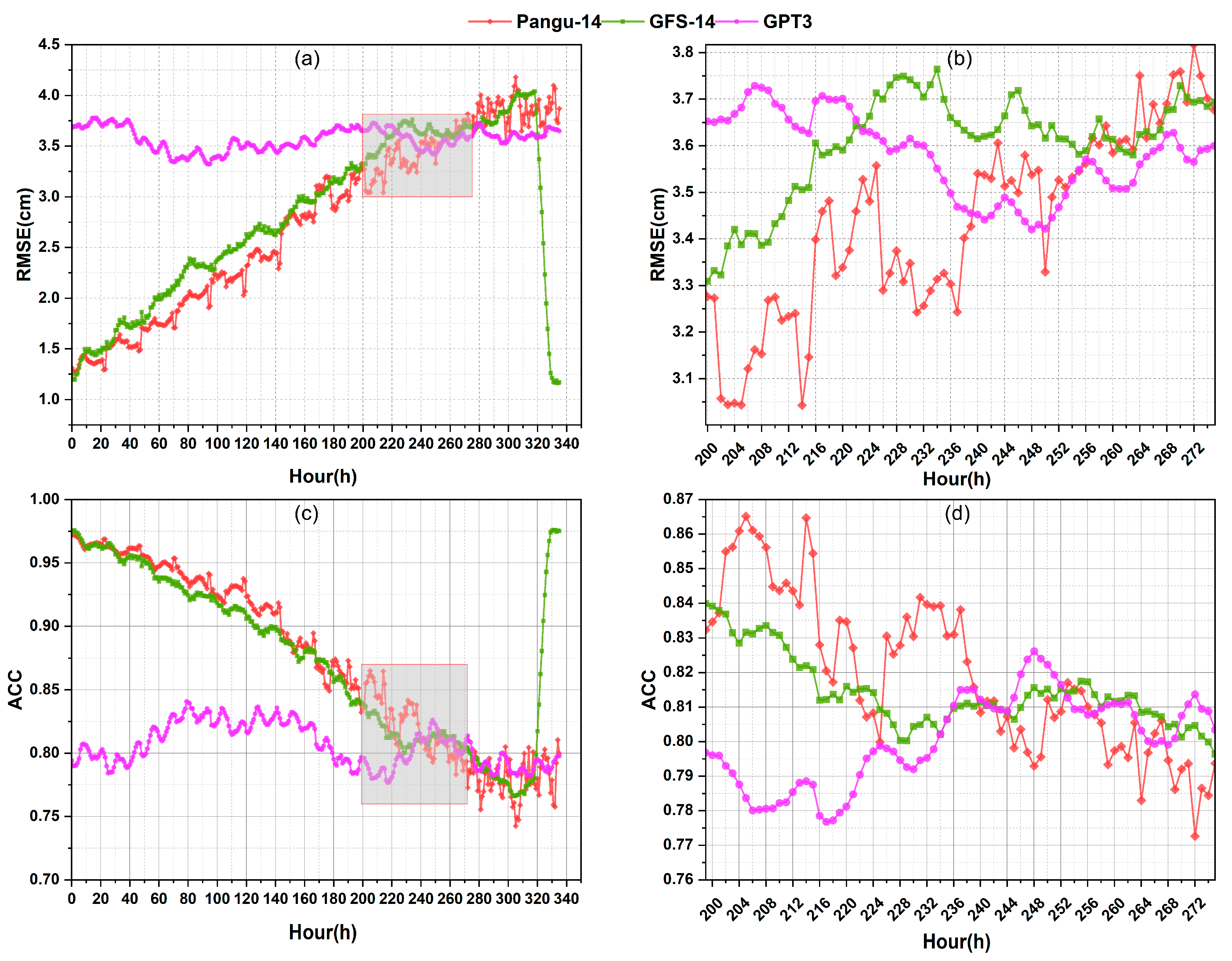
4.5. Accuracy Evaluation of RMSE in 7-Day and 14-Day ZTD Forecasting
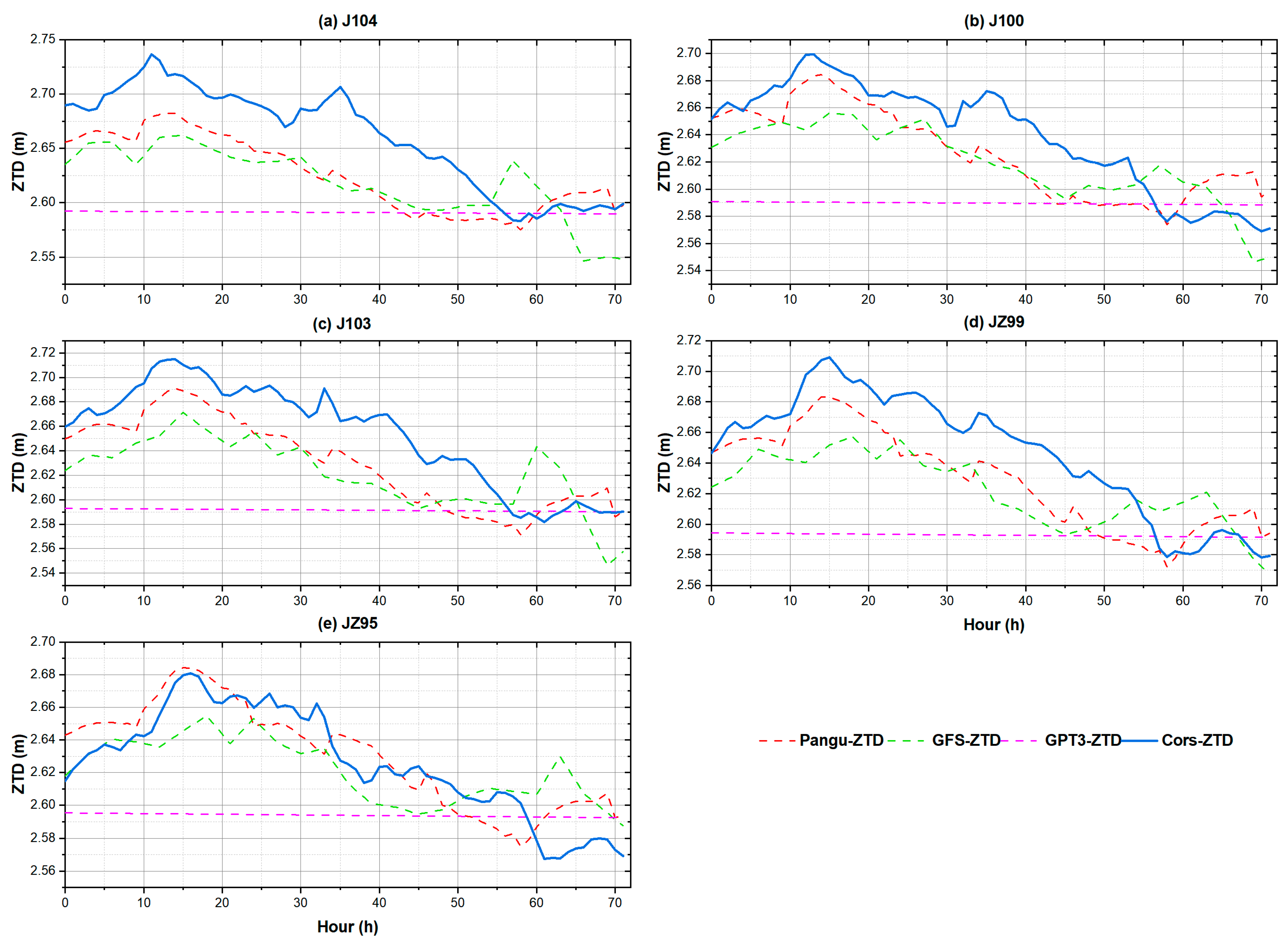
4.6. Accuracy Analysis of Models Under Complex Weather Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global Navigation Satellite Systems |
| ZTD | Zenith Total Delay |
| PWV | Precipitable Water Vapor |
| GPT3 | Global Pressure and Temperature 3 |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| NWP | Numerical Weather Prediction |
| GFS | Global Forecast System |
| IFS | Integrated Forecasting System |
| AI | Artificial Intelligence |
| NCEP | National Centers for Environmental Prediction |
| CMONOC | Crustal Movement Observation Network of China |
References
- Dousa, J.; Elias, M. An improved model for calculating tropospheric wet delay. Geophys. Res. Lett. 2014, 41, 4389–4397. [Google Scholar] [CrossRef]
- Huang, L.; Zhu, G.; Liu, L.; Chen, H.; Jiang, W. A global grid model for the correction of the vertical zenith total delay based on a sliding window algorithm. Gps Solut. 2021, 25, 98. [Google Scholar] [CrossRef]
- Li, H.; Zhu, G.; Kang, Q.; Huang, L.; Wang, H. A global zenith tropospheric delay model with ERA5 and GNSS-based ZTD difference correction. Gps Solut. 2023, 27, 154. [Google Scholar] [CrossRef]
- Huang, L.; Pan, A.; Chen, F.; Guo, F.; Li, H.; Liu, L. A novel global grid model for soil moisture retrieval considering geographical disparity in spaceborne GNSS-R. Satell. Navig. 2024, 5, 29. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q.; Liu, L.; Yao, Y.; Huang, L.; Chen, F.; Zhou, L.; Zhang, B. A refined zenith tropospheric delay model for Mainland China based on the global pressure and temperature 3 (GPT3) model and random forest. Gps Solut. 2023, 27, 172. [Google Scholar] [CrossRef]
- Li, S.; Jiang, N.; Xu, T.; Xu, Y.; Yang, H.; Zhang, Z.; Guo, A.; Wu, Y. A precipitation forecast model with a neural network and improved GPT3 model for Japan. Gps Solut. 2023, 27, 186. [Google Scholar] [CrossRef]
- Yuan, P.; Blewitt, G.; Kreemer, C.; Hammond, W.C.; Argus, D.; Yin, X.; Van Malderen, R.; Mayer, M.; Jiang, W.; Awange, J.; et al. An enhanced integrated water vapour dataset from more than 10 000 global ground-based GPS stations in 2020. Earth Syst. Sci. Data 2023, 15, 723–743. [Google Scholar] [CrossRef]
- Xiong, L.; Huang, L.; Mo, Z.; Chen, X.; Yang, Y.; Xie, S.; Li, J.; Liu, L. Evolution of GNSS-Derived Precipitable Water Vapor and Its Driving Factors During the “Dragon Boat Water” Rainfall Event in Guangxi, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 14308–14323. [Google Scholar] [CrossRef]
- Huang, L.; Zheng, Z.; Zhu, G.; Bi, H.; Li, H.; Liu, L. A Novel Method for Forecasting Global High-Resolution Precipitable Water Vapor with The Pangu-Weather System. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 14843–14854. [Google Scholar] [CrossRef]
- Xu, C.; Liu, C.; Yao, Y.; Wang, Q.; Wang, X. Tibetan zenith wet delay model with refined vertical correction. J. Geod. 2023, 97, 31. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Meng, X.; Li, J.; Zou, J.; Xu, Y. Establishment and assessment of a zenith wet delay (ZWD) augmentation model. Gps Solut. 2021, 25, 148. [Google Scholar] [CrossRef]
- Zhao, X.; Niu, Q.; Chi, Q.; Chen, J.; Liu, C. A new LSTM-based model to determine the atmospheric weighted mean temperature in GNSS PWV retrieval. Gps Solut. 2024, 28, 74. [Google Scholar] [CrossRef]
- Li, J.; Li, F.; Liu, L.; Yao, Y.; Huang, L.; Wang, Y. A weighted mean temperature forecast model based on fused data and generalized regression neural network and its impact on GNSS-Based precipitable water vapor estimation. IEEE Trans. Geosci. Remote 2024, 62, 4101914. [Google Scholar] [CrossRef]
- Huang, L.; Lu, D.; Chen, F.; Zhang, H.; Zhu, G.; Liu, L. A Deep Learning-Based Approach for Directly Retrieving GNSS Precipitable Water Vapor and Its Application in Typhoon Monitoring. IEEE Trans. Geosci. Remote 2024, 62, 4111712. [Google Scholar] [CrossRef]
- Hopfield, H.S. Two-quartic tropospheric refractivity profile for correcting satellite data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar] [CrossRef]
- Black, H.D. An easily implemented algorithm for the tropospheric range correction. J. Geophys. Res. 1978, 83, 1825–1828. [Google Scholar] [CrossRef]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio. Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Huang, L.; Jiang, W.; Liu, L.; Chen, H.; Ye, S. A new global grid model for the determination of atmospheric weighted mean temperature in GPS precipitable water vapor. J. Geod. 2019, 93, 159–176. [Google Scholar] [CrossRef]
- Ding, M. A neural network model for predicting weighted mean temperature. J. Geod. 2018, 92, 1187–1198. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Li, W.; Zhang, B.; Ou, J. A grid-based tropospheric product for China using a GNSS network. J. Geod. 2018, 92, 765–777. [Google Scholar] [CrossRef]
- Leandro, R.; Santos, M.; Langley, R.B. UNB neutral atmosphere models: Development and performance. In Proceedings of the 2006 National Technical Meeting of the Institute of Navigation, Monterey, CA, USA, 18–20 January 2006. [Google Scholar]
- Leandro, R.F.; Langley, R.B.; Santos, M.C. UNB3m_pack: A neutral atmosphere delay package for radiometric space techniques. Gps Solut. 2008, 12, 65–70. [Google Scholar] [CrossRef]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef]
- Lan, S.; Zhang, L.; Chen, X.; Yang, Y.; Xiong, S.; Tang, Y.; Huang, L.; Li, X. A novel model for the estimation of water vapor pressure and temperature considering diurnal variations in China. Adv. Space Res. 2025, 75, 515–529. [Google Scholar] [CrossRef]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Zhang, C.; Li, Y.; Li, J. A regional Zenith Tropospheric Delay (ZTD) model based on GPT3 and ANN. Remote Sens. 2021, 13, 838. [Google Scholar] [CrossRef]
- Zhao, Q.; Su, J.; Xu, C.; Yao, Y.; Zhang, X.; Wu, J. High-Precision ZTD model of altitude-related correction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 609–621. [Google Scholar] [CrossRef]
- Zhu, G.; Huang, L.; Yang, Y.; Li, J.; Zhou, L.; Liu, L. Refining the ERA5-based global model for vertical adjustment of zenith tropospheric delay. Satell. Navig. 2022, 3, 27. [Google Scholar] [CrossRef]
- Huang, L.; Zhu, G.; Peng, H.; Liu, L.; Ren, C.; Jiang, W. An improved global grid model for calibrating zenith tropospheric delay for GNSS applications. Gps Solut. 2022, 27, 17. [Google Scholar] [CrossRef]
- Huang, L.; Lan, S.; Zhu, G.; Chen, F.; Li, J.; Liu, L. A global grid model for the estimation of zenith tropospheric delay considering the variations at different altitudes. Geosci. Model. Dev. 2023, 16, 7223–7235. [Google Scholar] [CrossRef]
- Wilgan, K.; Hadas, T.; Hordyniec, P.; Bosy, J. Real-time precise point positioning augmented with high-resolution numerical weather prediction model. Gps Solut. 2017, 21, 1341–1353. [Google Scholar] [CrossRef]
- Du, Z.; Zhao, Q.; Yao, Y.; Zhu, H. Real-time tropospheric delay map retrieval using sparse GNSS stations. Gps Solut. 2023, 28, 12. [Google Scholar] [CrossRef]
- Xia, P.; Tong, M.; Ye, S.; Qian, J.; Fangxin, H. Establishing a high-precision real-time ZTD model of China with GPS and ERA5 historical data and its application in PPP. Gps Solut. 2022, 27, 2. [Google Scholar] [CrossRef]
- Huang, L.; Haohang, B.; Hongxing, Z.; Shitai, W.; Fasheng, L.; Lilong, L.; Jiang, W. An optimized BP neural network for modeling zenith tropospheric delay in the Chinese mainland using coupled particle swarm and genetic algorithm. Geo-Spat. Inf. Sci. 2025, 28, 1927–1942. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Li, W. Real-time wide-area precise tropospheric corrections (WAPTCs) jointly using GNSS and NWP forecasts for China. J. Geod. 2022, 96, 44. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Zus, F.; Heinkelmann, R.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Improving BeiDou real-time precise point positioning with numerical weather models. J. Geod. 2017, 91, 1019–1029. [Google Scholar] [CrossRef]
- Boehm, J.; Kouba, J.; Schuh, H. Forecast Vienna Mapping Functions 1 for real-time analysis of space geodetic observations. J. Geod. 2009, 83, 397–401. [Google Scholar] [CrossRef]
- Ding, J.; Chen, J.; Wang, J.; Zhang, Y. A novel method for tropospheric delay mapping function vertical modeling. J. Geod. 2024, 98, 37. [Google Scholar] [CrossRef]
- Li, J.; Yang, F.; Yuan, D.; Wang, H.; Song, S.; Tan, J.; Wen, Z. Unraveling the accuracy enigma: Investigating ZTD data precision in TUW-VMF3 and GFZ-VMF3 products using a comprehensive global GPS dataset. IEEE Trans. Geosci. Remote 2024, 62, 5800710. [Google Scholar] [CrossRef]
- Bi, K.; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Accurate medium-range global weather forecasting with 3D neural networks. Nature 2023, 619, 533–538. [Google Scholar] [CrossRef] [PubMed]
- Selz, T.; Craig, G.C. Can artificial intelligence-based weather prediction models simulate the butterfly effect? Geophys. Res. Lett. 2023, 50, e2023GL105747. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, Y.; Chen, J.; Zhang, Y. Short- to Medium-Term Weather Forecast Skill of the AI-Based Pangu-Weather Model Using Automatic Weather Stations in China. Remote Sens. 2025, 17, 191. [Google Scholar] [CrossRef]
- Huang, L.; Wang, Y.; Bi, H.; Zhu, G.; Liu, L.; Jiang, W. Initial results of atmospheric weighted mean temperature estimation with Pangu-Weather in real-time GNSS PWV retrieval for China. Gps Solut. 2025, 29, 48. [Google Scholar] [CrossRef]
- Xiong, S.; Mei, J.; Xu, X.; Shen, Z.; Huang, L. Methods and evaluation of AI-Based meteorological models for zenith tropospheric delay prediction. Remote Sens. 2024, 16, 4231. [Google Scholar] [CrossRef]
- Ding, J.; Mi, X.; Chen, W.; Chen, J.; Wang, J.; Zhang, Y.; Awange, J.L.; Soja, B.; Bai, L.; Deng, Y.; et al. Forecasting of tropospheric delay using AI foundation models in support of microwave remote sensing. IEEE Trans. Geosci. Remote 2024, 62, 5803019. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, R.; Nie, Z.; Li, Y.; Chen, Z.; Wang, T. Research on variety characteristics of mainland China troposphere based on CMONOC. Geod. Geodyn. 2018, 9, 411–417. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Wang, A.; Ding, J.; Zhang, Y. SHAtropE—A Regional Gridded ZTD Model for China and the Surrounding Areas. Remote Sens. 2020, 12, 165. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, X.; Zheng, Y.; Liu, C.; He, B. Real-time high-resolution tropospheric delay mapping based on GFS forecasts and GNSS. Gps Solut. 2024, 28, 175. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; Fan, S.; Cheng, Y. Water vapor-weighted mean temperature and its impact on the determination of precipitable water vapor and its linear trend. J. Geophys. Res-Atmos. 2016, 121, 833–852. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements. In FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Zhao, Q.; Wang, W.; Li, Z.; Du, Z.; Yang, P.; Yao, W.; Yao, Y. A high-precision ZTD interpolation method considering large area and height differences. Gps Solut. 2023, 28, 4. [Google Scholar] [CrossRef]
- Zhu, K.; Zhao, L.; Wang, W.; Zhang, S.; Liu, R.; Wang, J. Augment BeiDou real-time precise point positioning using ECMWF data. Earth Planets Space 2018, 70, 112. [Google Scholar] [CrossRef]
- Meng, X.; Jin, S.; Liu, C.; Zhang, G.; Zhang, Y. A high precision 3-D tropospheric delay model over China using ERA5 data. Adv. Space Res. 2025, 75, 2599–2613. [Google Scholar] [CrossRef]
- Jin, S.; Park, J.U.; Cho, J.H.; Park, P.H. Seasonal variability of GPS-derived zenith tropospheric delay (1994–2006) and climate implications. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Elsobeiey, M.E. Characteristic differences between IGS final and ray-traced tropospheric delays and their impact on precise point positioning and tropospheric delay estimates. Gps Solut. 2020, 24, 97. [Google Scholar] [CrossRef]
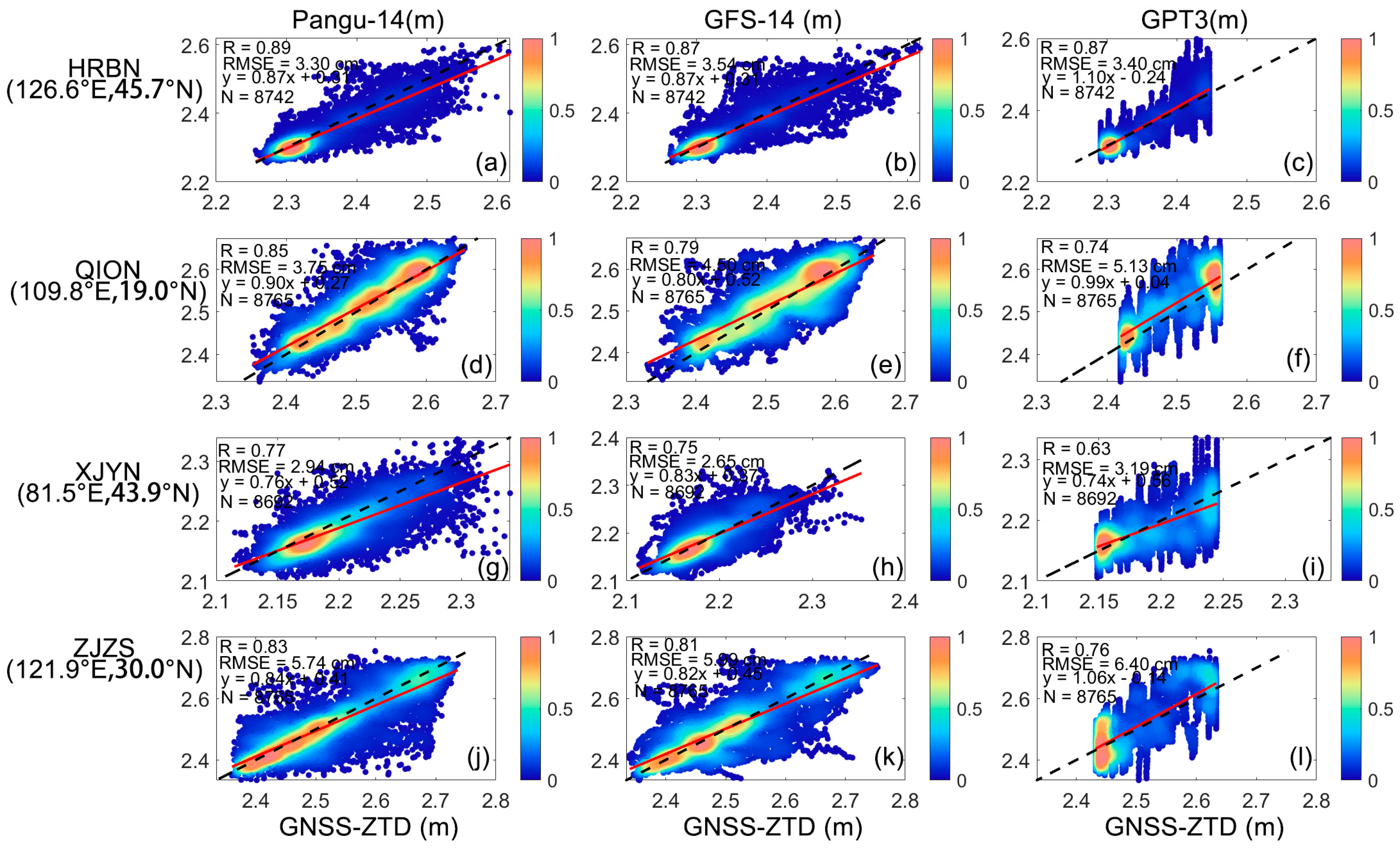
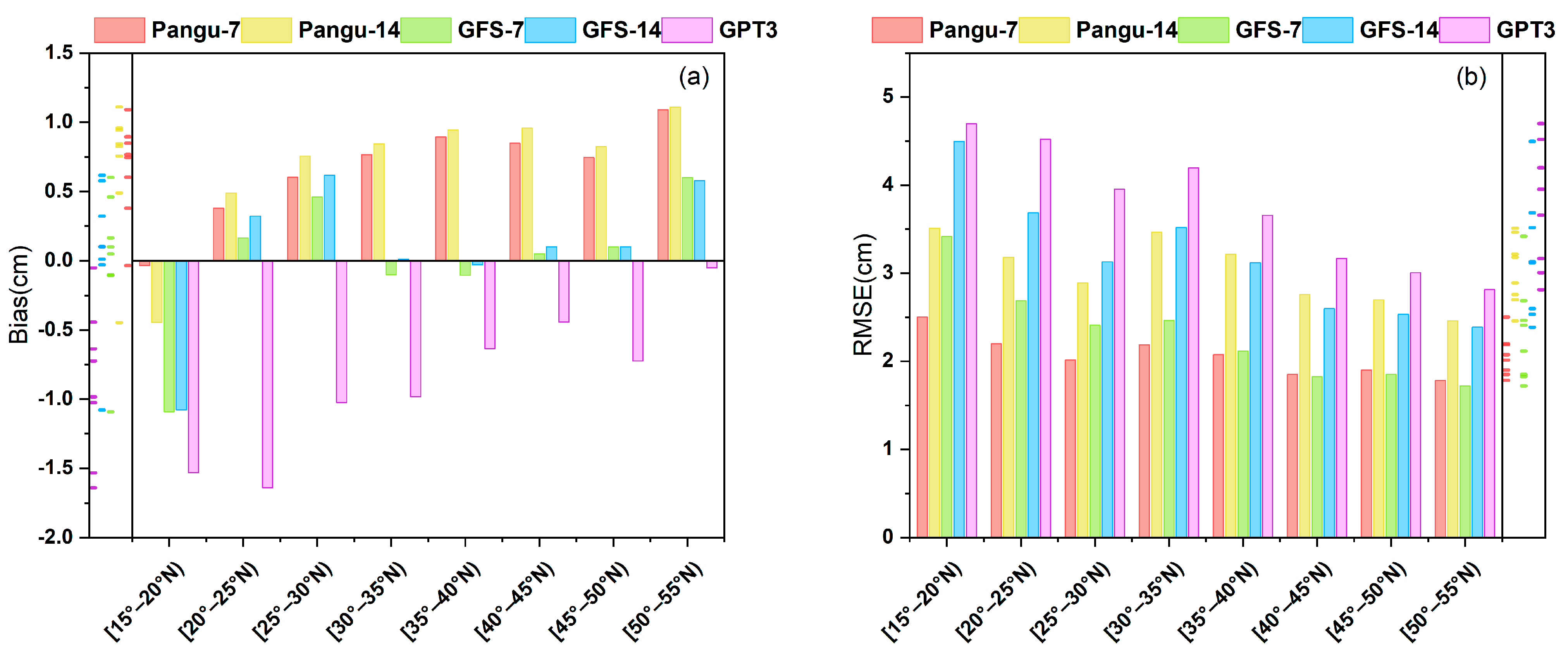
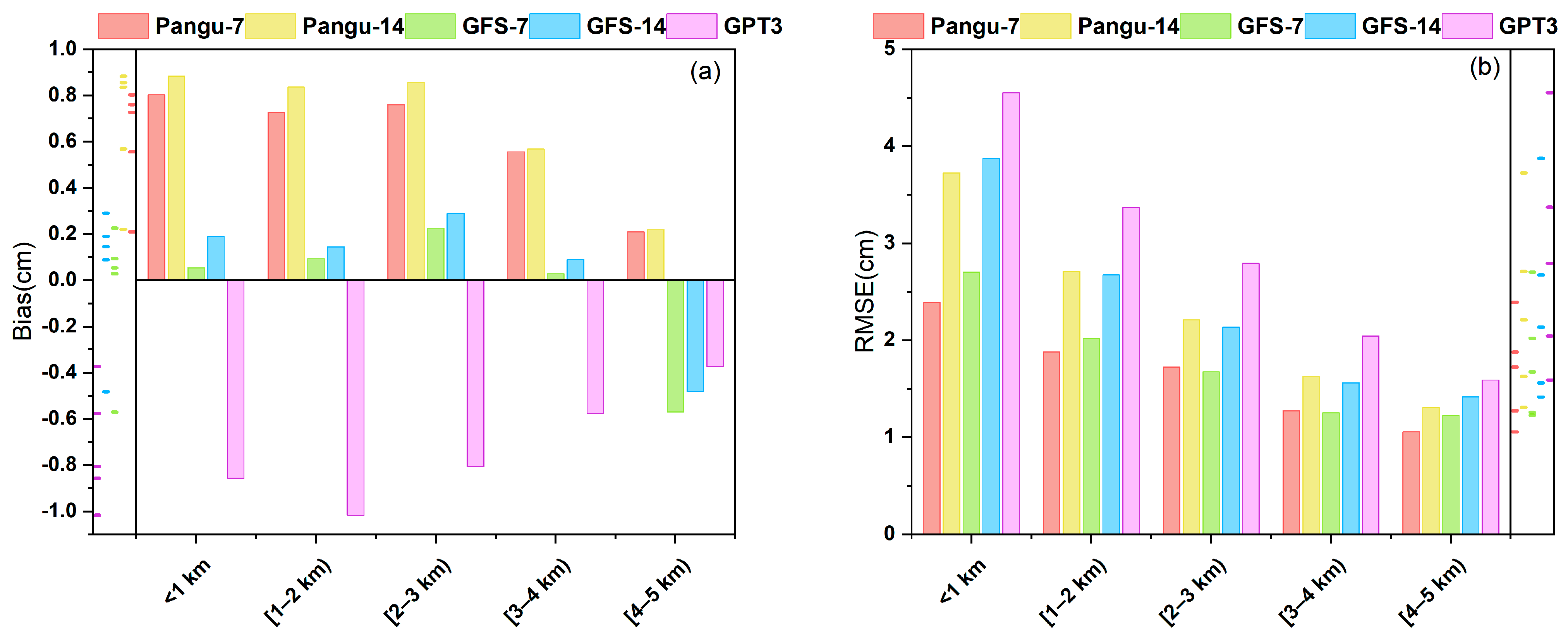
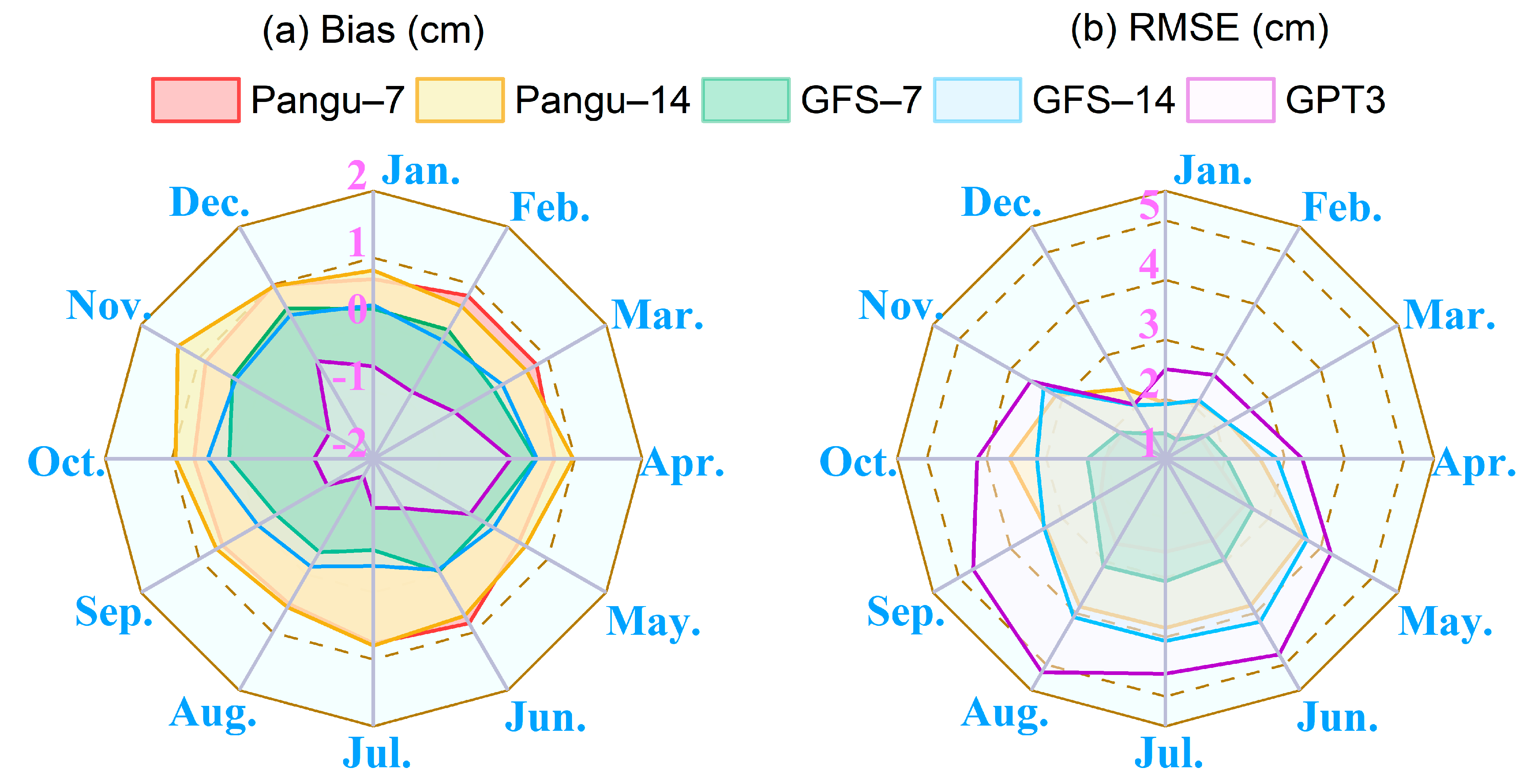
| Data | Temporal Resolution | Spatial Resolution | Time Latency | Data Type |
|---|---|---|---|---|
| GNSS | 5 s | - | Post-processing | Zenith total delays |
| Pangu-Weather | 1, 3, 6, 24 h | 0.25° × 0.25° | Forecasted | Meteorological parameters on pressure levels and surface |
| ERA5 | 1 h | 0.25° × 0.25° | Reanalyzed | Meteorological parameters on pressure levels and surface |
| GFS | 3 or 12 h | 0.25° × 0.25° | Forecasted | Meteorological parameters on pressure levels and surface |
| Model | Bias (cm) | RMSE (cm) | ||||
|---|---|---|---|---|---|---|
| Max | Min | Mean | Max | Min | Mean | |
| Pangu-7 | 1.95 | −0.95 | 0.73 | 3.94 | 0.61 | 1.99 |
| GFS-7 | 2.32 | −1.95 | 0.06 | 4.87 | 0.47 | 2.16 |
| Pangu-14 | 2.26 | −0.94 | 0.81 | 5.74 | 0.68 | 2.94 |
| GFS-14 | 2.78 | −2.29 | 0.16 | 5.94 | 0.70 | 2.98 |
| GPT3 | 2.80 | −3.51 | −0.86 | 6.65 | 1.20 | 3.61 |
| Model | Pangu-ZTD | GFS-ZTD | GPT3-ZTD | |||
|---|---|---|---|---|---|---|
| RMSE (cm) | Bias (cm) | RMSE (cm) | Bias (cm) | RMSE (cm) | Bias (cm) | |
| J104 | 4.28 | −3.44 | 5.14 | −4.13 | 8.30 | −6.94 |
| J100 | 2.62 | −1.38 | 2.96 | −2.05 | 6.33 | −5.04 |
| J103 | 2.97 | −2.33 | 4.22 | −3.16 | 7.39 | −6.17 |
| JZ99 | 2.50 | −1.78 | 3.52 | −2.42 | 6.61 | −5.39 |
| JZ95 | 1.71 | 0.43 | 2.23 | −0.46 | 4.52 | −3.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zhang, B.; Bi, H.; Huang, L.; Shi, B.; Ai, Q. Evaluation of Tropospheric Delays over China from the High-Resolution Pangu-Weather Model at Multiple Forecast Scales. Remote Sens. 2025, 17, 3164. https://doi.org/10.3390/rs17183164
Li S, Zhang B, Bi H, Huang L, Shi B, Ai Q. Evaluation of Tropospheric Delays over China from the High-Resolution Pangu-Weather Model at Multiple Forecast Scales. Remote Sensing. 2025; 17(18):3164. https://doi.org/10.3390/rs17183164
Chicago/Turabian StyleLi, Shuangping, Bin Zhang, Haohang Bi, Liangke Huang, Bo Shi, and Qingsong Ai. 2025. "Evaluation of Tropospheric Delays over China from the High-Resolution Pangu-Weather Model at Multiple Forecast Scales" Remote Sensing 17, no. 18: 3164. https://doi.org/10.3390/rs17183164
APA StyleLi, S., Zhang, B., Bi, H., Huang, L., Shi, B., & Ai, Q. (2025). Evaluation of Tropospheric Delays over China from the High-Resolution Pangu-Weather Model at Multiple Forecast Scales. Remote Sensing, 17(18), 3164. https://doi.org/10.3390/rs17183164








