Interval Determination Strategy for Bayesian Inversion of Seismic Source Parameters Under Uncertain Interval Conditions
Abstract
Highlights
- Two novel strategies—‘CFI’ (Converge First, Then Interval) and ‘IVI’ (Interval Value Iteration)—are proposed to prevent Markov Chain Monte Carlo (MCMC) algorithms from becoming trapped in local optima during the Bayesian inversion of seismic source parameters.
- The ‘IVI’ strategy, when paired with an MCMC algorithm using a normally distribut-ed step size, significantly reduces the root-mean-square error (RMSE) of the inversion results.
- Application to the 2022 Mw6.6 Menyuan earthquake demonstrates the method’s practicality, yielding fault parameters (depth, strike, dip, rake) closer to the GCMT solution with low fitting residuals.
- The strategies provide clear guidance for inversion settings: use ‘IVI’ when parameter ranges are unknown, ‘CFI’ when an approximate range is known, and standard con-straints only when both the interval and a reliable initial model are fully known.
Abstract
1. Introduction
2. Method
2.1. Bayesian Framework
2.2. Principles of MCMC Under the Bayesian Framework
2.3. Interval Determination Strategy
2.4. Avoiding the Inverse Problem of Deformation Constraints from InSAR Data
3. Synthetic Experiments
3.1. Synthetic Data
3.2. Synthetic Experiment Setup
3.3. Synthetic Experiment Results
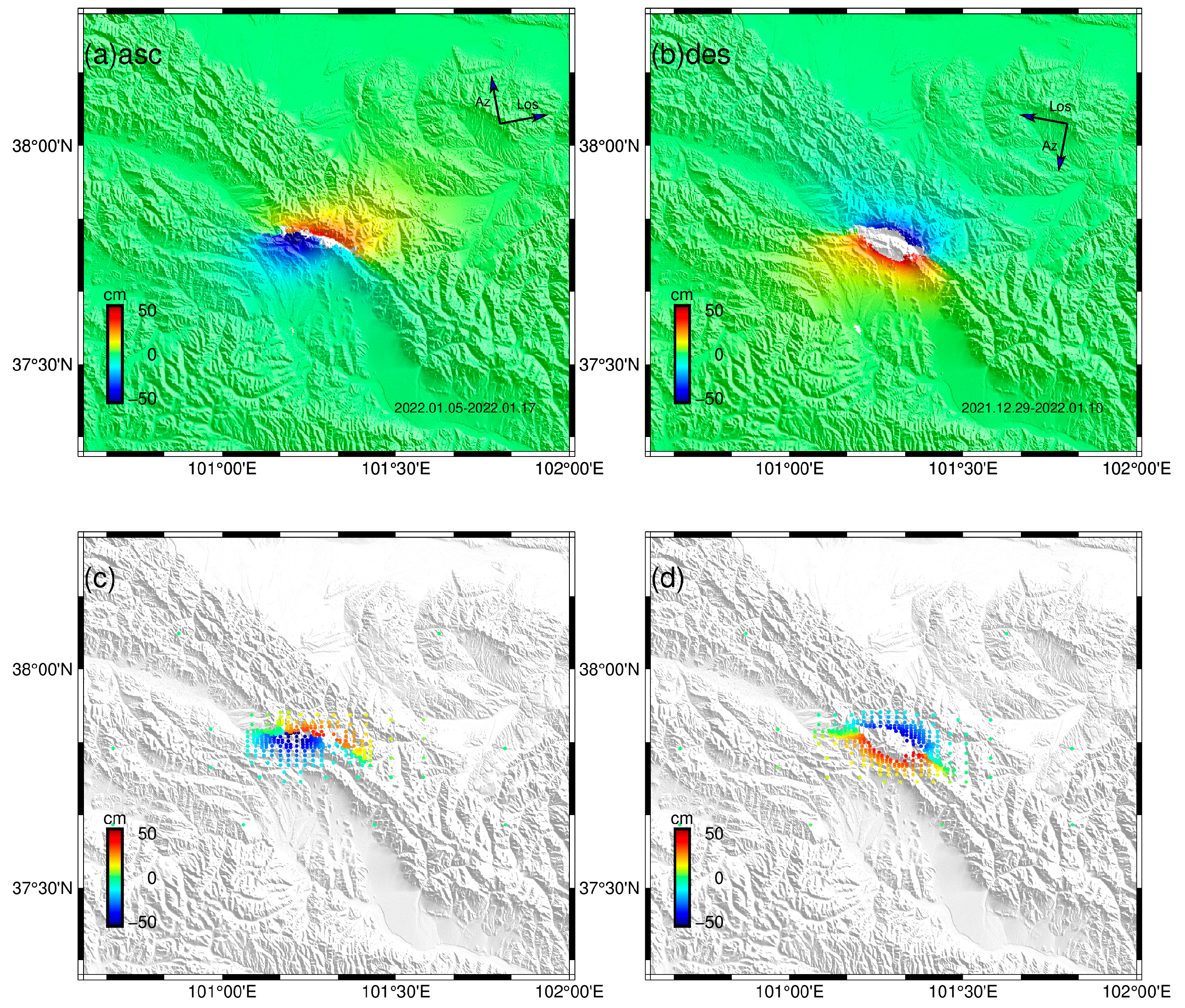
4. Application of the Menyuan Earthquake
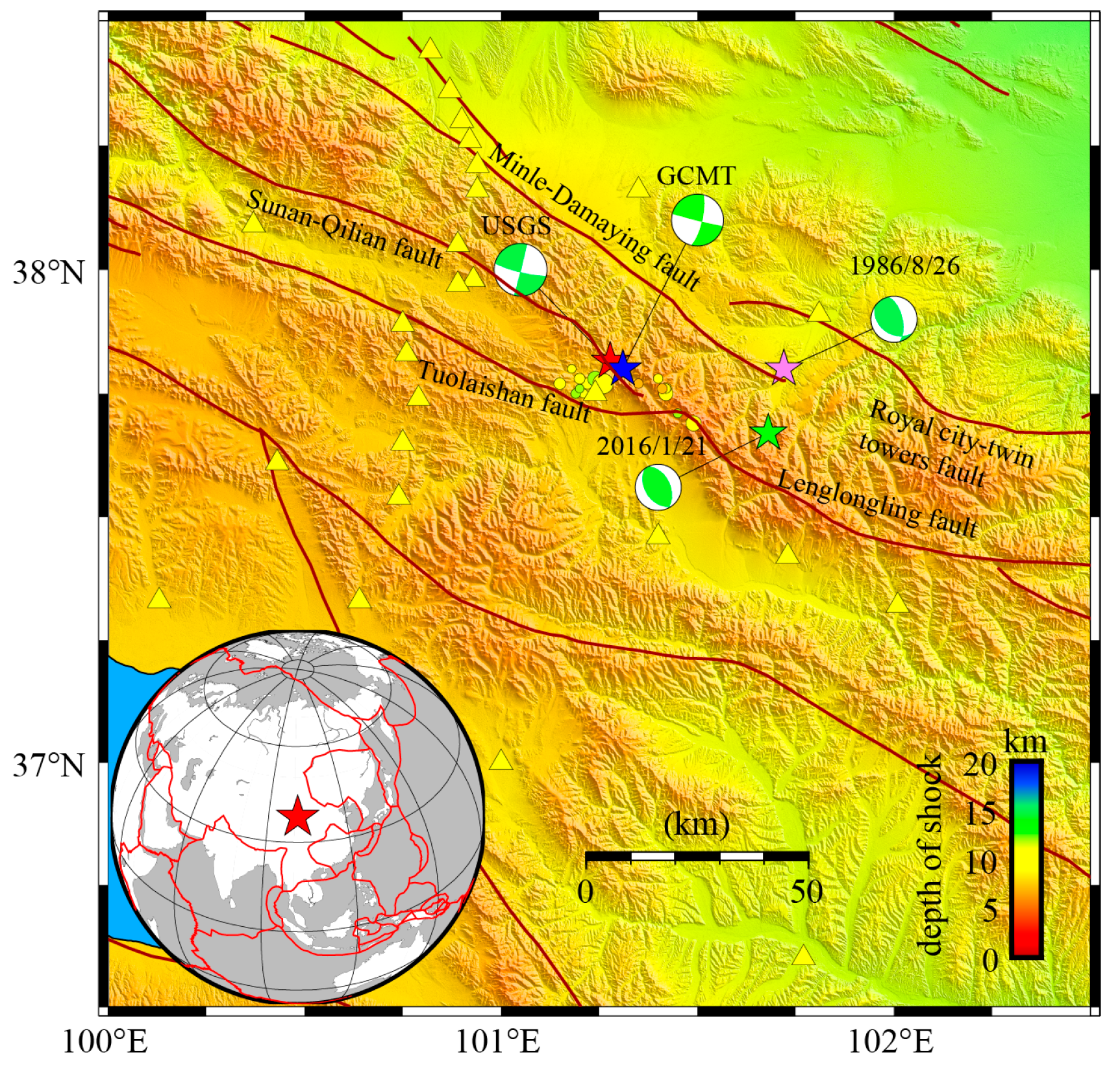
4.1. Background
4.2. Data and Model Set Up
4.3. Results
5. Discussion
6. Conclusions
- (1)
- When the range of seismic source parameters is unknown or ambiguous, Interval Determination Strategy 2 (IVI) should be adopted;
- (2)
- When an approximate range is known, Interval Determination Strategy 1 (CFI) is recommended;
- (3)
- When the interval is fully known and a reliable initial model can be obtained, the original interval constraint method should be used.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, C.; He, K. Advancements in Earthquake Cycle Deformation Research Based on Geodetic Observations. Geomat. Inf. Sci. Wuhan Univ. 2023, 48, 1736–1755. (In Chinese) [Google Scholar] [CrossRef]
- Funning, G.J.; Fukahata, Y.; Yagi, Y.; Parsons, B. Method for the joint inversion of geodetic and seismic waveform data using ABIC: Application to the 1997 Manyi, Tibet, earthquake. Geophys. J. Int. 2014, 196, 1564–1579. [Google Scholar] [CrossRef]
- Papadimitriou, E.; Karakostas, V.; Papazachos, C.; Foumelis, M.; Kiratzi, A.; Pikridas, C.; Bonatis, P.; Kostoglou, A.; Kourouklas, C.; Scordilis, E.; et al. The seismogenic structure of March 2021 Tyrnavos (central Greece) doublet (Mw6.3 and Mw6.0), constrained by aftershock locations and geodetic data. Geophys. J. Int. 2023, 235, 644–689. [Google Scholar] [CrossRef]
- Wang, L.; Li, H. GBO algorithm for seismic source parameters inversion. Geod. Geodyn. 2023, 14, 182–190. [Google Scholar] [CrossRef]
- Xi, C.; Wang, L.; Zhao, X.; Sun, Z.; Zhao, W.; Pang, M.; Wu, F. A simple weighting method for inverting earthquake source parameters using geodetic multisource data under Bayesian algorithm. Geophys. J. Int. 2024, 237, 1142–1156. [Google Scholar] [CrossRef]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar] [CrossRef]
- Picozzi, M.; Oth, A.; Parolai, S.; Bindi, D.; De Landro, G.; Amoroso, O. Accurate estimation of seismic source parameters of induced seismicity by a combined approach of generalized inversion and genetic algorithm: Application to The Geysers geothermal area, California. J. Geophys. Res. Solid Earth 2017, 122, 3916–3933. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Q.; Xu, Q.; Liu, G.; Hu, J. Source model and Coulomb stress change of the 2015 Mw 7.8 Gorkha earthquake determined from improved inversion of geodetic surface deformation observations. J. Geod. 2019, 93, 333–351. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, C. Adaptive multi-start Gauss-Newton approach for geodetic data inversion of earthquake source parameters. J. Geod. 2020, 94, 17. [Google Scholar] [CrossRef]
- Wang, L.; Xu, R.; Yu, F. Genetic Nelder-Mead neural network algorithm for fault parameter inversion using GPS data. Geod. Geodyn. 2022, 13, 386–398. [Google Scholar] [CrossRef]
- Xu, C.; Zheng, G.; Niu, J. Recent developments in seismological geodesy. Geod. Geodyn. 2016, 7, 157–164. [Google Scholar] [CrossRef]
- Simutė, S.; Boehm, C.; Krischer, L.; Gokhberg, A.; Vallée, M.; Fichtner, A. Bayesian Seismic Source Inversion With a 3-D Earth Model of the Japanese Islands. J. Geophys. Res. Solid Earth 2023, 128, e2022JB024231. [Google Scholar] [CrossRef]
- Wei, G.; Chen, K.; Meng, H. Bayesian Inversion of Finite-Fault Earthquake Slip Model Using Geodetic Data, Solving for Non-Planar Fault Geometry, Variable Slip, and Data Weighting. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025225. [Google Scholar] [CrossRef]
- Amey, R.M.J.; Hooper, A.; Morishita, Y. Going to any lengths: Solving for fault size and fractal slip for the 2016, Mw6.2 Central Tottori earthquake, Japan, using a transdimensional inversion scheme. J. Geophys. Res. Solid Earth 2019, 124, 4001–4016. [Google Scholar] [CrossRef]
- Amey, R.M.J.; Hooper, A.; Walters, R.J. A Bayesian method for incorporating self-similarity into earthquake slip inversions. J. Geophys. Res. Solid Earth 2018, 123, 6052–6071. [Google Scholar] [CrossRef]
- Bagnardi, M.; Hooper, A. Inversion of surface deformation data for rapid estimates of source parameters and uncertainties: A Bayesian approach. Geochem. Geophys. Geosystems 2018, 19, 2194–2211. [Google Scholar] [CrossRef]
- Izzatullah, M.; Van Leeuwen, T.; Peter, D. Bayesian seismic inversion: A fast sampling Langevin dynamics Markov chain Monte Carlo method. Geophys. J. Int. 2021, 227, 1523–1553. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, T. Bayesian slip inversion with automatic differentiation variational inference. Geophys. J. Int. 2022, 229, 546–565. [Google Scholar] [CrossRef]
- Zhao, X.; Curtis, A.; Zhang, X. Bayesian seismic tomography using normalizing flows. Geophys. J. Int. 2022, 228, 213–239. [Google Scholar] [CrossRef]
- Wang, L.; Sun, L.; Xu, G. An Improved Bayesian von Karman Regularization Method for the Joint Inversion of GNSS and InSAR Data. J. Surv. Eng. 2023, 149, 04022016. [Google Scholar] [CrossRef]
- Sun, L.; Wang, L.; Xu, G.; Wu, Q. A new method of variational Bayesian slip distribution inversion. J. Geod. 2023, 97, 10. [Google Scholar] [CrossRef]
- Wang, L.; Xi, C. An improved MCMC algorithm for inversion of source parameters using GPS data under Bayesian framework. Chin. J. Geophys. 2024, 67, 3367–3385. (In Chinese) [Google Scholar] [CrossRef]
- Pedersen, R.; Jónsson, S.; Árnadóttir, T.; Sigmundsson, F.; Feigl, K. Fault slip distribution of two June 2000 Mw6.5 earthquakes in South Iceland estimated from joint inversion of InSAR and GPS measurements. Earth Planet. Sci. Lett. 2003, 213, 487–502. [Google Scholar] [CrossRef]
- Wright, T.J.; Lu, Z.; Wicks, C. Source model for the Mw6.7, 23 October 2002, Nenana mountain earthquake (Alaska) from InSAR. Geophys. Res. Lett. 2003, 30, 18. [Google Scholar] [CrossRef]
- Wang, L.; Gao, H.; Feng, G.; Xu, W. Source parameters and triggering links of the earthquake sequence in central Italy from 2009 to 2016 analyzed with GPS and InSAR data. Tectonophysics 2018, 744, 285–295. [Google Scholar] [CrossRef]
- Wang, L.; Xu, R. Multistart Nelder–Mead neural network algorithm for earthquake source parameter inversion of 2017 Bodrum–Kos earthquake. J. Surv. Eng. 2021, 147, 04021014. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Chai, H.; Chen, K.; Wei, G.; Fang, R.; Zou, R.; Zhu, H. Coseismic Deformation Monitoring Using BDS-3 and Ultra-High Rate GNSS: A Case Study of the 2021 Maduo Mw7.4 Earthquake. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 946–954. (In Chinese) [Google Scholar] [CrossRef]
- Xiong, W.; Chen, W.; Wang, D.; Wen, Y.; Nie, Z.; Liu, G.; Dijin, W.; Yu, P.; Qiao, X.; Zhao, B. Coseismic slip and early afterslip of the 2021 Mw7.4 Maduo, China earthquake constrained by GPS and InSAR data. Tectonophysics 2022, 840, 229558. [Google Scholar] [CrossRef]
- Jiang, W.; Xu, C.; Li, Z.; Wu, Y.; Tan, K.; Geng, J.; Chun, Y.; Zheng, G.; Wen, Y.; He, K.; et al. Using space observation techniques to study temporal and spatial characteristics of seismogenic process, occurrence and deformation of the Qinghai Madoi Mw7.4 earthquake. Chin. J. Geophys. 2022, 65, 495–508. (In Chinese) [Google Scholar] [CrossRef]
- Fabris, M.; Battaglia, M.; Chen, X.; Menin, A.; Monego, M.; Floris, M. An integrated InSAR and GNSS approach to monitor land subsidence in the Po River Delta (Italy). Remote Sens. 2022, 14, 5578. [Google Scholar] [CrossRef]
- Lazos, I.; Papanikolaou, I.; Sboras, S.; Foumelis, M.; Pikridas, C. Geodetic Upper Crust Deformation Based on Primary GNSS and INSAR Data in the Strymon Basin, Northern Greece—Correlation with Active Faults. Appl. Sci. 2022, 12, 9391. [Google Scholar] [CrossRef]
- Shen, G.; Fu, W.; Guo, H.; Liao, J. Water body mapping using long time series Sentinel-1 SAR data in Poyang Lake. Water 2022, 14, 1902. [Google Scholar] [CrossRef]
- Brouwer, W.S.; Hanssen, R.F. A treatise on InSAR geometry and 3D displacement estimation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–11. [Google Scholar] [CrossRef]
- Hu, J.; Ding, X.; Zhang, L.; Sun, Q.; Li, Z.; Zhu, J.; Lu, Z. Estimation of 3-D surface displacement based on InSAR and deformation modeling. IEEE Trans. Geosci. Remote Sens. 2016, 55, 2007–2016. [Google Scholar] [CrossRef]
- Peltier, A.; Froger, J.L.; Villeneuve, N.; Catry, T. Assessing the reliability and consistency of InSAR and GNSS data for retrieving 3D-displacement rapid changes, the example of the 2015 Piton de la Fournaise eruptions. J. Volcanol. Geotherm. Res. 2017, 344, 106–120. [Google Scholar] [CrossRef]
- Feng, W.; Li, Z. PSO hybrid algorithm inversion strategy of source parameters under InSAR data constraints. Prog. Geophys. 2010, 25, 1189–1196. (In Chinese) [Google Scholar] [CrossRef]
- Wang, L.; Gao, H.; Feng, G. InSAR and GPS data were used to analyze the triggering relationship and stress influence of two Mw>6 earthquakes in southwestern Taiwan. Acta Geod. Et Cartogr. Sin. 2019, 60, 2578–2588. (In Chinese) [Google Scholar] [CrossRef]
- Lohman, R.B.; Simons, M. Some thoughts on the use of InSAR data to constrain models of surface deformation: Noise structure and data downsampling. Geochem. Geophys. Geosyst. 2005, 6, 2004GC000841. [Google Scholar] [CrossRef]
- Xu, G.; Xu, X.; Yi, Y.; Wen, Y.; Wang, Q.; Li, K.; Ren, J. Seismogenic structure of the 2022 Menyuan Mw6.6 earthquake, Qinghai Province, constrained by InSAR and Gaofen-7 observation. Chin. J. Geophys. 2022, 65, 4704–4724. (In Chinese) [Google Scholar] [CrossRef]
- He, L.; Feng, G.; Wang, Y.; Xiong, Z.; Gao, H.; Liu, X. Geodetic source models of the 2016–2022 Menyuan Earthquake sequence (Northeastern Tibet) inferred from InSAR and optical observations. Geophys. J. Int. 2024, 236, 470–479. [Google Scholar] [CrossRef]
- Li, K.; Tapponnier, P.; Xu, X.; Kang, W. The 2022 Ms 6.9 Menyuan earthquake: Surface rupture, Paleozoic suture re-activation, slip-rate and seismic gap along the Haiyuan fault system, NE Tibet. Earth Planet. Sci. Lett. 2023, 622, 118412. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, W.; Li, Y.; Shen, W.; He, Z.; Li, B.; Li, Q.; Jiao, Q.; Tian, Y. Coseismic rupture model and tectonic implications of the January 7, 2022, Menyuan Mw6.6 earthquake constraints from InSAR observations and field investigation. Remote Sens. 2022, 14, 2111. [Google Scholar] [CrossRef]
- Wang, J.; Ding, L.; He, J.; Cai, F.; Wang, C.; Zhang, Z. Research of seismogenic structures of the 2016 and 2022 Menyuan earthquakes, in the Northeastern Tibetan plateau. Remote Sens. 2023, 15, 742. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Song, C.; Han, B.; Chen, B.; Li, X.; Peng, J. Fault structure and slip mechanics of the 2022 Mw6.7 Menyuan earthquake revealed by coseismic rupture observations. Tectonophysics 2024, 872, 230192. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.; Gong, W.; Han, N.; Liu, Y.; Shan, X. Geodetic modeling of the 2022 Mw6.6 Menyuan earthquake: Insight into the strain-partitioned northern Qilian Shan fault system and implications for regional tectonics and seismic hazards. Geophys. J. Int. 2023, 233, 1987–2003. [Google Scholar] [CrossRef]
- Zuo, K.; Luo, J.; Zhao, C.; Chen, J.; Yin, X. Spatiotemporal distribution characteristics of seismicity and seismogenic environment in the Menyuan area, Qinghai Province. Chin. J. Geophys. 2023, 66, 1460–1480. (In Chinese) [Google Scholar] [CrossRef]
- Xu, X.; Wu, X.; Yu, G.; Li, K. Seismo-geological signatures for identifying M≥7.0 earthquake risk areas and their preliminary application in mainland China. Seismol. Geol. 2017, 39, 219–275. (In Chinese) [Google Scholar] [CrossRef]
- Lü, M.; Chen, K.; Chai, H.; Geng, J.; Zhang, S.; Fang, L. Joint inversion of InSAR and high-rate GNSS displacement waveforms for the rupture process of the 2022 Qinghai Menyuan M6.9 earthquake. Chin. J. Geophys. 2022, 65, 4725–4738. (In Chinese) [Google Scholar] [CrossRef]
- Li, Z.; Han, B.; Liu, Z.; Zhang, M.; Yu, C.; Chen, B.; Liu, H.; Du, J.; Zhang, S.; Zhu, W.; et al. Source Parameters and Slip Distributions of the 2016 and 2022 Menyuan, Qinghai Earthquakes Constrained by InSAR Observations. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 887–897. (In Chinese) [Google Scholar] [CrossRef]
- Feng, W.; He, X.; Zhang, Y.; Fang, L. Seismic faults of the 2022 Mw6.6 Menyuan, Qinghai earthquake and their implication for the regional seismogenic structures. Chin. Sci. Bull. 2023, 68, 254–270. (In Chinese) [Google Scholar] [CrossRef]
- Wan, Y.; Huang, S.; Wang, F.; Xu, Y.; Yu, H. Fault geometry and slip characteristics revealed by the 2022 Menyuan earthquake sequence. Chin. J. Geophys. 2023, 66, 2796–2810. (In Chinese) [Google Scholar] [CrossRef]
- Yang, H.; Wang, D.; Guo, R.; Xie, M.; Zang, Y.; Wang, Y.; Yao, Q.; Cheng, C.; An, Y.; Zhang, Y. Rapid report of the 8 January 2022 MS6.9 Menyuan earthquake, Qinghai, China. Earthq. Res. Adv. 2022, 2, 100113. [Google Scholar] [CrossRef]
- Xu, S. Co-seismic deformation filed and fault-slip distribution of the Menyuan Ms6.9 earthquake on January 8, 2022, constrained by GNSS observations. J. Earthq. Eng. 2023, 45, 401–409. (In Chinese) [Google Scholar] [CrossRef]
- Deng, Q. Active tectonics and earthquake activities in China. Earth Sci. Front. 2003, 10 (Suppl. S1), 66–73. (In Chinese) [Google Scholar]
- Maurer, J.; Johnson, K.; Wallace, L.; Hamling, I.; Williams, C.; Rollins, C.; Gerstenberger, M.; Van Dissen, R. Geodetic strain rates for the 2022 update of the New Zealand National Seismic Hazard Model. Bull. Seismol. Soc. Am. 2023, 114, 57–77. [Google Scholar] [CrossRef]


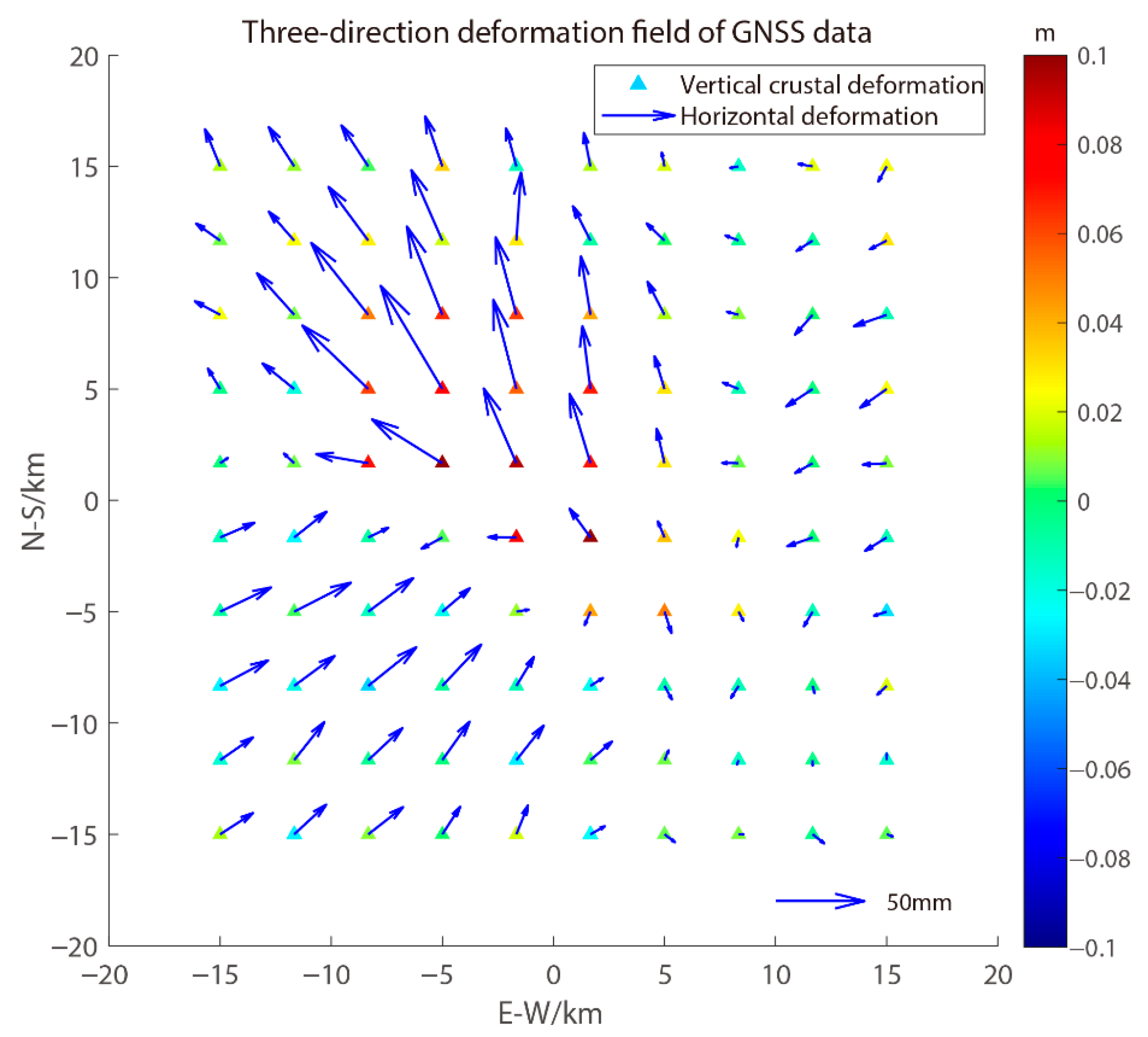

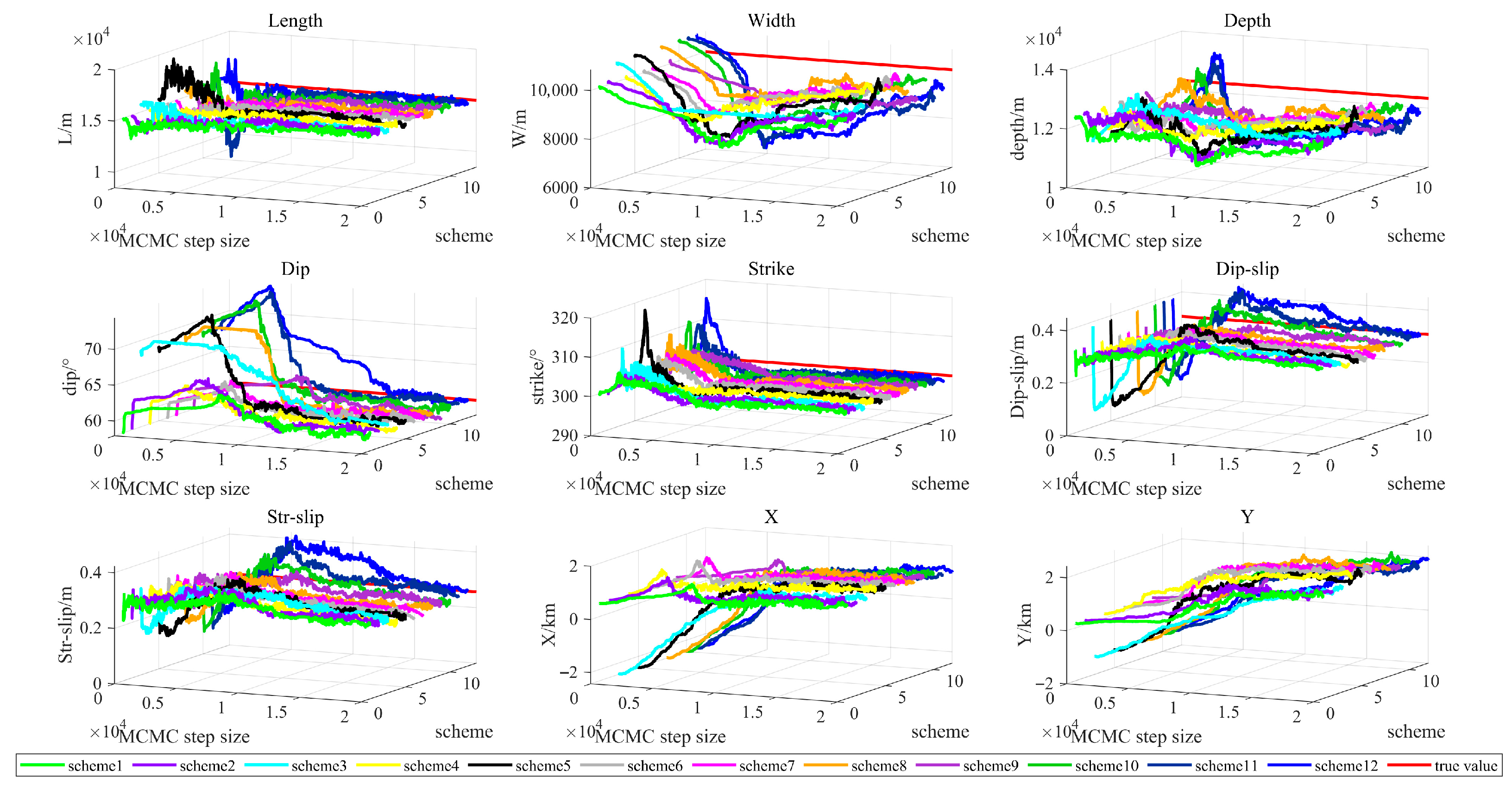
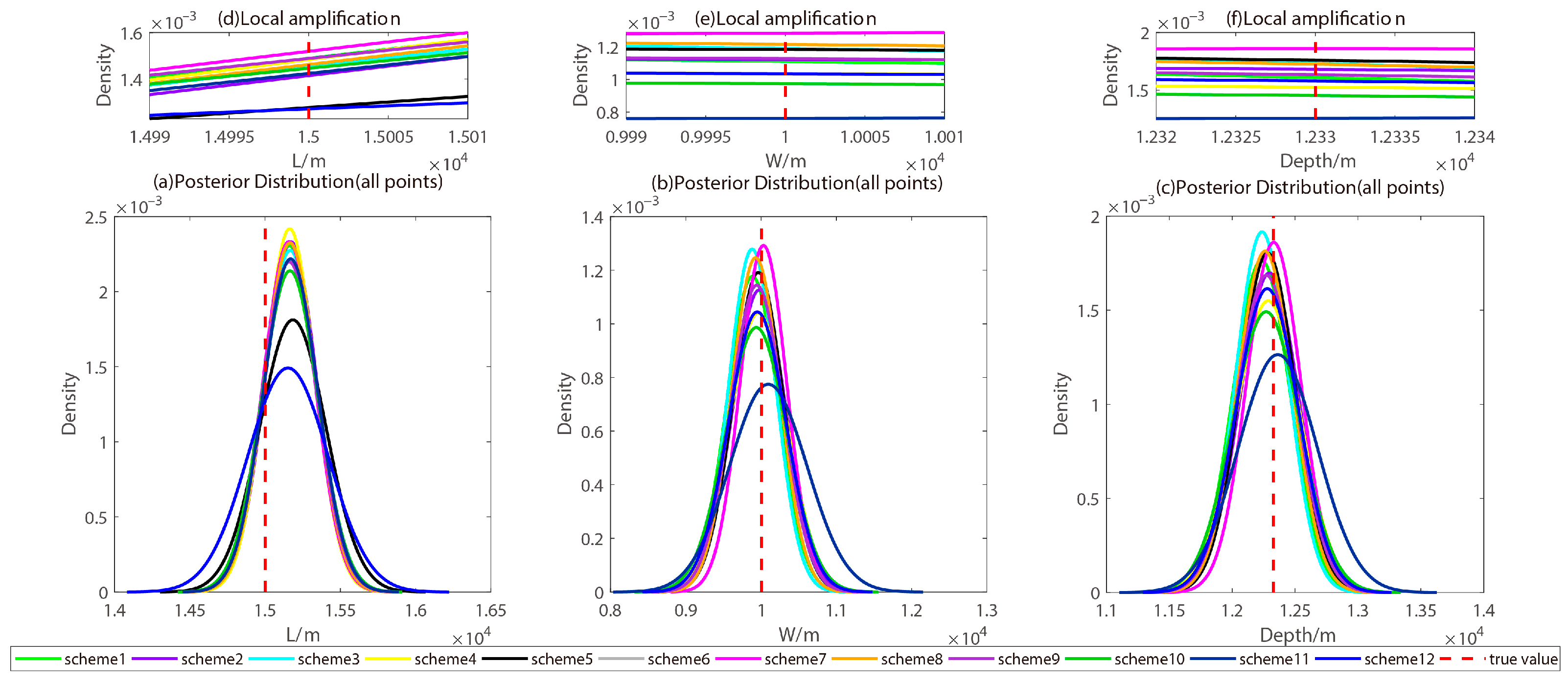



| Length/m | Width/m | Depth/m | Dip/° | Strike/° | X/m | Y/m | Strike-Slip/m | Dip-Slip/m | |
|---|---|---|---|---|---|---|---|---|---|
| lower limit a | 10,000 | 5000 | 1000 | 40 | 280 | −20,000 | −20,000 | 0 | 0 |
| upper limit a | 20,000 | 15,000 | 18,000 | 80 | 340 | 20,000 | 20,000 | 4 | 4 |
| lower limit b | 14,000 | 9000 | 11,000 | 50 | 290 | −3000 | −3000 | 0 | 0 |
| upper limit b | 16,000 | 11,000 | 13,000 | 70 | 310 | 3000 | 3000 | 0.4 | 0.4 |
| initial step size of MCMC | 100 | 100 | 100 | 1 | 1 | 10 | 10 | 0.1 | 0.1 |
| presupposed truth | 15,000 | 10,000 | 12,330 (bottom depth) | 60 | 300 | / | / | 0.25712 | 0.30642 |
| MPSO | 14,890 | 10,030 | 12,273 | 57.99 | 299.74 | 482.92 | 157.80 | 0.25402 | 0.31246 |
| Random interval generation | 15,629 | 10,812 | 11,254 | 68.27 | 302.65 | −2414 | −1329 | 0.21880 | 0.38300 |
| Scheme | Algorithm | Interval Constraint | Inversion Initial Value |
|---|---|---|---|
| Scheme 1 | Bagnardi and Hooper [16] MCMC algorithm | no interval constraint | MPSO provides the initial value |
| Scheme 2 | Bagnardi and Hooper [16] MCMC algorithm | A reasonable interval constraint | MPSO provides the initial value |
| Scheme 3 | Bagnardi and Hooper [16] MCMC algorithm | narrower interval constraint | random initial value |
| Scheme 4 | Bagnardi and Hooper [16] MCMC algorithm | A reasonable interval constraint (interval determination strategy 1) | MPSO provides the initial value |
| Scheme 5 | Bagnardi and Hooper [16] MCMC algorithm | narrow interval constraint (interval determination strategy 1) | random initial value |
| Scheme 6 | Wang and Xi [22] MCMC algorithm | no interval constraint | MPSO provides the initial value |
| Scheme 7 | Wang and Xi [22] MCMC algorithm | A reasonable interval constraint | MPSO provides the initial value |
| Scheme 8 | Wang and Xi [22] MCMC algorithm | narrower interval constraint | random initial value |
| Scheme 9 | Wang and Xi [22] MCMC algorithm | A reasonable interval constraint (interval determination strategy 1) | MPSO provides the initial value |
| Scheme 10 | Wang and Xi [22] MCMC algorithm | narrow interval constraint (interval determination strategy 1) | random initial value |
| Scheme 11 | Bagnardi and Hooper [16] MCMC algorithm | interval iteratively changed with sampling value (interval determination strategy 2) | random initial value |
| Scheme 12 | Wang and Xi [22] MCMC algorithm | interval iterative change with sampling value (interval determination strategy 2) | random initial value |
| RMSE of Each Scheme | Length/m | Width/m | Depth/m | Dip/° | Strike/° | Strike-Slip/m | Dip-Slip/m |
|---|---|---|---|---|---|---|---|
| Scheme 1 | 240.99 | 218.15 | 198.00 | 7.57 | 6.70 | 1.43 | 1.22 |
| Scheme 2 | 244.99 | 141.17 | 136.35 | 7.77 | 6.59 | 1.67 | 1.50 |
| Scheme 3 | 244.42 | 214.99 | 193.69 | 8.06 | 6.24 | 1.38 | 1.14 |
| Scheme 4 | 239.31 | 157.78 | 155.56 | 8.28 | 6.57 | 1.64 | 1.47 |
| Scheme 5 | 246.91 | 147.46 | 149.84 | 9.32 | 6.83 | 1.63 | 1.43 |
| Scheme 6 | 236.44 | 175.04 | 117.06 | 8.35 | 6.76 | 1.72 | 1.56 |
| Scheme 7 | 236.44 | 175.04 | 117.06 | 8.35 | 6.76 | 1.72 | 1.56 |
| Scheme 8 | 243.34 | 181.78 | 172.65 | 8.49 | 6.27 | 1.50 | 1.27 |
| Scheme 9 | 239.78 | 170.92 | 163.69 | 7.96 | 6.58 | 1.56 | 1.38 |
| Scheme 10 | 243.62 | 187.45 | 169.92 | 8.80 | 6.39 | 1.58 | 1.40 |
| Scheme 11 | 255.42 | 302.41 | 214.35 | 13.36 | 8.01 | 2.15 | 1.95 |
| Scheme 12 | 251.28 | 169.82 | 153.65 | 9.68 | 6.32 | 1.61 | 1.36 |
| RMSE of Each Scheme | Length/m | Width/m | Depth/m | Dip/° | Strike/° | Strike-Slip/m | Dip-Slip/m |
|---|---|---|---|---|---|---|---|
| Scheme 1 | 243.56 | 184.98 | 176.64 | 7.91 | 6.70 | 1.47 | 1.28 |
| Scheme 2 | 247.98 | 133.66 | 137.66 | 7.70 | 6.62 | 1.65 | 1.48 |
| Scheme 3 | 251.23 | 209.39 | 195.19 | 7.75 | 6.96 | 1.42 | 1.22 |
| Scheme 4 | 241.86 | 186.35 | 178.05 | 8.31 | 6.57 | 1.58 | 1.38 |
| Scheme 5 | 249.87 | 136.78 | 146.11 | 8.24 | 6.87 | 1.62 | 1.43 |
| Scheme 6 | 239.87 | 177.11 | 119.60 | 8.29 | 6.82 | 1.74 | 1.58 |
| Scheme 7 | 239.87 | 177.11 | 119.60 | 8.29 | 6.82 | 1.74 | 1.58 |
| Scheme 8 | 246.08 | 182.77 | 176.22 | 7.91 | 6.63 | 1.51 | 1.33 |
| Scheme 9 | 239.68 | 158.43 | 155.32 | 7.96 | 6.54 | 1.56 | 1.39 |
| Scheme 10 | 243.91 | 156.81 | 127.54 | 8.23 | 6.75 | 1.68 | 1.54 |
| Scheme 11 | 259.03 | 310.69 | 224.00 | 12.32 | 8.08 | 2.17 | 1.99 |
| Scheme 12 | 238.64 | 117.80 | 128.03 | 8.08 | 6.77 | 1.60 | 1.42 |
| Length/m | Width/m | Depth/m | Dip/° | Strike/° | X/m | Y/m | Strike-Slip/m | Dip–Slip/m | |
|---|---|---|---|---|---|---|---|---|---|
| lower limit | 2000 | 2000 | 0 | 50 | 80 | −20,000 | −20,000 | −1 | −1 |
| upper limit | 40,000 | 22,000 | 20,000 | 90 | 120 | 20,000 | 20,000 | 5 | 5 |
| initial step size of MCMC | 100 | 100 | 100 | 1 | 1 | 10 | 10 | 0.1 | 0.1 |
| Random interval generation | 15,152 | 11,708 | 13,006 | 75.68 | 96.87 | / | / | 3.49130 | 1.78740 |
| Scheme | Length/m | Width/m | Depth/m | Dip/° | Strike/° | X/m | Y/m | Strike-Slip/m | Dip-Slip/m | |
|---|---|---|---|---|---|---|---|---|---|---|
| Random interval generation | optimum | 17,008 | 10,878 | 13,263 | 89.49 | 107.87 | 669 | −3708 | 4.18083 | −0.09410 |
| mean | 17,598 | 10,636 | 13,450 | 89.32 | 107.80 | 98 | −3629 | 4.23621 | −0.04755 | |
| median | 17,238 | 10,611 | 13,431 | 89.42 | 107.93 | 417 | −3706 | 4.27682 | −0.04661 | |
| 2.5% | 17,030 | 10,460 | 13,281 | 88.93 | 107.02 | −1520 | −3733 | 3.97496 | −0.08821 | |
| 97.5% | 19,886 | 10,863 | 13,615 | 89.63 | 107.99 | 668 | −3302 | 4.31517 | −0.01307 | |
| East Longitude/° | North Latitude/° | Length/km | Depth/km | Strike/° | Dip/° | Slip/° | |
|---|---|---|---|---|---|---|---|
| ingle-fault model in this paper | 101.286 | 37.782 | 17 | 13.3 | 107.87 | 89.49 | 1.29 |
| 97.5% | 101.286 | 37.785 | 19.9 | 13.6 | 107.99 | 89.63 | 0.17 |
| CENC | 101.26 | 37.77 | / | 10 | / | / | / |
| GCMT | 101.31 | 37.80 | / | 14.8 | 104/14 | 82/89 | 1/172 |
| USGS | 101.278 | 37.815 | / | 13.0 | 104/13 | 88/75 | 15/178 |
| CEA-IGP Model 1 | / | / | / | 10 | 109/18 | 81/51 | 39/178 |
| CEA-IGP Model 2 | / | / | / | 4 | 192/284 | 69/82 | 172/21 |
| Xu et al. [40] | 101.28 | 37.79 | 13.9 | 0.24 | 106.5 | 80.4 | 3.7 |
| Li et al. [50] | / | / | 8.8 | / | 104/109 | 80/80 | 0.5 |
| Feng et al. [37] | 101.17–101.41 | 37.73–37.81 | 3.1–17.9 | / | 88.65–127.2 | 70.88 | / |
| Li et al. [43] | / | / | 20.10 | / | 106.89 | 86.83 | −5, −1 |
| Yang et al. [53] | / | / | / | / | / | 82 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Xi, C.; Xu, G.; Sun, Z.; Wu, F. Interval Determination Strategy for Bayesian Inversion of Seismic Source Parameters Under Uncertain Interval Conditions. Remote Sens. 2025, 17, 3151. https://doi.org/10.3390/rs17183151
Wang L, Xi C, Xu G, Sun Z, Wu F. Interval Determination Strategy for Bayesian Inversion of Seismic Source Parameters Under Uncertain Interval Conditions. Remote Sensing. 2025; 17(18):3151. https://doi.org/10.3390/rs17183151
Chicago/Turabian StyleWang, Leyang, Can Xi, Guangyu Xu, Zhanglin Sun, and Fei Wu. 2025. "Interval Determination Strategy for Bayesian Inversion of Seismic Source Parameters Under Uncertain Interval Conditions" Remote Sensing 17, no. 18: 3151. https://doi.org/10.3390/rs17183151
APA StyleWang, L., Xi, C., Xu, G., Sun, Z., & Wu, F. (2025). Interval Determination Strategy for Bayesian Inversion of Seismic Source Parameters Under Uncertain Interval Conditions. Remote Sensing, 17(18), 3151. https://doi.org/10.3390/rs17183151







