A Review of City-Scale Methane Flux Inversion Based on Top-Down Methods
Abstract
Highlights
- Top-down inversion studies at the city-scale reveal substantial discrepancies with bottom-up emission inventories, with posterior uncertainties typically ranging between 11% and 28%.
- Bayesian and hybrid (variational-ensemble Kalman) approaches demonstrate notable advantages: the former can effectively address issues of posterior uncertainty, while the latter strikes a balance between accuracy and computational efficiency.
- The observed inconsistencies underscore the necessity of advancing city-scale methane quantification methodologies to ensure robust and policy-relevant emission assessments.
- A comprehensive framework combining high-resolution inventories, coordinated observations, AI-enhanced modeling, and isotopic analysis can significantly advance the reliability of methane emission monitoring and support more effective climate policies at the city-scale.Second bullet.
Abstract
1. Introduction
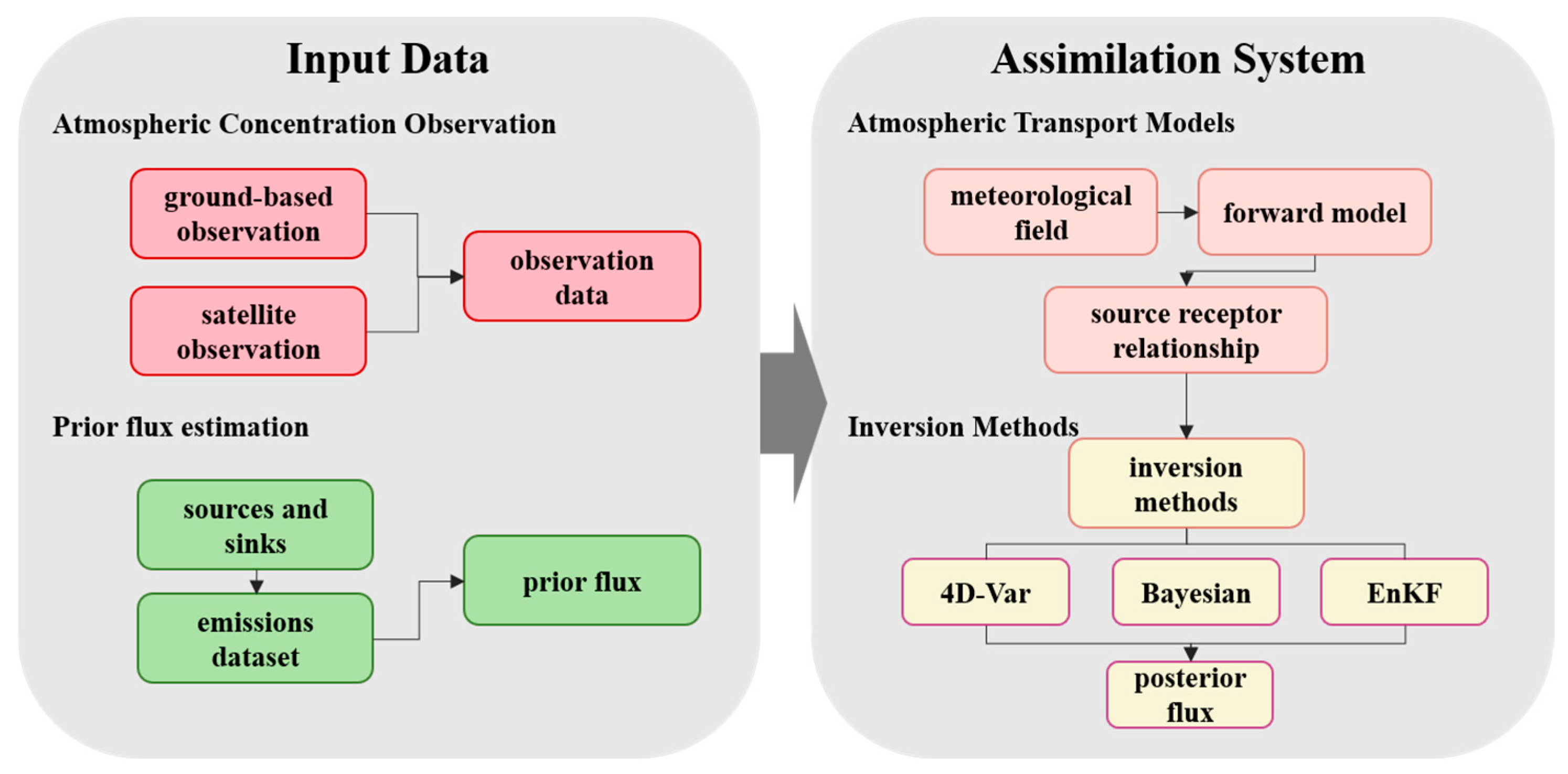
2. Top-Down Atmospheric Inversion Methods for CH4
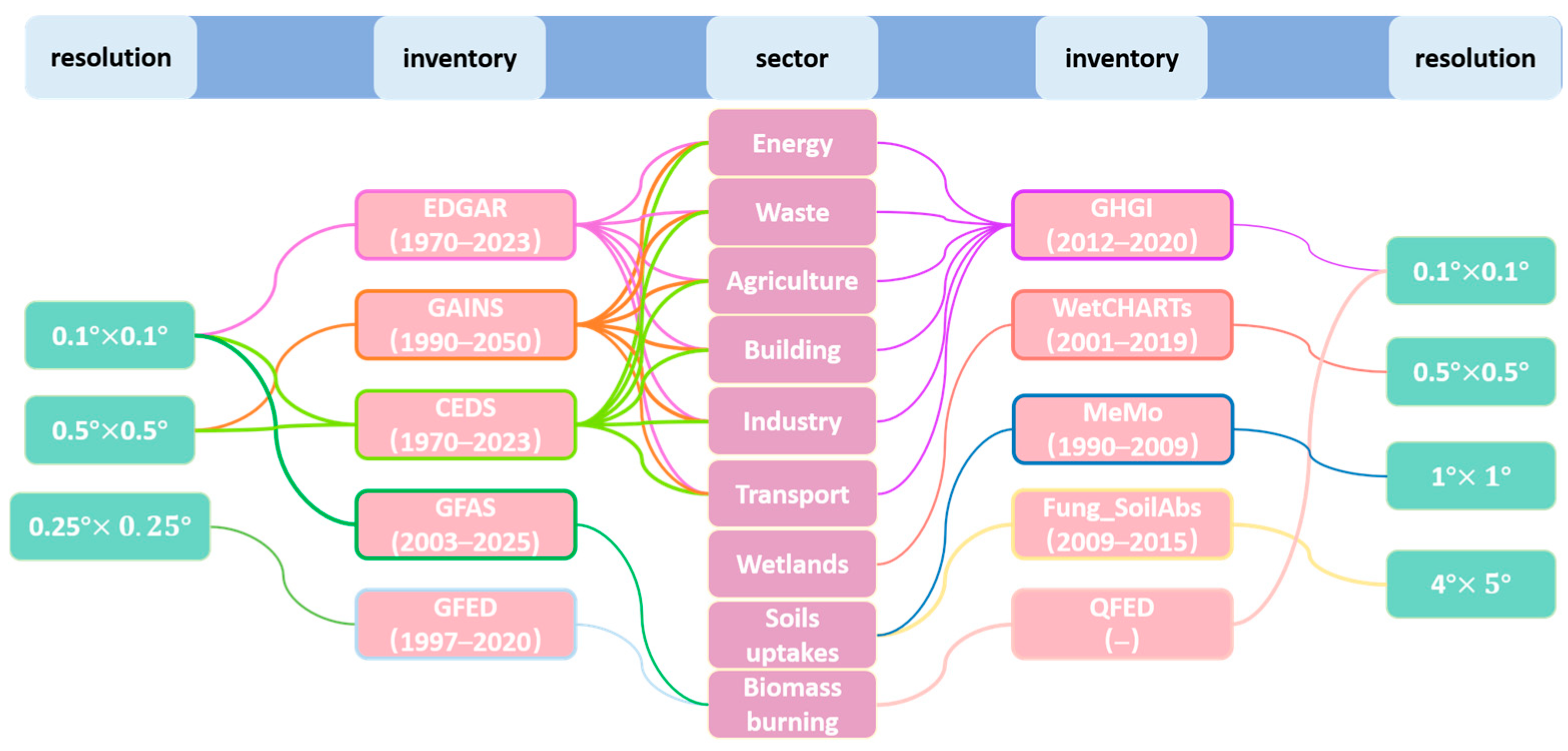
2.1. Emission Datasets for CH4
2.1.1. Anthropogenic Emission Inventory
2.1.2. Natural Source Emission Inventory
2.2. Observation of CH4 Concentration
2.2.1. Ground-Based Observations
2.2.2. Satellite Observations
2.3. Atmospheric Transport Models
2.4. Inversion Methods
2.4.1. Kalman Filter
2.4.2. 4D-Var Method
2.4.3. Bayesian Optimization
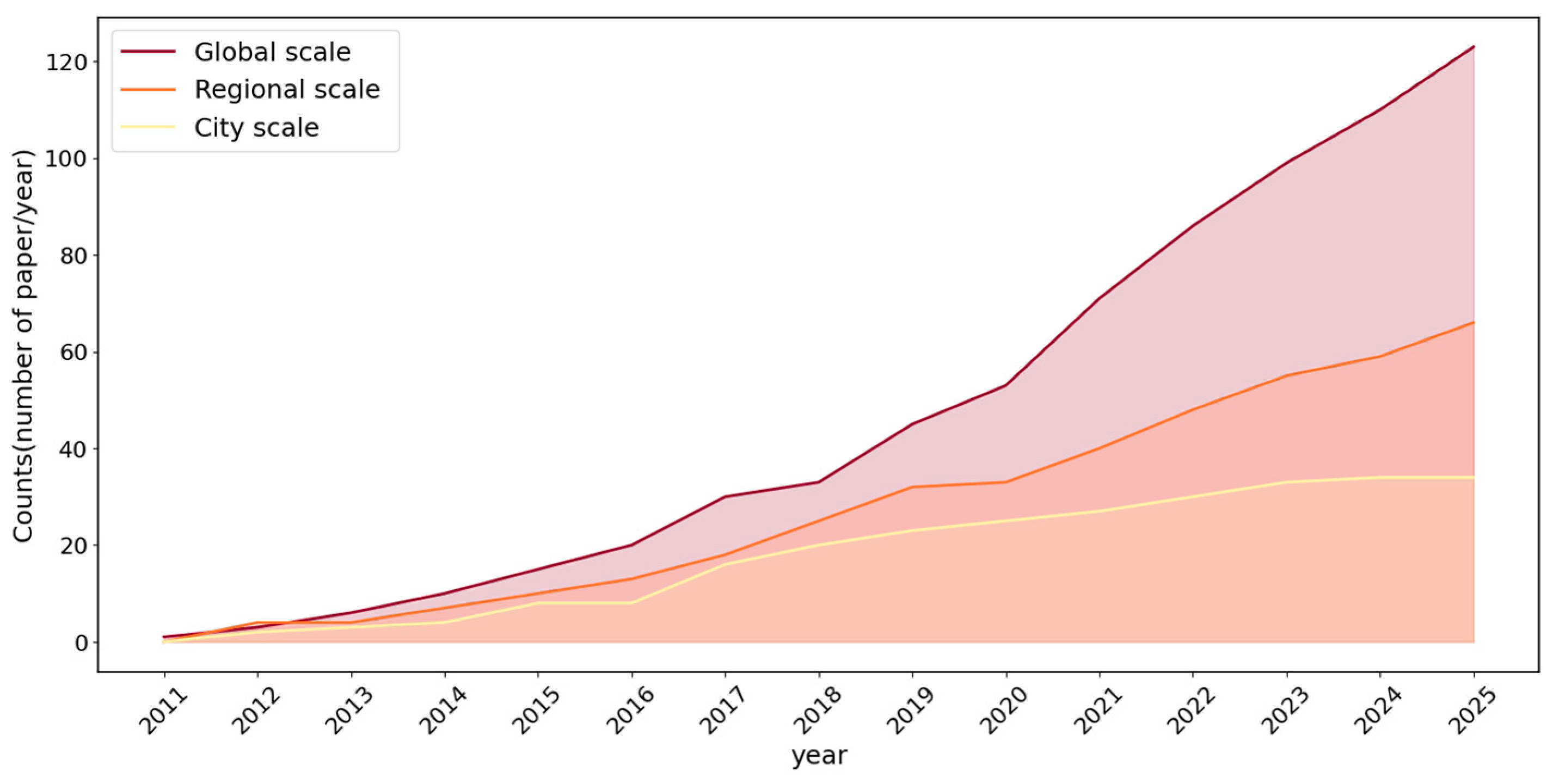
2.5. Applications to City Scale Inversions
2.5.1. Current Status of City-Scale Inventories
2.5.2. Application of Urban Observation Networks and Satellites in City Scale Inversion
2.5.3. Challenges of Atmospheric Transport Models at the City Scale
2.5.4. Applicability of Data Assimilation Methods at the City Scale
3. Top-Down Inversion of CH4 Flux at City Scales
3.1. CH4 Flux Inversion Results at the City Scale
3.2. Uncertainty Analysis of CH4 Flux at the City Scale
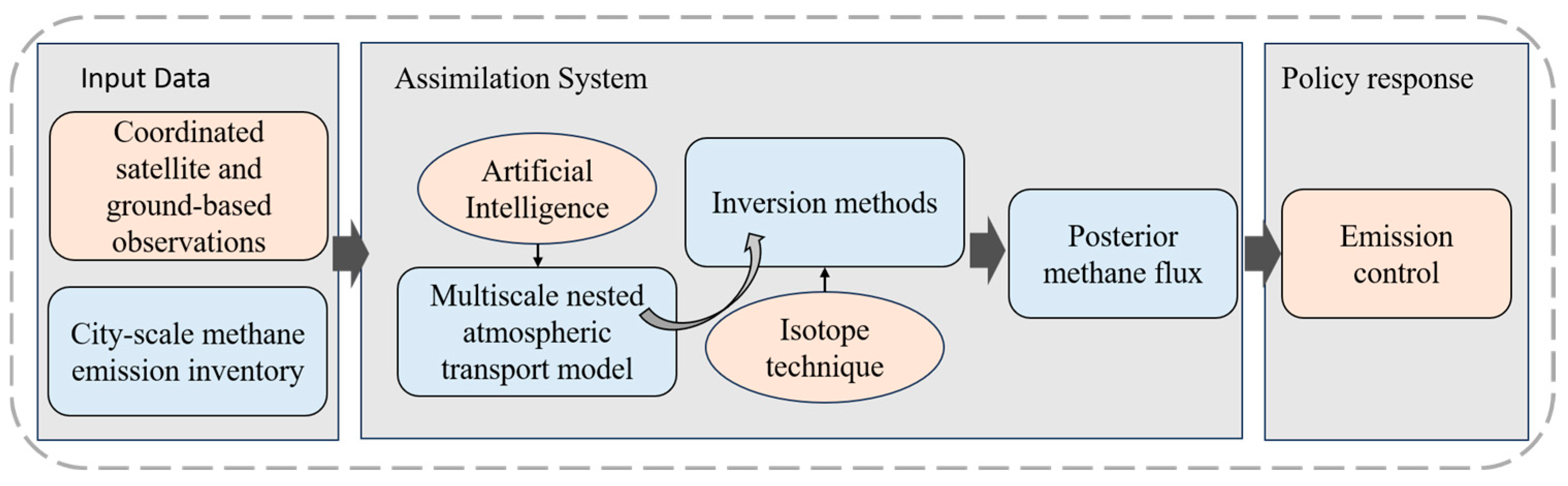
4. Future Prospects of Coordinated Satellite–Ground City-Scale CH4 Flux Inversions
4.1. Coordinated Satellite–Ground Observations
4.2. Application of Artificial Intelligence Technology
4.3. Methods for Distinguishing CH4 Sources
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EDGAR | Emissions Database for Global Atmospheric Research |
| CEDS | Community Emissions Data System |
| GAINS | Greenhouse Gas–Air Pollution Interactions and Synergies |
| FAOSTAT | Food and Agriculture Organization Corporate Statistical Database |
References
- Lee, H.; Calvin, K.; Dasgupta, D.; Krinner, G.; Mukherji, A.; Thorne, P.; Trisos, C.; Romero, J.; Aldunce, P.; Barret, K. IPCC, 2023: Climate Change 2023: Synthesis Report, Summary for Policymakers. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2023. [Google Scholar]
- Lenton, T.M.; Held, H.; Kriegler, E.; Hall, J.W.; Lucht, W.; Rahmstorf, S.; Schellnhuber, H.J. Tipping elements in the Earth’s climate system. Proc. Natl. Acad. Sci. USA 2008, 105, 1786–1793. [Google Scholar] [CrossRef]
- Forster, P.; Storelvmo, T.; Armour, K.; Collins, W.; Dufresne, J.-L.; Frame, D.; Lunt, D.; Mauritsen, T.; Palmer, M.; Watanabe, M. The Earth’s energy budget, climate feedbacks, and climate sensitivity. In Proceedings of the AGU Fall Meeting 2021, New Orleans, LA, USA, 13–17 December 2021. [Google Scholar]
- Saunois, M.; Martinez, A.; Poulter, B.; Zhang, Z.; Raymond, P.A.; Regnier, P.; Canadell, J.G.; Jackson, R.B.; Patra, P.K.; Bousquet, P. Global methane budget 2000–2020. Earth Syst. Sci. Data 2025, 17, 1873–1958. [Google Scholar] [CrossRef]
- Etminan, M.; Myhre, G.; Highwood, E.J.; Shine, K.P. Radiative forcing of carbon dioxide, methane, and nitrous oxide: A significant revision of the methane radiative forcing. Geophys. Res. Lett. 2016, 43, 12–614. [Google Scholar] [CrossRef]
- Janardanan, R.; Maksyutov, S.; Wang, F.; Nayagam, L.; Sahu, S.K.; Mangaraj, P.; Saunois, M.; Lan, X.; Matsunaga, T. Country-level methane emissions and their sectoral trends during 2009–2020 estimated by high-resolution inversion of GOSAT and surface observations. Environ. Res. Lett. 2024, 19, 034007. [Google Scholar] [CrossRef]
- National Academies of Sciences; Medicine, Division on Engineering; Physical Sciences; Space Studies Board; Committee on the Decadal Survey for Earth Science and Applications from Space. Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space; National Academies Press: Washington, DC, USA, 2019. [Google Scholar]
- Ito, A.; Patra, P.K.; Umezawa, T. Bottom-Up Evaluation of the Methane Budget in Asia and Its Subregions. Glob. Biogeochem. Cycles 2023, 37, e2023GB007723. [Google Scholar] [CrossRef]
- Chang, K.Y.; Riley, W.J.; Collier, N.; McNicol, G.; Fluet-Chouinard, E.; Knox, S.H.; Delwiche, K.B.; Jackson, R.B.; Poulter, B.; Saunois, M.; et al. Observational constraints reduce model spread but not uncertainty in global wetland methane emission estimates. Glob. Change Biol. 2023, 29, 4298–4312. [Google Scholar] [CrossRef]
- Solazzo, E.; Crippa, M.; Guizzardi, D.; Muntean, M.; Choulga, M.; Janssens-Maenhout, G. Uncertainties in the Emissions Database for Global Atmospheric Research (EDGAR) emission inventory of greenhouse gases. Atmos. Chem. Phys. 2021, 21, 5655–5683. [Google Scholar] [CrossRef]
- Cusworth, D.H.; Bloom, A.A.; Ma, S.; Miller, C.E.; Bowman, K.; Yin, Y.; Maasakkers, J.D.; Zhang, Y.; Scarpelli, T.R.; Qu, Z.; et al. A Bayesian framework for deriving sector-based methane emissions from top-down fluxes. Commun. Earth Environ. 2021, 2, 242. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Karstens, U.; Manning, A.J.; Saunois, M.; Tsuruta, A.; Berchet, A.; Vermeulen, A.T.; Arnold, T.; Janssens-Maenhout, G.; Hammer, S.; et al. Inverse modelling of European CH4 emissions during 2006–2012 using different inverse models and reassessed atmospheric observations. Atmos. Chem. Phys. 2018, 18, 901–920. [Google Scholar] [CrossRef]
- Liu, M.; van der A, R.; van Weele, M.; Eskes, H.; Lu, X.; Veefkind, P.; de Laat, J.; Kong, H.; Wang, J.; Sun, J.; et al. A New Divergence Method to Quantify Methane Emissions Using Observations of Sentinel-5P TROPOMI. Geophys. Res. Lett. 2021, 48, e2021GL094151. [Google Scholar] [CrossRef]
- Chandra, N.; Patra, P.K.; Fujita, R.; Höglund-Isaksson, L.; Umezawa, T.; Goto, D.; Morimoto, S.; Vaughn, B.H.; Röckmann, T. Methane emissions decreased in fossil fuel exploitation and sustainably increased in microbial source sectors during 1990–2020. Commun. Earth Environ. 2024, 5, 147. [Google Scholar] [CrossRef]
- Saunois, M.; Stavert, A.R.; Poulter, B.; Bousquet, P.; Canadell, J.G.; Jackson, R.B.; Raymond, P.A.; Dlugokencky, E.J.; Houweling, S.; Patra, P.K.; et al. The Global Methane Budget 2000–2017. Earth Syst. Sci. Data 2020, 12, 1561–1623. [Google Scholar] [CrossRef]
- Thompson, R.L.; Stohl, A.; Zhou, L.X.; Dlugokencky, E.; Fukuyama, Y.; Tohjima, Y.; Kim, S.Y.; Lee, H.; Nisbet, E.G.; Fisher, R.E.; et al. Methane emissions in East Asia for 2000–2011 estimated using an atmospheric Bayesian inversion. J. Geophys. Res. Atmos. 2015, 120, 4352–4369. [Google Scholar] [CrossRef]
- Qu, Z.; Jacob, D.J.; Shen, L.; Lu, X.; Zhang, Y.; Scarpelli, T.R.; Nesser, H.; Sulprizio, M.P.; Maasakkers, J.D.; Bloom, A.A.; et al. Global distribution of methane emissions: A comparative inverse analysis of observations from the TROPOMI and GOSAT satellite instruments. Atmos. Chem. Phys. 2021, 21, 14159–14175. [Google Scholar] [CrossRef]
- Du, M.; Kang, X.; Liu, Q.; Du, H.; Zhang, J.; Yin, Y.; Cui, Z. City-level livestock methane emissions in China from 2010 to 2020. Sci. Data 2024, 11, 251. [Google Scholar] [CrossRef]
- Hu, C.; Zhang, J.; Qi, B.; Du, R.; Xu, X.; Xiong, H.; Liu, H.; Ai, X.; Peng, Y.; Xiao, W. Global warming will largely increase waste treatment CH 4 emissions in Chinese megacities: Insight from the first city-scale CH4 concentration observation network in Hangzhou, China. Atmos. Chem. Phys. 2023, 23, 4501–4520. [Google Scholar] [CrossRef]
- Hemati, M.; Mahdianpari, M.; Nassar, R.; Shiri, H.; Mohammadimanesh, F. Urban methane emission monitoring across North America using TROPOMI data: An analytical inversion approach. Sci. Rep. 2024, 14, 9041. [Google Scholar] [CrossRef]
- de Foy, B.; Schauer, J.J.; Lorente, A.; Borsdorff, T. Investigating high methane emissions from urban areas detected by TROPOMI and their association with untreated wastewater. Environ. Res. Lett. 2023, 18, 044004. [Google Scholar] [CrossRef]
- Janssens-Maenhout, G.; Crippa, M.; Guizzardi, D.; Muntean, M.; Schaaf, E.; Dentener, F.; Bergamaschi, P.; Pagliari, V.; Olivier, J.G.; Peters, J.A. EDGAR v4. 3.2 Global Atlas of the three major greenhouse gas emissions for the period 1970–2012. Earth Syst. Sci. Data 2019, 11, 959–1002. [Google Scholar] [CrossRef]
- Hoesly, R.M.; Smith, S.J.; Feng, L.; Klimont, Z.; Janssens-Maenhout, G.; Pitkanen, T.; Seibert, J.J.; Vu, L.; Andres, R.J.; Bolt, R.M.; et al. Historical (1750–2014) anthropogenic emissions of reactive gases and aerosols from the Community Emissions Data System (CEDS). Geosci. Model Dev. 2018, 11, 369–408. [Google Scholar] [CrossRef]
- Amann, M.; Bertok, I.; Borken-Kleefeld, J.; Cofala, J.; Heyes, C.; Höglund-Isaksson, L.; Klimont, Z.; Nguyen, B.; Posch, M.; Rafaj, P. Cost-effective control of air quality and greenhouse gases in Europe: Modeling and policy applications. Environ. Model. Softw. 2011, 26, 1489–1501. [Google Scholar] [CrossRef]
- Tan, H.; Zhang, L.; Lu, X.; Zhao, Y.; Yao, B.; Parker, R.J.; Boech, H. An integrated analysis of contemporary methane emissions and concentration trends over China using in situ, satellite observations, and model simulations. Atmos. Chem. Phys. Discuss. 2021, 2021, 1–36. [Google Scholar] [CrossRef]
- Liu, M.; van der A, R.; van Weele, M.; Bryan, L.; Eskes, H.; Veefkind, P.; Liu, Y.; Lin, X.; de Laat, J.; Ding, J. Current potential of CH 4 emission estimates using TROPOMI in the Middle East. Atmos. Meas. Tech. 2024, 17, 5261–5277. [Google Scholar] [CrossRef]
- Zhang, Y.; Jacob, D.J.; Lu, X.; Maasakkers, J.D.; Scarpelli, T.R.; Sheng, J.-X.; Shen, L.; Qu, Z.; Sulprizio, M.P.; Chang, J.; et al. Attribution of the accelerating increase in atmospheric methane during 2010–2018 by inverse analysis of GOSAT observations. Atmos. Chem. Phys. 2021, 21, 3643–3666. [Google Scholar] [CrossRef]
- Maasakkers, J.D.; Jacob, D.J.; Sulprizio, M.P.; Turner, A.J.; Weitz, M.; Wirth, T.; Hight, C.; DeFigueiredo, M.; Desai, M.; Schmeltz, R. Gridded national inventory of US methane emissions. Environ. Sci. Technol. 2016, 50, 13123–13133. [Google Scholar] [CrossRef]
- IEA. Global Methane Tracker 2024. IEA 2024. Available online: https://www.iea.org/reports/global-methane-tracker-2024 (accessed on 7 August 2025).
- Bloom, A.A.; Bowman, K.W.; Lee, M.; Turner, A.J.; Schroeder, R.; Worden, J.R.; Weidner, R.; McDonald, K.C.; Jacob, D.J. A global wetland methane emissions and uncertainty dataset for atmospheric chemical transport models (WetCHARTs version 1.0). Geosci. Model Dev. 2017, 10, 2141–2156. [Google Scholar] [CrossRef]
- Wang, F.; Maksyutov, S.; Janardanan, R.; Tsuruta, A.; Ito, A.; Morino, I.; Yoshida, Y.; Kaiser, J.W.; Janssens-Maenhout, G.; Dlugokencky, E.; et al. Inversion Estimates of Methane Emission in the Middle East in 2010–2017 with GOSAT Observations. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 1082–1085. [Google Scholar]
- Darmenov, A.; da Silva, A. The Quick Fire Emissions Dataset (QFED): Documentation of Versions 2.1, 2.2 and 2.4: NASA Technical Report Series on Global Modeling Data Assimilation; NASA TM—104606. 2015; Volume 32, p. 183. Available online: https://ntrs.nasa.gov/citations/20180005253 (accessed on 7 August 2025).
- Murguia-Flores, F.; Arndt, S.; Ganesan, A.L.; Murray-Tortarolo, G.; Hornibrook, E.R. Soil Methanotrophy Model (MeMo v1. 0): A process-based model to quantify global uptake of atmospheric methane by soil. Geosci. Model Dev. 2018, 11, 2009–2032. [Google Scholar] [CrossRef]
- Zhao, Y.; Saunois, M.; Bousquet, P.; Lin, X.; Berchet, A.; Hegglin, M.I.; Canadell, J.G.; Jackson, R.B.; Hauglustaine, D.A.; Szopa, S.; et al. Inter-model comparison of global hydroxyl radical (OH) distributions and their impact on atmospheric methane over the 2000–2016 period. Atmos. Chem. Phys. 2019, 19, 13701–13723. [Google Scholar] [CrossRef]
- Nicely, J.M.; Salawitch, R.J.; Canty, T.; Anderson, D.C.; Arnold, S.R.; Chipperfield, M.P.; Emmons, L.K.; Flemming, J.; Huijnen, V.; Kinnison, D.E. Quantifying the causes of differences in tropospheric OH within global models. J. Geophys. Res. Atmos. 2017, 122, 1983–2007. [Google Scholar] [CrossRef]
- Duncan, B.N.; Anderson, D.C.; Fiore, A.M.; Joiner, J.; Krotkov, N.A.; Li, C.; Millet, D.B.; Nicely, J.M.; Oman, L.D.; St. Clair, J.M. Opinion: Beyond global means–novel space-based approaches to indirectly constrain the concentrations of and trends and variations in the tropospheric hydroxyl radical (OH). Atmos. Chem. Phys. 2024, 24, 13001–13023. [Google Scholar] [CrossRef]
- Shutter, J.D.; Millet, D.B.; Wells, K.C.; Payne, V.H.; Nowlan, C.R.; Abad, G.G. Interannual changes in atmospheric oxidation over forests determined from space. Sci. Adv. 2024, 10, eadn1115. [Google Scholar] [CrossRef] [PubMed]
- Crosson, E. A cavity ring-down analyzer for measuring atmospheric levels of methane, carbon dioxide, and water vapor. Appl. Phys. B 2008, 92, 403–408. [Google Scholar] [CrossRef]
- Dlugokencky, E.J.; Steele, L.P.; Lang, P.M.; Masarie, K.A. The growth rate and distribution of atmospheric methane. J. Geophys. Res. Atmos. 1994, 99, 17021–17043. [Google Scholar] [CrossRef]
- Röckmann, T.; Eyer, S.; Van Der Veen, C.; Popa, M.E.; Tuzson, B.; Monteil, G.; Houweling, S.; Harris, E.; Brunner, D.; Fischer, H. In situ observations of the isotopic composition of methane at the Cabauw tall tower site. Atmos. Chem. Phys. 2016, 16, 10469–10487. [Google Scholar] [CrossRef]
- Werle, P.; Slemr, F.; Maurer, K.; Kormann, R.; Mücke, R.; Jänker, B. Near-and mid-infrared laser-optical sensors for gas analysis. Opt. Lasers Eng. 2002, 37, 101–114. [Google Scholar] [CrossRef]
- Andrews, A.; Kofler, J.; Trudeau, M.; Williams, J.; Neff, D.; Masarie, K.; Chao, D.; Kitzis, D.; Novelli, P.; Zhao, C. CO2, CO, and CH 4 measurements from tall towers in the NOAA Earth System Research Laboratory’s Global Greenhouse Gas Reference Network: Instrumentation, uncertainty analysis, and recommendations for future high-accuracy greenhouse gas monitoring efforts. Atmos. Meas. Tech. 2014, 7, 647–687. [Google Scholar] [CrossRef]
- Cunnold, D.; Steele, L.; Fraser, P.; Simmonds, P.; Prinn, R.; Weiss, R.; Porter, L.; O’Doherty, S.; Langenfelds, R.; Krummel, P. In situ measurements of atmospheric methane at GAGE/AGAGE sites during 1985–2000 and resulting source inferences. J. Geophys. Res. Atmos. 2002, 107, ACH 20-18–ACH 20-21. [Google Scholar] [CrossRef]
- Franz, D.; Acosta, M.; Altimir, N.; Arriga, N.; Arrouays, D.; Aubinet, M.; Aurela, M.; Ayres, E.; López-Ballesteros, A.; Barbaste, M. Towards long-term standardised carbon and greenhouse gas observations for monitoring Europe’s terrestrial ecosystems: A review. Int. Agrophysics 2018, 32, 439–455. [Google Scholar] [CrossRef]
- Davis, S.P.; Abrams, M.C.; Brault, J.W. Fourier Transform Spectrometry; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Ehret, G.; Kiemle, C.; Wirth, M.; Amediek, A.; Fix, A.; Houweling, S. Space-borne remote sensing of CO2, CH4, and N2O by integrated path differential absorption lidar: A sensitivity analysis. Appl. Phys. B 2008, 90, 593–608. [Google Scholar] [CrossRef]
- Edner, H.; Ragnarson, P.; Spännare, S.; Svanberg, S. Differential optical absorption spectroscopy (DOAS) system for urban atmospheric pollution monitoring. Appl. Opt. 1993, 32, 327–333. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.C.; Blavier, J.-F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.; Sherlock, V.; Wennberg, P.O. The total carbon column observing network. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 2087–2112. [Google Scholar] [CrossRef]
- Hedelius, J.K.; Parker, H.; Wunch, D.; Roehl, C.M.; Viatte, C.; Newman, S.; Toon, G.C.; Podolske, J.R.; Hillyard, P.W.; Iraci, L.T.; et al. Intercomparability of XCO2 and XCH4 from the United States TCCON sites. Atmos. Meas. Tech. 2017, 10, 1481–1493. [Google Scholar] [CrossRef]
- De Mazière, M.; Thompson, A.M.; Kurylo, M.J.; Wild, J.D.; Bernhard, G.; Blumenstock, T.; Braathen, G.O.; Hannigan, J.W.; Lambert, J.-C.; Leblanc, T. The Network for the Detection of Atmospheric Composition Change (NDACC): History, status and perspectives. Atmos. Chem. Phys. 2018, 18, 4935–4964. [Google Scholar] [CrossRef]
- Plane, J.M.; Saiz-Lopez, A. UV-Visible differential optical absorption spectroscopy (DOAS). In Analytical Techniques for Atmospheric Measurement; Wiley Online Library: Hoboken, NJ, USA, 2006; pp. 147–188. [Google Scholar] [CrossRef]
- Frankenberg, C.; Platt, U.; Wagner, T. Iterative maximum a posteriori (IMAP)-DOAS for retrieval of strongly absorbing trace gases: Model studies for CH4 and CO2 retrieval from near infrared spectra of SCIAMACHY onboard ENVISAT. Atmos. Chemistry. Phys. 2005, 5, 9–22. [Google Scholar] [CrossRef]
- Parker, R.J.; Boesch, H.; Byckling, K.; Webb, A.J.; Palmer, P.I.; Feng, L.; Bergamaschi, P.; Chevallier, F.; Notholt, J.; Deutscher, N. Assessing 5 years of GOSAT Proxy XCH 4 data and associated uncertainties. Atmos. Meas. Tech. 2015, 8, 4785–4801. [Google Scholar] [CrossRef]
- Iwasaki, C.; Imasu, R.; Bril, A.; Yokota, T.; Yoshida, Y.; Morino, I.; Oshchepkov, S.; Wunch, D.; Griffith, D.W.; Deutscher, N.M. Validation of GOSAT SWIR XCO2 and XCH4 retrieved by PPDF-S method and comparison with full physics method. Sola 2017, 13, 168–173. [Google Scholar] [CrossRef]
- Yoshida, Y.; Kikuchi, N.; Morino, I.; Uchino, O.; Oshchepkov, S.; Bril, A.; Saeki, T.; Schutgens, N.; Toon, G.; Wunch, D. Improvement of the retrieval algorithm for GOSAT SWIR XCO 2 and XCH 4 and their validation using TCCON data. Atmos. Meas. Tech. 2013, 6, 1533–1547. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, L.; Zhang, X.; Cao, X. Methane retrieval algorithms based on satellite: A review. Atmosphere 2024, 15, 449. [Google Scholar] [CrossRef]
- Xiong, X.; Barnet, C.; Maddy, E.; Wei, J.; Liu, X.; Pagano, T.S. Seven years’ observation of mid-upper tropospheric methane from Atmospheric Infrared Sounder. Remote Sensing 2010, 2, 2509–2530. [Google Scholar] [CrossRef]
- Frankenberg, C.; Meirink, J.F.; Bergamaschi, P.; Goede, A.; Heimann, M.; Körner, S.; Platt, U.; van Weele, M.; Wagner, T. Satellite chartography of atmospheric methane from SCIAMACHY on board ENVISAT: Analysis of the years 2003 and 2004. J. Geophys. Res. Atmos. 2006, 111, D07303. [Google Scholar] [CrossRef]
- De Mazière, M.; Vigouroux, C.; Bernath, P.; Baron, P.; Blumenstock, T.; Boone, C.; Brogniez, C.; Catoire, V.; Coffey, M.; Duchatelet, P. Validation of ACE-FTS v2. 2 methane profiles from the upper troposphere to the lower mesosphere. Atmos. Chem. Phys. 2008, 8, 2421–2435. [Google Scholar] [CrossRef]
- Kuze, A.; Suto, H.; Shiomi, K.; Kawakami, S.; Tanaka, M.; Ueda, Y.; Deguchi, A.; Yoshida, J.; Yamamoto, Y.; Kataoka, F. Update on GOSAT TANSO-FTS performance, operations, and data products after more than 6 years in space. Atmos. Meas. Tech. 2016, 9, 2445–2461. [Google Scholar] [CrossRef]
- Jervis, D.; McKeever, J.; Durak, B.O.; Sloan, J.J.; Gains, D.; Varon, D.J.; Ramier, A.; Strupler, M.; Tarrant, E. The GHGSat-D imaging spectrometer. Atmos. Meas. Tech. 2021, 14, 2127–2140. [Google Scholar] [CrossRef]
- Lorente, A.; Borsdorff, T.; Butz, A.; Hasekamp, O.; aan de Brugh, J.; Schneider, A.; Wu, L.; Hase, F.; Kivi, R.; Wunch, D. Methane retrieved from TROPOMI: Improvement of the data product and validation of the first 2 years of measurements. Atmos. Meas. Tech. 2021, 14, 665–684. [Google Scholar] [CrossRef]
- Someya, Y.; Yoshida, Y.; Ohyama, H.; Nomura, S.; Kamei, A.; Morino, I.; Mukai, H.; Matsunaga, T.; Laughner, J.L.; Velazco, V.A. Update on the GOSAT TANSO–FTS SWIR Level 2 retrieval algorithm. Atmos. Meas. Tech. Discuss. 2022, 2022, 1–32. [Google Scholar] [CrossRef]
- Cusworth, D.H.; Jacob, D.J.; Varon, D.J.; Chan Miller, C.; Liu, X.; Chance, K.; Thorpe, A.K.; Duren, R.M.; Miller, C.E.; Thompson, D.R. Potential of next-generation imaging spectrometers to detect and quantify methane point sources from space. Atmos. Meas. Tech. 2019, 12, 5655–5668. [Google Scholar] [CrossRef]
- Jacob, D.J.; Varon, D.J.; Cusworth, D.H.; Dennison, P.E.; Frankenberg, C.; Gautam, R.; Guanter, L.; Kelley, J.; McKeever, J.; Ott, L.E.; et al. Quantifying methane emissions from the global scale down to point sources using satellite observations of atmospheric methane. Atmos. Chem. Phys. 2022, 22, 9617–9646. [Google Scholar] [CrossRef]
- Buchwitz, M.; De Beek, R.; Burrows, J.; Bovensmann, H.; Warneke, T.; Notholt, J.; Meirink, J.; Goede, A.; Bergamaschi, P.; Körner, S. Atmospheric methane and carbon dioxide from SCIAMACHY satellite data: Initial comparison with chemistry and transport models. Atmos. Chem. Phys. 2005, 5, 941–962. [Google Scholar] [CrossRef]
- Parker, R.J.; Webb, A.; Boesch, H.; Somkuti, P.; Barrio Guillo, R.; Di Noia, A.; Kalaitzi, N.; Anand, J.S.; Bergamaschi, P.; Chevallier, F. A decade of GOSAT Proxy satellite CH4 observations. Earth Syst. Sci. Data 2020, 12, 3383–3412. [Google Scholar] [CrossRef]
- Hasekamp, O.; Lorente, A.; Hu, H.; Butz, A.; de Brugh, J.; Landgraf, J. Algorithm Theoretical Baseline Document for Sentinel-5 Precursor Methane Retrieval; Netherlands Institute for Space Research: Leiden, The Netherlands, 2019. [Google Scholar]
- Lu, T.; Li, Z.; Fan, C.; He, Z.; Jiang, X.; Zhang, Y.; Gao, Y.; Xuan, Y.; de Leeuw, G. Global Methane Retrieval, Monitoring, and Quantification in Hotspot Regions Based on AHSI/ZY-1 Satellite. Atmosphere 2025, 16, 510. [Google Scholar] [CrossRef]
- Stein, A.F.; Draxler, R.R.; Rolph, G.D.; Stunder, B.J.; Cohen, M.D.; Ngan, F. NOAA’s HYSPLIT atmospheric transport and dispersion modeling system. Bull. Am. Meteorol. Soc. 2015, 96, 2059–2077. [Google Scholar] [CrossRef]
- Jacob, D.J.; Turner, A.J.; Maasakkers, J.D.; Sheng, J.; Sun, K.; Liu, X.; Chance, K.; Aben, I.; McKeever, J.; Frankenberg, C. Satellite observations of atmospheric methane and their value for quantifying methane emissions. Atmos. Chem. Phys. 2016, 16, 14371–14396. [Google Scholar] [CrossRef]
- Vojta, M.; Plach, A.; Thompson, R.L.; Stohl, A. A comprehensive evaluation of the use of Lagrangian particle dispersion models for inverse modeling of greenhouse gas emissions. Geosci. Model Dev. 2022, 15, 8295–8323. [Google Scholar] [CrossRef]
- Bey, I.; Jacob, D.J.; Yantosca, R.M.; Logan, J.A.; Field, B.D.; Fiore, A.M.; Li, Q.; Liu, H.Y.; Mickley, L.J.; Schultz, M.G. Global modeling of tropospheric chemistry with assimilated meteorology: Model description and evaluation. J. Geophys. Res. Atmos. 2001, 106, 23073–23095. [Google Scholar] [CrossRef]
- Krol, M.; Houweling, S.; Bregman, B.; Van den Broek, M.; Segers, A.; Van Velthoven, P.; Peters, W.; Dentener, F.; Bergamaschi, P. The two-way nested global chemistry-transport zoom model TM5: Algorithm and applications. Atmos. Chem. Phys. 2005, 5, 417–432. [Google Scholar] [CrossRef]
- Grell, G.A.; Peckham, S.E.; Schmitz, R.; McKeen, S.A.; Frost, G.; Skamarock, W.C.; Eder, B. Fully coupled “online” chemistry within the WRF model. Atmos. Environ. 2005, 39, 6957–6975. [Google Scholar] [CrossRef]
- Hass, H.; Jakobs, H.; Memmesheimer, M. Analysis of a regional model (EURAD) near surface gas concentration predictions using observations from networks. Meteorol. Atmos. Phys. 1995, 57, 173–200. [Google Scholar] [CrossRef]
- Stohl, A.; Forster, C.; Frank, A.; Seibert, P.; Wotawa, G. The Lagrangian particle dispersion model FLEXPART version 6.2. Atmos. Chem. Phys. 2005, 5, 2461–2474. [Google Scholar] [CrossRef]
- Lin, J.; Gerbig, C.; Wofsy, S.; Andrews, A.; Daube, B.; Davis, K.; Grainger, C. A near-field tool for simulating the upstream influence of atmospheric observations: The Stochastic Time-Inverted Lagrangian Transport (STILT) model. J. Geophys. Res. Atmos. 2003, 108, 4493. [Google Scholar] [CrossRef]
- Weil, J.C.; Sullivan, P.P.; Moeng, C.-H. The use of large-eddy simulations in Lagrangian particle dispersion models. J. Atmos. Sci. 2004, 61, 2877–2887. [Google Scholar] [CrossRef]
- Henze, D.K.; Hakami, A.; Seinfeld, J.H. Development of the adjoint of GEOS-Chem. Atmos. Chem. Phys. 2007, 7, 2413–2433. [Google Scholar] [CrossRef]
- Chevallier, F.; Fisher, M.; Peylin, P.; Serrar, S.; Bousquet, P.; Bréon, F.M.; Chédin, A.; Ciais, P. Inferring CO2 sources and sinks from satellite observations: Method and application to TOVS data. J. Geophys. Res. Atmos. 2005, 110, D24309. [Google Scholar] [CrossRef]
- Henne, S.; Brunner, D.; Oney, B.; Leuenberger, M.; Eugster, W.; Bamberger, I.; Meinhardt, F.; Steinbacher, M.; Emmenegger, L. Validation of the Swiss methane emission inventory by atmospheric observations and inverse modelling. Atmos. Chem. Phys. 2016, 16, 3683–3710. [Google Scholar] [CrossRef]
- Flesch, T.K.; Wilson, J.D.; Yee, E. Backward-time Lagrangian stochastic dispersion models and their application to estimate gaseous emissions. J. Appl. Meteorol. Climatol. 1995, 34, 1320–1332. [Google Scholar] [CrossRef]
- Stohl, A.; Seibert, P.; Arduini, J.; Eckhardt, S.; Fraser, P.; Greally, B.; Lunder, C.; Maione, M.; Mühle, J.; O’doherty, S. An analytical inversion method for determining regional and global emissions of greenhouse gases: Sensitivity studies and application to halocarbons. Atmos. Chem. Phys. 2009, 9, 1597–1620. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Segers, A.; Brunner, D.; Haussaire, J.-M.; Henne, S.; Ramonet, M.; Arnold, T.; Biermann, T.; Chen, H.; Conil, S.; et al. High-resolution inverse modelling of European CH4 emissions using the novel FLEXPART-COSMO TM5 4DVAR inverse modelling system. Atmos. Chem. Phys. 2022, 22, 13243–13268. [Google Scholar] [CrossRef]
- Thompson, R.L.; Stohl, A. FLEXINVERT: An atmospheric Bayesian inversion framework for determining surface fluxes of trace species using an optimized grid. Geosci. Model Dev. 2014, 7, 2223–2242. [Google Scholar] [CrossRef]
- Chen, Y.H.; Prinn, R.G. Estimation of atmospheric methane emissions between 1996 and 2001 using a three-dimensional global chemical transport model. J. Geophys. Res. Atmos. 2006, 111, D10307. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Bösch, H.; Dance, S. Estimating surface CO2 fluxes from space-borne CO2 dry air mole fraction observations using an ensemble Kalman Filter. Atmos. Chem. Phys. 2009, 9, 2619–2633. [Google Scholar] [CrossRef]
- Bishop, C.H.; Etherton, B.J.; Majumdar, S.J. Adaptive Sampling with the Ensemble Transform Kalman Filter. Part I: Theoretical Aspects. Mon. Weather Rev. 2001, 129, 420–436. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Bösch, H.; Parker, R.J.; Webb, A.J.; Correia, C.S.C.; Deutscher, N.M.; Domingues, L.G.; Feist, D.G.; Gatti, L.V.; et al. Consistent regional fluxes of CH4 and CO2 inferred from GOSAT proxy XCH4:XCO2 retrievals, 2010–2014. Atmos. Chem. Phys. 2017, 17, 4781–4797. [Google Scholar] [CrossRef]
- Voshtani, S.; Ménard, R.; Walker, T.W.; Hakami, A. Assimilation of GOSAT Methane in the Hemispheric CMAQ; Part I: Design of the Assimilation System. Remote Sens. 2022, 14, 371. [Google Scholar] [CrossRef]
- Bisht, J.S.H.; Patra, P.K.; Takigawa, M.; Sekiya, T.; Kanaya, Y.; Saitoh, N.; Miyazaki, K. Estimation of CH4emission based on an advanced 4D-LETKF assimilation system. Geosci. Model Dev. 2023, 16, 1823–1838. [Google Scholar] [CrossRef]
- Lorenc, A.C.; Rawlins, F. Why does 4D-Var beat 3D-Var? Q. J. R. Meteorol. Soc. 2005, 131, 3247–3257. [Google Scholar] [CrossRef]
- Gilbert, J.C.; Lemaréchal, C. Some numerical experiments with variable-storage quasi-Newton algorithms. Math. Program. 1989, 45, 407–435. [Google Scholar] [CrossRef]
- Meirink, J.F.; Eskes, H.J.; Goede, A.P.H. Sensitivity analysis of methane emissions derived from SCIAMACHY observations through inverse modelling. Atmos. Chem. Phys. 2006, 6, 1275–1292. [Google Scholar] [CrossRef]
- Meirink, J.F.; Bergamaschi, P.; Krol, M.C. Four-dimensional variational data assimilation for inverse modelling of atmospheric methane emissions: Method and comparison with synthesis inversion. Atmos. Chem. Phys. 2008, 8, 6341–6353. [Google Scholar] [CrossRef]
- . Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar] [CrossRef]
- Cui, Y.Y.; Brioude, J.; McKeen, S.A.; Angevine, W.M.; Kim, S.W.; Frost, G.J.; Ahmadov, R.; Peischl, J.; Bousserez, N.; Liu, Z.; et al. Top-down estimate of methane emissions in California using a mesoscale inverse modeling technique: The South Coast Air Basin. J. Geophys. Res. Atmos. 2015, 120, 6698–6711. [Google Scholar] [CrossRef]
- Sargent, M.R.; Floerchinger, C.; McKain, K.; Budney, J.; Gottlieb, E.W.; Hutyra, L.R.; Rudek, J.; Wofsy, S.C. Majority of US urban natural gas emissions unaccounted for in inventories. Proc. Natl. Acad. Sci. USA 2021, 118, e2105804118. [Google Scholar] [CrossRef]
- Jones, T.S.; Franklin, J.E.; Chen, J.; Dietrich, F.; Hajny, K.D.; Paetzold, J.C.; Wenzel, A.; Gately, C.; Gottlieb, E.; Parker, H. Assessing urban methane emissions using column-observing portable Fourier transform infrared (FTIR) spectrometers and a novel Bayesian inversion framework. Atmos. Chem. Phys. 2021, 21, 13131–13147. [Google Scholar] [CrossRef]
- Lauvaux, T.; Gurney, K.R.; Miles, N.L.; Davis, K.J.; Richardson, S.J.; Deng, A.; Nathan, B.J.; Oda, T.; Wang, J.A.; Hutyra, L. Policy-relevant assessment of urban CO2 emissions. Environ. Sci. Technol. 2020, 54, 10237–10245. [Google Scholar] [CrossRef]
- Wang, G.; Cui, R.; Di, J.; Wang, J.; Wang, Y.; Shang, Z.; Liu, X.; Tian, Q.; Wu, H.; Dong, L. Portable methane sensor system using miniature multi-pass cell for mobile monitoring of natural gas leaks. Sens. Actuators B Chem. 2025, 431, 137457. [Google Scholar] [CrossRef]
- Yan, G.; Zhang, L.; Zheng, C.; Zhang, M.; Zheng, K.; Song, F.; Ye, W.; Zhang, Y.; Wang, Y.; Tittel, F.K. Mobile vehicle measurement of urban atmospheric CH4/C2H6 using a midinfrared dual-gas sensor system based on interband cascade laser absorption spectroscopy. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Kohler, F.K.; Schaller, C.; Klemm, O. Quantification of urban methane emissions: A combination of stationary with mobile measurements. Atmosphere 2022, 13, 1596. [Google Scholar] [CrossRef]
- Leifer, I.; Melton, C.; Chang, C.S.; Blake, D.R.; Meinardi, S.; Kleinman, M.T.; Tratt, D.M. Validation of in situ and remote sensing-derived methane refinery emissions in a complex wind environment and chemical implications. Atmos. Environ. 2022, 273, 118900. [Google Scholar] [CrossRef]
- Lopez-Coto, I.; Ren, X.; Salmon, O.E.; Karion, A.; Shepson, P.B.; Dickerson, R.R.; Stein, A.; Prasad, K.; Whetstone, J.R. Wintertime CO2, CH4, and CO emissions estimation for the Washington, DC–Baltimore metropolitan area using an inverse modeling technique. Environ. Sci. Technol. 2020, 54, 2606–2614. [Google Scholar] [CrossRef]
- Pitt, J.R.; Lopez-Coto, I.; Hajny, K.D.; Tomlin, J.; Kaeser, R.; Jayarathne, T.; Stirm, B.H.; Floerchinger, C.R.; Loughner, C.P.; Gately, C.K. New York City greenhouse gas emissions estimated with inverse modeling of aircraft measurements. Elem. Sci. Anthr. 2022, 10, 00082. [Google Scholar] [CrossRef]
- Davis, K.J.; Deng, A.; Lauvaux, T.; Miles, N.L.; Richardson, S.J.; Sarmiento, D.P.; Gurney, K.R.; Hardesty, R.M.; Bonin, T.A.; Brewer, W.A. The Indianapolis Flux Experiment (INFLUX): A test-bed for developing urban greenhouse gas emission measurements. Elem. Sci. Anthr. 2017, 5, 21. [Google Scholar] [CrossRef]
- Umezawa, T.; Terao, Y.; Ueyama, M.; Kameyama, S.; Lunt, M.; France, J.L. Measurement report: Mobile measurements to estimate urban methane emissions in Tokyo. EGUsphere 2025, 2025, 1–24. [Google Scholar]
- Plant, G.; Kort, E.A.; Murray, L.T.; Maasakkers, J.D.; Aben, I. Evaluating urban methane emissions from space using TROPOMI methane and carbon monoxide observations. Remote Sens. Environ. 2022, 268, 112756. [Google Scholar] [CrossRef]
- Nesser, H.; Jacob, D.J.; Maasakkers, J.D.; Lorente, A.; Chen, Z.; Lu, X.; Shen, L.; Qu, Z.; Sulprizio, M.P.; Winter, M. High-resolution US methane emissions inferred from an inversion of 2019 TROPOMI satellite data: Contributions from individual states, urban areas, and landfills. Atmos. Chem. Phys. 2024, 24, 5069–5091. [Google Scholar] [CrossRef]
- Brioude, J.; Angevine, W.; McKeen, S.; Hsie, E.-Y. Numerical uncertainty at mesoscale in a Lagrangian model in complex terrain. Geosci. Model Dev. Discuss. 2012, 5, 967–991. [Google Scholar] [CrossRef]
- Yadav, V.; Duren, R.; Mueller, K.; Verhulst, K.R.; Nehrkorn, T.; Kim, J.; Weiss, R.F.; Keeling, R.; Sander, S.; Fischer, M.L. Spatio-temporally resolved methane fluxes from the Los Angeles Megacity. J. Geophys. Res. Atmos. 2019, 124, 5131–5148. [Google Scholar] [CrossRef]
- Bréon, F.; Broquet, G.; Puygrenier, V.; Chevallier, F.; Xueref-Remy, I.; Ramonet, M.; Dieudonné, E.; Lopez, M.; Schmidt, M.; Perrussel, O. An attempt at estimating Paris area CO2 emissions from atmospheric concentration measurements. Atmos. Chem. Phys. 2015, 15, 1707–1724. [Google Scholar] [CrossRef]
- Lauvaux, T.; Miles, N.L.; Deng, A.; Richardson, S.J.; Cambaliza, M.O.; Davis, K.J.; Gaudet, B.; Gurney, K.R.; Huang, J.; O’Keefe, D. High-resolution atmospheric inversion of urban CO2 emissions during the dormant season of the Indianapolis Flux Experiment (INFLUX). J. Geophys. Res. Atmos. 2016, 121, 5213–5236. [Google Scholar] [CrossRef]
- Pandey, S.; Houweling, S.; Segers, A. Order of magnitude wall time improvement of variational methane inversions by physical parallelization: A demonstration using TM5-4DVAR. Geosci. Model Dev. 2022, 15, 4555–4567. [Google Scholar] [CrossRef]
- Maksyutov, S.; Brunner, D.; Turner, A.J.; Zavala-Araiza, D.; Janardanan, R.; Bun, R.; Oda, T.; Patra, P.K. Applications of top-down methods to anthropogenic GHG emission estimation. In Balancing Greenhouse Gas Budgets; Elsevier: Amsterdam, The Netherlands, 2022; pp. 455–481. [Google Scholar]
- Liu, C.; Xiao, Q.; Wang, B. An Ensemble-Based Four-Dimensional Variational Data Assimilation Scheme. Part I: Technical Formulation and Preliminary Test. Mon. Weather Rev. 2008, 136, 3363–3373. [Google Scholar] [CrossRef]
- Zhao, M.; Tian, X.; Wang, Y.; Wang, X.; Ciais, P.; Jin, Z.; Zhang, H.; Wang, T.; Ding, J.; Piao, S. Slowdown in China’s methane emission growth. Natl. Sci. Rev. 2024, 11, nwae223. [Google Scholar] [CrossRef]
- Tian, X.; Feng, X. A non-linear least squares enhanced POD-4DVar algorithm for data assimilation. Tellus A Dyn. Meteorol. Oceanogr. 2015, 67, 25340. [Google Scholar] [CrossRef]
- Thompson, R.L.; Groot Zwaaftink, C.; Brunner, D.; Tsuruta, A.; Aalto, T.; Raivonen, M.; Crippa, M.; Solazzo, E.; Guizzardi, D.; Regnier, P. Effects of extreme meteorological conditions in 2018 on European methane emissions estimated using atmospheric inversions. Philos. Trans. R. Soc. A 2022, 380, 20200443. [Google Scholar] [CrossRef]
- Brunner, D.; Arnold, T.; Henne, S.; Manning, A.; Thompson, R.L.; Maione, M.; O’Doherty, S.; Reimann, S. Comparison of four inverse modelling systems applied to the estimation of HFC-125, HFC-134a, and SF 6 emissions over Europe. Atmos. Chem. Phys. 2017, 17, 10651–10674. [Google Scholar] [CrossRef]
- Wang, X.; Jacob, D.J.; Nesser, H.; Balasus, N.; Estrada, L.; Sulprizio, M.; Cusworth, D.H.; Scarpelli, T.R.; Chen, Z.; East, J.D. Quantifying urban and landfill methane emissions in the United States using TROPOMI satellite data. arXiv 2025, arXiv:2505.10835. [Google Scholar] [CrossRef]
- National Academies of Sciences, Medicine; Division on Earth, Board on Environmental Studies; Board on Energy, Environmental Systems; Board on Earth Sciences; Board on Atmospheric Sciences; Committee on Anthropogenic Methane Emissions in the United States. Improving Measurement and Presentation of Results. In Improving Characterization of Anthropogenic Methane Emissions in the United States; National Academies Press: Washington, DC, USA, 2018. [Google Scholar]
- Wang, Y.; Zhang, Y.; Tian, X.; Wang, X.; Yuan, W.; Ding, J.; Jiang, F.; Jin, Z.; Ju, W.; Liang, R. Towards verifying and improving estimations of China’s CO2 and CH4 budgets using atmospheric inversions. Natl. Sci. Rev. 2025, 12, nwaf090. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Kort, E.A.; Gourdji, S.; Karion, A.; Mueller, K.; Ware, J. Seasonally resolved excess urban methane emissions from the Baltimore/Washington, DC metropolitan region. Environ. Sci. Technol. 2019, 53, 11285–11293. [Google Scholar] [CrossRef] [PubMed]
- Duren, R.M.; Thorpe, A.K.; Foster, K.T.; Rafiq, T.; Hopkins, F.M.; Yadav, V.; Bue, B.D.; Thompson, D.R.; Conley, S.; Colombi, N.K. California’s methane super-emitters. Nature 2019, 575, 180–184. [Google Scholar] [CrossRef]
- Jeong, S.; Newman, S.; Zhang, J.; Andrews, A.E.; Bianco, L.; Bagley, J.; Cui, X.; Graven, H.; Kim, J.; Salameh, P. Estimating methane emissions in California’s urban and rural regions using multitower observations. J. Geophys. Res. Atmos. 2016, 121, 13,031–13,049. [Google Scholar] [CrossRef]
- Lu, X.; Jacob, D.J.; Zhang, Y.; Maasakkers, J.D.; Sulprizio, M.P.; Shen, L.; Qu, Z.; Scarpelli, T.R.; Nesser, H.; Yantosca, R.M.; et al. Global methane budget and trend, 2010–2017: Complementarity of inverse analyses using in situ (GLOBALVIEWplus CH4 ObsPack) and satellite (GOSAT) observations. Atmos. Chem. Phys. 2021, 21, 4637–4657. [Google Scholar] [CrossRef]
- Hong, X.; Gao, Y.; Wang, J.; Zhang, C.; Chen, H.; Ni, Y.; Wang, W.; Sun, Y.; Zhu, Y.; Tang, Z. Evaluating the performance of carbon dioxide and methane observations from carbon-monitoring satellite products over China. Sci. Total Environ. 2024, 955, 176896. [Google Scholar] [CrossRef]
- Mastrogiacomo, J.-P.; Crippa, M.; MacDonald, C.G.; Roehl, C.; Wunch, D. Estimating Urban CH4 Emissions from Satellite-Derived Enhancement Ratios of CH4, CO2, and CO. JGR Atmos. 2025, 130, e2025JD043394. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W.; Chueasa, B.; Wangwongchai, A. Artificial Intelligence and Numerical Weather Prediction Models: A Technical Survey. Nat. Hazards Res. 2025, 5, 306–320. [Google Scholar] [CrossRef]
- Chen, L.; Zhong, X.; Zhang, F.; Cheng, Y.; Xu, Y.; Qi, Y.; Li, H. FuXi: A cascade machine learning forecasting system for 15-day global weather forecast. Npj Clim. Atmos. Sci. 2023, 6, 190. [Google Scholar] [CrossRef]
- Chantry, M.; Lang, S.; Alexe, M.; Dramsch, J.; Raoult, B.; Clare, M.; Santa Cruz, M.; Hahner, S.; Adewoyin, R.; Pinault, F. AIFS-ECMWF’s Data-Driven Forecasting System. In Proceedings of the 105th Annual AMS Meeting 2025, New Orleans, LA, USA, 12–16 January 2025; p. 449087. [Google Scholar]
- Fillola, E.; Santos-Rodriguez, R.; Manning, A.; O’Doherty, S.; Rigby, M. A machine learning emulator for Lagrangian particle dispersion model footprints: A case study using NAME. Geosci. Model Dev. 2023, 16, 1997–2009. [Google Scholar] [CrossRef]
- Dadheech, N.; He, T.-L.; Turner, A. High-resolution greenhouse gas flux inversions using a machine learning surrogate model for atmospheric transport. EGUsphere 2024, 2024, 1–21. [Google Scholar] [CrossRef]
- Xu, X.; Sun, X.; Han, W.; Zhong, X.; Chen, L.; Gao, Z.; Li, H. Fuxi-da: A generalized deep learning data assimilation framework for assimilating satellite observations. npj Clim. Atmos. Sci. 2025, 8, 156. [Google Scholar] [CrossRef]
- Vaughan, A.; Mateo-Garcia, G.; Irakulis-Loitxate, I.; Watine, M.; Fernandez-Poblaciones, P.; Turner, R.E.; Requeima, J.; Gorroño, J.; Randles, C.; Caltagirone, M. AI for operational methane emitter monitoring from space. arXiv 2024, arXiv:2408.04745. [Google Scholar] [CrossRef]
- Tiemann, E.; Zhou, S.; Kläser, A.; Heidler, K.; Schneider, R.; Zhu, X.X. Machine learning for methane detection and quantification from space—A survey. arXiv 2024, arXiv:2408.15122. [Google Scholar]
- Whiticar, M.J.; Faber, E.; Schoell, M. Biogenic methane formation in marine and freshwater environments: CO2 reduction vs. acetate fermentation—Isotope evidence. Geochim. Cosmochim. Acta 1986, 50, 693–709. [Google Scholar] [CrossRef]
- Quay, P.; Stutsman, J.; Wilbur, D.; Snover, A.; Dlugokencky, E.; Brown, T. The isotopic composition of atmospheric methane. Glob. Biogeochem. Cycles 1999, 13, 445–461. [Google Scholar] [CrossRef]
- Zazzeri, G.; Lowry, D.; Fisher, R.; France, J.; Lanoisellé, M.; Grimmond, C.S.B.; Nisbet, E. Evaluating methane inventories by isotopic analysis in the London region. Sci. Rep. 2017, 7, 4854. [Google Scholar] [CrossRef]
- Defratyka, S.M.; Paris, J.-D.; Yver-Kwok, C.; Fernandez, J.M.; Korben, P.; Bousquet, P. Mapping urban methane sources in Paris, France. Environ. Sci. Technol. 2021, 55, 8583–8591. [Google Scholar] [CrossRef]
- Hopkins, F.M.; Kort, E.A.; Bush, S.E.; Ehleringer, J.R.; Lai, C.T.; Blake, D.R.; Randerson, J.T. Spatial patterns and source attribution of urban methane in the Los Angeles Basin. J. Geophys. Res. Atmos. 2016, 121, 2490–2507. [Google Scholar] [CrossRef]
- Peischl, J.; Ryerson, T.; Brioude, J.; Aikin, K.; Andrews, A.; Atlas, E.; Blake, D.; Daube, B.; De Gouw, J.; Dlugokencky, E. Quantifying sources of methane using light alkanes in the Los Angeles basin, California. J. Geophys. Res. Atmos. 2013, 118, 4974–4990. [Google Scholar] [CrossRef]
- Plant, G.; Kort, E.A.; Floerchinger, C.; Gvakharia, A.; Vimont, I.; Sweeney, C. Large fugitive methane emissions from urban centers along the US East Coast. Geophys. Res. Lett. 2019, 46, 8500–8507. [Google Scholar] [CrossRef]
- Della Rosa, M.M.; Jonker, A.; Waghorn, G.C. A review of technical variations and protocols used to measure methane emissions from ruminants using respiration chambers, SF6 tracer technique and GreenFeed, to facilitate global integration of published data. Anim. Feed Sci. Technol. 2021, 279, 115018. [Google Scholar] [CrossRef]
- Deighton, M.H.; Williams, S.R.O.; Hannah, M.C.; Eckard, R.J.; Boland, T.M.; Wales, W.J.; Moate, P.J. A modified sulphur hexafluoride tracer technique enables accurate determination of enteric methane emissions from ruminants. Anim. Feed Sci. Technol. 2014, 197, 47–63. [Google Scholar] [CrossRef]
- Cusworth, D.H.; Duren, R.M.; Ayasse, A.K.; Jiorle, R.; Howell, K.; Aubrey, A.; Green, R.O.; Eastwood, M.L.; Chapman, J.W.; Thorpe, A.K. Quantifying methane emissions from United States landfills. Science 2024, 383, 1499–1504. [Google Scholar] [CrossRef] [PubMed]
| Coordinate System | Representative Model | Reference |
|---|---|---|
| Eulerian Models | GEOS-Chem | Bey et al. [73] |
| TM5 | Krol et al. [74] | |
| WRF-Chem | Grell et al. [75] | |
| EURAD-IM | Hass et al. [76] | |
| Lagrangian Particle Dispersion Models | FLEXPART | Stohl et al. [77] |
| HYSPLIT | Stein et al. [70] | |
| STILIT | Lin et al. [78] | |
| LES-Driven LPDM | Weil et al. [79] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, Y.; de Leeuw, G.; Yao, X.; He, Z.; Wu, H.; Yang, Z. A Review of City-Scale Methane Flux Inversion Based on Top-Down Methods. Remote Sens. 2025, 17, 3152. https://doi.org/10.3390/rs17183152
Li X, Zhang Y, de Leeuw G, Yao X, He Z, Wu H, Yang Z. A Review of City-Scale Methane Flux Inversion Based on Top-Down Methods. Remote Sensing. 2025; 17(18):3152. https://doi.org/10.3390/rs17183152
Chicago/Turabian StyleLi, Xiaofan, Ying Zhang, Gerrit de Leeuw, Xingyu Yao, Zhuo He, Hailing Wu, and Zhuolin Yang. 2025. "A Review of City-Scale Methane Flux Inversion Based on Top-Down Methods" Remote Sensing 17, no. 18: 3152. https://doi.org/10.3390/rs17183152
APA StyleLi, X., Zhang, Y., de Leeuw, G., Yao, X., He, Z., Wu, H., & Yang, Z. (2025). A Review of City-Scale Methane Flux Inversion Based on Top-Down Methods. Remote Sensing, 17(18), 3152. https://doi.org/10.3390/rs17183152









