Estimating Methane Emissions by Integrating Satellite Regional Emissions Mapping and Point-Source Observations: Case Study in the Permian Basin

Abstract

Methane (CH₄) is known as the most potent greenhouse gas in the short term. With the growing urgency of mitigating climate change and monitoring CH₄ emissions, many emerging satellite systems have been launched in the past decade to observe CH₄ and other greenhouse gases from space. These satellites are either capable of pinpointing and quantifying super emitters or deriving regional emissions with a more frequent revisit time. This study aims to reconcile emissions estimated from point source satellites and those from regional mapping satellites, and to investigate the potential of integrating point-based quantification and regional-based quantification techniques. To do that, we quantified CH₄ emissions from the Permian Basin separately by applying the divergence method to the TROPOMI Level-2 data product, as well as an event-based approach using CH₄ plumes quantified by Carbon Mapper systems. The resulting annual CH₄ emissions estimates from the Permian Basin in 2024 are 1.83 ± 0.96 Tg and 1.26 [0.78, 2.02] Tg for divergence and event-based methods, respectively. The divergence-based emissions estimate shows a more comprehensive spatial distribution of emissions across the Permian Basin, whereas the event-based approach highlights the grid cells with the short-duration super-emitters. The emissions from grids with detectable emissions under both methods show strong agreement (R² ≈ 0.642). After substituting the overlap cells’ values from divergence-based emissions estimation with those from event-based estimation, the combined emissions estimate is 2.68 [1.88, 3.54] Tg, which is reconciled with Permian Basin emissions estimates from previous studies. We found that CH₄ emissions from the Permian Basin gradually reduced over the past five years. Furthermore, this case study indicates the potential for integrating estimations from both methods to generate a more comprehensive regional emissions estimate.

1. Introduction

Over the past decade, the adoption of low-Earth-orbit satellites to measure and quantify methane (CH₄) emissions has garnered significant attention [1]. Satellite data have become an important source to pinpoint the global super-emitters, reveal regional emissions, evaluate emissions benchmarks, and help the government to develop policy towards mitigating global warming and achieving the net-zero goal [2,3,4,5,6,7,8,9,10]. The rapid growth of applications has been largely facilitated by advancements in retrieval techniques, which, in turn, have driven the deployment of numerous satellites explicitly designed for the dedicated monitoring of CH₄ and other greenhouse gases (GHGs) (e.g., GHGSats, MethaneSat, and Tanager-1). Retrievals of the column-average CH₄ mixing ratio in the atmosphere require observing short-wave infrared (SWIR) radiation with frequencies ranging from 1.63 to 1.70 µm or 2.2 to 2.4 µm [1]. Therefore, several launched satellites are equipped with instruments that are also capable of detecting wavelengths sensitive to atmospheric CH₄ (e.g., Sentinel-2, Landsat-8).

Based on the spatial resolution of satellite observations, satellite systems can be classified as point-source detectors and regional mappers [1]. Point-source detectors, such as GHGSats, Worldview-3, EMIT, GESat, Sentinel-2, PRISMA, and Tanager-1, can pinpoint and quantify exact emission sources at the site-level, such as waste treatment plants, coal mines, oil and gas facilities, landfills, and other industrial sites [4,5,6,9,10,11,12]. The detection and quantification of several point-source detectors have already been verified in a past single-blind test study, which demonstrates the potential to detect emissions as low as 100 kg/h [13]. Conversely, observations from regional mappers such as Sentinel-5P TROPOMI, ENVISAT-SCIAMACHY, and GOSAT have a lower spatial resolution but can usually quantify emissions from entire basins or countries [14,15,16,17,18,19,20]; Furthermore, the newly launched MethaneSat can estimate both regional emissions and pinpoint CH₄ plumes at the site level [21,22]. Although some studies have also successfully identified the source using a regional mapper [22,23,24,25,26]. However, only super-emitters (i.e., emissions greater than 25,000 kg/h) can be detected due to the high minimum detection limit of regional mappers [24,27].

The performance of satellite systems is influenced by various atmospheric factors, including aerosol optical thickness, surface albedo, solar altitude, cloud cover, topographic roughness, and wind speed [28,29]. Some of these variables, such as persistent cloud cover and low solar altitude, systematically affect observations in high-latitude regions and areas near the equator [29]. While it is still premature to consider satellite observations the silver bullet solution, they provide valuable information across most high-emission regions globally and significantly reduce the temporal coverage gaps of the majority of anthropogenic emissions sources, particularly by integrating images from multiple satellites.

The finalized CH₄ emissions data product from satellite systems typically includes either a retrieved CH₄ concentration or mixing ratio map (also known as a level 2 data product) or regional quantification results (also known as a level 3 data product) or isolated CH₄ plume with visualization and associated quantification results (also known as a level 4 data product). Each type of data product supports different methods for estimating CH₄ emissions, depending on the scale of detail (regional scale vs. site scale) in the observations. The common quantification methods for point-source detectors include inverse Gaussian plume model [23], mass balance [30], integrated mass enhancement [10], and machine learning-based method [31]. For regional mappers, systematic quantification methods, such as Integrated Methane Inversion [32,33], as well as divergent methods, have been widely adopted over the past five years [7,16].

Previous studies have found a discrepancy in emission estimates between top-down (TD) and bottom-up (BU) approaches [34,35,36]. However, discrepancies can also exist between the two different TD approaches, such as those between point-source detectors and regional mappers. In this study, we present a reconciliation between regional emission estimates from regional mappers and aggregated plume-level quantifications from point-source detectors. Specifically, we apply the event-based methodology developed by Gao et al. [37], incorporating plume data published by Carbon Mapper and the divergence method developed by Liu et al. [7] with the TROPOMI Level-2 data product and the ECMWF Atmospheric Composition Reanalysis 4 dataset from Copernicus Atmosphere Monitoring Service (CAMS EAC4) to separately estimate emissions from the Permian Basin, US, for 2024. To ensure the singularity of the emission source sector and sufficient observational coverage, we selected Permian Basin BU estimation from the Global Fuel Exploitation Inventory (GFEI) v3 [38] and previous CH₄ emissions investigation results from Permian Basin as references.

This study is the first to integrate quantifications from point-source plumes and regional estimates to directly address the underestimation of short-duration, large-emission events. Regional mappers provide broad coverage over time, while point-source satellites provide plume-level snapshots but miss many emissions due to limited spatial coverage. By combining an event-based framework with divergence analysis, our method can improve the regional methane budget estimates, thereby reducing discrepancies between TD and BU approaches.

2. Materials and Methods

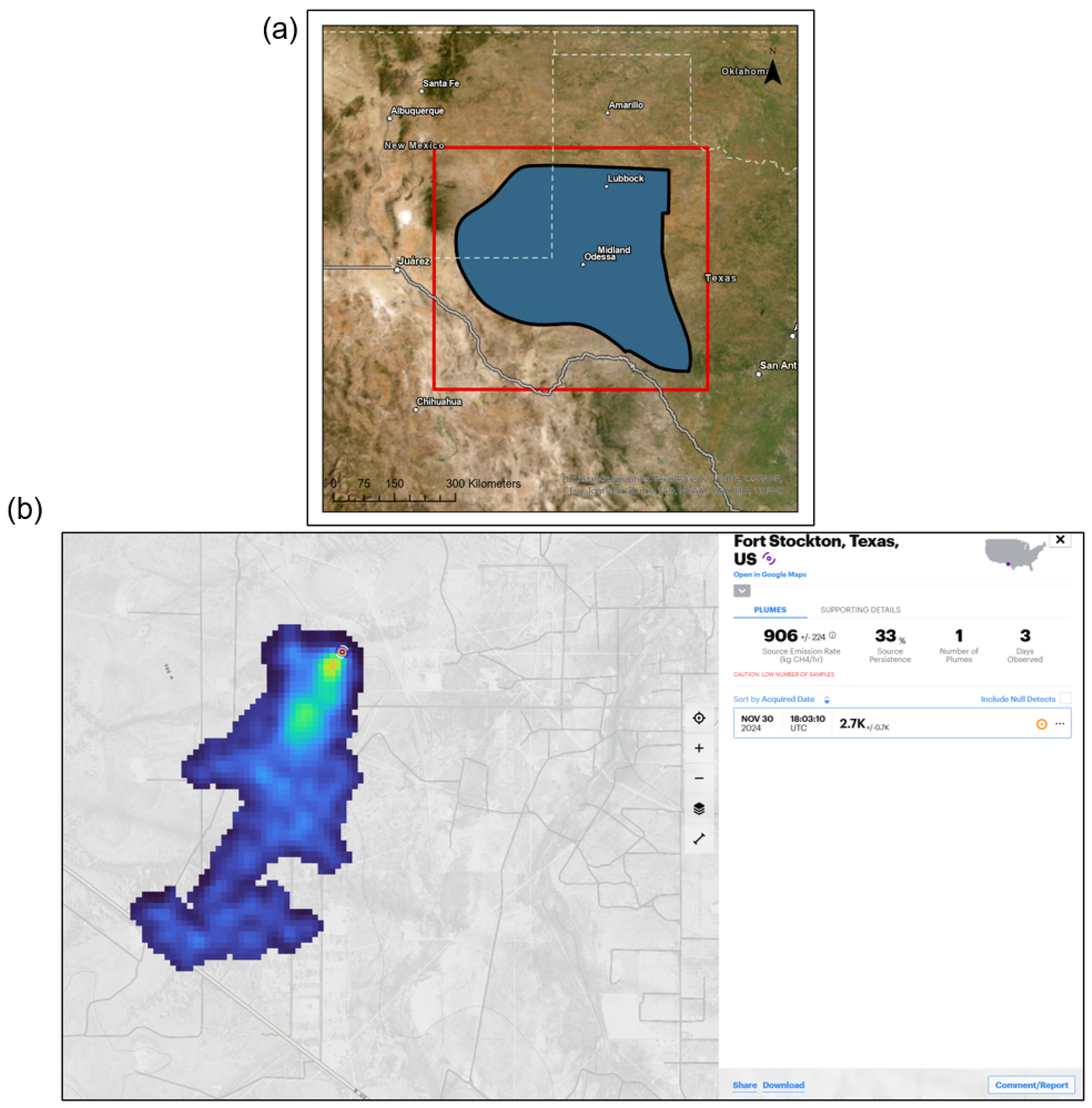
2.1. Study Area

The Permian Basin is the most productive oil and gas (O&G) basin in the United States [39], located in West Texas and southeastern New Mexico (see Figure 1a). Over the past five years, the Permian Basin has been consistently monitored and identified as the highest CH₄-emitting O&G region in the country [5,7,20,33]. For the divergence method, we estimate emissions for the entire Texas and the southeast corner of New Mexico. For the event-based method, we defined an extended study area (red highlighted region in Figure 1a) that encompasses the boundary of the Permian Basin, specifically, from 29 to 34.5 degrees north and −105.5 to −99.5 degrees west.

2.2. Regional CH₄ Emission Estimate—The Divergence Method

2.2.1. TROPOMI Level 2 Data Product

The TROPOspheric Monitoring Instrument (TROPOMI) onboard the Sentinel-5 Precursor satellite relies on passive remote sensing to measure atmospheric constituents, including CH₄. RemoTeC full-physics algorithm was applied to retrieve the atmospheric CH₄ total column (or concentrations) from Earth radiance measurements in the near-infrared (NIR, 675 nm to 775 nm) and shortwave infrared (SWIR, 2305–2385 nm) spectral bands [40,41]. The TROPOMI Level 2 data product provides daily observations of the column-mean dry air mixing ratio of CH₄ (XCH₄) across Texas, comprising 13 or 14 orbits per day [41]. To correct the underestimation of the TROPOMI XCH₄ data for low albedo, bias-corrected XCH₄ is also provided in the data product. The pixel size of the image product is approximately 7 km × 5.5 km for data collected after 6 August 2019. In this study, quality-assured TROPOMI level 2 XCH₄ observations (i.e., qa_value ≥ 0.5) from 1 January 2024 to 31 December 2024, were used for basin-level emission estimates via the divergence method.

2.2.2. Reanalysis Data from CAMS EAC4

To perform the divergent method developed by Liu et al. [7], atmospheric variables, including surface pressure, level-specific CH₄ column, the u and v wind components, were extracted from the CAMS EAC4 [42]. Different from the spatial resolution of TROPOMI XCH₄ observations, the spatial resolution of EAC4 data is 0.75° × 0.75° [42]. The EAC4 model does not rely on prior CH₄ emissions from bottom-up inventories such as the Emissions Database for Global Atmospheric Research (EDGAR) 8.0 or the GFEI v3. As a result, the distribution of CH₄ columns is primarily influenced by atmospheric transport and orography [16].

2.2.3. The Divergence Method

Figure 2 illustrates the detailed emissions estimation workflow developed by Liu et al. [7]. Equations and procedural steps are provided in Appendix A. The divergence method comprises three primary steps. First, we used the high-pass median filter to destrip and correct the bias caused by the satellite’s viewing angle [7]. Second, we calculated the average daily divergence using Equation (1). We downloaded the vertical column of CH₄ above planetary boundary layer (PBL) ($V_{CH4}^U$), as well as u- and v-wind components ($\mathbf{w}$) at the PBL from EAC4 (PBL is approximately 500 m above the surface, corresponding to model level 53 in EAC4). The $V_{CH4}$ and $V_{air}^{PBL}$ are total columns of CH₄ and dry air density used to retrieve TROPOMI’s column-mean dry air mixing ratio of CH₄, which can be directly assessed from TROPOMI Level 2 data product. To ensure that EAC4 data (0.75° × 0.75°) matches our predefined 0.25° grid cells, we downsampled the EAC4 data using bilinear interpolation [43]. Next, we calculated the daily CH₄ mixing ratio below the PBL ($X_d^{PBL}$) using Equation (2), as well as the regional background ($X_d^R$) of each grid cell using the lower 10 percentile of three surrounding cells (7 × 7 grid cells window). Then, the daily divergence ($D_d^s$) can be calculated by multiplying the CH₄ enhancement (i.e., the daily mixing ratio minus the regional background, $X_d^{PBL}-X_d^R$) by the air density column in the PBL ($A_d^{PBL}$).

$$E^{\prime }=\overline{D_d^s}=\overline{\nabla \left(\left(X_d^{PBL}-X_d^R\right)\times A_d^{PBL}\mathbf{w}\right)}$$

(1)

and

$$X_d^{PBL}={\displaystyle \frac{V_{\mathrm{CH}4}-V_{\mathrm{CH}4}^U}{V_{air}^{PBL}}}$$

(2)

This calculation was repeated for each day. Note that a single day may include more than one image (observation). To avoid underestimation [44], we first averaged the emissions divergence ($\overline{D_d^s}$) within each day and then averaged across all days to calculate the daily mean emissions for each grid cell ($E^{\prime }$). Finally, we applied a linear regression between emissions divergence and background divergence following the approach of Liu et al. [16] to generate the final emissions estimates (see Equation (A5) in Appendix A).

2.3. Event-Based CH₄ Emissions Estimate

2.3.1. CH₄ Plumes from Carbon Mapper

Carbon Mapper (https://carbonmapper.org/data (accessed on 14 April 2025)) is a non-profit organization that publishes CH₄ and CO₂ plumes detected by both airborne systems (Airborne Visible/Infrared Imaging Spectrometer–Next Generation [AVIRIS-NG], Global Airborne Observatory [GAO]) and satellite systems (EMIT, International Space Station [ISS], and Tanager-1), along with associated quantification results and source information [45]. Figure 1b shows a sample plume published on Carbon Mapper’s data portal. Several types of data products are available for download on the portal. In this study, we downloaded Level 4 products, which include plumes and sources, from both airborne and satellite platforms, covering the period from 1 January 2024 to 31 December 2024. Quantification results, uncertainty estimates, plume IDs, detection times, and plume coordinates from the L4A–Plume Emissions product, as well as source coordinates, plume IDs, scene IDs, observation scene names, and persistence from the L4B–Source Emissions product, were used for event creation in this study [46].

2.3.2. Event Creation

Figure 2 also presents the overall workflow for estimating regional emissions by aggregating discrete emission events. By utilizing emissions plumes and sources published by Carbon Mapper, we constructed emissions events using an event-based framework developed by Gao et al. [37]. According to the definition, only partially resolved events (PREs) are created in this study, which represent events measured using remote sensing technologies and require an estimated duration based on non-detections (i.e., the observations from aircraft and satellite systems conclude that no emissions are detected from the given source). The other two types of events are resolved events (RE), in which durations are determined using operational data, and unresolved events (UE), which are either not being measured or below the detection limit of the remote sensing technology.

Table A1. Three categories of emission event types.

Emission Event Type	Definition	Duration Determination	Emissions Quantity from Events	Uncertainty
Resolved Event (RE)	Events with durations determined using operational data/log	Extracted from operational data/log	Calculated	Only quantification uncertainty is considered
Partially Resolved Event (PRE)	Events with duration that are either measured by remote sensing technologies or estimated using null-detection and rules	Simulated by using proceedings and succeeding null-detection times	Calculated	Quantification uncertainty and duration estimation uncertainty
Unresolved Event (UE)	Events that are missing from annual emissions data	Simulated	(1) Simulate emissions that are not detected using POD checks (2) Simulate emissions by random sample RE and PRE	Estimated in the simulations

provides the definitions and descriptions of three types of events. Figure 3 illustrates an example of creating PRE using plume detection and non-detection data from Carbon Mapper systems.

Each emissions source on the ground can have multiple events that occur throughout the year, and each event has a finite number of detections and non-detections. Therefore, we can bookend each plume detection by using its proceeding and succeeding null-detections. The null-detections can be derived by accessing the plume name and scene name of each source for which the scene name does not relate to the plume is defined as a null-detection. When multiple plumes share the same null detections, we conclude that they represent the same event by following Allen’s interval algebra [47]. When there are no null detections, the first and last day of the year will be used to bind the event. Thus, the succeeding and proceeding null detections ($N{D}_{suceeding}$ and $N{D}_{proceeding}$) are 2024-01-01T00:00:00 and 2024-12-31T23:59:59 for 2024. Furthermore, the event rate ($Q_{PRE}$) is calculated by averaging the rates of all plumes included in the event. The difference between $N{D}_{suceeding}$ and $N{D}_{proceeding}$ is the observed duration. By combining the persistence [46], the number of plume detection days ($N_{plume}$) divided by the number of observation days ($N_{observe}$), and observed duration, the estimated event duration of each PRE ($D_{est}$) can be calculated by using equation as follows:

$$D_{est}=\left(N{D}_{suceeding}- N{D}_{proceeding}\right)\times {\displaystyle \frac{N_{plume}}{N_{observe}}}$$

(3)

and the total emissions of event can be calculated by using Equation (4).

$$E_{PRE}=Q_{PRE}\times D_{est}$$

(4)

2.3.3. Calculate Event-Based Emissions

We applied Equation (5) [37] to calculate the total emissions from all events of a given source.

$$E_{Total}={{\displaystyle \sum }}_{i_{RE}=1}^{N_{RE}}{E}_{R{E}_i}+{{\displaystyle \sum }}_{i_{PRE}=1}^{N_{PRE}}{E}_{PR{E}_i}+{{\displaystyle \sum }}_{i_{UE}=1}^{N_{UE}}{E}_{U{E}_{i }}={{\displaystyle \sum }}_{i_{PRE}=1}^{N_{PRE}}{Q}_{PR{E}_i}\times D_{es{t}_i}+{\overline{E}}_{UE\_sim}$$

(5)

where $N_{RE}$, $N_{PRE}$ and $N_{UE}$ indicate the number of resolved, partially resolved, and unresolved events, respectively. $E_{RE}$, $E_{PRE}$, and $E_{UE}$ represent total CH₄ emissions from given resolved, partially resolved, and unresolved events, respectively. Since operational data are not available, we only considered emissions from PREs and UEs in this study.

For each source, total emissions from PREs were calculated straightforwardly aggregating all emissions from PRE calculated using Equation (4). However, we need additional two steps to calculate emissions from UEs.

First, we derive distributions for the expected emission rate, event duration, and probability of occurrence based on the constructed PREs. The consolidated rate and duration of PREs usually follow right-skewed distributions, which mathematically can be expressed using exponential function (see Equation (6)). Additionally, the likelihood of event occurrence ($P_{occurence}$) for a given year can be approximately equal to the ratio between the number of detected plumes (plumes count) and number of observation attempts (scene count), which also can be expressed using exponential function.

$$P\left(v\right)=a{e}^{v^b}$$

(6)

where $v$ is either the rate or duration or probability of event occurrence sampled under the probability $P\left(v\right)$, and $a$ and $b$ are parameters required to fit different distributions.

$$P\left(v\right)={\displaystyle \frac{1}{v\times \sigma \sqrt{2\pi }}}\exp \left(-{\displaystyle \frac{{\left(lnv-\mu \right)}^2}{2{\sigma }^2}}\right)$$

(7)

where $\mu$ is the mean and $\sigma$ is standard deviation of rate or duration or probability of event occurrence.

Therefore, we use a log-normal probability density function (PDF; Equation (7)) to fit the empirically measured distributions of event rate ($Q_{dist}$), duration ($D_{dist}$), and probability of event occurrence ($P_{dist}$). The optimal $a$ and $b$ are used to create the expected rate ($Q_{exp\_dist}$), duration ($D_{exp\_dist}$), and probability of event occurrence ($P_{exp\_dist}$) distributions.

Second, we applied the Monte Carlo approach to extrapolate emissions of UEs for each source [37]. The Monte Carlo simulation begins by setting the timestamp to the start time of the simulation (2024-01-01T00:00:00) and initializing emissions from UEs ($E_{UE\_sim}$) to 0 kg. For each source, the simulation proceeds hourly and sample a $P_{occurence}$ from $P_{dist}$. Based on sampled $P_{occurence}$, we calculate the likelihood of no event occurrence ($P_{not\_occurence}$) by using 1 − $P_{occurence}$. Then a binomial distribution (with outcome of 0 or 1) can be created by using $P_{occurence}$ and $P_{not\_occurence}$. Next, we sample from the constructed binomial distribution. If an emission occurs, the emission rate ($q$) and duration ($d$) are sampled from the $Q_{exp\_dist}$ and $D_{exp\_dist}$, respectively. The $E_{UE\_sim}$ then updated by adding the emissions calculated from multiplying $q$ and $d$, and the simulation time is incremented by $d$. If no emission event occurs, the simulation time advances by one hour. This process is repeated until the end of the simulation time (2024-12-31T23:59:59). The $E_{UE\_sim}$ of a source is calculated by summing emissions from all sampled UEs. The simulation is repeated for 10⁵ iterations, and the median (${\overline{E}}_{UE\_sim}$), along with the 2.5th and 97.5th percentiles of the $E_{UE\_sim}$ distribution, are calculated to represent the simulated emissions from UEs and their associated uncertainty.

Finally, we calculate grid emissions ($E_{grid}$) by aggregating $E_{Total}$ of all point sources within each 0.25° grid cell (Equation (7)).

$$E_{grid}={{\displaystyle \sum }}_{k=1}^{N_s}{E}_{tota{l}_k}$$

(8)

3. Results

3.1. Divergence of CH₄ Emissions

Figure 4a illustrates the TROPOMI days (i.e., the number of days that TROPOMI have valid level 2 data) throughout 2024. The median number of TROPOMI days in our study region in 2024 is 140 days. By focusing on the Permian Basin, the median and average TROPOMI days are 184 days and 182 days, respectively. For 2024, the mean XCH₄ in the Permian Basin was 1917.12 ± 6.28 ppb (see Figure 4b). The concentration hotspots in the Permian Basin are located near the central Midland and the central Delaware Basins (highlighted in Figure 4b). The calculated divergence of CH₄ emissions using Equation (4) ranged from −15.11 to 16.60 kg/km²/hour prior to applying the linear regression correction (Figure 4c). The uncorrected divergence from hotspot grid cells near the Midland Basin was lower than that of grid cells in the Delaware Basin.

After the correction, the CH₄ emission divergence was adjusted to a range of 0 to 16.6 kg/km²/h (Figure 4d). By multiplying the area and normalizing it with the number of hours per year, we converted the calculated emissions per unit area and time into annual emissions estimates. As shown in Figure 4e, the total calculated CH₄ emissions of the Permian Basin were 1.83 Tg for the year 2024. Approximately 15% of grid cells contributed 83.6% of the total emissions (~1.53 Tg) within the Basin. The mean CH₄ emissions across all grid cells within the Permian Basin were 0.007 Tg, and the maximum CH₄ emissions were 0.097 Tg. We also applied the Monte Carlo approach developed by Liu et al. [16] to calculate the uncertainties associated with the estimated emissions. As indicated in Figure 4f, uncertainties of emissions per grid cell ranged from 44.51% to 167.10%. We calculated the root mean square error to represent the overall uncertainties in basin-level emissions estimation. Finally, our estimate for the Permian Basin for 2024 was 1.83 ± 0.96 Tg.

3.2. Event-Based CH₄ Emissions

A total of 1465 plumes and 656 sources were downloaded from the Carbon Mapper data portal. After aggregating the plumes and sources to our predefined 0.25° grid cells, the number of plumes per grid cell ranged from 0 to 228, with an average of 28 and a median of 6 plumes, respectively (Figure 5a). Similarly, the number of sources per grid cell ranged from 0 to 84, with an average of 13 and a median of 5 (Figure 5b).

Following the event-based framework proposed by Gao et al. [37], we constructed 565 partial resolved events (PREs) by combining plume and scene information from the source data. As shown in Figure 5c, the number of PREs per grid cell ranged from 1 to 90, with an average of 14 and a median of 3 events per grid cell. Figure 5a–c also show that the majority of plumes, sources, and constructed events were located near the Texas-New Mexico border, indicating the spatial observation coverage of the Carbon Mapper satellite systems.

Using the constructed events, we created the best-fit curves for event rate, duration, and occurrence probability distributions (Figure 5d–f). The mean and standard deviation for the event rate were 5.54 and 1.11, respectively, while those for the event duration were 6.42 and 2.48. The yielded best-fit parameters (a and b) are 0.000072 and −0.0006 for the rate and 0.0424 and −0.0004 for the duration. Similarly, the mean and standard deviation for emission event probability were −1.81 and 0.69, respectively, and the fitted exponential function parameters were a = 7.1 and b = −6.09. These curves were used to generate expected distributions and simulate UEs.

Figure 6a shows the map of estimated emissions aggregated from only PREs. The total CH₄ emissions in 2024 from only constructed PREs were estimated at 0.23 Tg, with a 95% confidence interval (CI) of [0.19, 0.27] Tg. Although the majority of Carbon Mapper plumes and sources were observed near the Texas-New Mexico border, the grid cells with the highest emissions (~0.043 Tg) from PREs were located in the central Midland basin. After incorporating simulated emissions from UEs (as shown in Figure 6b), the total estimated emissions for the Permian Basin increased to 1.26 Tg, with a 95% confidence interval of [0.78, 2.02] Tg. The Delaware Basin was highlighted from the simulation of UEs. In total, 1.03 Tg of previously unobserved emissions were simulated across 52 grid cells based on locations of published sources from Carbon Mapper. Emissions of grid cells near the northern Delaware Basin (i.e., border between New Mexico and Texas) increased significantly after adding emissions from UEs, ranging from 0.002 to 0.03 Tg.

In addition to the inherent uncertainty from individual plume quantification, two primary assumptions may also contribute to the uncertainty in emissions event estimation. First, the event-based framework assumes that each site can experience only one event during a given time period. In reality, multiple events may occur simultaneously. However, observation technologies (e.g., satellites) cannot resolve the number of concurrent events or the specific emitting equipment at a site. As a result, the quantification may represent the aggregation of multiple events. Thus, the simulated event could also be aggregation of multiple events. Second, since we use the rate and duration from measured events to estimate those of unmeasured events through fitted curves. If there are insufficient measurements of rates and durations, the fitted curve may fail to capture the true emissions profile of the site. Consequently, simulated emissions from UEs may also be inaccurate, as their rates and durations are sampled from these fitted distributions.

4. Discussion

Implications for Emission Reconciliation

Since the event-based method only estimates emissions where Carbon Mapper has detected sources, only 52 grid cells within the Permian Basin have event-based emissions estimates. Among them, 26 grid cells were found with emissions under the divergence method. We then further compared the grid-specific emissions from both methods. The mean and median differences in these 26 grid cells were 0.016 Tg and 0.015 Tg. The robust linear regression analysis reveals a strong positive correlation between emissions estimates from 26 grid cells that are available from the results of both methods (see Figure 7a). The total emissions estimated by the two methods were generally comparable (1.83 ± 0.96 Tg vs. 1.26 [0.78 Tg, 2.02 Tg]). Although emissions estimated using the event-based method were 0.57 Tg lower than those estimated using the divergence method, the uncertainty ranges of both estimates overlapped, with a 31.1% discrepancy, indicating agreement within statistical bounds.

A key limitation of the event-based method is its inability to estimate emissions in grid cells where no detectable emissions are present (i.e., emissions below ~100 kgCH₄/h). However, this method is particularly effective at capturing short-duration, high-emission events that may be smoothed out or missed in the time-averaged divergence-based approaches. For example, as shown in Figure 4e, the New Mexico portion (norther side) of the Delaware Basin was not highlighted using the divergence method alone, but was identified with notable emissions using the event-based method (Figure 6b).

To leverage the strengths of both approaches, we integrated the event-based estimates with the divergence-based regional estimates by substituting divergence-based values with event-based estimates in 26 grid cells where plume-derived results were available (see Figure 7b). By doing so, it is reasonable to believe the divergence-based emission estimate was corrected to include the instantaneous high emission events. This hybrid approach yielded a total CH₄ emission estimate of 2.68 Tg for the Permian Basin, with a 95% confidence interval of [1.88, 3.54] Tg. The overall uncertainty was estimated as the root mean square error across all grid cells (see Equation (A6)).

We compared the integrated emission estimate with previous CH₄ emission studies conducted between 2015 and 2023, as well as the bottom-up inventory provided in GFEI v3 [38]. A summary of referenced studies is provided in

Table A2. A summary of previous satellite-based CH₄ emissions studies in the Permian Basin.

References	Year of Investigation	Emission Rate	Uncertainty	Method	Unit	Doi
[49]	2010–2015	2.01	0.01	GOSAT inverse flux estimate—derived from [61]	Tg/year	https://doi.org/10.1038/s43247-021-00312-6
[20]	2018–2019	2.68	0.5	TROPOMI inverse flux estimate—O&G production	Tg/year	https://doi.org/10.1126/sciadv.aaz5120
	2018–2019	2.9	0.5	TROPOMI inverse flux estimate—basin total	Tg/year
[50]	2018–2020	2.9	0.4	TROPOMI inverse flux estimate	Tg/year	https://doi.org/10.5194/acp-22-11203-2022
	2018–2020	3.7	0.5	TROPOMI inverse flux estimate with an adjusted prior	Tg/year
[7]	2019	3.06	2.82—3.78	Divergence method: the continuity equation connecting the divergence (D), emission (E) and sink (S) for steady state.	Tg/year	https://doi.org/10.1029/2021GL094151
[52]	2018–2019	3.18	1.13	Gaussian integral mass balance method—TROPOMI/WFMD v1.2	Tg/year	https://doi.org/10.5194/acp-20-9169-2020
[53]	2018–2021	4.1	1.1	Automated detection of regions with persistently enhanced methane concentrations (TROPOMI) coupled with mass balance quantification method.	Tg/year	https://doi.org/10.5194/acp-24-10441-2024
[51]	2018–2020	3.7	0.9	Weekly TROPOMI inverse flux estimate	Tg/year	https://doi.org/10.5194/acp-23-7503-2023
[54]	2022–2023	2.69	0.86	Aggregation from GF-4 plume mapping	Tg/year	https://doi.org/10.1029/2024JD040870
[55]	2021	335 (2.9)	274–428 (2.4–3.7)	Measurement-based methane emissions inventory (EI-ME)	t/h (Tg/year)	https://doi.org/10.5194/essd-16-3973-2024

of Appendix B. The inversion-based emissions estimates, which rely on atmospheric transport models (e.g., GEOS-Chem) and prior emission information such as bottom-up inventories or source maps [20,33], often serve as a benchmark for other methods [7]. Past TROPOMI-based inverse flux estimates for the Permian Basin range from 2.9 ± 0.5 Tg/year (2019) to 3.7 ± 0.5 Tg/year (2020) [20,50,51]. In addition to inverse modeling, we compared our estimates with other techniques, including the divergence method [7], the Gaussian integral mass balance method [52,53], the point-source aggregation method [54], and a measurement-based inventory approach [55]. These studies reported Permian Basin emissions as follows:

• 3.06 Tg [2.82, 3.78] for 2019 [7];
• 3.18 ± 1.13 Tg averaged over 2018–2019 [52];
• 2.69 ± 0.86 Tg averaged over 2022–2023 [54];
• 2.93 Tg [2.4, 3.7] for 2021 [55].

Our combined estimate aligns well with the results from previous studies. Our integrated estimate is comparable but slightly lower than the previous estimates. Considering the reported decreasing trend of CH₄ emissions from the Permian Basin [51,56], it is reasonable to expect lower CH₄ emissions in 2024 compared to the emissions estimates derived in earlier periods.

We also found that the event-based estimate (1.26 Tg; 95% CI: [0.78, 2.02] Tg) was reconciled with the GFEI v3 bottom-up inventory (0.95 ± 0.52 Tg), which specifically focuses on the energy sector, respectively. This agreement provided further confidence in applying the event-based method to capture short-duration super emitters in regional emissions estimation.

Overall, the comparison of emissions estimates spanning 2018–2024 confirmed the decline of CH₄ emissions in the Permian Basin. This downward trend suggests that the impact of regulatory efforts, operational improvements, increased efficiency of leak detection and repair program with advanced detection techniques, and increased public and industry scrutiny on reducing CH₄ emission from O&G sector is noteworthy over the past six years [56,57]. Further investigations into emission reduction mechanisms are needed to unpack the precise causes.

5. Conclusions

In conclusion, both the divergence-based and event-based CH₄ emission approaches produce broadly consistent annual CH₄ emissions estimates for the Permian Basin in 2024. The divergence method, using TROPOMI observations, yields a total emission estimate of approximately 1.83 ± 0.96 Tg. In contrast, the point-source event-based method, utilizing data from Carbon Mapper systems and Monte Carlo estimation for undetected emissions, estimates a value of 1.26 Tg (95% CI: 0.78–2.02 Tg). By comparing overlapping grid cells where both methods produced estimates, the moderate correlation (R² ≈ 0.642) reasonably indicates the reconciled emissions estimates between the two methods.

Since the divergence method is based on daily averages, short-duration events within a day may be neglected. Therefore, the event-based method serves as a valuable complement by capturing short-duration super-emitter events using point-source data. The divergence-based emission estimate was then corrected by substituting divergence estimates with event-based values in the overlapping grid cells to include instantaneous high-emission events. The integrated estimate is 2.68 [1.88, 3.54] Tg and this is is close to the emission estimates derived from other approaches from previous studies.

Overall, this study demonstrates that point-source and regional satellite-based methods, though different in approach, can produce mutually consistent emission estimates when reconciled through the proposed methodology. Future research will focus on extending this comparison to multiple regions globally, evaluating the availability of emissions observations, and developing a streamlined workflow for combining both methods to advance CH₄ emission estimates in regions lacking prior data.