Integrating UAS Remote Sensing and Edge Detection for Accurate Coal Stockpile Volume Estimation
Abstract
Highlights
- UAS-based SfM with interpolated DTMs achieved ~2% error compared to LiDAR.
- Automated boundary detection enhanced accuracy in stockpile volume estimation.
- SfM–intDTM provides a cost-effective and scalable alternative to conventional surveying methods.
- The method supports both precise and regional monitoring and is adaptable to quarrying, agriculture, and forestry.
Abstract
1. Introduction
- To develop an automated edge detection approach using slope raster for precise stockpile boundary delineation;
- To evaluate the accuracy of coal stockpile volume estimates derived from the UAS photogrammetric approach in comparison to industry-standard LiDAR;
- To assess interpolation techniques for generating representative base surface information to enable volume estimation in cases where base surface data is unavailable.
2. Methodology
2.1. Study Area
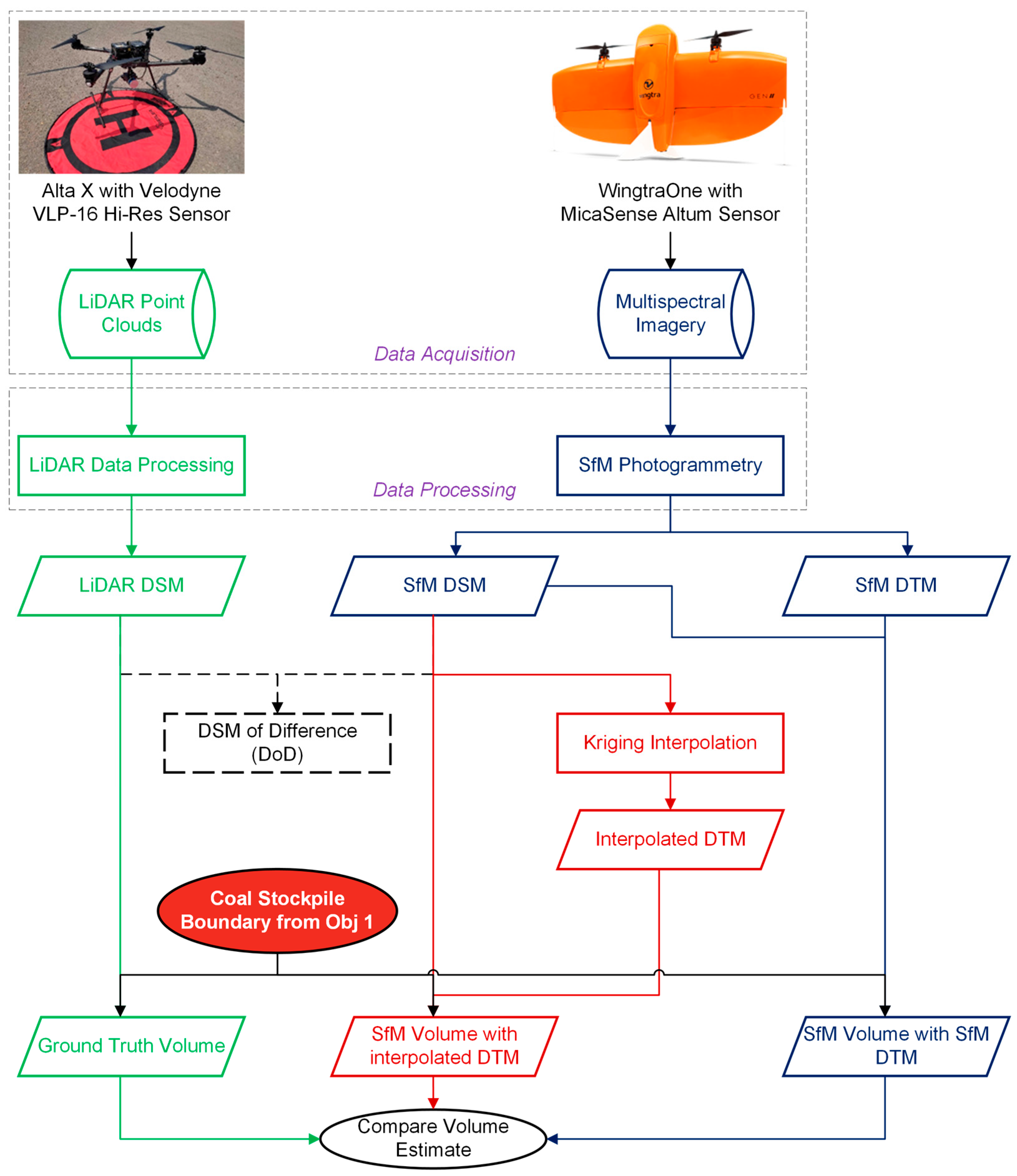
2.2. Overview of Methodology
2.3. Data Acquisition
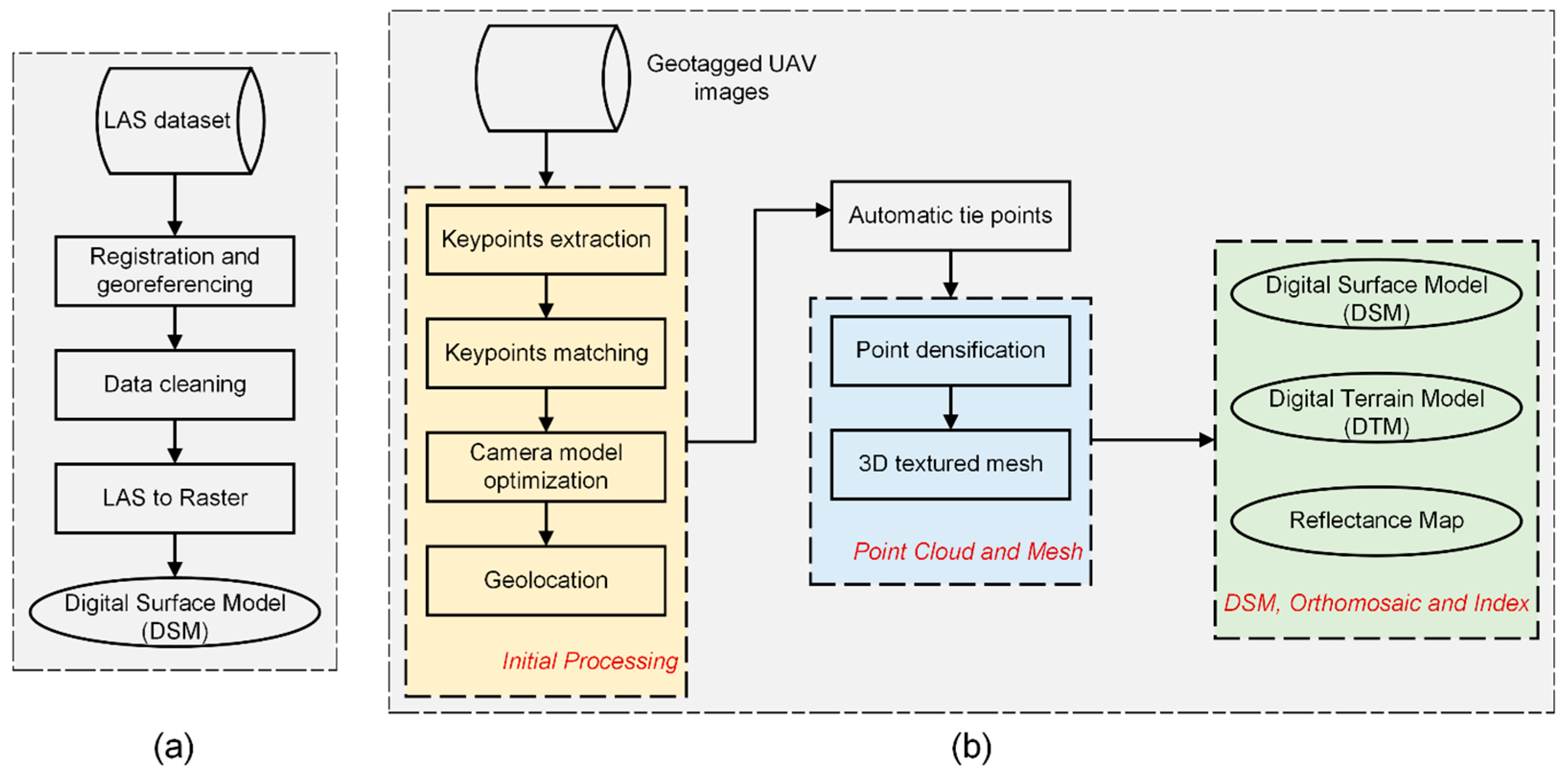
2.4. Data Processing
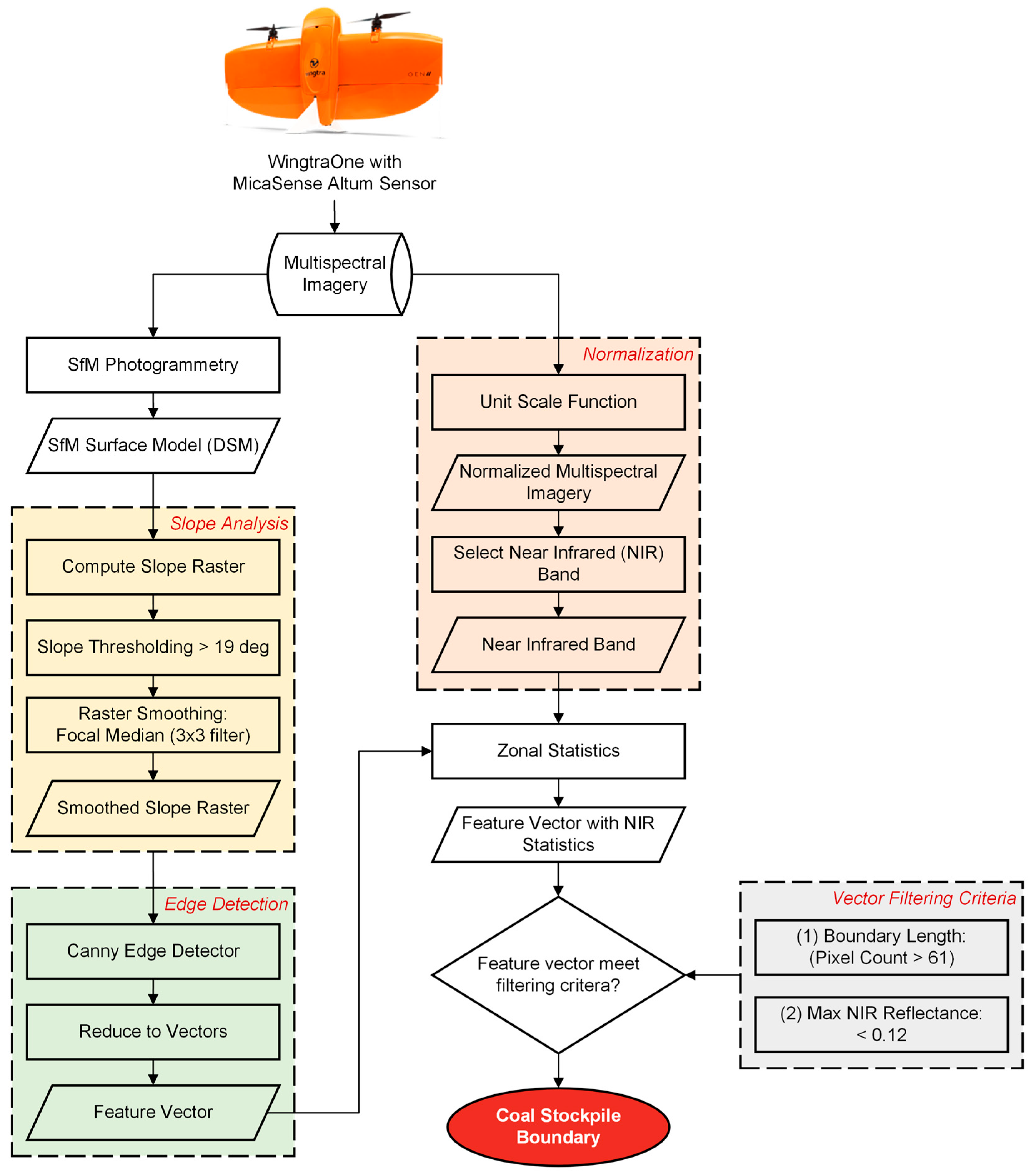
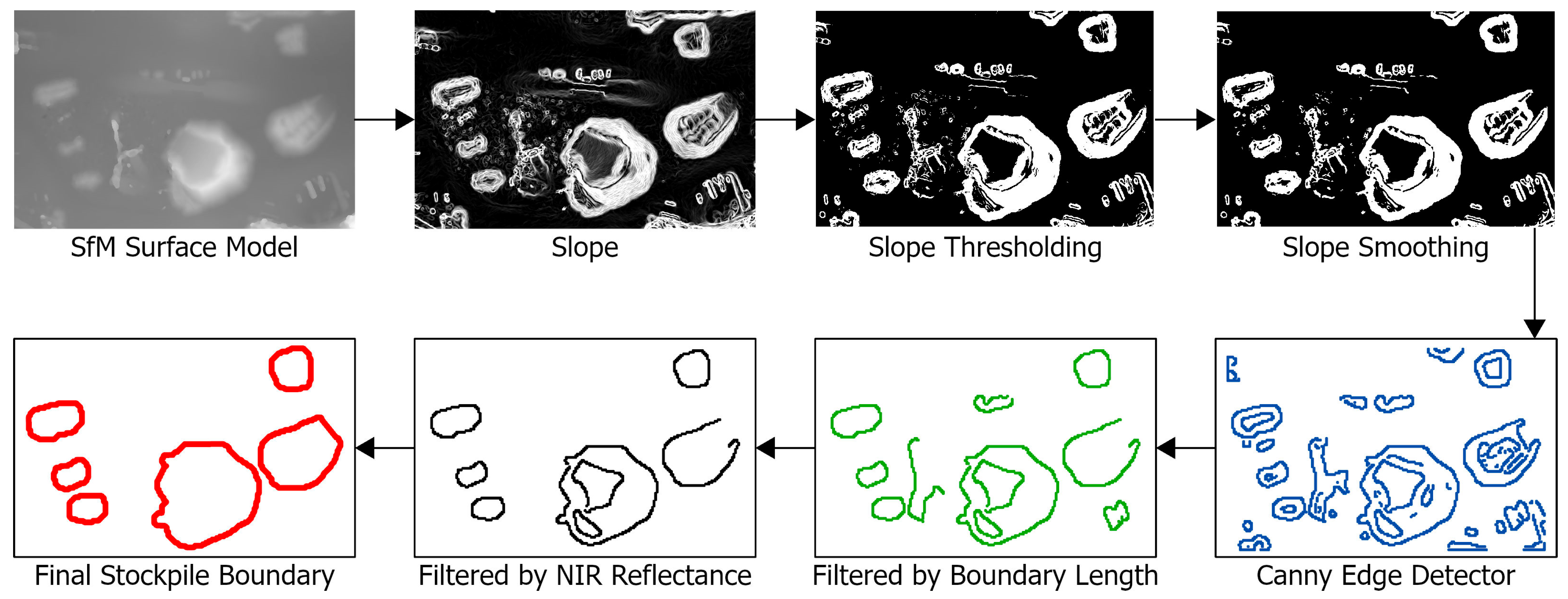
2.5. Stockpile Boundary Delineation
2.6. DSM of Difference (DoD)
2.7. Generating a Representative DTM for Coal Stockpiles Using Kriging Interpolation
2.8. Statistical Analysis
2.9. Evaluation Metrics
3. Results and Discussion
3.1. Stockpile Boundary Delineation
3.2. 3D Representation of Coal Stockpiles
3.3. DSM of Difference (DoD)
3.4. Difference in Terrain Elevation Across Different Approaches
3.5. Relative Accuracy of Volume Estimates
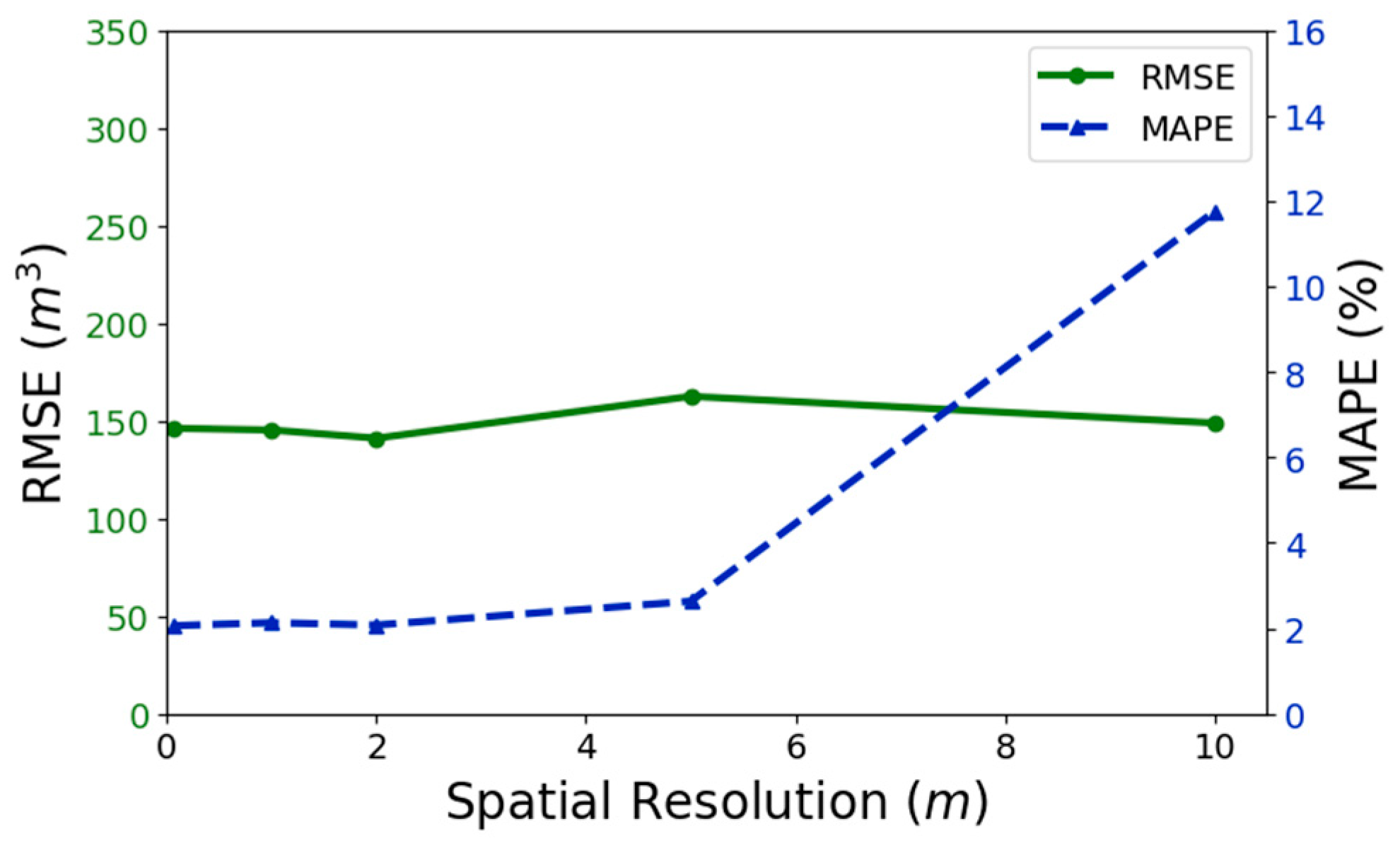
3.6. Effect of Spatial Resolution on Statistical Error Metrics
4. Future Works
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCC | Concordance Correlation Coefficient |
| CORS | Continuously Operating Reference Station |
| DSM | Digital Surface Model |
| DTM | Digital Terrain Model |
| DoD | DSM of Difference |
| FREO | Freeport |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| GCP | Ground Control Point |
| GSD | Ground Sampling Distance |
| IMU | Inertial Measurement Unit |
| IoU | Intersection over Union |
| LiDAR | Light Detection and Ranging |
| MAPE | Mean Absolute Percentage Error |
| NIR | Near-Infrared |
| ODOT | Ohio Department of Transportation |
| PPK | Post-Processed Kinematic |
| RTK | Real-Time Kinematic |
| RMSE | Root Mean Square Error |
| SfM | Structure-from-Motion |
| TLS | Terrestrial Laser Scanning |
| UAS | Unmanned Aerial System |
| VTOL | Vertical Take-off and Landing |
References
- Cao, D.; Zhang, B.; Zhang, X.; Yin, L.; Man, X. Optimization Methods on Dynamic Monitoring of Mineral Reserves for Open Pit Mine Based on UAV Oblique Photogrammetry. Measurement 2023, 207, 112364. [Google Scholar] [CrossRef]
- He, H.; Chen, T.; Zeng, H.; Huang, S. Ground Control Point-Free Unmanned Aerial Vehicle-Based Photogrammetry for Volume Estimation of Stockpiles Carried on Barges. Sensors 2019, 19, 3534. [Google Scholar] [CrossRef]
- Mantey, S.; Aduah, M.S. Comparative Analysis of Stockpile Volume Estimation Using UAV and GPS Techniques. Ghana Min. J. 2021, 21, 1–10. [Google Scholar] [CrossRef]
- Vacca, G. UAV Photogrammetry for Volume Calculations. A Case Study of an Open Sand Quarry. In Computational Science and Its Applications—ICCSA 2022 Workshops; Gervasi, O., Murgante, B., Misra, S., Rocha, A.M.A.C., Garau, C., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2022; Volume 13382, pp. 505–518. ISBN 978-3-031-10591-3. [Google Scholar]
- Liu, J.; Hasheminasab, S.M.; Zhou, T.; Manish, R.; Habib, A. An Image-Aided Sparse Point Cloud Registration Strategy for Managing Stockpiles in Dome Storage Facilities. Remote Sens. 2023, 15, 504. [Google Scholar] [CrossRef]
- Alsayed, A.; Nabawy, M.R.A. Stockpile Volume Estimation in Open and Confined Environments: A Review. Drones 2023, 7, 537. [Google Scholar] [CrossRef]
- Amaglo, W.Y. Volume Calculation Based on LiDAR Data; KTH Royal Institute of Technology: Stockholm, Sweden, 2021. [Google Scholar]
- Aber, J.S.; Marzolff, I.; Ries, J.B. Small-Format Aerial Photography: Principles, Techniques and Geoscience Applications; Elsevier Science: Amsterdam, The Netherlands; London, UK, 2010; ISBN 978-0-444-53260-2. [Google Scholar]
- Saratsis, G.; Xiroudakis, G.; Exadaktylos, G.; Papaconstantinou, A.; Lazos, I. Use of UAV Images in 3D Modelling of Waste Material Stock-Piles in an Abandoned Mixed Sulphide Mine in Mathiatis—Cyprus. Mining 2023, 3, 79–95. [Google Scholar] [CrossRef]
- Rohizan, M.H.; Ibrahim, A.H.; Abidin, C.Z.C.; Ridwan, F.M.; Ishak, R. Application of Photogrammetry Technique for Quarry Stockpile Estimation. IOP Conf. Ser. Earth Environ. Sci. 2021, 920, 012040. [Google Scholar] [CrossRef]
- Yin, H.; Tan, C.; Zhang, W.; Cao, C.; Xu, X.; Wang, J.; Chen, J. Rapid Compaction Monitoring and Quality Control of Embankment Dam Construction Based on UAV Photogrammetry Technology: A Case Study. Remote Sens. 2023, 15, 1083. [Google Scholar] [CrossRef]
- Pourreza, M.; Moradi, F.; Khosravi, M.; Deljouei, A.; Vanderhoof, M.K. GCPs-Free Photogrammetry for Estimating Tree Height and Crown Diameter in Arizona Cypress Plantation Using UAV-Mounted GNSS RTK. Forests 2022, 13, 1905. [Google Scholar] [CrossRef]
- Näsi, R.; Mikkola, H.; Honkavaara, E.; Koivumäki, N.; Oliveira, R.A.; Peltonen-Sainio, P.; Keijälä, N.-S.; Änäkkälä, M.; Arkkola, L.; Alakukku, L. Can Basic Soil Quality Indicators and Topography Explain the Spatial Variability in Agricultural Fields Observed from Drone Orthomosaics? Agronomy 2023, 13, 669. [Google Scholar] [CrossRef]
- Dronova, I.; Kislik, C.; Dinh, Z.; Kelly, M. A Review of Unoccupied Aerial Vehicle Use in Wetland Applications: Emerging Opportunities in Approach, Technology, and Data. Drones 2021, 5, 45. [Google Scholar] [CrossRef]
- Tomaštík, J.; Mokroš, M.; Surový, P.; Grznárová, A.; Merganič, J. UAV RTK/PPK Method—An Optimal Solution for Mapping Inaccessible Forested Areas? Remote Sens. 2019, 11, 721. [Google Scholar] [CrossRef]
- Eker, R.; Alkan, E.; Aydin, A. A Comparative Analysis of UAV-RTK and UAV-PPK Methods in Mapping Different Surface Types. Eur. J. For. Eng. 2021, 7, 12–25. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More; Springer: Wien, Austria; New York, NY, USA, 2008; ISBN 978-3-211-73012-6. [Google Scholar]
- Leandro, R.; Landau, H.; Nitschke, M.; Glocker, M.; Seeger, S.; Chen, X.; Deking, A.; BenTahar, M.; Zhang, F.; Ferguson, K.; et al. RTX Positioning: The Next Generation of Cm-Accurate Real-Time GNSS Positioning. In Proceedings of the 24th International technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 20–23 September 2011; pp. 1460–1475. [Google Scholar]
- Famiglietti, N.A.; Cecere, G.; Grasso, C.; Memmolo, A.; Vicari, A. A Test on the Potential of a Low Cost Unmanned Aerial Vehicle RTK/PPK Solution for Precision Positioning. Sensors 2021, 21, 3882. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, L.; Li, J.; Dai, W.; Lu, W.; Li, M. The Synergistic Effects of GCPs and Camera Calibration Models on UAV-SfM Photogrammetry. Drones 2025, 9, 343. [Google Scholar] [CrossRef]
- Shidiq, I.P.A.; Wibowo, A.; Kusratmoko, E.; Indratmoko, S.; Ardhianto, R.; Prasetyo Nugroho, B. Urban Forest Topographical Mapping Using UAV LIDAR. IOP Conf. Ser. Earth Environ. Sci. 2017, 98, 012034. [Google Scholar] [CrossRef]
- Hu, T.; Sun, X.; Su, Y.; Guan, H.; Sun, Q.; Kelly, M.; Guo, Q. Development and Performance Evaluation of a Very Low-Cost UAV-Lidar System for Forestry Applications. Remote Sens. 2020, 13, 77. [Google Scholar] [CrossRef]
- Elamin, A.; El-Rabbany, A. UAV-Based Multi-Sensor Data Fusion for Urban Land Cover Mapping Using a Deep Convolutional Neural Network. Remote Sens. 2022, 14, 4298. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Cheng, Y.-T.; Zhou, T.; Ravi, R.; Hasheminasab, S.; Flatt, J.; Troy, C.; Habib, A. Evaluation of UAV LiDAR for Mapping Coastal Environments. Remote Sens. 2019, 11, 2893. [Google Scholar] [CrossRef]
- Trepekli, K.; Balstrøm, T.; Friborg, T.; Fog, B.; Allotey, A.N.; Kofie, R.Y.; Møller-Jensen, L. UAV-Borne, LiDAR-Based Elevation Modelling: A Method for Improving Local-Scale Urban Flood Risk Assessment. Nat. Hazards 2022, 113, 423–451. [Google Scholar] [CrossRef]
- Velodyne LiDAR Puck: Real-Time 3D LiDAR Sensor. Available online: https://pdf.directindustry.com/pdf/velodynelidar/vlp-16-datasheets/182407-676097.html (accessed on 12 August 2025).
- MicaSense Altum and DLS 2 Integration Guide. Available online: https://support.micasense.com/hc/article_attachments/360073921173 (accessed on 12 August 2025).
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the Unmanned Aerial Vehicles (UAVs): A Comprehensive Review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry Using UAV-Mounted GNSS RTK: Georeferencing Strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Forte, M.; Neto, P.; Thé, G.; Nogueira, F. Altitude Correction of an UAV Assisted by Point Cloud Registration of LiDAR Scans. In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics, Paris, France, 6–8 July 2021; SCITEPRESS—Science and Technology Publications: Setúbal, Portugal, 2021; pp. 485–492. [Google Scholar]
- Mora, O.E.; Chen, J.; Stoiber, P.; Koppanyi, Z.; Pluta, D.; Josenhans, R.; Okubo, M. Accuracy of Stockpile Estimates Using Low-Cost sUAS Photogrammetry. Int. J. Remote Sens. 2020, 41, 4512–4529. [Google Scholar] [CrossRef]
- Kuinkel, M.S.; Zhang, C.; Liu, P.; Demirkesen, S.; Ksaibati, K. Suitability Study of Using UAVs to Estimate Landfilled Fly Ash Stockpile. Sensors 2023, 23, 1242. [Google Scholar] [CrossRef]
- Ajayi, O.G.; Ajulo, J. Investigating the Applicability of Unmanned Aerial Vehicles (UAV) Photogrammetry for the Estimation of the Volume of Stockpiles. Quaest. Geogr. 2021, 40, 25–38. [Google Scholar] [CrossRef]
- Dhakal, S. Mapping and Volume Estimation of Waste Coal in Abandoned Mine Lands Using Remote Sensing and Geospatial Techniques. Master’s Thesis, The Ohio State University, Columbus, OH, USA, 2024. [Google Scholar]
- Dhakal, S.; Shah, A.; Khanal, S. Monitoring Historical Waste Coal Piles Using Image Classification and Change Detection Algorithms on Satellite Images. Remote Sens. 2025, 17, 3041. [Google Scholar] [CrossRef]
- GEM Wiki. CCU Sexton Strip Mine; Global Energy Monitor (GEM): San Francisco, CA, USA, 2024. [Google Scholar]
- Esri. ArcGIS Pro Version 3.0.0: The World’s Leading Desktop GIS Software; Esri: Redlands, CA, USA, 2024. [Google Scholar]
- Pix4D Mapper Version 4.7.5; The Leading Photogrammetry Software for Professional Drone Mapping; Pix4D: Lausanne, Switzerland, 2024.
- Sharma, M.; Paige, G.B.; Miller, S.N. DEM Development from Ground-Based LiDAR Data: A Method to Remove Non-Surface Objects. Remote Sens. 2010, 2, 2629–2642. [Google Scholar] [CrossRef]
- McIlhagga, W. The Canny Edge Detector Revisited. Int. J. Comput. Vis. 2011, 91, 251–261. [Google Scholar] [CrossRef]
- Lee, K.; Lee, W.H. Earthwork Volume Calculation, 3D Model Generation, and Comparative Evaluation Using Vertical and High-Oblique Images Acquired by Unmanned Aerial Vehicles. Aerospace 2022, 9, 606. [Google Scholar] [CrossRef]
- Wilcoxon, F.; Katti, S.; Wilcox, R.A. Critical Values and Probability Levels for the Wilcoxon Rank Sum Test and the Wilcoxon Signed Rank Test; Selected Tables in Mathematical Statistics; American Cyanamid: Pearl River, NY, USA, 1970; Volume 1. [Google Scholar]
- Lin, L.I.-K. A Concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics 1989, 45, 255. [Google Scholar] [CrossRef]
- Torkan, M.; Janiszewski, M.; Uotinen, L.; Baghbanan, A.; Rinne, M. High-Resolution Photogrammetry to Measure Physical Aperture of Two Separated Rock Fracture Surfaces. J. Rock Mech. Geotech. Eng. 2024, 16, 2922–2934. [Google Scholar] [CrossRef]
- Julge, K.; Ellmann, A.; Köök, R. Unmanned Aerial Vehicle Surveying for Monitoring Road Construction Earthworks. Balt. J. Road Bridge Eng. 2019, 14, 1–17. [Google Scholar] [CrossRef]
- Kim, J.; Lee, Y.; Lee, M.-H.; Hong, S.-Y. A Comparative Study of Machine Learning and Spatial Interpolation Methods for Predicting House Prices. Sustainability 2022, 14, 9056. [Google Scholar] [CrossRef]
- Razas, M.A.; Hassan, A.; Khan, M.U.; Emad, M.Z.; Saki, S.A. A Critical Comparison of Interpolation Techniques for Digital Terrain Modelling in Mining. J. S. Afr. Inst. Min. Metall. 2023, 123, 53–62. [Google Scholar] [CrossRef]
- Alsayed, A.; Bana, F.; Arvin, F.; Quinn, M.K.; Nabawy, M.R.A. Experimental Evaluation of Multi- and Single-Drone Systems with 1D LiDAR Sensors for Stockpile Volume Estimation. Aerospace 2025, 12, 189. [Google Scholar] [CrossRef]
- Alsayed, A.; Nabawy, M.R.A. Indoor Stockpile Reconstruction Using Drone-Borne Actuated Single-Point LiDARs. Drones 2022, 6, 386. [Google Scholar] [CrossRef]
- Tucci, G.; Gebbia, A.; Conti, A.; Fiorini, L.; Lubello, C. Monitoring and Computation of the Volumes of Stockpiles of Bulk Material by Means of UAV Photogrammetric Surveying. Remote Sens. 2019, 11, 1471. [Google Scholar] [CrossRef]
- Rossi, P.; Mancini, F.; Dubbini, M.; Mazzone, F.; Capra, A. Combining Nadir and Oblique UAV Imagery to Reconstruct Quarry Topography: Methodology and Feasibility Analysis. Eur. J. Remote Sens. 2017, 50, 211–221. [Google Scholar] [CrossRef]



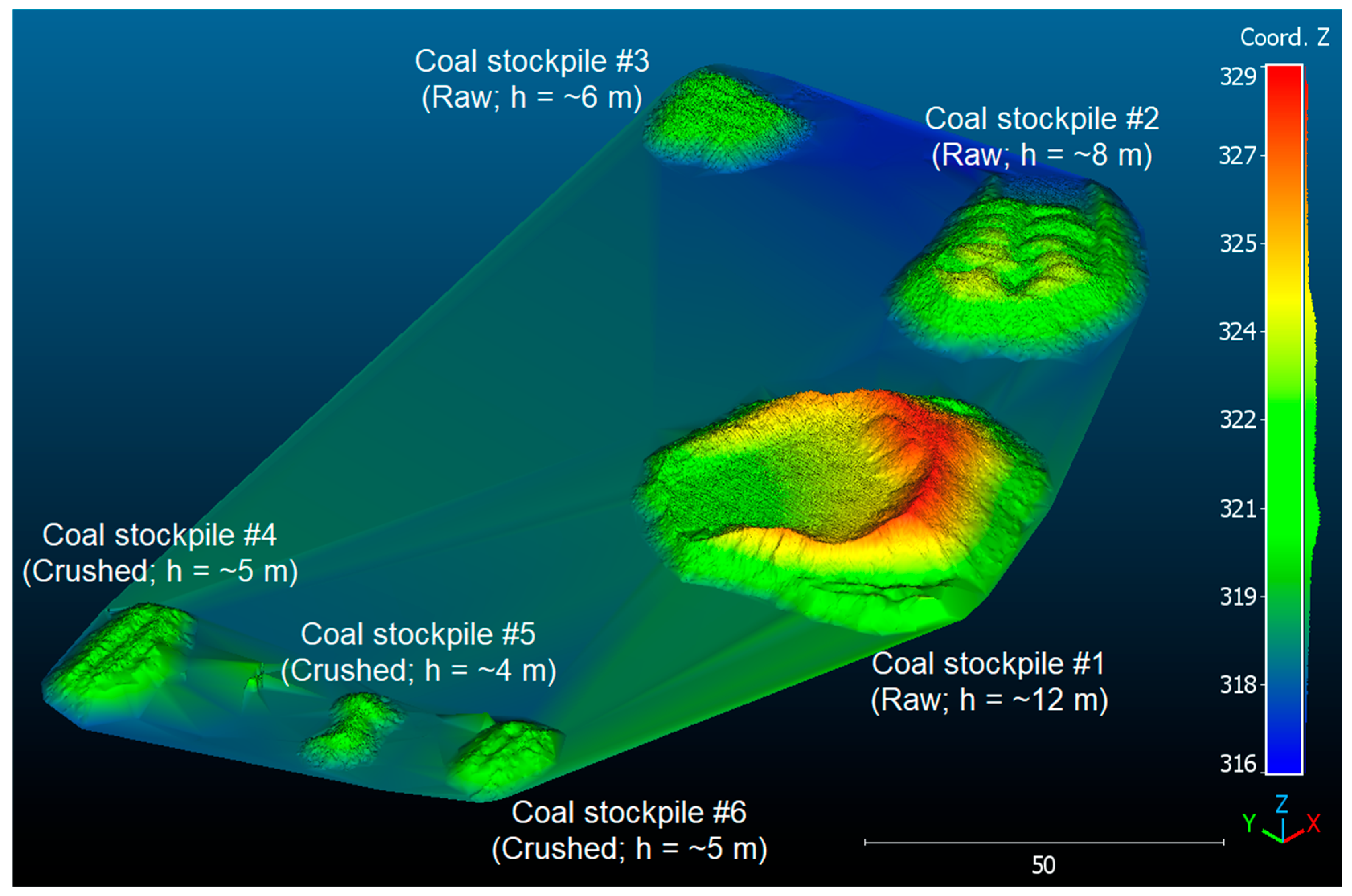


| Stockpile # | Type | Area of Intersection (m2) | Area of Union (m2) | IoU |
|---|---|---|---|---|
| 1 | Raw | 3219.3 | 3436.5 | 0.94 |
| 2 | Raw | 1625.3 | 2084.9 | 0.78 |
| 3 | Raw | 542.2 | 599.1 | 0.91 |
| 4 | Crushed | 621.2 | 817.0 | 0.76 |
| 5 | Crushed | 302.1 | 462.3 | 0.65 |
| 6 | Crushed | 338.1 | 505.9 | 0.67 |
| Stockpile # | Type | Volume (m3) | Difference in Volume (%) | |||
|---|---|---|---|---|---|---|
| LiDAR | SfM–DTM | SfM–intDTM | LiDAR vs. SfM–DTM | LiDAR vs. SfM–intDTM | ||
| 1 | Raw | 12,706.18 | 12,370.68 | 13,062.75 | 2.64 | −2.81 |
| 2 | Raw | 4319.38 | 4299.99 | 4329.78 | 0.45 | −0.24 |
| 3 | Raw | 892.96 | 869.17 | 871.76 | 2.66 | 2.37 |
| 4 | Crushed | 1028.22 | 1131.78 | 1009.41 | −10.07 | 1.83 |
| 5 | Crushed | 267.56 | 330.04 | 261.72 | −23.35 | 2.18 |
| 6 | Crushed | 383.84 | 433.00 | 372.58 | −12.81 | 2.93 |
| Metrics | LiDAR vs. SfM–DTM | LiDAR vs. SfM–intDTM | SfM–DTM vs. SfM–intDTM |
|---|---|---|---|
| CCC | 0.9994 | 0.9995 | 0.9979 |
| R2 | 99.990% | 99.994% | 99.978% |
| RMSE (m3) | 147.51 | 146.18 | 289.58 |
| MAPE (%) | 8.66% | 2.06% | 8.68% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhakal, S.; Manandhar, A.; Shah, A.; Khanal, S. Integrating UAS Remote Sensing and Edge Detection for Accurate Coal Stockpile Volume Estimation. Remote Sens. 2025, 17, 3136. https://doi.org/10.3390/rs17183136
Dhakal S, Manandhar A, Shah A, Khanal S. Integrating UAS Remote Sensing and Edge Detection for Accurate Coal Stockpile Volume Estimation. Remote Sensing. 2025; 17(18):3136. https://doi.org/10.3390/rs17183136
Chicago/Turabian StyleDhakal, Sandeep, Ashish Manandhar, Ajay Shah, and Sami Khanal. 2025. "Integrating UAS Remote Sensing and Edge Detection for Accurate Coal Stockpile Volume Estimation" Remote Sensing 17, no. 18: 3136. https://doi.org/10.3390/rs17183136
APA StyleDhakal, S., Manandhar, A., Shah, A., & Khanal, S. (2025). Integrating UAS Remote Sensing and Edge Detection for Accurate Coal Stockpile Volume Estimation. Remote Sensing, 17(18), 3136. https://doi.org/10.3390/rs17183136





