Abstract
Contextual features play a critical role in geospatial object detection by characterizing the surrounding environment of objects. In existing deep learning-based studies of 3D point cloud classification and segmentation, these features have been represented through geometric descriptors, semantic context (i.e., modeled by an attention-based mechanism), global-level context (i.e., through global aggregation), and textural representation (e.g., RGB, intensity, and other attributes). Even though contextual features have been widely explored, spatial contextual features that explicitly capture spatial autocorrelation and neighborhood dependency have received limited attention in object detection tasks. This gap is particularly relevant in the context of GeoAI, which calls for mutual benefits between artificial intelligence and geographic information science. To bridge this gap, this study presents a spatial autocorrelation encoder, namely SA-Encoder, designed to inform 3D geospatial object detection by capturing spatial autocorrelation representation as types of spatial contextual features. The study investigated the effectiveness of such spatial contextual features by estimating the performance of a model trained on them alone. The results suggested that the derived spatial autocorrelation information can help adequately identify some large objects in an urban-rural scene, such as buildings, terrain, and large trees. We further investigated how the spatial autocorrelation encoder can inform model performance in a geospatial object detection task. The results demonstrated significant improvements in detection accuracy across varied urban and rural environments when we compared the results to models without considering spatial autocorrelation as an ablation experiment. Moreover, the approach also outperformed the models trained by explicitly feeding traditional spatial autocorrelation measures (i.e., Matheron’s semivariance). This study showcases the advantage of the adaptiveness of the neural network-based encoder in deriving a spatial autocorrelation representation. This advancement bridges the gap between theoretical geospatial concepts and practical AI applications. Consequently, this study demonstrates the potential of integrating geographic theories with deep learning technologies to address challenges in 3D object detection, paving the way for further innovations in this field.
1. Introduction
Three-dimensional geospatial object detection plays a critical role in building accurate 3D models for state-of-the-art applications of geographic information science (GIScience). These applications span across digital earth [1,2], twin cities [3,4,5], and Building Information Modeling (BIM) [6,7,8], where 3D representations are important not only for visualizing but also for analysis and management of geospatial objects. In the domain of GIScience, the past decades have witnessed a remarkable evolution in 3D techniques, ranging from the development of data acquisition technologies (e.g., RGB-D camera and LiDAR (Light Detection and Ranging)) to the evolution of data processing and analyzing supported by computing technologies. Early studies naïvely represented 3D spatial objects, essentially reflecting the spatial location of the object in a 3D space. For example, objects were represented by spatial points in a 3D network [9] to describe the spatial relationship among them. Moreover, the representations of buildings were simply derived from blueprints [10,11,12] without their as-built status. However, nowadays, advancements in 3D techniques have made it possible to generate up-to-date and as-is representations of diverse geospatial objects, laying the foundation for the development of 3D geographical information systems (GIS) [2,13,14]. Therefore, there is a demand for accuracy and efficiency for 3D geospatial object detection.
An illustrative example of this is Tree Folio NYC (a digital twin of New York City’s urban canopy. Link: https://labs.aap.cornell.edu/daslab/projects/treefolio, accessed on 28 August 2025), which is a digital twin of New York City (NYC) Urban Canopy produced by the Design Across Scales Lab at Cornell University. It is a web-based GIS application designed to provide practitioners and stakeholders with a user-friendly platform for querying, analyzing, and visualizing the 3D point cloud representations of individual trees in NYC. The development of such applications requires the detection and extraction of trees from 3D point clouds. Due to the number of trees in NYC (approximately 8 million), it would become incredibly time-consuming and labor-intensive work if performed manually.
Three-dimensional deep learning algorithms can be potentially used to address this challenge. Deep learning for object detection in the 3D context has attracted unprecedented attention since the first deep neural network architecture, PointNet [15], which is a deep neural network designed to directly consume point cloud as input. PointNet demonstrates that permutation- and rotation-invariant design is the key to directly absorbing point clouds, shaping the development of neural network architectures in recent years. The variants of this architecture have been continuously serving as a key part in many cutting-edge architectures in recent studies [16,17,18,19]. Parallel to these advancements, the emergence of GeoAI—a synthesis of GIScience and Artificial Intelligence (AI)—marks a pivotal shift toward not only using cutting-edge AI methodologies to inform geospatial studies but also to enrich AI with geospatial insights (e.g., spatial autocorrelation and spatial heterogeneity) [20,21]. Responding to the call from Goodchild and Li [20,21] for mutual benefits between AI and GIScience, our study focuses on embedding a fundamental geographic principle—spatial autocorrelation, a measure of how attribute values correlated across space—into model design. Spatial autocorrelation is also known as spatial dependency, formally described by Tobler’s First Law of Geography and operationalized through statistical measures such as Moran’s I and semivariogram analysis. Traditional geostatistical methods quantify the similarity between observations as a function of their spatial separation, capturing both spatial continuity within features and spatial discontinuity across feature boundaries. Spatial autocorrelation is particularly relevant for large, spatially coherent geospatial objects (e.g., buildings, terrain, and high vegetation) where the spatial arrangement of attributes can be highly informative. Semivariance, one traditional spatial autocorrelation measurement, can be essentially quantified by an approach that evaluates pairwise differences in a neighborhood, such as using Matheron’s estimator [22] and Dowd’s estimator [23]. Chen [24] conducted a systematic investigation and proved the effectiveness of semivariance as a representation of spatial context in informing 3D deep learning, serving as an early effort to integrate geospatial statistics into related applications in the field of 3D object detection. However, it not only requires computationally intensive pre-calculation of semivariance but also relies on domain knowledge for the configuration of the estimation, hindering its integration into contemporary 3D object detection tasks. Therefore, we propose a learnt spatial autocorrelation representation, namely SA-Encoder, in this study. The encoder inherits this theoretical foundation by modeling local spatial dependency through lag-ordered pairwise differences between neighboring points. Rather than pre-computing semivariance with fixed parameters, the encoder embeds this process within a learnable architecture, enabling adaptive extraction of spatial autocorrelation patterns that are optimal for the specific dataset. In this way, the encoder extends a fundamental geospatial principle into a deep learning framework, integrating spatial autocorrelation theory for 3D object detection.
The proposed encoder not only enhances the capability of GIS in handling and interpreting 3D geospatial data but also paves the way for further investigation of geospatial insights that benefit AI models. The implications of this study are significant for various applications, including environmental monitoring, disaster management, and urban studies, where quick and accurate interpretation of spatial data is crucial. The contributions of this study are highlighted as follows:
- Enhanced geospatial object detection by spatial autocorrelation: The study underscores the effectiveness of spatial autocorrelation features for identifying diverse geospatial objects, embracing geographic theories, statistical methods, and deep learning advancements. It demonstrates the pivotal role of spatial theories in enriching AI technologies for geospatial object detection from complex environments.
- Automated spatial autocorrelation representation extraction: By developing SA-Encoder, which effectively extracts spatially explicit contextual representations, this research showcases an innovative integration of AI in geospatial analysis. This approach simplifies the application of traditional semivariance estimations, offering a streamlined and dataset-specific learning mechanism that informs the existing deep neural network for geospatial object detection.
The remainder of this article is organized as follows: Section 2 reviews the related literature with a focus on contextual features in object detection. Section 3 explains the proposed SA-Encoder for extracting the representation of spatial autocorrelation features. Section 4 demonstrates the 3D point cloud dataset used as an exemplary study case in urban and rural areas and outlines our experiments designed to investigate the effectiveness of the derived spatial autocorrelation features in informing model predictions. Moreover, the second experiment serves as an ablation study to verify the usefulness of the proposed neural network-based encoder. Section 5 reports the results of the experiments followed by discussion. Finally, the conclusions are presented in Section 6.
2. Literature Review
Spatial context was identified as an essential feature of imagery classification (a.k.a., imagery segmentation in the domain of computer vision nowadays) in traditional remotely sensed imagery [25,26,27]. Spatial autocorrelation, represented by a semivariogram and semivariance, is an important measure to quantify this phenomenon and has been used for imagery classification in the domain of remote sensing [26,28,29].
Spatial context is also important to the task of 3D object detection [30,31,32]. Spatial context can refer to various aspects in existing studies, such as geometry, texture, or any aggregated local and global features based on spatial neighbors. For example, Wan et al. developed a geometry-aware attention point network by using a weighted graph to represent local geometry [33]. Chen et al. demonstrated the importance of textual features by feeding semivariance-based spatial autocorrelation features [24]. Wang et al. represented local and global context by adopting neighborhood label aggregation and a global context learning module [34]. To improve the performance of deep learning architectures on 3D datasets, many studies have focused on using different feature extraction modules to improve deep learning models. We listed some of them within the scope of geospatial insights enhancing AI models. Wu et al. [17] presented an advanced method for 3D object detection in point clouds, improving upon Frustum PointNet [35] by incorporating local neighborhood information into point feature computation. This approach enhances the representation of each point through the neighboring features. The novel local correlation-aware embedding operation leads to superior detection performance on the KITTI dataset compared to the F-PointNet baseline. This method emphasizes the importance of local spatial relationships for 3D object detection in deep learning frameworks. Klemmer et al. [36] added a positional encoder using Moran’s I as an auxiliary task to enhance a graph neural network in interpolation tasks. Fan et al. [37] designed a module based on the distance between points to capture its local spatial context to inform object detection. Engelmann et al. [32] proposed a neural network to incorporate larger-scale spatial context in order to improve model performance by considering the interrelationship among subdivisions (i.e., blocks) of the point cloud. Chu et al. [38] leveraged local contextual information to enhance 3D point cloud completion tasks, with a focus on those occluded points during data collection. Li et al. [39] developed a full-level decoder aggregation module to capture long-range dependencies for better segmentation performance.
While most of the endeavors contribute to improving the model’s capability to derive discriminative features from spatial information, information from other channels seems to be overlooked [24]. Current LiDAR techniques often capture more information rather than only the position, such as intensity and RGB, while some special sensors can further collect other spectrum information, such as near infrared for thermal studies. Even though some studies integrate RGB as input [15,40,41], colors or textures are not explicitly focused on and limited considerations are taken in utilizing them. Chen et al. [24] pioneered a study with a focus on making more use of RGB information by explicitly incorporating semivariance variables to improve model performance, which are estimated based on the variation of observed color information and corresponding spatial lag distance. Viswanath et al. [42] claimed the importance of intensity or reflectivity in 3D point cloud segmentation and their results showed a significant increase in model performance on different large-scale datasets. By early 2025, contextual information suggested by other channels is still an emerging topic in a wide range of studies [38,43]. Extending the scope of Chen et al. [24], we investigate not only the spatial structure of point clouds but also the spatial variation of non-spatial attributes. Color or spectral information as well as the texture embedded within it is important for humans to recognize different objects [44,45]. Their importance becomes even more pronounced in applications where biophysical characteristics must be considered, for example, in species identification using multispectral sensors [46]. Accordingly, we emphasize the value of color and related attributes in geospatial object detection. We therefore call for broader exploration of non-spatial modalities—such as intensity, reflectivity, color, and spectral bands—as complementary sources of information to improve model performance. In doing so, we are contributing to an emerging shift of the current focus in 3D deep learning research from a reliance on spatial information toward a more balanced perspective that actively leverages multi-channel inputs.
3. Methodology
We demonstrate the role of the proposed SA-Encoder in a 3D object detection task using a deep learning architecture in Figure 1. The rest of this section explains the details of SA-Encoder and the corresponding rationale behind the design. SA-Encoder consists of two main modules, where the first module extracts lag-ordered pairwise differences and the other module is an encoder that extracts a robust representation of spatial autocorrelation. Section 3.1 provides an example of how lag-ordered pairwise differences are derived for one point, which serves as the input for the encoder described in Section 3.2. Since this encoder is designed to inform existing deep learning models for 3D object detection, we delineate our thoughts regarding the compatibility of how this encoder can integrated into an existing model. We provide practical examples in the section on experiments.
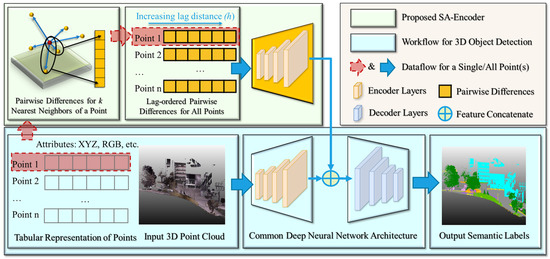
Figure 1.
Overall framework of 3D object detection with a common deep neural network. The role of the proposed spatial autocorrelation encoder (i.e., SA-Encoder) is to inform model performance by explicitly capturing the local spatial autocorrelation as a type of spatial contextual feature.
3.1. Spatial Autocorrelation and Lag-Ordered Pairwise Differences
A semivariogram is a measure of the spatial autocorrelation of a geographic variable. An experimental semivariogram can be represented by a curve consisting of a series of semivariances, , in a lag distance h, where the formula of Matheron’s semivariance [22] can be represented by Equations (1) and (2):
where Z(xi) is the observed value at location xi and d is the difference between observed values at xi and xi+h. In the context of a 3D LiDAR point cloud, Z(xi) can represent an observed value at a point, such as a color channel value (e.g., RGB values), reflectance at a specific band (e.g., near infrared), and intensity.
In this study, we use lag-ordered pairwise differences between a point and its neighbors as a representation for spatial autocorrelation-based context. We demonstrate the way to derive lag-ordered pairwise differences using one point as an example in Figure 2. Let OPD(i,k) represent a set of lag-ordered pairwise differences for a point at location xi and its k nearest neighbors:
where Δi,j is the absolute value of the pairwise differences of xi and a neighbor xj. Δi,j values are sorted ascendingly such that the lag distance (h) between xi and xj, :
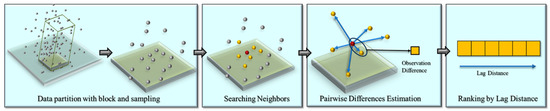
Figure 2.
Illustration of deriving lag-ordered pairwise differences for a single point and its neighbors. Data partitioning with blocks and sampling are the steps for preprocessing training data for deep learning-based 3D point cloud classification to regularize the input. The set of differences are sorted ascendingly by lag distance from nearby to distant pairs.
Data partitioning and subsampling are two essential steps in the preprocessing steps of cutting-edge 3D deep learning methods. This is due to considerations related to computing resources and the nature of neural networks that the input minibatch needs to be regularized [15]. The point cloud datasets directly collected by sensors such as LiDAR instruments commonly include millions of points, with the dataset often at a gigabyte level in size, which is too large to be efficiently or feasibly fed to the CPU and/or GPU [47]. On the other hand, neural networks require structured input, but the unstructured nature of 3D point clouds does not satisfy this requirement. Therefore, we have to perform data partitioning and subsampling to prepare structured and memory-manageable datasets for deep neural networks. These two steps are demonstrated as the first two steps in Figure 2. Data partitioning is implemented by using a particular size of blocks to subtract a subset from the original point cloud. Furthermore, a sampling method is conducted to sample from the subset to an anticipated number. Considering the unevenly distributed nature of 3D point clouds, this step is often performed by sampling with replacement. This is to overcome the case that the number of points within the subset does not reach the expected number of points per block.
Defining a neighborhood around a point is a prerequisite to compute pairwise differences. Due to the unstructured nature of a 3D point cloud, it is not feasible to use a fixed distance to identify the neighbors. The number of neighbors within a certain distance can vary across different points. In an extreme scenario, one point in point-sparse areas may not find a neighbor within a given distance. Therefore, it is essential to use the k nearest neighbor to identify the neighborhood. This idea is supported by many existing studies, such as PointNet++ [40], PointNext [19], and ConvPoint [41], using the kNN approach. kNN is thus adopted in this study to identify the neighbors of a point. One argument that is often associated with kNN is that the local neighborhood captured by kNN varies its size for different points, which may lead to inconsistent scales. We are aware of this difficulty brought by kNN that scales as well as features might be inconsistent, but this challenge can be mitigated through random sampling, as suggested by Klemmer et al. [36]. Additionally, Boulch [41] suggested that randomly sampling points to represent the same object within the same scene during the training process is a way to mitigate such inconsistencies.
We use tree searching provided by SciPy (https://scipy.org/) to implement kNN, which is more efficient than calculating all pair distances. Once the k nearest neighbors are identified, the pairwise differences are calculated between the center point (key point) and its neighbors. In the traditional calculation of semivariance, pairwise differences not only consider pairs between the key point and its neighbors but also all other pairs within the neighborhood. Therefore, the total number of pair differences is n×(n-1). We chose to use the former design because it was not only simpler in computational complexity but also powerful in terms of spatial autocorrelation representation in our preliminary experiments. Finally, we order the k nearest neighbors by their lag distances away from the key points, using this as a representation of initial context features of a point. The representation sorted by distance proved to be effective in graph-based geospatial object detection [33], while our study uses pairwise differences rather than the value of the point to represent its spatial autocorrelation. Subsequently, we applied this approach to all points in the block to prepare a dataset. We chose 16 as the k value to identify the nearest neighbor in this study, referring to the empirical setting from previous studies when aggregating features from neighbors [37,41].
3.2. Architecture Design of the Spatial Autocorrelation Encoder
Inspired by Chen et al. [24], who explicitly fed semivariance as a contextual feature for object detection, we aimed to automate the estimation process and derive dataset-dependent contextual embeddings by using a spatial autocorrelation encoder (an encoder is a module from a neural network that extracts features and generates a representation of input data; see [36] as an example) (see Figure 3). One important requirement for the design of the neural network architecture for 3D deep learning is that the derived representation of a point cloud should be permutation invariant to the original input [15]. PointNet uses max pooling as a symmetric function to make the output global signatures invariant in terms of permutation. ConvPoint [41] adopted a continuous convolution operation to ensure the convoluted features are permutation invariant to the input point cloud. The spatial dependency embeddings extracted by the proposed encoder are naturally ordered because the input unordered point and its neighbors to SA-Encoder will be resorted based on the lag distance.
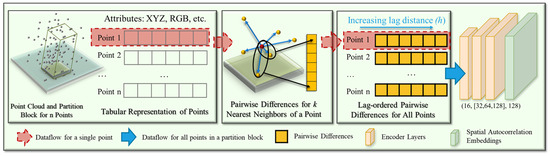
Figure 3.
Proposed spatial autocorrelation encoder for spatial autocorrelation feature extraction using deep learning. The multi-layer perceptron shares weights along the rows, which is equivalent to a 1-dimensional convolutional layer (see examples in [15,40]). The numbers in parenthesis are the number of input channels, the number of neurons in hidden layers, and the number of output channels.
Inspired by the design of shared weights in PointNet due to the tabular representation of a point cloud, we use a shared weights MLP as the encoder for lag-ordered pairwise differences, as shown in Figure 1, which has a similar structure as the tabular representation of the original point cloud. The chosen three-layer configuration [32] with ReLU activation functions follows a progressively increasing dimensionality to enable hierarchical feature abstraction. The first layer extracts low-level representations of pairwise differences, the second layer captures higher-order interactions, and the third layer provides a sufficiently expressive latent representation for downstream tasks. This gradual expansion is consistent with prior practice in point cloud learning (e.g., PointNet and its variants), where deeper layers with larger hidden dimensions are used to capture richer structural information. For activation functions, we selected ReLU, which is widely used in point cloud and deep learning models due to its computational simplicity, stability during optimization, and ability to mitigate vanishing gradient issues.
We also explored alternative MLP depths and hidden dimensions, but we found that a simple [32] configuration with ReLU activations offered the adequate balance between accuracy and efficiency, where deeper or wider networks increased computational costs without significant accuracy gains. Therefore, we selected this configuration as both empirically effective and theoretically consistent with established architectures in point cloud representation learning.
3.3. Feature Grouping to Embed the Encoder in a Neural Network Architecture
In a deep neural network, each feature extraction layer can extract the features from the previous layer (either input or hidden layers). In such a way, high-level features (from subsequent layers) can be eventually extracted, while the final abstract features should be adequately invariant to most local changes from early layers (e.g., input layer). In our design, we attempt to extract such high-level embedding features from the lag-ordered pairwise differences within a neighborhood and use these features along with embeddings from spatial and color information for the final prediction. The k nearest neighbors are identified for each point, and pairwise differences are estimated based on the values of the neighbors. The lag-ordered pairwise differences are fed into the spatial autocorrelation encoder (see Figure 3).
Aggregating local features to a larger scale (up to global scale, i.e., the entire block of a point cloud) can effectively improve model performance. By incorporating the spatial autocorrelation encoder module, we can concatenate the spatial dependency embeddings with other features in a layer of the neural network. There are three types [40] of grouping approaches (three settings of framework): single-scale point grouping (SSG), multi-scale point grouping (MSG), and multi-resolution point grouping (MRG). SSG is used to extract features in only one scale by layers of neural networks and only uses the final feature map for classification. MRG is extremely computationally expensive [40], in which larger-scale features are derived based on features at a smaller scale. MSG is a simple but effective approach to group layers at different scales, similar to the idea of skip connections [48]. The final features of points combine features of different scales, where features for each scale can be independently derived. Grouping approaches can also help to mitigate the impact of uneven distribution of point clouds. It is claimed in ref. [32] that MSG is a little higher than SSG in terms of accuracy. Therefore, we followed an MSG approach to group the features. We concatenate the local contextual features with the global and point-wise local features (see Section 4 Experiment 2 for details).
It is important to note that the MSG strategy in this study is not part of the spatial autocorrelation encoder itself. Rather, MSG describes how the output from the encoder is integrated into the main deep neural network for 3D object detection. In this implementation, PointNet serves as the main neural network architecture, which produces both single-point embedding and global feature embedding. The spatial autocorrelation encoder operates in parallel, generating spatial autocorrelation-based local contextual embeddings for each point based on lag-ordered pairwise differences. These local contextual embeddings are then concatenated with the point-wise features and the global features from PointNet. This concatenation across different feature scales (point-level, local-context level, and global-scene level) constitutes the MSG approach in the framework. By integrating the encoder-derived local context with the hierarchical features of PointNet, the model benefits from spatial autocorrelation features captured by the encoder and the spatial hierarchies learned by the main network, thereby improving the robustness of model performance in complex scenes.
4. Experiments
We designed two experiments, where one investigated the capability of SA-Encoder itself for 3D geospatial object detection, and the other examined how SA-Encoder can inform a common deep learning framework (PointNet is used as an example) in this task. The experiments were operated on a large-scale 3D point cloud dataset with urban and rural scenes specified in Section 4.1. The design of the experiments is detailed in Section 4.2.
4.1. Dataset
Semantic3D, introduced by Hackel et al. [49], stands as a substantial and diverse dataset specifically tailored for outdoor scene analysis. We selected this dataset because its context is close to GIS applications such as digital twins of cities, where it can serve as the original data for 3D modeling geospatial objects such as buildings, trees, traffic lights, and road surfaces. The Semantic3D dataset offers a detailed and complex dataset with 15 scenes, ranging from urban to rural. It covers a wide range of eight semantic categories, including man-made and natural terrains, high and low vegetation, structures such as buildings and hardscapes (e.g., road lights and fencing), scanning artefacts (e.g., dynamic noise during scanning), and vehicles (See Figure 4 for detail).
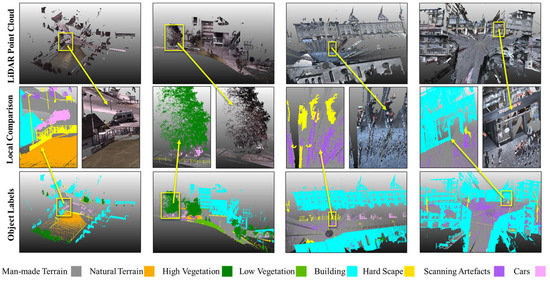
Figure 4.
Illustration of Semantic3D benchmark dataset for urban and rural areas. The first row is the raw LiDAR point clouds with RGB color. The last row shows the labels with discriminative colors for the scenes accordingly. The middle row shows a zoomed-in scope of the scenes with LiDAR point clouds and labels.
As we are moving toward the concept of twin cities, where urban environments are enriched with sensors and technology for better management and planning, the need for accurate and efficient processing of 3D spatial data becomes increasingly critical [1,4]. The ability to accurately segment and interpret these data can inform various aspects of smart city planning, including infrastructure development, environmental monitoring, and emergency response strategies [4,7,9,10,50,51]. The Semantic3D benchmark serves as a bridge between academic research and real-world applications. It provides common ground for researchers to test and compare their methodologies, fostering an environment of collaboration and continuous improvement. This is particularly important in fast-evolving fields such as GIS, where the gap between theoretical research and practical application needs to be constantly narrowed.
In our methodology, we chose nine of these scenes for our training dataset, selected in terms of the diversity of the scenes (e.g., urban and rural). The remaining six scenes were used for validation to examine the generalization capability of our model. For preprocessing, we adopted an 8 m block size for dataset partitioning, aligning with the recommendations of Boulch [41], and targeted a density of 4096 points per block. A block size of 8 m indicates that the dataset is divided by an 8 m grid, where each block covers an area of 8 m by 8 m. This setting is a good rule of thumb for a large-scale outdoor dataset, which is also supported in ref. [52]. This segmentation facilitates the handling and analysis of large datasets by breaking them down into more manageable units, allowing for detailed processing and analysis of each segment while maintaining the structural nature of spatial data. To maintain the quality of lag-ordered pairwise difference estimation, blocks containing fewer than 128 unique points were excluded. This approach addressed the issue of duplicated points in oversampled blocks by prioritizing unique point locations, ensuring that our model input was not skewed by artificial data replication. For example, when estimating lag-ordered pairwise differences, only unique points were taken into consideration. Otherwise, oversampled points could count toward k nearest neighbors, which could lead to a weak representation of spatial relationships within the dataset for accurate geospatial object detection.
There are two main challenges in the dataset, uneven point distribution and a long tail problem. The points within these scenes are not uniformly distributed; instead, they exhibit an extremely uneven spatial distribution owing to the nature of LiDAR data. This unevenness poses a unique challenge as it requires algorithms to be highly adaptable and sensitive to a wide variety of spatial contexts and densities. Furthermore, the classes exhibit extremely uneven distribution, known as a long tail problem. As suggested in Figure 5, the first four largest classes (i.e., buildings, man-made terrain, high vegetation, and natural terrain) represent approximately 90% of the whole dataset. In particular, the building class is approximately 45% of the points in the entire dataset. The remaining four classes, hard scape, low vegetation, cars, and scanning artefacts only represent <10% of the dataset. The ability to adequately represent non-uniform point cloud data is essential for developing sophisticated 3D deep learning models that can accurately interpret and interact with complex real-world environments. The Semantic3D dataset, therefore, serves as an invaluable resource for advancing research and development in 3D scene analysis and understanding.
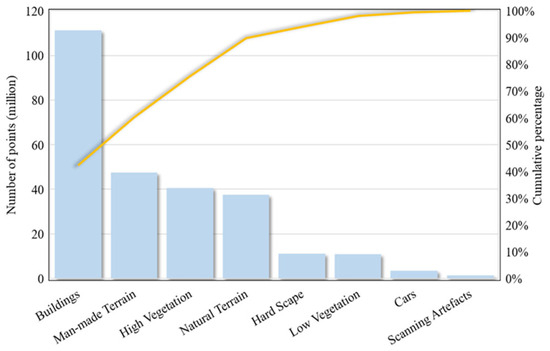
Figure 5.
Distribution of different classes in the Semantic3D dataset. The yellow line shows the cumulative percentage. The classes are imbalanced in terms of the number of points. A long tail problem can be observed where buildings, terrains, and high vegetation are dominant classes, and cars and scanning artefacts are minor classes.
4.2. Experiment Design
For the first experiment, we only used SA-Encoder following a pooling layer and a classification head (see Figure 6). We used the classification head of PointNet here not only because it is concise and powerful for deriving good representations [53] but also because of its compatibility to handle any type of input features. Cutting-edge architectures have a more sophisticated design, requiring an explicit feed of spatial information. For example, the neural network architecture designed in [37] requires explicit spatial information as input. In this case, we would not be able to explicitly examine the importance of the spatial contextual features as well as the effectiveness of SA-Encoder for geospatial object detection.
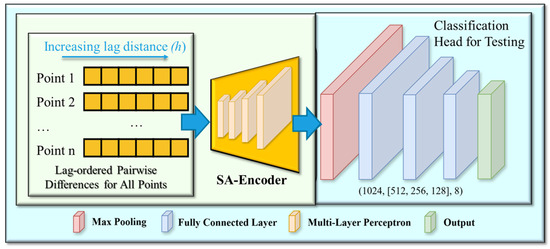
Figure 6.
Framework adopted in Experiment 1 to examine the effectiveness of SA-Encoder, consisting of the encoder, a pooling layer, and a classification head from PointNet. The multi-layer perceptron shares weights along the rows, which is equivalent to a 1-dimensional convolutional layer (see examples in [15,40]). The numbers in parenthesis are the number of input channels, the number of neurons in hidden layers, and the number of output channels.
The other experiment aimed to assess the effectiveness of the designed encoder in benefiting the 3D deep learning in terms of object detection (see Figure 7). In addition, we conducted a comparative analysis between our results and those from Chen et al. [24], who used a combination of spatial information, color information, and/or contextual information.
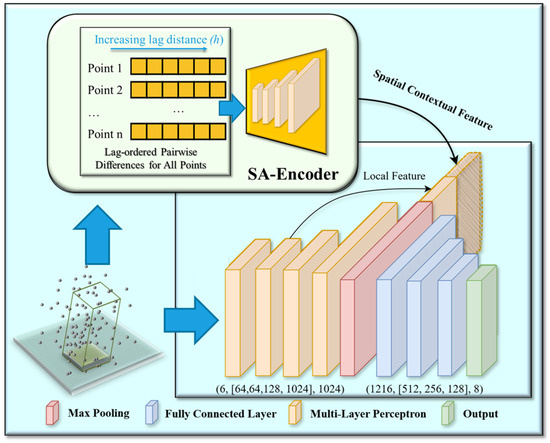
Figure 7.
Demonstration of framework adopted in Experiment 2, where SA-Encoder is embedded in the PointNet framework so that the model performance can be compared with the study [24] using the same architecture shown at bottom without the proposed encoder. The multi-layer perceptron shared weights along the rows, which is equivalent to a 1-dimensional convolutional layer (see examples in [15,40]). The numbers in parenthesis are the number of input channels, the number of neurons in hidden layers, and # output channels.
We conducted model training and validation for each treatment across 10 repetitions to mitigate uncertainties due to the stochastic nature of the training process, where the number was matched with that used in ref. [24] to make the results comparable. In this study, Intersection over Union (IoU) was used to measure model performance for each class. The mean Intersection over Union (mIoU), and Overall Accuracy (OA) were adopted to measure model performance on this dataset, as in ref. [24]. Consequently, we summarized the average performance measurements over the 10 repetitions. Furthermore, a one-tailed t-test was applied to examine if their mean values were significantly different. By employing the systematic approach, this experiment aimed to offer an in-depth understanding of the effectiveness of the module to inform 3D deep learning. The formulas of the measurements are given as follows:
where i indicate a single class, TP is True Positive (a.k.a., a hit), FP is False Positive (a.k.a., a false alarm), and FN is False Negative (a.k.a., a miss).
5. Results and Discussion
5.1. Investigating the Effectiveness of Lag-Ordered Pairwise Differences
Experiment 1 investigated the effectiveness of SA-Encoder for geospatial object detection. The measures are reported in Table 1 and a demonstration of the results is shown in Figure 8. It is interesting to see that the overall accuracy can achieve 63% while the input data are only lag-ordered pairwise differences without any explicit spatial locations or RGB information, which supports the moderate capability of such features in identifying geospatial objects. The results particularly suggest adequate performance for identifying large objects, such as buildings and high vegetation. This performance is especially visible on selected scenes, as shown in Figure 8.

Table 1.
Performance results for Experiment 1 averaged across repetitions.
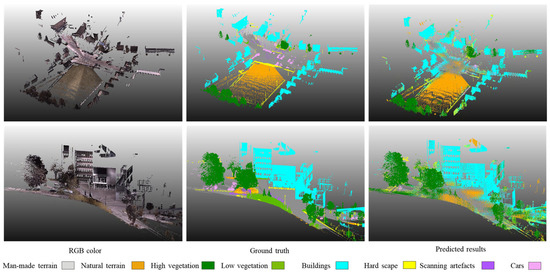
Figure 8.
Visualization of the prediction results on two example scenes using lag-ordered pairwise differences only as input. Lag-ordered pairwise differences only show adequate performance on objects with a large volume in the scene, such as high vegetation, natural/man-made terrains, and buildings.
The IoU values for each class show large differences across classes. The model performance on buildings and high vegetation reaches 63% and 54% in terms of IoU, respectively. The second tier of classes comprises man-made terrain and natural terrain, on which the model has IoU values of 39% and 38%, correspondingly. The rest of the classes, hardscapes, low vegetation, cars, and scanning artefacts, are not well detected by the model, leading to IoU values ranging from 0% to 12%.
We observed that model performance on different classes appears to be related to the proportion of the class within the dataset and the volume of the objects. As shown in Figure 5, buildings, man-made terrain, natural terrain, and high vegetation are the four largest classes, with a cumulative proportion of around 90% of the entire dataset. The model shows better performance on these four classes and appears far better than the rest of classes in terms of IoU. One potential reason that causes the diversity in the performance of the model on each class is the proportion of the class within the dataset [34]. Moreover, we found that this diversity is not only related to the proportion but also the volume of the objects in the scene. For example, even though man-made terrain has more points than the high vegetation class, the performance on high vegetation is better than that on man-made terrain. It suggests that lag-ordered pairwise differences have the capability to identify different objects, while it also appears to be sensitive to the volume of the objects. We attributed this finding to the nature of the data partitioning and sampling processes. During these processes, the number of points for objects in the original dataset directly impacts how many points from this object can be captured. Moreover, the volume of the object also impacts the analysis. For example, a cubic object (e.g., buildings and trees) tends to be captured with more points than a planar one since ground only exists on the floor surface of a block but cubic objects exist across the 3D space. Hardscapes, scanning artefacts, and cars take up a small volume, as well as the number of points, as opposed to the whole scene. Therefore, they might be less represented using pairwise differences, as the points sampled for them might be more subject to boundary effects.
Beyond dataset imbalance and object size, the intrinsic characteristics of each class also play a critical role in shaping detection outcomes. For example, buildings often present regular, planar, and orthogonal structures, producing stable geometric patterns and consistent spatial autocorrelation signatures that the encoder can effectively capture. High vegetation, although geometrically irregular, contains rich local texture and high variability in color and intensity, resulting in distinctive spatial-contextual features that support stronger classification performance than might be expected from proportion alone. By contrast, man-made terrain and natural terrain tend to share smoother surfaces and similar spectral properties, which increases the likelihood of misclassification between them despite their large representation in the dataset. Low vegetation poses further challenges because it frequently exists in transitional zones between terrain and high vegetation, where boundaries are spectrally and structurally ambiguous. For small-volume classes, such as scanning artefacts and cars, the limited and often inconsistent geometric or textural patterns across scenes can restrict the encoder’s ability to learn stable discriminative embeddings. These findings suggest that model performance is jointly determined by data availability, object size, and the degree to which a class’s geometry, surface texture, and spectral contrast produce distinctive spatial autocorrelation patterns.
Even though there were less represented classes, we still innovatively found the capability of lag-ordered pairwise differences as context features to identify many objects. As shown in Figure 8, buildings, trees, and terrain, even though there is confusion between natural terrain and man-made terrain, are reasonably identified by the model. The stronger performance observed for large-volume and spatially coherent geospatial objects, such as buildings, terrain, and high vegetation, can be explained by the way spatial autocorrelation operates. First, large objects typically contain many points with similar attribute values (e.g., elevation, color, or intensity) over extended spatial extents, producing a stronger and more stable autocorrelation signal. Second, this abundance of same-class points enhances statistical stability, making the derived contextual features less sensitive to noise. Third, in neighborhood-based analysis, points within large objects are more likely to have neighbors from the same object, ensuring that spatial context measures truly capture the object’s characteristics. By contrast, small or narrow objects (e.g., cars, poles, and fences) often suffer from boundary effects, where neighborhoods contain a mix of points from different classes, weakening the autocorrelation signal and reducing distinctiveness in the learned spatial patterns.
This experiment was designed to examine the intrinsic capability of the learned spatial autocorrelation representation when used as the sole input feature for 3D object detection. While models incorporating spatial coordinates and RGB information achieved higher accuracy, the results show that lag-ordered pairwise differences alone, as a representation of spatial autocorrelation, can effectively capture meaningful textural patterns, yielding moderate yet non-trivial classification performance. This outcome underscores that spatial autocorrelation features are not merely supplementary but can independently encode valuable contextual information. In the broader context of the call of GeoAI to integrate geospatial principles into artificial intelligence, these findings highlight how spatial dependency concepts can be integrated in deep learning frameworks to enhance the understanding of complex 3D geospatial data.
The visualization of the prediction results demonstrated confusion among classes, especially around the boundaries. For example, natural terrain and man-made terrain are not well distinguished by the model. Moreover, we also observed that some man-made surfaces were predicted as trees if the points were close to a tree. These results represent a challenge of the current method in that the spatial autocorrelation features of those points on boundaries may not adequately be represented since the neighboring points can come from other classes. This problem is also seen in the classification task on 2D remotely sensed imagery when spatial autocorrelation is considered. Myint [54] attempted to mitigate this challenge by excluding samples on boundaries during model training. Wu et al. [29] addressed the boundary issue by considering object-based spatial contextual features instead of window-based ones. However, further study has to be conducted to adapt these solutions from the 2D to 3D context so that this challenge can be well addressed.
5.2. Performance of the Spatial Autocorrelation Encoder
Experiment 2 investigated the effectiveness of the designed spatial autocorrelation encoder through an ablation study, along with results by Chen et al. [24], in which the two experiments from Chen’s study served as the two without such a neural network-based spatial autocorrelation encoder. In this section, we demonstrate the measurement statistics across the 10 repetitions (see details in Appendix A) in Table 2. We further demonstrate our results in Figure 9, compared with the results without using the encoder.

Table 2.
Statistical results across 10 repetitions.
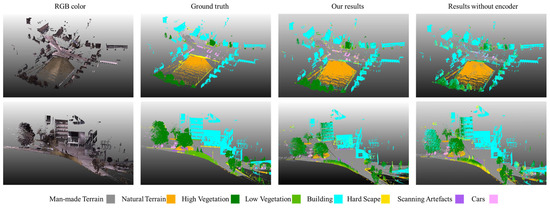
Figure 9.
Comparison between ground truth and the predicted results with/without the spatial autocorrelation encoder on two example scenes.
The OA and mIOU are 85.5% and 57.6%, respectively, providing a global measure of model performance on this dataset. The IoU values across the classes range from 26.8% (scanning artefacts) to 92.8% (man-made terrain). The same as reflected in Experiment 1, the classes with higher proportion from the original datasets tend to have better performance. For example, man-made terrain (IoU 92.8%), buildings (IoU 84.0%), natural terrain (IoU 78.7%), and high vegetation (IoU 66.1%) are the four classes on which the model best performs, while they are also the four largest classes with a cumulative proportion of 90% of the original dataset. We attributed their better performance to the amount of data compared to the rest of the classes. The model shows moderate performance on cars, with an IoU of 55.6%. Scanning artefacts, hardscapes, and low vegetation seem to be not well detected by the model, with IoU values ranging from 26.8% to 28.8%.
5.3. Comparative Ablation Analysis
We conducted a comparative analysis between the results from our study with those from Chen [24]. The two treatments in Chen’s study [24] were used to compare model performance using SA-Encoder. One treatment that used spatial information and color information was used as the baseline. Another treatment additionally taking Matheron’s semivariance was included in the comparison (see Table 3). We further compared model performance with SA-Encoder with the two identified treatments. A one-tailed t-test was performed against the baseline to explore its statistical significance (see Table 3).

Table 3.
Comparative analysis results of model performance among the baseline without spatial autocorrelation features, the model with Matheron’s semivariance, and the SA-Encoder-informed model.
For the global measurements, OA and mIOU, there is an increasing trend in accuracy as we consider spatial autocorrelation with more sophisticated measures. Without considering the spatial context, the two measurements are 81.95%, and 51.58%. Explicitly incorporating semivariance as a spatial context feature results in a 1–3% increase in the global measurements. Once we apply a neural network to directly learn spatial context embedded from lag-ordered pairwise differences, the accuracy improves 3.60%, and 6.00% for the two assessment measures, with the increase being significant at a 99% confidence interval.
Comparative analysis significantly underscores the advancement our study brings to the field of geospatial object detection using 3D deep learning. By directly learning spatial context embeddings from lag-ordered pairwise differences, our approach outperforms previous models trained on RGB and/or semivariance in terms of OA and mIOU. The substantial gains across various classes, particularly in categories such as high vegetation and cars, highlight the effectiveness of incorporating spatial autocorrelation features. The comparative results validate the advancement of the proposed encoder-based neural network approach over previous approaches in deriving spatial contextual features in geospatial object detection tasks. The statistical significance of these results emphasizes the critical role of spatial contextual features in enhancing 3D deep learning models, paving the way for future advancements in this rapidly evolving field.
Moreover, the comparison results provide empirical support for the encoder’s capability in mitigating the effect of a long-tail problem within the dataset. Several minority categories, such as cars and scanning artefacts, exhibit relatively larger performance gains compared to the most prevalent classes when using the proposed spatial autocorrelation encoder. The adaptability of the proposed method to such challenging data characteristics underscores its practical value for real-world 3D scene analysis.
6. Conclusions
This study introduces SA-Encoder to learn a spatial autocorrelation representation to inform 3D geospatial object detection. By leveraging lag-ordered pairwise differences, the encoder adaptively captures spatial dependencies. Our experiments demonstrated that SA-Encoder consistently improves detection accuracy across diverse urban and rural scenes, outperforming both the baseline model and the model absorbing pre-computed semivariance. Notably, the encoder proved especially effective for large, spatially coherent objects, such as buildings, terrain, and high vegetation, when it is used alone, while also yielding measurable gains for minority classes in a long-tail dataset when integrated with an existing model. This work advocates the broader importance of contextual information carried by non-spatial channels—such as RGB and intensity—for advancing geospatial object detection. Our findings highlight the potential of moving toward multi-channel 3D deep learning, where spatial and non-spatial attributes are jointly modeled to enrich feature representation.
While the proposed approach shows clear benefits, several limitations should be acknowledged. The evaluation was conducted on a single large-scale outdoor benchmark, which, although challenging and diverse, does not represent all possible environments, such as indoor or highly heterogeneous mixed scenes. The current implementation also uses fixed parameters for the number of nearest neighbors and block size, which may not be optimal across different object classes or spatial contexts. In addition, the integration was demonstrated within the PointNet architecture, and its effectiveness with other backbone networks remains untested.
Future work will focus on extending the evaluation to additional datasets covering different environments, developing adaptive parameter tuning strategies that account for object scale and local point density, and integrating the encoder with other state-of-the-art 3D deep learning architectures. Research into dynamic feature fusion methods that balance point-wise, local-context, and global features may further enhance robustness and generalization.
Our study started initially from the call for integrating GIScience and AI to enhance the development of state-of-the-art GIS applications, such as digital twin projects. By innovating in the realm of geospatial object detection, our study provides a foundation for future research and applications in urban studies, environmental monitoring, and beyond. The exploration and findings presented serve not only as remarkable progress witnessed in these domains but also as a bridge connecting the theoretical underpinnings of GIS with the practical applications of AI in 3D geospatial object detection.
Author Contributions
Conceptualization, T.C. and W.T.; methodology, T.C.; software, T.C.; validation, T.C.; formal analysis, T.C.; investigation, T.C.; resources, T.C., W.T., S.-E.C., and C.A.; data curation, T.C.; writing—original draft preparation, T.C.; writing—review and editing, T.C., W.T., S.-E.C., and C.A.; visualization, T.C.; supervision, W.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The dataset is available at https://www.semantic3d.net/.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Inference performance of 10 repetitions.

| Treat | OA | mIoU | Man-Made Terrain | Natural Terrain | High Vegetation | Low Vegetation | Buildings | Hardscape | Scanning Artefacts |
| 1 | 85.7% | 57.7% | 93.0% | 79.6% | 67.0% | 28.4% | 84.3% | 28.3% | 26.4% |
| 2 | 85.6% | 57.3% | 92.5% | 78.8% | 66.2% | 28.3% | 84.1% | 28.9% | 25.2% |
| 3 | 85.8% | 58.4% | 92.8% | 80.4% | 66.8% | 29.7% | 84.4% | 28.3% | 26.9% |
| 4 | 85.6% | 57.5% | 92.8% | 78.4% | 66.5% | 25.8% | 84.0% | 27.2% | 28.6% |
| 5 | 85.3% | 57.4% | 92.7% | 76.4% | 66.3% | 25.7% | 83.8% | 27.6% | 29.0% |
| 6 | 85.4% | 56.9% | 92.4% | 78.0% | 68.3% | 25.7% | 84.7% | 26.1% | 27.4% |
| 7 | 85.4% | 57.6% | 92.8% | 77.3% | 63.9% | 31.2% | 84.2% | 28.3% | 27.0% |
| 8 | 85.1% | 57.1% | 92.5% | 77.2% | 66.0% | 29.4% | 83.8% | 26.5% | 25.8% |
| 9 | 85.8% | 58.0% | 93.1% | 80.4% | 64.8% | 33.2% | 83.0% | 28.3% | 23.9% |
| 10 | 85.7% | 57.9% | 93.1% | 80.2% | 65.4% | 30.8% | 84.1% | 28.0% | 28.1% |
* Treat: treatment IDs. OA and mIoU: Overall Accuracy and mean Intersection over Union. The class label: Intersection over Union for each category.
References
- Guo, H.; Goodchild, M.; Annoni, A. Manual of Digital Earth; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Qin, K.; Li, J.; Zlatanova, S.; Wu, H.; Gao, Y.; Li, Y.; Shen, S.; Qu, X.; Yang, Z.; Zhang, Z. Novel UAV-based 3Dreconstruction using dense LiDAR point cloud and imagery: A geometry-aware 3D gaussian splatting approach. Int. J. Appl. Earth Obs. Geoinf. 2025, 140, 104590. [Google Scholar]
- Goodchild, M.F. Elements of an infrastructure for big urban data. Urban Inform. 2022, 1, 3. [Google Scholar] [CrossRef]
- Batty, M. Digital Twins in City Planning. Nat. Comput. Sci. 2023, 4, 192–199. [Google Scholar] [CrossRef]
- Syafiq, M.; Azri, S.; Ujang, U. CityJSON Management Using Multi-Model Graph Database to Support 3D Urban Data Management. In Proceedings of the 13th International Conference on Geographic Information Science (GIScience 2025), Christchurch, New Zealand, 26–29 August 2025; Schloss Dagstuhl–Leibniz-Zentrum für Informatik: Wadern, Germany, 2025. [Google Scholar]
- Goodchild, M.F. Introduction to urban big data infrastructure. In Urban Informatics; Springer: Berlin/Heidelberg, Germany, 2021; pp. 543–545. [Google Scholar]
- Batty, M. Agents, Models, and Geodesign. ArcNews 2013, 35, 1–4. [Google Scholar]
- Zbirovský, S.; Nežerka, V. Open-source automatic pipeline for efficient conversion of large-scale point clouds to IFCformat. Autom. Constr. 2025, 177, 106303. [Google Scholar] [CrossRef]
- Kwan, M.-P.; Lee, J. Emergency response after 9/11: The potential of real-time 3D GIS for quick emergency response inmicro-spatial environments. Comput. Environ. Urban Syst. 2005, 29, 93–113. [Google Scholar] [CrossRef]
- Evans, S.; Hudson-Smith, A.; Batty, M. 3-D GIS: Virtual London and beyond. An exploration of the 3-D GIS experience involved in the creation of virtual London. Cybergeo Eur. J. Geogr. 2006. [Google Scholar] [CrossRef]
- Batty, M.; Hudson-Smith, A. Urban simulacra: London. Archit. Des. 2005, 75, 42–47. [Google Scholar] [CrossRef]
- Batty, M. The new urban geography of the third dimension. Environ. Plan. B-Plan. Des. 2000, 27, 483–484. [Google Scholar] [CrossRef]
- Arav, R.; Wittich, D.; Rottensteiner, F. Evaluating saliency scores in point clouds of natural environments by learning surface anomalies. ISPRS J. Photogramm. Remote Sens. 2025, 224, 235–250. [Google Scholar] [CrossRef]
- Gao, K.; Lu, D.; He, H.; Xu, L.; Li, J.; Gong, Z. Enhanced 3D Urban Scene Reconstruction and Point Cloud Densification using Gaussian Splatting and Google Earth Imagery. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4701714. [Google Scholar]
- Qi, C.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Xie, J.; Xu, Y.; Zheng, Z.; Zhu, S.-C.; Wu, Y.N. Generative pointnet: Deep energy-based learning on unordered point sets for 3d generation, reconstruction and classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Wu, C.; Pfrommer, J.; Beyerer, J.; Li, K.; Neubert, B. Object detection in 3D point clouds via local correlation-aware point embedding. In Proceedings of the 2020 Joint 9th International Conference on Informatics, Electronics & Vision (ICIEV) and 2020 4th International Conference on Imaging, Vision & Pattern Recognition (icIVPR), Kitakyushu, Japan, 26–29 August 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Ren, D.; Ma, Z.; Chen, Y.; Peng, W.; Liu, X.; Zhang, Y.; Guo, Y. Spiking PointNet: Spiking neural networks for point clouds. Adv. Neural Inf. Process. Syst. 2024, 36, 41797–41808. [Google Scholar]
- Qian, G.C.; Li, Y.C.; Peng, H.W.; Mai, J.J.; Hammoud, H.A.A.K.; Elhoseiny, M.; Ghanem, B. PointNeXt: Revisiting PointNet plus plus with Improved Training and Scaling Strategies. Adv. Neural Inf. Process. Syst. 2022, 35, 23192–23204. [Google Scholar]
- Goodchild, M.F. The Openshaw effect. Int. J. Geogr. Inf. Sci. 2022, 36, 1697–1698. [Google Scholar] [CrossRef]
- Li, W. GeoAI and Deep Learning. In The International Encyclopedia of Geography; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Dowd, P.A. The Variogram and Kriging: Robust and Resistant Estimators. In Geostatistics for Natural Resources Characterization; Verly, G., David, M., Journel, A.G., Marechal, A., Eds.; Springer: Dordrecht, The Netherlands, 1984; pp. 91–106. [Google Scholar]
- Chen, T.; Tang, W.; Allan, C.; Chen, S.-E. Explicit Incorporation of Spatial Autocorrelation in 3D Deep Learning for Geospatial Object Detection. Ann. Am. Assoc. Geogr. 2024, 114, 2297–2316. [Google Scholar] [CrossRef]
- Miranda, F.P.; Carr, J.R. Application of the semivariogram textural classifier (STC) for vegetation discrimination using SIR-B data of the guiana shield, northwestern brazil. Remote Sens. Rev. 1994, 10, 155–168. [Google Scholar] [CrossRef]
- Miranda, F.P.; Fonseca, L.E.N.; Carr, J.R. Semivariogram textural classification of JERS-1 (Fuyo-1) SAR data obtained over a flooded area of the Amazon rainforest. Int. J. Remote Sens. 1998, 19, 549–556. [Google Scholar] [CrossRef]
- Miranda, F.P.; Fonseca, L.E.N.; Carr, J.R.; Taranik, J.V. Analysis of JERS-1 (Fuyo-1) SAR data for vegetation discrimination in northwestern Brazil using the semivariogram textural classifier (STC). Int. J. Remote Sens. 1996, 17, 3523–3529. [Google Scholar] [CrossRef]
- Miranda, F.P.; Macdonald, J.A.; Carr, J.R. Application of the semivariogram textural classifier (STC) for vegetation discrimination using SIR-B data of Borneo. Int. J. Remote Sens. 1992, 13, 2349–2354. [Google Scholar] [CrossRef]
- Wu, X.; Peng, J.; Shan, J.; Cui, W. Evaluation of semivariogram features for object-based image classification. Geo-Spat. Inf. Sci. 2015, 18, 159–170. [Google Scholar] [CrossRef]
- Mottaghi, R.; Chen, X.; Liu, X.; Cho, N.-G.; Lee, S.-W.; Fidler, S.; Urtasun, R.; Yuille, A. The role of context for object detection and semantic segmentation in the wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Pohlen, T.; Hermans, A.; Mathias, M.; Leibe, B. Full-resolution residual networks for semantic segmentation in street scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Engelmann, F.; Kontogianni, T.; Hermans, A.; Leibe, B. Exploring spatial context for 3D semantic segmentation of point clouds. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Wan, J.; Xu, Y.; Qiu, Q.; Xie, Z. A geometry-aware attention network for semantic segmentation of MLS point clouds. Int. J. Geogr. Inf. Sci. 2023, 37, 138–161. [Google Scholar] [CrossRef]
- Wang, J.; Fan, W.; Song, X.; Yao, G.; Bo, M.; Liu, Z. NLA-GCL-Net: Semantic segmentation of large-scale surveying point clouds based on neighborhood label aggregation (NLA) and global context learning (GCL). Int. J. Geogr. Inf. Sci. 2024, 38, 2325–2347. [Google Scholar] [CrossRef]
- Charles, R.Q.; Liu, W.; Wu, C.; Su, H.; Leonidas, J.G. Frustum pointnets for 3D object detection from RGB-D data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Klemmer, K.; Safir, N.S.; Neill, D.B. Positional encoder graph neural networks for geographic data. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 25–27 April 2023. [Google Scholar]
- Fan, S.; Dong, Q.; Zhu, F.; Lv, Y.; Ye, P.; Wang, F.-Y. SCF-net: Learning spatial contextual features for large-scale point cloud segmentation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 14504–14513. [Google Scholar]
- Chu, J.; Li, W.; Wang, X.; Ning, K.; Lu, Y.; Fan, X. Digging into Intrinsic Contextual Information for High-fidelity 3D Point Cloud Completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February 2025. [Google Scholar]
- Li, Y.; Ye, Z.; Huang, X.; HeLi, Y.; Shuang, F. LCL_FDA: Local context learning and full-level decoder aggregation network for large-scale point cloud semantic segmentation. Neurocomputing 2025, 621, 129321. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet plus plus: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Boulch, A. ConvPoint: Continuous convolutions for point cloud processing. Comput. Graph. 2020, 88, 24–34. [Google Scholar] [CrossRef]
- Viswanath, K.; Jiang, P.; Saripalli, S. Reflectivity is all you need! Advancing LiDAR semantic segmentation. IFAC-PapersOnLine 2025, 59, 43–48. [Google Scholar]
- Yang, L.; Hu, P.; Yuan, S.; Zhang, L.; Liu, J.; Shen, H.; Zhu, X. Towards Explicit Geometry-Reflectance Collaboration for Generalized LiDAR Segmentation in Adverse Weather. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, TN, USA, 11–15 June 2025. [Google Scholar]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Tso, B.; Olsen, R.C. Scene classification using combined spectral, textural and contextual information. Algorithms Technol. Multispectral Hyperspectral Ultraspectral Imag. X 2004, 5425, 135–146. [Google Scholar]
- Takhtkeshha, N.; Bocaux, L.; Ruoppa, L.; Remondino, F.; Mandlburger, G.; Kukko, A.; Hyyppä, J. 3D forest semantic segmentation using multispectral LiDAR and 3D deep learning. arXiv 2025, arXiv:2507.08025. [Google Scholar]
- Li, Z.; Hodgson, M.E.; Li, W. A general-purpose framework for parallel processing of large-scale LiDAR data. Int. J. Digit. Earth 2018, 11, 26–47. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. Semantic3D.net: A new large-scale point cloud classification benchmark. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, V-1-W1, 91–98. [Google Scholar] [CrossRef]
- Li, W.; Batty, M.; Goodchild, M.F. Real-time GIS for smart cities. Int. J. Geogr. Inf. Sci. 2020, 34, 311–324. [Google Scholar] [CrossRef]
- Batty, M. Virtual Reality in Geographic Information Systems. In Handbook of Geographic Information Science; Blackwell Publishing: Oxford, UK, 2008; pp. 317–334. [Google Scholar]
- Tang, W.; Chen, S.-E.; Diemer, J.; Allan, C.; Chen, T.; Slocum, Z.; Shukla, T.; Chavan, V.S.; Shanmugam, N.S. DeepHyd: A Deep Learning-Based Artificial Intelligence Approach for the Automated Classification of Hydraulic Structures from LiDAR and Sonar Data; North Carolina Department of Transportation, Research and Development Unit: Raleigh, NC, USA, 2022. [Google Scholar]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep Learning for 3D Point Clouds: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4338–4364. [Google Scholar] [CrossRef] [PubMed]
- Myint, S.W. Fractal approaches in texture analysis and classification of remotely sensed data: Comparisons with spatial autocorrelation techniques and simple descriptive statistics. Int. J. Remote Sens. 2003, 24, 1925–1947. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).