An Integrated Method for Dynamic Height Error Correction in GNSS-IR Sea Level Retrievals
Abstract
1. Introduction
2. Data and Methods
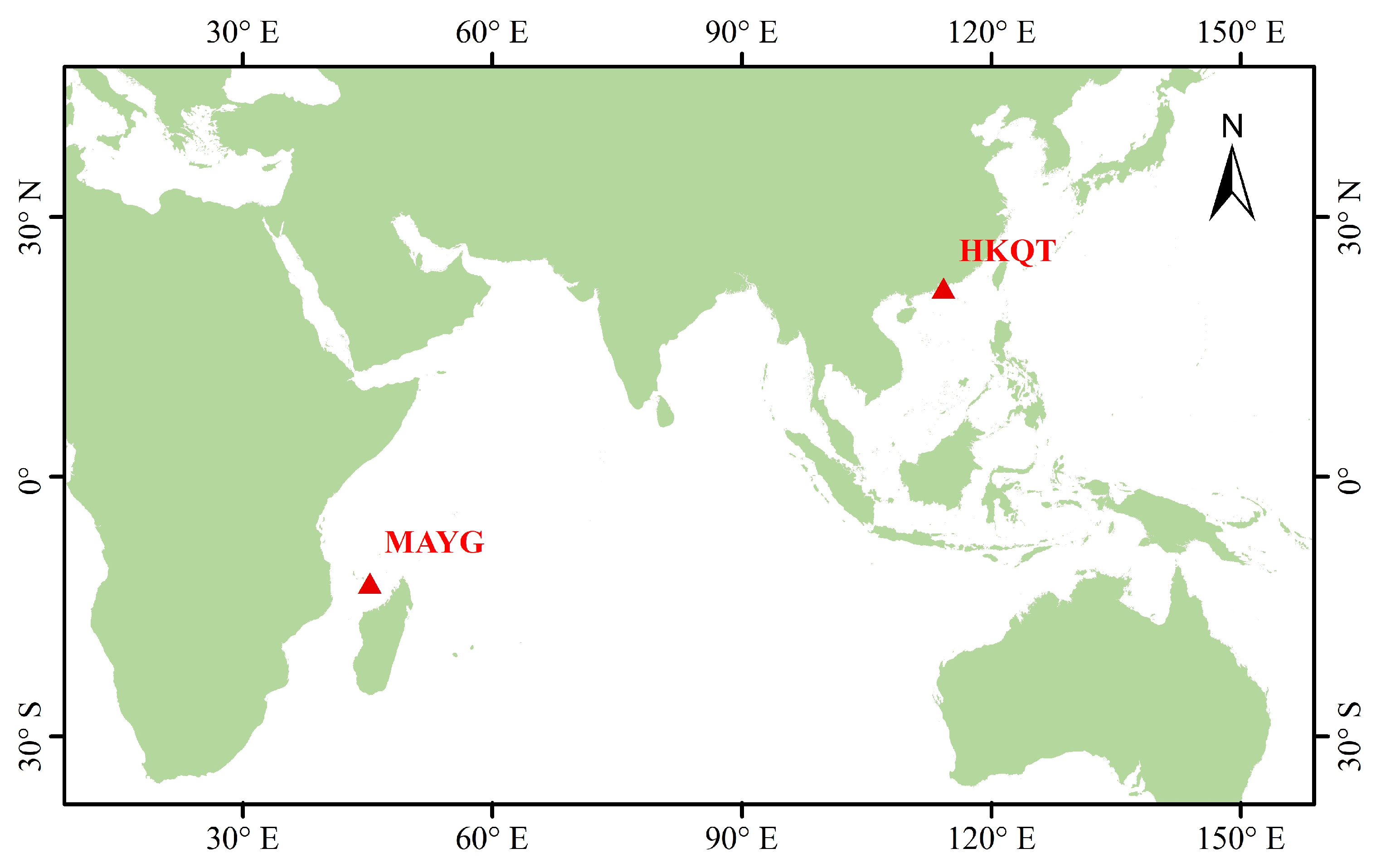
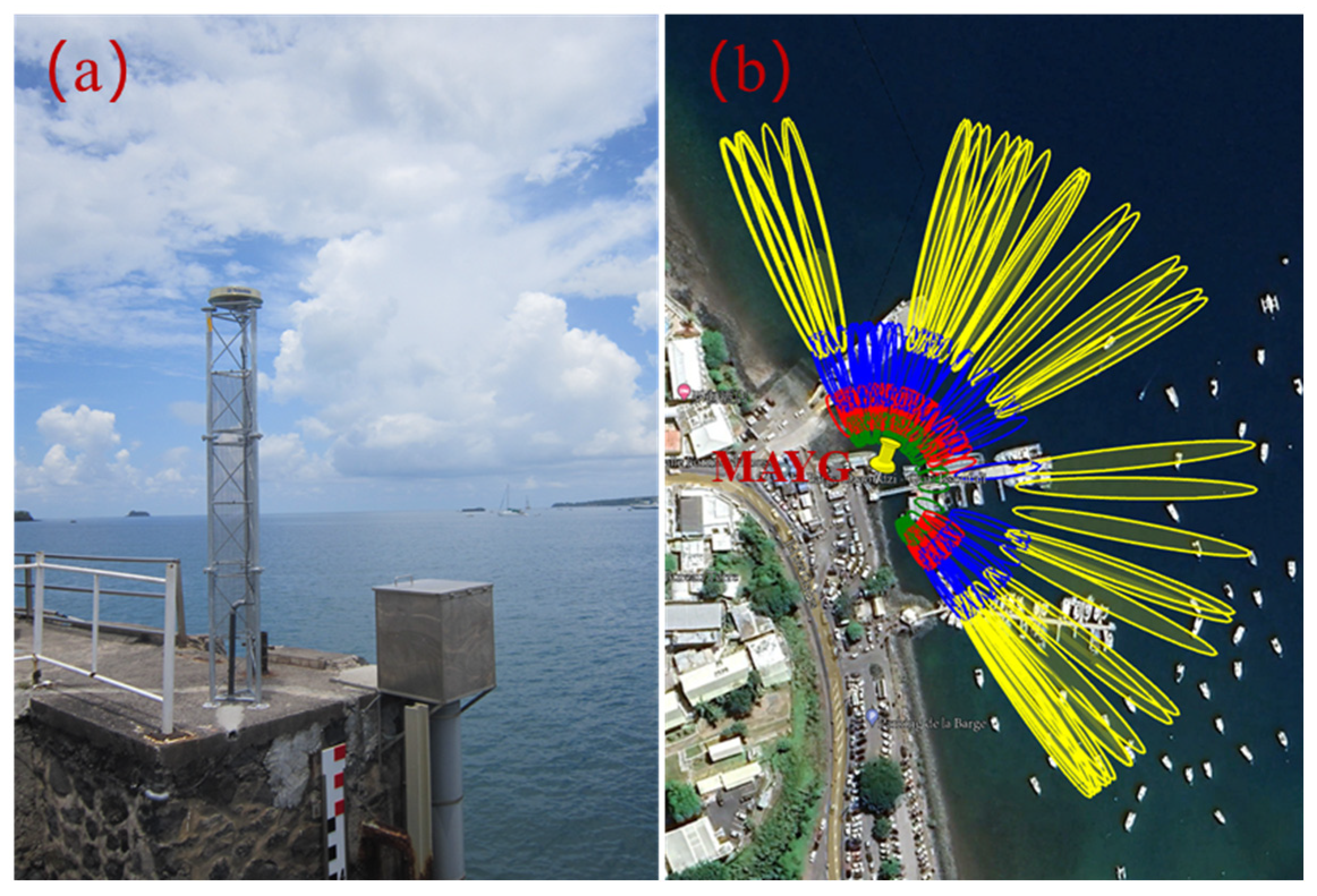
2.1. GNSS Sites and Data Description
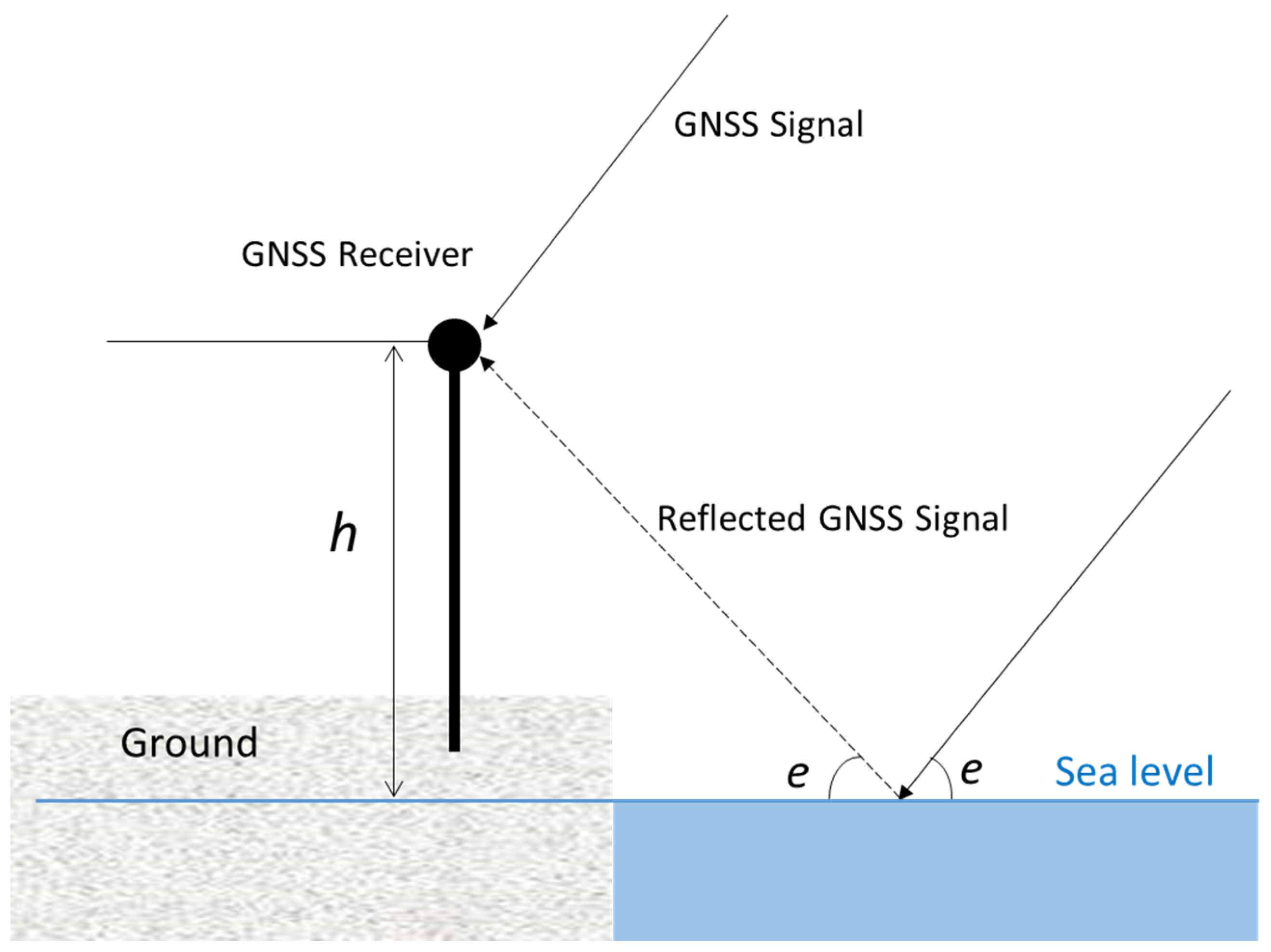
2.2. GNSS-IR
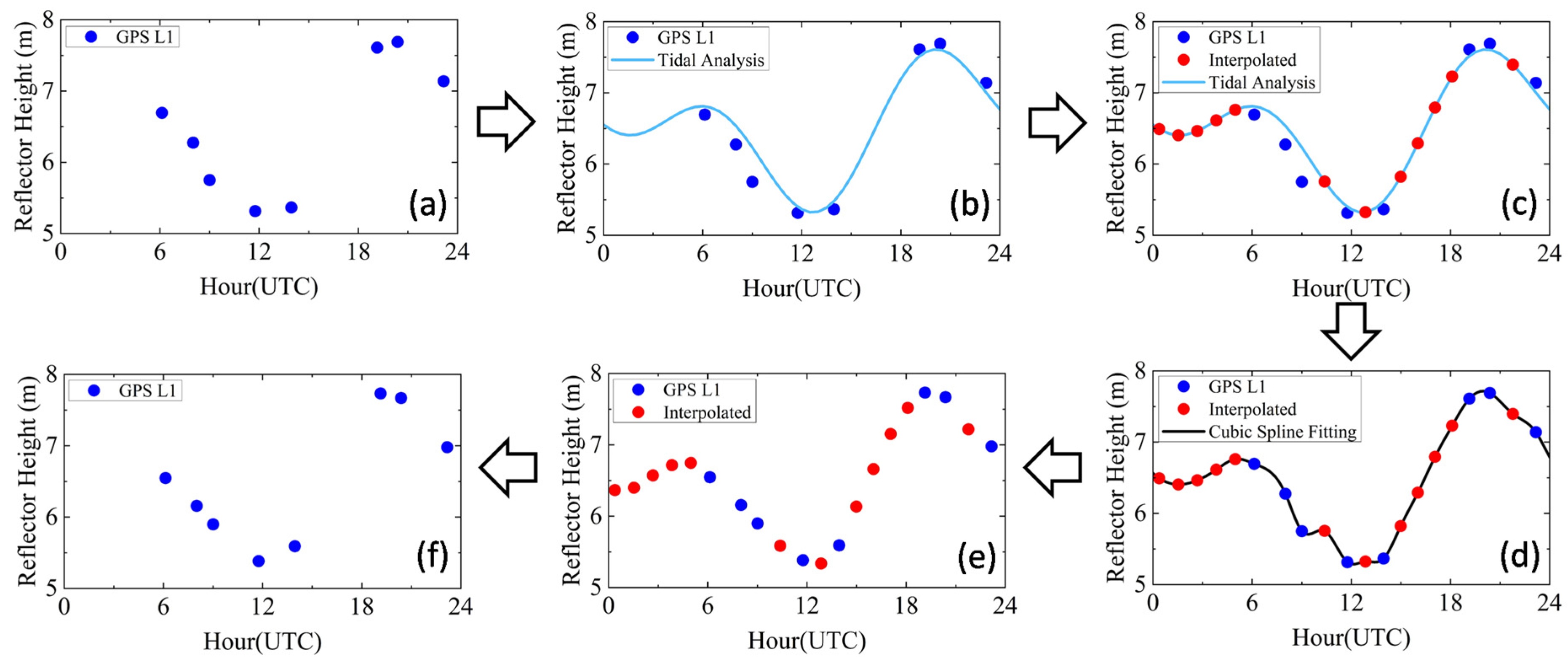
2.3. Tidal Analysis and Cubic Spline Fitting Methods for Dynamic Height Error Correction
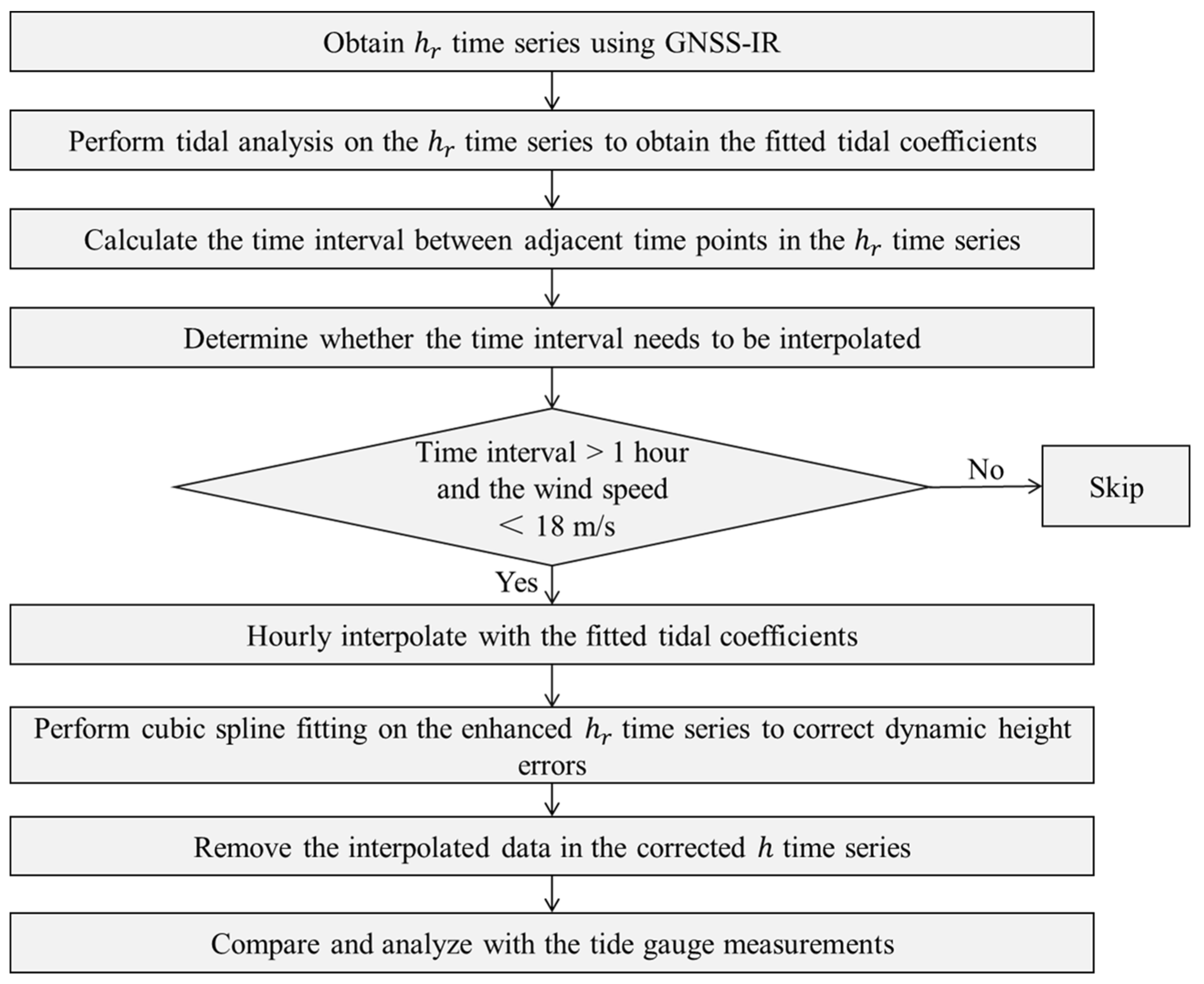
2.4. An Integrated Method for Dynamic Height Error Correction
3. Results
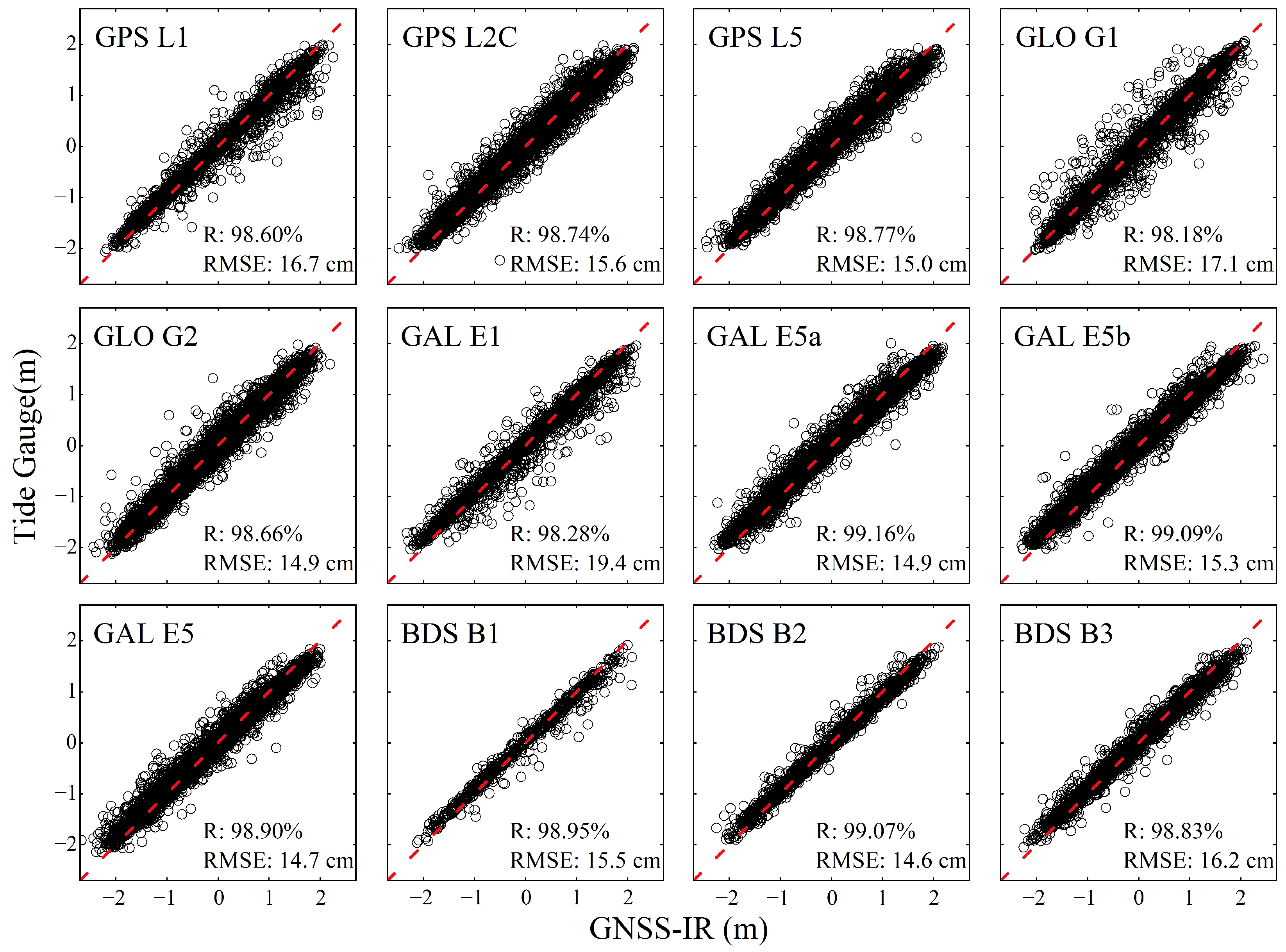
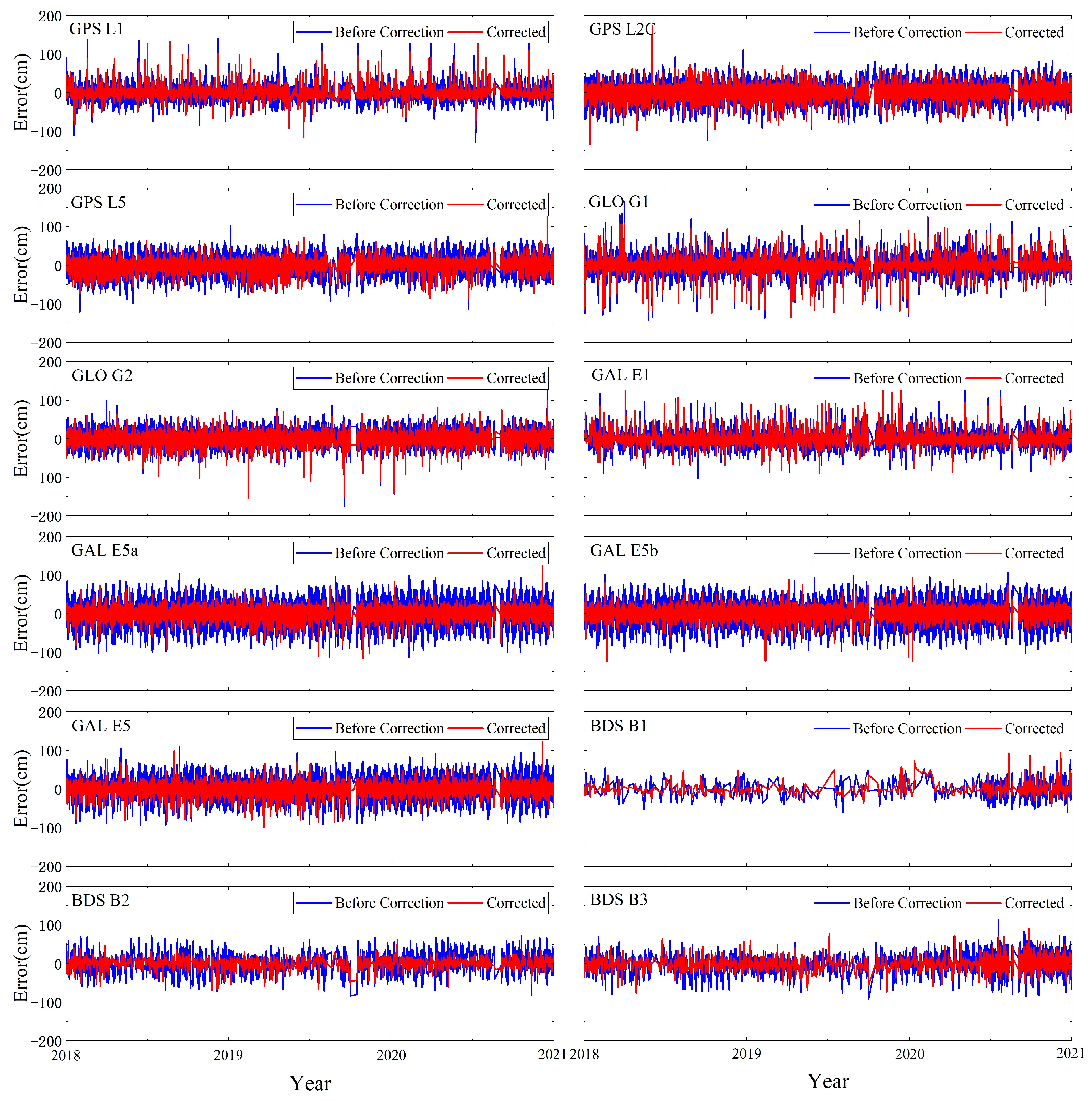
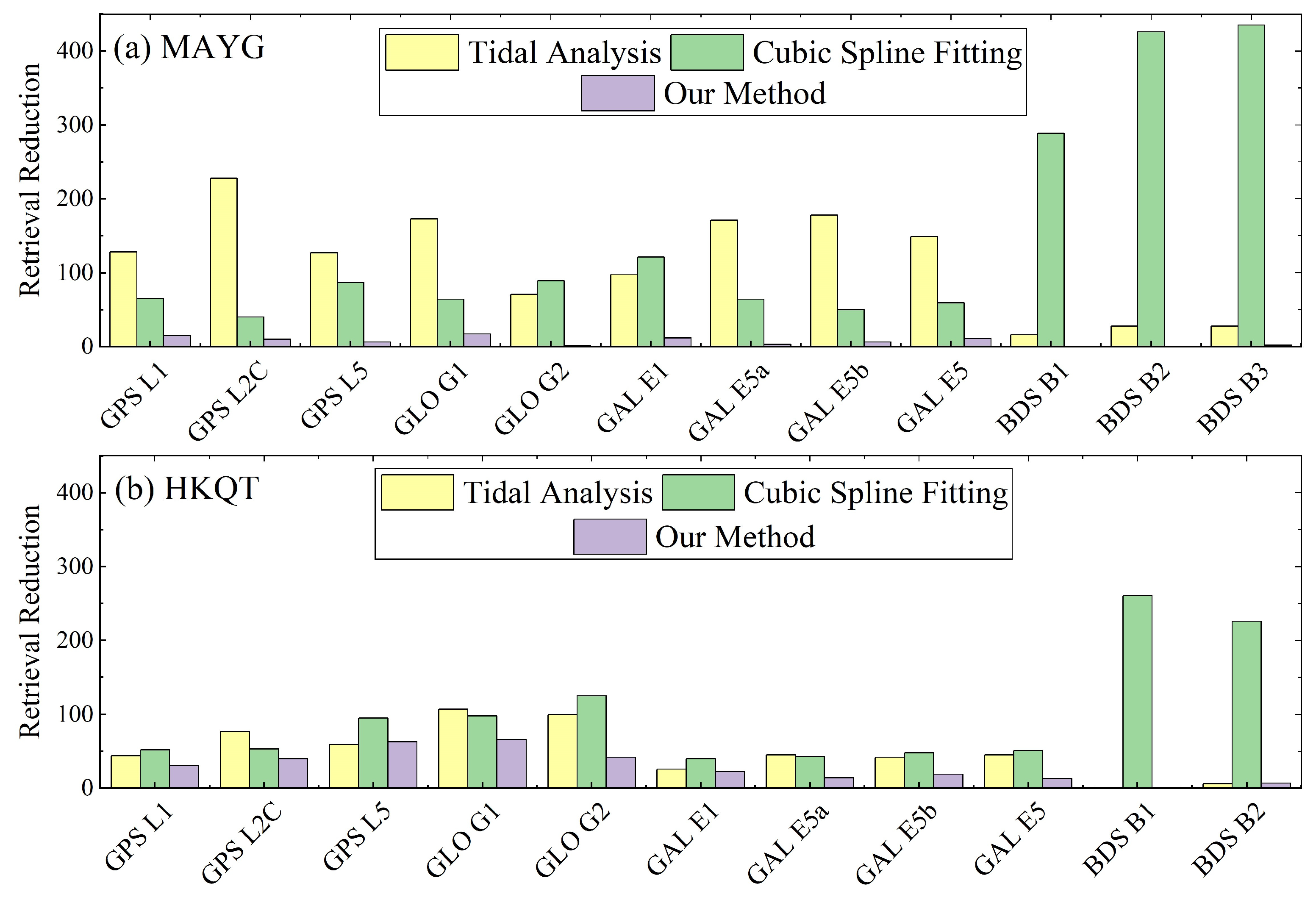
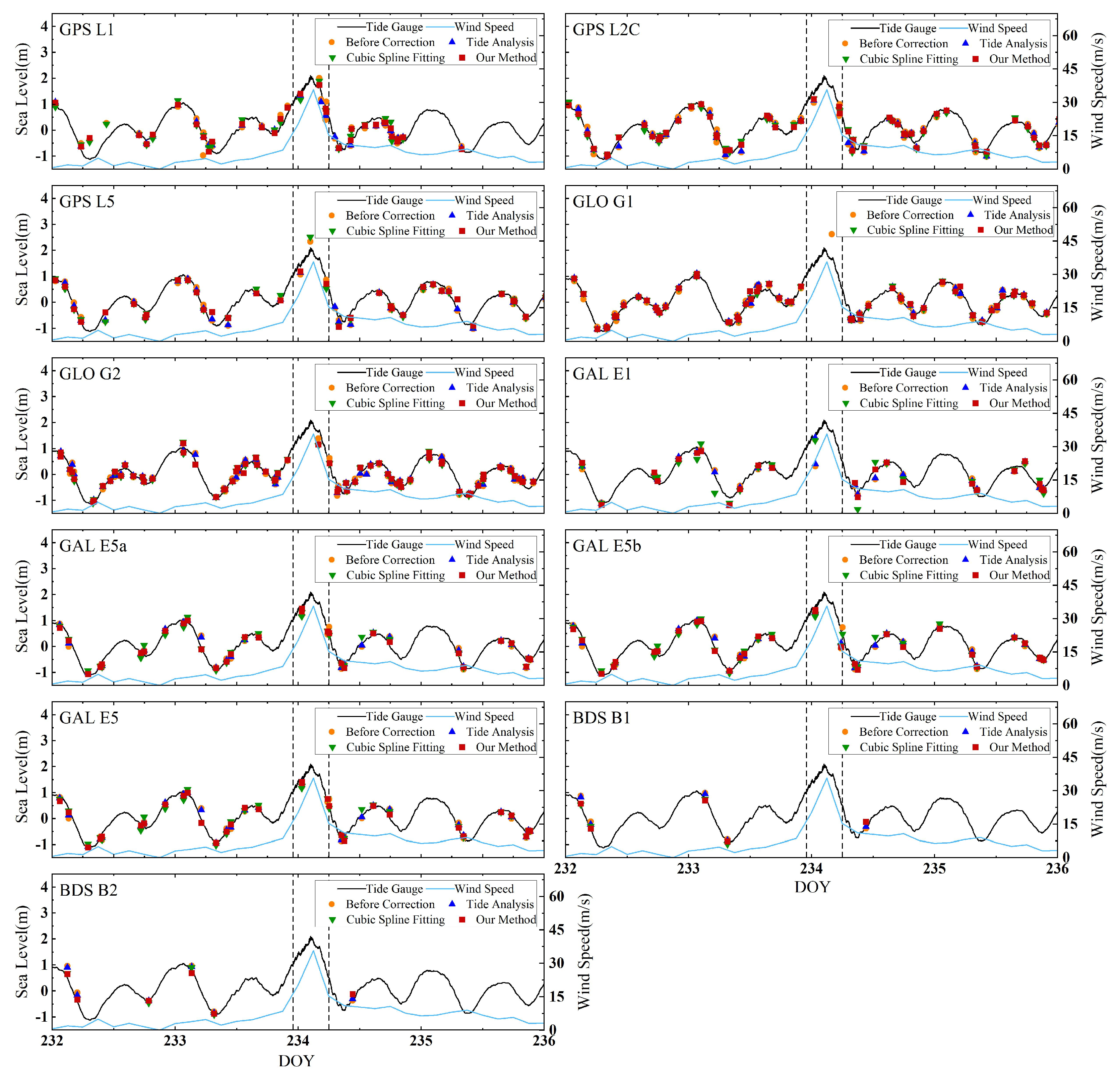
3.1. Correction Performance at MAYG
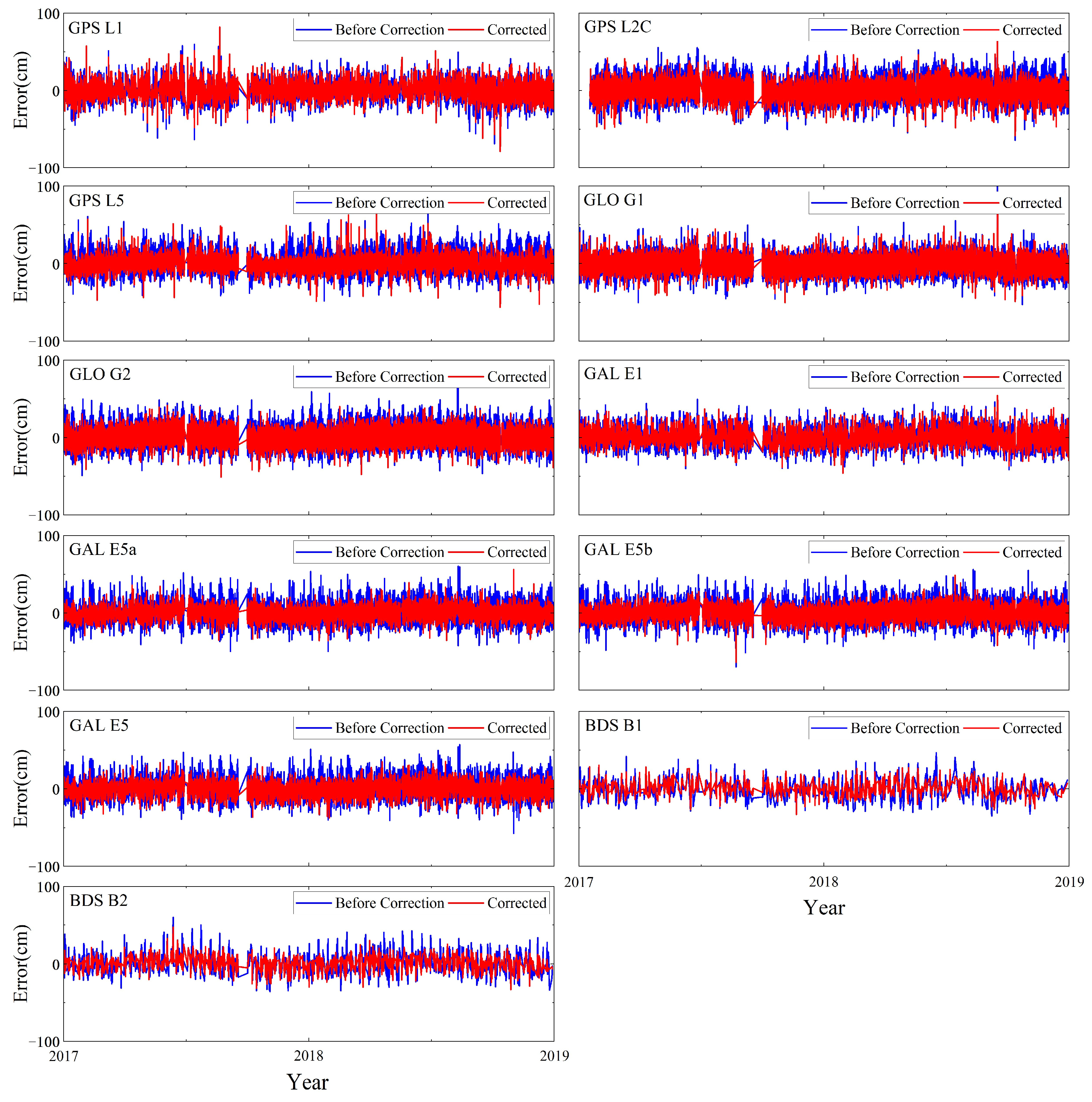
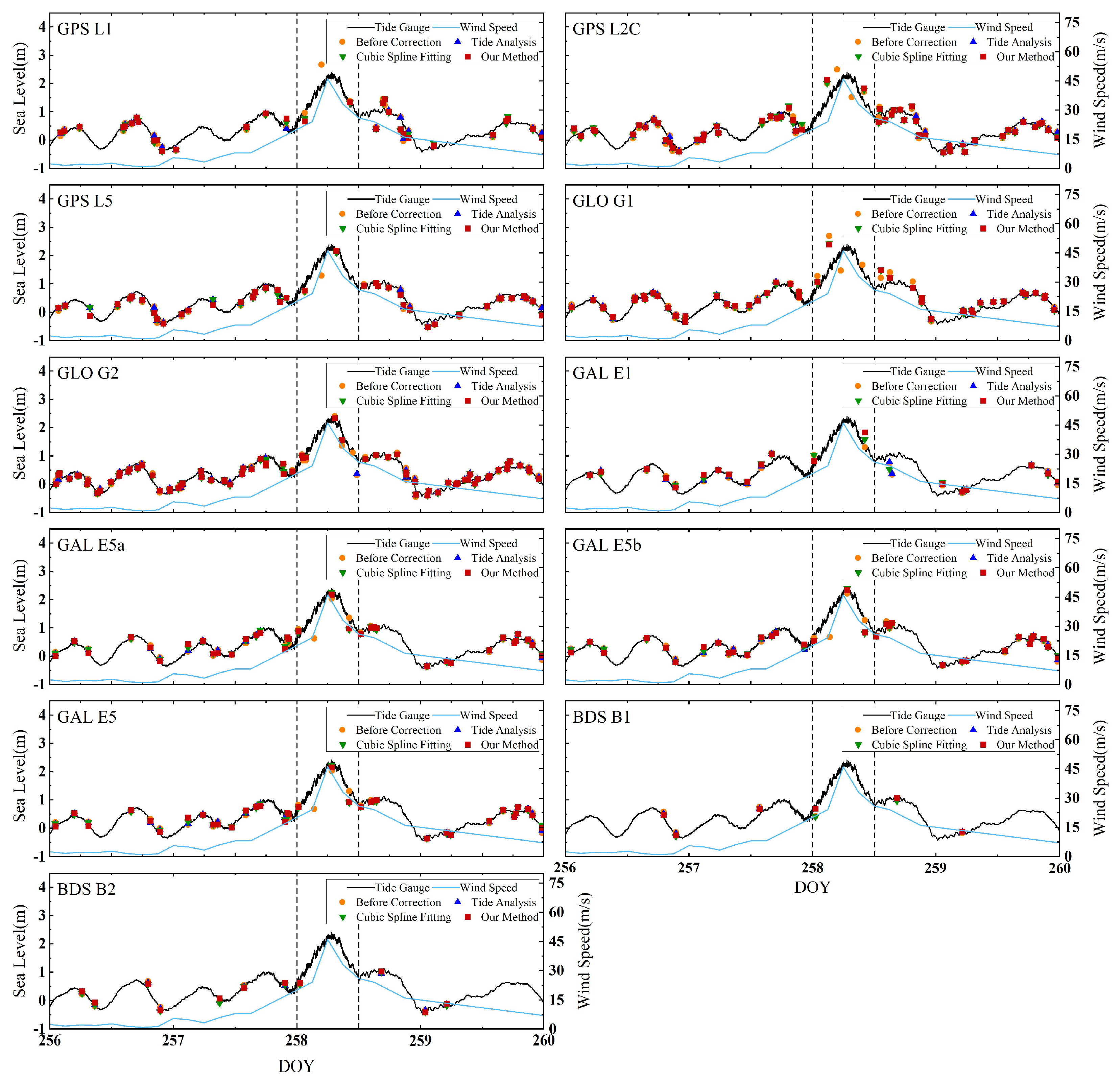
3.2. Correction Performance at HKQT
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schöne, T.; Schön, N.; Thaller, D. IGS tide gauge benchmark monitoring pilot project (TIGA): Scientific benefits. J. Geod. 2009, 83, 249–261. [Google Scholar] [CrossRef]
- Chepurin, G.A.; Carton, J.A.; Leuliette, E. Sea level in ocean reanalyses and tide gauges. J. Geophys. Res. Ocean 2014, 119, 147–155. [Google Scholar] [CrossRef]
- Cazenave, A.; Palanisamy, H.; Ablain, M. Contemporary sea level changes from satellite altimetry: What have we learned? What are the new challenges? Adv. Space Res. 2018, 62, 1639–1653. [Google Scholar] [CrossRef]
- Larson, K.M.; Löfgren, J.S.; Haas, R. Coastal sea level measurements using a single geodetic GPS receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef]
- Larson, K.M.; Ray, R.D.; Nievinski, F.G.; Freymueller, J.T. The accidental tide gauge: A GPS reflection case study from Kachemak Bay, Alaska. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1200–1204. [Google Scholar] [CrossRef]
- Larson, K.M.; Gutmann, E.D.; Zavorotny, V.U.; Braun, J.J.; Williams, M.W.; Nievinski, F.G. Can we measure snow depth with GPS receivers? Geophys. Res. Lett. 2009, 36, 41–52. [Google Scholar] [CrossRef]
- Larson, K.M.; Nievinski, F.G. GPS snow sensing: Results from the EarthScope plate boundary observatory. GPS Solut. 2013, 17, 41–52. [Google Scholar] [CrossRef]
- McCreight, J.L.; Small, E.E.; Larson, K.M. Snow depth, density, and SWE estimates derived from GPS reflection data: Validation in the western US. Water Resour. Res. 2014, 50, 6892–6909. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.D.; Bilich, A.L.; Braun, J.J.; Zavorotny, V.U. Use of GPS receivers as a soil moisture network for water cycle studies. Geophys. Res. Lett. 2008, 35, L24405. [Google Scholar] [CrossRef]
- Chew, C.; Small, E.E.; Larson, K.M. An algorithm for soil moisture estimation using GPS-interferometric reflectometry for bare and vegetated soil. GPS Solut. 2016, 20, 525–537. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, R.; Sun, B.; Wang, T.; Zhang, B.; Tu, J.; Nie, S.; Jiang, H.; Chen, K. GNSS-IR Soil Moisture Retrieval Using Multi-Satellite Data Fusion Based on Random Forest. Remote Sens. 2024, 16, 3428. [Google Scholar] [CrossRef]
- Liu, L.; Larson, K.M. Decadal changes of surface elevation over permafrost area estimated using reflected GPS signals. Cryosphere. 2018, 12, 477–489. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, L.; Larson, K.M.; Schaefer, K.M.; Zhang, J.; Yao, Y. GPS interferometric reflectometry reveals cyclic elevation changes in thaw and freezing seasons in a permafrost area (Barrow, Alaska). Geophys. Res. Lett. 2018, 45, 5581–5589. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, J.; Li, Z.; Peng, J. Ground surface elevation changes over permafrost areas revealed by multiple GNSS interferometric reflectometry. J. Geod. 2022, 96, 56. [Google Scholar] [CrossRef]
- Xu, T.; Wang, N.; He, Y.; Li, Y.; Meng, X.; Gao, F.; Lopez-Baeza, E. GNSS Reflectometry-Based Ocean Altimetry: State of the Art and Future Trends. Remote Sens. 2024, 16, 1754. [Google Scholar] [CrossRef]
- Löfgren, J.S.; Haas, R.; Scherneck, H.-G. Sea level time series and ocean tide analysis from multipath signals at five GPS sites in different parts of the world. J. Geodyn. 2014, 80, 66–80. [Google Scholar] [CrossRef]
- Löfgren, J.S.; Haas, R. Sea level measurements using multi-frequency GPS and GLONASS observations. EURASIP J. Adv. Signal Process. 2014, 2014, 50. [Google Scholar] [CrossRef]
- Roussel, N.; Ramillien, G.; Frappart, F.; Darrozes, J.; Gay, A.; Biancale, R.; Striebig, N.; Hanquiez, V.; Bertin, X.; Allain, D. Sea level monitoring and sea state estimate using a single geodetic receiver. Remote Sens. Environ. 2015, 171, 261–277. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Zhang, Q. Evaluation and combination of quad-constellation multi-GNSS multipath reflectometry applied to sea level retrieval. Remote Sens. Environ. 2019, 231, 111229. [Google Scholar] [CrossRef]
- Wang, J.; He, X.; Wang, X.; Song, M. Comparative analysis of dynamic correction method in tidal monitoring by GNSS-R. J. Geod. Geodyn. 2020, 40, 811–817. [Google Scholar]
- Strandberg, J.; Hobiger, T.; Haas, R. Improving GNSS-R sea level determination through inverse modeling of SNR data. Radio Sci. 2016, 51, 1286–1296. [Google Scholar] [CrossRef]
- Strandberg, J.; Hobiger, T.; Haas, R. Real-time sea-level monitoring using Kalman filtering of GNSS-R data. GPS Solut. 2019, 23, 61. [Google Scholar] [CrossRef]
- Larson, K.M.; Ray, R.D.; Williams, S.D. A 10-year comparison of water levels measured with a geodetic GPS receiver versus a conventional tide gauge. J. Atmos. Ocean. Technol. 2017, 34, 295–307. [Google Scholar] [CrossRef]
- Wang, X.; Niu, Z.; Chen, S.; He, X. A Correction Method of Height Variation Error Based on One SNR Arc Applied in GNSS–IR Sea-Level Retrieval. Remote Sens. 2022, 14, 11. [Google Scholar] [CrossRef]
- Wang, X.; Nan, Y.; He, X.; Song, M. GNSS-IR retrieval method with consideration of tidal periodicity of sea level. Acta Geod. Cartogr. Sin. 2024, 53, 482–492. [Google Scholar]
- Zhang, Z.; Hu, Y.; Gong, J.; Luo, Z.; Liu, X. Comparison and Analysis of Three Methods for Dynamic Height Error Correction in GNSS-IR Sea Level Retrievals. Remote Sens. 2024, 16, 3599. [Google Scholar] [CrossRef]
- Larson, K.M. GPS interferometric reflectometry: Applications to surface soil moisture, snow depth, and vegetation water content in the western United States. WIREs Water. 2016, 3, 775–787. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Bennett, G. The calculation of astronomical refraction in marine navigation. J. Navig. 1982, 35, 255–259. [Google Scholar] [CrossRef]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in 560 the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef]
- Stephenson, A. Harmonic Analysis of Tides Using TideHarmonics. 2016. Available online: https://CRAN.R-project.org/package=TideHarmonics (accessed on 30 June 2025).


| Satellite System | Frequency Band | Frequency (MHz) | Wavelength (m) |
|---|---|---|---|
| GPS | L1 | 1575.42 | 0.190 |
| L2C | 1227.6 | 0.244 | |
| L5 | 1176.45 | 0.255 | |
| GLONASS | G1 | ~1602 | ~0.187 |
| G2 | ~1246 | ~0.241 | |
| Galileo | E1 | 1575.42 | 0.190 |
| E5a | 1176.45 | 0.255 | |
| E5b | 1297.140 | 0.248 | |
| E5 (E5a + E5b) | 1191.795 | 0.252 | |
| BDS | B1 | 1561.098 | 0.192 |
| B2 | 1207.14 | 0.248 | |
| B3 | 1268.52 | 0.236 |
| Satellite System | Frequency Band | Uncorrected | Tidal Analysis | Cubic Spline Fitting | Our Method | ||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | ||
| GPS | L1 | 3958 | 25.5 | 3830 | 13.4 | 3893 | 21.7 | 3943 | 16.7 |
| L2C | 10,007 | 26.8 | 9779 | 15.6 | 9967 | 19.3 | 9997 | 15.6 | |
| L5 | 8587 | 27.9 | 8460 | 17.0 | 8500 | 20.3 | 8581 | 15.0 | |
| GLONASS | G1 | 6139 | 27.4 | 5966 | 12.9 | 6075 | 23.2 | 6122 | 17.1 |
| G2 | 8074 | 22.2 | 8003 | 13.3 | 7985 | 18.3 | 8073 | 14.9 | |
| Galileo | E1 | 3148 | 27.4 | 3050 | 16.9 | 3027 | 25.9 | 3136 | 19.4 |
| E5a | 9994 | 31.7 | 9823 | 21.4 | 9930 | 19.4 | 9991 | 14.9 | |
| E5b | 9156 | 30.6 | 8978 | 20.7 | 9106 | 20.4 | 9150 | 15.3 | |
| E5 | 8015 | 28.2 | 7866 | 18.4 | 7956 | 19.0 | 8004 | 14.7 | |
| BDS | B1 | 734 | 22.7 | 718 | 13.0 | 445 | 21.6 | 734 | 15.5 |
| B2 | 1434 | 29.0 | 1406 | 18.4 | 1008 | 24.1 | 1434 | 14.6 | |
| B3 | 2367 | 26.8 | 2339 | 17.5 | 1932 | 23.0 | 2365 | 16.2 | |
| Satellite System | Frequency Band | Uncorrected | Tidal Analysis | Cubic Spline Fitting | Our Method | ||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | ||
| GPS | L1 | 4113 | 16.3 | 4069 | 12.2 | 4061 | 15.3 | 4082 | 12.4 |
| L2C | 8854 | 14.9 | 8777 | 12.0 | 8801 | 12.2 | 8814 | 10.8 | |
| L5 | 7155 | 14.0 | 7096 | 11.0 | 7060 | 10.1 | 7092 | 9.2 | |
| GLONASS | G1 | 10,331 | 14.9 | 10,224 | 9.8 | 10,233 | 12.0 | 10,265 | 10.0 |
| G2 | 13,199 | 12.6 | 13,099 | 10.5 | 13,074 | 9.9 | 13,157 | 9.7 | |
| Galileo | E1 | 3297 | 15.1 | 3271 | 12.5 | 3257 | 14.5 | 3274 | 11.8 |
| E5a | 5325 | 13.7 | 5280 | 10.8 | 5282 | 11.9 | 5311 | 9.0 | |
| E5b | 5354 | 14.2 | 5312 | 11.2 | 5306 | 12.3 | 5335 | 9.7 | |
| E5 | 5303 | 13.3 | 5258 | 10.5 | 5252 | 11.6 | 5290 | 9.2 | |
| BDS | B1 | 717 | 14.5 | 716 | 12.0 | 456 | 13.5 | 716 | 11.1 |
| B2 | 1200 | 14.5 | 1194 | 12.2 | 974 | 13.0 | 1193 | 10.5 | |
| Satellite System | Frequency Band | Uncorrected | Tidal Analysis | Cubic Spline Fitting | Our Method | ||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | ||
| GPS | L1 | 37 | 28.8 | 29 | 14.4 | 29 | 22.4 | 33 | 20.4 |
| L2C | 51 | 20.1 | 48 | 15.9 | 51 | 12.7 | 51 | 11.7 | |
| L5 | 36 | 17.9 | 34 | 13.5 | 32 | 15.6 | 34 | 14.5 | |
| GLONASS | G1 | 56 | 18.8 | 54 | 11.1 | 53 | 9.8 | 55 | 10.5 |
| G2 | 71 | 15.7 | 68 | 12.8 | 65 | 13.8 | 70 | 12.8 | |
| Galileo | E1 | 26 | 28.3 | 26 | 26.8 | 24 | 26.0 | 23 | 16.5 |
| E5a | 32 | 20.5 | 29 | 16.8 | 32 | 16.8 | 31 | 9.2 | |
| E5b | 33 | 20.8 | 31 | 15.6 | 33 | 17.6 | 31 | 13.3 | |
| E5 | 32 | 19.0 | 30 | 15.2 | 31 | 17.7 | 31 | 9.1 | |
| BDS | B1 | 5 | 16.7 | 5 | 12.8 | 4 | 9.4 | 5 | 9.3 |
| B2 | 6 | 19.7 | 6 | 15.9 | 4 | 11.7 | 6 | 10.5 | |
| Satellite System | Frequency Band | Uncorrected | Tidal Analysis | Cubic Spline Fitting | Our Method | ||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | Number of Retrievals | RMSE (cm) | ||
| GPS | L1 | 31 | 22.5 | 26 | 16.7 | 30 | 19.2 | 30 | 19.3 |
| L2C | 56 | 21.3 | 42 | 13.8 | 54 | 18.2 | 54 | 18.9 | |
| L5 | 41 | 15.4 | 33 | 10.5 | 40 | 9.1 | 40 | 8.2 | |
| GLONASS | G1 | 49 | 21.5 | 39 | 7.8 | 46 | 16.3 | 47 | 15.8 |
| G2 | 75 | 14.7 | 63 | 12.3 | 72 | 10.9 | 73 | 11.6 | |
| Galileo | E1 | 21 | 22.1 | 19 | 21.6 | 20 | 20.3 | 19 | 17.4 |
| E5a | 36 | 20.3 | 25 | 7.3 | 35 | 10.3 | 35 | 12.0 | |
| E5b | 34 | 19.9 | 26 | 7.8 | 33 | 11.9 | 33 | 12.1 | |
| E5 | 36 | 19.1 | 26 | 7.9 | 35 | 9.8 | 35 | 11.1 | |
| BDS | B1 | 6 | 17.0 | 5 | 8.4 | 4 | 12.6 | 6 | 7.6 |
| B2 | 11 | 11.2 | 10 | 8.0 | 11 | 9.6 | 11 | 9.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Zhang, Z.; Liu, X. An Integrated Method for Dynamic Height Error Correction in GNSS-IR Sea Level Retrievals. Remote Sens. 2025, 17, 3076. https://doi.org/10.3390/rs17173076
Hu Y, Zhang Z, Liu X. An Integrated Method for Dynamic Height Error Correction in GNSS-IR Sea Level Retrievals. Remote Sensing. 2025; 17(17):3076. https://doi.org/10.3390/rs17173076
Chicago/Turabian StyleHu, Yufeng, Zhiyu Zhang, and Xi Liu. 2025. "An Integrated Method for Dynamic Height Error Correction in GNSS-IR Sea Level Retrievals" Remote Sensing 17, no. 17: 3076. https://doi.org/10.3390/rs17173076
APA StyleHu, Y., Zhang, Z., & Liu, X. (2025). An Integrated Method for Dynamic Height Error Correction in GNSS-IR Sea Level Retrievals. Remote Sensing, 17(17), 3076. https://doi.org/10.3390/rs17173076







