Study on the Design of Broadcast Ephemeris Parameters for Low Earth Orbit Satellites

Abstract

The integration of low Earth orbit (LEO) satellite constellations into the Global Navigation Satellite System (GNSS) has emerged as a prominent research focus, as LEO satellites can significantly enhance the precision of GNSS positioning, navigation, and timing (PNT) services. In the design of LEO navigation constellations, the development of an efficient broadcast ephemeris model is critical for delivering high-accuracy navigation solutions. This study extends the conventional 16-parameter Keplerian broadcast ephemeris model by proposing enhanced 18-, 20-, 22-, and 24-parameter models, ensuring compatibility with existing GNSS ephemeris standards. The performance of these models was evaluated using precise science orbit from five satellites at varying altitudes, ranging from 320 km to 1336 km. By analyzing fitting errors, Signal-in-Space Range Error (SISRE), and Message Size Bits (MSB) across different fitting arc durations and parameter counts, the optimal model configuration was identified. The results demonstrate that the 22-parameter model, which was constructed by augmenting the standard 16-parameter ephemeris with $(\dot{a}$, $\dot{n}$, $Crs3$, $Crc3$, $Crs1$, $Crc1$) delivers the best balance of accuracy and efficiency. With a fitting arc length of 20 min, the SISRE for the GRACE-A (320 km), GRACE-C (475 km), Sentinel-2A (786 km), HY-2A (966 km), and Sentinel-6A (1336 km) satellites were measured at 8.88 cm, 6.21 cm, 2.87 cm, 2.11 cm, and 0.75 cm, respectively. Meanwhile, the corresponding MSB remained compact at 501, 490, 491, 487, and 476 bits. These findings confirm that the proposed 22-parameter broadcast ephemeris model meets the stringent accuracy requirements for next-generation LEO-augmented GNSSs, paving the way for enhanced global navigation services.

1. Introduction

After 50 years of development, the Global Navigation Satellite System (GNSS) comprises four major systems with approximately 150 satellites, namely the U.S. GPS, Europe’s Galileo, Russia’s GLONASS, and China’s BDS [1,2,3]. GNSS can provide global users with all-weather, round-the-clock, and high-precision positioning, navigation, and timing (PNT) services, playing an irreplaceable role in disaster monitoring, transportation, economic development, geoscience research, and other fields [4,5,6]. Except for BDS, which adopts a multi-constellation combination of medium Earth orbit (MEO) satellites, geostationary orbit (GEO) satellites, and inclined geostationary orbit (IGSO) satellites, other GNSSs primarily use MEO satellites, while low Earth orbit (LEO) satellite constellations have not yet been adopted [7,8,9].

Many governments and enterprises around the world are constructing mega-LEO (Low Earth Orbit) satellite constellations. The State Council Information Office of the People’s Republic of China has mentioned that the design of the next-generation BeiDou Navigation System will integrate high, medium, and low-orbit constellations to achieve higher precision, greater security, and more user-friendly Positioning, Navigation, Timing, Remote Sensing, and Communication (PNTRC) services [10,11]. Companies such as OneWeb, SpaceX, Boeing, and Samsung are building mega-LEO satellite constellations to provide internet communications, Internet of Things, and navigation augmentation services [12]. With the widespread application of GNSS, issues such as weak signals prone to obstruction, interference, and spoofing have become increasingly evident. Signals transmitted by LEO satellites, with their higher power and broader bandwidth, can fundamentally address these problems [13,14,15]. The geometric configuration of LEO in the sky undergoes changes far more rapidly than that of GEO and MEO. This rapidly varying spatial distribution offers unique advantages for Precise Point Positioning (PPP). With more observation angles and more frequent orbit updates, the convergence time of positioning results can be significantly shortened [16,17,18]. In addition, the high-speed relative motion between satellites and receivers generates more significant Doppler frequency shifts, which makes LEO satellites promising to achieve more excellent performance in Doppler positioning [19,20,21]. Undoubtedly, LEO satellite constellations will play a pivotal role in future PNT systems [22,23,24]. However, the design of broadcast ephemeris schemes is a critical aspect of utilizing LEO satellites to provide PNT services.

Currently, broadcast ephemeris models are primarily divided into two types. The first is the Keplerian ephemeris model, which describes satellite motion by adding short-term and long-term perturbation parameters to the Keplerian elements. For example, the D1/D2 navigation messages broadcast by BeiDou-2 on the B1I/B3I signals and the B-CNAV1/B-CNAV2/B-CNAV3 navigation messages broadcast by BeiDou-3 on the B1C/B2a/B2b signals adopt this model [25,26]. Additionally, both GPS and Galileo also employ this type of broadcast ephemeris model. The second is the Cartesian ephemeris model, which describes satellite motion using coordinates, velocities, and numerical integration. Currently, only GLONASS adopts this ephemeris model [27]. Meng et al. designed an integration-type ephemeris model for LEO satellites and analyzed the impact of factors such as integration step size, integration method, and integration arc length on fitting accuracy [28]. Compared to the Cartesian ephemeris model, the Keplerian ephemeris model does not require users to perform complex numerical integration and more intuitively reflects the characteristics of satellite motion. However, the Keplerian ephemeris model has two well-known drawbacks: the difficulty in determining the perigee for near-circular orbits and the ambiguity in the right ascension of the ascending node (RAAN) when the orbital inclination approaches zero. To address these issues, many scholars and engineers have proposed solutions. For instance, Montenbruck and his team introduced a set of improved nonsingular Keplerian elements to avoid direct perigee calculation [29]. Xie et al. adopted a similar approach for designing LEO satellite broadcast ephemeris, achieving a fitting accuracy better than 10 cm [30]. Ruan and Choi et al. proposed rotating small-inclination orbits by 5° before fitting the orbital elements to resolve the ambiguity in RAAN definition [31,32]. This method has already been applied to the broadcast ephemeris of BeiDou GEO satellites. Meng and Du et al. pointed out that rotating the orbit to eliminate singularities in orbital fitting is not only time-consuming but also results in lower fitting accuracy compared to other orbit types. They proposed a new orbital element scheme that demonstrates superior performance in fitting accuracy for both GEO satellites and small-inclination LEO satellites [7,33].

As mentioned above, many researchers have designed various broadcast ephemeris models for LEO satellites, but most focus on achieving higher fitting accuracy while neglecting the design and analysis of the Least Significant Bit (LSB) and Message Size Bit (MSB). In terms of parameter scheme design, instead of redesigning a new set of broadcast ephemeris parameters or optimizing the Cartesian ephemeris model, we have chosen to introduce new parameters based on the existing 16-parameter model of GNSS broadcast ephemerides to achieve higher orbit fitting accuracy. The newly added parameters maintain the same types as those in the 16-parameter model but with adjusted orders and frequencies. This approach ensures that user algorithms remain largely consistent with those currently used for the ephemerides of GPS, BDS, and Galileo, thereby achieving strong compatibility. Furthermore, two notable limitations of the Keplerian broadcast ephemeris can be addressed through algorithm optimization and the introduction of constraint conditions. We adopt a solution similar to that proposed by Xie et al. to address the singularity issue in near-circular orbits. Additionally, science small-inclination LEO satellites are less common due to their limited service coverage and lower commercial value, and this study does not consider the ambiguity of RAAN caused by low orbital inclination.

In this study, we first introduce the ephemeris design scheme and user algorithm. In the subsequent sections, we present the calculation methods for LSB and MSB, as well as the ephemeris fitting process. Finally, we select precise science orbit from five LEO satellites at different orbital altitudes to analyze the influence of different parameter schemes, fitting arc lengths, and orbital altitudes on LSB, MSB, and fitting accuracy. Increasing the number of parameters can improve the orbital fitting accuracy of the ephemeris model, but it also leads to an increase in the length of navigation message. Moreover, different parameters vary in their efficiency in enhancing orbital fitting accuracy. After comprehensively considering the balance between fitting accuracy and MSB, it is recommended to adopt the 22-parameter ephemeris model.

2. Methods

2.1. Ephemeris Parameters Design

Both the GPS LNAV navigation message and the BeiDou D2 navigation message describe satellite motion using the six Keplerian elements ($a$, $e$, $i$, $\mathsf{\Omega }$, $\omega$, $M$) supplemented by nine perturbation parameters. These perturbation parameters can be divided into two categories: one corrects long-period variations in orbital elements ($\mathsf{\Delta }n,\dot{ \mathrm{i}}, \dot{\mathsf{\Omega }})$, while the other corrects short-period variations in satellite motion within the orbital coordinate system $(Crc2, Crs2, Cuc2, Cus2, Cic2, Cis2)$. Together with the reference epoch time $t_{oe}$, these form a total of 16 parameters. Additionally, the GPS CNAV navigation message and the BeiDou B-CNAV1 navigation message replace $\sqrt{a}$ with $a_{ref}+\mathsf{\Delta }a$ to reduce message length while retaining the original 16 ephemeris parameters. They also introduce ($\dot{a},\dot{n}$) to capture trend variations in the semimajor axis and mean motion.

Compared to MEO, GEO, and IGSO satellites, LEO satellites are more significantly affected by atmospheric drag and higher-order terms of Earth’s non-spherical gravitational perturbations, resulting in more complex dynamic characteristics. The 16-parameter ephemeris model cannot meet the required fitting accuracy. Therefore, we enhance the fitting precision by adding more perturbation parameters beyond the basic 16 parameters. The reason for not expanding the 18-parameter model (which includes $\dot{a}$ and $\dot{n}$) is that these terms are not the optimal choice for improving LEO ephemeris fitting accuracy.

Table 1. Descriptions of basic parameters and additional parameters.

Description	Basic Parameters	Additional Parameters
Ephemeris reference time	$t_{oe}$	-
Orbital elements	$\sqrt{a}, e, i_0, {\mathsf{\Omega }}_0, \omega , M_0$	-
Orbital element correction terms	$\mathsf{\Delta }n, \dot{i}, \dot{\mathsf{\Omega }}$	$\dot{a}, \dot{n}, \ddot{i}, \ddot{\mathsf{\Omega }}, \ddot{a}, \ddot{n}$
Along-track oscillating terms	$Cuc2, Cus2$	$Cuc1, Cus1, Cuc3, Cus3$
Cross-track oscillating terms	$Cic2, Cis2$	$Cic1, Cis1, Cic3, Cis3$
Radial oscillating terms	$Crc2, Crs2$	$Crc1, Crs1, Crc3, Crs3$

summarizes the ephemeris parameters, which include the first- and second-order time derivatives of the semimajor axis, mean motion, RAAN (Right Ascension of the Ascending Node), and inclination, as well as first- to third-order harmonic correction terms in the Along-track, Cross-track, and Radial directions.

When adding additional parameters to the basic parameter set, the following rules should be observed: For orbital element correction terms, first-order terms should be added before second-order terms. That is, $\dot{a}$ should be added prior to $\ddot{a}$, and $\ddot{a}$ should not be added alone. Harmonic correction terms (sine and cosine components) should be introduced in pairs. For example, $Cuc3$ and $Cus3$ should be added simultaneously [30]. In this study, we select parameters from the additional parameters and incorporate them into the Basic parameters to identify the optimal combination.

2.2. User Algorithm

Users need to use the user algorithm compatible with the broadcast ephemeris parameters to calculate the satellite coordinates in the Earth-Centered Earth-Fixed (ECEF) coordinate system. Additionally, in the fitting of broadcast ephemeris parameters, the derivative relationship between the satellite coordinates and the ephemeris parameters must be derived using the user algorithm. The following presents the user algorithm for calculating the satellite coordinates at time $t_k$, which includes all 16 basic parameters as well as all additional parameters, although in some schemes only a few of the additional parameters are used. The operations involving additional parameters in the user algorithm have been bolded for emphasis.

First, compute the orbital semi-major axis $a_k$ and the mean angular velocity $n$:

$$\begin{array}{l}a={\left(\sqrt{a}\right)}^2\\ a_k=a+\dot{\mathit{a}}\left({\mathit{t}}_{\mathit{k}}-{\mathit{t}}_{\mathit{o}\mathit{e}}\right)+{\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}\ddot{\mathit{a}}{({\mathit{t}}_{\mathit{k}}-{\mathit{t}}_{\mathit{o}\mathit{e}})}^{\mathbf{2}}\\ n=\sqrt{{\displaystyle \frac{\mu }{a^3}}}+\Delta n+\dot{\mathit{n}}\left({\mathit{t}}_{\mathit{k}}-{\mathit{t}}_{\mathit{o}\mathit{e}}\right)+{\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}\ddot{\mathit{n}}{({\mathit{t}}_{\mathit{k}}-{\mathit{t}}_{\mathit{o}\mathit{e}})}^{\mathbf{2}}\end{array}$$

(1)

where $\mu$ is the Earth’s gravitational constant, with a value of $\mu =3.986004418\times {10}^{14}$. Then, calculate the true anomaly $v_k$ and the uncorrected argument of latitude $\overline{u}$ based on Kepler’s equation:

$$\begin{array}{l}M=M_0+n\left(t_k-t_{oe}\right)\\ E-esinE=M\\ tan{\displaystyle \frac{v_k}{2}}=\sqrt{{\displaystyle \frac{1+e}{1-e}}}tan{\displaystyle \frac{E}{2}}\end{array}$$

(2)

$$\overline{u}=\omega +v_k$$

(3)

Next, compute the argument of latitude $u$, the radial distance $r$, and the inclination $i$:

$$\begin{array}{l}u=\overline{u}+\delta u\\ r=a_k\left(1-ecosE\right)+\delta r\\ i=i_0+\dot{i}\left(t_k-t_{oe}\right)+{\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}\ddot{\mathit{i}}{({\mathit{t}}_{\mathit{k}}-{\mathit{t}}_{\mathit{o}\mathit{e}})}^{\mathbf{2}}+\delta i\end{array}$$

(4)

where $\delta u$, $\delta r$, and $\delta i$ represent harmonic correction terms, computed as follows:

$$\begin{array}{l}\delta u=\mathit{C}\mathit{u}\mathit{s}\mathbf{1}\mathit{s}\mathit{i}\mathit{n}\overline{\mathit{u}}+\mathit{C}\mathit{u}\mathit{c}\mathbf{1}\mathit{c}\mathit{o}\mathit{s}\overline{\mathit{u}}+Cus2sin2\overline{u}+Cuc2cos2\overline{u}+\mathit{C}\mathit{u}\mathit{s}\mathbf{3}\mathit{s}\mathit{i}\mathit{n}\mathbf{3}\overline{\mathit{u}}+\mathit{C}\mathit{u}\mathit{c}\mathbf{3}\mathit{c}\mathit{o}\mathit{s}\mathbf{3}\overline{\mathit{u}}\\ \delta r=\mathit{C}\mathit{r}\mathit{s}\mathbf{1}\mathit{s}\mathit{i}\mathit{n}\overline{\mathit{u}}+\mathit{C}\mathit{r}\mathit{c}\mathbf{1}\mathit{c}\mathit{o}\mathit{s}\overline{\mathit{u}}+Crs2sin2\overline{u}+Crc2cos2\overline{u}+\mathit{C}\mathit{r}\mathit{s}\mathbf{3}\mathit{s}\mathit{i}\mathit{n}\mathbf{3}\overline{\mathit{u}}+\mathit{C}\mathit{r}\mathit{c}\mathbf{3}\mathit{c}\mathit{o}\mathit{s}\mathbf{3}\overline{\mathit{u}}\\ \delta i=\mathit{C}\mathit{i}\mathit{s}\mathbf{1}\mathit{s}\mathit{i}\mathit{n}\overline{\mathit{u}}+\mathit{C}\mathit{i}\mathit{c}\mathbf{1}\mathit{c}\mathit{o}\mathit{s}\overline{\mathit{u}}+Cis2sin2\overline{u}+Cic2cos2\overline{u}+\mathit{C}\mathit{i}\mathit{s}\mathbf{3}\mathit{s}\mathit{i}\mathit{n}\mathbf{3}\overline{\mathit{u}}+\mathit{C}\mathit{i}\mathit{c}\mathbf{3}\mathit{c}\mathit{o}\mathit{s}\mathbf{3}\overline{\mathit{u}}\end{array}$$

(5)

Furthermore, the right ascension of the ascending node is calculated as follows:

$$\mathsf{\Omega }={\mathsf{\Omega }}_0+\dot{\mathsf{\Omega }}\left(t_k-t_{oe}\right)+{\displaystyle \frac{\mathbf{1}}{\mathbf{2}}}\ddot{\mathbf{\Omega }}{({\mathit{t}}_{\mathit{k}}-{\mathit{t}}_{\mathit{o}\mathit{e}})}^{\mathbf{2}}-{\omega }_e{t}_k$$

(6)

where ${\omega }_e=7.292115\times {10}^{-5}$ rad/s is the Earth’s rotation rate. Finally, the satellite’s coordinates in ECEF are obtained as follows:

$$\left[\begin{array}{c}{x}_{sat}\\ y_{sat}\\ z_{sat}\end{array}\right]=R_3(-\mathsf{\Omega })R_1(-i)\left[\begin{array}{c}rcosu\\ rsinu\\ 0\end{array}\right]$$

(7)

2.3. Ephemeris Fitting Strategy

This study employs ($e_x$, $e_y$, $\lambda$) to replace ($e$, $\omega$, $M$) in order to address issues such as the ambiguity of the argument of perigee and mean anomaly in near-circular orbits, as well as the potential singularity in the design matrix. The two parameter sets are equivalent and can be transformed as follows:

$$\begin{array}{c}\begin{array}{ccc}{e}_x=ecos\omega & e_y=esin\omega & \lambda =\omega +M\end{array}\\ \begin{array}{ccc}e=\sqrt{e_x^{\mathit{2}}+e_y^{\mathit{2}}}& \omega =arctan({\displaystyle \frac{e_y}{e_x}})& M=\lambda -\omega \end{array}\end{array}$$

(8)

To ensure better compatibility with existing broadcast ephemeris schemes, ($e_x$, $e_y$, $\lambda$) is only used during the parameter fitting process and not adopted in the design of the ephemeris parameters.

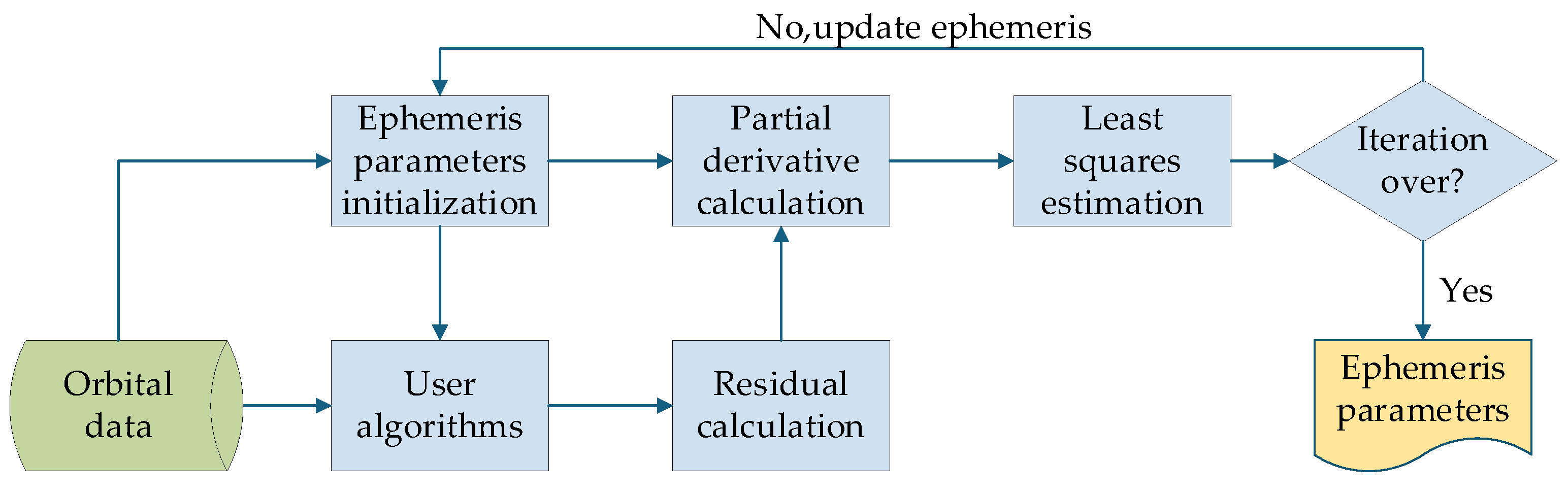
Figure 1 illustrates the workflow for LEO ephemeris parameter fitting in the ECEF. In the ephemeris parameter initialization phase, the satellite’s position and velocity at the reference epoch are converted into Keplerian orbital elements, with all correction terms set to zero. The user algorithm is then employed to compute the satellite coordinates at each epoch within the fitting arc. These computed coordinates are differenced with the orbital data to obtain residual vectors. Concurrently, the partial derivatives of the satellite coordinates in ECEF with respect to the ephemeris parameters are calculated for each epoch. The detailed methodology for computing these partial derivatives has been thoroughly described in the works of Cui and Xie [30,34] and is not reiterated here. Finally, a least-squares estimation is applied to determine the ephemeris parameters. As this constitutes a nonlinear parameter estimation problem, multiple iterative computations are required. The iteration termination criteria are defined as either the difference in root-mean-square (RMS) values of residual vectors between two consecutive iterations falling below 0.1 mm or the number of iterations exceeding 100.

2.4. SISRE Computation

The orbital coordinate system can more intuitively describe the ephemeris fitting error $∆\mathit{r}=\left[\begin{array}{ccc}{∆r}_R& {∆r}_A& {∆r}_C\end{array}\right]$, but it cannot directly illustrate the impact of fitting errors on user positioning. Users are more concerned about the Signal-in-Space Range Error (SISRE) caused by satellite orbits. This study focuses exclusively on orbital errors originating from ephemeris fitting, excluding contributions from orbit determination errors and clock biases. Since the line-of-sight direction between the satellite and the user cannot be obtained when evaluating ephemeris fitting errors, we adopt the calculation method proposed by Reid [12]:

$$SISRE=\sqrt{w_R^2{R}^2+w_{A,C}^2(A^2+C^2)}$$

(9)

where $R=rms\left({∆r}_R\right)$, $A=rms\left({∆r}_A\right)$, and $C=rms\left({∆r}_C\right)$ represent the RMS of the radial, along-track, and cross-track components of the orbit fitting errors, respectively. The weighting factors $w_R$ and $w_{A,C}$ reflect the relative contributions of orbital errors in different directions to the SISRE.

The values of $w_R$ and $w_{A,C}$ are dependent on orbital altitude. For instance, in BDS, GEO and IGSO satellites use $w_R=0.99$ and $w_{A,C}=0.089$, while MEO satellites adopt $w_R=0.98$ and $w_{A,C}=0.136$ [35].

Table 2. SISRE weight factors for different orbital altitudes LEOs.

Orbital Altitude (km)	${\mathit{w}}_{\mathit{R}}$	${\mathit{w}}_{\mathit{A},\mathit{C}}$	Orbital Altitude (km)	${\mathit{w}}_{\mathit{R}}$	${\mathit{w}}_{\mathit{A},\mathit{C}}$
400	0.419	0.642	1000	0.582	0.575
600	0.488	0.617	1200	0.618	0.556
800	0.540	0.595	1400	0.648	0.539

presents the specific values of $w_R$ and $w_{A,C}$ for LEO satellites with orbital altitudes ranging from 400 km to 1400 km, consistent with the approach employed by Xie, Meng, and colleagues in previous studies [28,30].

2.5. LSB and MSB Computation

The design of broadcast ephemeris should not only pursue higher fitting accuracy but also analyze the minimum word length required for each parameter to meet precision requirements, thereby reducing its demand on broadcast bandwidth. The LSB describes the representation accuracy of ephemeris parameters, i.e., the numerical truncation error incurred when ephemeris parameters are converted from the real number domain to the integer domain required for ephemeris broadcasting. In this study, the orbital error caused by numerical truncation is set to be on the millimeter scale. The MSB describes the number of bits required for broadcasting ephemeris parameters in the integer domain. During ephemeris compilation, it is necessary to design the number of MSB allocated to each ephemeris parameter to ensure the correct broadcasting of ephemeris parameters. The calculation process for the LSB and MSB of broadcast ephemeris parameters is as follows:

First, compute the partial derivatives of the satellite coordinates with respect to each broadcast ephemeris parameter, expressed as ${\displaystyle \frac{\mathit{\partial }\mathit{r}}{\mathit{\partial }{x}_i}}={\left[\begin{array}{ccc}{\displaystyle \frac{\mathit{\partial }{x}_{sat}}{\mathit{\partial }{x}_i}}& {\displaystyle \frac{\mathit{\partial }{y}_{sat}}{\mathit{\partial }{x}_i}}& {\displaystyle \frac{\mathit{\partial }{z}_{sat}}{\mathit{\partial }{x}_i}}\end{array}\right]}^T$. This vector has already been calculated during the ephemeris fitting process and will not be elaborated further here. Note that while the ephemeris fitting procedure computes partial derivatives with respect to ($e_x$, $e_y$, $\lambda$), the LSB calculation requires derivatives with respect to ($e$, $\omega$, $M$). The derivation is straightforward and is directly given below:

$$\begin{array}{c}{\displaystyle \frac{\mathit{\partial }\mathit{r}}{\mathit{\partial }e}}={\displaystyle \frac{\mathit{\partial }\mathit{r}}{\mathit{\partial }{e}_x}}\mathit{cos}\left(\omega \right)+{\displaystyle \frac{\mathit{\partial }\mathit{r}}{\mathit{\partial }{e}_y}}\mathit{sin}\left(\omega \right)\\ {\displaystyle \frac{\mathit{\partial }\mathit{r}}{\mathit{\partial }\omega }}=-e{\displaystyle \frac{\mathit{\partial }\mathit{r}}{\mathit{\partial }{e}_x}}\mathit{sin}\left(\omega \right)+e{\displaystyle \frac{\mathit{\partial }\mathit{r}}{\mathit{\partial }{e}_y}}\mathit{cos}\left(\omega \right)\\ {\displaystyle \frac{\mathit{\partial }\mathit{r}}{\mathit{\partial }M}}={\displaystyle \frac{\mathit{\partial }\mathit{r}}{\mathit{\partial }\lambda }}\end{array}$$

(10)

Therefore, according to the law of covariance propagation, the orbital computation error $∆\mathit{r}$ caused by broadcast ephemeris parameter errors ${∆x}_i$ can be expressed as follows:

$$∆\mathit{r}={\displaystyle \frac{\mathit{\partial }\mathit{r}}{\mathit{\partial }{x}_i}}{{∆x}_i}^2{{\displaystyle \frac{\mathit{\partial }\mathit{r}}{\mathit{\partial }{x}_i}}}^T$$

(11)

where the diagonal elements of the covariance matrix $∆\mathit{r}$ correspond to ${∆x}_{sat}^2$, ${∆y}_{sat}^2$, and ${∆z}_{sat}^2$.

Then, by setting $\sqrt{{∆x}_{sat}^2+{∆y}_{sat}^2+{∆z}_{sat}^2}=1 \mathrm{mm}$, the maximum truncation error of the broadcast ephemeris parameters can be calculated using the following equation:

$$\Delta X_i^{*}={\displaystyle \frac{0.001}{\sqrt{{\frac{\partial \mathit{r}}{\partial x_i}}^T\frac{\partial \mathit{r}}{\partial x_i}}}}=2^{d_i}$$

(12)

Finally, for parameter $x_i$, its message unit $2^{{LSB}_i}$, the corresponding parameter $X_i^b$ to be embedded in the message, and the required message size ${MSB}_i$ for broadcast parameter $X_i^b$ can be calculated according to the following equations:

$$\begin{array}{c}{LSB}_i=floor \left(d_i\right)\\ X_i^b=int({\displaystyle \frac{X_i}{2^{{LSB}_i}}})\\ {MSB}_i=ceiling \left({\mathit{log}}_2\left|X_i^b\right|\right)\end{array}$$

(13)

For the semi-major axis and eccentricity in the broadcast ephemeris, whose theoretical values are strictly positive, the valid range is $(0,+2^{M_i})$, requiring an information length of $L_i$ bits. For other parameters such as orbital inclination, right ascension of the ascending node, and perturbation terms, which can be either positive or negative, the range extends to $(-2^{M_i},+2^{M_i})$. These require an additional sign bit, resulting in an information length of $L_i+1$ bits.

Furthermore, each fitting arc yields a distinct set of broadcast ephemeris parameters with corresponding LSB and MSB values. The LSB values may vary across different fitting arcs, in which case the minimum LSB should be selected, while the maximum MSB should be adopted to accommodate all possible cases.

3. Results

This study selected precise science orbit (PSO) from five LEO satellites including GRACE-A/C, Sentinel-2A/6A, and HY-2A to evaluate and compare broadcast ephemeris design schemes. With orbital altitudes ranging from 320 km to 1300 km, these satellites comprehensively cover the typical altitude range of LEO applications. Analyzing the performance of different broadcast ephemeris design schemes across these satellites provides valuable insights for the development of LEO navigation constellations and the optimization of ephemeris parameter design.

Table 3. Basic orbit information for satellites used in this study.

Satellite Name	Attitude (km)	Inclination ($\mathbf{°}$)	Eccentricity	Period (min)	Orbit Data Date
GRACE-A	320	89	0.0021	90	1 June 2017
GRACE-C	475	89	0.0026	94	1 January 2024
Sentinel-2A	786	99	0.0013	101	1 January 2024
HY-2A	966	99	0.0013	104	1 January 2018
Sentinel-6A	1336	66	0.0006	112	1 January 2024

summarizes the orbital characteristics of these satellites.

We augmented the standard 16-parameter broadcast ephemeris by adding 2, 4, 6, and 8 additional parameters to analyze their effects on fitting errors in the radial, along-track, and cross-track directions, as well as on SISRE. Fitting arc lengths of 20 min and 30 min were selected.

Table 4. Fit error results for GACE-A in the along-track (A), cross-track (C), and radial (R) components, combined with SISREs, using 20/30 min fit intervals (unit: cm).

Number of Parameters	Additional Parameters	20 min				30 min
		A	C	R	SISRE	A	C	R	SISRE
16	-	41.75	7.71	24.95	37.66	96.99	21.60	67.37	90.78
18	$\dot{a}$$, \dot{n}$	22.16	7.54	13.79	20.77	57.64	21.30	42.67	56.46
	$Crs1, Crc1$	11.05	7.49	24.07	18.90	29.01	21.35	63.77	50.37
	$Cus1, Cuc1$	11.05	7.49	24.07	18.90	29.01	21.35	63.76	50.36
	$Crs3, Crc3$	11.66	7.49	15.62	15.01	32.05	21.38	38.80	39.80
20	$\dot{a}, \dot{n}, Crs3, Crc3$	7.15	7.50	9.71	10.41	21.26	21.32	26.18	29.48
	$\dot{a}, \dot{n}, Cus3, Cuc3$	6.66	7.50	13.51	11.88	18.36	21.30	41.35	34.99
	$Crs1$$, Crc1$$, Crs3$$, Crc3$	11.05	7.49	8.56	12.04	29.01	21.35	24.36	32.89
	$Cus1$$, Cuc1$$, Crs3$$, Crc3$	11.05	7.49	8.56	12.04	29.02	21.35	24.36	32.89
22	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$	6.90	7.50	5.40	8.88	19.98	21.30	16.80	25.80
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$	6.90	7.50	5.40	8.88	19.98	21.30	16.80	25.80
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis1$$, Cic1$	7.14	3.08	9.70	8.85	21.26	9.45	26.18	25.19
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis3$$, Cic3$	7.14	2.98	9.71	8.83	21.26	8.83	26.18	25.05
24	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$$, Cis3$$, Cic3$	6.89	2.98	5.40	6.96	19.95	8.83	16.80	20.58
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis3$$, Cic3$	6.89	2.98	5.40	6.96	19.95	8.83	16.80	20.58
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis1$$, Cic1$	6.89	3.08	5.40	6.99	19.95	9.44	16.80	20.76
	$\dot{a}$$, \dot{n}, Crs3$$, Crc3$$, Crs1$$, Crc1$$, \ddot{i}$$, \ddot{\mathsf{\Omega }}$	6.89	3.11	5.40	6.99	19.95	9.60	16.80	20.81

The underlined parts achieve the minimum fit Error of Specified Directional Component for the same number of parameters.

,

Table 5. Fit error results for GRACE-C in the along-track (A), cross-track (C), and radial (R) components, combined with SISREs, using 20/30 min fit intervals (unit: cm).

Number of Parameters	Additional Parameters	20 min				30 min
		A	C	R	SISRE	A	C	R	SISRE
16	-	33.29	5.47	18.09	29.40	82.35	17.08	52.99	75.64
18	$\dot{a}$$, \dot{n}$	17.22	5.32	10.02	15.82	47.84	16.78	32.05	45.63
	$Crs1, Crc1$	8.05	5.27	17.36	13.96	22.77	16.67	49.81	40.31
	$Cus1, Cuc1$	8.05	5.27	17.35	13.95	22.77	16.67	49.82	40.31
	$Crs3, Crc3$	8.43	5.27	10.87	10.76	24.78	16.68	28.59	30.52
20	$\dot{a}, \dot{n}, Crs3, Crc3$	5.05	5.26	6.94	7.44	16.10	16.71	19.01	22.41
	$\dot{a}, \dot{n}, Cus3, Cuc3$	4.69	5.26	9.79	8.65	14.05	16.70	30.88	27.05
	$Crs1$$, Crc1$$, Crs3$$, Crc3$	8.05	5.27	5.68	8.54	22.77	16.67	17.53	25.30
	$Cus1$$, Cuc1$$, Crs3$$, Crc3$	8.05	5.27	5.68	8.54	22.77	16.67	17.53	25.30
22	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$	4.87	5.26	3.69	6.21	15.25	16.70	12.12	19.70
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$	4.87	5.26	3.69	6.21	15.25	16.70	12.12	19.70
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis1$$, Cic1$	5.04	1.73	6.94	6.30	16.06	6.87	19.01	18.86
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis3$$, Cic3$	5.04	1.65	6.94	6.29	16.06	6.35	19.01	18.74
24	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$$, Cis3$$, Cic3$	4.86	1.65	3.69	4.77	15.19	6.34	12.12	15.40
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis3$$, Cic3$	4.86	1.65	3.69	4.77	15.19	6.34	12.12	15.40
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis1$$, Cic1$	4.86	1.73	3.69	4.79	15.20	6.87	12.12	15.54
	$\dot{a}$$, \dot{n}, Crs3$$, Crc3$$, Crs1$$, Crc1$$, \ddot{i}$$, \ddot{\mathsf{\Omega }}$	4.86	1.75	3.69	4.79	15.20	7.00	12.12	15.57

The underlined parts achieve the minimum fit Error of Specified Directional Component for the same number of parameters.

,

Table 6. Fit error results for Sentinel-2A in the along-track (A), cross-track (C), and radial (R) components, combined with SISREs, using 20/30 min fit intervals (unit: cm).

Number of Parameters	Additional Parameters	20 min				30 min
		A	C	R	SISRE	A	C	R	SISRE
16	-	24.40	2.60	11.76	20.81	65.37	10.49	38.01	58.21
18	$\dot{a}$$, \dot{n}$	10.89	2.37	5.54	9.51	28.13	7.91	16.74	25.57
	$Crs1, Crc1$	4.61	2.32	11.20	9.14	28.11	2.57	16.74	24.93
	$Cus1, Cuc1$	4.61	2.32	11.20	9.14	28.11	2.65	16.74	24.93
	$Crs3, Crc3$	4.85	2.32	6.45	6.30	13.44	7.77	15.70	16.80
20	$\dot{a}, \dot{n}, Crs3, Crc3$	2.56	2.33	3.50	3.71	10.05	10.07	11.80	13.99
	$\dot{a}, \dot{n}, Cus3, Cuc3$	2.35	2.33	5.39	4.71	8.75	10.07	20.32	18.13
	$Crs1$$, Crc1$$, Crs3$$, Crc3$	4.61	2.32	2.87	4.51	14.98	10.02	10.71	15.98
	$Cus1$$, Cuc1$$, Crs3$$, Crc3$	4.61	2.32	2.87	4.51	14.98	10.02	10.71	15.98
22	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$	2.47	2.33	1.59	2.87	9.55	10.07	6.74	11.79
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$	2.47	2.33	1.59	2.87	9.54	10.07	6.74	11.79
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis1$$, Cic1$	2.55	0.67	3.50	3.28	9.99	3.09	11.80	11.84
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis3$$, Cic3$	2.55	0.64	3.50	3.28	9.99	2.78	11.80	11.80
24	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$$, Cis3$$, Cic3$	2.47	0.64	1.59	2.29	9.48	2.78	6.74	9.09
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis3$$, Cic3$	2.46	0.64	1.59	2.28	9.48	2.78	6.74	9.09
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis1$$, Cic1$	2.46	0.67	1.59	2.29	9.48	3.09	6.74	9.15
	$\dot{a}$$, \dot{n}, Crs3$$, Crc3$$, Crs1$$, Crc1$$, \ddot{i}$$, \ddot{\mathsf{\Omega }}$	2.47	0.68	1.59	2.29	9.48	3.16	6.74	9.16

The underlined parts achieve the minimum fit Error of Specified Directional Component for the same number of parameters.

,

Table 7. Fit error results for HY-2A in the along-track (A), cross-track (C), and radial (R) components, combined with SISREs, using 20/30 min fit intervals (unit: cm).

Number of Parameters	Additional Parameters	20 min				30 min
		A	C	R	SISRE	A	C	R	SISRE
16	-	21.18	2.01	9.33	17.63	63.18	8.39	33.01	54.50
18	$\dot{a}$$, \dot{n}$	9.27	1.77	4.51	7.94	34.48	10.11	21.16	31.78
	$Crs1, Crc1$	3.36	1.71	8.80	7.30	14.98	10.02	35.42	29.51
	$Cus1, Cuc1$	3.36	1.71	8.80	7.30	14.98	10.02	35.43	29.51
	$Crs3, Crc3$	3.54	1.71	4.91	4.79	16.16	10.02	18.51	20.00
20	$\dot{a}, \dot{n}, Crs3, Crc3$	1.96	1.70	2.79	2.90	7.89	7.80	9.19	10.95
	$\dot{a}, \dot{n}, Cus3, Cuc3$	1.79	1.70	4.38	3.83	6.87	7.80	16.07	14.57
	$Crs1$$, Crc1$$, Crs3$$, Crc3$	3.36	1.71	1.88	3.19	12.37	7.77	8.35	12.78
	$Cus1$$, Cuc1$$, Crs3$$, Crc3$	3.36	1.71	1.88	3.19	12.37	7.77	8.35	12.78
22	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$	1.90	1.70	1.13	2.11	7.52	7.80	5.29	9.15
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$	1.89	1.70	1.13	2.11	7.52	7.79	5.29	9.15
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis1$$, Cic1$	1.95	0.38	2.79	2.61	7.84	2.16	9.19	9.34
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis3$$, Cic3$	1.95	0.36	2.79	2.61	7.84	1.94	9.19	9.31
24	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$$, Cis3$$, Cic3$	1.88	0.36	1.13	1.69	7.46	1.94	5.29	7.11
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis3$$, Cic3$	1.88	0.36	1.13	1.69	7.46	1.94	5.29	7.11
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis1$$, Cic1$	1.88	0.38	1.13	1.69	7.46	2.16	5.29	7.14
	$\dot{a}$$, \dot{n}, Crs3$$, Crc3$$, Crs1$$, Crc1$$, \ddot{i}$$, \ddot{\mathsf{\Omega }}$	1.88	0.39	1.13	1.69	7.46	2.21	5.29	7.15

The underlined parts achieve the minimum fit Error of Specified Directional Component for the same number of parameters.

and

Table 8. Fit error results for Sentinel-6A in the along-track (A), cross-track (C), and radial (R) components, combined with SISREs, using 20/30 min fit intervals (unit: cm).

Number of Parameters	Additional Parameters	20 min				30 min
		A	C	R	SISRE	A	C	R	SISRE
16	-	12.07	0.89	4.45	9.58	38.07	3.90	18.78	31.75
18	$\dot{a}$$, \dot{n}$	4.84	0.69	1.90	3.92	18.37	3.46	8.96	15.43
	$Crs1,Crc1$	1.43	0.64	4.14	3.49	6.78	3.34	17.27	14.37
	$Cus1, Cuc1$	1.43	0.64	4.14	3.49	6.78	3.34	17.28	14.37
	$Crs3, Crc3$	1.50	0.64	2.11	2.07	7.25	3.34	8.15	8.59
20	$\dot{a}, \dot{n}, Crs3, Crc3$	0.71	0.64	1.05	1.10	3.69	3.30	4.35	4.95
	$\dot{a}, \dot{n}, Cus3, Cuc3$	0.64	0.64	1.83	1.60	3.13	3.30	8.48	7.31
	$Crs1$$, Crc1$$, Crs3$$, Crc3$	1.43	0.64	0.69	1.28	6.78	3.34	3.88	6.33
	$Cus1$$, Cuc1$$, Crs3$$, Crc3$	1.43	0.64	0.69	1.28	6.78	3.34	3.88	6.33
22	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$	0.70	0.64	0.33	0.75	3.52	3.29	2.13	3.92
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$	0.78	0.65	0.33	0.80	3.52	3.29	2.13	3.92
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis1$$, Cic1$	0.71	0.12	1.05	0.99	3.68	0.84	4.35	4.35
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis3$$, Cic3$	0.71	0.12	1.05	0.99	3.68	0.75	4.35	4.34
24	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$$, Cis3$$, Cic3$	0.69	0.12	0.33	0.58	3.51	0.75	2.13	3.12
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis3$$, Cic3$	0.70	0.12	0.33	0.58	3.51	0.75	2.13	3.12
	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis1$$, Cic1$	0.73	0.12	0.33	0.60	3.51	0.83	2.13	3.13
	$\dot{a}$$, \dot{n}, Crs3$$, Crc3$$, Crs1$$, Crc1$$, \ddot{i}$$, \ddot{\mathsf{\Omega }}$	2.63	0.20	0.33	1.97	3.51	0.85	2.13	3.13

The underlined parts achieve the minimum fit Error of Specified Directional Component for the same number of parameters.

present the RMS fitting errors in the along-track, radial, and cross-track directions for the five satellites under different parameter combination schemes and fitting arc lengths, with corresponding SISRE statistics included in the tables. For comparison, the 16-parameter broadcast ephemeris model is also included in the tables. Although all possible schemes were tested, not all performed well. In some cases, adding parameters actually reduced fitting accuracy or even caused numerical instability leading to fitting failures. The tables list selected parameter design schemes worthy of discussion.

In the 16-parameter ephemeris scheme, all satellites exhibited a consistent characteristic: the largest fitting errors occurred in the along-track direction, followed by the radial direction, with the smallest errors in the cross-track direction. Consequently, reducing fitting errors in the along-track and radial directions is key to improving both fitting accuracy and SISRE. This also explains why perturbation parameters related to the cross-track direction rarely appear in the tables, such as $Cis1$, $Cic1$, $Cis3$, $Cic3$, and $\ddot{i}$.

When adding two additional parameters, the optimal choice for minimizing SISRE is $Crs3$ and $Crc3$. Although these parameters only reflect periodic variations in the radial direction, their coupling with other parameters effectively absorbs fitting errors in both the along-track and radial directions, thereby enhancing overall fitting accuracy and SISRE.

Unexpectedly, $(Crs1$, $Crc1$) and ($Cus1$, $Cuc1$) demonstrated identical improvements in fitting accuracy, although they are harmonic parameters in different directions. In the 18-parameter scheme, including these parameters minimized along-track fitting errors, but the radial errors remained significantly larger than those achieved with ($Crs3$, $Crc3)$. Furthermore, when the fitting arc length was set to 20 min, the radial fitting errors from ($\dot{a}$, $\dot{n}$) were smaller than those from ($Crs3$, $Crc3$). However, extending the fitting arc to 30 min reversed this trend, with ($\dot{a}$, $\dot{n}$) yielding larger radial errors than ($Crs3$, $Crc3$).

In the 20-parameter scheme, both ($Crs1$, $Crc1$, $Crs3$, $Crc3$) and ($Cus1$, $Cuc1$, $Crs3$, $Crc3$) achieve the minimum radial fitting errors. However, their along-track errors are significantly larger than those of the ($\dot{a}, \dot{n}, Crs3, Crc3$) scheme, preventing them from attaining the lowest SISRE. The ($\dot{a}$, $\dot{n}$, $Cus3$, $Cuc3$) scheme yields the smallest along-track errors, but its excessive radial errors preclude optimal SISRE performance. In contract, the ($\dot{a}$, $\dot{n}$, $Crs3$, $Crc3$) scheme balances errors across all three directions, achieving the lowest SISRE among all tested configurations. Notably, all four schemes exhibit identical cross-track errors (within 0.1 mm), as none incorporate cross-track perturbation parameters.

In the 22-parameter schemes, both the ($\dot{a}\dot{, n}$, $Crs3$, $Crc3$, $Crs1$, $Crc1$) and ($\dot{a}$, $\dot{n}$, $Crs3$, $Crc3$, $Cus1$, $Cuc1$) configurations achieve minimal SISRE values. An exception occurs for Sentinel-6A with a 20 min fitting arc, where the ($\dot{a}$, $\dot{n}$, $Crs3$, $Crc3$, $Crs1$, $Crc1$) scheme provides a 0.5 mm reduction in SISRE compared to the ($\dot{a}$, $\dot{n}$, $Crs3$, $Crc3$, $Cus1$, $Cuc1$) configuration. As previously demonstrated, ($Cus1$, $Cuc1$) and ($Crs1$, $Crc1$) provide equivalent improvements in fitting accuracy. Therefore, the optimal selection between these parameter sets should be based on their respective information length requirements.

In the 20-parameter scheme, the optimal solution tends to have equal fitting errors in the tangential, normal, and radial directions. The table also demonstrates the impact of adding normal harmonic terms and the second-order time rate of inclination on fitting accuracy. Compared to ($Cis3$, $Cic3$), ($Cis1$, $Cic1$) in the 22-parameter case better reduced the fitting error in the normal direction. A special case occurs when the fitting arc length of the Sentinel-6A satellite is set to 20 min, where the two schemes yield the same fitting error component in the normal direction. Both schemes outperform $\ddot{i}$ and $\ddot{\mathsf{\Omega }}$ in reducing the fitting error in the cross-track direction.

Table 9. MSB for different satellites with different schemes (unit: bit).

Additional Parameters	GRACE-A		GRACE-C		Sentinel-2A		HY-2A		Sentinel-6A
	20 min	30 min	20 min	30 min	20 min	30 min	20 min	30 min	20 min	30 min
-	350	345	346	342	347	346	349	346	342	339
$\dot{a}$$, \dot{n}$	396	392	390	390	394	393	397	394	384	384
$Crs1, Crc1$	392	387	391	380	384	387	390	385	380	380
$Cus1, Cuc1$	396	387	390	382	387	389	393	388	388	383
$Crs3, Crc3$	387	381	383	377	382	378	383	378	374	374
$\dot{a}, \dot{n}, Crs3, Crc3$	441	432	439	436	436	431	439	435	425	427
$\dot{a}, \dot{n}, Cus3, Cuc3$	433	427	427	427	431	425	431	430	418	417
$Crs1$$, Crc1$$, Crs3$$, Crc3$	431	418	426	416	430	417	425	414	414	416
$Cus1$$, Cuc1$$, Crs3$$, Crc3$	435	420	431	418	431	419	427	416	417	419
$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$	501	481	490	483	491	479	487	483	476	472
$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$	506	484	494	487	494	479	492	484	482	477
$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis1$$, Cic1$	508	487	497	487	495	483	495	485	478	476
$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cis3$$, Cic3$	490	467	481	467	481	465	478	467	465	462
$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$$, Cis3$$, Cic3$	543	514	535	511	531	514	530	515	516	511
$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis3$$, Cic3$	547	517	538	516	534	517	530	516	523	516
$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Cus1$$, Cuc1$$, Cis1$$, Cic1$	566	539	558	538	554	531	545	532	537	528
$\dot{a}$$, \dot{n}, Crs3$$, Crc3$$, Crs1$$, Crc1$$, \ddot{i}$$, \ddot{\mathsf{\Omega }}$	574	548	569	550	567	557	548	550	547	559

describes the number of bits required to broadcast information for five satellites under different parameter design schemes. Overall, each additional set of parameters requires approximately 40 more bits to be broadcast. Moreover, as the orbital altitude increases, the information length for the same parameter scheme tends to decrease. In the 18-parameter scheme, ($Crs3,\mathrm{ }Crc3$) can achieve both the smallest SISRE and save on information bit length. As mentioned earlier, in the 22-parameter ephemeris scheme, the schemes involving ($\dot{a}$, $\dot{n}$, $Crs3$, $Crc3$, $Crs1$, $Crc1$) and ($\dot{a}$, $\dot{n}$, $Crs3$, $Crc3$, $Cus1$, $Cuc1$) exhibit the same fitting error and SISRE, but the former saves approximately 4 bits in information length compared to the latter. The same holds true for the 24-parameter ephemeris, where schemes including ($Crs1$, $Crc1$) save more bits than those including ($Cus1$, $Cuc1$). Taking into account both SISRE and information length,

Table 10. Optimal LEO ephemeris parameter set for LEOs.

Number of Parameters	Additional Parameters
18	$Crs3, Crc3$
20	$\dot{a}, \dot{n}, Crs3, Crc3$
22	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$
24	$\dot{a}$$, \dot{n}$$, Crs3$$, Crc3$$, Crs1$$, Crc1$$, Cis3$$, Cic3$

presents the optimal schemes for broadcast ephemerides with different numbers of parameters. Subsequently, the 18-, 20-, 22-, and 24-parameter broadcast ephemerides refer to the schemes listed in Table 10.

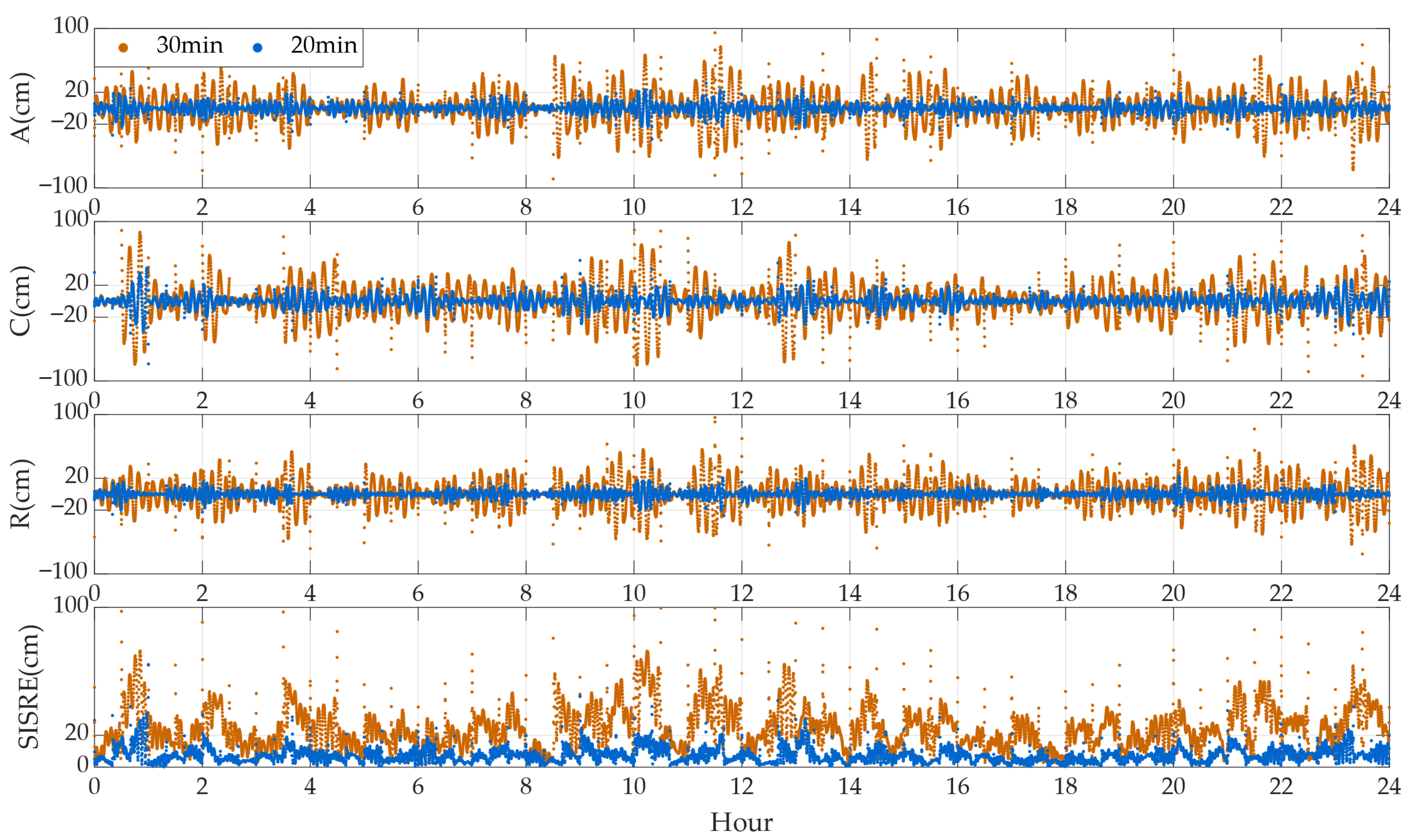
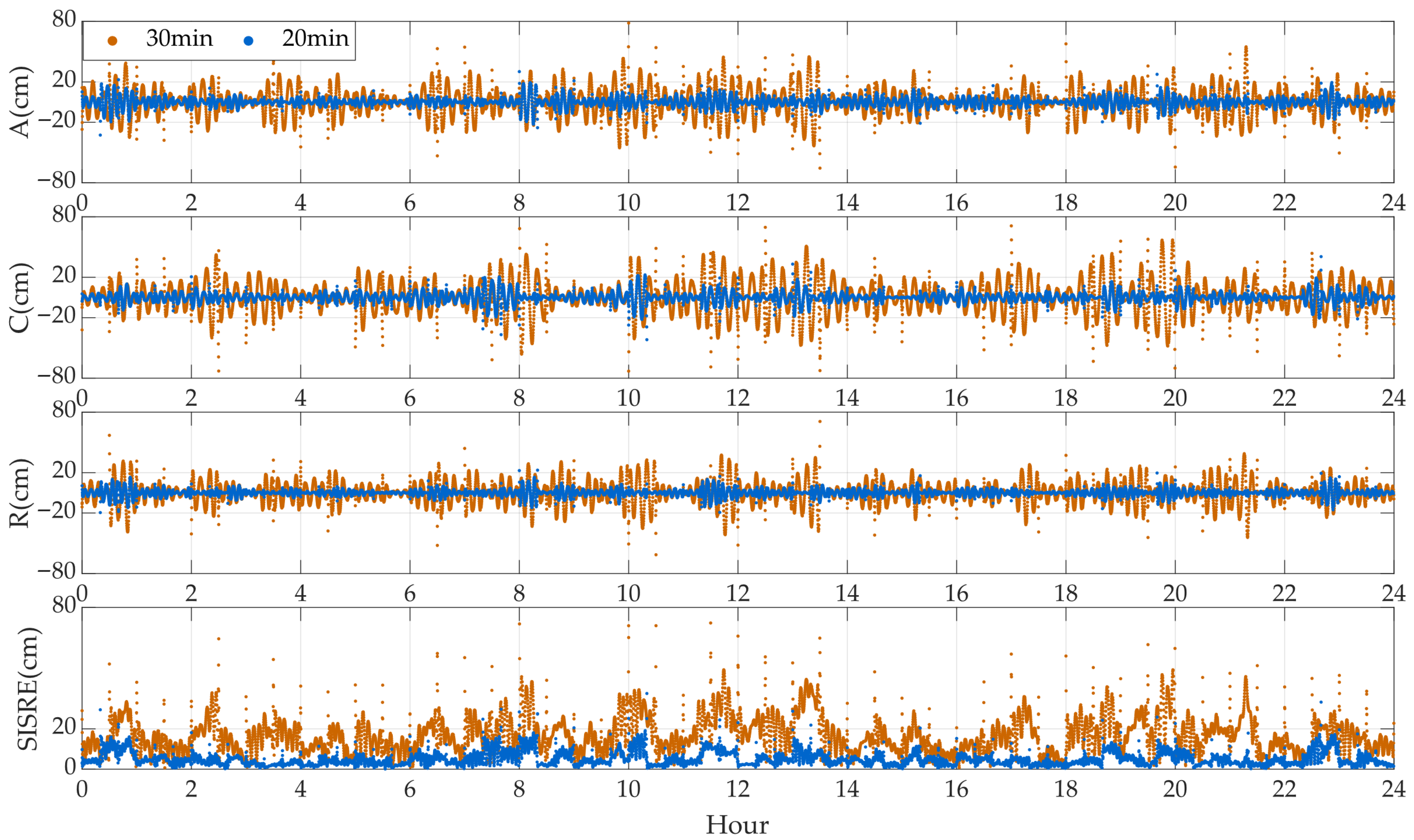
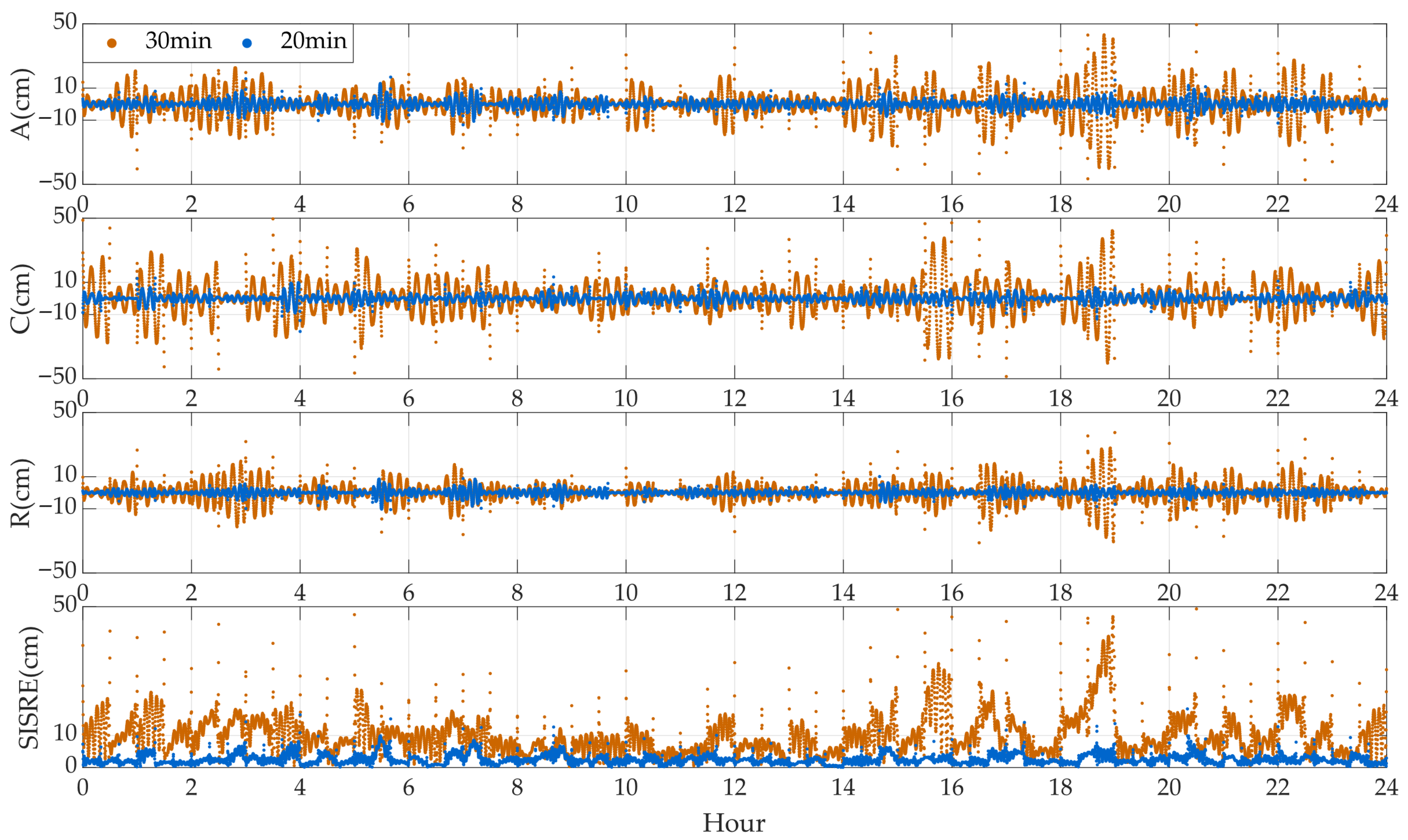
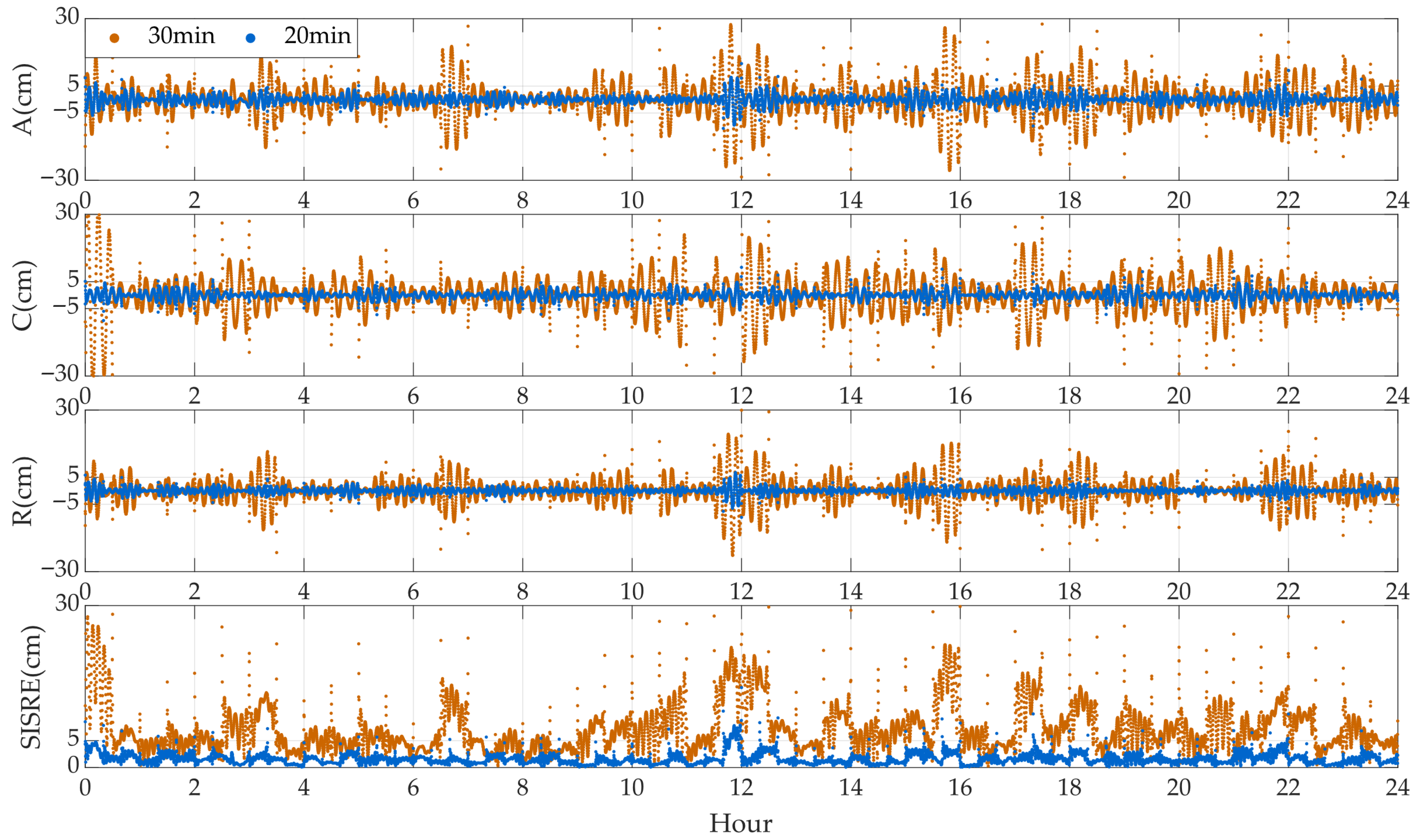
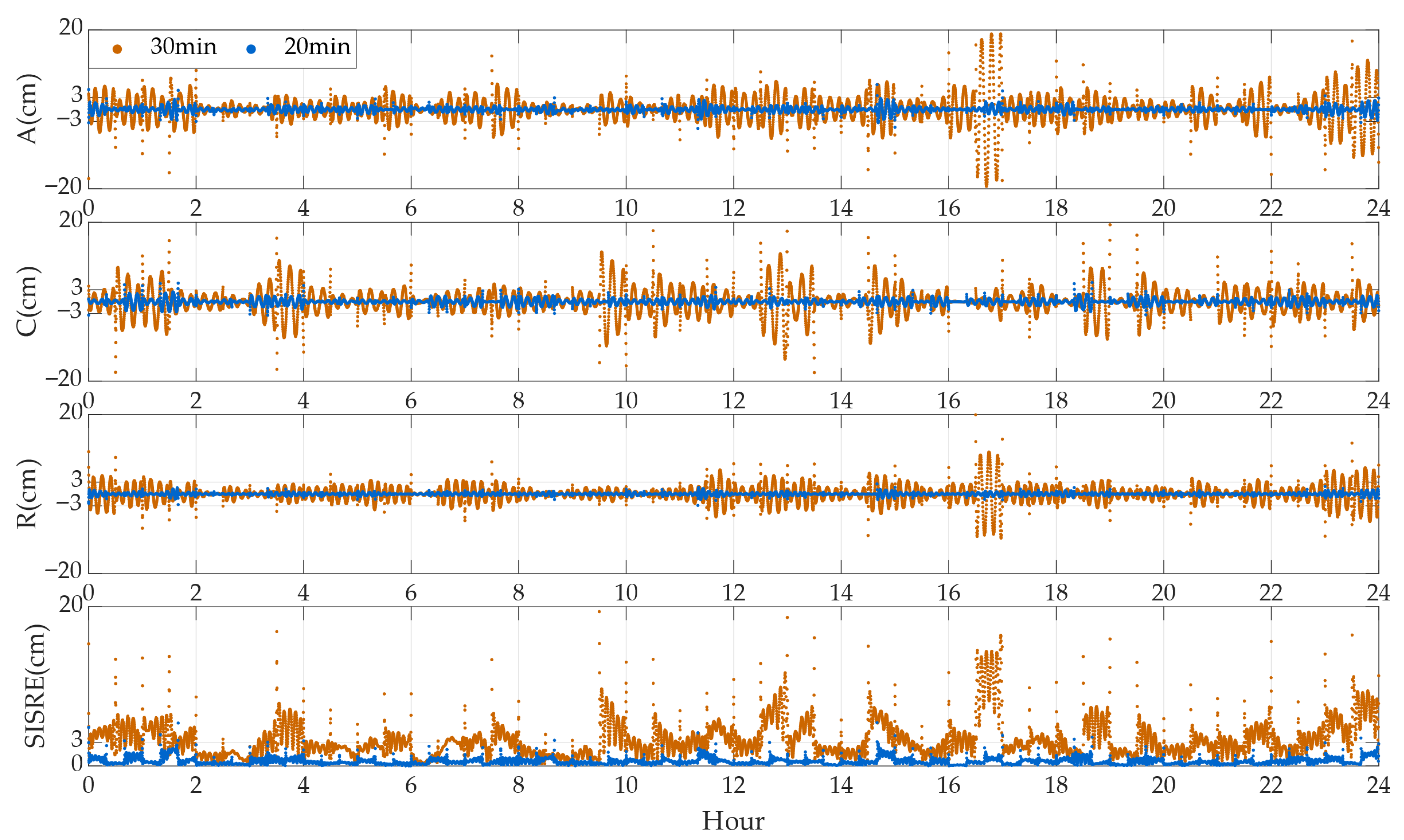
Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 presents the time series of fitting errors in the along-track (A), cross-track (C), and radial (R) directions, as well as the SISRE, for the five experimental satellites using the 22-parameter ephemeris model under fitting arc lengths of 20 min and 30 min.

The fitting errors significantly decrease as the satellite orbital altitude increases. Therefore, the axis ranges were adjusted accordingly for different satellites. From an overall perspective, when fitting an arc length of 20 min, for the GRACE-A satellite at an orbital altitude of 320 km and the GRACE-C satellite at 475 km, except for certain epochs, the fitting errors in all three directions are within ±20 cm, and the SISRE is within 20 cm. For the Sentinel-2A satellite at an orbital altitude of 786 km, the fitting errors in all three directions are within $\pm$20 cm, and the SISRE is within 10 cm. For the HY-2A satellite at an altitude of 966 km and the Sentinel-6A satellite at 1336 km, these metrics decrease to ±5 cm and 5 cm, and ±3 cm and 3 cm, respectively.

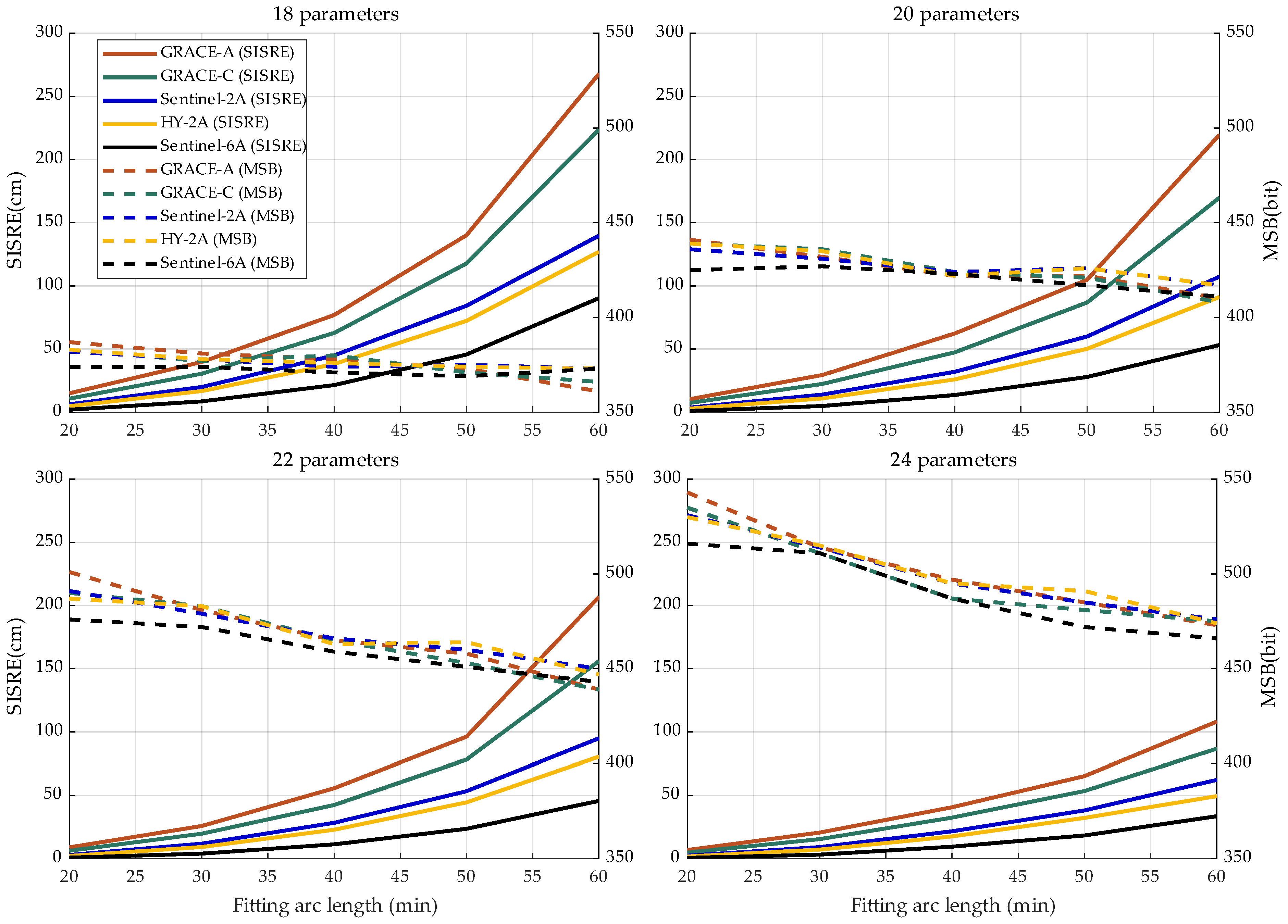
Figure 7 illustrates the changes in SISRE and message length for the five selected satellites under different parameter design schemes, corresponding to varying fitting arc lengths. Overall, as the fitting arc length increases, the SISRE for each satellite also increases, with an accelerating growth rate. In the 22-parameter ephemeris, when the fitting arc length of the Sentinel-6A satellite increases from 20 min to 30 min, the SISRE only rises from 0.75 cm to 3.92 cm, an increase of 3.17 cm. However, when the fitting arc length increases from 50 min to 60 min, the SISRE grows from 23.56 cm to 45.66 cm, an increase of 22.10 cm. On the other hand, the MSB decreases as the fitting arc length increases, and this reduction becomes more pronounced with a higher number of parameters. For the HY-2A satellite, in the 18-parameter ephemeris, the MSB for a 60 min fitting arc length is 10 bits less than that for a 20 min fitting arc length. In the 22-parameter ephemeris, the MSB for a 60 min fitting arc length is 56 bits less than that for a 20 min fitting arc length.

4. Discussion

In the aforementioned experiment, the direct application of the 16-parameter broadcast ephemeris model to LEO satellites results in significant fitting errors. Even for Sentinel-6A at an orbital altitude of 1300 km with a fitting arc of 20 min, the fitting error in the along-track direction exceeds 10 cm, and the SISRE is 9.58 cm. When the fitting arc is extended to 30 min, the SISRE increases to 31.75 cm, which is unacceptable. Moreover, the fitting errors in the along-track and cross-track directions are the primary challenges for improving fitting accuracy. In the 16-parameter model, preferentially adding correction terms such as ($\dot{a}$, $\dot{n}$, $Cus1$, $Cuc1$), and ($Crs3$, $Crc3$), which are strongly correlated with the along-track and cross-track directions, can significantly reduce fitting errors and thereby lower the SISRE. As the number of parameters increases, the fitting error and SISRE decrease accordingly, as more parameters can better absorb fitting errors. However, more parameters are not always better. On one hand, increasing parameters inevitably leads to longer information length, occupying more resources. On the other hand, a higher number of parameters can easily cause multicollinearity in the design matrix, leading to ambiguity in the Gram matrix and resulting in fitting errors.

As the fitting arc length increases, the fitting error also rises, which is inevitable. A longer fitting arc length means greater cumulative effects of orbital perturbations, and the influence of unmodeled perturbation terms becomes more pronounced. However, the information length decreases slightly because, for the same satellite, the longer fitting arc does not significantly change the LSB, while the numerical values of certain parameters decrease, leading to a reduction in the MSB.

Two additional limitations should be noted. First, the broadcast ephemeris design is based on the existing 16-parameter broadcast ephemeris model, and the added perturbation parameters merely adjust the order and harmonic period of the original perturbation terms. The dynamic characteristics of LEO satellites are more complex than those of medium and high Earth orbit satellites, so this approach may not be optimal. Second, the experiment used one day of orbital data to calculate the LSB and MSB, which introduces some degree of randomness. In engineering applications, a larger MSB and a smaller LSB should be adopted to enhance the robustness of the design scheme.

5. Conclusions

In this study, we designed different parameter schemes based on the 16-parameter Keplerian broadcast ephemeris and compared the performance of these schemes with different fitting arcs for satellites at different orbital altitudes. Using PSO from five satellites, we analyzed the variations in fitting error, SISRE, and MSB to determine the optimal schemes under different parameter counts. The schemes ($Crs3, Crc3$), ($\dot{a}, \dot{n}, Crs3, Crc3$), ($\dot{a}$, $\dot{n}$, $Crs3$, $Crc3$, $Crs1$, $Crc1$), and ($\dot{a}$, $\dot{n}$, $Crs3$, $Crc3$, $Crs1$, $Crc1$, $Cis3$, $Cic3$) were identified as the best solutions for adding 2, 4, 6, and 8 parameters, respectively. Under a fitting arc length of 20 min, these schemes improved the SISRE for the GRACE-C satellite (with an orbital altitude of approximately 500 km) and the HY-2A satellite (with an orbital altitude of approximately 1000 km) by 63.4%, 74.7%, 78.8%, and 83.8% and 72.8%, 83.5%, 88.0%, and 90.4%, respectively, compared to the 16-parameter ephemeris model. The information length increased by 10.6%, 26.9%, 41.6%, and 54.6% and 9.7%, 25.8%, 39.5%, and 51.9%, respectively. The ($Crs3, Crc3$) scheme was the most efficient in improving fitting accuracy and SISRE. Considering fitting accuracy, numerical stability, and information length, we recommend adopting the 22-parameter scheme ($\dot{a}$, $\dot{n}$, $Crs3$, $Crc3$, $Crs1$, $Crc1$).

It should be noted that this study focused only on the variations in fitting error and information length of different models with respect to the fitting arc length. Other factors, such as orbit prediction accuracy, ephemeris frame structure design, and user time to first fix, are also crucial for broadcast ephemeris design.