A Hybrid Short-Term Prediction Model for BDS-3 Satellite Clock Bias Supporting Real-Time Applications in Data-Denied Environments
Abstract
1. Introduction
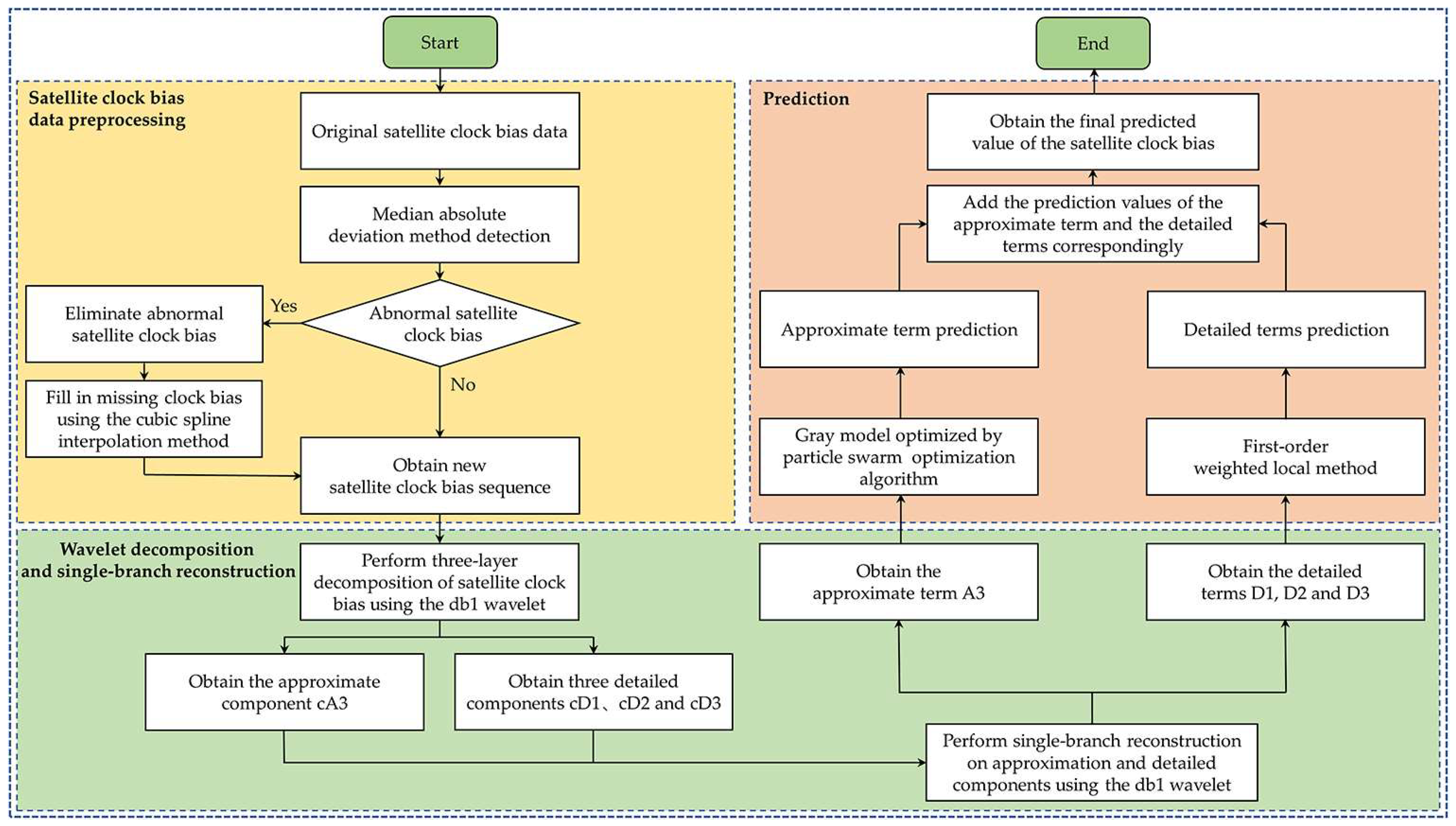
2. Establishment of Satellite Clock Bias Prediction Based on the WT-PGM-FWL Model
2.1. Preprocessing of Satellite Clock Bias
2.2. Principles of Decomposition and Reconstruction Algorithms for Satellite Clock Bias
2.2.1. Wavelet Transform
2.2.2. Decomposition and Reconstruction of Satellite Clock Bias
2.3. Gray Model Optimized by Particle Swarm Optimization Algorithm
2.3.1. Gray Model
2.3.2. Global Optimal Search for Parameters Based on Particle Swarm Optimization
2.4. First-Order Weighted Local Method
2.5. Satellite Clock Bias Prediction Integrated Gray Model Optimized by Particle Swarm Optimization and First-Order Weighted Local Method
- (1)
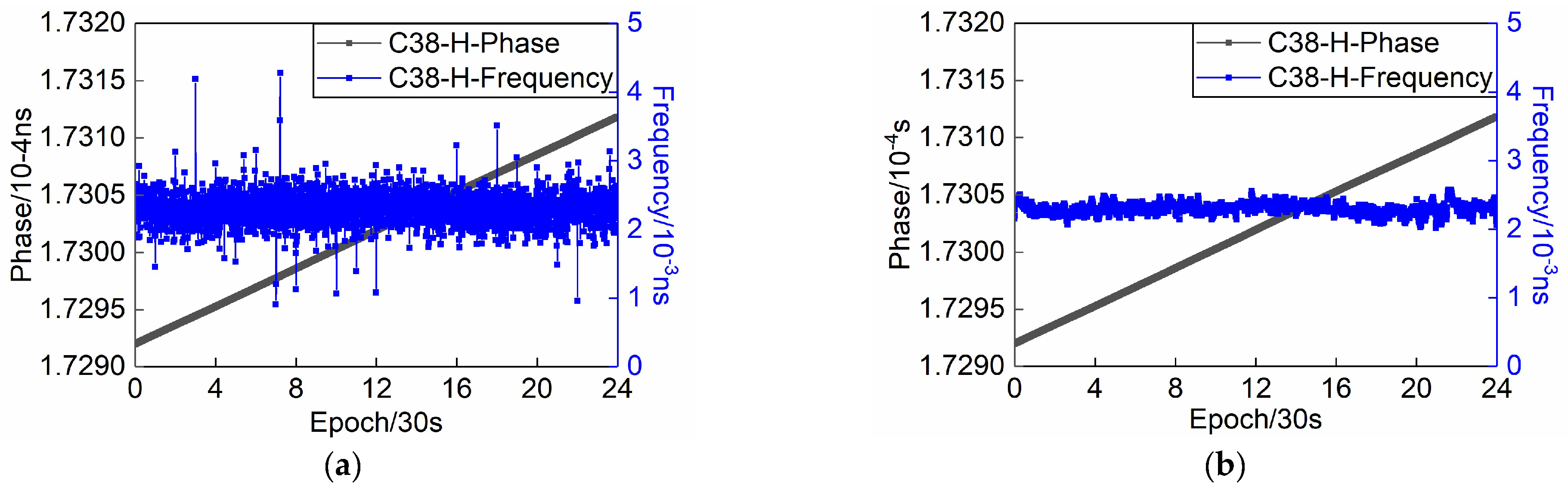
- SCB preprocessing. Owing to the frequent jumps in SCB, these data are severely unfavorable for the establishment of the model. Therefore, it is very important to check the quality of SCB before modeling. In the work, the MAD method with good tolerance and timeliness is adopted for gross errors and clock jump detection. After detecting the clock jumps or gross errors, they are excluded, and then the cubic spline interpolation method is employed to make up for the missing data.
- (2)
- SCB decomposition and reconstruction. The SCB is essentially a time series signal, and its phase information directly affects the accuracy of the subsequent SCB prediction. Moreover, the phase distortion will cause the physical meaning of approximate terms and detailed terms to deviate from reality. The db1 wavelet is the only wavelet with a strict linear phase in the Daubechies wavelet family. It can ensure that the phase delay of each component is strictly linear with the frequency in the process of three-layer decomposition and single-branch reconstruction. This fundamentally eliminates waveform distortion, ensuring the reliability of subsequent prediction. In this study, the db1 wavelet is used to perform three-level multi-resolution decomposition on the SCB to acquire the approximate component cA3 and three detailed components cD1, cD2, and cD3. Subsequently, the single-branch reconstruction of these components is performed to obtain the trend term A3 and the three detailed terms D1, D2, and D3. Because the db1 wavelet has symmetrical characteristics for the single-branch reconstruction of the signal, the trend term of the SCB decomposition shows a certain variation law after reconstruction, which meets the requirements of the PGM model for the modeling data. Meanwhile, the db1 wavelet has excellent linear phase characteristics, which makes it possible to decompose and reconstruct the signal without phase distortion.
- (3)
- Predict each component of SCB. The PGM model and the FWL method are adopted to predict the wavelet decomposed and reconstructed sequences, respectively. The trend term A3 is predicted using the PGM model; the three detailed terms D1, D2, and D3 are predicted using the FWL method.
- (4)
- The ultimate prediction of SCB. By adding the sequence of the trend term predicted by the PGM model to the sequence of the three detailed terms predicted by the FWL method, the ultimate SCB prediction can be acquired.
3. Experimental Results
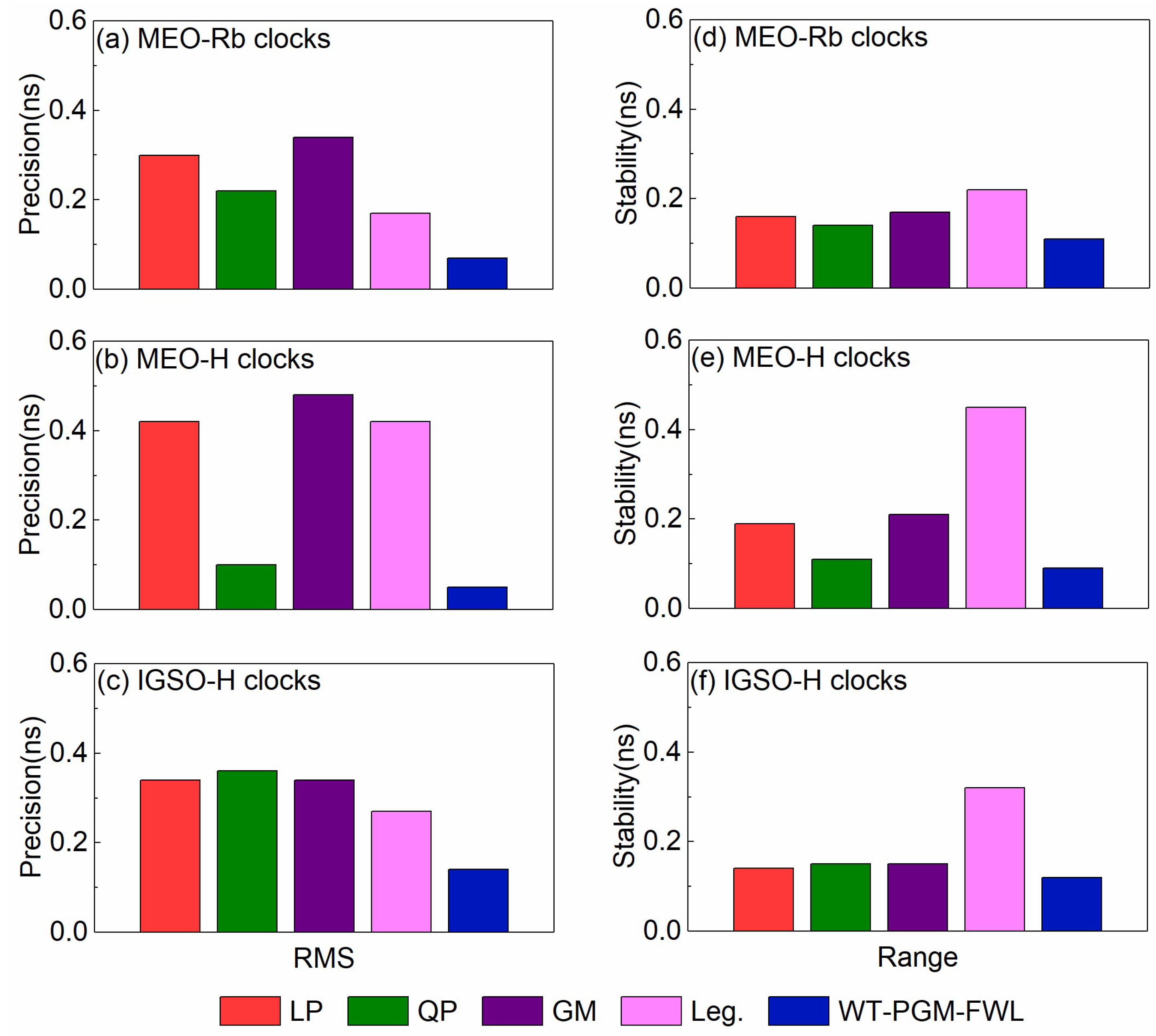
3.1. Modeling with 18 H Data to Predict Satellite Clock Bias of the Next 10 Min
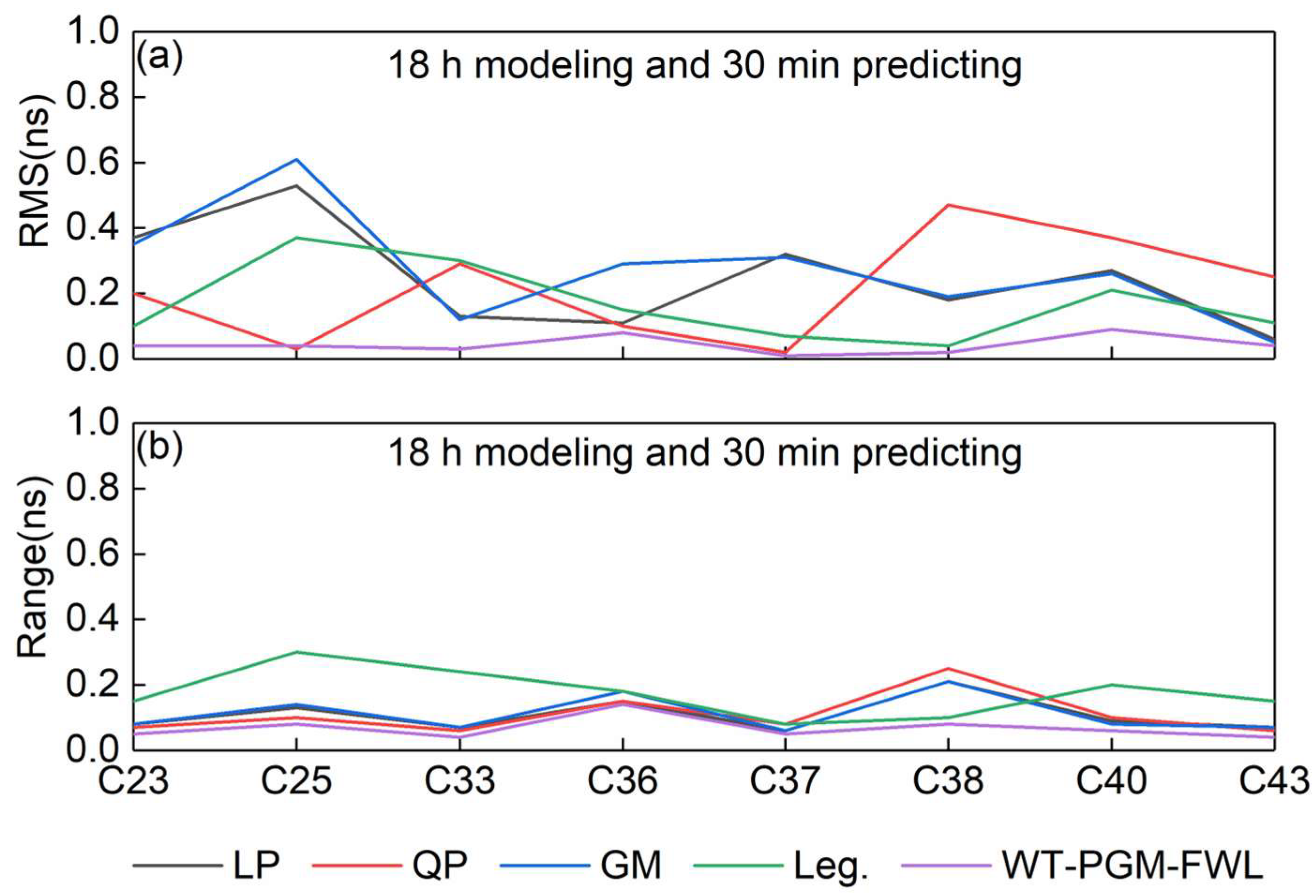
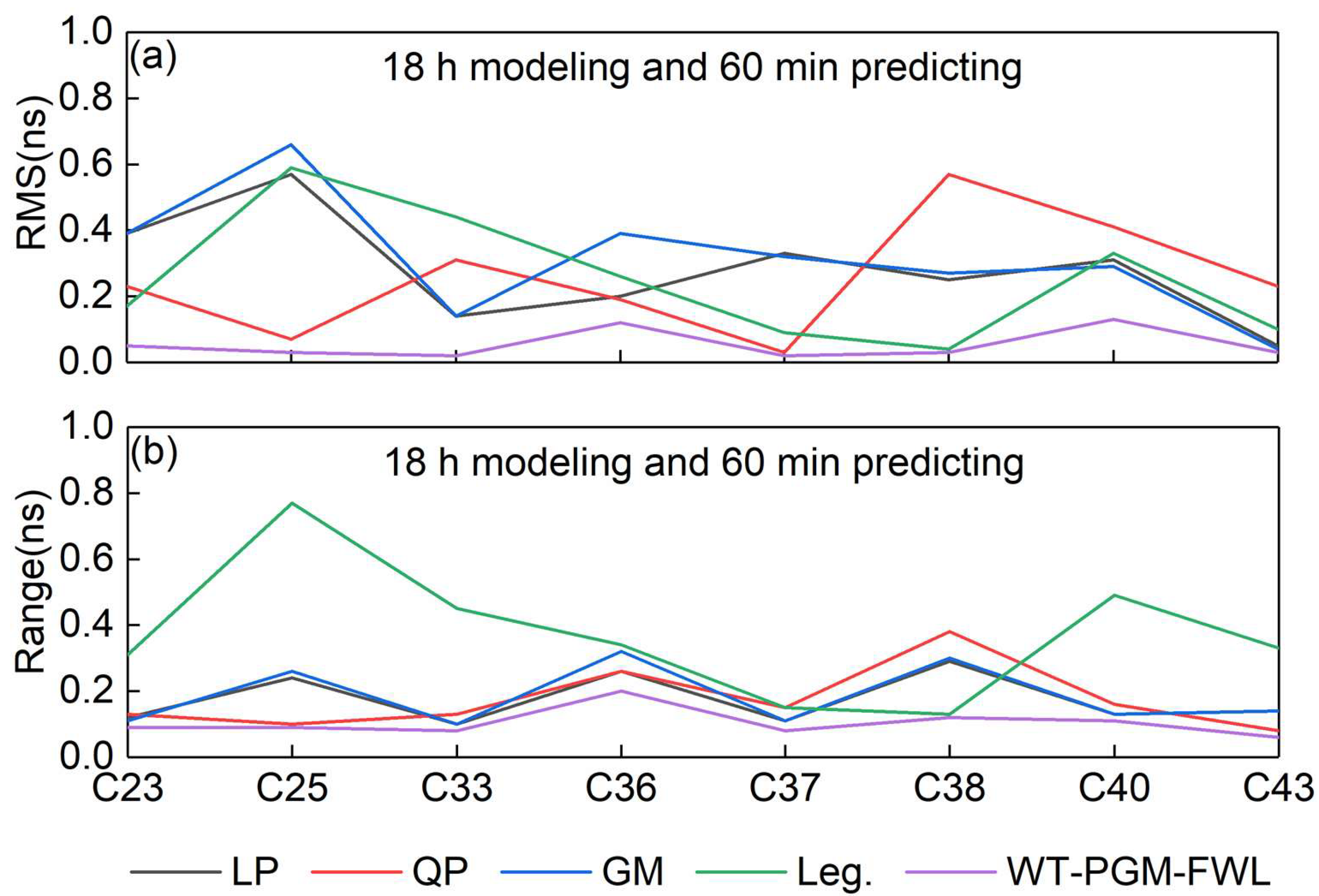
3.2. Modeling with 18 H Data to Predict Satellite Clock Bias of the Next 30 Min and 60 Min
3.3. Modeling with 20 H Data to Predict Satellite Clock Bias of the Next 60 Min
4. Discussion
5. Conclusions
- (1)
- Due to the high-frequency sensitivity of satellite atomic clocks, they are highly susceptible to complex space environmental factors, causing the output SCB to exhibit non-stationary and nonlinear trends. A single prediction model has certain limitations on SCB prediction and shows significant differences in predicting diverse types of clocks.
- (2)
- The WT-PGM-FWL model exhibits remarkable advantages in the precision and stability of SCB prediction, and its performance markedly exceeds that of several other models. Additionally, as the prediction time becomes longer, the WT-PGM-FWL model exhibits excellent robustness properties. The rate of error growth is significantly lower than that of other comparison models, and it can also maintain high prediction precision and stability.
- (3)
- The predictive precision and stability of the WT-PGM-FWL model for the SCB of hydrogen clocks are the same as those of rubidium clocks. It is not affected by the types of clocks and demonstrates good prediction ability for the SCB of diverse types of clocks. Furthermore, as the amount of modeling data increases, its prediction precision and stability exhibit little variation, and there is no phenomenon where the prediction precision and stability significantly decrease or increase.
- (4)
- For 30 min and 60 min predictions, the precision of the SCB products from the WT-PGM-FWL model all fall below 0.30 ns. Therefore, when users have poor communication and cannot obtain the RTS products, the SCB within a 1 h duration predicted by the WT-PGM-FWL model can be used in place of the RTS products, thereby guaranteeing the precision of RT-PPP over the 1 h period of communication interruption.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Yao, Z.; Mao, Y.; Xu, T.; Wang, D. Resilient satellite-based PNT system design and key technologies. Sci. China Ser. D-Earth Sci. 2025, 68, 669–682. [Google Scholar] [CrossRef]
- Geng, J.; Wen, Q.; Chen, G.; Dumitraschkewitz, P.; Zhang, Q. All-frequency IGS phase clock/bias product combination to improve PPP ambiguity resolution. J. Geod. 2024, 98, 48. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Manoj, D. Maintaining real-time precise point positioning during outages of orbit and clock corrections. GPS Solut. 2016, 21, 937–947. [Google Scholar]
- Wang, X.; Chai, H.; Wang, C. A high-precision short-term prediction method with stable performance for satellite clock bias. GPS Solut. 2020, 24, 105–115. [Google Scholar] [CrossRef]
- Huang, B.; Ji, Z.; Zhai, R.; Xiao, C.; Wang, Y. Clock bias prediction algorithm for navigation satellites based on a supervised learning long short-term memory neural network. GPS Solut. 2021, 25, 80. [Google Scholar] [CrossRef]
- Zhao, L.; Na, Z.; Li, L.; Cui, P. SSA-TCN: Satellite clock offset prediction during outages of RTS stream. GPS Solut. 2025, 29, 105–121. [Google Scholar] [CrossRef]
- Elsobeiey, M.; Al-Harbi, S. Performance of real-time Precise Point Positioning using IGS real-time service. GPS Solut. 2016, 20, 565–571. [Google Scholar] [CrossRef]
- Jaduszliwer, B.; Camparo, J. Past, present and future of atomic clocks for GNSS. GPS Solut. 2021, 25, 27. [Google Scholar] [CrossRef]
- Jin, S.; Su, K. PPP models and performances from single- to quad-frequency BDS observations. Satell. Navig. 2020, 1, 16. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Y.; Yuan, Y. PPP-RTK based on undifferenced and uncombined observations: Theoretical and practical aspects. J. Geod. 2019, 93, 1011–1024. [Google Scholar] [CrossRef]
- Li, B.; Ge, H.; Bu, Y.; Zheng, Y.; Yuan, L. Comprehensive assessment of real-time precise products from IGS analysis centers. Satell. Navig. 2022, 3, 12. [Google Scholar] [CrossRef]
- Hadas, T.; Bosy, J. IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Solut. 2015, 19, 93–105. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Q. BDS-3/GNSS satellite ultra-rapid clock offsets estimation model with the aid of onboard clock states Solution. Acta Geod. Cartogr. Sin. 2024, 53, 2268–2281. [Google Scholar]
- Yan, X.; Li, W.; Yang, Y.; Li, W.; Yang, Y.; Pan, X. BDS satellite clock prediction based on a semiparametric adjustment model considering model errors. Satell. Navig. 2020, 1, 11. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Q.; Min, Y.; Mao, Y.; Gong, Y. An improved model for BDS satellite ultra-rapid clock offsets prediction based on BDS-2 and BDS-3 combined estimation. Acta. Geod. Geophys. 2019, 54, 513–543. [Google Scholar] [CrossRef]
- Nie, Z.; Gao, Y.; Wang, Z.; Ji, S.; Yang, H. An approach to GPS clock prediction for real-time PPP during outages of RTS stream. GPS Solut. 2018, 22, 14. [Google Scholar] [CrossRef]
- Guo, J.; Xu, X.; Zhao, Q.; Liu, J. Precise orbit determination for quad-constellation satellites at Wuhan University: Strategy, result validation, and comparison. J. Geod. 2016, 90, 143–159. [Google Scholar] [CrossRef]
- Huang, G.; Cui, B.; Zhang, Q.; Fu, W.; Li, P. An Improved Predicted Model for BDS Ultra-Rapid Satellite Clock Offsets. Remote Sens. 2018, 10, 60. [Google Scholar] [CrossRef]
- Ye, S.; Zhao, L.; Song, J.; Chen, D.; Jiang, W. Analysis of estimated satellite clock biases and their effects on precise point positioning. GPS Solut. 2018, 22, 16. [Google Scholar] [CrossRef]
- Lv, K.; Cai, C.; Cai, Y.; Guan, W.; Fang, Y. Highly accurate short-term prediction of BDS-3 satellite clock bias based on SSA-ANFIS integrated modeling. GPS Solut. 2025, 29, 100–112. [Google Scholar] [CrossRef]
- Tu, R.; Zhang, P.; Zhang, R.; Liu, J.; Lu, X. Modeling and performance analysis of precise time transfer based on BDS triple-frequency un-combined observations. J. Geod. 2019, 93, 837–847. [Google Scholar] [CrossRef]
- Ai, Q.; Xu, T.; Sun, D.; Ren, L. The Prediction of BeiDou Satellite Clock Bias Based on Periodic Term and Starting Point Deviation Correction. Acta Geod. Cartogr. Sin. 2016, 45, 132–138. [Google Scholar]
- Huang, G. Research on Algorithms of Precise Clock Offset and Quality. Ph.D. Thesis, Chang’an University, Xi’an, China, 2012. [Google Scholar]
- Hauschild, A.; Montenbruck, O.; Steigenberger, P. Short-term analysis of GNSS clocks. GPS Solut. 2013, 17, 295–307. [Google Scholar] [CrossRef]
- Busca, G.; Wang, Q. Time prediction accuracy for a space clock. Metrologia 2003, 40, 265–269. [Google Scholar] [CrossRef]
- Lv, D.; Liu, G.; Ou, J.; Wang, S.; Gao, M. Prediction of GPS Satellite Clock Offset Based on an Improved Particle Swarm Algorithm Optimized BP Neural Network. Remote Sens. 2022, 14, 2407. [Google Scholar] [CrossRef]
- He, S.; Liu, J.; Zhu, X.; Dai, Z.; Li, D. Research on modeling and predicting of BDS-3 satellite clock bias using the LSTM neural network model. GPS Solut. 2023, 27, 108–119. [Google Scholar] [CrossRef]
- Huang, F.; Chen, Y.; Li, T.; Yuan, H.; Shan, Q. A Satellite Clock Bias Prediction Algorithm Based on Grey Model and Chaotic Time Series. Acta Electron. Sin. 2019, 47, 1416–1424. [Google Scholar]
- Sun, W.; Chen, J.; Hu, C.; Lin, Y.; Wang, M.; Zhao, H.; Zhao, R.; Fu, G.; Zhao, T. Clock bias prediction of navigation satellite based on BWO-CNN-BiGRU-attention model. GPS Solut. 2025, 29, 46–59. [Google Scholar] [CrossRef]
- Molaei, S.; Sabaei, M.; Taheri, J. MRM-PSO: An enhanced particle swarm optimization technique for resource management in highly dynamic edge computing environments. Ad Hoc Netw. 2025, 178, 103952. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, T.; Wei, Z.; Cai, S.; Long, R.; Liu, Z. Performance analysis of a novel solar-to-hydrogen system with energy storage via machine learning and particle swarm optimization. Energy 2025, 315, 134380. [Google Scholar] [CrossRef]
- Allaoui, M.; Belhaouari, B.; Hedjam, R.; Bouanane, K.; Kherfi, M. t-SNE-PSO: Optimizing t-SNE using particle swarm optimization. Expert. Syst. Appl. 2025, 269, 126398. [Google Scholar] [CrossRef]






| Orbits | PRN and Clock Types |
|---|---|
| IGSO (3) | 38 (H) 39 (H) 40 (H) |
| MEO (24) | 19 (Rb) 20 (Rb) 21 (Rb) 22 (Rb) 23 (Rb) 24 (Rb) 25 (H) 26 (H) 27 (H) 28 (H) 29 (H) 30 (H) 32 (Rb) 33 (Rb) 34 (H) 35 (H) 36 (Rb) 37 (Rb) 41 (Rb) 42 (Rb) 43 (H) 44 (H) 45 (H) 46 (H) |
| GEO (3) | 59 (H) 60 (H) 61 (H) |
| Model | RMS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MEO Rb | IGSO H | MEO H | All | Deviation Range | ||||||
| C23 | C33 | C36 | C37 | C38 | C40 | C25 | C43 | |||
| GM | 0.33 | 0.10 | 0.23 | 0.29 | 0.10 | 0.23 | 0.57 | 0.07 | 0.24 | 0.50 |
| WT-PGM-FWL | 0.04 | 0.04 | 0.17 | 0.02 | 0.03 | 0.07 | 0.05 | 0.02 | 0.06 | 0.15 |
| Model | Range | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MEO Rb | IGSO H | MEO H | All | Deviation Range | ||||||
| C23 | C33 | C36 | C37 | C38 | C40 | C25 | C43 | |||
| GM | 0.05 | 0.06 | 0.05 | 0.06 | 0.05 | 0.06 | 0.09 | 0.06 | 0.06 | 0.04 |
| WT-PGM-FWL | 0.03 | 0.04 | 0.03 | 0.05 | 0.03 | 0.05 | 0.06 | 0.04 | 0.04 | 0.03 |
| Clock Type | RMS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 18 H Modeling and 30 Min Predicting | 18 H Modeling and 60 Min Predicting | |||||||||
| LP | QP | GM | Leg. | WT-PGM-FWL | LP | QP | GM | Leg. | WT-PGM-FWL | |
| MEO-Rb | 0.23 | 0.15 | 0.27 | 0.16 | 0.04 | 0.27 | 0.19 | 0.31 | 0.24 | 0.05 |
| MEO-H | 0.30 | 0.14 | 0.33 | 0.24 | 0.04 | 0.31 | 0.15 | 0.35 | 0.35 | 0.06 |
| IGSO-H | 0.23 | 0.42 | 0.23 | 0.13 | 0.06 | 0.28 | 0.49 | 0.28 | 0.19 | 0.08 |
| All | 0.25 | 0.24 | 0.28 | 0.18 | 0.05 | 0.29 | 0.28 | 0.31 | 0.26 | 0.06 |
| Clock Type | RMS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 18 H Modeling and 30 Min Predicting | 18 H Modeling and 60 Min Predicting | |||||||||
| LP | QP | GM | Leg. | WT-PGM-FWL | LP | QP | GM | Leg. | WT-PGM-FWL | |
| MEO-Rb | 0.38 | 0.30 | 0.42 | 0.31 | 0.19 | 0.42 | 0.34 | 0.46 | 0.39 | 0.20 |
| MEO-H | 0.45 | 0.29 | 0.48 | 0.39 | 0.19 | 0.46 | 0.30 | 0.50 | 0.50 | 0.21 |
| IGSO-H | 0.38 | 0.47 | 0.38 | 0.28 | 0.21 | 0.43 | 0.64 | 0.43 | 0.34 | 0.23 |
| All | 0.40 | 0.35 | 0.43 | 0.33 | 0.20 | 0.44 | 0.43 | 0.46 | 0.41 | 0.21 |
| Clock Type | Range | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 18 H Modeling and 30 Min Predicting | 18 H Modeling and 60 Min Predicting | |||||||||
| LP | QP | GM | Leg. | WT-PGM-FWL | LP | QP | GM | Leg. | WT-PGM-FWL | |
| MEO-Rb | 0.09 | 0.09 | 0.10 | 0.16 | 0.07 | 0.15 | 0.17 | 0.16 | 0.31 | 0.11 |
| MEO-H | 0.10 | 0.08 | 0.11 | 0.23 | 0.06 | 0.19 | 0.09 | 0.20 | 0.55 | 0.08 |
| IGSO-H | 0.15 | 0.18 | 0.15 | 0.15 | 0.07 | 0.21 | 0.27 | 0.22 | 0.31 | 0.12 |
| All | 0.11 | 0.12 | 0.12 | 0.18 | 0.07 | 0.18 | 0.18 | 0.19 | 0.39 | 0.10 |
| Clock Type | 20 H Modeling and 60 Min Predicting | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMS | Range | |||||||||
| LP | QP | GM | Leg. | WT-PGM-FWL | LP | QP | GM | Leg. | WT-PGM-FWL | |
| MEO-Rb | 0.30 | 0.22 | 0.34 | 0.17 | 0.07 | 0.16 | 0.14 | 0.17 | 0.22 | 0.11 |
| MEO-H | 0.42 | 0.10 | 0.48 | 0.42 | 0.05 | 0.19 | 0.11 | 0.21 | 0.45 | 0.09 |
| IGSO-H | 0.34 | 0.36 | 0.34 | 0.27 | 0.14 | 0.14 | 0.15 | 0.15 | 0.32 | 0.12 |
| All | 0.35 | 0.23 | 0.39 | 0.29 | 0.09 | 0.16 | 0.13 | 0.18 | 0.33 | 0.11 |
| Clock Type | 20 H Modeling and 60 Min Predicting | ||||
|---|---|---|---|---|---|
| RMS | |||||
| LP | QP | GM | Leg. | WT-PGM-FWL | |
| MEO-Rb | 0.45 | 0.37 | 0.49 | 0.32 | 0.22 |
| MEO-H | 0.57 | 0.25 | 0.63 | 0.57 | 0.20 |
| IGSO-H | 0.49 | 0.55 | 0.49 | 0.42 | 0.29 |
| All | 0.50 | 1.17 | 0.54 | 0.44 | 0.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Yang, C.; Ding, Y.; Xue, Y.; Ge, Y. A Hybrid Short-Term Prediction Model for BDS-3 Satellite Clock Bias Supporting Real-Time Applications in Data-Denied Environments. Remote Sens. 2025, 17, 2888. https://doi.org/10.3390/rs17162888
Yu Y, Yang C, Ding Y, Xue Y, Ge Y. A Hybrid Short-Term Prediction Model for BDS-3 Satellite Clock Bias Supporting Real-Time Applications in Data-Denied Environments. Remote Sensing. 2025; 17(16):2888. https://doi.org/10.3390/rs17162888
Chicago/Turabian StyleYu, Ye, Chaopan Yang, Yao Ding, Yuanliang Xue, and Yulong Ge. 2025. "A Hybrid Short-Term Prediction Model for BDS-3 Satellite Clock Bias Supporting Real-Time Applications in Data-Denied Environments" Remote Sensing 17, no. 16: 2888. https://doi.org/10.3390/rs17162888
APA StyleYu, Y., Yang, C., Ding, Y., Xue, Y., & Ge, Y. (2025). A Hybrid Short-Term Prediction Model for BDS-3 Satellite Clock Bias Supporting Real-Time Applications in Data-Denied Environments. Remote Sensing, 17(16), 2888. https://doi.org/10.3390/rs17162888






