Retrieval of Wave Parameters from GNSS Buoy Measurements Using Spectrum Analysis: A Case Study in the Huanghai Sea
Abstract
1. Introduction
2. Methods and Principles
2.1. Statistical Inversion of Wave Period and Wave Height
2.2. Wave Period and Wave Height Inversion Based on Spectral Analysis
2.2.1. Theoretical Basis of Wave Spectrum Analysis
2.2.2. Wave Spectrum Estimation Method
- (1)
- Classical Spectral Estimation Methods
- Autocorrelation Function Method
- 2.
- Periodogram Method
- (2)
- Modern Spectral Estimation Methods
2.2.3. Calculation of Wave Characteristic Elements
2.3. Wave Direction Analysis Based on Directional Spectrum
3. Wave Data Acquisition and Signal Extraction
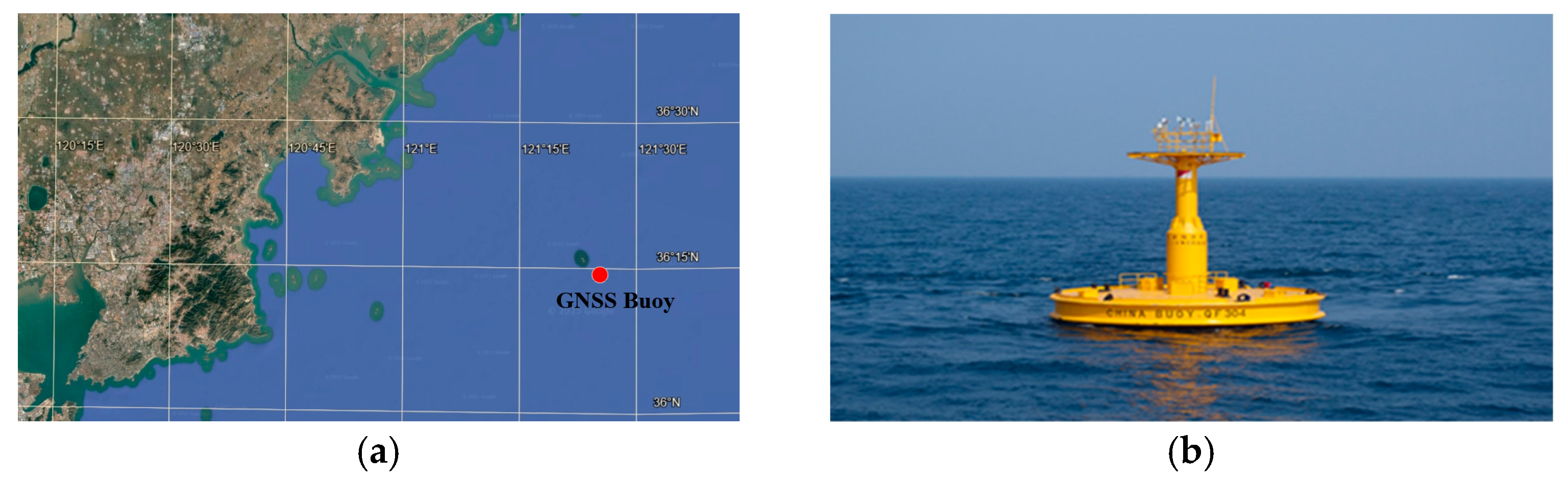
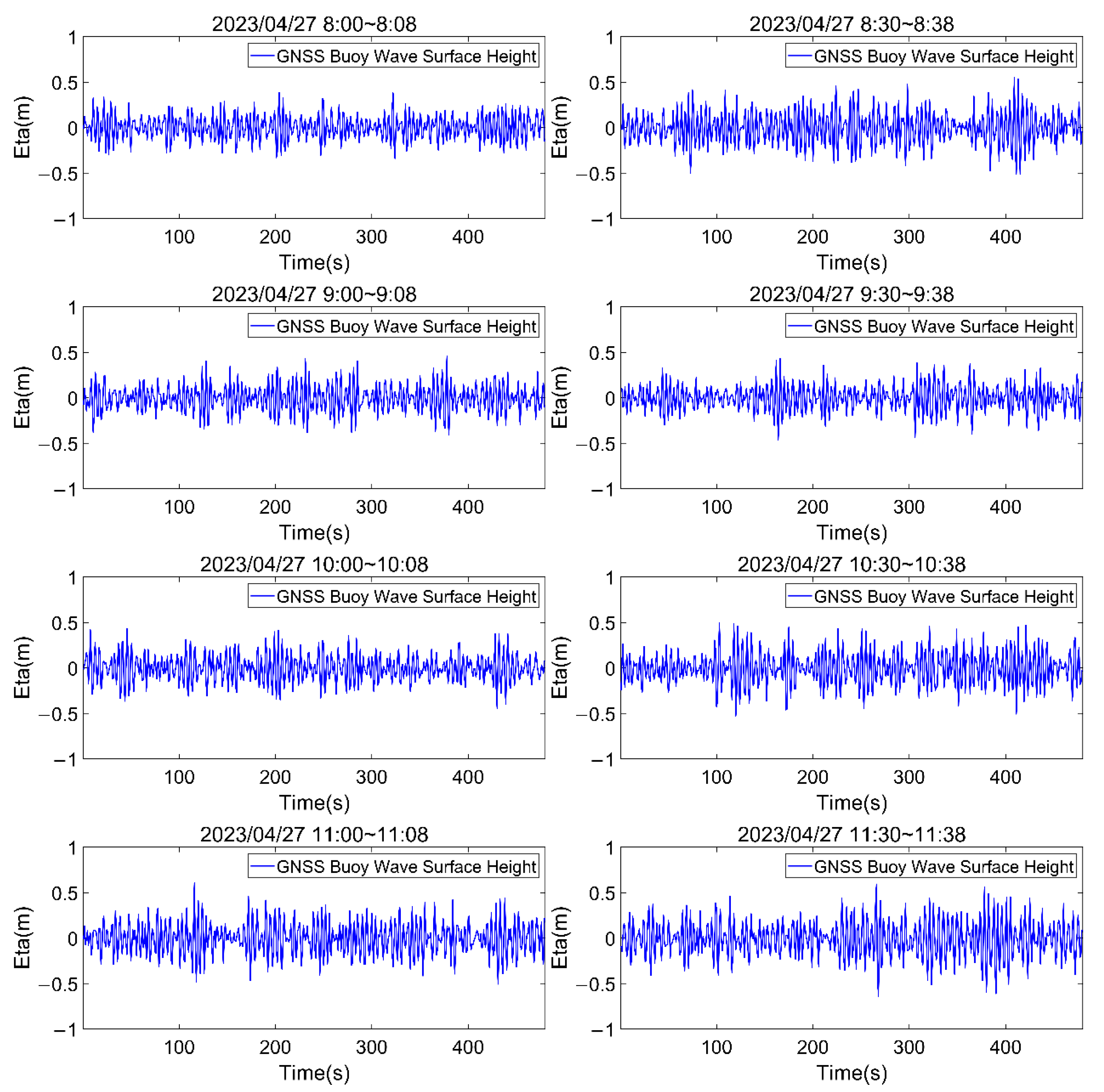
3.1. GNSS-Buoy-Based Data Collection and Processing
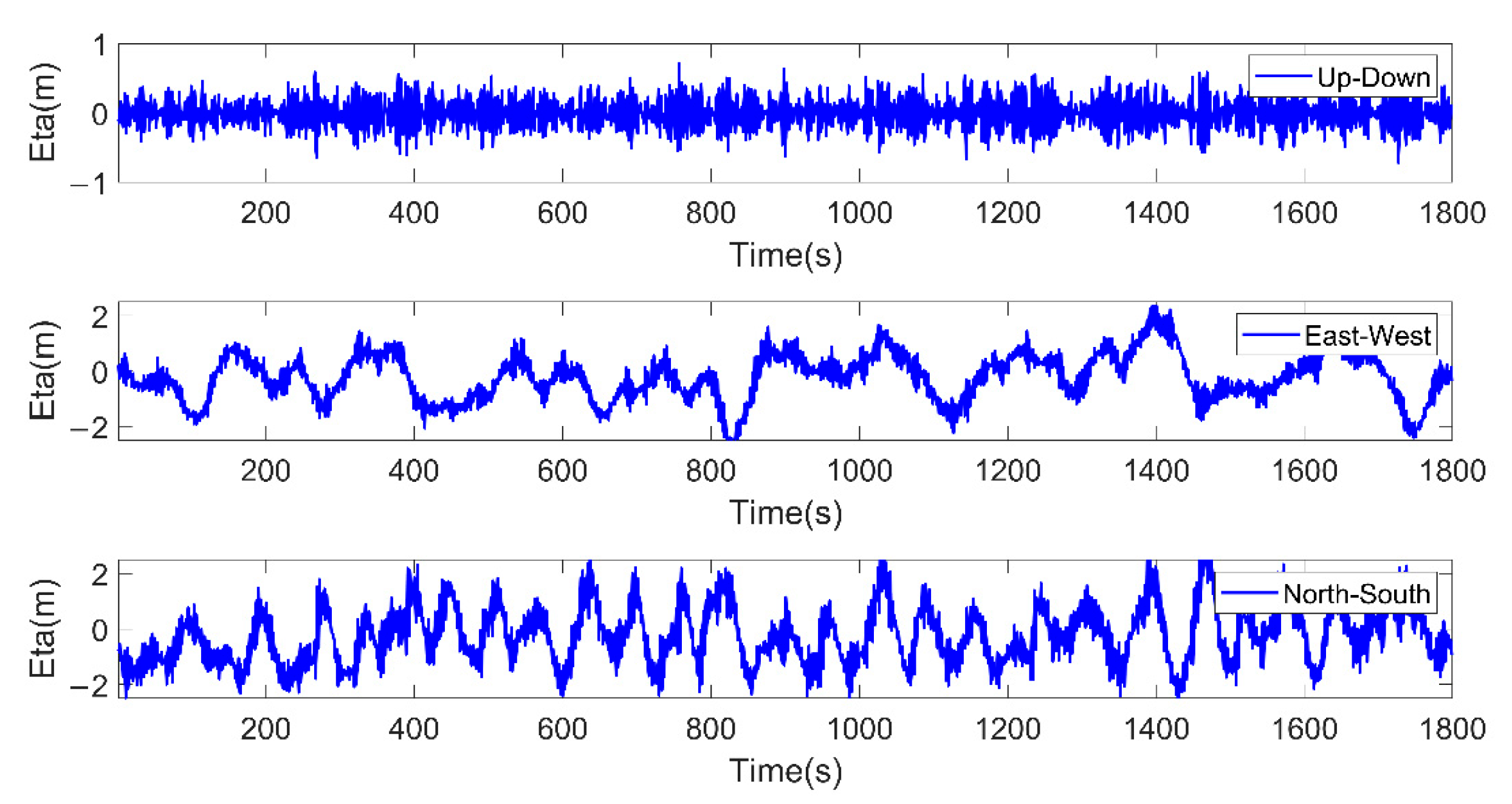
3.2. GNSS-Based Ocean Wave Signal Data Processing
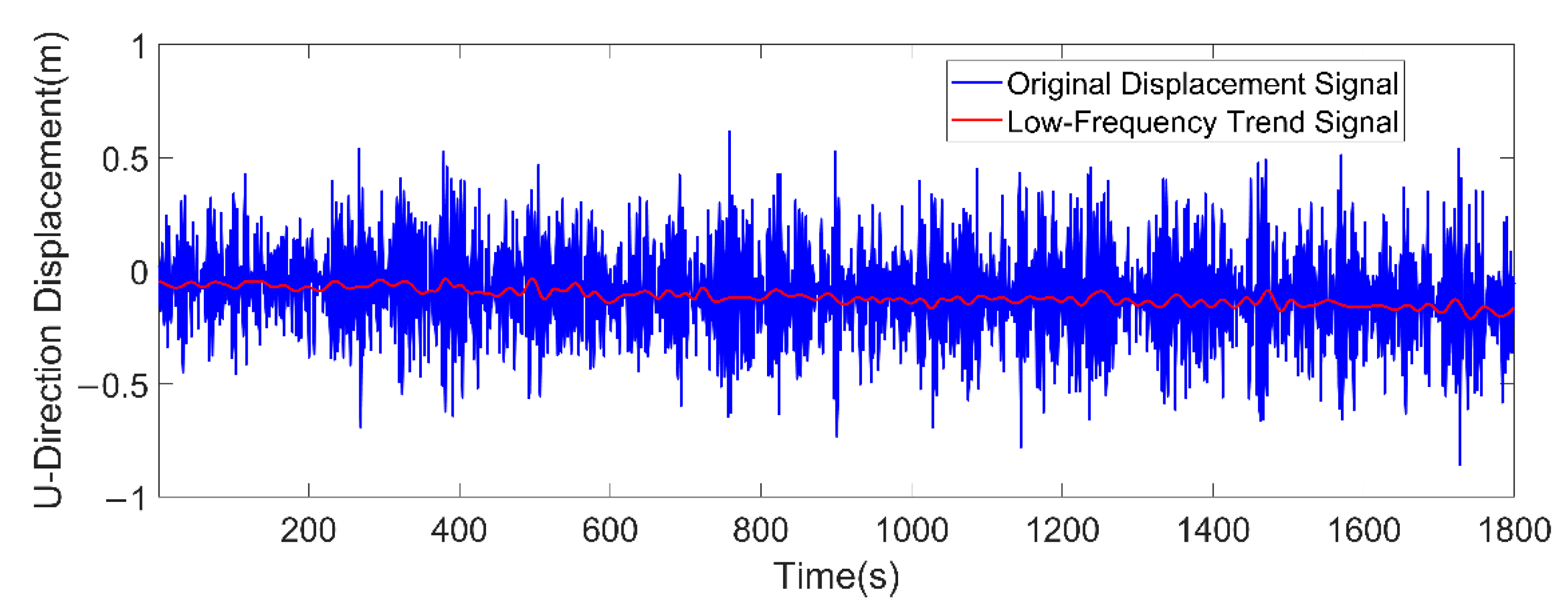
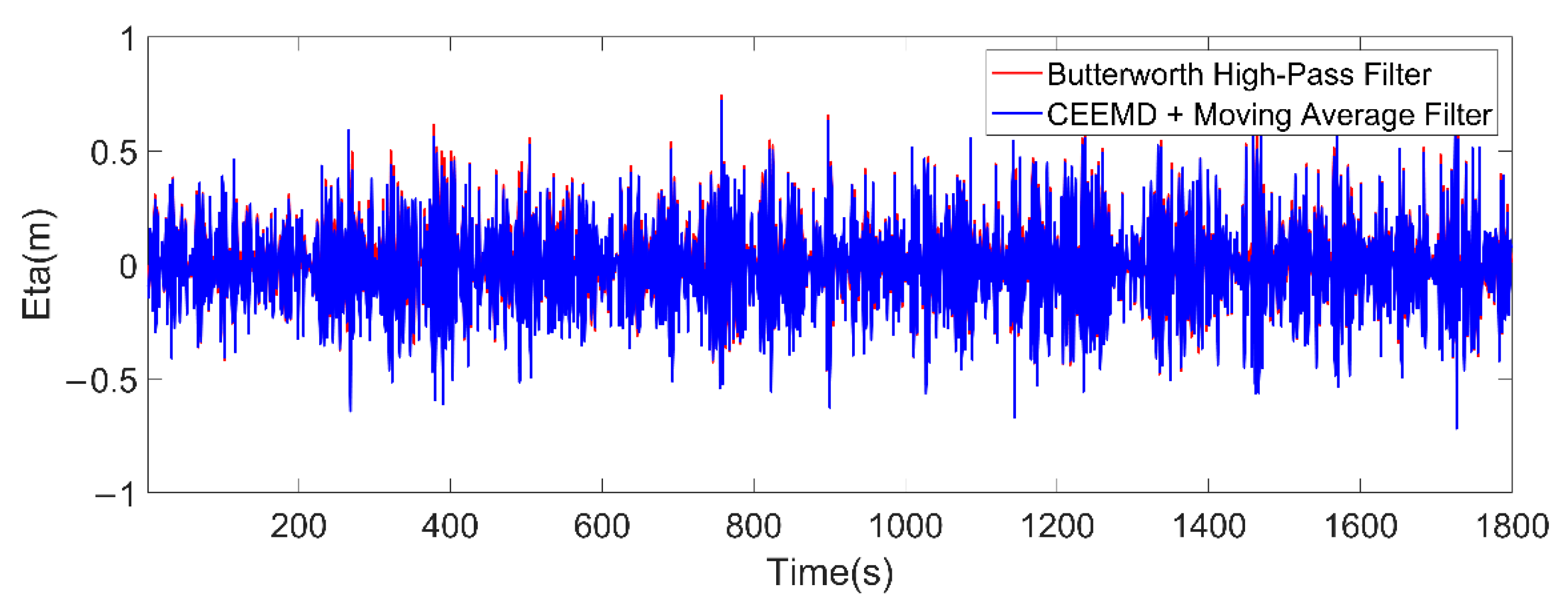
3.2.1. Ocean Wave Signal Separation and Extraction
3.2.2. Correction of Directional Spreading Function
- (1)
- Set all negative values in the directional spreading function to zero.
- (2)
- Redistribute the integrated area of the negative-valued portions to the positive-valued regions proportionally based on their respective weights.
- (3)
- Verify that the corrected directional spreading function satisfies the normalization condition (integral equals unity).
4. Analysis of Measured Wave Results
4.1. Wave Parameter Retrieval Based on Statistical Analysis
Wave Period and Height Estimation via Zero-Upcrossing Method
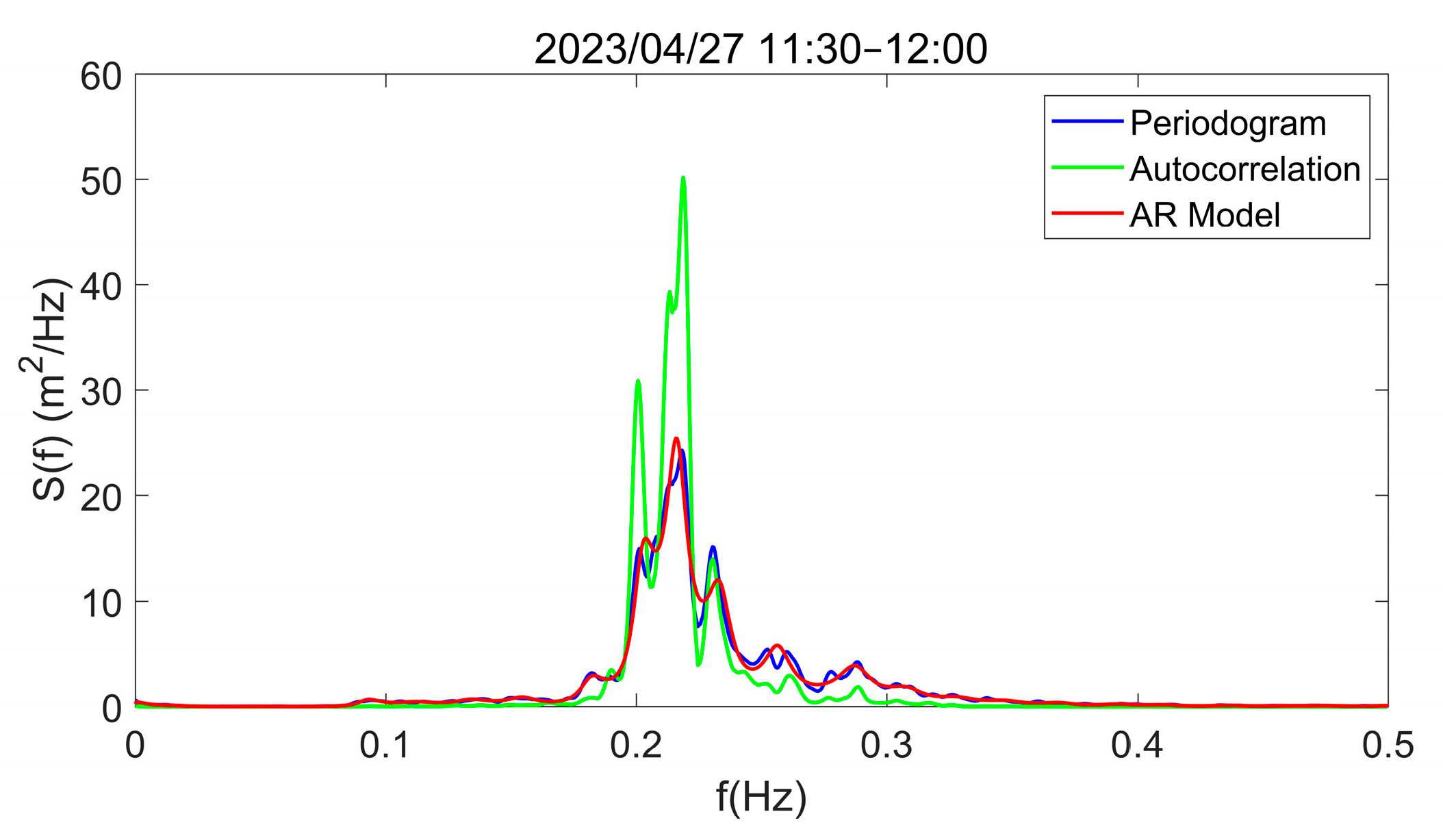
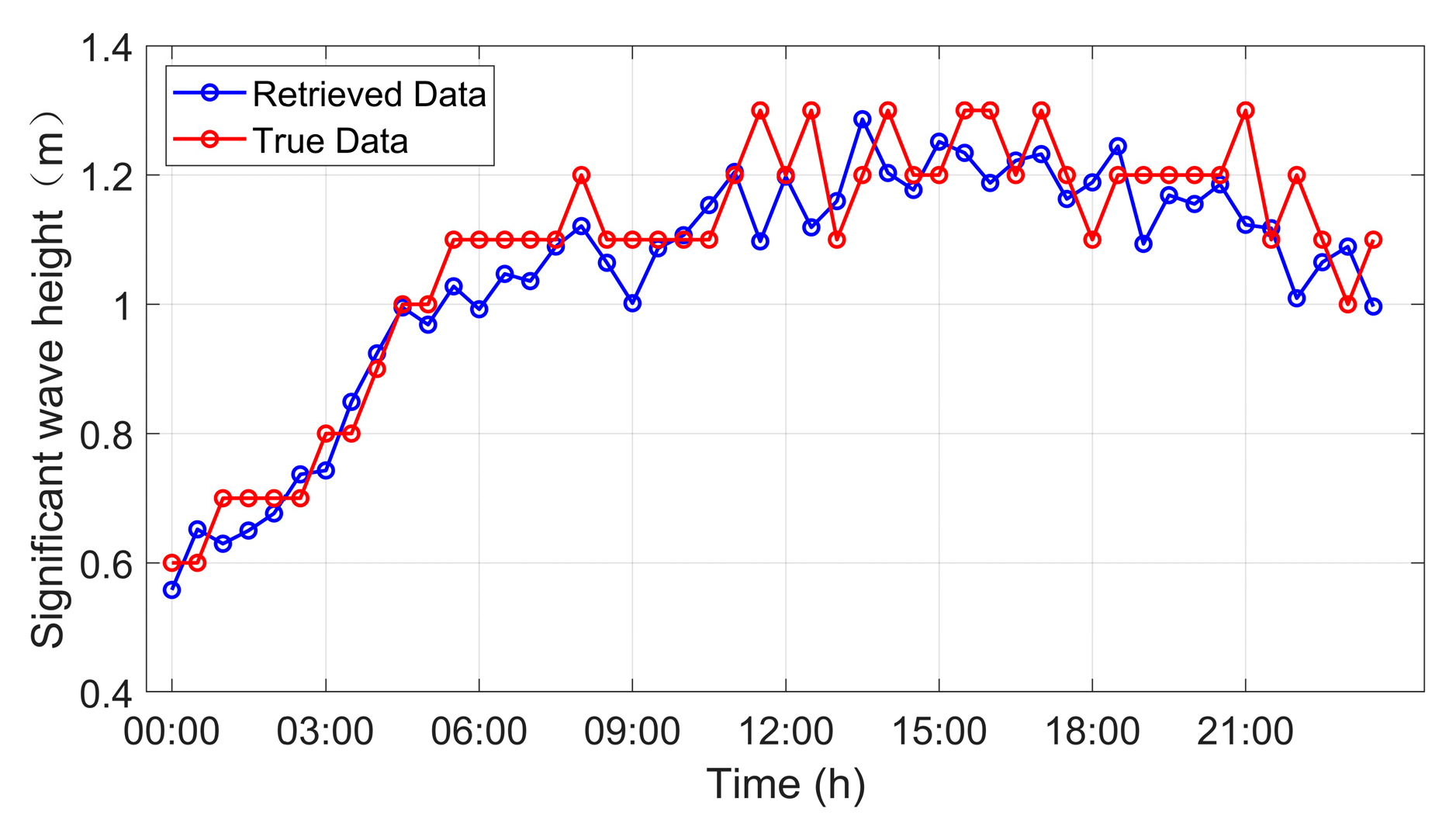
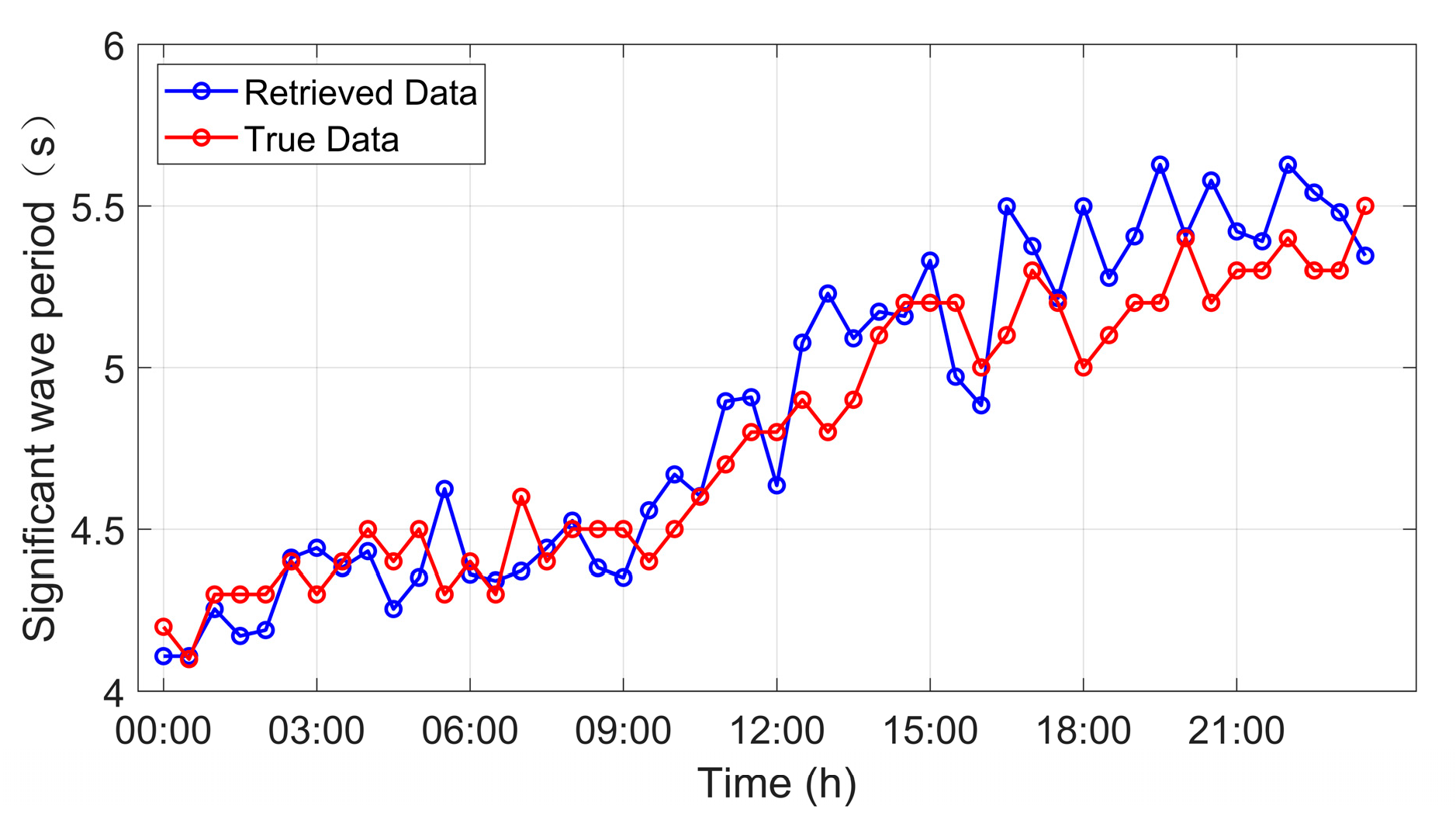
4.2. Wave Period and Height Retrieval Based on Spectral Analysis
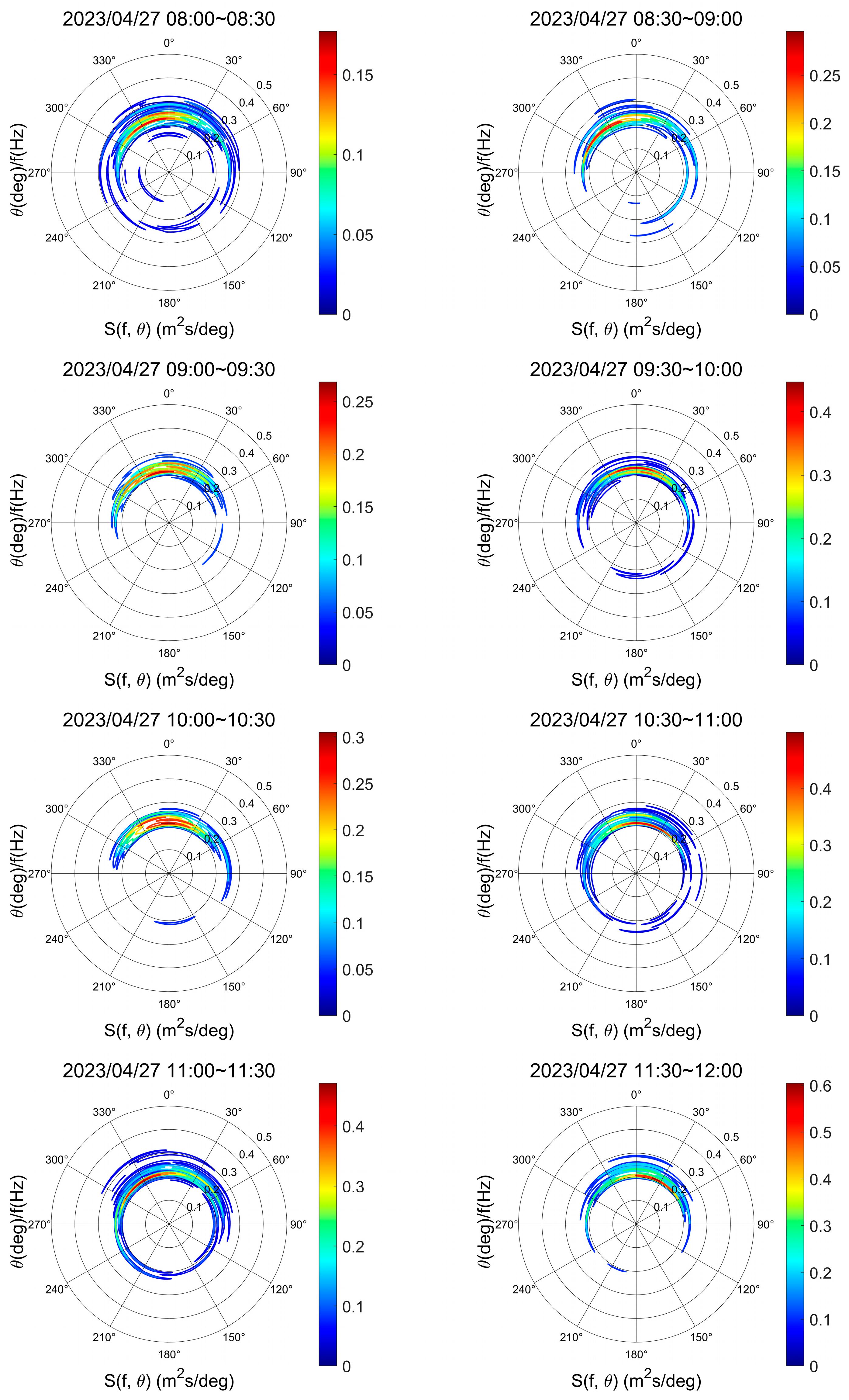
4.3. Wave Direction Retrieval Based on Directional Spectrum Analysis
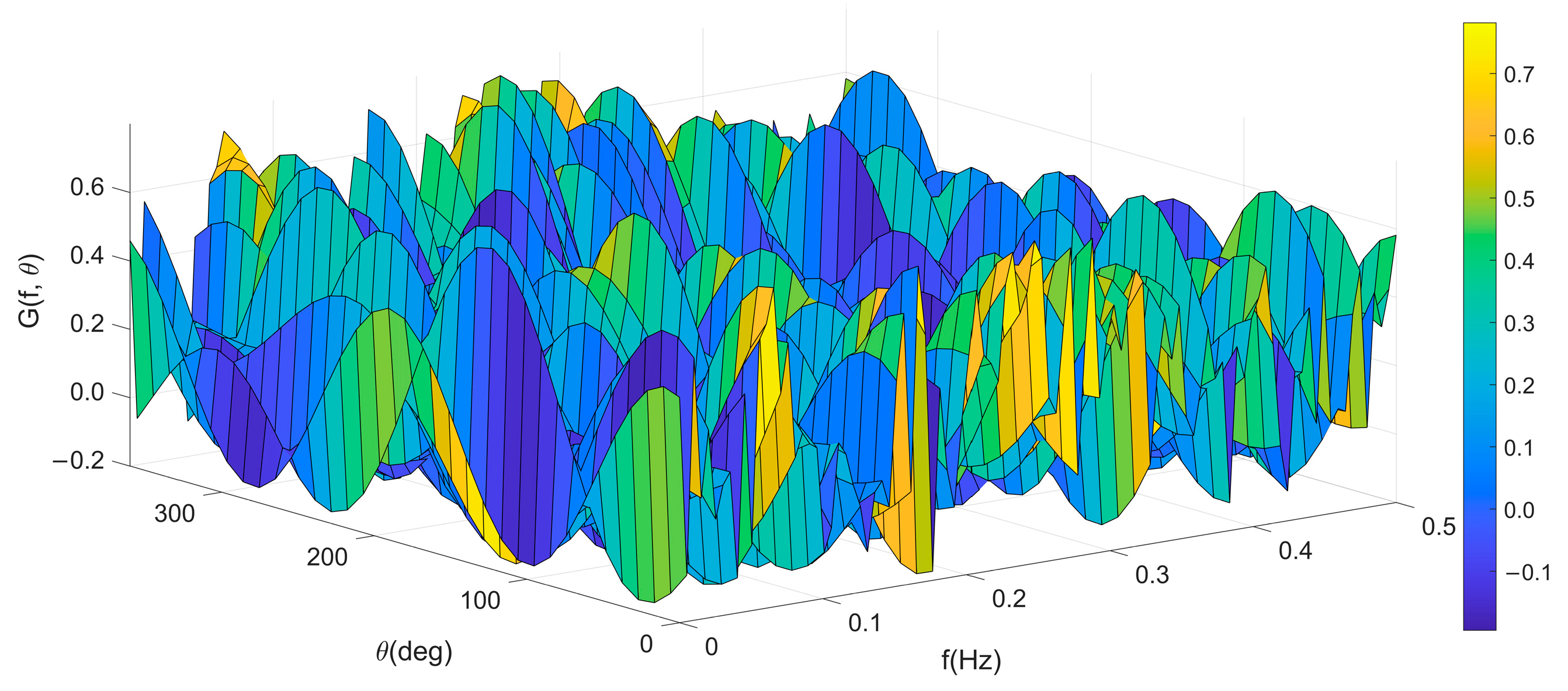
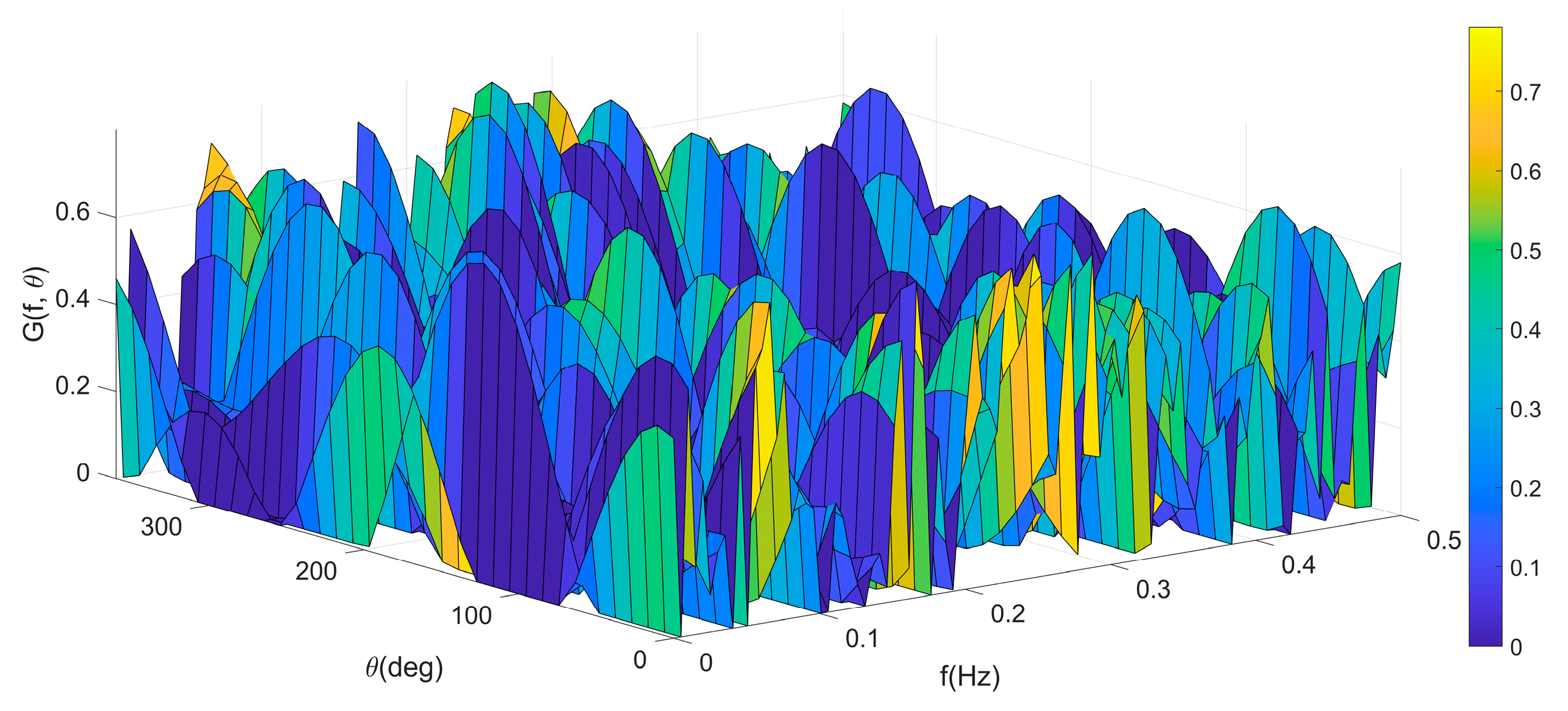
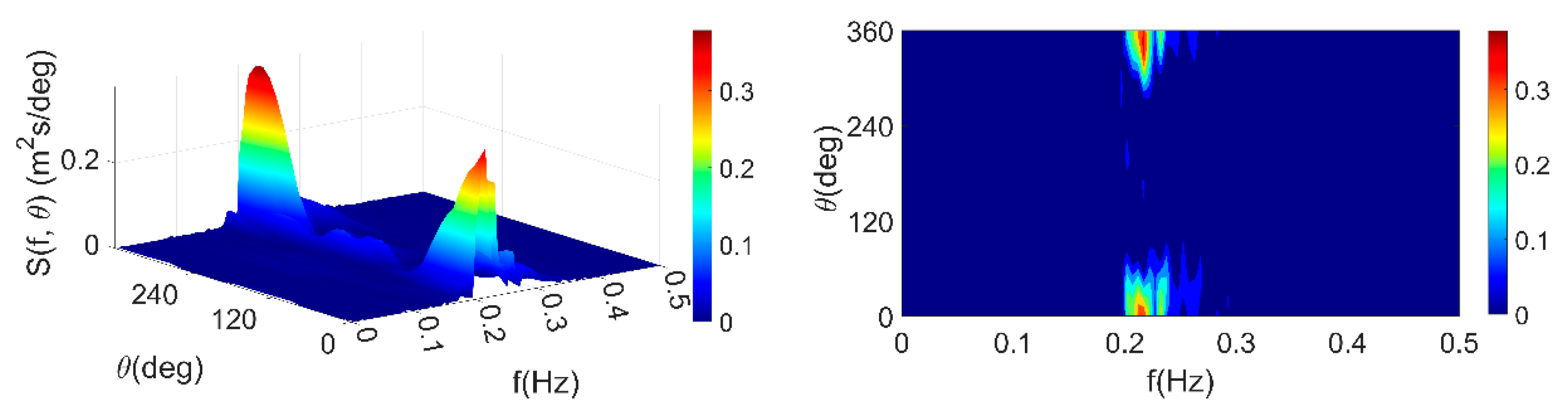
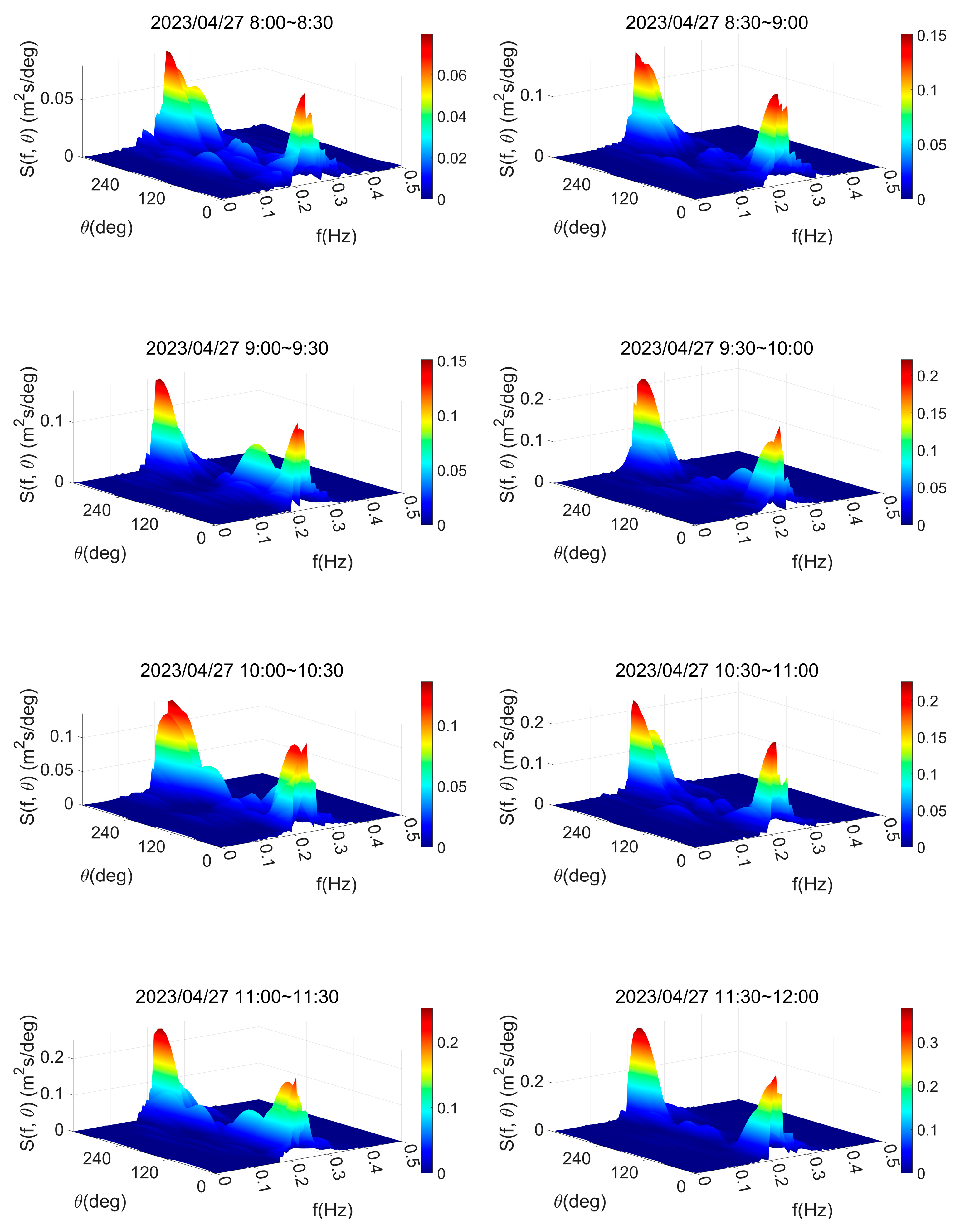
4.3.1. Three-Dimensional Wave Directional Spectrum Analysis
4.3.2. Analysis of Wave Direction–Height Relationship
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-1-139-46252-5. [Google Scholar]
- Kinsman, B. Wind Waves: Their Generation and Propagation on the Ocean Surface; Courier Corporation: North Chelmsford, MA, USA, 1984; ISBN 0-486-64652-1. [Google Scholar]
- Massel, S.R. Ocean Surface Waves: Their Physics and Prediction; World Scientific: Singapore, 2017; Volume 45, ISBN 981-322-839-3. [Google Scholar]
- He, Q.; Silliman, B.R. Climate Change, Human Impacts, and Coastal Ecosystems in the Anthropocene. Curr. Biol. 2019, 29, R1021–R1035. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, A.; Hasselmann, D.E.; Kruseman, P. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP). Ergaenzungsheft Dtsch. Hydrogr. Z. Reihe A 1973, 8, 1–15. [Google Scholar]
- Marques, O.B.; Feddersen, F.; MacMahan, J. An Effective Water Depth Correction for Pressure-Based Wave Statistics on Rough Bathymetry. J. Atmos. Ocean. Technol. 2024, 41, 1047–1062. [Google Scholar] [CrossRef]
- Mercier, P.; Thiébaut, M.; Guillou, S.; Maisondieu, C.; Poizot, E.; Pieterse, A.; Thiébot, J.; Filipot, J.-F.; Grondeau, M. Turbulence Measurements: An Assessment of Acoustic Doppler Current Profiler Accuracy in Rough Environment. Ocean Eng. 2021, 226, 108819. [Google Scholar] [CrossRef]
- Bruno, F.; Bianco, G.; Muzzupappa, M.; Barone, S.; Razionale, A.V. Experimentation of Structured Light and Stereo Vision for Underwater 3D Reconstruction. ISPRS J. Photogramm. Remote Sens. 2011, 66, 508–518. [Google Scholar] [CrossRef]
- Tannuri, E.A.; Simos, A.N.; Sparano, J.V.; Matos, V.L. Motion-Based Wave Estimation: Small-Scale Tests with a Crane-Barge Model. Mar. Struct. 2012, 28, 67–85. [Google Scholar] [CrossRef]
- Wyatt, L.R.; Thompson, S.P.; Burton, R.R. Evaluation of High Frequency Radar Wave Measurement. Coast. Eng. 1999, 37, 259–282. [Google Scholar] [CrossRef]
- Ma, C.; Pan, L.; Qiu, Z.; Liang, D.; Chen, G.; Yu, F.; Sun, H.; Sun, D.; Wu, W. Ocean Wave Inversion Based on a Ku/Ka Dual-Band Airborne Interferometric Imaging Radar Altimeter. Remote Sens. 2022, 14, 3578. [Google Scholar] [CrossRef]
- Tucker, M.J. Waves in Ocean Engineering: Measurement, Analysis, Interpretation; E. Horwood: New York, NY, USA, 1991; pp. 109–111. [Google Scholar]
- De Vries, J.J.; Waldron, J.; Cunningham, V. Field Tests of the New Datawell DWR-G GPA Wave Buoy. Sea Technol. 2003, 44, 50–55. [Google Scholar]
- Behrens, J.; Terrill, E.; Thomas, J.O. CDIP Wave Observations during Hurricanes Irma, Jose, and Maria, and a nor’easter. Shore Beach 2018, 86, 14–20. [Google Scholar]
- Bidlot, J.-R.; Holmes, D.J.; Wittmann, P.A.; Lalbeharry, R.; Chen, H.S. Intercomparison of the Performance of Operational Ocean Wave Forecasting Systems with Buoy Data. Weather Forecast. 2002, 17, 287–310. [Google Scholar] [CrossRef]
- Gorman, R.M. Estimation of Directional Spectra from Wave Buoys for Model Validation. Procedia Iutam 2018, 26, 81–91. [Google Scholar] [CrossRef]
- Fund, F.; Perosanz, F.; Testut, L.; Loyer, S. An Integer Precise Point Positioning Technique for Sea Surface Observations Using a GPS Buoy. Adv. Space Res. 2013, 51, 1311–1322. [Google Scholar] [CrossRef]
- Dawidowicz, K. Sea Level Changes Monitoring Using GNSS Technology—A Review of Recent Efforts. Acta Adriat. 2014, 55, 145–162. [Google Scholar]
- Zhu, L.; Yang, L.; Xu, Y.; Yang, F.; Zhou, X. Retrieving Wave Parameters from GNSS Buoy Measurements Using the PPP Mode. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Kato, T.; Terada, Y.; Tadokoro, K.; Kinugasa, N.; Futamura, A.; Toyoshima, M.; Yamamoto, S.; Ishii, M.; Tsugawa, T.; Nishioka, M. Development of GNSS Buoy for a Synthetic Geohazard Monitoring System. J. Disaster Res. 2018, 13, 460–471. [Google Scholar] [CrossRef]
- Lutsenko, V.I.; Lutsenko, I.V.; Popov, I.V.; Luo, Y.; Anh, N.X.; Guo, Q.; Zheng, Y. GNSS Signal Use for Sea Waves Monitoring. In Proceedings of the 2020 IEEE Ukrainian Microwave Week (UkrMW), Kharkiv, Ukraine, 21–25 September 2020; pp. 768–771. [Google Scholar]
- Yang, L.; Xu, Y.; Jiang, Y.; Mertikas, S.P.; Wang, Z.; Zhu, L.; Liu, N.; Lin, L. Retrieval of Ocean Wave Characteristics via Single-Frequency Time-Differenced Carrier Phases From GNSS Buoys. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4204512. [Google Scholar] [CrossRef]
- Gu, H.; Zhu, X.; Shan, R.; Zang, J.; Qian, L.; Lin, P. Evaluation of a GNSS for Wave Measurement and Directional Wave Spectrum Analysis. Ocean Eng. 2023, 270, 113683. [Google Scholar] [CrossRef]
- Liang, G.; Li, S.; Bao, K.; Wang, G.; Teng, F.; Zhang, F.; Wang, Y.; Guan, S.; Wei, Z. Development of GNSS Buoy for Sea Surface Elevation Observation of Offshore Wind Farm. Remote Sens. 2023, 15, 5323. [Google Scholar] [CrossRef]
- Shum, C.K.; Lee, H.; Abusali, P.A.M.; Braun, A.; de Carufel, G.; Fotopoulos, G.; Komjathy, A.; Kuo, C. Prospects of Global Navigation Satellite System (GNSS) Reflectometry for Geodynamic Studies. Adv. Space Res. 2011, 47, 1814–1822. [Google Scholar] [CrossRef]
- Jing, C.; Niu, X.; Duan, C.; Lu, F.; Di, G.; Yang, X. Sea Surface Wind Speed Retrieval from the First Chinese GNSS-R Mission: Technique and Preliminary Results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef]
- Ruffini, G.; Soulat, F.; Caparrini, M.; Germain, O.; Martín-Neira, M. The Eddy Experiment: Accurate GNSS-R Ocean Altimetry from Low Altitude Aircraft. Geophys. Res. Lett. 2004, 31, L12306. [Google Scholar] [CrossRef]
- Guerra, M.; Hay, A.E.; Karsten, R.; Trowse, G.; Cheel, R.A. Turbulent Flow Mapping in a High-Flow Tidal Channel Using Mobile Acoustic Doppler Current Profilers. Renew. Energy 2021, 177, 759–772. [Google Scholar] [CrossRef]
- Tomita, F.; Kido, M.; Iinuma, T.; Ohta, Y. GNSS-Acoustic Positioning Error in the Vertical Component Considering the Uncertainty of a Reference Sound Speed Profile. Mar. Geophys. Res. 2025, 46, 3. [Google Scholar] [CrossRef]
- Pérez Gómez, B.; Vilibić, I.; Šepić, J.; Međugorac, I.; Ličer, M.; Testut, L.; Fraboul, C.; Marcos, M.; Abdellaoui, H.; Álvarez Fanjul, E. Coastal Sea Level Monitoring in the Mediterranean and Black Seas. Ocean Sci. 2022, 18, 997–1053. [Google Scholar] [CrossRef]
- Lin, Y.-P.; Huang, C.-J.; Chen, S.-H. Variations in Directional Wave Parameters Obtained from Data Measured Using a GNSS Buoy. Ocean Eng. 2020, 209, 107513. [Google Scholar] [CrossRef]
- Lin, Y.-P.; Huang, C.-J.; Chen, S.-H.; Doong, D.-J.; Kao, C.C. Development of a GNSS Buoy for Monitoring Water Surface Elevations in Estuaries and Coastal Areas. Sensors 2017, 17, 172. [Google Scholar] [CrossRef]
- Lei, J.; Li, F.; Zhang, S.; Xiao, C.; Xie, S.; Ke, H.; Zhang, Q.; Li, W. Ocean Tides Observed from A GPS Receiver on Floating Sea Ice near Chinese Zhongshan Station, Antarctica. Mar. Geod. 2018, 41, 353–367. [Google Scholar] [CrossRef]
- Wang, F.; Yang, D.; Wang, J.; Xing, J.; Yu, Y. Shipborne GNSS Reflectometry for Monitoring Along-Track Significant Wave Height and Wind Speed. Ocean Eng. 2023, 281, 114935. [Google Scholar] [CrossRef]
- Rychlik, I.; Johannesson, P.; Leadbetter, M.R. Modelling and Statistical Analysis of Ocean-Wave Data Using Transformed Gaussian Processes. Mar. Struct. 1997, 10, 13–47. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, Y.; Benoit, M. Statistical Distributions of Free Surface Elevation and Wave Height for Out-of-Equilibrium Sea-States Provoked by Strong Depth Variations. Ocean Eng. 2024, 293, 116645. [Google Scholar] [CrossRef]
- Gryazin, D.G.; Belova, O.O.; Gleb, K.A.; Kovchin, M.I. Study of the Characteristics of Wave Buoys by Comparison Measurements. Oceanology 2018, 58, 742–748. [Google Scholar] [CrossRef]
- Dehghan, Y.; Sadrinasab, M.; Chegini, V.; Akhyani, M. Wave Spectrum Analysis for Southern Caspian Sea. Ocean Eng. 2023, 272, 113490. [Google Scholar] [CrossRef]
- Krogstad, H.E. Maximum Likelihood Estimation of Ocean Wave Spectra from General Arrays of Wave Gauges. Model. Identif. Control. 1988, 9, 81–97. [Google Scholar] [CrossRef]
- Liu, P.C. Wavelet Spectrum Analysis and Ocean Wind Waves. In Wavelet Analysis and Its Applications; Elsevier: Amsterdam, The Netherlands, 1994; Volume 4, pp. 151–166. ISBN 1874-608X. [Google Scholar]
- Joodaki, G.; Nahavandchi, H.; Cheng, K. Ocean Wave Measurement Using GPS Buoys. J. Geod. Sci. 2013, 3, 163–172. [Google Scholar] [CrossRef]
- Hashimoto, N. Analysis of the Directional Wave Spectrum from Field Data. Adv. Coast. Ocean Eng. 1997, 3, 103–144. [Google Scholar]
- Torabi, M.; Shahidi, R.; Gill, E.W. Ocean Surface Wave Parameter Estimation Using Periodogram Method. In Proceedings of the XXXVth URSI General Assembly and Scientific Symposium (URSI GASS), Sapporo, Hokkaido, Japan, 19–26 August 2023. [Google Scholar]
- Rasool, S.; Muttaqi, K.M.M.K.M. Modeling Ocean Waves and Investigation of Oceanic Wave Spectra for Wave-to-Wire System. J. Eng. Res. 2022, 10, 1–17. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Parameters Estimate of Autoregressive Moving Average and Autoregressive Integrated Moving Average Models and Compare Their Ability for Inflow Forecasting. J. Math. Stat. 2012, 8, 330–338. [Google Scholar] [CrossRef]
- Gryazin, D.; Gleb, K. A New Method to Determine Directional Spectrum of Sea Waves and Its Application to Wave Buoys. J. Ocean Eng. Mar. Energy 2022, 8, 269–283. [Google Scholar] [CrossRef]
- Krogstad, H.E.; Magnusson, A.K.; Donelan, M.A. Wavelet and Local Directional Analysis of Ocean Waves. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 28 May–2 June 2006; ISOPE: Mountain View, CA, USA, 2006; p. ISOPE-I-06-204. [Google Scholar]
- Donelan, M.; Babanin, A.; Sanina, E.; Chalikov, D. A Comparison of Methods for Estimating Directional Spectra of Surface Waves. J. Geophys. Res. Ocean. 2015, 120, 5040–5053. [Google Scholar] [CrossRef]
- Chang, Z.; Han, F.; Sun, Z.; Gao, Z.; Wang, L. Three-Dimensional Dynamic Sea Surface Modeling Based on Ocean Wave Spectrum. Acta Oceanol. Sin. 2021, 40, 38–48. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, S. Random Wave and Its Applications to Engineering, 4th ed.; Dalian University of Technology Press: Dalian, China, 2011; ISBN 978-7-5611-0466-8. [Google Scholar]
- Smith, S.W. The Scientist and Engineer’s Guide to Digital Signal Processing; California Technical Pub: Brisbane, CA, USA, 1997. [Google Scholar]
- Lyons, R.G. Understanding Digital Signal Processing, 3/E; Pearson Education India: Chennai, India, 1997; ISBN 81-317-6436-2. [Google Scholar]
- Panahi, R.; Shafieefar, M. Development of a Bi-Modal Directional Wave Spectrum. Ocean Eng. 2015, 105, 104–111. [Google Scholar] [CrossRef]




| Characteristic Value | Calculation Formula | Characteristic Value | Calculation Formula |
|---|---|---|---|
| Maximum wave height | Maximum wave period | ||
| Highest one-tenth wave height | Mean period of the highest one-tenth waves | ||
| Significant wave height | Significant wave period | ||
| Mean wave height | Mean wave period |
| Parameter | Configuration |
|---|---|
| Position Mode | Kinematic |
| Frequencies | L1 |
| Solution Type | Forward |
| Elevation Mask | 15.0 deg |
| Ephemeris Data | Broadcast |
| Navigation Systems | GPS/GLONASS/Galileo/BDS |
| Ambiguity Resolution | Instantaneous |
| Integer Validation Threshold | 3.0 |
| Data Period | Statistical Wave Height Parameters (m) | Number of Waves | |||
|---|---|---|---|---|---|
| 08:00–08:08 | 0.72 | 0.57 | 0.48 | 0.32 | 112 |
| 08:30–08:38 | 1.06 | 0.82 | 0.66 | 0.44 | 111 |
| 09:00–09:08 | 0.87 | 0.70 | 0.57 | 0.38 | 105 |
| 09:30–09:38 | 0.87 | 0.68 | 0.53 | 0.35 | 110 |
| 10:00–10:08 | 0.82 | 0.72 | 0.57 | 0.37 | 111 |
| 10:30–10:38 | 1.01 | 0.84 | 0.68 | 0.44 | 113 |
| 11:00–11:08 | 1.09 | 0.82 | 0.66 | 0.45 | 113 |
| 11:30–11:38 | 1.23 | 0.98 | 0.84 | 0.54 | 106 |
| Data Period | Statistical Wave Period Parameters (s) | |||
|---|---|---|---|---|
| 08:00–08:08 | 8.00 | 6.00 | 5.32 | 4.19 |
| 08:30–08:38 | 7.00 | 5.83 | 5.26 | 4.22 |
| 09:00–09:08 | 8.00 | 6.73 | 5.66 | 4.52 |
| 09:30–09:38 | 8.00 | 6.36 | 5.54 | 4.34 |
| 10:00–10:08 | 7.00 | 6.33 | 5.43 | 4.30 |
| 10:30–10:38 | 8.00 | 6.25 | 5.37 | 4.22 |
| 11:00–11:08 | 8.00 | 6.00 | 5.32 | 4.22 |
| 11:30–11:38 | 7.00 | 6.18 | 5.08 | 4.33 |
| Wave Parameters | Periodogram | Autocorrelation | AR Model | Zero-Crossing |
|---|---|---|---|---|
| Significant Wave Height (m) | 0.89 | 0.89 | 0.89 | 0.84 |
| Significant Wave Period (s) | 4.27 | 4.27 | 4.29 | 5.08 |
| Mean Wave Height (m) | 0.56 | 0.56 | 0.56 | 0.54 |
| Mean Wave Period (s) | 4.25 | 4.24 | 4.25 | 4.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Chang, X.; Tu, R.; Yan, S.; Wang, S.; Zhang, P. Retrieval of Wave Parameters from GNSS Buoy Measurements Using Spectrum Analysis: A Case Study in the Huanghai Sea. Remote Sens. 2025, 17, 2869. https://doi.org/10.3390/rs17162869
Wang J, Chang X, Tu R, Yan S, Wang S, Zhang P. Retrieval of Wave Parameters from GNSS Buoy Measurements Using Spectrum Analysis: A Case Study in the Huanghai Sea. Remote Sensing. 2025; 17(16):2869. https://doi.org/10.3390/rs17162869
Chicago/Turabian StyleWang, Jin, Xiaohang Chang, Rui Tu, Shiwei Yan, Shengli Wang, and Pengfei Zhang. 2025. "Retrieval of Wave Parameters from GNSS Buoy Measurements Using Spectrum Analysis: A Case Study in the Huanghai Sea" Remote Sensing 17, no. 16: 2869. https://doi.org/10.3390/rs17162869
APA StyleWang, J., Chang, X., Tu, R., Yan, S., Wang, S., & Zhang, P. (2025). Retrieval of Wave Parameters from GNSS Buoy Measurements Using Spectrum Analysis: A Case Study in the Huanghai Sea. Remote Sensing, 17(16), 2869. https://doi.org/10.3390/rs17162869






