Abstract
Land observation multispectral satellites (e.g., Landsat-8/9 and Sentinel-2) offer high spatial resolution but have limited spectral bands for water color observation and insufficient spectral resolution. This study proposes a spectral reconstruction model based on a residual neural network (Deep Spectral Reconstruction Learning Network, DSR-Net) to provide additional spectral bands support for nearshore water observations. The model is trained on 60 million pairs of quasi-synchronous reflectance data, and achieves stable reconstruction of 15 water color channels of the surface level reflectance for water pixels (ρw) from visible to near-infrared bands, considering sensor noise and atmospheric correction errors. Validation results based on AERONET-OC data show that the root mean square error of reconstructed ρw by DSR-Net ranges from 4.09 to 5.18 × 10−3, representing a reduction of 25% to 43% compared to original atmospheric correction results. The reconstruction accuracy reaches the observation level of the Sentinel-3/OLCI water color sensor and is universally applicable to different water categories, effectively supporting nearshore water color observation tasks such as colored dissolved organic matter inversion and cyanobacteria monitoring. The errors in the multispectral reflectance-based ρw primarily arise from sensor noise and atmospheric correction errors. After DSR-Net reconstruction, approximately 59% of the uncertainty caused by sensor noise and 38% of that caused by atmospheric correction errors are reduced. In summary, the spectral reconstruction products generated by DSR-Net not only significantly enhance the water color observation capabilities of current satellite sensors but also provide critical technical support for marine environmental monitoring and the design of next-generation sensors.
1. Introduction
The enhanced capabilities of land observation remote sensing sensors have facilitated their progressive application in coastal and inland water monitoring, enabling acquisition of observational data with improved spatial resolution. Recent studies demonstrate that land observation sensors (LOSs) can effectively quantify spatiotemporal variations in suspended particulate matter and chlorophyll-a concentrations in marine environments, with measurement accuracy reaching operational thresholds [1,2,3,4,5]. Nevertheless, inherent limitations persist compared to dedicated water color sensors (WCSs). Most LOSs prioritize spectral bands exhibiting strong atmospheric transmissivity (green, red, and near-infrared regions), while lacking dedicated spectral configurations for critical aquatic parameters such as colored dissolved organic matter (CDOM), phytoplankton pigment absorption characteristics (e.g., chlorophyll-a and phycocyanin), and fluorescence emission peaks. These spectral constraints not only reduce the robustness of water constituent retrieval algorithms but also limit their applicability for comprehensive aquatic environmental monitoring [6,7,8].
Spectral reconstruction techniques provide an effective solution to address spectral band limitations in water color observations and enhance the coastal monitoring capabilities of multispectral sensors. Studies have demonstrated that broadband spectral observations exhibit significant redundancy characteristics [9,10,11]. For instance, the panchromatic (PAN) band of Landsat-8, covering the 500–680 nm spectral range, partially overlaps with the red and green bands. After separating the overlapping regions, the PAN band provides additional spectral information not captured by the red and green bands. On the other hand, signals from adjacent spaced bands (Δλ ≤ 20 nm) display spectral redundancy, characterized by high inter-band correlations [12]. This property allows for complete spectral reconstruction in both pelagic and nearshore waters using a limited number of optimally selected bands (typically 5–15), achieving an optimal balance between signal-to-noise ratio (SNR) and data storage efficiency [12,13,14,15,16]. In summary, the core of spectral reconstruction techniques lies in leveraging the redundancy inherent in broadband signals along with the continuous nature of spectral curves to isolate or derive reflectance values for specific bands from known spectral information.
Building on these principles, spectral reconstruction approaches are broadly categorized into multivariate regressor models and intelligent learning models. Regressor models require a high correlation between the reconstructed band and the known bands. For example, Castagna et al. [17] and Niroumand-Jadidi and Bovolo [10] established a linear regression model calibrated for Landsat-8 that links the orange band (613 nm) with the PAN, green, and red bands. Reconstructed orange bands achieve accuracy comparable to that of the original red band, enabling applications in water color studies such as cyanobacterial bloom detection. Paulino et al. [18] developed a synthetic band generation method that tested three multivariate regression models on Sentinel-2 and Sentinel-3 image pairs to reconstruct eight visible bands, where linear regression achieved the highest accuracy with 28% bias relative to in situ observations. However, in Case-2 waters, the complexity of water color constituents (e.g., phytoplankton, CDOM, and non-algal particles) reduces inter-band correlations, increasing the challenge for regression. Recent breakthroughs in intelligent learning technologies for data mining and predictive modeling have provided novel pathways to fully exploit spectral continuity and redundancy. Niroumand-Jadidi and Bovolo [10] developed Deep OrAnge Band Learning Network (DOABLE-Net) trained on simulated hyperspectral data, successfully constructing a phycocyanin absorption band (620 nm) for Sentinel-2 sensors lacking PAN capability, thereby enabling reliable dynamic monitoring of cyanobacterial blooms. Banerjee et al. [9] utilized Hyperspectral Imager for the Coastal Ocean (HICO) data to establish hyperspectral-to-multispectral mapping relationships, reconstructing 76 bands (440–865 nm) for Sentinel-2, thereby providing cost-effective hyperspectral capabilities for water quality monitoring and algal bloom detection. Wang et al. [19] extended the spectral coverage of WCSs into near-blue ultraviolet (nbUV, 360–400 nm) through neural network modeling of correlations between visible and nbUV bands, subsequently deriving global distributions of the diffuse attenuation coefficients for downwelling irradiance (Kd, m−1) using reconstructed nbUV spectral data. While neural networks demonstrate superior multispectral reconstruction performance in optically complex Case-2 waters, critical limitations persist. First, model training remains contingent on the representativeness of simulated spectral datasets, which often fail to capture the full variability of in situ bio-optical conditions. Second, sensor-specific radiometric noise patterns and residual atmospheric correction errors, which are rarely quantified or integrated into the training process, introduce systematic biases. These error sources propagate cumulatively through subsequent processing stages, amplifying uncertainties in derived biogeochemical parameters.
This study employs the surface level reflectance for water pixels (ρw) as training data to establish nonlinear mapping relationships between spectral bands of LOSs and WCSs through a Deep learning-based Spectral Reconstruction Network (DSR-Net). The training dataset integrates quasi-synchronized observations from LOSs and WCSs, with rigorous quality control applied across spatial, temporal, and spectral dimensions, yielding approximately 60 million high-quality matched spectral pairs. Leveraging this dataset, DSR-Net achieves robust LOS-to-WCS spectral reconstruction while partially addressing sensor noise and residual atmospheric correction errors. Furthermore, this study systematically evaluates the reconstruction accuracy of DSR-Net across spectral bands, its operational applicability for nearshore water quality monitoring, and its comparative advantages over conventional reconstruction models. The investigation also elucidates error propagation mechanisms inherent in spectral reconstruction processes and identifies key factors influencing reconstruction fidelity through sensitivity analyses.
2. Data
2.1. Remote Sensing Data
This study employs high quality (cloud cover < 5%) remote sensing data from Landsat-8 (since 2013), Landsat-9 (since 2021), Sentinel-2 (since 2015) and Sentinel-3 (since 2016) acquired from their respective launch dates through 2023. The Operational Land Imager (OLI) on Landsat-8 and its successor (OLI-2) on Landsat-9 share close spectral configurations, forming a dual-satellite system (hereafter Landsat-8&9/OLI) that enhances temporal resolution through coordinated acquisitions. Notably, while their spectral bands are similar, the radiometric resolution differs: Landsat-9/OLI-2 provides 14-bit quantization, whereas Landsat-8/OLI provides 12-bit. Landsat-8&9/OLI comprises eight multispectral bands and a PAN band spanning the visible to shortwave infrared (SWIR) range. The visible and near-infrared (VNIR) bands have bandwidths of 20–75 nm and a SNR of approximately 110, while the PAN band integrates green, orange, and red signals across 500–680 nm. The Multispectral Imager (MSI) on Sentinel-2 features 13 spectral bands covering the visible to SWIR regions. In addition to VNIR bands, MSI incorporates four red-edge bands optimized for vegetation characterization. Sentinel-2/MSI VNIR bands exhibit bandwidths of 15–65 nm and a SNR of approximately 130.
In comparison, the Ocean and Land Color Imager (OLCI) onboard Sentinel-3 is characterized by narrow spectral bands (2.5–10 nm bandwidth in visible regions), enhanced SNRs (peak value > 1800), and high radiometric resolution. Beyond red, green, and blue bands that overlap with Landsat-8&9/OLI and Sentinel-2/MSI, OLCI includes specialized bands for phytoplankton fluorescence at 680 nm and phycocyanin absorption at 620 nm.
Regarding data accessibility, Level-1 products for Landsat-8&9/OLI, including top-of-atmosphere (TOA) reflectance as well as solar and satellite zenith and azimuth angles, are distributed by the United States Geological Survey (USGS) via EarthExplorer (https://earthexplorer.usgs.gov, accessed on 1 January 2025). Level-1 products for Sentinel-2/MSI and Sentinel-3/OLCI, including TOA reflectance as well as solar and satellite zenith and azimuth angles, are distributed by the Copernicus Data Space Ecosystem (https://dataspace.copernicus.eu, accessed on 1 January 2025).
2.2. In Situ Data
The AErosol RObotic NETwork—Ocean Color (AERONET-OC) system provides critical support for water color data calibration and quality assurance. Each station employs modified CIMEL radiometers measuring water color wavelengths (e.g., 412, 443, 488, 510, 551, 667, 870, and 1020 nm with about 10 nm bandwidth) to acquire key parameters: water-leaving radiance (Lw), normalized water-leaving radiance (Lwn), and aerosol optical thickness (τa). AERONET-OC data products are classified into three tiers: Level 1.0 (unscreened data), Level 1.5 (cloud cleared and quality-controlled data), and Level 2.0 (quality assured data) [20]. All tiers are publicly accessible through the AERONET portal (http://aeronet.gsfc.nasa.gov/, accessed on 1 January 2025). The f/Q-corrected products (Lwn_f/Q) were excluded from validation and analysis procedures due to concerns that chlorophyll concentration-based f/Q corrections, while effective for high-reflectance waters, may inadequately perform in turbid aquatic environments [20] and induce spectral overcorrection in suspended particulate matter-dominated systems [3]. To ensure maximum reliability and objectivity, this study utilizes Level 2.0 Lwn_IOP products [21]. ρw is calculated as Lwn/F0 × π, where F0 is the solar irradiance following Thuillier et al. [22]. For accuracy assessment, satellite observations were matched to AERONET-OC measurements within ±30 min of the overpass. When multiple AERONET-OC data met this criterion, linear interpolation was applied to the two spectra bracketing the overpass time. The eight AERONET-OC stations presented in Figure 1 were selected based on comprehensive criteria, including the requirement for a sufficient number of high-quality matchups with satellite observations [23,24] and the need for representation across diverse aquatic environments, specifically encompassing both coastal and offshore waters. This selection yielded a dataset comprising over 800 spectral observations spanning turbid waters, phytoplankton-dominant waters, algal bloom waters, inland waters, and open ocean waters to evaluate multi-source remote sensing data quality and reconstruction accuracy. Measuring periods of the selected stations and the number of matchups are provided in Table 1.
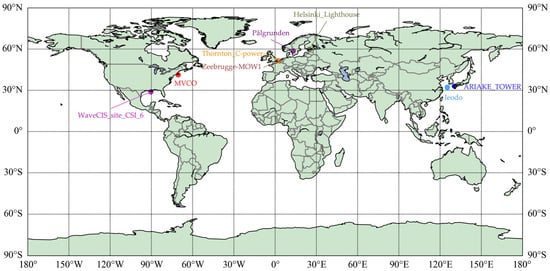
Figure 1.
Distribution of AERONET-OC stations used in this study.

Table 1.
The measuring periods and the number of matchups by multi-source remote sensing data at AERONET-OC stations.
3. Methods
3.1. Preprocess
ACOLITE v20231023 was employed to preprocess Landsat-8&9/OLI, Sentinel-2/MSI, and Sentinel-3/OLCI data, encompassing radiometric calibration, glint correction, atmospheric correction, and reprojection. Atmospheric correction utilized the dark spectrum fitting (DSF) method [3], which demonstrates robust performance across clear waters, terrestrial regions, and high-turbidity or highly productive Case-2 waters [3,25,26,27]. SWIR-based glint correction was applied to Landsat-8&9/OLI and Sentinel-2/MSI to mitigate sun glint contamination and ensure nadir-view reflectance accuracy [3,28]. Atmospherically corrected reflectance products were reprojected and resampled to a uniform 300 m spatial resolution using averaging over corresponding source pixels, aligning them with the Sentinel-3/OLCI observations.
3.2. Spatiotemporal–Spectral Data Matching
Discrepancies in overpass timing, spectral configurations, and atmospheric correction methodologies may undermine cross-sensor data coherence in multi-source remote sensing observations, particularly in dynamic coastal waters. The quasi-synchronous spectral dataset (its data sources are given in Supplementary File Tables S1–S3) requires comprehensive validation of spatiotemporal and spectral alignment prior to model training to ensure that LOS and WCS observations correspond to the identical target.
This study systematically analyzed spatiotemporal discrepancies in multi-source remote sensing data. In high-dynamic coastal waters (e.g., sediment front), bio-optical properties can exhibit rapid temporal variability, with remote sensing products showing pronounced spectral variability from water mass advection and dispersion. To ensure temporal consistency, a ±30-min synchronization threshold was implemented. For spatial alignment, the cross-correlation coefficient (Rc) served as the primary validation metric, calculated for co-located observation windows in multi-source imagery as defined in Equation (1):
In Equation (1), x and y represent the pixel matrices of the windows in LOS and WCS observation windows, respectively, where i and j denote row and column indices within the windows. and represent the mean pixel values of x and y, respectively. The window dimensions n and m were fixed at 25 pixels × 25 pixels, corresponding to a 7.5 km × 7.5 km observational footprint. Principal component analysis (PCA) was applied to the LOS and WCS imagery, with the first principal component selected as the feature-matching layer. A sliding-window search was performed within a ±0.9 km range centered on the WCS window’s geographic coordinates to compute Rc for each candidate window in the LOS imagery. This spatial buffer accommodated potential displacements from maximum 30-min temporal offsets at assumed 1.8 km/h current velocities. Observation windows were validated as spatially consistent when the maximum Rc exceeded 0.8. Both datasets were decomposed into 25 × 25-pixel windows to facilitate subsequent spectral angle calculations and model input processing.
Spectral angle (θSAM) [29] was adopted as an evaluation metric to assess spectral similarity between corresponding LOS and WCS bands. Its formulation is given by Equation (2):
In Equation (2), x and y are equal-length one-dimensional vectors containing the spatially averaged reflectance values per spectral band from corresponding LOS and WCS observation windows. These vectors preserve the shared spectral bands between sensors while collapsing spatial information through averaging. A θSAM threshold less than 10° was applied to synchronized observations to account for inherent variability from atmospheric correction errors, overpass timing discrepancies, and spatial resolution differences, while effectively filtering spectral anomalies caused by short-term hydrodynamic disturbances.
In addition to spatiotemporal–spectral consistency validation, the training dataset compilation integrated supplementary quality control criteria to ensure spectral coherence between LOS and WCS observations. Key metrics included the τa difference threshold at 550 nm (Δτa(550) < 0.5) for quasi-synchronized acquisitions and land cover classification restricted to the ocean. Using these constraints, the study systematically assembled quality-controlled quasi-synchronized reflectance data and τa(550), establishing a spatiotemporally consistent LOS-WCS spectral dataset. The integrated workflow from data filtering to product generation is schematically summarized in Figure 2.
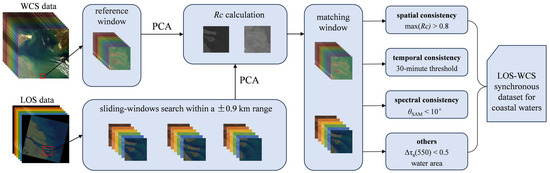
Figure 2.
Construction workflow of the LOS-WCS quasi-synchronous spectral observation dataset.
3.3. Construction and Refinement of the Training Dataset
The accuracy of spectral reconstruction is heavily relied on in the quality of the quasi-synchronous dataset. The error sources primarily originate from sensor noise and atmospheric correction. The error magnitude is modulated by atmospheric and surface conditions, solar and satellite geometries, spectral band configurations, and atmospheric correction methods [17].
Given the inherent error characteristics of LOS-WCS datasets, rigorous analysis of error propagation mechanisms is critical when utilizing these data for model training. To enhance reconstruction accuracy, Sentinel-3/OLCI spectra (as the reference output) were stringently controlled to minimize error contamination. When atmospheric correction refinements plateaued, bio-optical model-based filtering of corrected reflectance values proved effective for enhancing dataset quality. This study integrated multiple bio-optical frameworks [30,31] (detailed in Appendix A) to generate a 150,000-entry simulated spectral dataset spanning five water types: clear waters, phytoplankton-dominated waters, algal bloom waters, turbid waters, and extreme turbidity waters (≥25,000 spectra per class). Sentinel-3/OLCI spectra were validated by calculating θSAM against each simulated spectrum, and spectra exhibiting a minimum θSAM > 2° were classified as low-quality and excluded from the training dataset.
The training dataset was derived from the LOS-WCS dataset after bio-optical filtering. Subsequently, a training dataset comprising 60 million quasi-simultaneous spectra pairs was constructed. The WCS spectra originated from Sentinel-3/OLCI imagery, while the corresponding LOS spectra originated from Sentinel-2/MSI (26 million spectra) and Landsat-8&9/OLI (34 million spectra) imagery.
3.4. DSR-Net Model
The DSR-Net model utilized input parameters including the eight spectral bands of Landsat-8&9/OLI or eleven bands of Sentinel-2/MSI, solar and satellite geometries (solar zenith angle, satellite zenith angle, and relative azimuth angle), and τa(550) derived from ACOLITE. Fifteen VNIR bands from Sentinel-3/OLCI served as output targets, excluding bands with gas transmittance < 0.75, significant water absorption features, or limited relevance to water color applications. The spectral configurations of input and output bands are detailed in Figure 3.
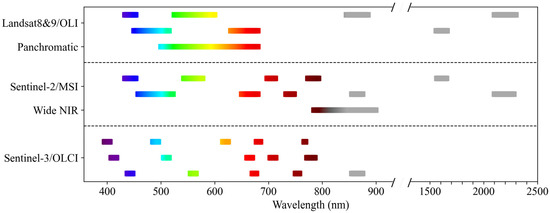
Figure 3.
Spectral band positions and bandwidths of Landsat-8&9/OLI and Sentinel-2/MSI served as input data, and Sentinel-3/OLCI served as output targets. Visible bands are colored according to their spectral regions, while near-infrared bands are indicated in gray.
The DSR-Net is designed and trained under three foundational assumptions: (1) input LOS reflectance inherently contains uncertainties arising from atmospheric correction error, atmospheric variability, solar and satellite geometries, sensor noise, adjacency effects, and so on; (2) bio-optically filtered Sentinel-3/OLCI reflectance aligns with natural aquatic spectral signatures, exhibiting minimal residual uncertainties from sun glint and adjacency effects; (3) nonlinear relationships exist between atmospheric correction errors and solar and satellite geometries, sensor wavelengths, ρw and τa(550).
Residual blocks mitigate gradient vanishing and are thus widely employed for complex spectral reconstruction problems [32,33,34]. DSR-Net employs a residual neural network architecture comprising 32 stacked residual convolutional blocks (Figure 4). Each block integrates two convolutional layers with ReLU activation functions and output scaling (×0.1), supplemented by residual skip connections to preserve gradient flow. This architecture addresses vanishing gradient challenges while optimizing feature reuse efficiency. The framework adapts channel dimensions to accommodate multi-source LOS data inputs, resolves nonlinear spectral mapping relationships between LOS and WCS bands, and achieves robust reconstruction through end-to-end training.
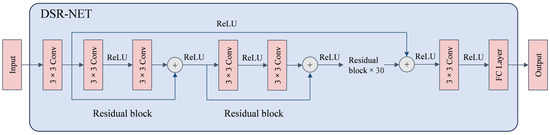
Figure 4.
Network structure of DSR-Net.
3.5. Uncertainty Quantification
3.5.1. Sensor Noise Quantification
The uncertainty in TOA reflectance induced by sensor noise (σnoise) can be estimated using the SNR, calculated as:
where Lref represents the reference radiance and F0 represents the solar irradiance at the TOA. Values of Lref and SNR were obtained from the World Meteorological Organization (https://space.oscar.wmo.int/, accessed on 1 January 2025), while Lref was extracted from sensor metadata. The corresponding spectral band parameters are compiled in Table 2, with complete σnoise analysis presented in Section 4.3.1.

Table 2.
Lref, SNR and F0 across sensors.
3.5.2. Atmospheric Correction Error Simulation
Building upon the 6SV radiative transfer model [35,36] that underpins ACOLITE’s DSF lookup tables, this study employs 6SV simulations to evaluate both bio-optical filtering performance and noise impacts on ρw.
For bio-optical filtering validation, the TOA reflectance, spectral band configurations, solar and satellite geometries (obtained from Sentinel-3/OLCI products), as well as the atmospheric and aerosol condition (inferred from the acquisition date and underlying surface conditions) are treated as known quantities, while τa(550) is input as a random variable into the 6SV radiative transfer model. Subsequent spectral validation against AERONET-OC measurements confirmed the filter’s capability to constrain uncertainties, with detailed analysis presented in Section 4.3.1.
In addition, the 6SV radiative transfer model was employed to rigorously evaluate the DSR-Net’s capacity to suppress atmospheric correction errors and sensor noise while elucidating error propagation dynamics. Isolated perturbations were introduced through two controlled scenarios: (1) sensor noise amplification through random noises (1.06 × 10−3) in TOA reflectance, doubling LOS noise and halving SNR, to quantify ρw uncertainties under degraded conditions; and (2) atmospheric correction uncertainty elevation via random τa(550) noise (3.6 × 10−2) to assess DSR-Net’s robustness against amplified atmospheric errors. Both scenarios were benchmarked against AERONET-OC measurement, enabling systematic quantification of error sources and their suppression, thereby validating DSR-Net’s efficacy in mitigating spectral reconstruction inaccuracies across diverse water and atmospheric conditions. Comprehensive analysis appears in Section 4.3.2.
3.6. Accuracy Assessment
The coefficient of determination (R2), root mean square error (RMSE), and percentage difference (PD) were employed to evaluate discrepancies between atmospheric corrected reflectance, reconstructed reflectance, and in situ measurements, thereby quantitatively assessing spectral quality and reconstruction performance. The computational formulations of these metrics are provided in Equations (4)–(6):
where xi represents in situ measured ρw, and yi represents either atmospheric corrected or model-reconstructed ρw. R2 quantifies the agreement between xi and yi, RMSE characterizes their absolute discrepancy, and the PD indicates their relative deviation. A positive PD value indicates overestimation in corrected or reconstructed reflectance, while a negative value indicates underestimation.
4. Results
4.1. Accuracy Assessment of the ACOLITE Products
This study conducted accuracy assessments of ρw products from Landsat-8&9/OLI, Sentinel-2/MSI, and Sentinel-3/OLCI utilizing AERONET-OC site data, yielding 88, 205, and 534 valid matchups, respectively. Sentinel-3/OLCI data underwent additional spectral filtering via bio-optical models (hereafter denoted as Sentinel-3*/OLCI) to remove outliers affected by sun glint, adjacency effects, and atmospheric correction error, retaining 396 high-quality ρw. The spectral matchup quantities and ρw product accuracy metrics for each sensor are summarized in Table 3.

Table 3.
Accuracy metrics of ρw products from Landsat-8&9/OLI, Sentinel-2/MSI, Sentinel-3/OLCI, and bio-optically filtered Sentinel-3/OLCI data. N denotes the number of matched site observations.
Comparative analysis demonstrated that Sentinel-3/OLCI and Sentinel-2/MSI achieve superior overall accuracy, with RMSE of 6.03 × 10−3 and 4.75 × 10−3, respectively, while Landsat-8&9/OLI exhibits a RMSE of 8.60 × 10−3. Systematic overestimation in blue spectral bands was observed across all sensors, consistent with land adjacency effects at coastal AERONET-OC stations as reported by Vanhellemont [3]. Following bio-optical spectral filtering, the total RMSE of the Sentinel-3 */OLCI dataset decreased to 3.75 × 10−3, demonstrating substantial accuracy improvement. While filtering partially mitigated blue-band overestimation in Sentinel-3/OLCI data, residual biases persist due to ambiguities in distinguishing blue-band signal variations caused by adjacency effects versus water component changes (e.g., reduced CDOM absorption). Future refinements in the atmospheric correction process may resolve these signal attribution challenges, though such advancements lie beyond the scope of this study.
4.2. Accuracy Assessment of the Reconstruction
The DSR-Net model was implemented using PyTorch (version 2.2.2) and trained on an NVIDIA GeForce RTX 4070 Ti GPU. After 5000 iterations (about 72 h), the L1 Loss [37] stabilized at 1.2 × 10−4, indicating that the DSR-Net model achieved full convergence. Table 4 shows the accuracy assessment of spectral reconstruction results for Landsat-8&9/OLI and Sentinel-2/MSI data.

Table 4.
Reconstruction accuracy for Landsat-8&9/OLI and Sentinel-2/MSI data. N denotes the number of matched site observations.
As demonstrated in Table 4, DSR-Net not only expands the usable spectral range of LOS data but also significantly enhances spectral accuracy across bands. This improvement is evidenced by elevated R2 values, reduced PD, and RMSE reductions of 25–43% compared to ACOLITE products. For Landsat-8&9/OLI, the total RMSE decreased by 4.51 × 10−3, accompanied by a PD reduction of 0.94, effectively mitigating systematic blue-band overestimation and achieving reconstruction accuracy comparable to the Sentinel-3/OLCI dataset. Sentinel-2/MSI exhibited substantial accuracy enhancements across all bands except 779 nm, with RMSE reductions ranging from 0.5 to 2.6 × 10−3. The marginal error increase at 779 nm post-reconstruction remains acceptable given Sentinel-3/OLCI’s inherent lower observational accuracy at this wavelength compared to Sentinel-2/MSI. Collectively, the reconstructed Sentinel-2/MSI spectral products surpass the quality of the original Sentinel-3/OLCI dataset and approach the performance of the bio-optically filtered Sentinel-3 */OLCI reference data.
To further evaluate DSR-Net’s applicability to complex Case-2 waters, four categories were extracted from the synchronized spectral dataset based on chlorophyll concentration (Chl, derived from the OC3S algorithm [38]), suspended particulate matter concentration (SPM, derived from the semi-empirical radiative transfer model [39,40,41]), and CDOM absorption at 443 nm (ag(443), derived from the quasi-analytical algorithm QAA_v6 [42,43]):
- Clear water: Chl < 2 μg/L, SPM < 5 mg/L and ag(443) < 1 m−1;
- Phytoplankton-dominated water: Chl ≥ 10 μg/L, SPM < 25 mg/L and ag(443) < 1.2 m−1;
- Turbid water: Chl < 10 μg/L, SPM ≥ 25 mg/L and ag(443) < 1.2 m−1;
- Mixed Case-2 waters: 2 μg/L ≤ Chl < 10 μg/L, 5 mg/L ≤ SPM < 25 mg/L and 0.6 m−1 ≤ ag(443) < 1.2 m−1.
This classification scheme, adapted from Banerjee et al. [9], was optimized based on the distribution of in situ matchups and prevailing marine conditions. Modifications included the following: (1) removing categories for algal bloom waters and extremely turbid waters lacking supporting measurements from AERONET-OC stations; (2) merging Case-2 waters with non-prominent optical components into the mixed Case-2 water category; and (3) slightly adjusting the concentration ranges for phytoplankton-dominated and turbid waters based on a literature review of coastal waters [44,45]. The reconstruction accuracy of DSR-Net was then systematically accessed across four water categories under diverse bio-optical conditions.
Table 5 summarizes the reconstruction accuracy of DSR-Net across four water categories. Overall, the DSR-Net model demonstrates strong robustness and generalization capability, with comprehensive R2 values exceeding 0.78 and RMSE remaining below 7.0 × 10−3, and with turbid waters exhibiting optimal performance (R2 = 0.92, RMSE = 5.25 × 10−3). Band-specific error analysis reveals distinct mechanisms: blue-band discrepancies primarily arise from reflectance overestimation due to land adjacency effects, while near-infrared band errors stem from weak water-leaving signals where sensor noise and atmospheric correction errors disproportionately obscure true hydrological signatures. In contrast, green bands demonstrate exceptional stability, particularly in phytoplankton-dominated waters, achieving R2 up to 0.92 in phytoplankton-dominated waters.

Table 5.
Reconstruction accuracy of DSR-Net for different water categories. N denotes the number of matched site observations.
4.3. Error Sources and Control
4.3.1. Error Sources
Given that the ρw from LOS data input to the DSR-Net model inherently contain uncertainties, this study quantitatively characterizes their sources and investigates error propagation mechanisms during spectral reconstruction. Following Castagna et al. [17], these uncertainties primarily originate from sensor noise and atmospheric correction error. While Table 3 summarizes the total errors across spectral bands, the analysis further categorizes these uncertainties as follows:
- 1.
- Sensor noise
The σnoise across spectral bands for different sensors are presented in Table 6. Sentinel-3 exhibits superior SNR characteristics, maintaining σnoise generally below 7.0 × 10−5. In contrast, LOS imagery demonstrates lower SNR performance, with σnoise ranging from 4.8 × 10−4 to 2.2 × 10−3.

Table 6.
σnoise across sensors.
- 2.
- Atmospheric correction errors
Spectral statistics (Table 3) indicate that approximately 26% of Sentinel-3/OLCI reflectance were rejected by bio-optical plausibility filtering, primarily attributed to overestimations of τa(550) inducing negative reflectance retrievals. Bio-optical filtering (as detailed in Section 3.3) is then performed on the 6SV simulation results (). As shown in Figure 5, comparisons between and AERONET-OC in situ measurements yield a RMSE of 3.97 × 10−3, marginally surpassing the observational accuracy of the Sentinel-3 */OLCI dataset.
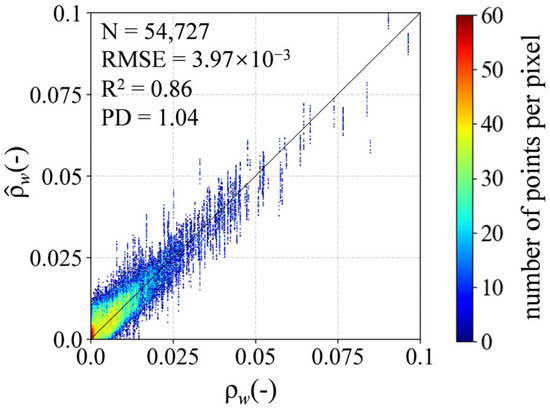
Figure 5.
Scatter plot of randomly generated ρw under bio-optical model filtering vs. AERONET-OC in situ measurements.
To further investigate the distribution patterns of atmospheric correction errors across water categories, four representative water categories were analyzed. As shown in Figure 6, ρw products of ACOLITE exhibit strong agreement with in situ measurements for all four water categories, except for systematic overestimations in the blue bands. Simulated ρw values gradually decrease as τa(550) increases, eventually being flagged as implausible by bio-optical models. Notably, while bio-optical constraints ensure the physical plausibility of ρw, they do not ensure absolute accuracy, particularly in blue bands where reflectance enhancements may ambiguously originate from reduced CDOM absorption or amplified adjacency effects. This critical uncertainty diminishes DSR-Net’s reconstruction fidelity in nearshore environments. Validation across the four water classes demonstrates that bio-optical data control methods remain effective under diverse water and aerosol conditions, successfully suppressing both over- and underestimation of τa(550) and improving ρw observational precision.
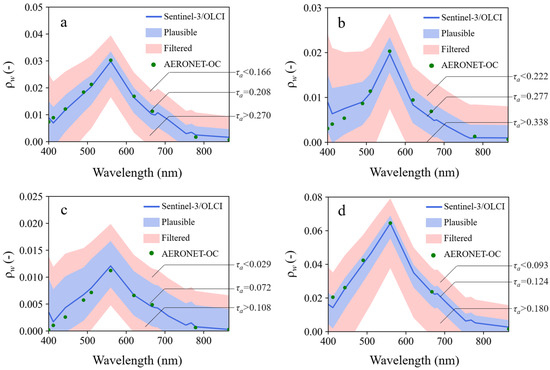
Figure 6.
Spectral filtering results for four Case-2 water categories. Green points represent AERONET-OC in situ measurements; blue lines denote ρw products of ACOLITE; blue shaded regions indicate bio-optically plausible reflectance ranges; red shaded regions identify atmospherically over-/under-corrected reflectance ranges. Case studies include (a) mildly turbid coastal waters (ARIKAKE TOWER, 26 November 2021); (b) chlorophyll-dominated waters (Helsinki Lighthouse, 24 July 2019); (c) inland lake waters (Pålgrunden, 23 July 2020); (d) sediment-dominated coastal waters (Zeebrugge-MOW1, 9 May 2017).
4.3.2. Error Propagation and Controls
Leveraging the isolated controlled variables detailed in Section 3.5.2, the error propagation and accuracy enhancement of the DSR-Net were systematically evaluated under amplified sensor noise and atmospheric correction error scenarios (Table 7 and Table 8). In sensor noise amplification, the DSR-Net demonstrated significant performance improvements, elevating the R2 from 0.78 to 0.94 while achieving a 59% reduction in RMSE. In atmospheric correction error amplification, comparable enhancements were observed with R2 increasing from 0.84 to 0.93 while achieving a 38% reduction in RMSE, thereby validating the model’s robust error suppression capacity. Spectral band analysis revealed wavelength-dependent efficacy, where shorter wavelengths (e.g., 443 nm) exhibited marked improvements (R2 increased from 0.56 to 0.79, RMSE reduced by 51%) compared to limited gains in longer bands (e.g., 865 nm), attributable to weak water-leaving signals. These findings highlight the comparable and non-negligible impacts of sensor noise and atmospheric correction errors, emphasizing the necessity to rigorously account for error propagation mechanisms and their cascading effects during spectral reconstruction.

Table 7.
Uncertainty in ρw and reconstruction results after introducing random errors (up to 1.06 × 10−3) to TOA reflectance.

Table 8.
Uncertainty in ρw and reconstruction results after introducing random errors (up to 3.6 × 10−2) to τa(550).
To systematically evaluate the reconstruction accuracy and robustness of DSR-Net across diverse water categories, Figure 7 illustrates the ρw for four water categories after introducing τa(550) noise of 3.6 × 10−2 and TOA reflectance noise of 1.06 × 10−3 during processing, alongside the corresponding DSR-Net spectral reconstruction results.
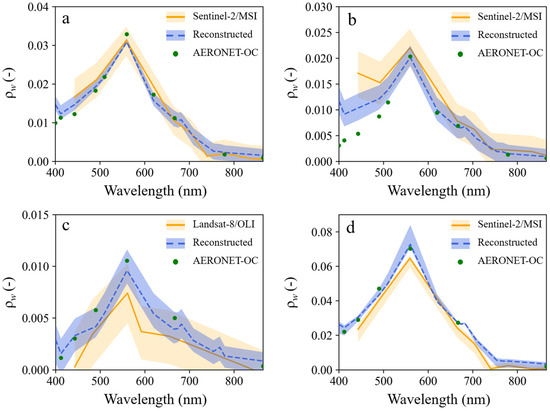
Figure 7.
ρw products for four Case-2 water categories under amplified sensor noise and atmospheric correction error scenarios, alongside corresponding DSR-Net reconstructed spectra. Green points denote AERONET-OC in situ measurements; orange lines denote ρw products of ACOLITE, with orange shaded areas indicating error-contaminated ranges; blue lines and shaded areas correspond to DSR-Net reconstructed ρw products and spectral ranges. Case studies include (a) mildly turbid waters (ARIAKE TOWER, 30 July 2021); (b) chlorophyll-dominated waters (Helsinki Lighthouse, 24 July 2019) (c) inland lake waters (Pålgrunden, 8 June 2014); (d) sediment-dominated waters (Zeebrugge-MOW1, 5 July 2019).
Following the amplified errors, the average RMSE across all water categories in Figure 7 increased to 2.27 × 10−3. After spectral reconstruction, spectral errors were significantly reduced across all wavelengths, with spectral shapes aligning more closely with in situ measurements and partial suppression of adjacency effects (e.g., Figure 7b), yielding a reduced average RMSE of 1.31 × 10−3. DSR-Net’s reconstructions further revealed observational accuracy variations in Sentinel-3/OLCI products across water categories: for mildly turbid or chlorophyll-dominated waters (Figure 7a,b), reflectance uncertainties were concentrated in blue and NIR bands, with error magnitudes substantially higher than those in red and green bands. In contrast, turbid waters (Figure 7d) exhibited predominant green band uncertainties, likely attributable to sensor limitations (band saturation) or inherent atmospheric correction model errors.
4.4. Application: Observation of CDOM and Cyanobacteria Blooms
To validate the reliability of DSR-Net reconstructed data and its observational advantages over LOSs, this study applied the reconstructed products to retrieve phycocyanin concentrations and CDOM absorption. Phycocyanin retrieval utilized the Phycocyanin Index (PCI), which exploits the absorption feature near 620 nm correlated with phycocyanin concentration to map spatiotemporal distributions of cyanobacterial blooms [46]. Previously, this algorithm could not be implemented for Sentinel-2 or Landsat-8&9 due to the absence of critical orange bands (e.g., 620 nm). Figure 8 illustrates the spatial distribution of a cyanobacterial bloom near the Helsinki Lighthouse station via PCI. DSR-Net achieved high-precision reconstruction of VNIR bands, with PCI retrievals (Figure 8d) showing strong consistency with Sentinel-3 products (Figure 8b) and in situ measurements (Figure 8c). Additionally, the DSR-Net partially mitigated reflectance overestimation caused by adjacency effects, though minor systematic overestimation persists in blue bands due to limitations in training data accuracy.
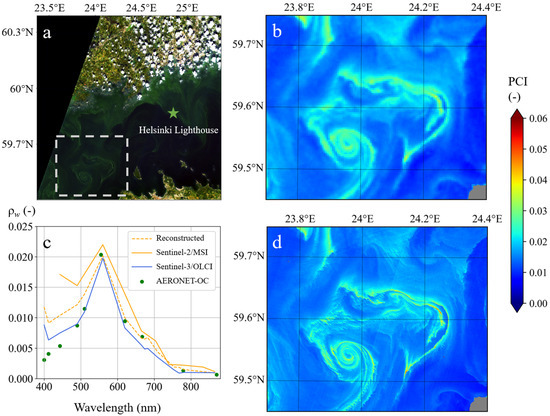
Figure 8.
PCI near the Helsinki_Lighthouse station based on Sentinel-3/OLCI data and Sentinel-2/MSI reconstructed spectra. (a) Sentinel-2/MSI true-color composite, the asterisk denotes the location of the Helsinki_Lighthouse station, and the dashed box outlines the retrieval area in (b,d); (b) PCI derived from Sentinel-3/OLCI data on 24 July 2019; (c) Comparison of synchronized Sentinel-2/MSI spectra, Sentinel-3/OLCI spectra, reconstructed spectra, and AERONET-OC in situ measurements; (d) PCI derived from the reconstructed spectra.
Another innovative contribution of DSR-Net lies in its ability to support the QAA_v6 through spectral reconstruction, enabling the estimation of CDOM absorption. QAA_v6 evolved from the QAA framework [47], which derives inherent optical properties (IOPs) from Lwn. In the QAA_v6, total water absorption is decomposed into contributions from pure seawater, phytoplankton pigments, detritus and minerals, and gelbstoff (e.g., CDOM). Consequently, QAA_v6 implementations require multiple water color bands (e.g., 443, 490, 555, and 670 nm) to resolve these absorption features. To address the limited spectral bands available on LOS, some researchers have developed simplified QAA variants with reduced band requirements [48]. This study proposes an alternative solution by leveraging DSR-Net-reconstructed spectra to fulfill QAA_v6’s spectral prerequisites. Figure 9 presents a synchronized ag(443) distribution derived from Sentinel-3/OLCI and reconstructed spectral data. The DSR-Net-based ag(443) product exhibits spatial consistency with Sentinel-3/OLCI outputs while demonstrating superior SNR and enhanced textural clarity in low-CDOM regions, underscoring the model’s potential for complex aquatic optical scenarios.
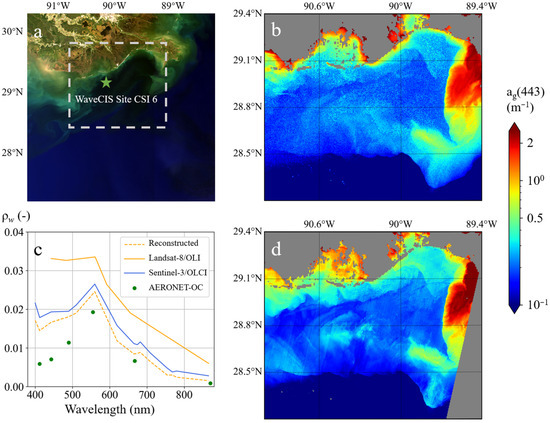
Figure 9.
Spatial distribution of ag(443) near the WaveCIS_site_CSI_6 station retrieved from Sentinel-3/OLCI and Landsat-8/OLI reconstructed spectra. (a) Sentinel-3/OLCI true-color composite, the asterisk denotes the location of the WaveCIS_site_CSI_6 station, and the dashed box outlines the retrieval area in (b,d); (b) ag(443) derived from Sentinel-3/OLCI data on 24 July 2019; (c) comparison of synchronized Landsat-8/OLI, Sentinel-3/OLCI spectra, reconstructed spectra, and AERONET-OC in situ measurements; (d) ag(443) derived from the reconstructed spectra.
5. Discussion
5.1. Reconstruction of Orange Band
LOS have become pivotal tools for coastal environmental monitoring due to their high-spatial-resolution capabilities. With the expanding applications of aquatic remote sensing, various spectral reconstruction techniques have emerged. The orange band, critical for water color observations, holds significant value in phycocyanin retrieval and related domains. This study conducts a cross comparison of orange band reconstruction methodologies, quantifying the performance of DSR-Net against existing models [10,17].
Figure 10 compares orange band reconstruction results from DSR-Net (a) with PAN-based methods (b and c). DSR-Net-reconstructed spectra exhibit strong agreement with in situ measurements, with only two outliers identified through comparison. Both points occur in hydrodynamically dynamic sediment frontal zones, likely due to temporal mismatches between field sampling and satellite overpass. Panels b and c shows the PAN-based results [10,17] and exhibit comparable predictive accuracy, with RMSE values of 9.21 × 10−3 and 1.04 × 10−2. The study demonstrates that DSR-Net achieves superior reconstruction accuracy compared to PAN-based methods, as its neural network architecture effectively addresses the impacts of sensor noise and atmospheric correction errors. In contrast, the performance of PAN-based methods remains heavily dependent on atmospheric correction precision. While additive noise can be partially mitigated through band arithmetic operations, multiplicative noise (e.g., adjacency effects) and significant atmospheric correction residuals undermine their robustness, particularly in optically complex environments such as turbid coastal zones or sediment-laden waters.
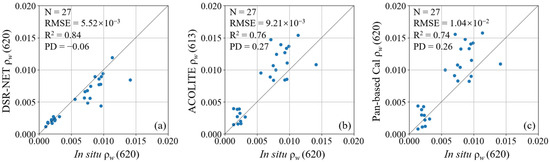
Figure 10.
Cross comparison of multiple orange band reconstruction methodologies against in situ measurements. (a) DSR-Net reconstruction at 620 nm; (b) ACOLITE reconstruction at 613 nm, following the methodology of Castagna et al. [17]; (c) PAN-based calibrated reconstruction at 620 nm, following the methodology of Niroumand-Jadidi and Bovolo [10].
5.2. Limitations and Improvements
The training dataset for spectral reconstruction may originate from in situ spectral measurements, bio-optical model simulations, or satellite observations. While in situ measurements (e.g., AERONET-OC) exhibit high credibility, their limited sample size and restricted coverage of water types hinder their ability to meet the large-scale dataset requirements of neural network training. Simulated reflectance from bio-optical models addresses data volume limitations but fails to account for sensor noise and atmospheric correction errors, reducing the generalization capability and robustness of trained models. Integrating considerations of data reliability, sample diversity, and model applicability, the use of quasi-synchronized LOS-WCS data as the DSR-NET training dataset is optimal. However, this approach faces the following limitations:
The spectral reconstruction process faces significant data imbalance across water categories, with approximately 50% of spectral data excluded during spatial feature matching due to insufficient coherence. Rejected samples predominantly originate from nearshore zones with strong vertical mixing, cloud/shadow-affected areas, and homogeneous open oceans lacking textural variation. The quasi-synchronized LOS-WCS dataset comprises 26% turbidity waters, 16% phytoplankton-dominated waters, and over 50% mixed Case-2 waters. Notably, algal bloom waters and extreme turbidity waters constitute a limited proportion of natural aquatic environments. The scarcity of spectral training samples for these optically extreme conditions, combined with the limited applicability of existing bio-optical models and atmospheric correction methods under high particle loads or algal biomass, significantly degrades DSR-Net’s accuracy in such environments. To enhance the generalizability and robustness of the DSR-Net model, it is necessary to expand the spectral sample library for extreme water color scenarios and develop new atmospheric correction methods with broad adaptability.
The precision of atmospheric correction critically determines DSR-Net accuracy, as atmospheric correction uncertainty dominates spectral reconstruction error budgets. Taking spectral band saturation and adjacency effects as examples, the former alters spectral shapes, increases spatial matching complexity, and leads to underestimation of reconstructed band reflectance; the latter systematically causes overestimation of blue-band reflectance in nearshore waters. Consequently, DSR-Net exhibits weaker performance in blue-band reconstruction, with a RMSE of approximately 7.01 × 10−3, significantly higher than those of red and green bands. Recent advances in mitigating land adjacency effects for Landsat-8/OLI and Sentinel-2/MSI atmospheric correction [49,50] offer promising pathways for future accuracy improvements. Additionally, sensor noise of LOS, comparable in magnitude to atmospheric correction errors, further exacerbates error accumulation. Although Section 4.3 has elucidated the propagation mechanisms of sensor noise and atmospheric correction errors, unresolved biases persist due to spatiotemporal mismatches, scale disparities (point vs. pixel observations), and divergent solar and satellite geometries between in situ and satellite datasets.
In summary, owing to the support of massive spectral datasets, DSR-Net’s spectral reconstruction no longer relies on spectral overlap, with accuracy primarily determined by the quality and scale of the quasi-synchronized spectral dataset. Even without a PAN band in Sentinel-2/MSI, the DSR-Net achieves band reconstruction at 620 nm, demonstrating accuracy comparable to Landsat-8&9/OLI. However, the black-box nature of neural networks currently limits the ability to systematically resolve the relationships among band quantity, observational precision, and reconstruction errors.
6. Conclusions
This study proposes DSR-Net, a deep residual neural network model for spectral reconstruction, aimed at addressing the limited spectral resolution of LOS in water monitoring. Results show that DSR-Net robustly reconstructs water color bands, increasing the number of reconstructed bands and improving reflectance accuracy.
A filtering method combining temporal threshold constraints and maximum cross-correlation analysis, along with bio-optical model-driven refinement, ensured spatiotemporal consistency in LOS-WCS datasets. This approach enhanced spectral quality, reducing errors in Sentinel-3 */OLCI products by 38% and lowering RMSE from 6.03 × 10−3 to 3.75 × 10−3. The resulting 60 million quasi-simultaneous spectra pairs provided a strong basis for model training in optically complex water environments.
The 32-layer residual convolutional architecture of DSR-Net accurately models nonlinear relationships between LOS and WCS bands. It achieves a 25–43% reduction in average RMSE after reconstruction, while effectively suppressing uncertainties from multiple error sources, including a 59% decrease in sensor noise-induced errors and a 38% reduction in atmospheric correction-related errors. Error analysis further indicates that most residual uncertainties in ρw originate from sensor noise and atmospheric correction, confirming the importance of comprehensive error handling. The model demonstrates stable reconstruction performance in various water environments, from turbid waters to phytoplankton-dominated systems, and consistently delivers spectral quality on par with or exceeding Sentinel-3/OLCI observations.
DSR-Net enables high-precision reconstruction of missing water color bands for Sentinel-2/MSI and Landsat-8&9/OLI, enhancing both accuracy and spectral dimensionality to meet the needs of advanced water color remote sensing applications such as cyanobacteria monitoring and CDOM inversion. Blue-band overestimation remains to be resolved through improved atmospheric correction. Future work should expand dataset diversity, integrate physical models with deep learning, and develop dynamic error compensation. Overall, DSR-Net provides a practical and innovative approach to LOS spectral reconstruction, supporting operational satellite applications and informing next-generation sensor design.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs17162860/s1, Table S1: Information on Landsat-8&9/OLI products used for DSR-Net training; Table S2: Information on Sentinel-2/MSI products used for DSR-Net training; Table S3: Information on Sentinel-3/OLCI products used for DSR-Net training.
Author Contributions
Conceptualization, R.T. and L.H.; software, R.T.; methodology, R.T. and B.G.; validation, R.T. and L.H.; formal analysis, R.T. and L.H.; funding acquisition, R.T., L.H., B.G. and C.Y.; data curation, R.T. and C.Y.; writing—original draft preparation, R.T., L.H. and B.G.; writing—review and editing, L.H., B.G. and C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Key R&D projects in Zhejiang Province, grant number 2023C03120; National Nature Science Foundation of China, grant number U2243226; Open Research Fund Program of Key Laboratory for Water Ecology Management and Protection in River Source Areas, Ministry of Water Resources, grant number 2024slbjh02; Consultation and Evaluation Program of the Department of Chinese Academy of Sciences, grant number 2020-ZW11-A-023; University Students Science and Technology Innovation Program of Zhejiang Province, grant number 2024R411A005.
Data Availability Statement
The Landsat-8&9 Level-1 data are available from https://glovis.usgs.gov/app, accessed on 1 January 2025. The Sentinel-2&3 Level-1 data are available from https://browser.dataspace.copernicus.eu, accessed on 1 January 2025. The AERONET data are available from https://aeronet.gsfc.nasa.gov, accessed on 1 January 2025. The ACOLITE code can be download from https://github.com/acolite/acolite, accessed on 1 January 2025. The 6SV code can be download from https://salsa.umd.edu/6spage.html, accessed on 1 January 2025.
Acknowledgments
We express our gratitude to everyone who helped us to successfully complete this research.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
ρw Simulation Using the Bio-Optical Model
To verify the quality of Sentinel-3 spectra, a large synthetic dataset encompassing a wide range of IOPs and ρw were generated. The construction of this dataset largely followed the methodology outlined in IOCCG-OCAG [30] to synthesize the extensive range of IOP spectra. An analytical model [51] was employed to compute ρw from these IOPs, thereby avoiding the computationally prohibitive time required to generate such a large dataset using Hydrolight. Studies have demonstrated that this model achieves an average accuracy within approximately 1% [19], indicating that the error introduced by using the analytical formulation for ρw in this study is negligible.
According to Golden et al. [47], ρw can be expressed by the sub-surface remote sensing reflectance (rrs) as
The relationship between rrs and IOPs from Lee et al. [51] was employed
where gw is governed by the phase function of molecular scattering and gp is governed by the phase function of particle scattering, and values of G0–2 are constants for a given light geometry and particle phase function.
The total absorption coefficient (a) and the total backscattering coefficient (bb) are the two key components constituting rrs. As described in IOCCG-OCAG [30], the a represents the sum of the absorptions by pure seawater (aw), phytoplankton pigments (aph), detrital and mineral particles (adm), and gelbstoff (ag). The contribution of each absorbing component can be expressed as
The bb represents the sum of the backscattering contributions from pure seawater (bbw), phytoplankton pigments (bbph), and detrital/mineral particles (bbdm). The contribution of each backscattering component can be expressed as
The aw and bbw are measurable, with values provided in IOCCG-OCAG [30]. The aph(λ) can be expressed as a function of chlorophyll-a concentration ([Cph], in µg/L) and the normalized spectral shape of pigments ()
where spectrum comes from the IOCCG-OCAG [30] and is divided into nine groups, [Cph] represents the chlorophyll-a concentration, ranging from 0.03 to 300 µg/L, covering oceanic waters to waters with phytoplankton blooms. The aph(λ) was simulated by randomly switching and [Cph].
In most natural water environments, the adm(440) exhibit correlations with the aph(440), expressed as
Parameters p1 and subsequent p2–6 were generated as controlled random values to produce optically plausible IOPs, with their reference ranges adopted the IOCCG-OCAG [30]. However, in relatively turbid waters, where SPM concentrations ([Cdm], in mg/L) significantly exceed those of phytoplankton and gelbstoff, the adm(440) is primarily determined by [Cdm] [31], expressed as
where [Cdm] ranges from 25 to 300 mg/L. The adm(λ) can be derived from adm(440) as
Values of Sdm are randomly selected within the range of 0.007–0.015 nm−1 following the IOCCG-OCAG [30].
Similarly to adm(λ), the ag(λ) exhibits a correlation with aph(440), expressed as
Values of Sg are randomly selected within the range of 0.01–0.02 nm−1 following the IOCCG-OCAG [30].
In most natural water environments, the bbph(λ) exhibits a correlation with the [Cph], expressed as
Bph is the backscattering ratio of phytoplankton and a value of 1% was taken. Similarly to bbph(λ), the bbdm(λ) exhibits a correlation with [Cph], expressed as
where Bdm depends on the selected phase function, and a value of 0.0183 was taken.
In relatively turbid waters, bbdm(λ) exhibits a correlation with [Cdm], expressed as
where ∂1–4 are constants given by Hong et al. [31].
In this modeling framework, [Cph] (ranges from 0.03 to 300 µg/L) and [Cdm] (ranges from 25 to 300 mg/L) serve as free variables. The generation of ρw follows the methodology of IOCCG-OCAG [30], with optimizations for turbid and extremely turbid waters (e.g., the Yangtze Estuary) based on Hong et al. [31]. For the clear waters, phytoplankton-dominated waters, and algal bloom waters categories, 100,000 spectrally resolved entries were generated using Equations (A1)–(A6) and (A8)–(A11). For turbid and extremely turbid waters, adm and bbdm are governed exclusively by [Cdm] (Equations (A7) and (A12)), thereby enhancing the model’s capacity to simulate spectra in sediment-dominated regions. An additional 50,000 spectral entries were generated for these water types.
References
- Luo, W.; Shen, F.; He, Q.; Cao, F.; Zhao, H.; Li, M. Changes in suspended sediments in the Yangtze River Estuary from 1984 to 2020: Responses to basin and estuarine engineering constructions. Sci. Total Environ. 2022, 805, 150381. [Google Scholar] [CrossRef]
- Tang, R.; Shen, F.; Pan, Y.; Ruddick, K.; Shang, P. Multi-source high-resolution satellite products in Yangtze Estuary: Cross-comparisons and impacts of signal-to-noise ratio and spatial resolution. Opt. Express 2019, 27, 6426. [Google Scholar] [CrossRef]
- Vanhellemont, Q. Adaptation of the dark spectrum fitting atmospheric correction for aquatic applications of the Landsat and Sentinel-2 archives. Remote Sens. Environ. 2019, 225, 175–192. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Turbid wakes associated with offshore wind turbines observed with Landsat 8. Remote Sens. Environ. 2014, 145, 105–115. [Google Scholar] [CrossRef]
- Kuhn, C.; de Matos Valerio, A.; Ward, N.; Loken, L.; Sawakuchi, H.O.; Kampel, M.; Richey, J.; Stadler, P.; Crawford, J.; Striegl, R.; et al. Performance of Landsat-8 and Sentinel-2 surface reflectance products for river remote sensing retrievals of chlorophyll-a and turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef]
- Beck, R.; Xu, M.; Zhan, S.; Liu, H.; Johansen, R.A.; Tong, S.; Yang, B.; Shu, S.; Wu, Q.; Wang, S.; et al. Comparison of Satellite Reflectance Algorithms for Estimating Phycocyanin Values and Cyanobacterial Total Biovolume in a Temperate Reservoir Using Coincident Hyperspectral Aircraft Imagery and Dense Coincident Surface Observations. Remote Sens. 2017, 9, 538. [Google Scholar] [CrossRef]
- Cao, Z.; Shen, M.; Kutser, T.; Liu, M.; Qi, T.; Ma, J.; Ma, R.; Duan, H. What water color parameters could be mapped using MODIS land reflectance products: A global evaluation over coastal and inland waters. Earth Sci. Rev. 2022, 232, 104154. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R.; Schluchter, W.M. A Novel Algorithm for Predicting Phycocyanin Concentrations in Cyanobacteria: A Proximal Hyperspectral Remote Sensing Approach. Remote Sens. 2009, 1, 758–775. [Google Scholar] [CrossRef]
- Banerjee, S.; Shanmugam, P. Novel method for reconstruction of hyperspectral resolution images from multispectral data for complex coastal and inland waters. Adv. Space Res. 2021, 67, 266–289. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F. Deep-Learning-Based Retrieval of an Orange Band Sensitive to Cyanobacteria for Landsat-8/9 and Sentinel-2. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3929–3937. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Song, R.; Zhao, X.; Zhao, K. MCT-Net: Multi-hierarchical cross transformer for hyperspectral and multispectral image fusion. Knowl. Based Syst. 2023, 264, 110362. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Hu, C.; Zibordi, G. Spectral interdependence of remote-sensing reflectance and its implications on the design of ocean color satellite sensors. Appl. Opt. 2014, 53, 3301–3310. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Prieur, L.; Morel, A. A three-component model of ocean colour and its application to remote sensing of phytoplankton pigments in coastal waters. Int. J. Remote Sens. 1989, 10, 1373–1394. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Hoge, F.E.; Platt, T.; Swift, R.N. Detection of phytoplankton pigments from ocean color: Improved algorithms. Appl. Opt. 1994, 33, 1081–1089. [Google Scholar] [CrossRef]
- Sun, D.; Hu, C.; Qiu, Z.; Wang, S. Reconstruction of hyperspectral reflectance for optically complex turbid inland lakes: Test of a new scheme and implications for inversion algorithms. Opt. Express 2015, 23, A718–A740. [Google Scholar] [CrossRef] [PubMed]
- Wernand, M.R.; Shimwell, S.J.; De Munck, J.C. A simple method of full spectrum reconstruction by a five-band approach for ocean colour applications. Int. J. Remote Sens. 1997, 18, 1977–1986. [Google Scholar] [CrossRef]
- Castagna, A.; Simis, S.; Dierssen, H.; Vanhellemont, Q.; Sabbe, K.; Vyverman, W. Extending Landsat 8: Retrieval of an Orange contra-Band for Inland Water Quality Applications. Remote Sens. 2020, 12, 637. [Google Scholar] [CrossRef]
- Paulino, R.S.; Martins, V.S.; Novo, E.M.L.M.; Barbosa, C.C.F.; Maciel, D.A.; Wanderley, R.L.D.N.; Portela, C.I.; Caballero, C.B.; Lima, T.M.A. Generation of robust 10-m Sentinel-2/3 synthetic aquatic reflectance bands over inland waters. Remote Sens. Environ. 2025, 318, 114593. [Google Scholar] [CrossRef]
- Wang, Y.; Lee, Z.; Wei, J.; Shang, S.; Wang, M.; Lai, W. Extending satellite ocean color remote sensing to the near-blue ultraviolet bands. Remote Sens. Environ. 2021, 253, 112228. [Google Scholar] [CrossRef]
- Zibordi, G.; Schuster, G.; Fabbri, B.E.; Kaitala, S.; Seppaelae, J.; Melin, F.; Berthon, J.; Holben, B.; Slutsker, I.; Giles, D.; et al. AERONET-OC: A Network for the Validation of Ocean Color Primary Products. J. Atmos. Ocean. Technol. 2009, 26, 1634–1651. [Google Scholar] [CrossRef]
- Lee, Z.P.; Du, K.; Voss, K.J.; Zibordi, G.; Lubac, B.; Arnone, R.; Weidemann, A. An inherent-optical-property-centered approach to correct the angular effects in water-leaving radiance. Appl. Opt. 2011, 50, 3155–3167. [Google Scholar] [CrossRef]
- Thuillier, G.; Hersé, M.; Labs, D.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.C.; Mandel, H. The Solar Spectral Irradiance from 200 to 2400 nm as Measured by the SOLSPEC Spectrometer from the Atlas and Eureca Missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Xu, Y.; Feng, L.; Zhao, D.; Lu, J. Assessment of Landsat atmospheric correction methods for water color applications using global AERONET-OC data. Int. J. Appl. Earth Obs. Geoinf. 2020, 93, 102192. [Google Scholar] [CrossRef]
- Xu, Y.; He, X.; Bai, Y.; Wang, D.; Zhu, Q.; Ding, X. Evaluation of Remote-Sensing Reflectance Products from Multiple Ocean Color Missions in Highly Turbid Water (Hangzhou Bay). Remote Sens. 2021, 13, 4267. [Google Scholar] [CrossRef]
- Cao, F.; Tzortziou, M. Capturing dissolved organic carbon dynamics with Landsat-8 and Sentinel-2 in tidally influenced wetland–estuarine systems. Sci. Total Environ. 2021, 777, 145910. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, W.; Tian, Y.Q.; Yu, Q. Monitoring dissolved organic carbon by combining Landsat-8 and Sentinel-2 satellites: Case study in Saginaw River estuary, Lake Huron. Sci. Total Environ. 2020, 718, 137374. [Google Scholar] [CrossRef] [PubMed]
- Vanhellemont, Q.; Ruddick, K. Atmospheric correction of Sentinel-3/OLCI data for mapping of suspended particulate matter and chlorophyll-a concentration in Belgian turbid coastal waters. Remote Sens. Environ. 2021, 256, 112284. [Google Scholar] [CrossRef]
- Harmel, T.; Chami, M.; Tormos, T.; Reynaud, N.; Danis, P. Sunglint correction of the Multi-Spectral Instrument (MSI)-SENTINEL-2 imagery over inland and sea waters from SWIR bands. Remote Sens. Environ. 2018, 204, 308–321. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- IOCCG Ocean Color Algorithm Working Group. Models, Parameters, and Approaches that Used to Generate Wide Range of Absorption and Backscattering Spectra. 2003. Available online: http://www.ioccg.org/groups/lee_data.pdf (accessed on 1 January 2025).
- Guanlin, H.; Fang, S.; Hong, S. Modeling of seawater reflectance in the Yangtze Estuary and the adjacent sea. J. East China Norm. Univ. 2012, 1, 37–46. [Google Scholar]
- Chen, W.; Zheng, X.; Lu, X. Hyperspectral Image Super-Resolution with Self-Supervised Spectral-Spatial Residual Network. Remote Sens. 2021, 13, 1260. [Google Scholar] [CrossRef]
- Zhang, P.; Weng, J.; Kang, Q.; Li, J. Reconstruction of High-Resolution Solar Spectral Irradiance Based on Residual Channel Attention Networks. Remote Sens. 2024, 16, 4698. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Song, R.; Li, Y.; Xie, W. Residual Augmented Attentional U-Shaped Network for Spectral Reconstruction from RGB Images. Remote Sens. 2020, 13, 115. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Kotchenova, S.Y.; Vermote, E.F.; Levy, R.; Lyapustin, A. Radiative transfer codes for atmospheric correction and aerosol retrieval: Intercomparison study. Appl. Opt. 2008, 47, 2215–2226. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss Functions for Image Restoration With Neural Networks. IEEE Trans. Comput. Imaging 2017, 3, 47–57. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Dall’Olmo, G.; Pardo, S.; van Dongen-Vogels, V.; Boss, E.S. Underway spectrophotometry along the Atlantic Meridional Transect reveals high performance in satellite chlorophyll retrievals. Remote Sens. Environ. 2016, 183, 82–97. [Google Scholar] [CrossRef]
- Shen, F.; Verhoef, W.; Zhou, Y.; Salama, M.S.; Liu, X. Satellite Estimates of Wide-Range Suspended Sediment Concentrations in Changjiang (Yangtze) Estuary Using MERIS Data. Estuaries Coasts. 2010, 33, 1420–1429. [Google Scholar] [CrossRef]
- Shen, F.; Zhou, Y.; Li, J.; He, Q.; Verhoef, W. Remotely sensed variability of the suspended sediment concentration and its response to decreased river discharge in the Yangtze estuary and adjacent coast. Cont. Shelf Res. 2013, 69, 52–61. [Google Scholar] [CrossRef]
- Shen, F.; Zhou, Y.; Peng, X.; Chen, Y. Satellite multi-sensor mapping of suspended particulate matter in turbid estuarine and coastal ocean, China. Int. J. Remote Sens. 2014, 35, 4173–4192. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Lee, Z.; Lubac, B.; Werdell, J.; Arnone, R. Update of the Quasi-Analytical Algorithm (QAA_v6) [R/OL]. 2014. Available online: https://www.ioccg.org/groups/software.html (accessed on 1 January 2025).
- Keith, D.; Milstead, B.; Walker, H.; Snook, H.; Szykman, J.; Wusk, M.; Kagey, L.; Howell, C.; Mellanson, C.; Drueke, C. Trophic status, ecological condition, and cyanobacteria risk of New England lakes and ponds based on aircraft remote sensing. J. Appl. Remote Sens. 2012, 6, 063577. [Google Scholar] [CrossRef]
- Zheng, G.; DiGiacomo, P.; Kaushal, S.; Yuen-Murphy, M.; Duan, S. Evolution of Sediment Plumes in the Chesapeake Bay and Implications of Climate Variability. Environ. Sci. Technol. 2015, 49, 6494–6503. [Google Scholar] [CrossRef]
- Qi, L.; Hu, C.; Duan, H.; Cannizzaro, J.; Ma, R. A novel MERIS algorithm to derive cyanobacterial phycocyanin pigment concentrations in a eutrophic lake: Theoretical basis and practical considerations. Remote Sens. Environ. 2014, 154, 298–317. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. Atmos. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Pitarch, J.; Vanhellemont, Q. The QAA-RGB: A universal three-band absorption and backscattering retrieval algorithm for high resolution satellite sensors. Dev. Implement. ACOLITE Remote Sens. Environ. 2021, 265, 112667. [Google Scholar] [CrossRef]
- Castagna, A.; Vanhellemont, Q. A generalized physics-based correction for adjacency effects. Appl. Opt. 2025, 64, 2719–2743. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Knudby, A.; Pahlevan, N.; Lapen, D.; Zeng, C. Sensor-generic adjacency-effect correction for remote sensing of coastal and inland waters. Remote Sens. Environ. 2024, 315, 114433. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Du, K. Effects of molecular and particle scatterings on the model parameter for remote-sensing reflectance. Appl. Opt. 2004, 43, 4957–4964. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).