Abstract
Localizing ground-penetrating radar (LGPR) benefits from deep subsurface coupling, ensuring robustness against surface variations and adverse weather. While LGPR is widely recognized as the complement of existing vehicle localization methods, its reliance on prior maps introduces significant challenges. Channel misalignment during traversal positioning and time-dimension distortion caused by non-uniform platform motion degrade matching accuracy. Furthermore, rain and snow conditions induce subsurface water-content variations that distort ground-penetrating radar (GPR) echoes, further complicating the localization process. To address these issues, we propose a weather-resilient adaptive spatio-temporal mask alignment algorithm for LGPR. The method employs adaptive alignment and dynamic time warping (DTW) strategies to sequentially resolve channel and time-dimension misalignments in GPR sequences, followed by calibration of GPR query sequences. Moreover, a multi-level discrete wavelet transform (MDWT) module enhances low-frequency GPR features while adaptive alignment along the channel dimension refines the signals and significantly improves localization accuracy under rain or snow. Additionally, a local matching DTW algorithm is introduced to perform robust temporal image-sequence alignment. Extensive experiments were conducted on both public LGPR datasets: GROUNDED and self-collected data covering five challenging scenarios. The results demonstrate superior localization accuracy and robustness compared to existing methods.
1. Introduction
The concept of localizing ground-penetrating radar (LGPR) was first introduced by Cornick et al. in 2016 [1]. Unlike vision-based systems, LGPR operates reliably under varying ground conditions and provides rich subsurface reflections, enabling accurate localization without dependence on stable visual environments credited on GPR’s performance [2,3]. As a result, this approach has attracted significant research attention [4,5,6,7,8,9]. The core principle of LGPR involves matching real-time GPR profiles with georeferenced profiles in a prebuilt map library to identify the best correspondence, thereby achieving re-localization on a prior map. This process can be viewed as an image retrieval task [10]. Consequently, positioning accuracy critically depends on high-precision registration between the prior map and the revisited GPR echoes images.
Since LGPR relies on image matching using priori maps, numerous studies have explored registration techniques for GPR A-scan, B-scan, and sequence images. For instance, ref. [11] proposed localization using GPR A-scans within a known underground map. Further, ref. [12] investigated faster R-CNN-based feature extraction from GPR B-scans, while [13] introduced a phase-symmetric feature descriptor to enhance GPR image registration by leveraging hyperbolic signatures. Nevertheless, ref. [7] demonstrated that single GPR scans from distinct scenes exhibit high similarity, risking false matches between different locations. In computer vision (CV) and LiDAR localization, this issue is typically mitigated via feature vector aggregation [14,15] or Siamese networks [16,17]. However, due to GPR’s limited vertical detection range [1,8], direct adoption of these methods degrades LGPR accuracy. To address this, refs. [7,18,19] employed GPR sequence images to improve LGPR precision.
However, LGPR exhibits fundamental distinctions from conventional wheel odometry, inertial navigation, and vision-based systems through its utilization of temporally acquired subsurface reflections instead of real-time measurements [1,10,20]. Specifically, in LGPR applications, the temporal acquisition mode is typically adopted, with subsequent distance normalization enabling the computation of ground-penetrating radar mile positions based on standard channel spacing. This methodology, however, introduces inherent sensitivity to platform movement: velocity fluctuations not only distort the dimensional accuracy of GPR reflection profiles but also compound ranging inaccuracies. While the GROUNDED dataset [10,21] addresses temporal synchronization through Savitzky–Golay filtering of multi-sensor timestamps, persistent misalignments occur in high-frame-rate GPR acquisitions owing to constrained detection ranges, resulting in compromised feature correspondence and degraded positioning performance. In addition, LGPR imposes stringent requirements on vehicle trajectory accuracy. As shown in Figure 1, channel deviations in the GPR array antenna, which occur between prior map collection and the online positioning phase, can alter the target echoes acquired from the same road segment. This variability leads to positioning inaccuracies caused by channel misalignment in the vehicle’s travel path. Lane deviations cause misaligned echo images at the same forward position, leading to incorrect matches, akin to viewpoint variations in CV positioning [22]. While LiDAR/CV mitigates such issues via rotation-invariant descriptors (e.g., spherical projection [23,24]), GPR’s sparse feature points limit their effectiveness. While the standard DTW method can address some of these issues, it fails to resolve the channel dimension deviation problem inherent in GPR sensors.
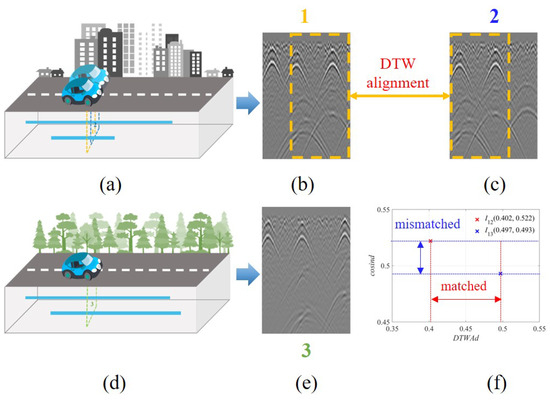
Figure 1.
Illustration of lane deviation effects on GPR echo signals. (a) Scene of lane deviation during two GPR mapping campaigns. (b,c) Underground echo images collected from the two deviated lanes in (a), (b) and (c) correspond to conditions 1 and 2 in (a), respectively. (d) GPR mapping scene at a location distinct from (a). (e) GPR echo image acquired at (d), (e) corresponds to condition 3 in (a). Despite the spatial proximity of (b,c), the echo patterns of (b,e) exhibit higher similarity. (f) Quantitative comparison of image distances between GPR echoes: cosine (cosine distance) and align (alignment-based distance).
To address the critical challenges in LGPR, including GPR data distorted induced by variable carrier velocity and lane offset, positioning mismatches caused by groundwater content variations during inclement weather (e.g., rain/snow) and computational complexity in GPR spatio-temporal feature extraction are investigated. We propose a novel framework employing adaptive alignment and dynamic time warping (DTW) strategies. Our approach generates bias-aware masks to sequentially rectify both channel and temporal misalignments in GPR sequences, followed by calibration of GPR maps. The methodology enables precise comparison between local features in query images and their semantically corresponding representations in reference maps. The system operates through three key phases. The first is that the generated correction masks adjust the GPR query sequences. Notably, our channel dimension calibration framework incorporates an adaptive parameter to generate mathematically constrained dimension masks, providing a complete solution to the systematic deviations depicted in Figure 1. The second group of low-frequency channel-dimensional features are extracted from both the map and query GPR time series. The third adaptive DTW performs spatio alignment of the processed sequences. This integrated approach demonstrates significant improvements in localization accuracy while enhancing the real-time capability of LGPR systems. We present a weather-resilient adaptive spatio-temporal mask alignment algorithm for LGPR, a novel framework with three key contributions:
- We develop an adaptive DTW algorithm that generates a map deviation-aware mask to address channel and temporal dimensional deformations in LGPR acquisition.
- We introduce a channel alignment module employing MDWT-based low-frequency signal enhancement, coupled with time-dimensional DTW local matching, to overcome challenges from both lane deviations and diverse weather conditions.
- Extensive evaluations on both the public GROUNDED dataset and self-collected data demonstrate the superior performance of the proposed method. The framework effectively eliminates positioning mismatches caused by lane deviations while significantly improving robustness under precipitation (rain/snow), surpassing state-of-the-art methods. Visualization results further validate its capability to mitigate channel misalignments and temporal feature distortions, highlighting its exceptional performance.
2. Preliminary
Since our proposed method builds upon DTW and MDWT, this section briefly reviews DTW and MDWT.
2.1. DTW
The dynamic time warping (DTW) algorithm employs a recursive approach to compute an optimal warping path for aligning two temporal sequences, where the path length quantifies their similarity. Initially developed for speech recognition [25,26], DTW has become a standard sequence alignment tool in this field due to its ability to synchronize time series with variable acquisition times and speeds. Subsequently, it has been successfully extended to diverse domains, including data mining [27] and image processing [28], establishing itself as a fundamental distance metric for time series analysis [29]. In visual location recognition, DTW was first adapted to align spatially distributed local features while measuring inter-image distances. For instance, ref. [30] utilized DTW to compare video sequences, effectively addressing temporal scale variations. Inspired by these advances, we propose the first application of DTW to LGPR. Specifically, we perform dynamic time regularization between GPR prior maps and query sequences to mitigate spatio-temporal misalignments. The core computation process is described as follows:
Given two GPR sequences and , the DTW distance is computed through the following three-step process. Firstly, we compute the pairwise Euclid distance matrix (or cosine distance), where each element represents the distance between frame and :
Secondly, using dynamic programming, we compute the accumulated cost matrix , where each entry stores the minimum cumulative distance up to :
The fundamental recursive formulation of DTW computes the minimal cumulative distance between the initial alignment point and current position , in which denotes the local distance metric between elements and of the respective time series. The minimization operation evaluates three distinct warping path transitions:
- Vertical movement V: progression in the reference sequence;
- Horizontal movement H: advancement in the query sequence;
- Diagonal movement D: simultaneous progression in both sequences.
Thirdly, we find an optimal alignment path in the matrix by minimizing the overall distance between sequence and . The optimal alignment between the two sequences is indicated by the elements of the optimal alignment path .
is derived by back-tracking from to , selecting the direction with the smallest accumulated cost at each step, where K is the length of the warping path (). The final sequence similarity is provided by the normalized cumulative cost:
where K is the length of the warping path.
This method ensures precise spatio-temporal alignment for visual place recognition under appearance changes. Emerging research evidence confirms DTW’s successful application in GPR data analysis [31], which substantiates the validity of our DTW-based approach to LGPR challenges.
2.2. MDWT
During GPR map and query acquisitions, matching images are typically captured at different times under varying weather conditions. Significantly, rainy and snowy environments induce shallow subsurface humidity variations that subsequently cause dielectric constant fluctuations. These variations critically influence electromagnetic wave time delays, thereby generating substantial image discrepancies. Consequently, to achieve robust positioning performance in adverse weather, more stable information extraction becomes essential for LGPR systems to effectively mitigate matching errors. Importantly, as demonstrated in [5,32], feature points from low-frequency B-scan components exhibit remarkable stability against moisture variations, clearly indicating that low-frequency-based registration offers superior reliability for LGPR applications. Accordingly, prior to channel-dimension alignment, we strategically employ multi-level DWT to enhance low-frequency components, as illustrated in Figure 2, which fundamentally improves weather-resistant matching capability. Consequently, we employ frequency-domain transformation to process GPR images, specifically utilizing the multi-level discrete wavelet transform (MDWT) with Symlet 4 as the wavelet basis to decompose the original image. Notably, this approach systematically enhances low-frequency information while simultaneously attenuating high-frequency components, thereby improving feature stability against environmental variations. The transformed representation effectively preserves structurally significant patterns while suppressing weather-induced noise components that predominantly reside in higher frequency bands. The MDWT operation is formally expressed as follows:
where denotes the MDWT operator. This approach systematically enhances low-frequency components while attenuating high-frequency noise, improving environmental robustness. The multi-level enhancement process proceeds as follows:
The enhanced reconstruction is computed through weighted synthesis:
where are high-frequency components (LH, HL, and HH) of an image post-MDWT, excluding the low-frequency LL sub-band. enhances level-k low-frequency components (), and suppresses high-frequency noise.
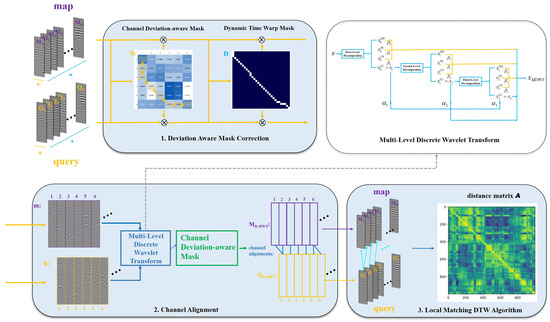
Figure 2.
Overview of the proposed framework. The proposed framework comprises three key components: (1) Deviation-aware mask correction: Compensates for map distortions induced by platform posture variations and motion speed changes (Section 3.1). (2) Channel alignment module: Addresses channel offsets caused by yaw deviations (Section 3.2). (3) Local matching DTW algorithm: Generates the alignment distance matrix for robust feature matching (Section 3.3); MDWT module: Extracts low-frequency features from aligned channel data to mitigate weather-dependent underground moisture variations (Section 2.2), the blue module illustrates the processing pipeline of the proposed methodology.
3. Methodology
This section presents the proposed framework, which consists of three key components: a deviation-aware mask, channel alignment, and localized feature matching. Figure 2 illustrates the overall pipeline of the proposed framework. The framework works as follows. Firstly, we use DTW to align two segments of raw GPR data collected at different times on the same road section, generating a deviation-aware mask. Secondly, the aligned data enter the channel alignment module, where MLDWT enhances low-frequency features. The processed signal is realigned in the channel dimension using the channel deviation-aware mask, improving alignment and reducing antenna-channel mismatch caused by track offset. Finally, we apply the local matching DTW algorithm. In the following section, we will elaborate on each module in detail.
3.1. Deviation-Aware Mask for GPR Sequence Calibration
To mitigate map deformation artifacts induced by lane deviations or platform velocity fluctuations during GPR data acquisition, we propose a novel two-stage mask calibration framework. The first stage generates a lane deviation mask for precise channel-dimension alignment of dual-channel GPR data. Building upon this, the second stage employs an optimized dynamic time warping (DTW) algorithm to construct a deviation-aware mask that achieves concurrent spatial and temporal registration of GPR sequences, as shown in Figure 2.
Consider two GPR sequences, and , exhibiting both spatial (cross-track) and temporal (along-track) distortions due to channel misalignments and non-uniform acquisition velocities during data collection. In the absence of precise prior information, direct sequence alignment becomes particularly challenging. To address this, we partition each sequence into N localized segments. For channel-dimensional DTW mask generation, we employ cosine distance as the fundamental similarity measure between subsequences, defined as , as shown in Equation (1). A smaller value indicates higher similarity between subsequences. We introduce an adaptive parameter to regulate diagonal shift weighting in our enhanced DTW formulation, yielding the channel-dimensional alignment mask (detailed in Section 3.2). Subsequently, mask generates channel-corrected sequences for both reference and query data, enabling temporal alignment through DTW with the Euclidean distance metric:
Following distance computation and DTW cost matrix generation, we obtain the cumulative DTW distance and perform path backtracking to derive the temporal alignment mask . This mask is then applied to generate the corrected GPR time series. Figure 3 demonstrates the comparative results between the query data and the prior map after offset-aware mask correction, showing significant improvement in alignment accuracy.
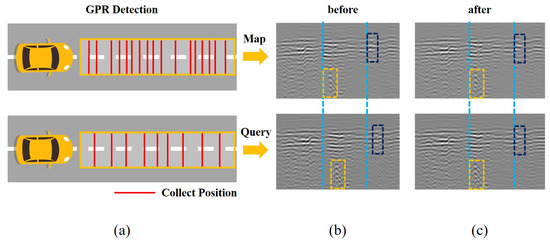
Figure 3.
Visualization of deviation-aware mask calibration for GPR sequence alignment. (a) GPR signal acquisition positions under varying platform speeds during map and query. (b) Time-domain comparison of a channel before calibration, showing significant temporal misalignment (yellow and blue boxes highlight identical features). (c) Post-calibration result, demonstrating corrected feature alignment in the B-scan.
3.2. Channel Alignment
Owing to the inherent operational characteristics of GPR systems, vehicles must precisely adhere to the prior map’s acquisition trajectory to obtain properly aligned GPR echo images in the antenna channel dimension. As demonstrated in Figure 4, any trajectory deviation causes channel dimension misalignment, introducing viewpoint discrepancies in the acquired B-scans. Direct application of cosine or Euclidean distance metrics under such misalignment conditions inevitably results in matching errors. To address this challenge, we propose an adaptive DTW-based block alignment method for GPR channel-dimensional B-scan registration. This approach computes the alignment distance between GPR time-series pairs while accounting for non-linear temporal deformations, thereby enabling robust similarity measurement.
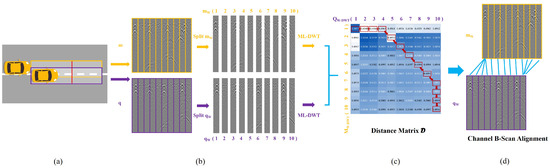
Figure 4.
Channel alignment module workflow. (a) Yaw-induced channel offset between map and query GPR data. (b) Each B-scan image is partitioned into W (W = 10 in Figure 4) uniform sub-regions, which subsequently undergo MDWT decomposition for localized low-frequency feature extraction. (c) Cosine distance matrix computation: A distance matrix is constructed from the localized low-frequency feature. (d) Channel-dimension alignment: dynamic time warping (DTW) is applied to matrix to generate the final channel alignment matrix.
As illustrated in Figure 4, the images of the GPR sequence map and query sequence are m and q, which are further segmented into channel-wise blocks separately, generating block sequences and . W must evenly divide the channel dimension in the along-track direction. Based on typical GPR channel dimensions and hardware limitations, we adopt W = 10 as a practical default value. While the choice of W impacts positioning accuracy, its selectable range is primarily determined by the GPR channel configuration. Consequently, the optimal practice is to set W as either the full channel dimension or a proper divisor thereof. Afterwards, they are sent to MDWT separately. The three-level DWT was chosen for optimal GPR signal analysis, balancing time-frequency resolution and computational efficiency. This decomposition depth simultaneously resolves shallow features and deep layers, while avoiding the inadequate resolution of fewer levels or the excessive fragmentation of deeper transforms. The weighting parameters and were empirically optimized to 1.5 and 0.2, respectively, effectively suppressing high-frequency noise components while amplifying relevant low-frequency signals in the GPR data.
The similarity measurement employs the cosine distance (defined in Section 3.1) between MDWT-processed low-frequency features (detailed in Section 2.2). This metric operates on vectorized B-scan pairs after DWT decomposition, with the distance . This local similarity measure enables pointwise comparison of time series characteristics, where decreasing distance values indicate higher feature similarity. From pairwise block comparisons, we construct a distance matrix . The DTW algorithm then identifies the optimal alignment path (The mask) , which is shown in Equation (3), with path coordinates establishing the temporal alignment between sequences and . The accumulated lane deviation-aware matrix is computed along the optimal path, with each element representing the minimum cost of the optimal path from to . The computation of is provided by Equation (2).
The fundamental recursive formulation of DTW computes the minimal cumulative distance between the initial alignment point and the current position , in which denotes the local distance metric between elements and of the respective time series. This recursive computation ensures optimal non-linear alignment while preserving temporal ordering constraints through systematic evaluation of all feasible warping paths. The proposed method introduces an adaptive deformation coefficient to the conventional DTW framework, enhancing its capability to accommodate feature variations while maintaining temporal alignment integrity. This modification addresses the limitations of standard DTW in handling non-linear distortions through a dynamically adjusted constraint parameter, as demonstrated in prior work [29]. The adaptive mechanism automatically regulates the warping path flexibility based on local feature characteristics, achieving improved alignment accuracy compared to traditional fixed-constraint approaches.
Here, is a predefined constant (typically set to 1), and corresponds to the index of the optimal matching feature in image for the reference feature in image . The warping path establishes spatio alignment between the two sequences from their initial positions to terminal coordinates , as illustrated in Figure 4. The exemplar alignment demonstrates that while the path primarily connects semantically equivalent channel-dimensional B-scan pairs (e.g., ), it necessarily incorporates some non-corresponding feature matches (e.g., ). These incidental alignments arise from trajectory deviations during GPR data acquisition, where the survey vehicle’s positional offset introduces content disparities between co-located regions of images and . Crucially, retaining these non-corresponding matches preserves the spatial coherence of local features and ensures metrologically sound distance computation between the B-scan images. To account for path length variability in dynamic time warping alignment, we employ normalized cumulative distance to derive a scale-invariant similarity measure between images and . The normalized distance metric is formulated as Equation (4). This normalization procedure effectively eliminates the dimensional bias introduced by varying warping path lengths while preserving the essential dissimilarity information between the compared B-scan sequences.
The proposed alignment methodology begins by computing a local distance matrix for each pair of GPR channel-dimensional B-scans. Subsequently, DTW is systematically applied to derive the cumulative distance matrix, thereby enabling precise temporal alignment of the channel-dimensional images. Notably, during this alignment process, an adaptive parameter is dynamically optimized to effectively modulate the diagonal path cost, consequently compensating for non-linear temporal distortions that may arise during data acquisition. Ultimately, as clearly demonstrated in Figure 4, this comprehensive procedure successfully yields a set of optimally aligned channel-dimensional B-scan distance measurements, which are characterized by enhanced accuracy and reliability for subsequent analytical processing.
3.3. Local Matching DTW Algorithm
Finally, we systematically compute pairwise distances between the channel-aligned map and query GPR time series using the local matching DTW algorithm, thereby generating a comprehensive distance matrix . Crucially, the matching performance is rigorously evaluated by identifying minimum-distance correspondences within matrix , which conclusively demonstrates the effectiveness of the proposed method under varying environmental conditions. Specifically, the consistent localization accuracy achieved through this approach verifies the method’s robustness against moisture-induced signal variations that typically degrade conventional GPR matching performance.
4. Experiment and Results Analysis
In this section, we first describe the data acquisition process and evaluation metrics adopted for the experiments. Subsequently, we conduct an ablation study to rigorously examine the influence of three critical components—namely, the deviation-aware mask (DAM), channel alignment (CA), and multi-level discrete wavelet transform (MDWT)—on LGPR performance under various weather conditions and different lane deviation scenarios. Finally, to comprehensively validate the efficacy of our framework, we compare the proposed method with state-of-the-art (SOTA) approaches, demonstrating its superior robustness and accuracy.
4.1. Data Acquisition and Data Pre-Processing
To rigorously validate the universality of the proposed method, we employ two complementary datasets: the publicly available GROUNDED dataset [21] and a self-collected dataset [5]. Both datasets comprehensively capture multiple traversals of identical routes under varying temporal conditions, with each route being recorded at least three times at different periods. Subsequently, we provide detailed descriptions of these datasets to facilitate reproducibility and demonstrate their suitability for evaluating our method. Finally, Table 1 presents the precise experimental configurations and dataset specifications for reference. In addition, the table summarizes the lengths of the chosen map and query sequences, the sampling interval, and the lane offset measured by RTK-GPS during acquisition.

Table 1.
Dataset specifications and parameters.
- GROUNDED dataset: To comprehensively characterize the experimental data, we utilize a unique large-scale LGPR dataset that currently represents the sole publicly available collection employing 11-channel 400 MHz GPR measurements. The dataset systematically incorporates three distinct weather conditions (rain, snow, and clear) while simultaneously encompassing seven diverse road environments, including highways, urban centers, and suburban areas. Furthermore, the dataset specifically addresses multi-lane mapping challenges through a carefully designed acquisition plan, thereby providing a robust testbed for evaluating LGPR performance across varying operational scenarios. In this study, Route5’s run56 (sunny) is selected as the map, while run57 (sunny), run90 (rainy), and run57 (snowy) serve as the query sequences.
- Self dataset: To ensure comprehensive data coverage, we employed a multi-channel GPR system to systematically acquire ground-penetrating radar data across various road surfaces in Changsha, China. The system configuration consists of a dual-row uniform antenna array comprising 20 radar channels with a total array width of 1.5 m, operating within a broad frequency range of 100–3000 MHz. While the nominal penetration depth reaches approximately 3 m, we note that actual penetration performance varies significantly depending on subsurface soil characteristics. Furthermore, to guarantee high-resolution data collection, we integrated a distance measurement instrument (DMI) that triggers the GPR system at precisely 7-cm intervals along each survey line. Importantly, our acquisition plan specifically addresses lane deviation challenges by intentionally collecting data with 0–5 channel offsets, while simultaneously ensuring environmental variability through repeated surveys of identical road sections under both sunny and rainy weather conditions. We selected non-yawed trajectories (self) under sunny conditions as the map, while sunny and rainy sequences served as queries. Additionally, we included sunny trajectories with intentional yaw deviations (self yaw), using the non-yawed sequence as the map and trajectories with two-lane and four-lane offsets as queries.
4.2. Valuation Metric
To objectively assess recognition performance, we primarily employ the -score as our evaluation metric, where ground truth is established through frame-level correspondences within each dataset. Specifically, we determine true positive matches by comparing query sequences with result sequences, requiring both the sequence distance to remain below a predetermined threshold and the recognition error to fall within acceptable tolerances (as detailed in Table 1). The best results are highlighted in bold.
4.3. Ablation Study
To systematically evaluate the contribution of each module in the proposed framework, we conduct comprehensive ablation experiments, with comparative results presented in Table 2. The baseline localization using original GPR data shows limited effectiveness, particularly under adverse weather conditions. In the GROUNDED dataset, we observe -scores of only 0.496 for sunny/sunny conditions and approximately 0.2 for sunny/rainy conditions. Similar trends are evident in the Self dataset, where the -score drops from 0.802 for sunny/sunny conditions to 0.285 during sunny/rainy conditions. These results highlight the significant challenges posed by weather-induced subsurface variations in traditional LGPR approaches. Our proposed framework demonstrates substantial improvements across all tested conditions. The adaptive spatio-temporal alignment strategy successfully maintains -scores above 0.9 in both sunny/sunny and sunny/rainy conditions for the GROUNDED dataset, while achieving 0.986 in the sunny/rainy conditions of the Self dataset. This enhanced performance is particularly notable given that rainfall typically causes more severe subsurface dielectric variations than snowfall due to greater moisture infiltration, making rainy conditions theoretically more challenging for GPR-based localization. The methodology also shows remarkable robustness to lane offset scenarios. In the Self dataset with intentional trajectory deviations, the system improves localization accuracy from baseline -scores of 0.78 (two-lane offset) and 0.577 (four-lane offset) to 0.901 and 0.845, respectively. This performance gain underscores the effectiveness of our channel alignment module in compensating for acquisition geometry variations. Notably, the relatively smaller performance gain for sunny/snowy conditions in the GROUNDED dataset (compared to sunny/rainy conditions) may be attributed to platform motion artifacts during data acquisition. As indicated in Table 3, advanced feature extraction techniques could potentially bridge this gap. Future work will explore the integration of learning-based approaches to further enhance localization robustness under such challenging conditions. Specifically, we analyze five distinct configurations:

Table 2.
-score comparison of different ablated versions.

Table 3.
-score comparison of SOTA.
- Proposed: the complete proposed method (Figure 2), representing our full proposed framework.
- No DAM: the variant excluding DAM calibration, where original dataset data undergo CA after MDWT filtering.
- No CA:a configuration without CA, utilizing cosine distance metrics on DAM calibrated MDWT data for single-image matching.
- No MDWT: an ablated version removing the MDWT module entirely.
- Original data: baseline performance using raw, unprocessed origin data.
This structured ablation approach enables the precise quantification of each component’s impact on overall system performance.
The ablation of the DAM module results in a significant degradation of positioning performance in both the GROUNDED and self-collected datasets, with particularly pronounced effects under varying weather conditions. To further investigate the DAM module’s influence on the LGPR task, we visualize the maps and queries under different weather conditions before and after DAM module processing, as illustrated in Figure 5.
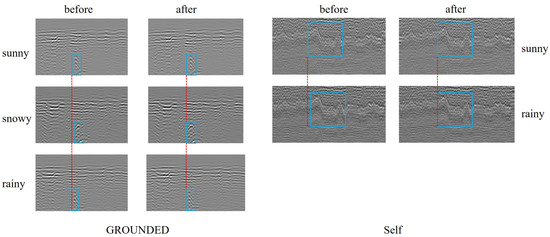
Figure 5.
Comparison of fifth-channel B-scans before and after DAM module processing in the time domain. (Left) GROUNDED dataset (map: sunny day; query: snowy/rainy day). (Right) Self-collected dataset (map: sunny day; query: rainy day). Blue boxes highlight GPR echoes from identical shallow subsurface features, while red dashed lines indicate alignment improvements after DAM processing.
Figure 5 demonstrates that the DAM module effectively corrects the GPR echo query by aligning it with the map’s shallow subsurface target echoes in both the GROUNDED and Self datasets. As analyzed in Section 3.1, this approach mitigates GPR map distortions caused by platform speed variations. Notably, despite the visual discrepancies between map and query echoes due to differing subsurface water content under varying weather conditions, the DAM module reliably captures consistent target features. Future work could further enhance the DAM module’s robustness in matching target echoes across weather conditions through advanced learning methods.
In Addition, the CA module significantly improves positioning accuracy in both the GROUNDED dataset and the Self (yaw) dataset, but its impact is less pronounced in the standard Self dataset. This discrepancy arises because the standard self-collected dataset maintains strict channel alignment during data acquisition, whereas both the GROUNDED dataset and the yaw-variant dataset exhibit GPR channel misalignment due to lane deviations.
We further evaluate the MDWT module and demonstrate its effectiveness in enhancing the robustness of LGPR tasks under varying weather conditions. On the GROUNDED dataset, the MDWT module improves the -score by 11% for snowy conditions and 5% for rainy conditions. The performance gain is more pronounced in the self-collected dataset, with -score improvements of 10% (sunny) and 20% (rainy). This discrepancy arises because the higher acquisition frequency of the self-collected dataset makes target echoes more susceptible to high-frequency noise interference. To validate this analysis, we provide visualizations of the self-collected dataset and further examine the MDWT module’s performance, as illustrated in the Figure 6.

Figure 6.
Visualization of map–query pairs in the self-collected dataset: (left) map (sunny) and (right) query (rainy), showing data before and after MDWT module processing. Corresponding cosine distance metrics between map and query are included for both processing states.
As shown in Figure 6, the MDWT module’s enhanced map-query matching capability under both clear and rainy conditions. Post-processing results show, firstly, improved distinctiveness of target feature echoes, secondly, reduced cosine distance between co-located map-query pairs, and thirdly effective compensation for subsurface water content variations. As analyzed before, the performance improvement is particularly significant for our self-collected dataset (operational bandwidth: 100–3000 MHz) compared to conventional 400 MHz systems, since the broader frequency range introduces additional high-frequency noise components that the MDWT module effectively suppresses.
Moreover, we compute the cosine distance matrix for localization using LGPR data ( Figure 7). In the cosine-distance heatmaps, smaller cosine distances between frames are represented by lighter colors, clearly demonstrating enhanced segment correspondence. Comparative analysis shows the proposed method significantly improves positioning accuracy under rainy conditions, as evidenced by the sharper diagonal pattern in the processed matrix versus the original data. The right sub-figure (proposed) exhibits a markedly clearer diagonal with more distinct light-colored segments, indicating superior inter-segment matching compared to the left sub-figure (original data).
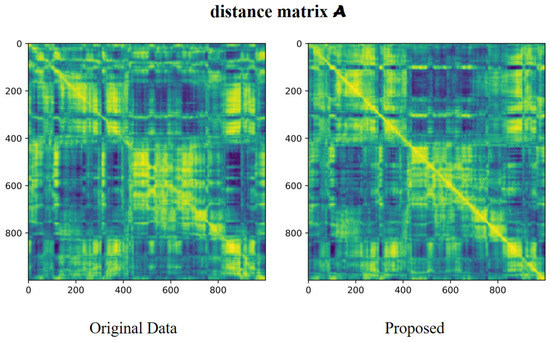
Figure 7.
Comparison of cosine distance matrices for local positioning using GPR data: (left) raw unprocessed data; (right) data processed with the proposed method. Experimental validation conducted using the GROUNDED dataset under sunny mapping and rainy query conditions.
In summary, as evidenced by the -score comparisons in Table 2, the proposed method demonstrates substantial positioning accuracy improvements across all experimental conditions. Specifically, the deviation-aware mask module yields remarkable performance gains, elevating -scores by 0.4–0.5 for both sunny and rainy conditions in the GROUNDED and Self datasets. Similarly, the channel alignment module proves particularly effective for challenging scenarios, improving -score by 0.2–0.3 in rainy/snowy sections of the GROUNDED dataset and lane-offset conditions in our Self data. Furthermore, the MDWT module shows consistent enhancement (-score = 0.2) for multi-weather positioning by effectively mitigating subsurface water content variations, with notably greater impact on our Self dataset. Moreover, baseline comparisons using raw GPR B-scan cosine distances further validate the proposed method’s superiority.
4.4. Comparison with the State-of-the-Art Methods
In order to rigorously validate the performance enhancement of our proposed LGPR method, systematic comparisons have been conducted against SOTA approaches encompassing both learning-based feature localization techniques and map alignment preprocessing solutions, including STU-Net [19] as a deep learning architecture for GPR echo feature extraction and enhancement, along with hybrid-driven recovery with low-frequency enhancement (LFE-MDP) [33], in addition to the widely adopted Savitzky–Golay filter [10] for LGPR preprocessing and the conventional fast DTW algorithm [34], all of which were re-implemented and retrained within our unified LGPR framework to ensure fair evaluation. Building upon our previous work [19,33], which demonstrated the superior performance of learning-based methods such as STU-Net and HRLE over alternative learning schemes for LGPR tasks, and considering that the Savitzky–Golay filter represents the current standard preprocessing approach in LGPR applications [7,10,18] while the fast DTW has been successfully applied across various computer vision applications [30,35], the quantitative comparison results presented in Table 3, the best results are highlighted in bold. clearly demonstrate significant performance improvements achieved by our proposed method across all , with particular emphasis on its unique advantages for subsurface sensing applications, including enhanced feature discrimination in challenging environments and improved robustness to signal variations.
Table 3 demonstrates the superior performance of our proposed method for LGPR localization. While both STU-Net and LFE-MDP learning methods show limited improvement over original data positioning in rainy/snowy conditions (in GROUNDED, 32.9%/36.6% and 36.1%/18% accuracy gains, respectively), their performance remains constrained by the inherent limitations of B-scan channel dimension features. Comparative analysis reveals HRLE’s better suitability for LGPR tasks (in GROUNDED and Self, 10–20% higher than STU-Net in sunny/sunny), confirming the importance of low-frequency information sensitivity in LGPR processing. However, neither learning-based approach effectively mitigates yaw-induced positioning errors. Furthermore, conventional methods (fast DTW and Savitzky–Golay filter) exhibit significantly lower robustness to weather variations compared to our proposed technique.
The Figure 8 presents precision–recall (PR) curves comparing the proposed method with baseline approaches across three distinct weather conditions in the GROUNDED dataset, quantitatively demonstrating the method’s superior robustness to environmental variations.
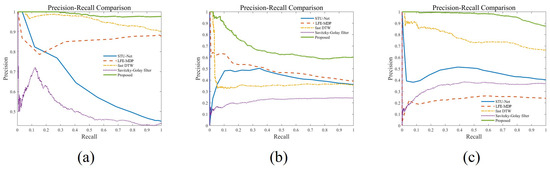
Figure 8.
Precision–recall (PR) performance comparison of state-of-the-art methods in the GROUNDED dataset under varying weather conditions: (a) sunny, (b) snowy, and (c) rainy days.
5. Conclusions
We present the proposed method, which fundamentally enhances LGPR accuracy by innovatively adapting DTW principles from audio processing while meticulously accounting for GPR data acquisition characteristics. Specifically, our technical contributions include four key components: the DAM correction module addressing speed variations in GPR platform motion; the CA module resolving channel mismatches induced by vehicle trajectory deviations; MDWT handling feature distortions from groundwater content fluctuations due to climatic variations; a novel local matching DTW algorithm integrating these solutions. Collectively, these innovations establish a robust framework for high-precision LGPR. Extensive experimental validation demonstrates our method’s consistent positioning accuracy across diverse weather conditions and channel offset scenarios, while comprehensive benchmarking confirms its superior performance over approaches on multiple datasets.
Author Contributions
Conceptualization, Y.C. and P.Z.; Methodology, Y.C., B.B. and P.Z.; Formal analysis, Y.C.; Writing—original draft, Y.C.; Writing—review & editing, B.B.; Visualization, Y.C.; Supervision, L.S. and C.C.; Funding acquisition, X.H. and T.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cornick, M.; Koechling, J.; Stanley, B.; Zhang, B. Localizing ground penetrating radar: A step toward robust autonomous ground vehicle localization. J. Field Robot. 2016, 33, 82–102. [Google Scholar] [CrossRef]
- Xu, L.; Winner, V.; Maurer, H. Gradient-constrained model parametrization in 3-D compact full waveform inversion. Geophys. J. Int. 2023, 232, 366–397. [Google Scholar] [CrossRef]
- Wang, X.; Yu, T.; Feng, D.; Li, B.; Ding, S. Spatiotemporal Optimization of GPR Full Waveform Inversion Based on Super-Resolution Technology. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5908413. [Google Scholar] [CrossRef]
- Ort, T.; Gilitschenski, I.; Rus, D. Autonomous navigation in inclement weather based on a localizing ground penetrating radar. IEEE Robot. Autom. Lett. 2020, 5, 3267–3274. [Google Scholar] [CrossRef]
- Bi, B.; Shen, L.; Zhang, P.; Huang, X.; Xin, Q.; Jin, T. TSVR-Net: An End-to-End Ground-Penetrating Radar Images Registration and Location Network. Remote Sens. 2023, 15, 3428. [Google Scholar] [CrossRef]
- Li, H.; Guo, J.; Song, D. Subsurface Feature-based Ground Robot/Vehicle Localization Using a Ground Penetrating Radar. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1716–1722. [Google Scholar]
- Zhang, P.; Zhi, S.; Yuan, Y.; Bi, B.; Xin, Q.; Huang, X.; Shen, L. Looking Beneath More: A Sequence-based Localizing Ground Penetrating Radar Framework. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 8515–8521. [Google Scholar]
- Zhang, K.; Chi, Y.; Guo, J.; Bai, C. Underground Robot Localization Based on Ground-Penetrating Radar. In Proceedings of the International Conference on Autonomous Unmanned Systems, Singapore, 26–28 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 3577–3588. [Google Scholar]
- Xu, J.; Lai, Q.; Wei, D.; Ji, X.; Shen, G.; Yuan, H. The Ground-Penetrating Radar Image Matching Method Based on Central Dense Structure Context Features. Remote Sens. 2024, 16, 4291. [Google Scholar] [CrossRef]
- Ort, T.; Gilitschenski, I.; Rus, D. GROUNDED: The Localizing Ground Penetrating Radar Evaluation Dataset. In Proceedings of the Robotics: Science and Systems, Virtual, 12–16 July 2021; Volume 2. [Google Scholar]
- Skartados, E.; Kargakos, A.; Tsiogas, E.; Kostavelis, I.; Giakoumis, D.; Tzovaras, D. Gpr antenna localization based on a-scans. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), A Coruña, Spain, 2–6 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Ni, Z.; Ye, S.; Shi, C.; Pan, J.; Zheng, Z.; Fang, G. A deep learning assisted ground penetrating radar localization method. J. Electron. Inf. Technol. 2022, 44, 1265–1273. [Google Scholar]
- Zhang, P.; Shen, L.; Wen, T.; Huang, X.; Xin, Q. Vector phase symmetry for stable hyperbola detection in ground-penetrating radar images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5107912. [Google Scholar] [CrossRef]
- Arandjelovic, R.; Gronat, P.; Torii, A.; Pajdla, T.; Sivic, J. NetVLAD: CNN architecture for weakly supervised place recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5297–5307. [Google Scholar]
- Arandjelovic, R.; Zisserman, A. All about VLAD. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1578–1585. [Google Scholar]
- Noh, H.; Araujo, A.; Sim, J.; Weyand, T.; Han, B. Large-scale image retrieval with attentive deep local features. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3456–3465. [Google Scholar]
- Ma, J.; Zhang, J.; Xu, J.; Ai, R.; Gu, W.; Chen, X. OverlapTransformer: An efficient and yaw-angle-invariant transformer network for LiDAR-based place recognition. IEEE Robot. Autom. Lett. 2022, 7, 6958–6965. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, X.; Chen, Y.; Bi, B.; Xu, Z.; Jin, T.; Huang, X.; Shen, L. EDENet: Echo Direction Encoding Network for Place Recognition Based on Ground Penetrating Radar. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 23–27 February 2025; Volume 39, pp. 10067–10075. [Google Scholar]
- Chen, Y.; Zhang, P.; Bi, B.; Shen, L.; Jin, T.; Huang, X. Spatial–Temporal U-Net for Localizing Ground-Penetrating Radar. IEEE Geosci. Remote Sens. Lett. 2025, 22, 3504905. [Google Scholar] [CrossRef]
- Stasewitsch, I.; Schattenberg, J.; Frerichs, L. Robust Monte Carlo Localisation Using a Ground Penetrating Radar. In Proceedings of the Iberian Robotics Conference, Sevilla, Spain, 23–25 November 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 247–258. [Google Scholar]
- Ort, T.; Gilitschenski, I.; Rus, D. GROUNDED: A localizing ground penetrating radar evaluation dataset for learning to localize in inclement weather. Int. J. Robot. Res. 2023, 42, 901–916. [Google Scholar] [CrossRef]
- Lu, F.; Chen, B.; Zhou, X.D.; Song, D. STA-VPR: Spatio-temporal alignment for visual place recognition. IEEE Robot. Autom. Lett. 2021, 6, 4297–4304. [Google Scholar] [CrossRef]
- Yin, H.; Wang, Y.; Ding, X.; Tang, L.; Huang, S.; Xiong, R. 3d lidar-based global localization using siamese neural network. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1380–1392. [Google Scholar] [CrossRef]
- Kim, G.; Kim, A. Scan context: Egocentric spatial descriptor for place recognition within 3d point cloud map. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 4802–4809. [Google Scholar]
- Deng, J.J.; Leung, C.H. Dynamic time warping for music retrieval using time series modeling of musical emotions. IEEE Trans. Affect. Comput. 2015, 6, 137–151. [Google Scholar] [CrossRef]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process. 2003, 26, 43–49. [Google Scholar] [CrossRef]
- Keogh, E.J.; Pazzani, M.J. Scaling up dynamic time warping for datamining applications. In Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, MA, USA, 20–23 August 2000; pp. 285–289. [Google Scholar]
- Maus, V.; Câmara, G.; Appel, M.; Pebesma, E. dtwsat: Time-weighted dynamic time warping for satellite image time series analysis in r. J. Stat. Softw. 2019, 88, 1–31. [Google Scholar] [CrossRef]
- Lu, F.; Chen, B.; Guo, Z.; Zhou, X. Visual sequence place recognition with improved dynamic time warping. In Proceedings of the 2019 IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI), Portland, OR, USA, 4–6 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1034–1041. [Google Scholar]
- Deng, Z.P.; Jia, K.B. A video similarity matching algorithm supporting for different time scales. In Proceedings of the 2008 Eighth International Conference on Intelligent Systems Design and Applications, Kaohsiung, Taiwan, 26–28 November 2008; IEEE: Piscataway, NJ, USA, 2008; Volume 3, pp. 570–574. [Google Scholar]
- Wen, J.; Huang, T.; Cui, X.; Zhang, Y.; Shi, J.; Jiang, Y.; Li, X.; Guo, L. Enhancing Image Alignment in Time-Lapse-Ground-Penetrating Radar through Dynamic Time Warping. Remote Sens. 2024, 16, 1040. [Google Scholar] [CrossRef]
- Luo, W.; Lee, Y.H.; Sun, H.H.; Ow, L.F.; Yusof, M.L.M.; Yucel, A.C. Tree roots reconstruction framework for accurate positioning in heterogeneous soil. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1912–1925. [Google Scholar] [CrossRef]
- Bi, B.; Shen, L.; Zhang, P.; Chen, Y.; Huang, X.; Jin, T. Hybrid-Driven with Low-Frequency Enhancement for LGPR Map Reconstruction. IEEE Sens. J. 2025, in press. [Google Scholar] [CrossRef]
- Salvador, S.; Chan, P. Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 2007, 11, 561–580. [Google Scholar] [CrossRef]
- Chen, A.P.; Lin, S.F.; Cheng, Y.C. Time registration of two image sequences by dynamic time warping. In Proceedings of the IEEE International Conference on Networking, Sensing and Control, Taipei, Taiwan, 21–23 March 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 1, pp. 418–423. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).