Abstract
The Yunyao Aerospace Constellation Program is the core project being developed by Yunyao Aerospace Technology Co., Ltd., Tianjin, China. It aims to provide scientific data for weather forecasting, as well as research on the ionosphere and neutral atmosphere. It is expected to launch 90 high time resolution weather satellites. Currently, the Yunyao space constellation provides nearly 16,000 BDS, GPS, GLONASS, and Galileo multi-system occultation profile products on a daily basis. This study initially calculates the precise orbits of Yunyao LEO satellites independently using each GNSS constellation, allowing the derivation of the neutral atmospheric refractive index profile. The precision of the orbit product was evaluated by comparing carrier-phase residuals (ranging from 1.48 cm to 1.68 cm) and overlapping orbits. Specifically, for GPS-based POD, the average 3D overlap accuracy was 4.93 cm, while for BDS-based POD, the average 3D overlap accuracy was 5.18 cm. Simultaneously, the global distribution, the local time distribution, and penetration depth of the constellation were statistically analyzed. BDS demonstrates superior performance with 21,093 daily occultation profiles, significantly exceeding GPS and GLONASS by 15.9% and 121%, respectively. Its detection capability is evidenced by 79.75% of profiles penetrating below a 2 km altitude, outperforming both GPS (78.79%) and GLONASS (71.75%) during the 7-day analysis period (DOY 169–175, 2023). The refractive index profile product was also compared with the ECWMF ERA5 product. At 35 km, the standard deviation of atmospheric refractivity for BDS remains below 1%, while for GPS and GLONASS it is found at around 1.5%. BDS also outperforms GPS and GLONASS in terms of the standard deviation in the atmospheric refractive index. These results indicate that Yunyao satellites can provide high-quality occultation product services, like for weather forecasting. With the successful establishment of the global BDS-3 network, the space signal accuracy has been significantly enhanced, with BDS-3 achieving a Signal-in-Space Ranging Error (SISRE) of 0.4 m, outperforming GPS (0.6 m) and GLONASS (1.7 m). This enables superior full-link occultation products for BDS.
1. Introduction
Radio occultation (RO) observations of the Global Navigation Satellite Systems (GNSS) serve as one of the observational data sources for global observing systems. These RO observations utilize the time delay in receiving GNSS satellite signals by Low Earth Orbit (LEO) satellites, which is caused by the refraction of these signals in the Earth’s atmosphere. As LEO satellite orbits around the Earth, GNSS satellites rise or set on the horizon, depending on their relative motion. Consequently, a series of observations provides vertical profiles of the Earth’s atmosphere, which are referred to as occultation observations [1]. In 1995, the Global Positioning System/Meteorology (GPS/MET) satellite was launched, marking the first validation of GPS occultation technology [2]. An increasing number of LEO satellites carrying occultation payloads have been deployed, including the Challenging Minisatellite Payload (CHAMP) [3], the Gravity Recovery and Climate Experiment (GRACE) [4], Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC) [1], COSMIC-2 [5], the Meteorological Operations Platform (MetOP), Fengyun-3C/D/E (FY-3C/D/E) [6,7,8], Sentinel-6 [9], and others.
High-precision orbits are essential to perform and achieve GNSS-RO. With the successful application of onboard GPS data to the TOPEX/Poseidon satellite [10] and the acquisition of a high-quality orbit, onboard GNSS precise orbit determination (POD) technology has become an important approach in GNSS RO data inversion. GNSS RO data inversion refers to the retrieval of atmospheric parameters from GNSS signal phase delays, including the derivation of bending angles and refractivity profiles via techniques such as the Abel transform [11]. In addition to the mentioned satellites, high-precision trajectories were computed for LEO satellites such as GOCE [12], Swarm [13], and Jason [14]. The relatively low cost and all-weather characteristics make onboard GPS orbit determination more applicable in the commercial aerospace field than Satellite Laser Ranging (SLR) orbit determination. On 31 July 2020, the Beidou Global Navigation Satellite System (BDS) was officially completed as a global network. Compared to BDS-2, the BDS-3 satellite orbit and clock accuracy have been gradually improved [15]. More and more LEO satellites are equipped with receivers capable of receiving BDS signals [16]. Research on orbit determination based on onboard BDS data is gradually increasing and developing [17]. Li et al. [18] conducted a comparison of overlapping arc segments of the FY-3C satellite based on single BDS and BDS/GPS combinations. The three-dimensional (3D) root mean square (RMS) value of the single BDS orbit is 8 cm, while the GPS/BDS combined POD accuracy is 3.9 cm. In 2021, China successfully launched the HY2D satellite, which carries both BDS and GPS signal receivers to achieve centimeter-level orbit determination. Three-dimensional orbit accuracies of 5.3 cm and 4.3 cm can be obtained using BDS and GPS, respectively [19].
Based on high-precision GNSS, the LEO satellite orbit, clock data, meteorological model and inversion algorithm, GNSS-RO technology allows us to obtain parameters related to Earth’s atmosphere, such as temperature, pressure, and refractivity [20]. Compared to radiosondes, GNSS-RO has the advantages of a high vertical resolution, global coverage, and all-day capability. The products obtained from GNSS-RO (e.g., the bending angle) can be used for numerical weather forecasting [21], which requires a large number of occultation events. The study by Harnisch et al. [22] showed that at least 16,000–20,000 occultation observations are needed daily to meet standard numerical forecasting requirements. With the launch of COSMIC-2, replacing COSMIC-1, the number of occultation events has nearly doubled. However, the number of occultation profiles generated by the six satellites is still far below the standards required for numerical forecasting. With the gradual improvement of numerical weather forecasting models [20], GNSS-RO products will bring greater social and economic benefits. As a result, more and more companies are becoming interested in meteorological constellations, such as Spire [23], GeoOptics [24], and PlanetIQ [25]. Tianjin Yunyao Aerospace Technology Co., Ltd, Tianjin, China. was established in March 2019. It is a high-tech company specializing in the research and development of meteorological satellite payloads (such as Global Navigation Satellite Systems-Reflected (GNSS-R), GNSS-RO, and Synthetic Aperture Radar (SAR)), meteorological data acquisition, and meteorological application services. The company launched its first operational satellite, the Tianjin University-1 (TJU-1) satellite, in December 2021 [26]. In August 2022, six operational satellites, TJBinhai-1 (BH01) and Y004–Y008, were launched. All six satellites are equipped with GPS, BDS, and GLONASS occultation receivers. Many of the current GNSS occultation constellations in orbit carry multiple GNSS systems to increase the number of occultation events observed by a single satellite. For example, the COSMIC-2 constellation carries GPS and GLONASS, the FengYun series satellites carry GPS and BDS, and the Spire constellation carries GPS, GLONASS, Galileo satellite navigation system (Galileo), and Quasi-Zenith Satellite System (QZSS). The products obtained from different systems’ inversion are not the same, as they are influenced by LEO and GNSS orbits, clock errors, receiver noise, and even Signal-in-Space Ranging Error (SISRE).
This study aims to evaluate the Yunyao LEO satellite constellation’s performance. In Section 2, the Yunyao satellite GNSS-RO processing system is introduced, including the observation model, orbit determination strategy, and software platform for onboard GNSS orbit determination. Also, the relevant GNSS-RO inversion algorithms are described. In Section 3, a phase residual accuracy assessment for onboard GPS and BDS orbit determination is presented, as well as an evaluation of the arc overlap precision. In Section 4, the Yunyao satellite’s precise orbits obtained in Section 3 are used to perform neutral atmosphere occultation inversion, and the accuracy of the refractivity products is assessed by comparison with the Reanalysis v5 (ERA5) background field from the European Centre for Medium-range Weather Forecasts (ECMWF). The analyzed results also indirectly reflect the correctness of the LEO satellite orbit obtained in Section 3. The number of neutral atmospheric products, penetration depth, and refractivity accuracy for the GPS, BDS, and GLONASS systems are statistically analyzed at different latitudes. As the BDS satellite orbits have unique characteristics, the refractivity accuracy and standard deviation (STDV) for the Medium Earth Orbit (MEO) and Inclined Geosynchronous Orbit (IGSO) are evaluated. The final conclusions are summarized in Section 5. This study aims to systematically evaluate the performance of the Yunyao LEO satellite constellation in neutral atmospheric sounding through multi-GNSS radio occultation, focusing on orbit determination accuracy, occultation inversion quality, and refractivity product validation for GPS, BDS, and GLONASS systems.
2. Processing
BinHai-1 and Y004–Y008 satellites are new types of weather observation (20 cm × 30 cm × 10 cm) CubeSats developed by Tianjin Yunyao Aerospace Technology Co., Ltd, Tianjin, China in collaboration with Chang Guang Satellite Technology Co., Ltd, Changchun, China. They operate in a sun-synchronous orbit at an altitude of approximately 533 km and provide all-weather GNSS neutral atmosphere and ionosphere occultation observations. These six satellites are an important part of the Yunyao constellation. Their names, launch dates, orbit heights, orbit inclinations, and local times are listed in Table 1. The receiving system’s frequency, the sampling rate, the usage of positioning, atmospheric, and ionospheric occultation channels are shown in Table 2. Closed-loop (CL) and open-loop (OL) tracking can be performed for the bottom of atmospheric occultation, greatly enhancing the depth of bottom detection.

Table 1.
Basic information on the Yunyao satellites.

Table 2.
Information about the Yunyao receiver and its receivable GNSS constellations.
The data obtained from the positioning and occultation antennas can be used to generate corresponding GNSS observation files and GNSS-RO raw data. LEO POD and excess phase calculations necessitate supporting GNSS satellite ephemerides and clock bias products. Considering the real-time requirements of atmospheric products and the fact that the majority of occultation events are from BDS, we use the GNSS Ultra products from Wuhan University [27], which provide GNSS orbit and clock correction at 5-min intervals.
2.1. LEO POD Strategies and Platform
The LEO satellite observes the pseudorange and phase measurements of the GNSS satellite, where the pseudorange () and phase () observation equations [28] are given below.
where represents the geometric distance in meters between the antenna phase center of the GNSS satellite and the LEO onboard receiver antenna phase center, is the clock error in seconds of the LEO satellite receiver, is the clock error of the GNSS satellite, is the ionospheric delay in meters, is the relativistic delay in meters, is the phase ambiguity term of in cycles, is the phase center deviation in meters of the LEO satellite receiver antenna, is the phase center deviation in meters of the GNSS satellite antenna, and is the observational noise in meters.
Shanghai Astronomical Observatory, Chinese Academy of Sciences, has developed the precise orbit determination program for LEO satellites, called Shanghai Astronomical Observatory Orbit Determination [29] (SHAOOD), taking into account the characteristics of LEO satellites such as altitude and disturbance forces, as well as its experience in spacecraft orbit determination. The strategy for LEO satellites plays a crucial role in achieving high-precision orbit. The orbit determination strategy includes the GNSS products, the length of the orbit arc, the resampling interval of the observation data, and the model selection. Considering factors such as the satellite orbit height, satellite-to-mass ratio, and solar panel design, suitable orbit determination strategies for the Yunyao small satellite can be studied and developed based on the receiver data using shared navigation antennas and satellite clocks. Table 3 provides more detailed information about the measurement models, dynamic models, and estimated parameters.

Table 3.
Precise orbit determination strategy for Yunyao satellites.
Furthermore, the consistency between the retrieved Level 2 refractivity profiles and the ECMWF ERA5 reanalysis is used as an additional criterion to validate the accuracy of the orbit solutions, given the sensitivity of neutral atmospheric retrievals to orbital precision.
The combination of two different frequencies can eliminate the majority of the first-order ionospheric delay during the precise orbit determination of LEO satellites if they are equipped with a dual-frequency receiver. However, after combining the observations, according to the error propagation law, the measurement noise will be amplified approximately three times due to the error propagation in the ionosphere-free linear combination, where large combination coefficients significantly increase the resulting noise level. The ionosphere-free combined observations are as follows:
where and represent the ionosphere-free pseudorange and phase observations, respectively, are two different frequencies of GNSS, and represent pseudorange observations at two frequencies, and and represent phase observations at two frequencies.
We use the dual-frequency ionosphere-free combination for the LEO satellite orbit determination. Therefore, when the receiver can collect pseudorange data and phase data at two frequencies, the navigation satellite can be considered available. At least four GNSS satellites are needed for the initial orbit determination, and other coefficients, such as the drag coefficients and empirical forces, are required to be estimated for a precise orbit determination. Therefore, the larger the number of navigational satellites that can be observed by the receiver, the more redundant observations there are, and the closer the calculated results will be to the true values. Given that the GLONASS constellation comprises only 24 satellites, it results in far fewer visible navigation signals than GPS. This study adopts the following processing strategy for atmospheric occultation data. Since both GLONASS positioning (which itself is an important source of ionospheric positioning data) and occultation measurements are handled on the same receiver board as GPS navigation and occultation signals, we first use the GPS occultation observations to precisely estimate the LEO satellite ephemerides and clock offsets. The resulting orbit and clock solutions are then applied to the excess-phase processing of both GPS and GLONASS occultation measurements, ensuring consistency and comparability in the atmospheric profile retrievals from the two systems. This approach not only maximizes the utility of GLONASS occultation data but also upholds the scientific rigor and objectivity of the inversion results.
As shown in Figure 1 and Figure 2, the receiver acquired a total of 83,712 epochs, with 95.78% (80,179 epochs) of these periods maintaining simultaneous tracking of at least four GPS satellites. When fewer than four satellites were available, 4.22% of the total number of epochs were observed, corresponding to 3533 epochs. Four or more observed BDS satellites accounted for 99.94% of the total number of epochs, that is, 83,671 epochs. When fewer than four satellites were available, only 0.05% of the total number of epochs were observed, that is, 42 epochs.
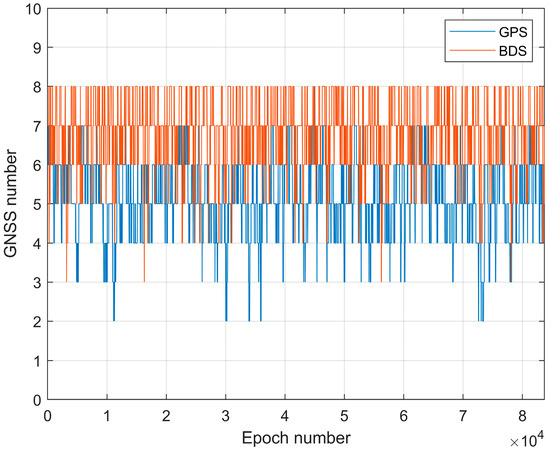
Figure 1.
Temporal variation in the number of successfully tracked BDS and GPS satellites by the receiver on satellite Y008 on 18 June 2023.
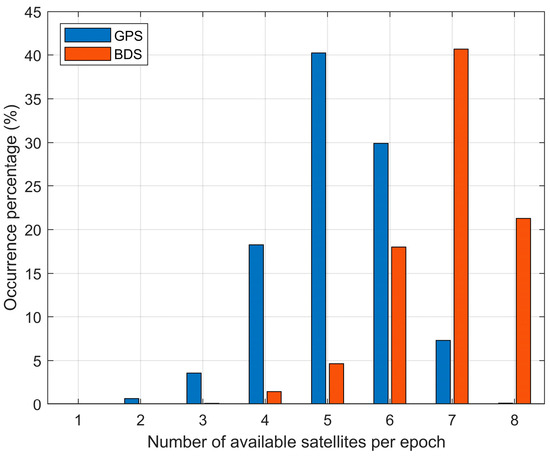
Figure 2.
Daily ratio of total available satellites of BDS or GPS observed by the receiver on satellite Y008 on 18 June 2023.
This receiver can detect 5.17 GPS satellites per epoch, 6.75 BDS satellites per epoch, and a total of 11.92 satellites when combining GPS and BDS. The two graphs above show that the receiver has the best performance in receiving BDS and slightly poorer performance in receiving GPS. The reason is that Yunyao’s onboard receiver has eight channels and two boards and can only receive 24 GPS satellites, whereas BDS can receive all BDS-2 and BDS-3 satellites except GEO satellites. When employing a single-system approach for orbit determination, BDS demonstrates the highest satellite availability, with most operational periods exceeding 4 visible satellites and typically maintaining 6–8 accessible satellites. In contrast, GPS primarily provides 4–6 satellites during single-system operation. Notably, both constellations satisfy orbit determination requirements for most operational scenarios when utilized independently, though BDS exhibits superior satellite geometry under typical conditions.
2.2. Extraction of the Neutral Atmospheric Excess Phase
The single-difference technique, which is the observation difference between the LEO satellite and a reference GNSS satellite, is used to eliminate clock frequency errors in LEO onboard receivers. By utilizing the precise orbits of LEO and GPS satellites, as well as GPS clock bias data, excess phase information from occultation observations can be obtained. During the occultation event, the LEO satellite simultaneously observes the signals from the occulted GPS satellite and another non-occulted reference GNSS satellite. Neglecting ambiguity and noise, the difference between LEO satellite observations and occultation GNSS observations and the observations of reference GNSS satellites are calculated as follows:
The superscripts o and r correspond to the LEO-GNSS occultation link and the LEO-GNSS reference GNSS signal link, respectively. The subscripts k = 1, 2 refer to L1 and L2, respectively. is the geometric distance between GNSS satellites and receivers. c is is the speed of light. and are the clock errors of the GNSS and LEO, respectively. induces phase delays in the neutral atmosphere. induces phase delays in the ionosphere [38].
where is the excess phase. To eliminate the LEO receiver clock error, the excess phase delay is essential for radio occultation processing and can be obtained by subtracting Equation (6) from Lk. Since the connection between the reference satellite and the LEO satellite is outside the neutral atmosphere, the term can be neglected, and the GNSS clock error is corrected using the GNSS clock bias solution.
The resulting for each frequency contains both neutral atmospheric and ionospheric delay information. These dual-frequency excess phases are then used in subsequent processing to separate the neutral atmospheric component from the ionospheric effects during bending angle retrieval.
2.3. Refractive Index Inversion
The Yunyao satellite’s radio occultation retrievals employ a hierarchical approach that integrates the geometric optic method [39] or single-path bending angle calculation below a 10 km altitude with full-spectrum inversion (FSI) [40] to resolve multipath propagation effects above this threshold. This hybrid fusion methodology generates continuous atmospheric profiles through optimal transition at the 10 km critical altitude determined by the atmospheric state analysis.
Atmospheric phase delay infers atmospheric Doppler shift [38] as follows:
where is the Doppler shift, c is the speed of light, is the excess phase obtained from Equation (7), is the GNSS frequency, and t is the observation time.
Under the assumption of a locally spherical symmetric atmosphere, the Doppler observation equation is used to convert the signal phase delay difference using the orbital ephemerides of the LEO and GNSS satellites into a bending angle profile as a function of the impact parameter. The relationship between the Doppler shift and the ray zenith angle is [39]
where is the ray direction vector of GNSS and LEO satellites, is the velocity vector of the GNSS transmitter relative to the receiver projected onto the plane of the occultation, is the zenith angle of the velocity component, is the zenith angle of the ray, is the distance of GNSS and LEO satellites, and is the bending angle.
Under the assumption of local spherical symmetry in the atmospheric medium, the relationship between the bending angle and the refractive index of the atmosphere, which is a function of impact parameters, in the process of signal propagation can be expressed by the following Abel equation [11]:
where x = nr is the refractive index multiplied by the radius, and a is the impact parameter. The integration is performed from the top of the atmosphere downward, with Earth’s ellipticity corrections applied to account for the planet’s non-spherical shape. This approach achieves high vertical resolution in the retrieved refractivity profiles, typically 100 m in the troposphere, allowing for detailed examinations of atmospheric structures.
This step yields two main geophysical parameters: the bending angle as a function of the impact parameter and the atmospheric refractivity profile obtained through Abel inversion.
3. LEO Precise Orbit Determination Result
3.1. POD Residual Analysis
For precise orbit determination, most of the observational errors have been corrected during the linearization of the observation equations, but there may still exist unconsidered errors, such as observation noise. The fitting residuals can indirectly reflect the level of the orbit determination observations and can be analyzed to preliminarily evaluate the level of the orbital parameter solution. When the quality of the observational data is good with accurate mechanical models and reasonable orbit determination strategies, then the fitting residuals of the observational data will be close to the observation noise. The smaller the orbit residuals, the higher the internal consistency accuracy. Figure 3 shows the statistical results of the carrier phase residuals’ root mean square (RMS) for six Yunyao satellites from 18 June 2023 to 24 June 2023 (DOY169–175).
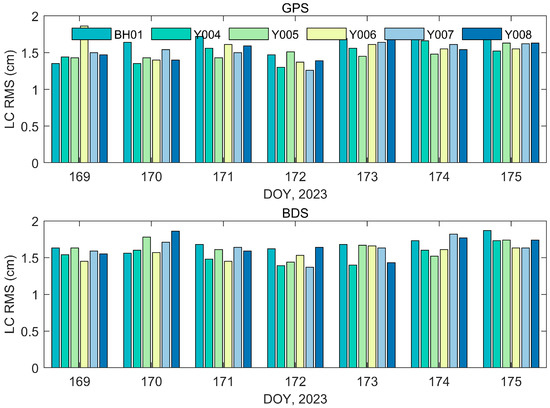
Figure 3.
RMS LC for GPS-based POD (upper panel) and BDS-based POD (lower panel).
Figure 3 displays the orbit residuals of GPS and BDS, which are roughly similar, ranging from 1.48 cm to 1.68 cm. Figure 4 shows the orbit residuals of GPS and BDS, which differ by about 14%, with GPS residuals being slightly smaller (1.48 cm vs. 1.68 cm). However, this difference of approximately 2 mm is negligible in the context of GNSS radio occultation, where Doppler measurement errors dominate. Therefore, for atmospheric occultation applications, the orbit precision derived from onboard GPS and BDS data can be considered effectively equivalent and stable.
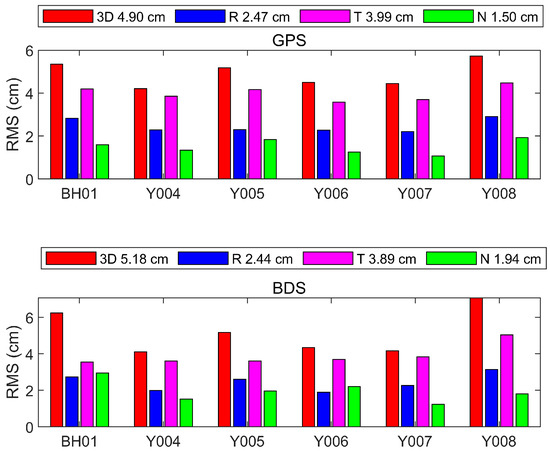
Figure 4.
RMS difference for the overlap comparison in 3D, radial (R), transverse (T), and normal (N) directions for GPS (upper panel) and BDS (lower panel).
3.2. Overlap Orbit Comparison
Overlap orbit comparison is a method of precise orbit determination in which two segment orbits are compared using observational data obtained before and after a given time period. The parameters calculated for each segment during different time periods are influenced by various factors, such as dynamic models, GNSS orbits, clock errors, and measurement data continuity, producing differences between the two segments. These differences can reflect the accuracy of the precise orbit. In order to evaluate the orbit determination accuracy of the six satellites using the overlap orbit comparison, two orbit determination segments are set up each day, with respective temporal windows defined as 00:00:00–17:59:59 and 12:00:00–23:59:59 (formatted in hh:mm:ss, i.e., hours:minutes:seconds). To avoid the impact of the orbit on the evaluation of the orbit accuracy, we compare the orbits after removing one hour on both sides of the overlap.
If only a single system (GPS) is used for the orbit determination, the accuracy can be within 3 cm in the R direction, 5 cm in the T direction and 2 cm in the N direction. The overlapping segment accuracy of the six satellites is approximately the same, and the 3D orbit accuracy of the satellites is maintained within 6 cm, allowing a good accuracy of atmospheric inversion at the top of the occultation.
If BDS is used as the single system for orbit determination, the accuracy for the six satellites is within 3 cm in the R direction, 5 cm in the T direction, and 3 cm in the N direction. The 3D mean value of the six satellites using on-board GPS data was 4.90 cm, and the 3D mean value using on-board BDS data was 5.18 cm.
4. Radio Occultation Result
To evaluate the cloud remote sensing neutral atmospheric occultation profiles, the ECWMF ERA5 product [41] was selected as the reference for comparison. The ERA5 product generated by ECMWF through the Copernicus Climate Change Service is internationally recognized as a standard background field, and the majority of meteorological products are evaluated for accuracy using it as the reference [42]. ECMWF’s quality management system is applicable to the development of global numerical models and data assimilation systems, allowing weather forecasts and monitoring of the Earth system for member countries, users, and stakeholders.
ERA5 can provide vertically oriented atmospheric information such as the barometric pressure, temperature, and humidity. The corresponding refractive index can be calculated using the following equation [43]:
where P is the pressure (hPa), T is the temperature (K), and e is the water vapor pressure (hPa). Although the terms involve physical units (e.g., hPa/K and hPa/K2), the resulting N is typically expressed in N-units (dimensionless). This expression is accurate to 0.5% in N for frequencies up to 30,000 MHz under typical ranges of temperature, pressure, and humidity.
4.1. Geographic Coverage and Local Time
Figure 5 and Figure 6 show the global distribution of occultation events for the six Yunyao satellites obtained from different GNSS systems and the local times of these events, respectively. As these Yunyao satellites have polar orbits, the occultation events are distributed worldwide. However, as these six satellites were launched from the same location at the same time, the local time is concentrated at approximately 11 UT and 22 UT, which has a moderate effect on the uniformity of time. However, Tianjin Yunyao Aerospace Technology Co., Ltd. will continue to launch satellites at different local times to meet the time requirements for meteorology.
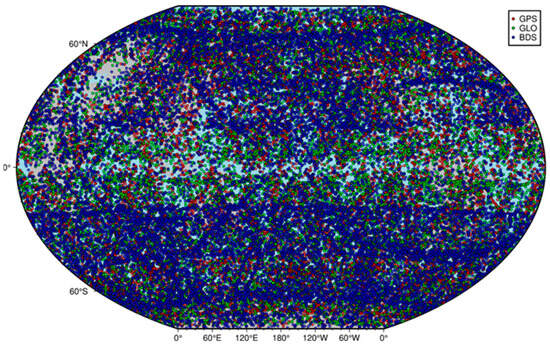
Figure 5.
Global distribution of BH01 and Y004-Y008 radio occultation events recorded from 18 June 2023 (DOY169) to 24 June 2023 (DOY175).
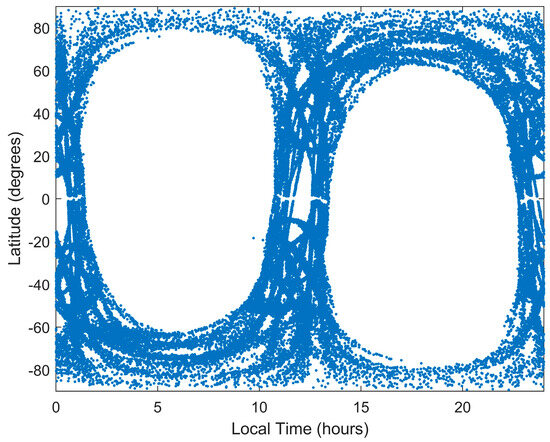
Figure 6.
Local time latitude distributions of radio occultation measurements for the Yunyao satellite constellation.
In this study, the BH01 and Y004-Y008 satellites were selected for neutral atmospheric occultation inversion. The period of analysis was 7 days, from the day of the year 169 to 175. Due to data access limitations and authorization constraints from the commercial satellite operator, this study focuses on a 7-day period, which provides a representative sample while ensuring the legality and transparency of data usage. Based on the precise LEO satellite orbits (i.e., Section 3), the occultation inversion for GPS and GLONASS was performed using the satellite-based GPS data to ensure consistency between different GNSS systems’ LEO satellite orbits and occultation products. Since GPS and GLONASS are on the same platform, only satellite-based GPS data was used for orbit determination. Similarly, the neutral atmospheric inversion for BDS was performed using the satellite-based BDS data. The obtained refractivity products were compared with the ERA5 background field. Statistical analysis was conducted to compare the number of occultation events for GPS, GLONASS, and BDS with intervals of 30° in latitude, as well as the relative accuracy (O-B/B)% (where O denotes the RO observation and B represents the ERA5 background field) of the inversion products compared to ERA5.
4.2. Penetration Depth
The occultation penetration depth products signify the GNSS constellation’s capability to probe the lower atmosphere. The introduction of open-loop techniques and the integration of high-power antennas [44] have allowed a significant improvement in the penetration depth. The minimum observable tangent-point height in GNSS-RO is governed not only by the atmospheric water vapor content but also by constellation-specific factors. First, differences in orbital inclination, altitude, and phasing among GPS, GLONASS, BeiDou, and Galileo lead to distinct geographic sampling patterns; in tropical regions, denser occultation events inherently traverse more humid layers, raising the effective detection floor. Second, differences in PRN (Pseudo-Random Noise) code lengths, modulation formats, and carrier-tracking loop bandwidths across GNSS constellations require customized Doppler prediction and loop parameter settings for each system. These technical variations affect the sensitivity of signal tracking in the lower atmosphere. Therefore, even though a common open-loop prediction model is used for all constellations, the combined influences of constellation-specific geometry, signal characteristics, and water vapor distribution result in distinct differences in the lowest altitudes that can be reached by each system (i.e., penetration height). Figure 7 shows the cumulative penetration depths at different altitudes for GPS, BDS, and GLONASS. The proportions of penetration depths below 1 km for GPS, BDS, and GLONASS are 55.12%, 58.67%, and 43.42%, respectively. Below 2 km, the penetration depths are 78.79%, 79.75%, and 71.75%, respectively. These results indicate that BDS exhibits the strongest detection capability, closely followed by GPS. However, as reported by Schreiner et al. [45], COSMIC-2 can achieve a penetration depth of 90% at 2 km, indicating a higher detection capability than that of BDS. The penetration height of GLONASS may have been culled to a certain extent due to quality control, resulting in a lower percentage of detections below 2 km when compared to GPS and BDS.
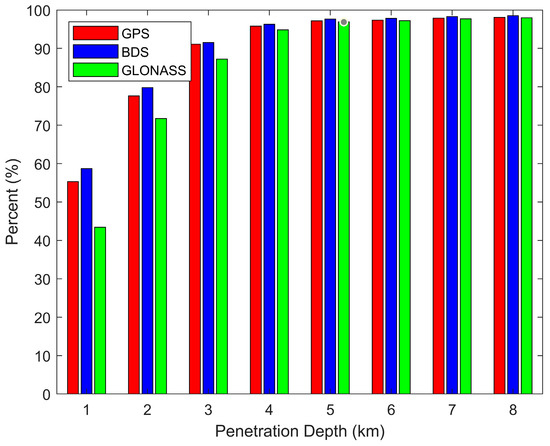
Figure 7.
Distribution of occultation profiles by penetration depth for different GNSS constellations.
4.3. Quality Assessment of Neutral Atmospheric Products Based on the ERA5 Evaluation
Figure 8 shows that during the 7-day period from the day of the year 169 to 175, the six Yunyao satellites collectively obtained 48,818 profiles. Specifically, 18,199 profiles were provided by GPS, 21,093 profiles were provided by BDS, and 9526 profiles were provided by GLONASS. The BDS system offered the highest number of observational data, followed by GPS, and GLONASS provided the lowest number of observational data.
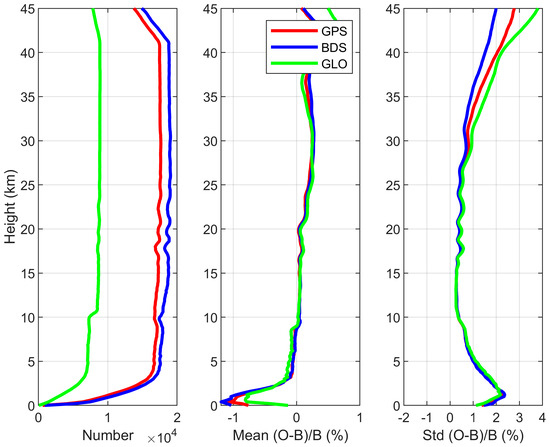
Figure 8.
Comparison of BH01 and Y004 − Y008 RO refractivity profiles with ERA5. The left panel indicates the number of contour profiles, the middle panel the mean bias, and the right panel the relative standard deviation.
The relative deviations, relative standard deviations, and event distribution quantities of the atmospheric profiles for GPS, BDS, and GLONASS are represented by the red, blue, and green lines, respectively, where ERA5 reanalysis products with a resolution of 0.25° and 37 layers are used as a reference. The relative standard deviation and relative deviation of the GPS, BDS, and GLONASS systems are roughly the same at 0–5 km. At altitudes above 27 km, the standard deviation of the BDS-derived profiles approaches 0% and remains closer to the true background field compared to the two other systems.
There are no large differences among the profiles of the various GNSS constellations between 3 km and 30 km. The results indicate a discernible positive bias in the mean deviation observed within the 20–35 km range. This systematic bias is considered to originate from limitations in the current algorithmic framework and parameterization scheme. Future iterations will incorporate targeted optimization of these components to achieve bias minimization approaching instrumental uncertainty levels.
In 35–45 km, there are significant differences in standard deviations among the profiles of different GNSS constellations, with BDS performing notably better than GPS and GLONASS. At 35 km, the standard deviation of atmospheric refractivity for BDS remains below 1%, while GPS and GLONASS are already around 1.5%. These deviations may result from differences in the precision of clock errors among different GNSS constellations. The poorer short-term stability of GLONASS clock errors [46] predominantly contributes to the differences in inversion product accuracy in the upper region. The short-term stability of GNSS clock errors may gradually deteriorate the accuracy of profiles above 30 km. In the case of LEO satellite orbital accuracy, which is roughly the same, the accuracy of the GNSS orbit and clock difference directly affects the inversion accuracy of the top of the occultation profile.
Another possibility is that the noise level of the BDS receiver is lower than that of GPS and GLONASS. Therefore, we evaluated the standard deviation of the numerical differences between the bending angles and climate models in the 60–80 km height region, which is considered a standard deviation (STDV) that can effectively represent the receiver’s noise and residuals. The average STDV can reflect the magnitude of noise in different systems, which affects the accuracy of the inversion products of these systems.
As shown in Figure 9, the STDV of BDS is superior to GPS and GLONASS. STDV values below 1 microrad account for 39% of all events for BDS, 35% for GPS, and less than 10% for GLONASS. The average values of BDS are better than GPS and GLONASS. This suggests that GLONASS has higher receiver noise, which can effectively explain why the profile accuracy of GLONASS is inferior to that of GPS and BDS.
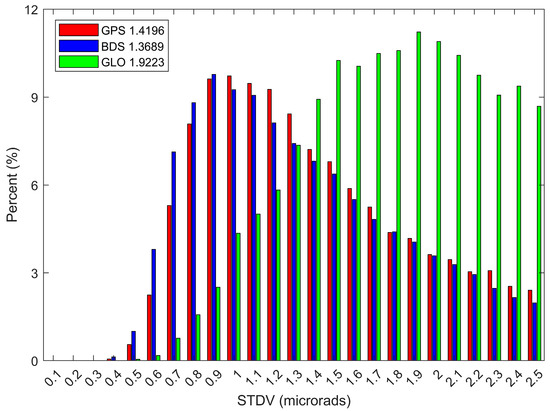
Figure 9.
Distributions of the standard deviation (STDV) at high-altitude bending angles for GPS, BDS, and GLONASS.
In Figure 10 and Figure 11, the standard deviation in the refractivity obtained for the MEO satellite is higher than that obtained for the IGSO satellite in the upper region. The STDV and average values of MEO are slightly better than those of IGSO. The percentage of MEO with an STDV less than 1 microrad is 45.53%, while for IGSO it is 22.27%. Currently, MEO mainly belongs to BDS-3, with its new frequency bands and higher performance atomic clocks, which improve the signal accuracy of BDS. By comparison, the main component of IGSO is BDS-2, which has a lower signal accuracy than BDS-3. This difference may be one of the reasons for why the STDV for MEO is smaller than for IGSO.
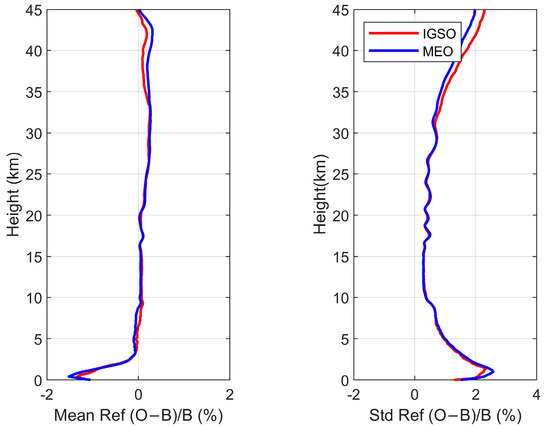
Figure 10.
Comparison between the refractive indexes derived from IGSO (red colored curve) and MEO (blue colored curve) satellite observations.
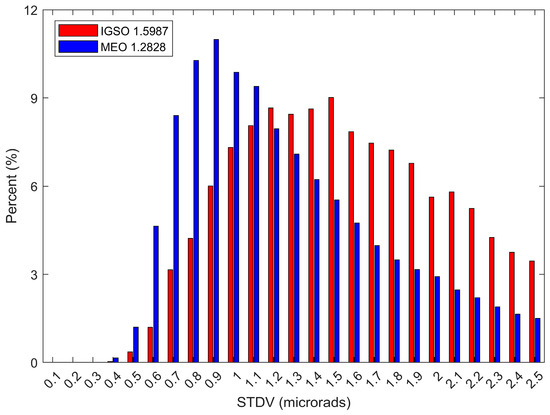
Figure 11.
IGSO and MEO distributions of high-altitude bending angle standard deviations.
The results presented above indicate that the occultation accuracy decreases from BDS to GPS and to GLONASS. This decrease may result from the BDS signal accuracy being higher than those of GPS (0.6 m) and GLONASS (1.7 m) [47] for LEO satellites with roughly equal accuracies (there is an approximately 2 mm difference in the accuracies of the orbit segments obtained from satellite-based GPS and satellite-based BDS). The spatial signal accuracy of GNSS controls the quality of the occultation products.
5. Conclusions
In this paper, GPS and BDS observation data from six Yunyao satellites were processed. Strategies were formulated to carry out a joint orbit determination using the GPS and BDS data. The Yunyao satellite orbits obtained separately from the satellite-based GPS data and satellite-based BDS data were used to perform neutral atmospheric occultation retrieval for different systems. The obtained refractive index products were compared with the ECMWF background field, and the main outcomes are summarized hereafter.
The precise orbit determination of the six Yunyao satellites was separately conducted using satellite-based GPS data and satellite-based BDS data. The orbit residuals for GPS and BDS are roughly similar, ranging from 1.48 cm to 1.68 cm. This indicates that the accuracy for both satellites is roughly equal and relatively stable. By comparing the overlapping arc segments for the orbit obtained from satellite-based GPS data, the average values in the R, T, and N directions for the six satellites are 2.47 cm, 3.99 cm, and 1.50 cm, respectively, and 4.93 cm in the 3D direction. For the orbit obtained from satellite-based BDS data, the average values in the R, T, and N directions for the six satellites are 2.44 cm, 3.89 cm, and 1.94 cm, respectively, and 5.18 cm in the 3D direction.
Using the obtained orbits mentioned above, neutral atmospheric occultation retrievals were carried out. The statistical analysis of neutral occultation products for a total of 7 days from DOY 169 to DOY 175 in 2023 shows that BDS has the highest number of occurrences. The percentage of events with a penetration depth below 2 km for the three systems is as follows: 78.79% for BDS, 79.75% for GPS, and 71.75% for GLONASS.
The refractive index products obtained from the Yunyao satellites were compared with ERA5. The occultation products obtained from the LEO satellite orbit inversion using BDS data are superior to those obtained using GPS and GLONASS data. In particular, the BDS products outperform the GPS and GLONASS products in terms of the standard deviation of the profiles at various latitudes at the top of the occultation. The distribution of the proportion of the STDV in the refractivity for the three systems was evaluated to explain the high accuracy of the BDS profiles. The average and proportion of STDV values below 1 microrad were better for BDS than for GPS and GLONASS. BDS produces three different types of orbits, and there are differences in the refractive index and STDV obtained from inversion using data from the IGSO and MEO satellites.
The successful completion of comprehensive construction of BDS-3 has endowed BDS with a high-quality and high-precision full-link GNSS occultation capability, providing global high-quality occultation product services.
Author Contributions
Conceptualization, writing—original draft preparation, writing—review and editing and methodology, H.Y. and N.F.; formal analysis and investigation, H.Y., N.F., Y.C. and W.D.; validation, M.W. and P.G.; funding acquisition, P.G. and M.W.; supervision, F.L., M.W., P.G., X.H. and F.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was partially supported by the National Natural Science Foundation of China (Grant Nos. 12273094 and 12273093).
Data Availability Statement
Satellite-borne GPS and BDS data are obtained from Tianjin Yunyao Aerospace Technology, Co. GPS, BDS, and GLONASS satellite orbits, clocks and Earth rotation parameters are provided by the Wuhan University (ftp://igs.gnsswhu.cn/ (accessed on 18 June 2023)). GNSS-RO data are obtained from Tianjin Yunyao Aerospace Technology, Co. ECWMF ERA5 data are provided by ECWMF (https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5 (accessed on 18 June 2023)).
Conflicts of Interest
Authors Naifeng Fu, Fenghui Li and Yan Cheng were employed by the company Tianjin Yunyao Aerospace Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Anthes, R.A. Exploring Earth’s Atmosphere with Radio Occultation: Contributions to Weather, Climate and Space Weather. Atmos. Meas. Tech. 2011, 4, 1077–1103. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Hardy, K.R.; Romans, L.J.; Schofield, J.T. Observing Tropospheric Water Vapor by Radio Occultation Using the Global Positioning System. Geophys. Res. Lett. 1995, 22, 2365–2368. [Google Scholar] [CrossRef]
- Wickert, J.; Reigber, C.; Beyerle, G.; König, R.; Marquardt, C.; Schmidt, T.; Grunwaldt, L.; Galas, R.; Meehan, T.K.; Melbourne, W.G.; et al. Atmosphere Sounding by GPS Radio Occultation: First Results from CHAMP. Geophys. Res. Lett. 2001, 28, 3263–3266. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The Gravity Recovery and Climate Experiment: Mission Overview and Early Results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Weiss, J.-P.; Schreiner, W.S.; Braun, J.J.; Xia-Serafino, W.; Huang, C.-Y. COSMIC-2 Mission Summary at Three Years in Orbit. Atmosphere 2022, 13, 1409. [Google Scholar] [CrossRef]
- Li, M.; Li, W.; Shi, C.; Jiang, K.; Guo, X.; Dai, X.; Meng, X.; Yang, Z.; Yang, G.; Liao, M. Precise Orbit Determination of the Fengyun-3C Satellite Using Onboard GPS and BDS Observations. J. Geod. 2017, 91, 1313–1327. [Google Scholar] [CrossRef]
- Tan, G.; Yang, G.; Wang, J.; Bai, W.; Sun, Y.; Hu, X.; Zhang, P.; Du, Q.; Wang, X.; Meng, X.; et al. Preliminary Accuracy Assessment of the F-Layer Worst-Case BDS Scintillation Observed by the GNOS Onboard the FY3D Satellite. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 10006–10016. [Google Scholar] [CrossRef]
- Yang, G.; Bai, W.; Wang, J.; Hu, X.; Zhang, P.; Sun, Y.; Xu, N.; Zhai, X.; Xiao, X.; Xia, J.; et al. FY3E GNOS II GNSS Reflectometry: Mission Review and First Results. Remote Sens. 2022, 14, 988. [Google Scholar] [CrossRef]
- Zhran, M. An Evaluation of GNSS Radio Occultation Atmospheric Profiles from Sentinel-6. Egypt. J. Remote Sens. Space Sci. 2023, 26, 654–665. [Google Scholar] [CrossRef]
- Yunck, T.P.; Bertiger, W.I.; Wu, S.C.; Bar-Sever, Y.E.; Christensen, E.J.; Haines, B.J.; Lichten, S.M.; Muellerschoen, R.J.; Vigue, Y.; Willis, P. First Assessment of GPS-based Reduced Dynamic Orbit Determination on TOPEX/Poseidon. Geophys. Res. Lett. 1994, 21, 541–544. [Google Scholar] [CrossRef]
- Gleisner, H.; Healy, S.B. A Simplified Approach for Generating GNSS Radio Occultation Refractivity Climatologies. Atmos. Meas. Tech. 2013, 6, 121–129. [Google Scholar] [CrossRef]
- Bock, H.; Jäggi, A.; Beutler, G.; Meyer, U. GOCE: Precise Orbit Determination for the Entire Mission. J. Geod. 2014, 88, 1047–1060. [Google Scholar] [CrossRef]
- Van Den Ijssel, J.; Encarnação, J.; Doornbos, E.; Visser, P. Precise Science Orbits for the Swarm Satellite Constellation. Adv. Space Res. 2015, 56, 1042–1055. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Zelensky, N.P.; Rowlands, D.D.; Lemoine, F.G.; Williams, T.A. The 1-Centimeter Orbit: Jason-1 Precision Orbit Determination Using GPS, SLR, DORIS, and Altimeter Data Special Issue: Jason-1 Calibration/Validation. Mar. Geod. 2010, 26, 399–421. [Google Scholar] [CrossRef]
- Chen, G.; Zhou, R.; Hu, Z.; Lv, Y.; Wei, N.; Zhao, Q. Statistical Characterization of the Signal-in-Space Errors of the BDS: A Comparison between BDS-2 and BDS-3. GPS Solut. 2021, 25, 112. [Google Scholar] [CrossRef]
- Chen, L.; Lv, F.; Yang, Q.; Xiong, T.; Liu, Y.; Yang, Y.; Pan, H.; Wang, S.; Liu, M.; He, R.; et al. Performance Evaluation of CentiSpace Navigation Augmentation Experiment Satellites. Sensors 2023, 23, 5704. [Google Scholar] [CrossRef]
- Li, W.; Yang, Q.; Du, X.; Li, M.; Zhao, Q.; Yang, L.; Qin, Y.; Chang, C.; Wang, Y.; Qin, G. LEO Augmented Precise Point Positioning Using Real Observations from Two CentispaceTM Experimental Satellites. GPS Solut. 2024, 28, 44. [Google Scholar] [CrossRef]
- Li, X.; Zhang, K.; Meng, X.; Zhang, W.; Zhang, Q.; Zhang, X.; Li, X. Precise Orbit Determination for the FY-3C Satellite Using Onboard BDS and GPS Observations from 2013, 2015, and 2017. Engineering 2020, 6, 904–912. [Google Scholar] [CrossRef]
- Peng, H.; Zhou, C.; Zhong, S.; Peng, B.; Zhou, X.; Yan, H.; Zhang, J.; Han, J.; Guo, F.; Chen, R. Analysis of Precise Orbit Determination for the HY2D Satellite Using Onboard GPS/BDS Observations. Remote Sens. 2022, 14, 1390. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, S.; Meng, X.; Wu, Y.; Lou, Y.; Lin, J. Undifferenced Processing of COSMIC-2 Radio Occultation Measurements with 1-Hz LEO Clock Corrections. GPS Solut. 2024, 28, 18. [Google Scholar] [CrossRef]
- Bai, W.; Deng, N.; Sun, Y.; Du, Q.; Xia, J.; Wang, X.; Meng, X.; Zhao, D.; Liu, C.; Tan, G.; et al. Applications of GNSS-RO to Numerical Weather Prediction and Tropical Cyclone Forecast. Atmosphere 2020, 11, 1204. [Google Scholar] [CrossRef]
- Harnisch, F.; Healy, S.B.; Bauer, P.; English, S.J. Scaling of GNSS Radio Occultation Impact with Observation Number Using an Ensemble of Data Assimilations. Mon. Weather Rev. 2013, 141, 4395–4413. [Google Scholar] [CrossRef]
- Bowler, N.E. An Assessment of GNSS Radio Occultation Data Produced by Spire. Q. J. R. Meteorol. Soc. 2020, 146, 3772–3788. [Google Scholar] [CrossRef]
- Chang, H.; Lee, J.; Yoon, H.; Morton, Y.J.; Saltman, A. Performance Assessment of Radio Occultation Data from GeoOptics by Comparing with COSMIC Data. Earth Planets Space 2022, 74, 108. [Google Scholar] [CrossRef]
- Zhran, M.; Mousa, A.; Wang, Y.; Hasher, F.F.B.; Jin, S. Assessment of Commercial GNSS Radio Occultation Performance from PlanetiQ Mission. Remote Sens. 2024, 16, 3339. [Google Scholar] [CrossRef]
- Gong, X.; Li, X.; Wang, P.; Wang, Q.; Wang, F.; Sang, J.; Gao, S. High-Precision Orbit Determination of the Small TJU-1 Satellite Using GPS, GLONASS, and BDS. IEEE Sens. J. 2023, 23, 13340–13350. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Guo, J.; Yang, C.; Zhao, Q. Near Real-Time Multi-GNSS Orbits, Clock and Observable-Specific Biases at Wuhan University. GPS Solut. 2024, 28, 191. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. Modeling and Assessment of Combined GPS/GLONASS Precise Point Positioning. GPS Solut. 2013, 17, 223–236. [Google Scholar] [CrossRef]
- Yuan, J.; Zhou, S.; Hu, X.; Yang, L.; Cao, J.; Li, K.; Liao, M. Impact of Attitude Model, Phase Wind-Up and Phase Center Variation on Precise Orbit and Clock Offset Determination of GRACE-FO and CentiSpace-1. Remote Sens. 2021, 13, 2636. [Google Scholar] [CrossRef]
- Förste, C.; Schmidt, R.; Stubenvoll, R.; Flechtner, F.; Meyer, U.; König, R.; Neumayer, H.; Biancale, R.; Lemoine, J.M.; Bruinsma, S.; et al. The GeoForschungsZentrum Potsdam/Groupe de Recherche de Gèodésie Spatiale Satellite-Only and Combined Gravity Field Models: EIGEN-GL04S1 and EIGEN-GL04C. J. Geod. 2008, 82, 331–346. [Google Scholar] [CrossRef]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H. The Planetary and Lunar Ephemeris DE 421. Interplanet. Netw. Prog. Rep. 2009, 42, 178. [Google Scholar]
- Petit, G.; Luzum, B. Technical Report: IERS Conventions; Verlag des Bundesamts fur Kartographie und Geodasie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Priestley, K.J.; Smith, G.L.; Thomas, S.; Cooper, D.; Lee, R.B.; Walikainen, D.; Hess, P.; Szewczyk, Z.P.; Wilson, R. Radiometric Performance of the CERES Earth Radiation Budget Climate Record Sensors on the EOS Aqua and Terra Spacecraft through April 2007. J. Atmos. Ocean. Technol. 2011, 28, 3–21. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the Global Ocean Tides: Modern Insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Rosengren, A.J.; Scheeres, D.J. Long-Term Dynamics of High Area-to-Mass Ratio Objects in High-Earth Orbit. Adv. Space Res. 2013, 52, 1545–1560. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 Empirical Model of the Atmosphere: Statistical Comparisons and Scientific Issues. J. Geophys. Res. Space Phys. 2002, 107, SIA 15-1–SIA 15-16. [Google Scholar] [CrossRef]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS Antenna Phase Center Model Igs08.Atx: Status and Potential Improvements. J. Geod. 2016, 90, 343–364. [Google Scholar] [CrossRef]
- Innerkofler, J.; Kirchengast, G.; Schwärz, M.; Marquardt, C.; Andres, Y. GNSS Radio Occultation Excess-Phase Processing for Climate Applications Including Uncertainty Estimation. Atmos. Meas. Tech. 2023, 16, 5217–5247. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Gurvich, A.S.; Kornblueh, L. Comparative Analysis of Radio holographic Methods of Processing Radio Occultation Data. Radio Sci. 2000, 35, 1025–1034. [Google Scholar] [CrossRef]
- Jensen, A.S.; Lohmann, M.S.; Benzon, H.H.; Nielsen, A.S. Full Spectrum Inversion of radio occultation signals. Radio Sci. 2003, 38, 1–6. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Steigenberger, P.; Boehm, J.; Tesmer, V. Comparison of GMF/GPT with VMF1/ECMWF and Implications for Atmospheric Loading. J. Geod. 2009, 83, 943–951. [Google Scholar] [CrossRef]
- Smith, E.K.; Weintraub, S. The Constants in the Equation for Atmospheric Refractive Index at Radio Frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V. Tracking Tropospheric Radio Occultation Signals from Low Earth Orbit. Radio Sci. 2001, 36, 483–498. [Google Scholar] [CrossRef]
- Schreiner, W.S.; Weiss, J.P.; Anthes, R.A.; Braun, J.; Chu, V.; Fong, J.; Hunt, D.; Kuo, Y.-H.; Meehan, T.; Serafino, W.; et al. COSMIC-2 Radio Occultation Constellation: First Results. Geophys. Res. Lett. 2020, 47, e2019GL086841. [Google Scholar] [CrossRef]
- Anthes, R.; Sjoberg, J.; Feng, X.; Syndergaard, S. Comparison of COSMIC and COSMIC-2 Radio Occultation Refractivity and Bending Angle Uncertainties in August 2006 and 2021. Atmosphere 2022, 13, 790. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Comparing the ‘Big 4’-A User’s View on GNSS Performance. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 407–418. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).