From Spaceborne LiDAR to Local Calibration: GEDI’s Role in Forest Biomass Estimation
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Reference AGBD Data
2.2.2. GEDI Data
2.3. GEDI-Derived AGBD Modeling
2.3.1. Random Forest
2.3.2. Geographically Weighted Regression
2.3.3. Multiscale Geographically Weighted Regression
2.4. Model Evaluation
3. Results
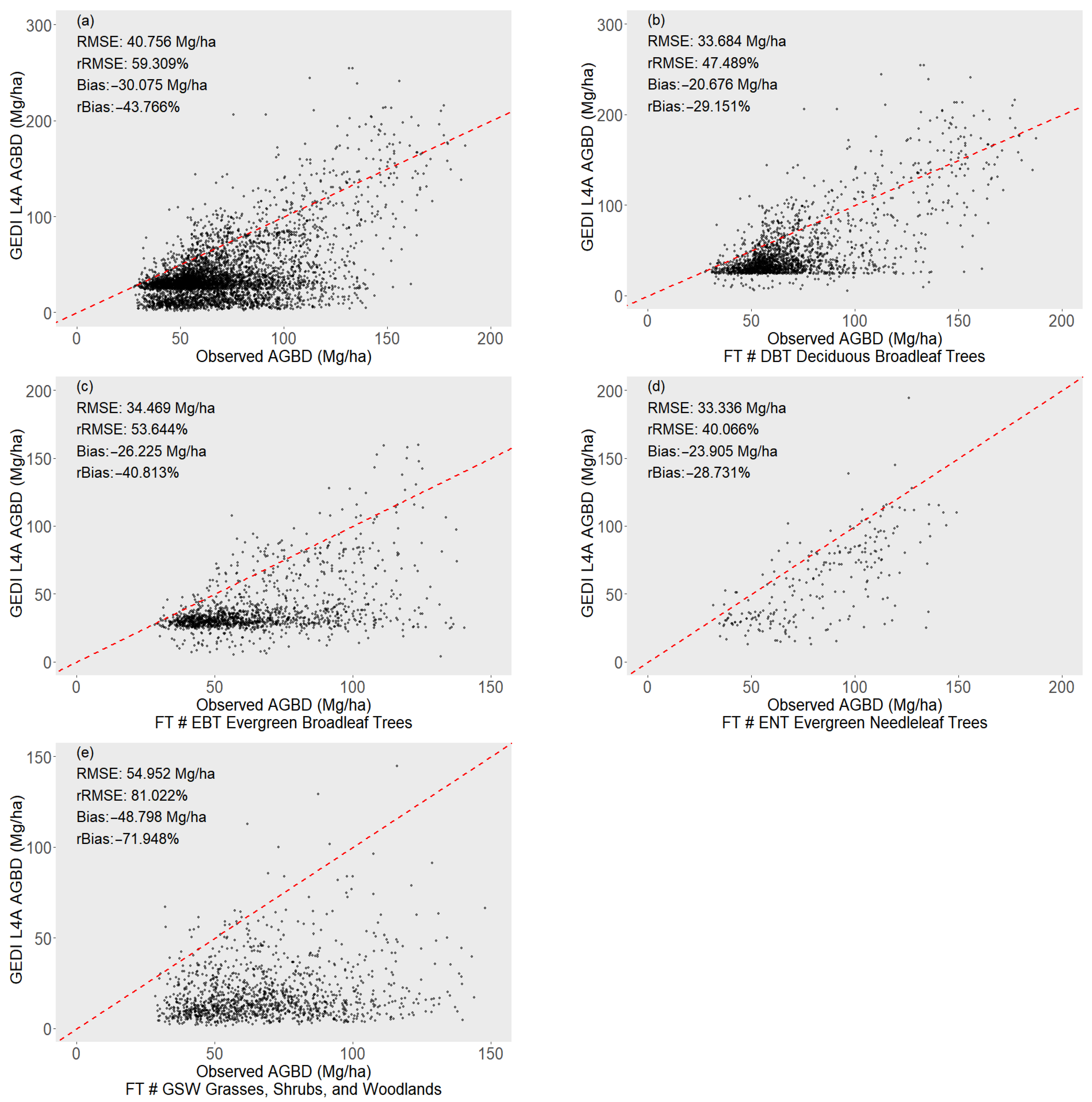
3.1. Validation of GEDI L4A Product
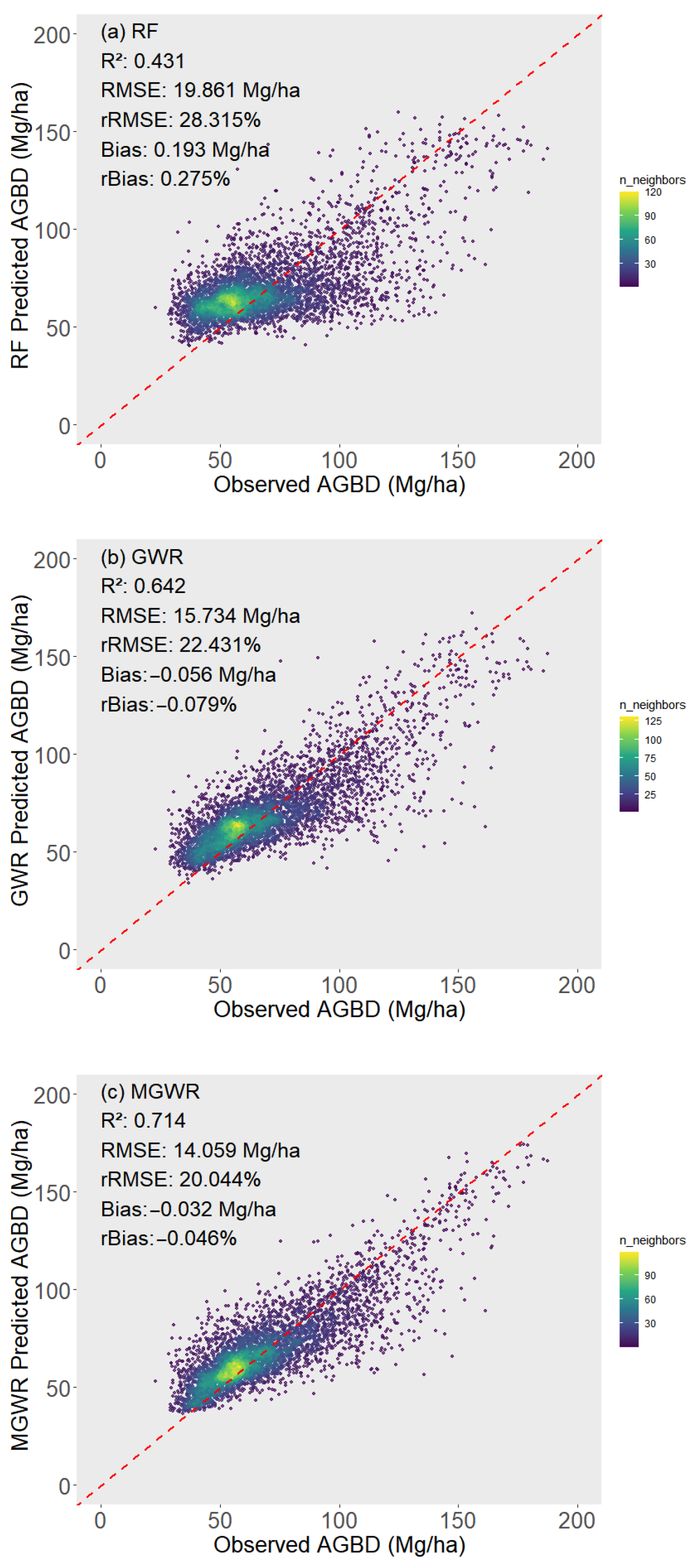
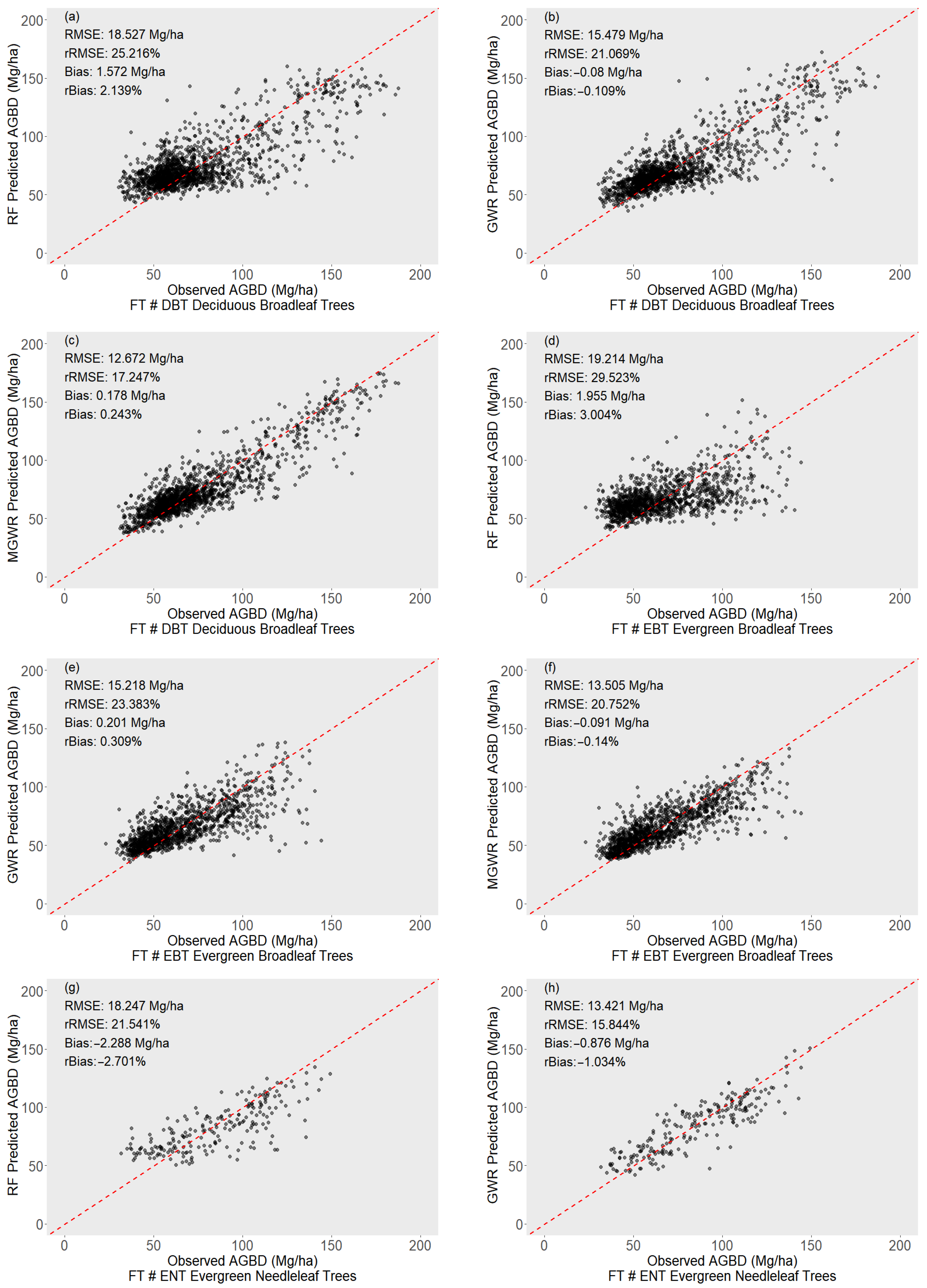
3.2. Performance of GEDI-Derived AGBD Models
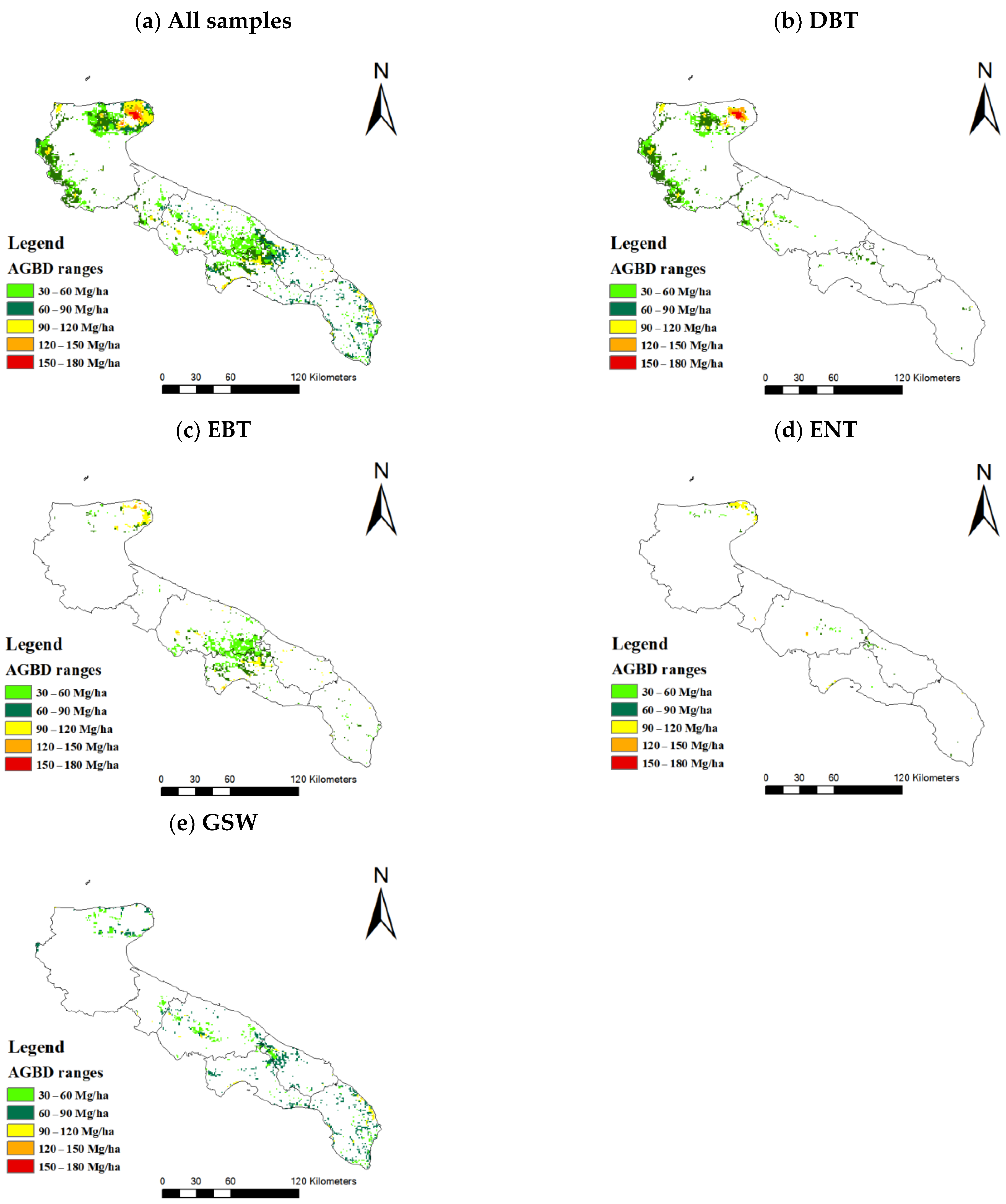
3.3. Mapping of AGBD Estimated from MGWR Model
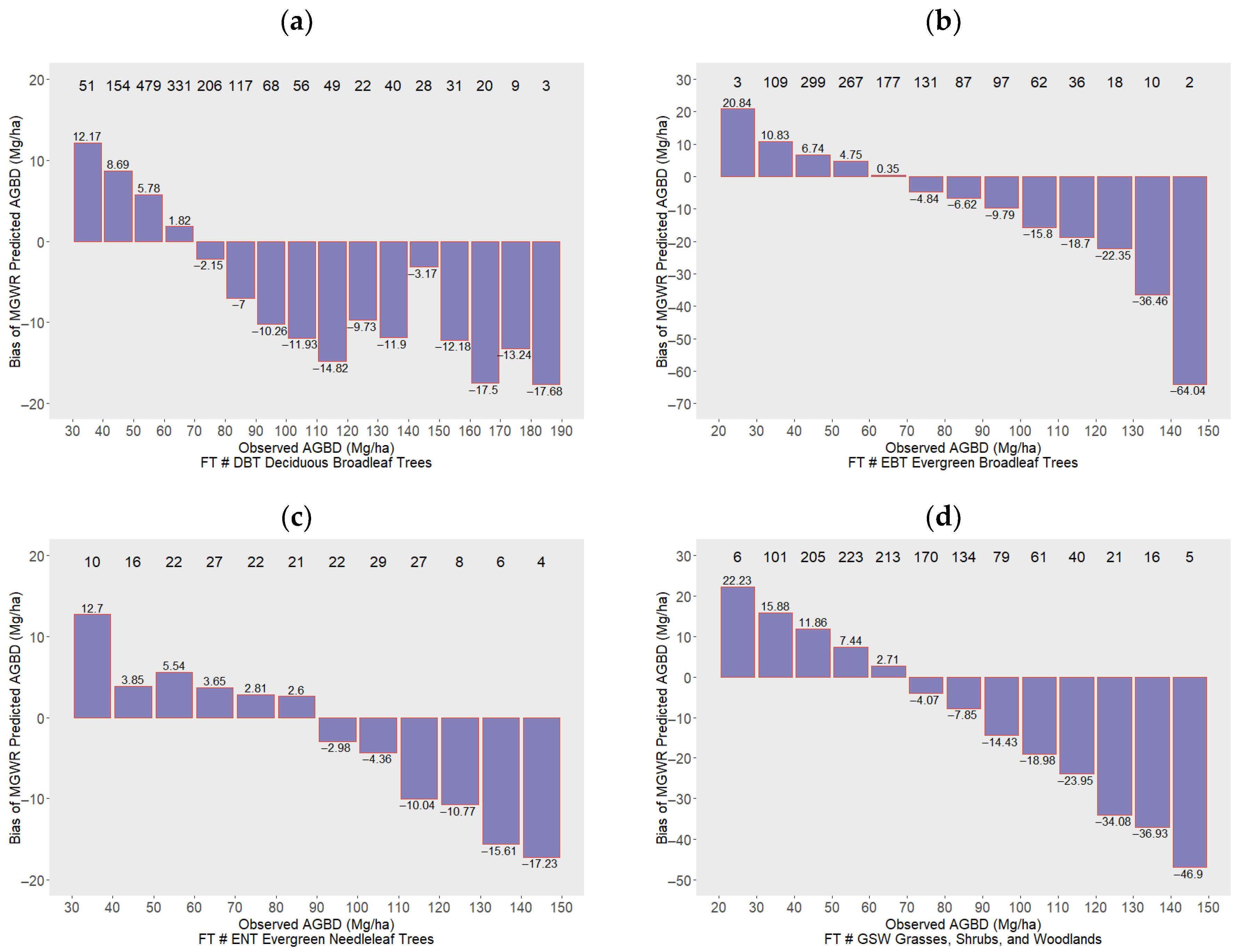
3.4. MGWR Model Bias Distribution Across Different AGBD Ranges
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Moreno-Fernández, D.; Díaz-Pinés, E.; Barbeito, I.; Sánchez-González, M.; Montes, F.; Rubio, A.; Cañellas, I. Temporal Carbon Dynamics over the Rotation Period of Two Alternative Management Systems in Mediterranean Mountain Scots Pine Forests. For. Ecol. Manag. 2015, 348, 186–195. [Google Scholar] [CrossRef]
- Sha, Z.; Bai, Y.; Li, R.; Lan, H.; Zhang, X.; Li, J.; Liu, X.; Chang, S.; Xie, Y. The Global Carbon Sink Potential of Terrestrial Vegetation Can Be Increased Substantially by Optimal Land Management. Commun. Earth Env. 2022, 3, 8. [Google Scholar] [CrossRef]
- Galidaki, G.; Zianis, D.; Gitas, I.; Radoglou, K.; Karathanassi, V.; Tsakiri–Strati, M.; Woodhouse, I.; Mallinis, G. Vegetation Biomass Estimation with Remote Sensing: Focus on Forest and Other Wooded Land over the Mediterranean Ecosystem. Int. J. Remote Sens. 2017, 38, 1940–1966. [Google Scholar] [CrossRef]
- Chirici, G.; Giannetti, F.; McRoberts, R.E.; Travaglini, D.; Pecchi, M.; Maselli, F.; Chiesi, M.; Corona, P. Wall-to-Wall Spatial Prediction of Growing Stock Volume Based on Italian National Forest Inventory Plots and Remotely Sensed Data. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101959. [Google Scholar] [CrossRef]
- Hu, T.; Su, Y.; Xue, B.; Liu, J.; Zhao, X.; Fang, J.; Guo, Q. Mapping Global Forest Aboveground Biomass with Spaceborne LiDAR, Optical Imagery, and Forest Inventory Data. Remote Sens. 2016, 8, 565. [Google Scholar] [CrossRef]
- Wang, P.; Tan, S.; Zhang, G.; Wang, S.; Wu, X. Remote Sensing Estimation of Forest Aboveground Biomass Based on Lasso-SVR. Forests 2022, 13, 1597. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Xi, X.; Pan, F.; Peng, D.; Zou, J.; Nie, S.; Qin, H. Fusion of Airborne LiDAR Data and Hyperspectral Imagery for Aboveground and Belowground Forest Biomass Estimation. Ecol. Indic. 2017, 73, 378–387. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A Survey of Remote Sensing-Based Aboveground Biomass Estimation Methods in Forest Ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, D. Improving Forest Aboveground Biomass Estimation Using Seasonal Landsat NDVI Time-Series. ISPRS J. Photogramm. Remote Sens. 2015, 102, 222–231. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Remote Sensing of Above-Ground Biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef]
- Shendryk, Y. Fusing GEDI with Earth Observation Data for Large Area Aboveground Biomass Mapping. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103108. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Chuvieco, E.; Danson, F.M. Estimating Biomass Carbon Stocks for a Mediterranean Forest in Central Spain Using LiDAR Height and Intensity Data. Remote Sens. Environ. 2010, 114, 816–830. [Google Scholar] [CrossRef]
- Dang, A.T.N.; Nandy, S.; Srinet, R.; Luong, N.V.; Ghosh, S.; Senthil Kumar, A. Forest Aboveground Biomass Estimation Using Machine Learning Regression Algorithm in Yok Don National Park, Vietnam. Ecol. Inform. 2019, 50, 24–32. [Google Scholar] [CrossRef]
- Jiang, F.; Kutia, M.; Ma, K.; Chen, S.; Long, J.; Sun, H. Estimating the Aboveground Biomass of Coniferous Forest in Northeast China Using Spectral Variables, Land Surface Temperature and Soil Moisture. Sci. Total Environ. 2021, 785, 147335. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Li, C.; Liu, Z. Forest Aboveground Biomass Estimation Using Landsat 8 and Sentinel-1A Data with Machine Learning Algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, N.; Wang, Y.; Li, M. A New Strategy for Improving the Accuracy of Forest Aboveground Biomass Estimates in an Alpine Region Based on Multi-Source Remote Sensing. GIScience Remote Sens. 2023, 60, 2163574. [Google Scholar] [CrossRef]
- Salazar Villegas, M.H.; Qasim, M.; Csaplovics, E.; González-Martinez, R.; Rodriguez-Buritica, S.; Ramos Abril, L.N.; Salazar Villegas, B. Examining the Potential of Sentinel Imagery and Ensemble Algorithms for Estimating Aboveground Biomass in a Tropical Dry Forest. Remote Sens. 2023, 15, 5086. [Google Scholar] [CrossRef]
- Ahmad, N.; Ullah, S.; Zhao, N.; Mumtaz, F.; Ali, A.; Ali, A.; Tariq, A.; Kareem, M.; Imran, A.B.; Khan, I.A.; et al. Comparative Analysis of Remote Sensing and Geo-Statistical Techniques to Quantify Forest Biomass. Forests 2023, 14, 379. [Google Scholar] [CrossRef]
- Arévalo, P.; Baccini, A.; Woodcock, C.E.; Olofsson, P.; Walker, W.S. Continuous Mapping of Aboveground Biomass Using Landsat Time Series. Remote Sens. Environ. 2023, 288, 113483. [Google Scholar] [CrossRef]
- Huang, T.; Ou, G.; Wu, Y.; Zhang, X.; Liu, Z.; Xu, H.; Xu, X.; Wang, Z.; Xu, C. Estimating the Aboveground Biomass of Various Forest Types with High Heterogeneity at the Provincial Scale Based on Multi-Source Data. Remote Sens. 2023, 15, 3550. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Ndikumana, E.; Vieilledent, G.; McKey, D.; Baghdadi, N. Potential Value of Combining ALOS PALSAR and Landsat-Derived Tree Cover Data for Forest Biomass Retrieval in Madagascar. Remote Sens. Environ. 2018, 213, 206–214. [Google Scholar] [CrossRef]
- Kumar, S.; Garg, R.D.; Govil, H.; Kushwaha, S.P.S. PolSAR-Decomposition-Based Extended Water Cloud Modeling for Forest Aboveground Biomass Estimation. Remote Sens. 2019, 11, 2287. [Google Scholar] [CrossRef]
- Sadeghi, Y.; St-Onge, B.; Leblon, B.; Prieur, J.-F.; Simard, M. Mapping Boreal Forest Biomass from a SRTM and TanDEM-X Based on Canopy Height Model and Landsat Spectral Indices. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 202–213. [Google Scholar] [CrossRef]
- Domingues, G.F.; Soares, V.P.; Leite, H.G.; Ferraz, A.S.; Ribeiro, C.A.A.S.; Lorenzon, A.S.; Marcatti, G.E.; Teixeira, T.R.; De Castro, N.L.M.; Mota, P.H.S.; et al. Artificial Neural Networks on Integrated Multispectral and SAR Data for High-Performance Prediction of Eucalyptus Biomass. Comput. Electron. Agric. 2020, 168, 105089. [Google Scholar] [CrossRef]
- Bouvet, A.; Mermoz, S.; Le Toan, T.; Villard, L.; Mathieu, R.; Naidoo, L.; Asner, G.P. An Above-Ground Biomass Map of African Savannahs and Woodlands at 25 m Resolution Derived from ALOS PALSAR. Remote Sens. Environ. 2018, 206, 156–173. [Google Scholar] [CrossRef]
- Schlund, M.; Davidson, M. Aboveground Forest Biomass Estimation Combining L- and P-Band SAR Acquisitions. Remote Sens. 2018, 10, 1151. [Google Scholar] [CrossRef]
- Qian, C.; Qiang, H.; Wang, F.; Li, M. Estimation of Forest Aboveground Biomass in Karst Areas Using Multi-Source Remote Sensing Data and the K-DBN Algorithm. Remote Sens. 2021, 13, 5030. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest Aboveground Biomass Estimation in Zhejiang Province Using the Integration of Landsat TM and ALOS PALSAR Data. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 1–15. [Google Scholar] [CrossRef]
- Yan, Y.; Lei, J.; Huang, Y. Forest Aboveground Biomass Estimation Based on Unmanned Aerial Vehicle–Light Detection and Ranging and Machine Learning. Sensors 2024, 24, 7071. [Google Scholar] [CrossRef]
- Brovkina, O.; Novotny, J.; Cienciala, E.; Zemek, F.; Russ, R. Mapping Forest Aboveground Biomass Using Airborne Hyperspectral and LiDAR Data in the Mountainous Conditions of Central Europe. Ecol. Eng. 2017, 100, 219–230. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Jacquemoud, S.; Gonçalves, G.; Silva, C.; Soares, P.; Tomé, M.; Pereira, L. Airborne Lidar Estimation of Aboveground Forest Biomass in the Absence of Field Inventory. Remote Sens. 2016, 8, 653. [Google Scholar] [CrossRef]
- Ene, L.T.; Næsset, E.; Gobakken, T.; Mauya, E.W.; Bollandsås, O.M.; Gregoire, T.G.; Ståhl, G.; Zahabu, E. Large-Scale Estimation of Aboveground Biomass in Miombo Woodlands Using Airborne Laser Scanning and National Forest Inventory Data. Remote Sens. Environ. 2016, 186, 626–636. [Google Scholar] [CrossRef]
- Ene, L.T.; Gobakken, T.; Andersen, H.-E.; Næsset, E.; Cook, B.D.; Morton, D.C.; Babcock, C.; Nelson, R. Large-Area Hybrid Estimation of Aboveground Biomass in Interior Alaska Using Airborne Laser Scanning Data. Remote Sens. Environ. 2018, 204, 741–755. [Google Scholar] [CrossRef]
- Chen, Q.; McRoberts, R.E.; Wang, C.; Radtke, P.J. Forest Aboveground Biomass Mapping and Estimation across Multiple Spatial Scales Using Model-Based Inference. Remote Sens. Environ. 2016, 184, 350–360. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Puletti, N.; Chen, Q.; Corona, P.; Papale, D.; Valentini, R. Above Ground Biomass and Tree Species Richness Estimation with Airborne Lidar in Tropical Ghana Forests. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 371–379. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Sun, Y.; Ruan, H.; Wang, G.; Dai, J.; She, G. Estimating Canopy Structure and Biomass in Bamboo Forests Using Airborne LiDAR Data. ISPRS J. Photogramm. Remote Sens. 2019, 148, 114–129. [Google Scholar] [CrossRef]
- Almeida, C.T.D.; Galvão, L.S.; Aragão, L.E.D.O.C.E.; Ometto, J.P.H.B.; Jacon, A.D.; Pereira, F.R.D.S.; Sato, L.Y.; Lopes, A.P.; Graça, P.M.L.D.A.; Silva, C.V.D.J.; et al. Combining LiDAR and Hyperspectral Data for Aboveground Biomass Modeling in the Brazilian Amazon Using Different Regression Algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- Rodríguez-Veiga, P.; Wheeler, J.; Louis, V.; Tansey, K.; Balzter, H. Quantifying Forest Biomass Carbon Stocks from Space. Curr. For. Rep. 2017, 3, 1–18. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-Resolution Laser Ranging of the Earth’s Forests and Topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Duncanson, L.; Neuenschwander, A.; Hancock, S.; Thomas, N.; Fatoyinbo, T.; Simard, M.; Silva, C.A.; Armston, J.; Luthcke, S.B.; Hofton, M.; et al. Biomass Estimation from Simulated GEDI, ICESat-2 and NISAR across Environmental Gradients in Sonoma County, California. Remote Sens. Environ. 2020, 242, 111779. [Google Scholar] [CrossRef]
- Kellner, J.R.; Armston, J.; Duncanson, L. Algorithm Theoretical Basis Document for GEDI Footprint Aboveground Biomass Density. Earth Space Sci. 2023, 10, e2022EA002516. [Google Scholar] [CrossRef]
- Duncanson, L.; Kellner, J.R.; Armston, J.; Dubayah, R.; Minor, D.M.; Hancock, S.; Healey, S.P.; Patterson, P.L.; Saarela, S.; Marselis, S.; et al. Aboveground Biomass Density Models for NASA’s Global Ecosystem Dynamics Investigation (GEDI) Lidar Mission. Remote Sens. Environ. 2022, 270, 112845. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G.; Mura, M.; Zolli, C.; Maselli, F.; Chiesi, M.; Bottai, L.; Chirici, G. The Potential of Multifrequency SAR Images for Estimating Forest Biomass in Mediterranean Areas. Remote Sens. Environ. 2017, 200, 63–73. [Google Scholar] [CrossRef]
- Li, X.; Wessels, K.; Armston, J.; Duncanson, L.; Urbazaev, M.; Naidoo, L.; Mathieu, R.; Main, R. Evaluation of GEDI Footprint Level Biomass Models in Southern African Savannas Using Airborne LiDAR and Field Measurements. Sci. Remote Sens. 2024, 10, 100161. [Google Scholar] [CrossRef]
- Mitsuhashi, R.; Sawada, Y.; Tsutsui, K.; Hirayama, H.; Imai, T.; Sumita, T.; Kajiwara, K.; Honda, Y. Re-Estimating GEDI Ground Elevation Using Deep Learning: Impacts on Canopy Height and Aboveground Biomass. Remote Sens. 2024, 16, 4597. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Wang, C.; Zhang, S.; Wang, R.; Wang, S.; Duan, J. Co-Kriging-Guided Interpolation for Mapping Forest Aboveground Biomass by Integrating Global Ecosystem Dynamics Investigation and Sentinel-2 Data. Remote Sens. 2024, 16, 2913. [Google Scholar] [CrossRef]
- Xu, L.; Yu, J.; Shu, Q.; Luo, S.; Zhou, W.; Duan, D. Forest Aboveground Biomass Estimation Based on Spaceborne LiDAR Combining Machine Learning Model and Geostatistical Method. Front. Plant Sci. 2024, 15, 1428268. [Google Scholar] [CrossRef]
- Dorado-Roda, I.; Pascual, A.; Godinho, S.; Silva, C.; Botequim, B.; Rodríguez-Gonzálvez, P.; González-Ferreiro, E.; Guerra-Hernández, J. Assessing the Accuracy of GEDI Data for Canopy Height and Aboveground Biomass Estimates in Mediterranean Forests. Remote Sens. 2021, 13, 2279. [Google Scholar] [CrossRef]
- Wu, L.; Du, J.; Liu, X.; Li, L.; Zhu, X.; Chen, X.; Gong, Y.; Li, Y. Comparative Analysis of Carbon Density Simulation Methods in Grassland Ecosystems: A Case Study from Gansu Province, China. Remote Sens. 2025, 17, 172. [Google Scholar] [CrossRef]
- Wang, J.; Du, H.; Li, X.; Mao, F.; Zhang, M.; Liu, E.; Ji, J.; Kang, F. Remote Sensing Estimation of Bamboo Forest Aboveground Biomass Based on Geographically Weighted Regression. Remote Sens. 2021, 13, 2962. [Google Scholar] [CrossRef]
- D’Este, M.; Elia, M.; Giannico, V.; Spano, G.; Lafortezza, R.; Sanesi, G. Machine Learning Techniques for Fine Dead Fuel Load Estimation Using Multi-Source Remote Sensing Data. Remote Sens. 2021, 13, 1658. [Google Scholar] [CrossRef]
- Burns, P.; Hakkenberg, C.R.; Goetz, S.J. Multi-Resolution Gridded Maps of Vegetation Structure from GEDI. Sci. Data 2024, 11, 881. [Google Scholar] [CrossRef]
- Simmavong, T.; Su, Y.; Deng, Y.; Wang, B.; Yao, Z.; Wu, J.; Sha, L.; Cao, M.; Lin, L. Forest Structure Predicts Aboveground Biomass Better than Community-Weighted Mean of Traits, Functional Diversity, Topography, and Soil in a Tropical Forest across Spatial Scales. For. Ecol. Manag. 2025, 578, 122457. [Google Scholar] [CrossRef]
- Fischer, R.; Knapp, N.; Bohn, F.; Shugart, H.H.; Huth, A. The Relevance of Forest Structure for Biomass and Productivity in Temperate Forests: New Perspectives for Remote Sensing. Surv. Geophys. 2019, 40, 709–734. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org (accessed on 20 February 2025).
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative Analysis of Modeling Algorithms for Forest Aboveground Biomass Estimation in a Subtropical Region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Spadoni, G.L.; Moris, J.V.; Vacchiano, G.; Elia, M.; Garbarino, M.; Sibona, E.; Ascoli, D. Active governance of agro-pastoral, forest and protected areas mitigates wildfire impacts in Italy. Sci. Total Environ. 2023, 890, 164281. [Google Scholar] [CrossRef]
- Zeng, N.; Ren, X.; He, H.; Zhang, L.; Zhao, D.; Ge, R.; Li, P.; Niu, Z. Estimating Grassland Aboveground Biomass on the Tibetan Plateau Using a Random Forest Algorithm. Ecol. Indic. 2019, 102, 479–487. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, Z.; Zhang, H.; Zhang, H.; Qiu, H. Aboveground Forest Biomass Estimation Using Tent Mapping Atom Search Optimized Backpropagation Neural Network with Landsat 8 and Sentinel-1A Data. Remote Sens. 2023, 15, 5653. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, W.; Ji, Y.; Marino, A.; Li, C.; Wang, L.; Zhao, H.; Wang, M. Estimation of Aboveground Biomass for Different Forest Types Using Data from Sentinel-1, Sentinel-2, ALOS PALSAR-2, and GEDI. Forests 2024, 15, 215. [Google Scholar] [CrossRef]
- Wang, N.; Sun, M.; Ye, J.; Wang, J.; Liu, Q.; Li, M. Spatial Downscaling of Forest Above-Ground Biomass Distribution Patterns Based on Landsat 8 OLI Images and a Multiscale Geographically Weighted Regression Algorithm. Forests 2023, 14, 526. [Google Scholar] [CrossRef]
- Giannico, V.; Garofalo, S.P.; Brillante, L.; Sciusco, P.; Elia, M.; Lopriore, G.; Camposeo, S.; Lafortezza, R.; Sanesi, G.; Vivaldi, G.A. Temporal Vine Water Status Modeling Through Machine Learning Ensemble Technique and Sentinel-2 Multispectral Images Under Semi-Arid Conditions. Remote Sens. 2024, 16, 4784. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Chen, L.; Ren, C.; Zhang, B.; Wang, Z.; Xi, Y. Estimation of Forest Above-Ground Biomass by Geographically Weighted Regression and Machine Learning with Sentinel Imagery. Forests 2018, 9, 582. [Google Scholar] [CrossRef]
- Propastin, P. Modifying Geographically Weighted Regression for Estimating Aboveground Biomass in Tropical Rainforests by Multispectral Remote Sensing Data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 82–90. [Google Scholar] [CrossRef]
- Shabrina, Z.; Buyuklieva, B.; Ng, M.K.M. Short-term rental platform in the urban tourism context: A geographically weighted regression (GWR) and a multiscale GWR (MGWR) approaches. Geogr. Anal. 2020, 53, 686–707. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale geographically weighted regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Liu, P.; Wu, C.; Chen, M.; Ye, X.; Peng, Y.; Li, S. A Spatiotemporal Analysis of the Effects of Urbanization’s Socio-Economic Factors on Landscape Patterns Considering Operational Scales. Sustainability 2020, 12, 2543. [Google Scholar] [CrossRef]
- Li, N.; Wu, H.; Ouyang, X. Localized Downscaling of Urban Land Surface Temperature—A Case Study in Beijing, China. Remote Sens. 2022, 14, 2390. [Google Scholar] [CrossRef]
- Wheeler, D.; Tiefelsdorf, M. Multicollinearity and Correlation among Local Regression Coefficients in Geographically Weighted Regression. J. Geogr. Syst. 2005, 7, 161–187. [Google Scholar] [CrossRef]
- Pascual, A.; Guerra-Hernández, J.; Armston, J.; Minor, D.M.; Duncanson, L.I.; May, P.B.; Kellner, J.R.; Dubayah, R. Assessing the Performance of NASA’s GEDI L4A Footprint Aboveground Biomass Density Models Using National Forest Inventory and Airborne Laser Scanning Data in Mediterranean Forest Ecosystems. For. Ecol. Manag. 2023, 538, 120975. [Google Scholar] [CrossRef]
- Rodda, S.R.; Nidamanuri, R.R.; Fararoda, R.; Mayamanikandan, T.; Rajashekar, G. Evaluation of Height Metrics and Above-Ground Biomass Density from GEDI and ICESat-2 Over Indian Tropical Dry Forests Using Airborne LiDAR Data. J. Indian. Soc. Remote Sens. 2024, 52, 841–856. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Kato, T.; Hayashi, M.; Fu, J.; Hiroshima, T. Accuracy Assessment of GEDI Terrain Elevation, Canopy Height, and Aboveground Biomass Density Estimates in Japanese Artificial Forests. Sci. Remote Sens. 2024, 10, 100144. [Google Scholar] [CrossRef]
- Sun, M.; Cui, L.; Park, J.; García, M.; Zhou, Y.; Silva, C.A.; He, L.; Zhang, H.; Zhao, K. Evaluation of NASA’s GEDI Lidar Observations for Estimating Biomass in Temperate and Tropical Forests. Forests 2022, 13, 1686. [Google Scholar] [CrossRef]
- Xu, L.; Shu, Q.; Fu, H.; Zhou, W.; Luo, S.; Gao, Y.; Yu, J.; Guo, C.; Yang, Z.; Xiao, J.; et al. Estimation of Quercus Biomass in Shangri-La Based on GEDI Spaceborne Lidar Data. Forests 2023, 14, 876. [Google Scholar] [CrossRef]
- Nikparvar, B.; Thill, J.-C. Machine Learning of Spatial Data. IJGI 2021, 10, 600. [Google Scholar] [CrossRef]
- Indirabai, I.; Nilsson, M. Estimation of above Ground Biomass in Tropical Heterogeneous Forests in India Using GEDI. Ecol. Inform. 2024, 82, 102712. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining Spectral Reflectance Saturation in Landsat Imagery and Corresponding Solutions to Improve Forest Aboveground Biomass Estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef]
- Mutanga, O.; Masenyama, A.; Sibanda, M. Spectral Saturation in the Remote Sensing of High-Density Vegetation Traits: A Systematic Review of Progress, Challenges, and Prospects. ISPRS J. Photogramm. Remote Sens. 2023, 198, 297–309. [Google Scholar] [CrossRef]
- Du, C.; Fan, W.; Ma, Y.; Jin, H.-I.; Zhen, Z. The Effect of Synergistic Approaches of Features and Ensemble Learning Algorithms on Aboveground Biomass Estimation of Natural Secondary Forests Based on ALS and Landsat 8. Sensors 2021, 21, 5974. [Google Scholar] [CrossRef] [PubMed]

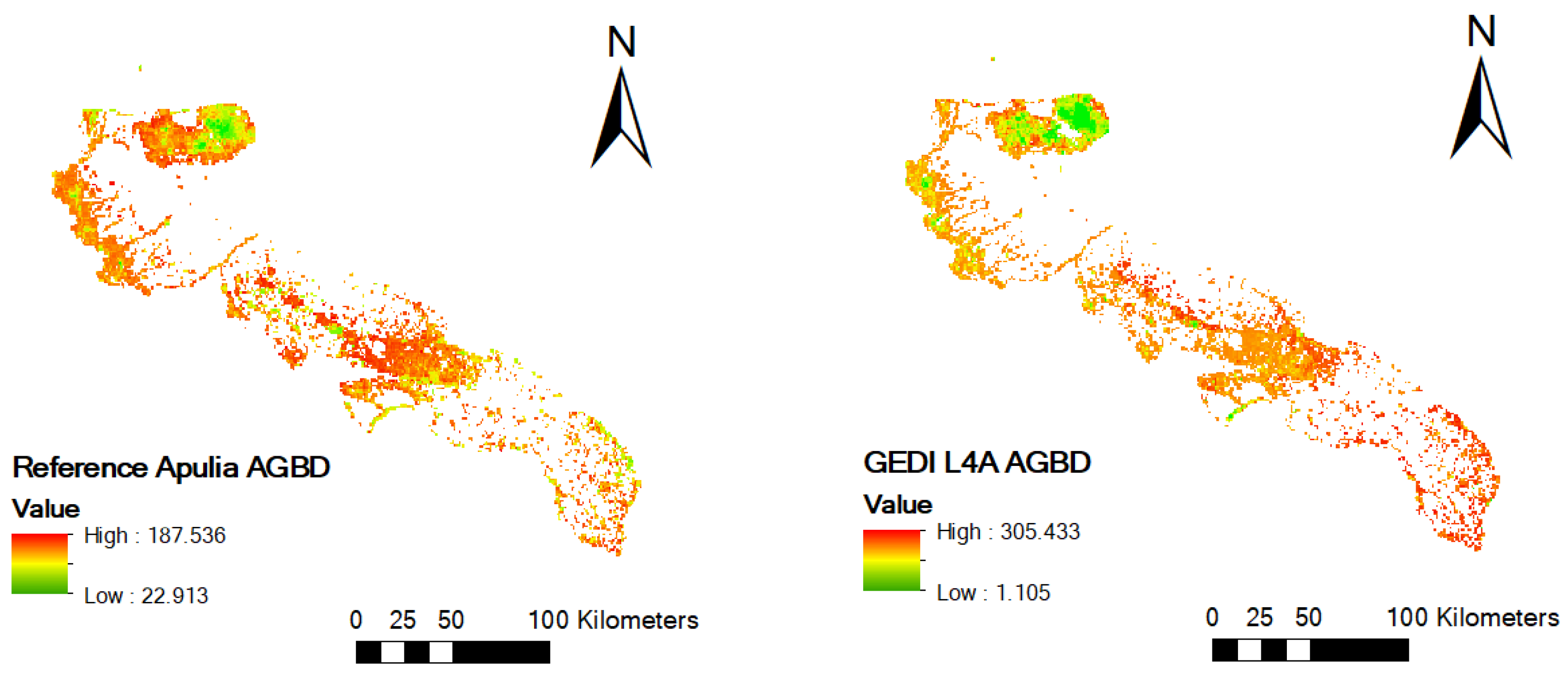

| GEDI Metric | Description |
|---|---|
| RH metrics (meters above the ground) | Relative height at percentile of returned energy, including RH50 and RH98. RH98 represents vegetation canopy, and RH50 provides information on the heights of subcanopy strata. |
| PAI (m2 m−2) | GEDI total plant area index that incorporates all canopy structural elements (e.g., branch and trunk) in addition to leaves. It is the indicator of the density of the canopy. |
| FHD (unitless) | Foliage height diversity (FHD), calculated from 1 m vertical bins in the foliage profile, normalized by the total plant area (PAI) index. It is a canopy structural index that describes the vertical heterogeneity of the foliage profile. A high FHD value means a complex forest structure. |
| Sensitivity (unitless) | Maximum canopy cover that can be penetrated all the way to the ground considering the SNR (signal-to-noise ratio) of the waveform. Higher sensitivity allows the laser to penetrate a denser canopy. |
| Cover (unitless) | Total canopy cover, defined as the percentage of the ground covered by the vertical projection of canopy material. It is a biophysical parameter that describes the spatially aggregated geometric properties of vegetation. |
| R2 | RMSE | rRMSE | Bias | rBias | |
|---|---|---|---|---|---|
| GEDI L4A | 40.756 | 59.309% | −30.075 | −43.766% | |
| RF | 0.431 | 19.861 | 28.315% | 0.193 | 0.275% |
| GWR | 0.674 | 15.024 | 21.419% | 0.078 | 0.111% |
| MGWR | 0.719 | 13.934 | 19.866% | −0.001 | −0.002% |
| PFT | RMSE | rRMSE (%) | Bias | rBias (%) | |
|---|---|---|---|---|---|
| Deciduous Broadleaf Trees (DBTs) | GEDI L4A | 33.684 | 47.489% | −20.676 | −29.151% |
| RF | 18.869 | 25.683% | 1.765 | 2.402% | |
| GWR | 15.479 | 21.069% | −0.080 | −0.109% | |
| MGWR | 12.672 | 17.247% | 0.178 | 0.243% | |
| Evergreen Broadleaf Trees (EBTs) | GEDI L4A | 34.469 | 53.644% | −26.225 | −40.813% |
| RF | 19.493 | 29.951% | 2.135 | 3.280% | |
| GWR | 15.218 | 23.383% | 0.201 | 0.309% | |
| MGWR | 13.505 | 20.752% | −0.091 | −0.140% | |
| Evergreen Needleleaf Trees (ENTs) | GEDI L4A | 33.336 | 40.066% | −23.905 | −28.731% |
| RF | 18.791 | 22.183% | −2.313 | −2.730% | |
| GWR | 13.421 | 15.844% | −0.876 | −1.034% | |
| MGWR | 11.976 | 14.138% | −0.871 | −1.028% | |
| Grasses, Shrubs, and Woodlands (GSWs) | GEDI L4A | 54.952 | 81.022% | −48.798 | −71.948% |
| RF | 22.537 | 32.899% | −3.171 | −4.629% | |
| GWR | 16.897 | 24.666% | −0.148 | −0.216% | |
| MGWR | 16.455 | 24.021% | −0.106 | −0.155% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, D.; Elia, M.; Cappelluti, O.; Huang, H.; Lafortezza, R.; Sanesi, G.; Giannico, V. From Spaceborne LiDAR to Local Calibration: GEDI’s Role in Forest Biomass Estimation. Remote Sens. 2025, 17, 2849. https://doi.org/10.3390/rs17162849
Lin D, Elia M, Cappelluti O, Huang H, Lafortezza R, Sanesi G, Giannico V. From Spaceborne LiDAR to Local Calibration: GEDI’s Role in Forest Biomass Estimation. Remote Sensing. 2025; 17(16):2849. https://doi.org/10.3390/rs17162849
Chicago/Turabian StyleLin, Di, Mario Elia, Onofrio Cappelluti, Huaguo Huang, Raffaele Lafortezza, Giovanni Sanesi, and Vincenzo Giannico. 2025. "From Spaceborne LiDAR to Local Calibration: GEDI’s Role in Forest Biomass Estimation" Remote Sensing 17, no. 16: 2849. https://doi.org/10.3390/rs17162849
APA StyleLin, D., Elia, M., Cappelluti, O., Huang, H., Lafortezza, R., Sanesi, G., & Giannico, V. (2025). From Spaceborne LiDAR to Local Calibration: GEDI’s Role in Forest Biomass Estimation. Remote Sensing, 17(16), 2849. https://doi.org/10.3390/rs17162849











