UAV-LiDAR-Based Study on AGB Response to Stand Structure and Its Estimation in Cunninghamia Lanceolata Plantations
Abstract
1. Introduction
2. Materials and Methods
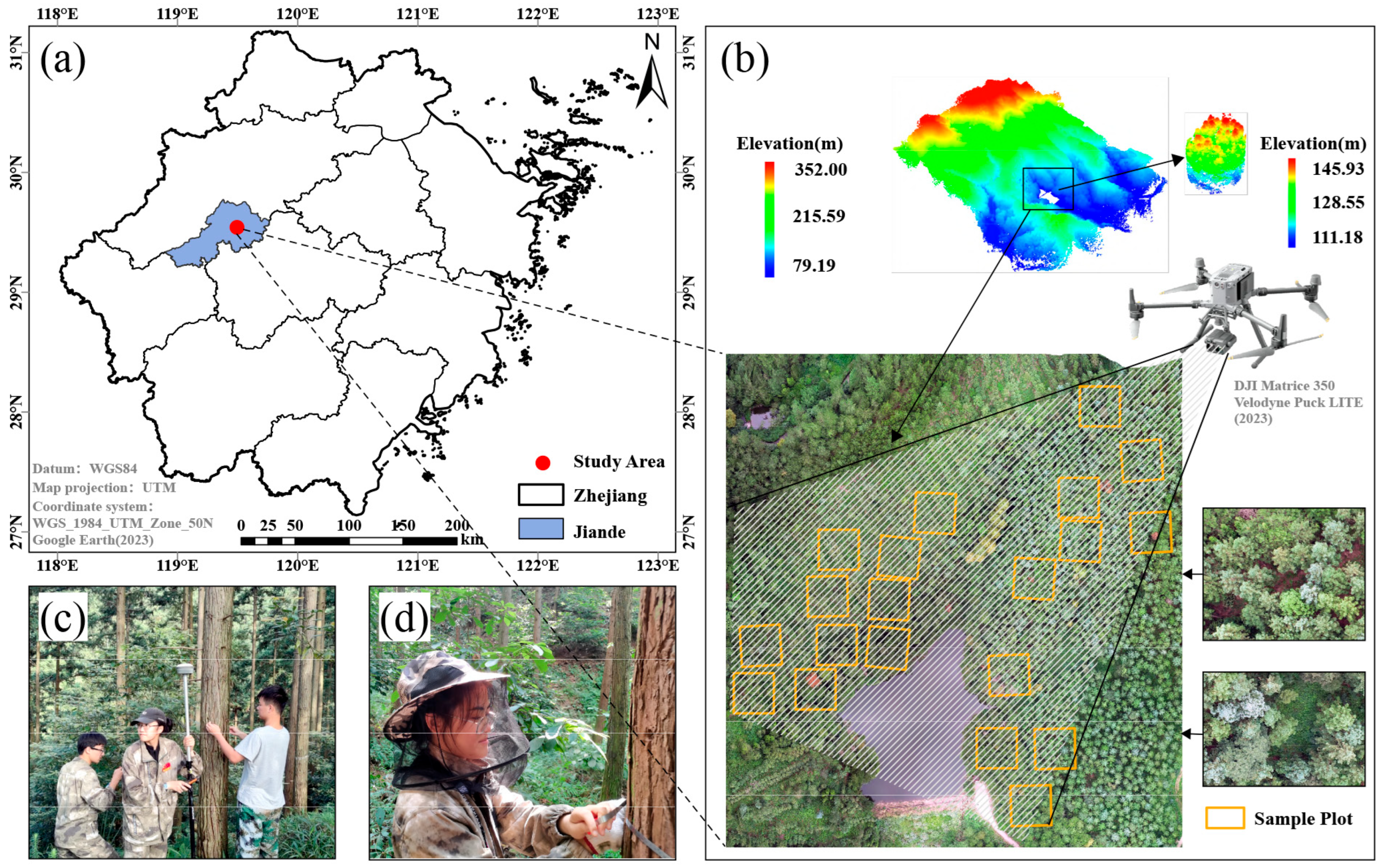
2.1. Overview of the Study Area
2.2. Data Acquisition and Processing
2.2.1. UAV-LiDAR Data
2.2.2. Ground Survey Data
2.2.3. LiDAR Data Matching with Field Data
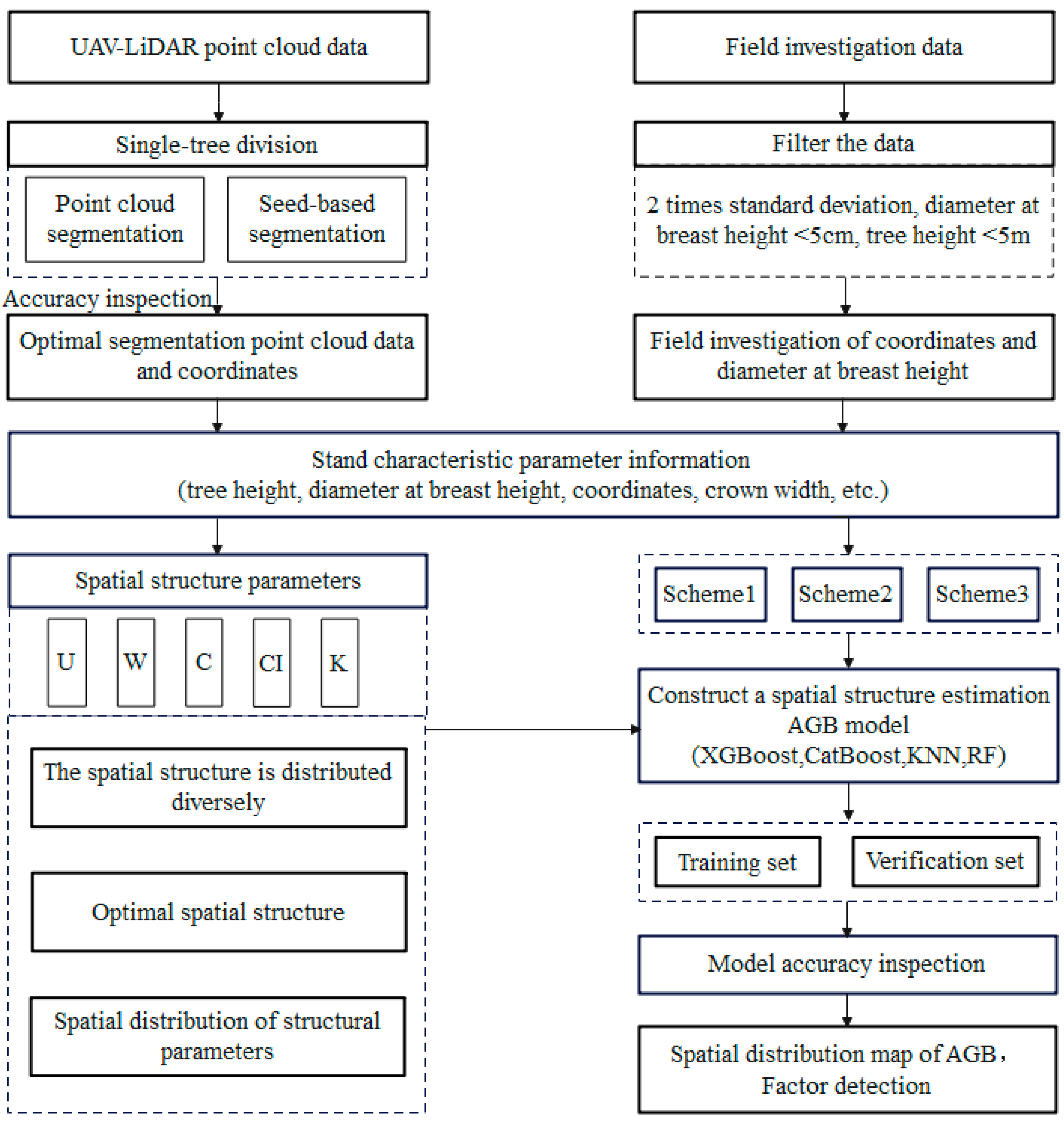
2.3. Technical Roadmap in the Paper
2.4. Segmentation and Evaluation of UAV Lidar Single Woods
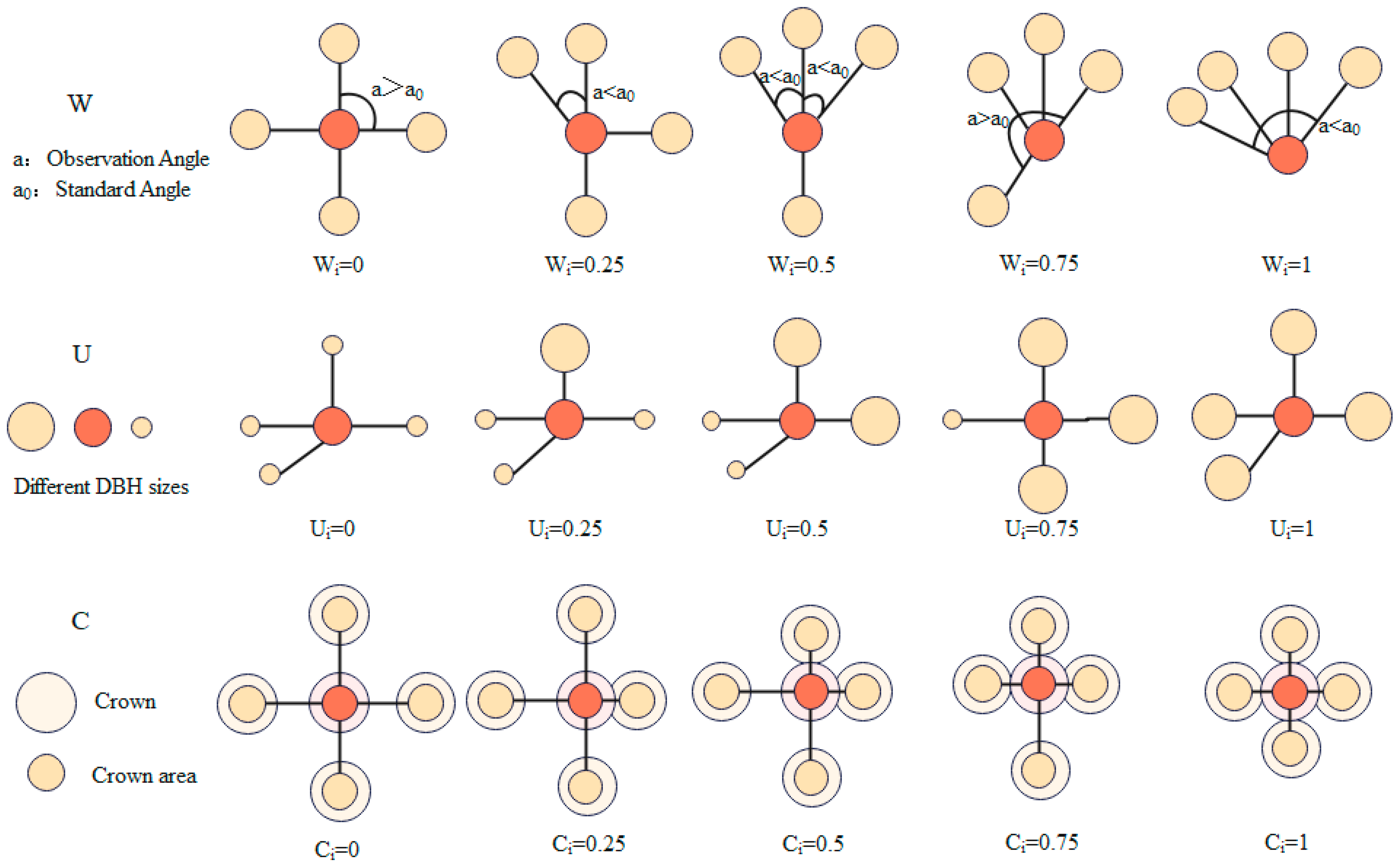
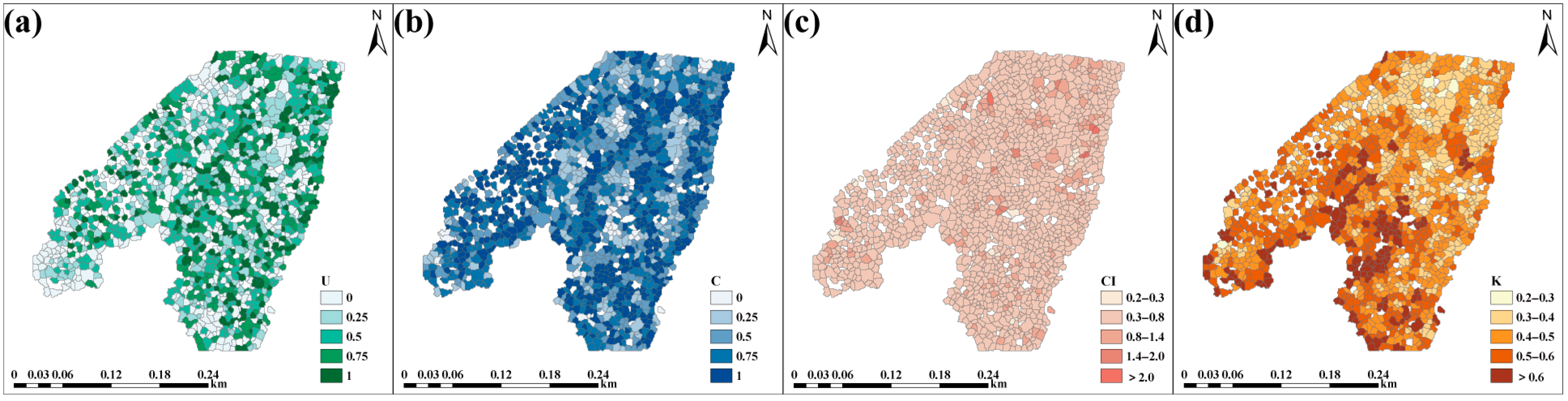
2.5. Methods for Calculating Stand Spatial Structure Parameters
2.6. Calculation of AGB for Single Wood in Ground Sample Plots
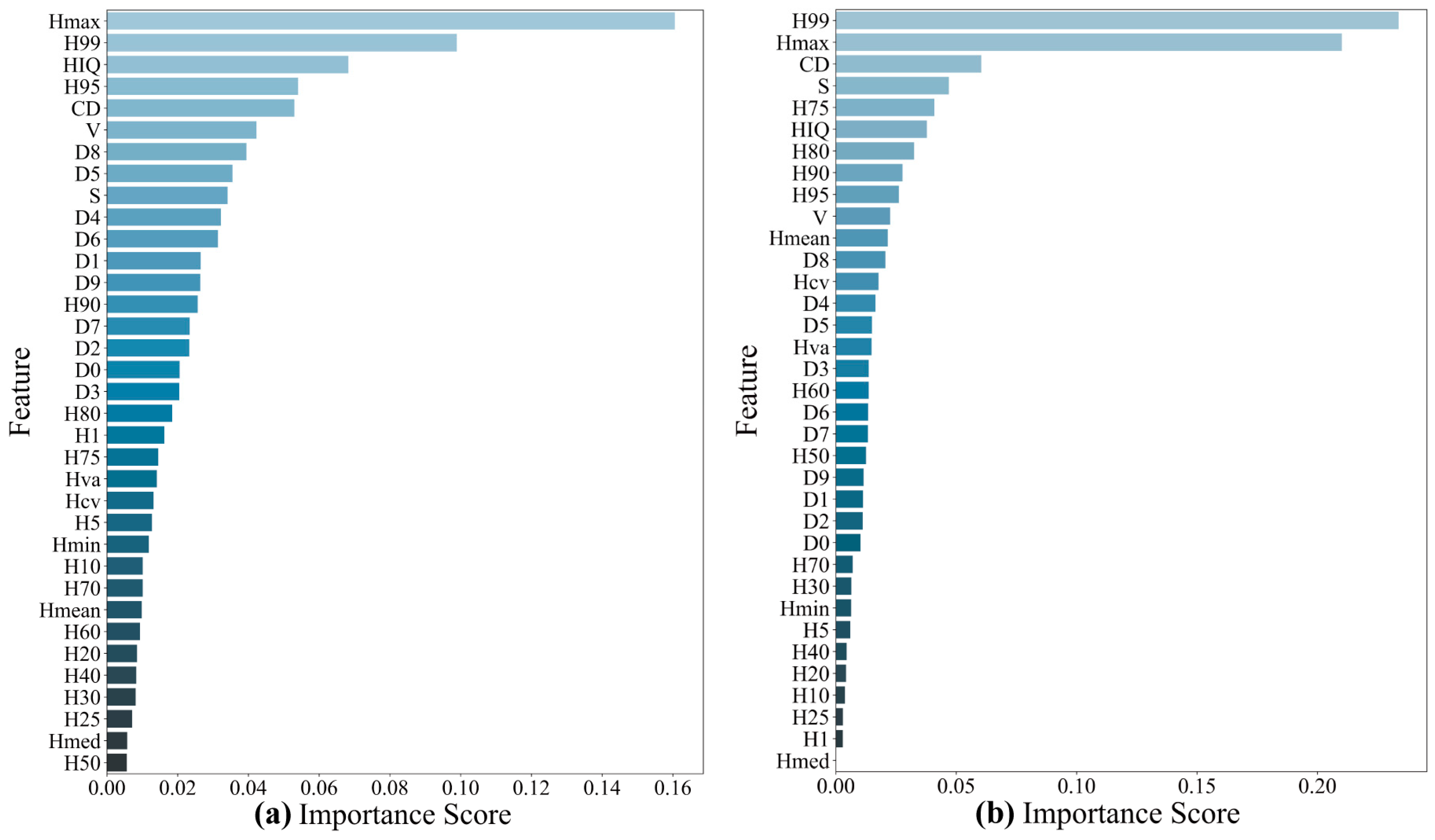
2.7. Extraction of LiDAR-Derived Feature Variables
2.8. AGB Estimation Model Schemes and Evaluation
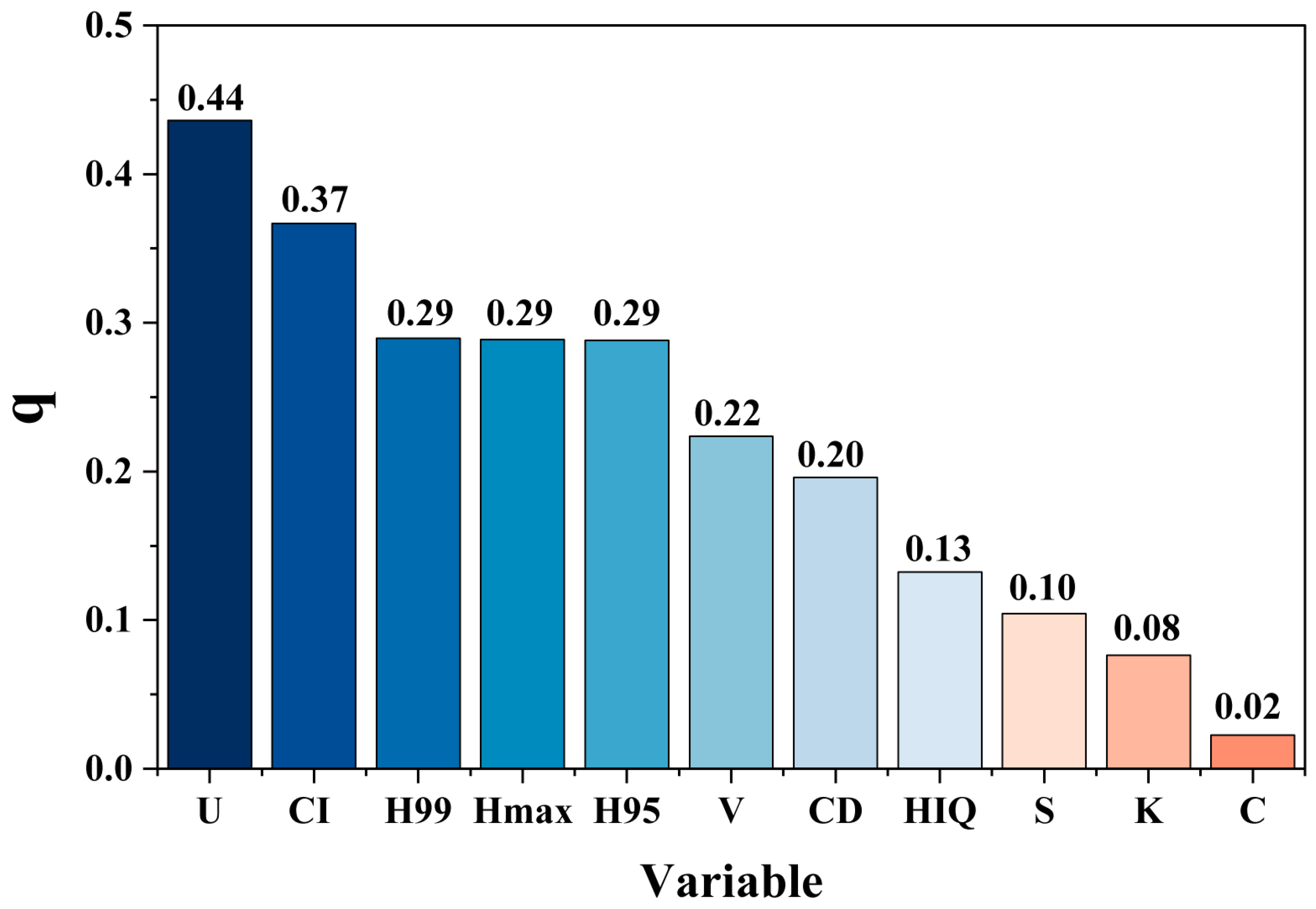
2.9. Geographical Detector Factor Analysis
3. Results
3.1. Individual Tree Segmentation Based on UAV-LiDAR
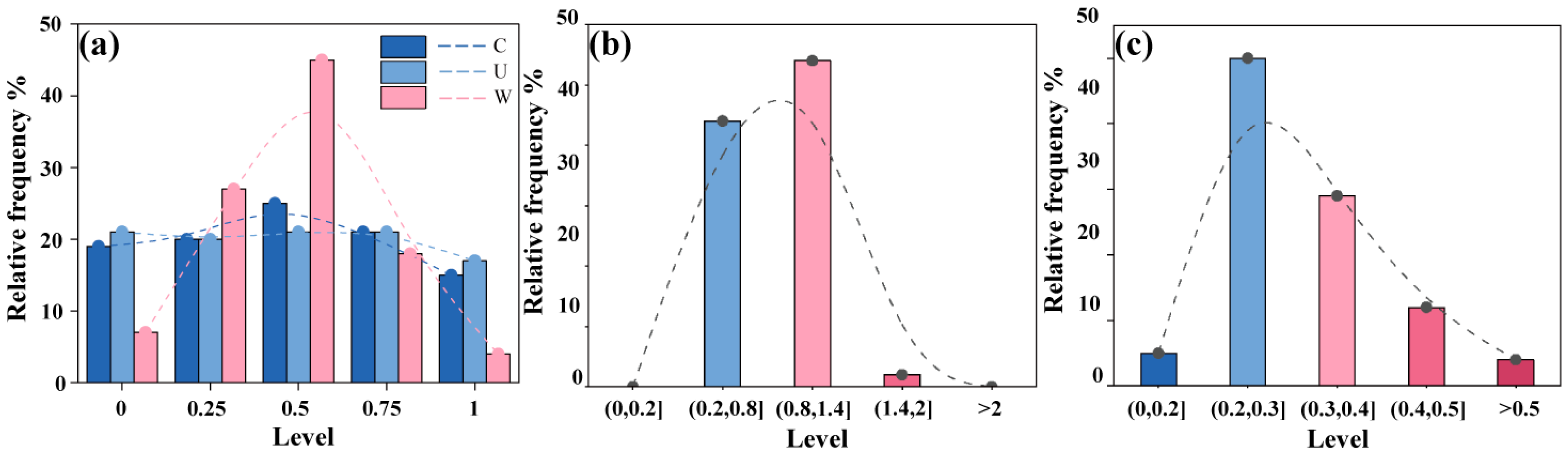
3.2. Multivariate Spatial Distribution Characteristics of Chinese Fir Forest Structure
3.2.1. Univariate Distribution
3.2.2. Bivariate Distribution
3.2.3. Trivariate Distribution
3.3. Correlation Analysis Between Stand Structure and AGB
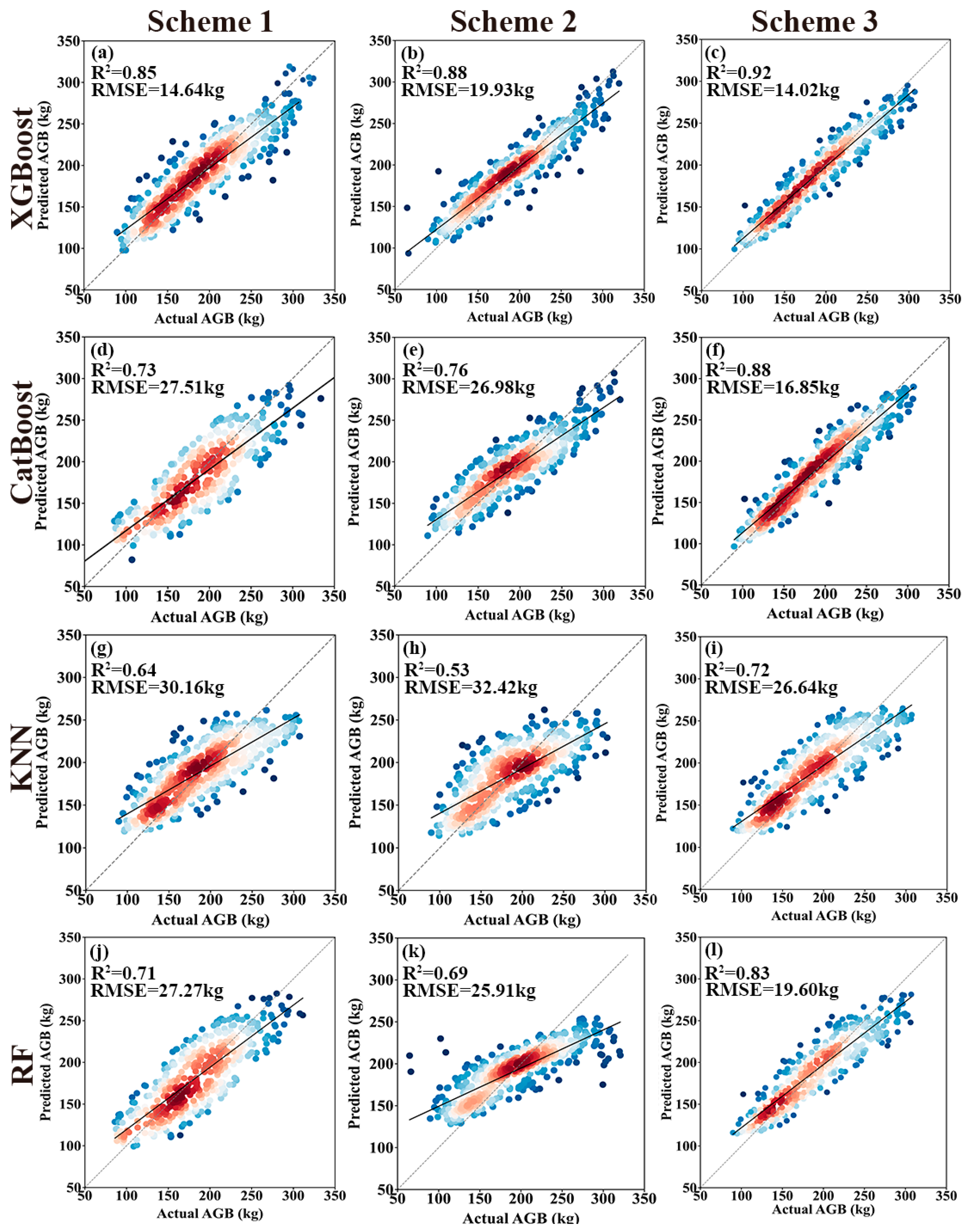
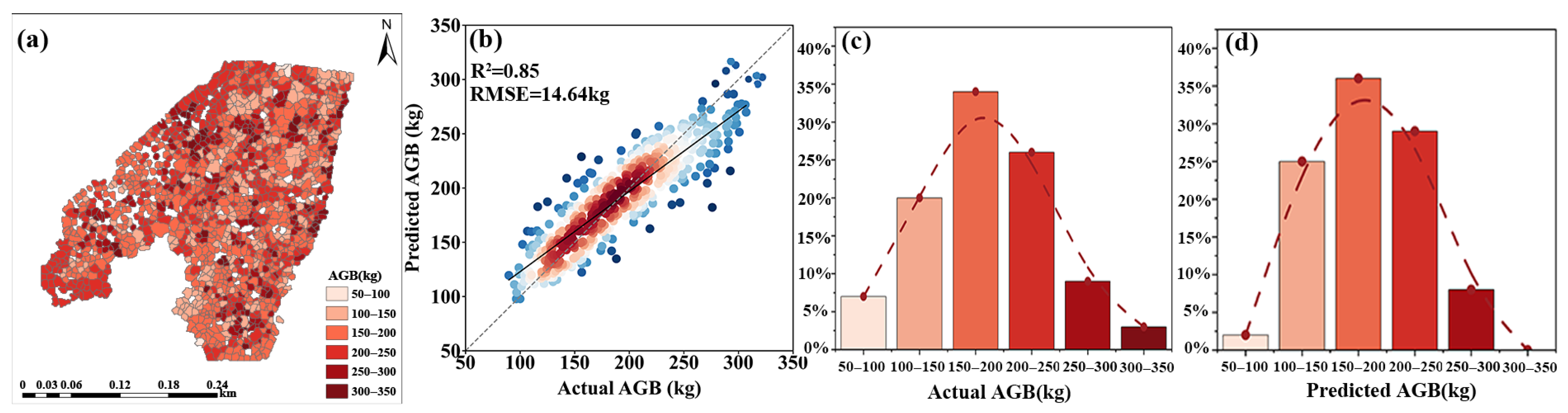
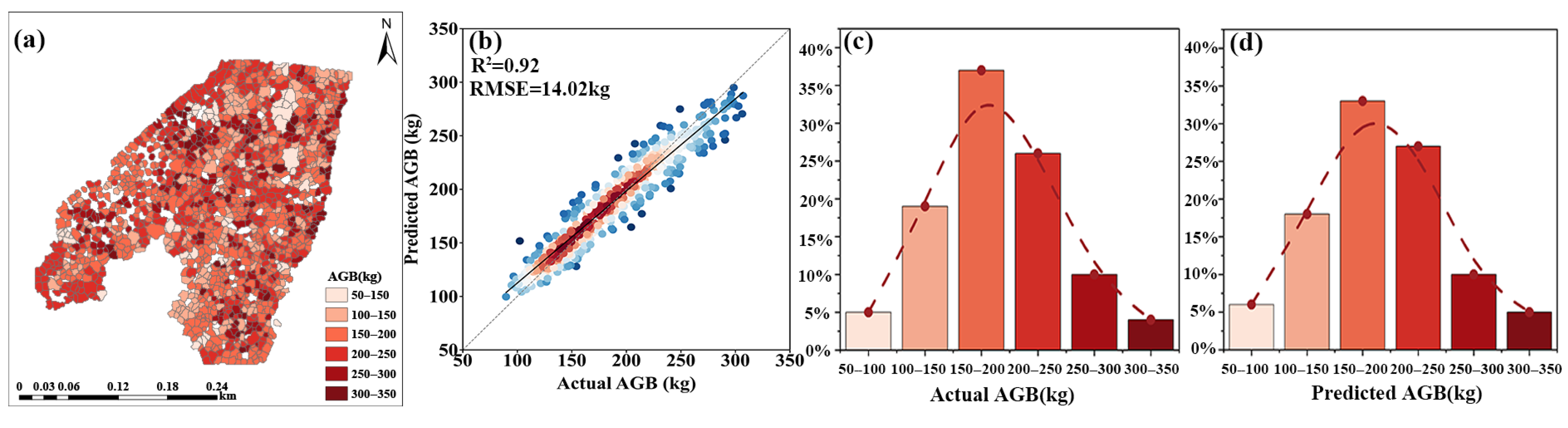
3.4. Construction of AGB Estimation Model and Accuracy Comparison
3.5. Spatial Distribution of AGB in Chinese Fir
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, M. Advances in study of forest spatial structure. Sci. Silvae Sin. 2010, 46, 117–122. [Google Scholar]
- Tang, M.; Tang, S.; Lei, X.; Li, X. Study on spatial structure optimizing model of stand selection cutting. Sci. Silvae Sin. 2004, 40, 25–31. [Google Scholar]
- Huang, T.; Ou, G.; Xu, H.; Zhang, X.; Wu, Y.; Liu, Z.; Zou, F.; Zhang, C.; Xu, C. Comparing Algorithms for Estimation of Aboveground Biomass in Pinus yunnanensis. Forests 2023, 14, 1742. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, H.; Ma, S.; Ren, M. Spatial structure diversity of semi-natural and plantation stands of larix gmelini in Changbai Mountains, northeastern China. J. Beijing For. Univ. 2015, 37, 48–58. [Google Scholar]
- Clark, P.J.; Evans, F.C. Distance to nearest neighbor as a measure of spatial relationships in populations. Ecology 1954, 35, 445–453. [Google Scholar] [CrossRef]
- Heggi, F. A simulation models for managing jack pine stands, Growth models for tree and stand simulation. For. Res. 1974, 1, 74–90. [Google Scholar]
- Li, Y.; Hui, G.; Wang, H.; Zhang, G.; Ye, S. Selection priority for harvested trees according to stand structural indices. iForest-Biogeosci. For. 2017, 10, 561–566. [Google Scholar] [CrossRef]
- Aguirre, O.; Hui, G.; von Gadow, K.; Jiménez, J. An analysis of spatial forest structure using neighbourhood-based variables. For. Ecol. Manag. 2003, 183, 137–145. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, J.; Zhou, G.; Yu, L.; Gong, X.; Meng, J. Logging Simulation of Natural Mixed Forest in Jinpen Mountain Based on Optimization of Spatial Structure. J. Southwest For. Univ. 2022, 42, 126–133. [Google Scholar]
- Dong, L.; Bettinger, P.; Liu, Z. Optimizing neighborhood-based stand spatial structure: Four cases of boreal forests. For. Ecol. Manag. 2022, 506, 119965. [Google Scholar] [CrossRef]
- Hui, G.; Hu, Y. Measuring Species Spatial Isolation in Mixed Forests. For. Res. 2001, 14, 23–27. [Google Scholar]
- Chen, A.; Xu, C.; Zhang, M.; Guo, J.; Xing, X.; Yang, D.; Xu, B.; Yang, X. Cross-scale mapping of above-ground biomass and shrub dominance by integrating UAV and satellite data in temperate grassland. Remote Sens. Environ. 2024, 304, 114024. [Google Scholar] [CrossRef]
- Tang, M.; Xu, W.; Chen, Y.; Deng, Y.; Zhao, M. Relationship between spatial structure and biomass of a close-to-nature Phyllostachys edulis stand in Tianmu Mountain. Sci. Silvae Sin. 2011, 47, 1–6. [Google Scholar]
- Li, Q.; Liu, Z.; Jin, G. Impacts of stand density on tree crown structure and biomass: A global meta-analysis. Agric. For. Meteorol. 2022, 326, 109181. [Google Scholar] [CrossRef]
- Yang, S.; Mao, K.; Yang, H.; Wang, Y.; Feng, Q.; Wang, S.; Miao, N. Stand characteristics and ecological benefits of Chinese Fir, Chinese Cedar, and mixed plantations in the mountainous areas of the Sichuan Basin. For. Ecol. Manag. 2023, 544, 121168. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Sun, Y.; Ruan, H.; Wang, G.; Dai, J.; She, G. Estimating canopy structure and biomass in bamboo forests using airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2019, 148, 114–129. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.Y.; Qiao, X.; Zhang, Y.; Jiang, M. The control of external and internal canopy structural heterogeneity on diversity and productivity relationship in a subtropical forest. For. Ecosyst. 2024, 11, 100246. [Google Scholar] [CrossRef]
- Liu, L.; Zeng, F.; Song, T.; Wang, K.; Du, H. Stand structure and abiotic factors modulate karst forest biomass in Southwest China. Forests 2020, 11, 443. [Google Scholar] [CrossRef]
- Saatchi, S.; Marlier, M.; Chazdon, R.L.; Clark, D.B.; Russell, A.E. Impact of spatial variability of tropical forest structure on radar estimation of aboveground biomass. Remote Sens. Environ. 2011, 115, 2836–2849. [Google Scholar] [CrossRef]
- Häbel, H.; Kuronen, M.; Henttonen, H.M.; Kangas, A.; Myllymäki, M. The effect of spatial structure of forests on the precision and costs of plot-level forest resource estimation. For. Ecosyst. 2019, 6, 8. [Google Scholar] [CrossRef]
- Yang, B.; Ma, R.; Zhai, J.; Du, J.; Bai, J.; Zhang, W. Stand spatial structure is more important than species diversity in enhancing the carbon sink of fragile natural secondary forest. Ecol. Indic. 2024, 158, 111449. [Google Scholar] [CrossRef]
- Zhang, B.; Li, X.; Du, H.; Zhou, G.; Mao, F.; Huang, Z.; Zhou, L.; Xuan, J.; Gong, Y.; Chen, C. Estimation of urban forest characteristic parameters using UAV-Lidar coupled with canopy volume. Remote Sens. 2022, 14, 6375. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, L.; Li, X.; Zhao, Y.; Yu, J.; Lv, L.; Du, H. Optimizing the Spatial Structure of Metasequoia Plantation Forest Based on UAV-LiDAR and Backpack-LiDAR. Remote Sens. 2023, 15, 4090. [Google Scholar] [CrossRef]
- Almeida, D.R.A.d.; Stark, S.C.; Chazdon, R.; Nelson, B.W.; César, R.G.; Meli, P.; Gorgens, E.; Duarte, M.M.; Valbuena, R.; Moreno, V.S.; et al. The effectiveness of lidar remote sensing for monitoring forest cover attributes and landscape restoration. For. Ecol. Manag. 2019, 438, 34–43. [Google Scholar] [CrossRef]
- Wang, W.; Pang, Y.; Du, L.; Zhang, Z.; Liang, X. Individual tree segmentation for airborne LiDAR point cloud data using spectral clustering and supervoxel-based algorithm. Natl. Remote Sens. Bull. 2022, 26, 1650–1661. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, Y.; Chen, C.; Li, X.; Mao, F.; Lv, L.; Yu, J.; Song, M.; Huang, L.; Chen, J.; et al. UAV-LiDAR Integration with Sentinel-2 Enhances Precision in AGB Estimation for Bamboo Forests. Remote Sens. 2024, 16, 705. [Google Scholar] [CrossRef]
- Fu, T.; Pang, Y.; Huang, Q.; Liu, Q.; Xu, G. Prediction of subtropical forest parameters using airborne laser scanner. J. Remote Sens. 2011, 15, 1092–1104. [Google Scholar]
- Cao, L.; Zhang, Z.; Yun, T.; Wang, G.; Ruan, H.; She, G. Estimating tree volume distributions in subtropical forests using airborne LiDAR data. Remote Sens. 2019, 11, 97. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, Y.; Li, X.; Lv, L.; Yu, J.; Song, M.; Huang, L.; Mao, F.; Du, H. Improving Chinese Fir Plantations DBH Inversion Accuracy Using Ensemble Learning Models Base on UAV-LiDAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 10846–10863. [Google Scholar] [CrossRef]
- Chen, J.; Li, X.; Huang, Z.; Xuan, J.; Chen, C.; Hu, M.; Tan, C.; Zhou, Y.; Zhao, Y.; Yu, J.; et al. Forest age estimation using UAV-LiDAR and Sentinel-2 data with machine learning algorithms-a case study of Masson pine (Pinus massoniana). Geo-Spat. Inf. Sci. 2024, 28, 1051–1071. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Q.; Pang, Y. Review on forest parameters inversion using LiDAR. J. Remote Sens. 2016, 20, 1138–1150. [Google Scholar]
- Qin, H.; Zhou, W.; Yao, Y.; Wang, W. Individual tree segmentation and tree species classification in subtropical broadleaf forests using UAV-based LiDAR, hyperspectral, and ultrahigh-resolution RGB data. Remote Sens. Environ. 2022, 280, 113143. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Cao, L.; Dai, J.-s.; Xu, J.-x.; Xu, Z.-q.; She, G.-h. Optimized extraction of forest parameters in subtropical forests based on airborne small footprint LiDAR technology. J. Beijing For. Univ. 2014, 36, 13–21. [Google Scholar]
- Næsset, E.; Bjerknes, K.-O. Estimating tree heights and number of stems in young forest stands using airborne laser scanner data. Remote Sens. Environ. 2001, 78, 328–340. [Google Scholar] [CrossRef]
- De Pauw, K.; Depauw, L.; Calders, K.; Caluwaerts, S.; Cousins, S.A.; De Lombaerde, E.; Diekmann, M.; Frey, D.; Lenoir, J.; Meeussen, C.; et al. Urban forest microclimates across temperate Europe are shaped by deep edge effects and forest structure. Agric. For. Meteorol. 2023, 341, 109632. [Google Scholar] [CrossRef]
- Li, P.; Shen, X.; Dai, J.; Cao, L. Comparisons and accuracy assessments of LiDAR-based tree segmentation approaches in planted forests. Sci. Silvae Sin. 2018, 54, 127–136. [Google Scholar]
- Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on the random forests technique. ISPRS J. Photogramm. Remote Sens. 2011, 66, 28–37. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Wu, X.; Shen, X.; Zhang, Z.; Cao, F.; She, G.; Cao, L. An Advanced Framework for Multi-Scale Forest Structural Parameter Estimations Based on UAS-LiDAR and Sentinel-2 Satellite Imagery in Forest Plantations of Northern China. Remote Sens. 2022, 14, 3023. [Google Scholar] [CrossRef]
- Lu, X.; Guo, Q.; Li, W.; Flanagan, J. A bottom-up approach to segment individual deciduous trees using leaf-off lidar point cloud data. ISPRS J. Photogramm. Remote Sens. 2014, 94, 1–12. [Google Scholar] [CrossRef]
- Alexander, C. Delineating tree crowns from airborne laser scanning point cloud data using Delaunay triangulation. Int. J. Remote Sens. 2009, 30, 3843–3848. [Google Scholar] [CrossRef]
- Zhu, B.-d.; Luo, H.-b.; Jin, J.; Yue, C.-r. Optimization of individual tree segmentation methods for high canopy density plantation based on UAV LiDAR. Sci. Silvae Sin. 2022, 58, 48–59. [Google Scholar]
- Dong, P.; Chen, Q. Principles of LiDAR Remote Sensing; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wang, H.; Zhang, G.; Hui, G.; Li, Y.; Hu, Y.; Zhao, Z. The influence of sampling unit size and spatial arrangement patterns on neighborhood-based spatial structure analyses of forest stands. For. Syst. 2016, 25, e056. [Google Scholar] [CrossRef]
- Cui, R.; Qi, S.; Wu, B.; Zhang, D.; Zhang, L.; Zhou, P.; Ma, N.; Huang, X. The influence of stand structure on understory herbaceous plants species diversity of platycladus orientalis plantations in Beijing, China. Forests 2022, 13, 1921. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Meng, Y.; Li, C.; Zhang, Z. Thinning effects on stand structure and carbon content of secondary forests. Forests 2022, 13, 512. [Google Scholar] [CrossRef]
- Hui, G.; Gadow, K. Quantitative Analysis of Forest Spatial Structure; Science and Technology Press: Beijing, China, 2003; pp. 16–18. [Google Scholar]
- Wang, P.; Jia, L.-m.; Wei, S.-p.; Wang, Q.-f. Analysis of stand spatial structure of Platycladus orientalis recreational forest based on Voronoi diagram method. J. Beijing For. Univ. 2013, 35, 39–44. [Google Scholar]
- Zhang, G.; Hui, G.; Zhang, G.; Zhao, Z.; Hu, Y. Telescope method for characterizing the spatial structure of a pine-oak mixed forest in the Xiaolong Mountains, China. Scand. J. For. Res. 2019, 34, 751–762. [Google Scholar] [CrossRef]
- Qin, L.; Zhang, M.; Zhong, S.; Yu, X. Model uncertainty in forest biomass estimation. Acta Ecol. Sin. 2017, 37, 7912–7919. [Google Scholar] [CrossRef][Green Version]
- Kim, Y.; Yang, Z.; Cohen, W.B.; Pflugmacher, D.; Lauver, C.L.; Vankat, J.L. Distinguishing between live and dead standing tree biomass on the North Rim of Grand Canyon National Park, USA using small-footprint lidar data. Remote Sens. Environ. 2009, 113, 2499–2510. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Moran, E.; Batistella, M.; Zhang, M.; Vaglio Laurin, G.; Saah, D. Aboveground forest biomass estimation with Landsat and LiDAR data and uncertainty analysis of the estimates. Int. J. For. Res. 2012, 2012, 436537. [Google Scholar] [CrossRef]
- Camarretta, N.; Ehbrecht, M.; Seidel, D.; Wenzel, A.; Zuhdi, M.; Merk, M.S.; Schlund, M.; Erasmi, S.; Knohl, A. Using airborne laser scanning to characterize land-use systems in a tropical landscape based on vegetation structural metrics. Remote Sens. 2021, 13, 4794. [Google Scholar] [CrossRef]
- de Almeida, C.T.; Galvao, L.S.; Aragão, L.E.d.O.C.e.; Ometto, J.P.H.B.; Jacon, A.D.; de Souza Pereira, F.R.; Sato, L.Y.; Lopes, A.P.; de Alencastro Graça, P.M.L.; de Jesus Silva, C.V.; et al. Combining LiDAR and hyperspectral data for aboveground biomass modeling in the Brazilian Amazon using different regression algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- Liu, K.; Shen, X.; Cao, L.; Wang, G.; Cao, F. Estimating forest structural attributes using UAV-LiDAR data in Ginkgo plantations. ISPRS J. Photogramm. Remote Sens. 2018, 146, 465–482. [Google Scholar] [CrossRef]
- Michałowska, M.; Rapiński, J. A review of tree species classification based on airborne LiDAR data and applied classifiers. Remote Sens. 2021, 13, 353. [Google Scholar] [CrossRef]
- Liu, H.; Fan, W.; Xu, Y.; Lin, W. Single tree biomass estimation based on UAV LiDAR point cloud. J. Cent. South Univ. For. Technol 2021, 41, 92–99. [Google Scholar]
- Xu, Y.; Zhen, J.; Jiang, X.; Wang, J. Mangrove species classification with UAV-based remote sensing data and XGBoost. Natl. Remote Sens. Bull. 2021, 25, 737–752. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, K.; Cao, J. Classification of coastal wetlands in the Pearl River Estuary using Zhuhai-1 hyperspectral imagery and XGBoost algorithm. Bull. Surv. Mapp. 2023, 12, 136–141. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Wang, X.; Yang, X.; Zhao, F.; An, B.; Huang, X. Estimation of Aboveground Biomass in the Arid Oasis Based on the Machine Learning Algorithm. Ecol. Environ. 2023, 32, 1007–1015. [Google Scholar]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of feature selection and catboost for prediction: The first application to the estimation of aboveground biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Zhang, C.; Ju, W.; Chen, J.M.; Li, D.; Wang, X.; Fan, W.; Li, M.; Zan, M. Mapping forest stand age in China using remotely sensed forest height and observation data. J. Geophys. Res. Biogeosci. 2014, 119, 1163–1179. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wang, J.-F.; Zhang, T.-L.; Fu, B.-J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Hui, G. A new parameter for stand spatial structure-neighbourhood comparison. For. Res. 1999, 12, 4–9. [Google Scholar]
- Geng, L.; Li, M.; Fan, W.; Wang, B. Individual tree structure parameters and effective crown of the stand extraction base on airborn LiDAR data. Sci. Silvae Sin. 2018, 54, 62–72. [Google Scholar]
- Yang, Q.; Su, Y.; Jin, S.; Kelly, M.; Hu, T.; Ma, Q.; Li, Y.; Song, S.; Zhang, J.; Xu, G.; et al. The influence of vegetation characteristics on individual tree segmentation methods with airborne LiDAR data. Remote Sens. 2019, 11, 2880. [Google Scholar] [CrossRef]
- Huang, L.; Zhen, Z.; Yinghui, Z. Stand spatial structure characterization of broad-leaved Pinus koraiensis forest based on multi-source LiDAR data. J. Cent. South Univ. For. Technol. 2023, 43, 36–50. [Google Scholar]
- Hui, G.-y.; Hu, Y.-b.; Zhao, Z.-h. Research Progress of Structure-based Forest Management. For. Res. 2018, 31, 85–93. [Google Scholar]
- Wu, D.-Y.; Dou, X.-W.; Tang, M.-P. Relationship between carbon stock and the structure of coniferous and broad-leaved mixed forest in Tianmu Mountains, China. J. Appl. Ecol. 2023, 34, 2029–2038. [Google Scholar]
- He, J.; Wang, X.; Wang, K.; Guo, W.; Liu, L.; Wang, F. Multivariate distribution of spatial structure parameters of Populus davidiana-Betula platyphylla secondary forest. J. Beijing For. Univ. 2021, 43, 22–33. [Google Scholar]
- Khan, M.N.I.; Shil, M.C.; Azad, M.S.; Sadath, M.N.; Feroz, S.; Mollick, A.S. Allometric relationships of stem volume and stand level carbon stocks at varying stand density in Swietenia macrophylla King plantations, Bangladesh. For. Ecol. Manag. 2018, 430, 639–648. [Google Scholar] [CrossRef]
- Protazio, J.M.B.; Souza, M.A.; Hernández-Díaz, J.C.; Escobar-Flores, J.G.; López-Sánchez, C.A.; Carrillo-Parra, A.; Wehenkel, C. A dynamical model based on the Chapman–Richards growth equation for fitting growth curves for four pine species in Northern Mexico. Forests 2022, 13, 1866. [Google Scholar] [CrossRef]
- Qiu, H.; Zhang, H.; Lei, K.; Hu, X.; Yang, T.; Jiang, X. A New Tree-Level Multi-Objective Forest Harvest Model (MO-PSO): Integrating Neighborhood Indices and PSO Algorithm to Improve the Optimization Effect of Spatial Structure. Forests 2023, 14, 441. [Google Scholar] [CrossRef]
- Lu, D.; Batistella, M.; Moran, E. Satellite estimation of aboveground biomass and impacts of forest stand structure. Photogramm. Eng. Remote Sens. 2005, 71, 967–974. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of variable selection and forest type on forest aboveground biomass estimation using machine learning algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T. Xgboost: Extreme Gradient Boosting; R Package Version 0.4-2. 2015, Volume 1, pp. 1–4. Available online: https://CRAN.R-project.org/package=xgboost (accessed on 3 June 2025).
- Huang, L.; Huang, Z.; Zhou, W.; Wu, S.; Li, X.; Mao, F.; Song, M.; Zhao, Y.; Lv, L.; Yu, J.; et al. Landsat-based spatiotemporal estimation of subtropical forest aboveground carbon storage using machine learning algorithms with hyperparameter tuning. Front. Plant Sci. 2024, 15, 1421567. [Google Scholar] [CrossRef]






| Parameters | UAV-LiDAR |
|---|---|
| transducers | H300-RT (1 pc) |
| maximum pitch angle | 30° |
| laser wavelength | 905 nm |
| altitude (aviation) | 60 m |
| flight speed | 8 m/s |
| maximum horizontal flight speed | 23 m/s |
| ranging accuracy | ±1 cm (0.5 cm) |
| scanning frequency | 20 Hz |
| scanning frequency | 300 kHz |
| wavelength | 905 nm |
| Statistical Characteristic | Min (cm) | Max (cm) | Average Value (cm) | Extremely Poor (cm) | Standard Deviation (cm) |
|---|---|---|---|---|---|
| DBH | 0.3 | 93.9 | 16.3 | 93.6 | 9.9 |
| Spatial Structure Parameters | Formulas | Account for | Partition |
|---|---|---|---|
| Neighborhood comparison | Kij = 1 when competing wood j is smaller in diameter at breast height than object wood i; otherwise Kij = 0 | Five classes of 0, 0.25, 0.5, 0.75, and 1 [48] | |
| Crowding degree | Yij = 1 when object wood i overlaps the crown projection of neighboring wood j; otherwise Y(ij) = 0 | Five classes of 0, 0.25, 0.5, 0.75, and 1 [48] | |
| Uniform angular scale | When the jth angle α is smaller than the standard angle α0, Zij = 1; otherwise Zij = 0 | Five classes of 0, 0.25, 0.5, 0.75, and 1 [48] | |
| Hegyi competition index | Lij is the distance between the object tree and the competing tree (m), di is the diameter at breast height (cm) of the object tree, dj is the diameter at breast height (cm) of the competing tree, and n is the number of competing trees (plants) of the object tree | (0, 0.2], (0.2, 0.8], (0.8, 1.4], (1.4, 2.0], and (2.0, ∞] [23] | |
| openness | Lij is the horizontal distance (m) between the object wood and the nearest neighbor wood j, Hij is the tree height (m) of the nearest neighbor wood at distance i, and n is the number of competing trees (plants) of the object wood | (0, 0.2], (0.2, 0.3], (0.3, 0.4], (0.4, 0.5], (0.5, ∞] [49] |
| ULS Feature Variable | Variable Description | Reference | |
|---|---|---|---|
| Height-Based Metrics [54] | Height Percentiles (H5, H10, H20, H25, H30, H40, H50, H60, H70, H75, H80, H90, H95, H99) | Percentiles of first-return height values (5th, 10th, 20th, 25th, 30th, 40th, 50th, 60th, 70th, 75th, 80th, 90th, 95th, and 99th) | [54,55,56] |
| Coefficient of Variation (Hcv) | Coefficient of variation of the first-return point cloud heights | ||
| Maximum Height (Hmax) | Maximum tree height from first-return point cloud | ||
| Variance (Hva) | Variance of first-return point cloud heights | ||
| Standard Deviation (Hstd) | Standard deviation of first-return point cloud heights | ||
| Median Height (Hmed) | Median of first-return point cloud heights | ||
| Mean Height (Hmean) | Mean value of first-return point cloud heights | ||
| Interquartile Range | Interquartile range of first-return point cloud heights | ||
| Root Mean Square Height (Hsq) | Root mean square of first-return point cloud heights | ||
| Cubic Mean Height (Hcm) | Cubic mean of first-return point cloud heights | ||
| Density-Based Metrics (DB) | Canopy Return Densities (D0, D1, D2, D3, D4, D5, D6, D7, D8, D9) | Percentage of points above certain height percentiles (10th to 90th) relative to total number of points | [57] |
| Canopy Structure Metrics (CS) | Crown Area (S) | Projected crown area calculated using a 2D convex hull algorithm | [58] |
| Crown Diameter (CD) | Average diameter of the crown point cloud: | ||
| Crown Volume (V) | Crown volume calculated using a 3D convex hull algorithm | ||
| Nt | No | Nc | r | p | F | |
|---|---|---|---|---|---|---|
| Point Cloud Segmentation | 430 | 123 | 91 | 78% | 82% | 80% |
| Seed Point-Based Segmentation | 521 | 64 | 59 | 89% | 90% | 89% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Zhao, Y.; Xu, J.; Fang, Q.; Xuan, J.; Huang, L.; Li, X.; Mao, F.; Sun, Y.; Du, H. UAV-LiDAR-Based Study on AGB Response to Stand Structure and Its Estimation in Cunninghamia Lanceolata Plantations. Remote Sens. 2025, 17, 2842. https://doi.org/10.3390/rs17162842
Cao Y, Zhao Y, Xu J, Fang Q, Xuan J, Huang L, Li X, Mao F, Sun Y, Du H. UAV-LiDAR-Based Study on AGB Response to Stand Structure and Its Estimation in Cunninghamia Lanceolata Plantations. Remote Sensing. 2025; 17(16):2842. https://doi.org/10.3390/rs17162842
Chicago/Turabian StyleCao, Yuqi, Yinyin Zhao, Jiuen Xu, Qing Fang, Jie Xuan, Lei Huang, Xuejian Li, Fangjie Mao, Yusen Sun, and Huaqiang Du. 2025. "UAV-LiDAR-Based Study on AGB Response to Stand Structure and Its Estimation in Cunninghamia Lanceolata Plantations" Remote Sensing 17, no. 16: 2842. https://doi.org/10.3390/rs17162842
APA StyleCao, Y., Zhao, Y., Xu, J., Fang, Q., Xuan, J., Huang, L., Li, X., Mao, F., Sun, Y., & Du, H. (2025). UAV-LiDAR-Based Study on AGB Response to Stand Structure and Its Estimation in Cunninghamia Lanceolata Plantations. Remote Sensing, 17(16), 2842. https://doi.org/10.3390/rs17162842








