Multimodal Prompt Tuning for Hyperspectral and LiDAR Classification
Abstract
1. Introduction
2. Related Work
2.1. HSI Representation
2.2. Fusion of HSI and LiDAR Data
2.3. Prompt Tuning
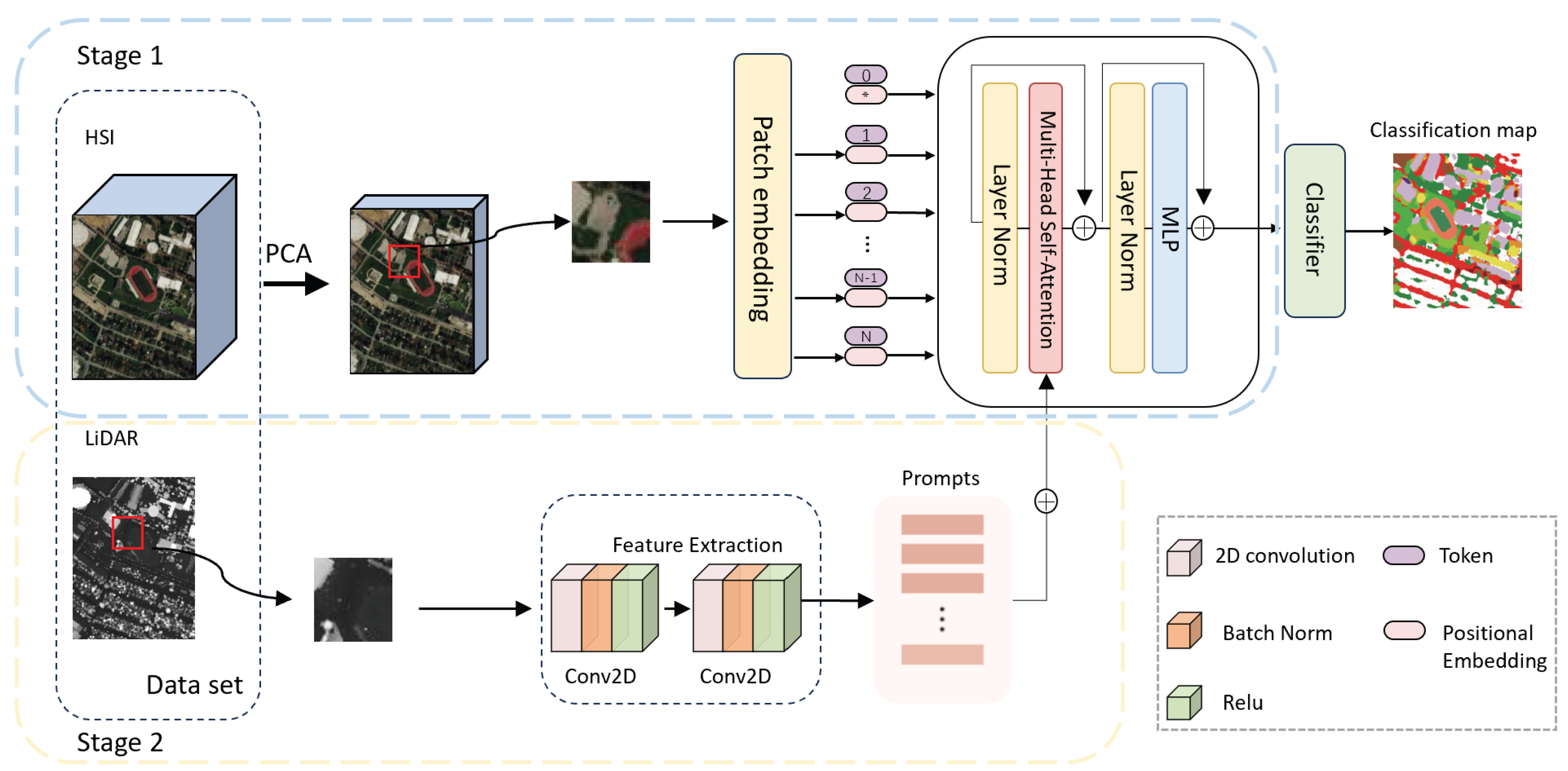
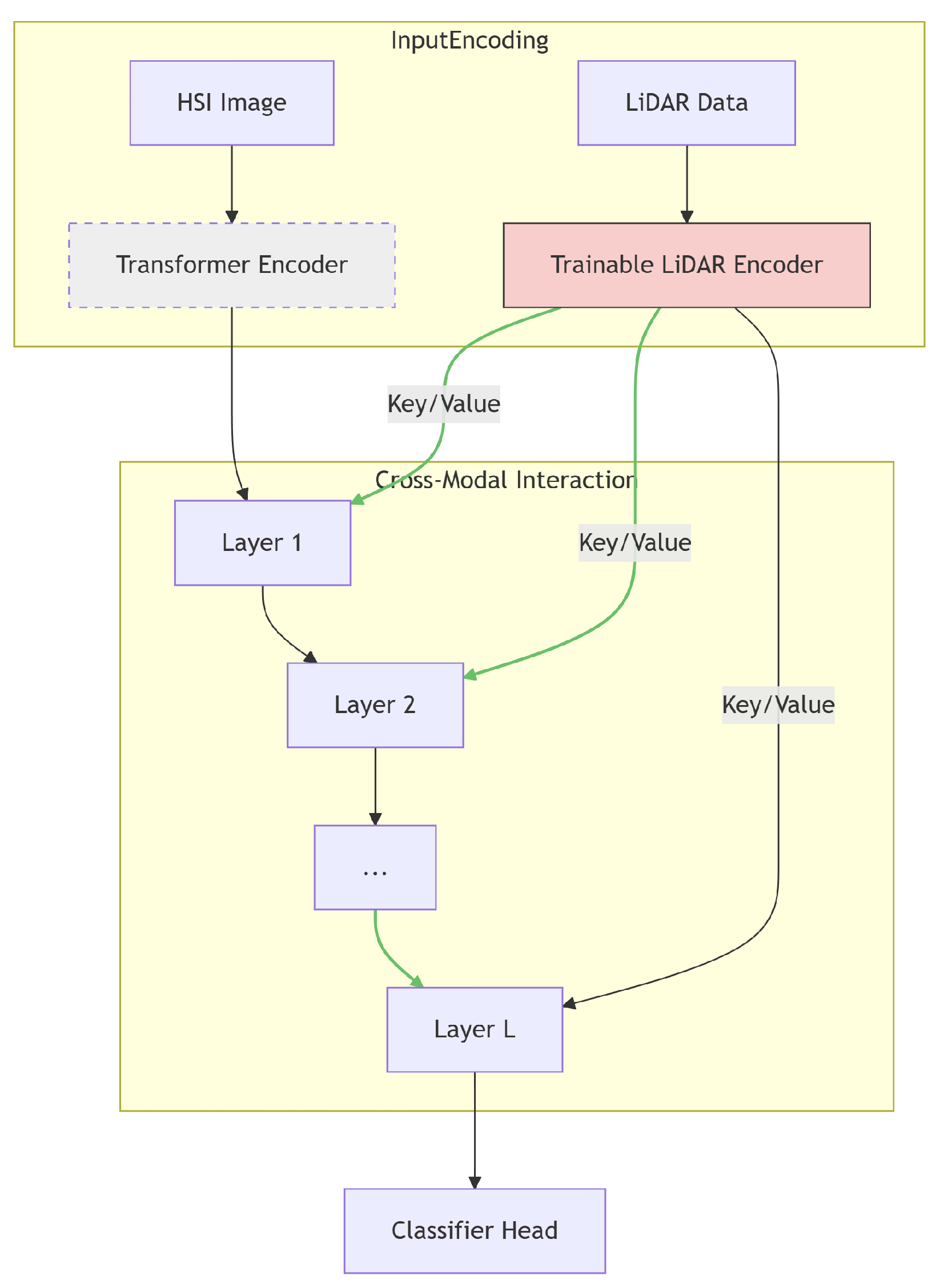
3. Methods
3.1. Overall Framework
3.2. First Stage: Learning the Spatial–Spectral Representation Across Multiple Datasets
3.3. Second Stage: LiDAR as Prompt for Tuning
4. Experiments
4.1. Dataset Description
- Indian Pines: This dataset was acquired by the AVIRIS sensor over an agricultural area, with an image size of pixels and 224 spectral bands. The dataset includes 16 classes and contains 21,025 labeled pixels.
- Salinas Valley: This dataset was collected by the AVIRIS sensor and originally consisted of 224 spectral bands. After removing 20 water absorption bands, 204 bands were retained. The imagery size is pixels. It contains 16 classes and 54,129 labeled pixels.
- Pavia University: This dataset was captured by the ROSIS-3 sensor and includes 115 spectral bands (reduced to 103 bands after discarding 12 noise bands) covering the range of 430–860 nm. The imagery size is pixels, with a spatial resolution of 1.3 m. It comprises 9 land-cover classes and 42,776 labeled pixels.
- KSC: Acquired by the NASA AVIRIS instrument over Florida on 23 March 1996, this dataset originally consisted of 224 bands. After removing water absorption and low-SNR bands, 176 bands were retained. The imagery size is pixels and it comprises 13 land-cover classes.
- Botswana: This dataset was acquired by the Hyperion sensor on NASA’s EO-1 satellite and consists of 242 spectral bands. The spatial resolution is 30 m, and the dataset captures a diverse range of environmental features, with pixels divided into 14 classes.
- Washington DC Mall: Released by the Spectral Information Technology Application Center of Virginia in 2013, this dataset includes 191 spectral bands. It has an image size of pixels and includes 7 land-cover classes, representing urban and natural environments.
- Houston 2013: Provided by the Hyperspectral Image Analysis Group and the NSF-funded Airborne Laser Mapping Center (NCALM). Originally created for the 2013 GRSS Data Fusion Competition, this dataset was provided through collaboration between the Hyperspectral Image Analysis Group and NSF’s NCALM. It features a 144-band hyperspectral image with pixel dimensions, representing 15 land-use classes. Table 1 enumerates the specific class labels and their respective training/test sample sizes in the Houston scene.
- MUUFL Gulfport: The ROSIS imaging spectrometer captured this dataset, which contains 72-band spectral data with pixel spatial coverage. Table 2 enumerates the land-use categories along with their respective training and validation sample sizes in the MUUFL study area.
- Trento: The hyperspectral imagery was acquired by the AISA Eagle system, comprising 63 spectral channels. Synchronized LiDAR measurements collected with an Optech ALTM 3100EA sensor share identical spatial coverage ( pixels at 1 m resolution). Table 3 provides the complete classification schema with training/testing sample allocations for the Trento study area.
4.2. Experimental Setup
4.2.1. Implementation Details
4.2.2. Compared Methods
- SVM: The classification process was executed using the support vector machine (SVM) implementation from the sklearn library, which utilizes a radial basis function kernel configuration. Key model parameters consisted of the regularization coefficient (C = 100) and convergence tolerance threshold (), with both values being determined through empirical optimization studies.
- RF: The Random Forest algorithm was implemented through the sklearn library, with four key hyperparameters configured as follows: the ensemble comprised 200 decision trees with a maximum depth of 10 for each tree, while node splitting required a minimum of three samples per leaf and considered up to 10 features at each split. All parameter values were carefully selected based on empirical validation to ensure optimal model performance.
- MLR: The logistic regression model was implemented using scikit-learn’s linear_model module, employing an L2 regularization penalty with the limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) optimization algorithm. To ensure convergence, the maximum iteration count was set to 5000. This classifier exclusively used hyperspectral data as input.
- KNN: The classification accuracy is highly sensitive to the neighborhood size (K). Using five-fold cross-validation on training data, we optimized K by testing candidate values and retaining the top-performing configuration.
- ENet [57]: This architecture includes two feature enhancement modules, the spatial attention enhancement module and the spectral enhancement module, which refine the spatial and spectral features of HS and LiDAR data, respectively. All other hyperparameters were set consistently with those in the original paper.
- FusAtNet [44]: This architecture processes hyperspectral (HS) data through a self-attention (SA) module to produce spectral–spatial attention maps, while strategically integrating LiDAR-derived features via a cross-attention fusion mechanism to enhance spatial representation learning. All architectural configurations and hyperparameters were kept consistent with the baseline implementation described in the reference study.
- ViT [58]: For ViT, the LiDAR and HS data were concatenated along the channel dimension. The model architecture consisted solely of encoder layers to facilitate joint classification of HS and LiDAR data.
- SpectralFormer [36]: This architecture integrates LiDAR and hyperspectral (HS) data through channel-wise concatenation while maintaining the original vision transformer (ViT) backbone structure for comparative consistency. The 64D spectral embeddings are processed through five transformer blocks, each comprising (1) four-head self-attention, (2) an 8D hidden layer MLP, and (3) GeLU activations.
- MTNet [12]: The fundamental concept involves employing transformer architectures to effectively extract both modality-specific characteristics and cross-modal correlations from hyperspectral and LiDAR datasets. Our implementation of MTNet was developed using the PyTorch 1.13.1 framework, with model optimization performed through the Adam adaptive learning algorithm to achieve parameter convergence. All architectural configurations and hyperparameters were kept consistent with the baseline implementation described in the reference study.
4.2.3. Evaluation Indicators
4.3. Classification Results
4.3.1. Quantitative Comparison
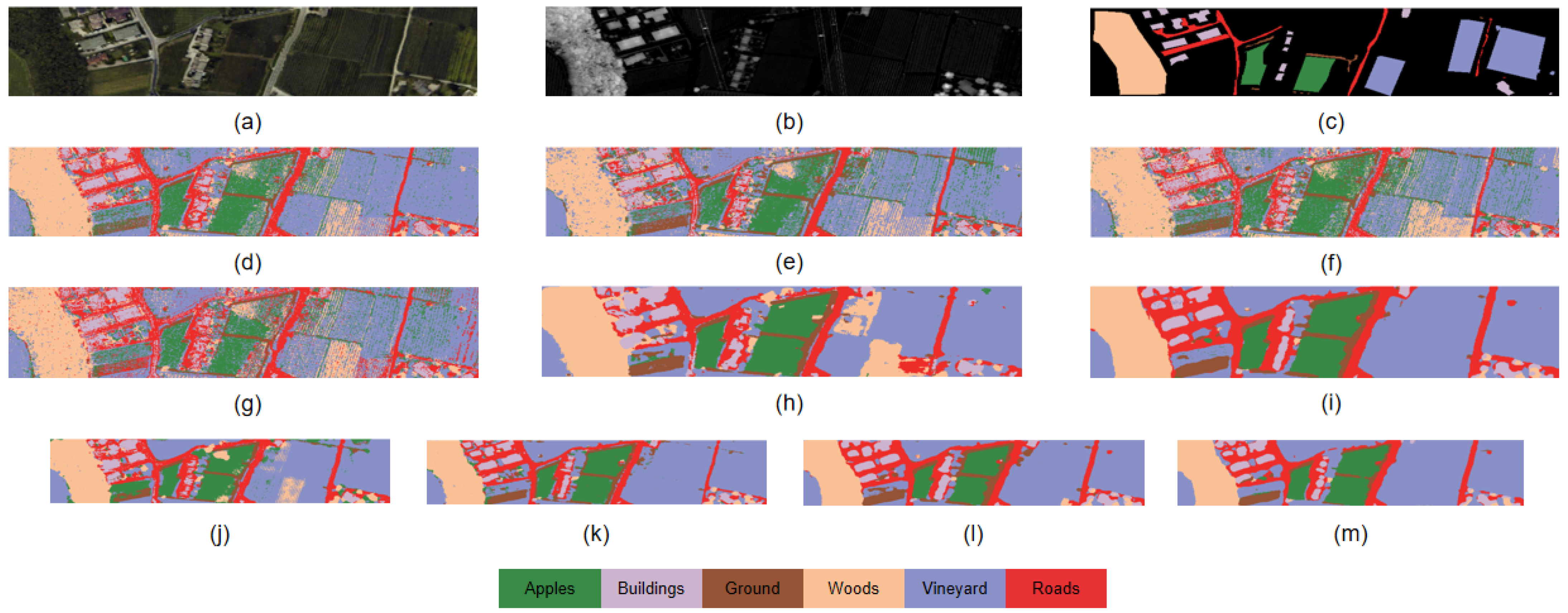
4.3.2. Qualitative Comparison
4.4. Ablation Study
4.4.1. Comparison of Different Components
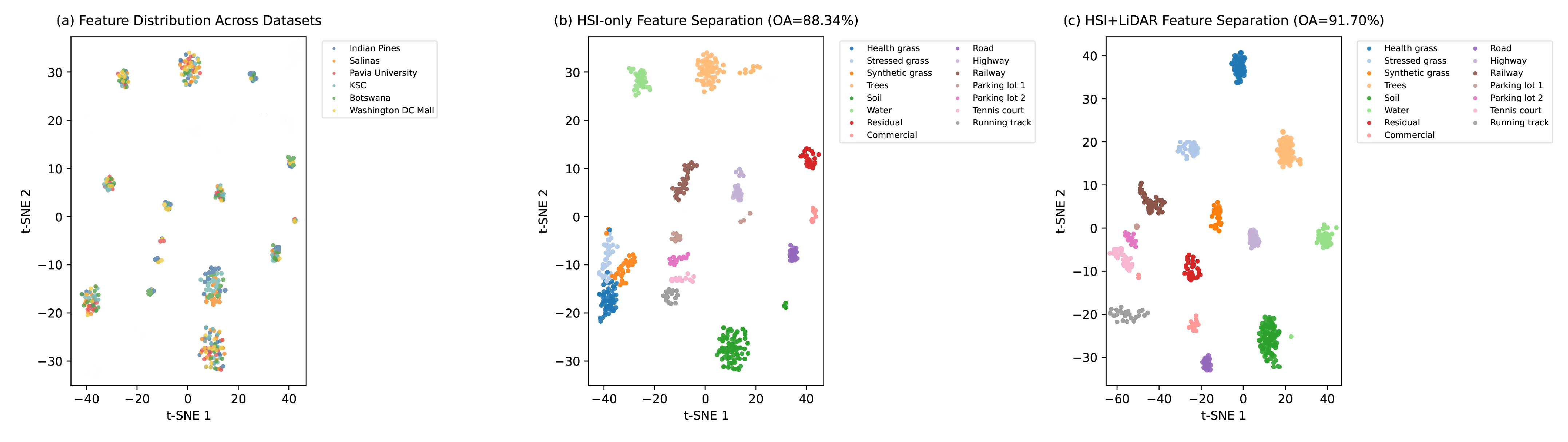
4.4.2. Feature Distribution Analysis
4.4.3. Prompt Method Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Landgrebe, D. Hyperspectral image data analysis. IEEE Signal Process. Mag. 2002, 19, 17–28. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, T.; Gao, G.; Ren, G.; Ma, Y.; Chanussot, J.; Jia, X. Multimodal hyperspectral remote sensing: An overview and perspective. Sci. China Inf. Sci. 2021, 64, 121301. [Google Scholar] [CrossRef]
- Ghamisi, P.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; Chi, M.; Anders, K.; Gloaguen, R.; et al. Multisource and multitemporal data fusion in remote sensing: A comprehensive review of the state of the art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef]
- Pedergnana, M.; Marpu, P.R.; Dalla Mura, M.; Benediktsson, J.A.; Bruzzone, L. Classification of remote sensing optical and LiDAR data using extended attribute profiles. IEEE J. Sel. Top. Signal Process. 2012, 6, 856–865. [Google Scholar] [CrossRef]
- Liao, W.; Pižurica, A.; Bellens, R.; Gautama, S.; Philips, W. Generalized graph-based fusion of hyperspectral and LiDAR data using morphological features. IEEE Geosci. Remote Sens. Lett. 2014, 12, 552–556. [Google Scholar] [CrossRef]
- Jia, S.; Zhan, Z.; Zhang, M.; Xu, M.; Huang, Q.; Zhou, J.; Jia, X. Multiple feature-based superpixel-level decision fusion for hyperspectral and LiDAR data classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1437–1452. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Shah, C.; Haut, J.M.; Du, Q.; Plaza, A. Spectral–spatial morphological attention transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5503615. [Google Scholar] [CrossRef]
- Xiu, D.; Pan, Z.; Wu, Y.; Hu, Y. MAGE: Multisource attention network with discriminative graph and informative entities for classification of hyperspectral and LiDAR data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5539714. [Google Scholar] [CrossRef]
- Xue, Z.; Tan, X.; Yu, X.; Liu, B.; Yu, A.; Zhang, P. Deep hierarchical vision transformer for hyperspectral and LiDAR data classification. IEEE Trans. Image Process. 2022, 31, 3095–3110. [Google Scholar] [CrossRef]
- Hang, R.; Li, Z.; Ghamisi, P.; Hong, D.; Xia, G.; Liu, Q. Classification of hyperspectral and LiDAR data using coupled CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4939–4950. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Zhang, S.; Meng, X.; Liu, Q.; Yang, G.; Sun, W. Feature-decision level collaborative fusion network for hyperspectral and LiDAR classification. Remote Sens. 2023, 15, 4148. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Tian, J. Local Manifold Learning-Based k-Nearest-Neighbor for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Hyperspectral Image Segmentation Using a New Bayesian Approach With Active Learning. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3947–3960. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Farrell, M.; Mersereau, R. On the impact of PCA dimension reduction for hyperspectral detection of difficult targets. IEEE Geosci. Remote Sens. Lett. 2005, 2, 192–195. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of hyperspectral images with regularized linear discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Ye, Q.; Zhao, H.; Li, Z.; Yang, X.; Gao, S.; Yin, T.; Ye, N. L1-Norm distance minimization-based fast robust twin support vector k-plane clustering. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 4494–4503. [Google Scholar] [CrossRef] [PubMed]
- Plaza, A.; Martinez, P.; Perez, R.; Plaza, J. A new method for target detection in hyperspectral imagery based on extended morphological profiles. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volume 6, pp. 3772–3774. [Google Scholar] [CrossRef]
- Licciardi, G.; Marpu, P.R.; Chanussot, J.; Benediktsson, J.A. Linear versus nonlinear PCA for the classification of hyperspectral data based on the extended morphological profiles. IEEE Geosci. Remote Sens. Lett. 2011, 9, 447–451. [Google Scholar] [CrossRef]
- Hou, B.; Huang, T.; Jiao, L. Spectral–Spatial Classification of Hyperspectral Data Using 3-D Morphological Profile. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2364–2368. [Google Scholar] [CrossRef]
- Qian, Y.; Ye, M.; Zhou, J. Hyperspectral image classification based on structured sparse logistic regression and three-dimensional wavelet texture features. IEEE Trans. Geosci. Remote Sens. 2012, 51, 2276–2291. [Google Scholar] [CrossRef]
- Jia, S.; Liao, J.; Xu, M.; Li, Y.; Zhu, J.; Sun, W.; Jia, X.; Li, Q. 3-D Gabor convolutional neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5509216. [Google Scholar] [CrossRef]
- Jia, S.; Hu, J.; Zhu, J.; Jia, X.; Li, Q. Three-dimensional local binary patterns for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2399–2413. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Zhang, H.; Gong, C.; Bai, Y.; Bai, Z.; Li, Y. 3-D-ANAS: 3-D Asymmetric Neural Architecture Search for Fast Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5508519. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Wu, H.; Prasad, S. Convolutional Recurrent Neural Networks for Hyperspectral Data Classification. Remote Sens. 2017, 9, 298. [Google Scholar] [CrossRef]
- Ma, Q.; Jiang, J.; Liu, X.; Ma, J. Deep Unfolding Network for Spatiospectral Image Super-Resolution. IEEE Trans. Comput. Imaging 2022, 8, 28–40. [Google Scholar] [CrossRef]
- Li, C.; Zhang, B.; Hong, D.; Yao, J.; Chanussot, J. LRR-Net: An Interpretable Deep Unfolding Network for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5513412. [Google Scholar] [CrossRef]
- Chen, R.; Vivone, G.; Li, G.; Dai, C.; Chanussot, J. An Offset Graph U-Net for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5520615. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 5998–6008. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations, Virtual, 3–7 May 2021. [Google Scholar]
- He, J.; Zhao, L.; Yang, H.; Zhang, M.; Li, W. HSI-BERT: Hyperspectral Image Classification Using the Bidirectional Encoder Representation From Transformers. IEEE Trans. Geosci. Remote Sens. 2020, 58, 165–178. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5518615. [Google Scholar] [CrossRef]
- He, C.; Sun, L.; Huang, W.; Zhang, J.; Zheng, Y.; Jeon, B. TSLRLN: Tensor subspace low-rank learning with non-local prior for hyperspectral image mixed denoising. Signal Process. 2021, 184, 108060. [Google Scholar] [CrossRef]
- Wang, Z.; Ziou, D.; Armenakis, C.; Li, D.; Li, Q. A comparative analysis of image fusion methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1391–1402. [Google Scholar] [CrossRef]
- Morchhale, S.; Pauca, V.P.; Plemmons, R.J.; Torgersen, T.C. Classification of pixel-level fused hyperspectral and lidar data using deep convolutional neural networks. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Xu, X.; Li, W.; Ran, Q.; Du, Q.; Gao, L.; Zhang, B. Multisource remote sensing data classification based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2017, 56, 937–949. [Google Scholar] [CrossRef]
- Su, Y.; Chen, J.; Gao, L.; Plaza, A.; Jiang, M.; Xu, X.; Sun, X.; Li, P. ACGT-Net: Adaptive cuckoo refinement-based graph transfer network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5521314. [Google Scholar] [CrossRef]
- Wu, X.; Hong, D.; Chanussot, J. Convolutional neural networks for multimodal remote sensing data classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5517010. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Hang, R.; Zhang, B.; Chanussot, J. Deep encoder–decoder networks for classification of hyperspectral and LiDAR data. IEEE Geosci. Remote Sens. Lett. 2020, 19, 5500205. [Google Scholar] [CrossRef]
- Mohla, S.; Pande, S.; Banerjee, B.; Chaudhuri, S. Fusatnet: Dual attention based spectrospatial multimodal fusion network for hyperspectral and lidar classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 92–93. [Google Scholar] [CrossRef]
- Chen, T.; Chen, S.; Chen, L.; Chen, H.; Zheng, B.; Deng, W. Joint Classification of Hyperspectral and LiDAR Data via Multiprobability Decision Fusion Method. Remote Sens. 2024, 16, 4317. [Google Scholar] [CrossRef]
- Wang, W.; Dai, J.; Chen, Z.; Huang, Z.; Li, Z.; Zhu, X.; Hu, X.; Lu, T.; Lu, L.; Li, H.; et al. InternImage: Exploring Large-Scale Vision Foundation Models With Deformable Convolutions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 14408–14419. [Google Scholar] [CrossRef]
- Sun, X.; Wang, P.; Lu, W.; Zhu, Z.; Lu, X.; He, Q.; Li, J.; Rong, X.; Yang, Z.; Chang, H.; et al. RingMo: A Remote Sensing Foundation Model With Masked Image Modeling. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5612822. [Google Scholar] [CrossRef]
- Lester, B.; Al-Rfou, R.; Constant, N. The Power of Scale for Parameter-Efficient Prompt Tuning. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, Punta Cana, Dominican Republic, 7–11 November 2021; pp. 3045–3059. [Google Scholar] [CrossRef]
- Jia, M.; Tang, L.; Chen, B.C.; Cardie, C.; Belongie, S.; Hariharan, B.; Lim, S.N. Visual Prompt Tuning. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2022; pp. 709–727. [Google Scholar] [CrossRef]
- Liu, P.; Yuan, W.; Fu, J.; Jiang, Z.; Hayashi, H.; Neubig, G. Pre-train, Prompt, and Predict: A Systematic Survey of Prompting Methods in Natural Language Processing. ACM Comput. Surv. 2023, 55, 195. [Google Scholar] [CrossRef]
- Tan, X.; Shao, M.; Qiao, Y.; Liu, T.; Cao, X. Low-Rank Prompt-Guided Transformer for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5520815. [Google Scholar] [CrossRef]
- Kong, Y.; Cheng, Y.; Chen, Y.; Wang, X. Joint Classification of Hyperspectral Image and LiDAR Data Based on Spectral Prompt Tuning. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5521312. [Google Scholar] [CrossRef]
- Zhou, L.; Geng, J.; Jiang, W. Joint classification of hyperspectral and LiDAR data based on position-channel cooperative attention network. Remote Sens. 2022, 14, 3247. [Google Scholar] [CrossRef]
- Wang, D.; Hu, M.; Jin, Y.; Miao, Y.; Yang, J.; Xu, Y.; Qin, X.; Ma, J.; Sun, L.; Li, C.; et al. HyperSIGMA: Hyperspectral Intelligence Comprehension Foundation Model. arXiv 2024, arXiv:2406.11519. [Google Scholar] [CrossRef] [PubMed]
- Braham, N.A.A.; Albrecht, C.M.; Mairal, J.; Chanussot, J.; Wang, Y.; Zhu, X.X. SpectralEarth: Training Hyperspectral Foundation Models at Scale. arXiv 2024, arXiv:2408.08447. [Google Scholar] [CrossRef]
- Hong, D.; Zhang, B.; Li, X.; Li, Y.; Li, C.; Yao, J.; Yokoya, N.; Li, H.; Ghamisi, P.; Jia, X.; et al. SpectralGPT: Spectral Remote Sensing Foundation Model. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 5227–5244. [Google Scholar] [CrossRef]
- Fang, S.; Li, K.; Li, Z. S2ENet: Spatial–spectral cross-modal enhancement network for classification of hyperspectral and LiDAR data. IEEE Geosci. Remote Sens. Lett. 2021, 19, 6504205. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, X.; Li, S.; Plaza, A. Hyperspectral Image Classification Using Groupwise Separable Convolutional Vision Transformer Network. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5511817. [Google Scholar] [CrossRef]


| Class | Land-Cover Type | Training | Testing | Total |
|---|---|---|---|---|
| 1 | Health grass | 198 | 1053 | 1251 |
| 2 | Stressed grass | 190 | 1064 | 1254 |
| 3 | Synthetic grass | 192 | 505 | 697 |
| 4 | Trees | 188 | 1056 | 1244 |
| 5 | Soil | 186 | 1056 | 1242 |
| 6 | Water | 182 | 143 | 325 |
| 7 | Residual | 196 | 1072 | 1268 |
| 8 | Commercial | 191 | 1053 | 1244 |
| 9 | Road | 193 | 1059 | 1252 |
| 10 | Highway | 191 | 1036 | 1227 |
| 11 | Railway | 181 | 1054 | 1235 |
| 12 | Parking lot 1 | 192 | 1041 | 1233 |
| 13 | Parking lot 2 | 184 | 285 | 469 |
| 14 | Tennis court | 181 | 247 | 428 |
| 15 | Running track | 187 | 473 | 660 |
| Class | Land-Cover Type | Training | Testing | Total |
|---|---|---|---|---|
| 1 | Trees | 150 | 23,096 | 23,246 |
| 2 | Mostly Grass | 150 | 4120 | 4270 |
| 3 | Mixed Ground Surface | 150 | 6732 | 6882 |
| 4 | Dirt and Sand | 150 | 1676 | 1826 |
| 5 | Road | 150 | 6537 | 6687 |
| 6 | Water | 150 | 316 | 466 |
| 7 | Building Shadow | 150 | 2083 | 2233 |
| 8 | Building | 150 | 6090 | 6240 |
| 9 | Sidewalk | 150 | 1235 | 1385 |
| 10 | Yellow Curb | 150 | 33 | 183 |
| 11 | Cloth Panels | 150 | 119 | 269 |
| Class | Land-Cover Type | Training | Testing | Total |
|---|---|---|---|---|
| 1 | Apple Trees | 129 | 3905 | 4034 |
| 2 | Buildings | 125 | 2778 | 2903 |
| 3 | Ground | 105 | 374 | 479 |
| 4 | Wood | 154 | 8969 | 9123 |
| 5 | Vineyard | 184 | 10,317 | 10,501 |
| 6 | Roads | 122 | 3052 | 3174 |
| Class Name | Traditional Classifiers | Deep Learning-Based Methods | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SVM | RF | MLR | KNN | S2ENet | FusAtNet | ViT | SpectralFormer | MTNet | Ours | |
| Health grass | 86.32 | 85.75 | 95.44 | 84.43 | 83.38 | 82.43 | 82.62 | 79.20 | 82.05 | 82.10 |
| Stressed grass | 97.18 | 98.12 | 96.15 | 96.05 | 94.92 | 98.40 | 97.18 | 96.05 | 97.74 | 98.54 |
| Synthetic grass | 99.80 | 97.62 | 99.80 | 99.60 | 97.23 | 87.33 | 100.00 | 93.27 | 96.24 | 100.00 |
| Trees | 98.11 | 96.78 | 92.05 | 98.39 | 99.53 | 97.35 | 96.88 | 96.67 | 97.82 | 100.00 |
| Soil | 98.20 | 95.83 | 96.88 | 96.69 | 100.00 | 99.05 | 97.35 | 99.91 | 99.05 | 100.00 |
| Water | 97.90 | 96.50 | 99.30 | 97.20 | 100.00 | 97.90 | 95.11 | 81.12 | 93.71 | 91.86 |
| Residual | 89.09 | 85.35 | 82.00 | 80.03 | 83.49 | 93.75 | 82.00 | 86.01 | 89.65 | 90.13 |
| Commercial | 54.32 | 47.20 | 59.35 | 57.46 | 92.78 | 94.68 | 57.17 | 75.78 | 88.32 | 95.79 |
| Road | 81.30 | 71.11 | 70.16 | 72.43 | 84.80 | 88.01 | 69.50 | 70.54 | 82.81 | 85.71 |
| Highway | 69.02 | 56.27 | 62.74 | 61.97 | 90.73 | 62.74 | 61.10 | 49.32 | 77.51 | 80.43 |
| Railway | 88.43 | 81.78 | 77.42 | 85.01 | 93.93 | 82.16 | 77.99 | 81.03 | 91.37 | 90.36 |
| Parking lot 1 | 64.65 | 44.19 | 69.74 | 51.97 | 80.60 | 87.61 | 63.31 | 75.41 | 76.08 | 81.13 |
| Parking lot 2 | 69.83 | 60.70 | 77.90 | 40.00 | 77.90 | 81.05 | 74.04 | 82.16 | 76.84 | 83.53 |
| Tennis court | 99.20 | 98.38 | 99.19 | 97.57 | 99.19 | 98.79 | 99.19 | 100.00 | 99.60 | 100.00 |
| Running track | 98.31 | 96.19 | 97.04 | 98.52 | 98.10 | 93.02 | 97.89 | 93.23 | 100.00 | 100.00 |
| OA (%) | 85.32 | 82.14 | 84.91 | 82.56 | 89.12 | 88.34 | 82.97 | 83.45 | 87.89 | 91.70 |
| AA (%) | 86.45 | 83.67 | 85.23 | 83.89 | 90.01 | 89.56 | 84.12 | 84.78 | 88.95 | 92.11 |
| Kappa×100 (%) | 82.38 | 78.14 | 81.29 | 79.01 | 86.32 | 85.27 | 80.03 | 81.05 | 84.21 | 91.00 |
| Class Name | Traditional Classifiers | Deep Learning-Based Methods | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SVM | RF | MLR | KNN | S2ENet | FusAtNet | ViT | SpectralFormer | MTNet | Ours | |
| Apples | 92.45 | 85.30 | 76.57 | 92.96 | 96.29 | 99.85 | 87.81 | 91.91 | 92.73 | 95.89 |
| Buildings | 84.59 | 85.57 | 67.28 | 83.12 | 99.93 | 99.32 | 82.83 | 89.02 | 96.36 | 99.33 |
| Ground | 98.93 | 86.90 | 94.39 | 96.52 | 93.32 | 66.58 | 95.99 | 93.85 | 95.19 | 97.12 |
| Woods | 96.91 | 95.56 | 80.28 | 93.79 | 99.99 | 98.46 | 96.68 | 93.56 | 97.00 | 98.87 |
| Vineyard | 77.67 | 80.94 | 62.46 | 66.68 | 99.74 | 96.40 | 77.47 | 94.60 | 87.63 | 99.77 |
| Roads | 70.22 | 64.65 | 72.18 | 68.91 | 83.55 | 90.47 | 68.58 | 60.98 | 86.11 | 92.31 |
| OA (%) | 84.47 | 83.00 | 72.52 | 82.67 | 97.80 | 95.01 | 84.89 | 87.32 | 92.36 | 98.13 |
| AA (%) | 86.79 | 83.15 | 75.53 | 83.66 | 95.47 | 91.84 | 84.89 | 87.32 | 92.50 | 97.22 |
| Kappa (%) | 79.84 | 77.42 | 63.21 | 77.12 | 96.93 | 93.12 | 79.86 | 83.21 | 89.65 | 97.80 |
| Class Name | Traditional Classifiers | Deep Learning-Based Methods | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SVM | RF | MLR | KNN | S2ENet | FusAtNet | ViT | SpectralFormer | MTNet | Ours | |
| Trees | 82.54 | 82.04 | 80.69 | 81.87 | 87.86 | 93.39 | 80.49 | 85.51 | 83.47 | 92.89 |
| Mostly grass | 81.04 | 79.10 | 81.55 | 80.68 | 86.14 | 84.64 | 81.29 | 75.46 | 79.61 | 87.71 |
| Mixed ground surface | 74.82 | 68.12 | 72.19 | 65.06 | 80.35 | 77.06 | 68.64 | 73.98 | 81.94 | 82.04 |
| Dirt and sand | 84.73 | 82.88 | 84.90 | 75.78 | 94.21 | 92.48 | 86.69 | 86.52 | 90.04 | 95.47 |
| Road | 87.50 | 84.86 | 73.58 | 88.11 | 89.17 | 86.57 | 86.97 | 88.73 | 90.52 | 90.79 |
| Water | 91.77 | 91.46 | 98.42 | 91.46 | 99.68 | 98.42 | 93.67 | 95.25 | 97.15 | 86.14 |
| Building shadow | 88.81 | 87.13 | 85.45 | 84.97 | 93.09 | 89.53 | 83.68 | 88.48 | 83.53 | 91.46 |
| Building | 78.77 | 72.56 | 72.17 | 71.61 | 90.59 | 94.98 | 83.89 | 77.19 | 81.13 | 92.98 |
| Sidewalk | 77.65 | 68.74 | 72.15 | 59.92 | 75.06 | 85.26 | 69.07 | 75.63 | 80.65 | 83.36 |
| Yellow curb | 97.27 | 94.54 | 95.63 | 86.34 | 93.94 | 81.82 | 95.42 | 93.94 | 91.77 | 100.00 |
| Cloth panels | 96.64 | 97.48 | 99.16 | 97.03 | 99.16 | 98.32 | 100.00 | 98.32 | 97.94 | 98.33 |
| OA (%) | 81.55 | 79.43 | 78.90 | 77.33 | 88.76 | 89.12 | 81.89 | 83.45 | 85.67 | 90.89 |
| AA (%) | 85.10 | 82.04 | 81.85 | 80.12 | 89.42 | 89.99 | 84.56 | 85.89 | 86.78 | 90.13 |
| Kappa×100 (%) | 78.42 | 75.89 | 75.21 | 73.24 | 86.79 | 87.32 | 78.54 | 81.23 | 83.21 | 89.35 |
| Dataset | Complexity | S2ENet | FusAtNet | ViT | SpectralFormer | MTNet | Ours |
|---|---|---|---|---|---|---|---|
| Houston | Parameters (M) | 0.289 | 37.315 | 0.089 | 0.279 | 0.308 | 0.41 |
| Training Time (s) | 261.31 | 1588.20 | 323.07 | 411.78 | 397.16 | 260.78 | |
| Trento | Parameters (M) | 0.172 | 41.073 | 0.089 | 0.131 | 0.127 | 0.19 |
| Training Time (s) | 77.31 | 399.74 | 73.15 | 79.48 | 81.74 | 76.61 | |
| MUUFL | Parameters (M) | 0.165 | 38.54 | 0.089 | 0.176 | 0.173 | 0.142 |
| Training Time (s) | 142.74 | 790.15 | 159.74 | 181.74 | 179.41 | 149.81 |
| Transformer | First Stage | Second Stage | Houston (OA) | Trento (OA) | MUUFL (OA) |
|---|---|---|---|---|---|
| ✓ | 83.01 | 89.95 | 82.75 | ||
| ✓ | ✓ | 88.34 | 92.34 | 88.26 | |
| ✓ | ✓ | 86.97 | 95.67 | 81.86 | |
| ✓ | ✓ | ✓ | 92.21 | 98.03 | 91.39 |
| Methods | Houston (OA) | Trento (OA) | MUUFL (OA) |
|---|---|---|---|
| Input-level prompt strategy | 87.34 | 95.91 | 90.17 |
| Cross-attention-based prompt | 92.21 | 98.03 | 91.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Yuan, X.; Yang, S.; Fu, G.; Zhao, C.; Xiong, F. Multimodal Prompt Tuning for Hyperspectral and LiDAR Classification. Remote Sens. 2025, 17, 2826. https://doi.org/10.3390/rs17162826
Liu Z, Yuan X, Yang S, Fu G, Zhao C, Xiong F. Multimodal Prompt Tuning for Hyperspectral and LiDAR Classification. Remote Sensing. 2025; 17(16):2826. https://doi.org/10.3390/rs17162826
Chicago/Turabian StyleLiu, Zhengyu, Xia Yuan, Shuting Yang, Guanyiman Fu, Chunxia Zhao, and Fengchao Xiong. 2025. "Multimodal Prompt Tuning for Hyperspectral and LiDAR Classification" Remote Sensing 17, no. 16: 2826. https://doi.org/10.3390/rs17162826
APA StyleLiu, Z., Yuan, X., Yang, S., Fu, G., Zhao, C., & Xiong, F. (2025). Multimodal Prompt Tuning for Hyperspectral and LiDAR Classification. Remote Sensing, 17(16), 2826. https://doi.org/10.3390/rs17162826









