Automated Landform Classification from InSAR-Derived DEMs Using an Enhanced Random Forest Model for Urban Transportation Corridor Hazard Assessment
Abstract
1. Introduction
- (1)
- We develop a fully automated landform classification framework tailored for highway corridor hazard assessment, leveraging high-resolution InSAR-derived DEMs.
- (2)
- We introduce a novel hybrid sampling strategy that effectively addresses class imbalance in landform datasets, significantly improving the recognition of minority landform types.
- (3)
- We provide a comprehensive evaluation of the proposed method against existing approaches, demonstrating its superiority in terms of classification completeness and accuracy.
2. Study Area
3. DEM Acquisition and Preprocessing
3.1. DEM Acquisition
3.2. DEM Sample Preprocessing
4. Methodology
4.1. Overview
4.2. RF Classification
4.3. Hybrid Sampling Algorithm
4.3.1. ODR Algorithm
- Based on the k-item nearest neighbors of all samples in the sample set T, mine and combine the minimum set of domain chains of this item and then form a chain table of associated sets about the sample set M according to the minimum set of domain chains of each sample in T.
- For all samples q in the majority class sample set M, the KNN algorithm is used to discriminate the samples in its associated set, and the number of correct judgments is set to A. Subsequently, delete q from the nearest neighbors of the sample set until the k + 1 nearest neighbors are added, then use the KNN algorithm to discriminate the results, and the number of correct judgments is set to B.
- Compare the values of A and B. If A > B, remove sample q as it is considered to have little effect on the classification of the training sample set T. Conversely, sample q is considered to have a large effect on the classifier.
- Compute the nearest opposing sample of all samples in M in the training sample set T and find the Euclidean distance ZP between them.
- According to the value of A − B from large to small (only in the case of A − B > 0), if the value of A − B is the same, the order of ZP from small to large is optimized. Then the majority class samples are deleted successively until the number of majority class samples decreases to the specified number, and the algorithm ends.
4.3.2. SVM-SMOTE Algorithm
4.4. Proposed Classifier for Highway Landform
- Dynamic Subset Generation: The process begins with the full “Highway Landform Training Set”. For each of the n decision trees to be built in the forest, a random sampling parameter αi (where i ranges from 1 to n) is generated within a predefined range. This parameter dictates the extent of undersampling for the majority class, ensuring that each tree’s subsequent training data will differ in size and composition. This step is critical for maintaining the diversity of the ensemble, a key factor for the model’s generalization ability.
- Hybrid Balancing: A hybrid sampling strategy, combining the ODR algorithm and the SVM-SMOTE algorithm, is then applied to the original training data based on the parameter αi. The ODR algorithm first removes a number of redundant majority class samples, followed by the SVM-SMOTE algorithm, which synthesizes new, high-quality minority class samples in data-sparse regions. This dual approach creates a “Training Subset i” that is not only numerically balanced but also features well-defined class boundaries.
- Ensemble Training and Voting: Each of the n “Training Subsets” is then used to train its corresponding “Decision Tree i”, yielding an individual “Result i”. Because each tree is trained on a unique and balanced dataset, it can adequately learn the characteristics of the minority classes without being overwhelmed by the majority classes. Finally, the individual results from all n decision trees are aggregated, and the final “Highway Landform Classification Result” is determined through a majority vote.
4.5. Validation
5. Results
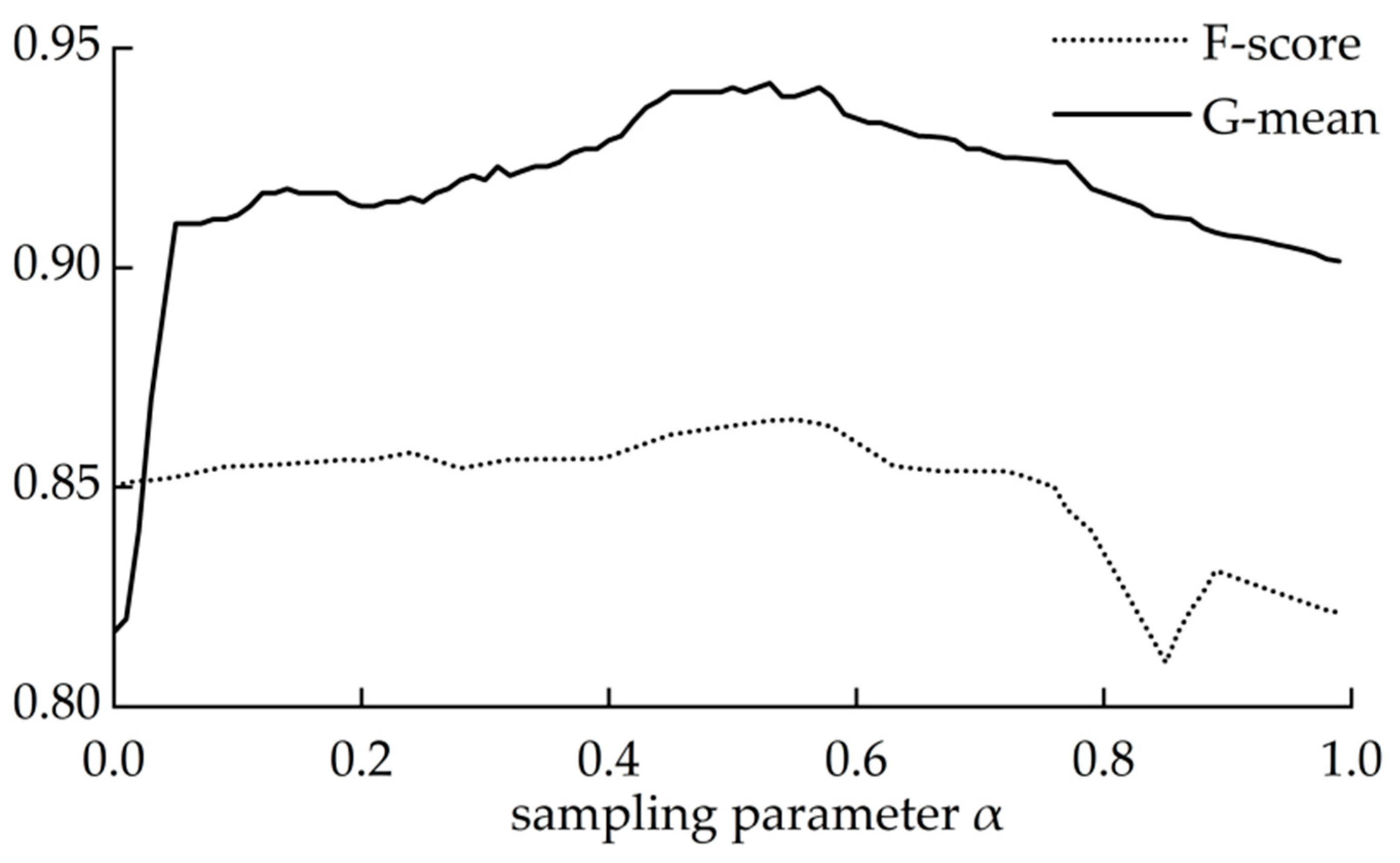
5.1. Parameter Optimization
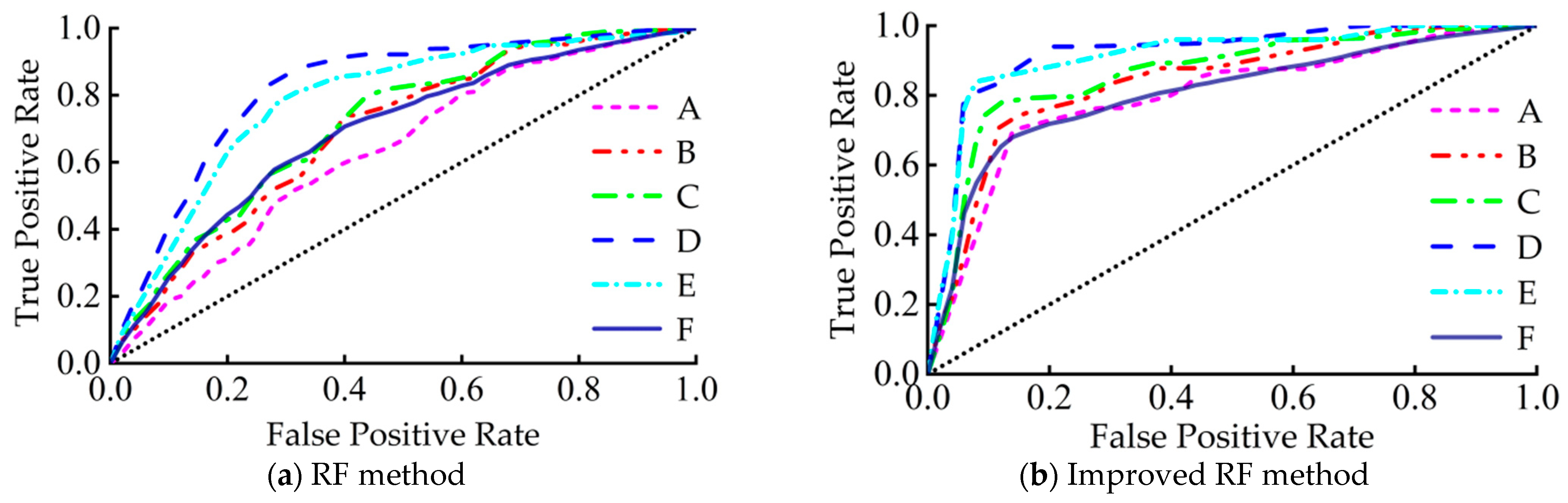
5.2. Accuracy Assessment
5.3. Comparative Classification Mapping
6. Discussion
6.1. Analysis of Classification Completeness
6.2. Comparison Between RF and Improved RF Method
6.3. Critical Evaluation and Practical Implications
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- JTG B01-2014; Technical Standard of Highway Engineering. People’s Communications Press: Beijing, China, 2014.
- JTG D20-2017; Design Specification for Highway Alignment. People’s Communications Press: Beijing, China, 2017.
- Al-Homoud, A.; Masanat, Y. A classification system for the assessment of slope stability of landforms along highway routes in Jordan. Environ. Geol. 1998, 34, 59–69. [Google Scholar] [CrossRef]
- Mihai, B.A.; Robert, D.; Savulescu, I. Geomorphotechnical Map for Railway Mainline Infrastructure Improvement. A case study from Romania. Géomorphologie Relief Process. Environ. 2014, 20, 79–90. [Google Scholar] [CrossRef]
- Hearn, G.; Pettifer, G. The role of engineering geology in the route selection, design and construction of a road across the Blue Nile gorge, Ethiopia. Bull. Eng. Geol. Environ. 2015, 75, 163–191. [Google Scholar] [CrossRef]
- Kadi, F.; Yildirim, F.; Saralioglu, E. Risk analysis of forest roads using landslide susceptibility maps and generation of the optimum forest road route: A case study in Macka, Turkey. Geocarto Int. 2019, 36, 1612–1629. [Google Scholar] [CrossRef]
- Sharma, S.; Bansal, V.K. Location-based planning and scheduling of highway construction projects in hilly landform using GIS. Can. J. Civ. Eng. 2018, 45, 570–582. [Google Scholar] [CrossRef]
- Choi, J.; Kim, S.; Heo, T.-Y.; Lee, J. Safety effects of highway landform types in vehicle crash model of major rural roads. KSCE J. Civ. Eng. 2011, 15, 405–412. [Google Scholar] [CrossRef]
- Oettl, D.; Sturm, P.; Pretterhofer, G.; Bacher, M.; Rodler, J.; Almbauer, R. Lagrangian Dispersion Modeling of Vehicular Emissions from a Highway in Complex landform. J. Air Waste Manag. Assoc. 2003, 53, 1233–1240. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Dang, W.; Liu, F.; Qingmiao, D. Evaluation of Highway Construction Impact on Ecological Environment of QingHai-Tibet Plateau. Environ. Eng. Manag. J. 2020, 19, 1157–1166. [Google Scholar] [CrossRef]
- Li, C.F.; Li, T.B.; Lan, F.; Wang, J.F.; Ren, Y.; Kou, X.M. Research on the distribution law of geohazards along the highways in the Western sichuan plateau gradient zone. Front. Earth Sci. 2025, 13, 1536412. [Google Scholar] [CrossRef]
- Yang, H.Z.; Dong, J.Y.; Guo, X.L. Geohazards and risk assessment along highway in Sichuan Province, China. J. Mt. Sci. 2023, 20, 1695–1711. [Google Scholar] [CrossRef]
- Tempa, K.; Chettri, N.; Aryal, K.R.; Gautam, D. Geohazard vulnerability and condition assessment of the Asian highway AH-48 in Bhutan. Geomat. Nat. Hazards Risk 2021, 12, 2904–2930. [Google Scholar] [CrossRef]
- Dong, Y.T.; Liu, B.B.; Zhang, L.; Liao, M.S.; Zhao, J. Fusion of Multi-Baseline and Multi-Orbit InSAR DEMs with landform Feature-Guided Filter. Remote Sens. 2018, 10, 1511. [Google Scholar] [CrossRef]
- Liu, S.J.; Tang, H.C.; Feng, Y.J.; Chen, Y.L.; Lei, Z.K.; Wang, J.F.; Tong, X.H. A Comparative Study of DEM Reconstruction Using the Single-Baseline and Multibaseline InSAR Techniques. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8512–8521. [Google Scholar] [CrossRef]
- Zhou, F.-B.; Meng, F.-Y.; Zou, L.-H.; Zhang, S.-S. A method for automatic classifying strip landforms in road area. J. Highw. Transp. Res. Dev. 2020, 37, 50–56. [Google Scholar] [CrossRef]
- Lei, J.; Li, S.; Fan, D.; Zhou, H.; Gu, F.; Qiu, Y.; Xu, B.; Liu, S.; Du, W.; Yan, Z.; et al. Classification and regionalization of the forming environment of windblown sand disasters along the Tarim Desert Highway. Sci. Bull. 2009, 53, 1–7. [Google Scholar] [CrossRef]
- Qi, H.-L.; Tian, W.-P.; Zhang, X.-R. Index system of landform regionalization for highway in China. Chang’an Daxue Xuebao (Ziran Kexue Ban)/J. Chang. Univ. (Nat. Sci. Ed.) 2011, 31, 33–38. (In Chinese) [Google Scholar] [CrossRef]
- Wang, J.; Li, K.; Shao, Y.; Zhang, F.; Wang, Z.; Guo, X.; Qin, Y.; Liu, X. Analysis of Combining SAR and Optical Optimal Parameters to Classify Typhoon-Invasion Lodged Rice: A Case Study Using the Random Forest Method. Sensors 2020, 20, 7346. [Google Scholar] [CrossRef]
- Singh, J.; Thakur, D.; Ali, F.; Gera, T.; Kwak, K.S. Deep Feature Extraction and Classification of Android Malware Images. Sensors 2020, 20, 7013. [Google Scholar] [CrossRef]
- Sayin, M.O.; Lin, C.-W.; Shiraishi, S.; Shen, J.; Basar, T. Information-Driven Autonomous Intersection Control via Incentive Compatible Mechanisms. IEEE Trans. Intell. Transp. Syst. 2019, 20, 912–924. [Google Scholar] [CrossRef]
- Shieh, J.L.; Haq, Q.M.U.; Haq, M.A.; Karam, S.; Chondro, P.; Gao, D.Q.; Ruan, S.J. Continual Learning Strategy in One-Stage Object Detection Framework Based on Experience Replay for Autonomous Driving Vehicle. Sensors 2020, 20, 6777. [Google Scholar] [CrossRef]
- Veronesi, F.; Hurni, L. Random Forest with semantic tie points for classifying landforms and creating rigorous shaded relief representations. Geomorphology 2014, 224, 152–160. [Google Scholar] [CrossRef]
- Qin, C.Z.; Zhu, A.X.; Qiu, W.L.; Lu, Y.J.; Li, B.-L.; Pei, T. Mapping soil organic matter in small low-relief catchments using fuzzy slope position information. Geoderma 2012, 171–172, 64–74. [Google Scholar] [CrossRef]
- Zhao, W.F.; Xiong, L.Y.; Ding, H.; Tang, G.-A. Automatic recognition of loess landforms using Random Forest method. J. Mt. Sci. 2017, 14, 885–897. [Google Scholar] [CrossRef]
- Csatáriné Szabó, Z.; Mikita, T.; Négyesi, G.; Varga, O.G.; Burai, P.; Takács-Szilágyi, L.; Szabó, S. Uncertainty and Overfitting in Fluvial Landform Classification Using Laser Scanned Data and Machine Learning: A Comparison of Pixel and Object-Based Approaches. Remote Sens. 2020, 12, 3652. [Google Scholar] [CrossRef]
- Huda, S.; Yearwood, J.; Jelinek, H.F.; Hassan, M.M.; Fortino, G.; Buckland, M. A Hybrid Feature Selection with Ensemble Classification for Imbalanced Healthcare Data: A Case Study for Brain Tumor Diagnosis. IEEE Access 2016, 4, 9145–9154. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Zhang, X.; Qi, D. Deep Learning Intrusion Detection Model Based on Optimized Imbalanced Network Data. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 8–11 October 2018; pp. 1128–1132. [Google Scholar] [CrossRef]
- Gao, W.; Huang, L.; Liu, S.; Dai, C. Artificial Bee Colony Algorithm Based on Information Learning. IEEE Trans. Cybern. 2015, 45, 2827–2839. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Batista, G.E.A.P.A.; Prati, R.C.; Monard, M.C. A study of the behavior of several methods for balancing machine learning training data. SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Lin, W.C.; Tsai, C.F.; Hu, Y.H.; Jhang, J.S. Clustering-based undersampling in class-imbalanced data. Inf. Sci. 2017, 409–410, 17–26. [Google Scholar] [CrossRef]
- Chawla, N.; Bowyer, K.; Hall, L.; Kegelmeyer, W. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. (JAIR) 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Tao, X.M.; Zhang, D.X.; Hao, S.Y.; Xu, P. Fault detection based on spectral clustering combined with under-sampling SVM under unbalanced datasets. Zhendong Yu Chongji/J. Vib. Shock 2013, 32, 30–36. [Google Scholar] [CrossRef]
- Wang, S.; Minku, L.L.; Yao, X. Resampling-Based Ensemble Methods for Online Class Imbalance Learning. IEEE Trans. Knowl. Data Eng. 2015, 27, 1356–1368. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.-Y.; Mao, B.-H. Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning. In Proceedings of the International Conference on Intelligent Computing, Hefei, China, 23–26 August 2005; Volume 3644, pp. 878–887. [Google Scholar]
- Tao, X.; Li, Q.; Ren, C.; Guo, W.; He, Q.; Liu, R.; Zou, J. Affinity and class probability-based fuzzy support vector machine for imbalanced data sets. Neural Netw. 2020, 122, 289–307. [Google Scholar] [CrossRef] [PubMed]
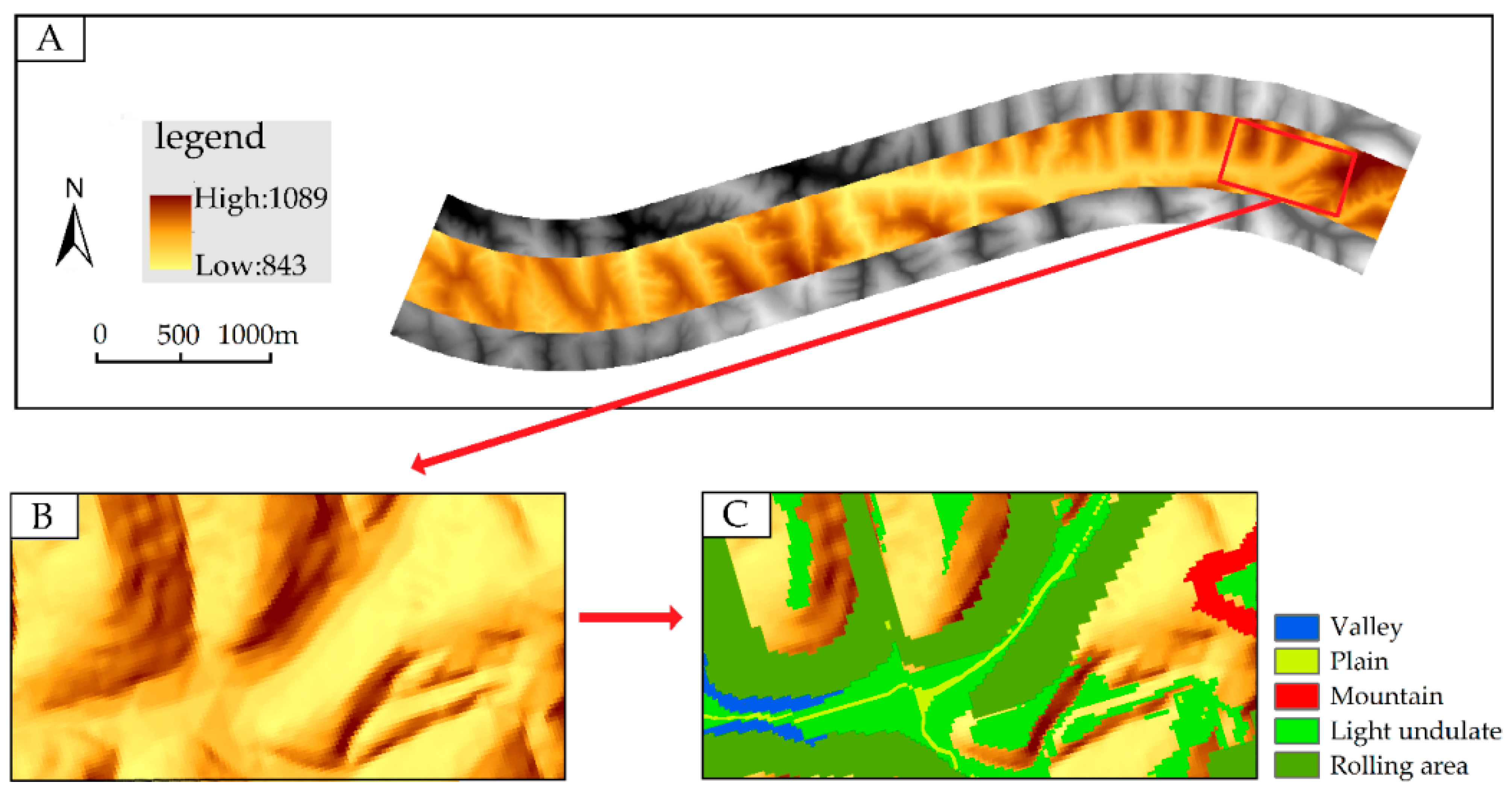



| Landform Types | Factors | ||
|---|---|---|---|
| Slope/(°) | Relative Elevation/(m) | Relief/(m) | |
| valley | 3~7 | / | <50 |
| plain | <3 | / | <30 |
| mountain | >20 | >200 | >120 |
| lightly undulating | 3~20 | <100 | 50–120 |
| rolling area | >20 | 100~200 | 50–120 |
| Landform Types | Training Dataset | Test Dataset | Total | Percentage |
|---|---|---|---|---|
| Valley | 1880 | 470 | 2350 | 2.85% |
| Plain | 1808 | 452 | 2260 | 2.74% |
| Mountain | 1984 | 496 | 2480 | 3.01% |
| Lightly undulating | 29,480 | 7370 | 36,850 | 44.70% |
| Rolling area | 30,808 | 7702 | 38,510 | 46.70% |
| Total | 65,960 | 16,490 | 82,450 | 100% |
| Model | Parameter | Optimal Threshold |
|---|---|---|
| RF algorithm | nFeatures nSamples nTrees | nFeatures = 2 nSamples = 2 nTrees = 500 |
| Hybrid sampling algorithm | k α | K = 5 α ∈ [0.4–0.6] |
| Valley | Plain | Mountain | Lightly Undulating | Rolling Area | |
|---|---|---|---|---|---|
| Valley | 58 | 1 | 0 | 0 | 0 |
| Plain | 0 | 56 | 0 | 0 | 0 |
| Mountain | 0 | 0 | 61 | 1 | 0 |
| Lightly undulating | 1 | 2 | 1 | 915 | 32 |
| Rolling area | 2 | 0 | 2 | 28 | 954 |
| Precision (%) | 96.5 | 95.9 | 96.1 | 98.0 | 99.1 |
| Recall (%) | 95.3 | 96.1 | 95.9 | 98.3 | 98.2 |
| F-score (%) | 95.9 | 96.5 | 96.0 | 98.1 | 98.6 |
| Over accuracy = 0.97; G-mean = 0.95 | |||||
| Study Area | Types | Valley (%) | Plain (%) | Mountain (%) | Lightly UnDulate (%) | Rolling Area (%) | Total (%) | Incomplete (%) |
|---|---|---|---|---|---|---|---|---|
| Study Area A | Rule-based method | 23.6 | 1.0 | 5.6 | 13.8 | 44.1 | 88.1 | 11.9 |
| Traditional RF | 35.0 | 1.0 | 5.6 | 14.3 | 44.1 | 100% | 0.0 | |
| Improved RF | 33.5 | 5.2 | 5.8 | 13.1 | 42.3 | 100.0 | 0.0 | |
| Study Area B | Rule-based method | 20.2 | 11.6 | 1.3 | 14.2 | 39.2 | 86.5 | 13.5 |
| Traditional RF | 33.1 | 11.6 | 1.3 | 14.9 | 39.2 | 100% | 0.0 | |
| Improved RF | 34.5 | 13.8 | 1.5 | 12.9 | 37.3 | 100.0 | 0.0 | |
| Study Area C | Rule-based method | 15.2 | 8.1 | 3.1 | 14.4 | 43.5 | 84.3 | 15.7 |
| Traditional RF | 30.7 | 8.1 | 3.1 | 14.6 | 43.5 | 100% | 0.0 | |
| Improved RF | 29.6 | 9.7 | 4.6 | 15.5 | 40.6 | 100.0 | 0.0 | |
| Study Area D | Rule-based method | 13.8 | 6.8 | 2.3 | 10.9 | 48.7 | 82.4 | 17.6 |
| Traditional RF | 31.3 | 6.8 | 2.3 | 11.0 | 48.7 | 100% | 0.0 | |
| Improved RF | 31.1 | 6.7 | 2.2 | 9.8 | 50.1 | 100.0 | 0.0 |
| Precision | Recall | F-Score | |
|---|---|---|---|
| Traditional RF | 83.8% | 87.1% | 86.5% |
| Improved RF | 97.1% | 96.8% | 97.0% |
| Type | Method | Precision (%) | Recall (%) | F-Score (%) |
|---|---|---|---|---|
| Valley | Traditional RF | 78.0% | 85.0% | 81.5% |
| Improved RF | 96.5% | 95.3% | 95.9% | |
| Plain | Traditional RF | 80.0% | 86.7% | 83.2% |
| Improved RF | 95.9% | 96.1% | 96.5% | |
| Mountain | Traditional RF | 82.0% | 87.0% | 84.5% |
| Improved RF | 96.1% | 95.9% | 96.0% | |
| Lightly undulating | Traditional RF | 86.0% | 91.3% | 88.6% |
| Improved RF | 98.0% | 98.3% | 98.1% | |
| Rolling area | Traditional RF | 87.0% | 89.5% | 88.2% |
| Improved RF | 99.1% | 98.2% | 98.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Hua, Y.; Zhu, J.; Meng, F. Automated Landform Classification from InSAR-Derived DEMs Using an Enhanced Random Forest Model for Urban Transportation Corridor Hazard Assessment. Remote Sens. 2025, 17, 2819. https://doi.org/10.3390/rs17162819
Zhu S, Hua Y, Zhu J, Meng F. Automated Landform Classification from InSAR-Derived DEMs Using an Enhanced Random Forest Model for Urban Transportation Corridor Hazard Assessment. Remote Sensing. 2025; 17(16):2819. https://doi.org/10.3390/rs17162819
Chicago/Turabian StyleZhu, Song, Yuansheng Hua, Jiasong Zhu, and Fanyi Meng. 2025. "Automated Landform Classification from InSAR-Derived DEMs Using an Enhanced Random Forest Model for Urban Transportation Corridor Hazard Assessment" Remote Sensing 17, no. 16: 2819. https://doi.org/10.3390/rs17162819
APA StyleZhu, S., Hua, Y., Zhu, J., & Meng, F. (2025). Automated Landform Classification from InSAR-Derived DEMs Using an Enhanced Random Forest Model for Urban Transportation Corridor Hazard Assessment. Remote Sensing, 17(16), 2819. https://doi.org/10.3390/rs17162819







