Marginal Contribution Spectral Fusion Network for Remote Hyperspectral Soil Organic Matter Estimation
Abstract
1. Introduction
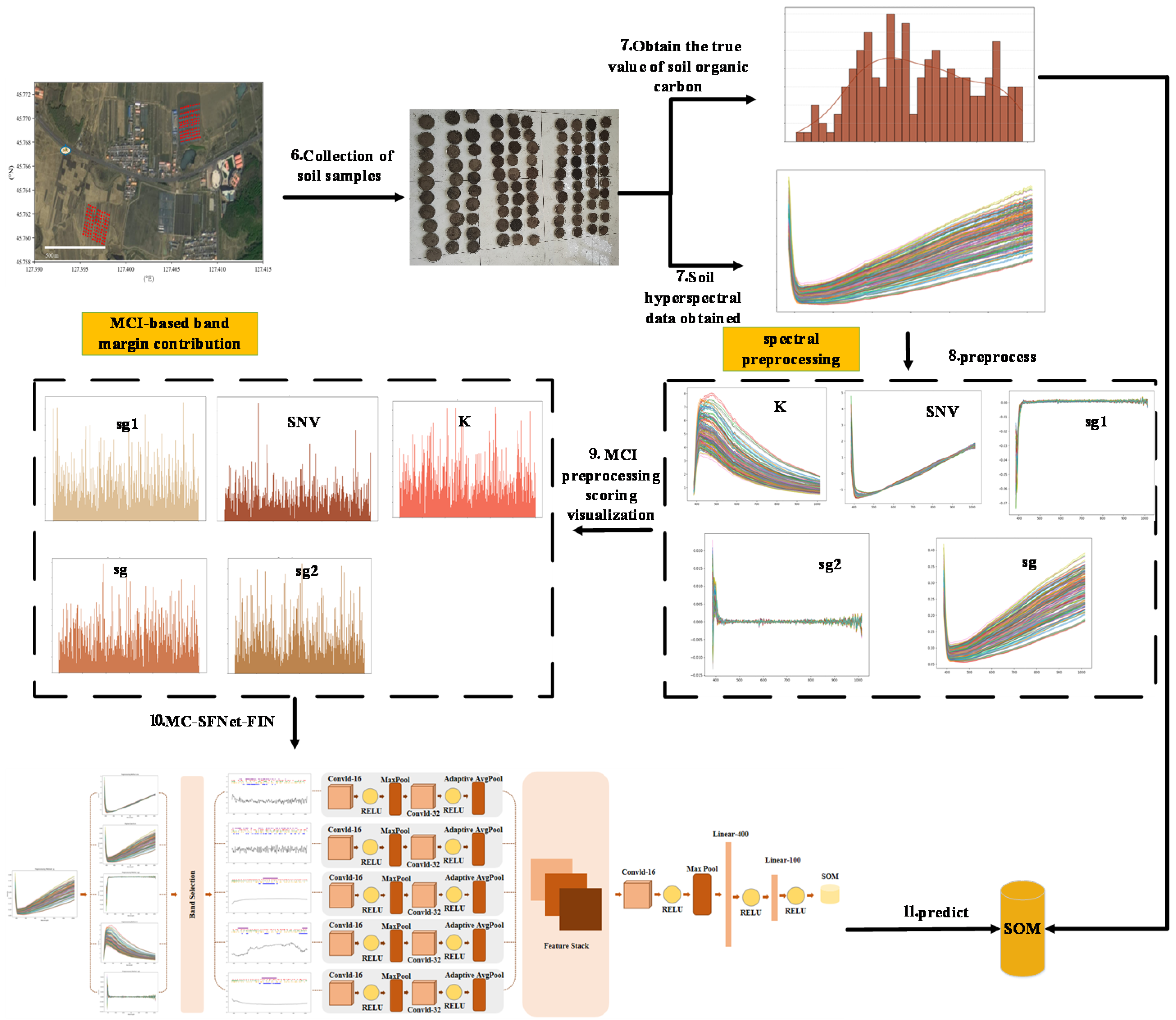
2. Proposed Method
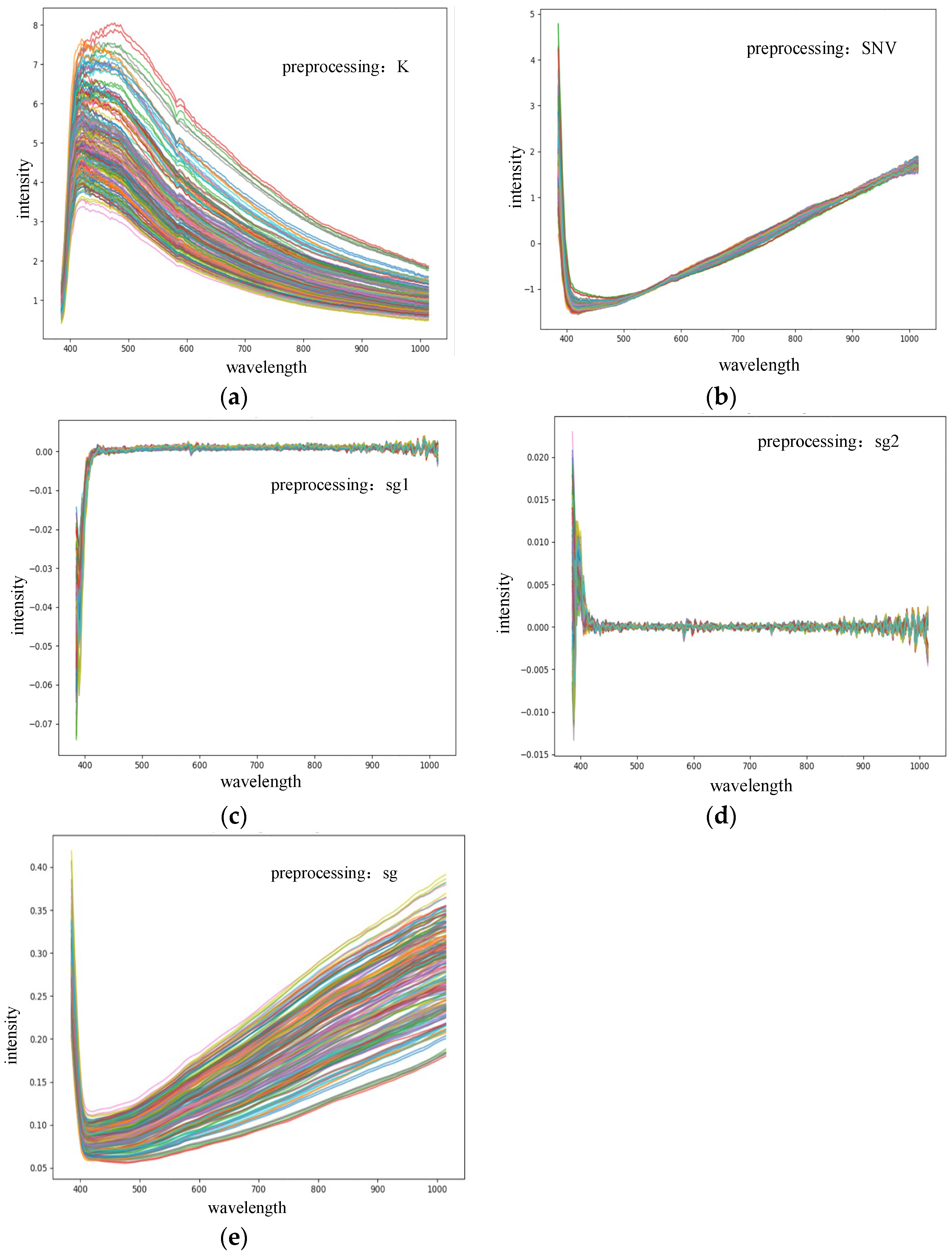
2.1. Spectral Preprocessing
2.2. Unified Permutation–Gain Analysis for Multi-Preprocessed Spectra
2.3. Marginal Contribution-Driven Spectral Fusion Network
3. Experiments
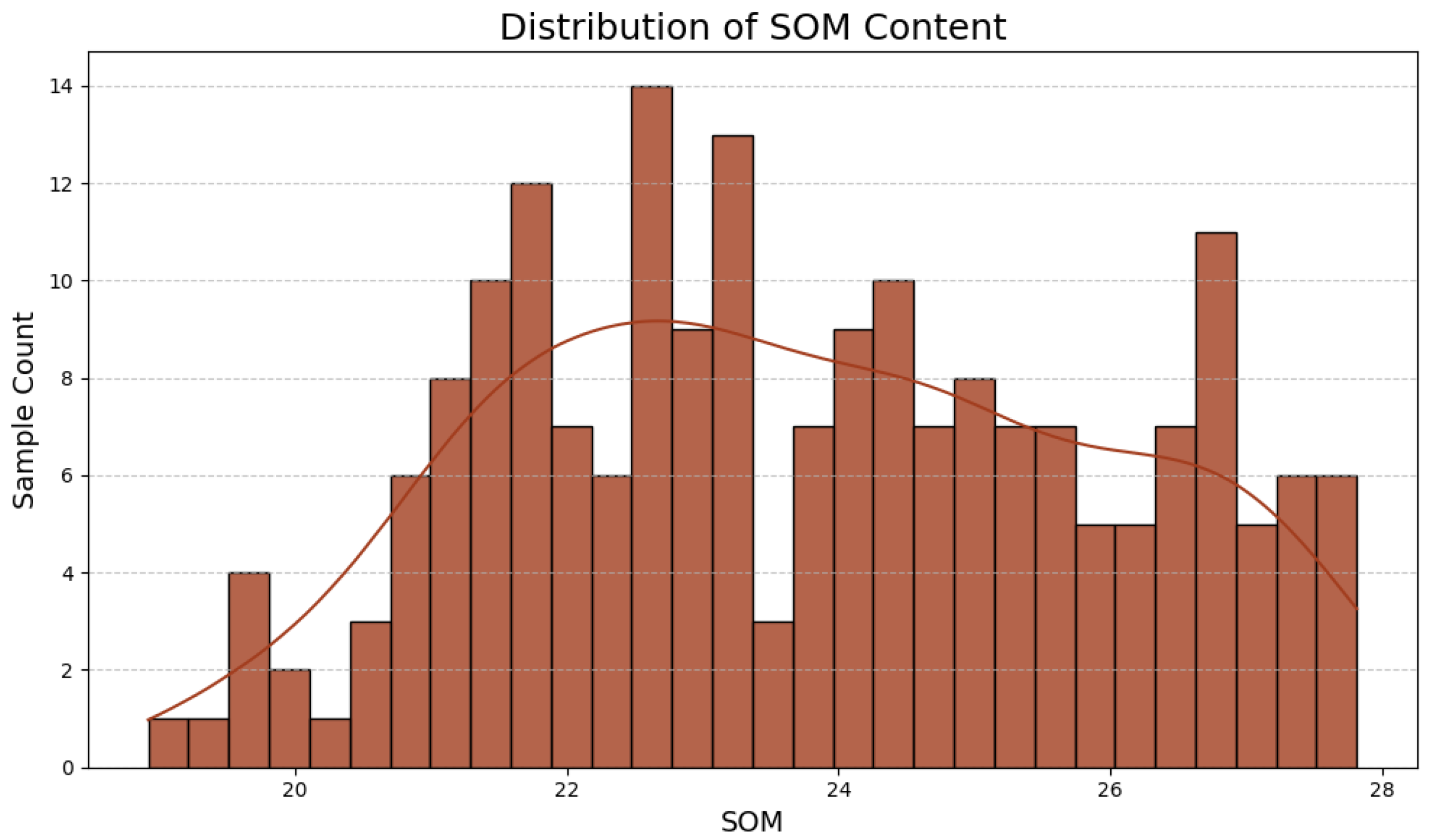
3.1. Experimental Settings
3.2. Evaluation Criteria
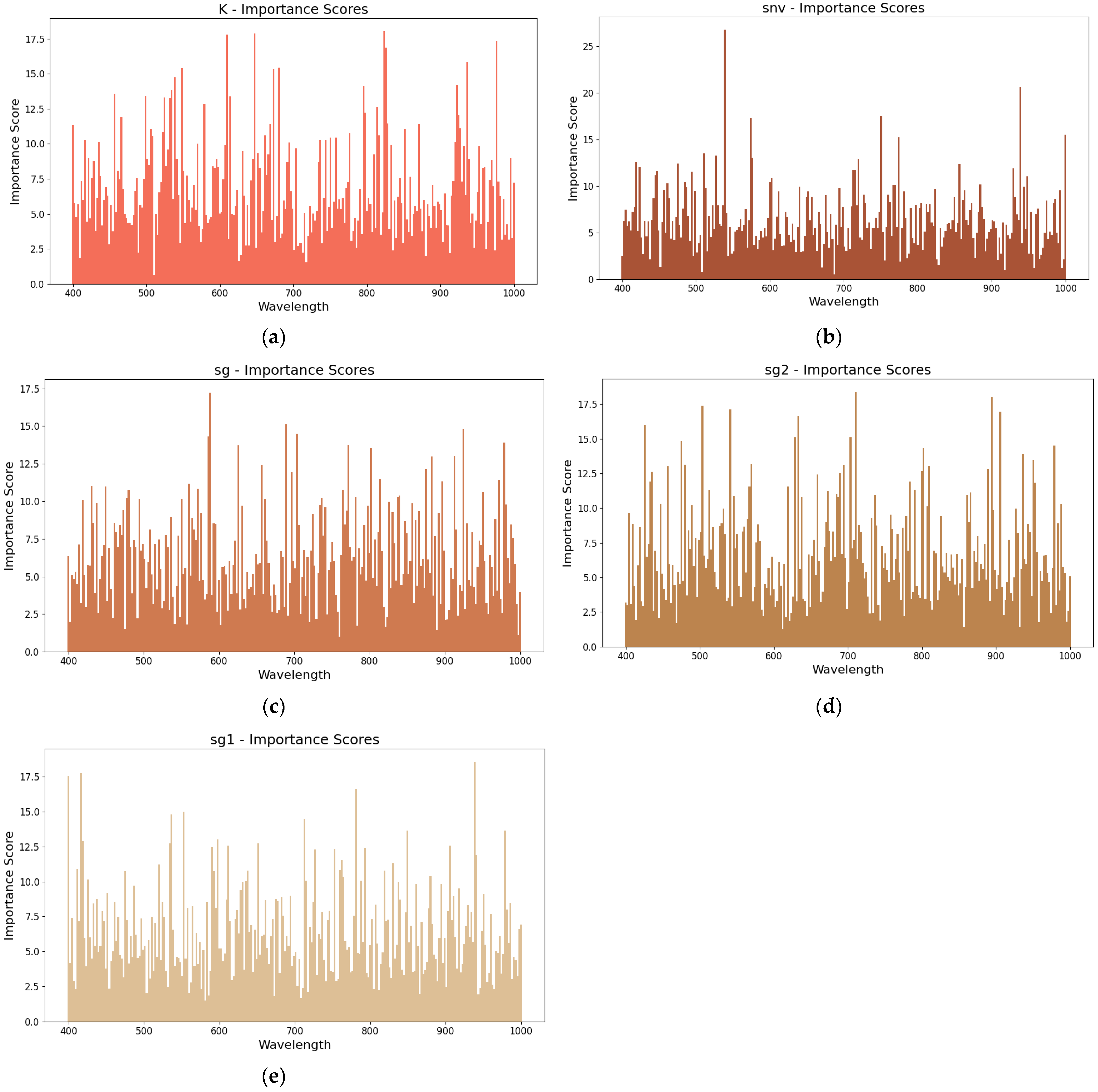
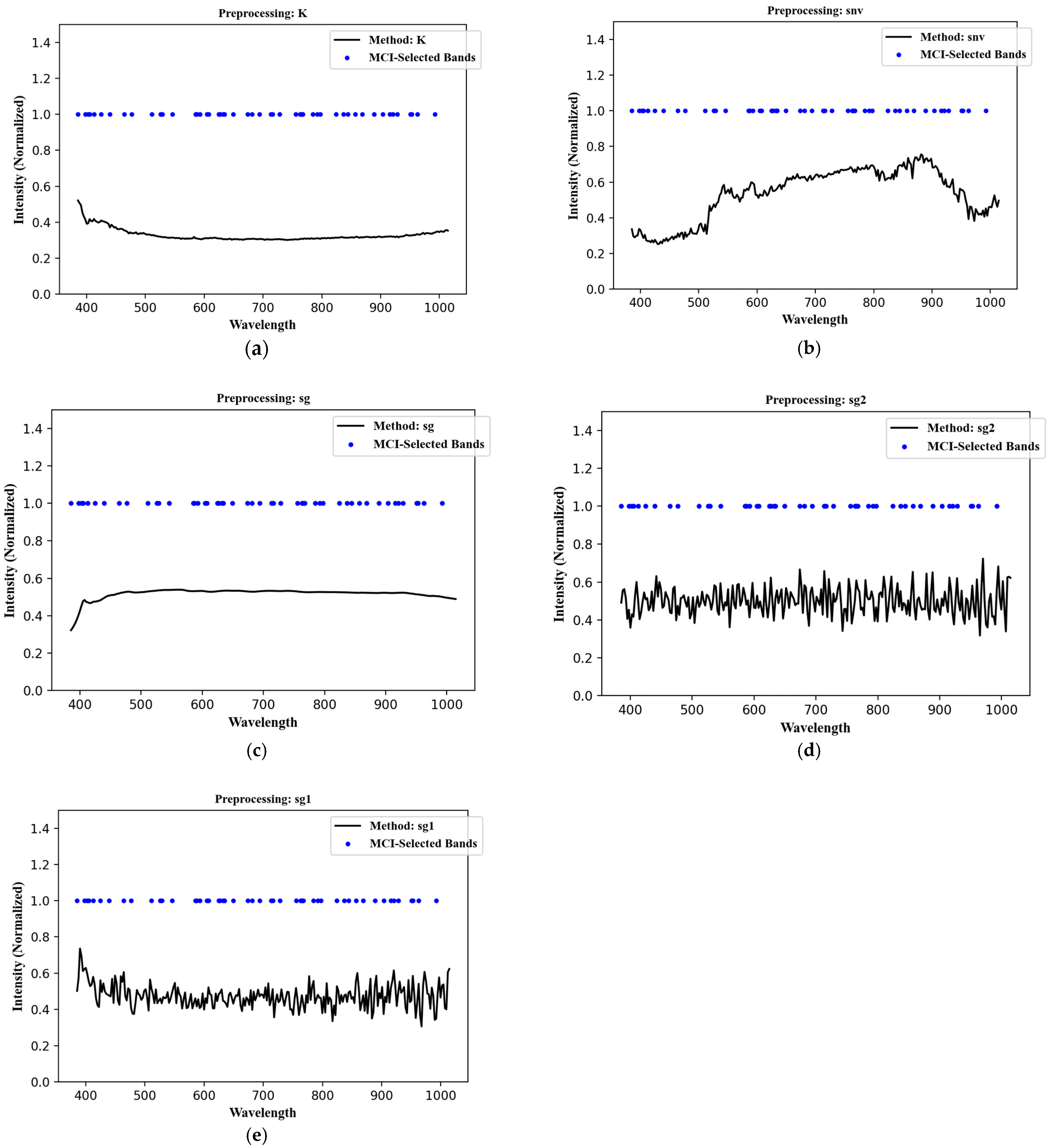
3.3. Interpretation of Wavelength Marginal Contributions
3.4. Comparative Performance Analysis of MC-SFNet
3.5. Generalization of Marginal Contribution-Driven Preprocessing for Enhanced Performance Across Machine Learning Models
3.6. Generalizability Experiments
4. Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Trivedi, M.Y.; Patel, B.I. A study on the impact of agri-entrepreneurship in the development of the agricultural sector resulting in the upliftment of the Indian economy. Int. J. Darshan 2024, 4, 2404. [Google Scholar] [CrossRef]
- Sanchez, P.A.; Ahamed, S.; Carré, F.; Hartemink, A.E.; Hempel, J.; Huising, J.; Lagacherie, P.; McBratney, A.B.; McKenzie, N.J.; Mendonca-Santos, M.d.L.; et al. Digital soil map of the world. Science 2009, 325, 680–681. [Google Scholar] [CrossRef]
- Gerke, J. The central role of soil organic matter in soil fertility and carbon storage. Soil Syst. 2022, 6, 33. [Google Scholar] [CrossRef]
- Tang, J.; Wang, Q.; Liu, D. A novel approach to spectral moisture interference correction for nitrogen and soil organic matter inversion in native black soils: Bayesian-optimized dynamic moisture mitigation. Ecol. Inform. 2025, 90, 103240. [Google Scholar] [CrossRef]
- Stevenson, A.; Zhang, Y.K.; Huang, J.Y.; Hu, J.; Paustian, K.; Hartemink, A.E. Rates of soil organic carbon change in cultivated and afforested sandy soils. Agric. Ecosyst. Environ. 2024, 360, 108785. [Google Scholar] [CrossRef]
- Ma, Y.Q.; Woolf, D.; Fan, M.S.; Qiao, L.; Li, R.; Lehmann, J. Global crop production increase by soil organic carbon. Nat. Geosci. 2023, 16, 1159–1165. [Google Scholar] [CrossRef]
- Lal, R. Soil carbon sequestration impacts on global climate change and food security. Science 2004, 304, 1623–1627. [Google Scholar] [CrossRef] [PubMed]
- Futa, B.; Gmitrowicz-Iwan, J.; Skersienė, A.; Šlepetienė, A.; Parašotas, I. Innovative soil management strategies for sustainable agriculture. Sustainability 2024, 16, 9481. [Google Scholar] [CrossRef]
- Shen, L.; Gao, M.; Yan, J.; Li, Z.-L.; Leng, P.; Yang, Q.; Duan, S.-B. Hyperspectral estimation of soil organic matter content using different spectral pre-processing techniques and PLSR method. Remote Sens. 2020, 12, 1206. [Google Scholar] [CrossRef]
- Francos, N.; Nasta, P.; Allocca, C.; Sica, B.; Mazzitelli, C.; Lazzaro, U.; D’urso, G.; Belfiore, O.R.; Crimaldi, M.; Sarghini, F.; et al. Mapping soil organic carbon stock using hyperspectral remote sensing: A case study in the Sele River Plain in Southern Italy. Remote Sens. 2024, 16, 897. [Google Scholar] [CrossRef]
- Yan, Y.; Yang, J.; Li, B.; Qin, C.; Ji, W.; Xu, Y.; Huang, Y. High-resolution mapping of soil organic matter at the field scale using UAV hyperspectral images with a small calibration dataset. Remote Sens. 2023, 15, 1433. [Google Scholar] [CrossRef]
- Bouslihim, Y.; Bouasria, A.; Minasny, B.; Castaldi, F.; Nenkam, A.M.; El Battay, A.; Chehbouni, A. Soil organic carbon prediction and mapping in Morocco using PRISMA hyperspectral imagery and meta-learner model. Remote Sens. 2025, 17, 1363. [Google Scholar] [CrossRef]
- Bouslihim, Y.; Bouasria, A. Potential of EnMAP hyperspectral imagery for regional-scale soil organic matter mapping. Remote Sens. 2025, 17, 1600. [Google Scholar] [CrossRef]
- Meng, X.; Bao, Y.; Ye, Q.; Liu, H.; Zhang, X.; Tang, H.; Zhang, X. Soil organic matter prediction model with satellite hyperspectral image based on optimized denoising method. Remote Sens. 2021, 13, 2273. [Google Scholar] [CrossRef]
- Cezar, E.; Alberton, T.A.; Lemos, E.F.; de Oliveira, K.M.; Sun, L.; Crusiol, L.G.T.; Rodrigues, M.; Reis, A.S.; Nanni, M.R. Estimating soil organic matter using proximal remote sensing: Performance evaluation of prediction models adjusted at local scale in the Brazilian Cerrado. Remote Sens. 2023, 15, 4397. [Google Scholar] [CrossRef]
- Rasooli, N.; Mirzaei, S.; Pignatti, S. Monitoring gypsiferous soils by leveraging advanced spaceborne hyperspectral imagery via spectral indices and a machine learning approach. Remote Sens. 2025, 17, 1914. [Google Scholar] [CrossRef]
- Lima, A.A.J.; Lopes, J.C.; Lopes, R.P.; de Figueiredo, T.; Vidal-Vázquez, E.; Hernández, Z. Soil organic carbon assessment using remote-sensing data and machine learning: A systematic literature review. Remote Sens. 2025, 17, 882. [Google Scholar] [CrossRef]
- Li, T.; Cui, L.; Wu, Y.; McLaren, T.I.; Xia, A.; Pandey, R.; Liu, H.; Wang, W.; Xu, Z.; Song, X.; et al. Soil organic carbon estimation via remote sensing and machine learning techniques: Global topic modeling and research trend exploration. Remote Sens. 2024, 16, 3168. [Google Scholar] [CrossRef]
- Nelson, D.W.; Sommers, L.E. Total carbon, organic carbon, and organic matter. In Methods of Soil Analysis, Part 3: Chemical Methods; Sparks, D.L., Ed.; Soil Science Society of America: Madison, WI, USA, 1996; pp. 961–1010. [Google Scholar] [CrossRef]
- Aj, S.; Adhikari, K.; Dharumarajan, S.; Lalitha, M. Remote sensing and geographic information system applications in mapping and assessment of soil resources. In Remote Sensing of Soils; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar] [CrossRef]
- Vavlas, N.-C.; Porre, R.; Meng, L.; Elhakeem, A.; van Egmond, F.; Kooistra, L.; De Deyn, G.B. Cover crop impacts on soil organic matter dynamics and its quantification using UAV and proximal sensing. Smart Agric. Technol. 2024, 9, 100621. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Webster, R. Predicting soil properties from the Australian soil visible–near infrared spectroscopic database. Eur. J. Soil Sci. 2012, 63, 848–860. [Google Scholar] [CrossRef]
- Shi, T.; Cui, L.; Wang, J.; Fei, T.; Chen, Y.; Wu, G. Comparison of multivariate methods for estimating soil total nitrogen with visible/near-infrared spectroscopy. Plant Soil 2013, 366, 363–375. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, J.L.; Tang, Y.L. Estimation and inversion of soil heavy metal arsenic (As) based on UAV hyperspectral platform. Microchem. J. 2024, 207, 112027. [Google Scholar] [CrossRef]
- Sun, M.; Yang, Y.; Li, S.; Yin, D.; Zhong, G.; Cao, L. A study on hyperspectral soil total nitrogen inversion using a hybrid deep learning model CBiResNet-BiLSTM. Chem. Biol. Eng. Q. 2024, 11, 157. [Google Scholar] [CrossRef]
- Zhong, Q.; Eziz, M.; Ainiwaer, M.; Sawut, R.; Hou, M. Hyperspectral estimation of mercury content of soil in oasis city in arid zones of China. Geocarto Int. 2024, 39, 2299147. [Google Scholar] [CrossRef]
- Subi, X.; Eziz, M.; Zhong, Q.; Li, X.G. Estimating the chromium concentration of farmland soils in an arid zone from hyperspectral reflectance by using partial least squares regression methods. Ecol. Indic. 2024, 161, 111987. [Google Scholar] [CrossRef]
- Zhao, W.; Wu, Z.; Yin, Z.; Li, D. Attention-based CNN ensemble for soil organic carbon content estimation with spectral data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6013105. [Google Scholar] [CrossRef]
- Kawamura, K.; Nishigaki, T.; Andriamananjara, A.; Rakotonindrina, H.; Tsujimoto, Y.; Moritsuka, N.; Rabenarivo, M.; Razafimbelo, T. Using a one-dimensional convolutional neural network on visible and near-infrared spectroscopy to improve soil phosphorus prediction in Madagascar. Remote Sens. 2021, 13, 1519. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Q.; Li, J. Soil moisture prediction using deep learning methods and hyperspectral data. Environ. Sci. Technol. 2023, 57, 789–801. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Wei, Y. Soil texture classification based on hyperspectral data and convolutional neural networks. J. Soil Sci. Environ. Manage. 2023, 45, 1123–1134. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, W.; Li, H.; Zhang, H.; Li, M.Z. Development of a vehicle-mounted soil organic matter detection system based on near-infrared spectroscopy and image information fusion. Measurement Sci. Technol. 2024, 35, 045501. [Google Scholar] [CrossRef]
- Patel, A.K.; Ghosh, J.K.; Pande, S.; Sayyad, S.U. Deep-learning-based approach for estimation of fractional abundance of nitrogen in soil from hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6495. [Google Scholar] [CrossRef]
- Barra, I.; Haefele, S.M.; Sakrabani, R.; Kebede, F. Soil spectroscopy with the use of chemometrics, machine learning and pre-processing techniques in soil diagnosis: Recent advances—A review. Trends Anal. Chem. 2021, 135, 116166. [Google Scholar] [CrossRef]
- Zhang, M.; Li, M.; Liu, W.; Cui, L.; Li, W.; Wang, H.; Wei, Y.; Guo, Z.; Wang, D.; Hu, Y.; et al. Analyzing the performance of statistical models for estimating leaf nitrogen concentration of Phragmites australis based on leaf spectral reflectance. Spectrosc. Lett. 2019, 52, 483–491. [Google Scholar] [CrossRef]
- He, J.; Liu, G.; Li, W.; Li, Z.; Li, Z. Inversion analysis of soil nitrogen content using hyperspectral images with different pre-processing methods. Ecol. Inform. 2023, 78, 102381. [Google Scholar] [CrossRef]
- Xu, X.B.; Ma, F.; Zhou, J.M.; Du, C.W. Applying convolutional neural networks (CNN) for end-to-end soil analysis based on laser-induced breakdown spectroscopy (LIBS) with less spectral pre-processing. Comput. Electron. Agric. 2022, 199, 107171. [Google Scholar] [CrossRef]
- Catav, A.; Fu, B.; Zoabi, Y.; Weiss-Meilik, A.; Shomron, N.; Ernst, J.; Sankararaman, S.; Gilad-Bachrach, R. Marginal contribution feature importance—An axiomatic approach for explaining data. Proc. Mach. Learn. Res. 2021, 139, 1324–1335. [Google Scholar] [CrossRef]
- Ye, S.; Weng, H.; Xiang, L.; Jia, L.; Xu, J. Synchronously predicting tea polyphenol and epigallocatechin gallate in tea leaves using Fourier transform–near-infrared spectroscopy and machine learning. Molecules 2023, 28, 5379. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Yang, H.; Zhang, S.; Li, L. Detection of defective features in Cerasus Humilis fruit based on hyperspectral imaging technology. Appl. Sci. 2023, 13, 3279. [Google Scholar] [CrossRef]
- Liu, X.; Tang, X.; Guo, J.; Lin, L.; Huang, F.; Robert, E. Concentration prediction of imidacloprid in water through the combination of Fourier transform infrared spectral data and 1D CNN with multilevel feature fusion. Desalination Water Treat. 2022, 274, 130–139. [Google Scholar] [CrossRef]
- Ou, D.; Tan, K.; Li, J.; Wu, Z.; Zhao, L.; Ding, J.; Wang, X.; Zou, B. Prediction of soil organic matter by Kubelka–Munk based airborne hyperspectral moisture removal model. Int. J. Appl. Earth Obs. Geoinf. 2023, 124, 103493. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Ji, R.; Wang, M.; Zheng, L. A deep learning-based method for screening soil total nitrogen characteristic wavelengths. Comput. Electron. Agric. 2021, 187, 106228. [Google Scholar] [CrossRef]
- Ma, X.; Wang, J.; Zhou, K.; Zhang, W.; Zhang, Z.; Zhou, S.; Bai, Y.; De Maeyer, P.; Van de Voorde, T. Quantitative evaluation of the impact of band optimization methods on the accuracy of the hyperspectral metal element inversion models. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104011. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, J.T.; Zhao, D. Band selection method for retrieving soil lead content with hyperspectral remote sensing data. In Earth Resources and Environmental Remote Sensing-GIS Applications; Michel, U., Civco, D.L., Eds.; Proceedings of SPIE 2010; SPIE: Bellingham, WA, USA, 2010; Volume 7831, p. 78311K. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, X.Y.; Cai, W.S.; Shao, X.G. Combination of heuristic optimal partner wavelengths for variable selection in near-infrared spectral analysis. J. Chemom. 2018, 32, e2971. [Google Scholar] [CrossRef]
- Chander Goud, S.; Subhash, O.; Goud, C.; Sarma, T.H.; Bindu, C.S. Optimal wavelength selection in hyperspectral images using improved K-means clustering with spectral similarity measures. In Proceedings of the 2023 IEEE International Conference on Artificial Intelligence in Engineering and Technology (IICAIET), Kota Kinabalu, Malaysia, 12–14 September 2023. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.L. Deep spectral clustering with regularized linear embedding for hyperspectral image clustering. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5509311. [Google Scholar] [CrossRef]
- Liu, B.Y.; Guo, B.F.; Zhuo, R.X.; Dai, F. Estimation of soil organic carbon content by Vis-NIR spectroscopy combining feature selection algorithm and local regression method. Rev. Bras. Cienc. Solo 2023, 47, e0230067. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems; 2017; pp. 4765–4774. Available online: https://dl.acm.org/doi/10.5555/3295222.3295230 (accessed on 8 August 2025).
- Zhong, L.; Guo, X.; Ding, M.; Ye, Y.; Zhu, Q.; Guo, J.; Wu, J.; Zeng, X. Spatial mapping of topsoil total nitrogen in mountainous and hilly areas of southern China using a continuous convolution neural network. Catena 2023, 229, 107228. [Google Scholar] [CrossRef]
- Misbah, K.; Laamrani, A.; Voroney, P.; Khechba, K.; Casa, R.; Chehbouni, A. Ensemble band selection for quantification of soil total nitrogen levels from hyperspectral imagery. Remote Sens. 2024, 16, 2549. [Google Scholar] [CrossRef]
- Pan, S.; Liu, Z.; Han, Y.; Zhang, D.; Zhao, X.; Li, J.; Wang, K. Using the Pearson’s correlation coefficient as the sole metric to measure the accuracy of quantitative trait prediction: Is it sufficient? Front. Plant Sci. 2024, 15, 1480463. [Google Scholar] [CrossRef]
- Gao, Z.L.; Wang, W.Q.; Wang, H.J.; Li, R.Y. Selection of spectral parameters and optimization of estimation models for soil total nitrogen content during fertilization period in apple orchards. Horticulturae 2024, 10, 358. [Google Scholar] [CrossRef]
- Ma, Y.; Jiang, Q.G.; Meng, Z.G.; Liu, H.X. Black soil organic matter content estimation using hybrid selection method based on RF and GABPSO. Spectrosc. Spect. Anal. 2018, 38, 181–187. [Google Scholar]
- Hati, K.M.; Sinha, N.; Mohanty, M.; Jha, P.; Londhe, S.; Sila, A.; Towett, E.; Chaudhary, R.; Jayaraman, S.; Vassanda Coumar, M.; et al. Mid-infrared reflectance spectroscopy for estimation of soil properties of Alfisols from Eastern India. Sustainability 2022, 14, 94883. [Google Scholar] [CrossRef]
- Shen, Z.; Viscarra Rossel, R.A. Automated spectroscopic modelling with optimised convolutional neural networks. Sci. Rep. 2021, 11, 208. [Google Scholar] [CrossRef] [PubMed]
- Zhong, L.; Guo, X.; Ding, M.; Ye, Y.; Jiang, Y.; Zhu, Q.; Li, J. SHAP values accurately explain the difference in modeling accuracy of convolution neural network between soil full-spectrum and feature-spectrum. Comput. Electron. Agric. 2024, 217, 108627. [Google Scholar] [CrossRef]
- Cao, L.; Sun, M.; Yang, Z.; Jiang, D.; Yin, D.; Duan, Y. A Novel Transformer-CNN Approach for Predicting Soil Properties from LUCAS Vis-NIR Spectral Data. Agronomy 2024, 14, 1998. [Google Scholar] [CrossRef]
- Canero, F.M.; Rodriguez-Galiano, V.; Aragones, D. Machine Learning and Feature Selection for Soil Spectroscopy: An Evaluation of Random Forest Wrappers to Predict Soil Organic Matter, Clay, and Carbonates. Heliyon 2024, 10, e30228. [Google Scholar] [CrossRef]
- Lin, L.; Gao, Z.; Liu, X. Estimation of soil total nitrogen using the synthetic color learning machine (SCLM) method and hyperspectral data. Geoderma 2020, 380, 114664. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
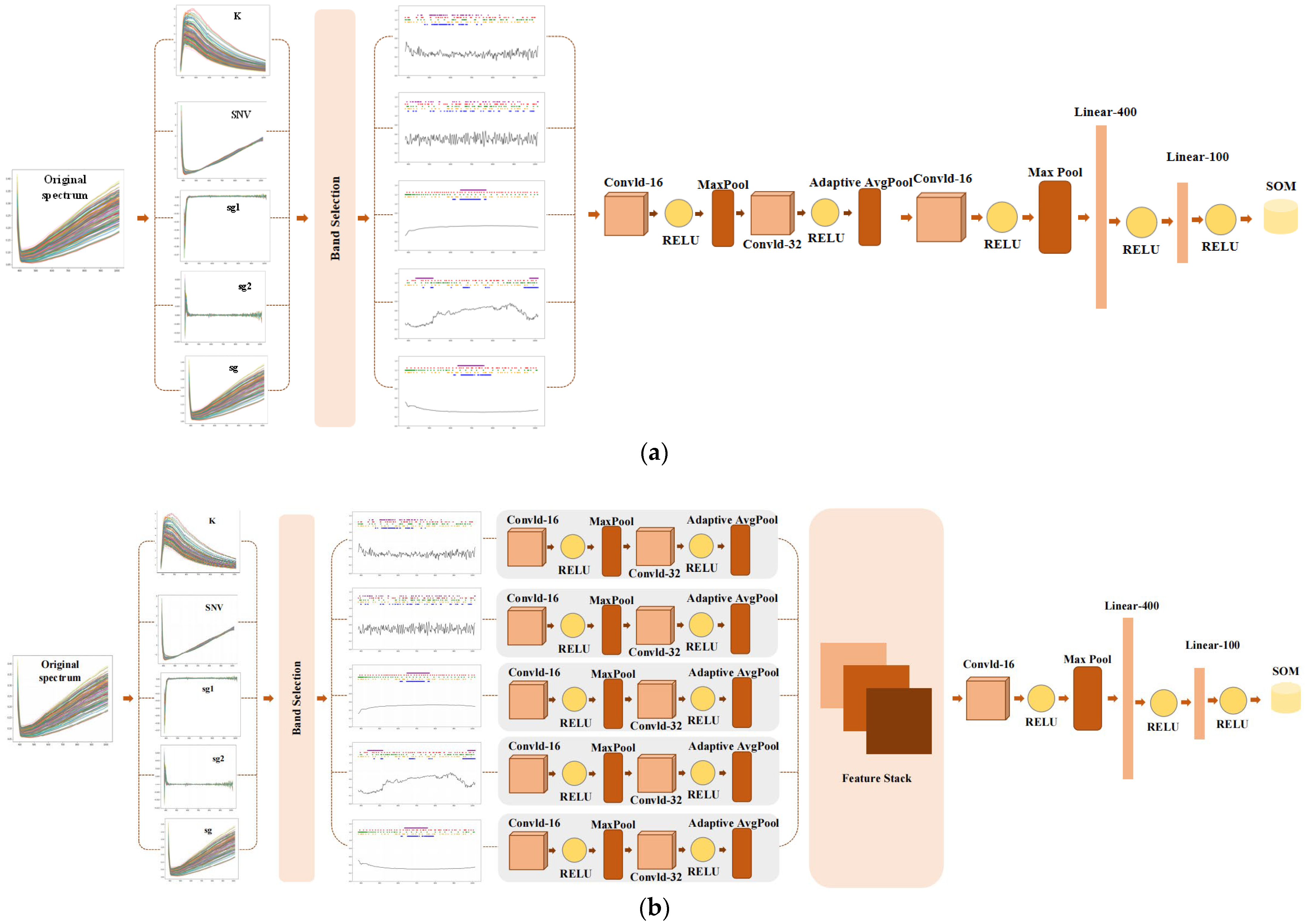

| Layer Type | Output Shape |
|---|---|
| Input | (batch_size, preprocess, features) |
| Conv1d | (batch_size, 16, features) |
| Max Pooling | (batch_size, 16, features/2) |
| Conv1d | (batch_size, 32, features/2) |
| Max Pooling | (batch_size, 32, features/4) |
| Adaptive Pooling | (batch_size, 32, 128) |
| Global Conv1d | (batch_size, 32, global_output) |
| Linear Layer 1 | (batch_size, 400) |
| ReLU | (batch_size, 400) |
| Linear Layer 2 | (batch_size, 100) |
| ReLU | (batch_size, 100) |
| Output | (batch_size, 1) |
| Model | |||||||
|---|---|---|---|---|---|---|---|
| RF [55] | plsr [56] | svm [57] | 1D-CNN [58] | Transformer [59] | MC-SFNet-WIN | MC-SFNetFIN | |
| R2 | 0.73 ± 0.09 | 0.59 ± 0.08 | 0.72 ± 0.10 | 0.71 ± 0.15 | 0.75 ± 0.14 | 0.78 ± 0.09 | 0.80 ± 0.08 |
| RMSE | 1.11 ± 0.19 | 1.37 ± 0.07 | 1.13 ± 0.17 | 1.15 ± 0.27 | 1.07 ± 0.26 | 1.00 ± 0.16 | 0.97 ± 0.15 |
| PCC | 0.86 ± 0.05 | 0.78 ± 0.05 | 0.86 ± 0.06 | 0.85 ± 0.05 | 0.89 ± 0.06 | 0.90 ± 0.05 | 0.90 ± 0.05 |
| Preprocessing | ||||||
|---|---|---|---|---|---|---|
| SG [39] | SG1 [40] | SG2 | SNV [41] | MCI-Driven | ||
| RF [55] | R2 | 0.41 | 0.50 | 0.17 | 0.71 | 0.75 |
| RMSE | 1.66 | 1.52 | 1.95 | 1.15 | 1.08 | |
| PCC | 0.66 | 0.73 | 0.42 | 0.85 | 0.87 | |
| plsr [56] | R2 | 0.56 | 0.23 | −0.27 | 0.48 | 0.61 |
| RMSE | 1.41 | 1.87 | 2.41 | 1.53 | 1.33 | |
| PCC | 0.77 | 0.63 | 0.43 | 0.74 | 0.79 | |
| svm [57] | R2 | 0.29 | 0.71 | 0.15 | 0.73 | 0.75 |
| RMSE | 1.81 | 1.16 | 1.99 | 1.12 | 1.07 | |
| PCC | 0.56 | 0.85 | 0.41 | 0.86 | 0.88 | |
| 1D-CNN [58] | R2 | 0.27 | 0.59 | 0.16 | 0.71 | 0.78 |
| RMSE | 1.83 | 1.38 | 1.96 | 1.17 | 1.00 | |
| PCC | 0.55 | 0.78 | 0.45 | 0.84 | 0.89 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Liu, D.; Wang, Q.; Li, J.; Liao, J.; Sun, J. Marginal Contribution Spectral Fusion Network for Remote Hyperspectral Soil Organic Matter Estimation. Remote Sens. 2025, 17, 2806. https://doi.org/10.3390/rs17162806
Tang J, Liu D, Wang Q, Li J, Liao J, Sun J. Marginal Contribution Spectral Fusion Network for Remote Hyperspectral Soil Organic Matter Estimation. Remote Sensing. 2025; 17(16):2806. https://doi.org/10.3390/rs17162806
Chicago/Turabian StyleTang, Jiaze, Dan Liu, Qisong Wang, Junbao Li, Jingxiao Liao, and Jinwei Sun. 2025. "Marginal Contribution Spectral Fusion Network for Remote Hyperspectral Soil Organic Matter Estimation" Remote Sensing 17, no. 16: 2806. https://doi.org/10.3390/rs17162806
APA StyleTang, J., Liu, D., Wang, Q., Li, J., Liao, J., & Sun, J. (2025). Marginal Contribution Spectral Fusion Network for Remote Hyperspectral Soil Organic Matter Estimation. Remote Sensing, 17(16), 2806. https://doi.org/10.3390/rs17162806







