Identification of Dominant Controlling Factors and Susceptibility Assessment of Coseismic Landslides Triggered by the 2022 Luding Earthquake

Abstract

Coseismic landslides are geological events in which slopes, either on the verge of instability or already in a fragile state, experience premature failure due to seismic shaking. On 5 September 2022, an Ms 6.8 earthquake struck Luding County, Sichuan Province, China, triggering numerous landslides that caused severe casualties and property damage. This study systematically interprets 13,717 coseismic landslides in the Luding earthquake’s epicentral area, analyzing their spatial distribution concerning various factors, including elevation, slope gradient, slope aspect, plan curvature, profile curvature, surface cutting degree, topographic relief, elevation coefficient variation, lithology, distance to faults, epicentral distance, peak ground acceleration (PGA), distance to rivers, fractional vegetation cover (FVC), and distance to roads. The analytic hierarchy process (AHP) was improved by incorporating frequency ratio (FR) to address the subjectivity inherent in expert scoring for factor weighting. The improved AHP, combined with the Pearson correlation analysis, was used to identify the dominant controlling factor and assess the landslide susceptibility. The accuracy of the model was verified using the area under the receiver operating characteristic (ROC) curve (AUC). The results reveal that 34% of the study area falls into very-high- and high-susceptibility zones, primarily along the Moxi segment of the Xianshuihe fault and both sides of the Dadu river valley. Tianwan, Caoke, Detuo, and Moxi are at particularly high risk of coseismic landslides. The elevation coefficient variation, slope aspect, and slope gradient are identified as the dominant controlling factors for landslide development. The reliability of the proposed model was evaluated by calculating the AUC, yielding a value of 0.845, demonstrating high reliability. This study advances coseismic landslide susceptibility assessment and provides scientific support for post-earthquake reconstruction in Luding. Beyond academic insight, the findings offer practical guidance for delineating priority zones for risk mitigation, planning targeted engineering interventions, and establishing early warning and monitoring strategies to reduce the potential impacts of future seismic events.

1. Introduction

Landslides are widespread natural disasters around the world, frequently occurring in countries such as China [1], the United States [2], Japan [3], and Italy [4]. Earthquakes are recognized as one of their principal triggers, and in many cases, the destruction caused by earthquake-induced landslides can surpass that of the seismic shaking itself [2,5]. China lies at the convergence of two major seismic zones—the Pacific Ring of Fire and the Eurasian seismic belt. The ongoing compression from the Pacific, Indian, and Philippine Sea plates leads to the development of numerous active fault zones, rendering the country highly susceptible to frequent and sometimes devastating earthquakes [6]. Several recent earthquakes in China, such as the 2008 Wenchuan (Ms 8.0), 2010 Yushu (Ms 7.1), 2013 Ya’an (Ms 7.0), 2014 Ludian (Ms 6.5), and 2017 Jiuzhaigou (Ms 7.0) events, have all resulted in widespread coseismic landslides. China is geographically characterized by numerous mountains and hills, with mountainous areas covering about 70% of the country’s land. This vast mountainous terrain provides geographical conditions with high potential for coseismic landslides. In particular, the mountainous canyon regions of western China feature highly complex geological conditions, with densely distributed active faults and frequent strong earthquakes, leading to severe coseismic landslides. On 5 September 2022, at 12:52 p.m., an Ms 6.8 earthquake struck Luding County in Ganzi Prefecture, Sichuan Province. The epicenter was located at 102.08°E and 29.59°N, with a focal depth of 16 km and a maximum intensity of IX. This seismic event triggered a large number of landslides, causing heavy casualties and considerable economic losses. As a result, carrying out regional coseismic landslide susceptibility analyses is critically important for disaster prevention, risk reduction, and guiding future urban development in earthquake-prone areas.

Coseismic landslide susceptibility assessment involves estimating the probability of landslides triggered by an earthquake within a given region. A reliable and detailed landslide inventory produced after the seismic event is essential for such assessments [7,8]. To this end, multiple research groups have interpreted landslides induced by the Luding earthquake using pre- and post-event multi-source satellite imagery or UAV aerial photographs, thereby compiling coseismic landslide inventories. Nevertheless, the presence of cloud cover has led to the significant underrepresentation of landslides in high-elevation mountainous zones above 2500 m, particularly on the western side of the seismogenic fault [9,10,11,12]. Shao et al. used cloud-free post-earthquake remote sensing images to conduct a comprehensive interpretation of landslides in the entire Luding earthquake-affected area [13]. They provided a more complete supplement to previous landslide inventories, resulting in the most comprehensive and reliable coseismic landslide inventory for Luding to date. Therefore, we used this updated landslide inventory as the fundamental data for the coseismic landslide susceptibility assessment.

Methods for coseismic landslide susceptibility assessment generally fall into three categories. Engineering geological analysis methods rely on expert experience and historical analogies to qualitatively evaluate slope stability [14], while mechanics-based methods use numerical simulation or physical modeling to quantitatively analyze slope failure under seismic loading [15,16,17,18,19]. Statistical regression models, including the frequency ratio (FR) [20], information value [21], and weights of evidence [22], remain widely used due to their practicality and ability to integrate multiple influencing factors. Although machine learning approaches such as logistic regression, artificial neural networks, and support vector machines [7,23,24] have been introduced to reduce subjectivity and improve predictive accuracy, they often require large, high-quality landslide inventories and typically lack interpretability, limiting their use in disaster mitigation planning.

In response to the urgent need for accurate coseismic landslide susceptibility assessments in the wake of the Ms 6.8 Luding earthquake, this study aims to systematically identify and quantify the dominant factors controlling landslide occurrence in the epicentral area. Specifically, we develop a refined landslide inventory based on remote sensing interpretation and field validation. We then apply an improved FR–AHP (analytic hierarchy process)–Pearson correlation coefficient coupling approach to assess landslide susceptibility. The main objectives are to (1) generate an objective and high-resolution susceptibility map of the Luding region, (2) elucidate the spatial relationship between landslide distribution and key geomorphological, geological, and seismic factors, and (3) verify the predictive performance of the proposed model. The anticipated outcomes include a more reliable understanding of coseismic landslide mechanisms and a susceptibility zoning map that can support targeted mitigation strategies. Importantly, the results can inform post-earthquake reconstruction planning, the delineation of high-risk zones, and the development of disaster prevention and preparedness policies in seismically active mountainous areas.

The remainder of this paper is organized as follows. Section 2 introduces the geographical and geological setting of the study area. Section 3 describes the data sources, selection of influencing factors, analytical methods, including the AHP and FR models, and the methodological framework. Section 4 provides the results of the coseismic landslide susceptibility assessment and its validation. Section 5 discusses the mechanisms by which controlling factors influence the distribution of coseismic landslides, as well as the impact of seismogenic faults on landslide spatial patterns, and outlines the limitations of this study, research prospects, and disaster mitigation recommendations. Finally, Section 6 summarizes the main conclusions of this study.

2. Study Area

To assess the spatial distribution and controlling factors of coseismic landslides, this study focuses on the Ms 6.8 Luding earthquake that occurred at 12:52 PM on 5 September 2022 in Luding County, Sichuan Province (Figure 1). According to the China Earthquake Networks Center, the epicenter was located in the Hailuogou Glacier Forest Park near Moxi Town (102.08°E, 29.59°N), with a focal depth of approximately 16 km and a maximum seismic intensity of IX. The earthquake triggered numerous landslides, resulting in 93 fatalities, 25 missing persons, over 270 injuries, and widespread damage to infrastructure and buildings [9,25]. It was generated by the Moxi segment of the left-lateral strike–slip Xianshuihe fault [26]. Considering the concentration of coseismic landslides in the vicinity of this fault segment, a 963.77 km² area surrounding the fault was delineated as the study area for landslide susceptibility assessment.

Situated on the southeastern margin of the Tibetan Plateau, the study area encompasses part of the Hengduan Mountains. It features highly dissected alpine terrain, with deep gorges and steep slopes that are particularly sensitive to earthquake-induced failures. The topography descends from west to east and from north to south, ranging from a maximum elevation of 4668 m at Wanglangbao in the northwest to a minimum of 874 m in the lower reaches of the Dadu river. The average elevation is 2312 m, and the total relief reaches 3736 m. This pronounced topographic relief plays a significant role in slope instability under seismic loading.

Tectonic uplift and faulting have not only shaped the regional geomorphology, but also play a central role in controlling seismic hazards. The Xianshuihe fault zone is one of the most active strike–slip fault systems in western China, with 17 earthquakes of magnitude greater than 6.5 recorded in the past 300 years [27,28]. This frequent seismic activity underscores the long-term instability of the region and its high landslide susceptibility under strong shaking. To quantify ground motion during the Luding earthquake, a peak ground acceleration (PGA) zoning map was generated based on seismic station data within 150 km of the epicenter. The PGA values in the study area range from 0.23 g to 0.65 g, providing a key input for subsequent susceptibility modeling.

The exposed strata in the study area range from the Sinian to the Quaternary systems, including Silurian, Devonian, Carboniferous, Permian, and Triassic formations. The dominant lithologies include granite, quartzite, marble, limestone, and slate, which are unevenly distributed across the fault zone (Figure 2). Long-term tectonic activity and weathering have led to highly fractured rock masses with well-developed structural planes, providing favorable conditions for slope failures under seismic excitation.

The Dadu river, the main river in the study area, flows from north to south along a deep, rugged canyon. Within the study area, the river extends for approximately 50 km with a vertical drop of 266 m and an average channel gradient of 5.32‰. Three major right-bank tributaries—the Moxi river, Wandong river, and Tianwan river—converge into the main river. These river valleys align with zones of intense coseismic landslide activity, highlighting the interaction between fluvial incision, seismic ground motion, and hillslope instability. Combined with steep terrain, climatic factors further exacerbate slope instability. The region experiences a subtropical monsoon climate influenced by the southeastern and southwestern monsoons, as well as cold air masses from the Tibetan Plateau. The annual average temperature is 15.5 °C, and the mean annual precipitation is approximately 664.4 mm [12]. The intense rainfall during the wet season and rapid surface runoff in confined catchments can saturate soils and reduce slope stability, which is particularly critical under post-seismic or co-seismic conditions.

3. Materials and Methodology

3.1. Sources of Data

The datasets required for the landslide susceptibility assessment of the 2022 Luding earthquake are listed in

Table 1. Sources of data required for the coseismic landslide susceptibility assessment.

Data	Source	Spatial Resolution
Coseismic landslide inventory	Data collection, remote-sensing interpretation, and field survey	--
Satellite image	https://www.ovital.com, (accessed on 28 November 2022)	1:200,000
DEM	https://www.gscloud.cn/, (accessed on 28 November 2022)	30 m
River network	Manual sketching	--
Strata chronology	https://geocloud.cgs.gov.cn, (accessed on 28 November 2022)	1:200,000
PGA	https://data.earthquake.cn/index.html, (accessed on 21 May 2024)	--
Fractional vegetation cover, (FVC)	https://www.gscloud.cn/, (accessed on 14 April 2020)	30 m
Road network	https://www.usgs.gov	--

. They include: ① a remote sensing-interpreted seismic landslide inventory database, ② a 30 m resolution digital elevation model (DEM), ③ a 1:200,000 scale vector geological map, ④ a satellite imagery map at a 1:200,000 scale, and ⑤ a vector PGA distribution map of the 2022 Luding earthquake.

The visual interpretation of landslides was performed using a human–machine interactive approach, based on field surveys and optical satellite imagery. The dataset employed in this research comprises pre-earthquake satellite imagery collected between 1 June 2022 and 5 September 2022, alongside post-earthquake planet images primarily obtained from 8 September 2022 to 30 December 2022. By comparing high-resolution remote sensing data captured before and after the event, a total of 13,717 landslides were delineated across the study region, covering an overall area of 39.27 km². The maximum landslide extent reached 120,747 m², while the smallest was 16 m², with an average landslide area of approximately 3451 m². In addition, a two-week field survey was conducted to verify the coseismic nature of selected mapped landslides through on-site observations [29]. Figure 1 presents the spatial distribution of the interpreted coseismic landslides.

3.2. Selection of Coseismic Landslide Influencing Factors

Coseismic landslides are controlled by a combination of topographic, geological, seismic, hydrological, and anthropogenic factors [30]. The selection of influencing factors in this study was based on: (1) previous research findings on earthquake-induced landslides [9]; (2) the availability and quality of spatial data [13]; and (3) relevance to the Luding region’s geomorphic and engineering context [9]. Fifteen factors were finally selected to represent the primary physical and environmental controls on landslide susceptibility.

3.2.1. Topographic Factors

(1) Elevation (EL): Derived from the 30 m resolution DEM, represents the absolute altitude;

(2) Slope gradient (SG): Derived from the DEM using the slope tool in ArcGIS (v10.8). It indicates the rate of elevation change over horizontal distance in degrees and is a key factor influencing slope stability, with steeper slopes being more susceptible to failure under seismic loading [31];

(3) Slope aspect (SA): Derived from the DEM using the aspect tool in ArcGIS. It represents the downslope direction of the steepest elevation change and has been reclassified into eight compass and one flat directions [9];

(4) Plan curvature (PLC) and profile curvature (PRC): The plan curvature can be derived by computing the aspect of the slope gradient map, whereas the profile curvature can be obtained by performing a second derivative of the slope gradient based on the DEM. Plan curvature and profile curvature respectively characterize the morphological variations in terrain convexity and concavity in the horizontal and vertical directions [9];

(5) Surface cutting depth (SCD): Surface cutting depth is defined as the difference between the mean elevation and the minimum elevation within a given neighborhood, reflecting the degree of surface incision and erosion [32];

(6) Topographic relief (TR): The topographic relief within the study area can be derived using statistical tests and the maximum elevation difference approach. Topographic relief is defined as the elevation difference between the highest and lowest points within a neighborhood, reflecting the macro-scale variability of terrain elevation [33];

(7) Elevation variation coefficient (EVC): The coefficient of elevation variation, defined as the ratio of the standard deviation to the mean elevation within a given area (see Equation (1)), serves as a standardized geomorphological index. Unlike slope gradient or topographic relief, it is primarily employed for tectonic feature identification and the prediction of landslide distribution [34].

$$\mathrm{E}\mathrm{l}\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{v}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{c}\mathrm{o}\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}={\displaystyle \frac{\sigma \left(h\right)}{\overline{h}}}$$

(1)

In this equation, $\sigma \left(h\right)$ represents the standard deviation of elevation, reflecting the degree of elevation dispersion, while $\overline{h}$ denotes the mean elevation within the area.

3.2.2. Geological and Seismic Factors

(1) Lithology (LI): The original lithology data were provided in vector format. Multiple lithological categories were consolidated into seven types relevant to slope stability. Subsequently, the vector data were rasterized at a spatial resolution of 30 m to enable spatial analysis and modeling;

(2) Distance to faults (DTFA)/Epicentral distance (ED): The original fault and epicenter location were obtained as vector data. Euclidean distance analysis was performed in ArcGIS to create raster layers representing the shortest distance from each grid cell to the nearest fault or the epicenter;

(3) PGA: PGA data were collected from seismic stations published on the China Earthquake Networks Center website The point data were interpolated in ArcGIS to generate a continuous raster layer representing the spatial distribution of PGA.

3.2.3. Hydrological and Anthropogenic Factor

(1) Distance to rivers (DTRI)/roads (DTRO): The original river network and road network were obtained as vector data. Euclidean distance analysis was performed in ArcGIS to generate raster layers representing the shortest distance from each grid cell to the nearest river or road;

(2) FVC: Satellite imagery with a 30 m resolution was obtained from the Geospatial Data Cloud. The FVC was then derived in ENVI (v5.3) based on the NDVI (normalized difference vegetation index) method to quantify vegetation density across the study area.

3.3. Coseismic Landslide Susceptibility Assessment Methods

3.3.1. Frequency Ratio Method

The FR method estimates the likelihood of landslide occurrence by analyzing the distribution of landslides across different classified intervals of each influencing factor [35,36]. In this study, the FR technique was applied to explore the relationships between coseismic landslides and 15 selected factors, as shown in Equation (2). An $FR$ value below 1 implies that the corresponding factor interval is less susceptible to coseismic landslides, whereas an $FR$ value above 1 suggests higher susceptibility, and a value equal to 1 indicates no clear effect [37]. To quantify the contribution of individual factors to the distribution of coseismic landslides, the frequency ratio of a single factor ($fr$) was calculated using Equation (3) through a weighted summation of the frequency ratios of its classified intervals. The weights were assigned based on the proportion of landslides occurring within each class. The resulting $fr$ value effectively reflects the influence of the corresponding factor on the spatial distribution of coseismic landslides.

$$FR={\displaystyle \frac{n_i/N}{s_i/S}}$$

(2)

$$fr=\sum [FR\times (n_i/N\left)\right]$$

(3)

In the equation: $n_i$ denotes the number of landslides within each classified interval, $N$ represents the total number of landslides in the study area, $s_i$ is the area of each classified category, and $S$ is the total area of the study region. $i$ represents the classification under the influencing factor.

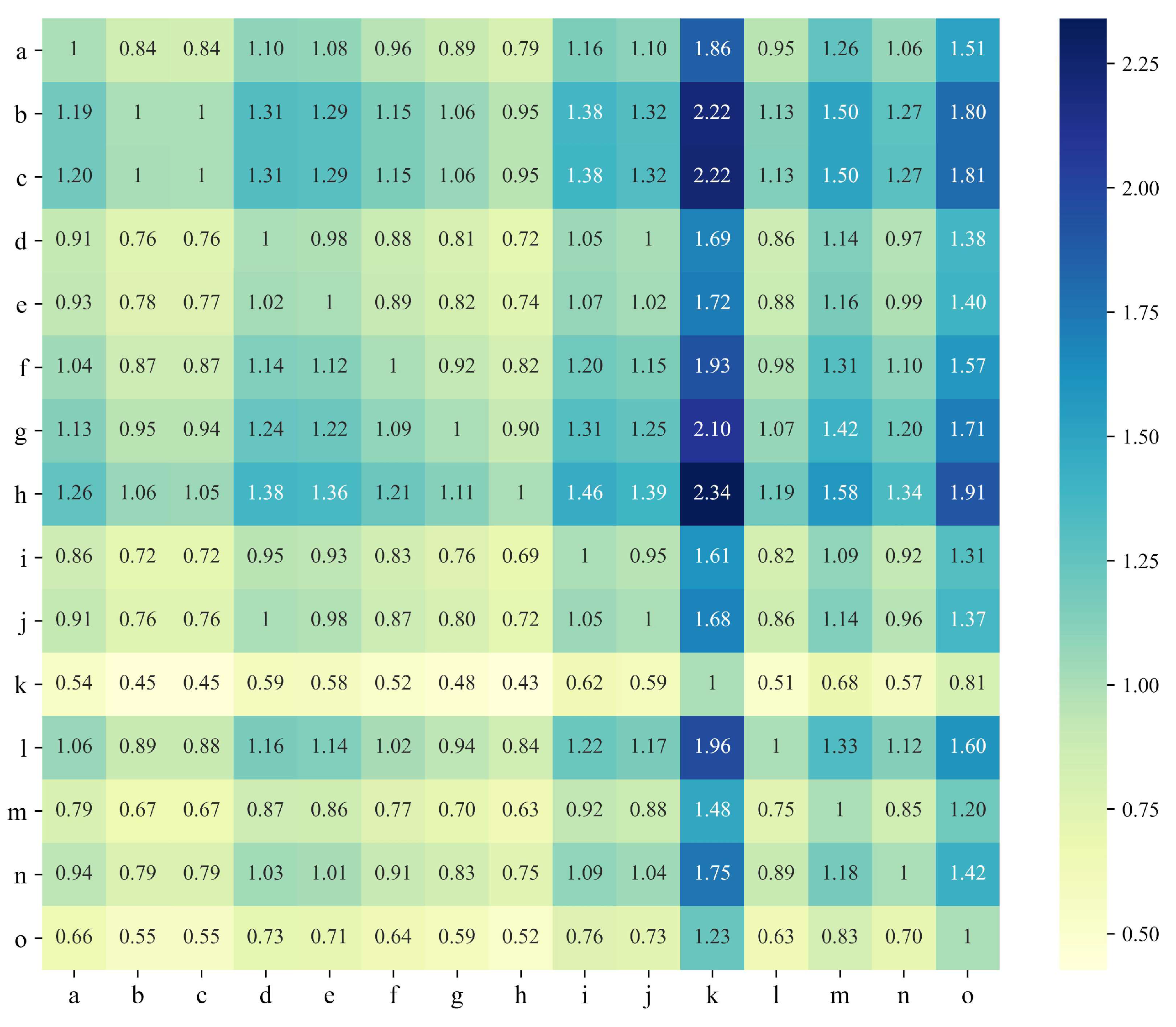
3.3.2. Analytical Hierarchy Process

AHP is widely used in landslide susceptibility assessments. The occurrence of coseismic landslides depends on multiple factors, including seismic forces, terrain features, and geological settings, which makes it a typical multi-criteria evaluation challenge. The AHP, originally introduced by Saaty, remains a widely recognized and effective tool for handling such complex assessments [38,39,40,41]. This approach has been extensively utilized in evaluating hazards associated with typhoons [42], landslides [43,44], spontaneous coal combustion [45], avalanches [46], flood risks [47,48,49], and other natural disasters. The AHP method is also one of the effective approaches for assessing coseismic landslide susceptibility [50]. However, the traditional method has three main limitations: first, it relies on expert judgment for pairwise comparisons, introducing subjectivity and failing to quantify the weight of each factor. Second, in the absence of a disaster database, the results of the AHP method are expressed as a range of scores, rather than the actual probability of disaster occurrence. Third, in seismic landslide susceptibility assessment, including more influencing factors does not always enhance the analysis. On the contrary, low-correlation factors may compromise the accuracy of the evaluation. The basic steps of the AHP method include:

(1)

Establish a hierarchical structure model, clarifying the relationships between influencing factors. By defining recursive interactions among influencing factors at the criterion and sub-criterion levels, the hierarchical structure model is developed;

(2)

Build the judgment matrix, which serves as the foundation of the AHP approach. This process entails conducting pairwise comparisons to evaluate the relative significance of factors within the sub-criterion layer corresponding to each criterion, resulting in a judgment matrix. In traditional AHP, the relative importance of two factors is qualitatively expressed as equally important, slightly important, moderately important, strongly important, and extremely important, and is quantified using a scale of 1, 3, 5, 7, and 9. In the context of coseismic landslide susceptibility and multi-criteria analysis, the feasibility of replacing expert judgment with data-driven indicators has already been demonstrated [51]. In this paper, the judgment matrix is constructed by pairwise comparison of the $fr$ values between the influencing factors;

(3)

To confirm the reliability of the weights calculated from the judgment matrix, a consistency evaluation is conducted based on Equations (4) and (5);

$$CI={\displaystyle \frac{{\lambda }_{max}-n}{n-1}}$$

(4)

$$CR=CI/RI$$

(5)

In this equation, $CI$ represents the consistency index, ${\lambda }_{max}$ is the maximum eigenvalue of the judgment matrix, and $n$ is the order of the matrix, $RI$ refers to the average random consistency index, with values taken from

Table 2. Values of the random index ($\mathit{R}\mathit{I}$).

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
RI	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46	1.49	1.52	1.54	1.56	1.58	1.59

. If $CI=0$, it indicates perfect consistency in the matrix. Conversely, the larger the $CI$ value, the worse the consistency of the matrix. $CR$ is the consistency ratio, and a $CR$ value of less than 0.1 is generally required. If the $CR$ value is below 0.1, the matrix passes the consistency test; otherwise, the matrix needs to be revised.

(4)

Calculate the overall weight of each influencing factor. After passing the consistency test, normalize the weight of each influencing factor at all levels to compute the comprehensive weight value (${\omega }_{i }$), and create a ranking table of the comprehensive weights of the influencing factors.

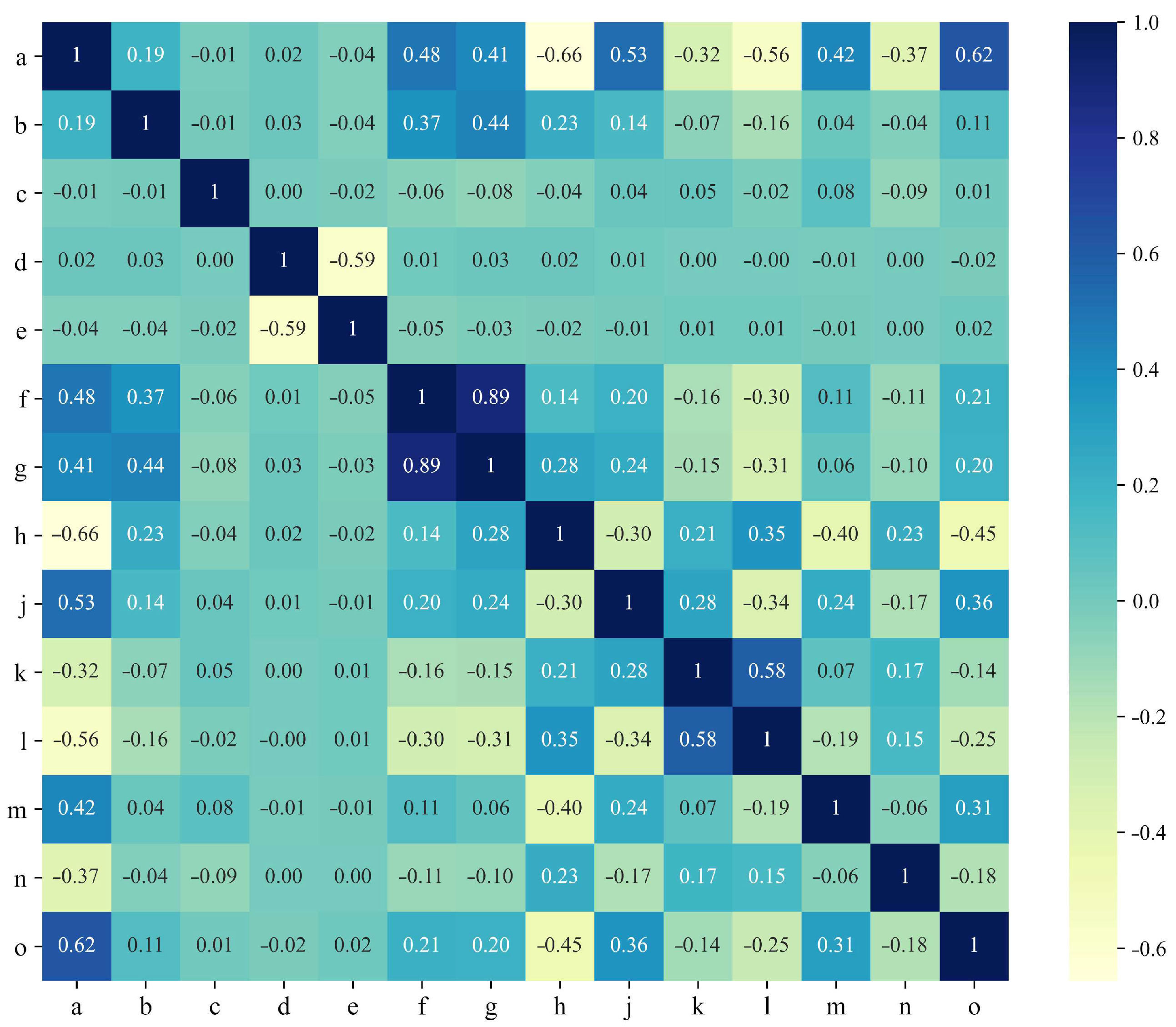
3.3.3. Pearson Correlation Coefficient

As a statistical metric, the Pearson correlation coefficient evaluates how strongly two continuous variables are linearly related. In this study, it was applied to assess the degree of correlation among the selected landslide conditioning factors. Identifying strongly correlated factors is essential to mitigate multicollinearity, which can bias the determination of factor weights and affect the reliability of susceptibility models. Given two variables, X and Y, where variable X contains n sample observations $(x_1,x_2,x_3,\cdot \cdot \cdot {,\mathrm{x}}_n)$ and variable Y contains n observations $({\mathrm{y}}_1,y_2,y_3,\dots {,\mathrm{y}}_n)$, the Pearson correlation coefficient is defined as follows [52]:

$$r={\displaystyle \frac{{\sum }_{i=1}^n\left(X_i - \overline{x}\right)\left(y_i - \overline{y}\right)}{\sqrt{{\sum }_{i=1}^n{\left(X_i - \overline{x}\right)}^2}\sqrt{{\sum }_{i=1}^n{\left(y_i - \overline{y}\right)}^2}}}$$

(6)

The value of r ranges within [−1, 1]. The larger the $r$ value, the stronger the linear relationship between variables $X$ and $Y$. When $r$ = 1, $X$ and $Y$ are perfectly positively correlated; when $r$ = −1, $X$ and $Y$ are perfectly negatively correlated; and when $r$ = 0, $X$ and $Y$ are uncorrelated. Generally, if the correlation coefficient $r$ > 0.5, variables $X$ and $Y$ are considered to have a high correlation.

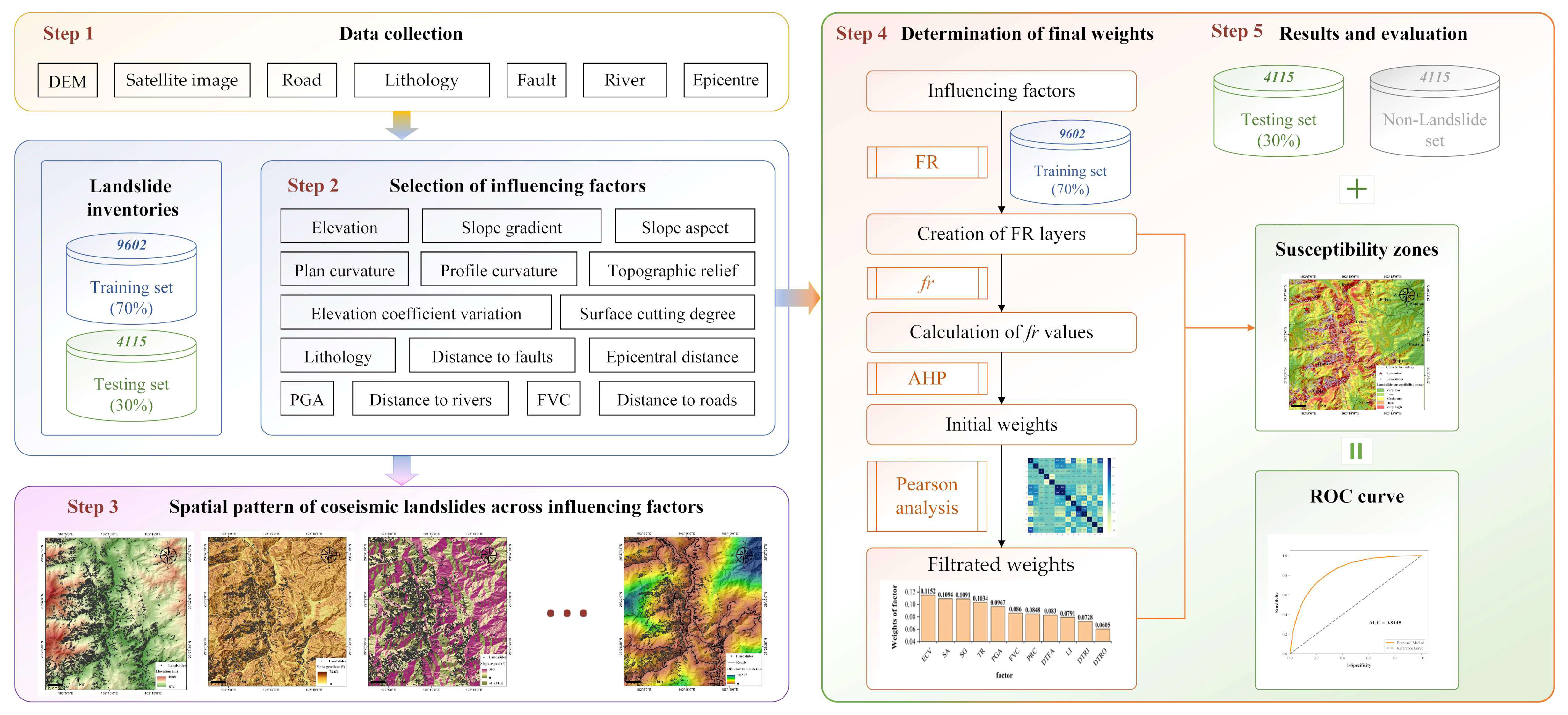
3.4. Methodology Flow

Coseismic landslides are typically triggered by seismic forces that initiate slope failure at the head scarp and propagate downslope under gravitational influence. This failure mechanism indicates that the spatial response to seismic triggering is most directly expressed at the initiation zone, while the deposition zone is more influenced by post-failure movement and terrain constraints [53,54]. Therefore, to accurately capture the initiation characteristics of coseismic landslides, the highest elevation point within each landslide polygon—generally located near the head scarp—was extracted from the elevation raster and used as the representative landslide location for subsequent analysis.

Step 1 Data collection: Based on this rationale, landslide polygons interpreted from remote sensing were overlaid on the DEM to extract the highest point within each polygon, representing the landslide scarp. These representative points served as the basic spatial units for susceptibility modeling. The scarp points were then randomly divided into training and testing sets at a 7:3 ratio to facilitate model construction and validation. Having established representative scarp points as the modeling units, the next step involves identifying the relevant environmental and seismic factors that influence the occurrence of coseismic landslides in the study area.

Step 2 Selection of influencing factors: Fifteen influencing factors were selected based on their relevance to slope stability under seismic excitation, covering topographic, geological, seismic, hydrological, and anthropogenic domains. These included: elevation, slope gradient, slope aspect, plan curvature, profile curvature, surface cutting depth, topographic relief, elevation variation coefficient, lithology, distances to faults, epicentral distance, peak ground acceleration (PGA), distances to rivers, fractional vegetation cover (FVC), and distances to roads. The inclusion of these factors draws on extensive prior research into coseismic landslide susceptibility. After identifying the influencing factors, it is essential to quantitatively assess their spatial correlation with coseismic landslide distribution. This not only guides the understanding of factor relevance, but also lays the foundation for weight assignment in the modeling process.

Step 3 Correlation analysis of influencing factors and coseismic landslides: To evaluate the relationship between each factor and the spatial occurrence of landslides, the natural breaks method in GIS was applied to classify the factor values. Then, the FR method was used to calculate the landslide occurrence probability within each class. This process provides a preliminary understanding of how each factor influences landslide distribution and formed the basis for subsequent weight determination.

Step 4 Determination of final weights: To objectively quantify the contribution of each factor, $fr$ was calculated. These data-driven $fr$ values were then integrated into the AHP as quantitative references for expert scoring, thus reducing the subjectivity of traditional AHP. To avoid multicollinearity and enhance model robustness, Pearson correlation analysis was conducted to identify pairs of strongly correlated factors. Factors showing high inter-correlation but contributing relatively low weight were filtered out to refine the input set. While FR provides a useful measure of individual factor importance, a comprehensive weighting scheme is needed to account for the relative importance of all factors simultaneously. Thus, the next step involves integrating the FR-based indicators into a modified analytic hierarchy framework.

Step 5 Results and evaluation: Finally, the FR layers of the filtered factors and their normalized weights were combined using a weighted overlay based on Equation (7), resulting in the coseismic landslide susceptibility map for the 2022 Luding earthquake.

$$LSI=\sum {\omega }_j·F{R}_j$$

(7)

Note: $LSI$ is the landslide susceptibility index; ${\omega }_{j }$ is the normalized weight value of the $j$ th filtrated influencing factors; and $F{R}_j$ is the $j$ th filtrated frequency ratio of the influencing factors. $j$ is the number of filtrated influencing factors.

To evaluate the predictive performance of the susceptibility model, a receiver operating characteristic (ROC) curve was generated. The area under the ROC curve (AUC) served as a quantitative measure of the model’s accuracy in distinguishing landslide from non-landslide areas, thus validating the effectiveness of the susceptibility assessment. The overall methodology is depicted in Figure 3.

4. Results and Analysis

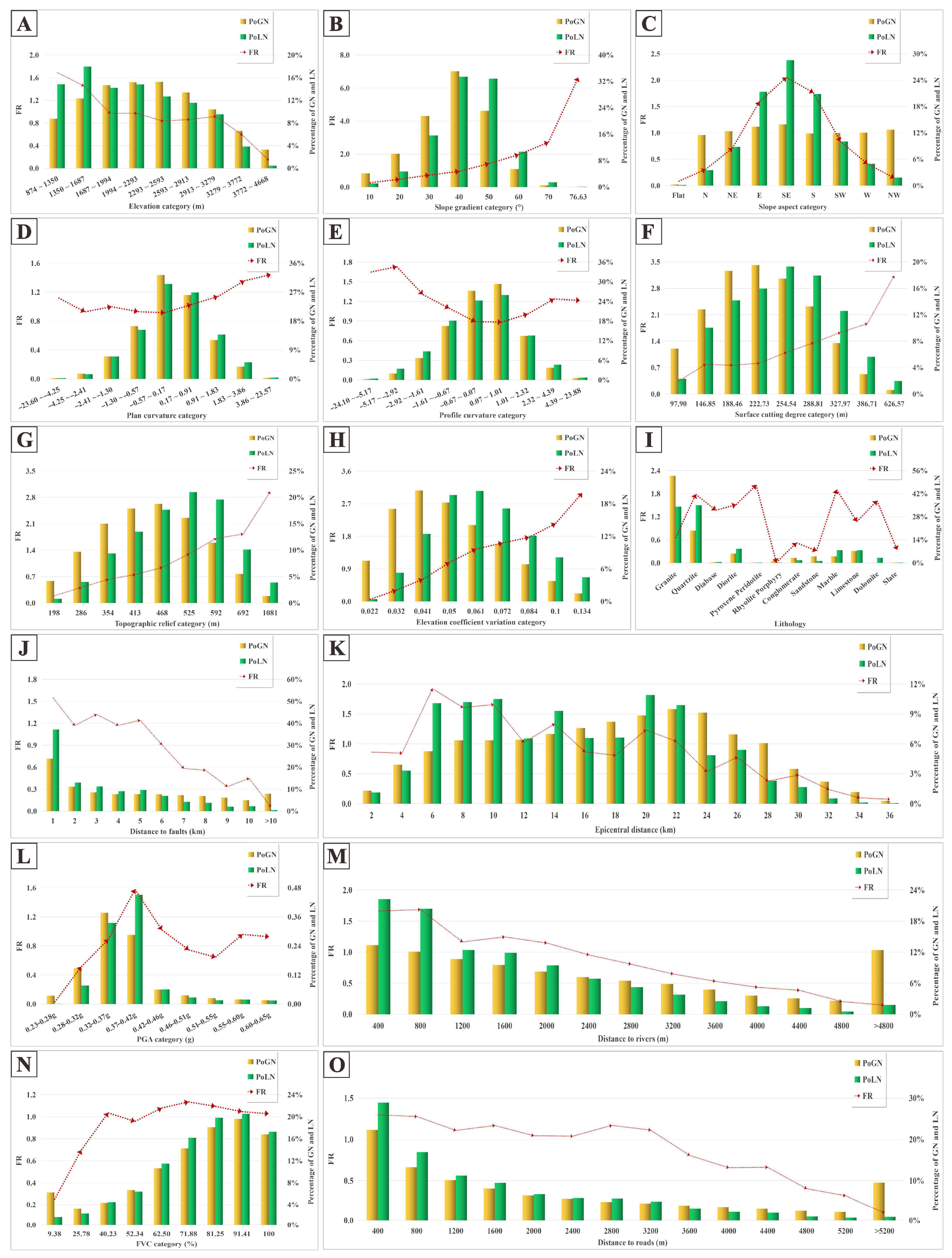
4.1. Spatial Pattern of Coseismic Landslides Across Influencing Factors

Using ArcGIS, spatial layers for 15 influencing factors were obtained. Continuous variables were classified using the reclassification tool, while lithology, as a discrete variable, was classified according to its actual distribution. Secondly, a total of 13,717 coseismic landslides were detected within the study region. These landslide samples were divided into training (9602 samples) and testing sets (4115 samples) with a ratio of 7:3. Finally, using Equation (1), the frequency ratio for each classification of influencing factors was calculated. Further, spatial distribution maps of coseismic landslide susceptibility factors (Figure 4) along with their corresponding relationship curves (Figure 5) were generated to examine the spatial patterns of landslides across the different influencing factors. The findings are summarized as follows:

(1) Topographic Conditions: As shown in Figure 5A, within the elevation ranges of 874–1994 m and 3279–4668 m, the $FR$ value decreases significantly with increasing elevation. In the elevation range of 1994–3279 m, the $FR$ value shows a slight decrease with increasing elevation, but the change is not pronounced. The susceptibility of coseismic landslides is strongly positively correlated with slope, surface dissection depth, terrain roughness, and elevation variation coefficient, showing the greatest $FR$ values and steepest slopes within the top two categories of these factors (Figure 5B,F–H). Plan curvature is calculated based on slope direction, describing the terrain characteristics in the horizontal direction [55]. Within the plan curvature range of −23.60–0.17, the $FR$ value slightly decreases as the curvature increases, whereas in the range of 0.17–23.57, the $FR$ value increases with curvature. Profile curvature describes the complexity of the terrain [56,57]. Within the profile curvature range of −24.10–0.07, the $FR$ value decreases as the curvature increases, whereas in the range of 0.07–23.88, the $FR$ value increases with curvature.

(2) Geological Conditions: Lithology is a crucial influencing factor, as different lithologies exhibit varying strengths, playing a decisive role in slope stability [58]. Figure 5I illustrates that granite is the dominant lithology in the study area, comprising 52.77% of the total surface, with quartzite being the second most prevalent, at 19.60%. Approximately 69% of coseismic landslides occur evenly distributed across granite and quartzite formations. Pyroxene peridotite and marble regions show the highest $FR$ values, with the greatest density of coseismic landslide development.

(3) Seismic motion conditions show that, within 5 km of the fault, the $FR$ value gradually decreases as the distance from the fault increases, but remains above 1; beyond 5 km, the $FR$ value continues to decline with increasing distance from the fault (Figure 4J and Figure 5J). The Xianshuihe fault zone, which generated the Luding earthquake, is associated with a high concentration of large landslides, as illustrated in Figure 1. According to Figure 5K, the $FR$ value initially rises with epicentral distance before stabilizing, reaching a peak of 1.92 within the 4–6 km range, indicating the highest coseismic landslide density near the fault at this distance. Analysis of PGA shows that approximately 85% of coseismic landslides occur within the 0.23–0.42 g PGA range, and the $FR$ value shows an increasing trend with increasing PGA. The $FR$ value is highest at 0.37–0.42 g PGA, reaching 1.58, indicating the greatest density of coseismic landslides. Within the 0.42–0.65 g PGA range, the $FR$ value decreases initially and then increases with stronger ground motion, with the minimum $FR$ value corresponding to the 0.51–0.55 g PGA range.

(4) Rivers and FVC: Figure 5M shows that both the number of coseismic landslides and the $FR$ values exhibit a significant decreasing trend with increasing distance from rivers. The highest concentration of coseismic landslides occurs within 0–800 m of rivers, accounting for 25.48% of all landslides; the $FR$ value peaks at 1.68 within the 400–800 m interval. This suggests that river erosion at slope bases significantly influences coseismic landslide formation. The fractional vegetation cover (FVC), which ranges from 0 to 1, indicates vegetation density, with higher values representing denser coverage. As shown in Figure 5N, there is an overall positive correlation between coseismic landslide frequency and FVC, with $FR$ values increasing within the 0–40.23% FVC range. When FVC exceeds 40.23%, the $FR$ value increases slightly with FVC, but the change is minimal; within the 62.50–71.88% FVC range, the $FR$ value is highest, indicating the greatest density of coseismic landslides.

(5) Human Engineering Activities: As shown in Figure 5O, within a distance of 0–2800 m from roads, the $FR$ value decreases slightly with increasing distance from roads, but the change is minimal. Beyond 2800 m from roads, the $FR$ value steadily decreases as distance increases, approaching zero once the distance surpasses 5200 m. The density of coseismic landslides is highest within the 0–400 m range from roads.

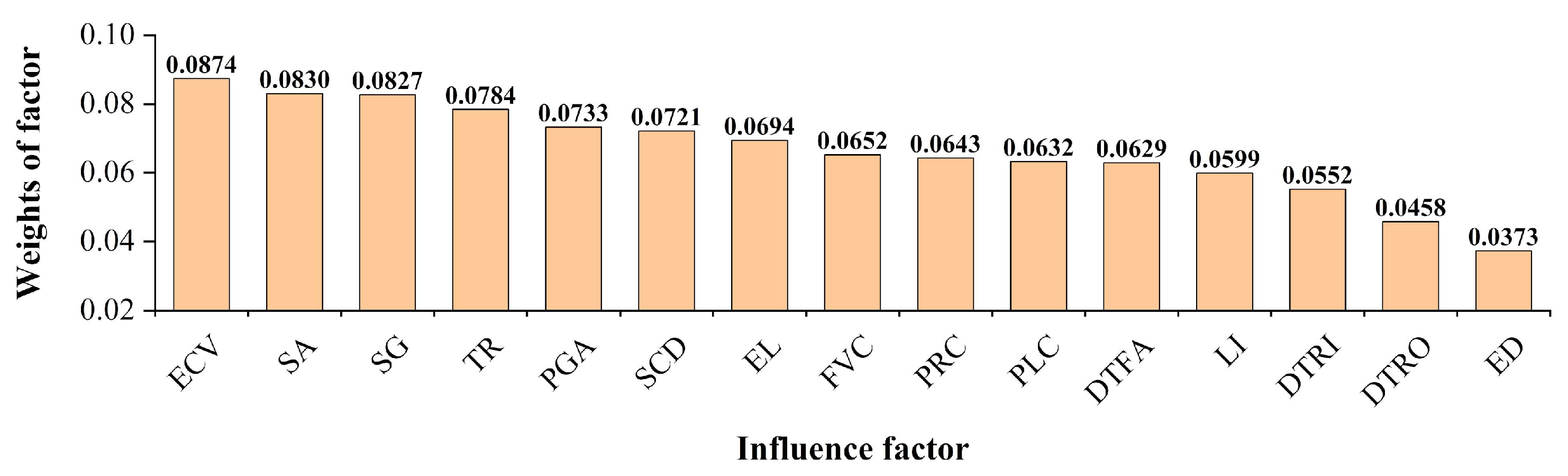
4.2. Determination of Initial Weights for Influence Factors

After the correlation between each influencing factor and coseismic landslide susceptibility was determined, the $fr$ values for all 15 factors were computed from their respective FR raster layers following Equation (2). The results are summarized in

Table 3. Landslide count-based weighted summation of the frequency ratio for all influence factors.

Factor	Elevation	Slope Gradient	Slope Aspect	Plan Curvature	Profile Curvature
$fr$	0.1235	0.1472	0.1476	0.1124	0.1144
Factor	Surface cutting degree	Topographic relief	Elevation coefficient variation	Lithology	Distance to faults
$fr$	0.1282	0.1394	0.1554	0.1066	0.1119
Factor	Epicentral distance	PGA	Distance to rivers	FVC	Distance to roads
$fr$	0.0664	0.1304	0.0982	0.116	0.0816

.

Constructing the judgment matrix is a crucial step for determining the weights of influence factors. The core step in constructing the judgment matrix is to compare the influence factors pairwise to determine their relative importance. Conventional AHP approaches depend heavily on expert opinions to assign relative weights to influencing factors, introducing considerable subjectivity. In contrast, this study utilizes the $fr$ values to quantitatively reflect the relative significance of each factor (Figure 6), thereby minimizing the subjectivity inherent in the traditional AHP method.

After normalization, the eigenvector associated with the maximum eigenvalue of the judgment matrix serves as the weight vector. The largest eigenvalue was computed as 15, with the corresponding eigenvector being {0.264, 0.314, 0.315, 0.240, 0.244, 0.274, 0.298, 0.332, 0.228, 0.239, 0.142, 0.278, 0.210, 0.248, 0.174}. After normalization, the weight ranking of the influence factors for coseismic landslides was obtained (Figure 7). The CR value of the judgment matrix, calculated using Equations (4) and (5), was found to be, which is well below 0.1, and the distribution of weights among the influencing factors is appropriate.

4.3. Correlation Analysis of Influence Factors and Normalization of Filtrated Weights

When assessing coseismic landslide susceptibility, high autocorrelation among influence factors can lead to redundancy and reduce modeling accuracy [59]. Therefore, it is necessary to conduct a correlation analysis among the influencing factors to eliminate those with high inter-factor correlations, thereby ensuring relative independence among the remaining factors and improving the scientific validity and reliability of the modeling results. Using the multi-value extraction tool on the GIS platform, raster values from the 15 layers shown in Figure 4 were extracted to the attribute table of the landslide scarp points in the testing set. The attribute table was imported into SPSS (v26.0) software to conduct Pearson correlation analysis among the 15 influencing factors (Equation (6)), as illustrated in Figure 8. A correlation coefficient |$r$| ≤ 0.5 indicates a weak correlation between the two factors [60]. The results indicate that elevation has significant correlations with elevation variation coefficient, distance to road, PGA, and distance to fault. Distance to epicenter shows a strong correlation with PGA, plan curvature with profile curvature, and surface cutting depth with terrain roughness. Based on the obtained weights in Section 4.2, factors with smaller weights were removed. Consequently, elevation, distance to epicenter, planar curvature, and surface cutting depth were excluded. Finally, the weights of the remaining factors were renormalized, resulting in the filtrated influence factor weight ranking for the Luding study area (Figure 9). Here, the term “filtered weight” refers to the final normalized weights calculated after removing highly correlated factors identified through Pearson correlation analysis. Figure 8 shows that the elevation variation coefficient is the most important influence factor, with a weight of 0.1152, followed by slope aspect and slope degree, both with weights around 0.11. Compared with other influencing factors, distance to road is the least important factor, with a weight of 0.0605.

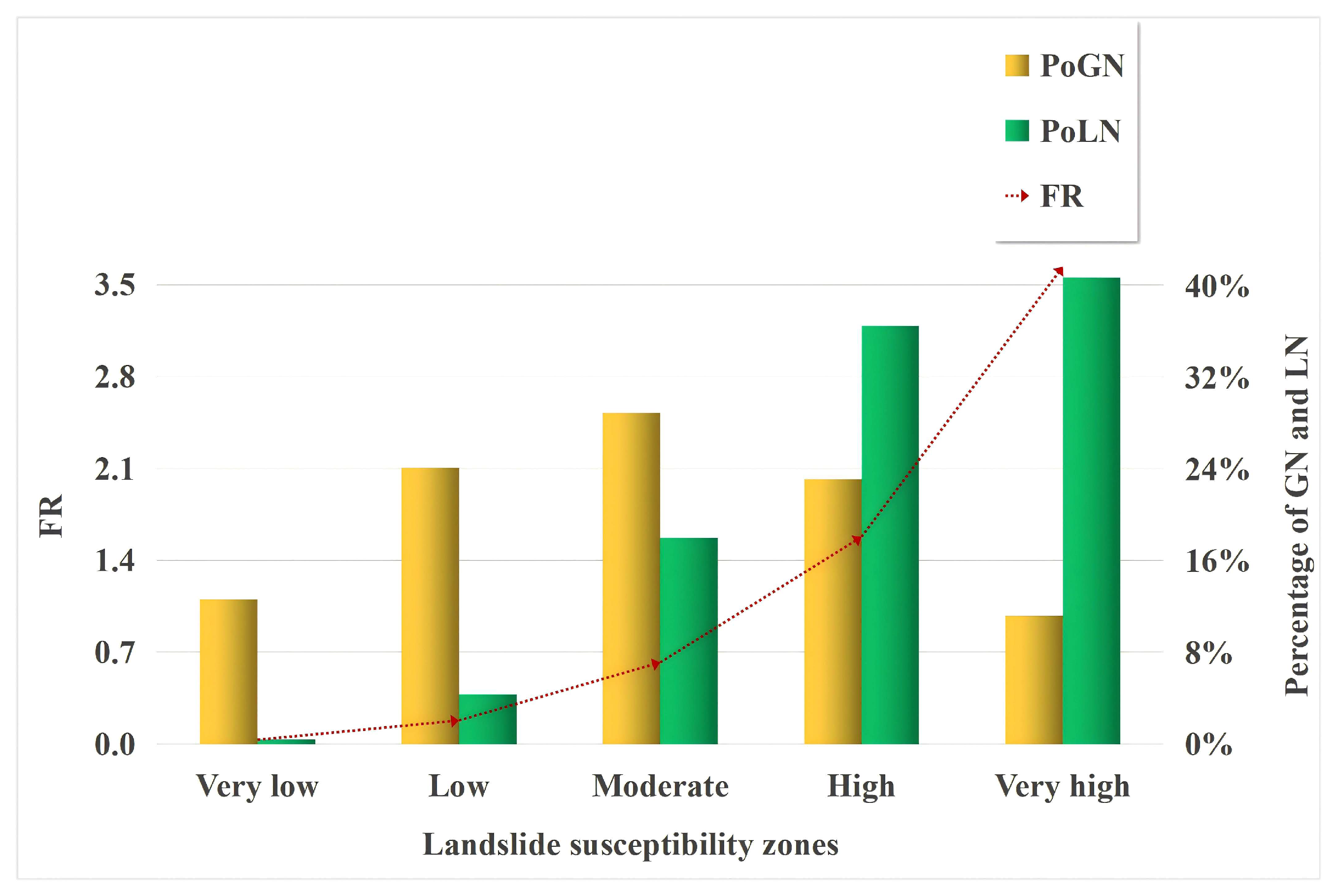
4.4. Mapping of Coseismic Landslide Susceptibility Zoning

After the filtrated weights of the influence factors were obtained, the FR raster layers derived in Section 4.3, together with the filtrated weights presented in Figure 9, were applied in Equation (7). A weighted overlay of the filtered FR raster layers and their corresponding weights was then performed to compute the coseismic landslide susceptibility index for the study area. Based on the values of the coseismic landslide susceptibility index, the study area was classified into five categories—very high, high, moderate, low, and very low susceptibility (Figure 10)—using the Natural Breaks (Jenks) method, which is widely used in landslide susceptibility mapping to identify natural groupings within the data and minimize intra-class variance.

Figure 10 illustrates that zones with very high and high landslide susceptibility are primarily located along the banks of the Dadu river and near the Xianshupoihe fault zone. The concentration of high-susceptibility areas in tectonically active and steep terrain highlights the significant roles of fault proximity, river erosion, and slope gradient in controlling landslide occurrences. Figure 11 illustrates the statistical distribution of landslides across the susceptibility zones. The results show that both the percentage of landslide numbers (PoLN) and the FR increase markedly from the very-low- to the very-high-susceptibility classes. The very high susceptibility zones have the highest proportion of landslides (about 40%) and the highest $FR$ value (over 3.5), indicating strong spatial clustering of coseismic landslides. In contrast, the very-low-susceptibility zone contains few landslides and has an $FR$ value near zero, suggesting low susceptibility. Overall, the patterns of PoGN, PoLN, and FR support the reliability and effectiveness of the zoning results.

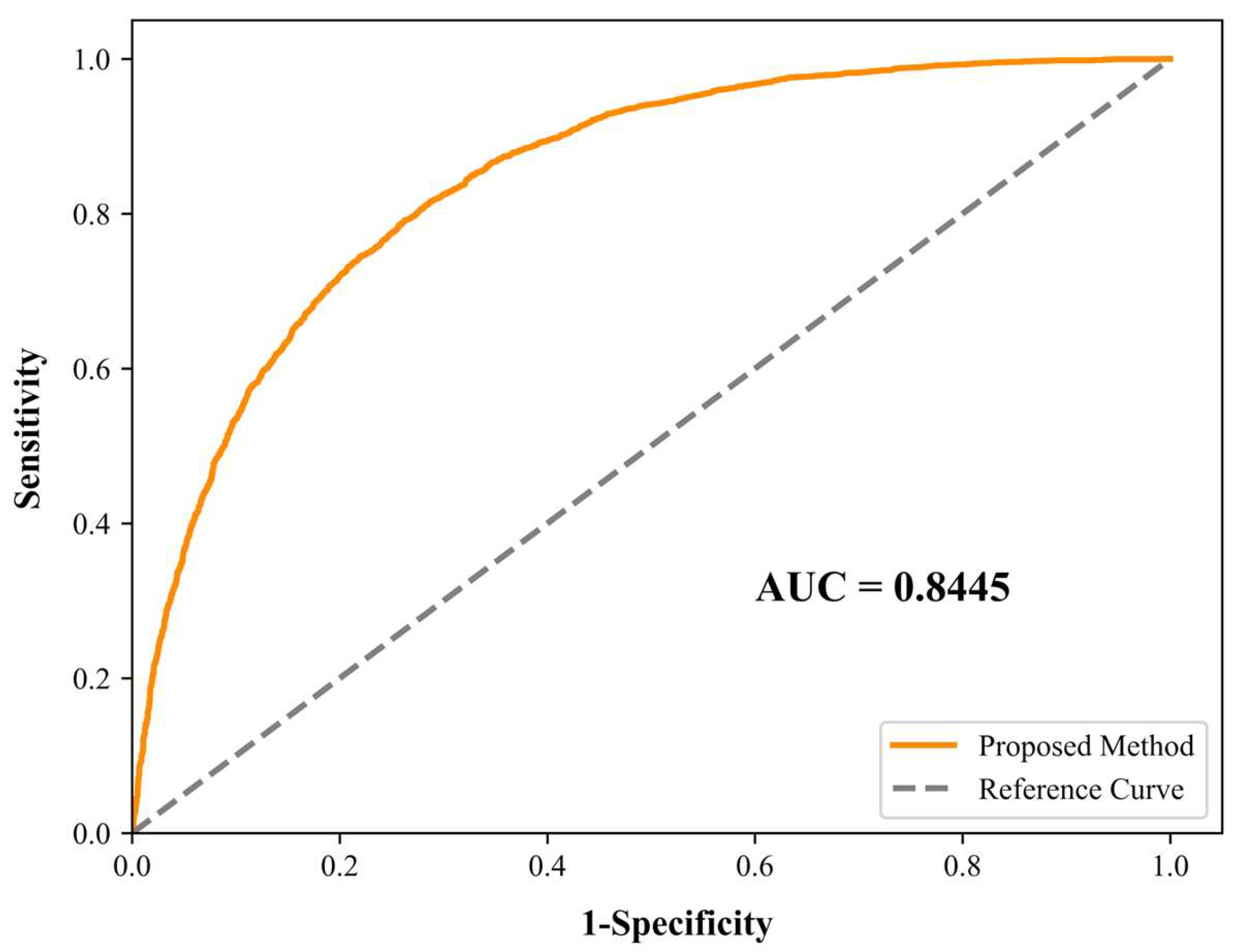
4.5. Validation of Coseismic Landslide Susceptibility Zoning Results

The accuracy of the coseismic landslide susceptibility zoning results was evaluated using the area under the ROC curve (AUC) [61]. AUC values range from 0.5 to 1.0, with values above 0.7 indicating satisfactory model performance and those above 0.9 reflecting outstanding predictive accuracy [62]. The ROC curve plots the true positive rate (TPR) against the false positive rate (FPR) under various threshold settings, providing a visual measure of model performance. Specifically, the true positive rate (sensitivity) is shown on the y-axis, while the false positive rate (1-Specificity) is shown on the x-axis (see Equations (8) and (9)).

$$Sensitivity={\displaystyle \frac{TP}{TP+FN}}$$

(8)

$$Specificity={\displaystyle \frac{TN}{FR+TN}}$$

(9)

where $TP$ = true positives (correctly predicted landslide points); $FN$ = false negatives (actual landslide points predicted as non-landslide); $TN$ = true negatives (correctly predicted non-landslide points); $FP$ = false positives (actual non-landslide points predicted as landslide).

In this research, 30% of the landslide scarp points (4115 in total) were randomly selected as the testing dataset. Slope units were extracted using the hydrological analysis method in ArcGIS, resulting in 44,018 units across the study area. Excluding the slope units containing all landslide scarp points from the training and testing sets, the study area’s elevation raster layer was used as the base map. The purpose of using slope units is to subdivide the terrain into homogeneous morphological units that better capture the spatial variability of topographic, geological, and triggering factors. This unit-based approach enables more accurate modeling of landslide susceptibility by reducing internal heterogeneity within each mapping unit [33]. To ensure a balanced and representative dataset, we randomly selected non-landslide units from the remaining slope units that do not intersect any mapped landslides. This random sampling approach is commonly used in landslide susceptibility studies to avoid sampling bias and to ensure that non-landslide samples are distributed across different terrain and geological conditions. This helps the model to learn the contrast between landslide-prone and stable areas effectively. After excluding units containing all training or testing landslides using the Intersect tool in ArcGIS software, raster center points with the highest elevation in each slope were extracted as landslide scarp points, yielding 30,513 samples. For slope units lacking raster center point coverage, a total of 8846 slope center points were extracted. During data preprocessing, 180 slope units near the boundary of the study area were identified as lacking valid raster center points and were thus excluded. The remaining 43,838 slope units were retained, from which 4115 landslide scarp points were randomly selected to form the testing dataset for model validation. Using the multi-value extraction tool, susceptibility index values corresponding to the testing points were obtained. Subsequently, the ROC curve was then generated, and the corresponding AUC value computed. As illustrated in Figure 12, an AUC of 0.8445 indicates that the coseismic landslide susceptibility zoning model has strong predictive capability.

5. Discussion

5.1. Controlling Factors of the Coseismic Landslides

The areas classified as high and very high susceptibility for landslides triggered by the Luding earthquake closely align with the actual coseismic landslide distribution interpreted from remote sensing data (Figure 11 and Figure 12), supporting the reliability of the susceptibility zoning results in this study. The findings highlight the elevation variation coefficient as the dominant factor influencing coseismic landslides. Defined as the ratio of the standard deviation of elevation to the mean elevation, this coefficient captures the extent of surface incision and erosion across the region. A higher elevation variation coefficient indicates more significant surface erosion and incision [63]. Coseismic landslide susceptibility increases with increasing elevation variation coefficient (Figure 4H), meaning that regions with more pronounced surface erosion and incision typically reflect higher tectonic activity, intense river downcutting, and the development of steep slopes. It also implies that these slopes have undergone prolonged unloading deformation and exhibit extensively developed rock mass fracturing, leading to reduced rock quality and strength—conditions favorable for coseismic landslide initiation. Furthermore, Yang et al. proposed using two quantitative geomorphic parameters, slope gradient and elevation variation coefficient, to identify active faults [64]. They discovered that, in the high-mountain gorge region of the Yarlung Tsangpo river, east of Namcha Barwa, the elevation variation coefficient map revealed discontinuous, linear low-value bands along active fractured fault zones. A comparable pattern was identified in this study near the Xianshuihe fault zone, further supporting the use of the elevation variation coefficient as a quantitative geomorphic indicator for detecting active faults. Moreover, the notably high elevation variation coefficient observed on slopes flanking the Xianshuihe fault reflects intense erosion processes, which in turn supply abundant loose material that facilitates the occurrence of large landslides in proximity to the fault zone. This also reflects the basic fact that the rocks along the fault’s fractured zone are less resistant to erosion than the surrounding bedrock.

Slope aspect emerged as the second most important factor, likely due to three reasons. First, research on the 2008 Wenchuan earthquake found that slopes aligned with the direction of fault movement were more susceptible to landslides [65]. A similar pattern was observed in landslides triggered by the Luding earthquake, where the initial slope directions of most landslides in the western mountain gorge region were S, SE, and E, consistent with the SE strike–slip direction of the fault (Figure 4C), further supporting this observation. This reflects that the SE extension of the seismogenic fault was a primary cause of landslides, as seismic surface waves encountered free faces, where wave reflection and other effects caused tension cracks and ejection failures in the slope’s surface rock. Second, remote sensing imagery (Figure 1) reveals that, in the western mountainous gorge area of the study region, the majority of coseismic landslides occurred on sun-facing slopes, while relatively few were observed on shaded slopes. Snow cover was observed on shaded mountain tops, indicative of glacial geomorphology. Glaciers can play a role in moderating seismic activity and controlling landslide scale. Where glacier thickness approaches local slope height, glaciers can reduce the topographic amplification effect of seismic shaking [66]. Sunward-facing slopes, exposed to solar radiation, had melted snow cover, and glacier retreat exposed steeper, higher terrain, enhancing the topographic amplification of seismic shaking [63]. This amplification effect is most pronounced near steep slopes, mountain tops, and ridges [67,68]. Third, Figure 4N,I illustrate that, in the western part of the study area, sun-facing slopes tend to have denser vegetation cover, whereas shaded slopes exhibit relatively sparse vegetation. Coseismic landslides primarily developed on hard rocks, such as quartzite and granite. The roots of plants can secrete organic acids that absorb minerals from rocks, altering their composition. Roots can infiltrate rock fissures, gradually expanding them. This process, particularly in already fractured rocks, can cause rock disintegration, providing ample material for coseismic landslide development. In summary, the role of slope aspect as the second most important factor is driven by a complex mechanism that integrates multiple factors influencing the development of coseismic landslides.

Slope gradient is the third most important factor, with coseismic landslide susceptibility increasing as slope gradient increases (Figure 5C). This observation is consistent with the spatial patterns of landslides triggered by the 2008 Wenchuan earthquake, as well as by the 2016 Kaikoura earthquake in New Zealand, and the 2004 Niigata Chuetsu earthquake in Japan, where slope gradient was also identified as a key conditioning factor [38,69,70]. Steeper slopes are more unstable, and thus have higher susceptibility to coseismic landslides. Distance to rivers is the factor with the lowest weight. As shown in Figure 4M, in the western region of the study area, the Hailiu river and Sala Pond river—both tributaries of the Dadu river—are located at a considerable distance from the seismogenic fault. Both the elevation variation coefficient and slope gradient are small, indicating gentle slopes and low topographic relief, which result in a sparse distribution of coseismic landslides, reducing the influence of rivers on landslides. The elevation variation coefficient, derived from elevation factors, reflects geomorphological differences. Roads and faults are located near valleys, and from the valley to the mountain peak, elevation increases with distance from roads and faults. Additionally, seismic waves exhibit amplification with elevation, meaning that peak ground acceleration (PGA) tends to increase at higher altitudes. Consequently, the elevation, elevation variation coefficient, distance to roads, PGA, and distance to faults show strong correlations. Since seismic energy is usually concentrated near the epicenter, The PGA values in the central and northern parts of the study area generally decrease as the distance from the epicenter increases. Plan curvature and profile curvature characterize the terrain’s horizontal and vertical features, respectively. Coseismic landslides tend to develop on convex or concave surfaces in the horizontal direction and at curvature transition points in the profile (Figure 4D,E). Surface dissection depth and terrain relief describe the degree of surface erosion and topographic variation, both of which are factors reflecting geomorphological differences. The greater the surface dissection, the more steep and tall the slopes that develop are. These slopes tend to have a long history of unloading deformation, with highly fractured rock masses, which promote the occurrence of coseismic landslides. Therefore, epicentral distance is strongly correlated with PGA, plan curvature, profile curvature, surface cutting degree, and topographic relief.

5.2. Influence of the Seismogenic Fault

Figure 1 illustrates that the tributary valleys of the Dadu river on the western side of the study area are oriented nearly perpendicular to the Xianshuihe fault, with a visually discernible concentration of large landslides near the so-called “locked section.” This pattern appears consistent with the “locked section effect” proposed by Xu and Li, based on observations from the 2008 Wenchuan earthquake [71]. Similar clustering near locked fault segments has also been noted in other studies [72]. According to this hypothesis, earthquake energy may be preferentially released in the vicinity of a locked segment due to shear rupture and accumulated strain, thereby intensifying local ground shaking and triggering more frequent and larger landslides [2,71]. However, while this explanation is plausible, it may oversimplify the complex interactions between seismic energy distribution, fault geometry, and topographic amplification. For instance, the steep terrain, lithological variations, and pre-existing slope conditions in the study area could also contribute to the observed landslide concentration. Furthermore, the generalizability of the “locked section effect” remains debated, as its influence may vary across tectonic settings and seismic events. Thus, although the current pattern may support the locked-section hypothesis, further multidisciplinary investigations are warranted to establish causality. The observed concentration of large landslides within the locked section of the Xianshuihe fault during the Luding earthquake appears to support the interpretation that this segment acted as the primary seismogenic source. However, this spatial pattern may not exclusively reflect fault mechanics. It could also be influenced by factors such as pre-existing slope instabilities, lithological contrasts, and topographic amplification effects. Hanging wall effects have similarly been reported for the 1999 Mw 7.6 Chi-Chi earthquake in Taiwan, the 2005 Mw 7.6 Kashmir earthquake in Pakistan, and the 2008 Wenchuan earthquake, where greater landsliding was observed on the hanging wall relative to the footwall. For the Xianshuihe fault, a higher density of landslides on its western side [13], aligned with the aftershock distribution [73], suggests a possible thrust component in addition to strike-slip motion. Nevertheless, such an interpretation should be treated with caution, as asymmetric ground shaking or rupture directivity may also account for the observed distribution. Field surveys have identified thrust–fold contact structures between the hanging wall and the fault zone (Figure 13), providing preliminary structural indications. Further detailed geophysical and structural investigations are needed to validate the composite movement hypothesis. The measured strike and dip of the fault zone were 256°∠42°. After the Luding earthquake, some research teams processed InSAR data and obtained coseismic surface displacements. The findings revealed a maximum uplift of about 15 cm on the western side of the Xianshuihe fault and a maximum subsidence of 14 cm on the eastern side [73,74]. Additionally, coseismic fault modeling results suggested that the deformation in the epicentral region and to the north was primarily characterized by sinistral strike–slip motion with a minor thrust component [75,76]. Based on these observations, we infer that the Moxi segment of the Xianshuihe fault likely includes a thrust component in its movement. This hypothesis requires further verification by future research teams.

5.3. Limitations and Research Prospects

Landslide inventories are crucial data for landslide susceptibility assessment, especially the quality of the landslide inventory [77]. The reliability of a landslide inventory is influenced by factors including scale, data acquisition methods, and the resolution of remote sensing images [78]. However, many current inventories remain incomplete because they often fail to differentiate between landslide initiation and deposition areas [79]. In this study, the Luding coseismic landslide inventory was updated through the integration of remote sensing data and field surveys. We extracted the highest elevation points of the landslide polygons as the initiation zones of the coseismic landslides [66], using these as inputs for the model to improve the quality of the Luding coseismic landslide inventory.

From the viewpoint of administrative divisions, the area most susceptible to landslides triggered by the Luding earthquake are mainly located within the townships of Tianwan, Caoke, Detuo, and Moxi. These townships show high landslide susceptibility, and efforts should be made to enhance InSAR-based hazard identification and dynamic monitoring of deformed bodies to prevent further exacerbation of potential landslide hazards during rainfall. In the Wandong township area, the fractured slope rock mass, influenced by the Xianshuihe fault zone, has led to a high density of landslides. Numerous landslide deposits have accumulated to form a small barrier dam in the upper section of the Wandong river. Although the dam has breached, a substantial amount of loose material remains in the riverbed, which could easily trigger debris flows during rainfall events. This poses a significant challenge for post-earthquake reconstruction, highlighting the need for special attention to be paid to the potential geological disaster chain risks in this area. In contrast to the monotonic use of a single method for evaluating coseismic landslide susceptibility by other scholars [38,67,80], this research utilized a combined FR-AHP -Pearson model to evaluate landslides induced by the Luding earthquake. The traditional AHP method, while widely used, suffers from inherent subjectivity in weight assignment; for a single case study, different experts may assign different scores, leading to inconsistent and non-unique results. In contrast, this study’s FR–AHP–Pearson model integrates data-driven weighting and correlation filtering, resulting in a more robust susceptibility model with improved predictive accuracy (AUC = 84.45%) [35,81,82].

Despite the improvements achieved in this study, several limitations remain that warrant critical consideration. First, although the updated landslide inventory enhances the spatial accuracy of the dataset, small-scale or vegetation-obscured landslides may still be underrepresented due to limitations inherent in optical remote sensing techniques. This omission could introduce a scale bias, particularly affecting the model’s sensitivity to micro-topographic features. Second, the susceptibility model was constructed based on the 2022 Luding earthquake, which, while representative of strike–slip fault-induced landslides in southwestern China, may not fully capture the variability associated with different tectonic regimes or lithological conditions. Thus, the model’s generalizability remains uncertain without multi-event or cross-regional validation. Third, the model adopted PGA as the sole seismic parameter to represent ground shaking. While PGA is widely used, it lacks the capacity to characterize the energy duration and cumulative effects of shaking, which are better reflected by parameters such as Arias intensity or cumulative absolute velocity [83]. Neglecting these may oversimplify the earthquake–ground response relationship in complex terrain.

To address these limitations, future studies should incorporate multi-temporal landslide inventories derived from high-resolution imagery and SAR data to improve detection completeness. In addition, expanding the model to include diverse seismic events and integrating richer seismic metrics could significantly enhance robustness. Moreover, we plan to explore machine learning-based frameworks—such as random forests and convolutional neural networks—to better capture nonlinear interactions and spatial heterogeneity in landslide susceptibility modeling.

6. Conclusions

In this research, an FR-AHP-Pearson integrated model was employed to evaluate the susceptibility of coseismic landslides caused by the 2022 Luding Ms 6.8 earthquake. The proposed approach effectively mitigates multicollinearity while retaining interpretability, thereby enabling a more robust determination of factor weights. By using landslide scarp points as the primary input data, the model better captures the spatial response of slopes to seismic shaking. These improvements help to overcome the key limitations of previous studies, including excessive subjectivity in weight assignment, inadequate treatment of correlated factors, and difficulties in applying machine learning models in data-scarce regions. The main conclusions are as follows:

(1)

An updated landslide inventory for the Luding earthquake was created, documenting 13,717 landslides within the study area, covering a total area of 39.27 km².

(2)

The study area was divided into five susceptibility categories, with very-high- and high-susceptibility zones mainly located along the Dadu river and the Moxi segment of the Xianshuihe fault. Particularly, towns such as Tianwan, Caoke, Detuo, and Moxi fall within the very high susceptibility zone, warranting focused landslide hazard investigations.

(3)

The elevation variation coefficient, slope aspect, and slope gradient are the main controlling factors of coseismic landslide distribution. Coseismic landslide susceptibility is highest when the elevation variation coefficient is between 0.1 and 0.134, the slope aspect is southeast, and the slope gradient ranges from 70° to 76.63°.

(4)

The coseismic landslide susceptibility model established using the FR-AHP-Pearson model achieved a prediction accuracy of 0.8445, indicating high accuracy, and can be widely applied in coseismic landslide susceptibility assessment.