OSSMDNet: An Omni-Selective Scanning Mechanism for a Remote Sensing Image Denoising Network Based on the State-Space Model

Abstract

Remote sensing images often degrade during acquisition due to various environmental factors, leading to noise contamination and loss of texture details. Existing methods based on convolutional neural networks (CNNs) are limited by their local receptive fields, making it difficult to effectively model long-range dependencies. Although Transformers possess global modeling capabilities, they face high computational costs and poor scalability in high-resolution remote sensing images. To address these challenges, this paper proposes an efficient remote sensing image denoising network—OSSMDNet—based on the Mamba network and incorporating an omni-directional selective scanning mechanism (OSSM). Its advantages include (1) introducing a multi-directional state-space modeling mechanism to enhance spatial structure perception capabilities and mitigate the limitations of traditional unidirectional modeling; (2) OSSMDNet is designed based on the Mamba architecture, achieving efficient fusion of global context and local details while maintaining linear computational complexity. On multiple remote sensing and natural image denoising datasets such as CBSD68 and DOTA, OSSMDNet significantly outperforms existing CNN-, Transformer-, and Mamba-based methods in terms of Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) metrics, with PSNR and SSIM values 0.14 dB and 0.0033 higher than the most iconic Mamba baseline method, respectively. This demonstrates that the proposed OSSMDNet achieves an excellent balance between accuracy and efficiency.

1. Introduction

Remote sensing images are typically captured via satellite or airborne sensors across multiple spectral bands, enabling large-area, high-resolution observations over time. It has been widely applied in key fields such as land cover and land use analysis [1], environmental protection [2], water body detection or coastline monitoring [3,4], and urban planning [5,6]. For example, in water body detection or coastline monitoring, noise in remote sensing images can significantly reduce boundary accuracy and spectral consistency. With increasing demands for high-quality and clear remote sensing images, ensuring image clarity has become increasingly important. However, due to the inherent limitations of remote sensing imaging equipment and external environmental influences, remote sensing images are inevitably corrupted by various types of noise during processes such as compression, transmission, and storage. This degradation not only reduces image clarity but also severely compromises the accuracy of downstream tasks such as object detection [7,8,9] and semantic segmentation [10,11,12]. Therefore, effective noise removal from remote sensing images remains a fundamental and critical challenge.

In recent years, significant progress has been made in remote sensing image denoising, particularly for multispectral, hyperspectral, and radar data [13]. Traditional methods, including low-rank approximation [14], sparse representation [15,16], non-local means [17], conditional random fields [18], and curvelet transform [19], have demonstrated success in hyperspectral image denoising. With the rapid development of Artificial Intelligence technology, deep learning-based denoising methods have received wide attention. Specifically, convolutional neural networks (CNNs) have become powerful frameworks for image denoising tasks. For instance, Hou et al. [20] proposed an improved DnCNN (Denoising Convolutional Neural Network) [21] model for remote sensing image denoising. The original DnCNN [21], based on residual learning, demonstrated outstanding performance across various types of image degradation, significantly outperforming traditional techniques such as block-matching and 3D filtering (BM3D) [22]. Building upon this foundation, researchers, including Canavoy et al. [23], Zheng et al. [24], Zhang et al. [25], and Zamir et al. [26], have proposed more advanced CNN-based denoising algorithms. Nonetheless, the inherently local receptive fields of CNNs constrain their ability to capture long-range dependencies, resulting in suboptimal reconstruction of structural textures, repetitive patterns, and symmetric features spanning large spatial regions.

Vision Transformers incorporating joint attention mechanisms have been introduced into image denoising tasks. For example, Huang et al. [27] proposed MDDA-Former, a novel architecture integrating multi-dimensional dynamic attention and self-attention mechanisms within a U-Net framework to capture global semantic information and enhance restoration accuracy. Similarly, Yin et al. [28] developed CSFormer, a Swin Transformer-based denoising model that employs cross-scale feature fusion to enrich feature representation and facilitate multi-scale self-attention modeling. However, as we know, Transformer-based models face insurmountable difficulties in terms of computational complexity and other aspects.

Recently, the structured state-space model Mamba (SSM) has emerged as a promising alternative for image denoising. Mamba [29], rooted in continuous linear time-invariant systems and discretized for deep learning, offers linear computational complexity and strong capability in modeling long-range dependencies. To enable efficient sequence modeling, it incorporates selective state updates and parallel scanning mechanisms. Wen et al. [30] introduced the nested S-shaped scanning (NSS) strategy and a sequence mixing attention (SSA) module to preserve spatial continuity and local structure, leading to the Mamba-based image restoration model MatIR. Guo et al. [31] proposed MambaIR (Mamba for Image Restoration), a simple baseline that integrates local enhancement and channel attention to address local pixel forgetting and channel redundancy in low-level vision tasks. The advantage of Mamba in image processing lies in efficient modeling of long-range dependencies, but its spatial modeling capabilities, training stability, and structural generality remain inferior to those of CNNs and Transformers, limiting its widespread application in high-resolution image tasks.

For solving these challenges, we propose OSSMDNet—an Omni-Selective Scanning Mechanism for a remote sensing image denoising network based on the state space model [32]. The main contributions of this study are summarized as follows:

(1)

We designed an end-to-end image denoising framework based on Mamba, enabling efficient training and inference. It offers a competitive alternative to traditional CNN and Transformer architectures for remote sensing image restoration.

(2)

We propose a Deep Feature Extraction Module (DEFM), which introduces the omni-selective scanning model based on Mamba for long-range dependency modeling and a Local Residual Module (LRB) to capture fine-grained spatial details, enabling multi-level feature extraction and fusion from both global and local perspectives.

(3)

We construct a new benchmark dataset for remote sensing image denoising. Extensive experiments demonstrate that OSSMDNet outperforms both classical methods and state-of-the-art methods in restoring high-quality natural images and remote sensing images.

The remainder of this paper is organized as follows: related works on image denoising are introduced in Section 2 including image denoising methods based on CNNs, Transformers, and state-space models. Section 3 presents the architecture of the proposed OSSMDNet, detailing its components and design rationale. In Section 4, the construction of the remote sensing image denoising dataset is described, the experimental configuration is outlined, and the results, including a comprehensive comparison with state-of-the-art methods, is demonstrated. Finally, conclusions and outlooks of the paper are summarized in Section 5.

2. Related Works

Remote sensing images are often degraded during the acquisition process by various factors such as sensor noise, atmospheric interference, and signal transmission errors. These disturbances cause diverse noise that significantly impair subsequent tasks including classification, detection, and object recognition. Consequently, image denoising, as a fundamental step in remote sensing image preprocessing, has witnessed substantial advances over the past decades, evolving from traditional filtering techniques to deep learning-based image restoration methods, with particularly notable progress in the remote sensing domain.

Traditional denoising methods: Traditional image denoising techniques mainly focus on spatial and transform domain methods. Gaussian filtering [33] and median filtering [34] are representative examples, aiming to suppress noise through local smoothing or nonlinear statistics. While effective for simple noise types, they often blur image details and struggle with high-resolution remote sensing data. Transform-domain methods, such as wavelet [35], curvelet [36], and contourlet transform [37], enhance multiscale denoising performance by better preserving structural features. In addition, non-local methods such as Non-Local Means (NLM) [38] and BM3D [22], along with low-rank and sparse representation techniques [39,40,41], have achieved improved results by exploiting image redundancy. However, these methods primarily rely on manually designed filters or predefined thresholds in the transform domain, performing well under fixed noise models but often struggling with complex and non-uniform noise distributions, frequently resulting in fine blurred details in images.

Deep Learning-Based Methods: Deep learning has significantly advanced image denoising, with CNNs and Transformers emerging as two dominant paradigms. CNN-based methods, such as DnCNN [21] and FFDNet [42], leverage convolutional hierarchies and residual learning to effectively extract local features and suppress noise. These methods have been widely applied to RGB images, hyperspectral images [43], and Synthetic Aperture Radar (SAR) images [44]. Despite their efficiency and compatibility with end-to-end training, CNNs are inherently limited by their local receptive fields, which restricts their ability to model long-range dependencies and preserve global structural information. To address this limitation, Transformer-based models incorporate global self-attention mechanisms, enabling them to capture long-distance correlations and restore fine textures more effectively. Notable examples include Restormer (Restoration Transformer) [45], SwinIR [46], and Uformer [47], which use multi-scale and hierarchical designs to achieve state-of-the-art results. However, the quadratic computational and memory complexity of self-attention mechanisms pose significant challenges for real-time deployment, particularly when processing high-resolution remote sensing images or operating under resource constraints. Although CNN-based models have made notable progress in image denoising, their limited local receptive fields hinder effective modeling of long-range dependencies, which leads to suboptimal performance in complex image scenarios. In contrast, Transformers provide strong global modeling capabilities and can substantially enhance image restoration, but their high computational cost, especially when processing high-resolution images, restricts their practical deployment.

Emerging State-Space Models: Structured state-space models (SSMs) have recently become an efficient alternative to CNNs and Transformers for sequence modeling, offering linear time complexity and strong ability to model long-range dependencies. Mamba [29] is one such model that has demonstrated promising results in image restoration by balancing computational efficiency and denoising performance. Unlike traditional filtering methods that lack global modeling and edge preservation, CNNs focus on local features but have difficulty maintaining large-scale consistency, while Transformers are good at global context modeling but require high computational resources and are challenging to deploy. Mamba overcomes these limitations with lightweight architecture and robust performance, making it a strong candidate for remote sensing image denoising. Recent work has expanded the application of Mamba in hyperspectral image denoising. Liu et al. [48] proposed HSIDMamba (HSDM), which uses bidirectional continuous scanning to better capture spatial and spectral dependencies efficiently. Fu et al. [49] developed SSUMamba, applying spatial and spectral continuous scanning in multiple directions with bidirectional SSM to improve noise suppression and local texture recovery, combined with a direction-aware scanning module to reduce scanning bias [50]. MambaHR [51] combines the state space module with the channel attention mechanism to achieve spectral–spatial fusion, focusing on hyperspectral image restoration. The SSM captures global dependencies, while the channel attention module enhances the interaction between spectral channels while maintaining spectral continuity and image details. These advances show that Mamba provides a powerful and efficient framework for complex remote sensing image denoising tasks.

Unlike traditional neural network architectures, Mamba relies entirely on selective gating mechanisms, eliminating the need for attention or feedforward layers and resulting in a purely recursive modeling framework with linear time complexity. By incorporating input-dependent parameterization, Mamba integrates the modeling flexibility of Transformers with the computational efficiency of state-space models. This approach not only preserves the linear computational complexity of SSMs but also substantially improves the ability of models to capture long-range contextual dependencies.

3. Methodology

In this section, we present the fundamental concepts of state-space models, detail the implementation of Mamba, and introduce the architecture of the proposed OSSMDNet.

3.1. Preliminaries

The state-space model (SSM), originally developed in control theory, provides a mathematical framework for modeling dynamic systems. Its core concept is to describe the evolution of the internal state of system using continuous-time linear differential equations. Specifically, the internal state $h(t)$ and the observed output $y(t)$ of the system are linked through a set of state and output equations, which incorporate the system input $x(t)$, state $h(t)$, and output $y(t)$, and are parameterized by matrices A, B, C, and D. This formulation enables the model to accurately capture the input-driven dynamics of the system. The general form of the equations is as follows:

$$h^{\prime }(t)=Ah(t)+Bx(t),$$

(1)

$$y(t)=Ch(t)+Dx(t),$$

(2)

where $x(t)\in R^L$ represents the input sequence, $h(t)\in R^L$ denotes the hidden state that facilitates the mapping from $x(t)$ to $y(t)\in R^M$, $h^{\prime }(t)\in R^L$ denotes the derivative of $h(t)$, and A, B, C, and D correspond to the state transition matrix, input matrix, output matrix, and direct transmission matrix, respectively. To enable implementation in discrete-time frameworks, such as neural networks, the zero-order hold (ZOH) method is employed to discretize Equations (1) and (2), resulting in the following iterative update formulation:

$$h_t^{\prime }=\overline{A}{h}_{t-1}+\overline{B}{x}_t,$$

(3)

$$y_t=C{h}_t+D{x}_t,$$

(4)

$$\overline{A}=e^{∆A},$$

(5)

$$\overline{B}={(\Delta t\cdot A)}^{-1}(e^{\Delta t\cdot A}-I)\cdot \Delta t\cdot B,$$

(6)

where $\overline{A}$, $\overline{B}$ are the state space matrix corresponding to discrete time, and $\Delta t$ denotes the time step. The OSSMamba we introduced utilizes the omni-selection scanning mechanism, which allows us to effectively capture the features of long-sequence signals using a simple architecture, effectively improving the capabilities of noise removal and detail restoration.

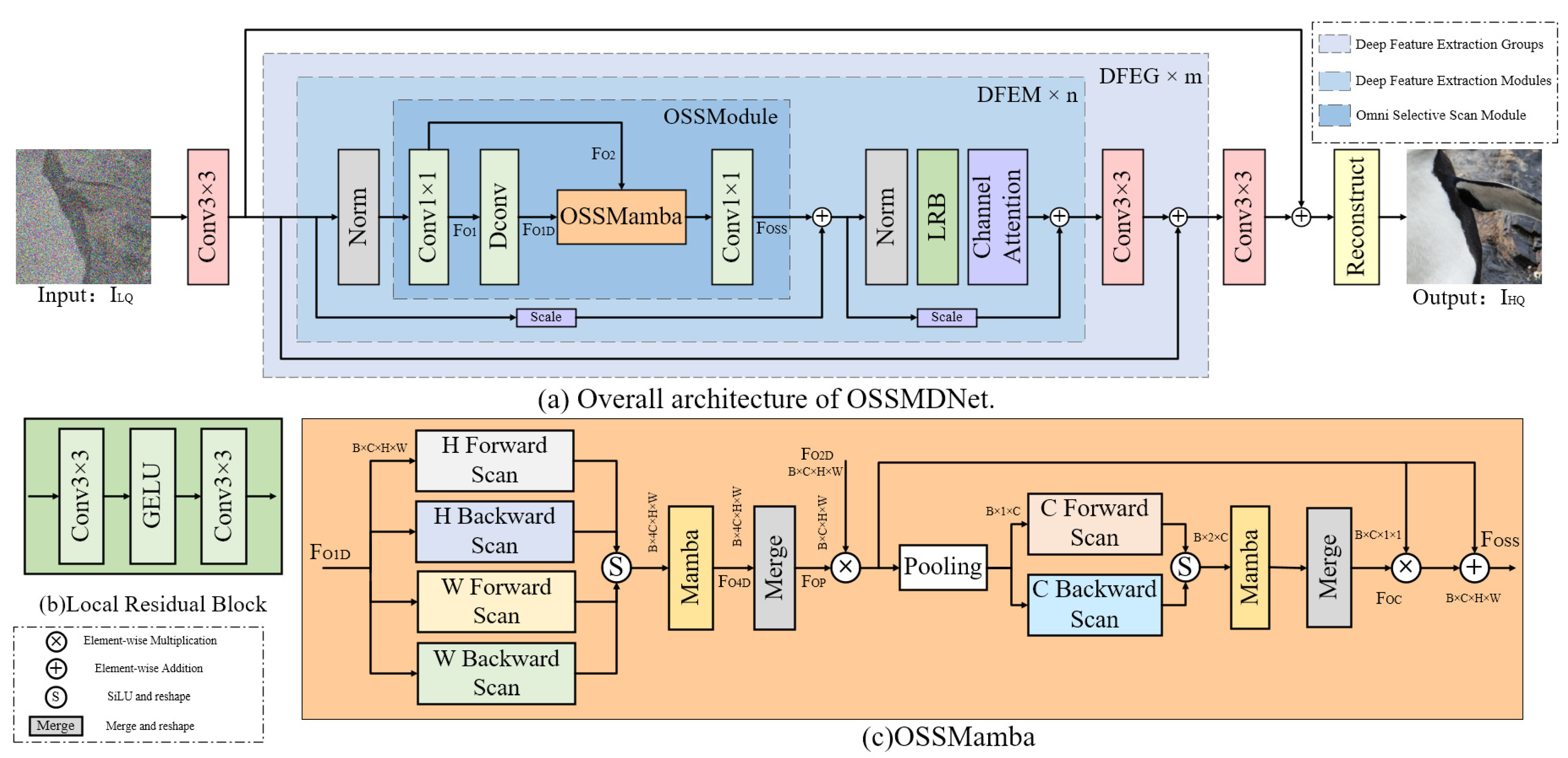
3.2. OSSMDNet Architecture

The overall architecture of the proposed OSSMDNet for remote sensing images is depicted in Figure 1.

As shown in Figure 1a, the proposed OSSMDNet mainly consists of three components: a shallow extraction section, a deep feature extraction module, and an image reconstruction section.

(1)

Shallow feature extraction stage: The input image $I_{LQ}$ first undergoes preliminary processing in a shallow feature extraction stage, which mainly consists of a 3 × 3 convolution layer that extracts shallow features $F_s$ from the input image to enhance the ability of images to represent details. The formula is as follows:

$$F_s=Conv(I_{LQ}),$$

(7)

where $I_{LQ}\in R^{H\times W\times 3}$ denotes the input low-quality image, $F_s\in R^{H\times W\times C}$ indicates the extracted shallow features, H and W specify the image dimensions for the height and width, and $C$ represents the number of output channels in the convolutional layer. The step determines both the quantity and representational capacity of the extracted features.

(2)

Deep Feature Extraction Group (DFEG): DFEG is composed of multiple DFEG modules stacked in sequence, aiming to progressively extract deeper information from shallow features. Each DFEG contains six Deep Feature Extraction Modules (DFEM) and an additional convolutional layer. As the core unit of deep feature extraction, DFEM combines the proposed OSSMamba module and a custom scanning mechanism to effectively capture long-range dependencies for expressing remote contextual information. Therefore, DFEG not only promotes the restoration of similarity between spatially adjacent pixels, improving the expression of local features, but also aids in the precise reconstruction of image details. The mathematical expression for multiple stacked DFEGs is:

$$F_D^l=m\times Conv(n\times DFEM(F_s))+F_s,$$

(8)

where $m$ represents the number of DFEG modules, $n$ denotes the number of DFEM, $l$ denotes the layer index within the deep feature extraction stage, $l\in \{1,2,\dots ,L\}$, $L$ specify the total number of layers in this stage, and $D$ signifies “Deep” to distinguish deep features $F_D$ from shallow features $F_s$.

(3)

Image Reconstruction Stage: This stage restores the image to its original RGB resolution through a convolutional mapping process, applies residual enhancement by combining the result with the input image, and finally performs denormalization to recover the original value range, yielding a high-quality output image $I_{HQ}$, as shown in the following formula:

$$I_{HQ}=reconstruct(F_D^l)$$

(9)

The entire process integrates multi-level features and effectively leverages information extracted at various stages to restore image details and textures, thereby enhancing the overall quality of the reconstructed image. The final convolutional mapping, which restores the image to its original resolution, plays a crucial role in converting the learned feature representations into a visually coherent result that aligns with human perceptual expectations.

3.3. Deep Feature Extraction Module (DFEM)

The DFEM module consists of normalization (LayerNorm), OSSModule, local residual block (LRB), and channel attention (CA) mechanism. After normalization, pixel values are mapped to a specific range, which can accelerate training convergence and improve model stability. OSSModule, as a core component, utilizes Mamba to capture long-range dependencies, enabling comprehensive scanning and modeling across multiple dimensions. As illustrated in Figure 1a, the structure of the first half of the DFEM can be formalized as follows:

$$Z^l=OSSModule(LN(F_D^l))+s\cdot F_D^l.$$

(10)

In the DFEM design, the latter half consists of normalization, LRB, and CA mechanisms. Figure 1b illustrates the design of LRB, which consists of a convolutional layer and an activation function. This module further refines the extracted features to enhance representational capabilities, thereby addressing the local pixel forgetting issue introduced by the SSM. In other words, due to the bias of the structure toward global modeling, the serialization of data disrupts local spatial structures, and the lack of a local detail modeling mechanism leads to insufficient image detail recovery. The LRB is defined by the following equation:

$$F_{LRB}=Conv(GELU(Conv(F_D^l))).$$

(11)

By introducing convolutional layers with residual structures to compensate for the loss of local features and fully utilizing local pixel information, the image restoration performance is improved. Additionally, since standard Mamba suffers from channel redundancy issues in image processing, namely, a large number of hidden states leads to inefficient utilization of certain channel information, the CA mechanism is introduced to guide the model to focus on learning cross-channel discriminative representations. The latter part of this process can be expressed as:

$$F_D^{l+1}=CA(LRB(LN(Z^l)))+s\cdot Z^l,$$

(12)

where the incorporation of skip connections facilitates the retention of original feature information, alleviates the vanishing gradient problem, and enhances the learning and optimization capabilities of network.

3.4. OSSMamba Block Design Details

As shown in Figure 1a, the OSSModule is a composite building block that primarily consists of three components:

(1)

A 1 × 1 convolution layer;

(2)

A depth-wise convolution layer;

(3)

A core OSSMamba mechanism.

The 1 × 1 convolution layer performs preliminary processing on the normalized input, generating two parallel information streams that serve as the foundation for subsequent feature extraction. The depth-wise convolution layer extracts spatial features from one of these streams. Specifically, after passing through the 1 × 1 convolution layer, the input feature map is split into two information streams, denoted as $F_{O1}$ and $F_{O2}\in R^{B\times C\times H\times W}$. Stream $F_{O1}$ is processed by the deep convolution layer to produce the output $F_{O1D}$. The resulting streams, $F_{O1D}$ and $F_{O2}$, are then fed into OSSMamba through two different locations.

OSSMamba, illustrated in Figure 1c, serves as a key component comprising a bidirectional scanning mechanism and an enhanced Mamba block based on Mamba (S6) [29]. Its output is refined by a 1 × 1 convolution layer, which adjusts the feature dimensions to better align with subsequent processing and fusion stages, thereby facilitating efficient information transmission and representation. Furthermore, the skip connection incorporates a learnable scaling factor that modulates the contribution of residual information. Specifically, the output of the OSSMamba is combined with the original input features in a weighted manner, as defined by Formula (13):

$$F_{OP}=Mamba(SiLU(BidirectionalScan(F_{O1D}))),$$

(13)

where $BidirectionalScan()$ refers to a bidirectional scanning mechanism along the vertical and horizontal directions (i.e., H Forward Scan, H Backward Scan, W Forward Scan, and W Backward Scan) to comprehensively capture the two-dimensional spatial structure of the input feature map $F_{O1D}$. The enhanced feature representation, denoted as $F_{OP}$, serves as the basis for planar feature modeling. Inspired by UVM-Net [52], the approach is further extended to simultaneously capture both spatial and channel-wise dependencies. Specifically, a channel-wise bidirectional scanning mechanism is introduced and applied to the feature map $F_{O2}$, which enables joint modeling of the relationships between the two-dimensional spatial structures and inter-channel dependencies. This process is formalized as follows:

$$F_{OSS}=Mamba(SiLU(ChannelScan(Pooling(F_{OP}{F}_{O2}))))\cdot F_{O2}+F_{O2},$$

(14)

where $Pooling()$ denotes the pooling operation, and $ChannelScan()$ refers to the channel-wise bidirectional scanning mechanism. The process begins by multiplying $F_{OP}$ and $F_{O2}$, followed by a pooling operation, and finally performing bidirectional scanning along the channel dimension. This approach reduces computational complexity while enabling comprehensive modeling of channel information, ultimately producing $F_{OC}$. By fusing planar and channel information through residual connections, we obtain $F_{OSS}$, which represents the final result of comprehensive scanning and modeling.

As shown in Figure 2, the process includes omni-directional selective scanning and bidirectional channel scanning methods, involving six different directions: from the top-left corner to the bottom-right corner, from the bottom-right corner to the top-left corner, and from the bottom-left corner to the top-right corner and its reverse, as well as Channel Forward Scan and Channel Backward Scan. This multi-directional scanning enables the comprehensive extraction of spatial dependencies across the entire image plane. The resulting features from each directional pass are subsequently stacked and reshaped to form a unified representation, which is then fed into a Mamba block for sequential modeling. By incorporating six-directional scanning of image features, the model can more thoroughly capture image information, thereby overcoming the limitations of the original unidirectional modeling Mamba. This mechanism effectively integrates information from both spatial and channel dimensions, allowing the model to gain a deeper and more accurate understanding of the image content. In the context of complex image restoration tasks, this multi-directional scanning strategy enables the model to learn richer feature representations, thereby significantly improving the quality and accuracy of the reconstructed images.

3.5. Loss Function

To improve the robustness and reconstruction quality of the optimization process in remote sensing image denoising tasks, this paper uses the Charbonnier loss function as the training objective function. This loss is a smooth approximation of the L1 loss, combining the edge retention capability of L1 and the numerical stability of L2, and is expressed as follows:

$$L_{char}(\widehat{y},y)={\displaystyle \frac{1}{N}}{\displaystyle {\sum }_{i=1}^N\sqrt{{({\widehat{y}}_i-y_i)}^2+\epsilon }},$$

(15)

where ${\widehat{y}}_i$ denotes the predicted value of the model, $y_i$ is the ground truth value, $N$ is the total number of pixels, and $\epsilon$ is a small positive constant (such as 1 × 10⁻⁶) introduced to prevent numerical instability.

Compared to traditional L1 and L2 losses, the Charbonnier loss is smoother in regions close to zero, exhibits stronger gradient stability, and is less sensitive to outliers. These characteristics make it particularly suitable for image restoration problems in low-level visual tasks that require high fidelity in edge and texture structure preservation. The effectiveness of the Charbonnier loss has been extensively validated in multiple classical tasks such as image deblurring, super-resolution, and image denoising [53].

We chose the Charbonnier loss primarily due to its excellent edge preservation capability and numerical stability during training, which are critical for restoring weak structural details in remote sensing images. Additionally, we explored various loss functions, including perceptual loss, SSIM loss, and Huber loss. However, experiments demonstrated that the Charbonnier loss achieved superior quantitative metrics and subjective visual quality within our proposed OSSMDNet framework, making it the final choice for this study.

3.6. FLOPs, Computation Complexity and Robustness Analysis

When designing OSSMDNet, we meticulously balanced the representational capacity of the model with computational efficiency. The total number of trainable parameters in OSSMDNet is approximately 4 million, which is comparable to or even lower than that of current state-of-the-art Transformer-based denoising frameworks. For a typical input size of 128 × 128 pixels, the computational load, measured in terms of floating-point operations (FLOPs), is approximately 64 GFLOPs. This computational efficiency primarily stems from the linear complexity of the proposed Omni-Selective Scanning Modules (OSSModules), which effectively substitute the quadratic-complexity self-attention mechanisms commonly employed in traditional Transformer architectures.

As a core architectural component, the Depth Feature Extraction Module (DEFM) integrates structured state-space blocks with multi-directional scanning operations (including vertical, horizontal, diagonal, and anti-diagonal orientations) to enable comprehensive feature aggregation. This omni-directional scanning strategy significantly enhances the capacity of the model for spatial continuity preservation and fine-grained texture modeling, while mitigating the inherent anisotropy of receptive fields. As a result, OSSMDNet demonstrates superior robustness in addressing common challenges in high-resolution remote sensing imagery, such as geometric distortions and spatial misalignments caused by sensor motion, terrain undulation, or orthorectification errors.

Compared to traditional CNN-based and Transformer-based modules, OSSMDNet achieves linear spatial complexity O(N), thereby substantially reducing both memory footprint and inference latency. This characteristic makes the framework particularly suitable for processing large-scale remote sensing datasets, such as those obtained from high-resolution satellites or aerial imaging platforms.

In terms of robustness, extensive empirical evaluations under varying levels of synthetic and real-world noise demonstrate that OSSMDNet consistently maintains stable denoising performance. The synergistic combination of the global selective scanning mechanism and local residual connections empowers the model to adapt dynamically to nonstationary or spatially heterogeneous noise distributions, while effectively preserving structural integrity and semantic consistency, especially in scenes containing fine-scale land cover textures or man-made objects.

In summary, OSSMDNet achieves an effective trade-off between model expressiveness, computational cost, and denoising robustness, making it a promising and scalable solution for real-world remote sensing image restoration tasks that demand high fidelity, computational efficiency, and structural preservation.

4. Experiments

4.1. Experimental Setup

To evaluate the effectiveness and feasibility of the proposed method, we conducted experiments across multiple image restoration tasks, including both classical and remote sensing image denoising. For classical image denoising, the DIV2K [54] and Flickr2K [55] datasets were used for training. In the case of remote sensing image denoising, 2278 images from the DOTA dataset [56] were randomly selected as the training set.

The test datasets for classical image denoising included BSD68 [57], Kodak24 [58], McMaster [59], and Urban100 [60]. For remote sensing image denoising, the evaluation was performed by 600 and 198 images random sampled from AID [61] and WHU-RS19, which cover 30 and 19 distinct scene categories, respectively. Additionally, 967 images from the DOTA dataset, excluding those used for training, were selected as supplementary test samples to further validate the performance of model on remote sensing data.

To increase data diversity and enhance the generalization capability of the model during training, a series of data augmentation techniques were applied, including:

(1)

Horizontal flipping—mirroring images along the horizontal axis;

(2)

Random rotation—rotating images by 90°, 180°, or 270°;

(3)

Image cropping—dividing the original images into 128 × 128 patches.

All experiments were conducted on a workstation equipped with an NVIDIA RTX 4060Ti GPU (16GB VRAM). The model was trained using the Adam optimizer [62] with a fixed learning rate of 1e-4 and a batch size of 1 for 50,000 iterations. The learning rate remained constant throughout the training process to ensure sufficient convergence and feature extraction stability.

4.2. Evaluation Indicators

To comprehensively evaluate the performance of the proposed model on image denoising tasks, we adopted two widely used image quality evaluation metrics: Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM).

PSNR quantifies the pixel-level difference between the restored image and the reference (ground-truth) image, with higher values indicating superior restoration quality. PSNR is defined as follows:

$$PSNR=10\cdot {\log }_{10}({\displaystyle \frac{MA{X}^2}{MSE}}),$$

(16)

where $MAX$ denotes the maximum possible pixel value of the image (typically 255), and $MSE$ represents the mean squared error.

SSIM assesses the similarity between two images from three perspectives: luminance, contrast, and structural information. Compared to PSNR, SSIM better aligns with human visual perception, providing a more comprehensive evaluation of image quality. SSIM is defined as follows:

$$SSIM(x,y)={\displaystyle \frac{(2{\mu }_x{\mu }_y+C_1)(2{\sigma }_{xy}+C_2)}{({\mu }_x^2+{\mu }_y^2+C_1)({\sigma }_x^2+{\sigma }_y^2+C_2)}},$$

(17)

where ${\mu }_x$, ${\mu }_y$ represents the mean brightness, ${\sigma }_x^2$, ${\sigma }_y^2$ the variance, ${\sigma }_{xy}$ the covariance, and $C_1$, $C_2$ a constant used to stabilize numerical values.

In this study, both metrics were computed in the RGB color space on the test images, and average results across multiple standard datasets were reported. The proposed OSSMDNet method was compared against several state-of-the-art image denoising approaches, including CNN-based models (e.g., DnCNN [21], DRUNet [63]), Transformer-based models (e.g., SCUNet [64], Restormer [45]), and models based on the Mamba architecture (e.g., MambaIR [30]). All five categories of methods were trained under consistent settings with identical parameter configurations to ensure a fair comparison.

4.3. Classic Image Denoising Tasks

To visually evaluate the performance of various methods on image denoising tasks, we tested models trained on natural images and compared their denoising results on simulated datasets, including BSD68, Kodak24, McMaster, and Urban100, under different noise levels. The comparison included classic CNN-based methods such as DnCNN, DRUNet, and SCUNet, Transformer-based Restormer, Mamba-based MambaIR, and our proposed OSSMDNet.

The test results for classical image denoising are presented in Figure 3 (noise level 25) and 4 (noise level 50). Using Figure 4 as an illustrative example, the following observations can be made: As shown in Figure 4a, the high-definition reference image clearly displays the texture and structural details of the scene. Figure 4e presents the noisy input image with a noise level of 50, where colored Gaussian noise is uniformly distributed across the entire image. Figure 4b illustrates the result produced by DnCNN, which shows limited denoising capability. Residual noise remains noticeable in the output, negatively affecting the overall visual quality. The aircraft fuselage appears significantly blurred, and the star pattern is barely distinguishable. Figure 4c shows the result from SCUNet, which achieves stronger noise suppression, leaving virtually no visible noise in the image. However, this comes at the cost of over-smoothing, particularly in regions rich in texture. Fine-grained details are lost, and both the aircraft fuselage and star pattern remain blurred, indicating insufficient preservation of image structure. Figure 4d demonstrates that DRUNet achieves a good balance between noise removal and detail preservation. The aircraft fuselage regains its basic contours, and the pentagram is recognizable in both shape and color. Nonetheless, some deformation remains visible in the star-shaped region. As shown in Figure 4f, Restormer is capable of removing noise to a certain extent. However, it tends to over-smooth the image. Although the denoised result appears clean and smooth at first glance, a closer inspection reveals blurred textures and a lack of realism. In Figure 4g, MambaIR demonstrates strong noise suppression capabilities, but its ability to restore fine details remains limited. The rear section of the aircraft is poorly reconstructed, exhibiting noticeable structural distortion.

In contrast, the proposed OSSMDNet delivers superior visual quality. As shown in Figure 4h, it can effectively remove most noise while avoiding excessive smoothing of textures. In edge-rich and structurally detailed areas, such as the aircraft and pentagram patterns, fine details are well preserved. The denoised images are cleaner, more natural, and visually closer to the original noise-free images. These results demonstrate that OSSMDNet achieves an optimal balance between noise suppression and detail preservation, resulting in superior visual fidelity.

We conducted a quantitative statistical analysis of the denoising performance under two different noise levels (σ = 25 and σ = 50), as presented in

Table 1. Comparison results between OSSMDNet and both classic and advanced denoising methods at noise levels of 25 and 50 on classic image datasets.

DataSets	Noise Level	DnCNN		DRUNet		SCUNet		Restormer		MambaIR		OSSMDNet
		PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
CBSD68	25	30.46	0.8700	30.89	0.8816	30.92	0.8833	30.50	0.8839	30.99	0.8841	31.03	0.8858
	50	27.01	0.7654	27.63	0.7898	27.61	0.7894	26.37	0.7787	27.70	0.7917	27.74	0.7913
Kodak24	25	31.33	0.8614	31.95	0.8772	31.92	0.8782	31.68	0.8786	32.10	0.8807	32.11	0.8819
	50	27.99	0.7645	28.80	0.7946	28.76	0.7938	26.67	0.7866	28.92	0.7982	28.92	0.7977
McMaster	25	31.43	0.8684	32.25	0.8896	32.26	0.8913	31.13	0.8491	32.47	0.8918	32.47	0.8924
	50	28.07	0.7827	29.16	0.8239	29.16	0.8234	26.08	0.7282	29.31	0.8241	29.32	0.8249
Urban100	25	30.02	0.8969	30.87	0.9125	30.72	0.9110	30.56	0.9033	31.25	0.9173	31.30	0.9188
	50	26.04	0.8001	27.51	0.8457	27.33	0.8437	26.09	0.8256	27.89	0.8545	27.96	0.8553

. For clarity, the best results are highlighted in bold, while the second-best results are underlined. This allows for a comprehensive evaluation of the robustness and effectiveness of each method across varying noise intensities.

At a noise level of σ = 25, OSSMDNet consistently outperformed other methods on multiple datasets. On the CBSD68 test set, it achieved average PSNR improvements of 0.57 dB and 0.53 dB over DnCNN and Restormer, respectively. Compared with advanced CNN-based methods such as DRUNet and SCUNet, OSSMDNet demonstrated gains of 0.14 dB and 0.11 dB, respectively. Even against MambaIR, a state-of-the-art method based on the Mamba architecture, OSSMDNet maintained a marginal advantage of 0.04 dB.

At the higher noise level of σ = 50, the superiority of OSSMDNet became even more pronounced. On the Urban100 dataset, it outperformed DnCNN and Restormer by 1.92 dB and 1.87 dB in average PSNR, respectively, clearly demonstrating its robustness under severe noise conditions. It also achieved improvements of 0.45 dB over DRUNet and 0.63 dB over SCUNet. When compared to MambaIR, OSSMDNet still delivered a PSNR gain of 0.07 dB.

In summary, these experimental results comprehensively demonstrate that OSSMDNet possesses superior denoising capabilities and stronger generalization performance across different noise levels on natural image datasets.

4.4. Remote Sensing Image Denoising Task

Similarly, to validate the performance of the proposed OSSMDNet for remote sensing denoising task, we designed a unified experiment setting and retrained six mainstream image denoising methods. All models were trained under consistent settings, including a uniform input image size (128 × 128), the same optimizer Adam, and a fixed learning rate scheduling strategy (initial learning rate set to 1 × 10⁻⁴ and kept constant throughout training). Each model was trained for 50,000 iterations.

Figure 5 presents the denoising visualization results of different methods on the AID dataset with a noise level of 25, while Figure 6 shows the results on the WHU-RS19 dataset with a noise level of 50. Taking Figure 6 as an example, in the high-resolution original image (Figure 6a), the red and white disks, along with the surrounding textures, are clearly visible. However, the noisy image (Figure 6e) is severely degraded due to the presence of dense noise. As shown in Figure 6b, after denoising with DnCNN, the red and white disks and the lower-right region appear blurry, with residual noise still visible around the disks. This indicates the limited capability of DnCNN in both denoising and detail restoration. In Figure 6c,d, the SCUNet and DRUNet methods manage to partially recover the textures around the disks, but the disk centers remain blurred, suggesting moderate performance in preserving fine details. In contrast, although Restormer demonstrates strong denoising ability as shown in Figure 6f, it suffers from significant over-smoothing, leading to the loss of texture details around the disks. This implies that a substantial amount of structural information is discarded during the denoising process.

By comparison, as shown in Figure 6g, the MambaIR results and those of OSSMDNet in Figure 6h exhibit enhanced texture recovery around the disks, along with partial restoration of the building on the right side of the image. These results indicate that both methods achieve effective denoising while better preserving fine structural details, with OSSMDNet particularly excelling in balancing noise removal and detail preservation.

As shown in

Table 2. Comparison results between OSSMDNet and the most classic and advanced denoising methods on remote sensing images with noise levels of 25 and 50.

DataSets	Noise Level	DnCNN		DRUNet		SCUNet		Restormer		MambaIR		OSSMDNet
		PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
AID	25	32.15	0.8740	32.57	0.8827	32.61	0.8829	32.52	0.8850	32.50	0.8806	32.64	0.8839
	50	28.82	0.7703	29.63	0.8045	29.64	0.8019	28.80	0.7935	29.70	0.8047	29.72	0.8067
DOTA	25	32.97	0.8823	33.66	0.8930	33.69	0.8926	33.54	0.8893	33.44	0.8879	33.74	0.8940
	50	29.76	0.7971	30.72	0.8283	30.73	0.8261	29.61	0.8120	30.81	0.8289	30.84	0.8305
WHU-RS19	25	32.57	0.8946	32.97	0.9018	33.03	0.9030	32.39	0.9025	32.90	0.9000	33.08	0.9035
	50	28.75	0.7952	29.92	0.8309	29.91	0.8293	28.25	0.8174	30.00	0.8315	30.04	0.8334

, the PSNR and SSIM values obtained by the six different denoising methods under different test sets are presented. It can be seen that the proposed OSSMDNet model achieves the best PSNR and SSIM among all comparison methods, demonstrating excellent denoising performance and strong practical application potential.

Under moderate noise conditions with a standard deviation of σ = 25, OSSMDNet outperforms the classic CNN-based method DnCNN and the Transformer-based Restormer by 0.49 dB and 0.12 dB in average PSNR on the AID dataset, respectively. Even compared to state-of-the-art CNN-based models such as DRUNet and SCUNet, OSSMDNet still achieves gains of 0.07 dB and 0.03 dB, respectively. This advantage is even more pronounced on the WHU-RS19 dataset, where OSSMDNet surpasses DRUNet by 0.10 dB in average PSNR.

Under high noise conditions (σ = 50), the superiority of OSSMDNet becomes even more evident. On the DOTA dataset, it achieves an average PSNR that is 1.08 dB higher than DnCNN, 1.23 dB higher than Restormer, and approximately 0.11 dB and 0.09 dB higher than DRUNet and SCUNet, respectively. These results clearly demonstrate the robustness and effectiveness of OSSMDNet in handling complex, high-noise environments.

4.5. Downstream Classification Experimental Verification

To further substantiate the superiority of the proposed OSSMDNet, supervised classification experiments were conducted on denoised remote sensing images to evaluate the impact of various denoising methods on classification performance.

As shown in Figure 7, when the noise level is σ = 50, the denoising results of various methods are visually compared. Figure 7c–h present the results of DnCNN, SCUNet, DRUNet, Restormer, MambaIR, and OSSMDNet, respectively, while Figure 7a shows the original high-resolution image and Figure 7e shows the noisy version. The denoised images conducted a pixel-level classification. Figure 8 further illustrates the classification outcomes of different denoising methods with Support Vector Machine (SVM). As shown in Figure 8a, a three-class scheme was applied to the original high-resolution image, categorizing pixels into buildings (red), trees (green), and roads (blue). In this image, buildings dominate, trees are sparsely distributed, and roads form distinct linear patterns. However, in the noisy image (Figure 8e), the classification scheme degrades to only two categories: one category is trees, and the other is buildings. This is because roads are incorrectly classified as trees. In addition, it can be seen that some buildings are also incorrectly labeled as trees, indicating that noise has a significant impact on classification accuracy. We have marked these eight classification result images simply (as indicated by the yellow and blue boxes in the figure). By visually comparing the classification results within the yellow boxes, where the green fill represents classified trees, we can see that, using the high-definition image Figure 8a (HQ) as the standard, the classification result image closest to it is Figure 8h (OSSMDNet). Similarly, the classification situation within the blue boxes is the same. The blue-filled areas represent the classified road sections. Through visual comparison, Figure 8h (OSSMDNet) classification result image remains the closest to Figure 8a (HQ) classification results.

Specifically, based on the classification results from Figure 8b–h, DnCNN, DRUNet, SCUNet, and Restormer tend to overclassify tree areas, resulting in a significantly higher number of pixels labeled as trees compared to the high-resolution reference image. This is primarily due to incomplete noise removal, which causes some building areas to be mistaken for trees. MambaIR shows a degree of improvement but still exhibits a slightly higher proportion of tree-classified pixels, and mislabels parts of buildings, particularly in the left-central and lower regions, as trees, leading to an overall accuracy that remains lower than that of the original image. In contrast, OSSMDNet produces results most similar to the high-resolution reference. Roads appear as clear linear structures, and tree regions are properly distributed among buildings, demonstrating its strong noise suppression ability and accurate restoration of textures and structural details. Among all methods, OSSMDNet delivers the most significant improvement in classification accuracy, which is critical for remote sensing image analysis.

As shown in

Table 3. Comparison of accuracy results for supervised classification after denoising using different image denoising methods.

Evaluation Indicators	DnCNN	DRUNet	SCUNet	Restormer	MambaIR	OSSMDNet	Noisy	Raw
Overall accuracy(OA) (%)	92.96%	95.47%	96.57%	97.83%	98.33%	99.76%	77.10%	100%
Kappa Improvement (%)	84.06%	91.51%	93.42%	96.21%	97.77%	98.43%	47.60%	100%

, we adopt the classification performance of the original high-resolution image as the baseline (i.e., normalized to 100%) and conduct a relative comparison of classification accuracy after applying various denoising methods. Under severe noise interference, the performance of remote sensing images in downstream classification tasks degrades significantly, with a normalized Overall Accuracy (OA) of only 77.10% and a Kappa coefficient of 47.60%. This indicates that the presence of noise severely disrupts the spatial structures and spectral signatures of the imagery, thus compromising the reliability of subsequent object recognition and land-cover classification tasks.

After applying several representative deep learning-based denoising models, classification performance improves substantially, listed as follows: DnCNN-denoised images increase the normalized OA to 92.96%, and the Kappa coefficient to 84.06%; DRUNet, benefiting from residual dense connections that promote feature reuse, further elevates the OA and Kappa to 95.47% and 91.51%, respectively; SCUNet, which integrates spatial-channel attention mechanisms to enhance texture detail representation, improves the OA to 96.57% and the Kappa to 93.42%; Restormer, leveraging the long-range dependency modeling capacity of the Transformer architecture, achieves 97.83% OA and 96.21% Kappa; MambaIR, as the first state-space model tailored for image restoration, further improves performance to 98.33% OA and 97.77% Kappa; OSSMDNet, which integrates the global context modeling capability of Mamba with an omni-directional selective scanning mechanism, achieves the best results in terms of both structure preservation and texture recovery. It attains a normalized OA of 99.76% and a Kappa coefficient of 98.43%, outperforming MambaIR by 1.43% and 0.66%, respectively, and yielding results closest to the original high-resolution image.

Therefore, OSSMDNet demonstrates superior denoising robustness and excellent adaptability to downstream tasks, effectively preserving fine-grained spatial features and structural consistency. These results suggest that OSSMDNet offers strong practical potential for high-fidelity remote sensing image processing and real-world Earth observation applications.

4.6. Ablation Experiments

To further analyze the contributions of key components in our architecture, we conducted ablation studies examining the effects of OSSMamba, CA mechanism, LRB, and the number of stacked OSSMamba modules. All models were trained on the natural RGB image denoising task using the Charbonnier loss function. The results are summarized in

Table 4. Impact of different network configurations for OSSMDNet.

Method	OSSMamba	CA	LRB	Number of Stacks	PSNR(dB)	SSIM
OSSMDNet	√	√	√	[6,6,6,6,6,6]	27.96	0.8555
OSSMDNet-v1	×	√	√	[6,6,6,6,6,6]	26.97	0.8287
OSSMDNet-v2	√	×	√	[6,6,6,6,6,6]	27.94	0.8553
OSSMDNet-v3	√	√	×	[6,6,6,6,6,6]	27.75	0.8505
OSSMDNet-v4	√	√	√	[1,1,1,1,1,1]	27.46	0.8451

.

Table 5. Test results of different network configurations with different test sets.

Datasets	Noise Level	OSSMDNet		OSSMDNet-v1		OSSMDNet-v2		OSSMDNet-v3		OSSMDNet-v4
		PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
CBSD68	50	27.74	0.7913	27.38	0.7769	27.72	0.7913	27.67	0.7895	27.59	0.7890
Kodak24		28.92	0.7977	28.42	0.7774	28.92	0.7980	28.80	0.7945	28.67	0.7931
McMaster		29.32	0.8249	28.77	0.8072	29.32	0.8246	29.18	0.8203	28.98	0.8158
Urban100		27.96	0.8555	26.97	0.8287	27.94	0.8553	27.75	0.8505	27.46	0.8451

shows a quantitative comparison of the values of PSNR and SSIM after denoising various natural datasets using various ablation experiment models at a noise level of 50.

Impact of the OSSMamba module: To evaluate the effectiveness of the OSSMamba module, we conducted an ablation study using the OSSMDNet-v1 variant, in which the network was trained for 50,000 iterations without incorporating OSSMamba. As shown in Table 4, under high noise conditions (σ = 50), the PSNR values on four benchmark datasets, including CBSD, dropped by an average of approximately 0.60 dB compared to the complete OSSMDNet model. This noticeable performance decline underscores the critical importance of state-space modeling in remote sensing image denoising, particularly for effectively capturing two-dimensional spatial dependencies.

The OSSMamba module is specifically designed to exploit the strengths of the Mamba architecture. By integrating the sequential modeling power of state-space models, OSSMamba effectively captures both global structural dependencies and fine-grained local details within images. Compared to traditional denoising approaches, such as CNN-based methods with limited receptive fields and Transformer-based models with high computational overhead, OSSMamba offers a more efficient and scalable solution for modeling complex spatial relationships in noisy remote sensing images. This validates the essential contribution of OSSMamba to the superior denoising performance of the full OSSMDNet model.

Effect of the CA Mechanism: To assess the contribution of the CA mechanism within OSSMDNet, we conducted an ablation experiment by removing this component and retraining the network, resulting in the OSSMDNet-v2 variant. As shown in the evaluation results, the PSNR values dropped by approximately 0.02 dB compared to the full model. Although the decline is relatively small, it confirms the positive role of the CA mechanism in enhancing the performance stability of the model and in reducing redundancy across feature channels.

Specifically, the CA mechanism helps the network to selectively focus on the most informative and relevant channels during image restoration. By suppressing less useful or redundant channel responses, it improves the representational efficiency of the network. In the context of image denoising, this mechanism allows the model to better distinguish between noise and useful image structures, thereby enabling more precise noise suppression and detail preservation. These results highlight that even seemingly modest architectural components, such as CA, can contribute meaningfully to overall denoising effectiveness.

Effect of the LRB: In the OSSMDNet-v4 variant, we removed the LRB from OSSModule to assess their specific role in image denoising tasks. This adjustment resulted in a 0.14 dB decrease in average PSNR, indicating that the introduction of LRB significantly enhances local feature modeling capabilities and makes a positive contribution to overall denoising performance.

The effectiveness of LRB primarily stems from its explicit modeling capability of local information, which is often relatively weak in architectures that primarily focus on global modeling. For example, while stacking multiple DFEGs helps capture long-range dependencies and multi-scale semantic information in images, it may also weaken sensitivity to local spatial correlations. Additionally, the sequence scanning structure of Mamba can disrupt spatial continuity between pixels during image-to-sequence conversion, making it difficult to effectively preserve local neighborhood structures (e.g., edges, textures, etc.).

In contrast, convolutional operations are inherently suited for modeling local features. By filtering, fusing, and enhancing feature maps through sliding convolutional kernels, they can highlight key regions in images while suppressing irrelevant information. Therefore, integrating carefully designed convolutional layers with nonlinear activation functions in the LRB can effectively compensate for the absence of a local consistency modeling mechanism in the Mamba architecture.

Specifically, LRB not only helps preserve basic visual attributes of images, such as color fidelity, edge sharpness, and structural contours, but also further integrates advanced features reflecting long-range dependencies and semantic associations. By establishing a more balanced representation between local details and global structure, LRB significantly improves image reconstruction quality, enabling the model to maintain overall structural consistency while preserving fine-grained information, thereby achieving notable improvements in both denoising accuracy and visual quality.

Stacking Effect of the OSSMamba: In OSSMDNet-v5, the number of stacked OSSModules was reduced to one, effectively removing the stacking effect. This modification led to a notable PSNR decrease of 0.31 dB, emphasizing the importance of stacking OSSMamba modules. As a core architectural component, stacking these modules significantly boosts the denoising performance of the model.

As shown in Figure 9, we present the visual comparison results of four ablation experiments under a noise level of 50, alongside the high-definition reference image and the output of our complete method. Using the high-quality image in Figure 9a as a reference, Figure 9b depicts the denoising result of our proposed OSSMDNet. It can be observed that our full model demonstrates significant advantages in noise suppression, almost completely eliminating background noise. Meanwhile, it also excels in restoring structural image details, particularly in the edge clarity of red letters on a white background and the reconstruction of the red sports car’s parking area, including the rear contours and the vertical pole. In contrast, the result of OSSMDNet-v1 shows a substantial amount of residual noise, with the entire image appearing visibly distorted. The ground textures are severely degraded, the red sports car’s parking region suffers from strong motion blurring, and the vertical pole is nearly unrecognizable, indicating weak detail preservation capabilities. The output of OSSMDNet-v2 is visually close to that of the complete model, exhibiting strong denoising performance and effective structural retention. For instance, the red car’s rear shows minimal trailing artifacts, and the vertical pole is restored with relatively high accuracy. In OSSMDNet-v3, the reconstruction performance degrades to some extent. The vertical pole at the rear of the car appears faded in color, with surrounding regions exhibiting blur and trailing, suggesting insufficient capacity to model complex structures. The result from OSSMDNet-v4 still presents noticeable red trailing around the vehicle’s rear, blurry edges around the parking area, and imprecise recovery of the vertical pole, alongside certain deformations in the ground texture. Overall visual quality remains suboptimal.

In summary, the step-by-step visual comparison highlights the concrete contributions of each module to image restoration. These results further validate that the proposed OSSMDNet strikes an effective balance between noise removal and structure preservation, offering superior perceptual quality and adaptability to downstream tasks.

5. Conclusions

In this paper, we proposed OSSMDNet, a novel remote sensing image denoising framework that integrates the Mamba state-space model with an Omni-Selective Scanning Mechanism. By addressing the limitations of CNNs in modeling long-range dependencies and reducing the high computational cost of Transformers, OSSMDNet enables efficient global–local feature interaction with linear complexity. The introduced directional state-space scanning enhances structural continuity modeling, contributing to improved texture and detail restoration. Extensive experiments on both natural and remote sensing datasets demonstrate that OSSMDNet consistently surpasses representative CNN-based, Transformer-based, and state-space-based models in PSNR and SSIM, while significantly reducing inference latency. These results confirm that our method achieves a better balance between denoising accuracy and computational efficiency, making it a practical and scalable solution for high-resolution image restoration tasks.

Although the PSNR and SSIM results show measurable numerical improvements, the perceptual quality of reconstructed images may sometimes appear visually similar. We acknowledge that numerical gains do not always translate into perceptual enhancements. Therefore, future work will explore the integration of texture-aware strategies, including perceptual loss, style loss, and texture-guided reconstruction mechanisms, to further enhance the visual realism and structural fidelity of denoised outputs. This direction is expected to improve not only quantitative evaluation metrics but also the subjective visual quality of results, particularly in complex real-world remote sensing scenarios.

Furthermore, we plan to extend OSSMDNet to the domain of hyperspectral image (HSI) denoising, where maintaining spectral correlation is essential. By incorporating spectral modeling strategies, such as spectral-spatial attention mechanisms or inter-band consistency constraints, we aim to enhance the network’s ability to jointly represent spectral and spatial features. This extension is expected to broaden the applicability of OSSMDNet to more advanced Earth observation tasks that require high-dimensional data integrity and strong robustness to noise.