An Improved InTEC Model for Estimating the Carbon Budgets in Eucalyptus Plantations
Abstract
1. Introduction
2. Methods
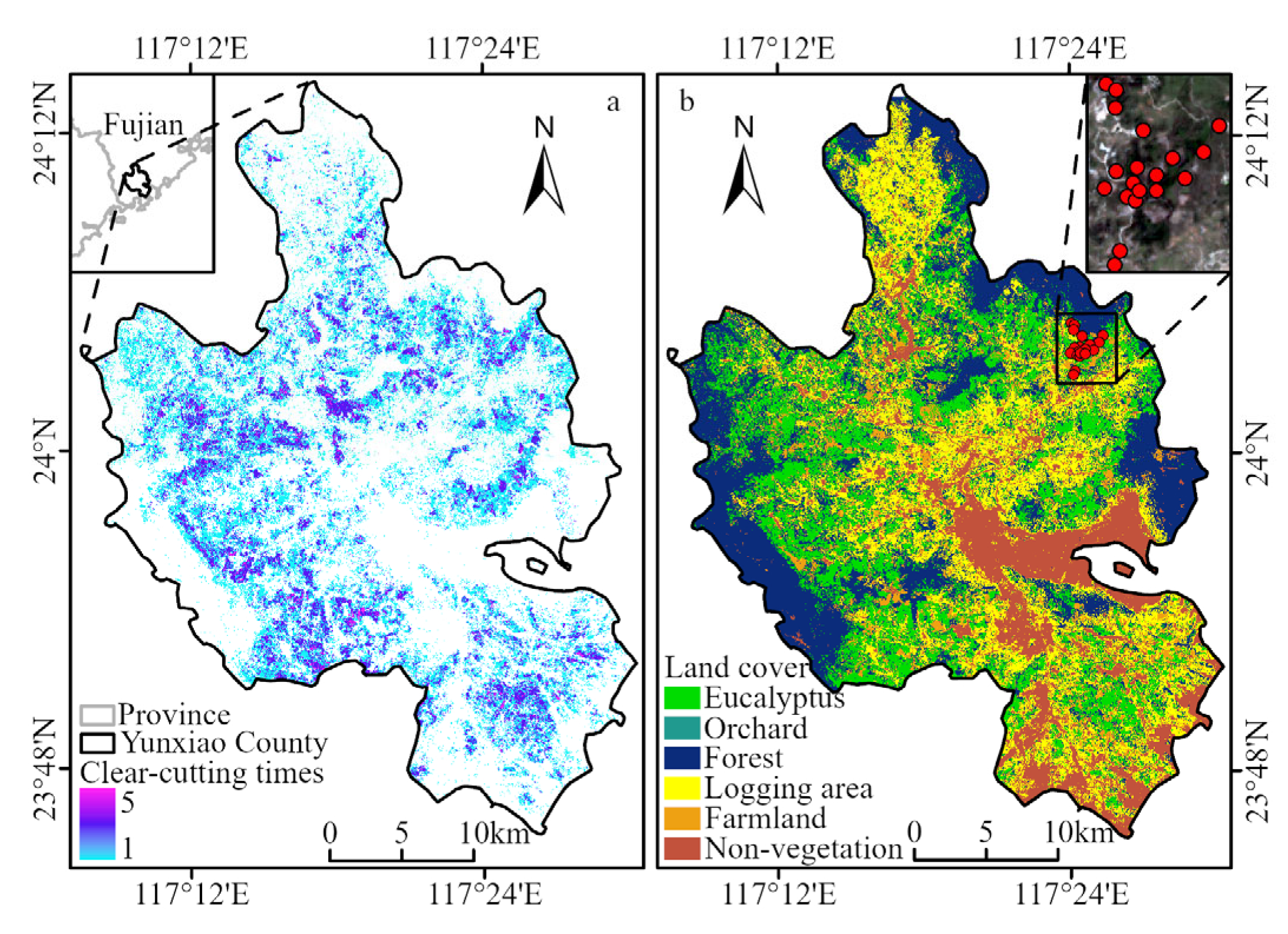
2.1. Study Area and Data
2.1.1. Study Area
2.1.2. Data Collection and Preprocessing
2.2. InTEC Model and Improvement
2.2.1. Basic Principles and Key Parameters of InTEC Model
2.2.2. Optimizing Key Modules of InTEC Model
2.3. Accuracy Evaluation
2.4. Spatiotemporal Variation Characteristics Analysis
3. Results
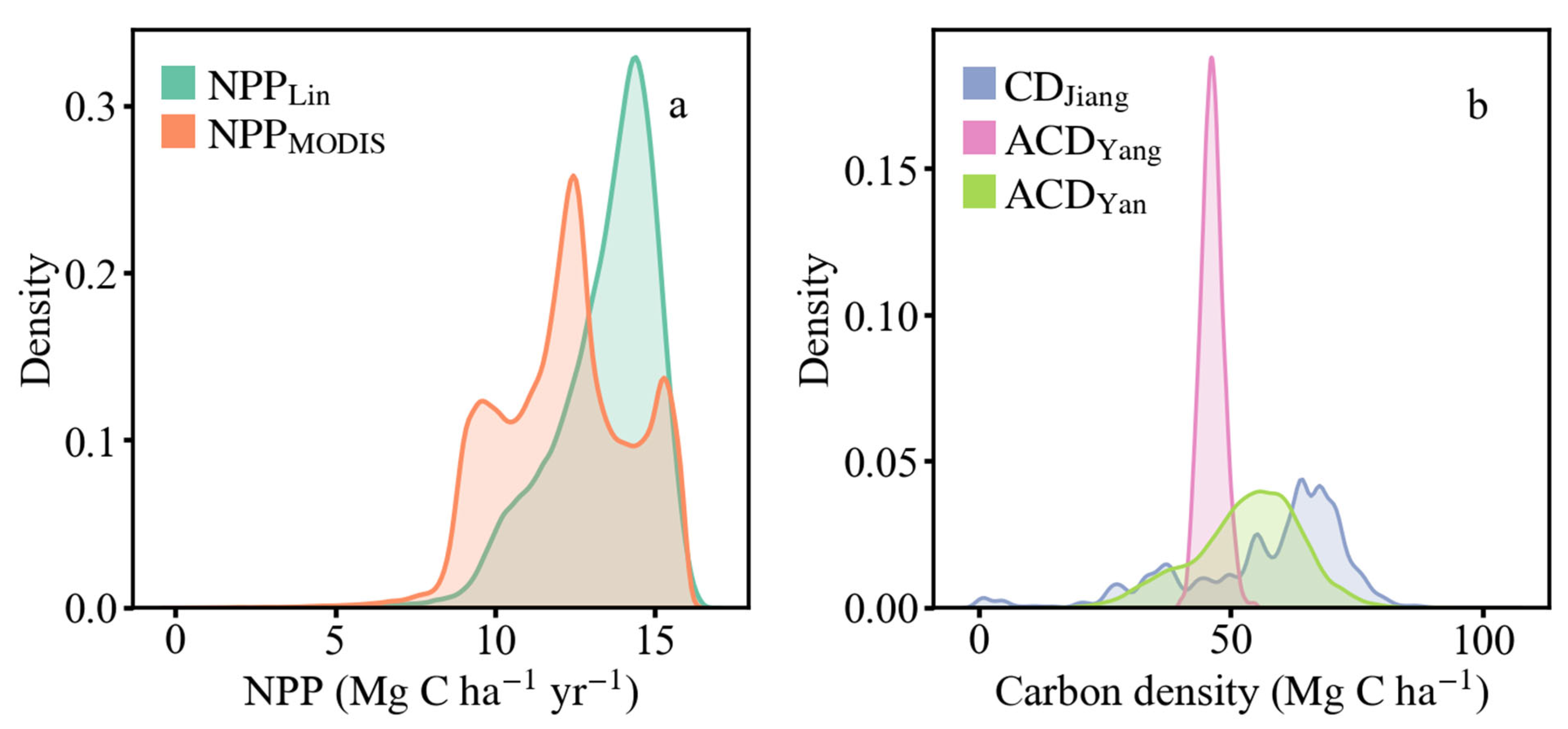
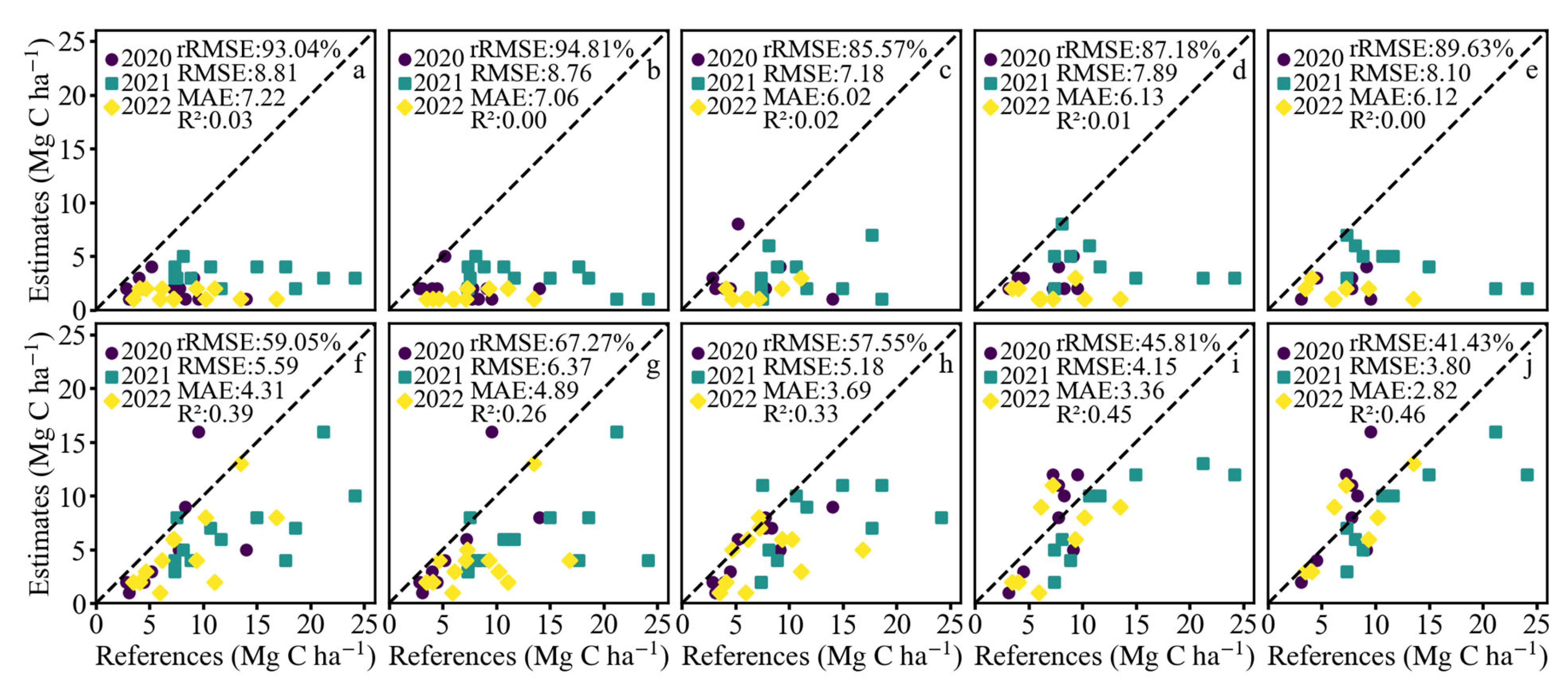
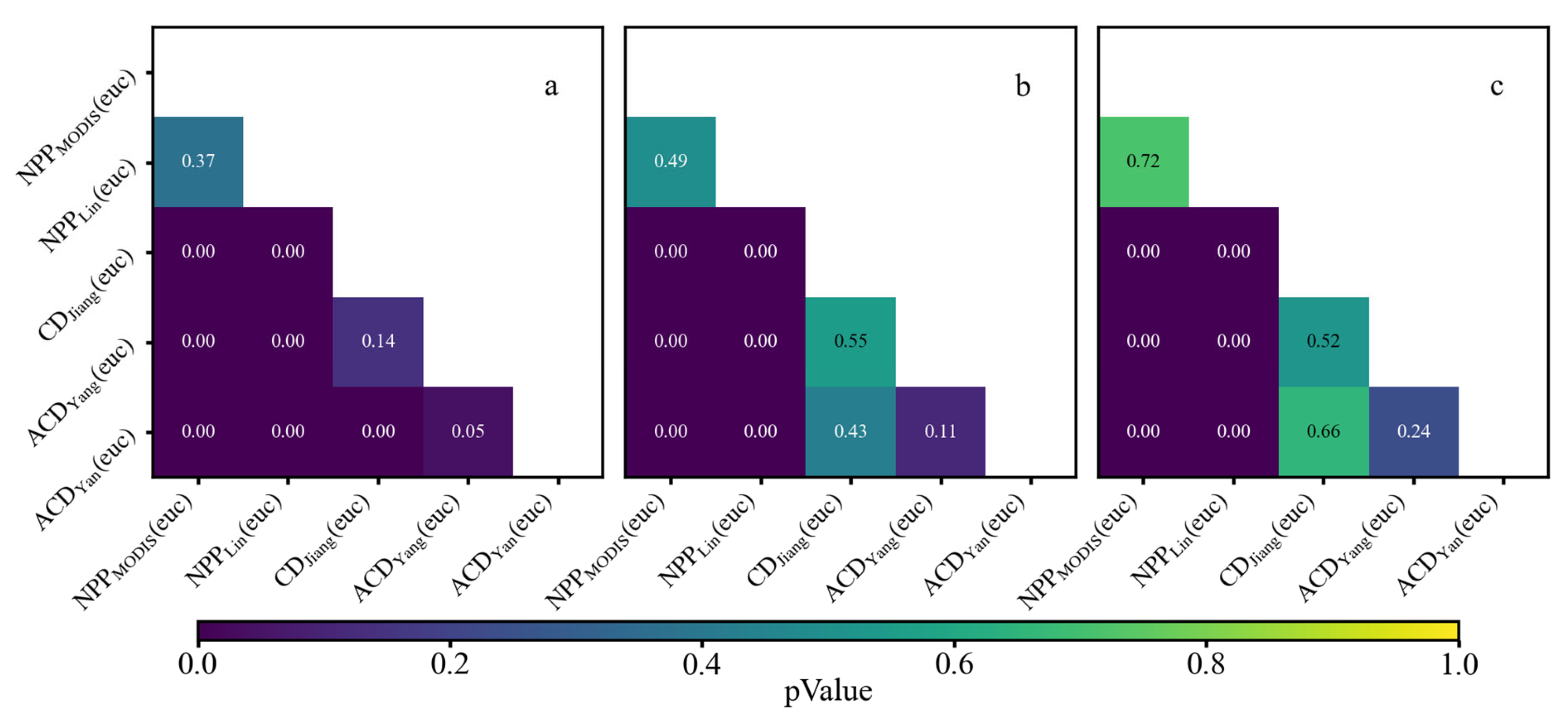
3.1. Evaluation of Simulation Result
3.1.1. Accuracy Evaluation of InTECeuc Model
3.1.2. Accuracy Evaluation of InTECDA Model
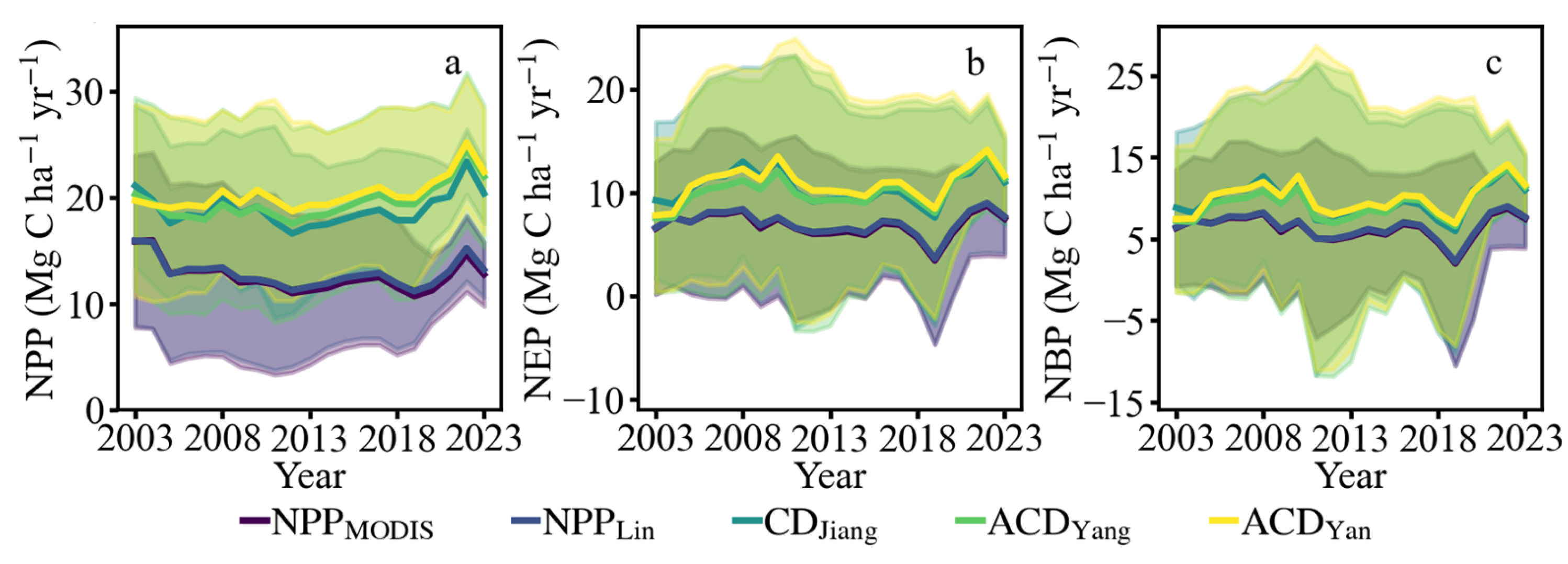
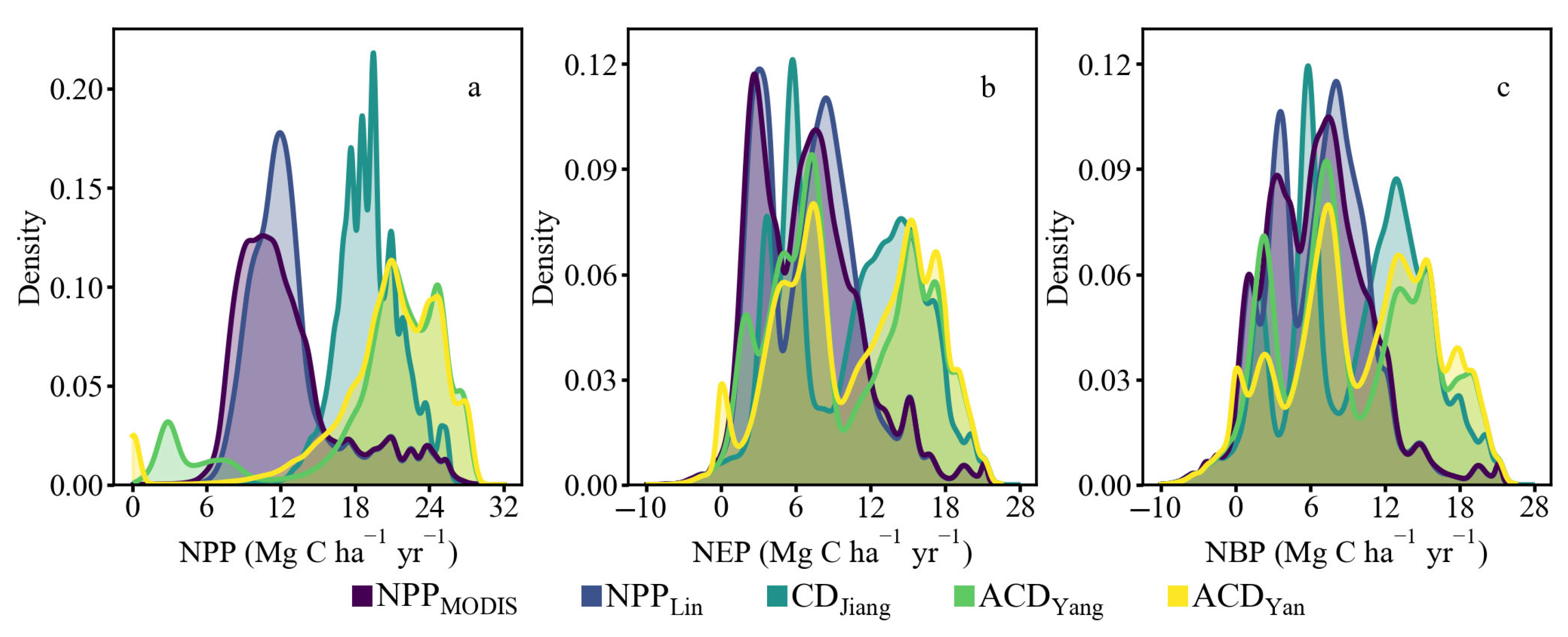
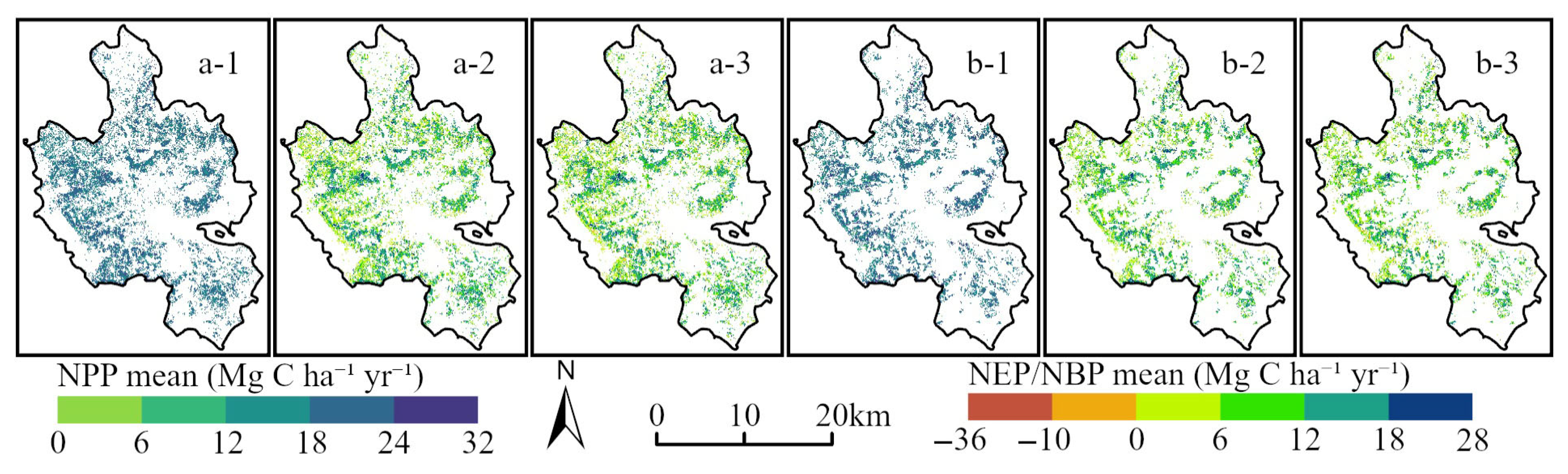
3.2. Spatiotemporal Variation Characteristics of Eucalyptus Carbon Budgets with InTECeuc Model
3.2.1. Temporal Variation Characteristics of Carbon Budgets
3.2.2. Spatial Variation Characteristics
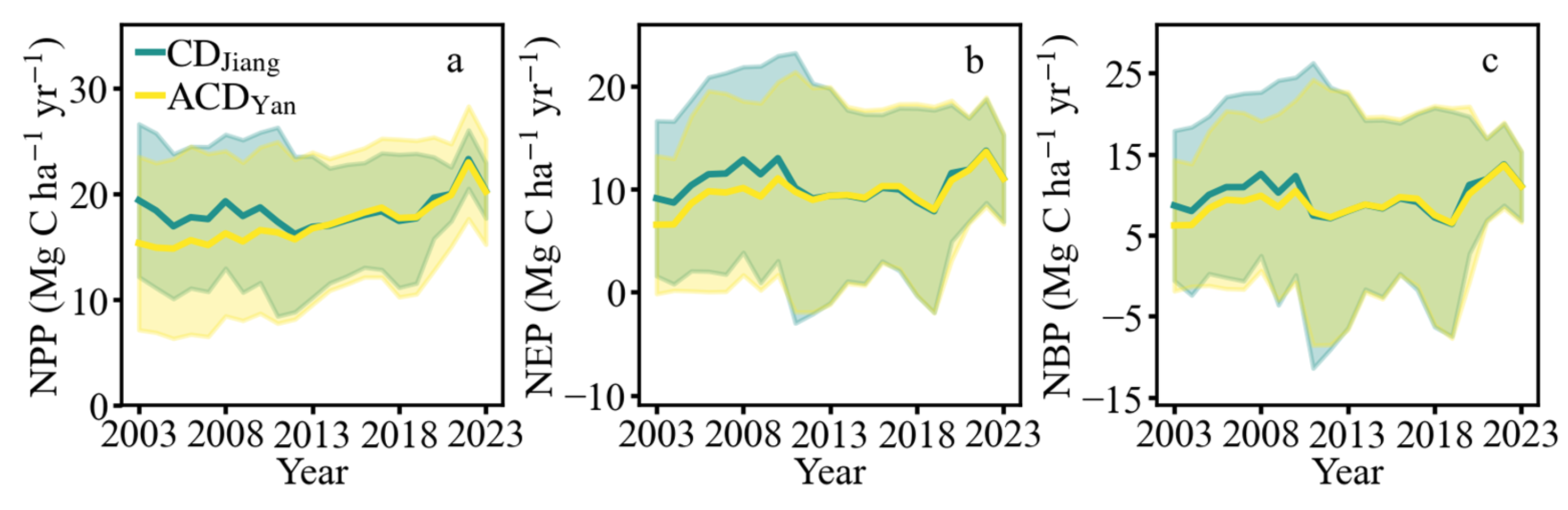
3.3. Spatiotemporal Variation Characteristics of Eucalyptus Carbon Budgets with InTECDA Model
3.3.1. Temporal Variation Characteristics
3.3.2. Spatial Variation Characteristics of InTECDA Model
4. Discussion
4.1. The Performance of Improved InTEC Model
4.2. Carbon Budgets of Eucalyptus
4.3. Limitations and Potential Improvements
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, K.; Yang, H.; Tao, S.; Su, Y.; Guan, H.; Ren, Y.; Hu, T.; Li, W.; Xu, G.; Chen, M.; et al. Carbon Storage through China’s Planted Forest Expansion. Nat. Commun. 2024, 15, 4106. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X. Geographical Spatial Distribution and Productivity Dynamic Change of Eucalyptus Plantations in China. Sci. Rep. 2021, 11, 19764. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ye, D.; Liang, H.; Zhu, H.; Qin, L.; Zhu, Y.; Wen, Y. Effects of Successive Rotation Regimes on Carbon Stocks in Eucalyptus Plantations in Subtropical China Measured over a Full Rotation. PLoS ONE 2015, 10, e0132858. [Google Scholar] [CrossRef] [PubMed]
- Keenan, T.F.; Williams, C.A. The Terrestrial Carbon Sink. Annu. Rev. Environ. Resour. 2018, 43, 219–243. [Google Scholar] [CrossRef]
- Li, Q.; Zhu, J.; Feng, Y.; Xiao, W. Carbon Stocks and Carbon Sequestration Capacity of the Main Plantations in China. J. Northwest For. Univ. 2016, 31, 1–6. [Google Scholar] [CrossRef]
- Lan, X.; Du, H.; Song, T.; Zeng, F.; Peng, W.; Liu, Y.; Fan, Z.; Zhang, J. Vegetation Carbon Storage in the Main Forest Types in Guangxi and the Related Influencing Factors. Acta Ecol. Sin. 2019, 39, 2043–2053. [Google Scholar] [CrossRef]
- Li, D.; Lu, D.; Wu, Y.; Luo, K. Retrieval of Eucalyptus Planting History and Stand Age Using Random Localization Segmentation and Continuous Land-Cover Classification Based on Landsat Time-Series Data. GIScience Remote Sens. 2022, 59, 1426–1445. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, D.; Zhu, Y.; Peng, H.; Xie, H. A Review of Forest Carbon Cycle Models on Spatiotemporal Scales. J. Clean. Prod. 2022, 339, 130692. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, L.; Chen, J.; Ju, W.; Feng, X.; Wu, W. Relationships between Net Primary Productivity and Stand Age for Several Forest Types and Their Influence on China’s Carbon Balance. J. Environ. Manag. 2011, 92, 1651–1662. [Google Scholar] [CrossRef]
- Yu, Y.; Fan, W.; Yang, X. Estimation of Forest NPP in Xiaoxing’an Mountains in 1901–2008. Sci. Silvae Sin. 2014, 50, 16–23. [Google Scholar]
- Zheng, J.; Mao, F.; Du, H.; Li, X.; Zhou, G.; Dong, L.; Zhang, M.; Han, N.; Liu, T.; Xing, L. Spatiotemporal Simulation of Net Ecosystem Productivity and Its Response to Climate Change in Subtropical Forests. Forests 2019, 10, 708. [Google Scholar] [CrossRef]
- Li, X.; Du, H.; Zhou, G.; Mao, F.; Zheng, J.; Liu, H.; Huang, Z.; He, S. Spatiotemporal Dynamics in Assimilated-LAI Phenology and Its Impact on Subtropical Bamboo Forest Productivity. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102267. [Google Scholar] [CrossRef]
- Wang, J.; Wu, C.; Zhang, C.; Ju, W.; Wang, X.; Chen, Z.; Fang, B. Improved Modeling of Gross Primary Productivity (GPP) by Better Representation of Plant Phenological Indicators from Remote Sensing Using a Process Model. Ecol. Indic. 2018, 88, 332–340. [Google Scholar] [CrossRef]
- Running, S.; Zhao, M. MODIS/Terra Net Primary Production Gap-Filled Yearly L4 Global 500m SIN Grid V061 [Data Set]; NASA EOSDIS Land Processes Distributed Active Archive Center: Sioux Falls, SD, USA, 2021. [Google Scholar] [CrossRef]
- Lin, S.; Huang, X.; Zheng, Y.; Zhang, X.; Yuan, W. An Open Data Approach for Estimating Vegetation Gross Primary Production at Fine Spatial Resolution. Remote Sens. 2022, 14, 2651. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP Products across Multiple Biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- Turner, J.; Lambert, M.J. Nutrient Cycling in Age Sequences of Two Eucalyptus Plantation Species. For. Ecol. Manag. 2008, 255, 1701–1712. [Google Scholar] [CrossRef]
- Rajab Pourrahmati, M.; Le Maire, G.; Baghdadi, N.; Alvares, C.A.; Stape, J.L.; Scolforo, H.F.; Campoe, O.C.; Nouvellon, Y.; Guillemot, J. Integrating MODIS-Derived Indices for Eucalyptus Stand Volume Estimation: An Evaluation of MODIS Gross Primary Productivity. Front. Remote Sens. 2025, 6, 1588387. [Google Scholar] [CrossRef]
- Yang, Q.; Niu, C.; Liu, X.; Feng, Y.; Ma, Q.; Wang, X.; Tang, H.; Guo, Q. Mapping High-Resolution Forest Aboveground Biomass of China Using Multisource Remote Sensing Data. GIScience Remote Sens. 2023, 60, 2203303. [Google Scholar] [CrossRef]
- Jiang, X.; Li, D.; Li, G.; Lu, D. Eucalyptus Carbon Stock Estimation in Subtropical Regions with the Modeling Strategy of Sample Plots—Airborne LiDAR—Landsat Time Series Data. For. Ecosyst. 2023, 10, 100149. [Google Scholar] [CrossRef]
- Li, X.; Liu, F.; Ma, C.; Hou, J.; Zheng, D.; Ma, H.; Bai, Y.; Han, X.; Vereecken, H.; Yang, K.; et al. Land Data Assimilation: Harmonizing Theory and Data in Land Surface Process Studies. Rev. Geophys. 2024, 62, e2022RG000801. [Google Scholar] [CrossRef]
- Li, X.; Ma, H.; Ran, Y.; Wang, X.; Zhu, G.; Liu, F.; He, H.; Zhang, Z.; Huang, C. Terrestrial Carbon Cycle Model-Data Fusion: Progress and Challenges. Sci. China Earth Sci. 2021, 64, 1645–1657. [Google Scholar] [CrossRef]
- Liu, L.; Song, B. Calculating the Carbon Sequestration Rate of Terrestrial Ecosystems: Methods, Progress and Challenges. Trans. Atmos. Sci. 2022, 45, 321–331. [Google Scholar]
- Zhu, H.; Wu, M.; Jiang, F.; Vossbeck, M.; Kaminski, T.; Xing, X.; Wang, J.; Ju, W.; Chen, J.M. Assimilation of Carbonyl Sulfide (COS) Fluxes within the Adjoint-Based Data Assimilation System—Nanjing University Carbon Assimilation System (NUCAS v1.0). Geosci. Model Dev. 2024, 17, 6337–6363. [Google Scholar] [CrossRef]
- Cheng, W.; Dan, L.; Deng, X.; Feng, J.; Wang, Y.; Peng, J.; Tian, J.; Qi, W.; Liu, Z.; Zheng, X.; et al. Global Monthly Gridded Atmospheric Carbon Dioxide Concentrations under the Historical and Future Scenarios. Sci. Data 2022, 9, 83. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Zhou, F.; Ciais, P.; Miao, C.; Yang, T.; Jia, Y.; Zhou, X.; Klaus, B.-B.; Yang, T.; Yu, G. Human Activities Aggravate Nitrogen-Deposition Pollution to Inland Water over China. Natl. Sci. Rev. 2020, 7, 430–440. [Google Scholar] [CrossRef]
- Yan, S.; He, G.; Zhang, X. Forest Aboveground Biomass Products in China, 2013–2021. Sci. Data Bank 2023, 118, 103275. [Google Scholar] [CrossRef]
- Du, H.; Zeng, F.; Wang, K.; Song, T.; Wen, Y.; Li, C.; Peng, W.; Liang, H.; Zhu, H.; Zeng, Z. Dynamics of Biomass and Productivity of Three Major Plantation Types in Southern China. Acta Ecol. Sin. 2014, 34, 2712–2724. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Pan, Y.; Birdsey, R.; Kattge, J. Relationships between Net Primary Productivity and Forest Stand Age in U.S. Forests. Global Biogeochem. Cycles 2012, 26, GB3009. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, M.; Chen, H.; Adams, J. Global Pattern of NPP to GPP Ratio Derived from MODIS Data: Effects of Ecosystem Type, Geographical Location and Climate. Glob. Ecol. Biogeogr. 2009, 18, 280–290. [Google Scholar] [CrossRef]
- Krug, J.; Koehl, M.; Riedel, T.; Bormann, K.; Rueter, S.; Elsasser, P. Options for Accounting Carbon Sequestration in German Forests. Carbon Balance Manag. 2009, 4, 5. [Google Scholar] [CrossRef]
- Chen, W.; Chen, J.; Cihlar, J. An Integrated Terrestrial Ecosystem Carbon-Budget Model Based on Changes in Disturbance, Climate, and Atmospheric Chemistry. Ecol. Modell. 2000, 135, 55–79. [Google Scholar] [CrossRef]
- Ju, W.M.; Chen, J.M.; Harvey, D.; Wang, S. Future Carbon Balance of China’s Forests under Climate Change and Increasing CO2. J. Environ. Manag. 2007, 85, 538–562. [Google Scholar] [CrossRef]
- Li, D.; Zhang, C.; Ju, W.; Liu, L. Forest Net Primary Productivity Dynamics and Driving Forces in Jiangxi Province, China. Chin. J. Plant Ecol. 2016, 40, 643–657. [Google Scholar] [CrossRef][Green Version]
- Chen, W.; Chen, J.; Liu, J.; Cihlar, J. Approaches for Reducing Uncertainties in Regional Forest Carbon Balance. Global Biogeochem. Cycles 2000, 14, 827–838. [Google Scholar] [CrossRef]
- Le Dimet, F.-X.; Talagrand, O. Variational Algorithms for Analysis and Assimilation of Meteorological Observations: Theoretical Aspects. Tellus A Dyn. Meteorol. Oceanogr. 1986, 38, 97–110. [Google Scholar] [CrossRef]
- Hogue, T.S.; Sorooshian, S.; Gupta, H.; Holz, A.; Braatz, D. A Multistep Automatic Calibration Scheme for River Forecasting Models. J. Hydrometeorol. 2000, 1, 524–542. [Google Scholar] [CrossRef]
- Rahnamay Naeini, M.; Yang, T.; Sadegh, M.; AghaKouchak, A.; Hsu, K.; Sorooshian, S.; Duan, Q.; Lei, X. Shuffled Complex-Self Adaptive Hybrid EvoLution (SC-SAHEL) Optimization Framework. Environ. Model. Softw. 2018, 104, 215–235. [Google Scholar] [CrossRef]
- Kangrang, A.; Prasanchum, H.; Sriworamas, K.; Ashrafi, S.M.; Hormwichian, R.; Techarungruengsakul, R.; Ngamsert, R. Application of Optimization Techniques for Searching Optimal Reservoir Rule Curves: A Review. Water 2023, 15, 1669. [Google Scholar] [CrossRef]
- Zheng, X.; Weng, X.; OU, L.; REN, Y. Allometric Equation and Biomass Estimation of Eucalyptus in Fujian. J. Univ. Chin. Acad. Sci. 2024, 41, 321–333. [Google Scholar]
- McKight, P.E.; Najab, J. Kruskal-Wallis Test. In The Corsini Encyclopedia of Psychology; John Wiley & Sons: Hoboken, NJ, USA, 2010; p. 1. ISBN 9780470479216. [Google Scholar]
- Yu, Z.; Zhou, G.; Liu, S.; Sun, P.; Agathokleous, E. Impacts of Forest Management Intensity on Carbon Accumulation of China’s Forest Plantations. For. Ecol. Manag. 2020, 472, 118252. [Google Scholar] [CrossRef]
- Wen, L.; Wang, K.; Zeng, F.; Peng, W.; Du, H.; Li, S.; Song, T. Carbon Storage and Its Distribution in Eucalyptus Urophylla×E.Grandis Plantations at Different Stand Ages. Acta Bot. Boreali-Occident. Sin. 2014, 34, 1676–1684. [Google Scholar] [CrossRef]
- Tao, Y.; Feng, J.; Ma, L.; Long, W.; Cao, S. Carbon Storage and Distribution of Massion Pine, Chinese Fir and Eucalyptus Plantations at Liuzhou, Guangxi Province. Ecol. Environ. 2011, 20, 1608–1613. [Google Scholar]
- Zhang, Y.; Lu, D.; Jiang, X.; Li, Y.; Li, D. Forest Structure Simulation of Eucalyptus Plantation Using Remote-Sensing-Based Forest Age Data and 3-PG Model. Remote Sens. 2023, 15, 183. [Google Scholar] [CrossRef]
- Miehle, P.; Livesley, S.J.; Feikema, P.M.; Li, C.; Arndt, S.K. Assessing Productivity and Carbon Sequestration Capacity of Eucalyptus Globulus Plantations Using the Process Model Forest-DNDC: Calibration and Validation. Ecol. Modell. 2006, 192, 83–94. [Google Scholar] [CrossRef]
- Colmanetti, M.A.A.; Cuadra, S.V.; Lamparelli, R.A.C.; Bortolucci, J., Jr.; Cabral, O.M.R.; Campoe, O.C.; de Castro Victoria, D.; Barioni, L.G.; Galdos, M.V.; Figueiredo, G.K.D.A.; et al. Implementation and Calibration of Short-Rotation Eucalypt Plantation Module within the ECOSMOS Land Surface Model. Agric. For. Meteorol. 2022, 323, 109043. [Google Scholar] [CrossRef]
- Guedes, B.S.; Olsson, B.A.; Sitoe, A.A.; Egnell, G. Net Primary Production in Plantations of Pinus Taeda and Eucalyptus Cloeziana Compared with a Mountain Miombo Woodland in Mozambique. Glob. Ecol. Conserv. 2018, 15, e00414. [Google Scholar] [CrossRef]
- Cleverly, J.; Vote, C.; Isaac, P.; Ewenz, C.; Harahap, M.; Beringer, J.; Campbell, D.I.; Daly, E.; Eamus, D.; He, L.; et al. Carbon, Water and Energy Fluxes in Agricultural Systems of Australia and New Zealand. Agric. For. Meteorol. 2020, 287, 107934. [Google Scholar] [CrossRef]
- Cabral, O.M.R.; Gash, J.H.C.; Rocha, H.R.; Marsden, C.; Ligo, M.A.V.; Freitas, H.C.; Tatsch, J.D.; Gomes, E. Fluxes of CO2 above a Plantation of Eucalyptus in Southeast Brazil. Agric. For. Meteorol. 2011, 151, 49–59. [Google Scholar] [CrossRef]
- Silva, M.R.F.; McHugh, I.; Peixoto Neto, A.M.L.; Pauwels, V.R.N.; Cartwright, I.; Daly, E. Trading a Little Water for Substantial Carbon Gains during the First Years of a Eucalyptus Globulus Plantation. Agric. For. Meteorol. 2022, 318, 108910. [Google Scholar] [CrossRef]
- Walter, K.; Don, A.; Flessa, H. No General Soil Carbon Sequestration under Central European Short Rotation Coppices. GCB Bioenergy 2015, 7, 727–740. [Google Scholar] [CrossRef]
- Tong, X.; Brandt, M.; Yue, Y.; Ciais, P.; Rudbeck Jepsen, M.; Penuelas, J.; Wigneron, J.-P.; Xiao, X.; Song, X.-P.; Horion, S.; et al. Forest Management in Southern China Generates Short Term Extensive Carbon Sequestration. Nat. Commun. 2020, 11, 129. [Google Scholar] [CrossRef]
- Rodrigues, A.; Pita, G.; Mateus, J.; Kurz-Besson, C.; Casquilho, M.; Cerasoli, S.; Gomes, A.; Pereira, J. Eight Years of Continuous Carbon Fluxes Measurements in a Portuguese Eucalypt Stand under Two Main Events: Drought and Felling. Agric. For. Meteorol. 2011, 151, 493–507. [Google Scholar] [CrossRef]
- Jia, K.; Yu, Y.; Yang, X.; Fan, W. Assimilation and NEP Estimation of Soil Respiration Rate by Ensemble Kalman Filter Algorithm. J. Northeast For. Univ. 2024, 52, 77–84. [Google Scholar] [CrossRef]
- Rossi, F.S.; Della-Silva, J.L.; Teodoro, L.P.R.; Teodoro, P.E.; Santana, D.C.; Baio, F.H.R.; Morinigo, W.B.; Crusiol, L.G.T.; La Scala, N.; da Silva, C.A. Assessing Soil CO2 Emission on Eucalyptus Species Using UAV-Based Reflectance and Vegetation Indices. Sci. Rep. 2024, 14, 20277. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Tschieder, E.; Marshall, J.D.; Binkley, D. Carbon Budget at the Individual-Tree Scale: Dominant Eucalyptus Trees Partition Less Carbon Belowground. New Phytol. 2024, 242, 1932–1943. [Google Scholar] [CrossRef]







| Data | Name | Description | Time | Resolution | Source |
|---|---|---|---|---|---|
| Model Input Data | Climate Data | Monthly average temperature, total monthly precipitation, average monthly radiation, average monthly vapor pressure | 1960–2023 | 30 m | This Study |
| Soil Data | Soil depth, soil texture data | - | 1 km | National Qinghai–Tibet Plateau Science Data Center | |
| Wetness index, Water table | - | 30 m | This Study | ||
| Eucalyptus Data | Eucalyptus distribution, harvest frequency, and harvest timing data | 1986–2021 | 30 m | [7] | |
| CO2 Concentration | Station observation data | 2013–2022 | - | https://www.gml.noaa.gov accessed on 12 February 2024 | |
| Satellite Data Inversion | 1850–2013 | 1° | [25] | ||
| Nitrogen Deposition | Simulated Data | 1980–2013 | 0.5° | [26] | |
| LAI | Calculated using Sentinel-2 data | 2020 | 30 m | This Study | |
| Reference-year NPP | MODIS NPP (NPPMODIS) | 2020 | 500 m | [14] | |
| Lin GPP (NPPLin) | 2020 | 30 m | [15] | ||
| Reference-year Biomass/Carbon Density | Aboveground carbon density from Yang et al. (ACDYang) | 2019 | 30 m | [19] | |
| Aboveground carbon density from Yan et al. (ACDYan) | 2013–2021 | 30 m | [27] | ||
| Carbon density from Jiang et al. (CDJiang) | 2020–2021 | 30 m | [20] | ||
| Validation Data | Plot survey data (CDPlots) | 15 plots, collected semi-annually | 2021–2024 | - | - |
| Carbon Allocation | Turnover Rate | ||
|---|---|---|---|
| Allocation coefficient to stem | 0.4624 | Wood turnover rate | 0.0288 |
| Allocation coefficient to coarse root | 0.2226 | Coarse root turnover rate | 0.0448 |
| Allocation coefficient to leaf | 0.1190 | Leaf turnover rate | 0.2948 |
| Allocation coefficient to fine root | 0.1960 | Fine root turnover rate | 1.0000 |
| Parameter | CDPlots | CDJiang | ACDYan | Parameter | CDPlots | CDJiang | ACDYan |
|---|---|---|---|---|---|---|---|
(Mg C ha−1 yr−1) | [10, 500] | [10, 500] | [10, 500] | 1.0 | 1.0 | 0.2 | |
(Mg C ha−1) | [0, 1] | [1, 10] | [1, 10] | 1.0 | 1.0 | 0.3 | |
(Mg C ha−1 yr−1) | [1000, 3000] | [1000, 3000] | [1000, 3000] | 1.0 | 1.0 | 0.8 | |
(Mg C ha−1 yr−1) | [100, 2500] | [100, 2500] | [100, 2500] | 1.0 | 1.0 | 1.0 | |
| 3.0 | 3.0 | 3.0 | 2.0 | 2.0 | 2.0 | ||
| 1.0 | 1.0 | 1.0 |
| Model | Validated Variable | rRMSE (%) |
|---|---|---|
| 3-PG | Aboveground carbon stocks | 15.70 |
| Forest-DNDC | Total aboveground C | 17.88 |
| InTECDA | Carbon density | 18.25 |
| ECOSMOS | Total stem biomass | 29.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhou, M.; Luo, K.; Wu, Y.; Li, D. An Improved InTEC Model for Estimating the Carbon Budgets in Eucalyptus Plantations. Remote Sens. 2025, 17, 2741. https://doi.org/10.3390/rs17152741
Li Z, Zhou M, Luo K, Wu Y, Li D. An Improved InTEC Model for Estimating the Carbon Budgets in Eucalyptus Plantations. Remote Sensing. 2025; 17(15):2741. https://doi.org/10.3390/rs17152741
Chicago/Turabian StyleLi, Zhipeng, Mingxing Zhou, Kunfa Luo, Yunzhong Wu, and Dengqiu Li. 2025. "An Improved InTEC Model for Estimating the Carbon Budgets in Eucalyptus Plantations" Remote Sensing 17, no. 15: 2741. https://doi.org/10.3390/rs17152741
APA StyleLi, Z., Zhou, M., Luo, K., Wu, Y., & Li, D. (2025). An Improved InTEC Model for Estimating the Carbon Budgets in Eucalyptus Plantations. Remote Sensing, 17(15), 2741. https://doi.org/10.3390/rs17152741





