Freezing Fog Microphysics and Visibility Based on CFACT Feb 19 Case

Abstract

The objective of this study is to analyze microphysical parameters affecting visibility parameterizations of a freezing fog case that occurred on 19 February 2022, during the Cold Fog Amongst Complex Terrain (CFACT) project conducted in a high-elevation alpine valley in Utah, USA. Observations are collected using visibility, droplet spectra, ice crystal spectra, and aerosol spectral instruments, as well as in-situ meteorological instruments. Particle phase is determined from relative humidity with respect to water (RH_w) as well as ground cloud imaging probe (GCIP), ceilometer (CL61) depolarization ratio, and icing accumulation on the platforms. Results showed that freezing droplet density can affect visibility (Vis) up to 100 m during Vis less than 1 km. In addition, increasing volume can lead to up to a 2 μm increase in droplet radius due to a change in the chemical composition of aerosols from Sodium Chloride (NaCl) to Ammonium Nitrate (NH₄NO₃). Overall, comparisons suggested that Vis parameterizations are highly variable, and freezing fog conditions resulted in lower Vis values compared to warm fog microphysical parameterizations. Furthermore, riming of freezing fog conditions can lead to more than 50% uncertainty in Vis. It is concluded that changing aerosol composition and freezing fog droplet density and riming can play a major role in Vis simulations.

1. Introduction

Fog, composed of droplets, ice crystals, or mixed phase particles, with a horizontal Vis less than 1 km is defined for aviation applications [1]. The decrease in Vis due to fog significantly impacts human activities in various fields such as transportation, shipping, ecosystem, healthcare, and aviation, marine, and military operations; therefore, inaccurate forecasts of foggy conditions can lead to significant economic losses and loss of human lives [2,3]. Furthermore, its microphysical and dynamical environments are still not properly known, and freezing fog (FFG) creates further issues related to icing effects and low Vis conditions (the definitions used in this work are provided in Abbreviations part).

FFG consists of suspended tiny, supercooled droplets (SDs) in the air at/or near Earth’s surface that often reduces Vis less than 1 km for −10 °C ≤ T ≤ 0 °C at the saturation levels with respect to water (RH_w~100%) [3]. SD’s formation and survival in colder temperatures can be possible down to about −40 °C [4,5]. These SDs can freeze in the air and reduce Vis compared to warm fog (WFG) conditions, and depending on particle density, upon contact with the surfaces, leads to icing conditions.

Cold fog, including FFG and ice fog (IFG), over regions of complex terrain has not yet received sufficient attention from the research community [6,7]. For several decades, most fog experiments focused on WFG conditions, and most experiments have taken place along the California coast [8,9,10]. Although WFG and FFG are physically identical, their Vis for the same droplet number concentration (N_d) with changing particle density (for water as ρ_w and ice as ρ_i) can be significantly different [11]. Gultepe et al. [12] suggested that FFG droplets can enlarge their size due to decreasing density; therefore, FFG Vis can be lower than WFG due to increasing droplet size.

Recent field programs have been conducted in mountainous regions [13,14] to study fog-affected stable atmospheric boundary layers. These studies have emphasized dynamical processes without focusing on microphysical (MP) processes. The Local and Non-local Fog Experiment (LANFEX) concentrated radiation-fog formation in complex terrain but did not focus on cold fog [15]. A pilot cold-fog field experiment was conducted as part of the Mountain Terrain Atmospheric Modeling and Observations (MATERHORN) program in the mountains of Utah [16,17]. MATERHORN project outcomes were limited due to a lack of FFG events and MP (droplet size spectra) and aerosol measurements.

Cold fog conditions, in addition to FFG, can also include IFG [17,18] and mixed-phase fog types. Pu et al. [7] presented an overview of the cold fog conditions in the high-elevation alpine terrain of Utah during the CFACT project using various platforms and instruments. In the context of CFACT, they stressed that Vis due to IFG based on Weather Research and Forecast Model (WRF) runs, was not simulated accurately at least 50% of the time. This might be due to limited cloud condensation nuclei (CCN) and ice nuclei (IN) parameterizations leading to lower N_d or ice number concentration (N_i) and underestimating the saturation rates in an atmospheric boundary layer (ABL) with smaller RH_w values. FFG conditions were also studied by Gultepe et al. [19], who stated that FFG conditions were highly possible in marine environments when the air temperature (T_a) falls below to about 0 °C, and can be detected by the Rosemount Icing Detector (RID).

The life cycle of cold fog involves complex interactions between various scales of atmospheric motion (from synoptic-scale to micro-scale e.g., turbulent motion), thermodynamical processes, and a delicate balance between radiation, turbulence, thermodynamics, and MP processes [20,21]. The intensity of turbulence, together with the turbulence dissipation rate occurring during the life cycle of radiation fog, were studied by [22,23,24], who suggested that turbulence intensity plays an important role over the fog life cycle. Gultepe et al. [24] developed a Vis physical parameterization using eddy dissipation rate to improve the Vis prediction. The nature of the interaction between fog dynamics and MP processes is complex and still not fully understood properly [25]. Later work suggested that improvements in nucleation processes can reduce the uncertainties in the estimation of Vis. Because of limited FFG experiments, new field observations of cold fog conditions can be used to better evaluate the life cycle (including formation, development, and dissipation) and MP structure of FFG [2].

Cold fog formation processes can be dominated by large-scale patterns, including ridging and cold-air advection as well as collision processes and mixing of air pockets of different temperatures and moisture contents [26]. Cold pool type fog formation is an example of mountain FFG formation [15,27]. Cold fog, described as supercooled fog, can also significantly affect marine and aviation operations. Examples of these types of fog are FFG occurrences at the cold surfaces in marine environments. Therefore, FFG studies are very important for aircraft icing, marine shipping, and wire icing, and need to be further studied when the air is saturated with respect to water near 0 °C and below.

Meteorological conditions, such as the environment T_a, dew point temperature (T_d), and RH_w, as well as CCN/IN, and droplet growth rate, along with turbulence and vertical air velocity, play an important role in N_d prediction, thereby affecting Vis estimation [28,29]. In this regard, Gultepe et al. [30] suggested that accurate predictions of both N_d and Liquid Water Content (LWC) are critical for Vis prediction, and that parameterizations that only use LWC, as suggested in [31,32], are insufficient. Vis is usually diagnosed in the post-processing stage of forecast model outputs that utilize the Stoelinga–Warner [32] study, leading to large uncertainties in fog Vis prediction [19,33]. In fact, FFG conditions are not represented well in numerical weather prediction (NWP) model studies because of scale issues and underestimating N_d; therefore, FFG predictions need to be improved.

The single-moment and double-moment microphysical schemes often used in NWP models were applied to analyze cloud/fog MP parameters. LWC is usually a prognostic variable, and N_d is assumed as a fixed value or is obtained either deterministically or prognostically by making several assumptions about the physical terms affecting N_d. If N_d is not fixed, a modified gamma distribution is usually assumed to represent fog droplet size distribution (DSD), which is used to obtain N_d. Previous studies have found that fog forecasting is sensitive to the choice of Vis algorithm [2,34,35,36,37]. These studies indicated that a Vis algorithm may work well for a specific fog type but not for all fog types. In fact, FFG conditions have not been studied in detail using NWP models. This point needs to be further studied and FFG droplet density should be emphasized for Vis simulations.

The objectives of this study are to evaluate the MP processes leading to FFG formation. The main objectives of this work are to (1) evaluate the influence of large-scale synoptic conditions and aerosol composition effect on Vis, (2) investigate Vis change related to droplet growth mechanisms, and (3) develop physical parameterizations for FFG prediction. In the analysis, the synoptic and atmospheric conditions responsible for the development of FFG conditions are evaluated. The influence of chemical composition on CCN activation during particle-to-droplet transition processes was investigated using the Kappa (κ)-Köhler method. To improve freezing fog prediction, new parameterizations were developed and assessed in comparison with existing formulations reported in the literature.

The paper is composed of six sections, as follows: Section 1 provides the Introduction. Section 2 focuses on synoptic conditions as well as the CFACT field campaign and observations. Section 3 summarizes the method being used and Section 4 provides the results. Finally, Section 5 and Section 6 are given for discussions and conclusions, respectively.

2. Field Campaign and Observations

This section involves the CFACT campaign location and observations that include a summary of the instruments. Nine fog cases were conducted during the CFACT field campaign to investigate various mountainous weather patterns and cold fog conditions. Additional details are given in Pu et al. [7]. In this work, the IOP 8 (19 February 2022) freezing fog event is selected for the analysis because of its unique weather conditions.

2.1. Project Location and Observations

The CFACT field campaign took place in Heber Valley, Utah, USA, during the winter of 2022 from 5 January to 28 February 2022. The project was designed to capture the temporal and spatial variability of cold fog using ground-based, airborne, and remote sensing platforms. During the campaign, numerical simulations using the WRF model were performed to predict the formation and dissipation of cold fog. The CFACT study area (see Figure 1a) is centered at approximately 40.50°N, 111.42°W and is located about 50 km southeast of Salt Lake City. Heber Valley is an alpine basin characterized by suburban and agricultural land cover, surrounded by canyons and high-elevation mountains. The Provo River runs through the valley from the Jordanelle Reservoir and flows into Deer Creek Reservoir, which lies at an elevation of 1652 m [7]. The highest surrounding peaks reach up to 3500 m, particularly to the west and southwest of the valley.

Cold-air pool fog, together with IFG, has often been observed in the Heber Valley during cold seasons. The field campaign was funded by the National Science Foundation (NSF) and instrumentation support was provided by the Lower Atmospheric Observing Facilities (LAOF) managed by the National Center for Atmospheric Research (NCAR), specifically by its Earth Observing Laboratory (EOL) [7]. The University of Utah (UU) and Ontario Technical University (OntTecU) also participated in the project design and performing campaign observations. The CFACT field deployment included two supersites and nine satellite sites that were composed of an aerosol measurement trailer, an MP measurement site [34], and eight low-cost weather stations [7]. Figure 1b summarizes project location and supersites used in the study.

At the Deer Creek Supersite (DC SS), in-situ ground-based measurements were collected by several instruments, including the present weather detectors and visibility sensor (PWD22), broadband radiometers (Kipp and Zonen—CMP21), cloud droplet spectrometer (Droplet Measurement Technologies—DMT—FM120), a ground-based cloud imaging probe (DMT—GCIP), a scanning mobility particle sizer (TSI—SMPS), Total Air Sampler (Airmetric MiniVol) (MTAS), 3D sonic anemometer (Campbell Scientific CSAT3), hygrothermometers (Sensiron—SHT85), and celiometers (Vaisala—CL31 and CL61) (see Figure 1c and

Table 1. Shows the instruments used in this study used during the CFACT project. DC SS indicates Deer Creek Supersite, MP: Microphysics site, AT: Aerosol Trailer, S: Sounding Site, and FT: Flux Tower. Parameters in column 4 are Vis (visibility), PR (precipitation rate), T_a (air temperature), β_h (horizontal backscattering ratio), RH (relative humidity), N_d (droplet number concentration), LWC (liquid water content), MVD (mean volume diameter), N_a (aerosol number concentration), u, v, and w (wind components), dir (wind direction), U_h (wind speed), MSL (mean sea level), a.g.l. (above ground level), H (a.g.l. height) and P (pressure).

Site	Lat Lon and Elevation (m, MSL)	Instrument	Measured or Retrieved Parameters	H (a.g.l., m)	Manufacturer
DC MP	40.488 320°N 111.468 143°W 1659m	Present Weather Detector (PWD22)	Vis < 20 km and PR (mm/h—10 min interval), Ta	5	Vaisala Inc., Vantaa, Finland
		Celiometer (CL31)	Horizontal looking βh	1.5	Vaisala Inc., Vantaa, Finland
		Weather Transmitter (WXT520)	Ta/RH/Uh/dir	1.5	Vaisala Inc., Vantaa, Finland
		Cloud particle Spectrometer Fog Monitor (FM120)	Nd, LWC, MVD from Size Distribution (2–50 μm, 30 size bins)	2	DMT, Boulder, CO, USA
		Ground-based cloud imaging probe (GCIP)	Cloud particle size distribution (10–1000 μm)	3	DMT, Boulder, CO, USA
DC AT	40.489 940°N, 111.470 331°W 1661m	Scanning Mobility Particle Sizer (SMPS Model 3938)	Na size distribution in 128 bin (8 nm to 19.81 mm)	2	TSI Inc, Minneapolis, MN, USA
		MiniVol Tactical Air Sampler (MTAS)	(PM10 Filters—smaller than 10 μm)	2	Airmetric, Eugene, OR, USA
DC S	40.489027°N 111.470164°W 1660 m	Celiometer (CL61)	Vertical looking β and depolarization ratio	2	Vaisala Inc., Vantaa, Finland, USA
DC FT	40.490101°N 111.464737°W 1659 m	Broadband Radiometer (CMP21)	4-component radiation	2	Kipp and Zonen, Delft, Netherlands
		Hygrothermometer (SHT85)	Ta, RH	2	Sensirion, Stäfa, Switzerland
		3D sonic anemometer (CSAT3)	u, v, w, dir	2	Campbell Scientific, Logan, UT, USA
		Nanobarometer	P	2	Paroscientific Inc., Redmond, WA, USA

). With these instruments, fog MP properties, including LWC or ice water content (IWC), mean volume diameter (MVD), N_d, aerosol composition, particle shape, infrared (IR) and shortwave (SW) up-down radiative fluxes, and vapor mixing ratio (q_v) and 3D wind components, as well as atmospheric profiles of extinction coefficient (β_ext) and depolarization, were obtained. The CL31 was oriented in the horizontal direction to detect the horizontal extent of the fog. Vertical profiles of β_ext were obtained using a CL61 with depolarization capability. The observations used in the analysis were collected at the Deer Creek Microphysics supersite (DC MP) and at the Aerosol Trailer (DC AT) site. Spectral measurements of droplet microphysics (30 channels between 2–50 μm) were measured by FM120 at 1Hz sampling rate. The FM120 measurements were averaged over 1-min intervals to match the temporal resolution of the PWD visibility data. However, when compared with the SMPS measurements, a 5-min averaging interval was applied to ensure consistency between the datasets. The GCIP data were only used for discriminating droplets from ice crystals that likely affected Vis.

Aerosol composition and spectral measurements were performed using various instruments at the DC SS and DC AT. These instruments were used to evaluate the physical and chemical properties of aerosols (Figure 1b) and the results are summarized in Table 1. In-situ size-resolved measurements of ambient aerosols were obtained using a TSI Inc. SMPS, operating over a size range from 8 nm to 19.81 mm across 128 bins, as described in Carrillo-Cardenas et al. [38]. The SMPS measurements, collected at 5-min scan intervals, were used to quantify aerosol physical properties. Additionally, Teflon filters were collected using Airmetrics MTAS at a flow rate 5 L min⁻¹ for particulate matter (PM₁₀; size < 10 μm). Using SMPS and Teflon filters, aerosol physical and chemical properties are analyzed to show the aerosol impact on freezing fog conditions from 8 nm up to 10s of micrometer size range.

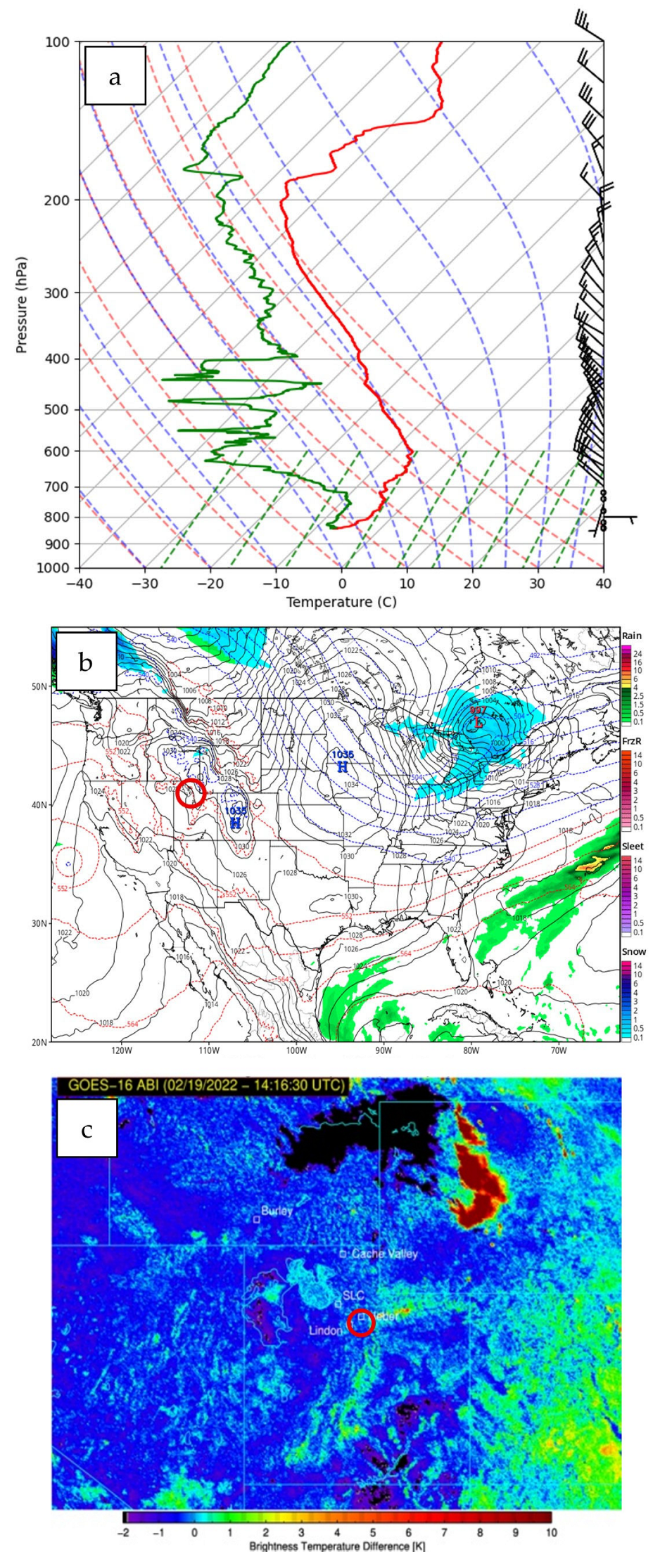
2.2. Synoptic Weather Systems

Synoptic systems can affect the cold fog life cycle. Usually, cold high-pressure (HP) systems with clear skies lead to cold fog (IFG or FFG) formation that is related to infrared cooling [18,34]. In addition to synoptic conditions, local meteorological factors also influence FFG formation, particularly over mountainous slopes and valleys [39]. During the FFG event that occurred on 19 February 2022, its unique physical conditions led to supercooled FFG formation. The fog occurred between 05:30 and 14:20 UTC. Specifically, an HP system dominated the Heber Valley, which led to FFG formation. Figure 2 shows a radiosonde profile, the US Global Forecast Model (GFS) model forecast, and the Shortwave infrared (SWIR)-IR temperature difference based on Geostationary Operational Environmental Satellites (GOES-R). Figure 2a shows that the surface ABL was saturated with respect to water (RH_w~100%) and winds were relatively calm (<2 m s⁻¹). Figure 2b shows the pressure centers, 6-h precipitation rate (color bar), and 500 mb thickness. The FFG event in this case was directly related to the HP system moving from NW to SE with its center at ~1030 mb over the Heber Valley. The SWIR-IR difference (Figure 2c) is less than 1–2 °C and indicates the likely presence of cold foggy regions.

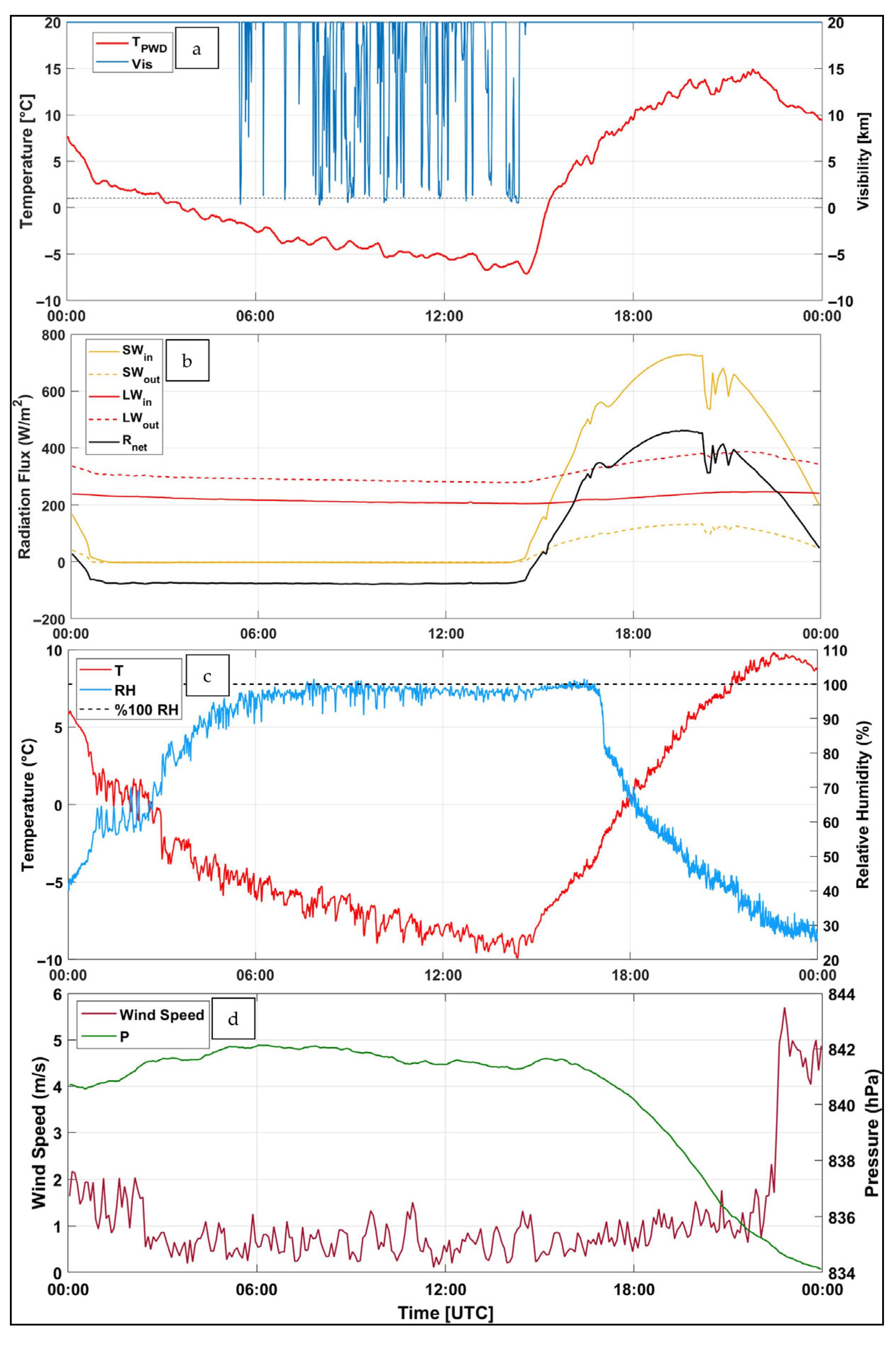
2.3. Observations

Figure 3a shows time series of T_a and Vis from the PWD. FFG occurred during IOP 8 between 05:30 and 14:20 UTC, during which Vis decreased down to about 300 m and T_a decreased from −2 °C to −7.1 °C. Note that T_a values from PWD (T_PWD) are about 3 °C higher than environmental T_a measurements because T_PWD sensor was located inside PWD pole. On this day, the fog event continued until the downward short wave radiative flux (SWRF) reached 100 Wm⁻² (Figure 3b). A detailed analysis of radiative fluxes is provided in the results section. Figure 3c shows the time series of T_a and RH_w where, during fog occurrence, RH_w is found to be about 100%, indicating that during FFG conditions, T_a ranged between 0 °C and −10 °C. In the same time period, pressure (P) increased from 840.5 mb to 842 mb and wind speed (U_h) decreased from 2 m s⁻¹ down to about 0.5–1 m s⁻¹ (Figure 3d).

CL31_h (horizontal looking) and CL61_v (vertical looking) provided the backscatter coefficient (β) time-height cross-sections at the DC SS MP, as shown in Figure 4. It is important to note that the ceilometer-based fog-top heights cannot be accurate because of strong extinction of transmitted light when a large number of fog liquid droplets exists, but this was not the case during the Feb 19 case. Figure 4 suggests that fog formation on 19 Feb case was very patchy, and its duration was between 30 min and 60 min. Figure 4a shows time series of CL31, indicating that the top of the fog layer was about 200 m. Figure 4b,c show CL61 and linear depolarization ratio (LDR) time-height cross sections, respectively. The LDR indicates that the lowest foggy layer was noisy but β shows high values.

3. Method

In the analysis, microphysical processes associated with a FFG event that occurred on 19 February 2022 are investigated. First, the κ-Köhler approach is used to show aerosol chemical composition effect on droplet activation and growth, then Vis is calculated using FM120 spectral measurements for FFG fog conditions. Measurement issues are provided in the next section. Second, to simulate the time-dependent growth of an individual droplet during the initial 30-min period of the fog event min of the fog event, the droplet growth equation is used and the critical radius (r_c) and critical saturation ratio (S_c) values are derived from the Köhler curve [40]. Vis estimations were obtained based on Gultepe et al. [24], using MP parameters (droplet radius (r), LWC, and N_d) retrieved from FM-120 measurements. The results are then evaluated by comparing them with direct visibility measurements from PWD; these results are provided in the discussion section. The following sections provide κ-Köhler theory application with aerosol composition effects, droplet growth equation, aerosol impact on FFG conditions, and the freezing fog MP parameterizations. These sections are related to the aerosol composition from filter samples, FM120 MP measurements, and PWD Vis data.

3.1. Aerosol Composition Impact on Droplet Size

Köhler equation is described for the activation of cloud droplets. Similar to clouds, the saturation ratio with respect to water (S) during FFG formation is given by Pruppacher and Klett [40] as:

$$\mathrm{S}\left(\mathrm{r}\right)={\displaystyle \frac{{\mathrm{e}}^{\mathrm{*}}\left(\mathrm{r}\right)}{{\mathrm{e}}_{\mathrm{s},\mathrm{w}}\left(\mathrm{\infty }\right)}}=1+{\displaystyle \frac{\mathrm{a}}{\mathrm{r}}}-{\displaystyle \frac{\mathrm{b}}{{\mathrm{r}}^3}}.$$

(1)

In Equation (1), e*(r) and e_s,w(∞) equilibrium vapor pressure over a solution droplet and saturated water vapor pressure over a flat pure water surface (see Abbreviations part). The effects of droplet curvature (Kelvin’s term) and solute concentration (Raoult’s term) on droplet growth are provided in 2nd and 3rd terms of Equation (1), where a $={\displaystyle \frac{2{\sigma }_{\mathrm{w}}}{{\rho }_{\mathrm{l}}{\mathrm{R}}_{\mathrm{v}}{\mathrm{T}}_{\mathrm{a}}}}$ and $\mathrm{b}={\displaystyle \frac{3\mathrm{i}{\mathrm{m}}_{\mathrm{s}}{\mathrm{M}}_{\mathrm{w}}}{4\pi {\rho }_{\mathrm{l}}{\mathrm{M}}_{\mathrm{S}}}}$. In coefficient a, σ_w is the surface tension of water in air, ρ_l the density of water, R_v the specific gas constant of water vapor, and T_a the air temperature in K. In coefficient b, i is the Van’t Hoff factor, m_s the solute mass, M_w the molecular weight of water, and M_s the molecular weight of solute. The point at which the S reaches a level where droplets form is defined as the S_c corresponding to the r_c. The r_c and S_c are given, respectively, as:

$${\mathrm{r}}_{\mathrm{c}}=\sqrt{{\displaystyle \frac{3\mathrm{b}}{\mathrm{a}}}},$$

(2)

and

$${\mathrm{S}}_{\mathrm{c}}=1+\sqrt{{\displaystyle \frac{4{\mathrm{a}}^3}{27\mathrm{b}}}}.$$

(3)

S_c indicates the minimum saturation ratio for a droplet to grow on its own while r_c indicates the minimum radius at which the solution droplet will become active, leading to particle growth.

To simplify the complex chemical requirements of the Köhler theory, a method describing CCN activity using a single hygroscopicity parameter (κ), the κ-Köhler theory, was developed by Petters and Kreidenweis [41] to define the saturation ratio as follows:

$$\mathrm{S}={\mathrm{a}}_{\mathrm{w}}\exp \left({\displaystyle \frac{4{\sigma }_{\mathrm{s}/\mathrm{a}}{\mathrm{M}}_{\mathrm{w}}}{\mathrm{R}\mathrm{T}{\rho }_{\mathrm{w}}\mathrm{D}}}\right),$$

(4)

where R is the universal gas constant, D is the diameter of the droplet, and a_w is the activity of water in solution. The κ is defined through its effect on the water activity of the solution:

$${\mathrm{a}}_{\mathrm{w}}={\displaystyle \frac{1}{1+\kappa \frac{{\mathrm{V}}_{\mathrm{s}}}{{\mathrm{V}}_{\mathrm{w}}}}},$$

(5)

where V_s is the volume of the dry particulate matter and V_w is the volume of the water.

Using Equations (1)–(5), r_c and S are calculated for NaCl and NH₄NO₃ aerosol compositions based on studies by Carrillo-Cardenas et al. [38] and Chow et al. [42]. The mass concentration estimates of the elemental composition from the Teflon filter samples were calculated using mass reconstruction equations from the Interagency Monitoring of Protected Visual Environment (IMPROVE) network, as specified by Chow et al. [42], using Airmetric MiniVol samplings. The IMPROVE equation set estimates the contributions of components such as salt, organic matter (OM), organic carbon (OC), geological minerals (Soil), ammonium nitrate, and ammonium sulfate ((NH₄)₂SO₄) [42]. However, the Teflon filters used in this study were analyzed only for inorganic species. This analysis is applied to droplet growth equations to study aerosol composition effects on droplet growth and Vis.

3.2. Droplet Growth During Freezing Fog Event

To show the effect of aerosol composition on Vis, we need to provide a droplet growth equation as a function of droplet size. The cloud droplet size growth rate is given by Pruppacher and Klett [40] as:

$$\mathrm{r}{\displaystyle \frac{\mathrm{d}\mathrm{r}}{\mathrm{d}\mathrm{t}}}={\displaystyle \frac{(\mathrm{S}-1)-\mathrm{a}/\mathrm{r}+\mathrm{b}/{\mathrm{r}}^3}{{\mathrm{F}}_{\mathrm{k}}+{\mathrm{F}}_{\mathrm{d}}}},$$

(6)

where F_k and F_d are provided, respectively, as:

$${\mathrm{F}}_{\mathrm{k}}=\left({\displaystyle \frac{\mathrm{L}}{{\mathrm{R}}_{\mathrm{v}}{\mathrm{T}}_{\mathrm{a}}}}-1\right){\displaystyle \frac{{\rho }_{\mathrm{l}}\mathrm{L}}{\mathrm{K}\mathrm{T}\mathrm{a}}}\approx {\displaystyle \frac{{\rho }_{\mathrm{l}}\mathrm{L}{\mathrm{v}}^2}{\mathrm{K}{\mathrm{R}}_{\mathrm{v}}{\mathrm{T}}_{\mathrm{a}}^2}},\mathrm{a}\mathrm{n}\mathrm{d} {\mathrm{F}}_{\mathrm{d}}={\displaystyle \frac{{\rho }_{\mathrm{l}}{\mathrm{R}}_{\mathrm{v}}{\mathrm{T}}_{\mathrm{a}}}{{\mathrm{D}}_{\mathrm{v}}{\mathrm{e}}_{\mathrm{s}}\left({\mathrm{T}}_{\mathrm{a}}\right)}}.$$

(7)

In Equation (7), the F_k is related to heat conduction as a function of T_a. The L_v is latent heat of vaporization and K is the thermal conductivity. The ρ_l is the droplet water density, but for freezing fog, it should be replaced with the density of ice (ρ_i) as 0.91 g cm⁻³. The effect of density on freezing droplet growth and Vis is calculated using Equation (6), which is related to Equation (7) with particle density parameter. The F_d above is the water vapor diffusion term, which is a function of the saturated vapor pressure (e_s), T_a, and the water vapor diffusion coefficient in air (D_v), Beard and Pruppacher [43], which is given as:

$${\mathrm{D}}_v=2.11\times {10}^{-5}{\left({\displaystyle \frac{{\mathrm{T}}_{\mathrm{a}}}{{\mathrm{T}}_0}}\right)}^{1.94}\left({\displaystyle \frac{{\mathrm{P}}_0}{\mathrm{P}}}\right)$$

(8)

where T₀ and P₀ are surface values of air temperature and pressure, respectively. Then, Equation (6) can be used to emphasize aerosol composition impact on droplet growth.

3.3. Freezing Droplet Effect on Extinction Coefficient

In fog conditions, Vis can be obtained by direct measurement of the extinction coefficient from the difference between the transmitted and received radiation or by using MP droplet spectral measurements such as N_d, LWC, and effective radius (r_eff) (or MVD). Generally, Vis is obtained using either PWD-based direct measurements of the extinction or fog microphysical spectral measurements using FM120, but the results cannot be the same for both Vis calculations due to measurement issues such as wind speed and directions [24]. To show aerosol impact on Vis, we first need to obtain Vis as a function of LWC and N_d (or MVD) where N_d is related to aerosol number concentration (N_a).

Based on Koschmieder’s law [44], Vis is defined as a function of a brightness contrast threshold (C) and β_ext. The visibility range then can be defined as:

$$\mathrm{V}\mathrm{i}\mathrm{s}={\displaystyle \frac{-\mathrm{l}\mathrm{n}\left(\mathrm{C}\right)}{{\beta }_{\mathrm{e}\mathrm{x}\mathrm{t}}}},$$

(9)

In Equation (9), C is defined as a threshold value at which the human eye can recognize an object at a certain distance in daytime conditions and is taken as 0.05 in meteorological applications [34]. β_ext is calculated for water droplets as:

$${\beta }_{\mathrm{e}\mathrm{x}\mathrm{t}}={\int }_{\mathrm{i}=1}^{\mathrm{m}}\pi {\mathrm{Q}}_{\mathrm{e}\mathrm{f}\mathrm{f}}\left(\mathrm{r}\right)\mathrm{n}\left(\mathrm{r}\right){\mathrm{r}}^2\mathrm{d}\mathrm{r},$$

(10)

where m represents the number of particle spectral bins and Q_eff is the extinction efficiency, which is ~2 for spherical large water droplets at visible wavelengths according to Mie theory. The n(r) and r² denote particle number concentration and spherical particle cross-sectional area, respectively. For freezing droplets, Equation (10) becomes:

$${\beta }_{\mathrm{e}\mathrm{x}\mathrm{t}}={\int }_{\mathrm{i}=1}^{\mathrm{m}}\pi {\mathrm{Q}}_{\mathrm{e}\mathrm{f}\mathrm{f}}(\mathrm{r}+\Delta \mathrm{r})\mathrm{n}(\mathrm{r}+\Delta \mathrm{r}){\mathrm{r}}^2\mathrm{d}\mathrm{r},$$

(11)

where Δr represents the difference between freezing droplet radius (r_i) and liquid droplet radius (r_w). The r_i is then calculated as:

$${\mathrm{r}}_{\mathrm{i}}{=\mathrm{r}}_{\mathrm{w}}+\Delta \mathrm{r}={\mathrm{r}}_{\mathrm{w}}{\left[{\displaystyle \frac{{\rho }_{\mathrm{w}}}{{\rho }_{\mathrm{i}}}}\right]}^{1/3}.$$

(12)

Equation (12) is used to calculate the difference between freezing fog and liquid fog, and that is used to obtain Vis differences between FFG and WFG.

3.4. Microphysical Parameterizations

FFG particles can be WFG droplets, but if droplets freeze, the volume of spherical ice particles become greater than liquid droplets. To develop visibility parameterization for freezing fog, MP parameters are needed for both the liquid (like N_d, LWC, MVD) and ice forms (such as N_i, IWC, MVD_ice). It can be estimated that visibility for ice crystals (Vis_ice) can be different than visibility with respect to liquid droplets (Vis_liq) because frozen droplet density can lead to formation of larger particle sizes.

Using warm fog microphysical spectral measurements, Gultepe et al. [24,34] developed a parametrization based on the theory of extinction of visible light in a volume of fog droplets as:

$$\mathrm{V}\mathrm{i}\mathrm{s}={\displaystyle \frac{-\left(\frac{4}{3}\right)\mathrm{l}\mathrm{n}(\epsilon ){\rho }_{\mathrm{w}}\sum _{\mathrm{r}1}^{\mathrm{r}2}\mathrm{n}\left(\mathrm{r}\right){\mathrm{r}}^3\Delta \mathrm{r}}{{\mathrm{Q}}_{\mathrm{eff} }\mathrm{L}\mathrm{W}\mathrm{C}\sum _{\mathrm{r}1}^{\mathrm{r}2}\mathrm{n}\left(\mathrm{r}\right){\mathrm{r}}^2\Delta \mathrm{r}}}.$$

(13)

Equation (13) can be simplified and used as a theoretical model for parameterizations:

$$\mathrm{V}\mathrm{i}\mathrm{s}=5.216{\displaystyle \frac{{\rho }_{\mathrm{w}}{\mathrm{r}}_{\mathrm{e}\mathrm{f}\mathrm{f}}}{{\mathrm{Q}}_{\mathrm{eff} }\mathrm{L}\mathrm{W}\mathrm{C}}},$$

(14)

where ρ_w is 1000 kg m⁻³. Visibility can be obtained from Equation (14) if the effective radius (r_eff) and LWC are obtained from FM120 measurements. For the calculation of FFG microphysical parameters, LWC and N_d are replaced with IWC and N_i, respectively. The r and LWC values in Equations (13) and (14) can be presented as freezing droplet radius when we assume as ice (r_i) and IWC for freezing droplets, respectively [17]. The final equations used for WFG and FFG are obtained, respectively, as:

$${\mathrm{Vis}}_{\mathrm{liq}} =\alpha {\left[{\displaystyle \frac{{\rho }_{\mathrm{w}}}{{\mathrm{Q}}_{\mathrm{e}\mathrm{f}\mathrm{f}}{\mathrm{N}}_{\mathrm{d}}\mathrm{L}\mathrm{W}\mathrm{C}}}\right]}^{\gamma },$$

(15)

and

$${\mathrm{Vis}}_{\mathrm{ice}}=\alpha {\left[{\displaystyle \frac{{\rho }_{\mathrm{i}}}{{\mathrm{Q}}_{\mathrm{e}\mathrm{f}\mathrm{f}}{\mathrm{N}}_{\mathrm{i}}\mathrm{I}\mathrm{W}\mathrm{C}}}\right]}^{\gamma },$$

(16)

where ρ_i is 917 kg m⁻³, Q_eff ~2 for large particles, and α and γ are regression constants. The ice crystal number concentration (N_i) (# cm⁻³) and IWC (g m⁻³) are obtained from FM120 spectral measurements.

Assuming that Q_eff, ρ_w, and ρ_i are constants, Equations (15) and (16) can be rewritten, correspondingly, as:

$${\mathrm{Vis}}_{\mathrm{liq}} =\alpha {\left[{\displaystyle \frac{1}{{\mathrm{N}}_{\mathrm{d}}\mathrm{L}\mathrm{W}\mathrm{C}}}\right]}^{\gamma },$$

(17)

and

$${\mathrm{Vis}}_{\mathrm{ice}}=\alpha {\left[{\displaystyle \frac{1}{{\mathrm{N}}_{\mathrm{i}}\mathrm{I}\mathrm{W}\mathrm{C}}}\right]}^{\gamma }.$$

(18)

Equations (17) and (18) are used to obtain Vis based on liquid droplets and frozen droplets, respectively. In NWP models, visibility is usually diagnosed using the post-processed model outputs. If numerical forecast model simulations can resolve MP processes at small time and space scales in ABL, Vis can also be predicted diagnostically. This bulk parametrization of the cloud MP parameters does not need a droplet spectrum at each time-step, which increases calculation time significantly. Therefore, the above equations are used to show freezing fog impact on Vis, and the results are given in the next section.

4. Results

The results related to the FFG event on 19 February 2022 are presented in this section. First, time series of microphysical parameters are given. Second, the influence of aerosol chemical composition on Vis and droplet growth are provided using theoretical and observational data. Finally, the impact of water phase (liquid vs. ice) on Vis is evaluated, and a newly developed, site-specific visibility parameterization is introduced.

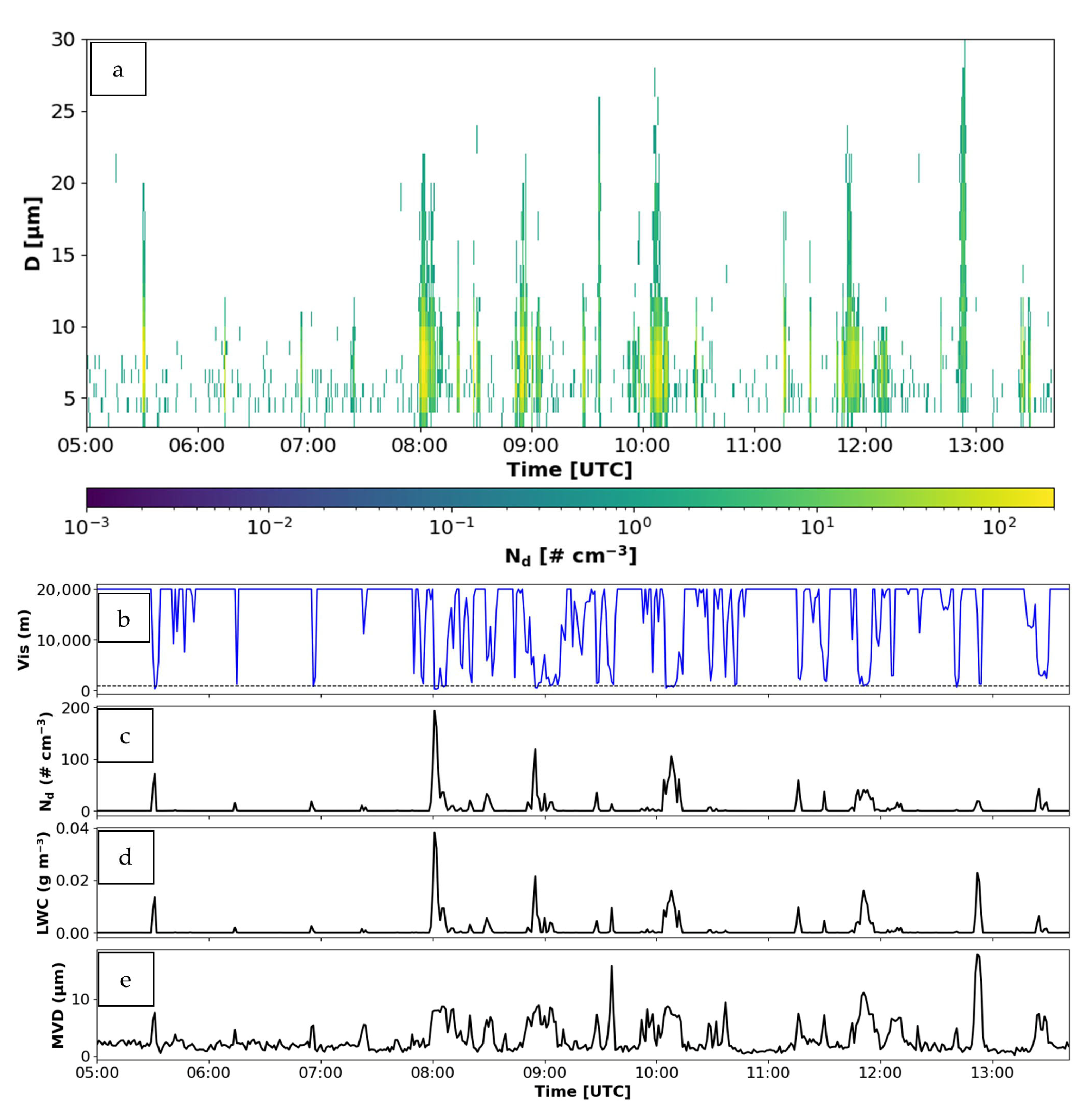
4.1. Time Series of Microphysical Parameters

Time series of droplet spectra obtained from the FM120 are shown in Figure 5a. The color bar indicates contours of N_d. Several foggy segments are seen from 08:00 to 13:00 UTC where N_d values for each segment indicate strong temporal variability. Measured Vis, N_d, LWC, and MVD parameters are shown in Figure 5b and Figure 5c–e, respectively. Vis measurements were obtained from PWD at 1-min sampling rate and microphysical parameters are obtained from 1-s FM120 measurements. To enable a consistent comparison between the two datasets, FM120 data were visualized as 1-min averages using a moving average. Figure 5b shows the freezing fog event that is clearly observed between 05:30 to 13:40 UTC, during which Vis decreased to as low as 300 m. The N_d values reached up to 200 cm⁻³ (Figure 5c). During this FFG event, the LWC (Figure 5d) was less than 0.05 g m⁻³. Although the MVD was usually less than 10 µm (Figure 5e), it reached occasionally up to 20 µm. This characteristic of MVD was consistent with measurements of PWD Vis because decreasing Vis matched well with increasing N_d and MVD.

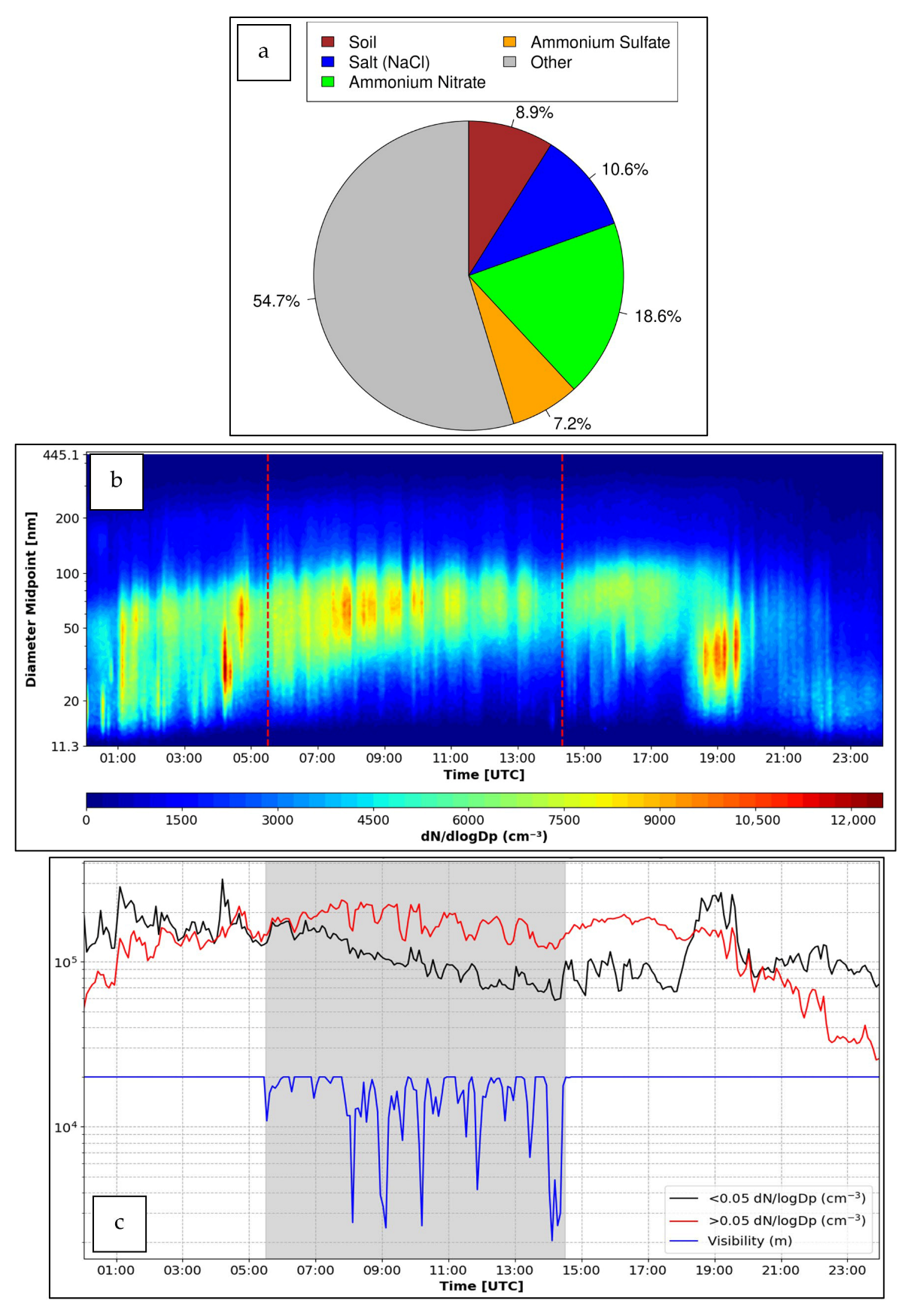
4.2. Aerosol Chemical and Physical Effects on Visibility

Aerosol chemical and physical characteristics affect fog MP properties. Figure 6a shows aerosol chemical composition for a 24 h period from 18 February 21:09 to 19 February 20:43 UTC for a MiniVol flow rate of 5 L min⁻¹. Figure 6a displays the aerosol mass distribution from nine Teflon filters, showing that 45.3% of the mass is made up of inorganic compounds, while the remaining 54.7% is labeled as “Other”. NaCl and NH₄NO₃ compounds are the most common type of CCN or IN.

A time series of aerosol number size distribution from SMPS is shown in Figure 6b. N_a spectral density reached its maximum at about 10⁴ cm⁻³ with diameter of 40–80 nm size interval during freezing fog conditions. On Figure 6b, after 05:30 UTC, a rapid decrease in N_a when D < 40 nm was observed but at about 19:00 UTC, small N_a values were consistent with newly formed CCN particles after evaporation of water molecules from aerosol particles.

To show a comparison between PWD Vis versus N_a, time series of PWD Vis and N_a for small aerosols particles (N_as) with D < 0.05 μm and large aerosols particles (N_al) with D > 0.05 μm are shown in Figure 6c. Overall, decreasing Vis was consistent with decreasing N_as, suggesting increasing N_d. The N_al also indicated the same result, but its values were higher than N_as during fog but less before and after the fog event, indicating that large aerosols were acting as CCN.

4.3. Aerosol Composition Effect on Droplet Growth

Fog nucleation chemical properties are another factor affecting fog formation [45,46]. Figure 7a,b is obtained using Equations (1)–(5) and displays the classic and κ-Köhler curves for NaCl and NH₄NO₃ with Raoult and Kelvin effects. Calculations were performed using the dry aerosol density of 2200 kg m⁻³, I = 2, T_a = 268.15, and σ_w = 0.0756 Nm⁻¹, and are used in the calculations. Using the classical Köhler approach, S_c and r_c were calculated as 1.0015 and 0.608 µm for NaCl, and as S_c = 1.0020 and r_c = 0.463 µm for NH₄NO_3. Using the κ-Köhler approach, the corresponding values were obtained as r_c = 0.555 µm and S_c = 1.0016 for NaCl, and r_c = 0.431 µm and S_c = 1.0021 for NH₄NO₃. If a droplet has grown to critical radius (r > r_c), it is called an activated droplet, and can grow up to 100 µm [47], while collision-coalescence processes lead to large particles. Figure 7a,b shows that for higher S values, smaller aerosol particles can be activated. In Figure 7c, κ-Köhler curves are plotted for NaCl using κ = 1 and κ = 1.33 in order to demonstrate the effect of the κ parameter. These values were selected within the experimentally observed range of κ = 0.91–1.33 reported by Petters et al. [41]. It is seen in Figure 7 that r_c for NH₄NO₃ is smaller than for NaCl aerosols, and this suggests that NH₄NO₃ aerosols will activate earlier than NaCl aerosols. Using NaCl and NH₄NO₃ aerosols, droplet growth rate is obtained using Equation (6). The result is shown in Figure 7d, in which NaCl particles acting as CCN led to formation of droplets of sizes 2 µm smaller than for the NH₄NO₃ aerosol case.

4.4. Freezing Fog and Density Effects on Vis

FFG occurs either when droplets in the air are supercooled (T_a~0 °C) or, on the ground, touch on the surfaces like aircraft and ships as well as ground structures. Assuming that the N_d = N_i in the air after freezing conditions, droplet size and volume change as a function ice crystal density. If we assume N_d = N_i and m_w = m_i (water mass = ice crystal mass), it can be shown, using Equation (14), that an estimated volume difference between droplet and ice crystal mass can be about 8.3% due to the lower density of ice. To investigate the impact of this density-related size change on Vis estimates, using N_d spectra obtained from FM120 measurements (filtered using N_d > 1 cm⁻³ and LWC > 0.005 g m⁻³ [48]), we calculated the differences between Vis_liq and Vis_ice, and the results are shown in Figure 8a. This figure shows that difference can reach up to about 80 m, which is significant compared to 1 km Vis criteria. Similarly, without using any filtering of the data, Vis differences between the FFG and IFG cases can be up to 1 km depending on Vis magnitude (Figure 8b).

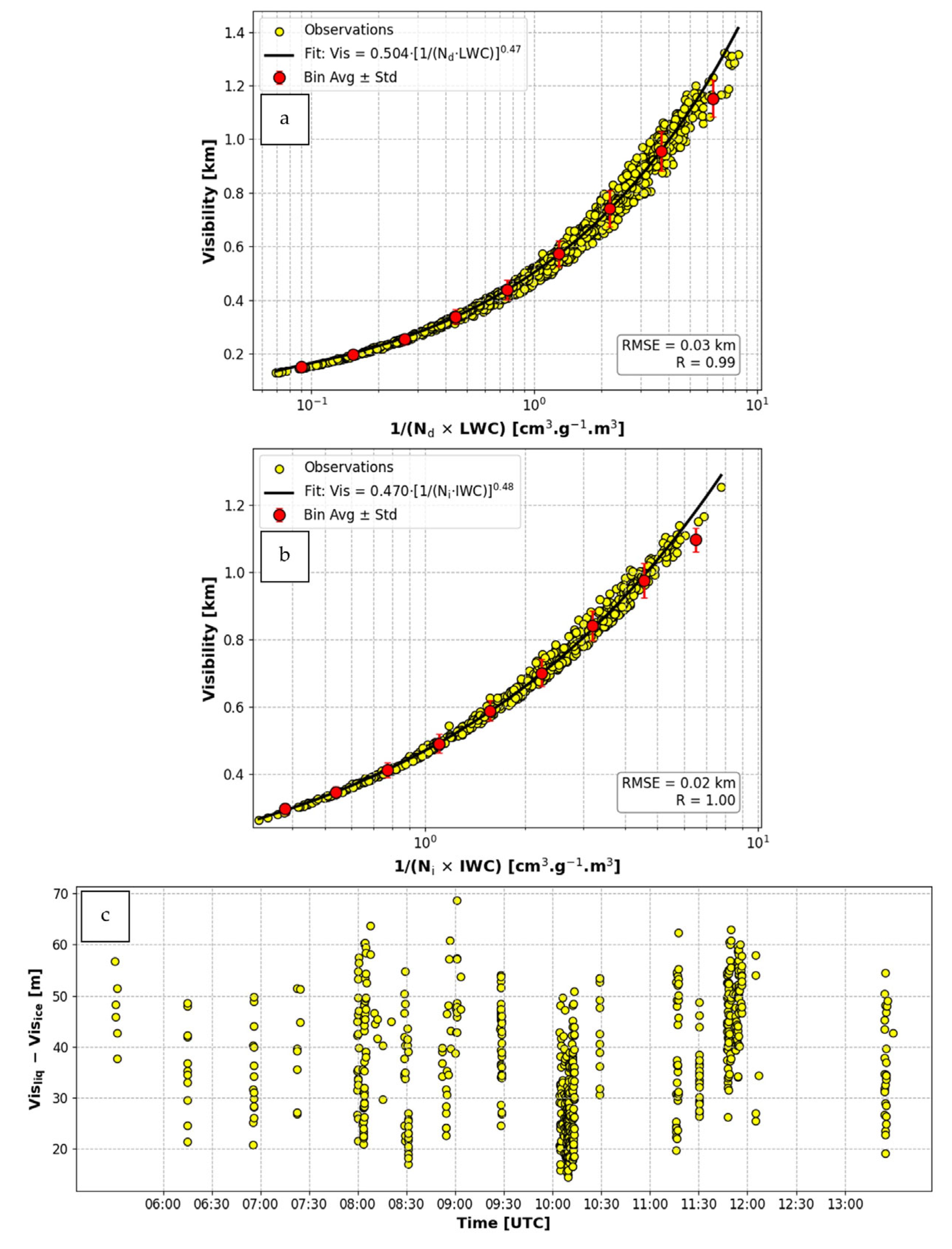
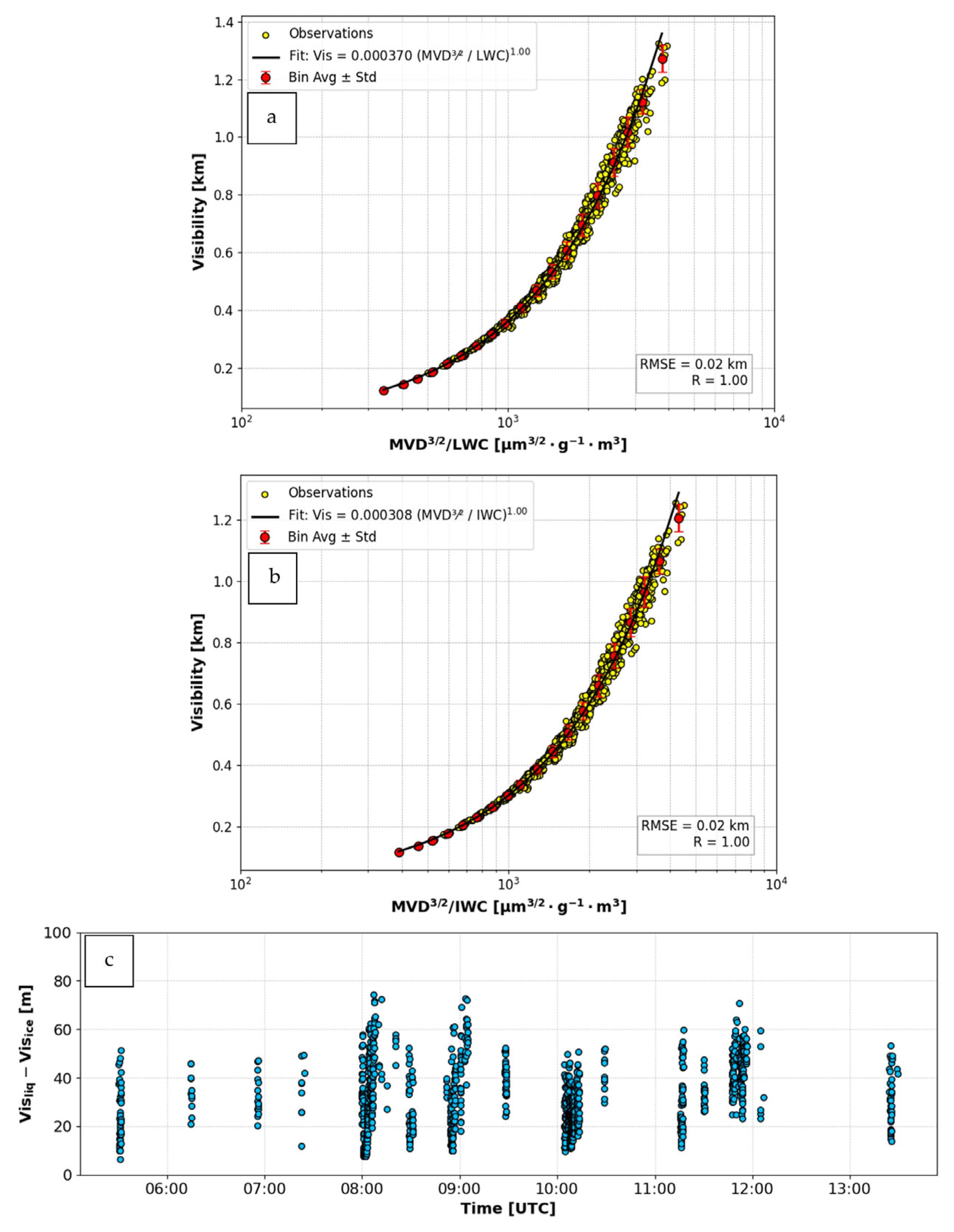
4.5. Visibility Parameterization

Visibility parameterization can be derived in different ways using (1) bulk MP parameters such as LWC (IWC), N_d (N_i), and MVD (for liquid droplets as MVD_liq and ice crystals as MVD_ice), and (2) assumed particle size distribution parameters [24]. Here, the first method is applied, and the results are compared with theoretical estimations and previously developed parameterizations. It should be noted that the results are site-specific and depend on the measurements. Similar to Gultepe et al. [17,19], Vis was estimated using Equation (9), derived from Koshimider law based on β_ext calculation using FM120 spectral measurements. Both liquid droplets and ice particles are assumed to be spherical. Vis for supercooled liquid fog droplets or spherical ice crystals are calculated using Equations (17) and (18), respectively, and then Vis is plotted as a function of fog index (FI = 1/(N_d LWC) [17]). Figure 9a,b show Vis as a function of FI, including observed data points and a fit with standard deviations (Sd) values. The fitted visibility parameterizations for the liquid and ice phases are given as:

$${\mathrm{V}\mathrm{i}\mathrm{s}}_{\mathrm{l}\mathrm{i}\mathrm{q}}=0.504\cdot {\left({\mathrm{N}}_{\mathrm{d}}\cdot \mathrm{L}\mathrm{W}\mathrm{C}\right)}^{-0.47},$$

(19)

and

$${\mathrm{V}\mathrm{i}\mathrm{s}}_{\mathrm{i}\mathrm{c}\mathrm{e}}=0.431\cdot {\left({\mathrm{N}}_{\mathrm{i}}\cdot \mathrm{I}\mathrm{W}\mathrm{C}\right)}^{-0.48}.$$

(20)

The fits on Figure 9a,b had root mean square errors as 30 m and 20 m, respectively, but maximum error can be up to 100 m for both fits. Figure 9c shows differences (mean as 31.16 m) between Vis for liquid droplets and spherical ice crystals conditions. This shows that if a FFG (with spherical ice crystals) event happens, fog Vis can decrease up to 70 m.

5. Discussion

Fog prediction can be important for aviation and marine environments as well as economic and ecosystem planning. The rapid changes in fog intensity (represented with Vis) are related to the short time and spatial scales as well as nonlinear relationships between surface and atmospheric conditions. There are several methods for fog prediction that includes the rule-based techniques [49,50], statistical [51,52] and numerical forecasting [51,52,53,54], and integrated nowcasting methods [55,56]. Lately, artificial intelligence (AI) techniques are being applied for Vis predictions based on observations and NWP models [57].

Here, some issues related to Vis predictions and measurements are provided that include fog size changes at the cold temperatures, uncertainty in measuring and calculation of Vis, particle density, as well as theoretical concepts.

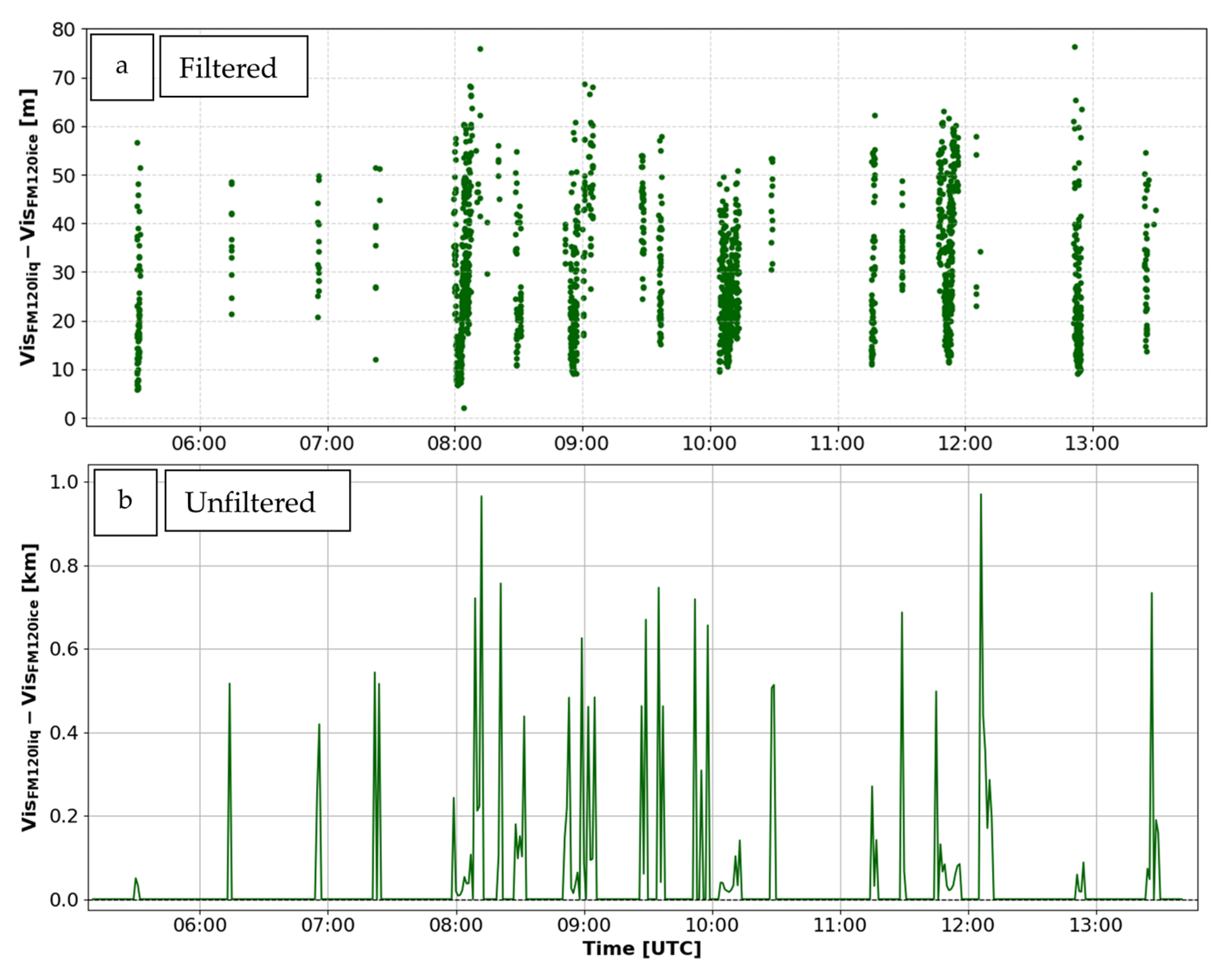
5.1. Freezing Droplet Size Effect on Vis Calculations

The Vis parameterization formula is modified to obtain Vis as a function of MVD when droplet freezes up. For this purpose, Equation (13) as a function of MVD can be expressed as follows:

$${\mathrm{N}}_{\mathrm{d}}=\left({\displaystyle \frac{1}{\mathrm{k}}}\right){\displaystyle \frac{\mathrm{L}\mathrm{W}\mathrm{C}}{\mathrm{M}\mathrm{V}{\mathrm{D}}^3}},$$

(21)

where k = (4/3)πρ. By replacing N_d in Equations (17) and (18) with Equation (21), Vis can be rewritten for liquid droplets as:

$${\mathrm{V}\mathrm{i}\mathrm{s}}_{\mathrm{l}\mathrm{i}\mathrm{q}}=\alpha {\left[\left({\displaystyle \frac{1}{{\mathrm{k}}_{\mathrm{liq}}}}\right){\displaystyle \frac{\mathrm{L}\mathrm{W}\mathrm{C}}{\mathrm{M}\mathrm{V}{\mathrm{D}}^{3/2}}}\right]}^{-2\gamma },$$

(22)

and for freezing droplets (ice particles) as:

$${\mathrm{V}\mathrm{i}\mathrm{s}}_{\mathrm{i}\mathrm{c}\mathrm{e}}=\alpha {\left[\left({\displaystyle \frac{1}{{\mathrm{k}}_{\mathrm{ice}}}}\right){\displaystyle \frac{\mathrm{I}\mathrm{W}\mathrm{C}}{(\mathrm{M}\mathrm{V}{\mathrm{D}+\Delta \mathrm{r})}^{3/2}}}\right]}^{-2\gamma }.$$

(23)

In Equations (22) and (23), k_liq = (4/3)πρ_w, k_ice = (4/3)πρ_ice. Figure 10a shows Vis versus MVD and LWC and Figure 10b Vis versus MVD and IWC, along with best fits to the observations. Figure 10c shows the difference between them based on fits (Vis_liq − Vis_ice). This difference can be up to about 60–70 m. Note that this figure shows the effect of size enlargement due to icing conditions, and it can be important for Vis_ice predictions. Therefore, freezing fog particle size enlargement should be added to Vis calculations that can affect up to 10% variation in Vis estimates.

5.2. Uncertainty in Measurement of Microphysical Parameters

Measurements of droplet spectra can be highly affected by the wind speed (U_h) and direction. Here, true air speed (TAS) used was about 25 m s⁻¹ (measured). If TAS decreases due to changing wind direction changes, N_d increases significantly. This uncertainty can be assumed as negligible during low U_h conditions. Figure 11a shows U_h rose plot and Figure 11b conditional T_a plot with respect to wind speed criteria. The wind speed was typically less than 1 m s⁻¹ during Feb 19 (Figure 11a), and cold air advection was both northerly and easterly, but T was usually between −6 °C and −9 °C. This suggests that the freezing fog event formed in a stable atmospheric boundary layer. Figure 11c shows the ice particle density effect on Vis calculated using Equation (14), assuming ρ_i = 0.9 g cm⁻³ (glazed ice) and 0.5 g cm⁻³ (rimed ice). This plot shows that ice crystal density effect on Vis can be very large, up to 4–8 km, and is related to Vis magnitude. Further research on ABL ice fog conditions is needed to better evaluate Vis predictions.

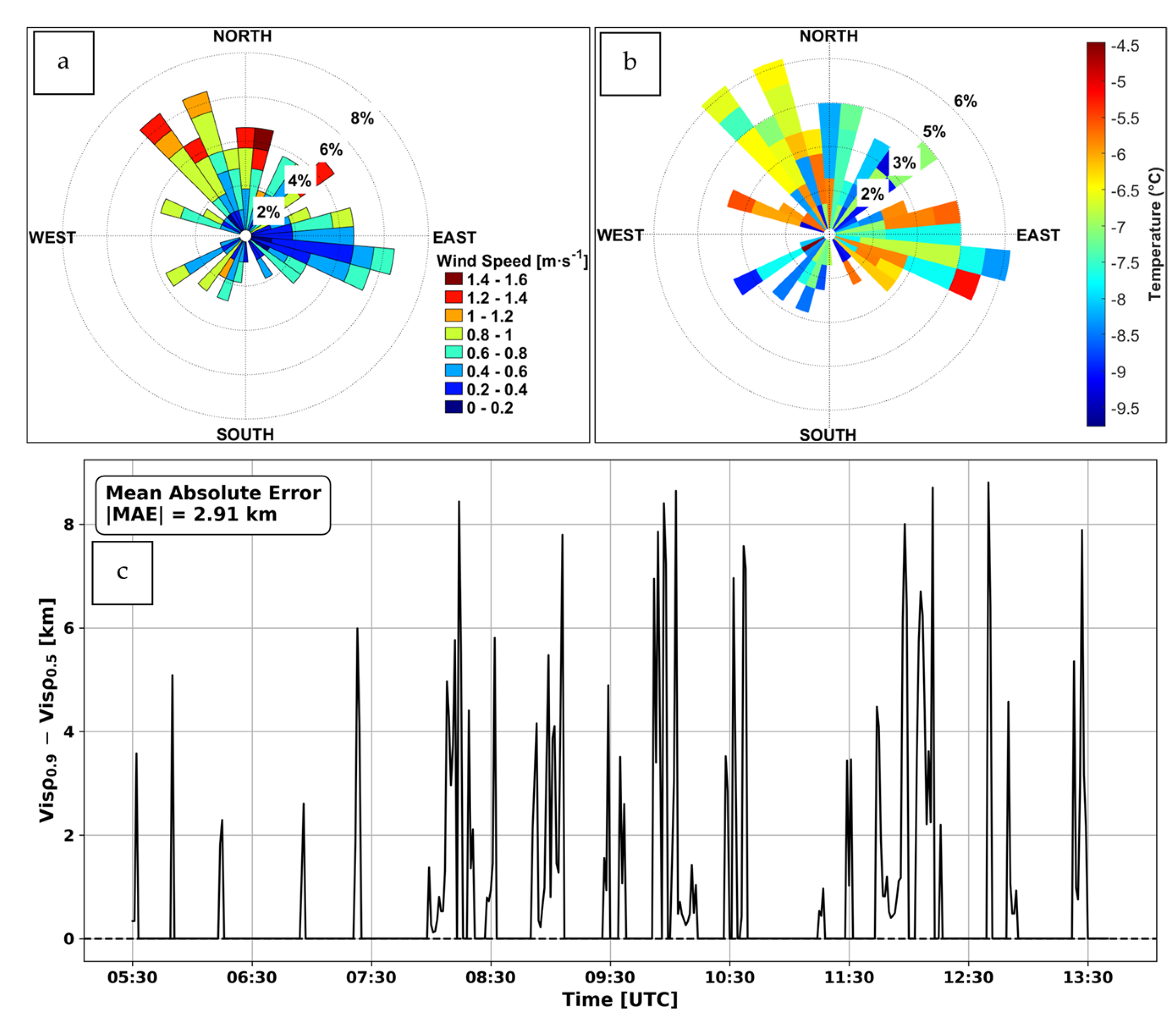
5.3. FM120 and PWD Vis Comparison

In the literature, significant differences have been stated for Vis obtained from PWD and FM120 measurements [58]. These differences can be due to various reasons, including calibration errors, assumed coefficients in the calculations, as well as averaging time and space scales. Figure 12a and Figure 12b shows PWD and FM120 Vis time series, and the differences in Vis comparisons for liquid and freezing droplets (spherical ice crystals) are shown in Figure 12c and Figure 12d, respectively. As indicated by the figures, ΔVis for both liquid (Figure 12c) and ice cases (Figure 12d) can be more than a few km. Further research is needed to better understand these differences.

5.4. Visibility Comparisons Using Observations and Parameterizations

Verification of the bulk parameterization equations derived here is obtained using FM120 Vis values calculated from the droplet spectra. Determining the visibility, Gultepe et. al. [19] developed a parameterization as:

$$\mathrm{Vis}={\displaystyle \frac{1.002}{{\left(\mathrm{L}\mathrm{W}\mathrm{C}\times {\mathrm{N}}_{\mathrm{d}}\right)}^{0.6473}}}$$

(24)

Equation (24) is compared with the Kunkel [31] method that used β_ext values directly related to LWC for visibility calculation. The β_ext as a function of LWC is given by Kunkel [31] as:

$${\beta }_{\mathrm{ext} }=144.7\mathrm{L}\mathrm{W}{\mathrm{C}}^{\mathrm{a}}.$$

(25)

where a = 0.88.

Figure 13 shows Vis versus LWC scatter plot for Equations (9), (14), (22), (24) and (25), assuming various fixed r_eff and using N_d = 10 and 100 cm⁻³. Vis values from Equation (24) [19] for marine environmental conditions are relatively higher than the current work. With N_d = 100 cm⁻³, Vis comparisons are found to be comparable to the parameterized ones of the current work. Using Equation (14) with r_eff = 5 µm, Gultepe et al.’s [24] Vis values are also found to be comparable with the current work results. Overall, the variability among the results suggests that Vis parameterizations are highly dependent on variability in microphysical parameters and for FFG conditions. It is found out that ρ_ice changes due to riming can also play an important role for significantly reducing Vis. This suggests that decreasing ice crystal density can further reduce Vis when riming take a place.

6. Conclusions

Vis associated with freezing fog conditions in an alpine mountain valley was studied. Microphysical parameters including LWC (IWC), N_d (N_i), and MVD (or r_eff) along with dynamic parameters were studied using observations obtained during a fog event that occurred on 19 February 2022 during the CFACT campaign. Aerosol and droplet spectral characteristics are used to study FFG Vis parameterizations considering aerosol composition and particle density. Based on the results, the following conclusions are drawn:

• Synoptic weather conditions are found to affect local fog conditions and colder temperature advection likely created instability for FFG formation over the complex terrain. Moving an HP system over the project area (e.g., Heber Valley) was a reason for FFG formation.
• Freezing fog can occur at temperatures as low as −10 °C when IR cooling at night happens.
• Freezing fog dissipation is initiated after sunrise with increasing SW radiative heating.
• Aerosol composition effect on Vis can be significant and can reach up to 1000 m at low LWC values, and droplet size can increase up to 2 µm affecting Vis.
• Aerosols had an occurrence of 54.7.3% based on Teflon filter observation and were not included in the analysis. Only inorganic components are considered based on availability of the observations. Among the inorganic components, soil-based aerosols accounted for 8.9%, NaCl for 10.6%, NH₄NO₃ for 18.6%, and (NH₄)₂SO₄ for 7.2%.
• Freezing droplet density with riming can be an important factor reducing Vis down to at least 50% but freezing fog density can affect Vis at about 10% during FFG event.
• Differences in Vis parameterizations suggest that FFG and WFG conditions can be different, and this can be more than 50% when the crystal shape and density change significantly.
• Large differences between PWD Vis and FM120 Vis can be significant and reach up to 1 km, and that needs to be further researched.

Overall, because of a possible increase in T_a based on climate simulations, FFG events are expected to increase in the northern latitudes and that can lead to much lower Vis values. This suggests that cold fog intensity (Vis) in FFG events will likely increase over the high mountainous and polar regions. For this reason, further cold fog studies need to be performed, and an ice fog project should be considered in the northern latitudes.