Application and Comparison of Satellite-Derived Sea Surface Temperature Gradients to Identify Seasonal and Interannual Variability off the California Coast: Preliminary Results and Future Perspectives
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methods
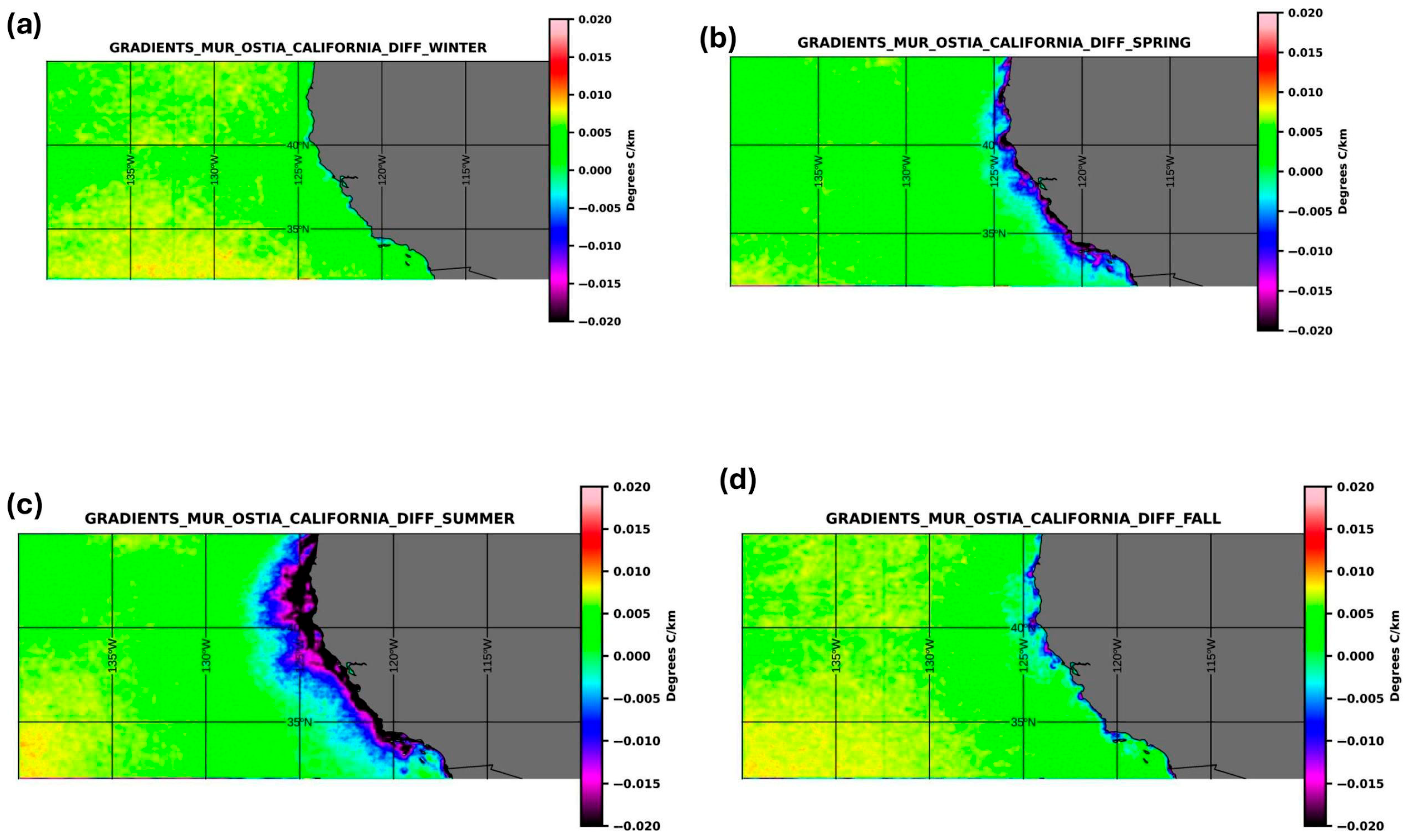
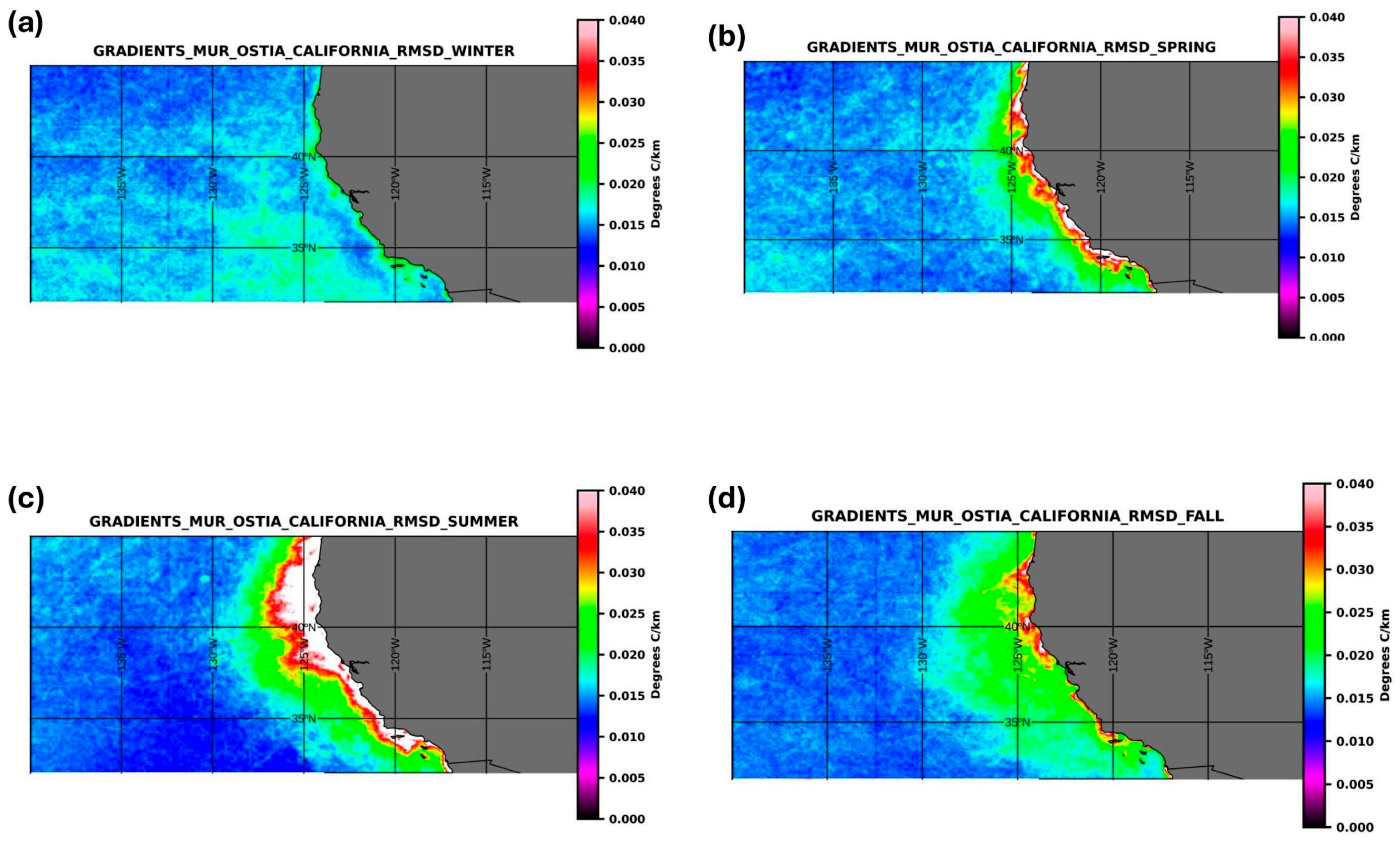
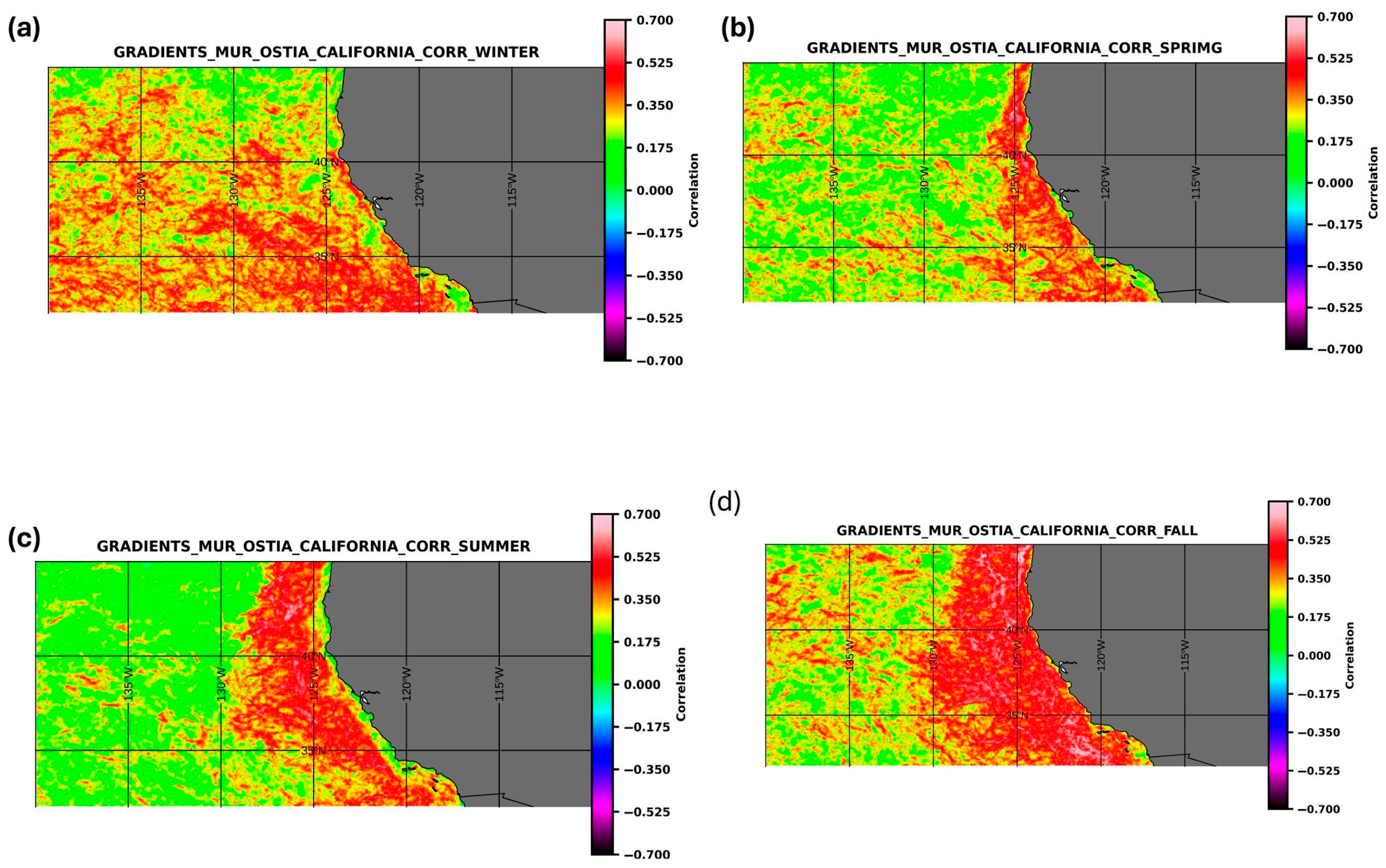
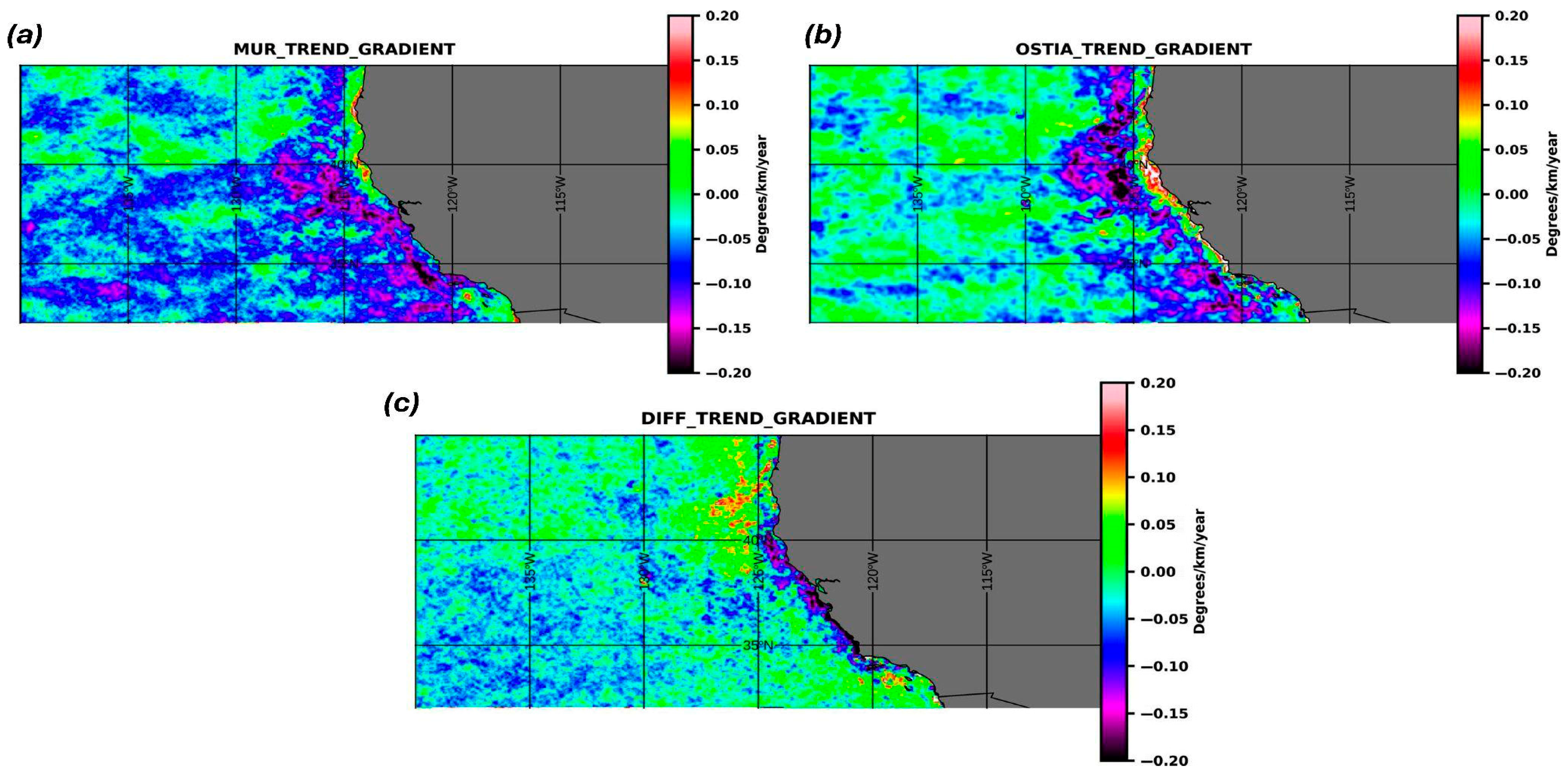
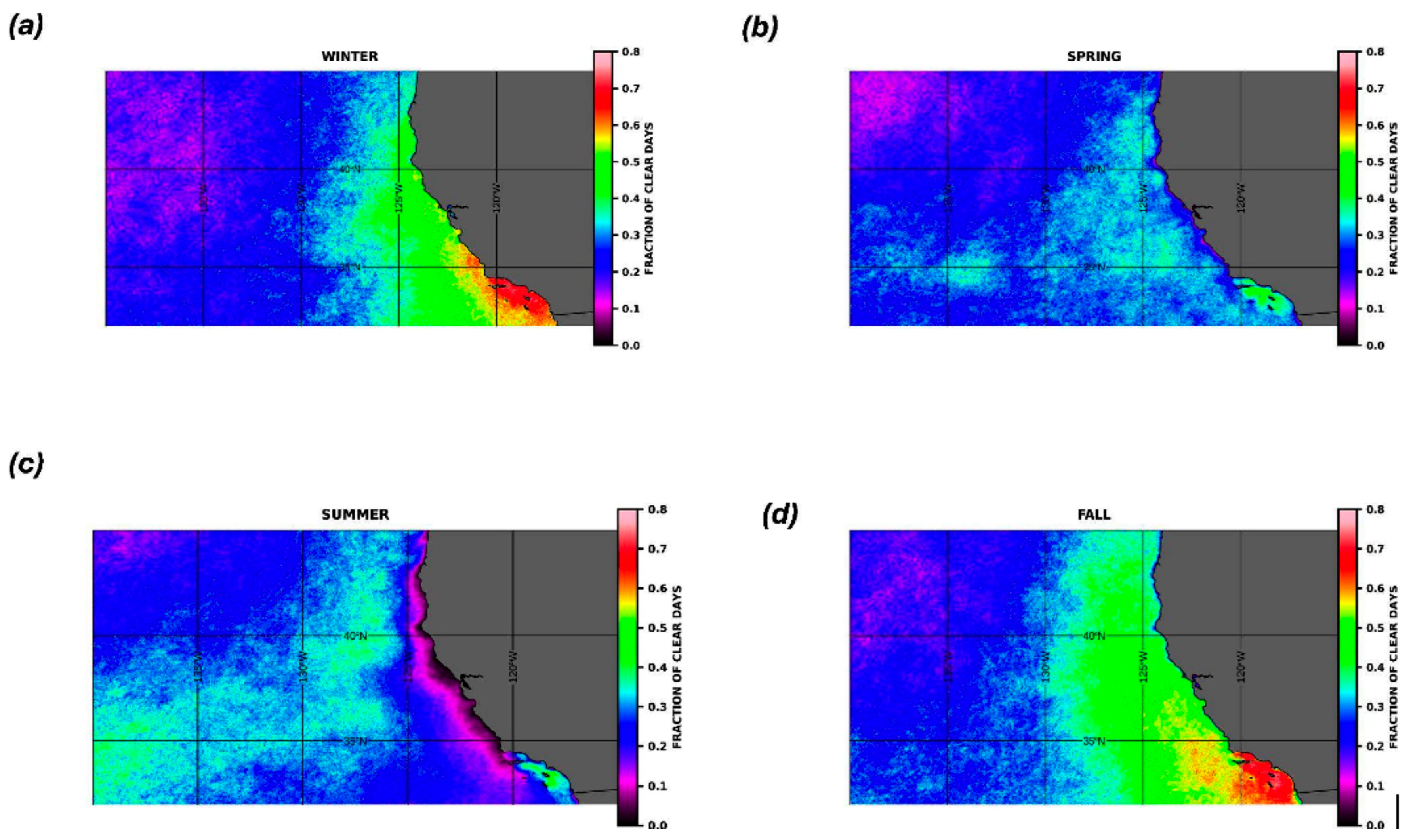
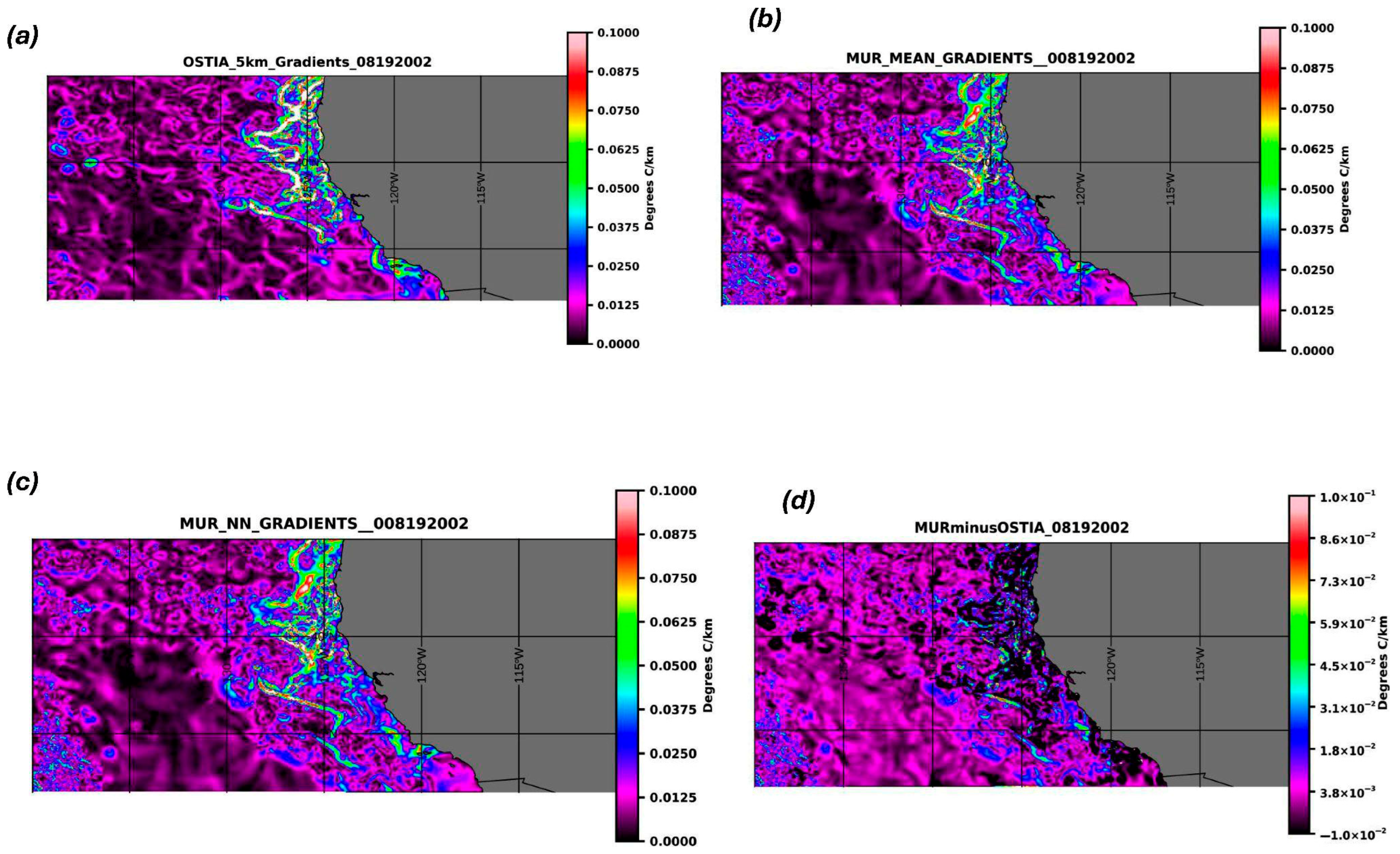
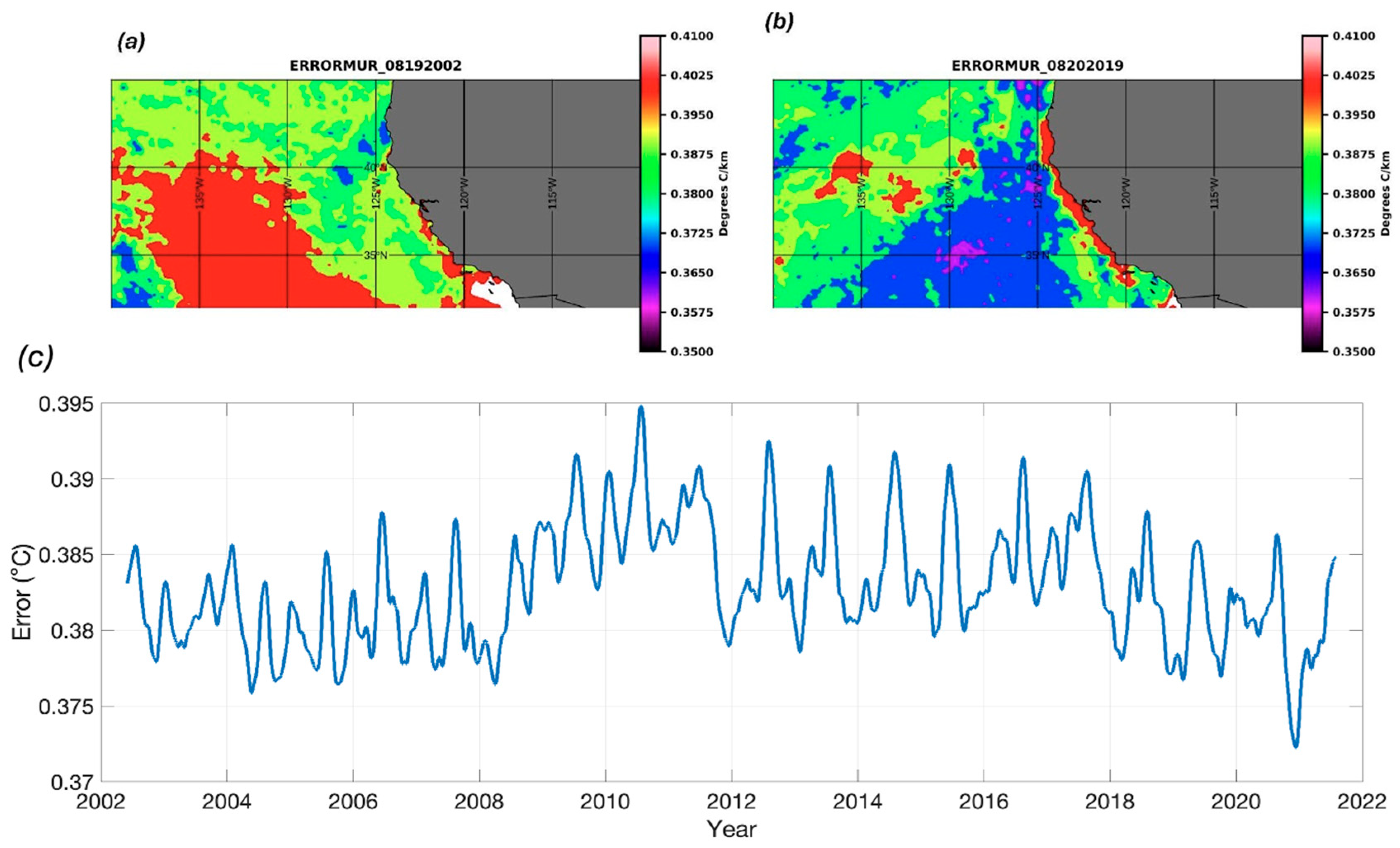
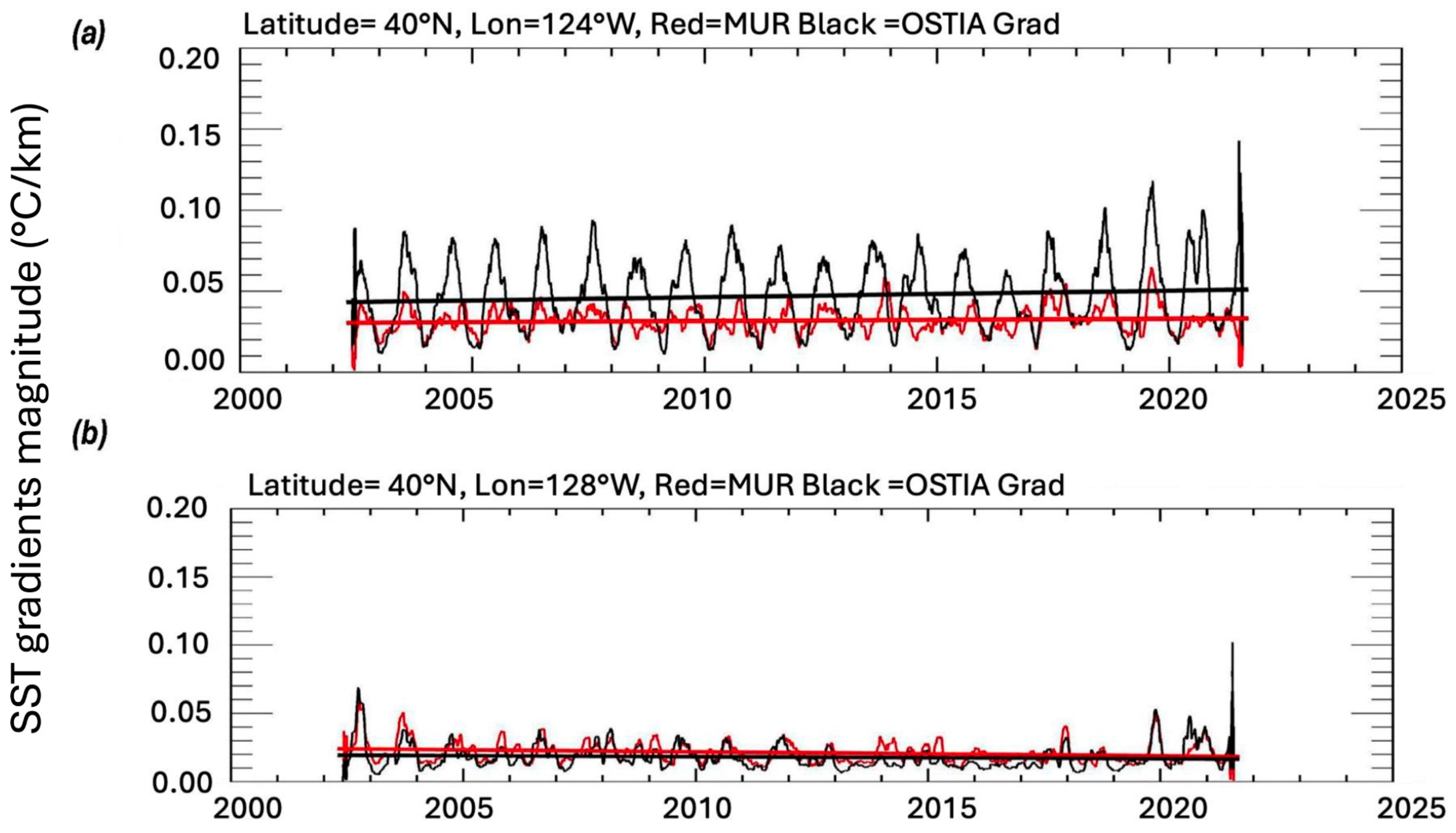
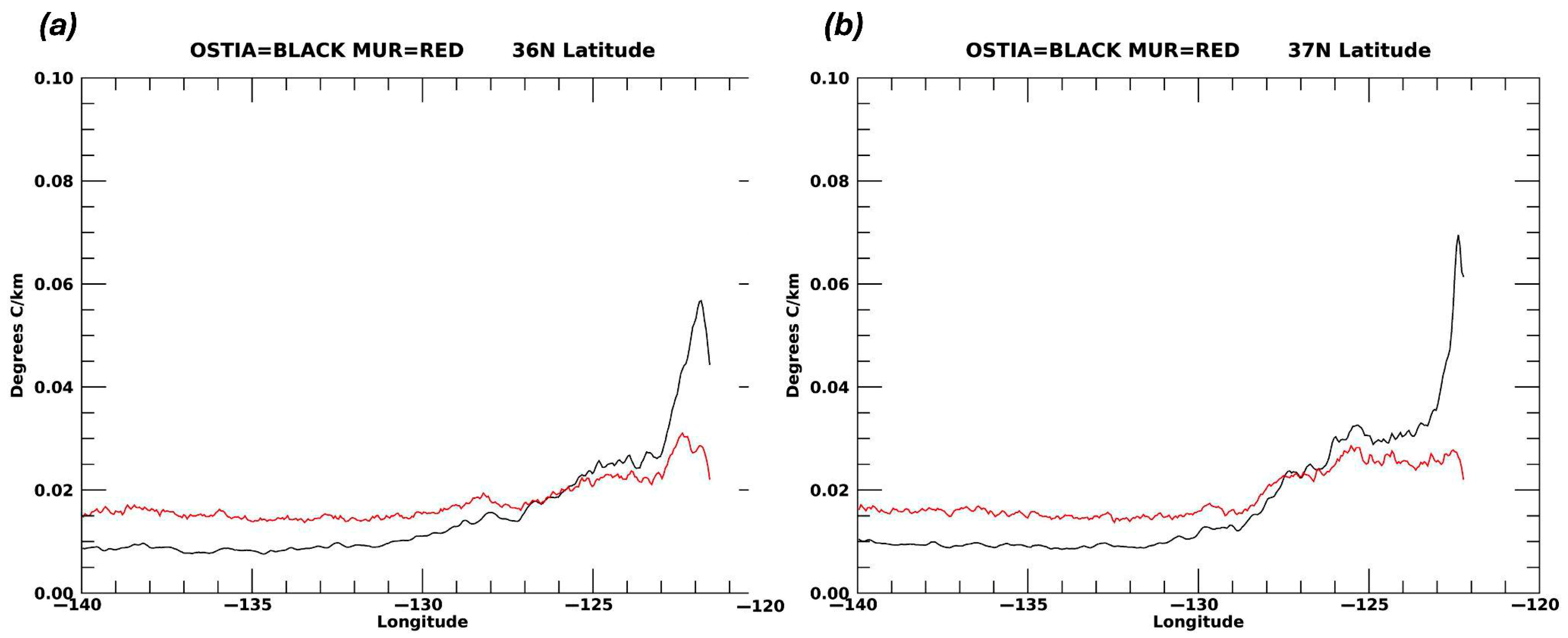
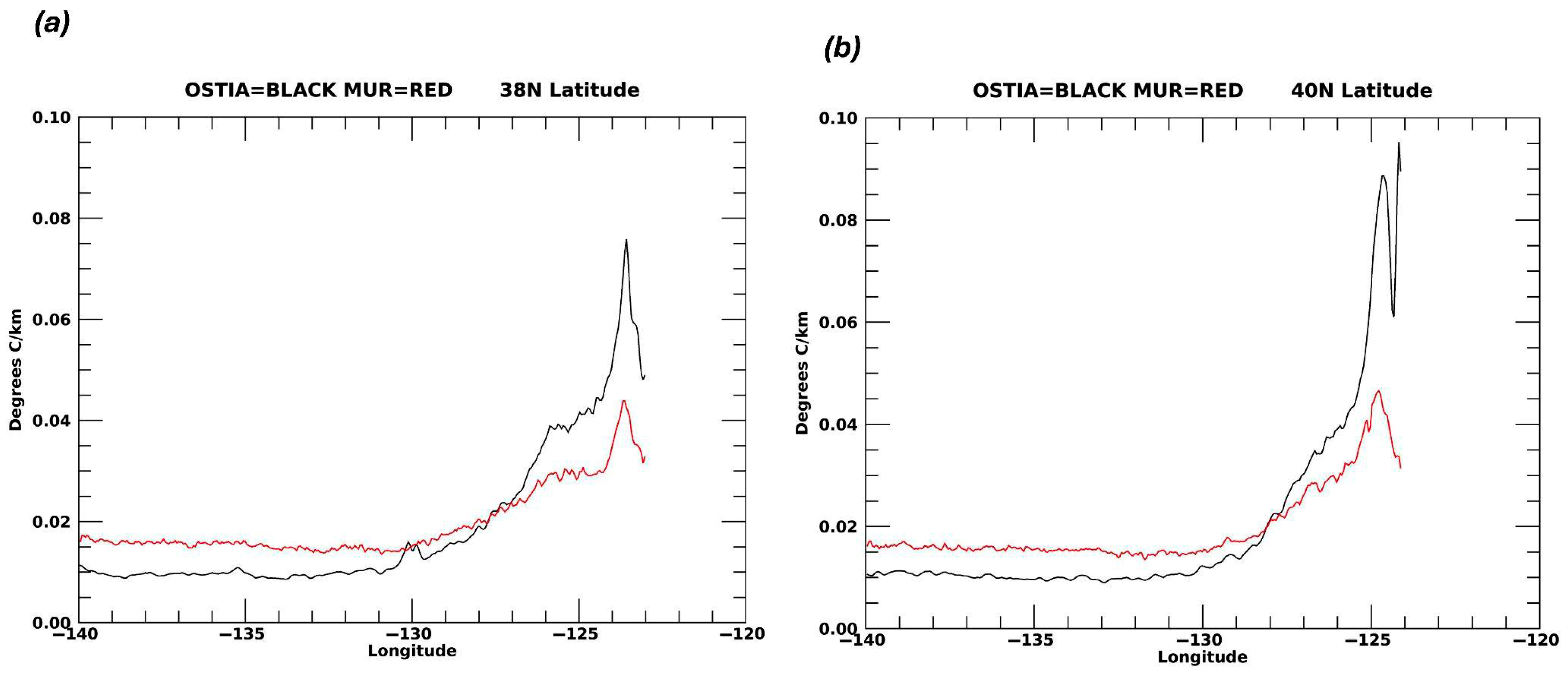
3. Results
4. Discussion
4.1. Seasonal Signal
4.2. Trend Analysis
4.3. Analysis of Differences Between MUR and OSTIA Seasonal Gradients
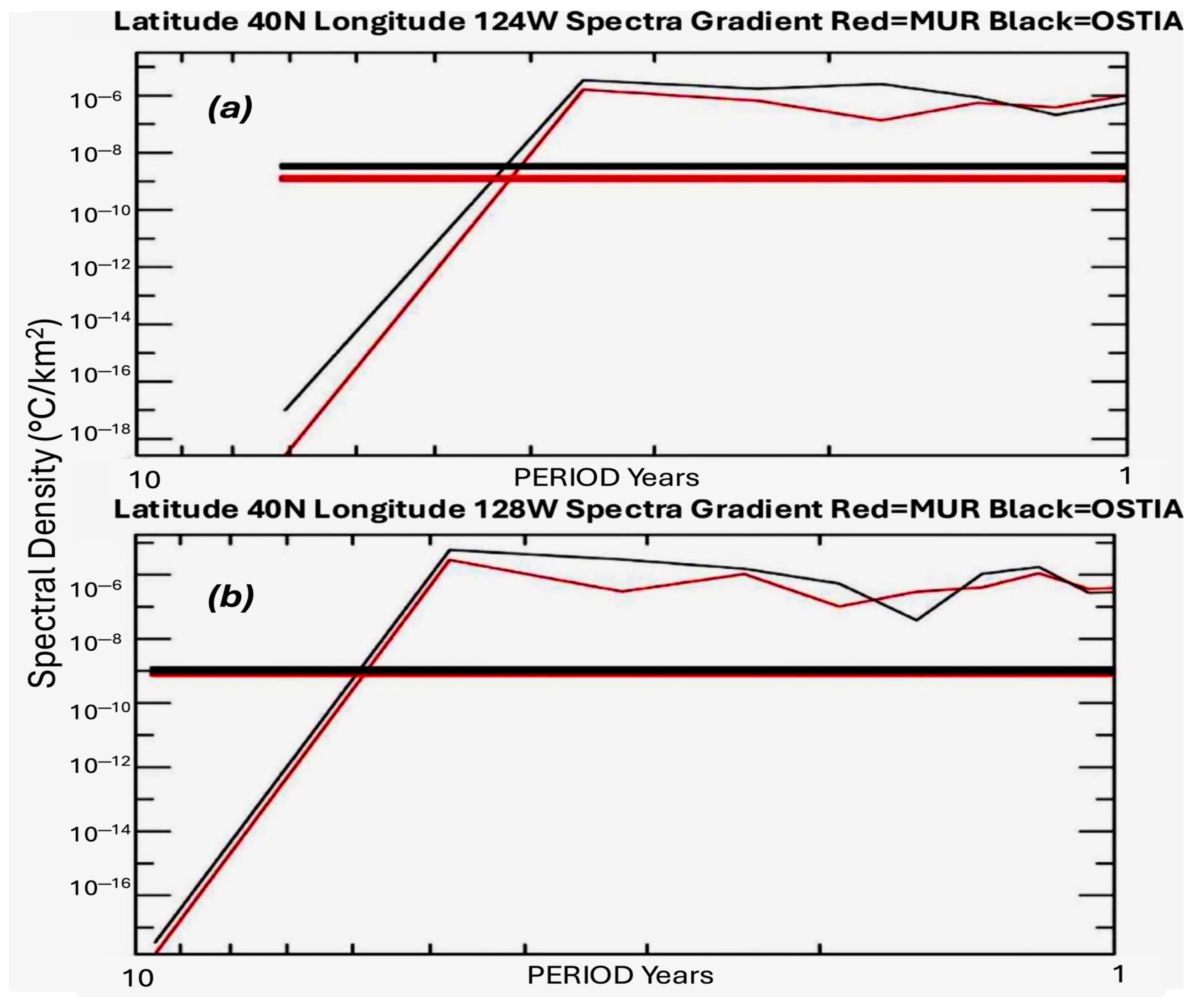
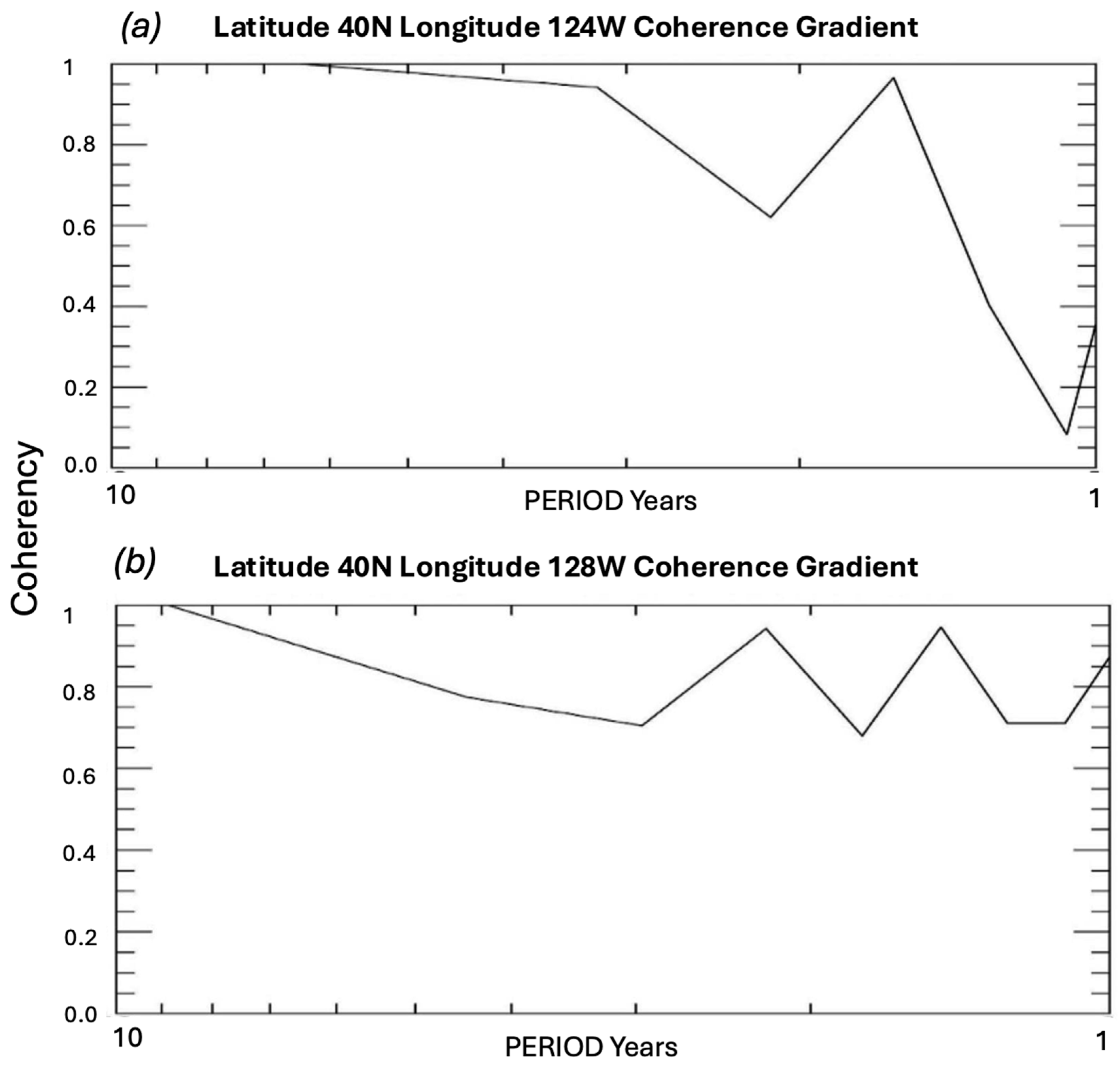
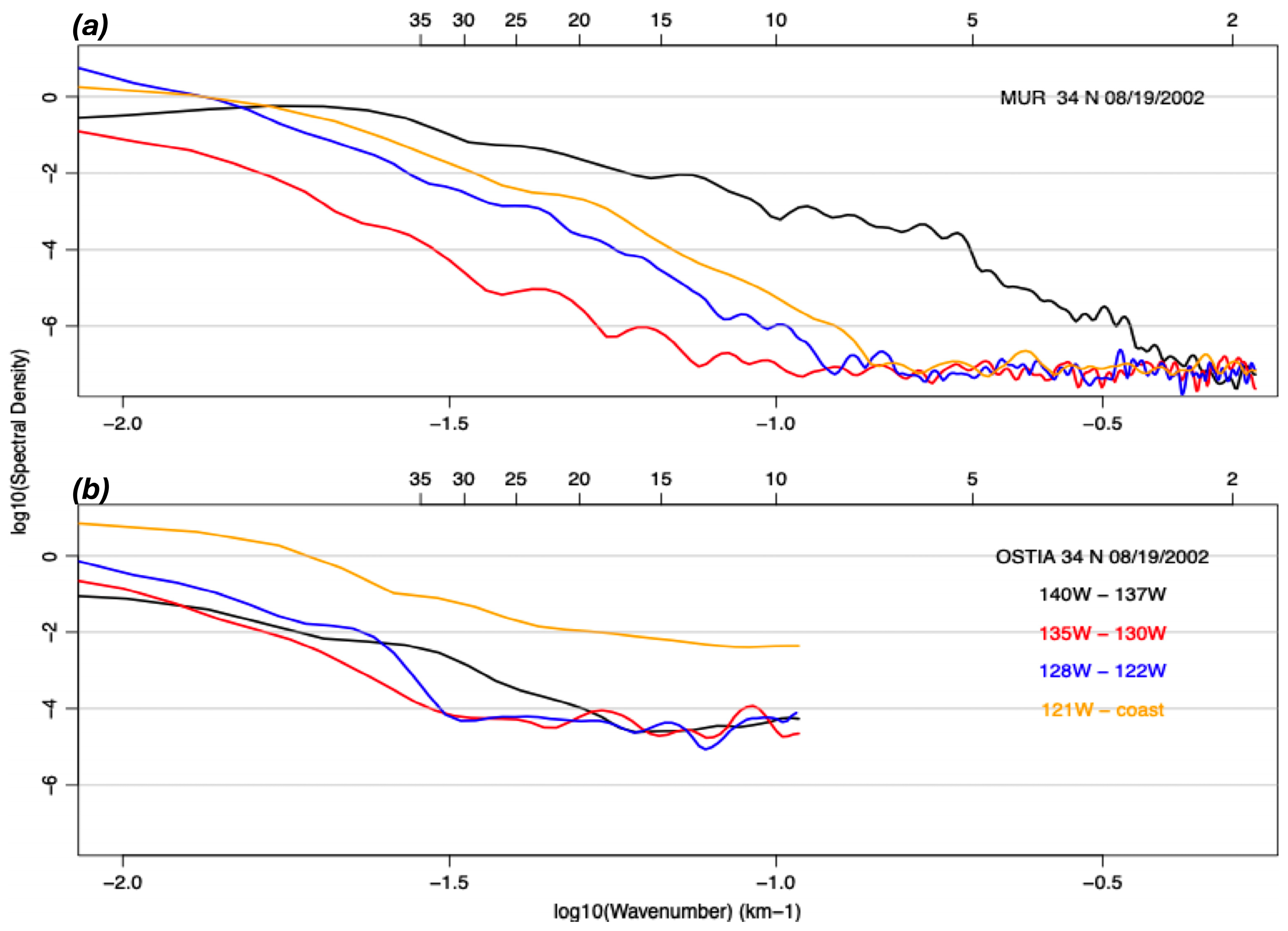
4.4. Spectra and Coherence
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, Y.; Cornillon, P. A comparison of satellite-derived sea surface temperature fronts using two edge detection algorithms. Deep Sea Res. Part II Top. Stud. Oceanogr. 2015, 119, 40–47. [Google Scholar] [CrossRef]
- Belkin, I.M.; Cornillon, P.C. Fronts in the world ocean’s large marine ecosystems. Ices Cm 2007, 500, 21. [Google Scholar]
- Vazquez-Cuervo, J.; Torres, H.S.; Menemenlis, D.; Chin, T.; Armstrong, E.M. Relationship between SST gradients and upwelling off Peru and Chile: Model/satellite data analysis. Int. J. Remote Sens. 2017, 38, 6599–6622. [Google Scholar] [CrossRef]
- Castro, S.L.; Emery, W.J.; Wick, G.A.; Tandy, W., Jr. Submesoscale sea surface temperature variability from UAV and satellite measurements. Remote Sens. 2017, 9, 1089. [Google Scholar] [CrossRef]
- Messager, C.; Swart, S. Significant atmospheric boundary layer change observed above an Agulhas Current warm cored eddy. Adv. Meteorol. 2016, 2016, 3659657. [Google Scholar] [CrossRef]
- Warner, T.T.; Lakhtakia, M.N.; Doyle, J.D.; Pearson, R.A. Marine atmospheric boundary layer circulations forced by Gulf Stream sea surface temperature gradients. Mon. Weather. Rev. 1990, 118, 309–323. [Google Scholar] [CrossRef]
- Barsugli, J.J.; Battisti, D.S. The basic effects of atmosphere–ocean thermal coupling on midlatitude variability. J. Atmos. Sci. 1998, 55, 477–493. [Google Scholar] [CrossRef]
- Nilsson, J. Propagation, diffusion, and decay of SST anomalies beneath an advective atmosphere. J. Phys. Oceanogr. 2000, 30, 1505–1513. [Google Scholar] [CrossRef]
- Woollings, T.; Hoskins, B.; Blackburn, M.; Hassell, D.; Hodges, K. Storm track sensitivity to sea surface temperature resolution in a regional atmosphere model. Clim. Dyn. 2010, 35, 341–353. [Google Scholar] [CrossRef][Green Version]
- Zheng, Y.; Bourassa, M.A.; Hughes, P. Influences of sea surface temperature gradients and surface roughness changes on the motion of surface oil: A simple idealized study. J. Appl. Meteorol. Climatol. 2013, 52, 1561–1575. [Google Scholar] [CrossRef]
- Rascle, N.; Molemaker, J.; Marié, L.; Nouguier, F.; Chapron, B.; Lund, B.; Mouche, A. Intense deformation field at oceanic front inferred from directional sea surface roughness observations. Geophys. Res. Lett. 2017, 44, 5599–5608. [Google Scholar] [CrossRef]
- Frenger, I.; Gruber, N.; Knutti, R.; Münnich, M. Imprint of Southern Ocean eddies on winds, clouds and rainfall. Nat. Geosci. 2013, 6, 608–612. [Google Scholar] [CrossRef]
- Holligan, P. Biological implications of fronts on the northwest European continental shelf. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1981, 302, 547–562. [Google Scholar] [CrossRef]
- Vazquez-Cuervo, J.; Gomez-Valdes, J.; Bouali, M.; Miranda, L.E.; Van der Stocken, T.; Tang, W.; Gentemann, C. Using saildrones to validate satellite-derived sea surface salinity and sea surface temperature along the California/Baja Coast. Remote Sens. 2019, 11, 1964. [Google Scholar] [CrossRef]
- Wick, G.A.; Jackson, D.L.; Castro, S.L. Assessing the ability of satellite sea surface temperature analyses to resolve spatial variability—The northwest tropical Atlantic ATOMIC region. Remote Sens. Environ. 2023, 284, 113377. [Google Scholar] [CrossRef]
- Rio, M.H.; Santoleri, R. Improved global surface currents from the merging of altimetry and sea surface temperature data. Remote Sens. Environ. 2018, 216, 770–785. [Google Scholar] [CrossRef]
- Ciani, D.; Rio, M.H.; Nardelli, B.B.; Etienne, H.; Santoleri, R. Improving the altimeter-derived surface currents using sea surface temperature (SST) data: A sensitivity study to SST products. Remote Sens. 2020, 12, 1601. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; García-Ladona, E.; González-Haro, C.; Turiel, A.; Rosell-Fieschi, M.; Company, J.B.; Padial, A. High-Resolution Ocean Currents from Sea Surface Temperature Observations: The Catalan Sea (Western Mediterranean). Remote Sens. 2021, 13, 3635. [Google Scholar] [CrossRef]
- Buongiorno Nardelli, B.; Cavaliere, D.; Charles, E.; Ciani, D. Super-Resolving Ocean Dynamics from Space with Computer Vision Algorithms. Remote Sens. 2022, 14, 1159. [Google Scholar] [CrossRef]
- Umbert, M.; Hoareau, N.; Turiel, A.; Ballabrera-Poy, J. New blending algorithm to synergize ocean variables: The case of SMOS sea surface salinity maps. Remote Sens. Environ. 2014, 146, 172–187. [Google Scholar] [CrossRef]
- Droghei, R.; Buongiorno Nardelli, B.; Santoleri, R. A new global sea surface salinity and density dataset from multivariate observations (1993–2016). Front. Mar. Sci. 2018, 5, 84. [Google Scholar] [CrossRef]
- Chelton, D.B.; Esbensen, S.K.; Schlax, M.G.; Thum, N.; Freilich, M.H.; Wentz, F.J.; Gentemann, C.L.; McPhaden, M.J.; Schopf, P.S. Observations of coupling between surface wind stress and sea surface temperature in the eastern tropical Pacific. J. Clim. 2001, 14, 1479–1498. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Samelson. Summertime coupling between sea surface temperature and wind stress in the California Current System. J. Phys. Oceanogr. 2007, 37, 495–517. [Google Scholar] [CrossRef]
- Vazquez-Cuervo, J.; García-Reyes, M.; Gómez-Valdés, J. Identification of Sea Surface Temperature and Sea Surface Salinity Fronts along the California Coast: Application Using Saildrone and Satellite Derived Products. Remote Sens. 2023, 15, 484. [Google Scholar] [CrossRef]
- Huyer, A. Coastal upwelling in the California Current system. Prog. Oceanogr. 1983, 12, 259–284. [Google Scholar] [CrossRef]
- Checkley, D.M., Jr.; Barth, J.A. Barth. Patterns and processes in the California Current System. Prog. Oceanogr. 2009, 83, 49–64. [Google Scholar] [CrossRef]
- Chavez, F.P.; Messié, M. A comparison of eastern boundary upwelling ecosystems. Prog. Oceanogr. 2009, 83, 80–96. [Google Scholar] [CrossRef]
- Koračin, D.; Dorman, C.E.; Lewis, J.M.; Hudson, J.G.; Wilcox, E.M.; Torregrosa, A. Marine fog: A review. Atmos. Res. 2014, 143, 142–175. [Google Scholar] [CrossRef]
- Rykaczewski, R.R.; Checkley, D.M., Jr. Influence of ocean winds on the pelagic ecosystem in upwelling regions. Proc. Natl. Acad. Sci. USA 2008, 105, 1965–1970. [Google Scholar] [CrossRef]
- Bakun, A. Global climate change and intensification of coastal ocean upwelling. Science 1990, 247, 198–201. [Google Scholar] [CrossRef]
- Sydeman, W.J.; García-Reyes, M.; Schoeman, D.S.; Rykaczewski, R.R.; Thompson, S.A.; Black, B.A.; Bograd, S.J. Climate change and wind intensification in coastal upwelling ecosystems. Science 2014, 345, 77–80. [Google Scholar] [CrossRef]
- Rykaczewski, R.R.; Dunne, J.P.; Sydeman, W.J.; García-Reyes, M.; Black, B.A.; Bograd, S.J. Poleward displacement of coastal upwelling-favorable winds in the ocean’s eastern boundary currents through the 21st century. Geophys. Res. Lett. 2015, 42, 6424–6431. [Google Scholar] [CrossRef]
- Quilfen, Y.; Shutler, J.; Piolle, J.F.; Autret, E. Recent trends in the wind-driven California current upwelling system. Remote Sens. Environ. 2021, 261, 112486. [Google Scholar] [CrossRef]
- Bograd, S.J.; Jacox, M.G.; Hazen, E.L.; Lovecchio, E.; Montes, I.; Buil, M.P.; Shannon, L.J.; Sydeman, W.J.; Rykaczewski, R.R. Climate change impacts on eastern boundary upwelling systems. Annu. Rev. Mar. Sci. 2023, 15, 303–328. [Google Scholar] [CrossRef]
- Bustos, D.F.; Narváez, D.A.; Dewitte, B.; Oerder, V.; Vidal, M.; Tapia, F. Revisiting historical trends in the Eastern Boundary Upwelling Systems with a machine learning method. Front. Mar. Sci. 2024, 11, 1446766. [Google Scholar] [CrossRef]
- Bakun, A.; Black, B.A.; Bograd, S.J.; Garcia-Reyes, M.; Miller, A.J.; Rykaczewski, R.R.; Sydeman, W.J. Anticipated effects of climate change on coastal upwelling ecosystems. Curr. Clim. Change Rep. 2015, 1, 85–93. [Google Scholar] [CrossRef]
- García-Reyes, M.; Koval, G.; Sydeman, W.J.; Palacios, D.; Bedriñana-Romano, L.; DeForest, K.; Silva, C.M.; Sepúlveda, M.; Hines, E. Most eastern boundary upwelling regions represent thermal refugia in the age of climate change. Front. Mar. Sci. 2023, 10, 1158472. [Google Scholar] [CrossRef]
- Cayula, J.F.; Cornillon, P. Cloud detection from a sequence of SST images. Remote Sens. Environ. 1996, 55, 80–88. [Google Scholar] [CrossRef]
- Minnett, P.J.; Kilpatrick, K.A.; Podestá, G.P.; Evans, R.H.; Szczodrak, M.D.; Izaguirre, M.A.; Williams, E.J.; Walsh, S.; Reynolds, R.M.; Bailey, S.W.; et al. Skin sea-surface temperature from VIIRS on Suomi-NPP—NASA continuity retrievals. Remote Sens. 2020, 12, 3369. [Google Scholar] [CrossRef]
- Chin, T.M.; Vazquez-Cuervo, J.; Armstrong, E.M. A multi-scale high-resolution analysis of global sea surface temperature. Remote Sens. Environ. 2017, 200, 154–169. [Google Scholar] [CrossRef]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The operational sea surface temperature and sea ice analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- García-Reyes, M.; Largier, J.L. Seasonality of coastal upwelling off central and northern California: New insights, including temporal and spatial variability. J. Geophys. Res. Ocean. 2012, 117, C03028. [Google Scholar] [CrossRef]
- García-Reyes, M.; Largier, J. Observations of increased wind-driven coastal upwelling off central California. J. Geophys. Res. Ocean 2010, 115, C04011. [Google Scholar] [CrossRef]
- Meneghesso, C.; Seabra, R.; Broitman, B.R.; Wethey, D.S.; Burrows, M.T.; Chan, B.K.; Guy-Haim, T.; Ribeiro, P.A.; Rilov, G.; Santos, A.M.; et al. Remotely-sensed L4 SST underestimates the thermal fingerprint of coastal upwelling. Remote Sens. Environ. 2020, 237, 111588. [Google Scholar] [CrossRef]
- Jacox, M.G.; Moore, A.M.; Edwards, C.A.; Fiechter, J. Spatially resolved upwelling in the California Current System and its connections to climate variability. Geophys. Res. Lett. 2014, 41, 3189–3196. [Google Scholar] [CrossRef]
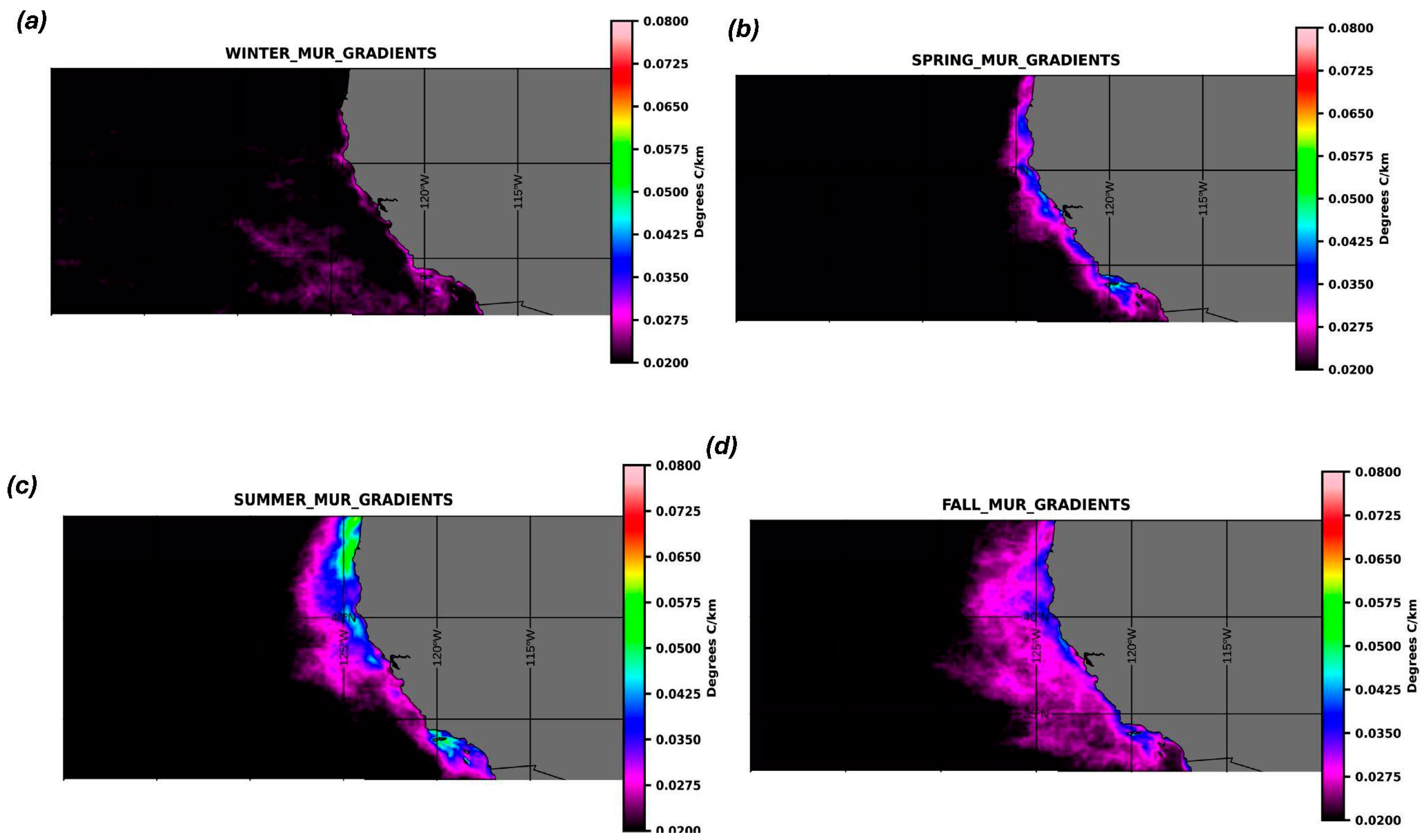
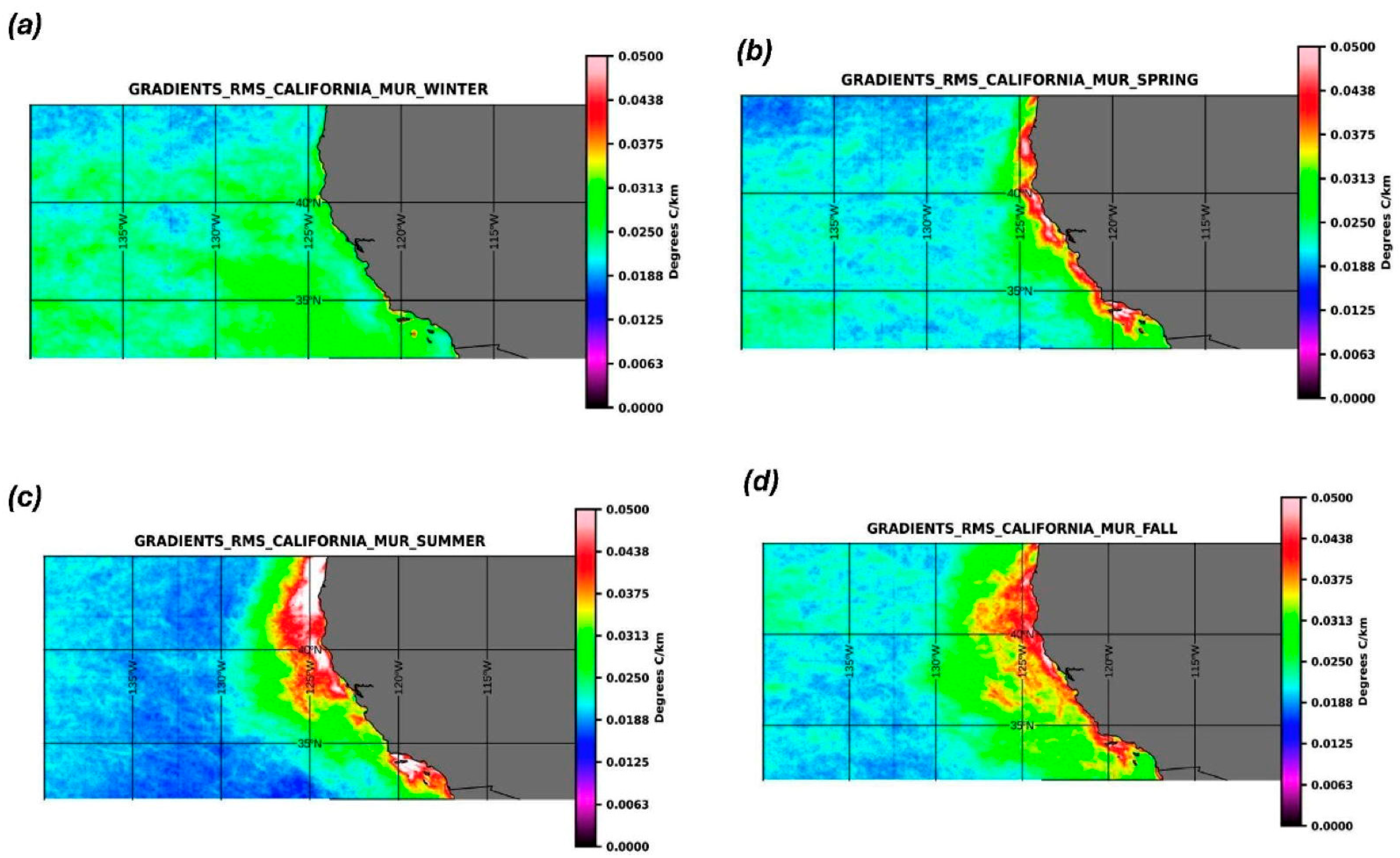
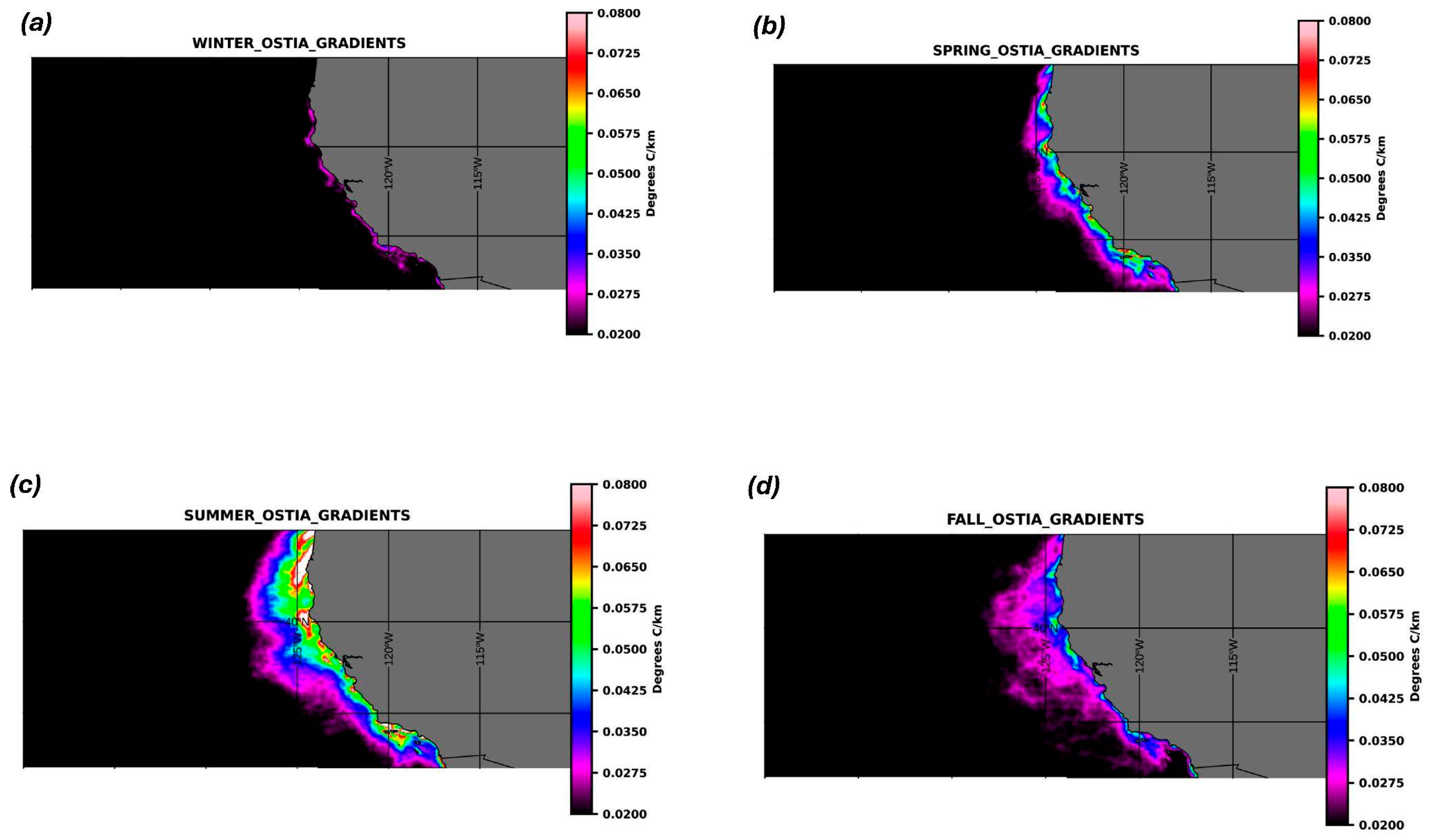
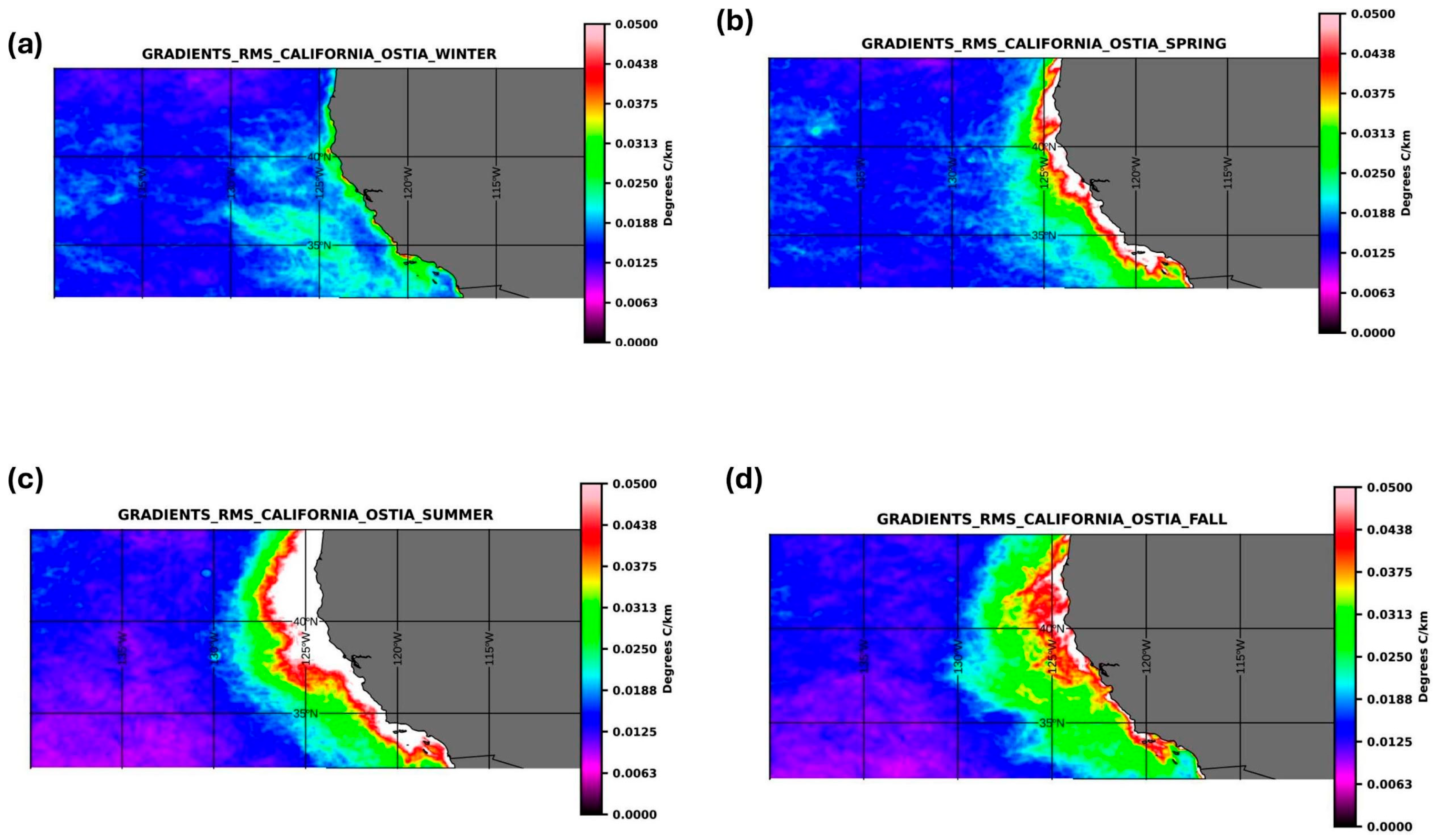



| Season | OSTIA (°C/km) | MUR (°C/km) |
|---|---|---|
| Winter | 0.0379 | 0.0363 |
| Spring | 0.0913 | 0.0512 |
| Summer | 0.1115 | 0.0602 |
| Fall | 0.0690 | 0.0470 |
| MEAN | Nearest Neighbor | |
|---|---|---|
| Mean OSTIA (°C) | 0.013 | 0.013 |
| Mean MUR (°C) | 0.016 | 0.016 |
| RMS OSTIA (°C) | 0.014 | 0.014 |
| RMS MUR (°C) | 0.014 | 0.014 |
| Bias (°C) | 0.002 | 0.002 |
| Correlation | 0.63 | 0.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vazquez-Cuervo, J.; García-Reyes, M.; Wethey, D.S.; Ciani, D.; Gomez-Valdes, J. Application and Comparison of Satellite-Derived Sea Surface Temperature Gradients to Identify Seasonal and Interannual Variability off the California Coast: Preliminary Results and Future Perspectives. Remote Sens. 2025, 17, 2722. https://doi.org/10.3390/rs17152722
Vazquez-Cuervo J, García-Reyes M, Wethey DS, Ciani D, Gomez-Valdes J. Application and Comparison of Satellite-Derived Sea Surface Temperature Gradients to Identify Seasonal and Interannual Variability off the California Coast: Preliminary Results and Future Perspectives. Remote Sensing. 2025; 17(15):2722. https://doi.org/10.3390/rs17152722
Chicago/Turabian StyleVazquez-Cuervo, Jorge, Marisol García-Reyes, David S. Wethey, Daniele Ciani, and Jose Gomez-Valdes. 2025. "Application and Comparison of Satellite-Derived Sea Surface Temperature Gradients to Identify Seasonal and Interannual Variability off the California Coast: Preliminary Results and Future Perspectives" Remote Sensing 17, no. 15: 2722. https://doi.org/10.3390/rs17152722
APA StyleVazquez-Cuervo, J., García-Reyes, M., Wethey, D. S., Ciani, D., & Gomez-Valdes, J. (2025). Application and Comparison of Satellite-Derived Sea Surface Temperature Gradients to Identify Seasonal and Interannual Variability off the California Coast: Preliminary Results and Future Perspectives. Remote Sensing, 17(15), 2722. https://doi.org/10.3390/rs17152722









