An Underground Goaf Locating Framework Based on D-InSAR with Three Different Prior Geological Information Conditions
Abstract
1. Introduction
2. Study Area and Datasets
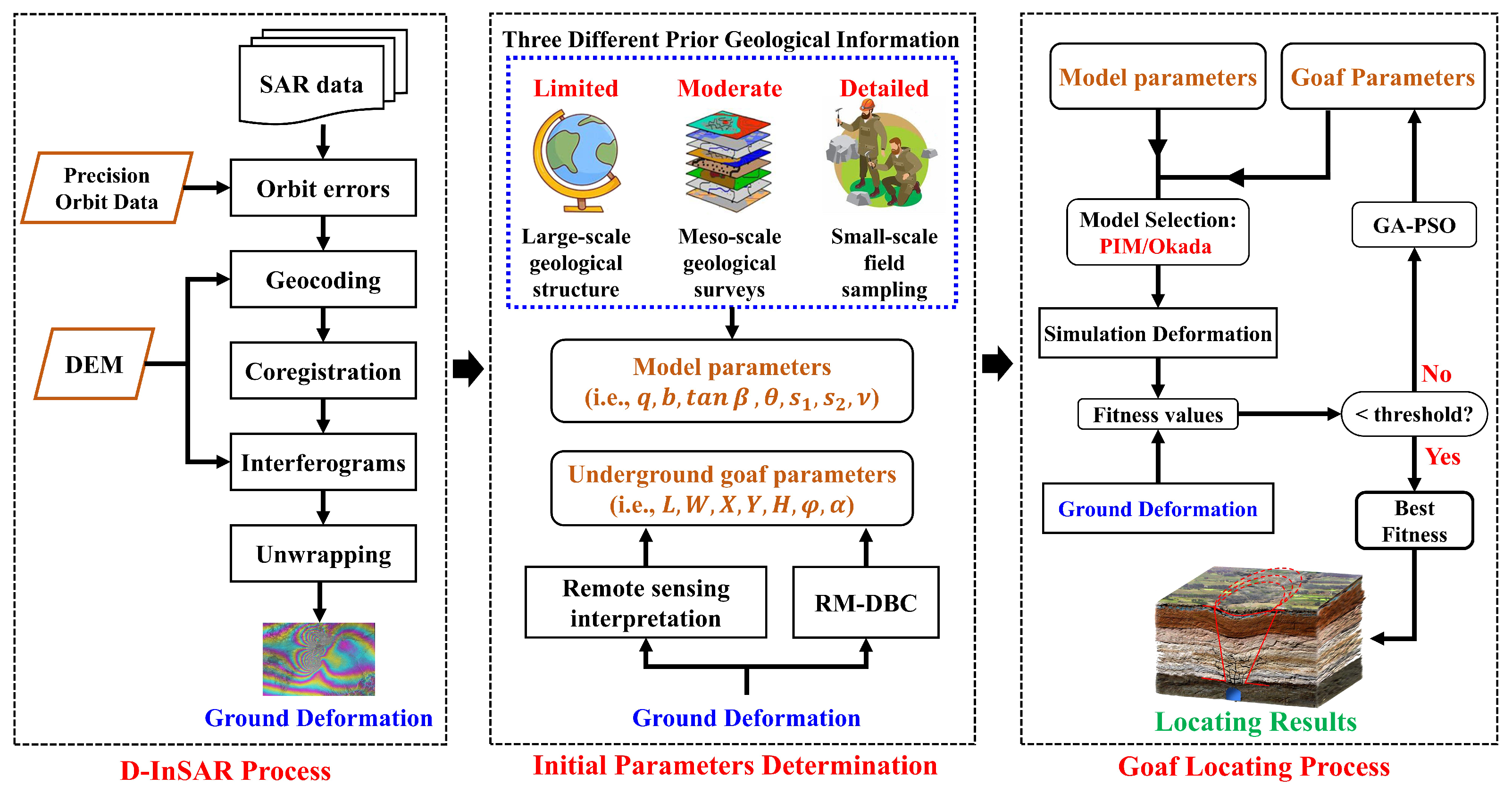
3. Technical Principles
- Time-series line-of-sight (LOS) deformation retrieval through D-InSAR process (Differential Interferometric Synthetic Aperture Radar);
- Model parameter definition under three different prior geological information conditions (detailed/moderate/limited);
- Use the RM-DBC for estimating azimuth and establishing constraint boundaries of PIM and ODM;
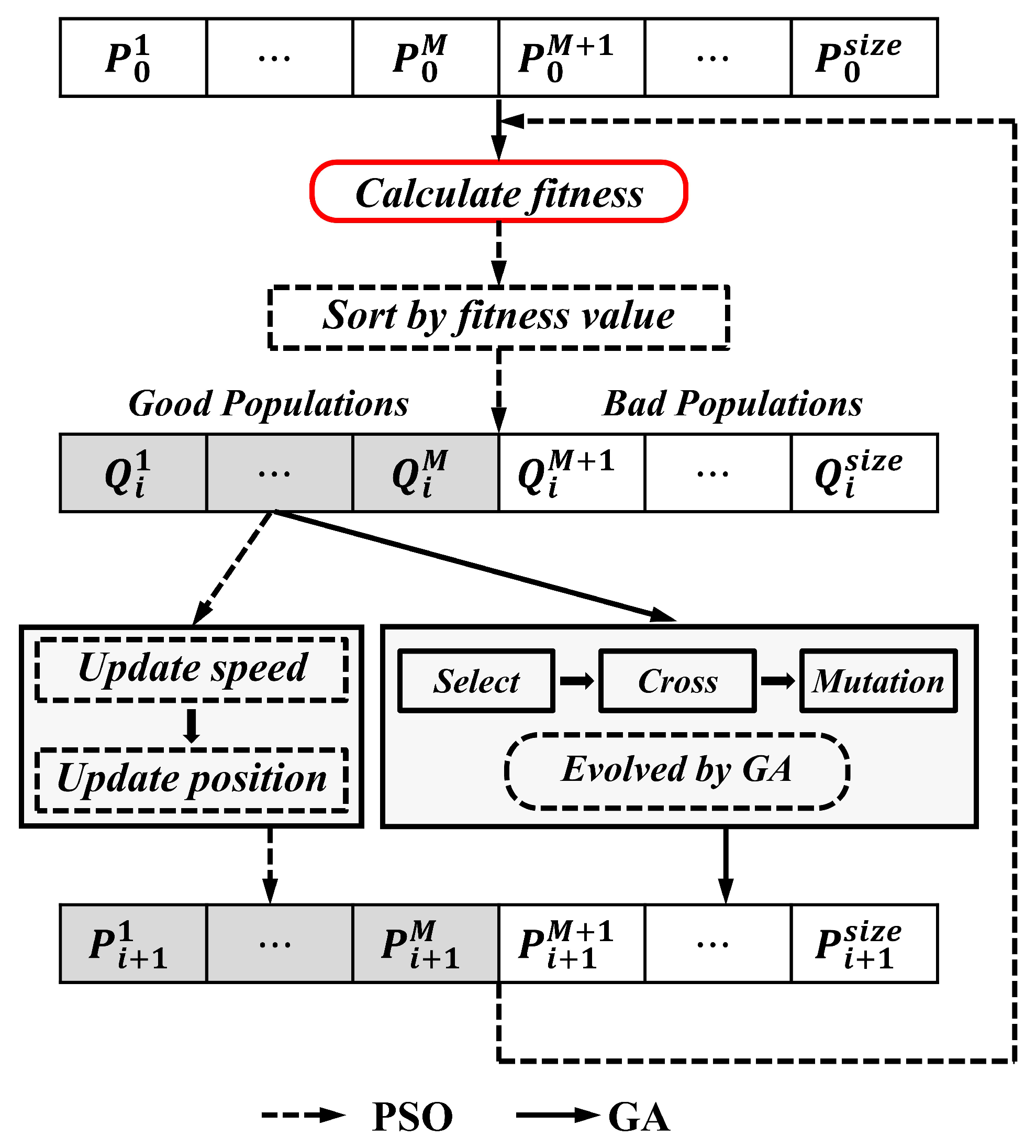
- Estimate other parameters by using the GA-PSO algorithm to estimate goaf parameters.
3.1. Differential InSAR
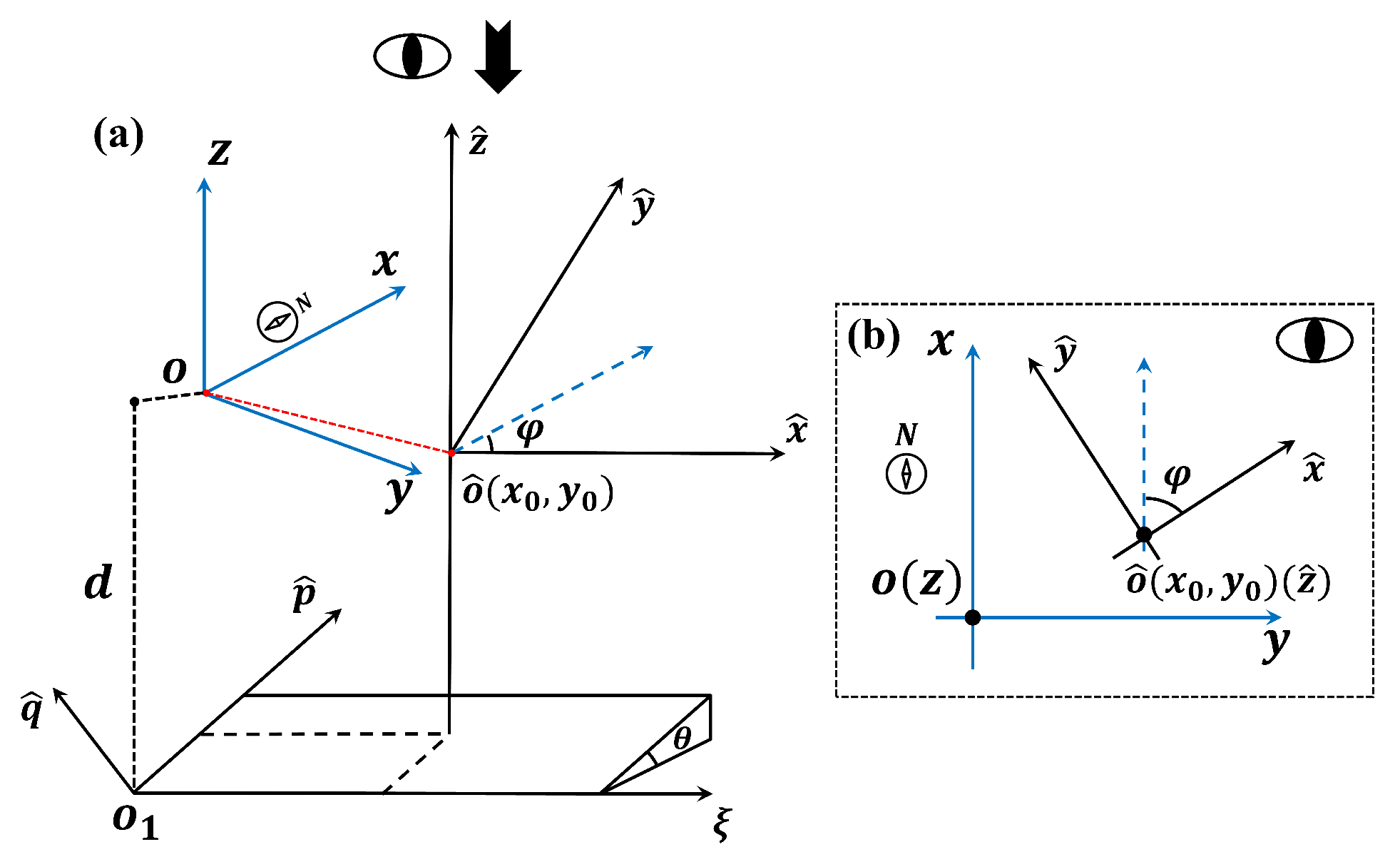
3.2. Probability Integral Model
3.3. Okada Dislocation Model
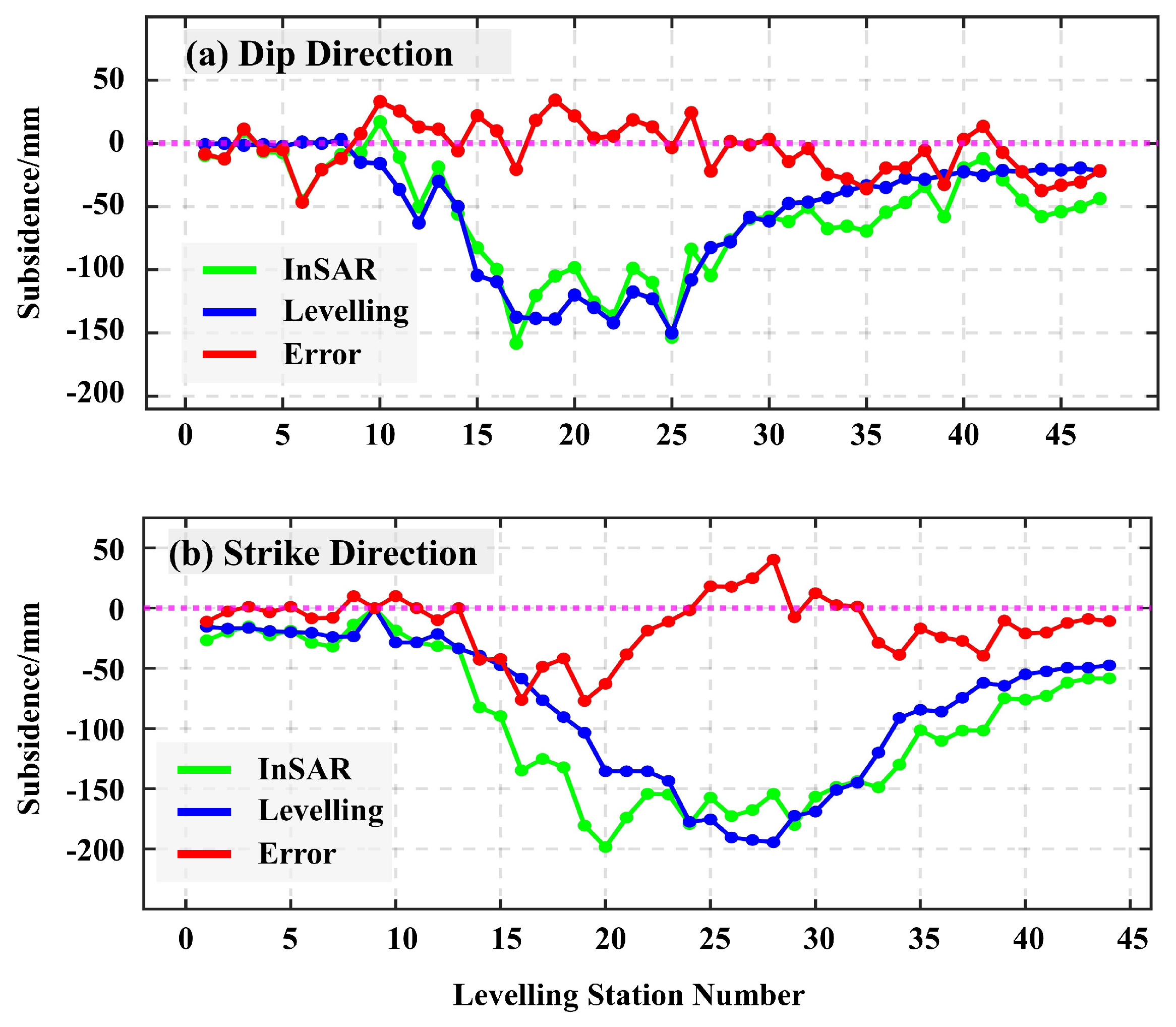
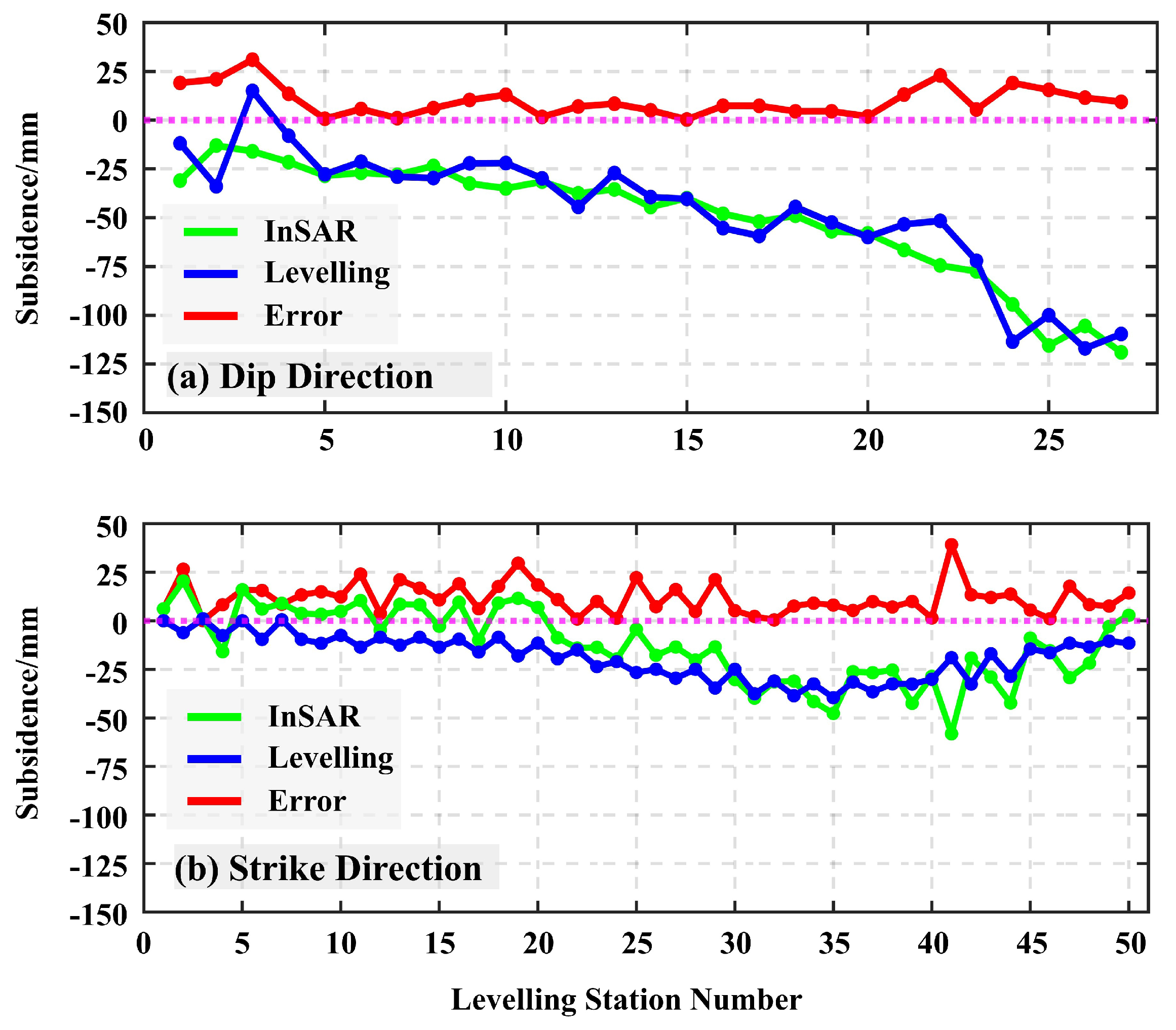
3.4. Underground Goaf Locating
3.4.1. Geologic Parameter Acquisition
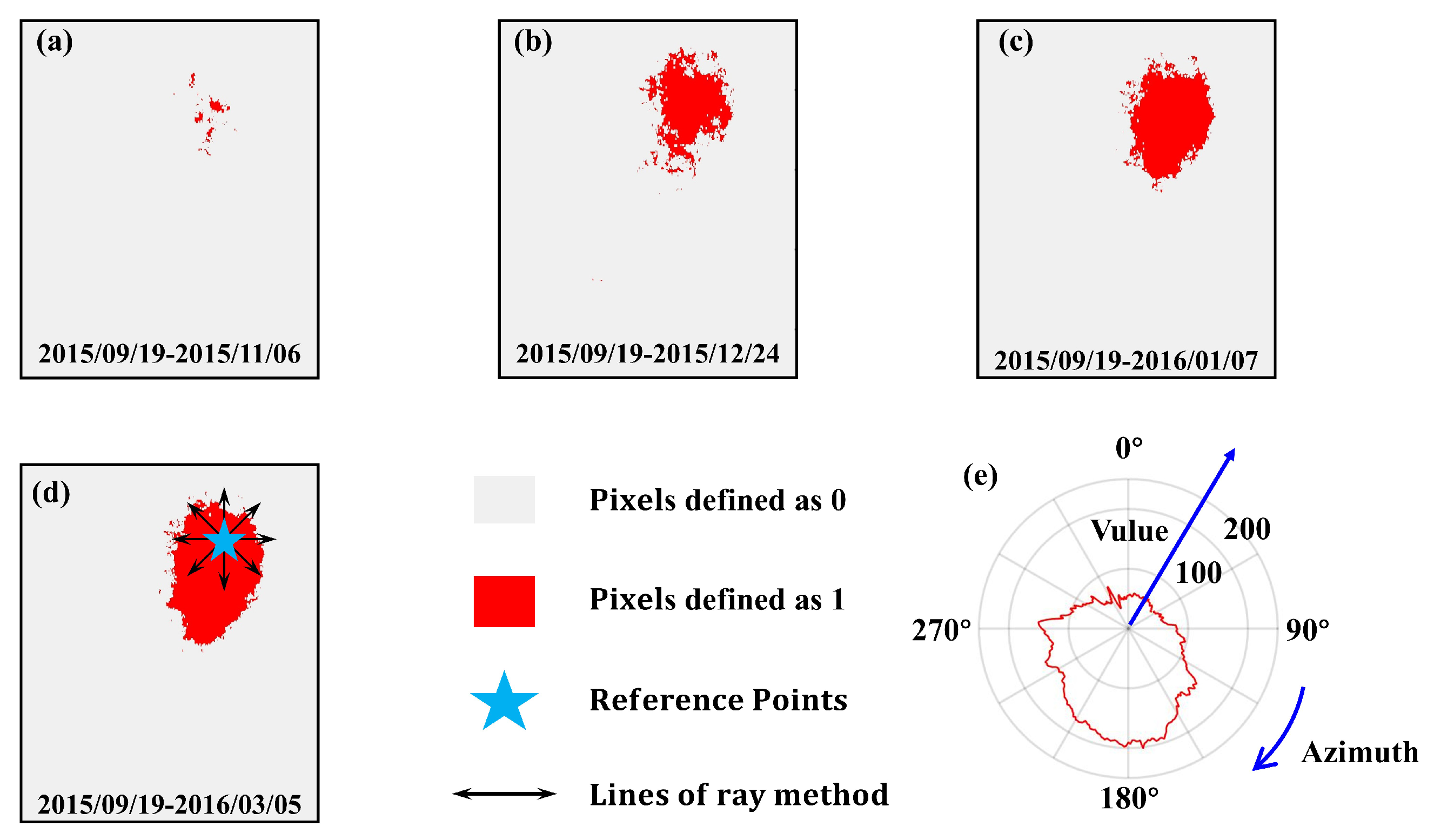
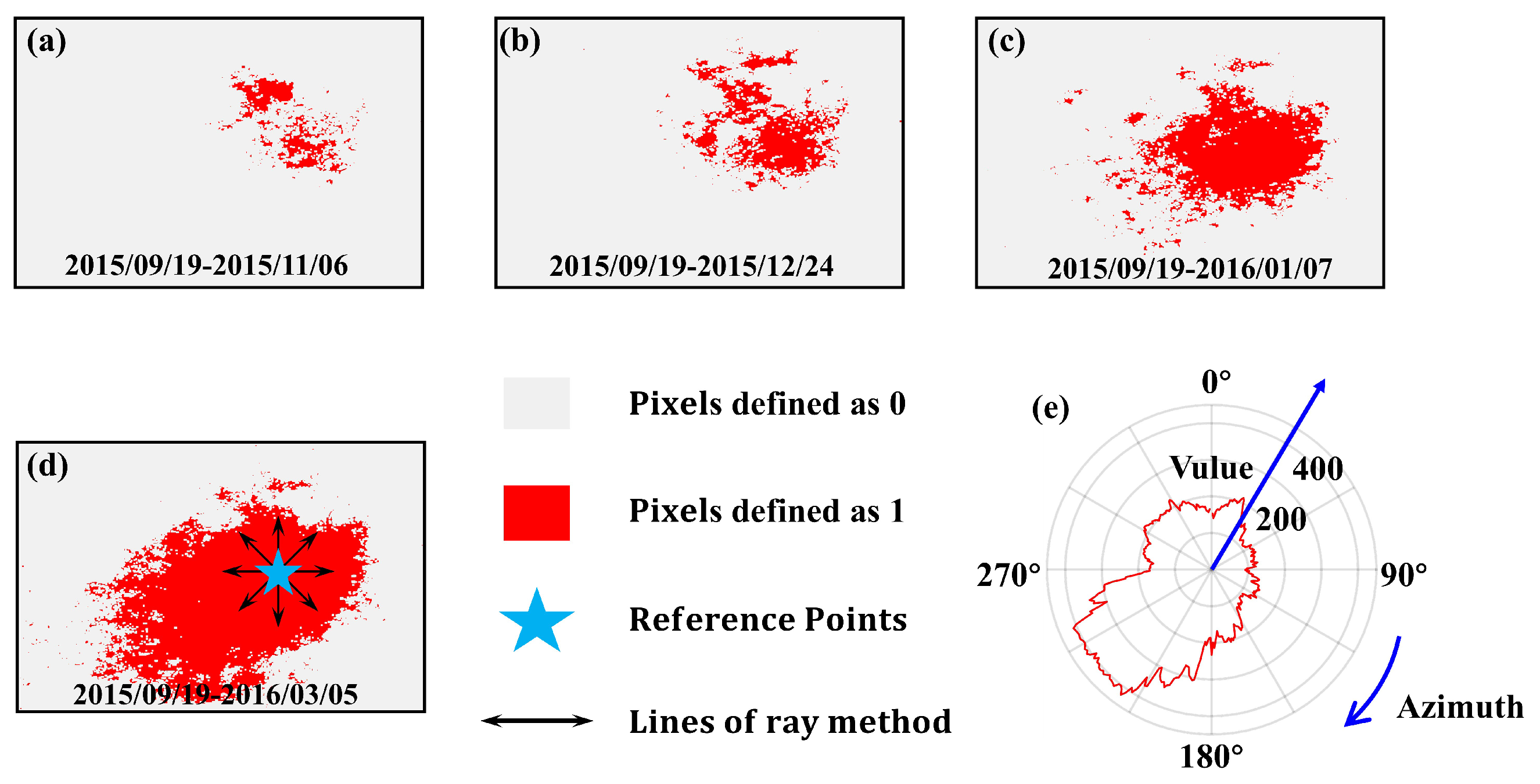
3.4.2. Mining Azimuth Estimation
- Select a stable region (considered to be deformation-free) from the InSAR-derived accumulated deformation results, and establish adaptive thresholds according to the average value of this region;
- Convert LOS displacement maps into binary matrices based on the thresholds to highlight subsidence features;
- Define the the maximum subsidence point as the origin, and then 1°-stepped ray projections from the origin point were applied for accumulating activated pixel counts along each azimuthal path;
- The direction with the highest sum of pixel values is regarded as the azimuth angle.
3.4.3. Goaf Parameters Estimation
4. Results Analysis
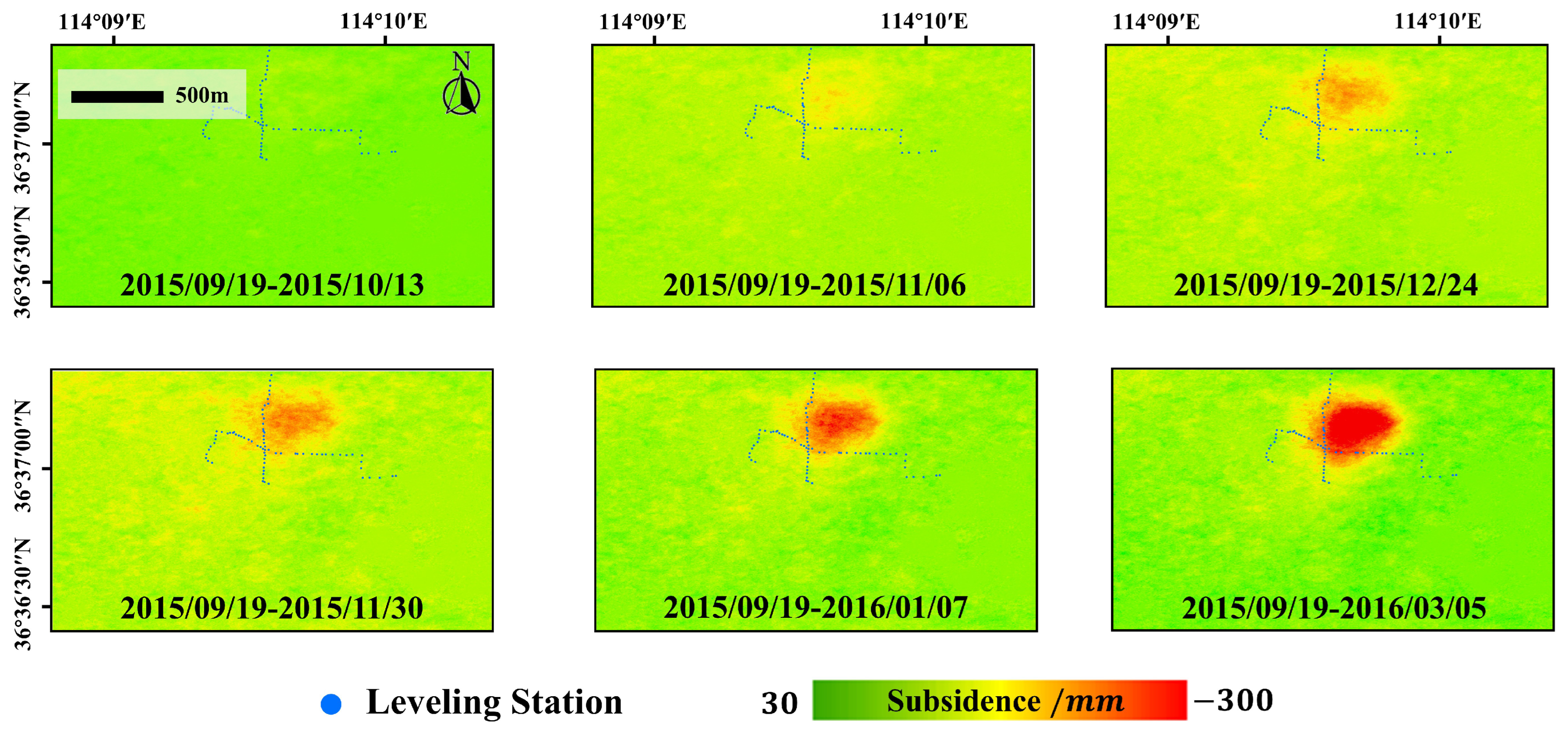
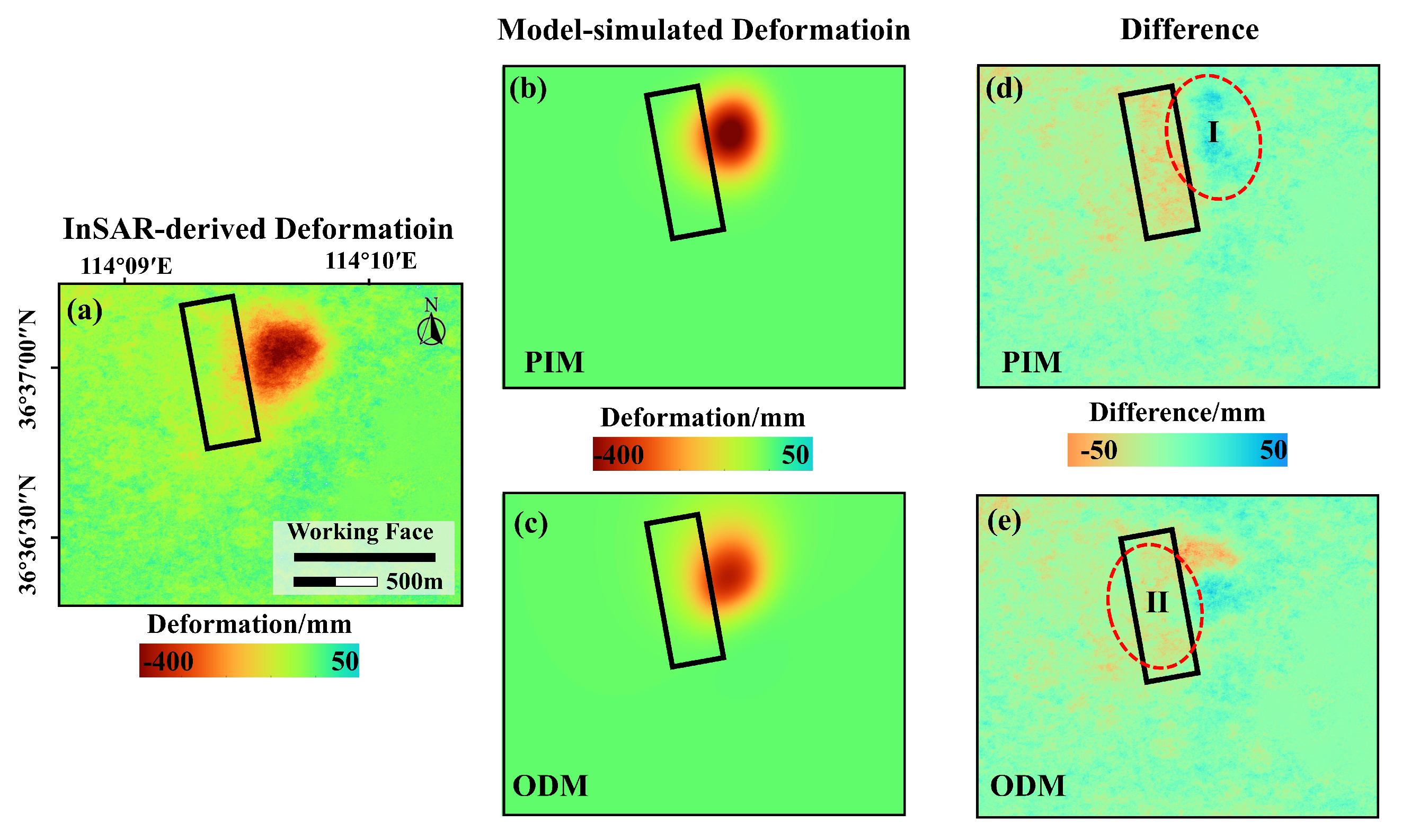
4.1. InSAR-Derived Deformation Result
4.2. Azimuth Estimation and Model Parameters Selection
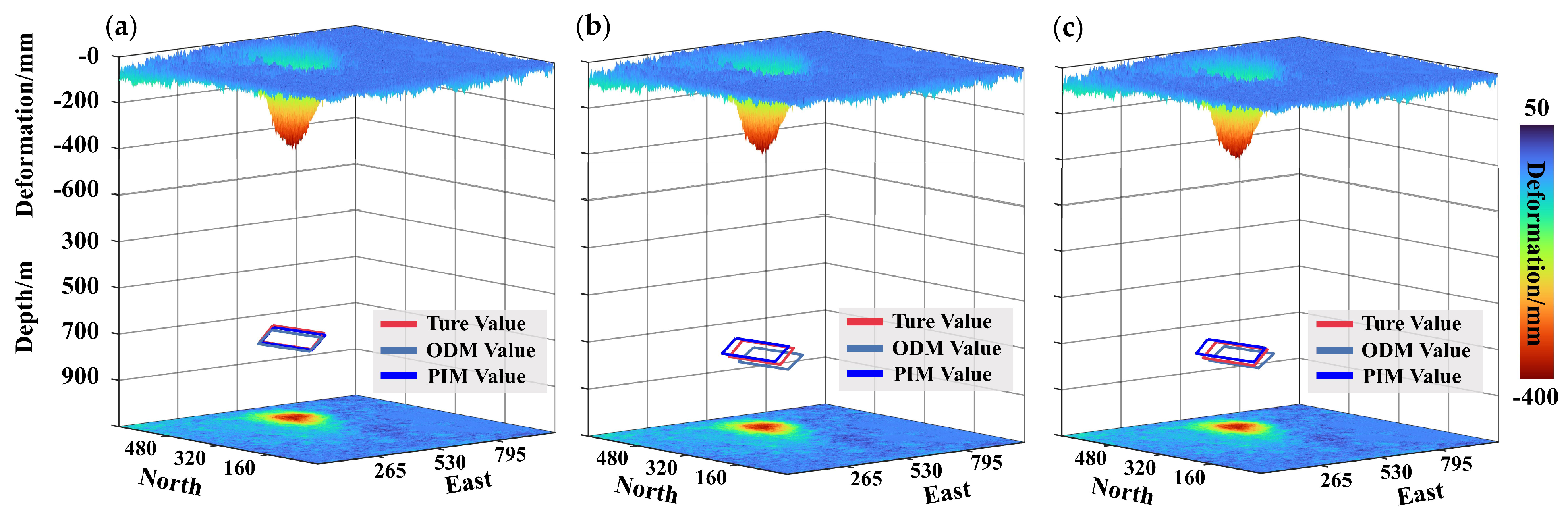
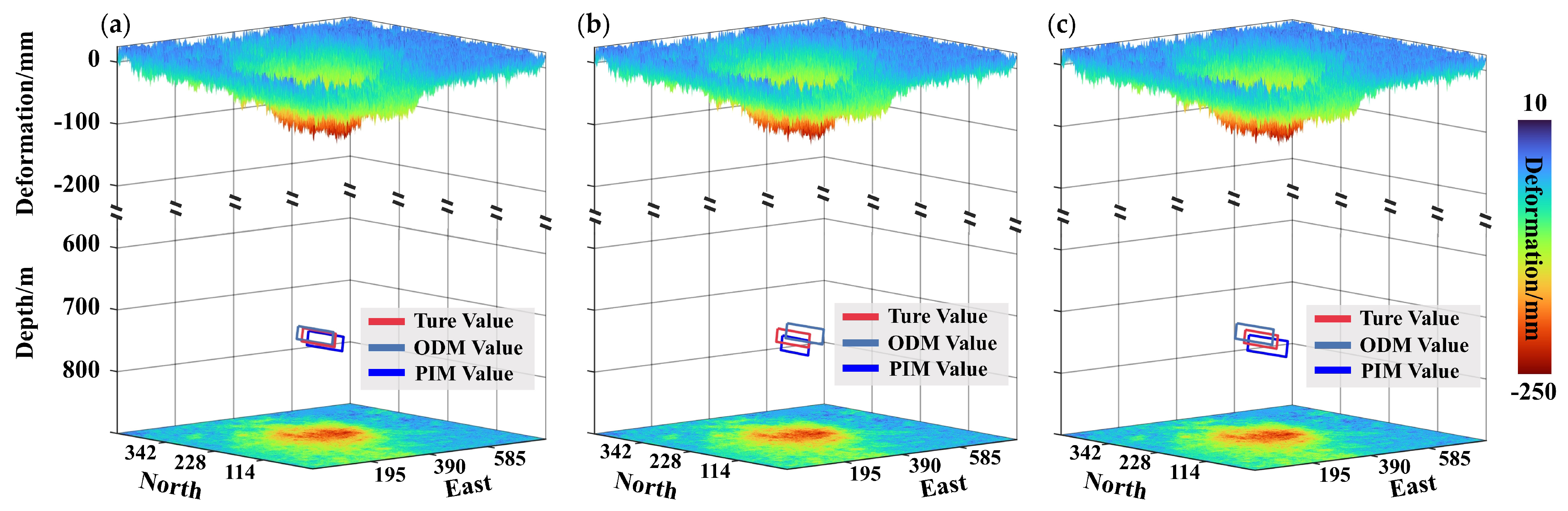
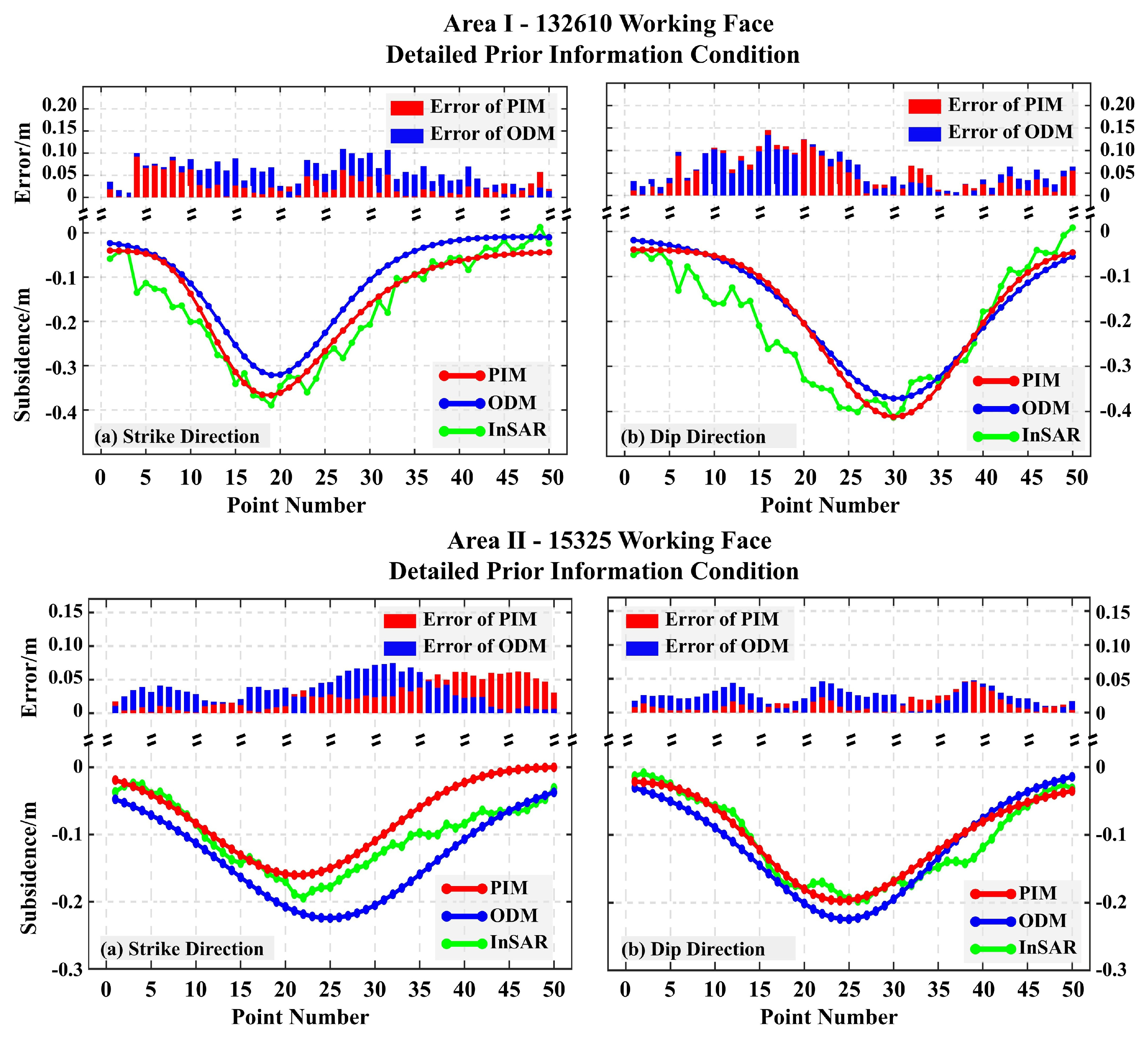
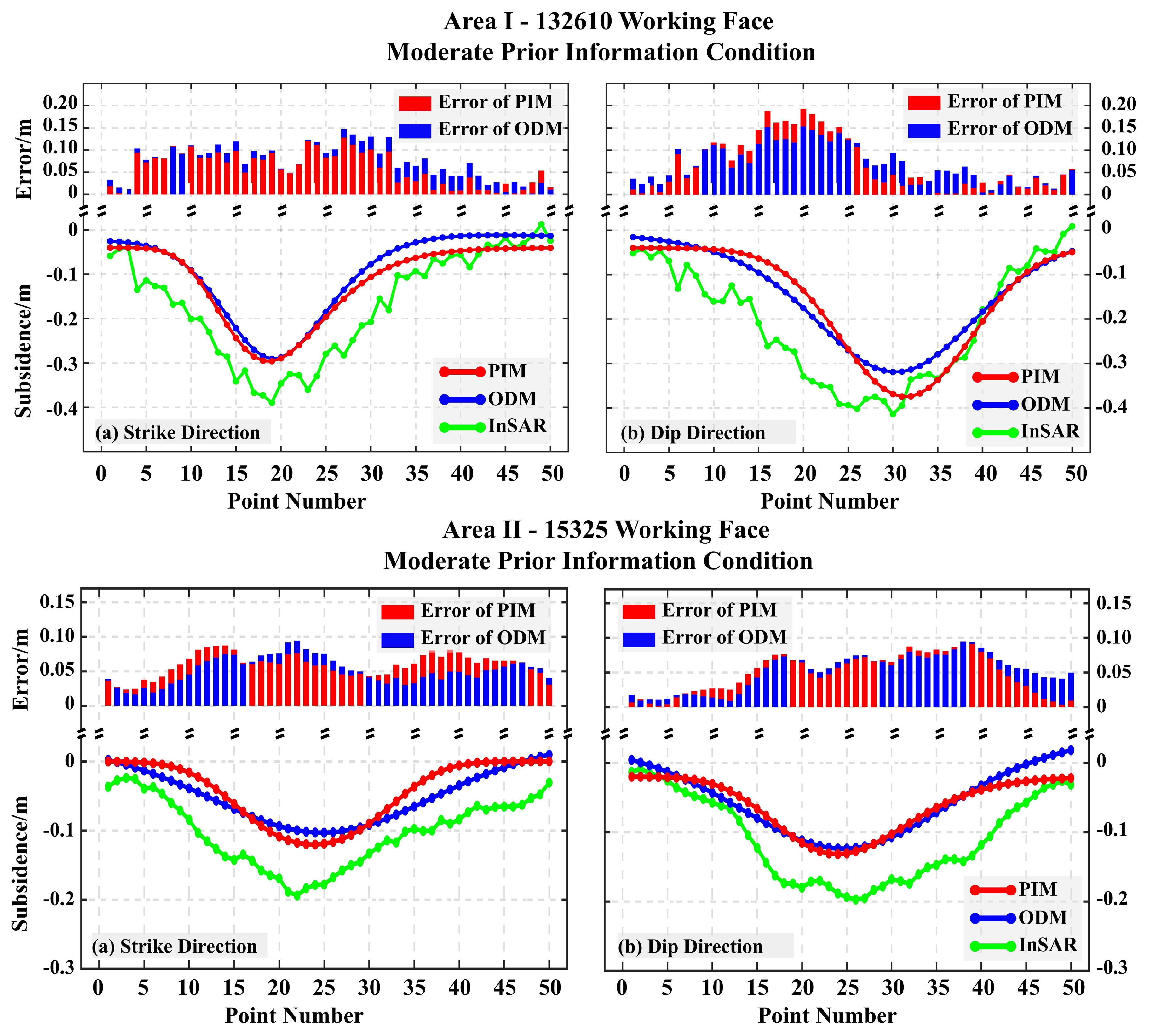
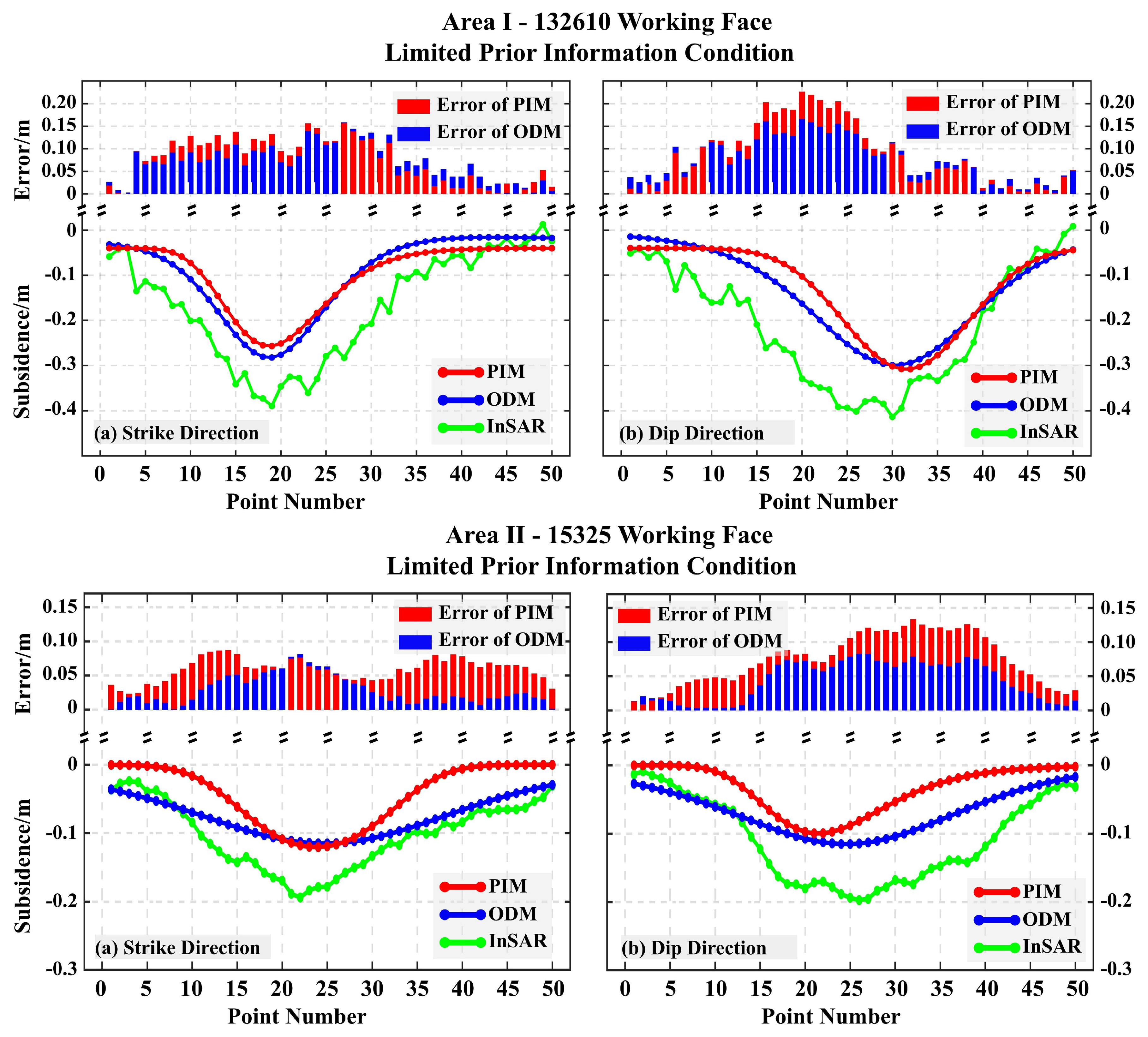
4.3. Goaf Locating Under Different Priori Information
5. Discussion
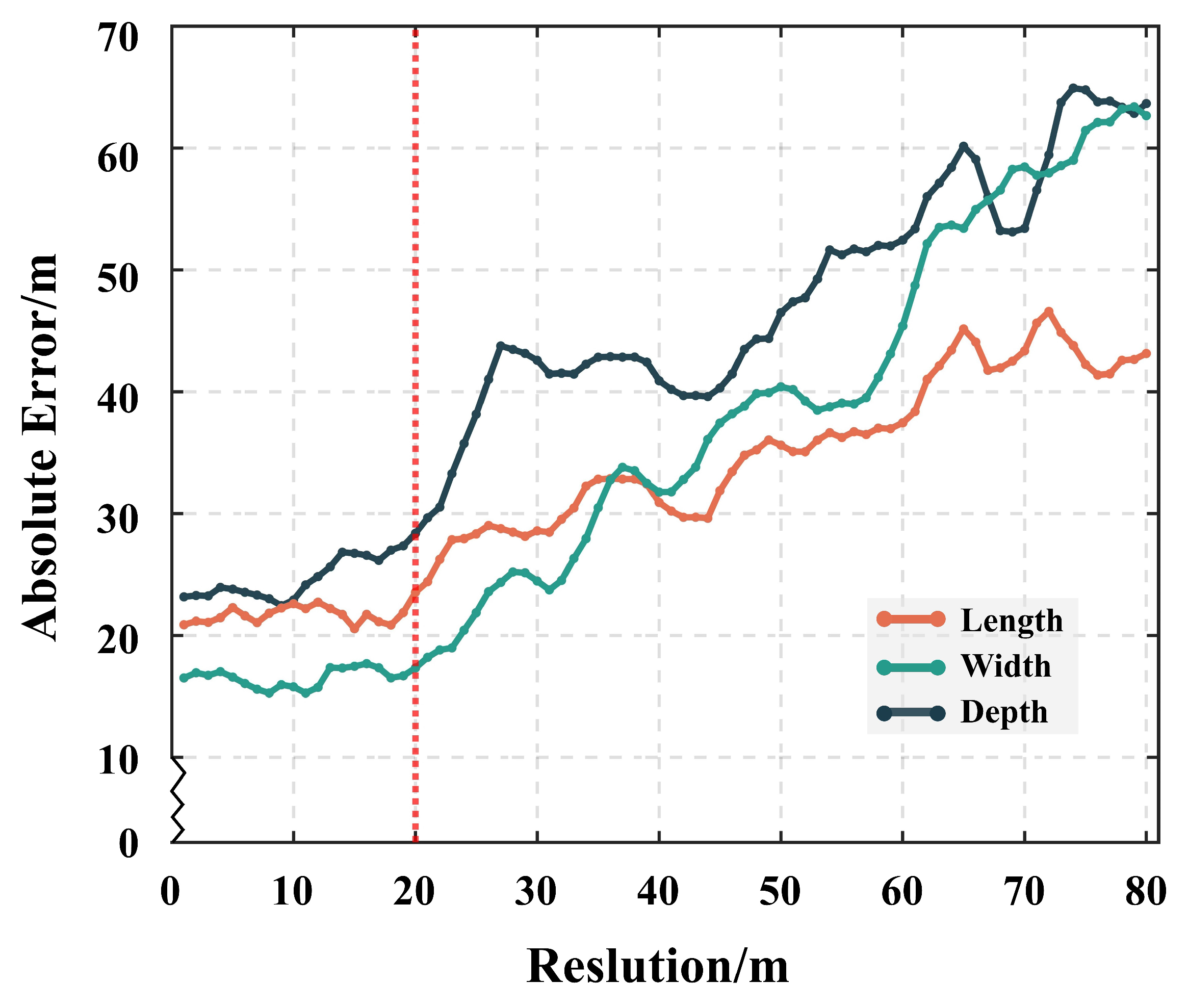
5.1. Impact of SAR Spatial Resolution on Goaf Locating Accuracy
5.2. Influence of Determining Azimuth in Advance
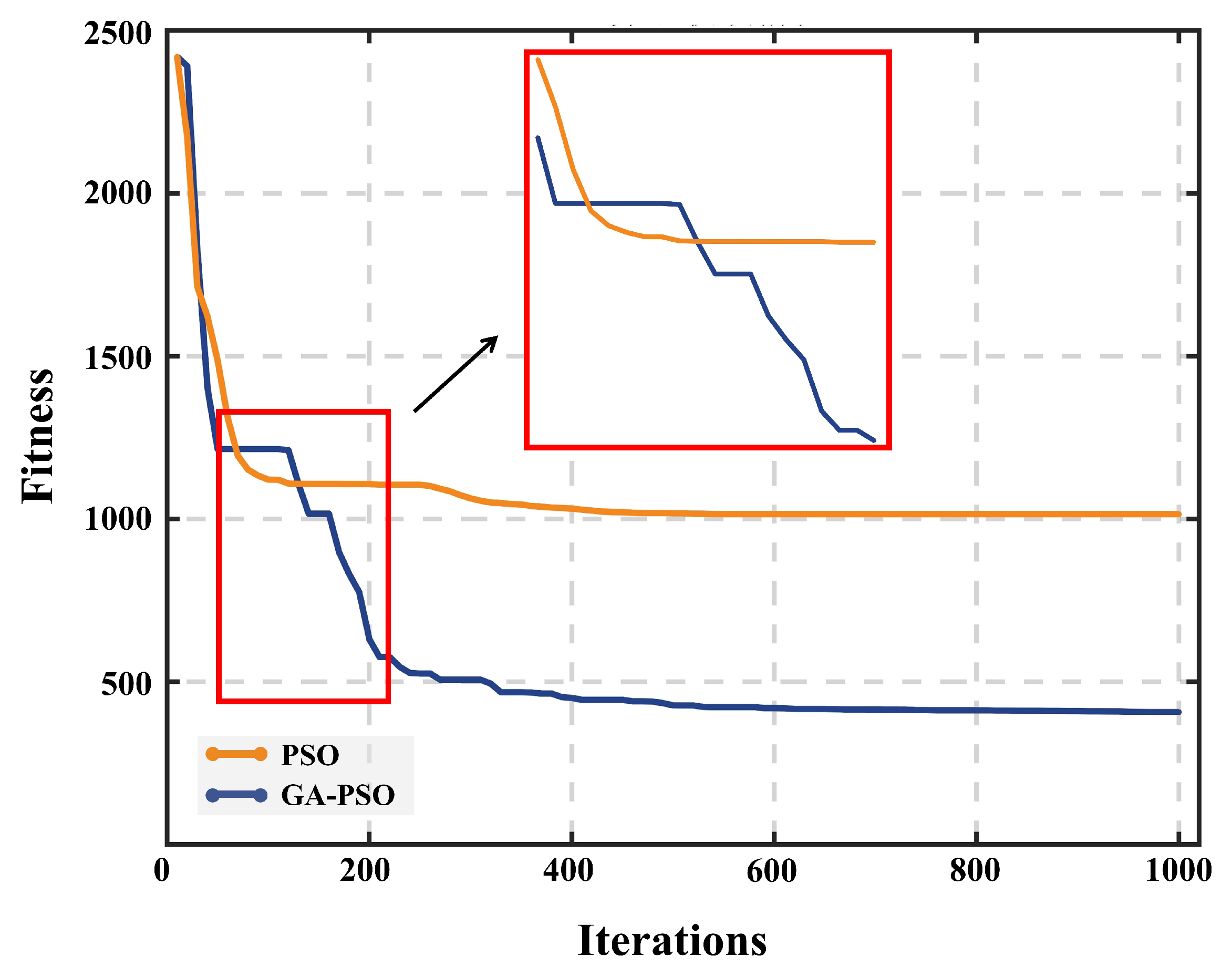
5.3. Comparisons of Non-Hybrid and Hybrid Optimization Algorithms
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- The Energy Institute. Statistical Review of World Energy; The Energy Institute: London, UK, 2024. [Google Scholar]
- Xia, Y. Research on the Key Technologies of InSAR/GIS Monitoring for Illegal Underground Mining in Coal Mining Area. Ph.D Thesis, China University of Mining and Technology, Xuzhou, China, 2020. [Google Scholar]
- Fan, H.D.; Cheng, D.; Deng, K.Z.; Chen, B.Q.; Zhu, C.G. Subsidence monitoring using D-InSAR and probability integral prediction modelling in deep mining areas. Emp. Surv. Rev. 2015, 47, 438–445. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Wang, Y.; Wu, L. Use of SAR/InSAR in mining deformation monitoring, parameter inversion, and forward predictions: A review. IEEE Geosci. Remote Sens. Mag. 2020, 8, 71–90. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Fan, H.; Zheng, C.; Liu, J. Position inversion of goafs in deep coal seams based on DS-InSAR data and the probability integral methods. Remote Sens. 2021, 13, 2898. [Google Scholar] [CrossRef]
- Maus, V.; Werner, T.T. Impacts for half of the world’s mining areas are undocumented. Nature 2024, 625, 26–29. [Google Scholar] [CrossRef] [PubMed]
- Zahorec, P.; Pašteka, R.; Papčo, J.; Putiška, R.; Mojzeš, A.; Kušnirák, D.; Plakinger, M. Mapping hazardous cavities over collapsed coal mines: Case study experiences using the microgravity method. Near Surf. Geophys. 2021, 19, 353–364. [Google Scholar] [CrossRef]
- Chang, J.; Su, B.; Malekian, R.; Xing, X. Detection of water-filled mining goaf using mining transient electromagnetic method. IEEE Trans. Ind. Inform. 2019, 16, 2977–2984. [Google Scholar] [CrossRef]
- Zhu, J.; Li, Z.; Hu, J. Research Progress and Methods of InSAR for Deformation Monitoring. Acta Geod. Cartogr. Sin. 2017, 46, 1717–1733. [Google Scholar] [CrossRef]
- Gao, H.; Liao, M.; Liu, X.; Xu, W.; Fang, N. Source geometry and causes of the 2019 Ms6. 0 Changning earthquake in Sichuan, China based on InSAR. Remote Sens. 2022, 14, 2082. [Google Scholar] [CrossRef]
- Anantrasirichai, N.; Biggs, J.; Albino, F.; Bull, D. A deep learning approach to detecting volcano deformation from satellite imagery using synthetic datasets. Remote Sens. Environ. 2019, 230, 111179. [Google Scholar] [CrossRef]
- Cai, J.; Liu, G.; Jia, H.; Zhang, B.; Wu, R.; Fu, Y.; Xiang, W.; Mao, W.; Wang, X.; Zhang, R. A new algorithm for landslide dynamic monitoring with high temporal resolution by Kalman filter integration of multiplatform time-series InSAR processing. Int. J. Appl. Earth Obs. Geoinf. 2022, 110, 102812. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Y.; Zhao, F.; Wang, T.; Zhang, K.; Fan, H.; Zhou, D.; Zhang, L.; Yan, S.; Diao, X.; et al. Monitoring and Analysis of the Collapse at Xinjing Open-Pit Mine, Inner Mongolia, China, Using Multi-Source Remote Sensing. Remote Sens. 2024, 16, 993. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Yan, S.; Shao, Y.; Zhou, H.; Li, Y. Ground subsidence characteristics associated with urbanization in East China analyzed with a Sentinel-1A-based InSAR time series approach. Bull. Eng. Geol. Environ. 2019, 78, 4003–4015. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Huo, W.; Zhao, F.; Hu, Z.; Wang, T.; Song, R.; Liu, J.; Zhang, L.; Fernández, J.; et al. Ground Deformation Monitoring over Xinjiang Coal Fire Area by an Adaptive ERA5-Corrected Stacking-InSAR Method. Remote Sens. 2023, 15, 1444. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, G.; Wang, T.; Liu, J.; Zhao, F.; Feng, H.; Dang, L.; Peng, K.; Zhang, L. Research on Multi-source Remote Sensing Detection of Concealed Fire Sources in Coalfields. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 1651–1661. [Google Scholar] [CrossRef]
- Hu, Z.; Ge, L.; Li, X.; Zhang, K.; Zhang, L. An underground-mining detection system based on DInSAR. IEEE Trans. Geosci. Remote Sens. 2012, 51, 615–625. [Google Scholar] [CrossRef]
- Du, S.; Wang, Y.; Zheng, M.; Zhou, D.; Xia, Y. Goaf locating based on InSAR and probability integration method. Remote Sens. 2019, 11, 812. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Yi, H.; Feng, G.; Hu, J.; Wu, L.; Preusse, A.; Wang, Y.; Papst, M. Locating and defining underground goaf caused by coal mining from space-borne SAR interferometry. ISPRS J. Photogramm. Remote Sens. 2018, 135, 112–126. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, F.; Wang, Y.; Zhang, N.; Zhou, D.; Diao, X.; Zhao, X. An Algorithm for Locating Subcritical Underground Goaf Based on InSAR Technique and Improved Probability Integral Model. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5214914. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Y.; Du, S.; Zhao, F.; Wang, T.; Zhang, N.; Zhou, D.; Diao, X. A Goaf-Locating Method Based on the D-InSAR Technique and Stratified Okada Dislocation Model. Remote Sens. 2024, 16, 2741. [Google Scholar] [CrossRef]
- He, L.; Wang, X.; Liu, C.; Tang, Y.; Zhang, X.; Kang, J.; Guo, C.; He, R. Time series interferometric synthetic aperture radar-based modeling and analysis of complex land subsidence caused by multi-seam coal mining on the Liaohe Plain, China. J. Appl. Remote Sens. 2022, 16, 024512. [Google Scholar] [CrossRef]
- Wang, R.; Wu, K.; He, Q.; He, Y.; Gu, Y.; Wu, S. A novel method of monitoring surface subsidence law based on probability integral model combined with active and passive remote sensing data. Remote Sens. 2022, 14, 299. [Google Scholar] [CrossRef]
- Kinoshita, Y.; Furuta, R. Slow slip event displacement on 2018 offshore Boso Peninsula detected by Sentinel-1 InSAR time-series analysis with numerical weather model assistance. Geophys. J. Int. 2024, 237, 75–89. [Google Scholar] [CrossRef]
- Sheikhalishahi, M.; Ebrahimipour, V.; Shiri, H.; Zaman, H.; Jeihoonian, M. A hybrid GA–PSO approach for reliability optimization in redundancy allocation problem. Int. J. Adv. Manuf. Technol. 2013, 68, 317–338. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent scatterer interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Zheng, M.; Deng, K.; Fan, H.; Du, S. Monitoring and analysis of surface deformation in mining area based on InSAR and GRACE. Remote Sens. 2018, 10, 1392. [Google Scholar] [CrossRef]
- Aspri, A.; Beretta, E.; Mazzucato, A.L.; De Hoop, M.V. Analysis of a model of elastic dislocations in geophysics. Arch. Ration. Mech. Anal. 2020, 236, 71–111. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar] [CrossRef]


| Interferogram Pairs | Spatial Baseline | Time Baseline |
|---|---|---|
| 20151013–20151106 | 47.1835 m | 24 d |
| 20151106–20151130 | 3.8988 m | 24 d |
| 20151130–20151224 | 13.3323 m | 24 d |
| 20151224–20160117 | −43.7693 m | 24 d |
| 20160117–20160305 | −37.7825 m | 48 d |
| Rock Properties | Rock Category | Q | Poisson’s Ratio |
|---|---|---|---|
| soft | topsoil/loam | 1 | 0.35–0.5 |
| medium soft | sandy mudstone/mudstone | 0.6 | 0.25–0.35 |
| medium hard | medium sandstone/siltstone | 0.4 | 0.15–0.25 |
| hard | granite/fine-grained sandstone | 0.2 | 0.1–0.15 |
| soft | P | 0.00 | 0.03 | 0.07 | 0.11 | 0.15 | 0.19 | 0.23 | 0.27 | 0.3 |
| 0.76 | 0.82 | 0.88 | 0.95 | 1.01 | 1.08 | 1.14 | 1.20 | 1.25 | ||
| medium hard | P | 0.3 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 | 0.65 | 0.70 |
| 1.26 | 1.35 | 1.45 | 1.54 | 1.64 | 1.73 | 1.82 | 1.91 | 2.00 | ||
| hard | P | 0.70 | 0.75 | 0.80 | 0.85 | 0.910 | 0.95 | 1.00 | 1.05 | 1.10 |
| 2.00 | 2.10 | 2.20 | 2.30 | 2.40 | 2.50 | 2.60 | 2.70 | 2.80 |
| Rock Properties | Thickness | p | q | Poisson’s Ratio |
|---|---|---|---|---|
| soft | 20 m | 0.03 | 0.465 | 0.4 |
| medium hard | 400 m | 0.22 | 0.56 | 0.18 |
| hard | 344/320 m | 0.12 | 0.51 | 0.12 |
| - | True | Detailed | Moderate | Limited | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PIM | ODM | Error (abs) | Error (rel) | PIM | ODM | Error (abs) | Error (rel) | PIM | ODM | Error (abs) | Error (rel) | ||||
| L | 291 | 314 | 321 | 23/30 | 7.9/10.3% | 328 | 330 | 37/39 | 12.7/13.1% | 343 | 252 | 52/39 | 17.8/13.4% | ||
| W | 165 | 174 | 181 | 9/16 | 5.3/9.5% | 183 | 180 | 18/15 | 10.9/9.1% | 140 | 148 | 25/22 | 15.1/13.3% | ||
| D | 774 | 774 | 774 | 0 | 0 | 752 | 801 | 22/27 | 2.9/3.5% | 728 | 195 | 46/21 | 5.9/2.7% | ||
| X | 563 | 568 | 570 | 18.03 m /25.24 m | – | 556 | 570 | 19.43 m /27.47 m | – | 553 | 559 | 23.36 m /14.42 m | – | ||
| Y | 480 | 475 | 473 | 484 | 472 | 482 | 476 | ||||||||
| 31° | 28° | 33° | 3/2° | – | 37° | 32° | 6/4° | – | 35° | 42° | 4/11° | – | |||
| 169° | 167° | 167° | 2° | – | 167° | 167° | 2° | – | 167° | 167° | 2° | – | |||
| - | True | Detailed | Moderate | Limited | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PIM | ODM | Error (abs) | Error (rel) | PIM | ODM | Error (abs) | Error (rel) | PIM | ODM | Error (abs) | Error (rel) | ||||
| L | 493 | 469 | 541 | 24/48 | 4.9/9.7% | 553 | 544 | 60/51 | 12.2/10.3% | 582 | 570 | 89/77 | 18.1/15.6% | ||
| W | 142 | 152 | 163 | 10/21 | 7.0/14.8% | 125 | 161 | 17/19 | 10.6/13.4% | 169 | 161 | 27/19 | 19.0/13.4% | ||
| D | 740 | 740 | 740 | 0 | 0 | 772 | 715 | 32/25 | 4.3/3.4% | 768 | 720 | 46/21 | 3.8/2.8% | ||
| X | 380 | 385 | 371 | 18.03 m /32.45 m | – | 370 | 391 | 31.89 m /31.74 m | – | 388 | 371 | 33.39 m /32.45 m | – | ||
| Y | 250 | 245 | 259 | 242 | 243 | 240 | 259 | ||||||||
| 13° | 15° | 12° | 2/1° | – | 12° | 15° | 1/2° | – | 8° | 17° | 5/4° | – | |||
| 236° | 234° | 234° | 2° | – | 236° | 236° | 2° | – | 236° | 236° | 2° | – | |||
| Method | Azimuth | Length | Width | Depth | Center Coordinate | Inclined Angle |
|---|---|---|---|---|---|---|
| True Value | 169° | 291 m | 165 m | 774 m | (563, 480) | 31° |
| RM-DBC | 167° | 314 m | 174 m | 774 m | (568, 475) | 28° |
| Direct Inversion | 151° | 332 m | 183 m | 774 m | (575, 471) | 33° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Wang, Y.; Zhao, F.; Ma, Z.; Zou, G.; Wang, T.; Zhang, N.; Huo, W.; Diao, X.; Zhou, D.; et al. An Underground Goaf Locating Framework Based on D-InSAR with Three Different Prior Geological Information Conditions. Remote Sens. 2025, 17, 2714. https://doi.org/10.3390/rs17152714
Zhang K, Wang Y, Zhao F, Ma Z, Zou G, Wang T, Zhang N, Huo W, Diao X, Zhou D, et al. An Underground Goaf Locating Framework Based on D-InSAR with Three Different Prior Geological Information Conditions. Remote Sensing. 2025; 17(15):2714. https://doi.org/10.3390/rs17152714
Chicago/Turabian StyleZhang, Kewei, Yunjia Wang, Feng Zhao, Zhanguo Ma, Guangqian Zou, Teng Wang, Nianbin Zhang, Wenqi Huo, Xinpeng Diao, Dawei Zhou, and et al. 2025. "An Underground Goaf Locating Framework Based on D-InSAR with Three Different Prior Geological Information Conditions" Remote Sensing 17, no. 15: 2714. https://doi.org/10.3390/rs17152714
APA StyleZhang, K., Wang, Y., Zhao, F., Ma, Z., Zou, G., Wang, T., Zhang, N., Huo, W., Diao, X., Zhou, D., & Shen, Z. (2025). An Underground Goaf Locating Framework Based on D-InSAR with Three Different Prior Geological Information Conditions. Remote Sensing, 17(15), 2714. https://doi.org/10.3390/rs17152714






