Abstract
Aerosols play an important role in global meteorology and climate, as well as in air transport and human health, but there are still many unknowns on their effects and importance, in particular for the coarser (giant and ultragiant) aerosol particles. In this study, we aim to exploit the synergy between Raman lidar and Ka-band cloud radar to enlarge the size range in which aerosols can be observed and characterized. To this end, we developed an inversion technique that retrieves the aerosol microphysical properties based on cloud radar reflectivity and linear depolarization ratio. We applied this technique to a 6-year-long dataset, which was created using a recently developed methodology for the identification of giant aerosols in cloud radar measurements, with measurements from Potenza in Italy. Similarly, using collocated and concurrent lidar profiles, a dataset of aerosol microphysical properties using a widely used inversion technique complements the radar-retrieved dataset. Hence, we demonstrate that the combined use of lidar- and radar-derived aerosol properties enables the inclusion of particles with radii up to 12 µm, which is twice the size typically observed using atmospheric lidar alone.
1. Introduction
Aerosols can have multiple effects on different systems, such as the atmosphere and the climate, the biosphere, public health, and air transportation. Aerosols can affect the meteorological and climate system by interacting with solar radiation and therefore inducing changes in the Earth’s radiation balance (radiative forcing). This can happen via radiation scattering and absorption and through their potential role as as cloud condensation nuclei (CCN) and ice nuclei (IN), altering the clouds’ properties. Their impact on the biosphere can happen via atmospheric deposition, which is an important route of supply of trace elements and nutrients to the oceans [1], which is especially important to oligotrophic ecosystems. Moreover, aerosols can have infectious, allergenic, or toxic effects on living organisms, impacting health and agriculture on local, regional, and global scales [2]. Finally, they can affect air transport by causing disruption to air traffic (as happened during the spring of 2010 due to the Eyjafjallajökull volcano eruption in Iceland [3]) and by posing a safety challenge and a cost increase for aviation (i.e., by airborne mineral dust [4]).
The aerosols’ effects and their importance depend on their characteristics. Aerosols have a highly variable chemical composition and size distribution [5], due to their numerous sources and varying formation mechanisms. Their sizes range from a few nanometers to hundreds of micrometers; they can be of primary (particles emitted directly to the atmosphere) or of secondary origin (produced in the atmosphere) and of natural or anthropogenic origin. Primary aerosols consist of both inorganic and organic components. Inorganic primary aerosols are relatively large (often larger than 1 µm) and originate from sea spray, mineral dust, and volcanoes. These coarse aerosols have short atmospheric lifetimes, typically of only a few days [6]. Coarse particles reduce the single-scattering albedo of shortwave radiation, increase radiative absorption [7], and enhance the absorption of longwave radiation [8], possibly causing a net atmospheric warming [9]. Aerosols can act as Cloud Condensation Nuclei (CCN) and Ice Nuclei (IN), which can determine to a large extent cloud microstructure and, consequently, cloud albedo and the dynamic response of clouds to aerosol-induced changes in precipitation [10]. The aerosol size distribution, and in particular the availability of Giant CCN (GCCN), can have a major impact on cloud development and rain formation [11]. By acting as GCCN, giant (>1 µm radius) and ultragiant particles (>2.5 µm radius) can determine the concentration of the initial cloud droplets, the clouds albedo and lifetime, and the precipitation formation, expediting especially warm rain processes [12,13]. In addition, depending on their composition, they can also act as IN. Mineral dust, for instance, is an efficient IN [14], with the bigger particles with larger surface areas being the first to nucleate [15]. Furthermore, the presence of GCCN can impact the radiative balance, and neglecting large particles may lead to significant overestimation (up to 45%) of direct aerosol radiative forcing despite very small aerosol optical depths (∼0.05 at 0.5 µm) [16]. Dust particles larger than 20 µm in diameter have been regularly observed to remain airborne during long-range transport [17], and volcanic ultragiant particles from Iceland were detected in Italy with a Ka-band radar by Madonna et al. [18,19].
Current models fail to explain the transport of coarse-mode particles (>5 µm) to long distances from their sources [20], and climate model simulations often limit particle diameters to only <10 µm [21], with giant and ultragiant aerosols being largely underestimated by aerosol transport models [22]. However, the incorporation of coarse particles is important, as the radiative effect of dust is especially sensitive to the coarse dust mode [23]. Coarse mineral dust particles tend to be under-represented in climate models, given that coarse particles in the model are deposited too quickly, resulting in an underestimation of dust mass in the atmosphere [24]. Méndez Harper et al. [20] found that electrostatic effects could help explain the longer-than-predicted atmospheric residence times for particles larger than a few microns, and Drakaki et al. [17] also found that the modelled lifetimes of the coarser particles are shorter than those observed, highlighting the necessity of upgrading the existing model parametrization schemes of dust life-cycle components in order to improve the assessment of the dust-related impacts within the Earth–atmosphere system.
In order to improve knowledge on the impact and effects of aerosols in their whole size distribution, it is important for coarse aerosols to be measured, studied and monitored, which should contribute to better representation in aerosol models. In this study, we aim to enlarge the size range in which aerosols can be measured and monitored and in which their microphysical properties can be retrieved through the combination of concurrent Raman lidar and Ka-band radar measurements. Multiwavelength Raman lidars, often equipped with polarization capabilities, are now one of the main instruments used to measure and characterize aerosols, allowing aerosol microphysical properties to be observed for particles of up to a few microns. The retrieval of microphysical properties typically relies on regularization techniques to solve an ill-posed inverse problem e.g., [25,26,27,28]. The use of independent extinction and backscatter measurements improves inversion accuracy by reducing the number of assumptions needed, such as the assumption of the lidar ratio value [29]. Nonetheless, challenges remain for coarse particles, primarily due to weaker Raman signals and reduced sensitivity at common lidar wavelengths [30]. Recent advances include synergistic approaches combining lidar and sun photometer data and the usage of ensemble-based methods to improve the constraint of solutions and quantification of uncertainties [31,32]. Furthermore, the development of enhanced instrumentation continues to drive improvements in algorithm accuracy and reliability e.g., [28,33]. On the other hand, Ka-band cloud radars can detect giant aerosol particles far from their source [19,34]. Accordingly, in this work, we identified the giant aerosol layers measured by the cloud radar by applying the recently developed methodology by Gumà-Claramunt et al. [34] to a 6-year-long dataset in Potenza (Italy), and then we found concurrent lidar measurements. In doing so, we were able to synergistically use the measurements of the two instruments in order to enlarge the aerosol size range that could be measured, as lidar has a better sensitivity to small size aerosols, and cloud radar can detect coarser particles. Afterwards, we retrieved the aerosol microphysical properties separately for each case and instrument, using a well-established inversion method for the lidar and a newly developed one for the radar. This methodology enables a comprehensive characterization of the aerosol population, spanning from ultrafine to ultragiant particle size ranges.
This study is structured as follows: the instrumentation and the methodology are presented in Section 2. In Section 3, we present the aerosol observations with the cloud radar and the Raman lidars and the results of the microphysical properties’ retrieval. The discussion of the study’s findings, their implications, and possible future research directions are in Section 4. Finally, the conclusions are in Section 5.
2. Materials and Methods
2.1. Instruments
The observational site where this study was carried out is the CNR-IMAA Atmospheric Observatory (CIAO, www.ciao.imaa.cnr.it, accessed on 28 May 2025), located in Tito Scalo, Potenza, Southern Italy, on the Apennine mountains (N, E), 760 m above sea level (a.s.l.) and less than 150 km from the west, south, and east coasts [35]. The site is in a plain surrounded by low mountains (<1300 m a.s.l.) and has a coastal Mediterranean climate (Köppen type Csb) characterized by dry, warm summers and wet, cold winters [34]. The site is of particular interest for studying aerosol properties because it is affected by quite a large number of Saharan dust intrusions per year [36,37], and it is located 300 km far from the Etna volcano [38]. Moreover, CIAO is part of the Aerosol, Clouds and Trace Gases Research Infrastructure (ACTRIS), of the Global Climate Observing System (GCOS) Reference Upper-Air Network (GRUAN) [39], and of the Integrated Carbon Observation System (ICOS) network [40]. Furthermore, in the last few years, the observatory has undergone a major upgrade with the addition of multiple aerosol in situ instruments [41].
The main instruments used in this study are a Ka-band Doppler radar and two multiwavelength Raman lidars.
The millimetre-wavelength Doppler cloud radar (MIRA36, manufactured by METEK GmbH, Elmshorn, Germany) operated at CIAO between 2009 and 2022, when it was upgraded to a MIRA35 cloud radar (also manufactured by METEK GmbH, Elmshorn, Germany). The MIRA36 system was a mono-static magnetron-based pulsed Ka-Band Doppler radar operating at 8.45 mm wavelength (35.5 GHz), with a sensitivity of −55 dBZ at 1 km and −40.3 dBZ at 5 km [35]. According to its configuration, the time and range resolution were 10 s and 30 m, respectively. A linearly polarized signal was transmitted, while co- and cross polarized signals were received simultaneously to detect Doppler spectra and the linear depolarization ratio (LDR). Of the Doppler spectra, the signal-to-noise ratio (SNR), the Doppler velocity (VEL), the peak width (RMS), and the equivalent reflectivity (Z) were retrieved.
The lidar systems operating at CIAO are part of the European Aerosol Research LIdar NETwork (EARLINET). During the study period, lidar observations were performed three times a week according to the regular EARLINET schedule (one day-time and two night-time measurements) plus, on average, one to two CALIPSO (Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations) satellite correlative measurements during day-time and one to two during the night for each 16-day CALIPSO repetition cycle [42]. Two multiwavelength Raman lidar systems were in operation at CIAO during the period considered for this study: PEARL (Potenza EArlinet Raman Lidar) and MUSA (Multiwavelength System for Aerosol). Both systems were built at the CNR-IMAA Atmospheric Observatory, in Tito Scalo, Italy, and emitted at three laser wavelengths (355, 532 and 1064 nm); they had three channels devoted to the detection of the elastically backscattered radiation and two channels used to detect the Raman radiation backscattered from the atmospheric molecules at 387 and 607 nm, allowing independent measurements of the aerosol particle backscatter and light extinction coefficients and therefore of the aerosol particle light extinction to backscatter ratio (hereinafter lidar ratio) at 532 nm and 355 nm [43,44]. During day-time, when Raman signals are not usable due to strong solar background, the backscatter coefficient is retrieved from elastic signals using the iterative method described by Di Girolamo et al. [45]. Moreover, both MUSA and PEARL were designed to perform particle depolarization measurements at 532 nm. The temporal resolution was of 1 min for both systems, whilst the vertical resolution of the MUSA raw profiles was 3.75 m, and the PEARL resolution was 7.5 m at 1064 nm and 15 m at 355 and 532 nm [35].
2.2. Aerosol Observations
According to their different operating wavelengths, which are between four and five orders of magnitude further away (8.45 mm for the radar vs 355–1064 nm for the lidars),Raman lidars and Ka-band radars are sensitive to different particle sizes. Therefore, this study uses synergistically cloud radar and Raman lidar to enlarge the size range in which aerosols can be observed and characterized. Consequently, an approximately 6-year-long dataset (March 2009–June 2015) is explored for simultaneous lidar and cloud radar aerosol observations. This time interval was chosen based on having the longest uninterrupted data record due to maintenance, tests, and temporary instrument shut-downs, as in Gumà-Claramunt et al. [34].
For the identification of aerosol observations in the cloud radar measurements, we applied the methodology developed by Gumà-Claramunt et al. [34]. The methodology, in a nutshell, detects giant and ultragiant aerosols by first identifying non-hydrometeorological lofted layers and, second, separating them into aerosols or insects by applying the findings of several entomology studies regarding the insects behaviour in the atmosphere.
After the identification of the aerosols and insects lofted layers in the cloud radar measurements, we search for concurrent lidar measurements. The lidar observations correspond to aerosols only; cloud cases are not considered, and insects are not detected by the lidar because of its operating principles. Nonetheless, we decided to classify the lidar aerosol cases according to the target observed by the cloud radar to investigate if the aerosol properties vary.
2.3. Microphysical Properties Retrieval
The inversion of the radar and lidar data for the aerosol microphysical properties’ retrieval must be carried out separately, given that the two instruments observe different parts of the aerosol size distribution. Therefore, the aerosol microphysical properties are retrieved for the lidar and radar data separately, as depicted in Figure 1. For the radar data, we have developed a code that retrieves the aerosol effective radius (which is the surface-area-weighted mean radius) from the measured reflectivity and linear depolarization ratio (LDR) values by using a scattering database that we created using the T-matrix scattering code developed by Mishchenko et al. [46]. For the lidar data, we used the inversion code developed by Veselovskii et al. [47].
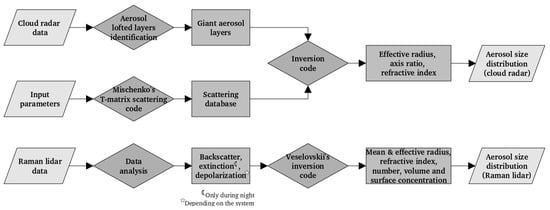
Figure 1.
Aerosol size distribution inversion scheme. The retrieval of microphysical properties is carried out separately for the cloud radar and the multiwavelength Raman lidar aerosol observations, obtaining one aerosol size distribution for the measurements of each instrument.
2.3.1. Cloud Radar
The inversion algorithm used to obtain the aerosol microphysical properties from the cloud radar measurements consists of two steps: the creation of a scattering database and the inversion of the data.
Scattering Database Generation
In every scattering process, either the degree or the nature of the electromagnetic wave polarization can change. A convenient way to describe the polarization state of light is through the Stokes vector. The Stokes vector can be defined through a set of ideal measurements [48] and is defined as
where the Stokes parameters, Sn, are a complete description of the state of light [49]. S0 represents the total intensity beam, S1 the horizontally or vertically polarized light, S2 the or polarized light, and S3 the circularly polarized light. The P parameters in the Stokes vector refer to the measured intensities (or power) of light in specific polarization states; PH is the power of horizontally polarized light, PV is the power of vertically polarized light, P45 is the power of light polarized at , P135 is the power of light polarized at (or from horizontal), PR is the power of right-hand circularly polarized light, and PL is power of left-hand circularly polarized light [50].
The change in the state of light caused by the scattering processes can be defined as
where Si and Ss are the incident and scattered light state in the format of Stokes vectors, and F is the Müller matrix:
The elements of this matrix depend on the direction of radiation propagation and the wavelength and completely describe the properties of a scattering element [50].
We used the T-matrix scattering code developed by Mishchenko et al. [46] to create our scattering database. This code computes orientationally-averaged light-scattering characteristics for ensembles of non-spherical axially symmetric particles. Here, it is solved for randomly oriented spheroids. The main parameter defining spheroids is the axis ratio, which is the ratio between their horizontal and vertical axes. The axis ratio for prolate spheroids is lower than 1, while it is over 1 for oblate spheroids. When the axis ratio is equal to 1, the particle is a sphere. Random particle orientation was selected to simplify the initial implementation of the aerosol size distribution inversion scheme based on cloud radar observations, even though the alignment of aerosol particles can have a notable impact on the reflectivity and, especially, on the LDR results, as shown in Madonna et al. [19].
We computed the scattering parameters for a large set of randomly oriented particles at the cloud radar wavelength, considering the combination of a large number of values of effective radius, axis ratio, refractive index, and number concentration, resulting in over 3 million combinations. The ranges considered for the listed parameters are reported in Table 1. We set the effective radius range in the aerosol coarse mode, from 1 µm up to 50 µm. The axis ratio varied between 0.1 and 10, which is the difference between the two spheroid axes up to a factor of ten.

Table 1.
Input parameters for the T-matrix calculations at the cloud radar wavelength (8.45 mm). In the axis ratio, “h” and “v” stand for horizontal and vertical axes, respectively.
In the same way as in Gumà-Claramunt et al. [34], the refractive index was defined according to Adams et al. [51], who found that volcanic particles at 35.5 GHz have a real refractive index of 2.45 ± 0.12 and an imaginary refractive index of 0.43 ± 0.11. Since these values correspond to volcanic particles only, the range was slightly extended from 2.20 to 2.70 for the real part and from 0.2 to 0.65 for the imaginary part. The number concentration was set to the range – 10 cm−3 according to Lasher-Trapp and Stachnik [52], who studied the variability of giant and ultragiant aerosols over the eastern Great Lakes region during a campaign with aircraft data. Finally, the scattering angle was set for backscatter, and random particle orientation was selected.
From the Müller matrix, which is the output of Mishchenko’s scattering code, we obtain the reflectivity and LDR [53]:
where Fii corresponds to the Müller matrix elements (Equation (3)) and N to the number concentration.
Also using the elements from the Müller matrix, the LDR can be calculated as follows [53]:
Therefore, our scattering database comprises all the reflectivity and LDR values corresponding to all the possible combinations of effective radius, axis ratio, refractive index, and number concentration within the ranges of Table 1.
Inversion Algorithm
Figure 2 illustrates the methodology used to retrieve the microphysical properties of a giant aerosol layer inverting radar data. It uses the measured reflectivity and LDR values as input. First, the inversion is performed for each layer pixel, and then the mean layer properties are calculated considering all the pixels.
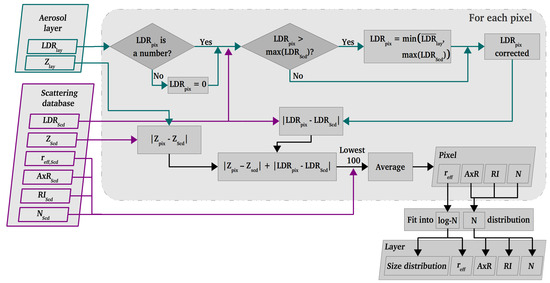
Figure 2.
Flowchart of the radar inversion methodology, where “” corresponds to effective radius, “AxR” to axis ratio, “RI” to refractive index, and “N” to number concentration. The subscripts “Lay”, “Scd”, and “pix” correspond to layer, scattering database, and pixel, respectively.
First, the LDR values that are outside of range are corrected to allow the inversion methodology to converge for them. The corrections applied are the following:
- if the pixel LDR is below the instrumental sensitivity, the LDR value is set to zero;
- if the pixel LDR is higher than the maximum LDR present in the scattering database (∼–10 dB), the LDR value is set to the mean LDR value of the layer;
- if the pixel and the mean layer LDR values are higher than the maximum LDR present in the scattering database, the LDR value is set to the maximum LDR value in the scattering database.
These corrections might have an impact on the inversion results, as they are, in fact, lowering the LDR input values. This is presented in more detail in the Results section (Section 3.2.1). By correcting the LDR values out of range, though, we account for their reflectivity values instead of leaving them out of the following steps of the inversion methodology. Otherwise, no solutions would be found for them, and they would be excluded.
For the second correction, the code was tested, setting the values of the pixels to the maximum LDR value in the scattering database, but a better agreement was found between the reflectivity and LDR measurements and the estimated values when using the mean LDR value of the layer. The differences between these two are reported in Table 2 for a single case; similar results were found across all the layers. The differences between the measured and retrieved values, in dB, were lower for both reflectivity and LDR when the values with high LDR values were set to the mean LDR of the layer that they belong to. In future versions of the inversion methodology, more possibilities should be included in the scattering database to be able to account for these pixels without these assumptions.

Table 2.
Reflectivity and LDR differences for the layer of 19 June 2013 19:27–19:57 UTC (case B), depending on the correction applied to LDR values which are higher than the maximum scattering database LDR value (referred to as “High LDR” in the table). The “Scd” subscript refers to the scattering database.
In the following step, the absolute differences between each pixel value and the scattering database values are computed, both for reflectivity and LDR.
Next, the absolute differences for the reflectivity and LDR for each pixel are aggregated. Then, the particle properties corresponding to the lowest hundred values (or less, if the absolute difference is over 1 dB) are averaged to obtain the mean pixel effective radius, axis ratio, complex refractive index, and number concentration. The retrieval, in this way, is constrained, obtaining the properties relative to the Z and LDR pairs which are closest to the measured values.
In the last step, the layer properties are estimated from the values of their pixels. To obtain the aerosol layer’s size distribution and its effective radius, the individual pixel values are fit into a mono-modal log-normal distribution. For simplicity, we approximate the distributions of axis ratio, complex refractive index, and number concentration using Gaussian fits, though we note that in reality, these properties often follow log-normal or bounded distributions [54].
2.3.2. Lidar
The retrieval of microphysical properties for the aerosol layers observed with lidar has been achieved using the algorithm by Veselovskii et al. [47]. The algorithm is based on a model of oriented spheroids for the inversion of multiwavelength lidar data and estimates the aerosol size distribution; the complex refractive index; and the number, surface, and volume concentrations. The aerosols are modelled as a mixture of two aerosol components: one composed only of spherical particles and the second composed of non-spherical particles. The non-spherical component is an ensemble of randomly oriented spheroids with size-independent shape distribution. This approach was integrated into an algorithm retrieving aerosol properties from the observations with a Raman lidar based on a triple Nd:YAG laser. Such a lidar provides three backscatter coefficients, two extinction coefficients, and the particle depolarization ratio at a single or multiple wavelengths. To test the model, simulations were performed for a bimodal particle size distribution typical of desert dust particles. The uncertainty of the retrieved particle surface, volume concentration, and effective radius for 10% measurement errors is estimated to be below 30% [47].
The retrieval algorithm consists of a comparison between precalculated synthetic optical data (spheres and spheroid kernel functions) and the optical extensive properties retrieved from lidar measurements. As the algorithm is solving an undetermined problem, the values of the radius (minimum and maximum) and of the complex refractive index are varied, and several thousands of solutions are found. Then, every solution is characterized by discrepancy (a difference between experimental data and data calculated from solutions). Finally, the solutions are ranged, and ∼1% of solutions are averaged.
To perform a retrieval, it is necessary to constrain the range of the solutions first. The constraints used for this study can be found in Table 3.

Table 3.
Range of parameters used for the retrieval of the lidar microphysical properties with the inversion algorithm from Veselovskii et al. [30].
In our study, the input variables used correspond to the three aerosol particle backscatter coefficients (at 355, 532 and 1064 nm) and the two aerosol particle light extinction coefficients (at 355 and 532 nm) obtained from the Raman lidar measurements. We choose not to use particle linear depolarization for two reasons: (a) when the volume fraction of spheroids in the model distribution is 100%, the results obtained from the 3 + 2 + 1 set are close to the results obtained in the absence of depolarization (3 + 2 set), and no significant improvement is observed [47]; (b) particle linear depolarization is not available for all the cases.
From our lidar measurements, the mean layer optical properties were calculated and processed with the algorithm in Veselovskii et al. [47] to retrieve the particles’ microphysical properties, which correspond to the average of all the solutions that have a lower discrepancy between the measured and retrieved values (∼1% of the solutions).
3. Results
In this section, we first present the aerosol observations with the cloud radar and the Raman lidars (Section 3.1), and we then show the results of the microphysical properties’ retrieval (Section 3.2).
3.1. Aerosol Observations
Following Gumà-Claramunt et al. [34], we identified 328 giant aerosol layers from six years of cloud radar measurements at CIAO (March 2009–June 2015). The maximum number of layers was observed during summer, a secondary maximum was observed in spring, and a minimum was detected during winter [34].
By comparing the lidar measurements performed during the same time period and the giant aerosol radar dataset, 22 cases of simultaneous aerosol measurements were found. A list of simultaneous cloud radar and lidar observations can be found in Appendix A; Table A1 contains the lidar cases corresponding to cloud radar giant aerosol observations, and Table A2 showss those corresponding to cloud radar insect observations.
In the following, we present two examples of concurrent measurements: Case A corresponds to mixed dust measurements, while Case B is related to smoke observations. For each of them, we will first present the lidar analysis, and then we will compare it to the cloud radar reflectivity and LDR.
3.1.1. Case A: 29 July 2013
This measurement corresponds to observations of Saharan dust aerosol particles based on the values of the aerosol particle light backscatter Ångström exponent (from now on the Ångström backscatter-related exponent), the values of the aerosol particle light backscatter linear depolarization ratio (from now on the particle depolarization ratio), and the back-trajectory analysis. The lidar measurements were performed at CIAO on 29 July 2013 between 13:59 and 14:59 UTC and are presented in Figure 3.
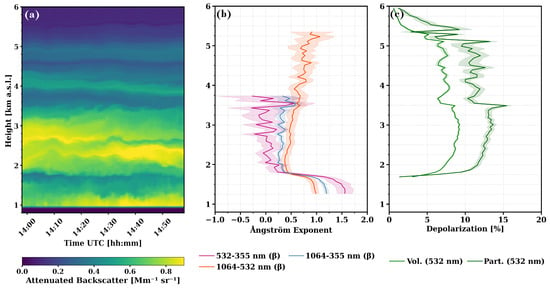
Figure 3.
(a) Time–height evolution of the of the 1064 nm attenuated backscatter coefficient for 29 July 2013 between 13:59 and 14:59 UTC, measured by MUSA, and profiles of the (b) aerosol particle light backscatter Ångström exponent (or Ångström backscatter-related exponent) and (c) volume (Vol.) and linear particle (Part.) depolarization ratio. The vertical resolution is 30 m. The shadowed areas correspond to statistical errors.
Figure 3a presents the time-range evolution of the observed aerosol by means of the attenuated backscatter coefficient at 1064 nm. Aerosols are observed from the ground up to 5 km a.s.l., with the main aerosol layer located in the range of 1.8 to 3.4 km. Thin aerosol layers are also found up to 5 km. Below 1.7 km, the convective boundary layer (CBL) is also evident, as it was well separated from the free tropospheric aerosol throughout the measurement duration.
Figure 3b,c display the two available intensive optical properties: the Ångström backscatter-related exponent and the particle depolarization ratio. The backscatter-related Ångström exponents (Figure 3b) are separated into two parts with different characteristics. The first part exhibits values greater than 1 up to 1.7 km a.s.l., indicating small particles typically originating from anthropogenic activities within the CBL. The second displays values well below 1 and above 1.8 km, suggesting the existence of bigger particles. Figure 3c shows the atmosphere light backscatter linear depolarization ratio (hereinafter the volume depolarization ratio) and the particle depolarization ratio, which are indicative of the sphericity of the particles. The atmospheric backscatter linear depolarization ratio is the total (or volume) linear depolarization ratio and includes contributions both from molecules (Rayleigh scattering) and aerosols (Mie scattering); it is a directly measured quantity and reflects the overall depolarization in the atmosphere. The particle depolarization ratio, instead, is a particle-only depolarization ratio and is derived from the total depolarization ratio after subtracting the molecular (Rayleigh) contribution using a retrieval or correction algorithm. Similar to Figure 3b, the upper layer particle depolarization ratio values are well above 10% e.g., [55] and correspond to non-spherical particles. The particle depolarization ratio and backscatter-related Ångström exponents highlight the mixing of dust particles e.g., [56]. For the lower layer, it was not possible to retrieve the particle depolarization ratio due to low SNR.
To identify the travelled path and sources, the FLEXPART model was used in backward mode. The simulation was performed considering a 7-day-long period. The FLEXPART total column sensitivity plot (Figure 4) indicates the path travelled by the aerosols prior to arriving at the measuring site. It shows that the air-parcels followed a northward movement over the Italian peninsula before looping towards the north-west of Africa. Therefore, it is likely that the observed layers originated in NW Saharan regions and crossed the heavily polluted area of Po valley and big urban areas along the west coast of Italy prior to their arrival over the observational site. Therefore, the FLEXPART back-trajectory and observed lidar optical parameters agree in their identification of mixed dust aerosol particles.
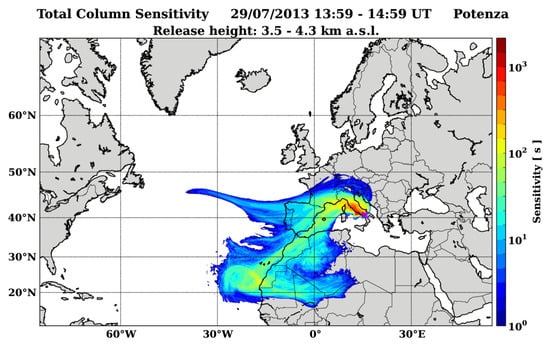
Figure 4.
Total column sensitivity for a 7-day FLEXPART back-trajectory analysis starting on 29 July 2013 (from 13:59 to 14:59 UTC) at between 3.5 and 4.3 km a.s.l.
The lidar and radar temporal evolutions and profiles are reported in Figure 5. The attenuated backscatter coefficient at 1064 nm (Figure 5a) shows the vertical stratification of the layers seen by the lidar, whilst the radar lofted layer can be observed between 3.5 and 4.2 km a.s.l. in Figure 5b. The lidar aerosol backscatter coefficient (hereinafter backscatter) and the radar reflectivity profiles (Figure 5c) show various aerosol layers. The lidar identified multiple layers in two distinct areas (as described for Figure 3), one directly affected by the CBL and the other containing coarse aerosol in the free troposphere. The radar, instead, identified three layers: the first from the ground up to 2 km, the second from 2 to 3 km, and the third from 3.5 to 4.2 km. However, we are only interested in the third layer, which was classified as a giant aerosol layer following the methodology in Gumà-Claramunt et al. [34]. The enhanced signal up to 3.5 km a.s.l. is evident for both instruments and is expected considering the observations took place from 13:59 to 14:59 UTC, when the CBL was fully developed. The radar lofted layer location coincides in height with the lidar layer from 3.5 to 4.2 km a.s.l. The depolarization comparison (Figure 5d) also presents different behaviour for the profiles using the two instruments: while the lidar particle depolarization ratio is almost constantly above 1.8 km a.s.l., the highest radar LDR values were measured in the CBL, whilst they range between −26 and −12 dB in the lofted layer. The differences in the vertical structure of the profiles can be attributed to the sensitivity of the two instruments to different particle sizes, number concentrations, and orientations in the profile. For the upper lidar layer (4.6–5.6 km a.s.l.), for example, there is only radar signal in two of the vertical bins, which may be an indication of a lower concentration and/or smaller size of giant aerosols.
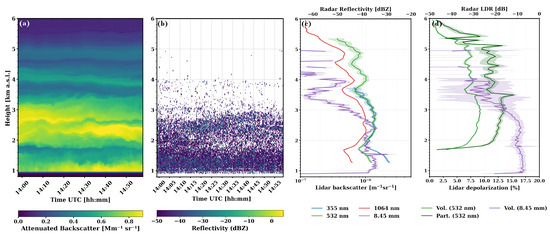
Figure 5.
Temporal evolution of the lidar 1064 nm attenuated backscatter coefficient (a) and radar reflectivity (b) on 29 July 2013 between 13:59 and 14:59 UTC. (c) Lidar aerosol backscatter coefficient at 355 nm, 532 nm, and 1064 nm and the radar reflectivity at 8.45 mm, both retrieved for the same time period. (d) Lidar volume and particle depolarization ratio at 532 nm and radar volume linear depolarization ratio at 8.45 mm, both retrieved for the same time period. The shaded areas correspond to the statistical error.
3.1.2. Case B: 19 June 2013
The second case study refers to aerosol from biomass burning, as observed at CIAO on 19 June 2013 from 19:27 to 19:57 UTC; it is presented in Figure 6.
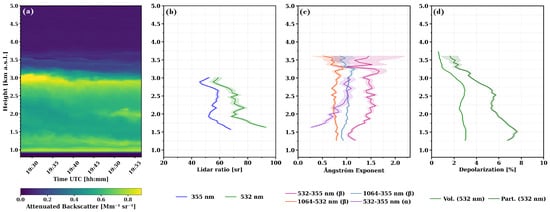
Figure 6.
(a) Time–height evolution of the attenuated backscatter coefficient at 1064 nm for 19 June 2013 between 19:27 and 19:57 UTC, as measured by MUSA, and profiles of (b) lidar ratio, (c) aerosol particle light backscatter- () and extinction-related () Ångström exponent, (d) volume depolarization ratio, and particle depolarization ratio. The vertical resolution of the optical property profiles is 210 m, and the shadowed areas correspond to the statistical error.
The time–height evolution of the attenuated backscatter coefficient at 1064 nm is shown in Figure 6a. A stratified aerosol load was measured from the ground up to 3.5 km a.s.l., showing an aerosol layer located near the ground, which represents the well-mixed residual layer and a thicker optical layer extending from 2.7 to 3.2 km a.s.l. From the data analysis, the aerosol extinction-to-backscatter ratio (hereinafter the lidar ratio) (Figure 6b) is around 60 sr at 355 nm and 80 sr at 532 nm within the residual layer up to about 2.7 km; it could not be retrieved for the upper layer owing to low SNR in the extinction profiles. The backscatter- and extinction-related Ångström exponents (Figure 6c) are values that approximately correspond to absorbing particles. The relatively small values of the particle depolarization ratio (5–6%; Figure 6d) correspond to slightly depolarizing particles. Therefore, from the values of the lidar intensive optical properties and according to studies in the literature e.g., [57,58], we can deduce that, most likely, the observed aerosols correspond to smoke or urban aerosol particles.
The possible origin and transport path of the measured aerosols were investigated using the FLEXPART model and the active fire product from MODIS (MODerate-resolution Imaging Spectroradiometer). The FLEXPART total column sensitivity plot (Figure 7a) indicates the path travelled by the aerosols prior to arriving at the measuring site. The air masses followed an eastward direction towards Greece and then moved north and, finally, extended westward. The MODIS active fire product detects fires in 1 km pixels that are burning at the time of overpass under relatively cloud-free conditions using a contextual algorithm [59]. In this case (Figure 7b), it identified several active fires along the path of the air masses before the aerosol layers were observed. Hence, the source of the observed layer may be the presence of forest fires burning over the Balkans.
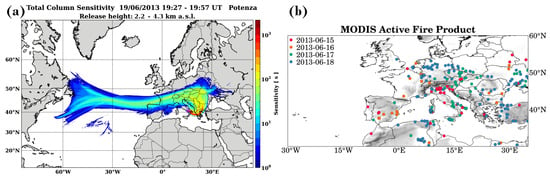
Figure 7.
(a) Total column sensitivity for a 7-day FLEXPART back-trajectory starting on 19 June 2013 (from 19:27 to 19:57 UTC) between 2.2 and 3.3 km a.s.l.; (b) MODIS active fire product 1, 2, 3 and 4 days prior to 19 June 2013.
The lidar and radar measurements for this case are presented in Figure 8.
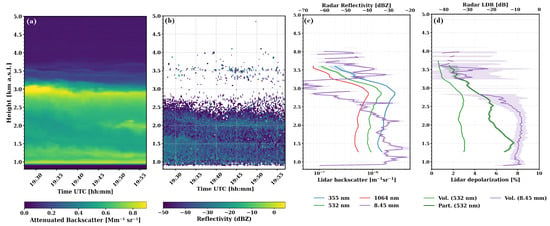
Figure 8.
Temporal evolution of the lidar 1064 nm attenuated backscatter coefficient (a) and radar reflectivity (b) on 19 June 2013 between 19:27 and 19:57 UTC. (c) Lidar aerosol backscatter coefficient at 355 nm, 532 nm, and 1064 nm, and radar reflectivity at 8.45 mm. (d) Lidar volume and particle depolarization ratio at 532 nm and radar volume linear depolarization ratio at 8.45 mm. All the profiles are for the same time period, and the shaded areas correspond to the statistical error.
The lidar temporal evolution (Figure 8a) and its corresponding backscatter profiles (Figure 8c) illustrate the presence of the residual layer and the biomass burning plume, which is located around 2.8 km a.s.l., where the backscatter signal is maximum. The radar (Figure 8b,c) identified the residual layer up to 2.7 km a.s.l., while a lofted layer is located between 3.2 and 4 km a.s.l. As in the case previously presented, the vertical structure measured by the two instruments differs; the lofted layer identified by the radar is slightly above the one measured by the lidar. The depolarization profiles (Figure 8d) show that the lidar particle depolarization ratio ranges from 8 to 2%, decreasing with height. The radar LDR values are at their maximum within the atmospheric boundary layer due to the presence of insects and/or giant aerosols, and they are lower in the lofted layer (from −38 to −12 dB). As in the previous case, we attribute the differences on the aerosol vertical structure as observed by the two instruments to their different sensitivity and the multimodal aerosols’ size distribution throughout the atmospheric column.
3.2. Microphysical Properties’ Retrieval
In this subsection, we present the inversion results from the cloud radar and the lidar measurements separately, and then combined. Afterwards, we show the results to provide specific examples.
3.2.1. Cloud Radar Inversion Results
Next, the inversion algorithm performance is evaluated by comparing the measured reflectivity and LDR to their estimated values for different scenarios, depending on the LDR pixel values compared to the sensitivity threshold and the maximum LDR value present in the scattering database (referred to in this section as LDRmax).
In Figure 9, this comparison is displayed for Case B (19 June 2013), where Original corresponds to the measured values and Outputto the inversion methodology retrieval. The rest of the categories are presented to illustrate the different retrieval scenarios depending on the LDR correction values applied. In Figure 9a, the estimated reflectivity (Output, blue line) reproduces well the measured radar reflectivity (Original, purple line), suggesting a good performance of our inversion methodology. The yellow line (Output (null LDR)) corresponds to the pixels for which LDR is null or equal to 0. The proportion of pixels for which this condition is met increases with lower reflectivity values due to the instrument sensitivity. The teal line (Output (0 < LDR < LDRmax)) corresponds to the pixels where the LDR is not corrected. The green line (Output (LDR < LDRmax)) shows the estimated results for all the pixels below the maximum value in the scattering database (LDRmax), including those with null LDR values, and it closely follows the original values. Finally, the red line (Output (LDR > LDRmax)) presents the results for the LDR pixel values that were corrected for high values. After adding the green and red lines (Output, blue line), the values are closer to the input than if we just consider the pixels with an LDR value lower than LDRmax (Output (LDR < LDRmax), green line), and therefore we decided to correct the high values of LDR instead of keeping them out of the inversion procedure.
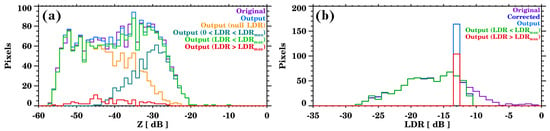
Figure 9.
(a) Reflectivity and (b) LDR performance for Case B (19 June 2013). “Original” corresponds to the cloud radar measurements and “Output” to the retrieval. In parentheses, different subsets of pixels are presented according to their LDR in comparison to the radar sensitivity and the maximum LDR value in the scattering database (LDRmax).
The agreement is also satisfactory regarding the performance of the LDR inversion (Figure 9b). The values measured by the radar are depicted with the purple line (Original), spanning from −30 to 0 dB. The LDR values over the scattering database maximum LDR value (LDRmax) were, in this case, corrected with the mean LDR of the layer (∼−13 dB). The dark blue line (Corrected) presents the original values with this correction applied. The retrieval (Output, light blue line) is very close to the used input (Corrected, dark blue line). The output for the LDR pixels to which no correction was applied (Output (LDR < LDRmax), green line) is in quite a good agreement with the measured values (Original, purple line) up to almost −10 dB. The retrieval for the corrected pixels (Output (LDR > LDRmax), red line) is centred at the mean LDR of the layer, which is the value that these higher LDR values were corrected with. It becomes clear that our retrieval algorithm underestimates the LDR values, and therefore, the scattering database should be enlarged to include higher LDR values (e.g., considering different particles’ orientation).
The reflectivity and LDR differences between the original and the retrieved values for the same case are presented in Table 4. The first row refers to all the layer points, including the corrected LDR values, and the difference is −44.5 dB for reflectivity and −43.4 dB for LDR. The lowest differences correspond to the pixels for which the LDR was null, which indicates either that the particles were spherical or that the LDR values were below the sensitivity threshold. The retrieval, therefore, relies mainly on the reflectivity values, which explains the lower difference. The highest differences correspond to the pixels in which the LDR values were not corrected (0 < LDR ≤ LDRmax), which are associated with larger pixel LDR variability. Considering all the pixels with null LDR and the non-corrected (LDR ≤ LDRmax), the discrepancies are very close to those considering the whole layer, which is also the case for the pixels in which the LDR was corrected for being too high (LDR > LDRmax).

Table 4.
Difference between the reflectivity and LDR values measured by the cloud radar, and the values retrieved by the inversion algorithm for Case B (19 June 2013). In the range of application, LDR corresponds to the pixels’ LDR values, whilst LDRmax corresponds to the maximum LDR value in the scattering database. In parentheses, values are expressed in dB. N/A means that values are not available.
The described inversion method was applied to all the cloud radar observations of giant aerosol lofted layers. The performance of the method in terms of difference is presented in Table 5 for both reflectivity and LDR. The difference averaged for all the cases is for the reflectivity and for the LDR. The difference is one order of magnitude higher for the LDR, which can be attributed to the corrections to the pixels that had values measured above the maximum value in the scattering database. The worst performance has discrepancies that are two orders of magnitude higher for both parameters ( and , respectively). The best performance for the reflectivity has a difference of and of for the LDR.

Table 5.
Discrepancies in reflectivity and LDR between the measurements and values retrieved by the inversion method for all the giant aerosol cases. In parentheses, values expressed in dB.
Figure 10 shows the frequency distributions of reflectivity and LDR for all the aerosol layers as measured by the radar (purple line) and as retrieved by our method (blue line). The reflectivity plot (Figure 10a) shows a fair agreement between the two distributions, where the centers of the distributions (between −40 and −30 dB) coincide. The inversion method, though, generally overestimates reflectivity values over −30 dB and underestimates them below −40 dB. Accordingly, the lower discrepancies from Table 5 correspond to layers with mean reflectivity values in the −40–−30 dB range, and the highest ones to layers at the edges of the distribution. The reason for these discrepancies is probably linked to the LDR pixels’ correction.
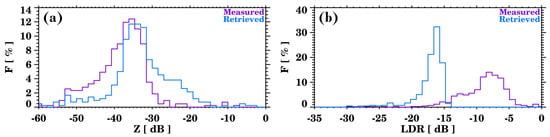
Figure 10.
Frequency distributions of the measured and retrieved (a) reflectivity and (b) linear depolarization ratio (LDR) values for all the giant aerosol layers measured by the Ka-band radar. The retrieved values were obtained using our newly developed inversion methodology.
In the LDR plot (Figure 10b), the effect of the correction of pixel values over the maximum LDR value in the scattering database is obvious: the frequency’s distribution is shifted towards lower LDR values for the retrieval. This impacts the retrieval, and especially the axis ratio.
The reflectivity and LDR differences between the original and the retrieved values that we have presented for Case B (Figure 9 and in Table 4) are quite similar to the mean situation when considering all the giant aerosol layers (Table 5).
The effective radius resulting from the inversion for all the layers (Figure 11a) ranges between 1.5 and 7 µm and has a bimodal distribution. The first maximum is around 3 µm and the second between 4 and 5 µm. The corresponding size parameter is between and , in agreement with the Rayleigh regime assumption embedded in the retrieval method. The number concentration (Figure 11b) is found to be between 0.10 and 1 cm−3, with maximum values in the region 0.4–0.8 cm−3. The mean geometric radius of the aerosol distribution (Figure 11c) extends between 1 and 12 µm, and the maximum radii are found in the range 1–3 µm. The frequency decreases with aerosol size, which suggests that the smallest aerosols reach the observational site more frequently compared to bigger ones, as one would expect according to their respective settling velocities.
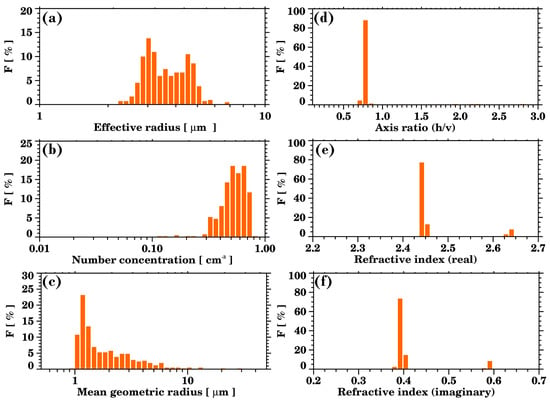
Figure 11.
Frequency distributions of the retrieved aerosol: (a) effective radius, which is the surface-area-weighted mean radius; (b) number concentration; (c) mean geometric radius; (d) axis ratio (horizontal/vertical axis); and (e) real and (f) imaginary parts of the refractive index.
The aerosol particle sizes and number concentration results retrieved by our algorithm are in line with the observational measures by Exton et al. [60], who found total particle concentrations of about 0.1–0.5 in the 5–150 µm range, even though in the frequency distribution, the portion of particles over 5 µm is low. They also fall in the range of the measurements by Lasher-Trapp and Stachnik [52], who detected giant to ultragiant aerosol particles spanning approximately from 5 µm to 50 µm in diameter (2.5–25 µm in radius) in concentrations between 10−3 and 10 by using airborne probes. Instead, the retrieved number concentrations are higher than those measured during the First Aerosol Characterization Experiment (ACE-1), in which researchers measured particles with dry radii in the order of 6 to 12 µm in concentrations between 10−4 and 10−2 cm−3 [12].
The axis ratio (horizontal/vertical axis) frequency distribution (Figure 11d) indicates that more than 90% of the aerosol particles are prolate, with axis ratios between 0.7 and 0.8. A small portion of the aerosols are oblate, with axis ratios around 2, and almost none are spherical. These findings are consistent with our hypothesis of giant particles, which mainly comprise dust, pollen, and volcanic materials; hence, there are irregular shaped aerosol types [61,62,63]. Considering that our retrieval algorithm underestimates LDR values, though, it is likely that the aerosol particles’ irregularity is underestimated.
The refractive index depends on the aerosols’ composition and size distribution and on the incident wavelength. The real part accounts for refraction, while the imaginary part handles the attenuation. The real part of the refractive index (Figure 11e) oscillates, mainly, between 2.43 and 2.47, and for a few cases, it is between 2.62 and 2.65. The imaginary part of the refractive index (Figure 11f) fluctuates around 0.4, and for a few cases, it is between 0.57 and 0.6. This suggests, that, in general, the observed aerosol particles are less absorbing than the volcanic particles studied by Adams et al. [51]. Given the observational site’s location and climatology, this is in line with what we would expect, as volcanic aerosols are generally more absorbing with respect to desert dust, which leads to higher SSA. The values of SSA depend on the aerosol’s composition, size, and wavelength. Reported values at 440 nm, for example, are for volcanic particles [64] and for dust particles [65]. The estimation of the refractive index of aerosols is important given that it has an impact on the SSA and, therefore, can impact the radiative budget.
3.2.2. Lidar Inversion Results
The inversion code by Veselovskii et al. [47] uses three aerosol backscatter coefficients and two aerosol extinction coefficients as input, and therefore it can be only applied to the night-time measurements, when the aerosol particle light extinction coefficient (hereinafter extinction) profiles are available (they cannot be retrieved in an independent way during day-time because the Raman backscattered signal cannot be measured accurately due to solar background radiation). All the input optical properties were available for 11 out of the 25 night-time measurements, for which we performed the inversion. Not all the optical properties were available for all the cases, which may be due to low SNR values or to quality assurance of the estimated properties.
When we classify the cases according to the cloud radar observed target, five correspond to aerosol and six to insect observations. We decided to perform the inversion for all the lidar cases independently of the cloud radar-observed target in order to increase the number of cases for which we could retrieve the microphysical properties and to infer if there are any differences depending on the presence or not of giant aerosols in the atmosphere.
Figure 12 reports the number, surface, and volume distribution for each individual case (a, b and c respectively) and the mean distribution of all the cases according to the target observed by the radar (d, e and f). The number distribution describes how many particles exist per unit volume of air for each particle size, and it is dominated by small particles. The surface distribution represents the total surface area of particles per unit volume of air for each size, and it typically peaks at intermediate sizes. The volume distribution describes the total volume of particles per unit volume of air for each size, and it is usually dominated by larger particles (coarse mode).
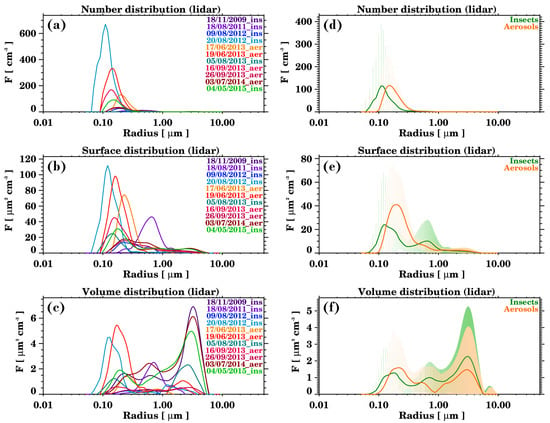
Figure 12.
Number, surface, and volume distribution for all the night-time lidar cases, using Veselevskii’s algorithm. In the left panels (a–c), the distributions are plotted for each of the cases, and the legend indicates the date and the target detected by the cloud radar (“aer” stands for aerosols and “ins” for insects). In the right panels (d–f), the distributions correspond to averaging all the individual distributions depending on the target observed by the cloud radar. The vertical lines correspond to the standard deviation.
In Figure 12a, the number distribution for each case shows that most of the particles fall in the size range 0.06–1 µm. The number concentration reaches up to 670 cm−3 but for most cases is lower than 150 cm−3. In Figure 12b, the surface distributions reveal the existence of a minor mode in the region 1–6 µm. This indicates that even in low number concentration, some coarse particles are detected by the lidar. The surface concentration is, in general, lower than 50 µm2 cm−3 but in some cases reaches up to 100 µm2 cm−3. The volume concentration in Figure 12c shows that not all the distributions are bimodal. Some distributions are trimodal, and their corresponding radii ranges are from 0.1 to 0.3 µm, between 0.3 and 1 µm, and from 1 to 6 µm radius. No differences in the distributions of all the individual cases could be observed depending on the detection of aerosols or insects (hereinafter target) by the cloud radar.
To infer whether differences exist in the number, surface area, and volume distributions when aerosols or insects are detected by the cloud radar, the distributions were averaged based on the corresponding radar targets. Figure 12d shows the number distribution for all the lidar aerosol cases averaged depending on the cloud radar-detected target. In this case, the distributions are slightly different: the aerosol radii when insects are observed by the cloud radar (between 0.06 and 0.13 µm) is lower than when aerosols are also observed (between 0.09 and 0.14 µm). The number concentration in both cases, though, is similar. Figure 12e presents the surface distribution in the same way. For the cloud radar insect observations, two modes are observed, the second from 0.3 to 1 µm, while for radar aerosol observations, there is one main mode between 0.10 and 1 µm. The surface concentration is slightly higher for the aerosol cases. Figure 12f reports the volume distribution, which has three modes both for cloud radar aerosols and insects. In this case, the distributions are relatively closer than before, and the volume concentration is also quite similar.
In conclusion, in the studied cases, it was possible to observe particles with lidar with radii between 0.1 and 6 µm, with mean radii being below 1 µm. To investigate whether the lidar retrievals capture a coarse aerosol fraction closer to the larger particles detected by the cloud radar, the lidar retrievals were grouped according to the radar target classification. This analysis revealed some differences in the aerosol size distributions (number, surface, and volume). For instance, the aerosol mean radius was larger in cases where the cloud radar detected giant aerosol particles. This aligns with expectations, suggesting that lidar measurements can retrieve the microphysical properties of the smallest and likely more numerous fraction of giant aerosols. However, due to the limited number of cases available for this analysis, these findings should be viewed as indicative rather than definitive.
3.2.3. Combined Inversion Results
By combining the aerosol size distribution from the lidar and the radar, it is possible to enhance the range of the measured aerosol size distribution. The particles observed by the lidar are mainly between 0.1 and 1 µm, sometimes detecting particles up to 6 µm, whereas the aerosols detected by the radar have radii between 1 and 12 µm. The aerosol particle size distribution is retrieved up to 50 µm. Nevertheless, given the nature of the kernel function of the inversion algorithm, the size distribution is prone to significant uncertainties at the edges of the size distribution, even with small uncertainties in the input data.
Next, we present the results of the number, surface, and volume distribution inversions for two specific cases. We want to illustrate the advantages of using lidar and radar data together by displaying the retrieved size distributions together in the same figures. As the microphysical properties needed for the lidar inversion could not be retrieved from the lidar measurements for the previously presented Case A, owing to background contamination during day-time conditions, we are going to present the results for Cases B (19 June 2013) and C (3 July 2014).
Case B: 19 June 2013
As we described previously, smoke aerosol particles were observed on 19 June 2013. Figure 13 shows the number, surface, and volume distributions retrieved with the lidar and radar inversions both together and separately. The inversions were performed for the 2–2.5 km a.s.l. layer measured by the lidar and for the 3.2–4 km a.s.l. layer measured by the radar, both from 19:27 to 19:57 UTC. The number distribution (Figure 13a) shows that the number of particles below 0.4 µm is predominant, whilst the number concentration of particles with radii over 1 µm is negligible. In the surface distribution graph (Figure 13b), particles below 0.4 µm still predominate, although coarser particles generate three secondary maxima. The first and second secondary maxima are seen by the lidar (∼1 µm and ∼3 µm) and the third by the radar (∼7 µm). A partial overlap between the third lidar mode and the radar mode is present. The volume distribution (Figure 13c) shows a similar behaviour to that of surface distribution, with the first lidar mode being less intense and the radar mode more intense and centred at ∼9 µm instead of at ∼7 µm. In this case, the partial overlap between the third lidar mode and the radar mode is more evident, between 2 and 6 µm approximately. This indicates that the lidar detected a small fraction of the coarser particles seen by radar.
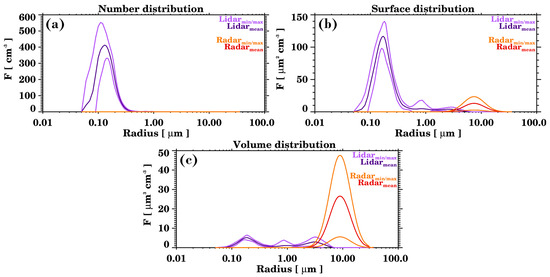
Figure 13.
Case B: (a) number, (b) surface, and (c) volume size distribution for the layers observed on 19 June 2013 from 19:27 to 19:57 UTC. For the lidar, the inversion was performed for the layer between 2.0 and 2.5 km a.s.l.; for the radar; and for the lofted layer between 3.2 and 4 km a.s.l.
This case is an example of how to obtain an enlarged aerosol size distribution by combining Raman lidar and cloud radar information. The Raman lidar can be used to retrieve the size distribution for aerosols in the Aitken and in the accumulation mode, as well as for a small part of the coarse mode. The cloud radar can be used to retrieve the size distribution for coarse-mode aerosols.
The mean microphysical properties retrieved from the radar and lidar measurements for this case can be found in Table 6. The effective and mean radius are larger for the aerosols detected by the radar, and the number concentration is much higher for the lidar-detected aerosol particles. The complex refractive index is different for both instruments, and the different input values for the two inversion methods bias the retrieved mean values, as this parameter depends both on the particle type and the wavelength. The axis ratio for the radar shows that the particles were aspherical (specifically prolate).

Table 6.
Case B: aerosol microphysical properties retrieved from the radar and lidar measurements for the smoke case on 19 June 2013. In the axis ratio, “h” and “v” stand for horizontal and vertical axis, respectively. The – sign means that the variable is not available.
The discrepancies in aerosol microphysical properties retrieved from radar and lidar measurements are substantial and can be primarily attributed to the differing operating wavelengths and sensitivities of the two instruments. In terms of particle size, these differences arise from the relative scale of the aerosol particle size compared to each instrument’s wavelength; radar typically detects larger aerosols, whereas lidar is more sensitive to smaller ones. Consequently, the number concentration retrieved by lidar tends to be higher, which is consistent with its sensitivity to smaller, more numerous particles. Finally, the observed differences in complex refractive index can be linked to its wavelength dependence and to variations in aerosol particle composition [66].
Case C: 3 July 2014
An intense dust layer was observed by the lidar between 3.6 and 5.7 km a.s.l. on 3 July 2014 from 21:09 to 21:39 UTC, with values of particle depolarization ratio around 30%, extinction- and backscatter-related Ångström exponents between 0 and 1 and lidar ratio values in the 40–60 sr range, in line with dust aerosol particles in studies from the literature, e.g., [55]. The concurrent giant aerosol layer was observed by the radar between 2.6 and 3.5 km a.s.l. from 22:57 to 23:27 UTC.
The corresponding number, surface, and volume distributions for these layers are shown in Figure 14. The number distribution (Figure 14a) shows that the number of aerosol particles below 1 µm is predominant, and no contribution from larger aerosols is observed. The surface distribution (Figure 14b) for aerosols detected by the lidar has two modes: a main mode from 0.07 to 2 µm radius and a smaller one from 2 to 8 µm. The surface distribution for the aerosols, as measured by the radar, spans from 1 to 12 µm approximately. Therefore, there is an overlap between the aerosol radii measured by the two instruments. In the volume distribution (Figure 14c), this overlap between the coarse aerosols observed by lidar and by radar is even more evident. As in the previous case, the combined information is able to provide an enlarged aerosol size distribution.
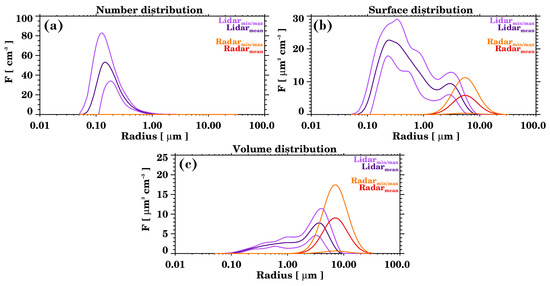
Figure 14.
Case C: (a) number, (b) surface, and (c) volume size distributions for the layers observed on 3 July 2014. The lidar inversion was performed for the layer between 3.6 and 5.7 km a.s.l. from 21:09 to 21:39 UTC. The radar inversion was performed for the layer between 2.6 and 3.5 km a.s.l. from 22:57 to 23:27 UTC.
The mean aerosol microphysical properties retrieved from the radar and lidar measurements for this case are given in Table 7. The effective and mean radius is larger for the aerosols detected by the radar, and the number concentration is two orders of magnitude higher for the lidar. The axis ratio retrieved from the radar data suggests the existence of non-spherical aerosol particles. As for Case B, the differences in aerosol microphysical properties between the lidar and the radar are considerable.

Table 7.
Case C: aerosol microphysical properties retrieved from the radar and lidar measurements for the dust case on 3 July 2014. In the axis ratio, “h” and “v” stand for horizontal and vertical axis, respectively. The – sign means that the variable is not available.
4. Discussion
In this study, we used simultaneous lidar and Ka-band radar aerosol measurements synergistically in order to enlarge the portion of the aerosol size distribution that can be observed and characterized using two different remote sensing technologies. While lidars are commonly used to characterize aerosols, cloud radars are used for the first time to complement lidar observations.
We applied the methodology introduced in Gumà-Claramunt et al. [34] to detect giant aerosols in Ka-band radar observations and developed a novel inversion technique to retrieve their microphysical properties. Leveraging the combined use of radar and lidar retrievals, this study extends the measurable and characterizable portion of the aerosol size distribution. Consequently, the methodology presented in this study offers valuable insights into aerosol microphysical properties, particularly for coarser aerosols.
A total of 22 concurrent lidar and cloud radar aerosol measurements were found for the considered 6-year-long study period. The shape of the backscatter and particle depolarization ratio profiles indicated a mismatch in the vertical structure of the layers, which, as expected, suggests that the instruments observe different parts of the size spectrum in accordance with their different operating wavelengths.
The aerosol microphysical properties were retrieved independently for the two instruments. For the inversion of the lidar data, the methodology developed by Veselovskii et al. [47] was used. For the inversion of the radar data, a new retrieval was designed and presented, using T-matrix calculations from Mishchenko et al. [46]. The reflectivity values retrieved by our methodology reproduced the measured radar reflectivity fairly well, especially for the most frequently observed mean layer’s reflectivity values (between −40 and −30 dB). The inversion method, though, tends to underestimate reflectivity values below −40 dB and to overestimate those over −30 dB. The LDR values tend to be underestimated by the methodology, with the retrieved values being lower than those measured by the radar. The differences between the measured and the estimated reflectivity and LDR values affected the retrieval of the aerosol microphysical properties. The estimated axis ratio, for example, was likely closer to one (sphere) than it should be, due to underestimation of the LDR values. In order to estimate the effect of the reflectivity and LDR discrepancies on the retrieval of the aerosol microphysical properties, a more in-depth analysis should be performed, which could include the use of synthetic data to evaluate the accuracy of the estimates. The difference averaged for all the cases is for the reflectivity and for the LDR. Therefore, the difference is one order of magnitude higher for the LDR, which can be attributed to the LDR corrections applied. This suggests that our method could be improved by including more possibilities in the scattering database, which should account for the higher LDR values. This could involve, for example, including pairs of reflectivity and LDR values for ice-coated particles or particles’ alignment, as reported in Madonna et al. [19]. Therefore, it is important to emphasize that, in its current state, the cloud radar inversion methodology yields results for mineral aerosols only. Moreover, the retrieval of the aerosol microphysical properties can be affected by other sources of uncertainty, such as instrument sensitivity, the used dielectric constant, multiple scattering effects in dense layers, assumptions of particle shapes, and systematic errors. To better understand the effect that these errors and uncertainties can have on the retrieval, an in-depth sensitivity study should be performed to evaluate each of the factors individually.
Selected individual cases have been used to illustrate how Raman lidar and cloud radar measurements can complement one another, thereby extending the size range over which aerosols can be effectively observed and characterized. The combination of the aerosol size distributions, which were retrieved individually from the lidar and the radar measurements, enabled the measurement of an enlarged aerosol size distribution. For the study dataset, it spans approximately from 60 nm to 12 µm radius. With the addition of the aerosol cloud radar measurements, it was possible to retrieve information for aerosol particles over 6 µm, which was the maximum aerosol particle radius retrieved using lidar information only. Both systems measured aerosols with a radius in the 1–6 µm range.
The enhanced aerosol size distribution offers unprecedented insights and a better understanding of aerosols, which might be useful for aerosol transport models’ tuning and evaluation. Nevertheless, further work is needed to better understand the role and importance of these particles in the atmosphere. Furthermore, we lacked an impact study and a clear methodology through which to actually merge the size distributions from the two instruments. For this, different parameters will need to be considered, such as the different field of view of the two instruments, their sensitivities to particle sizes, and retrieval-related uncertainties; such parameters may be obtained using a weighted average, a transition function, or a more elaborate method.
Also, it is important to note that this methodology was developed based solely on the data from one observational site; therefore, an evaluation of whether our method can be applied to other observational sites will be needed.
In the future, a longer dataset may be considered, which apart from reducing the uncertainties arising from the limited dataset would enable a thorough validation of the results. Since the retrieval of the aerosols’ microphysical properties from the radar measurements is based solely on the reflectivity and LDR measurements, the evaluation of the uncertainties and the validation of the results also using independent datasets is very important. CIAO is equipped with numerous instruments enabling direct dataset comparisons (e.g., AERONET and in situ measurements). Furthermore, campaign datasets with airborne in situ sampling (e.g., PRE-TECT [67]) can offer unprecedented insights into our methodology.
To obtain a longer dataset, the two methodologies employed in this study for the detection and characterization of giant aerosols using cloud radar observations could be implemented operationally. This would expand the cloud radar dataset related to giant aerosols and facilitate near-real-time monitoring of their presence in the atmosphere—for example, involving volcanic and dust intrusions—owing to the continuous operation of the radars. In conjunction with the increasingly frequent measurement schedule of the EARLINET network, this could support the expansion of the dataset utilized in this study and enable a more comprehensive analysis.
5. Conclusions
This study successfully extends the observable portion of aerosol size distribution using remote sensing techniques. By combining Raman lidar and Ka-band radar observations of a six-year dataset collected in Potenza, Italy, we retrieved aerosol microphysical properties within a size range of approximately 60 nm to 12 µm. This represents a significant improvement over the 60 nm to 6 µm range retrievable with lidar measurements alone.
To accomplish this, independent inversion algorithms were applied to the lidar and radar datasets. The retrieved aerosol size distributions corresponding to each instrument are presented separately, showing their respective contributions. While the inversion algorithm applied to the lidar data is well established and widely used within the lidar remote sensing community, the radar inversion algorithm was newly developed as part of this study. As such, several areas for improvement are identified, including the expansion of the reference scattering database, enlargement of the dataset, a comprehensive evaluation of associated uncertainties, and the need for further validation against independent observations.
Although the methodology requires further development and comprehensive evaluation, the extension of the measurable aerosol size range represents a significant advancement, particularly with respect to giant and ultragiant aerosol particles. These aerosol particles are still not well understood and are often underestimated in atmospheric transport models.
Author Contributions
Conceptualization, A.A., F.M. and P.G.-C.; methodology, P.G.-C. and F.M.; software, P.G.-C.; validation, A.A. and F.M.; formal analysis, A.A. and P.G.-C.; data curation, A.A. and P.G.-C.; resources, G.P.; writing—original draft preparation, P.G.-C.; writing—review and editing, A.A., F.M., N.P., B.D.R., C.-A.P. and M.R.; visualization, P.G.-C.; supervision, A.A. and F.M.; project administration, A.A.; funding acquisition, G.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Community through the ACTRIS Research Infrastructure Action under the 7th Framework Programme under ACTRIS Grant Agreement n° 262254 and ITaRS Grant Agreement n° 289923, by the Italian national project “Programma Operativo Nazionale (PON) Regione Basilicata 2000/2006”, and by IR0000032—ITINERIS, Italian Integrated Environmental Research Infrastructures System (D.D. no. 130/2022—CUP B53C22002150006), funded by the EU—Next-Generation EU PNRR-Mission 4 “Education and Research”—Component 2: “From research to business”—Investment 3.1: “Fund for the realization of an integrated system of research and innovation infrastructure”.
Data Availability Statement
Data Availability Statement: The MIRA36 Ka-band Doppler radar data can be accessed on the CLOUDNET website (https://cloudnet.fmi.fi/search/data?site=potenza, accessed on 30 May 2025), whilst the lidar data is available in the ACTRIS-EARLINET Database (https://data.earlinet.org, accessed on 30 May 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACTRIS | Aerosol, Clouds and Trace Gases Research Infrastructure |
| AERONET | Aerosol Robotic Network |
| CALIPSO | Cloud–Aerosol Lidar and Infrared Pathfinder Satellite Observations |
| CCN | Cloud Condensation Nuclei |
| CIAO | CNR-IMAA Atmospheric Observatory |
| CBL | Convective Boundary Layer |
| EARLINET | European Aerosol Research LIdar NETwork |
| FLEXPART | FLEXible PARTicle dispersion model |
| GCOS | Global Climate Observing System |
| GRUAN | GCOS Reference Upper-Air Network |
| ICOS | Integrated Carbon Observation System |
| IN | Ice Nuclei |
| LDR | Linear Depolarization Ratio |
| MUSA | Multiwavelength System for Aerosol |
| PEARL | Potenza EArlinet Raman Lidar |
| RMS | Peak Width |
| SNR | Signal-to-Noise Ratio |
| UTC | Coordinated Universal Time |
| VEL | Doppler Velocity |
| Z | Equivalent Reflectivity |
Appendix A. List of Cases

Table A1.
Lidar measurements performed at the site simultaneously to cloud radar giant aerosol observations.
Table A1.
Lidar measurements performed at the site simultaneously to cloud radar giant aerosol observations.
| Conditions | System | Case | Date | Time UTC [hh:mm] |
|---|---|---|---|---|
| Day | MUSA | 1 | 12/05/2013 | 10:52–12:20 |
| 2 (A) | 29/07/2013 | 13:59–14:59 | ||
| 3 | 05/08/2013 | 13:00–13:56 | ||
| 4 | 23/09/2013 | 13:05–13:35 | ||
| 5 | 25/08/2014 | 14:12–15:12 | ||
| 6 | 12/01/2015 | 12:39–13:09 | ||
| 7 | 12/01/2015 | 14:30–15:00 | ||
| PEARL | 8 | 13/07/2009 | 10:32–11:02 | |
| 9 | 10/05/2010 | 14:00–14:15 | ||
| 10 | 13/05/2010 | 11:55–12:03 | ||
| 11 | 20/05/2013 | 12:10–13:11 | ||
| Night | MUSA | 12 (B) | 19/06/2013 | 19:27–19:57 |
| 13 | 16/09/2013 | 18:15–18:43 | ||
| 14 | 19/09/2013 | 19:09–20:09 | ||
| 15 | 23/09/2013 | 17:40–18:56 | ||
| 16 | 26/09/2013 | 18:00–18:59 | ||
| 17 | 18/02/2014 | 17:52–18:23 | ||
| 18 (C) | 03/07/2014 | 21:09–21:39 | ||
| 19 | 16/10/2014 | 19:00–19:30 | ||
| PEARL | 20 | 13/07/2009 | 19:45–21:15 | |
| 21 | 19/04/2010 | 20:03–20:33 | ||
| 22 | 17/06/2013 | 19:27–21:13 |

Table A2.
Lidar measurements performed at the site simultaneously to cloud radar insect observations.
Table A2.
Lidar measurements performed at the site simultaneously to cloud radar insect observations.
| Conditions | System | Case | Date | Time UTC [hh:mm] |
|---|---|---|---|---|
| Day | MUSA | 23 | 08/08/2011 | 12:39–12:59 |
| 24 | 29/08/2012 | 10:44–11:04 | ||
| 25 | 29/08/2012 | 13:23–13:53 | ||
| 26 | 25/10/2012 | 11:55–13:51 | ||
| Night | MUSA | 27 | 18/11/2009 | 00:00–00:30 |
| 28 | 26/08/2010 | 18:52–19:37 | ||
| 29 | 18/08/2011 | 19:15–19:35 | ||
| 30 | 09/08/2012 | 20:47–21:18 | ||
| 31 | 22/07/2013 | 19:21–21:40 | ||
| 32 | 05/08/2013 | 18:54–19:28 | ||
| 33 | 22/05/2014 | 19:29–21:10 | ||
| 34 | 23/06/2014 | 20:00–21:00 | ||
| 35 | 25/06/2014 | 00:10–00:50 | ||
| 36 | 30/06/2014 | 20:08–20:38 | ||
| 37 | 03/07/2014 | 19:33–20:33 | ||
| 38 | 04/08/2014 | 21:50–22:20 | ||
| 39 | 04/05/2015 | 20:40–21:20 | ||
| 40 | 29/05/2015 | 21:51–22:51 |
References
- Jickells, T.D.; Baker, A.R.; Chance, R. Atmospheric transport of trace elements and nutrients to the oceans. Phil. Trans. R. Soc. A 2016, 374, 20150286. [Google Scholar] [CrossRef] [PubMed]
- Fröhlich-Nowoisky, J.; Kampf, C.J.; Weber, B.; Huffman, J.A.; Pöhlker, C.; Andreae, M.O.; Lang-Yona, N.; Burrows, S.M.; Gunthe, S.S.; Elbert, W.; et al. Bioaerosols in the Earth system: Climate, health, and ecosystem interactions. Atmos. Res. 2016, 182, 346–376. [Google Scholar] [CrossRef]
- Pappalardo, G.; Mona, L.; D’Amico, G.; Wandinger, U.; Adam, M.; Amodeo, A.; Ansmann, A.; Apituley, A.; Alados Arboledas, L.; Balis, D.; et al. Four-dimensional distribution of the 2010 Eyjafjallajökull volcanic cloud over Europe observed by EARLINET. Atmos. Chem. Phys. 2013, 13, 4429–4450. [Google Scholar] [CrossRef]
- Scherllin-Pirscher, B.; Nickovic, S.; Votsis, A.; Cvetkovic, B.; Amiridis, V.; Bolic, T.; Brenot, H.; Brock, G.; Clarkson, R.J.; Durant, A.; et al. Airborne Soil-Derived Dust Hazards in Aviation. Bull. Am. Meteorol. Soc. 2025, 106, E125–E145. [Google Scholar] [CrossRef]
- Putaud, J.P.; Van Dingenen, R.; Alastuey, A.; Bauer, H.; Birmili, W.; Cyrys, J.; Flentje, H.; Fuzzi, S.; Gehrig, R.; Hansson, H.; et al. A European aerosol phenomenology—3: Physical and chemical characteristics of particulate matter from 60 rural, urban, and kerbside sites across Europe. Atmos. Environ. 2010, 44, 1308–1320. [Google Scholar] [CrossRef]
- Myhre, G.; Myhre, C.E.; Samset, B.H.; Storelvmo, T. Aerosols and their Relation to Global Climate and Climate Sensitivity. Nat. Educ. Knowl. 2013, 4, 7. [Google Scholar]
- Ryder, C.L.; Highwood, E.J.; Rosenberg, P.D.; Trembath, J.; Brooke, J.K.; Bart, M.; Dean, A.; Crosier, J.; Dorsey, J.; Brindley, H.; et al. Optical properties of Saharan dust aerosol and contribution from the coarse mode as measured during the Fennec 2011 aircraft campaign. Atmos. Chem. Phys. 2013, 13, 303–325. [Google Scholar] [CrossRef]
- Otto, S.; de Reus, M.; Trautmann, T.; Thomas, A.; Wendisch, M.; Borrmann, S. Atmospheric radiative effects of an in situ measured Saharan dust plume and the role of large particles. Atmos. Chem. Phys. 2007, 7, 4887–4903. [Google Scholar] [CrossRef]
- Kok, J.F.; Ridley, D.A.; Zhou, Q.; Miller, R.L.; Zhao, C.; Heald, C.L.; Ward, D.S.; Albani, S. Smaller desert dust cooling effect estimated from analysis of dust size and abundance. Nat. Geosci. 2017, 10, 274–278. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Andreae, M.O.; Asmi, A.; Chin, M.; de Leeuw, G.; Donovan, D.P.; Kahn, R.; Kinne, S.; Kivekäs, N.; Kulmala, M.; et al. Global observations of aerosol-cloud-precipitation-climate interactions. Rev. Geophys. 2014, 52, 750–808. [Google Scholar] [CrossRef]
- Dagan, G.; Koren, I.; Altaratz, O. Aerosol effects on the timing of warm rain processes. Geophys. Res. Lett. 2015, 42, 4590–4598. [Google Scholar] [CrossRef]
- Feingold, G.; Cotton, W.; Kreidenweis, S.; Davis, J. The Impact of Giant Cloud Condensation on Drizzle Formation in Stratocumulus: Implications for Cloud Radiative Properties. J. Atmos. Sci. 1999, 56, 4100–4117. [Google Scholar] [CrossRef]
- Eagan, R.; Hobbs, P.; Radke, L. Measurements of CCN and cloud droplet size distribution in the vicinity of forest fires. J. Appl. Meteor. 1974, 13, 553–557. [Google Scholar] [CrossRef]
- DeMott, P.J.; Sassen, K.; Poellot, M.R.; Baumgardner, D.; Rogers, D.C.; Brooks, S.D.; Prenni, A.J.; Kreidenweis, S.M. African dust aerosols as atmospheric ice nuclei. Geophys. Res. Lett. 2003, 30, 1732. [Google Scholar] [CrossRef]
- Möhler, O.; Field, P.R.; Connolly, P.; Benz, S.; Saathoff, H.; Schnaiter, M.; Wagner, R.; Cotton, R.; Krämer, M.; Mangold, A.; et al. Efficiency of the deposition mode ice nucleation on mineral dust particles. Atmos. Chem. Phys. 2006, 6, 3007–3021. [Google Scholar] [CrossRef]
- Kassianov, E.; Pekour, M.; Barnard, J. Aerosols in central California: Unexpectedly large contribution of coarse mode to aerosol radiative forcing. Geophys. Res. Lett. 2012, 39, L20806. [Google Scholar] [CrossRef] [PubMed]
- Drakaki, E.; Amiridis, V.; Tsekeri, A.; Gkikas, A.; Proestakis, E.; Mallios, S.; Solomos, S.; Spyrou, C.; Marinou, E.; Ryder, C.L.; et al. Modeling coarse and giant desert dust particles. Atmos. Chem. Phys. 2022, 22, 12727–12748. [Google Scholar] [CrossRef]
- Madonna, F.; Amodeo, A.; D’Amico, G.; Mona, L.; Pappalardo, G. Observation of non-spherical ultragiant aerosol using a microwave radar. Geophys. Res. Lett. 2010, 37, L21814. [Google Scholar] [CrossRef]
- Madonna, F.; Amodeo, A.; D’Amico, G.; Pappalardo, G. A study on the use of radar and lidar for characterizing ultragiant aerosol. Geophys. Res. 2013, 118, 10056–10071. [Google Scholar] [CrossRef]
- Méndez Harper, J.; Harvey, D.; Huang, T.; McGrath, J., III; Meer, D.; Burton, J.C. The lifetime of charged dust in the atmosphere. PNAS Nexus 2022, 1, pgac220. [Google Scholar] [CrossRef]
- Huneeus, N.; Schulz, M.; Balkanski, Y.; Griesfeller, J.; Prospero, J.; Kinne, S.; Bauer, S.; Boucher, O.; Chin, M.; Dentener, F.; et al. Global dust model intercomparison in AeroCom phase I. Atmos. Chem. Phys. 2011, 11, 7781–7816. [Google Scholar] [CrossRef]
- Ginoux, P.; Prospero, J.; Gill, T.; Hsu, N. Natural and anthropogenic dust: From sources to radiative forcing derived from satellite data and GFDL climate model. In Proceedings of the Fall Meeting, American Geophysical Union, San Francisco, CA, USA, 5–9 December 2011. [Google Scholar]
- van der Does, M.; Knippertz, P.; Zschenderlein, P.; Harrison, R.G.; Stuut, J.B.W. The mysterious long-range transport of giant mineral dust particles. Sci. Adv. 2018, 4, eaau2768. [Google Scholar] [CrossRef]
- Ratcliffe, N.G.; Ryder, C.L.; Bellouin, N.; Woodward, S.; Jones, A.; Johnson, B.; Wieland, L.M.; Dollner, M.; Gasteiger, J.; Weinzierl, B. Long-range transport of coarse mineral dust: An evaluation of the Met Office Unified Model against aircraft observations. Atmos. Chem. Phys. 2024, 24, 12161–12181. [Google Scholar] [CrossRef]
- Müller, D.; Ansmann, A.; Mattis, I.; Wandinger, U.; Althausen, D.; Dubovik, O. Retrieval of physical particle properties from multiwavelength lidar measurements. Appl. Opt. 1999, 38, 2346–2357. [Google Scholar] [CrossRef]
- Veselovskii, I.; Kolgotin, A.; Griaznov, V.; Müller, D.; Wandinger, U.; Ansmann, A. Inversion with regularization for the retrieval of tropospheric aerosol parameters from multiwavelength lidar sounding. Appl. Opt. 2002, 41, 3685–3699. [Google Scholar] [CrossRef] [PubMed]
- Böckmann, C.; Mironova, I.; Müller, D.; Schneidenbach, L.; Nessler, R. Microphysical aerosol parameters from multiwavelength lidar. J. Opt. Soc. Am. A 2005, 22, 518–528. [Google Scholar] [CrossRef] [PubMed]
- McLean, C.N.; Müller, D.; Hsiao, T.C.; Baars, H.; Yin, D.; Lin, T.H.; Chang, S.C. Aerosol microphysical properties from multiwavelength Raman and depolarization lidar: A study in Central Taiwan during springtime pollution events. Atmos. Meas. Tech. 2021, 14, 3851–3866. [Google Scholar]
- Ansmann, A.; Müller, D. Lidar and atmospheric aerosol particles. Atmos. Environ. 2005, 39, 3125–3137. [Google Scholar] [CrossRef]
- Veselovskii, I.; Kolgotin, A.; Griaznov, V.; Müller, D.; Franke, K.; Whiteman, D.N. Inversion of multiwavelength Raman lidar data for retrieval of bimodal aerosol size distribution. Appl. Opt. 2004, 43, 1180–1195. [Google Scholar] [CrossRef]
- Lopatin, A.; Dubovik, O.; Chaikovsky, A.; Boers, R.; Goloub, P.; Litvinov, P.; Derimian, Y.; Fedotenko, T.; Tanré, D. Enhancement of aerosol characterization using synergy of lidar and sun-photometer coincident observations: The GARRLiC algorithm. Atmos. Meas. Tech. 2013, 6, 2065–2088. [Google Scholar] [CrossRef]
- Müller, D.; Bravo-Aranda, J.A.; Guerrero-Rascado, J.L.; Granados-Muñoz, M.J.; Antonovich, A.; Dubovik, O.; Alados-Arboledas, L. Synergetic aerosol characterization from lidar and sun photometer observations: Method improvements and applications. J. Quant. Spectrosc. Radiat. Transf. 2013, 133, 646–653. [Google Scholar] [CrossRef]
- Chang, F.L.; Müller, D.; Yin, D.; McLean, C.N.; Tsai, F.; Tsai, C.; Hsiao, T.C. Bayesian optimization of aerosol microphysical retrievals from multiwavelength Raman lidar. Atmos. Meas. Tech. 2022, 15, 1747–1763. [Google Scholar]
- Gumà-Claramunt, P.; Madonna, F.; Amodeo, A.; Bauer-Pfundstein, M.; Papagiannopoulos, N.; Rosoldi, M.; Pappalardo, G. Giant Aerosol Observations with Cloud Radar: Methodology and Effects. Remote Sens. 2025, 17, 419. [Google Scholar] [CrossRef]
- Madonna, F.; Amodeo, A.; Boselli, A.; Cornacchia, C.; Cuomo, V.; D’Amico, G.; Giunta, A.; Mona, L.; Pappalardo, G. CIAO: The CNR-IMAA advanced observatory for atmospheric research. Atmos. Meas. Tech. 2011, 4, 1191–1208. [Google Scholar] [CrossRef]
- Mona, L.; Papagiannopoulos, N.; Basart, S.; Baldasano, J.; Binietoglou, I.; Cornacchia, C.; Pappalardo, G. EARLINET dust observations vs. BSC-DREAM8b modeled profiles: 12-year-long systematic comparison at Potenza, Italy. Atmos. Chem. Phys. 2014, 14, 8781–8793. [Google Scholar] [CrossRef]
- De Rosa, B.; Mytilinaios, M.; Amodeo, A.; Colangelo, C.; D’Amico, G.; Dema, C.; Gandolfi, I.; Giunta, A.; Gumà-Claramunt, P.; Laurita, T.; et al. Observations of Saharan Dust Intrusions over Potenza, Southern Italy, During 13 Years of Lidar Measurements: Seasonal Variability of Optical Properties and Radiative Impact. Remote Sens. 2025, 17, 453. [Google Scholar] [CrossRef]
- Pappalardo, G.; Amodeo, A.; Mona, L.; Pandolfi, M.; Pergola, N.; Cuomo, V. Raman lidar observations of aerosol emitted during the 2002 Etna eruption. Geophys. Res. Lett. 2004, 31, L05120-1. [Google Scholar] [CrossRef]
- Rosoldi, M.; Coppa, G.; Merlone, A.; Musacchio, C.; Madonna, F. Intercomparison of Vaisala RS92 and RS41 Radiosonde Temperature Sensors under Controlled Laboratory Conditions. Atmosphere 2022, 13, 773. [Google Scholar] [CrossRef]
- Lapenna, E.; Buono, A.; Mauceri, A.; Zaccardo, I.; Cardellicchio, F.; D’Amico, F.; Laurita, T.; Amodio, D.; Colangelo, C.; Di Fiore, G.; et al. ICOS Potenza (Italy) Atmospheric Station: A New Spot for the Observation of Greenhouse Gases in the Mediterranean Basin. Atmosphere 2025, 16, 57. [Google Scholar] [CrossRef]
- Laurita, T.; Mauceri, A.; Cardellicchio, F.; Lapenna, E.; De Rosa, B.; Trippetta, S.; Mytilinaios, M.; Amodio, D.; Giunta, A.; Ripepi, E.; et al. CIAO main upgrade: Building up an ACTRIS-compliant aerosol in situ laboratory. Atmos. Meas. Tech. 2025, 18, 2373–2396. [Google Scholar] [CrossRef]
- Pappalardo, G.; Wandinger, U.; Mona, L.; Hiebsch, A.; Mattis, I.; Amodeo, A.; Ansmann, A.; Seifert, P.; Linné, H.; Apituley, A.; et al. EARLINET correlative measurements for CALIPSO: First intercomparison results. J. Geophys. Res. Atmos. 2010, 115, D00H19. [Google Scholar] [CrossRef]
- Ansmann, A.; Riebesell, M.; Weitkamp, C. Measurement of atmospheric aerosol extinction profiles with a Raman lidar. Opt. Lett. 1990, 15, 746–748. [Google Scholar] [CrossRef]
- Pappalardo, G.; Amodeo, A.; Pandolfi, M.; Wandinger, U.; Ansmann, A.; Bösenberg, J.; Matthias, V.; Amiridis, V.; Tomasi, F.D.; Frioud, M.; et al. Aerosol lidar intercomparison in the framework of the EARLINET project. 3. Raman lidar algorithm for aerosol extinction, backscatter, and lidar ratio. Appl. Opt. 2004, 43, 5370–5385. [Google Scholar] [CrossRef]
- Di Girolamo, P.; Ambrico, P.F.; Amodeo, A.; Boselli, A.; Pappalardo, G.; Spinelli, N. Aerosol observations by lidar in the nocturnal boundary layer. Appl. Opt. 1999, 38, 4585–4595. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Mackowski, D.W. T-matrix computations of light scattering by nonspherical particles: A review. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 535–575. [Google Scholar] [CrossRef]
- Veselovskii, I.; Dubovik, O.; Kolgotin, A.; Lapyonok, T.; Di Girolamo, P.; Summa, D.; Whiteman, D.; Mishchenko, M.; Tanre, M. Application of randomly oriented spheroids for retrieval of dust particle parameters from multiwavelength lidar measurements. J. Geophys. Res. 2010, 115, D21203. [Google Scholar] [CrossRef]
- Bass, M.; DeCusatis, C.; Enoch, J.; Lakshminarayanan, V.; Li, G.; Mac-Donald, C.; Mahajan, V.; Stryland, E.V. Handbook of Optics, Third Edition Volume I: Geometrical and Physical Optics, Polarized Light, Components and Instrument, 3rd ed.; McGraw-Hill Professional: New York, NY, USA, 2009. [Google Scholar]
- Van de Hulst, H. Light Scattering by Small Particles; Dover Publications: Mineola, NY, USA, 1981. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Adams, R.; Perger, F.; Rose, W.; Kostinski, A. Measurements of the complex dielectric constant of volcanic ash from 4 to 19 GHz. J. Geophys. Res. 1996, 101, 8175–8185. [Google Scholar] [CrossRef]
- Lasher-Trapp, S.; Stachnik, J.P. Giant and ultragiant aerosol particle variability over the eastern Great Lakes region. J. Appl. Meteorol. Climatol. 2007, 46, 651–659. [Google Scholar] [CrossRef][Green Version]
- Vivekanandan, J.; Adams, W.; Bringi, V. Rigorous approach to polarimetric radar modeling of hydrometeor orientation distributions. J. Appl. Meteorol. 1991, 30, 1053–1063. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J.; King, M.D.; Tanré, D.; Slutsker, I. Variability of absorption and optical properties of key aerosol types observed in worldwide locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar] [CrossRef]
- Groß, S.; Esselborn, M.; Weinzierl, B.; Wirth, M.; Fix, A.; Petzold, A. Aerosol classification by airborne high spectral resolution lidar observations. Atmos. Chem. Phys. 2013, 13, 2487–2505. [Google Scholar] [CrossRef]
- Papagiannopoulos, N.; Mona, L.; Amodeo, A.; D’Amico, G.; Gumà Claramunt, P.; Pappalardo, G.; Alados-Arboledas, L.; Guerrero-Rascado, J.L.; Amiridis, V.; Kokkalis, P.; et al. An automatic observation-based aerosol typing method for EARLINET. Atmos. Chem. Phys. 2018, 18, 15879–15901. [Google Scholar] [CrossRef]
- Amiridis, V.; Giannakaki, E.; Balis, D.; Gerasopoulos, E.; Pytharoulis, I.; Zanis, P.; Kazadzis, S.; Melas, D.; Zerefos, C. Smoke injection heights from agricultural burning in Eastern Europe as seen by CALIPSO. Atmos. Chem. Phys. 2010, 10, 11567–11576. [Google Scholar] [CrossRef]
- Burton, S.; Ferrare, R.; Vaughan, M.; Omar, A.; Rogers, R.; Hostetler, C.; Hair, J. Aerosol classification from airborne HSRL and comparisons with the CALIPSO vertical feature mask. Atmos. Meas. Tech. 2013, 6, 1397–1412. [Google Scholar] [CrossRef]
- Giglio, L.; Boschetti, L.; Roy, D.; Humber, M.; Hall, J.; Zubkova, M.; Schroeder, W.; Justice, C. MODIS Active Fire Product. Available online: https://firms.modaps.eosdis.nasa.gov/active_fire/ (accessed on 29 July 2025).
- Exton, H.J.; Latham, J.; Park, P.M.; Smith, M.H.; Allan, R.R. The Production and Dispersal of Maritime Aerosol. In Oceanic Whitecaps: And Their Role in Air-Sea Exchange Processes; Monahan, E.C., Niocaill, G.M., Eds.; Springer: Dordrecht, The Netherlands, 1986; pp. 175–193. [Google Scholar] [CrossRef]
- Huang, Y.; Kok, J.F.; Kandler, K.; Lindqvist, H.; Nousiainen, T.; Sakai, T.; Adebiyi, A.; Jokinen, O. Climate Models and Remote Sensing Retrievals Neglect Substantial Desert Dust Asphericity. Geophys. Res. Lett. 2020, 47, e2019GL086592. [Google Scholar] [CrossRef]
- Martin, R.S.; Mather, T.A.; Pyle, D.M.; Power, M.; Allen, A.G.; Aiuppa, A.; Horwell, C.J.; Ward, E.P.W. Composition-resolved size distributions of volcanic aerosols in the Mt. Etna plumes. J. Geophys. Res. Atmos. 2008, 113, D17211. [Google Scholar] [CrossRef]
- Li, M.; Tian, C.F.; Idrees, M.; Pathak, M.; Xiong, X.H.; Gao, X.F.; Wang, X.R. Pollen Morphology in Sorbus L. (Rosaceae) and Its Taxonomic Implications. Plants 2023, 12, 3318. [Google Scholar] [CrossRef]
- Derimian, Y.; Dubovik, O.; Tanre, D.; Goloub, P.; Lapyonok, T.; Mortier, A. Optical properties and radiative forcing of the Eyjafjallajökull volcanic ash layer observed over Lille, France, in 2010. J. Geophys. Res. Atmos. 2012, 117, D00U25. [Google Scholar] [CrossRef]
- Barreto, A.; García, R.D.; Guirado-Fuentes, C.; Cuevas, E.; Almansa, A.F.; Milford, C.; Toledano, C.; Expósito, F.J.; Díaz, J.P.; León-Luis, S.F. Aerosol characterisation in the subtropical eastern North Atlantic region using long-term AERONET measurements. Atmos. Chem. Phys. 2022, 22, 11105–11124. [Google Scholar] [CrossRef]
- Zhang, Y.; Saito, M.; Yang, P.; Schuster, G.; Trepte, C. Sensitivities of Spectral Optical Properties of Dust Aerosols to Their Mineralogical and Microphysical Properties. J. Geophys. Res. Atmos. 2024, 129, e2023JD040181. [Google Scholar] [CrossRef]
- National Observatory of Athens, in the Frame of ACTRIS. The PRE-TECT Campaign: Revealing the Secrets of Desert Dust. Available online: http://pre-tect.space.noa.gr/ (accessed on 11 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).