Mechanisms of Ocean Acidification in Massachusetts Bay: Insights from Modeling and Observations
Abstract
1. Introduction
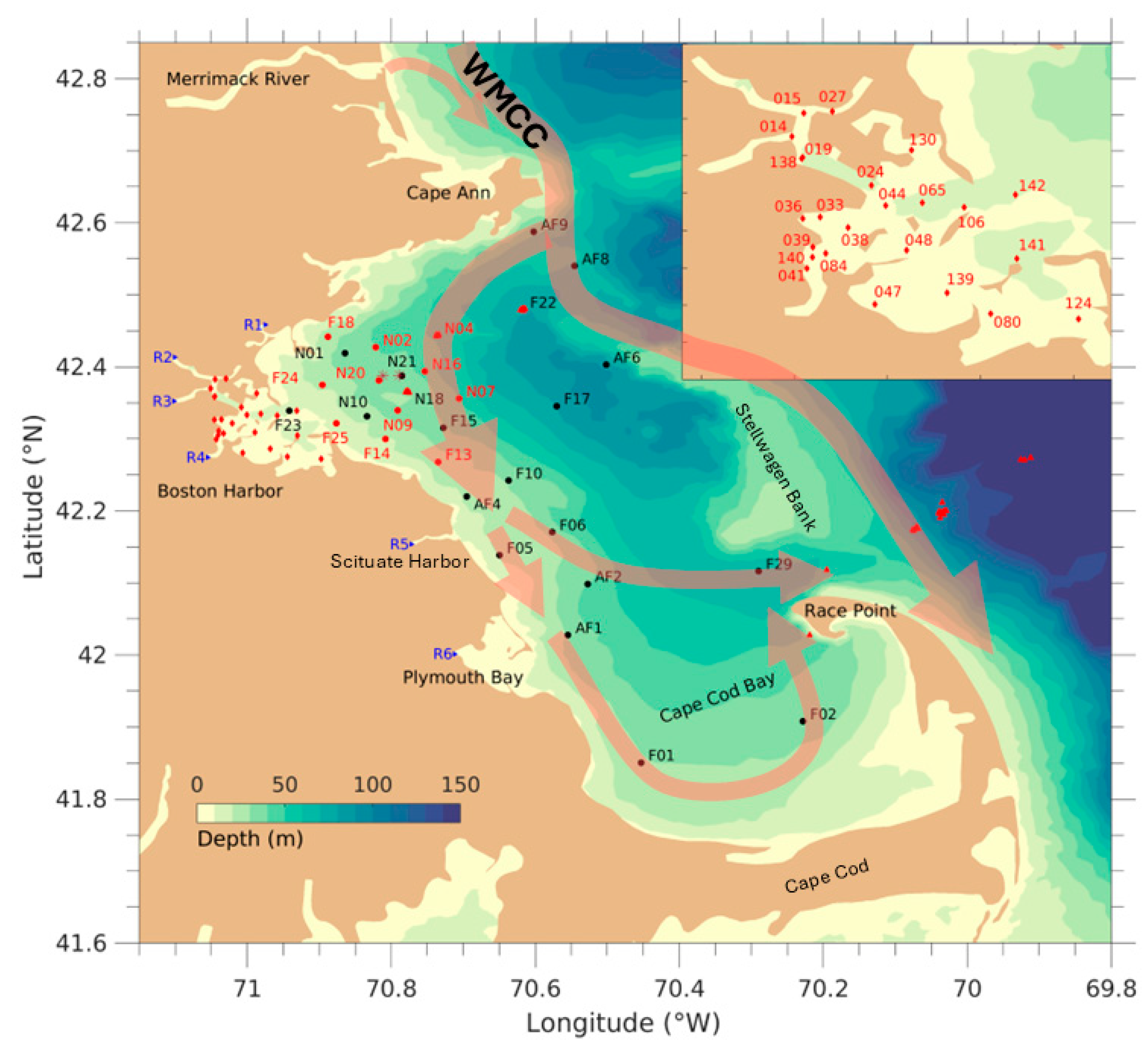
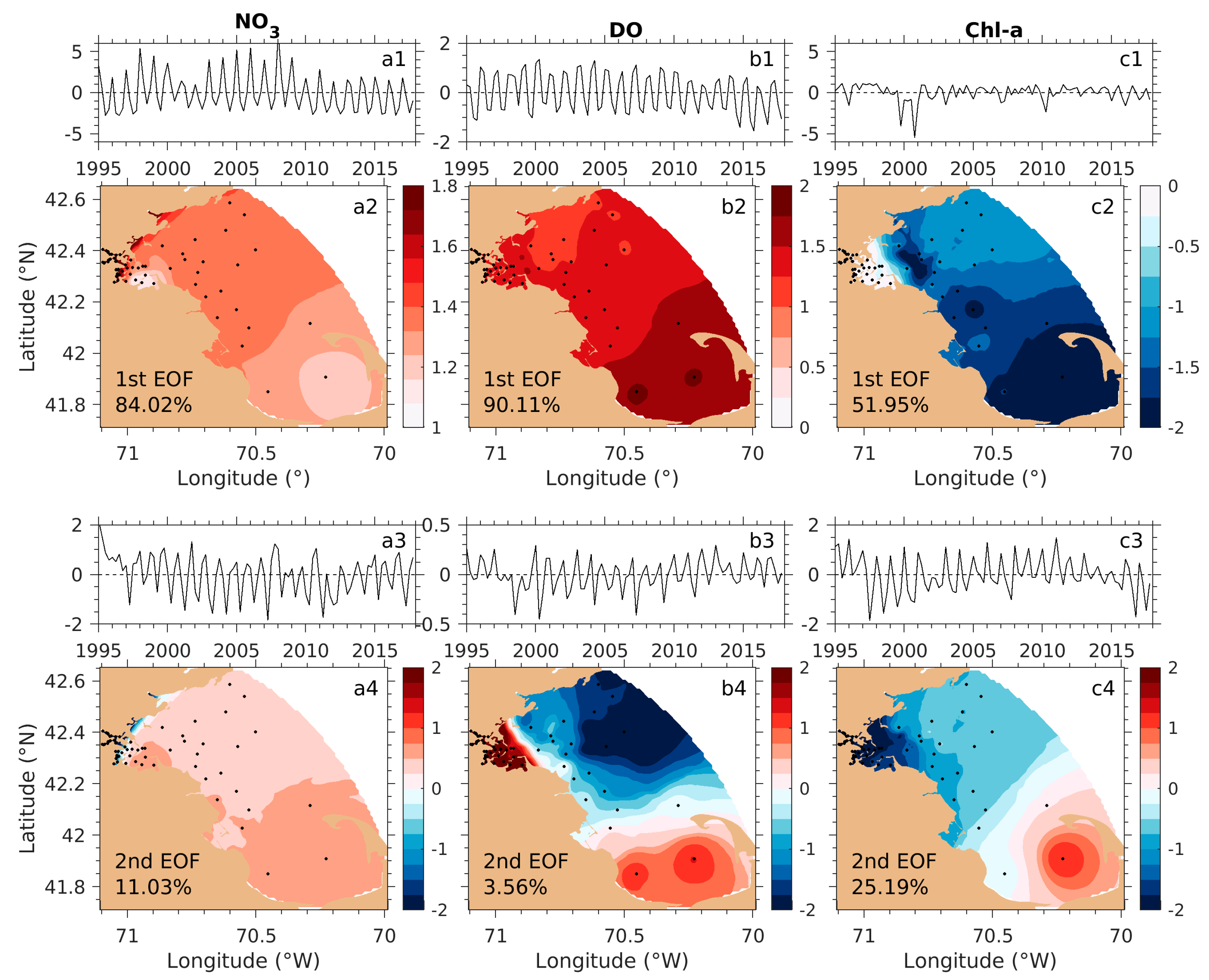
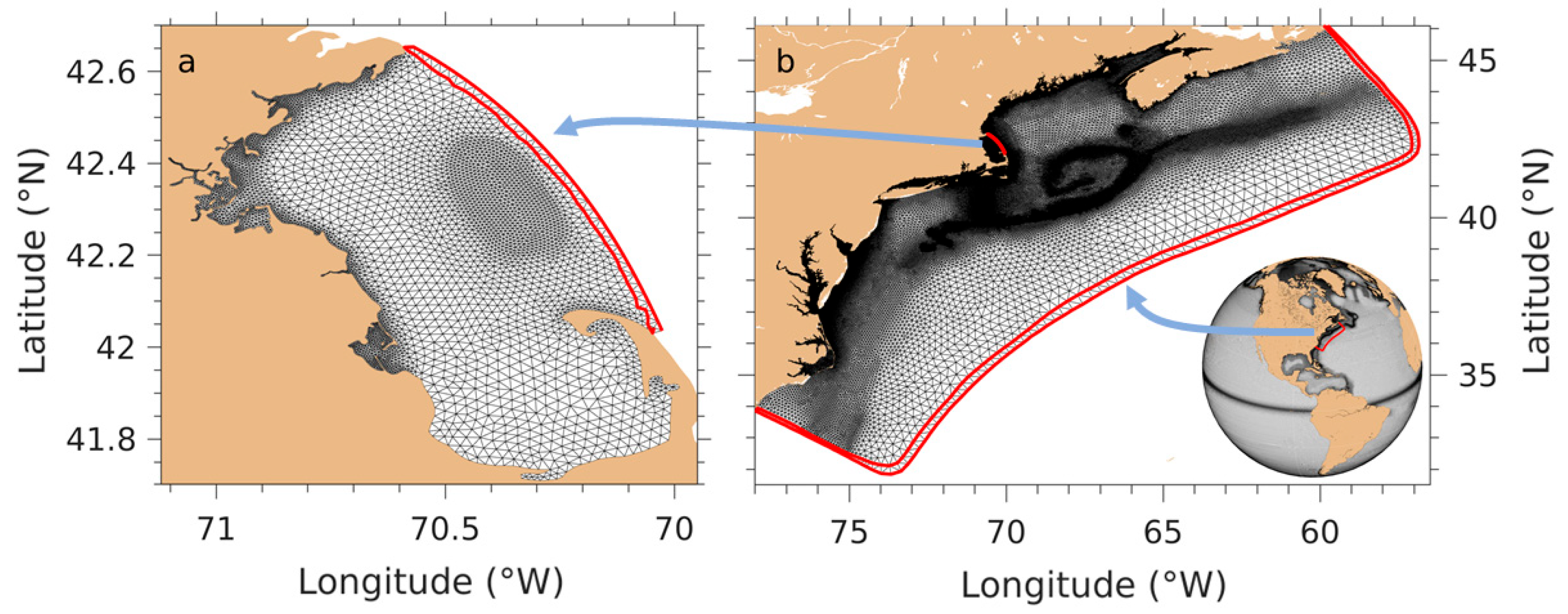
2. The Model, Numerical Designs, and Data
2.1. NeBEM
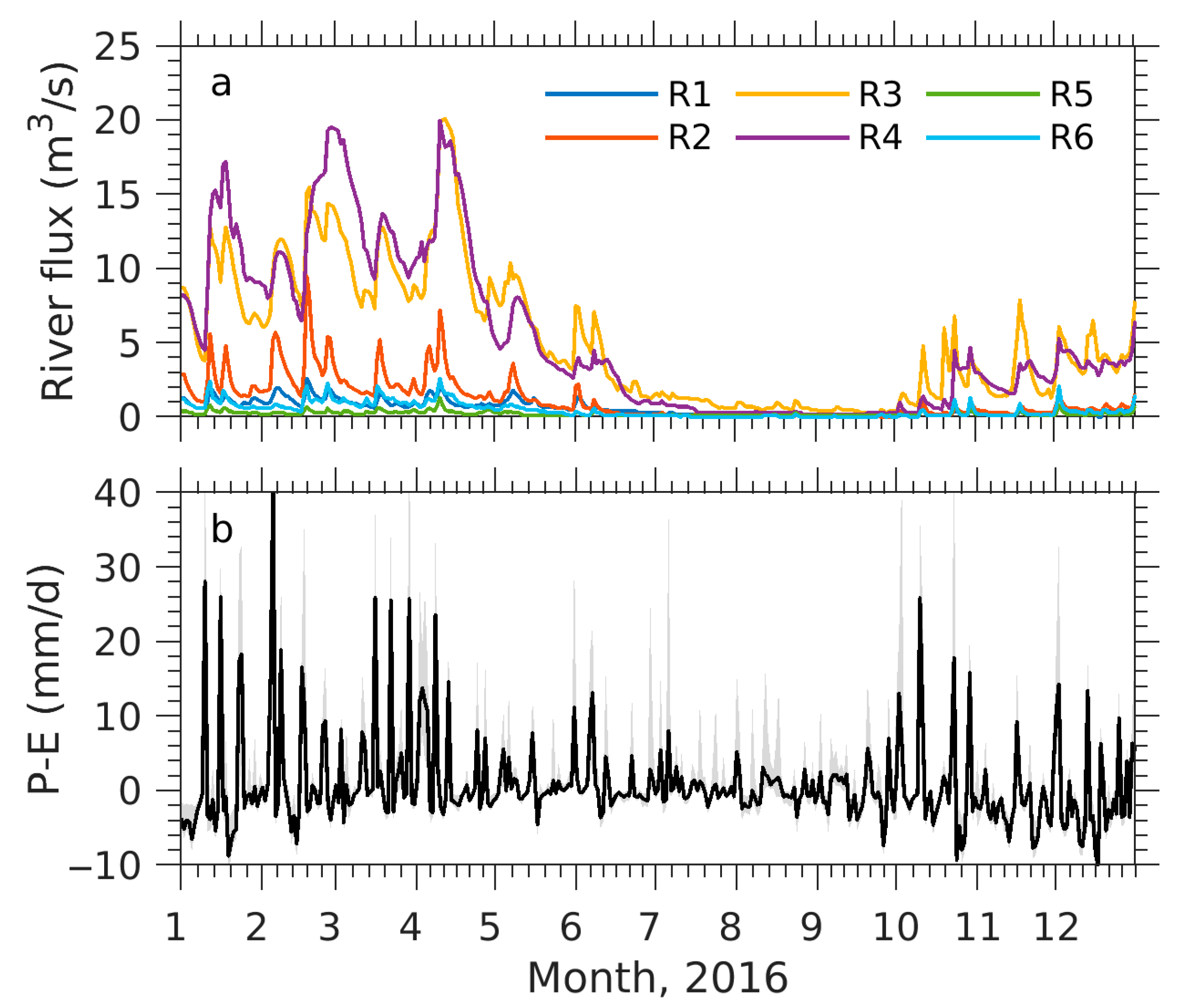
2.2. Numerical Experiment Designs
2.3. Data and Model Assessment Skills
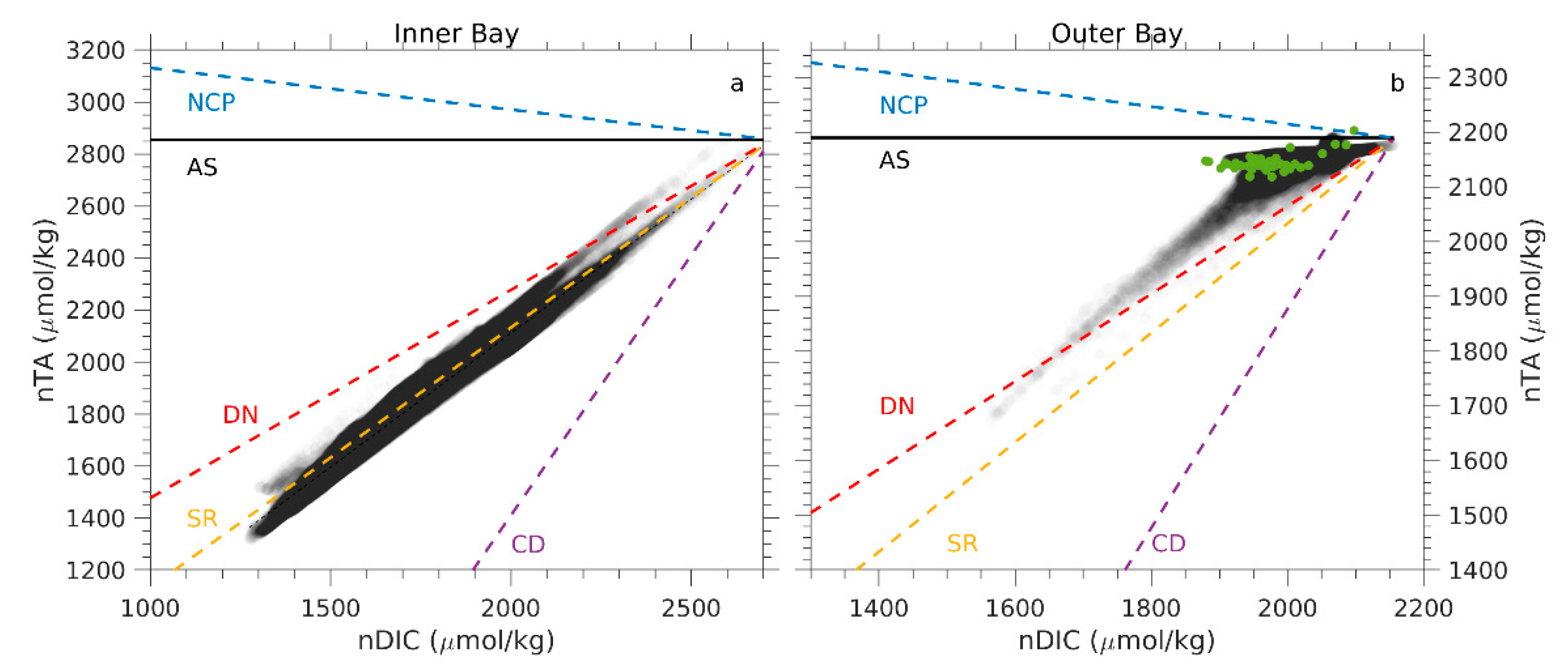
2.4. Salinity Normalization Approach
3. Results
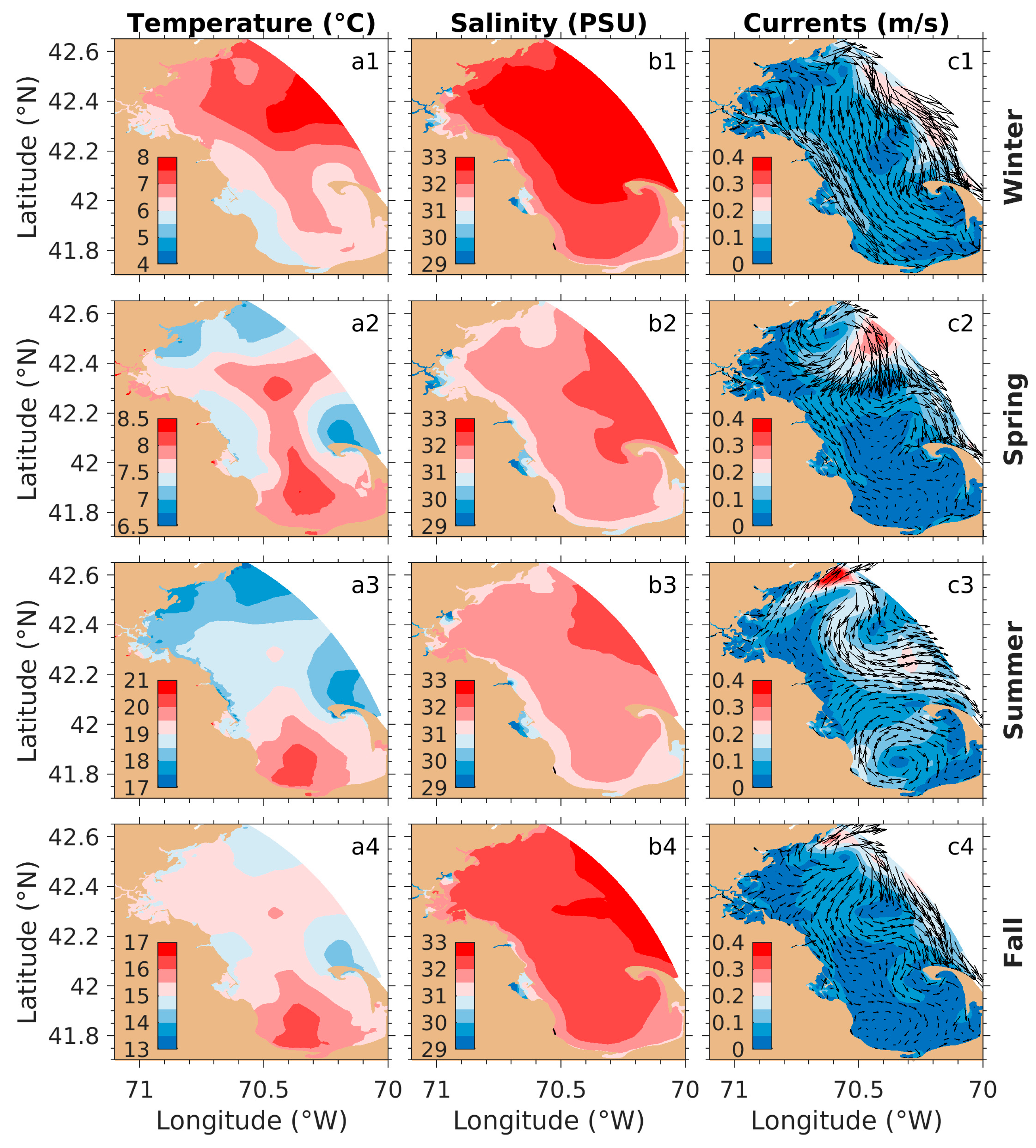
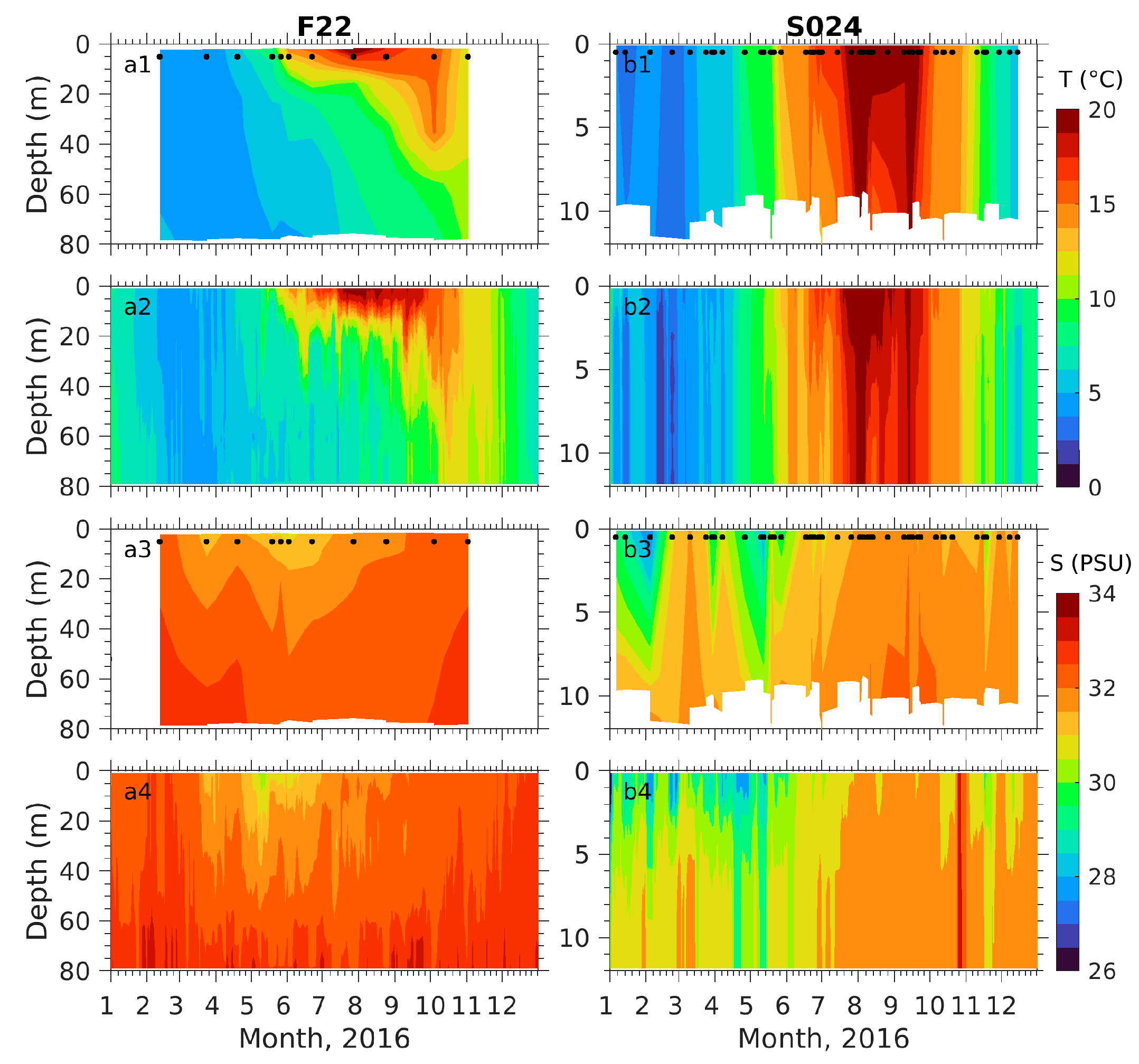
3.1. Physical Fields
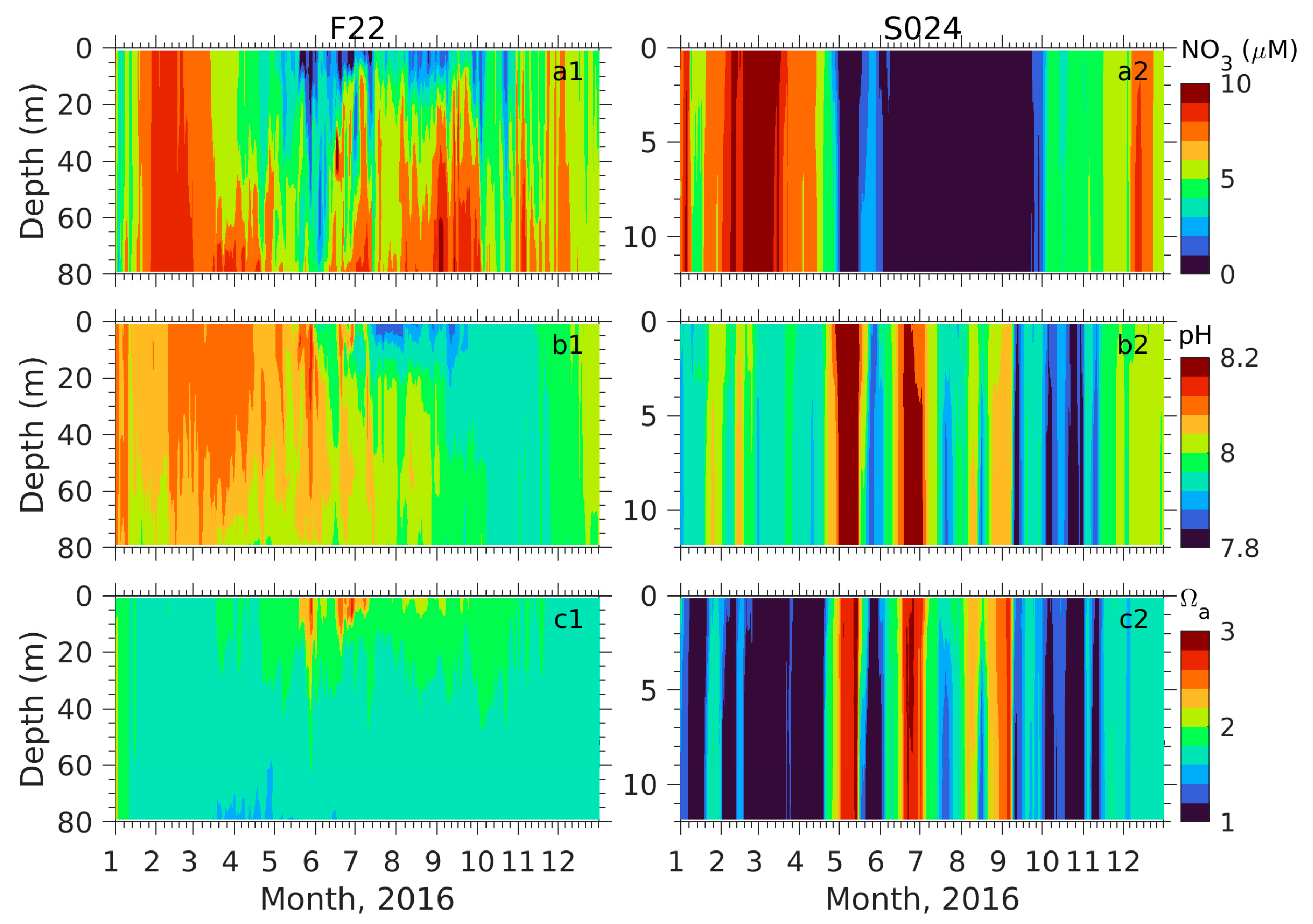
3.2. Biogeochemical Fields
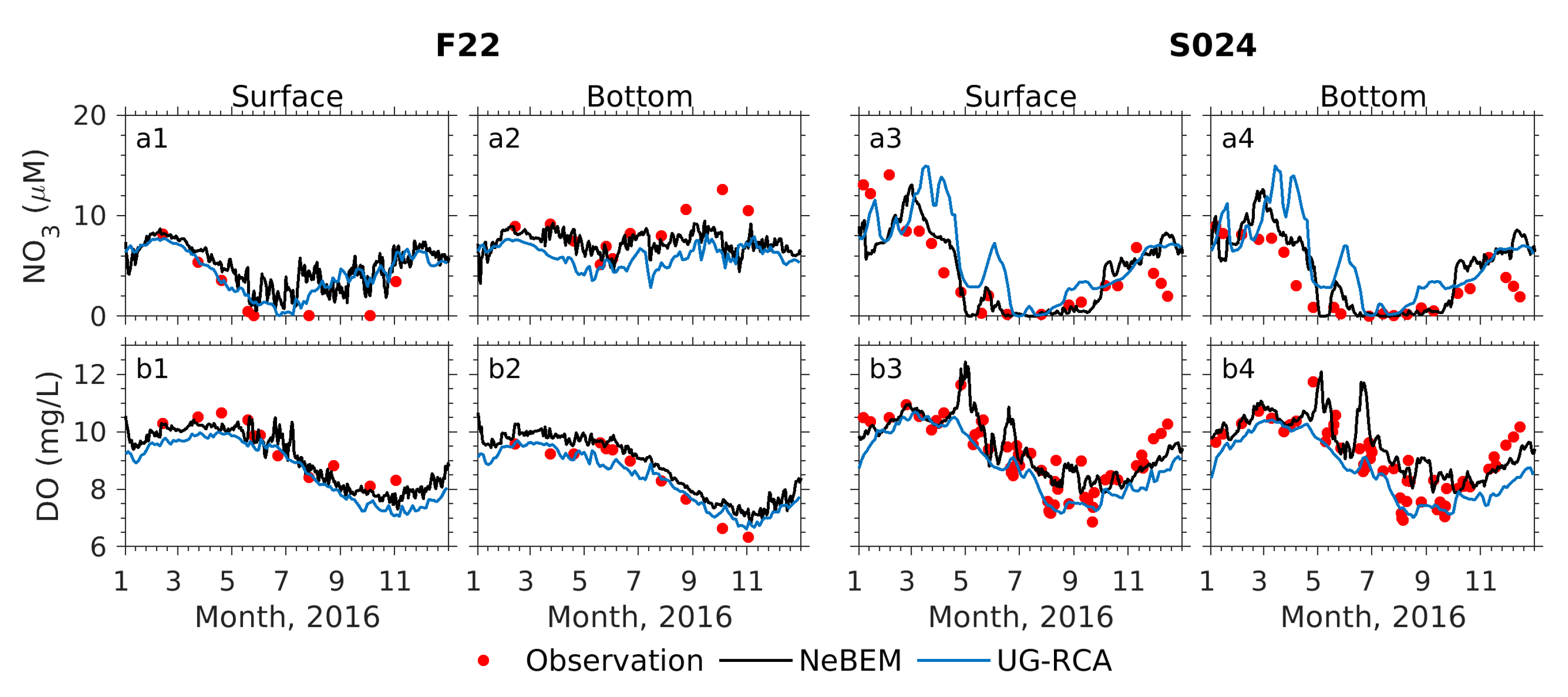
3.2.1. Comparison with Observations
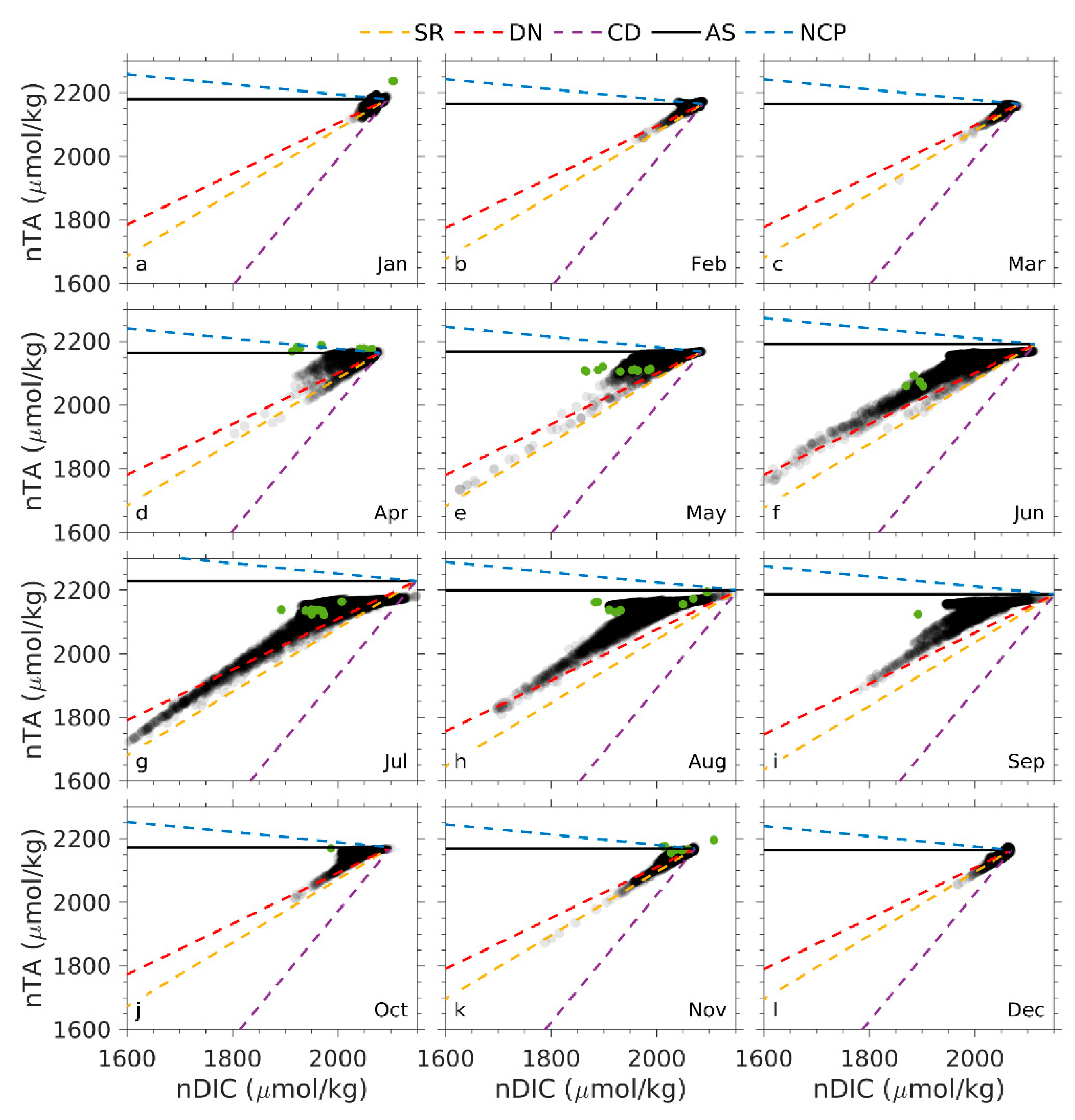
3.2.2. Seasonal Distributions
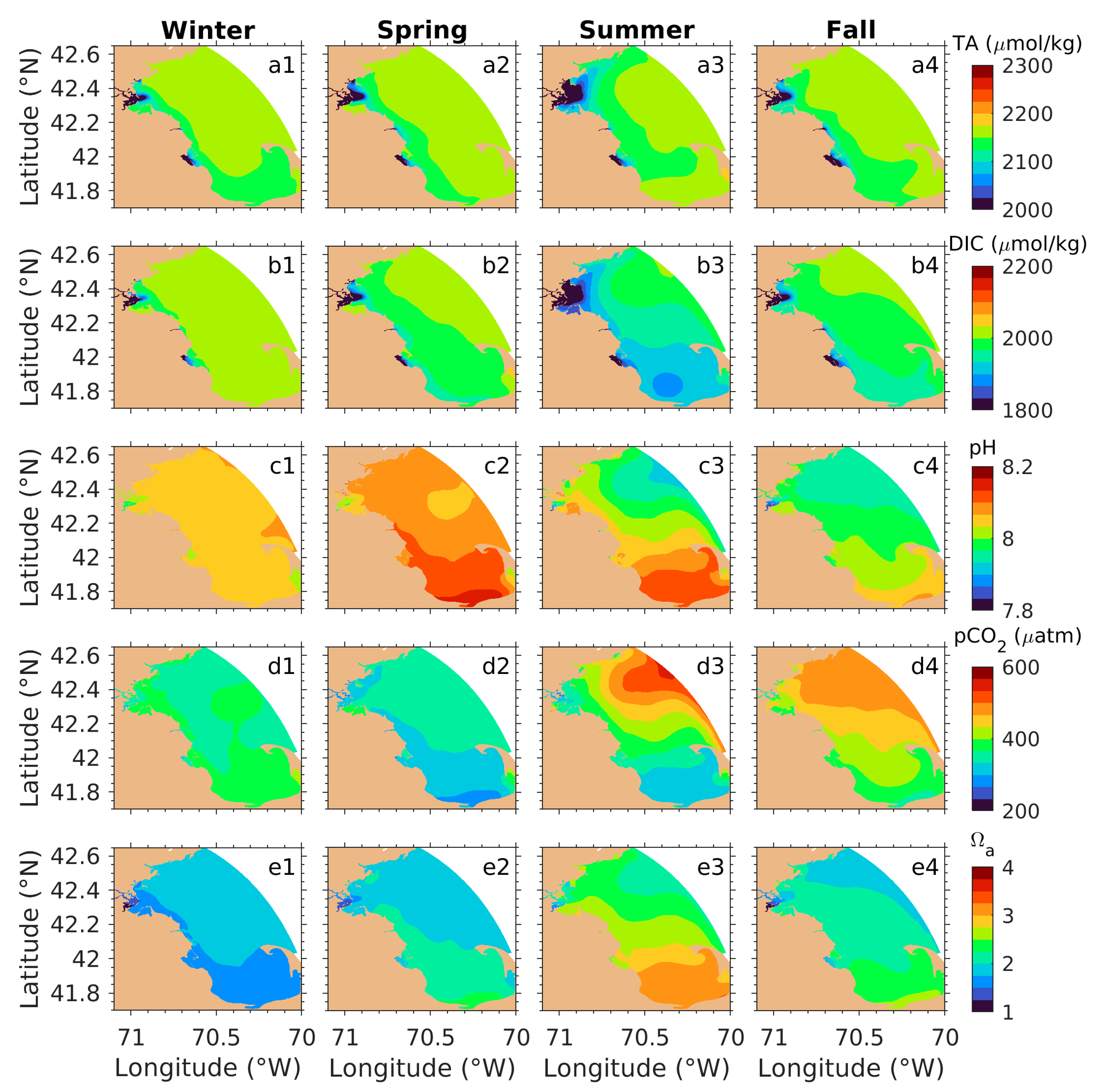
3.3. Quantitative Model Skill Assessment
4. Discussion
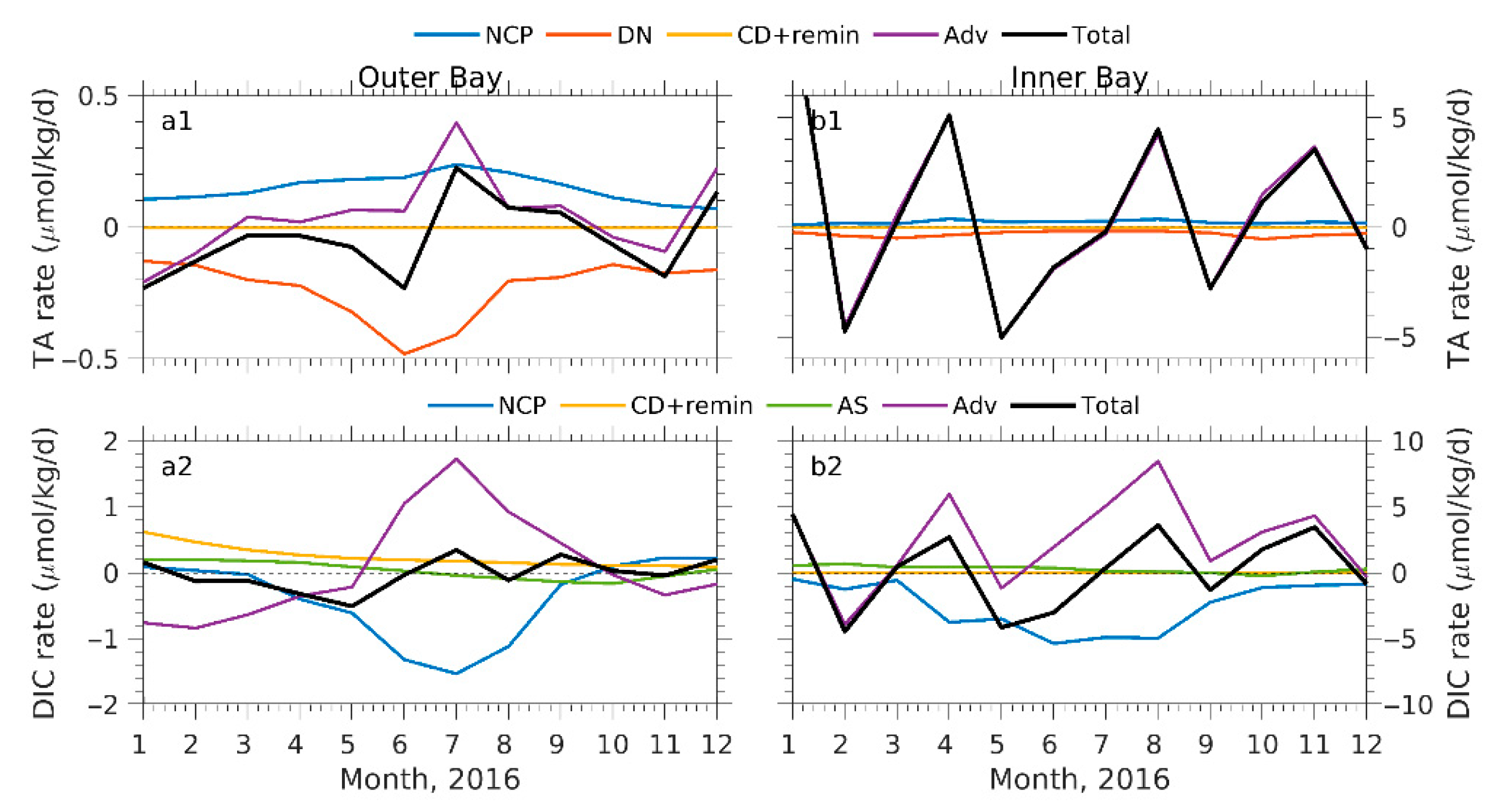
4.1. Processes Contributing to TA and DIC Variations
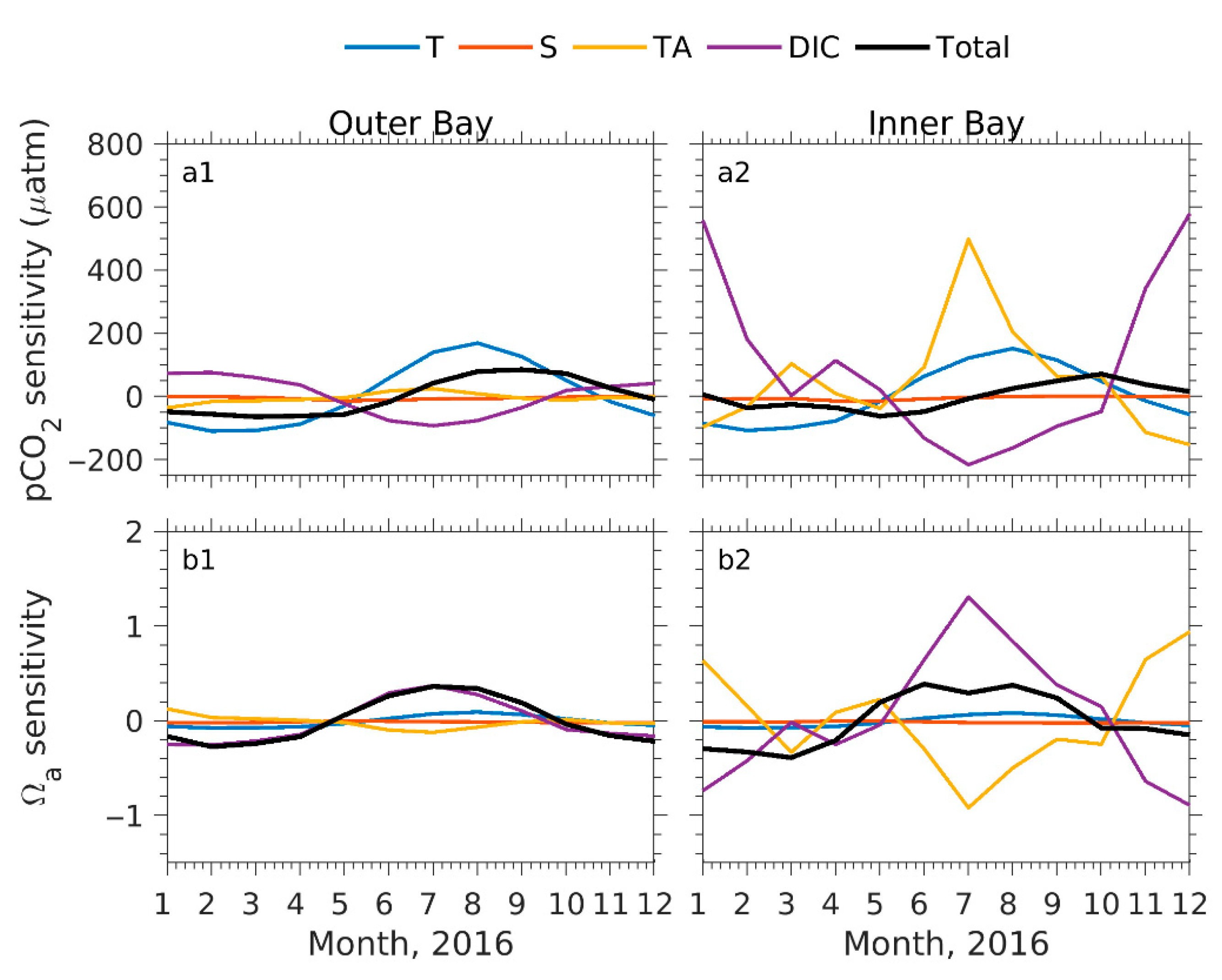
4.2. Processes Attributing to Seasonal pCO2 and Ωa Cycles
4.3. Inter-Model Comparisons
4.3.1. NeBEM vs. UG-RCA Performance Comparison
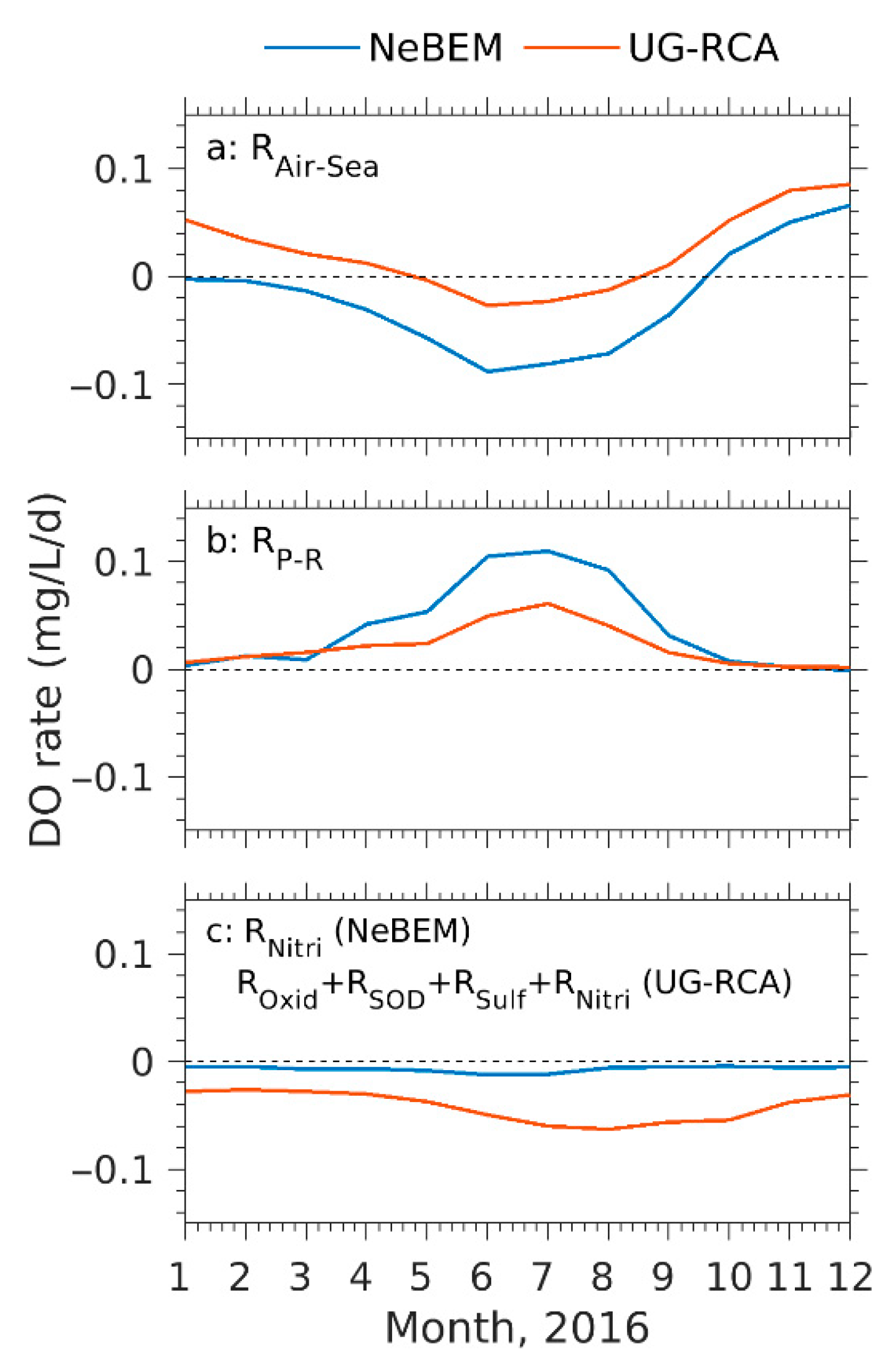
4.3.2. Biological Processes Influencing Dissolved Oxygen
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Results and Discussions for Other Key Ecosystem Variables
Appendix A.1. Model–Data Comparisons
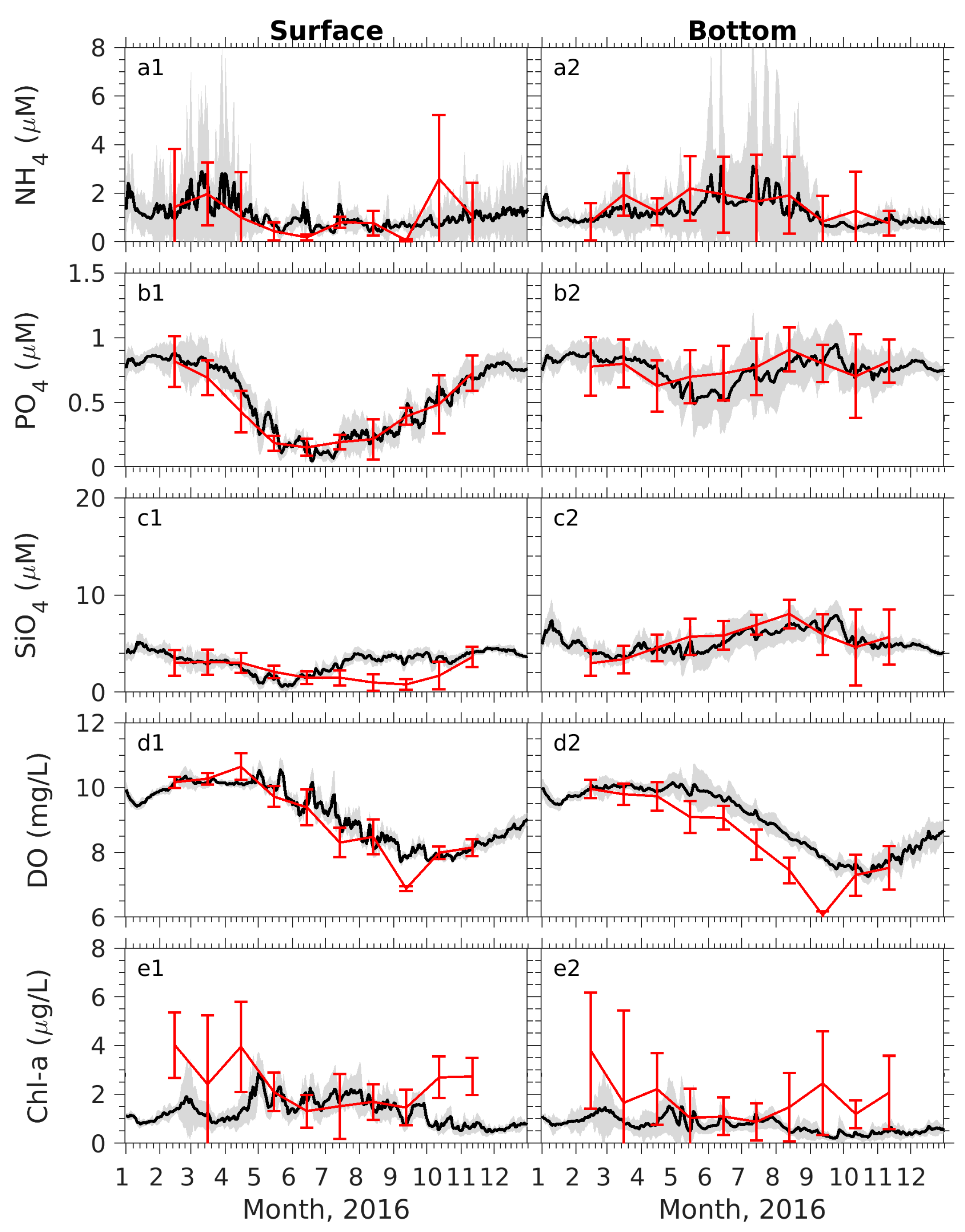

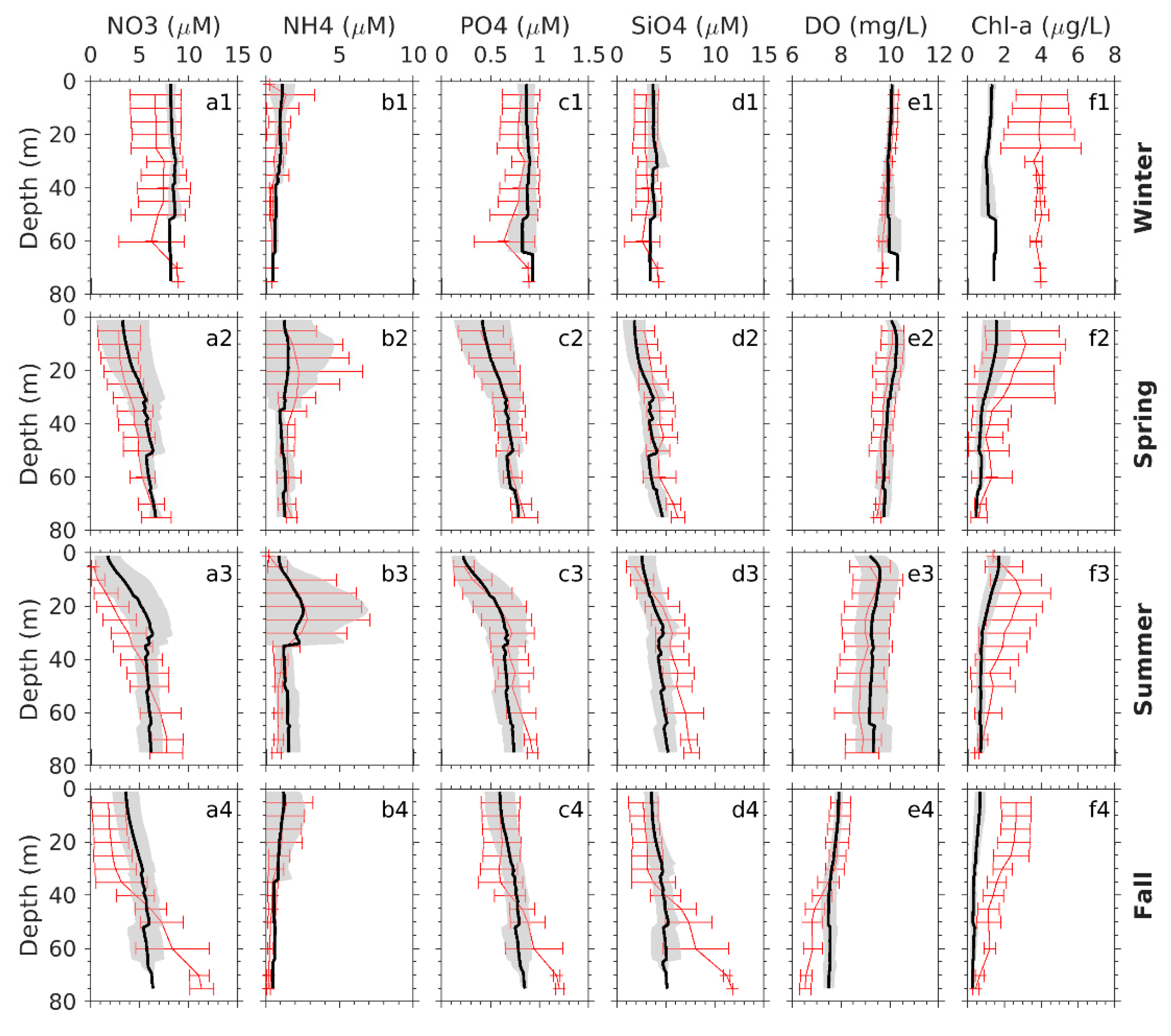
Appendix A.2. Spatial Variability Patterns

References
- Salisbury, J.; Green, M.; Hunt, C.; Campbell, J. Coastal acidification by rivers: A threat to shellfish? Eos Trans. Am. Geophys. Union 2008, 89, 513. [Google Scholar] [CrossRef]
- Salisbury, J.; Vandemark, D.; Hunt, C.W.; Campbell, J.W.; McGillis, W.R.; McDowell, W.H. Seasonal observations of surface waters in two Gulf of Maine estuary-plume systems: Relationships between watershed attributes, optical measurements and surface pCO2. Estuar. Coast. Shelf Sci. 2008, 77, 245–252. [Google Scholar] [CrossRef]
- Prasad, M.B.K.; Kaushal, S.S.; Murtugudde, R. Long-term pCO2 dynamics in rivers in the Chesapeake Bay watershed. Appl. Geochem. 2013, 31, 209–215. [Google Scholar] [CrossRef]
- Wallace, R.B.; Baumann, H.; Grear, J.S.; Aller, R.C.; Gobler, C.J. Coastal ocean acidification: The other eutrophication problem. Estuar. Coast. Shelf Sci. 2014, 148, 1–13. [Google Scholar] [CrossRef]
- Gledhill, D.K.; White, M.M.; Salisbury, J.; Thomas, H.; Mlsna, I.; Liebman, M.; Mook, B.; Grear, J.; Candelmo, A.C.; Chambers, R.C.; et al. Ocean and coastal acidification off New England and Nova Scotia. Oceanography 2015, 28, 182–197. [Google Scholar] [CrossRef]
- Salisbury, J.; Vandemark, D.; Hunt, C.; Campbell, J.; Jonsson, B.; Mahadevan, A.; McGillis, W.; Xue, H. Episodic riverine influence on surface DIC in the coastal Gulf of Maine. Estuar. Coast. Shelf Sci. 2009, 82, 108–118. [Google Scholar] [CrossRef]
- Xue, P.; Chen, C.; Qi, J.; Beardsley, R.C.; Tian, R.; Zhao, L.; Lin, H. Mechanism studies of seasonal variability of dissolved oxygen in Mass Bay: A multi-scale FVCOM/UG-RCA application. J. Mar. Syst. 2014, 131, 102–119. [Google Scholar] [CrossRef]
- Lagerloef, G.S.; Bernstein, R.L. Empirical orthogonal function analysis of advanced very high-resolution radiometer surface temperature patterns in Santa Barbara Channel. J. Geophys. Res. Ocean 1988, 93, 6863–6873. [Google Scholar] [CrossRef]
- Preisendorfer, R.W. Principal Component Analysis in Meteorology and Oceanography (Developments in Atmospheric Science); Mobley, C.D., Ed.; Elsevier Science: Oxford, UK, 1988; Volume 17. [Google Scholar]
- Bigelow, H.B. Physical Oceanography of the Gulf of Maine; U.S. Government Printing Office: Washington, DC, USA, 1927. [Google Scholar]
- Butman, B. Hydrography and low frequency currents associated with the spring runoff in Massachusetts Bay Memories. Soc. R. Des. Sci. Liege 1976, 6, 247–275. [Google Scholar]
- Xue, P.; Chen, C.; Beardsley, R.C. Observing system simulation experiments of dissolved oxygen monitoring in Massachusetts Bay. J. Geophys. Res. Ocean 2012, 117, C05014. [Google Scholar] [CrossRef]
- Zhao, L.Z.; Tian, R.C.; Xue, P.; Chen, C.; Leo, W.S.; Mickelson, M.J. Modeling 2010 in Massachusetts Bay Using the Unstructured-Grid Bays Eutrophication Model; Report 2011-09; Massachusetts Water Resources Authority: Boston, MA, USA, 2011; 118p. [Google Scholar]
- Geyer, W.R.; Gardner, G.B.; Brown, W.S.; Irish, J.D.; Butman, B.; Loder, T.C.; Signell, R.P. Physical Oceanographic Investigation of Massachusetts and Cape Cod Bays; The Massachusetts Environmental Trust: Boston, MA, USA, 1992. [Google Scholar]
- Butman, B.; Bothner, M.H.; Lightsom, F.L.; Gutierrez, B.T.; Alexander, P.S.; Martini, M.A.; Strahle, W.S. Long-Term Oceanographic Observations in Western Massachusetts Bay Offshore of Boston, Massachusetts: Data Report for 1989–2000; US Geological Survey: Reston, VA, USA, 2002. [Google Scholar]
- Chen, C.; Zhao, L.; Gallager, S.; Ji, R.; He, P.; Davis, C.; Beardsley, R.C.; Hart, D.; Gentleman, W.C.; Wang, L.; et al. Impact of larval behaviors on dispersal and connectivity of sea scallop larvae over the northeast US shelf. Prog. Oceanogr. 2021, 195, 102604. [Google Scholar] [CrossRef]
- Franks, P.J.; Chen, C. Plankton production in tidal fronts: A model of Georges Bank in summer. J. Mar. Res. 1996, 54, 631–651. [Google Scholar] [CrossRef]
- Franks, P.J.S.; Chen, C. A 3-D prognostic model study of the ecosystem over Georges Bank and adjacent coastal regions. Part II: Coupled biological and physical model. Deep Sea Res. 2001, 48, 457–482. [Google Scholar] [CrossRef]
- Tian, R.; Chen, C.; Qi, J.; Ji, R.; Beardsley, R.C.; Davis, C. Model study of nutrient and phytoplankton dynamics in the Gulf of Maine: Patterns and drivers for seasonal and interannual variability. ICES J. Mar. Sci. 2015, 72, 388–402. [Google Scholar] [CrossRef]
- Zang, Z.; Ji, R.; Feng, Z.; Chen, C.; Li, S.; Davis, C.S. Spatially varying phytoplankton seasonality on the Northwest Atlantic Shelf: A model-based assessment of patterns, drivers, and implications. ICES J. Mar. Sci. 2021, 78, 1920–1934. [Google Scholar] [CrossRef]
- Wang, L. Simulating Ocean Acidification in the Northeast, U.S. Region Using a Fully Coupled Three-Dimensional Biogeochemistry and Ecosystem Model. Ph.D Thesis, University of Massachusetts Dartmouth, North Dartmouth, MA, USA, 2023. [Google Scholar]
- Wang, L.; Chen, C.; Salisbury, J.; Beardsley, R.C.; Motyka, J. Modeling of Ocean Acidification in the Massachusetts Bay and Boston Harbor: 1-D Experiments; Ecological Modelling: San Diego, CA, USA, 2025; under review. [Google Scholar]
- Zhao, L.Z.; Tian, R.C.; Xue, P.; Chen, C.; Leo, W.S.; Mickelson, M.J. Modeling 2012 in Massachusetts Bay Using the Unstructured-Grid Bays Eutrophication Model; Report 2015-02; Massachusetts Water Resources Authority: Boston, MA, USA, 2013; 102p. [Google Scholar]
- Zhao, L.; Chen, C.; Beardsley, R.C.; Codiga, D.L.; Leo, W.S. Simulations of 2015 Hydrodynamics and Water Quality in the Massachusetts Bay System Using the Bays Eutrophication Model; Report 2016-16; Massachusetts Water Resources Authority: Boston, MA, USA, 2016; 112p. [Google Scholar]
- Butenschön, M.; Clark, J.; Aldridge, J.N.; Allen, J.I.; Artioli, Y.; Blackford, J.; Bruggeman, J.; Cazenave, P.; Ciavatta, S.; Kay, S.; et al. ERSEM 15.06: A generic model for marine biogeochemistry and the ecosystem dynamics of the lower trophic levels. Geosci. Model. Dev. 2016, 9, 1293–1339. [Google Scholar] [CrossRef]
- Chen, C.; Beardsley, R.C.; Cowles, G.; Qi, J.; Lai, Z.; Gao, G.; Stuebe, D.; Xu, Q.; Xue, P.; Ge, J.; et al. An Unstructured-Grid, Finite-Volume Community Ocean Model: FVCOM User Manual; Sea Grant College Program, Massachusetts Institute of Technology: Cambridge, MA, USA, 2012. [Google Scholar]
- Keller, A.A.; Taylor, C.; Oviatt, C.; Dorrington, T.; Holcombe, G.; Reed, L. Phytoplankton production patterns in Massachusetts Bay and the absence of the 1998 winter–spring bloom. Mar. Biol. 2001, 138, 1051–1062. [Google Scholar] [CrossRef]
- Zhao, L.; Beardsley, R.C.; Chen, C.; Codiga, D.L.; Wang, L. Simulations of 2016 Hydrodynamics and Water Quality in the Massachusetts Bay System Using the Bays Eutrophication Model; Report 2017-13; Massachusetts Water Resources Authority: Boston, MA, USA, 2017; 111p. [Google Scholar]
- Chen, C.; Gao, G.; Zhang, Y.; Beardsley, R.C.; Lai, Z.; Qi, J.; Lin, H. Circulation in the Arctic Ocean: Results from a high-resolution coupled ice-sea nested Global-FVCOM and Arctic-FVCOM system. Prog. Oceanogr. 2016, 141, 60–80. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.; Beardsley, R.C.; Gao, G.; Lai, Z.; Curry, B.; Lee, C.M.; Lin, H.; Qi, J.; Xu, Q. Studies of the Canadian Arctic Archipelago water transport and its relationship to basin-local forcings: Results from AO-FVCOM. J. Geophys. Res. Ocean 2016, 121, 4392–4415. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.; Beardsley, R.C.; Gao, G.; Qi, J.; Lin, H. Seasonal and interannual variability of the Arctic sea ice: A comparison between AO-FVCOM and observations. J. Geophys. Res. Ocean 2016, 121, 8320–8350. [Google Scholar] [CrossRef]
- Chen, C.; Beardsley, R.C.; Hu, S.; Xu, Q.; Lin, H. Using MM5 to hindcast the ocean surface forcing fields over the Gulf of Maine and Georges Bank region. J. Atmos. Ocean. Technol. 2005, 22, 131–145. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Godfrey, J.S.; Wick, G.A.; Edson, J.B.; Young, G.S. Cool-skin and warm-layer effects on sea surface temperature. J. Geophys. Res. Oceans 1996, 101, 1295–1308. [Google Scholar] [CrossRef]
- Millero, F.J.; Lee, K.; Roche, M. Distribution of alkalinity in the surface waters of the major oceans. Mar. Chem. 1998, 60, 111–130. [Google Scholar] [CrossRef]
- Lee, K.; Tong, L.T.; Millero, F.J.; Sabine, C.L.; Dickson, A.G.; Goyet, C.; Park, G.H.; Wanninkhof, R.; Feely, R.A.; Millero, F.J.; et al. Global relationships of total alkalinity with salinity and temperature in surface waters of the world’s oceans. Geophys. Res. Lett. 2006, 33, L19605. [Google Scholar] [CrossRef]
- Land, P.E.; Shutler, J.D.; Findlay, H.S.; Girard-Ardhuin, F.; Sabia, R.; Reul, N.; Piolle, J.-F.; Chapron, B.; Quilfen, Y.; Salisbury, J.; et al. Salinity from space unlocks satellite—based assessment of ocean acidification. Environ. Sci. Technol. 2015, 49, 1987–1994. [Google Scholar] [CrossRef]
- Fassbender, A.J.; Alin, S.R.; Feely, R.A.; Sutton, A.J.; Newton, J.A.; Byrne, R.H. Estimating total alkalinity in the Washington State coastal zone: Complexities and surprising utility for ocean acidification research. Estuaries Coasts 2017, 40, 404–418. [Google Scholar] [CrossRef]
- Courtney, T.A.; Cyronak, T.; Griffin, A.J.; Andersson, A.J. Implications of salinity normalization of seawater total alkalinity in coral–reef metabolism studies. PLoS ONE 2021, 16, e0261210. [Google Scholar] [CrossRef] [PubMed]
- McGarry, K.; Siedlecki, S.A.; Salisbury, J.; Alin, S.R. Multiple linear regression models for reconstructing and exploring processes controlling the carbonate system of the northeast US from basic hydrographic data. J. Geophys. Res. Ocean 2021, 126, e2020JC016480. [Google Scholar] [CrossRef]
- Metzl, N.; Fin, J.; Monaco, C.L.; Mignon, C.; Alliouane, S.; Bombled, B.; Boutin, J.; Bozec, Y.; Comeau, S.; Conan, P.; et al. An updated synthesis of ocean total alkalinity and dissolved inorganic carbon measurements from 1993 to 2023: The SNAPO-CO2-v2 dataset. Earth Syst. Sci. Data 2025, 17, 1075–1100. [Google Scholar] [CrossRef]
- Salisbury, J.E. Dissolved Inorganic Carbon, Total Alkalinity, pH, Nutrients and Other Variables Collected from Profile and Discrete Sample Observations Using CTD, Niskin Bottle, and Other Instruments from NOAA Ship Gordon Gunter off the US East Coast During the East Coast Ocean Acidification (GU-15-04 ECOA1) from 2015-06-20 to 2015-07-23 (NCEI Accession 0159428); Version 2.2; Dataset; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2017. [Google Scholar]
- Salisbury, J.E.; Shawn, S.M. Dissolved Inorganic Carbon, Total Alkalinity, PH, Nutrients and Other Variables Collected from Discrete Profile Observations Using CTD, Niskin Bottle, and Other Instruments in the East Coast of the U.S. and Canada During the 2nd East Coast Ocean Acidification (ECOA2 or ECOA-2) Cruise from 2018-06-25 to 2018-07-29 (NCEI Accession 0196419); Dataset; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2019. [Google Scholar]
- Wang, Z.A.; Gareth, L.; Cynthia, P.H.; Amy, M.E. Discrete Profile Measurements of Dissolved Inorganic Carbon, Total Alkalinity, Dissolved Oxygen, Temperature and Salinity During the R/V Tioga Ten Cruises in Wilkinson Basin of the Gulf of Maine from 2013-05-21 to 2015-02-15 (NCEI Accession 0172591); Dataset; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2018. [Google Scholar]
- Libby, P.S.; Geyer, W.R.; Keller, A.A.; Turner, J.T.; Borkman, D.; Oviatt, C.A.; Hunt, C.D. 2002 Annual Water Column Monitoring Report; Report 2003-09; Massachusetts Water Resources Authority: Boston, MA, USA, 2003; 111p. [Google Scholar]
- Libby, P.S.; Geyer, W.R.; Keller, A.A.; Turner, J.T.; Borkman, D.; Oviatt, C.A. 2003 Annual Water Column Monitoring Report; Report 2004-07; Massachusetts Water Resources Authority: Boston, MA, USA, 2004; 154p. [Google Scholar]
- OSPAR; Villars, M.; de Vries, I.; Bokhorst, M.; Ferreira, J.; Gellers-Barkmann, S.; Kelly-Gerreyn, B.; Lancelot, C.; Mensguen, A.; Moll, A.; et al. Report of the ASMO Modelling Workshop on Eutrophication Issues, 5–8 November 1996, The Hague, The Netherlands; Report for Commission Report; Netherlands Institute for Coastal and Marine Management RIKZ: The Hague, The Netherlands, 1998. [Google Scholar]
- Allen, J.I.; Somerfield, P.J.; Gilbert, F.J. Quantifying uncertainty in high-resolution coupled hydrodynamic-ecosystem models. J. Mar. Syst. 2007, 64, 3–14. [Google Scholar] [CrossRef]
- Sutherland, J.; Walstra, D.J.R.; Chesher, T.J.; Van Rijn, L.C.; Southgate, H.N. Evaluation of coastal area modelling systems at an estuary mouth. Coast. Eng. 2004, 51, 119–142. [Google Scholar] [CrossRef]
- Olsen, A.; Key, R.M.; Van Heuven, S.; Lauvset, S.K.; Velo, A.; Lin, X.; Schirnick, C.; Kozyr, A.; Tanhua, T.; Hoppema, M.; et al. The Global Ocean Data Analysis Project version 2 (GLODAPv2)—An internally consistent data product for the world ocean. Earth Syst. Sci. Data 2016, 8, 297–323. [Google Scholar] [CrossRef]
- Melrose, D.C.; Rebuck, N.D.; Townsend, D.W.; Thomas, M.A.; Taylor, C.C. Ammonia, Silicate, Phosphate, Nitrite+Nitrate, Dissolved Oxygen, and Other Variables Collected from Profile and Discrete Sample Observations Using CTD, Nutrient Autoanalyzer, and Other Instruments from NOAA Ship Delaware II, NOAA Ship Gordon Gunter, NOAA Ship Henry, B. Bigelow, NOAA Ship Okeanos Explorer, and NOAA Ship Pisces in the Gulf of Maine, Georges Bank, and Mid-Atlantic Bight from 2009-11-03 to 2016-08-19 (NCEI Accession 0127524); Dataset; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2015. [Google Scholar]
- Friis, K.; Körtzinger, A.; Wallace, D.W. The salinity normalization of marine inorganic carbon chemistry data. Geophys. Res. Lett. 2003, 30, 1085. [Google Scholar] [CrossRef]
- Burdige, D.J. 5.09-Estuarine and coastal Sediments—Coupled biogeochemical cycling. Treatise Estuar. Coast. Sci. 2011, 5, 279–316. [Google Scholar]
- Hunt, C.W.; Salisbury, J.E.; Vandemark, D. Controls on buffering and coastal acidification in a temperate estuary. Limnol. Oceanogr. 2022, 67, 1328–1342. [Google Scholar] [CrossRef]
- Krumins, V.; Gehlen, M.; Arndt, S.; Van Cappellen, P.; Regnier, P. Dissolved inorganic carbon and alkalinity fluxes from coastal marine sediments: Model estimates for different shelf environments and sensitivity to global change. Biogeosciences 2013, 10, 371–398. [Google Scholar] [CrossRef]
- Sippo, J.Z.; Maher, D.T.; Tait, D.R.; Holloway, C.; Santos, I.R. Are mangroves drivers or buffers of coastal acidification? Insights from alkalinity and dissolved inorganic carbon export estimates across a latitudinal transect. Glob. Biogeochem. Cycles 2016, 30, 753–766. [Google Scholar] [CrossRef]
- Cai, W.J.; Huang, W.J.; Luther, G.W., III.; Pierrot, D.; Li, M.; Testa, J.; Xue, M.; Joesoef, A.; Mann, R.; Brodeur, J.; et al. Redox reactions and weak buffering capacity lead to acidification in the Chesapeake Bay. Nat. Commun. 2017, 8, 369. [Google Scholar] [CrossRef]
- Vandemark, D.; Salisbury, J.E.; Hunt, C.W.; Shellito, S.M.; Irish, J.D.; McGillis, W.R.; Sabine, C.L.; Maenner, S.M. Temporal and spatial dynamics of CO2 air-sea flux in the Gulf of Maine. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Van Heuven, S.M.A.C.; Pierrot, D.; Rae, J.W.B.; Lewis, E.; Wallace, D.W.R. MATLAB Program Developed for CO2 System Calculations; ORNL/CDIAC-105b; Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, US Department of Energy: Oak Ridge, TN, USA, 2011; 530p. [Google Scholar]
- Signorini, S.R.; Mannino, A.; Najjar, R.G.; Friedrichs, M.A.; Cai, W.J.; Salisbury, J.; Wang, Z.A.; Thomas, H.; Shadwick, E. Surface ocean pCO2 seasonality and sea-air CO2 flux estimates for the North American east coast. J. Geophys. Res. Ocean 2013, 118, 5439–5460. [Google Scholar] [CrossRef]
- HydroQual Inc. Bays Eutrophication Model (BEM): Modeling Analysis for the Period 1992–1994; Report 2000-02; Massachusetts Water Resources Authority: Boston, MA, USA, 2000; 158p. [Google Scholar]
- HydroQual Inc; Signell, R.P. Calibration of the Massachusetts and Cape Cod Bays Hydrodynamic Model: 1998–1999; Report 2001-12; Massachusetts Water Resources Authority: Boston, MA, USA, 2001; 170p. [Google Scholar]
- Jiang, M.S.; Zhou, M. Bays Eutrophication Model (BEM) Model Verification for the Period: 2000–2001; Report 2004-09; Massachusetts Water Resources Authority: Boston, MA, USA, 2004; 90p. [Google Scholar]
- Tian, R.C.; Chen, C.S.; Xu, Q.C.; Xue, P.F.; Cowles, G.W.; Beardsley, R.; Rothschild, B. Massachusetts Bay Eutrophication Model: 2006–2007 Simulation; Report 2009-11; Massachusetts Water Resources Authority: Boston, MA, USA, 2009; 147p. [Google Scholar]
- Zhao, L.; Chen, C.; Vallino, J.; Hopkinson, C.; Beardsley, R.C.; Lin, H.; Lerczak, J. Wetland-estuarine-shelf interactions in the Plum Island Sound and Merrimack River in the Massachusetts coast. J. Geophys. Res. Ocean 2010, 115. [Google Scholar] [CrossRef]
- Durbin, E.G.; Durbin, A.G.; Beardsley, R.C. Springtime nutrient and chlorophyll—A concentrations in the southwestern Gulf of Maine. Cont. Shelf Res. 1995, 15, 433–450. [Google Scholar] [CrossRef]



| Parameter | Unit | Value |
|---|---|---|
| Sinking velocity for small-size POM | m/day | 0.1 (1.0) |
| Sinking velocity for medium-size POM | m/day | 0.5 (5.0) |
| Sinking velocity for large-size POM | m/day | 1.0 (10.0) |
| Remineralization rate for benthic DOM | 1/day | 0.1 (0.001) |
| Remineralization rate for benthic POM | 1/day | 0.05 (0.0025) |
| Remineralization rate for benthic refractory matter | 1/day | 0.01 (0.001) |
| River | Annual | Winter | Spring | Summer | Fall |
|---|---|---|---|---|---|
| Saugus | 0.6 ± 0.5 | 0.9 ± 0.5 | 1.0 ± 0.3 | 0.3 ± 0.3 | 0.2 ± 0.1 |
| Mystic | 1.2 ± 1.4 | 2.1 ± 1.8 | 2.0 ± 1.2 | 0.2 ± 0.4 | 0.3 ± 0.2 |
| Charles | 5.2 ± 4.5 | 7.7 ± 3.6 | 9.4 ± 4.0 | 1.7 ± 1.7 | 1.9 ± 1.7 |
| Neponset | 5.3 ± 5.4 | 8.6 ± 4.7 | 10.3 ± 4.9 | 1.1 ± 1.2 | 1.4 ± 1.3 |
| North | 0.2 ± 0.2 | 0.3 ± 0.1 | 0.3 ± 0.2 | 0.1 ± 0.1 | 0.2 ± 0.1 |
| Jones | 0.5 ± 0.5 | 0.8 ± 0.5 | 0.9 ± 0.5 | 0.1 ± 0.1 | 0.2 ± 0.2 |
| Score Color | Score | CF | PB | ARMAE |
|---|---|---|---|---|
| Excellent and very good | <1 | <20 | <0.2 | |
| Good | 1–2 | 20–40 | 0.2–0.4 | |
| Reasonable | 2–3 | / | 0.4–0.7 | |
| Poor and bad | >3 | >40 | 0.7–1.0 |
| T | S | NO3 | NH4 | PO4 | SiO4 | DO | Chl-a | pH | |
|---|---|---|---|---|---|---|---|---|---|
| CF | 0.05 | 0.10 | 0.72 | 0.42 | 0.53 | 0.73 | 0.48 | 0.84 | 0.76 |
| PB | 0.49 | 0.09 | 48.94 | −9.83 | −2.15 | −11.71 | 1.82 | −51.13 | 0.74 |
| ARMAE | 0.02 | 0.01 | 0.58 | 0.66 | 0.25 | 0.40 | 0.02 | 0.54 | 0.01 |
| T | S | NO3 | NH4 | PO4 | SiO4 | DO | Chl-a | pH | |
|---|---|---|---|---|---|---|---|---|---|
| CF | 0.11 | 0.20 | 0.49 | 0.79 | 1.21 | 0.67 | 0.49 | 1.07 | 0.97 |
| PB | 0.59 | −0.23 | −9.00 | −11.64 | −45.74 | −0.52 | 3.25 | −65.41 | 1.43 |
| ARMAE | 0.04 | 0.01 | 0.49 | 0.79 | 0.54 | 0.74 | 0.03 | 0.70 | 0.02 |
| NO3 (μM) | NH4 (μM) | PO4 (μM) | SiO4 (μM) | DO (mg/L) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MB | BH | MB | BH | MB | BH | MB | BH | MB | BH | |
| NeBEM | 6.1 ± 1.7 | 3.7 ± 0.3 | 1.5 ± 0.2 | 1.6 ± 0.2 | 0.6 ± 0.0 | 0.3 ± 0.3 | 3.4 ± 0.3 | 3.3 ± 1.7 | 9.4 ± 0.2 | 9.2 ± 0.3 |
| UG-RCA | 3.8 ± 0.5 | 5.4 ± 1.4 | 0.9 ± 0.8 | 2.1 ± 0.3 | 0.5 ± 0.1 | 0.7 ± 0.1 | 2.6 ± 1.0 | 6.1 ± 1.2 | 8.9 ± 0.4 | 8.6 ± 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Chen, C.; Salisbury, J.; Li, S.; Beardsley, R.C.; Motyka, J. Mechanisms of Ocean Acidification in Massachusetts Bay: Insights from Modeling and Observations. Remote Sens. 2025, 17, 2651. https://doi.org/10.3390/rs17152651
Wang L, Chen C, Salisbury J, Li S, Beardsley RC, Motyka J. Mechanisms of Ocean Acidification in Massachusetts Bay: Insights from Modeling and Observations. Remote Sensing. 2025; 17(15):2651. https://doi.org/10.3390/rs17152651
Chicago/Turabian StyleWang, Lu, Changsheng Chen, Joseph Salisbury, Siqi Li, Robert C. Beardsley, and Jackie Motyka. 2025. "Mechanisms of Ocean Acidification in Massachusetts Bay: Insights from Modeling and Observations" Remote Sensing 17, no. 15: 2651. https://doi.org/10.3390/rs17152651
APA StyleWang, L., Chen, C., Salisbury, J., Li, S., Beardsley, R. C., & Motyka, J. (2025). Mechanisms of Ocean Acidification in Massachusetts Bay: Insights from Modeling and Observations. Remote Sensing, 17(15), 2651. https://doi.org/10.3390/rs17152651





