A New Signal Separation and Sampling Duration Estimation Method for ISRJ Based on FRFT and Hybrid Modality Fusion Network
Abstract
1. Introduction
- 1.
- Signal separation: Efficiently extracting the jamming component from intricate mixed signal, a prerequisite for subsequent analysis [9].
- 2.
- Robust estimation: Mitigating the impact of inevitable signal distortions (e.g., energy loss, feature degradation) introduced during separation, which can otherwise compromise the accuracy of parameter estimation [10].
- 1.
- Limited Efficacy in Complex Signal Separation: Many existing methods struggle with intricate signal mixtures, particularly those involving coexisting suppressive and deceptive jamming with significant time–frequency overlap, leading to degraded separation performance. Most current research focuses on simpler scenarios, often limited to ISRJ and target echoes.
- 2.
- Suboptimal Balance between Parameter Estimation and Jamming Suppression: Precise ISRJ parameter estimation, which is crucial for optimizing subsequent electromagnetic countermeasure strategies, is often compromised by approaches that heavily prioritize jamming suppression.
- 3.
- Algorithm Complexity versus Real-Time Constraints: The high computational demands of numerous advanced signal-processing algorithms and deep learning models frequently conflict with the stringent real-time processing requirements essential for radar system operation.
2. Signal Modeling
2.1. Interrupted Sampling Repeater Jamming
2.2. SMSP Jamming
2.3. Noise Convolution Jamming
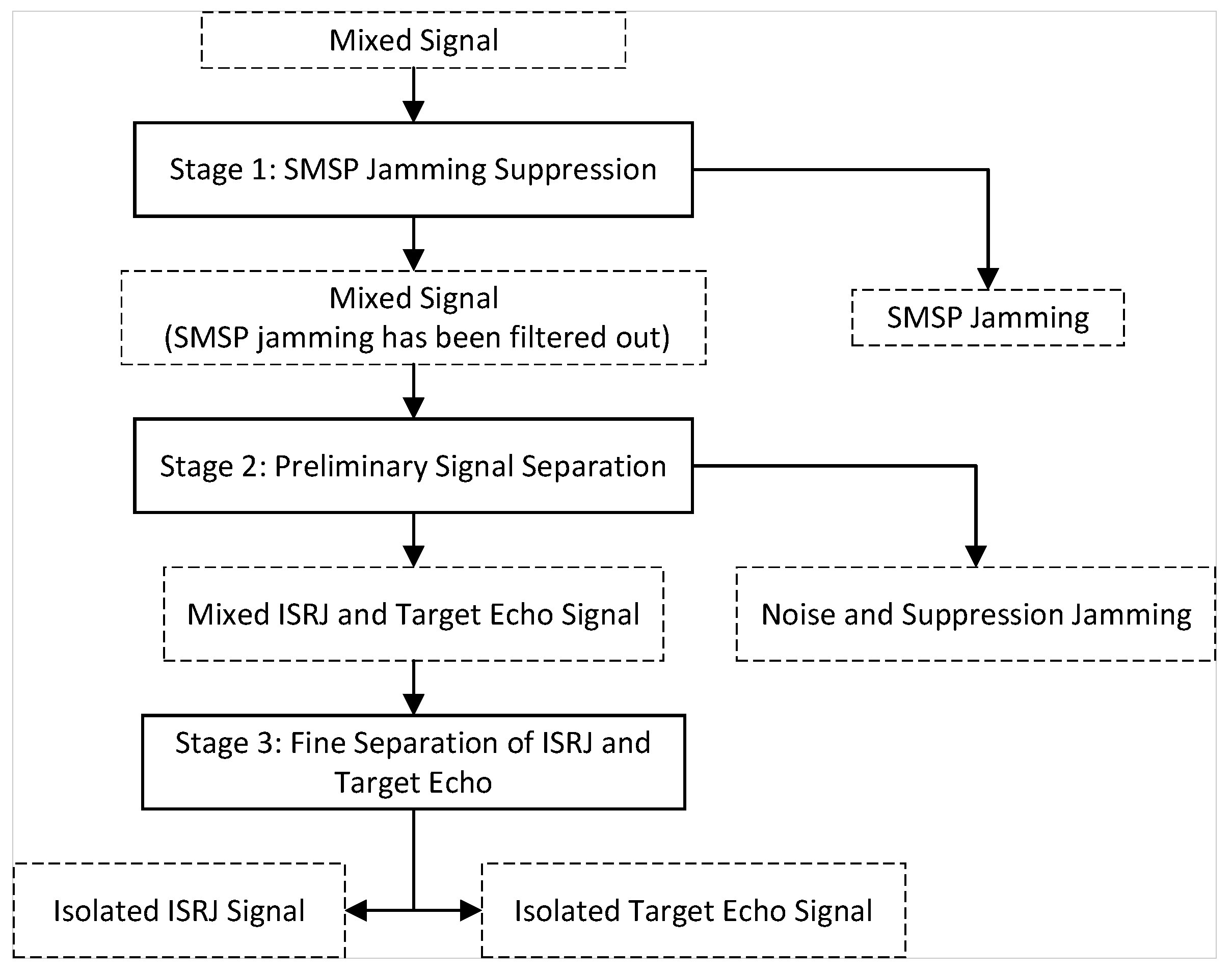
3. Signal Segregation and Key Time–Frequency Block Extraction for Hybrid Modality Fusion Network
3.1. Signal Separation
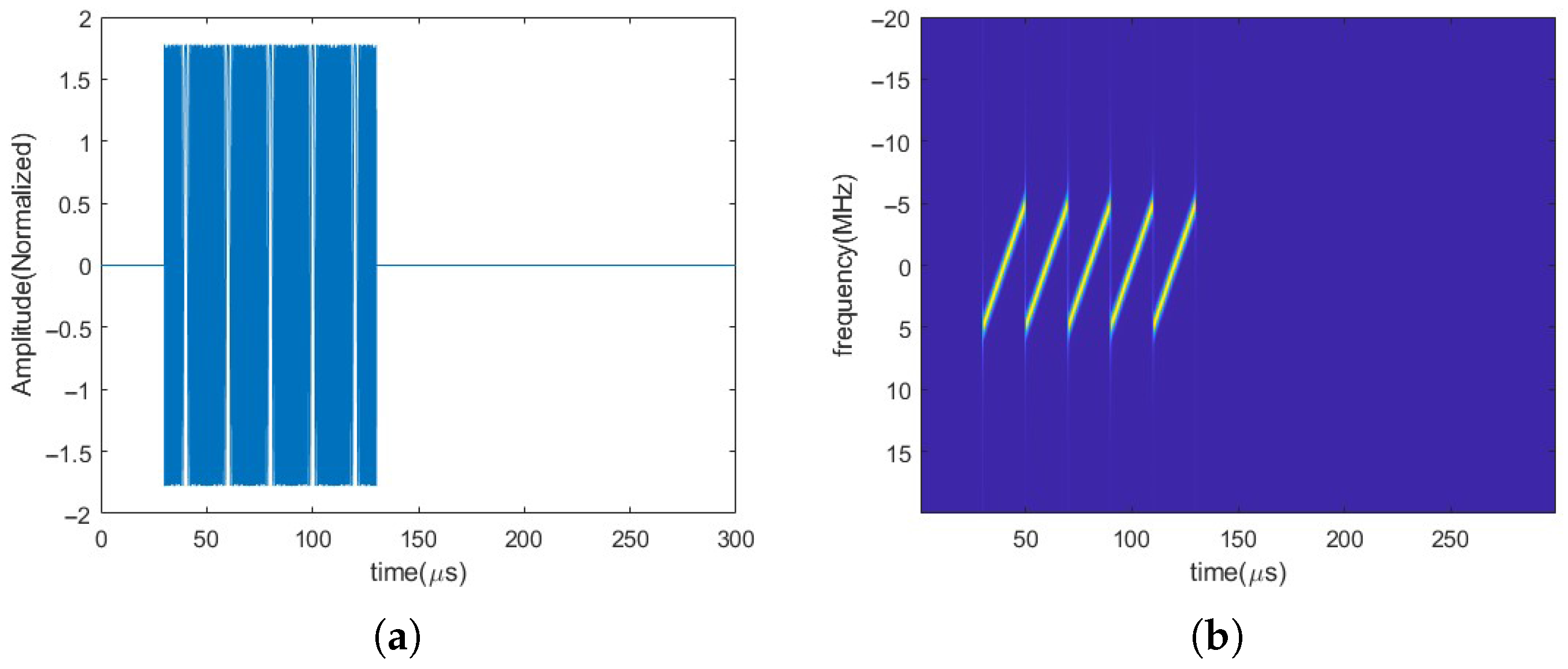
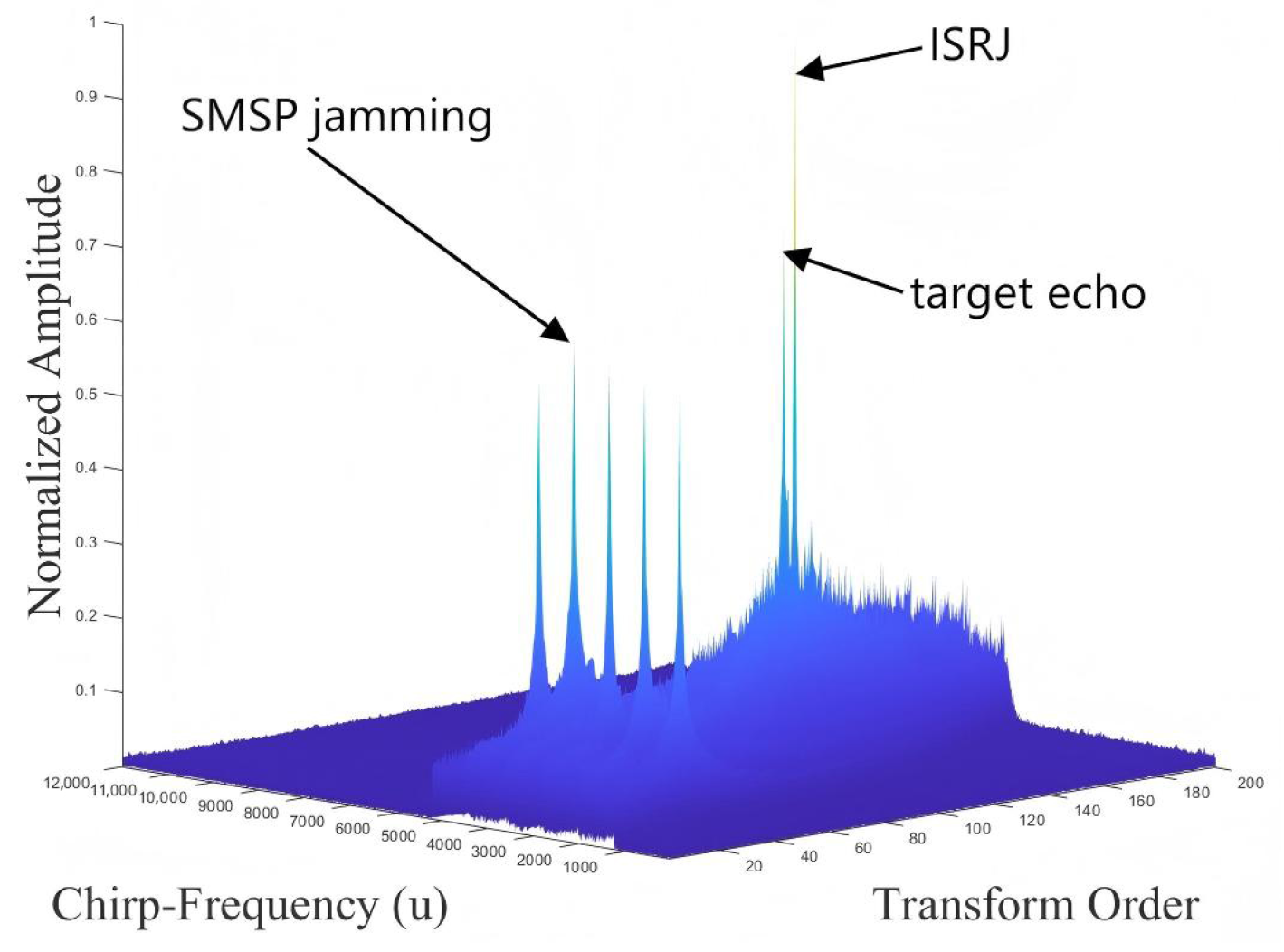
3.2. Feature Analysis of the Mixed Signal
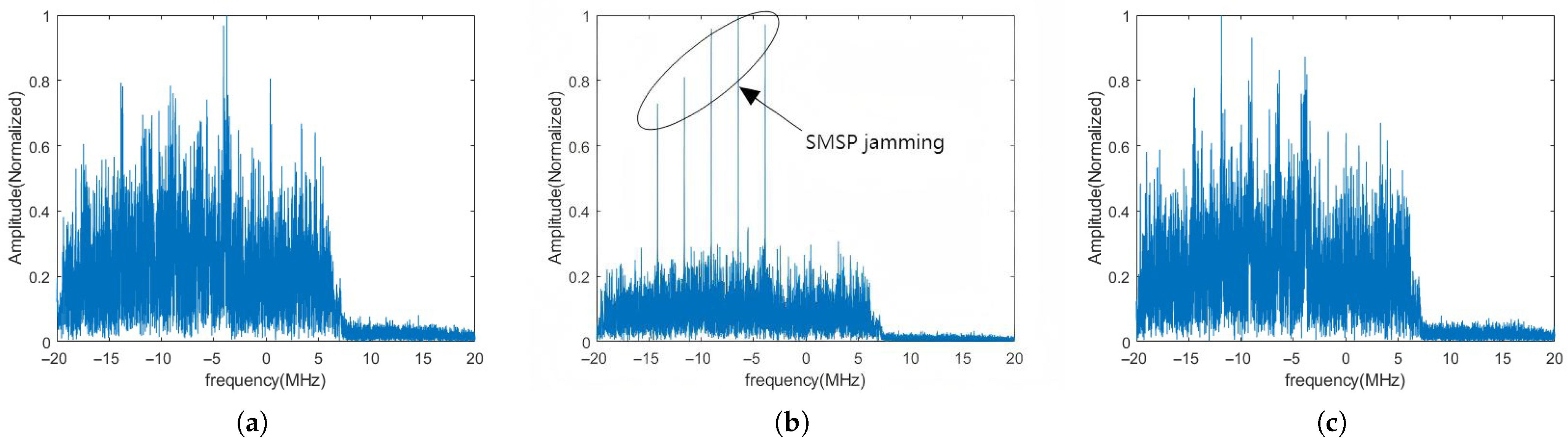
3.3. SMSP-Jamming Suppression Using FRFT
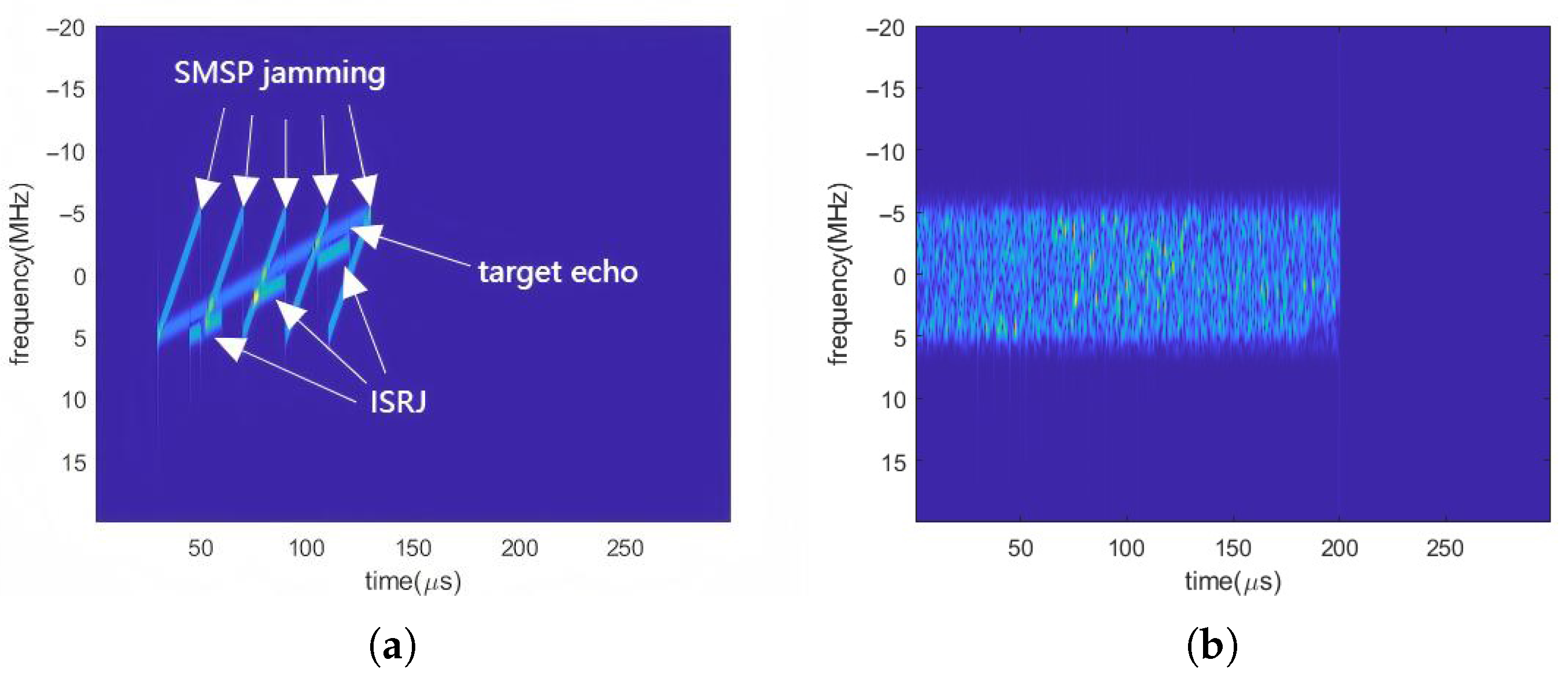
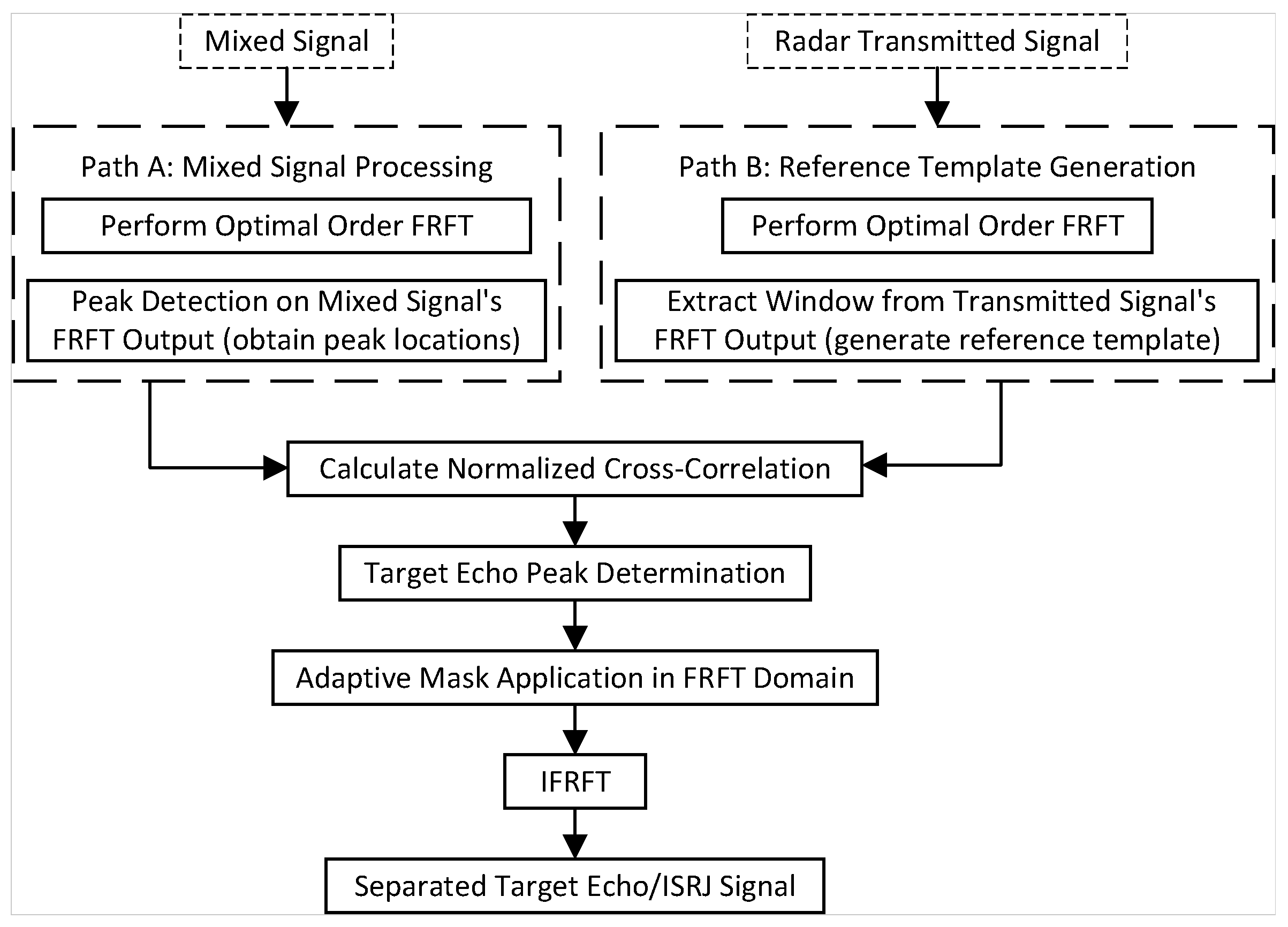
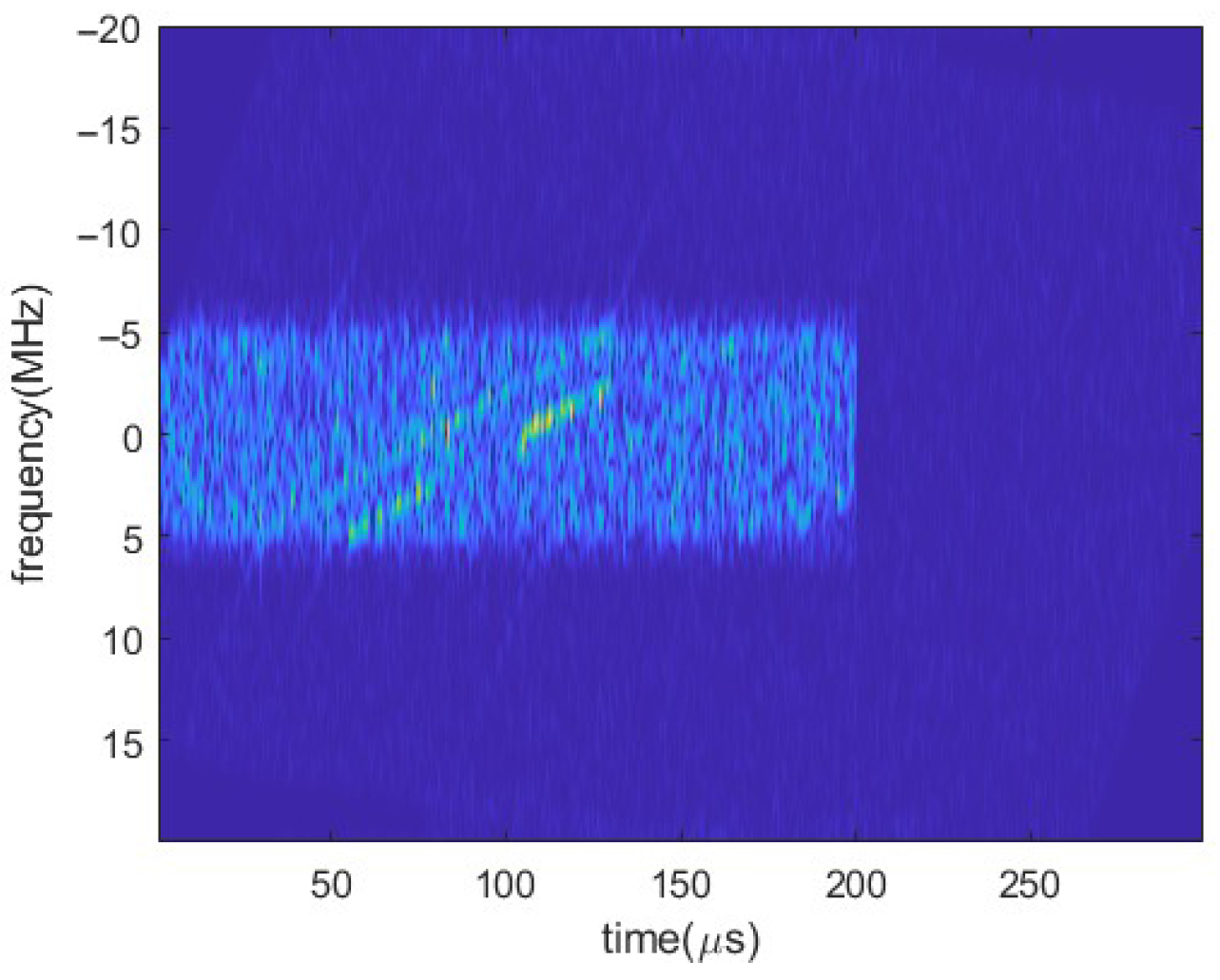
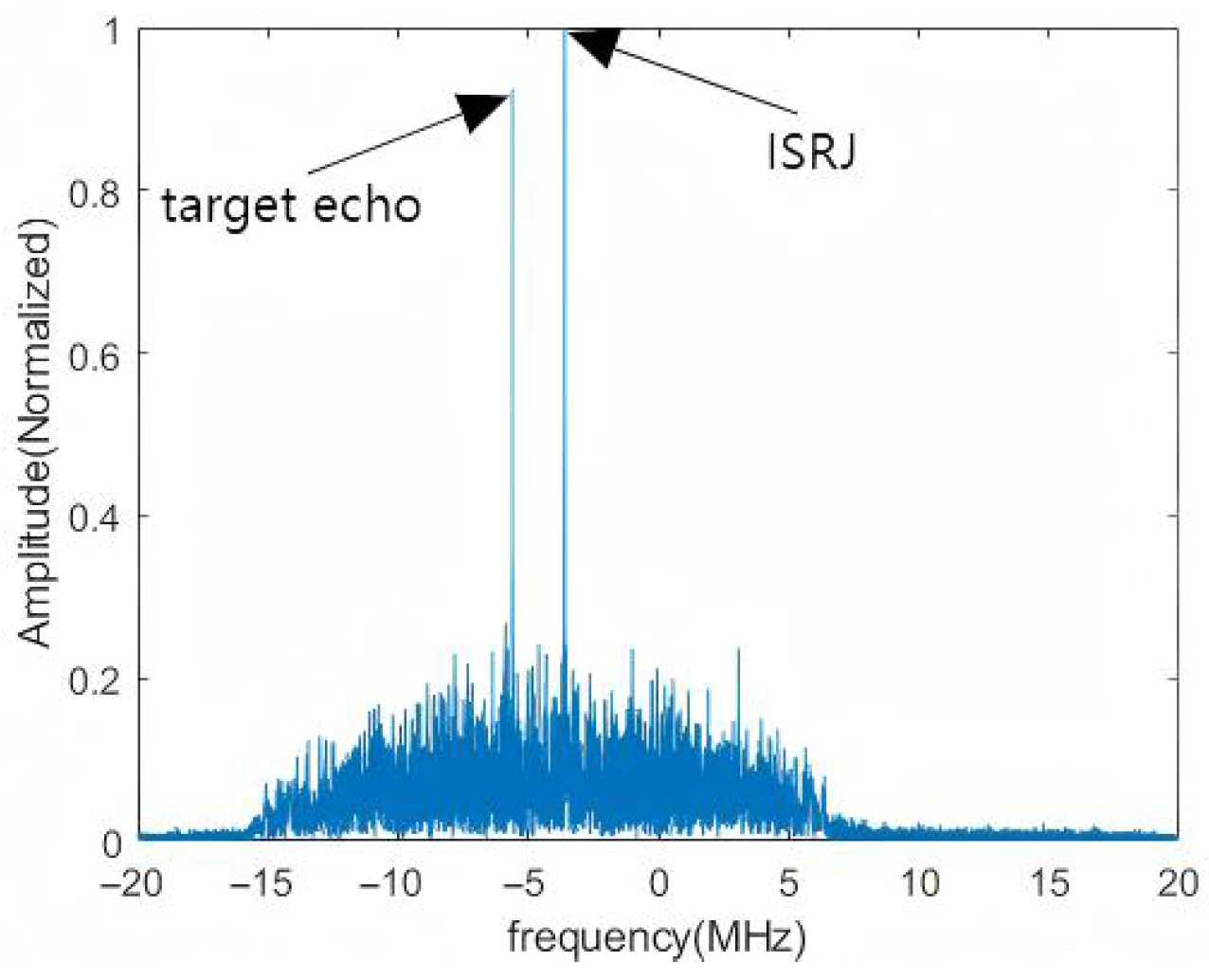
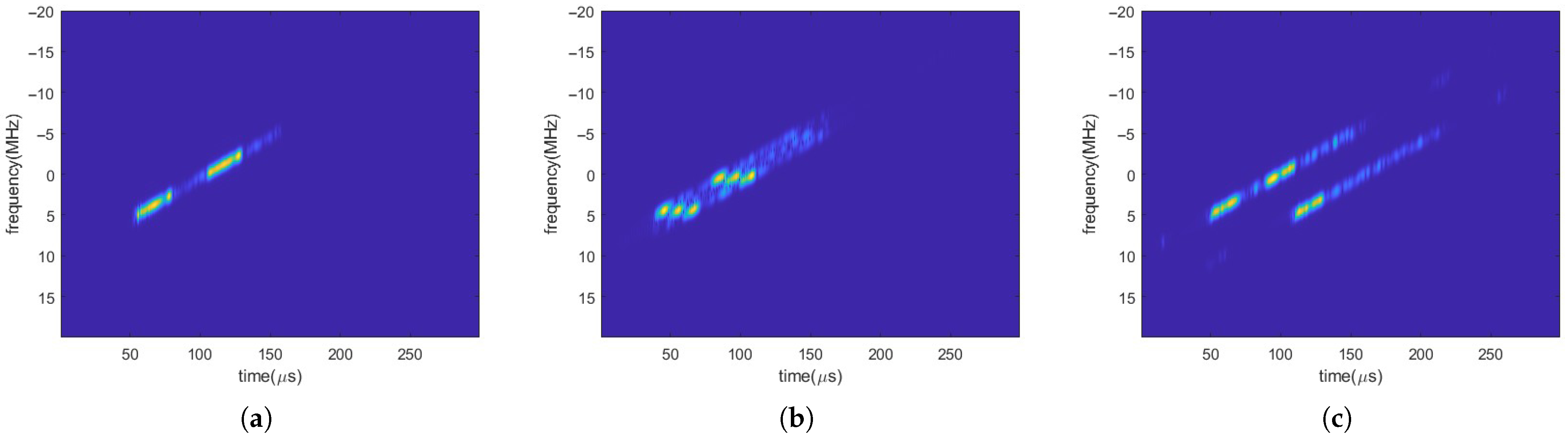
3.4. ISRJ and Echo Signal Separation
- 1.
- Reference Template Generation: The reference template is derived from the transmitted signal . First, its -order FRFT-squared magnitude, , is computed. The template is then defined as a window of length L extracted from , precisely centered at ’s main peak position , using a relative coordinate . L is chosen to encompass the main lobe and key side lobes, thereby capturing the characteristic peak shape.
- 2.
- Peak Detection: Detect peaks in to obtain the peak positions .
- 3.
- Template Matching: For each peak in , centered at , extract a window of the same length L, where . Calculate the Normalized Cross-Correlation [37] between and the reference template .The range of is [−1, 1], where a value closer to 1 indicates higher shape similarity. The peak with the highest Normalized Cross-Correlation coefficient with the reference template is selected and identified as the target echo peak .
- 4.
- Time–Frequency Masking: After obtaining the peak position of the target echo, adaptive time–frequency masking is implemented to separate the ISRJ signal. The design of the mask depends on the separation objective:
- Case 1: Separate and extract the ISRJ signal. Its definition is as shown in Equation (11):
where represents the time–frequency region where the target echo signal is primarily distributed, and represents the time–frequency region where the ISRJ signal is primarily distributed.- Case 2: Separate and extract the target echo signal. Its definition is as shown in Equation (12):
This mask is applied to the FRFT representation of the original signal to obtain the processed time–frequency distribution :Subsequently, the time-domain signal is reconstructed from through an IFRFT. The signal will primarily contain the desired signal component (either the ISRJ signal or the target echo), while the other signal component is effectively suppressed, thus achieving selective separation of the two types of signals.
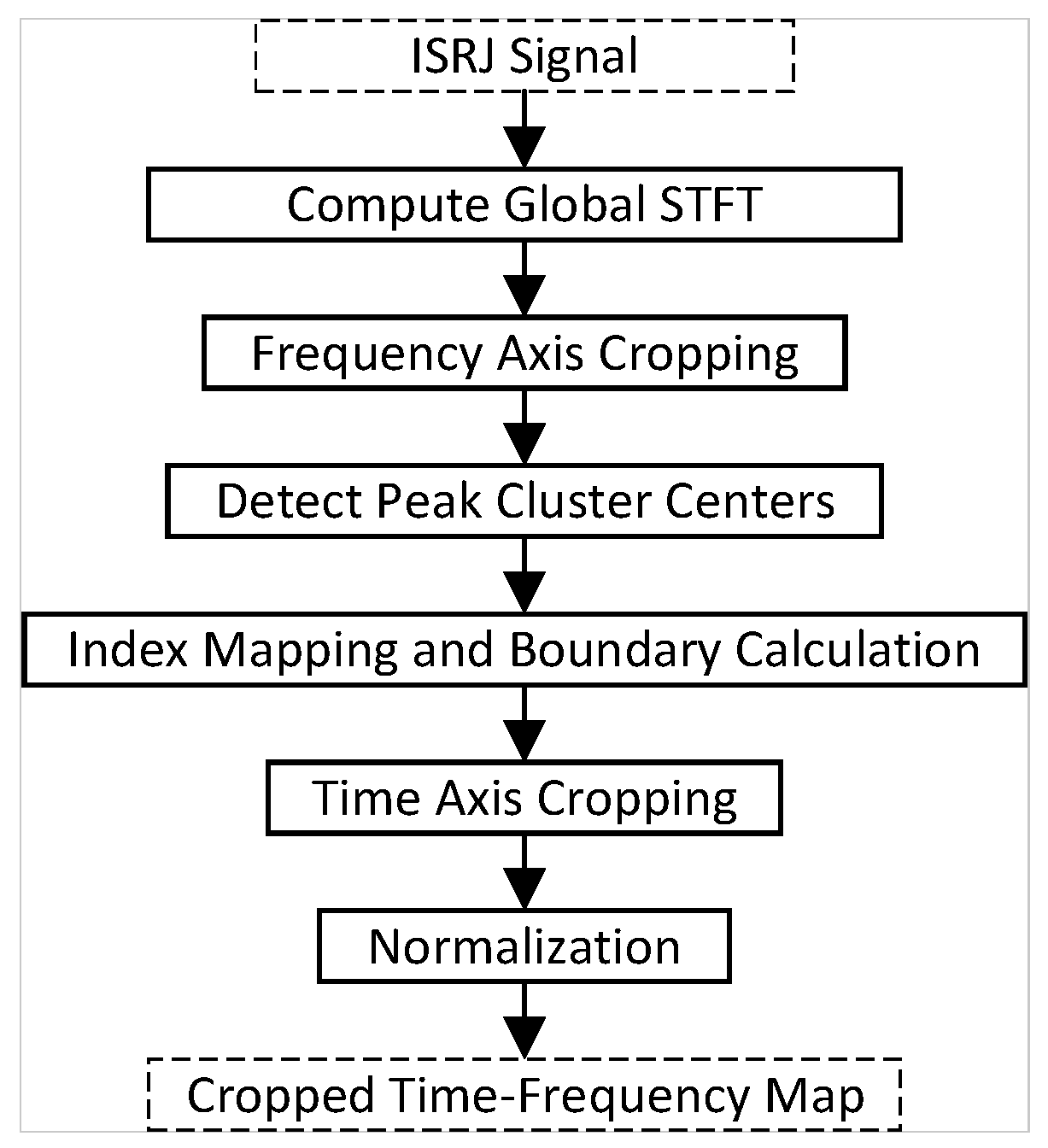
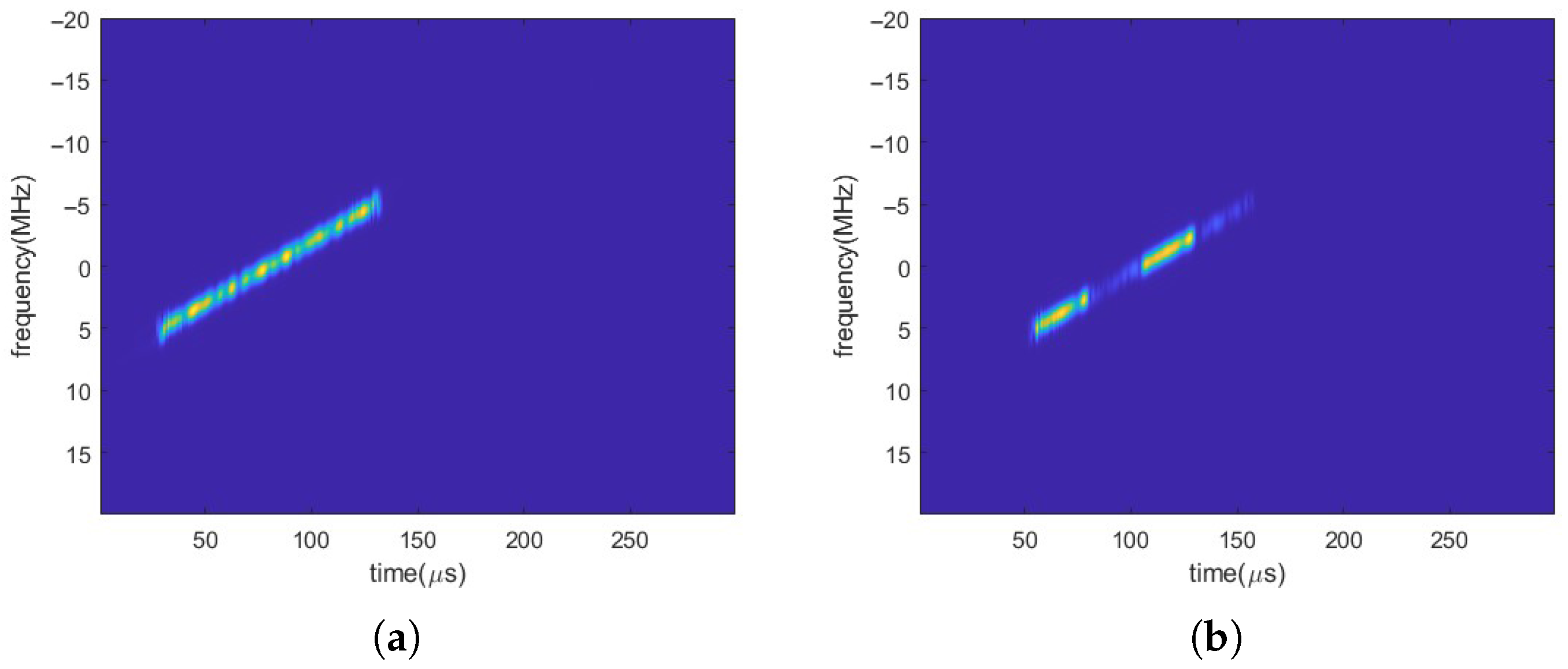
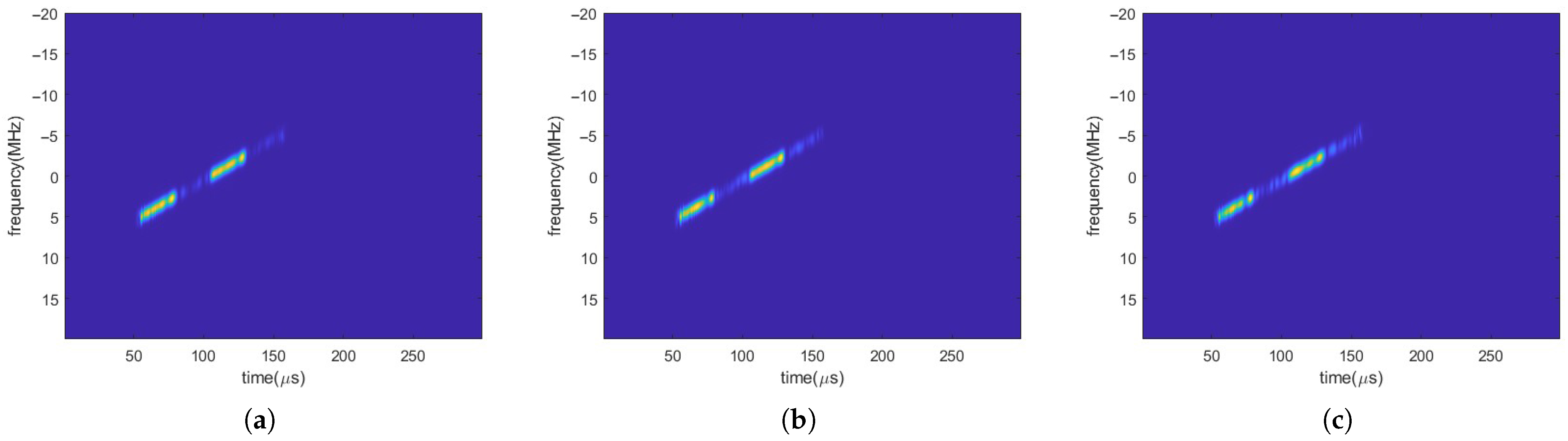
3.5. Time–Frequency Region of Interest Extraction
- 1.
- Global STFT Calculation: Perform STFT on the ISRJ signal to obtain the global time–frequency spectrum .
- 2.
- Frequency axis cropping: Given that the bandwidth of the ISRJ signal is usually narrower than the bandwidth of the radar-transmitted signal, first perform frequency axis cropping on the global time–frequency spectrum based on the spectral range of the radar-transmitted signal ( and ).
- 3.
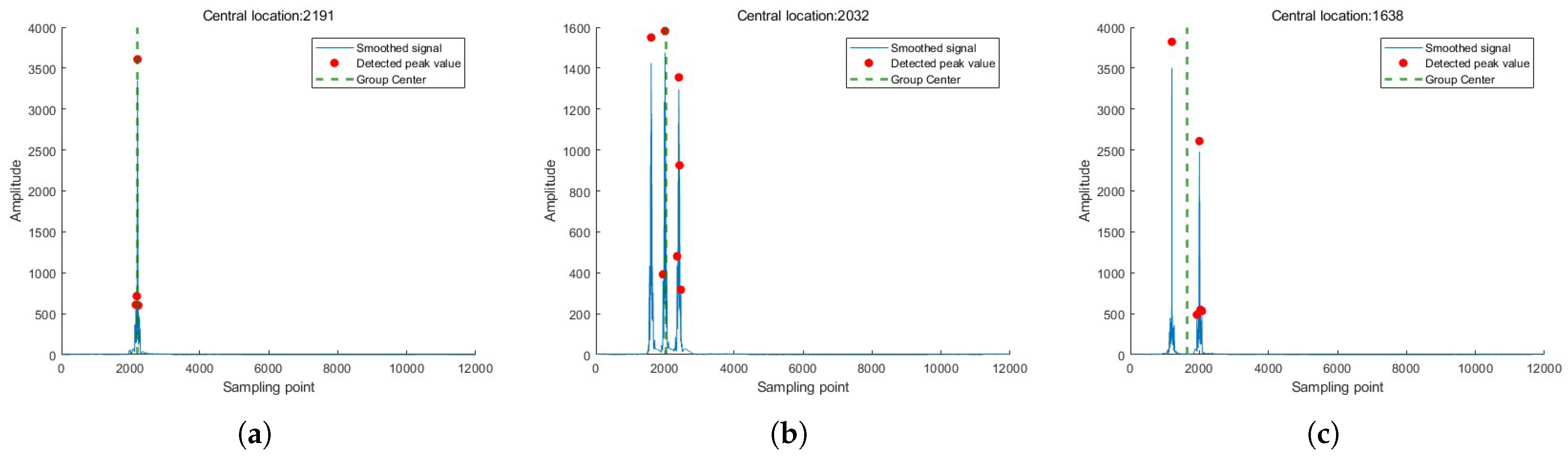
- Peak Cluster Center Detection: To locate the active intervals of the signal on the time axis, perform matched filtering on the ISRJ signal to obtain the output . Then, apply a peak cluster center detection algorithm to its magnitude . This detection integrates signal smoothing [38], adaptive threshold setting, multi-conditional peak screening, and cluster center calculation [39], thereby robustly estimating the core regions of signal energy on the time axis of the matched filter output.
- 4.
- Index Mapping and Calculation: Map the peak cluster centers from the time axis of the matched-filter output to the time axis of the STFT.
- 5.
- Time Axis Cropping: Based on the calculated and , perform time-axis cropping on the frequency-cropped time–frequency matrix to extract the time–frequency representation of the region where the jamming signal primarily exists:
- 6.
- Standardized Output: To facilitate use by subsequent processing modules, the cropped time–frequency matrix is embedded into the center of a predefined fixed-size matrix through zero-padding, resulting in a standardized-size output, .
4. ISRJ Signal Sampling Duration Estimation Based on Hybrid Modality Fusion Network
4.1. Feature Extraction
4.1.1. ISRJ Time-Domain Waveform Feature Extraction
- 1.
- Basic Statistical Features: Calculate the mean, median, variance, skewness, kurtosis, and maximum value of the envelope . These statistics describe the central tendency, dispersion, shape, and peak level of the amplitude distribution.
- 2.
- Signal Activity and Variability Features: Extract the duty cycle of the amplitude (reflecting signal activity or intermittency), the rate of amplitude change (characterizing the rate of change and fluctuation of the envelope), and the crest factor (measuring the prominence of peaks).
- 3.
- Energy and Sparsity Features: Calculate the average power of the signal (characterizing the average energy level), the power spectral entropy (reflecting the concentration of energy in the time domain), and the L1/L2 norm ratio (measuring the sparsity of the signal).
- 4.
- Amplitude Autocorrelation Features: Extract the position of the first significant non-zero delay peak of the normalized autocorrelation function of . This feature helps capture the periodicity or repetitive patterns of the envelope and plays an auxiliary role in distinguishing different forwarding modes.
4.1.2. Time-Domain Feature Extraction of ISRJ Signal After Matched Filtering
- 1.
- Pulse Peak Characteristic Statistics: First, detect all pulse peaks in the amplitude envelope and record their total number. Second, for the amplitudes of the detected peaks, calculate their mean, median, standard deviation, and maximum value to quantify the statistical distribution characteristics of pulse intensity.
- 2.
- Pulse Repetition Interval [41] Statistical Analysis: Extract the sequence of time intervals between adjacent pulse peaks and calculate the mean, median, standard deviation, minimum, and maximum values of this sequence. These statistics aim to characterize the pulse repetition time structure of the ISRJ signal.
- 3.
- Pulse Peak Position Distribution Features: Calculate the standard deviation of the occurrence times of all detected pulse peaks. This value is used to measure the dispersion of pulses on the time axis. Additionally, determine the precise time positions of the first and last pulse peaks to define the duration range of the entire effective pulse sequence.
- 4.
- Macroscopic Characteristics of the Amplitude Envelope After Matched Filtering: Calculate the mean of the amplitude envelope as an indicator of the overall energy or average intensity of the signal after matched filtering. Simultaneously, extract the position of the first significant non-origin peak of its normalized autocorrelation function to detect the macroscopic periodic structure of the amplitude envelope after matched filtering.
4.1.3. Jamming-Type Encoding
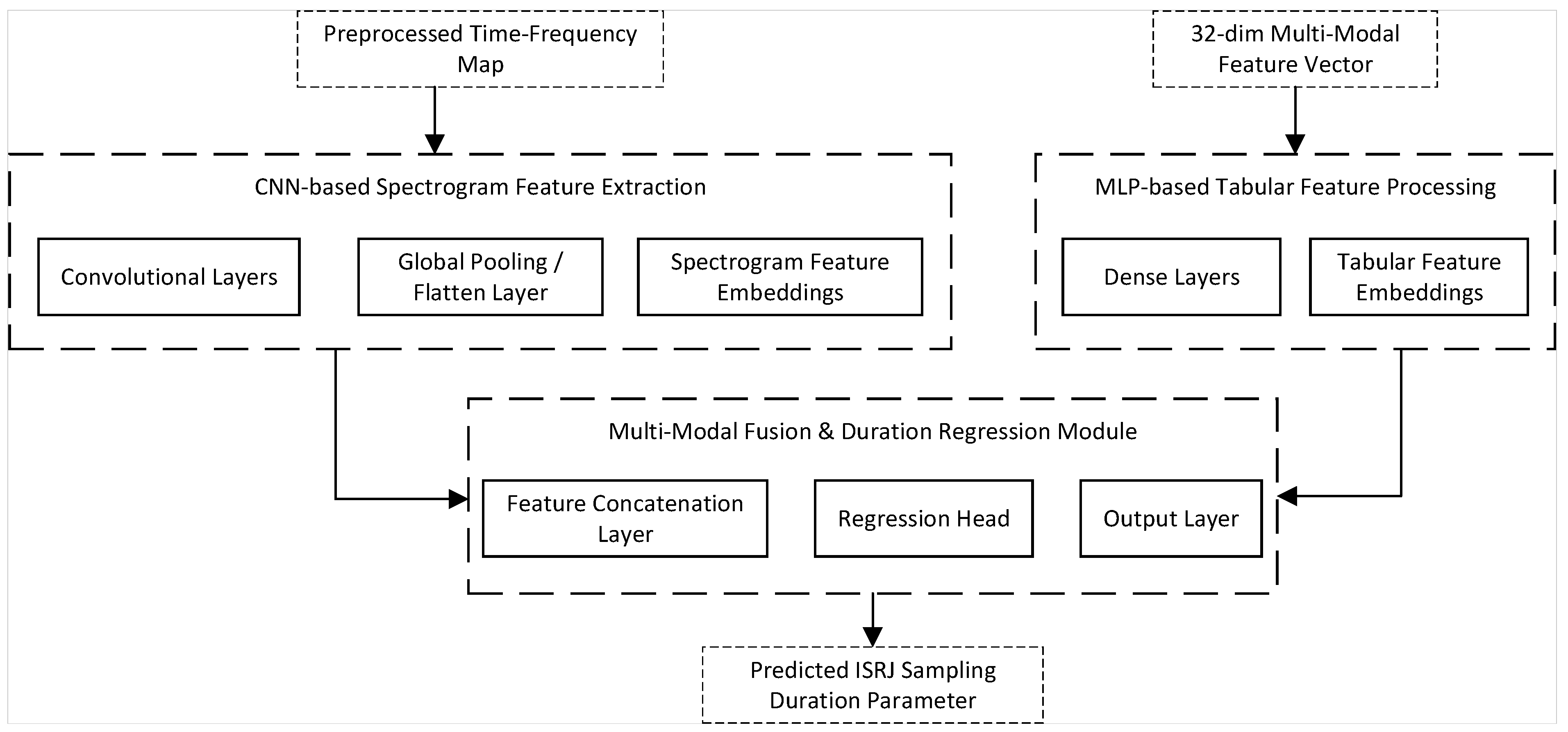
4.2. Hybrid Modality Fusion Network
- Time–Frequency Representation and Convolutional Feature Extraction: This paper selects the spectrogram as a core input branch for the network to capture the dynamic details of the signal spectrum evolving over time [42]. This high-dimensional time–frequency representation is fed into a convolutional neural network (CNN) module, which, through its hierarchical feature learning capability, can adaptively extract and encode complex time–frequency patterns sensitive to the sampling duration.
- Explicit Incorporation of Feature Vectors and A Priori Knowledge: The model additionally integrates a low-dimensional feature vector . It provides a physically meaningful and compact representation of the signal’s key physical attributes, especially those directly reflecting sampling behavior. The introduction of such features helps compensate for information loss due to spectrogram distortion. More critically, this a priori knowledge, directly related to the sampling duration, can guide the model, making its learning process more focused on the accurate estimation of the target parameter.
- CNN Feature Extraction Module: This module processes the high-dimensional TFR input . Its core is a CNN-processing unit. This unit typically consists of stacked convolutional layers, non-linear activation functions, batch normalization layers [43], and pooling layers. Convolutional layers utilize learned convolutional kernels to extract patterns with local time–frequency characteristics. After passing through the CNN-processing unit and subsequent global pooling and flattening operations, the high-dimensional time–frequency feature map is ultimately mapped to a fixed-dimension time–frequency latent feature vector. This vector can be regarded as a projection of the original spectrogram into a latent semantic space highly relevant to the sampling duration prediction task.
- MLP Feature Vector Processing Module: As indicated in the “MLP-based Tabular Feature Processing” part of Figure 14, this module receives the low-dimensional engineered feature vector . Its core is an MLP-processing unit. This unit is composed of multiple fully connected layers, non-linear activation functions, and batch normalization layers, supplemented by Dropout regularization [44]. This module ultimately outputs a fixed-dimension engineered feature latent vector . Its dimension is carefully designed for effective fusion with the time–frequency features extracted by the CNN.
- Feature Fusion and Regression Prediction Module: This module integrates heterogeneous features from the preceding parallel branches and outputs the estimated ISRJ sampling duration. As shown in Figure 14, first, the time–frequency latent feature vector output by the CNN module and the engineered feature latent vector output by the MLP module are concatenated along the feature dimension. This forms a higher-dimensional fused feature vector . Subsequently, the fused feature vector is fed into a regression head for processing. The regression head internally contains a regression-processing unit. Its role is to perform further non-linear transformations and information refinement on the fused high-dimensional features to extract the final abstract representation most relevant to the target prediction. Finally, through an output layer, this final feature representation is mapped to the target prediction value, i.e., the predicted sampling duration of the ISRJ signal .
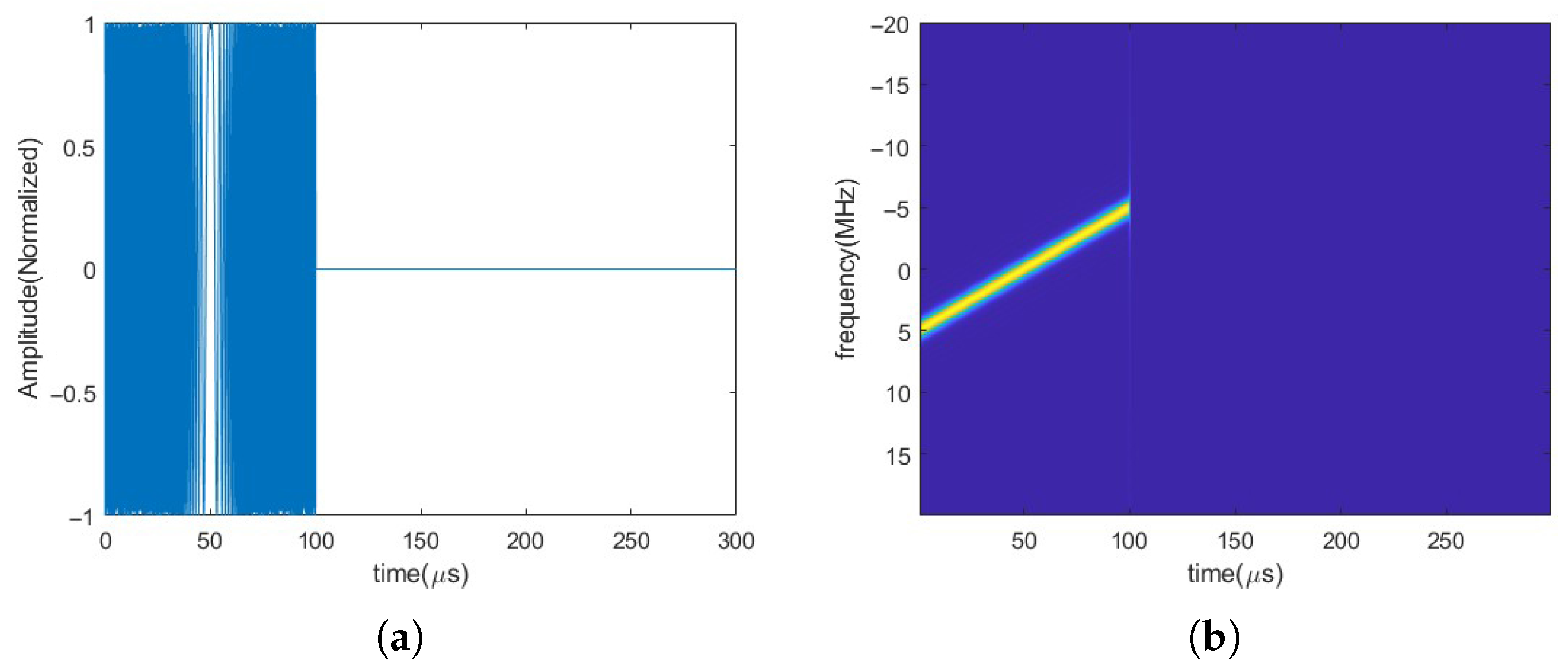
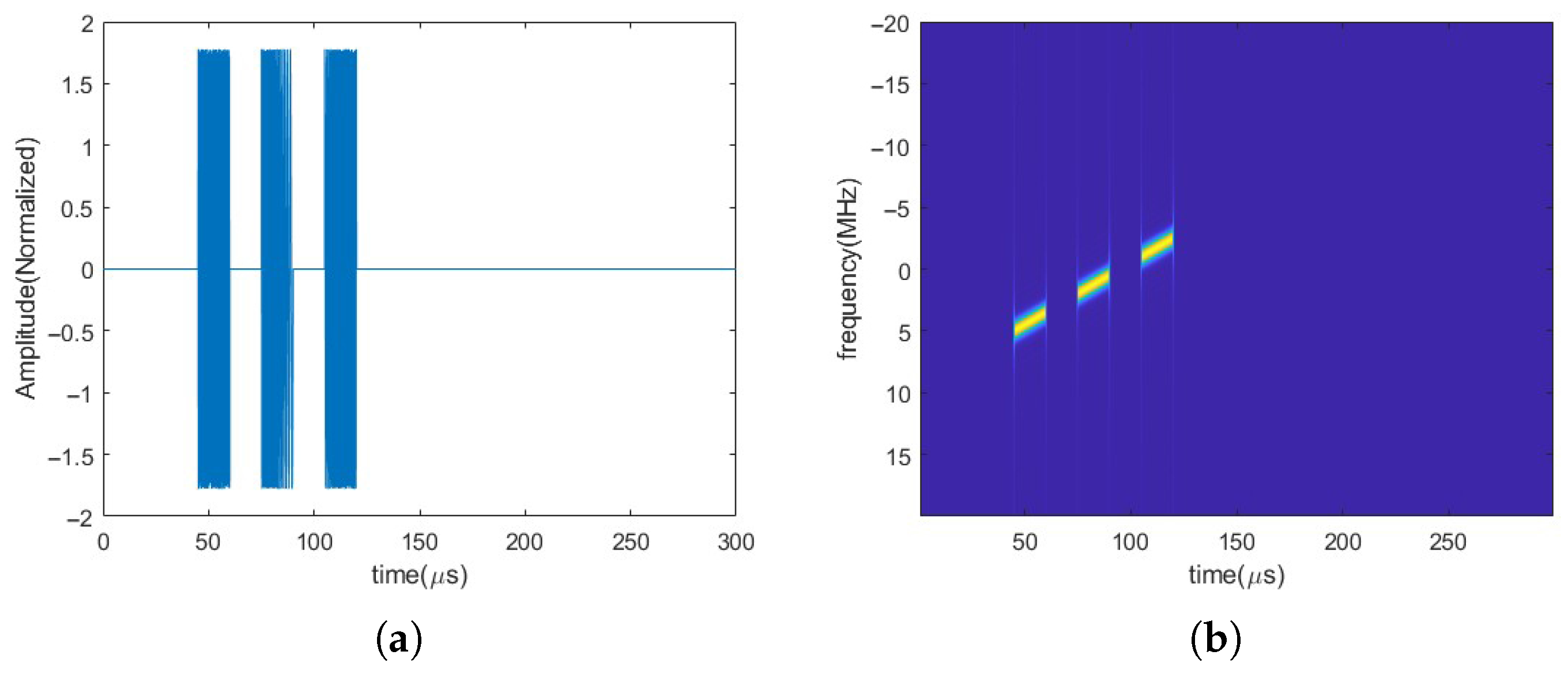
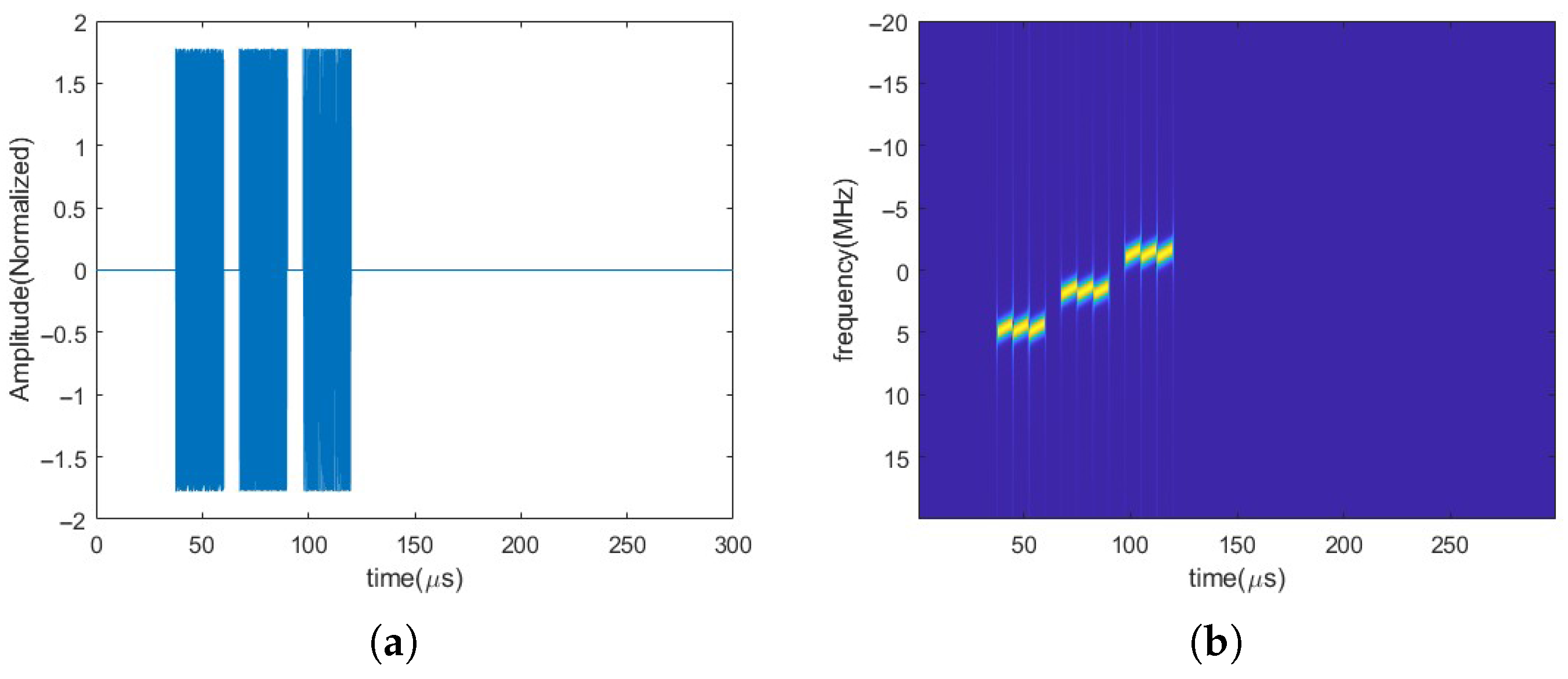
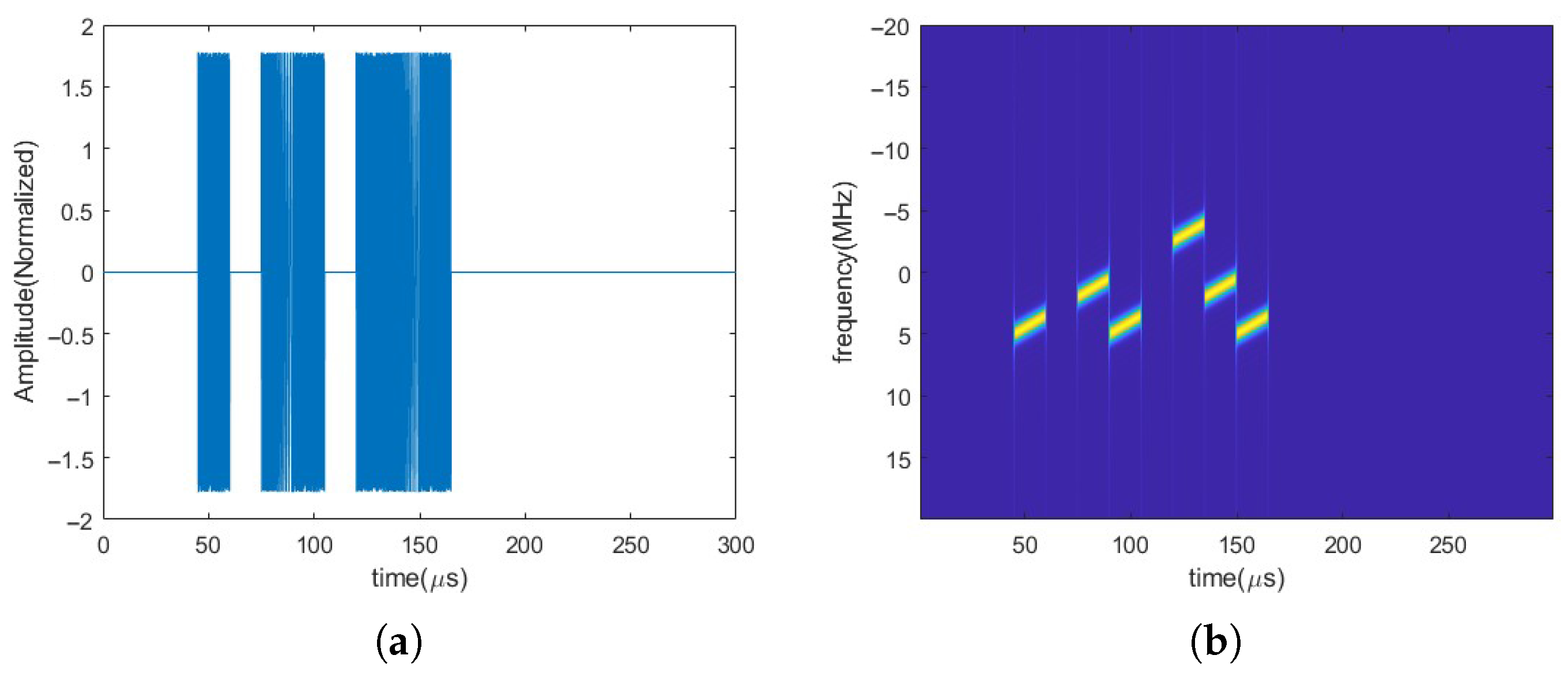
5. Simulation Analysis
5.1. Mixed-Signal Separation
5.1.1. SMSP Jamming Filtering
5.1.2. Extraction of ISRJ and Target Echo Signal
5.1.3. Time–Frequency Map Cropping
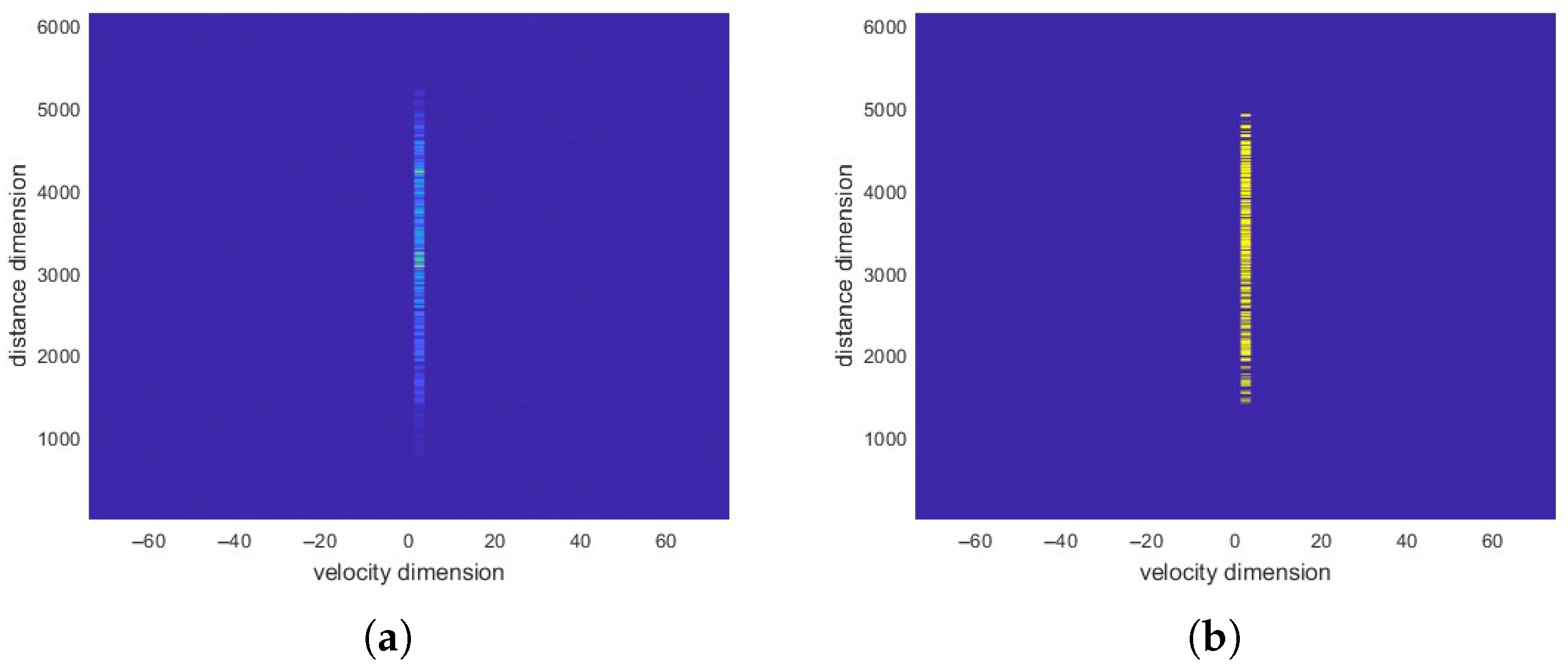
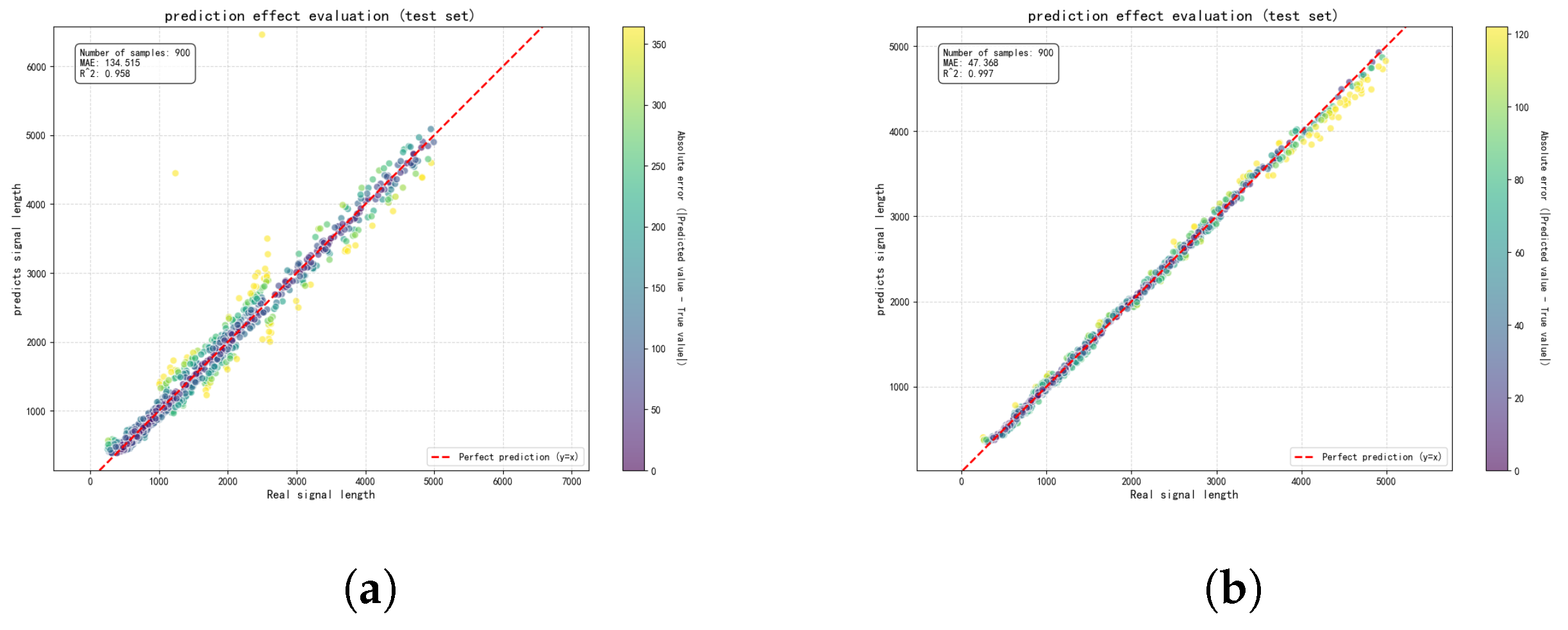
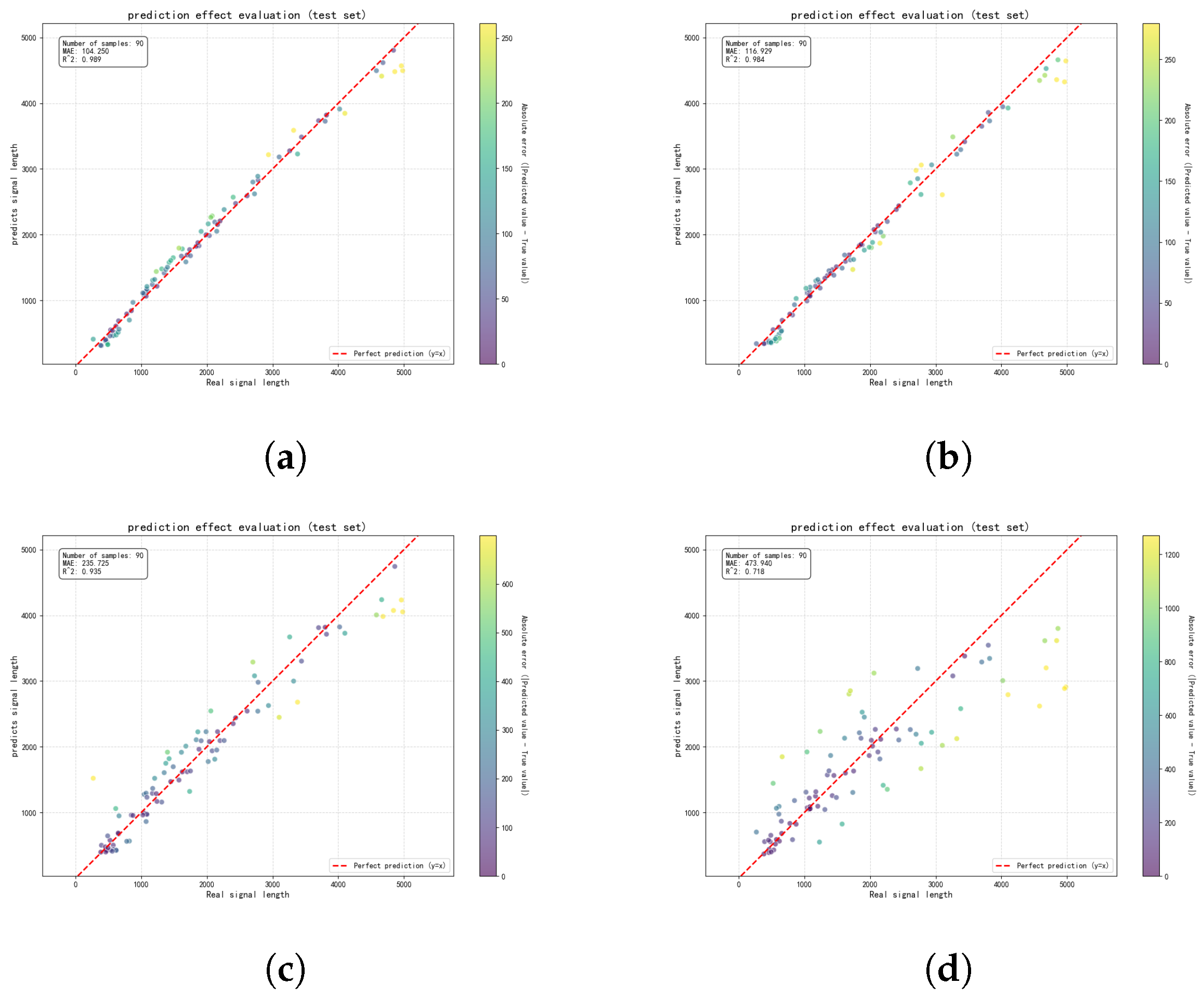
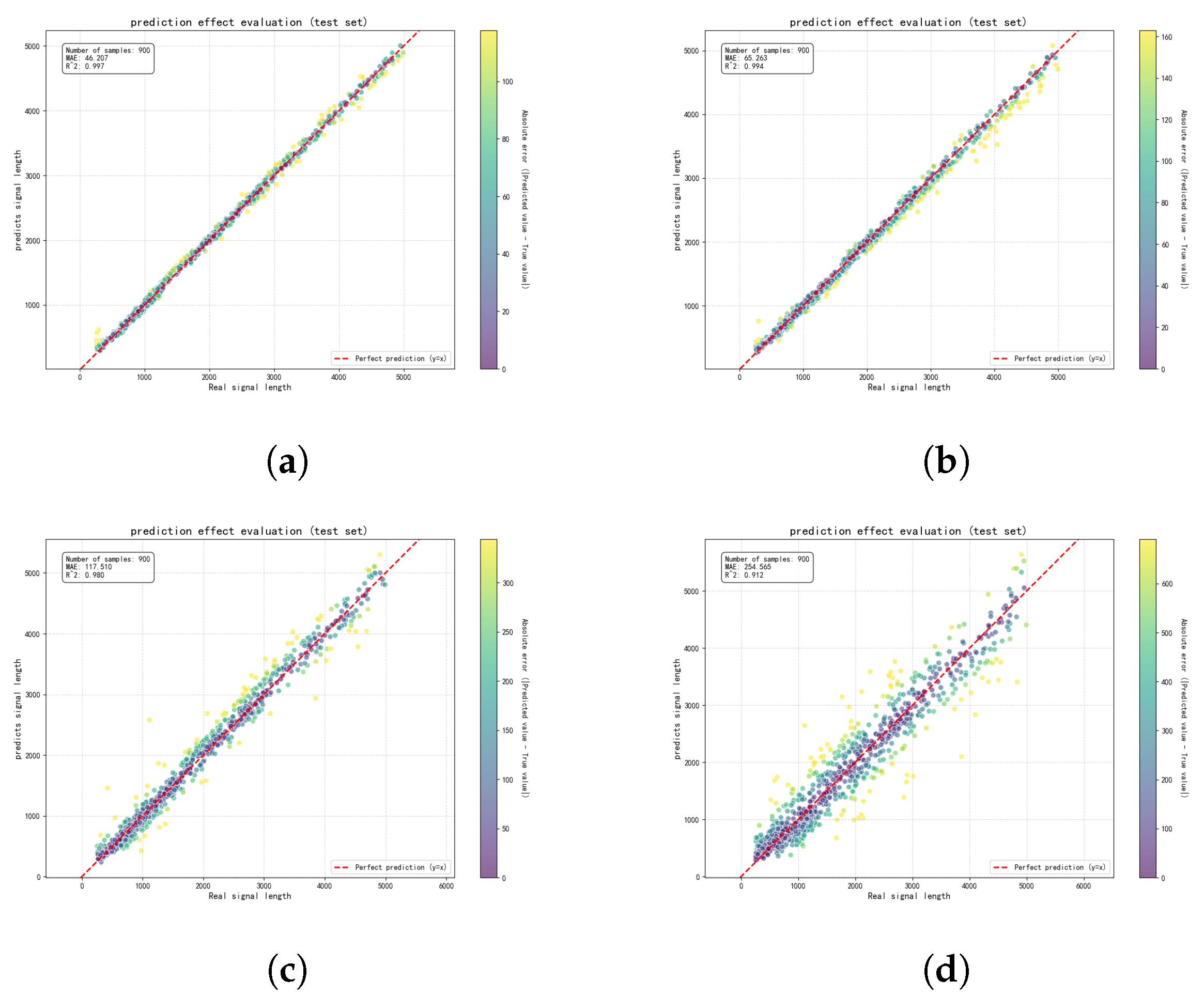
5.1.4. ISRJ Parameter Estimation Results
6. Results
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Liu, Y.; Wang, C. Multi-Domain Fusion Network for Active Jamming Recognition in Cognitive Radar. Remote Sens. 2025, 17, 1723. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, L.; Guo, Z. A Radar Compound Jamming Recognition Method Based on Blind Source Separation. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 9073–9084. [Google Scholar] [CrossRef]
- Pan, Y.; Xie, D.; Zhao, Y.; Wang, X.; Huang, Z. Overview of Radar Jamming Waveform Design. Remote Sens. 2025, 17, 1218. [Google Scholar] [CrossRef]
- Han, R.; Li, X.; Xu, X.; Zhang, Z.; Zhang, T. Adaptive Reconnaissance and Suppressive Jamming Strategy Generation Based on Reinforcement Learning. IEEE Trans. Aerosp. Electron. Syst. 2025, early access. [Google Scholar] [CrossRef]
- Li, Q.; Guo, Y.; Zhang, P.; Xu, H.; Zhang, L.; Chen, Z.; Huang, Y. Deception Velocity-Based Method to Discriminate Physical Targets and Active False Targets in a Multistatic Radar System. Remote Sens. 2024, 16, 382. [Google Scholar] [CrossRef]
- Orduyilmaz, A.; Ispir, M.; Serin, M.; Efe, M. Ultra wideband spectrum sensing for cognitive electronic warfare applications. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019. [Google Scholar]
- Lei, Z.; Qu, Q.; Chen, H.; Zhang, Z.; Dou, G.; Wang, Y. Mainlobe Jamming Suppression With Space-Time Multichannel via Blind Source Separation. IEEE Sens. J. 2023, 23, 17042–17053. [Google Scholar] [CrossRef]
- Lv, Q.; Liu, L.; Wu, Y.; Peng, M.; Quan, Y. A Framework for Compound Interrupted Sampling Repeater Jamming Parameter Measurement. IEEE Trans. Instrum. Meas. 2025, 74, 2507704. [Google Scholar] [CrossRef]
- Liu, Q.; Sui, X.; Chen, X.; Liang, Z.; Zhu, R. Jamming suppression by blind source separation: From a perspective of spatial band-pass filters. J. Syst. Eng. Electron. 2025, 1–8. [Google Scholar] [CrossRef]
- Luo, W.; Jin, H.; Li, H.; Duan, K. Radar Main-Lobe Jamming Suppression Based on Adaptive Opposite Fireworks Algorithm. IEEE Open J. Antennas Propag. 2021, 2, 138–150. [Google Scholar] [CrossRef]
- Lu, L.; Gao, M. A Truncated Matched Filter Method for Interrupted Sampling Repeater Jamming Suppression Based on Jamming Reconstruction. Remote Sens. 2022, 14, 97. [Google Scholar] [CrossRef]
- Lu, L.; Gao, M. An Improved Sliding Matched Filter Method for Interrupted Sampling Repeater Jamming Suppression Based on Jamming Reconstruction. IEEE Sens. J. 2022, 22, 9675–9684. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, Y.; Su, H.; Wang, Z.; Bao, Q.; Pan, J. Research on an Intra-Pulse Orthogonal Waveform and Methods Resisting Interrupted-Sampling Repeater Jamming within the Same Frequency Band. Remote Sens. 2023, 15, 3673. [Google Scholar] [CrossRef]
- Chao, Z.; Liu, Q.; Tao, Z. Research on DRFM Repeater Jamming Recognition. J. Signal Process. 2017, 33, 911–917. [Google Scholar] [CrossRef]
- Liu, M.; Chen, J.; Pan, X.; Zhao, F. Parameter Estimation for Interrupted-Sampling Jamming Recognition Based on Piecewise Shannon Entropy. In Proceedings of the 2022 International Applied Computational Electromagnetics Society Symposium (ACES-China), Xuzhou, China, 9–12 December 2022. [Google Scholar]
- Liu, L.; Lv, Q.; Liu, J.; Wu, Y.; Quan, Y. Adaptive Parameter Estimation for Compound Interrupted Sampling and Repeating Jamming. IEEE Signal Process. Lett. 2024, 31, 496–500. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Chen, H.; Liu, W.; Zhu, Y.; Luo, J.; Ni, L. Interrupted-Sampling Repeater Jamming Countermeasure Based on Intrapulse Frequency–Coded Joint Frequency Modulation Slope Agile Waveform. Remote Sens. 2024, 16, 2810. [Google Scholar] [CrossRef]
- Han, B.; Qu, X.; Yang, X.; Li, W.; Zhang, Z. DRFM-Based Repeater Jamming Reconstruction and Cancellation Method with Accurate Edge Detection. Remote Sens. 2023, 15, 1759. [Google Scholar] [CrossRef]
- Zhe, Z. Radar Signal Recognition and Parameter Estimation Based on FRFT. Master’s Thesis, Harbin Engineering University, Harbin, China, 2020. [Google Scholar]
- Wen, Z.; Liu, M.; Chen, Y.; Zhao, N.; Nallanathan, A.; Yang, X. Multi-Component LFM Signal Parameter Estimation for Symbiotic Chirp-UWB Radio Systems. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 1608–1619. [Google Scholar] [CrossRef]
- Deng, J.; Sun, Z.; Li, X.; Cui, G. ASC-BSS-Based Parameter Estimation Method for Multiple LFM Pulses With Aliasing Effect From Passive Radar. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 5132–5144. [Google Scholar] [CrossRef]
- Wang, P.; Yang, J.; Du, Y. A fast algorithm for parameter estimation of multi-component LFM signal at low SNR. In Proceedings of the 2005 International Conference on Communications, Circuits and Systems, Hong Kong, China, 27–30 May 2005; Volume 2, pp. 765–768. [Google Scholar]
- Gong, S.; Wei, X.; Li, X. ECCM scheme against interrupted sampling repeater jammer based on time-frequency analysis. J. Syst. Eng. Electron. 2014, 25, 996–1003. [Google Scholar] [CrossRef]
- Ji, H. Parameter Estimation of LFM Signal Based on Radon-WDL Transform and Its Application. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2017. [Google Scholar]
- Tingyu, N. Research on Parameter Estimation Algorithm of LPI Radar Signals Based on T-F Analysis. Master’s Thesis, Xidian University, Xi’an, China, 2017. [Google Scholar]
- Xie, Q.; Wang, Z.; Wen, F.; He, J.; Truong, T.K. Coarray Tensor Train Decomposition for Bistatic MIMO Radar with Uniform Planar Array. IEEE Trans. Antennas Propag. 2025, early access. [Google Scholar] [CrossRef]
- Hao, L. Research on Radar Jamming Suppression Based on Jamming Cognition. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2021. [Google Scholar]
- Duong, V.M.; Vesely, J.; Hubacek, P.; Janu, P.; Tran, X.L. Detection and parameter estimation of intra-pulse modulated radar signals in complex interference environments+. SN Appl. Sci. 2023, 5, 184. [Google Scholar] [CrossRef]
- Shi, Z.; Wu, H.; Zhu, X.; Wang, W.; Ni, X.; Zhang, J. Interrupted sampling forwarding jamming parameter estimation based on YOLOv7-tiny. In Proceedings of the 2024 IEEE 7th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 31 July–2 August 2024; pp. 144–149. [Google Scholar]
- Meng, Y.; Yu, L.; Wei, Y. Multiple information cognition of interrupted sampling repeater jamming in complex scenes. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 2176–2179. [Google Scholar]
- He, X.; Liao, K.; Peng, S.; Tian, Z.; Huang, J. Interrupted-Sampling Repeater Jamming-Suppression Method Based on a Multi-Stages Multi-Domains Joint Anti-Jamming Depth Network. Remote Sens. 2022, 14, 3445. [Google Scholar] [CrossRef]
- Chao, Z.; Liu, Q.; Cheng, H. Time-frequency Analysis Techniques for Recognition and Suppression of Interrupted Sampling Repeater Jamming. J. Radars 2019, 8, 100–106. [Google Scholar]
- Li, Y. Research on the Identification and Inhibition of SMSP and C&I Distance False Target Spoof Interference. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2012. [Google Scholar]
- Wang, Y.; Liu, G.; Ma, X.; Song, C.; Jin, G.; Li, L. A Convolution Modulation Jamming Method Based on the Optimal Combination of Noise Templates. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4008905. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.; Lu, X.; Zhang, Y. SDBD: A Hierarchical Region-of-Interest Detection Approach in Large-Scale Remote Sensing Image. IEEE Geosci. Remote Sens. Lett. 2017, 14, 699–703. [Google Scholar] [CrossRef]
- Chen, R.; Wang, Y. Universal FRFT-based algorithm for parameter estimation of chirp signals. J. Syst. Eng. Electron. 2012, 23, 495–501. [Google Scholar] [CrossRef]
- Wei, S.D.; Lai, S.H. Fast Template Matching Based on Normalized Cross Correlation with Adaptive Multilevel Winner Update. IEEE Trans. Image Process. 2008, 17, 2227–2235. [Google Scholar] [CrossRef]
- Liu, P.; Huang, W.; Zhang, W.; Li, F. An EMD-SG Algorithm for Spectral Noise Reduction of FBG-FP Static Strain Sensor. IEEE Photonics Technol. Lett. 2017, 29, 814–817. [Google Scholar] [CrossRef]
- Chen, H.; Maharatna, K. An Automatic R and T Peak Detection Method Based on the Combination of Hierarchical Clustering and Discrete Wavelet Transform. IEEE J. Biomed. Health Inform. 2020, 24, 2825–2832. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Ma, C.X.; Zhou, Y.R.; Luo, M.X.; Zhang, K.B. Multi-Feature Fusion for Enhancing Image Similarity Learning. IEEE Access 2019, 7, 167547–167556. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Si, W. PRI modulation recognition and sequence search under small sample prerequisite. J. Syst. Eng. Electron. 2023, 34, 706–713. [Google Scholar] [CrossRef]
- Huang, J.; Chen, B.; Yao, B.; He, W. ECG Arrhythmia Classification Using STFT-Based Spectrogram and Convolutional Neural Network. IEEE Access 2019, 7, 92871–92880. [Google Scholar] [CrossRef]
- Fagbohungbe, O.; Qian, L. The Effect of Batch Normalization on Noise Resistant Property of Deep Learning Models. IEEE Access 2022, 10, 127728–127741. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Z.Q.J. Implicit Regularization of Dropout. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 4206–4217. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Radar-transmitted-signal pulse width | 100 |
| Radar-transmitted-signal bandwidth | 10 MHz |
| Radar-transmitted-signal chirp rate | 100 GHz |
| Sampling rate | 40 MHz |
| ISDRJ-sampling-duration range | 10–50 |
| ISPRJ-sampling-duration range | 5–25 |
| ISCRJ-sampling-duration range | 5–25 |
| SMSP-jamming decimation factor range | 2–8 |
| SNR | 5 dB |
| SJR (Deception Jamming) | −5 dB |
| SJR (Suppression Jamming) | −8 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhu, C.; Song, Z.; Wang, Z.; Wang, F. A New Signal Separation and Sampling Duration Estimation Method for ISRJ Based on FRFT and Hybrid Modality Fusion Network. Remote Sens. 2025, 17, 2648. https://doi.org/10.3390/rs17152648
Wang S, Zhu C, Song Z, Wang Z, Wang F. A New Signal Separation and Sampling Duration Estimation Method for ISRJ Based on FRFT and Hybrid Modality Fusion Network. Remote Sensing. 2025; 17(15):2648. https://doi.org/10.3390/rs17152648
Chicago/Turabian StyleWang, Siyu, Chang Zhu, Zhiyong Song, Zhanling Wang, and Fulai Wang. 2025. "A New Signal Separation and Sampling Duration Estimation Method for ISRJ Based on FRFT and Hybrid Modality Fusion Network" Remote Sensing 17, no. 15: 2648. https://doi.org/10.3390/rs17152648
APA StyleWang, S., Zhu, C., Song, Z., Wang, Z., & Wang, F. (2025). A New Signal Separation and Sampling Duration Estimation Method for ISRJ Based on FRFT and Hybrid Modality Fusion Network. Remote Sensing, 17(15), 2648. https://doi.org/10.3390/rs17152648






