Radar Monitoring and Numerical Simulation Reveal the Impact of Underground Blasting Disturbance on Slope Stability
Abstract
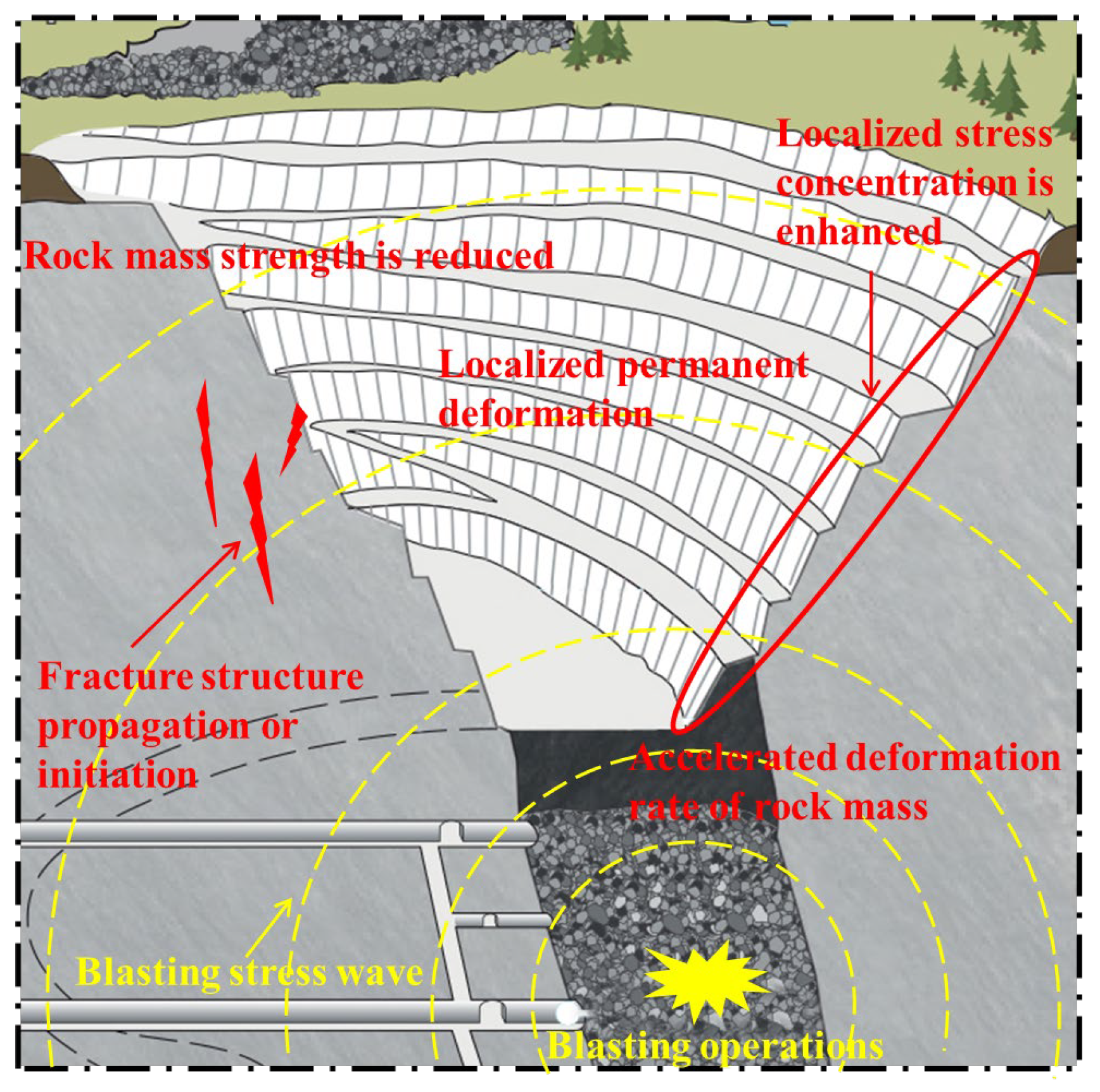
1. Introduction
2. Materials and Methods
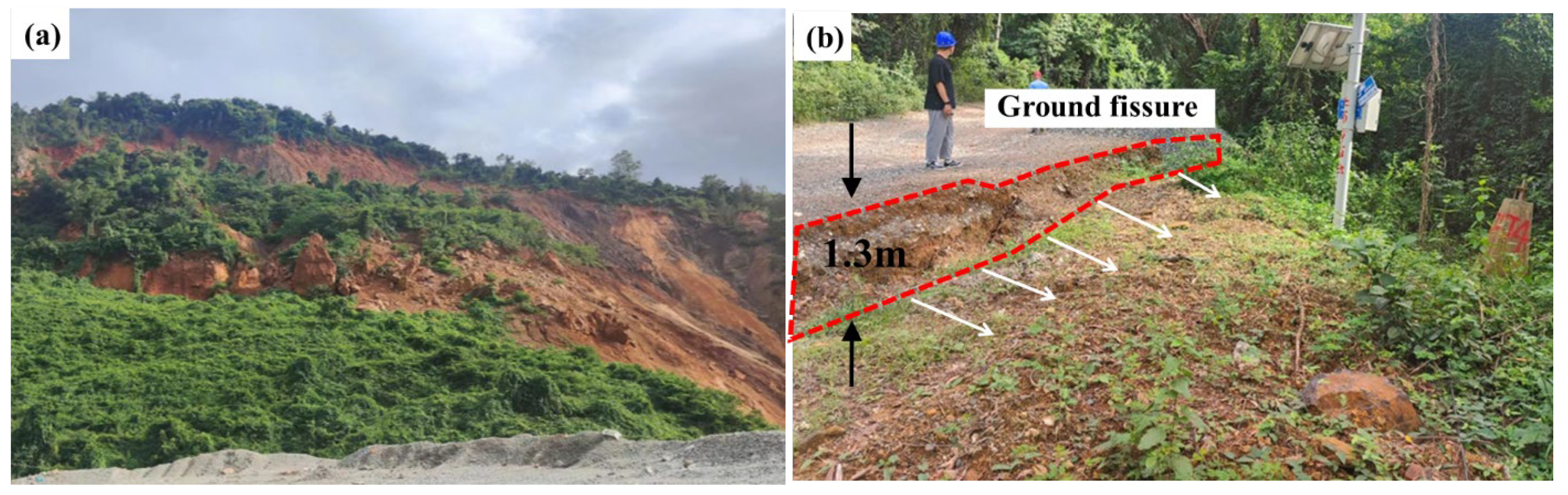
2.1. Research Area
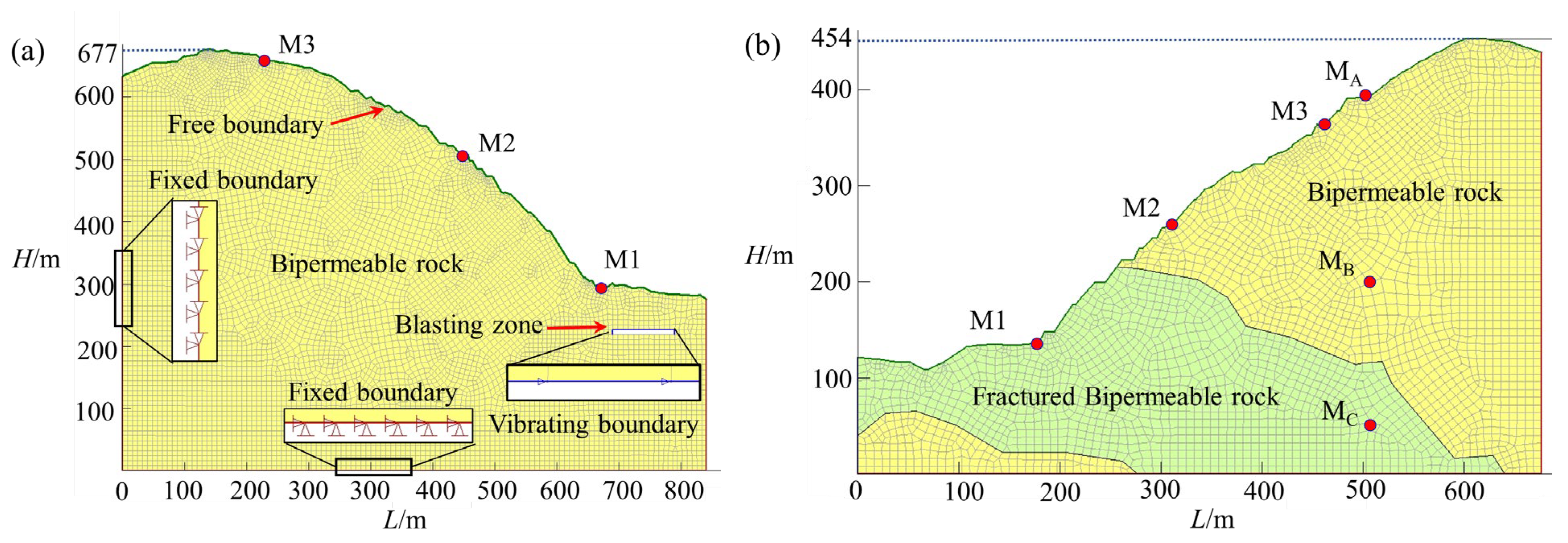
2.2. Dynamic Response Analysis Model of Slope
2.3. Slope Surface Deformation Monitoring Using Radar and Correlation Analysis with Blasting Activities
3. Results
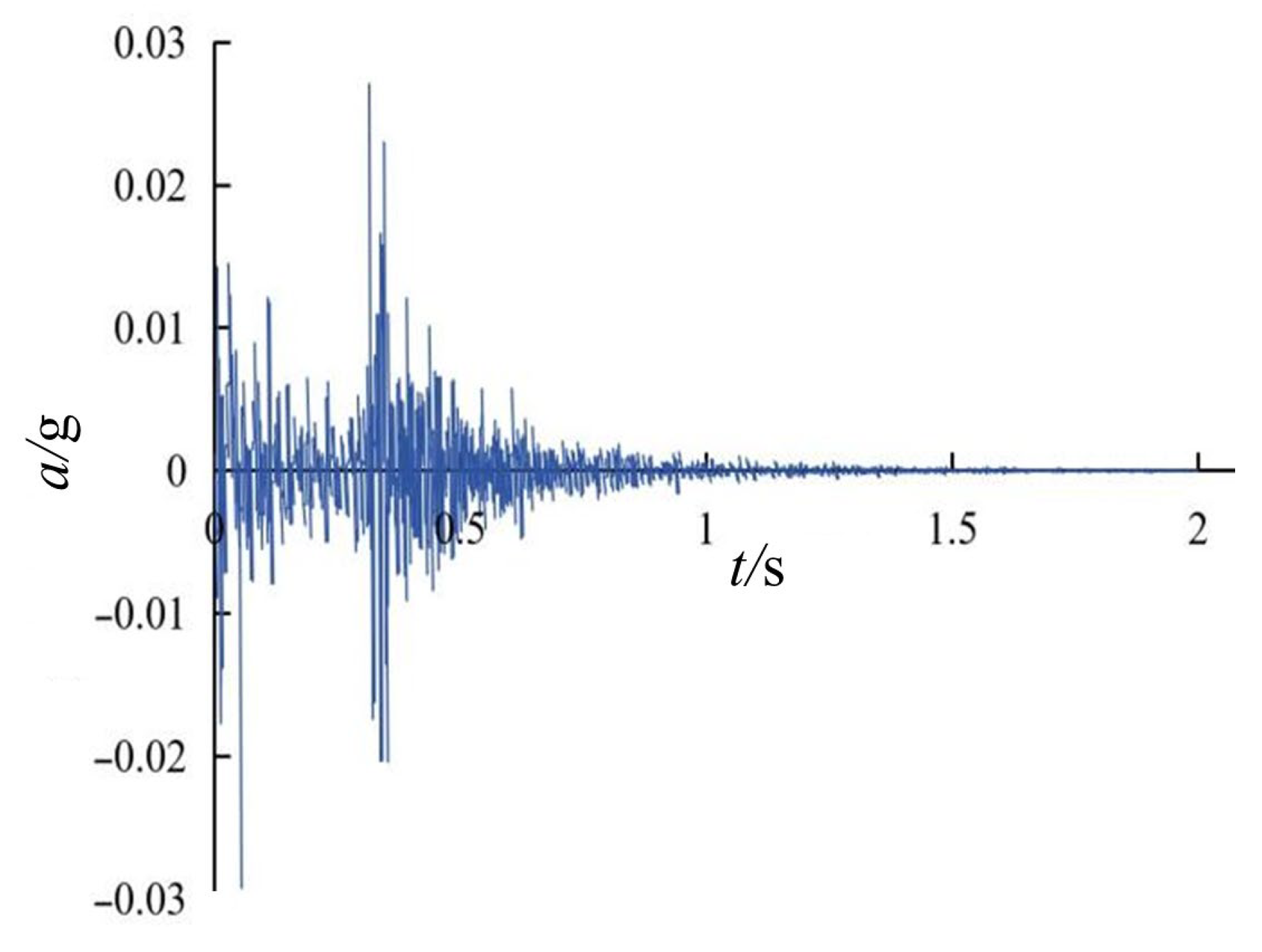
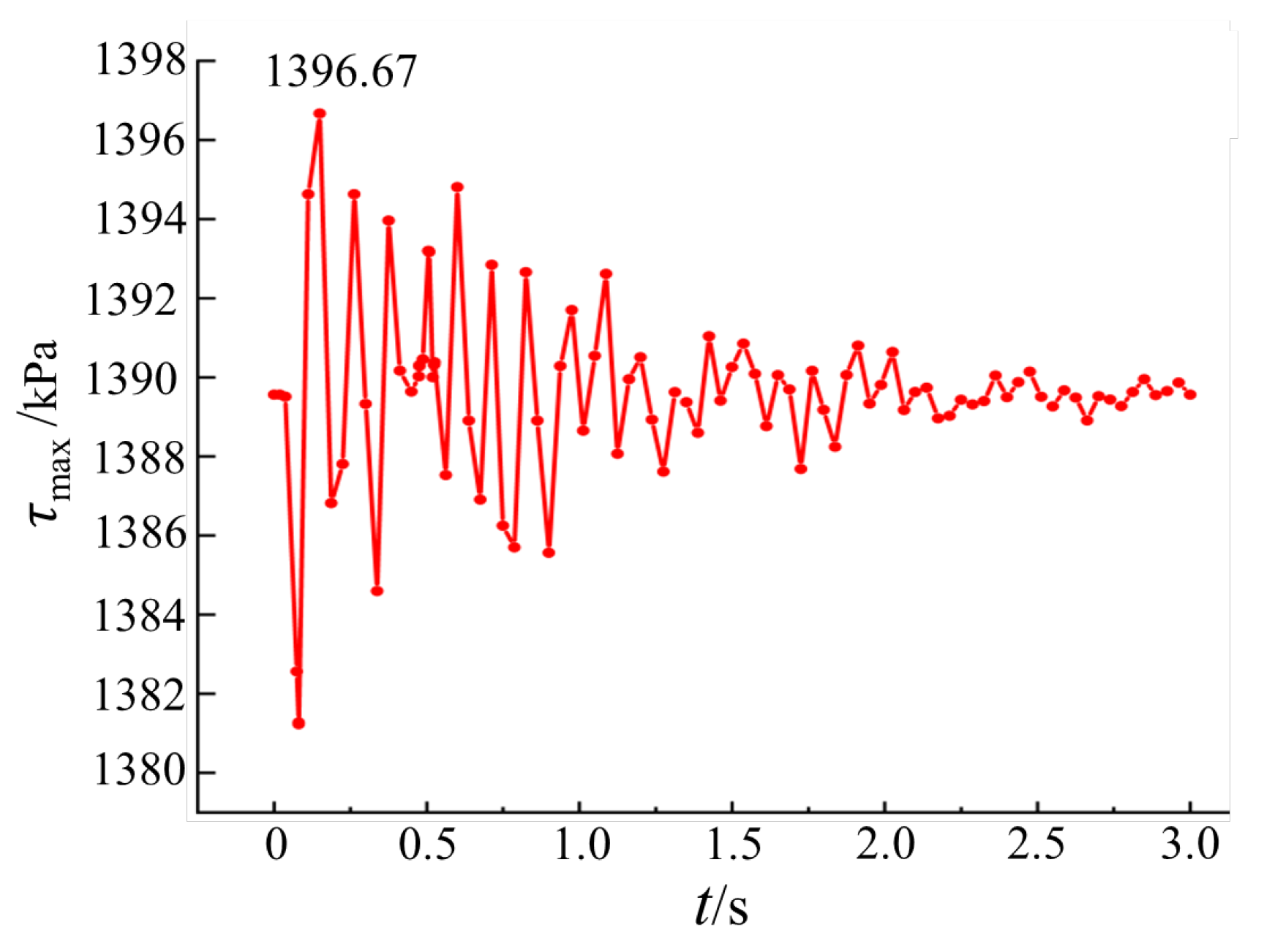
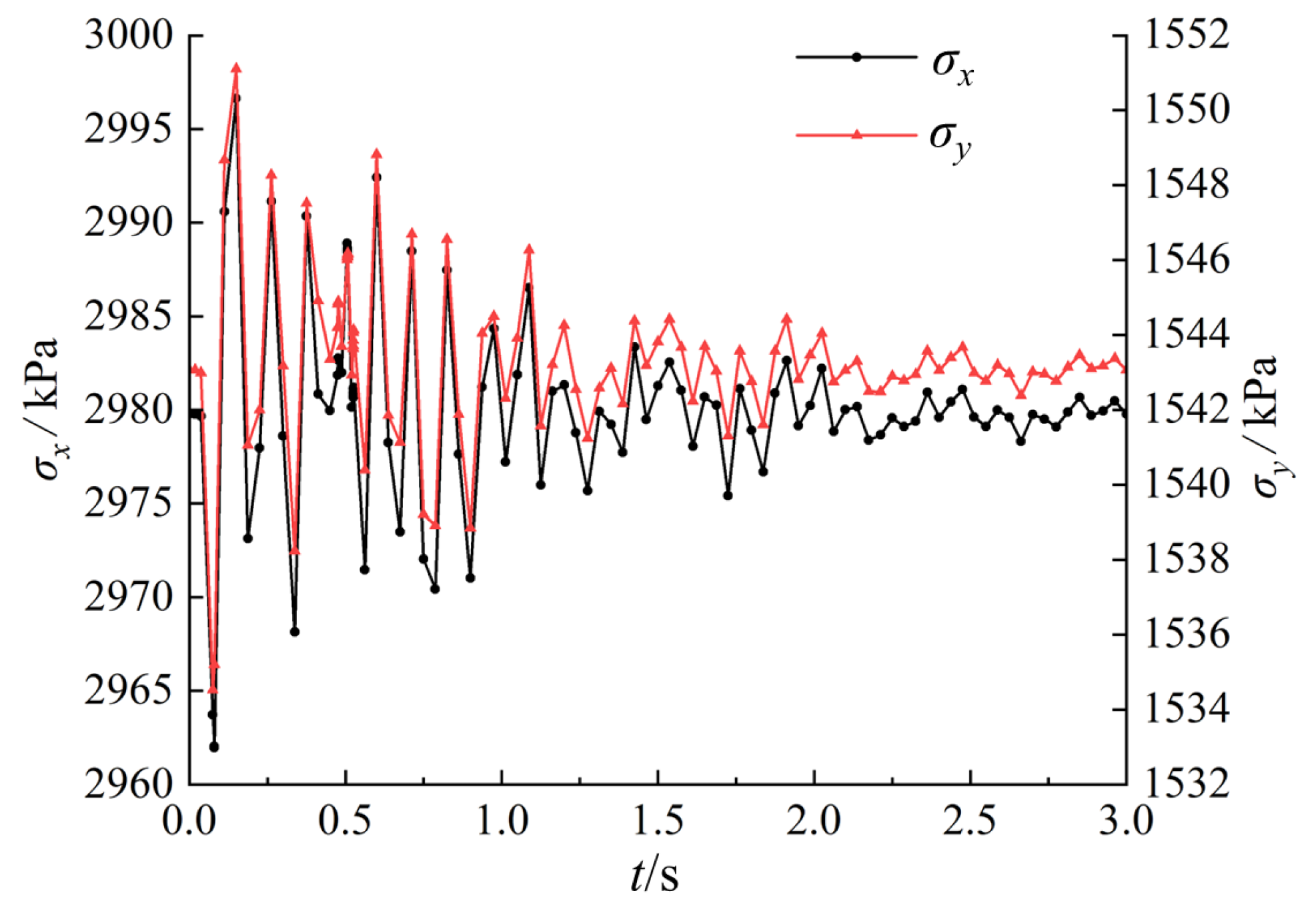
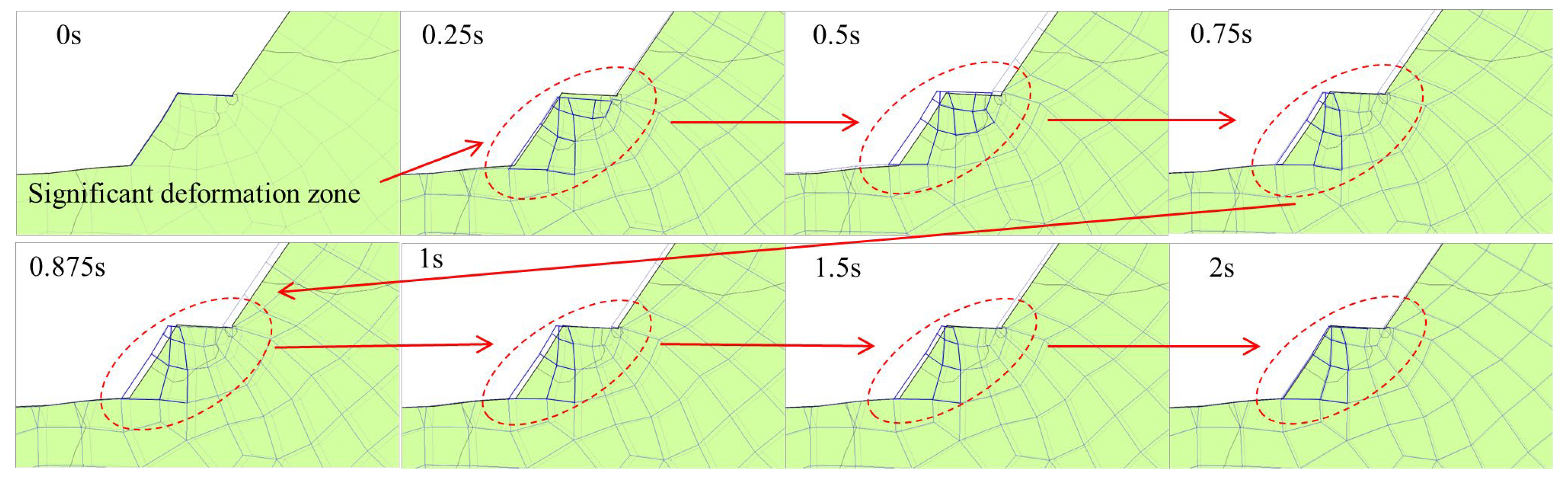
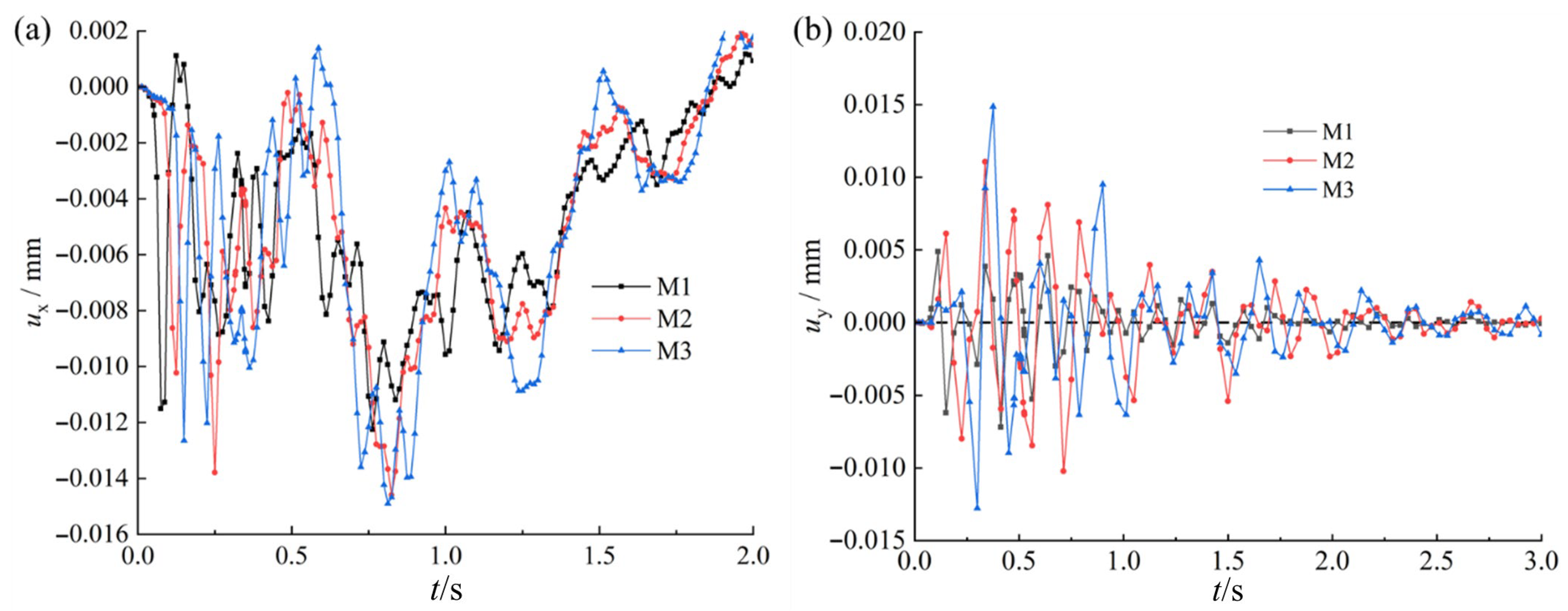
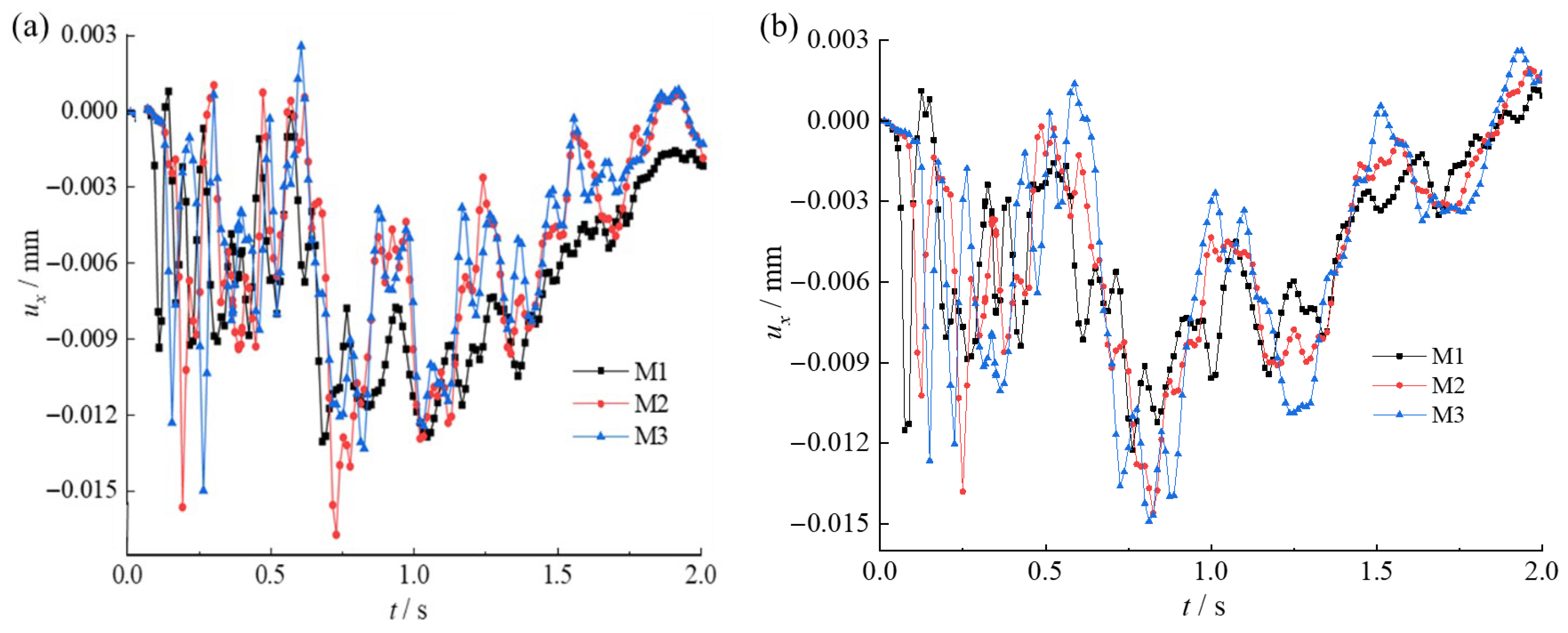
3.1. Analysis of Slope Dynamic Response Under Blasting Vibration
- (1)
- During the initial phase of blasting vibration generation and propagation (0–0.5 s), displacement responses at all monitoring points fluctuate dramatically, displaying an overall trend of initial decrease followed by increase, with displacement values exhibiting large-amplitude oscillations alternating between positive and negative values. The cumulative displacement formed during this phase comprises two components: elastic deformation displacement, which gradually recovers as vibration acceleration attenuates, and irreversible residual displacement.
- (2)
- During the sustained propagation phase of blasting vibration (0.5–1 s), blasting vibration acceleration rapidly attenuates, with all displacement values during this phase being negative, reflecting that displacement responses are primarily elastic with relatively small permanent deformation.
- (3)
- During the late propagation phase of blasting vibration (1–2 s), displacement gradually transitions from negative to positive values, exhibiting an overall slow increasing trend, indicating gradual attenuation of elastic displacement and continuous accumulation of permanent displacement.
- (4)
- Regarding differences in slope displacement responses, displacement fluctuation amplitudes at eastern slope monitoring points are generally smaller than those at the western slope. Combined with geological survey results and analysis of model rock stratum distribution, the eastern slope contains extensive loose rock strata with poor rock mass integrity and local fault and fracture structures, significantly enhancing vibration wave energy absorption and attenuation effects, resulting in relatively weak vibration displacement responses in this region. In contrast, the western slope exhibits superior rock stratum integrity and structural stability, displaying more sensitive displacement responses under vibration. Even after significant vibration acceleration attenuation, it still demonstrates pronounced vibration lag and sustained fluctuations.
- (5)
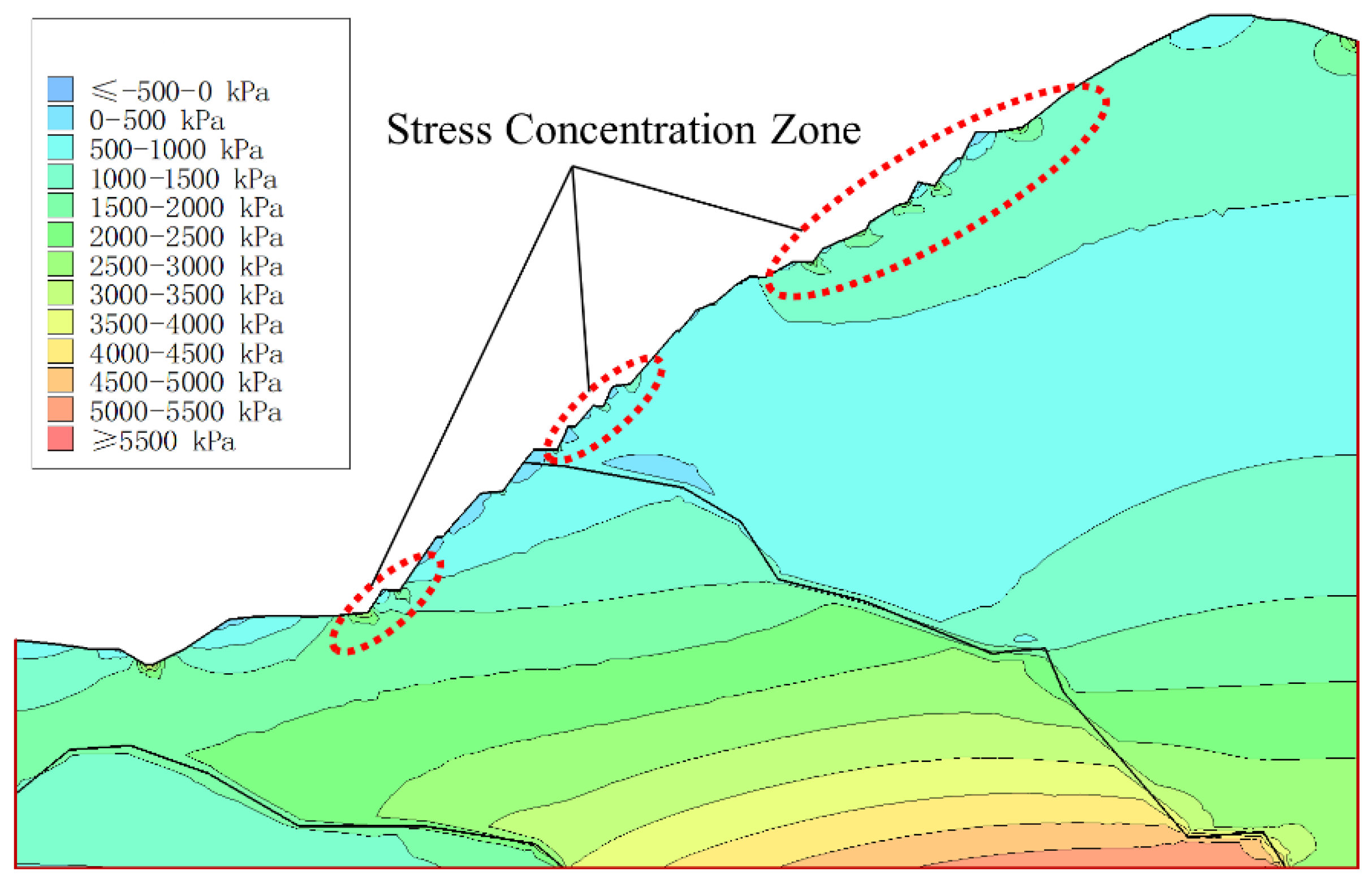
- During the middle and later stages of blasting vibration propagation, monitoring points located at higher elevations consistently exhibit greater displacement magnitudes compared to those at lower elevations on the same slope. This observation reflects a characteristic “elevation effect,” wherein increasing elevation amplifies particle velocity and acceleration responses to blasting vibrations, thereby intensifying the resulting displacement.
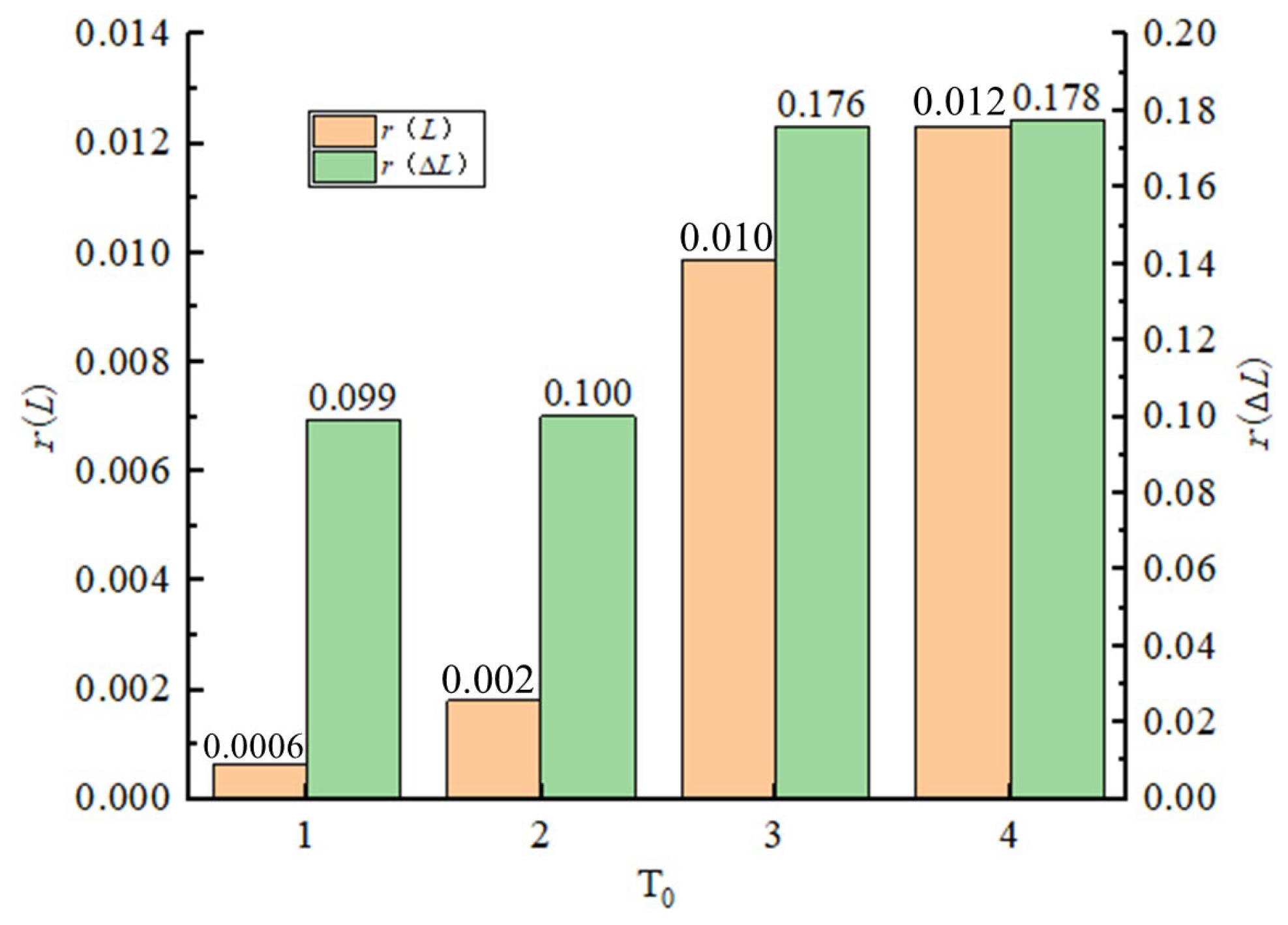
3.2. Correlation Between Underground Blasting Activities and Slope Surface Deformation
4. Discussion
5. Conclusions
- (1)
- The simulation results combined with field investigations indicate that blasting vibrations exhibit typical short-duration, high-amplitude pulse characteristics, with stress variations in the horizontal direction significantly exceeding those in the vertical direction. This suggests that horizontal dynamic loading is the critical trigger for slope shear failure. Furthermore, the intensity of the rock mass vibration response induced by blasting disturbances increases with elevation, with monitoring points at the slope crest exhibiting significantly higher velocity and acceleration, marking it as the most dynamically sensitive hazard zone. The eastern slope, characterized by poor rock mass integrity and pronounced variations in the factor of safety, represents the primary current instability zone, whereas the western slope remains relatively stable overall but still presents localized disturbance responses requiring attention.
- (2)
- By introducing the Pearson correlation coefficient combined with slope radar remote sensing technology, this study, for the first time, reveals a strong correlation between blasting sequences and slope deformation. In slope areas undergoing slow creep, both the magnitude and spatial extent of deformation increased following blasting events. Specifically, cumulative deformation increased by 10.13% and 34.06% at one and six hours after blasting, respectively, indicating a significant lag effect. These findings suggest that blasting vibrations may trigger or exacerbate short-term slope deformations, highlighting the necessity for enhanced post-blasting monitoring and assessment. Future work will focus on refining dynamic models and integrating long-term monitoring data to enhance predictive capabilities.
- (3)
- Mechanistically, the impact of blasting disturbances on slope stability can be understood through three interconnected processes: abrupt changes in the instantaneous stress field, stress redistribution caused by deformation within the rock mass, and the cumulative accumulation of fatigue damage over time. Repeated blasting accelerates the initiation, propagation, and coalescence of microcracks, facilitating the formation of continuous shear zones or slip surfaces. This progressive damage evolution may transform localized instabilities into large-scale slope failures. Therefore, blasting disturbances not only affect the short-term mechanical equilibrium of the slope but also have potential long-term impacts on stability through cumulative effects, warranting significant attention.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, Y.G.; Yang, Z.W.; Huang, S.L.; Lu, W.B.; Zhao, G. A new safety control method of blasting excavation in high rock slope with joints. Rock Mech. Rock Eng. 2020, 53, 3015–3029. [Google Scholar] [CrossRef]
- Chen, Y.K.; Xu, J.H.; Huo, X.H.; Wang, J.C. Numerical Simulation of Dynamic Damage and Stability of a Bedding Rock Slope under Blasting Load. Shock Vib. 2019, 2019, 9616859. [Google Scholar] [CrossRef]
- Kesimal, A.; Ercikdi, B.; Cihangir, F. Environmental impacts of blast-induced acceleration on slope instability at a limestone quarry. Environ. Geol. 2008, 54, 381–389. [Google Scholar] [CrossRef]
- Ozdogan, M.; Deliormanli, A. Determination of possible failure surfaces in an open-pit slope caused by underground production. Boll. Geof. Teor. Appl. 2020, 6, 199–218. [Google Scholar]
- Li, Q.; Wang, Y.; Li, X.; Gong, B. Rainfall-mining coupling effects on slope failure mechanism and evolution process: A case study of open-pit to underground mining. Water 2024, 16, 740. [Google Scholar] [CrossRef]
- Ge, Y.; Wang, H.; Liu, G.; Chen, Q.; Tang, H. Automated identification of rock discontinuities from 3D point clouds using a convolutional neural network. Rock Mech. Rock Eng. 2025, 58, 3683–7000. [Google Scholar] [CrossRef]
- Lu, Y.; Jin, C.; Wang, Q.; Han, T.; Chen, L.J. Modeling study on cumulative damage effects and safety control criterion of open-pit final slope under blasting. Rock Mech. Rock Eng. 2024, 57, 2081–2101. [Google Scholar] [CrossRef]
- Gou, Y.G.; Shi, L.Z.; Huo, X.F.; Yu, Z.; Chen, Y.M. Propagation and prediction of blasting vibration on ground surface induced by underground mining with comparison to vibration inside rock. Rock Mech. Rock Eng. 2024, 57, 10283–10306. [Google Scholar] [CrossRef]
- Chand, K.; Koner, R. Failure zone identification and slope stability analysis of mine dump based on realistic 3d numerical modeling. Geotech. Geol. Eng. 2023, 42, 543–560. [Google Scholar] [CrossRef]
- Widodo; Phanjaya, H.; Prassetyo, S.H.; Ganda, M.S.; Made, A.R.; Ridho, K.W. Dynamic slope stability subject to blasting vibrations: A case study of the jakarta-bandung high-speed railway tunnel. Transp. Infrastruct. Geotech. 2022, 10, 774–794. [Google Scholar] [CrossRef]
- Chen, Y.L.; Liu, G.Y.; Li, N.; Du, X.; Wang, S.R.; Azzam, R. Stability evaluation of slope subjected to seismic effect combined with consequent rainfal. Eng. Geol. 2020, 266, 105461. [Google Scholar] [CrossRef]
- Tao, H.; Zhang, M.M.; Gong, L.; Shi, X.; Wang, Y.J.; Yang, G.Q.; Lei, S.W. The mechanism of slope instability due to rainfall-induced structural decay of earthquake-damaged loess. Earthq. Res. Adv. 2022, 2, 100137. [Google Scholar] [CrossRef]
- Zhang, J.W.; Chen, S.; Wang, T.Y.; Wu, F.B. Study on correlation between ground motion parameters and soil slope seismic response. Bull. Eng. Geol. Environ. 2022, 81, 226. [Google Scholar] [CrossRef]
- Jiang, N.; Zhou, C.; Lu, S.; Zhang, Z. Propagation and prediction of blasting vibration on slope in an open pit during underground mining. Tunn. Undergr. Space Technol. 2017, 70, 409–421. [Google Scholar] [CrossRef]
- Song, D.Q.; Quan, X.R.; Chen, Z.; Xu, D.K.; Liu, C.; Liu, X.L.; Wang, E.Z. Influence of Lithology on the Characteristics of Wave Propagation and Dynamic Response in Rocky Slope Sites Subject to Blasting Load Via the Discrete Element Method. Lithosphere 2024, 2024, 2023302. [Google Scholar] [CrossRef]
- Wu, X.G.; Zhu, D.Y.; Lu, H.; Li, L.M. Simulation research on blasting of an open pit mine slope considering elevation conditions and slope shape factors. Front. Earth Sci. 2024, 12, 1417895. [Google Scholar] [CrossRef]
- Li, X.S.; Li, Q.H.; Hu, Y.J.; Chen, Q.S.; Peng, J.; Xie, Y.L.; Wang, J.W. Study on three-dimensional dynamic stability of open-pit high slope under blasting vibration. Lithosphere. 2021, 2021, 6426550. [Google Scholar] [CrossRef]
- Hu, Y.G.; Lu, W.B.; Wu, X.X.; Liu, M.S.; Li, P. Numerical and experimental investigation of blasting damage control of a high rock slope in a deep valley. Eng. Geol. 2018, 237, 12–20. [Google Scholar] [CrossRef]
- Yang, J.H.; Dai, J.H.; Yao, C.; Jiang, S.H.; Zhou, C.B.; Jiang, Q.H. Estimation of rock mass properties in excavation damage zones of rock slopes based on the Hoek-Brown criterion and acoustic testing. Int. J. Rock Mech. Min. Sci. 2020, 126, 104192. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, C.; Xie, S.D.; Liu, Y. Research on the prediction model of blasting vibration velocity in the dahuangshan mine. Appl. Sci. 2022, 12, 5849. [Google Scholar] [CrossRef]
- Hu, Y.G.; Liu, M.S.; Wu, X.X.; Zhao, G.; Li, P. Damage-vibration couple control of rock mass blasting for high rock slopes. Int. J. Rock Mech. Min. Sci. 2018, 103, 134–144. [Google Scholar] [CrossRef]
- Nath, S.; Tripathi, A.; Singh, A.K.R.; Verma, H.K.R.; Rai, N. Blast damage induced degradation in rock mass parameters of Himalayan jointed rock slopes: A parametric study. J. Earth Syst. Sci. 2025, 134, 87. [Google Scholar] [CrossRef]
- Bazzi, H.; Noferesti, H.; Farhadian, H. Modelling the effect of blast-induced vibrations on the stability of a faulted mine slope. J. S. Afr. Inst. Min. Metall. 2020, 120, 591–597. [Google Scholar] [CrossRef]
- Yuan, K.; Ma, C.; Guo, G.; Wang, P. Slope failure of Shilu metal mine transition from open-pit to underground mining under excavation disturbance. Appl. Sci. 2024, 14, 1055. [Google Scholar] [CrossRef]
- Dai, J.H.; Yang, J.H.; Yao, C.; Hu, Y.G.; Zhang, X.B.; Jiang, Q.H.; Zhou, C.B. Study on the mechanism of displacement mutation for jointed rock slopes during blasting excavation. Int. J. Rock Mech. Min. Sci. 2022, 150, 105032. [Google Scholar] [CrossRef]
- Zhang, L.M.; Ning, Z.G.; Miao, S.J.; Feng, Z.M.; Sun, J.L.; Cai, M.F.; Xi, X. Experimental and numerical investigations on the mixed-mode fracture of granite under offset three-point bending loads. Rock Mech. Rock Eng. 2025, in press. [Google Scholar]
- Ray, S.K.; Sarkar, M.; Singh, T.N. Effect of cyclic loading and strain rate on the mechanical behaviour of sandstone. Int. J. Rock Mech. Min. Sci. 1999, 36, 543–549. [Google Scholar] [CrossRef]
- Singh, S.K. Fatigue and strain hardening behaviour of graywacke from the Flagstaff Formation. New South Wales. Eng. Geol. 1989, 26, 171–179. [Google Scholar] [CrossRef]
- Tien, Y.M.; Lee, D.H.; Juang, C.H. Strain, pore pressure and fatigue characteristics of sandstone under various load conditions. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1990, 27, 283–289. [Google Scholar] [CrossRef]
- Yang, F.; Huang, Z.W.; Dai, Z.Y.; Liu, S.F.; Zhao, L.H. Stability analysis of multi-stage blasting rock slopes based on the Hoek-Brown criterion considering cumulative disturbance. Eng. Geol. 2025, 52, 108077. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Hu, B.; Li, J.; Zhong, Z.X.; Chang, S.X. Analysis of swallowtail mutation instability of slope with weak interlayer under blasting disturbance. Phys. Scr. 2024, 99, 55037. [Google Scholar] [CrossRef]




| Rock Type | Density (kg/m3) | Friction Angle (°) | Cohesion (kPa) | Poisson’s Ratio | Elastic Modulus (GPa) |
|---|---|---|---|---|---|
| Dual-permeability rock | 2814.82 | 11.89 | 0.241 | 0.21 | 81.08 |
| Hematite | 3675.68 | 38.38 | 1.396 | 0.23 | 112.905 |
| Loose rock layer | 2814.82 | 4.52 | 0.057 | 0.2 | 52.582 |
| ID | Mean | Standard Deviation | Variance | Minimum | Maximum |
|---|---|---|---|---|---|
| M1 | 0.000287 | 0.00187 | 0.000003 | −0.00719 | 0.00488 |
| M2 | −0.000255 | 0.00358 | 0.000013 | −0.01022 | 0.01106 |
| M3 | −0.000471 | 0.00345 | 0.000012 | −0.01277 | 0.01485 |
| Monitoring Point | Mean | Standard Deviation | Variance | Minimum | Maximum | |
|---|---|---|---|---|---|---|
| Velocity (mm/s) | MA | 0.18115 | 0.20358 | 0.04145 | 0.00223 | 0.98950 |
| MB | 0.13064 | 0.13105 | 0.01717 | 0.00223 | 0.59927 | |
| MC | 0.11085 | 0.133 | 0.01769 | 0.00369 | 0.67087 | |
| Acceleration (g) | MA | 0.00158 | 0.00192 | 0.000004 | 0.00001 | 0.01048 |
| MB | 0.00142 | 0.0016 | 0.000003 | 0.00002 | 0.00615 | |
| MC | 0.00137 | 0.00142 | 0.000002 | 0.00001 | 0.00718 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; He, Z.; Wang, P.; Tan, W.; Ma, Q.; Wang, C.; Cai, M.; Chen, Y. Radar Monitoring and Numerical Simulation Reveal the Impact of Underground Blasting Disturbance on Slope Stability. Remote Sens. 2025, 17, 2649. https://doi.org/10.3390/rs17152649
Ma C, He Z, Wang P, Tan W, Ma Q, Wang C, Cai M, Chen Y. Radar Monitoring and Numerical Simulation Reveal the Impact of Underground Blasting Disturbance on Slope Stability. Remote Sensing. 2025; 17(15):2649. https://doi.org/10.3390/rs17152649
Chicago/Turabian StyleMa, Chi, Zhan He, Peitao Wang, Wenhui Tan, Qiangying Ma, Cong Wang, Meifeng Cai, and Yichao Chen. 2025. "Radar Monitoring and Numerical Simulation Reveal the Impact of Underground Blasting Disturbance on Slope Stability" Remote Sensing 17, no. 15: 2649. https://doi.org/10.3390/rs17152649
APA StyleMa, C., He, Z., Wang, P., Tan, W., Ma, Q., Wang, C., Cai, M., & Chen, Y. (2025). Radar Monitoring and Numerical Simulation Reveal the Impact of Underground Blasting Disturbance on Slope Stability. Remote Sensing, 17(15), 2649. https://doi.org/10.3390/rs17152649








