Intelligent Recognition and Parameter Estimation of Radar Active Jamming Based on Oriented Object Detection
Abstract
1. Introduction
2. Jamming Signal Model
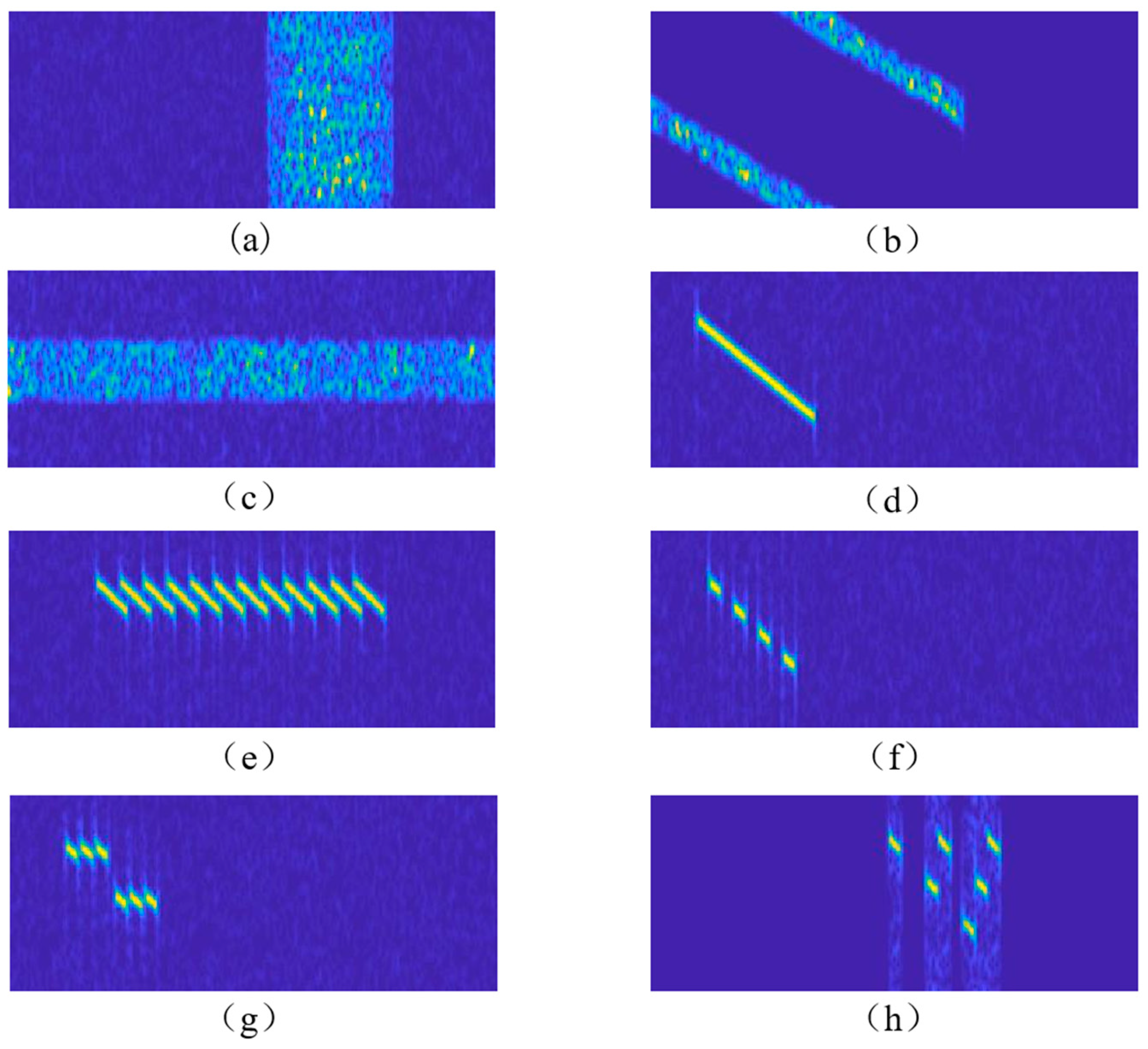
2.1. Noise Convolution Jamming
2.2. Swept Jamming
2.3. Aiming Jamming
2.4. Full Pulse Forwarding Jamming
2.5. Mono-Pulse Dense Forwarding Jamming
2.6. Interrupted Sampling and Direct Repeater Jamming
2.7. Interrupted Sampling and Periodic Repeater Jamming
2.8. Interrupted Sampling and Cyclic Repeater Jamming
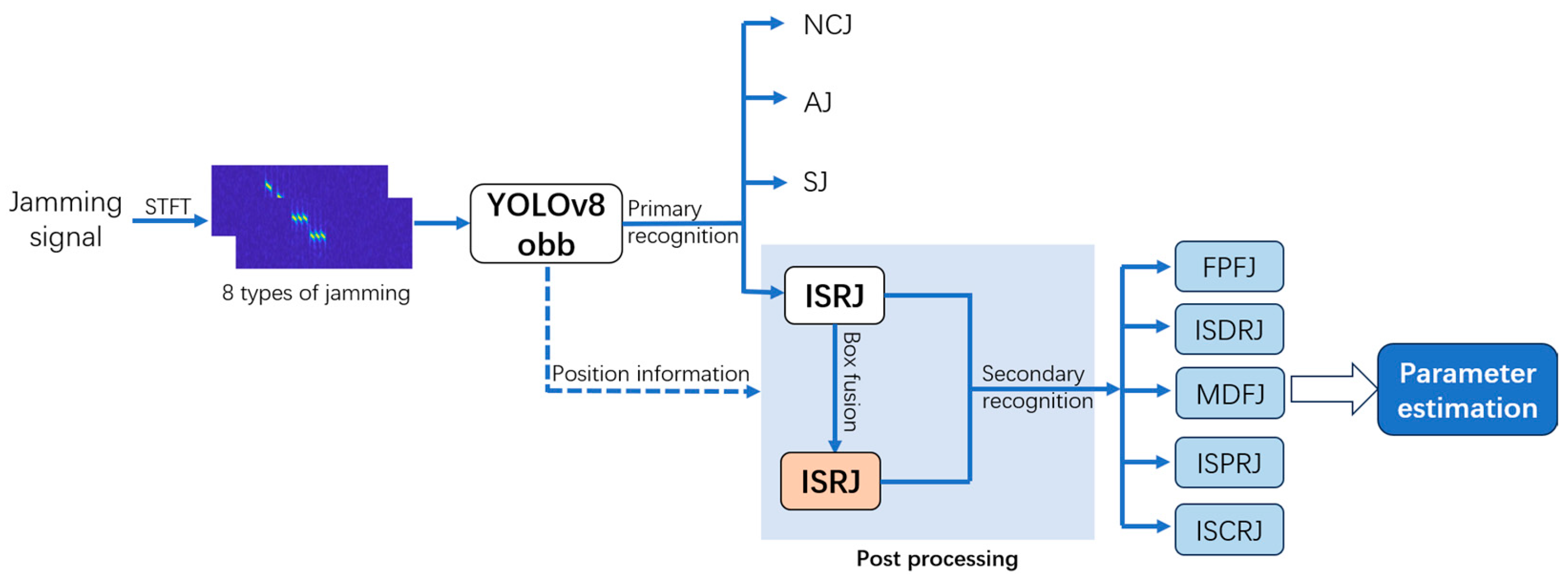
3. The Proposed Method
3.1. Data Preprocessing
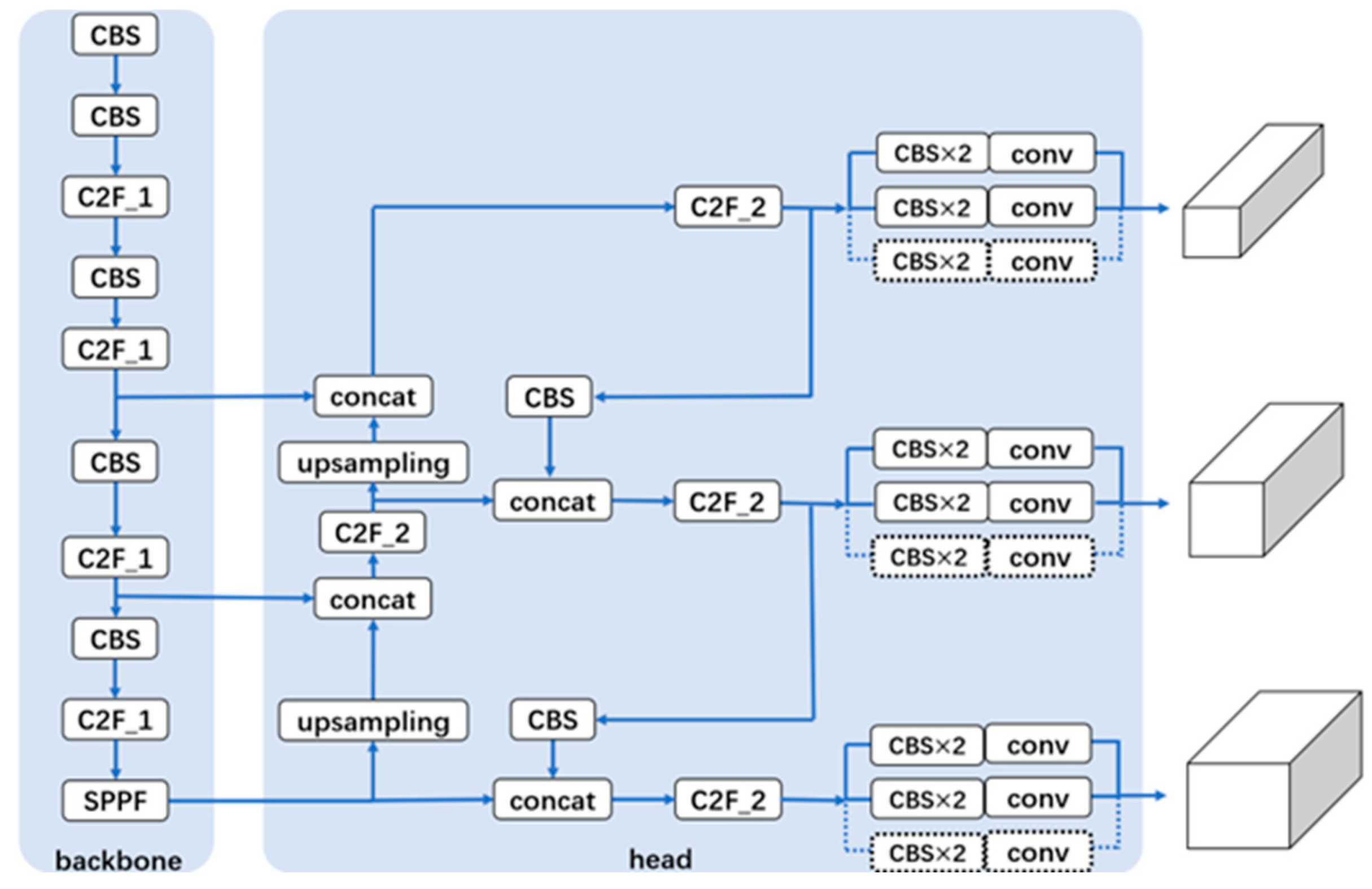
3.2. YOLOv8 OBB
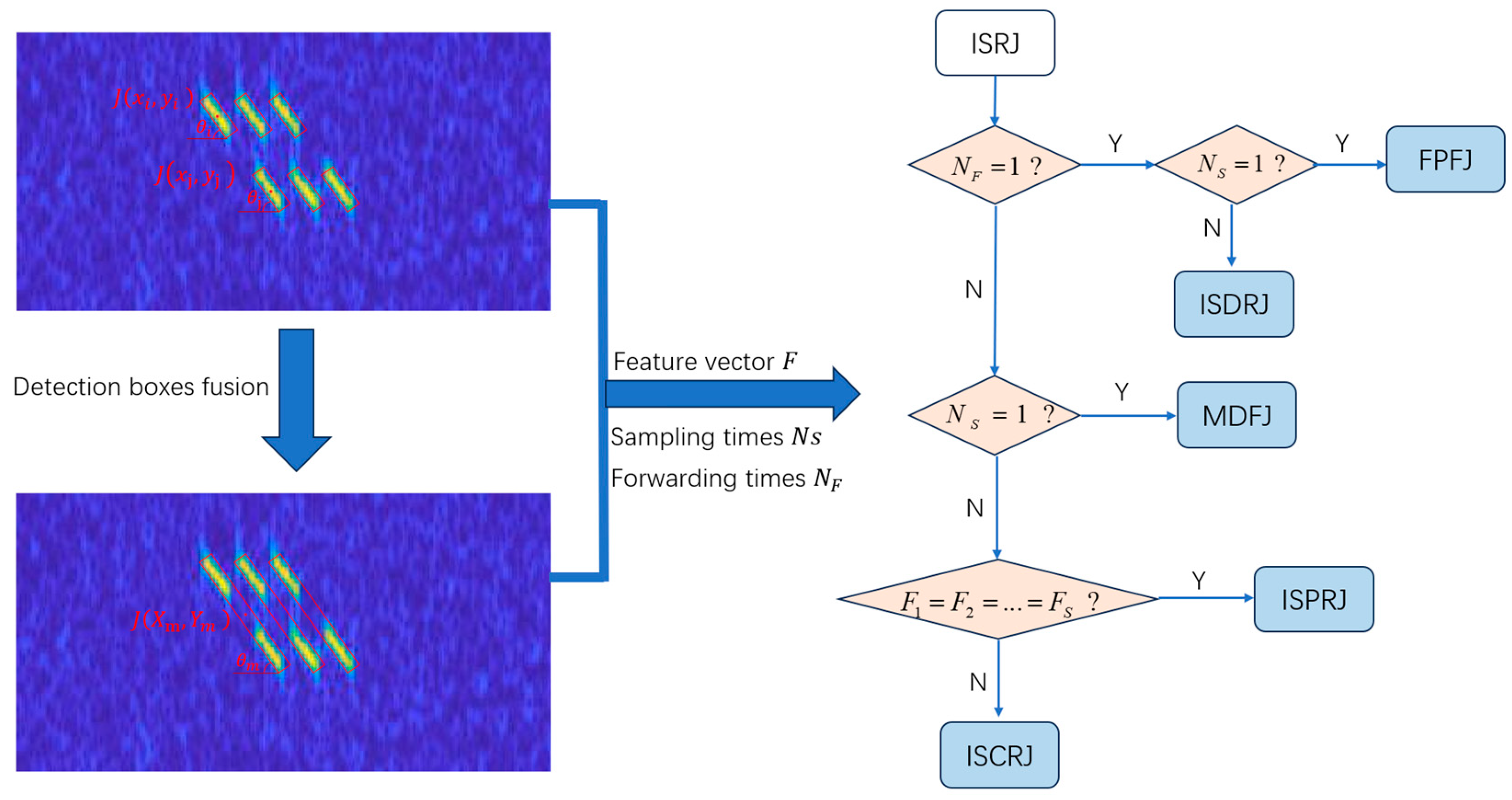
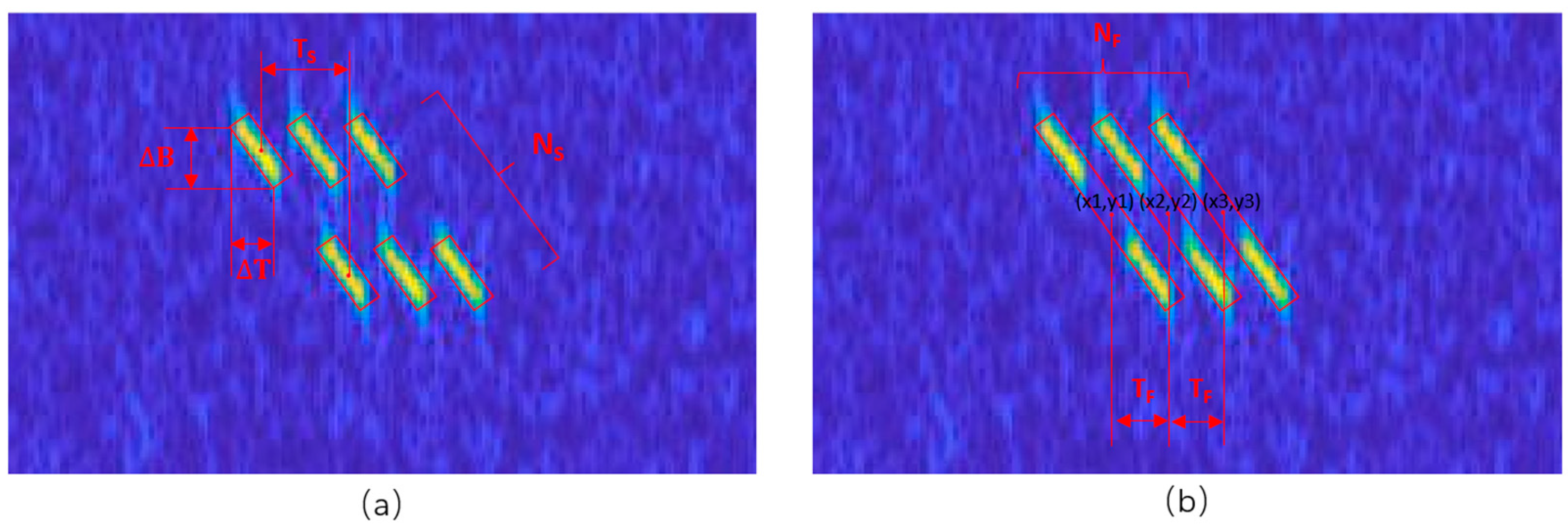
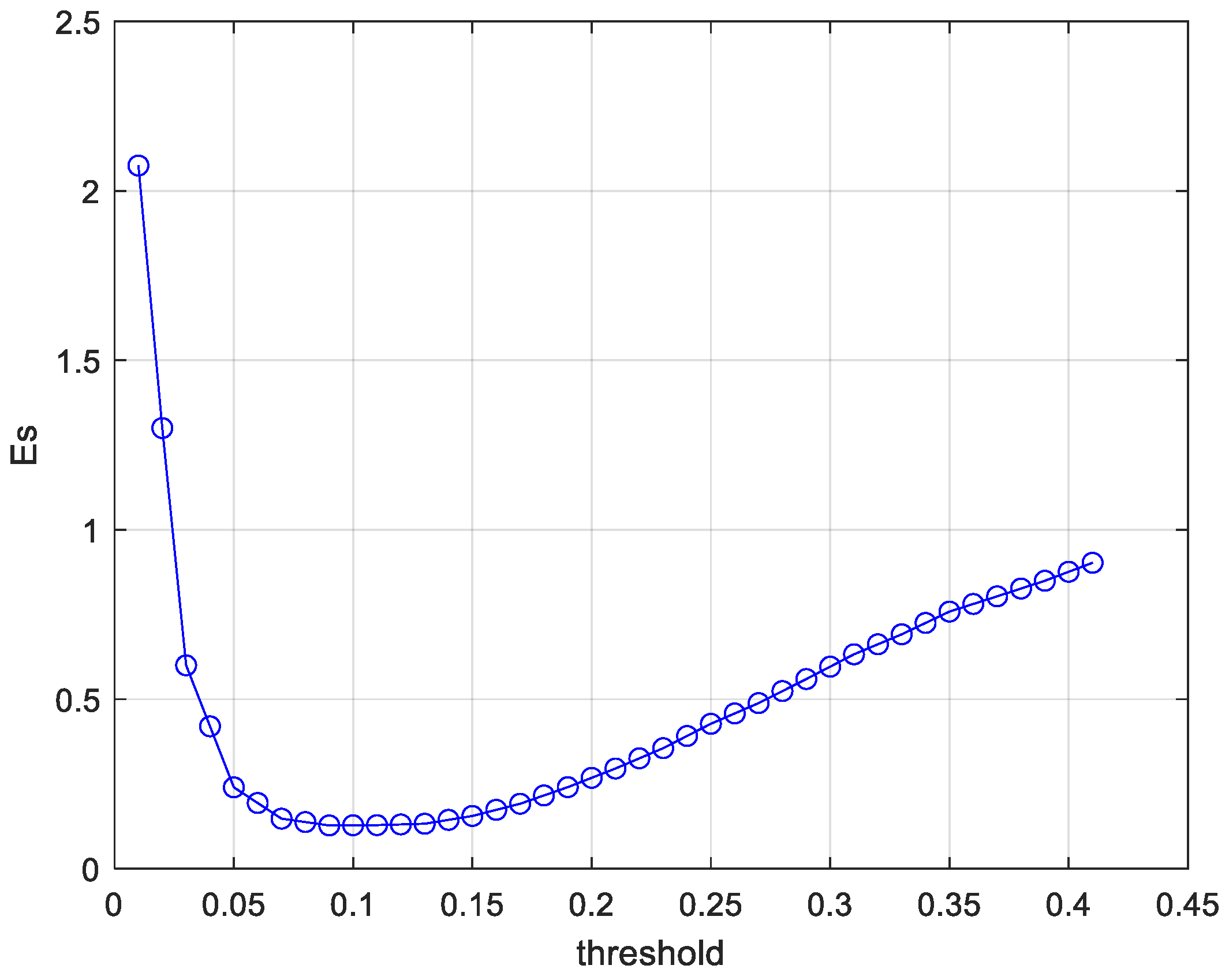
3.3. Post-Processing Algorithm
| Algorithm 1. Procedures of detection box fusion |
| Input: Detection boxes information and the threshold . |
Output: Parameter feature vector .
|
3.4. Parameter Estimation
4. Simulation Experiment and Result Analysis
4.1. Experimental Conditions
4.1.1. Jamming Simulation
4.1.2. Dataset Construction
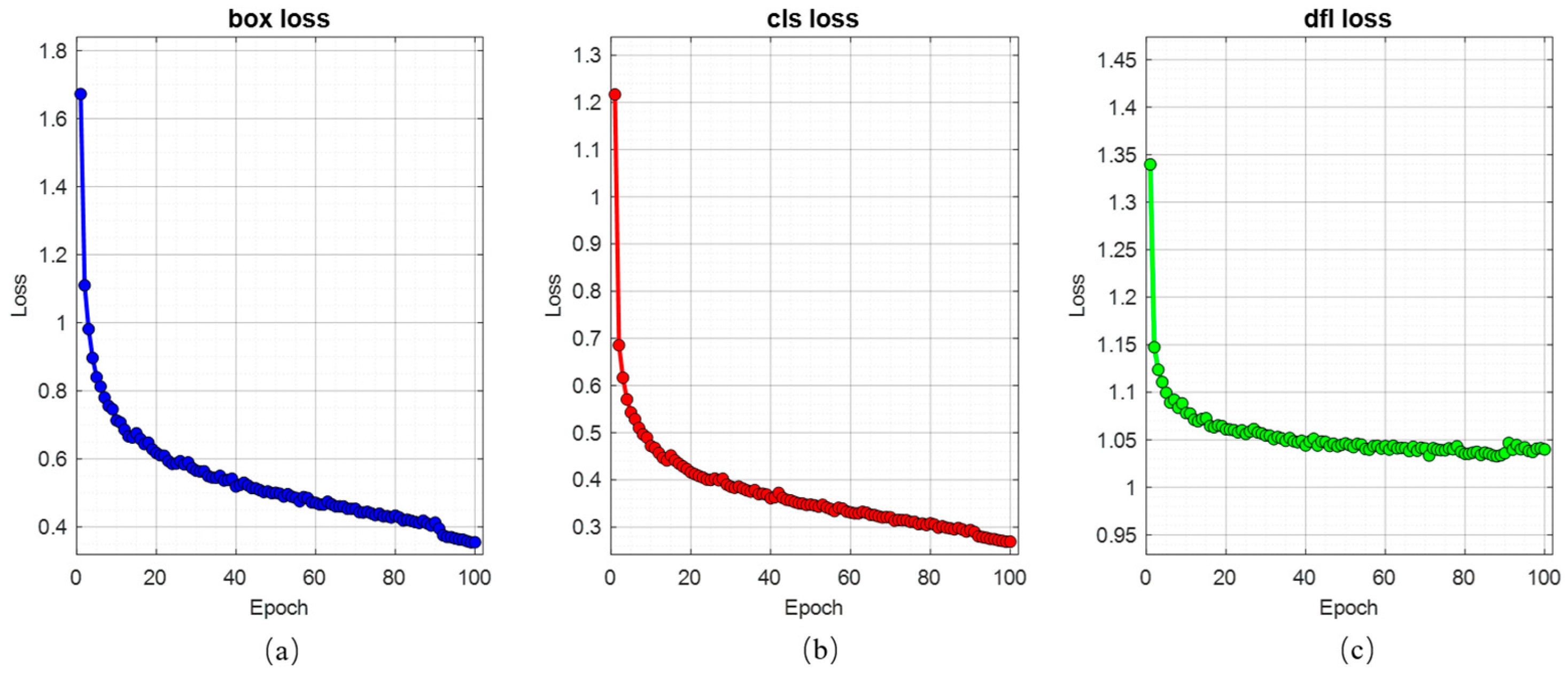
4.1.3. Training of the Network
4.2. Simulation and Result Analysis
4.2.1. Error Simulation Experiment
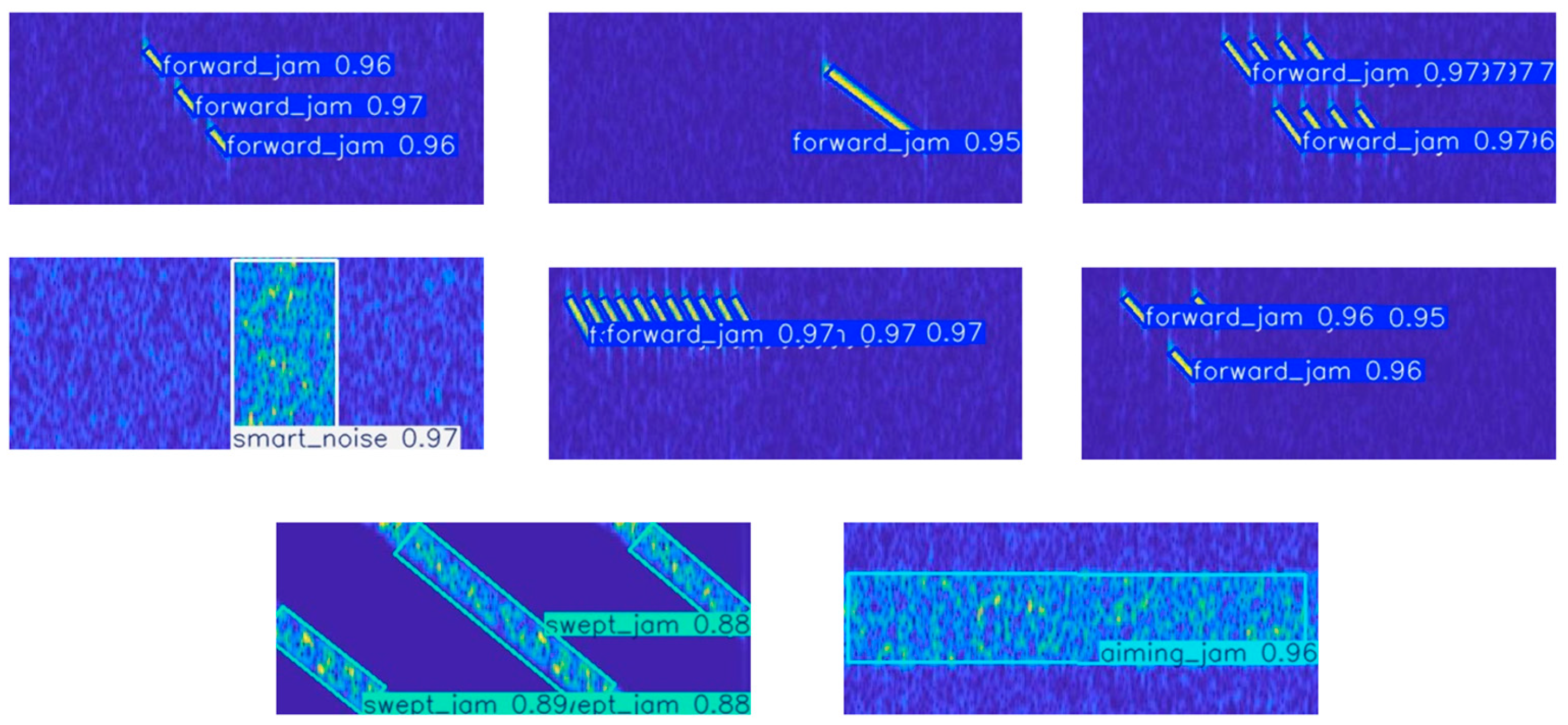
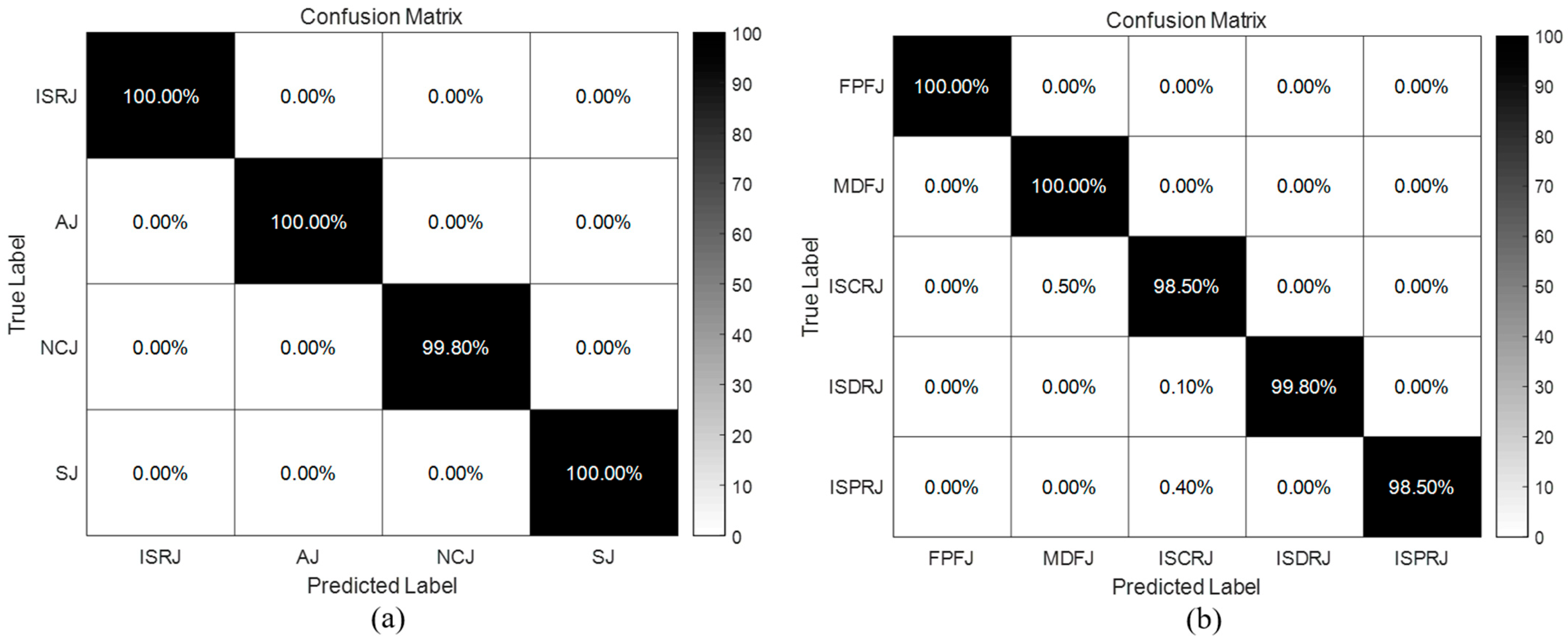
4.2.2. Analysis of Detection and Recognition Results
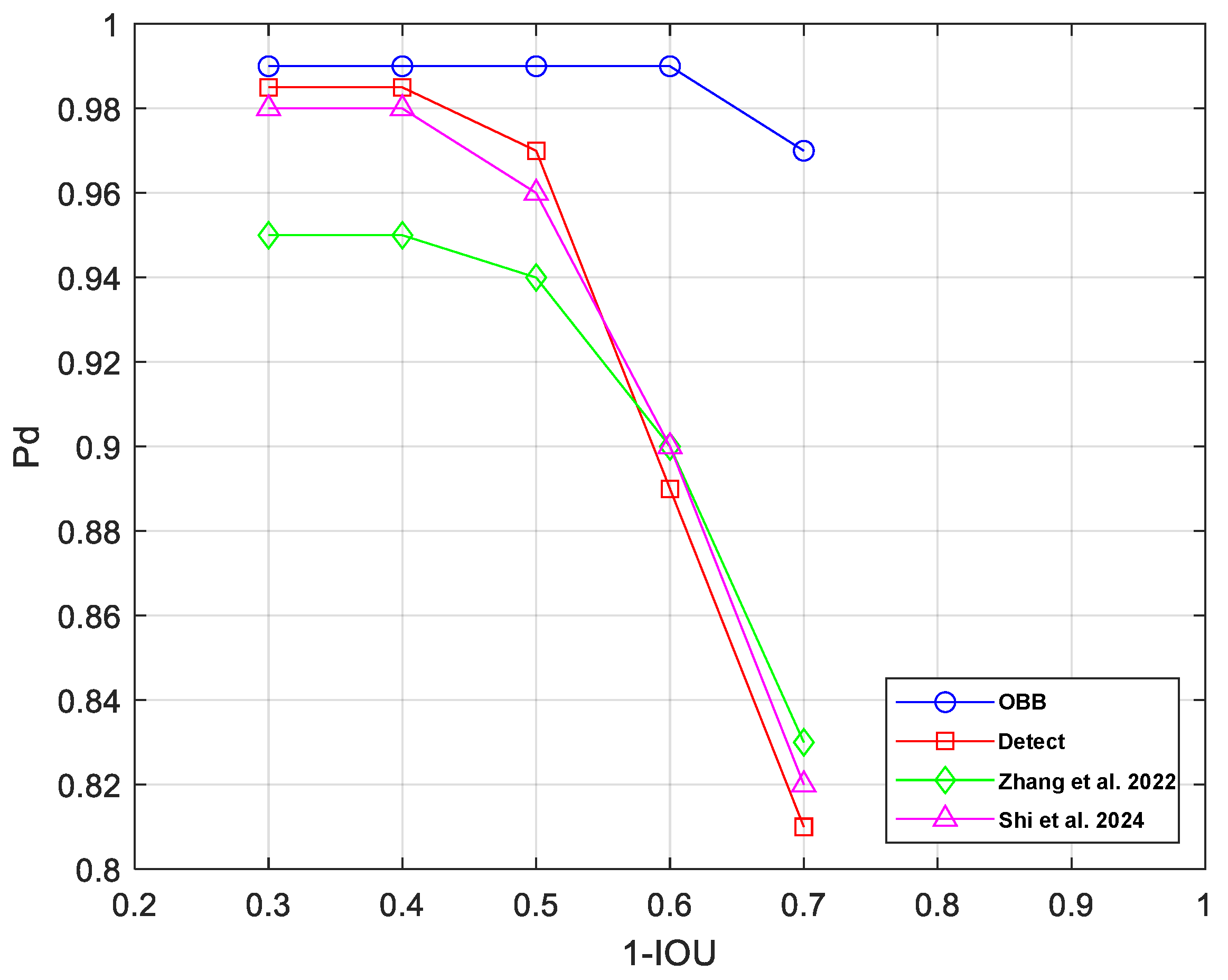
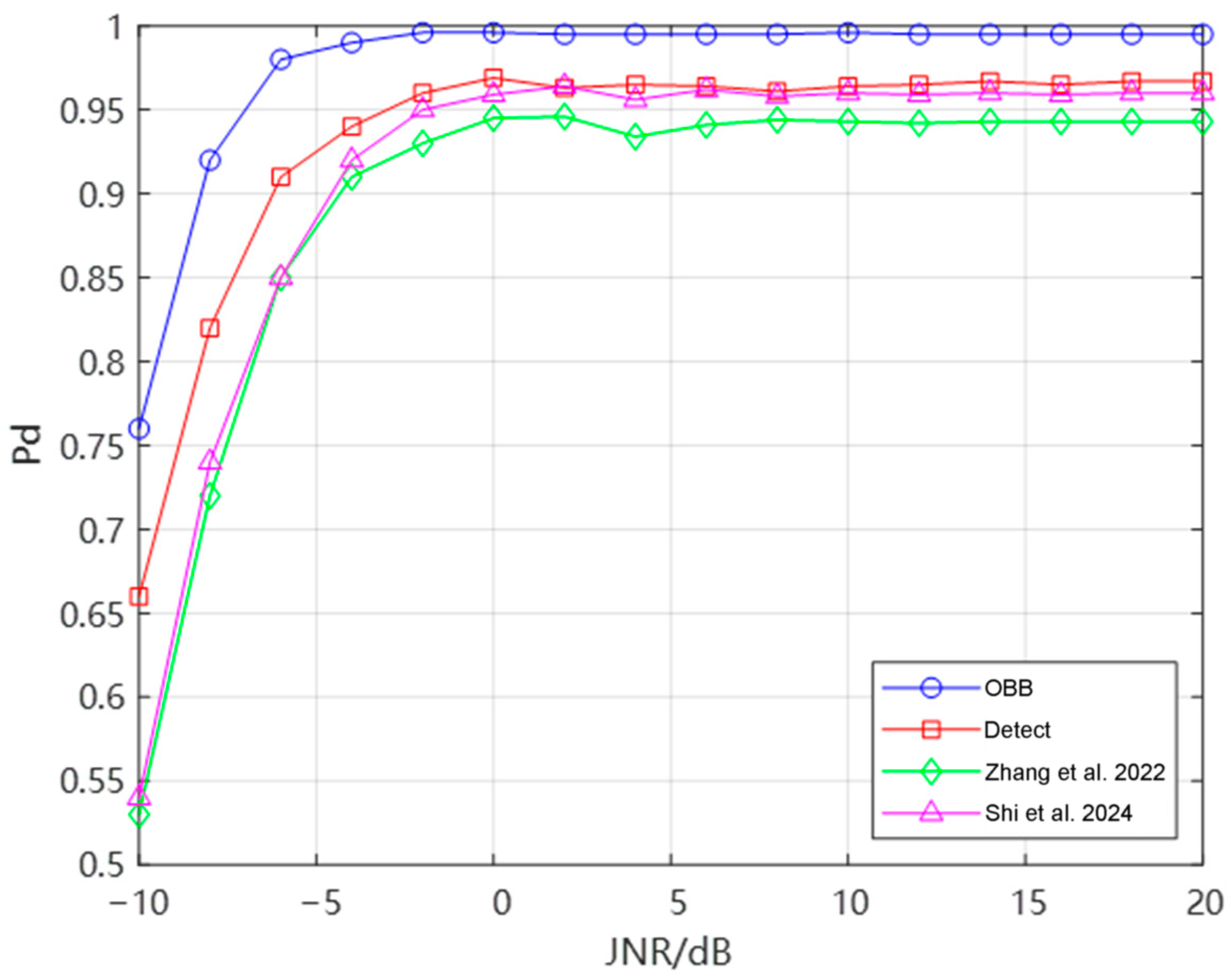
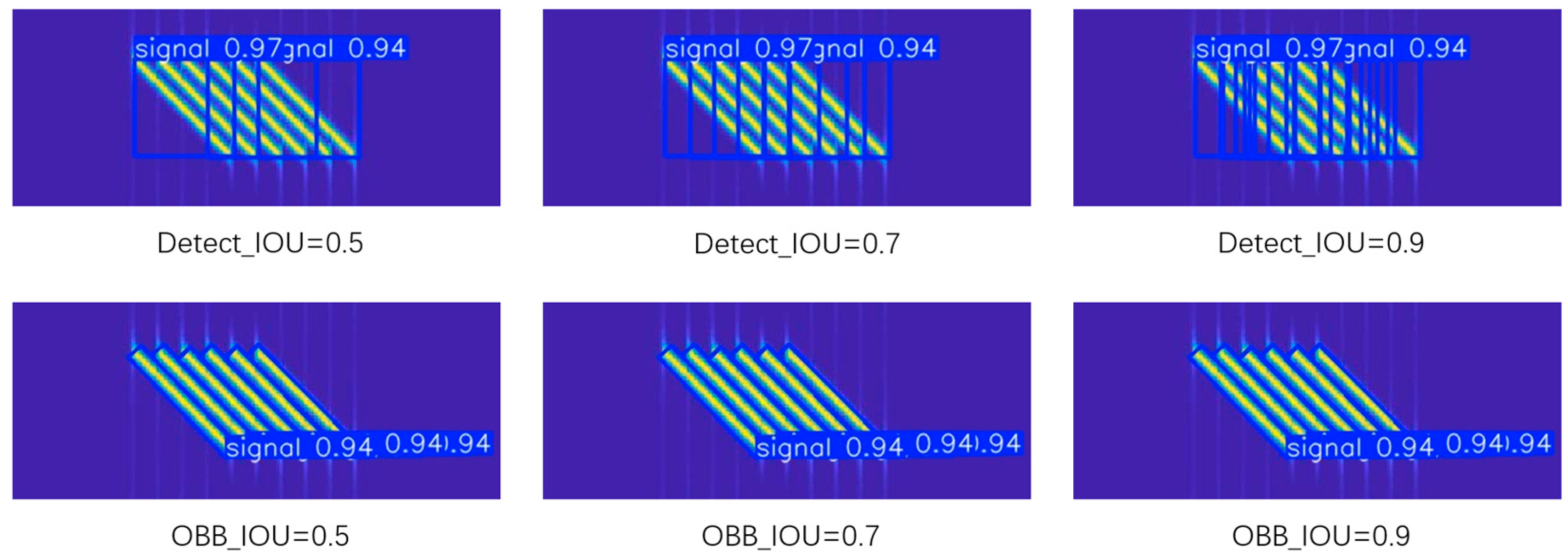
4.2.3. NMS and the Result of Detection Probability
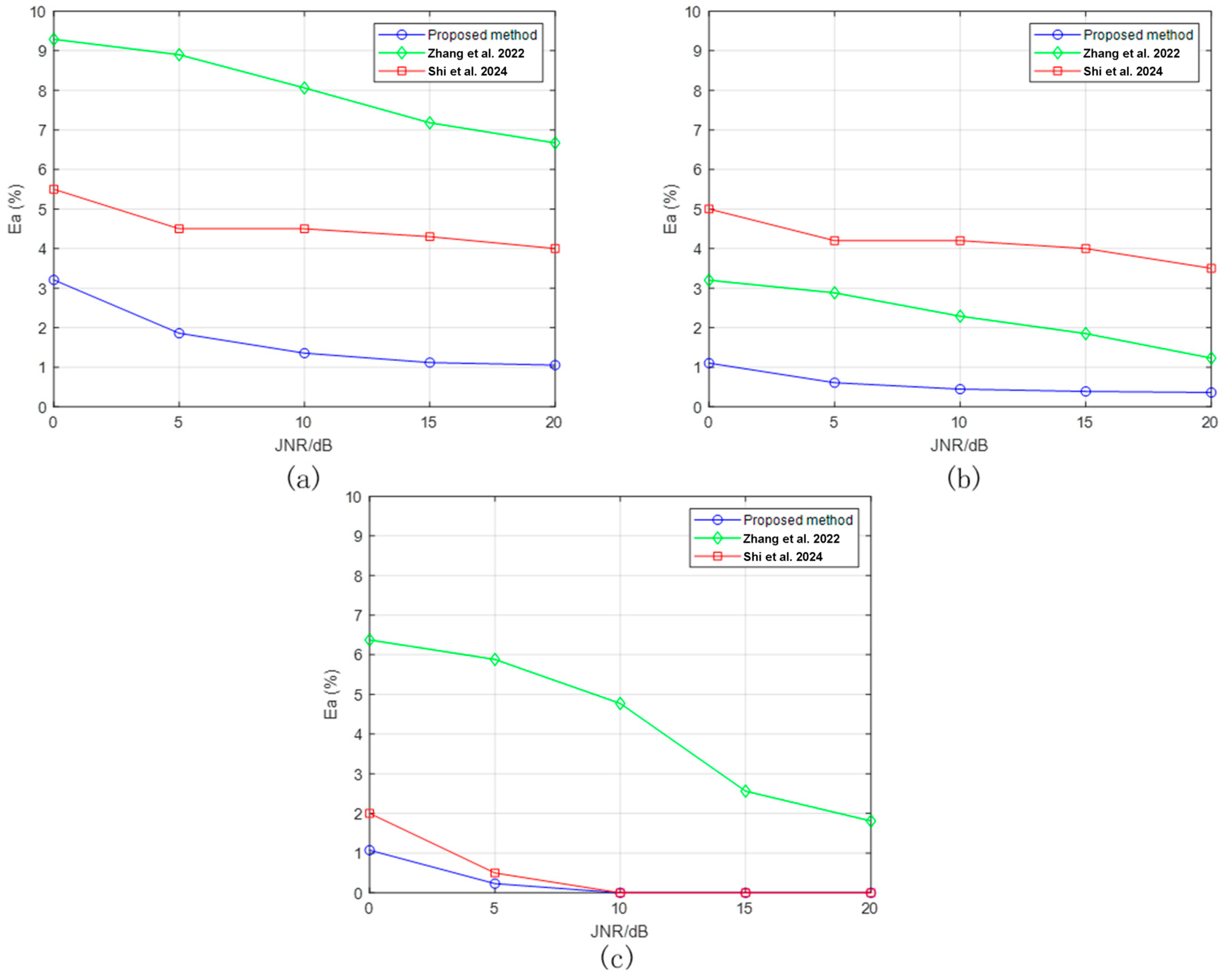
4.3. Analysis of Parameter Estimation Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnston, S.L. Radar electronic counter-countermeasures. IEEE Trans. Aerosp. Electron. Syst. 2007, 14, 109–117. [Google Scholar] [CrossRef]
- Orlando, D. A novel noise jamming detection algorithm for radar applications. IEEE Signal Process. Lett. 2016, 24, 206–210. [Google Scholar] [CrossRef]
- Feng, D.; Xu, L.; Pan, X.; Wang, X. Jamming wideband radar using interrupted-sampling repeater. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1341–1354. [Google Scholar] [CrossRef]
- Kwak, C.M. Application of DRFM in ECM for pulse type radar. In Proceedings of the 2009 34th International Conference on Infrared, Millimeter, and Terahertz Waves, Busan, Republic of Korea, 21–25 September 2009. [Google Scholar]
- Lu, L.; Gao, M. An improved sliding matched filter method for interrupted sampling repeater jamming suppression based on jamming reconstruction. IEEE Sens. J. 2022, 22, 9675–9684. [Google Scholar] [CrossRef]
- Zheng, H.; Jiu, B.; Liu, H. Waveform design based ECCM scheme against interrupted sampling repeater jamming for wideband MIMO radar in multiple targets scenario. IEEE Sens. J. 2021, 22, 1652–1669. [Google Scholar] [CrossRef]
- Greco, M.; Gini, F.; Farina, A. Radar detection and classification of jamming signals belonging to a cone class. IEEE Trans. Signal Process. 2008, 56, 1984–1993. [Google Scholar] [CrossRef]
- Zhao, S.; Zhou, Y.; Zhang, L.; Guo, Y.; Tang, S. Discrimination between radar targets and deception jamming in distributed multiple-radar architectures. IET Radar Sonar Navig. 2017, 11, 1124–1131. [Google Scholar] [CrossRef]
- Yang, X.; Ruan, H. Active deception jamming identification method based on bispectrum analysis. J. Detect. Control. 2018, 40, 122–127. [Google Scholar]
- Zhou, H.; Dong, C.; Wu, R.; Xu, X.; Guo, Z. Feature fusion based on Bayesian decision theory for radar deception jamming recognition. IEEE Access 2021, 9, 16296–16304. [Google Scholar] [CrossRef]
- Liu, L.; Yang, H.; Xiao, G. Time-frequency domain feature extraction algorithm based on linear discriminant analysis. Syste. Eng. Electron. 2019, 41, 2184–2190. [Google Scholar]
- Tian, X.; Tang, B. Active deception jamming recognition of radar based on normalized wavelet decomposition power ratio. J. Data Acquisit. Process. 2013, 28, 416–420. [Google Scholar]
- Zhou, C.; Liu, Q.; Chen, X. Parameter estimation and suppression for DRFM-based interrupted sampling repeater jammer. IET Radar Sonar Navig. 2018, 12, 56–63. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Zhang, J. A novel parameter estimation method for ISRJ. In Proceedings of the 2nd International Conference on Electronic Materials and Information Engineering, Hangzhou, China, 15–17 April 2022. [Google Scholar]
- Geng, Z.; Yan, H.; Zhang, J.; Zhu, D. Deep-learning for radar: A survey. IEEE Access 2021, 9, 141800–141818. [Google Scholar] [CrossRef]
- Lv, Q.; Quan, Y.; Feng, W.; Sha, M.; Dong, S.; Xing, M. Radar deception jamming recognition based on weighted ensemble CNN with transfer learning. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–11. [Google Scholar] [CrossRef]
- Meng, Y.; Yu, L.; Wei, Y. Multiple information cognition of interrupted sampling repeater jamming in complex scenes. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021. [Google Scholar]
- Shao, G.; Chen, Y.; Wei, Y. Deep fusion for radar jamming signal classification based on CNN. IEEE Access 2020, 8, 117236–117244. [Google Scholar] [CrossRef]
- Shao, G.; Chen, Y.; Wei, Y. Convolutional neural network-based radar jamming signal classification with sufficient and limited samples. IEEE Access 2020, 8, 80588–80598. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, L.; Guo, Z. Recognition of radar compound jamming based on convolutional neural network. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7380–7394. [Google Scholar] [CrossRef]
- Gao, M.; Li, H.; Jiao, B.; Hong, Y. Simulation research on classification and identification of typical active jamming against LFM radar. In Proceedings of the Eleventh International Conference on Signal Processing Systems, Chengdu, China, 31 December 2019. [Google Scholar]
- Fan, P.; Wu, Y.; Wei, Y.; Guo, G.; Peng, Z. A method of jamming recognition based on multi-domain joint convolutional neural network. In Proceedings of the International Conference on Electronic Information Engineering and Computer Communication, Nanchang, China, 4 May 2022. [Google Scholar]
- Yu, X.; Wang, W.; Wu, H.; Bo, J.; Zhang, J.; Meng, J. Multi-domain feature fusion based radar deception jamming recognition method. In Proceedings of the 2023 IEEE 7th International Symposium on Electromagnetic Compatibility, Hangzhou, China, 20–23 October 2023. [Google Scholar]
- Luo, Z.; Cao, Y.; Yeo, T.S.; Wang, Y.; Wang, F. Few-shot radar jamming recognition network via time-frequency self-attention and global knowledge distillation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Zhu, X.; Wu, H.; He, F.; Yang, Z.; Meng, J.; Ruan, J. YOLO-CJ: A Lightweight Network for Compound Jamming Signal Detection. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 6807–6821. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, Z.; Zhou, C.; Liu, Q.; Long, T. Radar compound jamming cognition based on a deep object detection network. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 3251–3263. [Google Scholar] [CrossRef]
- Shi, Z.; Wu, H.; Zhu, X.; Wang, W.; Ni, X.; Zhang, J. Interrupted sampling forwarding jamming parameter estimation based on YOLOv7-tiny. In Proceedings of the 2024 IEEE 7th International Conference on Electronic Information and Communication Technology, Xi’an, China, 31 July–2 August 2024. [Google Scholar]
- Xie, A.; Liu, X.; Wu, Q.; Liu, Z.; Xiao, S. Recognition and Suppression of Slice Repeater Jamming Based on Coded Waveform. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 7466–7480. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Q.; Pan, X.; Wang, J.; Zhao, F. SAR image transform based on amplitude and frequency shifting joint modulation. IEEE Sens. J. 2025, 25, 7043–7052. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, Y.; Liu, X.; Gu, Z.; Xu, Z.; Xiao, S. ISAR Image Transform via Joint Intra pulse and Inter pulse Periodic coded Phase Modulation. IEEE Sens. J. 2025, in press. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.; Liu, X.; Feng, D.; Sun, G. A Flexible Range-Doppler Modulation Method for Pulse-Doppler Radar Using Phase-Switched Screen. IEEE Trans. Antennas Propag. 2025, in press. [Google Scholar] [CrossRef]
- Lv, Q.; Quan, Y.; Sha, M.; Feng, W.; Xing, M. Deep neural network-based interrupted sampling deceptive jamming countermeasure method. IEEE J.-STARS 2022, 15, 9073–9085. [Google Scholar] [CrossRef]
- Neemat, S.; Krasnov, O.; Yarovoy, A. An interference mitigation technique for FMCW radar using beat-frequencies interpolation in the STFT domain. IEEE Trans. Microw. Theory Tech. 2018, 67, 1207–1220. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Vairavasundaram, S. Yolo-based object detection models: A review and its applications. Multimed. Tools Appl. 2024, 83, 83535–83574. [Google Scholar] [CrossRef]
- Hosang, J.; Benenson, R.; Schiele, B. Learning non-maximum suppression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hawaii, HI, USA, 21–26 July 2017. [Google Scholar]
| Jamming Types | Parameters | Value Range |
|---|---|---|
| NCJ | JNR | 0~20 dB |
| SJ | JNR Sweep frequency cycle Sweep bandwidth | 30~60 dB 40~80 us 20 MHz |
| AJ | JNR | 0~20 dB |
| FPFJ | JNR Bandwidth Pulse width | 0~20 dB 5~15 MHz 10~25 us |
| MDFJ | JNR Forward period Forward times Duty | 0~20 dB 2~5 us 8~12 35%~45% |
| ISDRJ | JNR Slice number Duty | 0~20 dB 2~4 45%~60% |
| ISPRJ | JNR Slice number Forward period Forward times Duty | 0~20 dB 2~3 2~3 us 2~4 45%~60% |
| ISCRJ | JNR Sampling times Sampling period | 0~20 dB 2~3 1.875~5 us |
| FPFJ | 1.398% | 1.477% | ----- | 0 | ----- | 0 |
| MDFJ | 0.879% | 0.871% | ----- | 0 | 1.120% | 0.021% |
| ISDRJ | 1.542% | 1.808% | 0.577% | 0.075% | ----- | 0.300% |
| ISPRJ | 1.289% | 1.542% | 0.464% | 0.433% | 0.844% | 0.167% |
| ISCRJ | 1.857% | 1.772% | 0.669% | 0.633% | ----- | 0.900% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Guo, Y.; Feng, W.; Hu, X.; Gong, J.; Zhang, Y. Intelligent Recognition and Parameter Estimation of Radar Active Jamming Based on Oriented Object Detection. Remote Sens. 2025, 17, 2646. https://doi.org/10.3390/rs17152646
Lu J, Guo Y, Feng W, Hu X, Gong J, Zhang Y. Intelligent Recognition and Parameter Estimation of Radar Active Jamming Based on Oriented Object Detection. Remote Sensing. 2025; 17(15):2646. https://doi.org/10.3390/rs17152646
Chicago/Turabian StyleLu, Jiawei, Yiduo Guo, Weike Feng, Xiaowei Hu, Jian Gong, and Yu Zhang. 2025. "Intelligent Recognition and Parameter Estimation of Radar Active Jamming Based on Oriented Object Detection" Remote Sensing 17, no. 15: 2646. https://doi.org/10.3390/rs17152646
APA StyleLu, J., Guo, Y., Feng, W., Hu, X., Gong, J., & Zhang, Y. (2025). Intelligent Recognition and Parameter Estimation of Radar Active Jamming Based on Oriented Object Detection. Remote Sensing, 17(15), 2646. https://doi.org/10.3390/rs17152646