Abstract
With the rapid advancement of space technology, satellites are playing an increasingly vital role in fields such as Earth observation, communication and navigation, space exploration, and military applications. Efficiently deploying satellite missions under multi-objective, multi-constraint, and dynamic environments has become a critical challenge in the current aerospace domain. This paper integrates the concepts of game theory and proposes a distributed collaborative task model suitable for on-orbit satellite mission planning. A two-player impulsive maneuver game model is constructed using differential game theory. Based on the ideas of Nash equilibrium and distributed collaboration, multi-agent technology is applied to the distributed collaborative task planning, achieving collaborative allocation and countermeasure strategies for multi-objective and multi-satellite scenarios. Experimental results demonstrate that the method proposed in this paper exhibits good adaptability and robustness in multiple impulse scheduling, maneuver strategy iteration, and heterogeneous resource utilization, providing a feasible technical approach for mission planning and game confrontation in satellite clusters.
1. Introduction
Space is a critical domain for safeguarding national security and conducting international competition and cooperation. Since the 21st century, major space-faring nations have been racing to develop their space capabilities, and space has gradually become the pinnacle of great power rivalry and strategic competition [1]. With the continuous advancement of aerospace technology, the future battlefield landscape will extend from traditional land, sea, and air domains to outer space [2], and space operations will emerge as the new frontier in military competition. In particular, the deployment of new-generation remote sensing and communication satellites has rapidly increased global demand for spatial data and information services, which now exhibit characteristics of diversity and high timeliness [3,4]. Against this backdrop, effectively deploying satellite missions under conditions of limited resources and ever-changing objectives has become a pivotal challenge in future space operations.
Satellite mission planning is a complex systems engineering task that involves multiple constraints, including orbital maneuvering [5], mission scheduling [6], and resource allocation [7]. To address the multiple challenges of target timeliness, dynamic environmental changes, and multi-satellite coordination, traditional single-objective or single-satellite mission planning methods can no longer meet the demands of modern aerospace systematic operations and efficient resource utilization [8]. Therefore, current satellite mission planning urgently requires comprehensive optimization under multi-objective, multi-constraint, and dynamic environments, utilizing advanced algorithms and theoretical tools to enhance the execution efficiency and reliability of satellite missions. With the continuous development of technology, satellite mission planning will play a crucial role in future space operations, becoming a key component in ensuring national space security and effective operational capabilities.
2. Related Work
Distributed collaborative task planning initially achieved success in ground-based multi-agent systems [9] and robot networks [10], and later gradually extended to satellite swarm applications [11]. The multi-robot task planning and “task game” concepts mentioned by Skrzypczyk [12] provided inspiration for satellite distributed task planning. Martin et al. [13] further validated, in the Modular Open Network Architecture (MONARCH), that distributed simulation and task allocation optimization can significantly improve collaboration efficiency. In response to the collaborative needs within satellite systems, Chen Qifeng [14] realized distributed autonomous formation keeping and task planning through a multi-agent negotiation mechanism, demonstrating good robustness and adaptability, especially under highly dynamic conditions. Wang et al. [15] further studied a distributed collaborative dynamic task planning algorithm based on multi-agent hybrid learning, which maintains good adaptability in multiple complex task scenarios. Additionally, Liu Yuan [16] combined distributed online algorithms with game theory to provide rapid allocation and optimization ideas for multi-player space pursuit–evasion task planning, thereby greatly reducing the time required for task scheduling.
With the enhancement of computational capabilities and the infiltration of artificial intelligence technologies, the connotation of distributed collaborative task planning in satellite mission planning has continuously expanded. Zheng [17] proposed a distributed autonomous task allocation model for high-density dynamic environments, improving the task completion rate and resource utilization efficiency of multi-satellite systems by adjusting task priorities and resource allocations in real time. Kim [18] utilized a response threshold model for distributed task searching in unmanned aerial vehicles, providing a referential multi-agent system example for collaboration mechanism optimization in satellite mission planning. Pei Jianwen [19] pointed out in his study that after integrating intelligent optimization algorithms, distributed collaboration exhibits more prominent performance in task execution efficiency and dynamic adaptability. Fei [20] modeled multi-satellite collaborative task scheduling using a genetic algorithm, achieving significant computational efficiency improvements in task priority ranking and resource reconfiguration. It can be observed that when the swarm size increases and the environment changes constantly, a single centralized planning model struggles to consider global optimality and real-time performance, whereas distributed collaboration can maximize global benefits through multi-node communication and local optimization.
This paper, focusing on distributed heterogeneous cluster task planning based on Nash equilibrium, integrates methodologies from game theory and distributed optimization, achieving efficient collaboration of multiple objectives and satellites in complex constellation attack–defense confrontations and resource-limited scenarios. It addresses the deficiencies in previous studies that overlooked issues such as “multi-objective compatibility” and “multi-agent joint game”, providing new solutions for task planning in heterogeneous satellite clusters. The research findings not only enrich the theoretical system of space mission planning but also provide technical support for future intelligent and distributed satellite collaborative operations.
3. Modeling of Heterogeneous Cluster Deployment Tasks
This section establishes a theoretical framework for heterogeneous cluster mission planning, starting from the orbital coordinate system and equations of relative motion. Firstly, from the perspective of coordinate systems, the geocentric inertial coordinate system and the orbital coordinate system are defined. The geocentric inertial coordinate system is used to describe the motion of satellites within the Earth’s gravitational field, while the orbital coordinate system is employed to depict the relative motion of satellites with respect to a primary satellite. Secondly, considering the orbital deployment requirements of satellites in actual missions, a satellite state transition model based on the equations of relative motion is proposed.
3.1. Definition and Transformation of Coordinate Systems
- (1)
- Geocentric inertial coordinate system
The geocentric inertial coordinate system, denoted as (), has its origin set at the center of mass of a spherical Earth. The axis is perpendicular to the equatorial plane and aligned with the direction of the Earth’s rotational angular velocity. The axis lies within the equatorial plane and points towards the direction of the J2000.0 vernal equinox. The axis is also located within the equatorial plane, and the three axes form a right-handed coordinate system. The three axes of this coordinate system do not change with time in inertial space, exhibiting constancy. This coordinate system is commonly used to describe the motion of celestial bodies around the Earth (S). The motion state of a satellite within the Earth’s gravitational field can be characterized through orbital dynamics equations in this coordinate system, as illustrated in Figure 1.
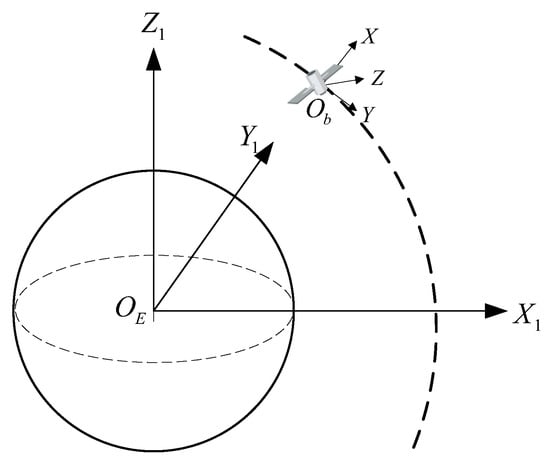
Figure 1.
The geocentric inertial coordinate system and the satellite orbital coordinate system.
- (2)
- Orbital coordinate system
The orbital coordinate system, denoted as (), is also referred to as the local orbital coordinate system. It is a coordinate system that changes with the motion of the primary satellite. The origin of the orbital coordinate system is typically set at the position of the primary satellite. The axis points from the geocenter towards . The axis is aligned with the orbital motion direction of the reference primary satellite. The and axes together form the orbital plane, and the axis, together with the orbital plane formed by the and axes, constitutes a right-handed system, as illustrated in Figure 1.
3.2. Equations of Relative Motion
When executing close-range collaborative detection tasks in satellite constellations, the distance between satellites of both sides is relatively close, and the motion between satellites can be described as relative motion. Under the premise of satisfying the following assumptions, the well-known Clohessy–Wiltshire (CW) equations can be employed to depict the relative motion between satellites. The fundamental assumptions are as follows:
- (1)
- For satellite cluster missions in medium-high altitude low Earth circular orbits (LEO), when the mission duration does not exceed several orbital periods, the effects of atmospheric drag perturbation and J2 perturbation on spacecraft can be neglected [21].
- (2)
- A virtual satellite moving along a circular orbit is selected near the participating satellites as the origin of the reference orbit.
- (3)
- When the distance between the participating spacecraft and the origin of the reference orbit is much smaller than the orbital radius of the reference orbit, the second-order and higher-order terms in the relative orbital dynamic equations can be ignored, as the influence of these higher-order terms on the relative motion is minimal at this time.
In a region of near-Earth orbit where distances are close, a virtual reference satellite (primary satellite) is selected, and its orbit serves as the reference orbit. The center of mass of the reference satellite is taken as the origin of the coordinate system to establish a satellite orbital coordinate system , as illustrated in Figure 2. In the coordinate system of the reference satellite, the equations of motion of a satellite relative to the reference satellite can be expressed as:
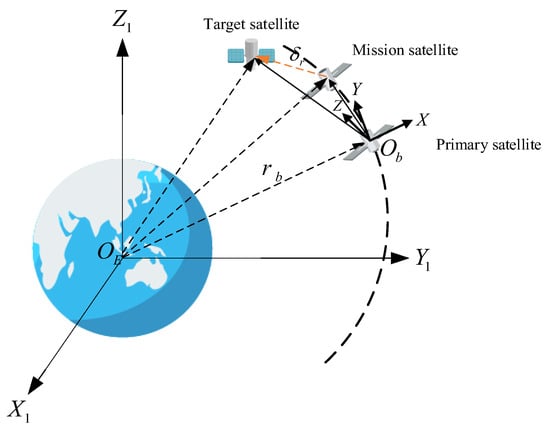
Figure 2.
Establishment of satellite relative motion scenarios and relevant reference frames.
Here, represents the angular velocity of the reference orbit, and its expression is given by .
4. Optimization Design for Satellite Game Mission Deployment Based on Co-Evolution
4.1. Differential Game Model
When both the mission satellite and the target satellite possess maneuvering capabilities, their trajectories are not solely determined by unilateral strategies but are jointly shaped by their mutual game-playing and interactive behaviors. In response to this scenario, this section constructs a model based on differential game theory and solves it using a cooperative game algorithm, aiming to optimize the best control strategies between the detecting satellite and the target satellite. The entire mission process of the task satellite can be described as first approaching the target satellite, then maintaining operation for a certain duration while meeting mission requirements. Therefore, the complete mission can be divided into two phases: the approach phase and the sustained phase.
For the approach phase, the mission satellite’s strategy is to optimize the control variables to minimize the loss function corresponding to its mission scenario within the maximum flight time . The control parameters of the mission satellite include the total mission time , the maneuvering times , the impulse magnitudes , the angles between the impulses and the plane, as well as the angles between their projections in the frame and the -axis. Here, , where denotes the maximum number of impulse maneuvers. The optimization model of the mission satellite can be expressed in the following form:
represent the control strategies of the target satellite, which influence the optimal strategies of the mission satellite. is the total mission time for the mission satellite to execute the approach phase, and is the maximum value of a single impulse for the mission satellite. The constraints ensure that the control variables of the mission satellite remain within the physically achievable and mission-compliant ranges, thereby guaranteeing the practical feasibility of the optimization problem.
At the end of the approach phase, the mission satellite has already met all requirements except for the duration. Therefore, during the sustaining phase, the mission satellite does not need to optimize the mission time. The optimization model for the mission satellite is as follows:
The loss function of the target satellite is independent of the mission phase, and its optimization objective does not necessarily solely involve evading the mission satellite. In practice, different objectives can be set for the target satellite according to varying requirements to make it more intelligent. This article outlines two objectives for the target satellite design. The first objective is to maintain a safe distance to avoid collisions with the mission satellite, specifically by maximizing the distance from the mission satellite during the engagement process. The second objective is to be as close as possible to the primary satellite. The control variables of the target satellite include the maneuvering times , the impulse magnitudes , the angles between the impulses and the plane, as well as the angles between their projections in the frame and the -axis. Here, , where denotes the maximum number of impulse maneuvers. Similar to the calculation method of the loss function for the mission satellite, for a game-playing duration of tr, the loss function of the target satellite can be expressed as
Here, represents the minimum safe distance for the target satellite.
During the approach phase, the game-playing duration is equal to the mission duration of the mission satellite. During the sustaining phase, the game-playing duration is the minimum sustainable duration . The strategy of the target satellite is to optimize parameters such as impulse timings and magnitudes within the maximum flight time to minimize its loss function. The optimization model for the target satellite is as follows:
Here, represent the control strategies of the detected satellite, denotes the upper limit of a single impulse magnitude for the detected satellite, and represents the minimum time interval between two impulse maneuvers of the target satellite.
The co-evolution problem involving a mission satellite and a target satellite requires finding a saddle-point solution that satisfies the following equation under given constraints:
where the terms represent the optimal control strategy of the task satellite. The terms represent the optimal control strategy of the target satellite.
The solutions of Equations (11) and (12) represent saddle-point solutions in the differential game. This indicates that the task satellite and target satellite will reach a stable state during the game process. Their strategies oppose each other to some extent and achieve an optimal balance.
Specifically, the task satellite’s optimal strategy maximizes its own benefits while considering the target satellite’s responses and making reasonable adjustments. The target satellite’s optimal strategy maximizes its own objectives while avoiding collisions with the task satellite.
4.2. Design of Co-Evolutionary Algorithm
Co-evolution is a biological or systematics concept that describes the phenomenon where two or more interacting systems or species adapt to each other and evolve jointly during their interactions. This concept is not only widely applied in biology but has also been introduced into fields such as computer science, artificial intelligence, and optimization algorithms. In the context of satellite gaming, the co-evolutionary mechanism can be integrated with optimization algorithms like Particle Swarm Optimization (PSO), Genetic Algorithm (GA), and Zebra Optimization Algorithm (ZOA) as a strategy for cooperation and competition among multiple satellites. Each satellite in the swarm can be regarded as an individual. During the game, each satellite selects its strategy based on the strategies of others. Through multiple generations of iterations, the strategies within the satellite swarm are continuously optimized. Each generation of satellites adapts and adjusts its strategies based on the strategies of others, ultimately reaching an equilibrium state. In long-term gaming, the satellite swarm can find the optimal balance between cooperation and competition, thereby achieving complex orbital control and space missions.
The core idea of co-evolution is the joint evolution of the mission satellite population and the target satellite population through mutual influence. For each individual mission satellite, the individuals with the optimal loss functions are selected from the target satellite population. The mission satellite then competes against these target satellites individually, and the average value of the mission satellite’s loss function is recorded as its individual loss function. Similarly, for each individual target satellite, the individuals with the optimal loss functions are selected from the mission satellite population. The target satellite then competes against these mission satellites individually, and the average value of the target satellite’s loss function is recorded as its individual loss function. Through this setup, both the target satellite and mission satellite populations update themselves based on the optimal individuals from the opposing population. The two populations compete with each other and optimize individually. Eventually, when the competition reaches a stable state, the optimal solution to the differential game model is obtained, and the iteration termination condition is met.
The flowchart of the co-evolutionary algorithm is shown in Figure 3.
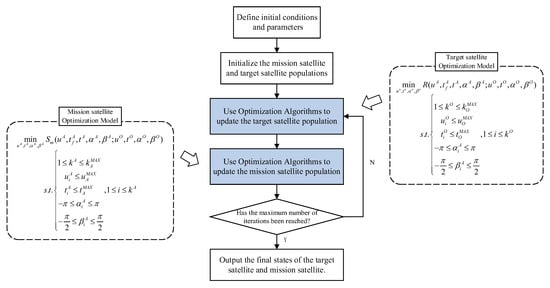
Figure 3.
Flow of the co-evolutionary algorithm.
The specific steps of the co-evolutionary algorithm are as follows:
Step 1: Define the initial conditions and relevant parameters for the optimization process. This involves determining the initial states of the mission satellite and the target satellite, the optimization ranges of the control variables, and the initial parameters of the optimization algorithm.
Step 2: Initialize the populations of the mission satellite and the target satellite. For the control variables of both populations, an initial position is uniformly and randomly selected within their respective optimization ranges to serve as the initial individuals.
Step 3: Update the target satellite population using the optimization algorithm. The target satellite population is updated based on its loss function.
Step 4: Update the mission satellite population using the optimization algorithm. The mission satellite population is updated based on its loss function.
Step 5: Determine whether the maximum number of iterations has been reached. Check if the current iteration count has reached the preset maximum number of iterations. If not, return to Step 3 to continue the iteration process.
Step 6: Select the optimal individuals from both populations. The finally selected optimal individuals represent the best-performing strategies during the confrontation process, ensuring that both the mission satellite and the target satellite minimize their respective losses.
5. Distributed Heterogeneous Cluster Task Planning Based on Nash Equilibrium
5.1. Construction of a Task Planning Model for Heterogeneous Clusters
The system consists of several small detection satellites deployed in different orbits. These satellites perform collaborative detection tasks in a dynamic space environment. When facing multi-target tracking or sudden detection demands, the system needs rapid response and task re-planning capabilities. In this task planning process, orbit maneuver optimization and multi-target allocation are two core problems. The goal is to ensure detection quality while minimizing energy consumption.
Suppose the system has a total of intelligent satellites denoted as . The detection method of the intelligent satellites follows that described in the first part. The objective function is , where represents two types of detection scenarios, and represents the mission phases, namely the approach phase and the sustaining phase. When takes a value of 0, it indicates mission success. For an intelligent satellite, successful missions in both the approach phase and the sustaining phase result in and both being 0. There are target satellites denoted as . When an intelligent satellite detects a target satellite, its task failure rate is defined as:
Here, is a 0–1 matrix, where the horizontal axis and vertical axis represent the indices of the intelligent satellites and the target satellites, respectively. The higher the value of , the lower the mission success rate. Thus, minimizing maximizes the mission success rate.
Time cost of detection is the maximum time taken by any intelligent satellite to complete its task. By normalizing this time cost by dividing it by the maximum endurance time of the intelligent satellites, the time cost is obtained as follows:
The application of impulse velocity changes by intelligent satellites consumes fuel. The total amount of velocity change can be used to reflect the fuel consumption. Similar to the approach for handling time cost, the maximum impulse amount is used for normalization, resulting in the total fuel consumption as follows:
Here, represents the total remaining impulse capacity of the -th intelligent satellite, where represents the total velocity impulse required for the i-th intelligent satellite to maneuver and detect the j-th target satellite.
For a task assignment strategy , covering a greater number of target satellites is a crucial objective. The proportion of target satellites not covered by the strategy, denoted as , can be defined as follows:
The comprehensive effectiveness is obtained by calculating the weighted average of all effectiveness values using certain weights , as follows:
The objective of the planning is to minimize . Regarding the multi-satellite collaborative detection mission system, the Nash equilibrium strategy set requires that all participating mission nodes in the system satisfy the following condition:
Here, represents the comprehensive effectiveness evaluation function for node , denotes the optimal strategy for node , and is the strategy space of node . The notation refers to all nodes in the system except node .
The comprehensive effectiveness function of the -th node is not only related to its own decision variables but also influenced by the decision variables of other nodes . According to the definition of Nash equilibrium, when each sub-node solves its problem, it requires the strategy information of other nodes. Therefore, a communication network among nodes is necessary for distributed task planning, enabling sufficient information exchange. Figure 4 shows solution process for distributed task planning based on Nash equilibrium theory.
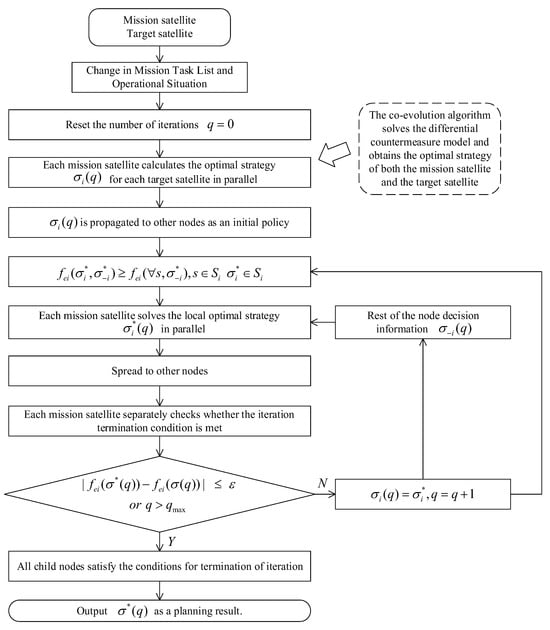
Figure 4.
Solution process for distributed task planning based on Nash equilibrium theory.
5.2. Description of the Simulation Scenario
A heterogeneous satellite cluster composed of two intelligent satellites (D1–D2) is deployed in geostationary orbit. These satellites possess space situational awareness capabilities and are responsible for safeguarding the operational security of critical space facility X. The orbital parameters of facility X and the two intelligent satellites are listed in Table 1. Additionally, two detection satellites (A1–A2) are present in orbit, tasked with conducting scientific observations of the intelligent satellites. In this scenario, the intelligent satellites must optimize their orbital maneuvers to maintain a safe distance from the detection satellites, while the detection satellites adjust their orbits to achieve optimal observation conditions. Through intelligent task planning, both satellite types fulfill their respective mission requirements while ensuring space safety. Figure 5 shows the satellite cluster cooperative mission scenario.

Table 1.
The orbital parameters of facility X and the two intelligent satellites.
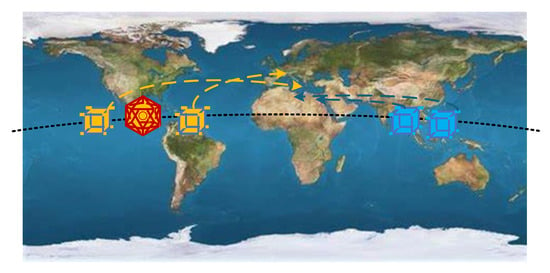
Figure 5.
The satellite cluster cooperative mission scenario.
Each intelligent satellite (D1–D2) has a maximum single impulse of 2 m/s, with a minimum interval of 200 s between maneuvers and a maximum of 30 maneuvers. Their orbital data are provided in Table 1. The detection satellites (A1–A2) are adapted for two mission scenarios, with specific parameters listed in Table 2. Each detection satellite has a maximum single impulse of 1 m/s, a minimum interval of 400 s, and a maximum of 30 maneuvers (orbital data in Table 3). Four performance metrics are evaluated: detection success rate, fuel consumption, time cost, and target coverage. The proposed Zebra Optimization Algorithm is applied, with parameter settings detailed in Table 4.

Table 2.
Detection satellite attributes.

Table 3.
The orbital parameters of detection satellites.

Table 4.
Optimization parameter settings.
6. Result Analysis
6.1. Efficiency Convergence Result
Figure 6 illustrates the change process of the comprehensive efficiency function with the number of iterations. It can be observed from the figure that after four iterations, the curve of the efficiency function gradually stabilizes, indicating that through multiple rounds of strategy optimization, the nodes have essentially reached a Nash equilibrium, and further strategy adjustments among them are unlikely to reduce their own losses.
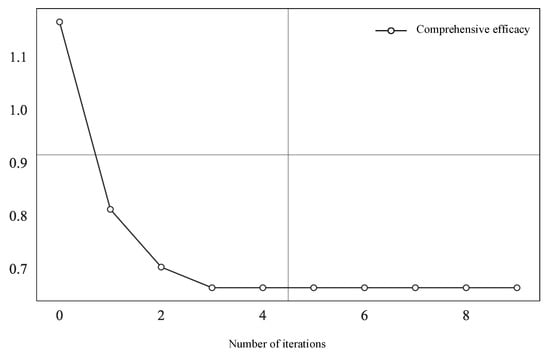
Figure 6.
The change of the efficiency function.
6.2. Spatial Positions and Impulse Conditions
Figure 7 shows the operational trajectories of two detection satellites (A1–A2) and two intelligent satellites (D1–D2) in three-dimensional orbital space. Solid and dashed lines of different colors represent the orbital paths of different numbered detection and intelligent satellites. The figure clearly demonstrates that each intelligent satellite achieves a relatively favorable deployment position through strategic maneuvers, effectively avoiding potential collisions with detection satellites. Meanwhile, the corresponding detection satellites attempt to obtain optimal observation conditions through complex maneuver trajectories to accomplish their missions. This dynamic process reflects the game characteristics between the two parties in orbital space and reveals the importance of orbital maneuvers and coordinated deployment in achieving detection missions.
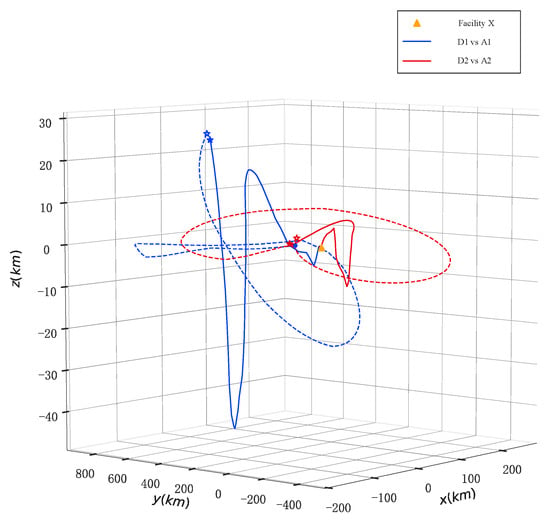
Figure 7.
Three-dimensional spatial paths of satellite constellations.
Table 5 presents the impulse statistics of detection and intelligent satellites during the entire mission period, including mission duration, total impulse, and number of impulses. The data show that the mission completion times for the two intelligent satellites (D1–D2) are 125,580 s and 116,500 s, respectively, with both reaching or approaching 30 impulses. The two detection satellites (A1–A2) performed 23 and 27 impulses, respectively, with impulse amounts smaller than their corresponding intelligent satellites. The statistical results indicate that both sides adopted high-frequency impulse strategies during the mission, demonstrating highly intense dynamic game characteristics.

Table 5.
Impulse statistics for detection and intelligent satellites.
Through precise impulse strategies, the intelligent satellites effectively optimized orbit adjustments and maneuver strategies, achieving superior spatial deployment and maintaining safe distances, while the detection satellites attempted to achieve optimal detection through flexible maneuver trajectories. These results reflect the importance and complexity of strategy selection in multi-to-multi scenarios. Overall, all intelligent satellites demonstrated excellent maneuverability and tactical execution capabilities, achieving superior comprehensive scheduling effects through reasonable impulse strategies during the game process. This indicates that satellite clusters can achieve effective resource coordination and strategy optimization in multi-objective mission environments.
6.3. Feature Variations
To further understand the details of each intelligent and detection satellite in different scenarios, Figure 8, Figure 9, Figure 10 and Figure 11 show the evolution of relative distances, illumination angles, and capture angles for each satellite pair.
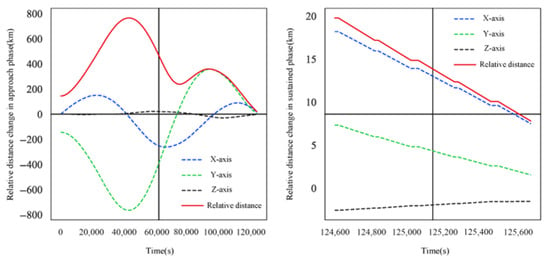
Figure 8.
Relative distance of intelligent satellite D1 during its evasion of detection satellite A1.
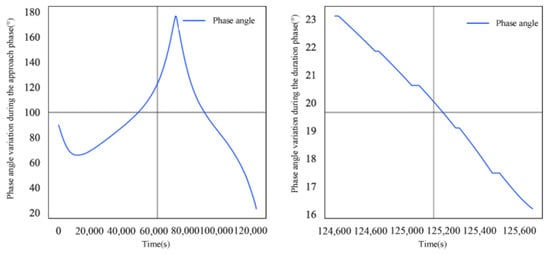
Figure 9.
Illumination angle of intelligent satellite D1 during its evasion of detection satellite A1.
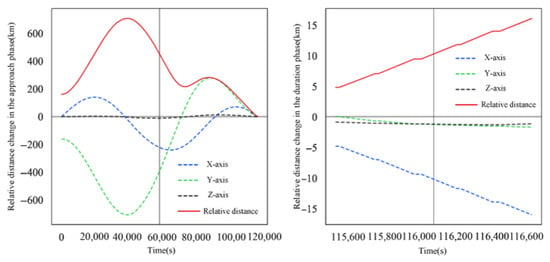
Figure 10.
Relative distance of intelligent satellite D2 during its evasion of detection satellite A2.
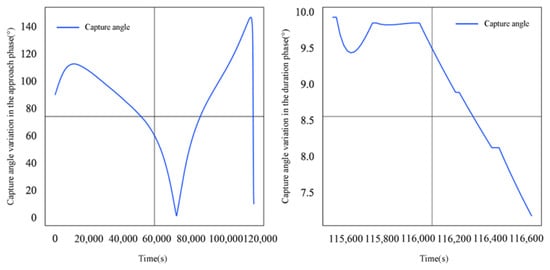
Figure 11.
Capture angle of intelligent satellite D2 during its evasion of detection satellite A2.
Figure 8 and Figure 9 display the dynamic changes in relative distance and illumination angle for intelligent satellite D1 during its evasion of detection satellite A1 in the approach and sustained phases, respectively.
From Figure 8 and Figure 9, it can be observed that the relative distance first increases and then decreases over time during the approach phase, while the illumination angle fluctuates significantly. After the approach phase, the illumination angle is constrained within 40°, indicating that D1 positioned itself more favorably through multiple impulse maneuvers during evasion. Through precise orbit adjustments, A1 continuously optimized its relative position, effectively mitigating the negative impact of the illumination angle on mission execution and ensuring optimal angle configuration during detection. In the sustained phase, the relative distance between the two gradually decreases, indicating that the detection satellite continues to approach the intelligent satellite while remaining within safe distance limits. The illumination angle continues to decrease, demonstrating the detection satellite’s capability for effective target detection. The results show that intelligent satellite D1 successfully avoided collision with detection satellite A1 while maintaining stability. Throughout the process, D1 employed flexible maneuver strategies multiple times to avoid collision, while A1 ensured successful mission completion through precise impulse strategies and accurate orbit control, further validating the method’s efficiency and robustness in dynamic missions.
Figure 10 and Figure 11 show the dynamic changes in relative distance and capture angle between intelligent satellite D2 and detection satellite A2 during the approach and sustained phases of evasion.
It can be seen that, during the approach phase, the dynamic adjustment process between intelligent satellite D2 and detection satellite A2 was constrained not only by relative distance but also required strict control of the capture angle within acceptable limits. The figures show that the relative distance between the satellites gradually decreased and eventually converged to within 20 km, while the capture angle reduced to below 10°. This indicates that the optimization strategy during the approach phase satisfied A1’s detection mission constraints while maintaining a safe distance from D2. In the sustained phase, the relative distance between the two gradually increased, reflecting their continued optimization of control strategies during the dynamic process. However, the capture angle exhibited significant fluctuations, likely caused by complex trajectory changes resulting from dynamic maneuver adjustments during this phase. Although these fluctuations reflect the intensity of maneuvers to some extent, the capture angle remained within mission-required thresholds overall, demonstrating the optimization algorithm’s robustness in handling dynamic changes.
7. Conclusions
Overall, during multi-to-multi space collaborative detection in geostationary orbit, intelligent satellites avoided collisions with detection satellites through strategy optimization, while detection satellites achieved comprehensive observation of intelligent satellites through efficient mission planning and optimization strategies, demonstrating their maneuverability and collaborative detection advantages in complex space environments. Furthermore, a good balance was achieved between detection success rate, fuel consumption, mission time cost, and target coverage. The proposed algorithm demonstrated high applicability and robustness under complex constraints, validating the performance and application value of the Nash equilibrium-based distributed heterogeneous cluster task planning method in complex detection scenarios.
The results clearly demonstrate the strong capability of the Nash equilibrium-based distributed task planning method in coordinating heterogeneous satellite cluster missions. The algorithm not only maximizes detection success rate but also significantly optimizes key metrics such as fuel consumption and mission time cost. By introducing a weighted optimization mechanism for comprehensive performance metrics, the proposed method exhibits high adaptability and robustness under multi-objective constraints, ensuring balanced optimization of all mission metrics when facing complex space mission requirements. This fully proves the broad application potential of the Nash equilibrium-based distributed task planning method in complex space detection missions. Particularly for future more complex dynamic space missions requiring efficient cluster coordination and intelligent mission planning, this study provides an effective method with significant academic value and practical importance.
Author Contributions
Conceptualization, H.G., J.W., Q.Y. and D.Z.; methodology, H.G., P.W. and D.Z.; software, H.G., J.W., P.W. and D.Z.; validation, X.X., J.W., Q.Y., P.W. and D.Z.; formal analysis, H.G., X.X. and Q.Y.; investigation, H.G., J.W., X.X. and Q.Y.; resources, H.G., J.W., X.X. and Q.Y.; data curation, H.G., J.W., P.W. and D.Z.; writing—original draft preparation, H.G., J.W., P.W. and D.Z.; writing—review and editing, H.G., J.W., P.W. and D.Z.; visualization, H.G., J.W., P.W. and D.Z.; supervision, Q.Y. and D.Z.; project administration, H.G., Q.Y. and D.Z.; funding acquisition, H.G., Q.Y. and D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grants 52377215, 51977177); Northwestern Polytechnical University Education and Teaching Reform Research Project (2025JGG03); Shanghai Academy of Spaceflight Technology Funded project (SAST2023-088); the “Double world-class project” discipline construction fund of Northwestern Polytechnical University (WH00001049).
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, Y.; Zhang, W. Analysis and Reflection on the Space Security Situation. China Aerosp. 2024, 21–26. (In Chinese) [Google Scholar] [CrossRef]
- Liu, S. Task Planning and Orbit Optimization for Multi-Satellite Interception. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2018. (In Chinese). [Google Scholar]
- Fourati, F.; Alouini, M.S. Artificial intelligence for satellite communication: A review. Intell. Converg. Netw. 2021, 2, 213–243. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, Y.; Zhao, B.; Chanussot, J.; Hong, D.; Yao, J. Progress and challenges in intelligent remote sensing satellite systems. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1814–1822. [Google Scholar] [CrossRef]
- Farquhar, R.W.; Muhonen, D.P.; Newman, C.R.; Heubergerg, H.S. Trajectories and orbital maneuvers for the first libration-point satellite. J. Guid. Control. 1980, 3, 549–554. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, L.; Cheng, J.; Zhou, J.; Wang, Y. Task scheduling and attitude planning for agile earth observation satellite with intensive tasks. Aerosp. Sci. Technol. 2019, 90, 23–33. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, C.; Kuang, L.; Wu, S.; Huang, H.; Qian, Y. High-efficient resource allocation in data relay satellite systems with users behavior coordination. IEEE Trans. Veh. Technol. 2018, 67, 12072–12085. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.; Liu, L.; Liu, L.; Lan, D.; Jiang, H.; Wan, S. Aerial edge computing on orbit: A task offloading and allocation scheme. IEEE Trans. Netw. Sci. Eng. 2022, 10, 275–285. [Google Scholar] [CrossRef]
- Wang, R.; Xing, J.; Wang, P.; Wang, C. Research Review on Multi-Agent Cooperative Control of Ground Unmanned Systems. J. Dyn. Control. 2016, 14, 97–108. [Google Scholar]
- Ferreira, B.A.; Petrović, T.; Orsag, M.; Dios, J.R.F.; Bogdan, S. Distributed allocation and scheduling of tasks with cross-schedule dependencies for heterogeneous multi-robot teams. IEEE Access 2024, 12, 74327–74342. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, D. Distributed Imaging Satellite Mission Planning Based on Multi-Agent. IEEE Access 2023, 11, 65530–65545. [Google Scholar] [CrossRef]
- Skrzypczyk, K. Game theory based task planning in multi-robot systems. Int. J. Simul. 2005, 6, 50–60. [Google Scholar]
- Martin, M.; Lyke, J. Modular Open Network ARCHitecture (MONARCH): Transitioning plug-and-play to aerospace. In Proceedings of the Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013. [Google Scholar]
- Chen, Q.; Wu, W.; Dai, J. Research on Distributed Autonomous Configuration Maintenance Planning of Satellite Systems Based on Multi-Agent Negotiation. J. Astronaut. 2008, 29, 517–521. [Google Scholar]
- Wang, C.; Li, J.; Jing, N.; Wang, J.; Chen, H. A Distributed Cooperative Dynamic Task Planning Algorithm for Multiple Satellites Based on Multi-agent Hybrid Learning. Chin. J. Aeronaut. 2011, 24, 493–505. [Google Scholar] [CrossRef]
- Liu, Y.; Ye, D.; Hao, Y. Distributed Online Algorithm for Multi-Agent Space Pursuit-Evasion Mission Planning. J. Aeronaut. China 2016, 29, 1709–1720. [Google Scholar] [CrossRef]
- Zheng, Z.; Guo, J.; Gill, E. Distributed onboard mission planning for multi-satellite systems. Aerosp. Sci. Technol 2019, 89, 111–122. [Google Scholar] [CrossRef]
- Kim, M.H.; Baik, H.; Lee, S. Response threshold model based UAV search planning and task allocation. Intell. Robot. Syst. 2014, 75, 625–637. [Google Scholar] [CrossRef]
- Pei, J.; Li, L. Research on Distributed Cooperative Optimization Algorithm for Satellite Task Planning. Aerosp. Eng. 2020, 47, 231–238. [Google Scholar]
- Fei, H.; Zhang, X.; Long, J. Towards Multi-Satellite Collaborative Computing via Task Scheduling Based on Genetic Algorithm. Aerospace 2023, 10, 95. [Google Scholar] [CrossRef]
- Wang, Z. Research on Dynamics Modeling and Control of Distributed Satellites. Ph.D. Thesis, University of National Defense Science and Technology, Changsha, China, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).