Estimation of Footprint-Scale Across-Track Slopes Based on Elevation Frequency Histogram from Single-Track ICESat-2 Photon Data of Strong Beam
Abstract
1. Introduction
2. Materials and Methods
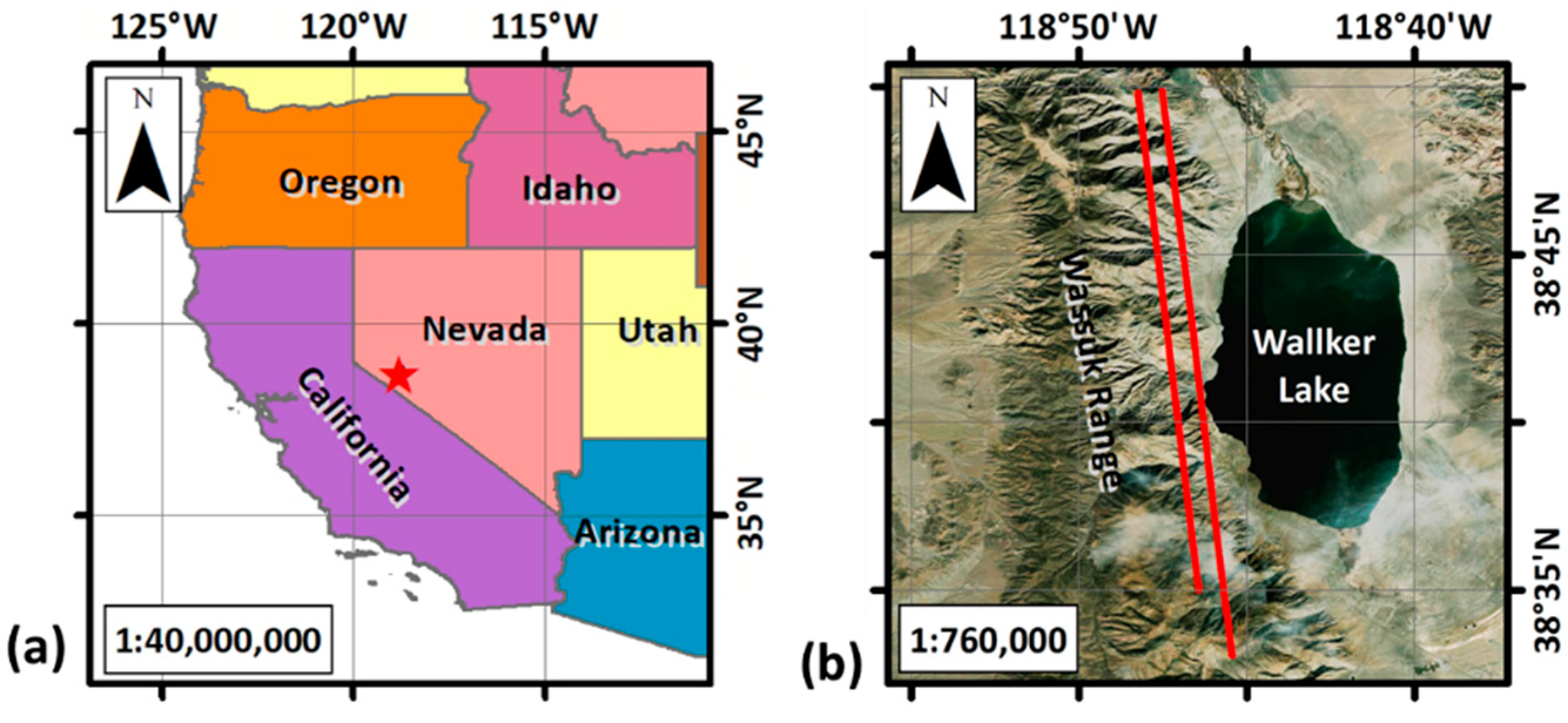
2.1. Study Area
2.2. ICESat-2 Data
2.3. ALS Data
3. Methods
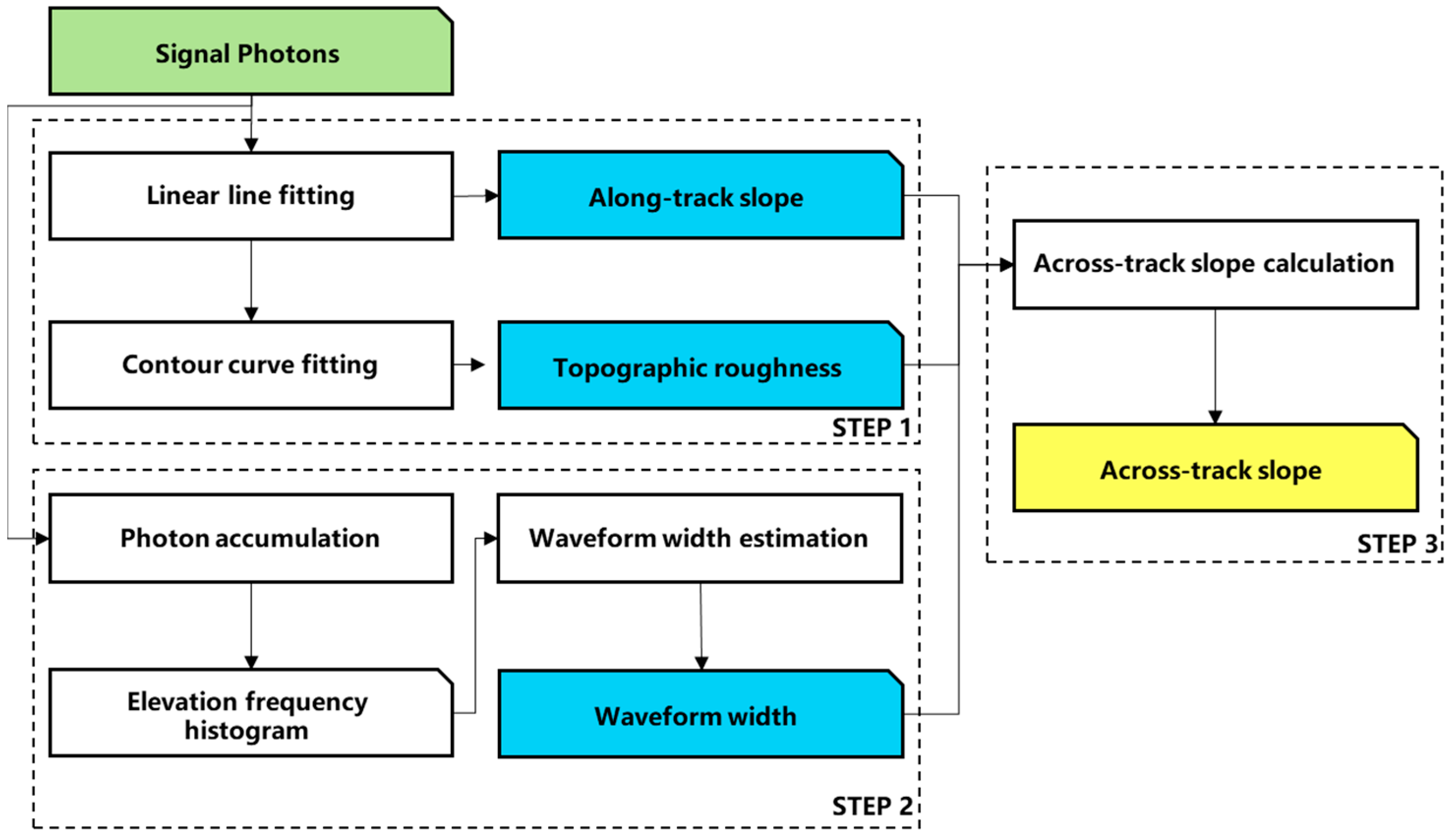
3.1. Retrieval of Across-Track Slope
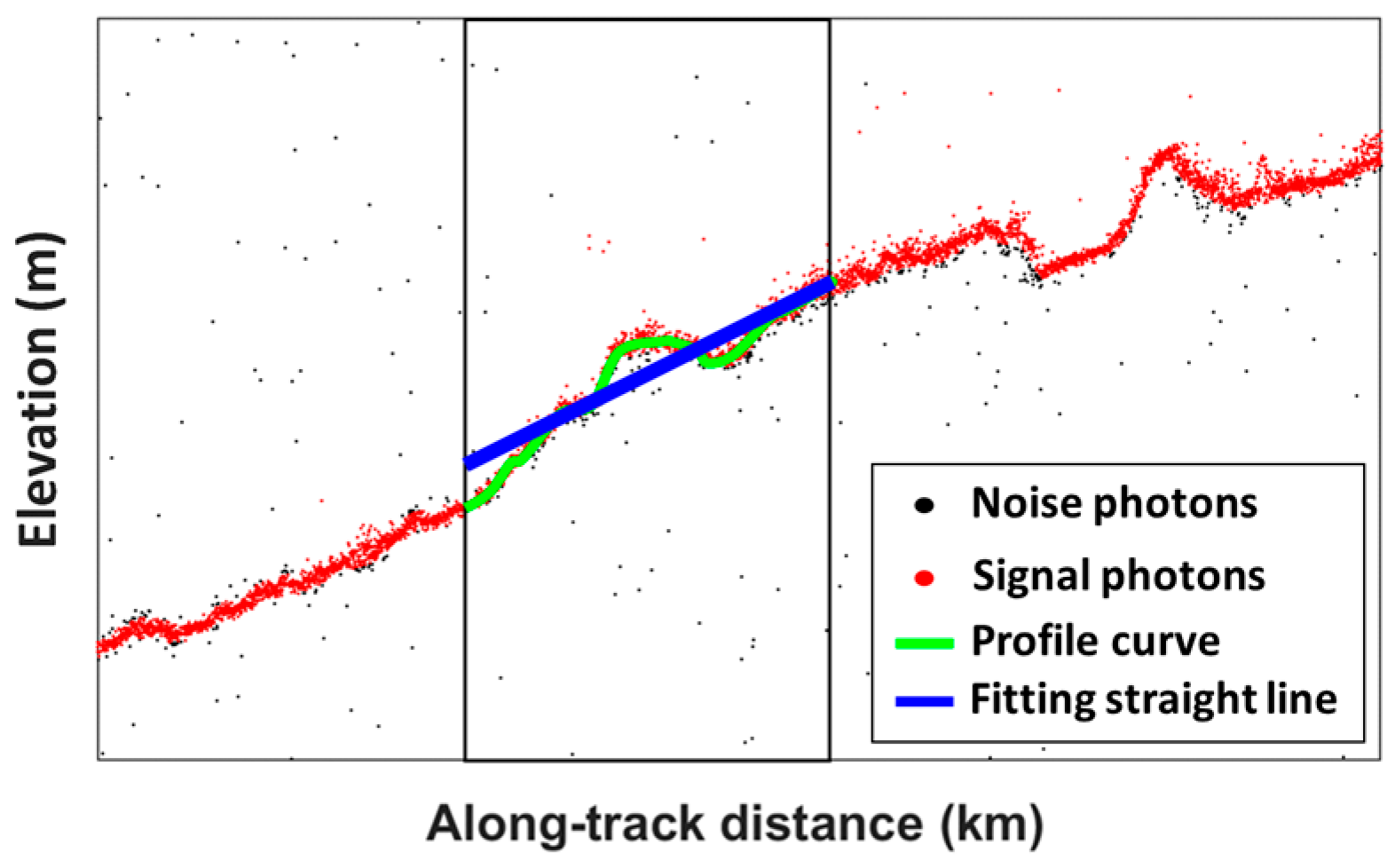
3.1.1. Deriving Along-Track Slope and Roughness Based on Photon Data
3.1.2. Generating EFH Based on Photon Data
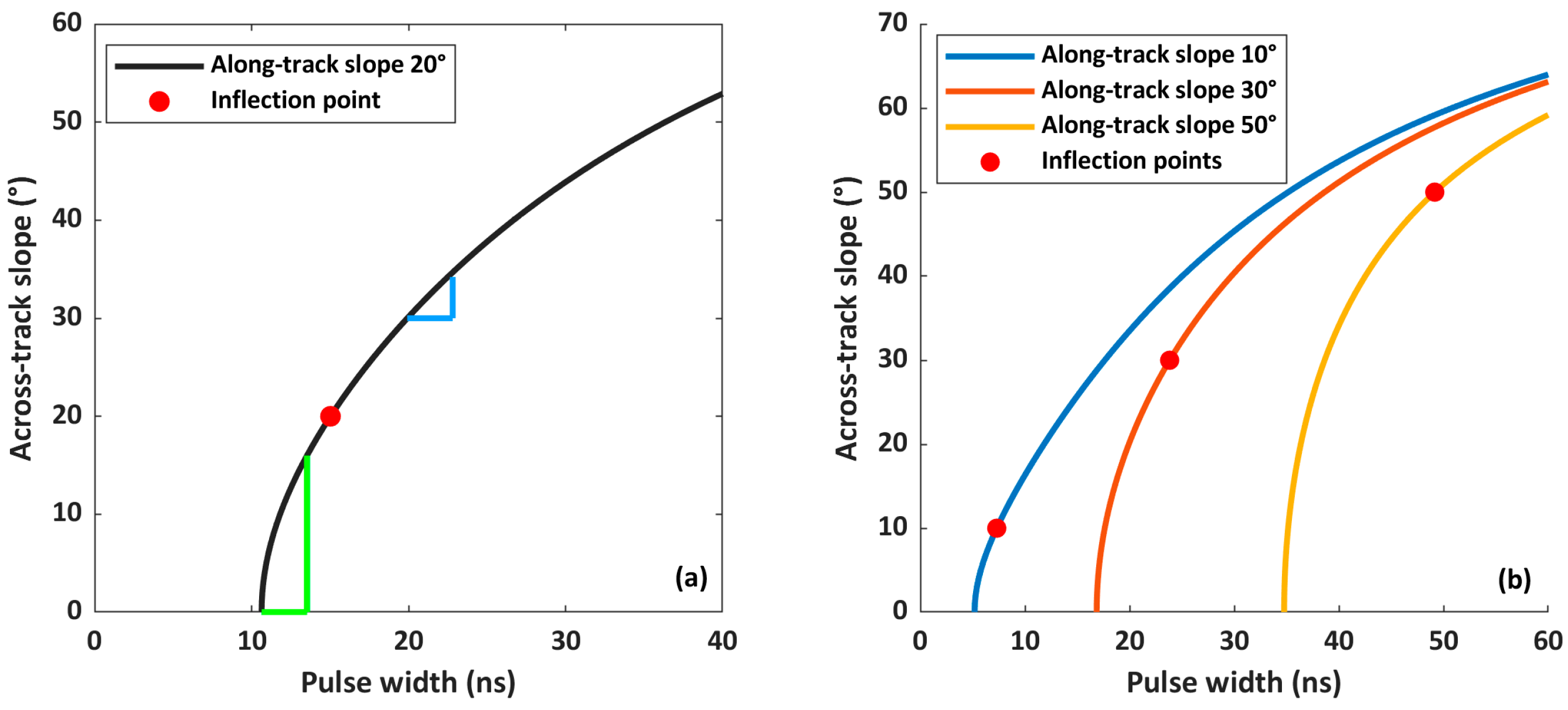
3.1.3. Estimating Across-Track Slope Based on EFH Waveform
3.2. Accuracy Validation
4. Results and Discussion
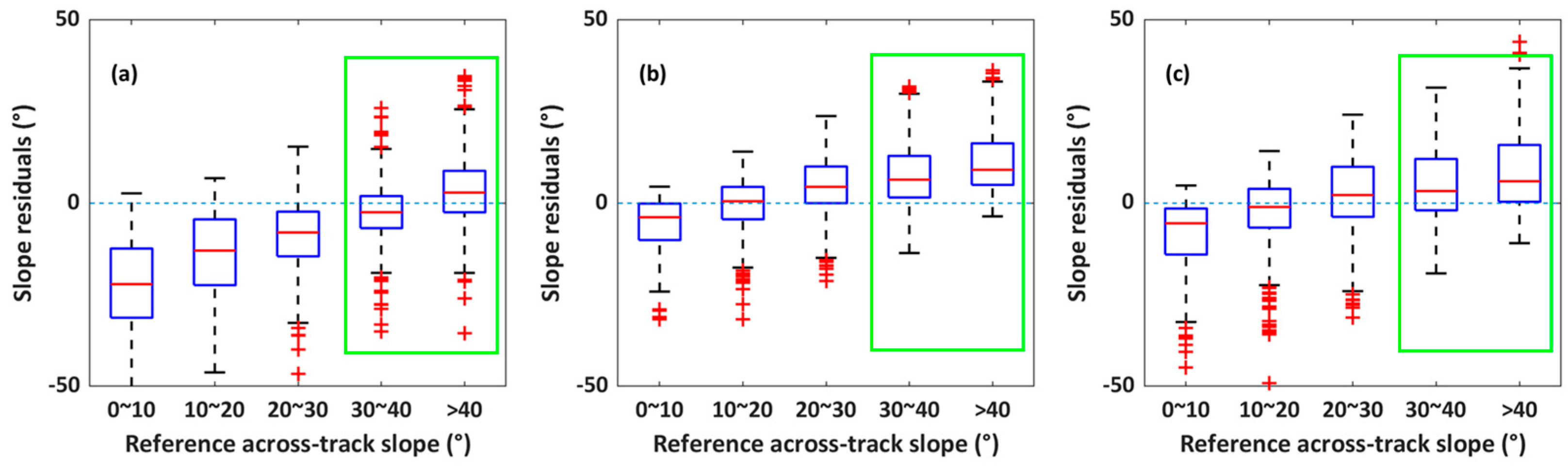
4.1. Accuracy of Retrieved Across-Track Slope
4.2. Topographic Applicability Assessment
5. Discussion
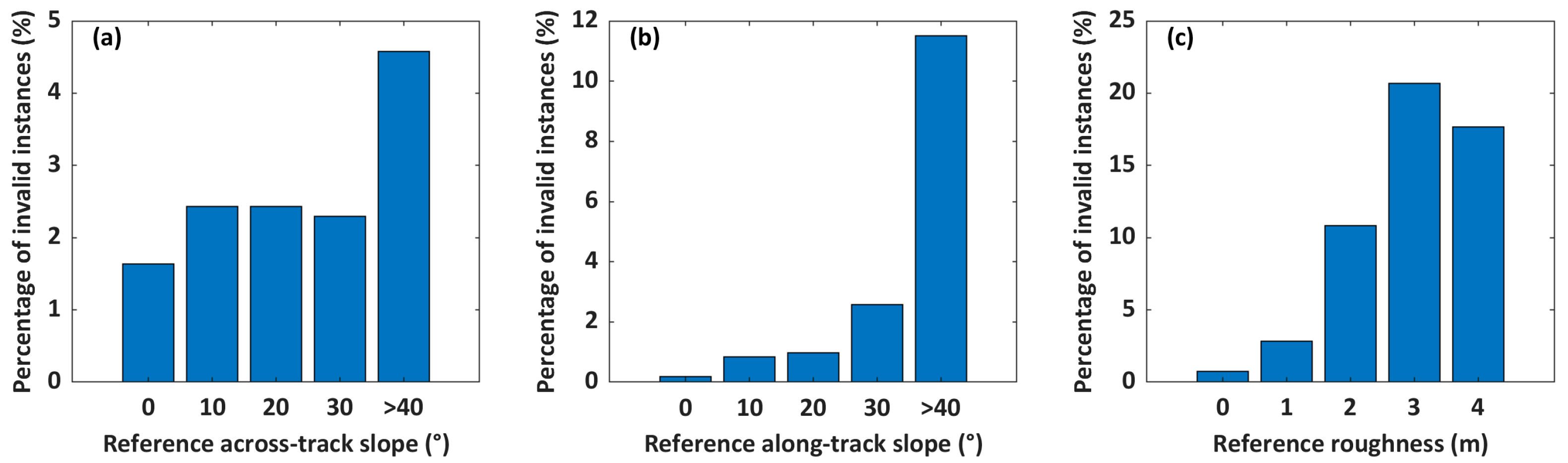
5.1. Invalid Instance Analysis
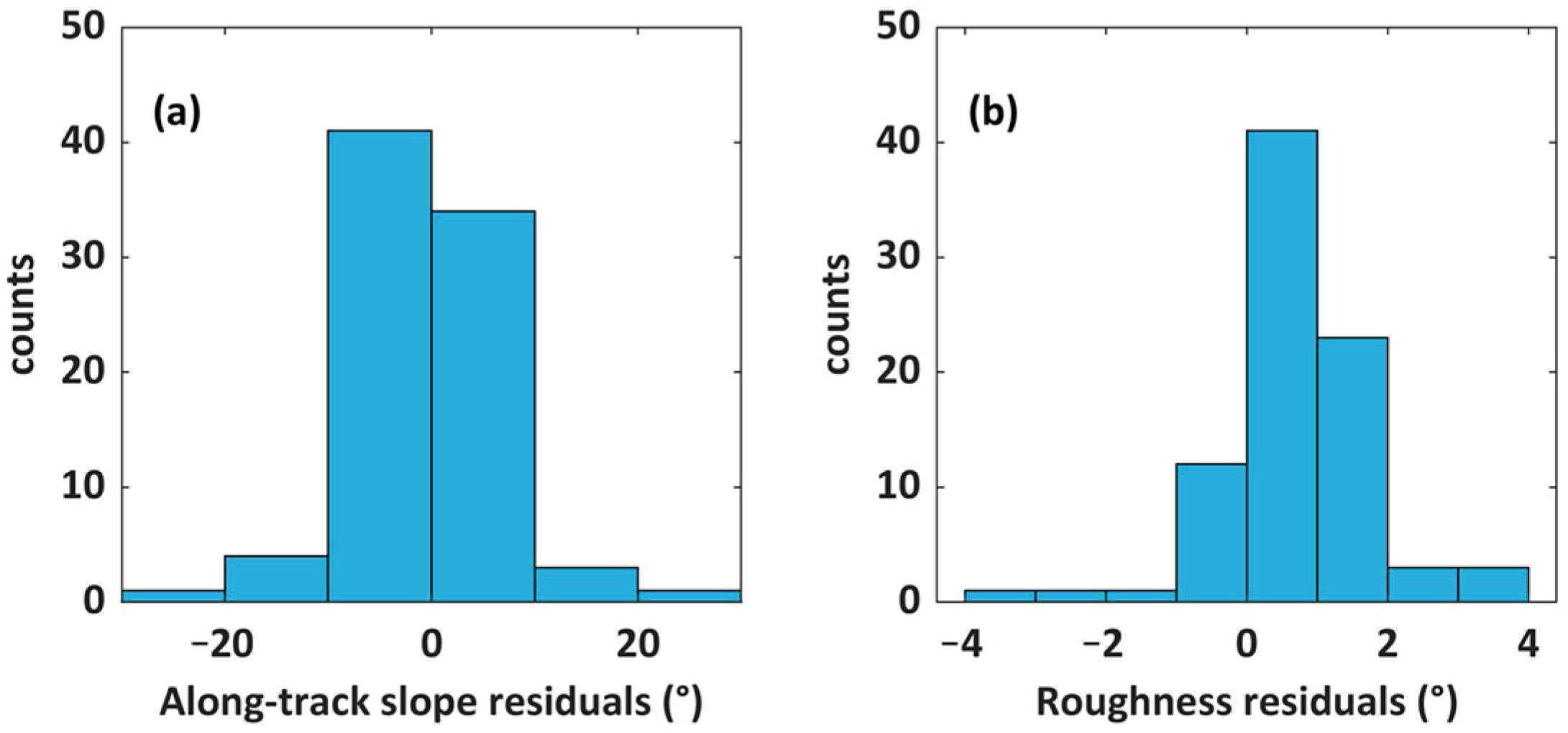
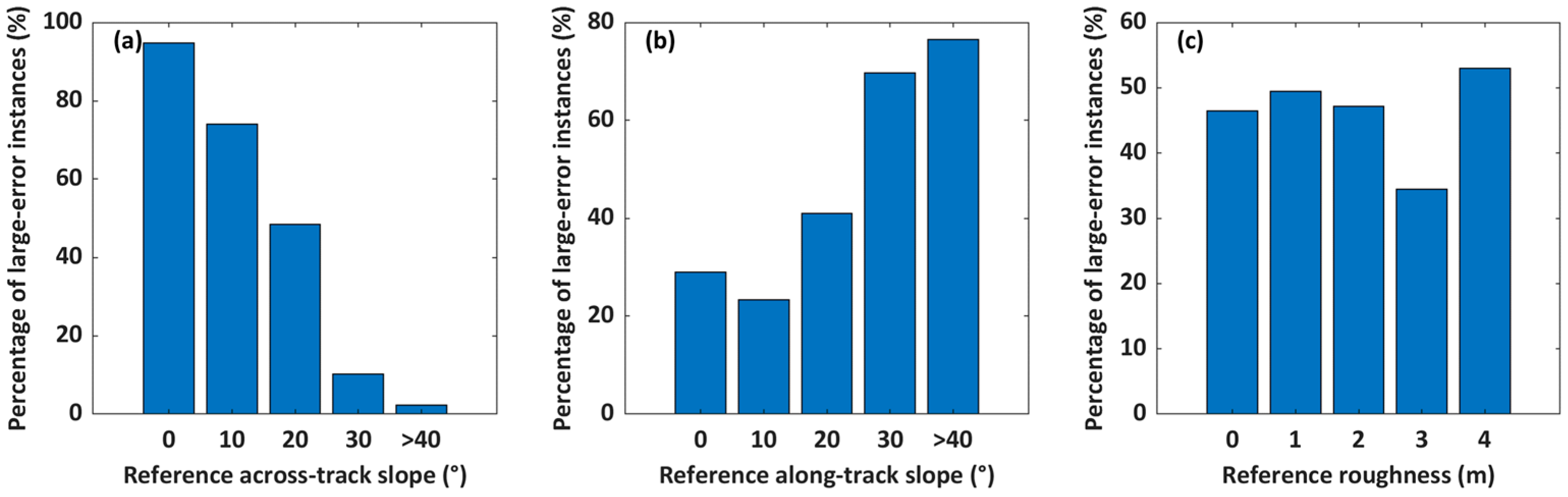
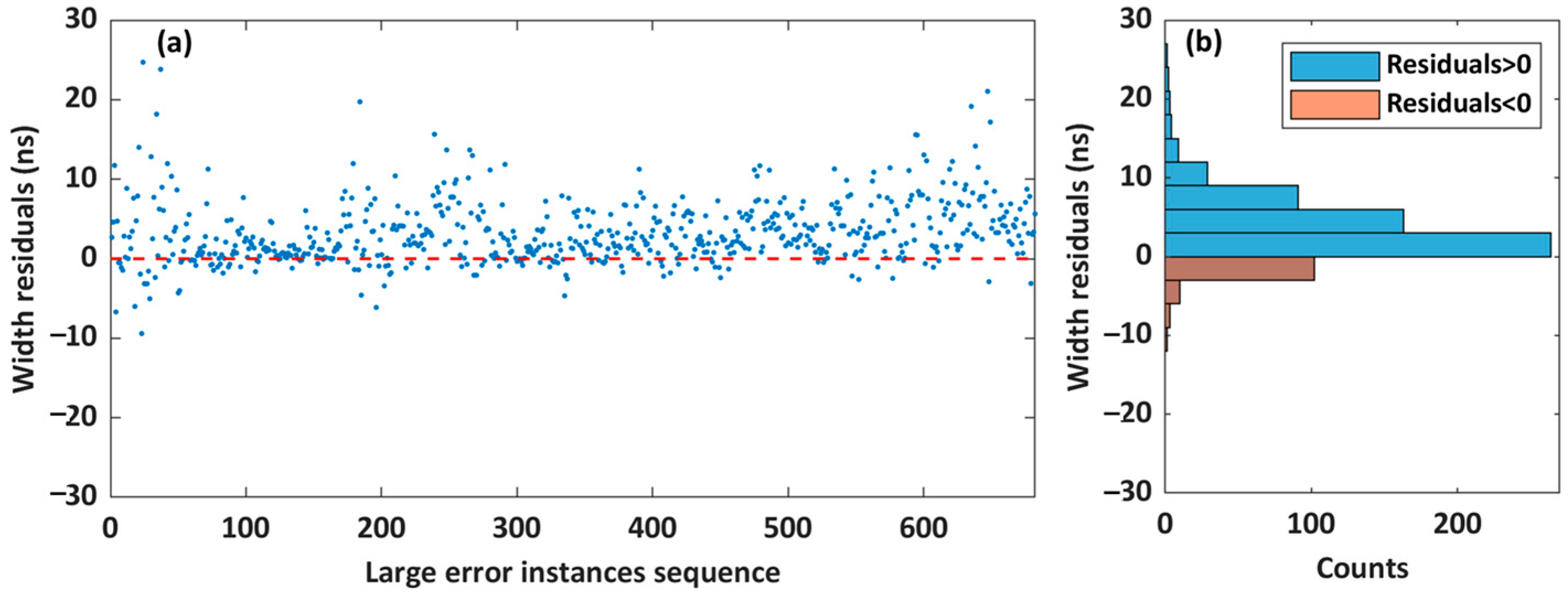
5.2. Large-Error Instance Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hilbert, C.; Schmullius, C. Influence of Surface Topography on ICESat/GLAS Forest Height Estimation and Waveform Shape. Remote Sens. 2012, 4, 2210–2235. [Google Scholar] [CrossRef]
- del Rosario Gonzalez-Moradas, M.; Viveen, W. Evaluation of ASTER GDEM2, SRTMv3. 0, ALOS AW3D30 and TanDEM-X DEMs for the Peruvian Andes against Highly Accurate GNSS Ground Control Points and Geomorphological-Hydrological Metrics. Remote Sens. Environ. 2020, 237, 111509. [Google Scholar] [CrossRef]
- Fricker, G.A.; Synes, N.W.; Serra-Diaz, J.M.; North, M.P.; Davis, F.W.; Franklin, J. More than Climate? Predictors of Tree Canopy Height Vary with Scale in Complex Terrain, Sierra Nevada, CA (USA). For. Ecol. Manag. 2019, 434, 142–153. [Google Scholar] [CrossRef]
- Eitel, J.U.; Höfle, B.; Vierling, L.A.; Abellán, A.; Asner, G.P.; Deems, J.S.; Glennie, C.L.; Joerg, P.C.; LeWinter, A.L.; Magney, T.S. Beyond 3-D: The New Spectrum of Lidar Applications for Earth and Ecological Sciences. Remote Sens. Environ. 2016, 186, 372–392. [Google Scholar] [CrossRef]
- Muscarella, R.; Kolyaie, S.; Morton, D.C.; Zimmerman, J.K.; Uriarte, M. Effects of Topography on Tropical Forest Structure Depend on Climate Context. J. Ecol. 2020, 108, 145–159. [Google Scholar] [CrossRef]
- Yu, J.; Liu, H.; Wang, L.; Jezek, K.C.; Heo, J. Blue Ice Areas and Their Topographical Properties in the Lambert Glacier, Amery Iceshelf System Using Landsat ETM+, ICESat Laser Altimetry and ASTER GDEM Data. Antarct. Sci. 2012, 24, 95–110. [Google Scholar] [CrossRef]
- Giardino, M.; Perotti, L.; Lanfranco, M.; Perrone, G. GIS and Geomatics for Disaster Management and Emergency Relief: A Proactive Response to Natural Hazards. Appl. Geomat. 2012, 4, 33–46. [Google Scholar] [CrossRef]
- Cao, G.; Wei, X.; Ye, J. Fireground Recognition and Spatio-Temporal Scalability Research Based on ICESat-2/ATLAS Vertical Structure Parameters. Forests 2024, 15, 1597. [Google Scholar] [CrossRef]
- Evans, I.S. Geomorphometry and Landform Mapping: What Is a Landform? Geomorphology 2012, 137, 94–106. [Google Scholar] [CrossRef]
- Schillaci, C.; Braun, A.; Kropáček, J. Terrain Analysis and Landform Recognition. In Geomorphological Techniques (Online Edition); Clarke, N.E., Nield, J.M., Eds.; British Society for Geomorphology: London, UK, 2015. [Google Scholar]
- Zhao, G.; Xue, H.; Ling, F. Assessment of ASTER GDEM Performance by Comparing with SRTM and ICESat/GLAS Data in Central China. In Proceedings of the 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010; pp. 1–5. [Google Scholar]
- Carabajal, C.C.; Harding, D.J. SRTM C-Band and ICESat Laser Altimetry Elevation Comparisons as a Function of Tree Cover and Relief. Photogramm. Eng. Remote Sens. 2006, 72, 287–298. [Google Scholar] [CrossRef]
- Braun, A.; Fotopoulos, G. Assessment of SRTM, ICESat, and Survey Control Monument Elevations in Canada. Photogramm. Eng. Remote Sens. 2007, 73, 1333–1342. [Google Scholar] [CrossRef]
- Carabajal, C.C.; Harding, D.J. ICESat Validation of SRTM C-Band Digital Elevation Models. Geophys. Res. Lett. 2005, 32, 22. [Google Scholar] [CrossRef]
- Wessel, B.; Huber, M.; Wohlfart, C.; Marschalk, U.; Kosmann, D.; Roth, A. Accuracy Assessment of the Global TanDEM-X Digital Elevation Model with GPS Data. ISPRS J. Photogramm. Remote Sens. 2018, 139, 171–182. [Google Scholar] [CrossRef]
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Tridon, D.B.; Bräutigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M. Generation and Performance Assessment of the Global TanDEM-X Digital Elevation Model. ISPRS J. Photogramm. Remote Sens. 2017, 132, 119–139. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance Evaluation of GEDI and ICESat-2 Laser Altimeter Data for Terrain and Canopy Height Retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Mallet, C.; Bretar, F. Full-Waveform Topographic Lidar: State-of-the-Art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Magruder, L.A.; Brunt, K.M. Performance Analysis of Airborne Photon- Counting Lidar Data in Preparation for the ICESat-2 Mission. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2911–2918. [Google Scholar] [CrossRef]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat Mission. Geophys. Res. Lett. 2005, 32, L21S01. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, X.; Gong, P.; Huang, H.; Li, Z. and Li, X. Earth Science Applications of ICESat/GLAS: A Review. Int. J. Remote Sens. 2011, 32, 8837–8864. [Google Scholar] [CrossRef]
- Kwok, R.; Zwally, H.J.; Yi, D. ICESat Observations of Arctic Sea Ice: A First Look. Geophys. Res. Lett. 2004, 31, 16. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D. The Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2): Science Requirements, Concept, and Implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neumann, T.A.; Brenner, A.C.; Hancock, D.W.; Harbeck, K.; Luthcke, S.; Robbins, J.; Saba, J.; Gibbons, A. Ice, Cloud, and Land Elevation Satellite-2 Project Algorithm Theoretical Basis Document for Global Geolocated Photons (ATL03); NASA Goddard Space Flight Center: Greenbelt, MD, USA, June 2018. [Google Scholar]
- Patterson, P.L.; Healey, S.P.; Ståhl, G.; Saarela, S.; Holm, S.; Andersen, H.-E.; Dubayah, R.O.; Duncanson, L.; Hancock, S.; Armston, J. Statistical Properties of Hybrid Estimators Proposed for GEDI—NASA’s Global Ecosystem Dynamics Investigation. Environ. Res. Lett. 2019, 14, 065007. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping Global Forest Canopy Height through Integration of GEDI and Landsat Data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Shendryk, Y. Fusing GEDI with Earth Observation Data for Large Area Aboveground Biomass Mapping. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103108. [Google Scholar] [CrossRef]
- Spinhirne, J.D.; Palm, S.P.; Hart, W.D.; Hlavka, D.L.; Welton, E.J. Cloud and Aerosol Measurements from GLAS: Overview and Initial Results. Geophys. Res. Lett. 2005, 32, 22. [Google Scholar] [CrossRef]
- Magruder, L.A.; Webb, C.E.; Urban, T.J.; Silverberg, E.C.; Schutz, B.E. ICESat Altimetry Data Product Verification at White Sands Space Harbor. IEEE Trans. Geosci. Remote Sens. 2007, 45, 147–155. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Frappart, F. Comparative Analysis of GEDI’s Elevation Accuracy from the First and Second Data Product Releases over Inland Waterbodies. Remote Sens. 2022, 14, 340. [Google Scholar] [CrossRef]
- Gong, P.; Li, Z.; Huang, H.; Sun, G.; Wang, L. ICESat GLAS Data for Urban Environment Monitoring. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1158–1172. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W. The Ice, Cloud, and Land Elevation Satellite–2 Mission: A Global Geolocated Photon Product Derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef]
- Magruder, L.A.; Brunt, K.M.; Alonzo, M. Early ICESat-2 on-Orbit Geolocation Validation Using Ground-Based Corner Cube Retro-Reflectors. Remote Sens. 2020, 12, 3653. [Google Scholar] [CrossRef]
- Parrish, C.E.; Magruder, L.A.; Neuenschwander, A.L.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinski, M. Validation of ICESat-2 ATLAS Bathymetry and Analysis of ATLAS’s Bathymetric Mapping Performance. Remote Sens. 2019, 11, 1634. [Google Scholar] [CrossRef]
- Xu, N.; Ma, Y.; Zhou, H.; Zhang, W.; Zhang, Z.; Wang, X.H. A Method to Derive Bathymetry for Dynamic Water Bodies Using ICESat-2 and GSWD Data Sets. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Bagnardi, M.; Kurtz, N.T.; Petty, A.A.; Kwok, R. Sea Surface Height Anomalies of the Arctic Ocean from ICESat-2: A First Examination and Comparisons with CryoSat-2. Geophys. Res. Lett. 2021, 48, e2021GL093155. [Google Scholar] [CrossRef]
- Herzfeld, U.C.; Lawson, M.; Trantow, T.; Nylen, T. Airborne Validation of ICESat-2 ATLAS Data over Crevassed Surfaces and Other Complex Glacial Environments: Results from Experiments of Laser Altimeter and Kinematic GPS Data Collection from a Helicopter over a Surging Arctic Glacier (Negribreen, Svalbard). Remote Sens. 2022, 14, 1185. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y.; Wang, C.; Li, L. Accelerated Glacier Mass Loss over Svalbard Derived from ICESat-2 in 2019–2021. Atmosphere 2022, 13, 1255. [Google Scholar] [CrossRef]
- Herrmann, J.; Magruder, L.A.; Markel, J.; Parrish, C.E. Assessing the Ability to Quantify Bathymetric Change over Time Using Solely Satellite-Based Measurements. Remote Sens. 2022, 14, 1232. [Google Scholar] [CrossRef]
- Palm, S.P.; Selmer, P.; Yorks, J.; Nicholls, S.; Nowottnick, E. Planetary Boundary Layer Height Estimates from ICESat-2 and CATS Backscatter Measurements. Front. Remote Sens. 2021, 2, 716951. [Google Scholar] [CrossRef]
- Malambo, L.; Popescu, S.C. Assessing the Agreement of ICESat-2 Terrain and Canopy Height with Airborne Lidar over US Ecozones. Remote Sens. Environ. 2021, 266, 112711. [Google Scholar] [CrossRef]
- Liu, M.; Popescu, S. Estimation of Biomass Burning Emissions by Integrating ICESat-2, Landsat 8, and Sentinel-1 Data. Remote Sens. Environ. 2022, 280, 113172. [Google Scholar] [CrossRef]
- Feng, T.; Duncanson, L.; Montesano, P.; Hancock, S.; Minor, D.; Guenther, E.; Neuenschwander, A. A Systematic Evaluation of Multi-Resolution ICESat-2 ATL08 Terrain and Canopy Heights in Boreal Forests. Remote Sens. Environ. 2023, 291, 113570. [Google Scholar] [CrossRef]
- Li, X.; Xu, L.; Wang, C. Terrain Slope Calculation from Waveform of Airborne LiDAR. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 6259–6262. [Google Scholar]
- Li, X.; Xu, L.; Tian, X.; Kong, D. Terrain Slope Estimation within Footprint from ICESat/GLAS Waveform: Model and Method. J. Appl. Remote Sens. 2012, 6, 063534. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Dong, P.; Li, G.; Xi, X.; Wang, P.; Yang, X. A Novel Model for Terrain Slope Estimation Using ICESat/GLAS Waveform Data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 217–227. [Google Scholar] [CrossRef]
- Howat, I.M.; Smith, B.E.; Joughin, I.; Scambos, T.A. Rates of Southeast Greenland Ice Volume Loss from Combined ICESat and ASTER Observations. Geophys. Res. Lett. 2008, 35, 17. [Google Scholar] [CrossRef]
- Rinne, E.J.; Shepherd, A.; Palmer, S.; van den Broeke, M.R.; Muir, A.; Ettema, J.; Wingham, D. On the Recent Elevation Changes at the Flade Isblink Ice Cap, Northern Greenland. J. Geophys. Res. Earth Surf. 2011, 116, F3. [Google Scholar] [CrossRef]
- Yi, D.; Zwally, H.J.; Sun, X. ICESat Measurement of Greenland Ice Sheet Surface Slope and Roughness. Ann. Glaciol. 2005, 42, 83–89. [Google Scholar] [CrossRef]
- Zhu, X.; Nie, S.; Wang, C.; Xi, X.; Li, D.; Li, G.; Wang, P.; Cao, D.; Yang, X. Estimating Terrain Slope from ICESat-2 Data in Forest Environments. Remote Sens. 2020, 12, 3300. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 Land and Vegetation Product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Bincai, C.A.O.; Yong, F.; Zhenzhi, J.; Li, G.A.O.; Haiyan, H.U. Implementation and Accuracy Evaluation of ICESat-2 ATL08 Denoising Algorithms. Bull. Surv. Mapp. 2020, 518, 25–30. [Google Scholar]
- Neuenschwander, A.L.; Popescu, S.C.; Nelson, R.F.; Harding, D.; Pitts, K.L.; Robbins, J. ATLAS/ICESat-2 L3A Land and Vegetation Height, Version 1; NASA National Snow and Ice Data Center DAAC: Boulder, CO, USA, 2019. [Google Scholar]
- Xing, Y.; Huang, J.; Gruen, A.; Qin, L. Assessing the Performance of ICESat-2/ATLAS Multi-Channel Photon Data for Estimating Ground Topography in Forested Terrain. Remote Sens. 2020, 12, 2084. [Google Scholar] [CrossRef]
- Zhao, R.; Hu, Q.; Liu, Z.; Li, Y.; Zhang, K. A Pseudo-Waveform-Based Method for Grading ICESat-2 ATL08 Terrain Estimates in Forested Areas. Forests 2024, 15, 2113. [Google Scholar] [CrossRef]
- Corcoran, F.; Parrish, C.E. Diffuse Attenuation Coefficient (Kd) from ICESat-2 ATLAS Spaceborne Lidar Using Random-Forest Regression. Photogramm. Eng. Remote Sens. 2021, 87, 831–840. [Google Scholar] [CrossRef]
- Neumann, T.A.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S.B.; Rebold, T. ATLAS/ICESat-2 L2A Global Geolocated Photon Data, Version 4; NASA National Snow and Ice Data Center DAAC: Boulder, CO, USA, 2021. [Google Scholar]
- Dietrich, J.T.; Magruder, L.A.; Holwill, M. Monitoring Coastal Waves with ICESat-2. J. Mar. Sci. Eng. 2023, 11, 2082. [Google Scholar] [CrossRef]
- Gardner, C.S. Ranging Performance of Satellite Laser Altimeters. IEEE Trans. Geosci. Rem. Sens. 1992, 30, 1061–1072. [Google Scholar] [CrossRef]
- Gardner, C.S. Target Signatures for Laser Altimeters: An Analysis. Appl. Opt. 1982, 21, 448–453. [Google Scholar] [CrossRef]
- Frigge, M.; Hoaglin, D.C.; Iglewicz, B. Some Implementations of the Boxplot. Am. Stat. 1989, 43, 50–54. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. The Potential Impact of Vertical Sampling Uncertainty on ICESat-2/ATLAS Terrain and Canopy Height Retrievals for Multiple Ecosystems. Remote Sens. 2016, 8, 1039. [Google Scholar] [CrossRef]





| Across-Track Slope Range (°) | 0–10 | 10–20 | 20–30 | 30–40 | >40 |
|---|---|---|---|---|---|
| Segment number | 366 | 988 | 1029 | 829 | 306 |
| MAE | RMSE | MEAN | Invalid Segment | |
|---|---|---|---|---|
| Our method | 11.45° | 10.45° | −8.26° | 88 (2.51%) |
| ICESat-2 team method | 11.61° | 10.61° | 8.90° | 1137 (32.32%) |
| Plane fitting method | 12.51° | 10.53° | −2.67° | 362 (10.29%) |
| Methods | Indicators | Reference Across-Track Slope (°) | ||||
|---|---|---|---|---|---|---|
| 0–10 | 10–20 | 20–30 | 30–40 | >40 | ||
| Our method | Median | −22.10 | −12.93 | −7.98 | −2.47 | 2.90 |
| IQR | 18.89 | 17.96 | 12.19 | 8.75 | 11.32 | |
| Whisker range | 54.77 | 56.15 | 48.21 | 35.02 | 45.26 | |
| ICESat-2 team method | Median | −3.84 | 0.55 | 4.47 | 6.43 | 9.12 |
| IQR | 9.96 | 8.84 | 10.01 | 11.34 | 11.34 | |
| Whisker range | 29.51 | 31.74 | 38.77 | 43.52 | 36.96 | |
| Plane fitting method | Median | −5.49 | −1.03 | 2.23 | 3.32 | 5.99 |
| IQR | 12.56 | 10.60 | 13.66 | 14.01 | 15.51 | |
| Whisker range | 37.67 | 36.80 | 48.38 | 50.72 | 50.07 | |
| Methods | Factors | Reference Across-Track Slope (°) | ||||
|---|---|---|---|---|---|---|
| 0–10 | 10–20 | 20–30 | 30–40 | >40 | ||
| Our method | Invalid | 6 (1.64%) | 24 (2.43%) | 25 (2.43%) | 19 (2.29%) | 14 (4.58%) |
| Outliers | 0 (0%) | 1 (0.10%) | 5 (0.49%) | 21 (2.53%) | 13 (4.25%) | |
| ICESat-2 team method | Invalid | 100 (27.32%) | 334 (34.82%) | 290 (28.18%) | 265 (31.97%) | 148 (48.04%) |
| Outliers | 5 (1.37%) | 11 (1.11%) | 8 (0.78%) | 6 (0.72%) | 4 (1.31%) | |
| Plane fitting method | Invalid | 22 (6.01%) | 96 (9.72%) | 88 (8.55%) | 100 (12.06%) | 56 (18.30%) |
| Outliers | 7 (1.91%) | 19 (1.92%) | 7 (0.68%) | 0 (0%) | 4 (1.31%) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhou, H.; Ma, Y.; Li, S.; Wang, H. Estimation of Footprint-Scale Across-Track Slopes Based on Elevation Frequency Histogram from Single-Track ICESat-2 Photon Data of Strong Beam. Remote Sens. 2025, 17, 2617. https://doi.org/10.3390/rs17152617
Zhang Q, Zhou H, Ma Y, Li S, Wang H. Estimation of Footprint-Scale Across-Track Slopes Based on Elevation Frequency Histogram from Single-Track ICESat-2 Photon Data of Strong Beam. Remote Sensing. 2025; 17(15):2617. https://doi.org/10.3390/rs17152617
Chicago/Turabian StyleZhang, Qianyin, Hui Zhou, Yue Ma, Song Li, and Heng Wang. 2025. "Estimation of Footprint-Scale Across-Track Slopes Based on Elevation Frequency Histogram from Single-Track ICESat-2 Photon Data of Strong Beam" Remote Sensing 17, no. 15: 2617. https://doi.org/10.3390/rs17152617
APA StyleZhang, Q., Zhou, H., Ma, Y., Li, S., & Wang, H. (2025). Estimation of Footprint-Scale Across-Track Slopes Based on Elevation Frequency Histogram from Single-Track ICESat-2 Photon Data of Strong Beam. Remote Sensing, 17(15), 2617. https://doi.org/10.3390/rs17152617








