A Hybrid ANN–GWR Model for High-Accuracy Precipitation Estimation
Abstract
1. Introduction
2. Methodology
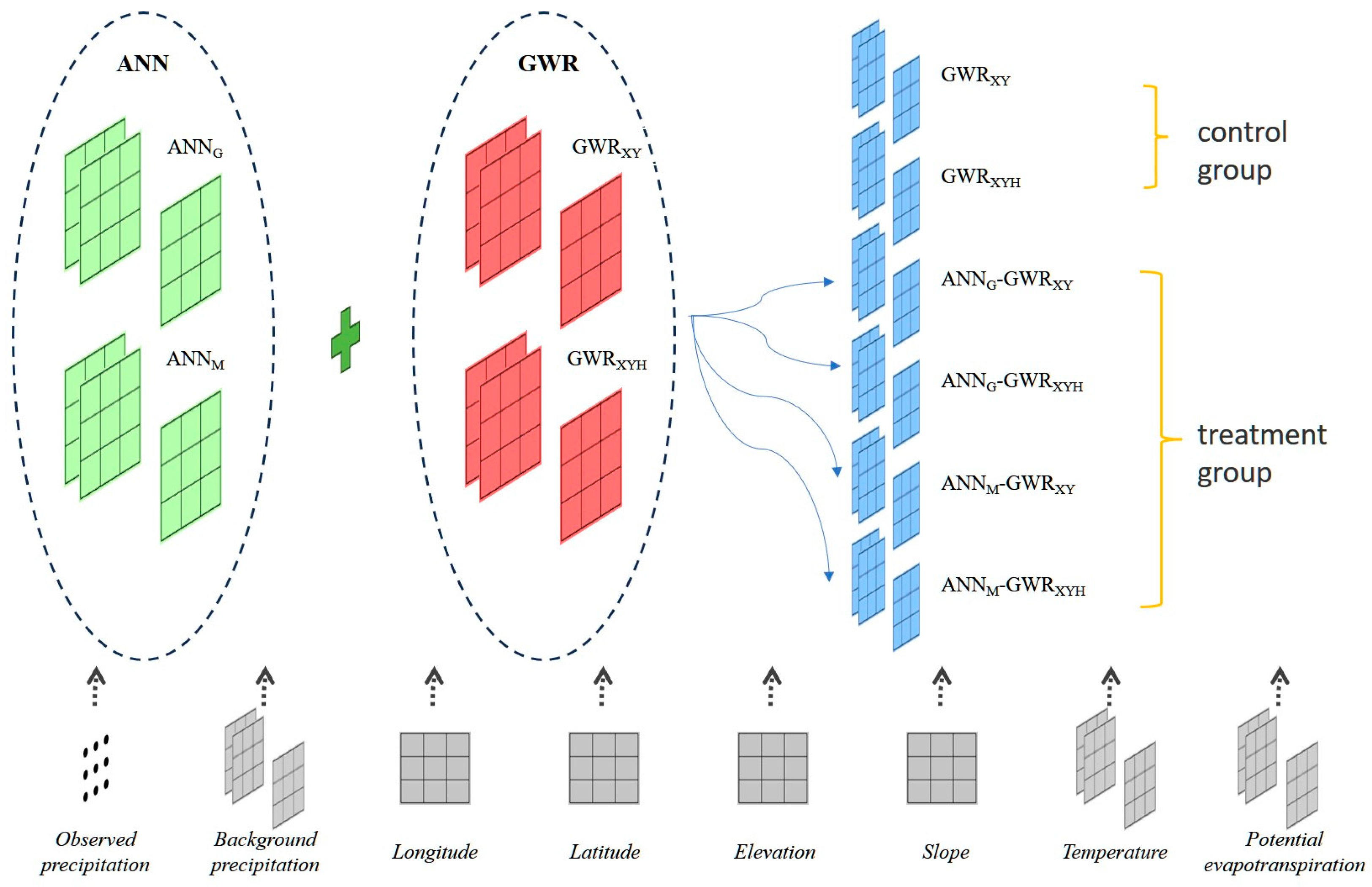
2.1. Integrated ANN–GWR Framwork
- Experiment 1: In this setup, the six input variables include geographic information (latitude, longitude), elevation, slope, temperature, and potential evapotranspiration (referred to as ANNG);
- Experiment 2: This setup incorporates all seven input variables: geographic information (latitude, longitude), elevation, slope, temperature, potential evapotranspiration, and background field precipitation (referred to as ANNM).
- Scenario 1: PANN = 0 and PGWR = 1
- Scenario 2: PANN = 0 and PGWR = 0
- Scenario 3: PANN = 1 and PGWR = 1
- Scenario 4: PANN = 1 and PGWR = 0
2.2. Validation and Error Decomposition
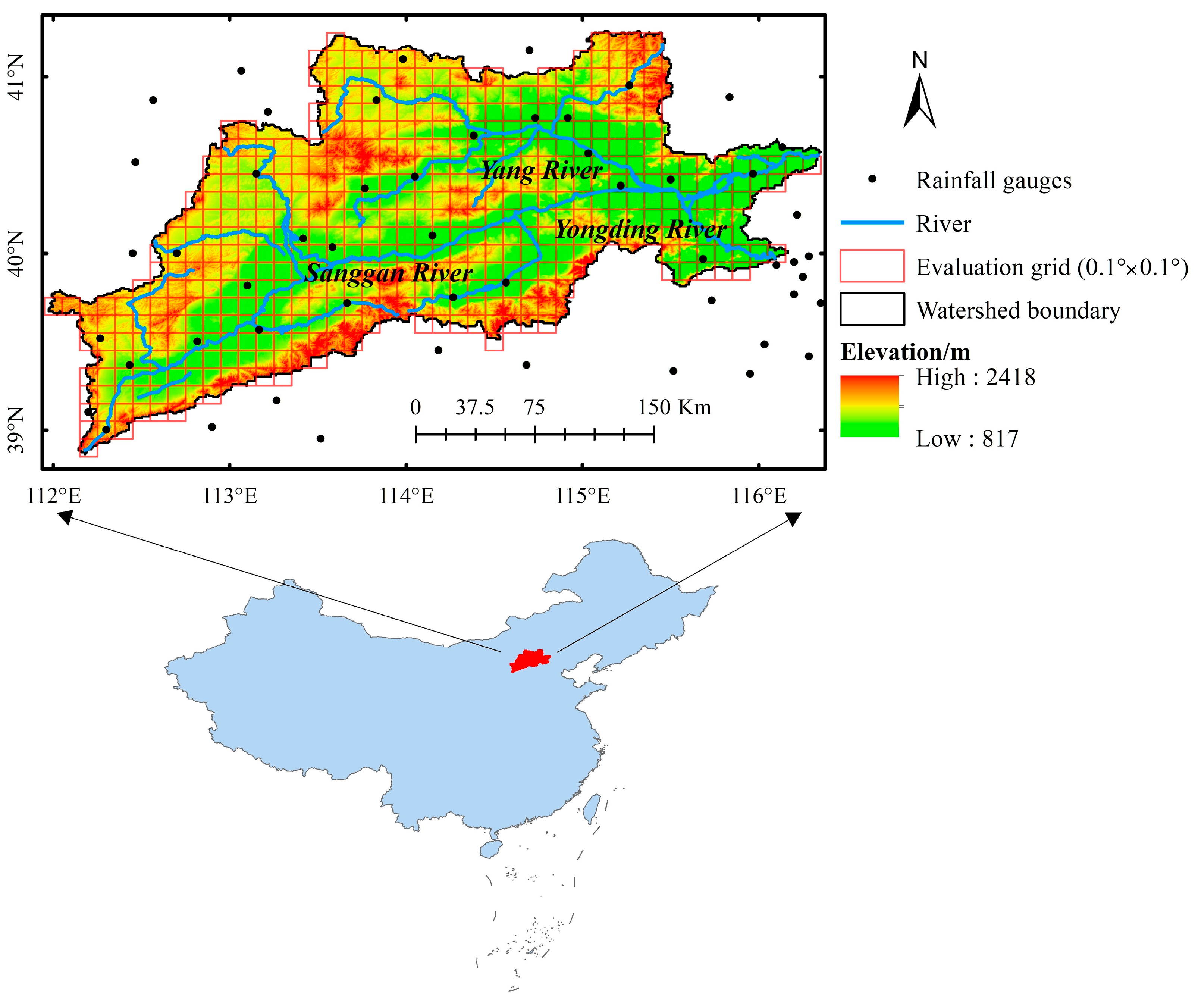
3. Study Area
3.1. Geographical Setting
3.2. Climatic Characteristics
- Annual precipitation: 360–650 mm (mean: 486 mm), with 80% concentrated in summer months (June to August);
- Extreme rainfall events: Heavy precipitation (>50 mm/day) occurs 3–5 times annually, primarily during July–August;
3.3. Data Source and Processing
4. Results
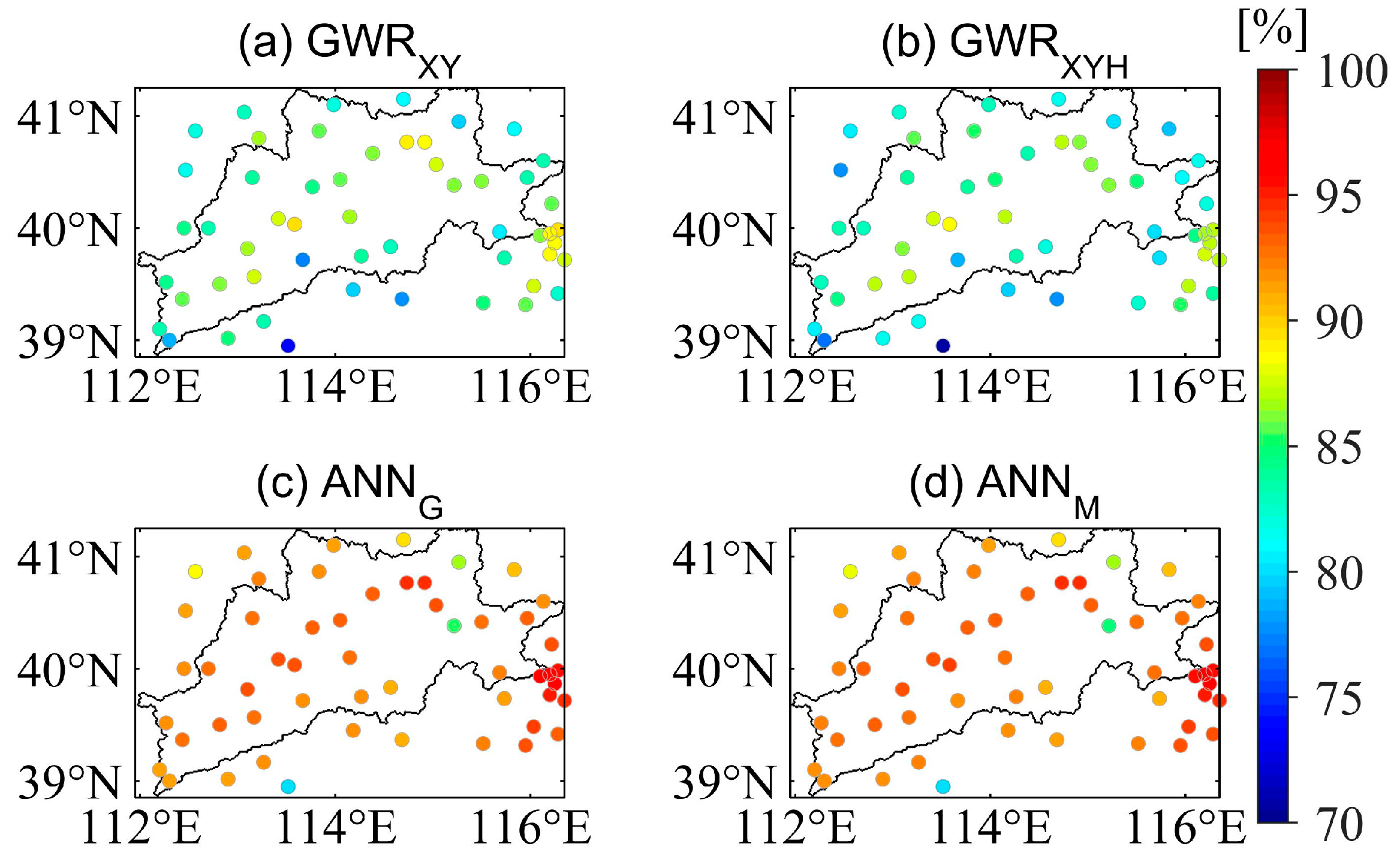
4.1. Accuracy of Precipitation Classification by the ANN Module
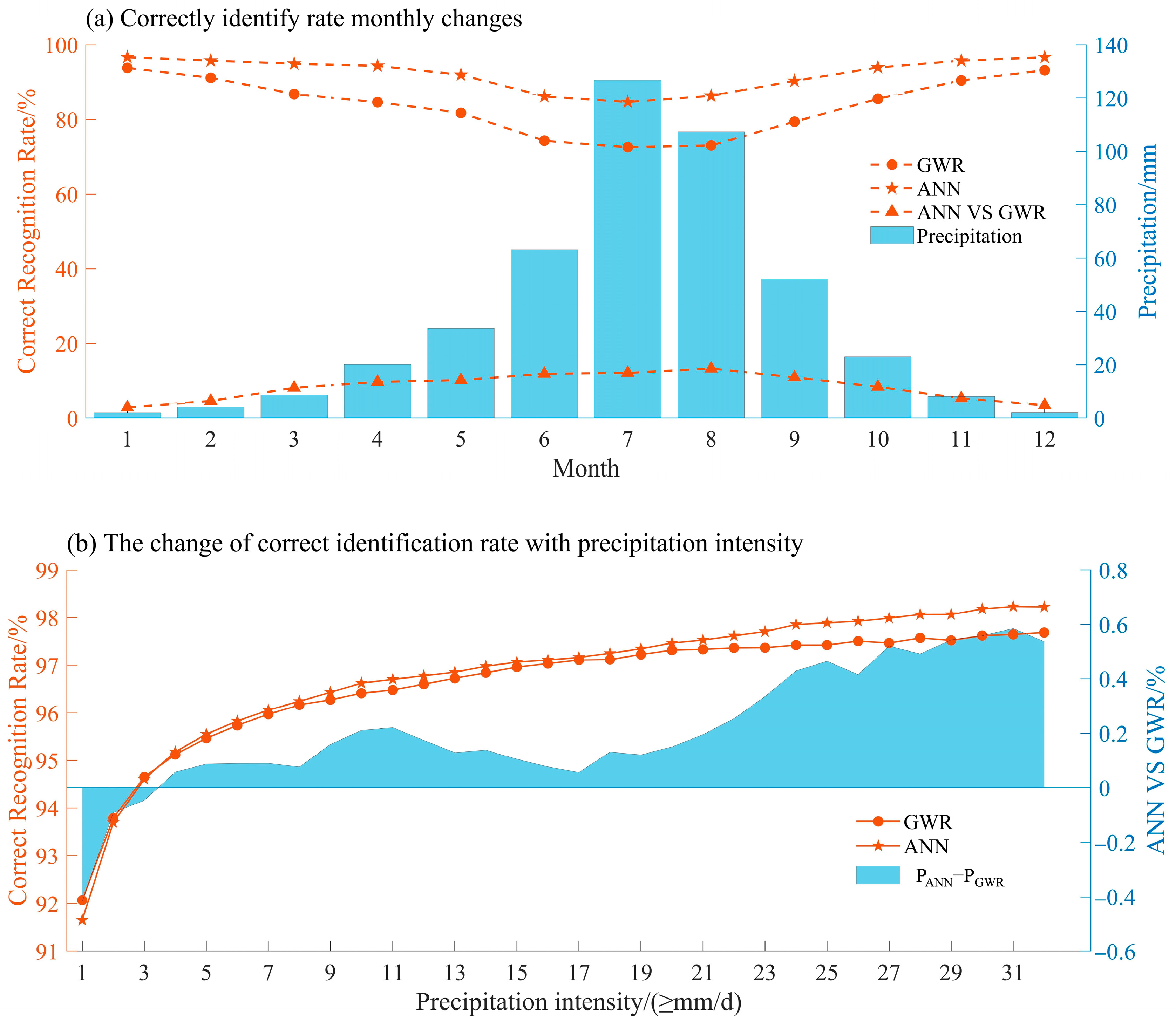
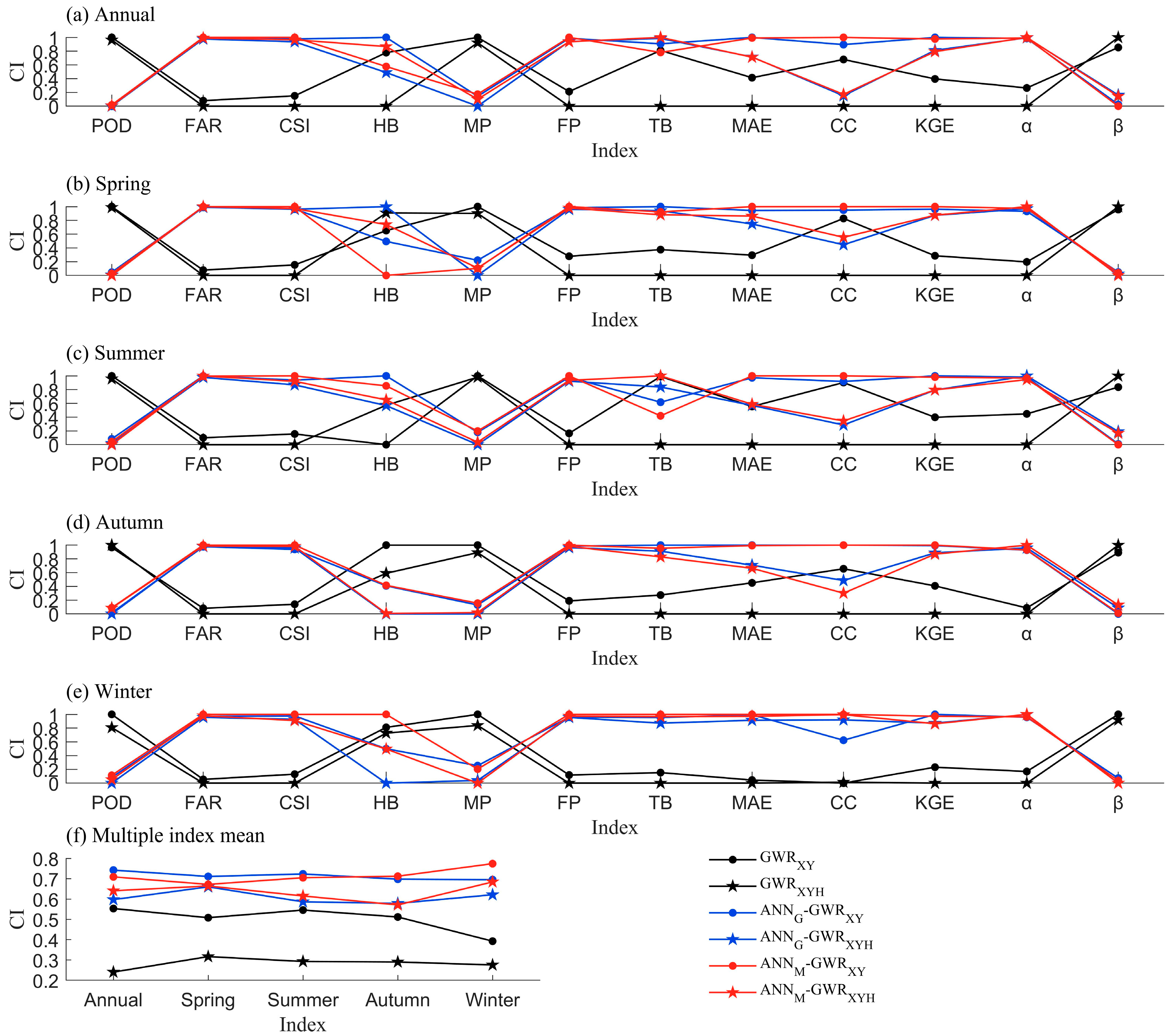
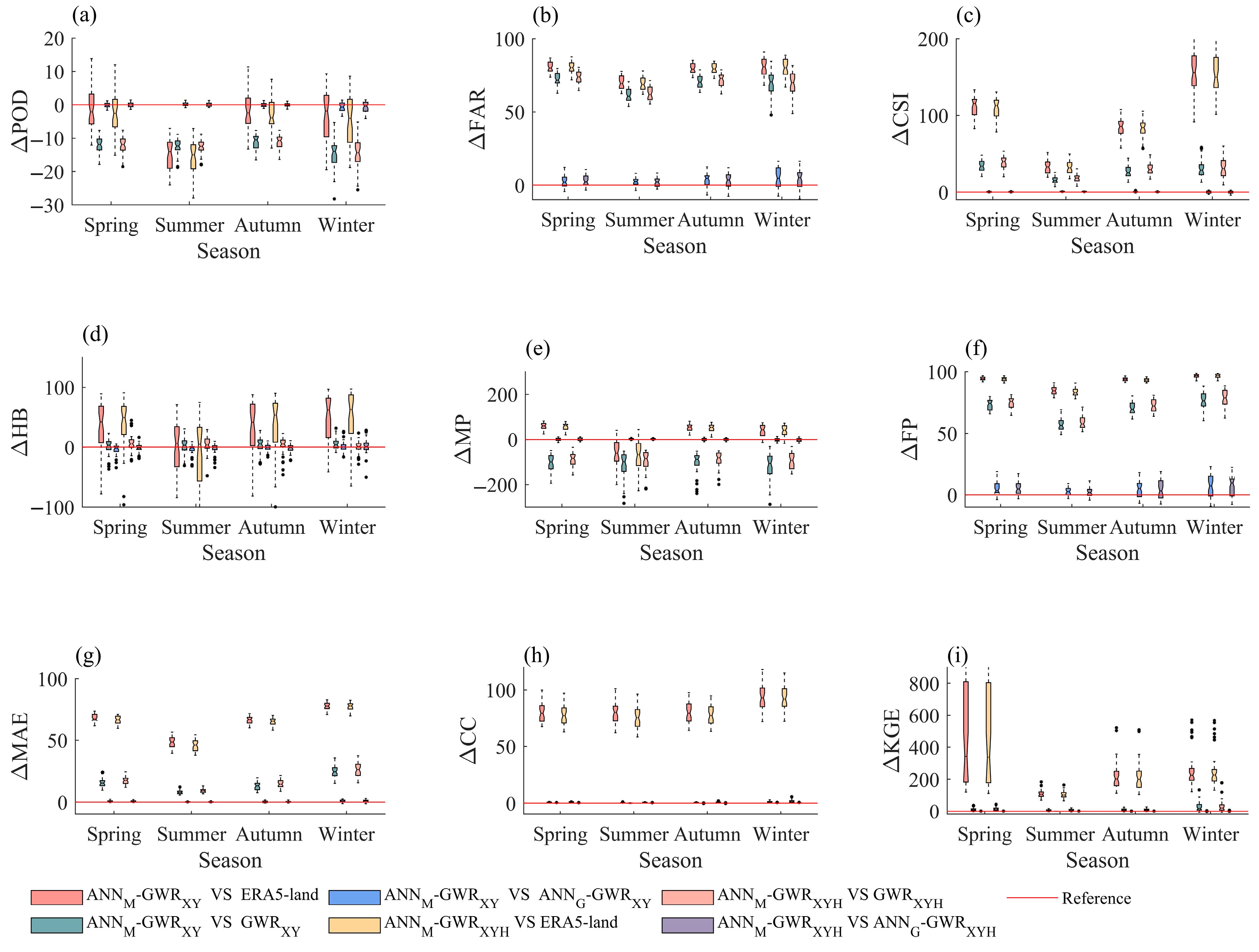
4.2. Gain of ANN–GWR Model Compared to GWR Model
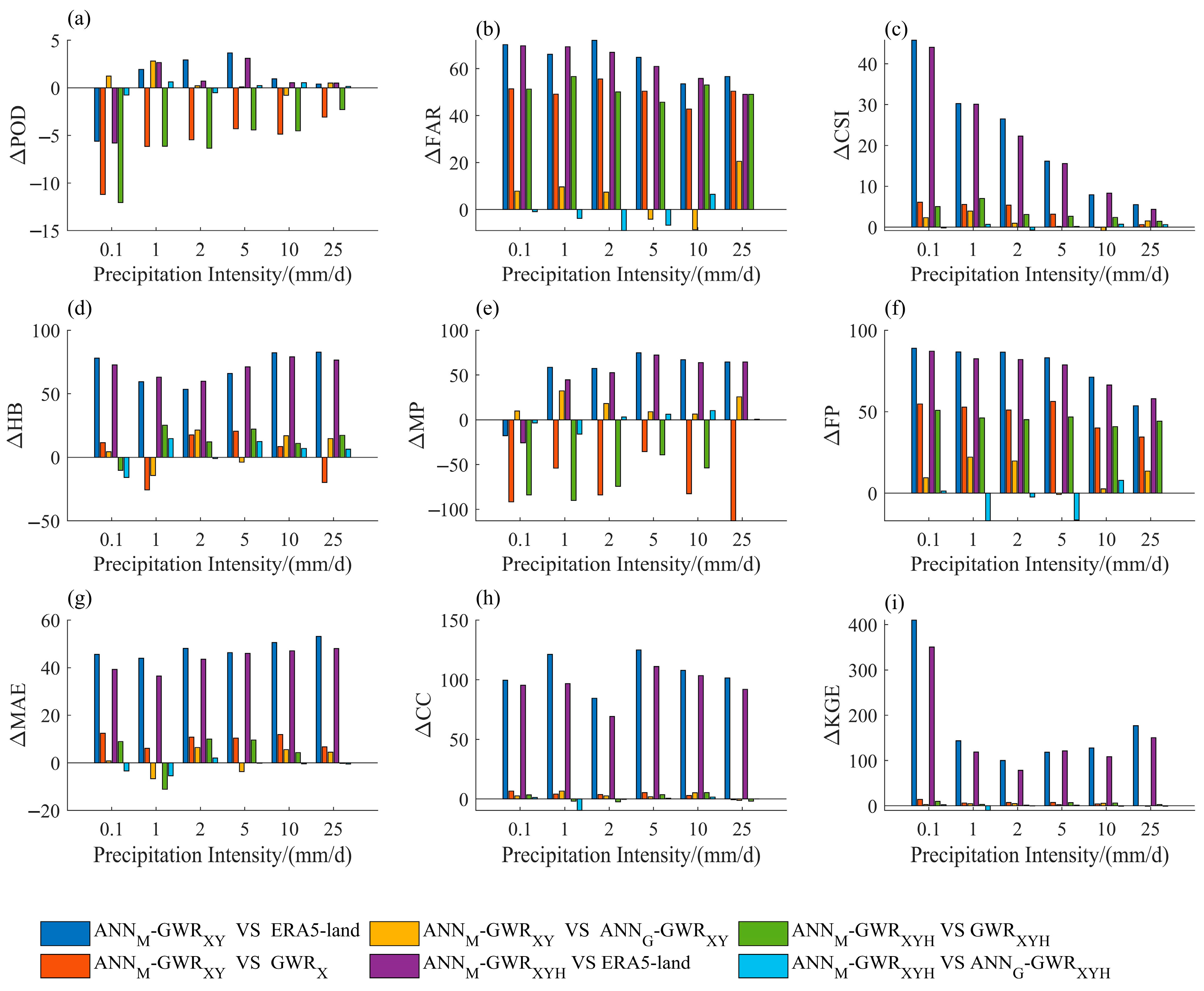
4.3. Model Gains Across Different Precipitation Intensities
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Libertino, A.; Sharma, A.; Lakshmi, V.; Claps, P. A global assessment of the timing of extreme rainfall from TRMM and GPM for improving hydrologic design. Environ. Res. Lett. 2016, 11, 054003. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Ma, M.; Liu, R.; Wen, Y.; Hong, Y. Can near-real-time satellite precipitation products capture rainstorms and guide flood warning for the 2016 summer in South China? IEEE Geosci. Remote Sens. Lett. 2017, 14, 1208–1212. [Google Scholar] [CrossRef]
- Fu, Y.; Xia, J.; Yuan, W.; Xu, B.; Wu, X.; Chen, Y.; Zhang, H. Assessment of multiple precipitation products over major river basins of China. Theor. Appl. Climatol. 2016, 123, 11–22. [Google Scholar] [CrossRef]
- Pereira, P.; Oliva, M.; Misiune, I. Spatial interpolation of precipitation indexes in Sierra Nevada (Spain): Comparing the performance of some interpolation methods. Theor. Appl. Climatol. 2016, 126, 683–698. [Google Scholar] [CrossRef]
- Antal, A.; Guerreiro, P.M.P.; Cheval, S. Comparison of spatial interpolation methods for estimating the precipitation distribution in Portugal. Theor. Appl. Climatol. 2021, 145, 1193–1206. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Pai, D.S.; AghaKouchak, A. From TRMM to GPM: How well can heavy rainfall be detected from space? Adv. Water Resour. 2016, 88, 1–7. [Google Scholar] [CrossRef]
- Shawky, M.; Moussa, A.; Hassan, Q.K.; El-Sheimy, N. Performance assessment of sub-daily and daily precipitation estimates derived from GPM and GSMaP products over an arid environment. Remote Sens. 2019, 11, 2840. [Google Scholar] [CrossRef]
- Mekonnen, K.; Melesse, A.M.; Woldesenbet, T.A. Spatial evaluation of satellite-retrieved extreme rainfall rates in the Upper Awash River Basin, Ethiopia. Atmos. Res. 2021, 249, 105297. [Google Scholar] [CrossRef]
- Hayashi, Y.; Tebakari, T.; Hashimoto, A. A Comparison Between Global Satellite Mapping of Precipitation Data and High-Resolution Radar Data–A Case Study of Localized Torrential Rainfall over Japan. J. Disaster Res. 2021, 16, 786–793. [Google Scholar] [CrossRef]
- Batista, F.F.; Rodrigues, D.T.; e Silva, C.M.S. Analysis of climatic extremes in the Parnaíba River Basin, Northeast Brazil, using GPM IMERG-V6 products. Weather. Clim. Extrem. 2024, 43, 100646. [Google Scholar] [CrossRef]
- Wang, Q.J.; Schepen, A.; Robertson, D.E. Merging seasonal rainfall forecasts from multiple statistical models through Bayesian model averaging. J. Clim. 2012, 25, 5524–5537. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J. A high spatiotemporal gauge-satellite merged precipitation analysis over China. J. Geophys. Res. Atmos. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Sideris, I.V.; Gabella, M.; Erdin, R.; Germann, U. Real-time radar–rain-gauge merging using spatio-temporal co-kriging with external drift in the alpine terrain of Switzerland. Q. J. R. Meteorol. Soc. 2014, 140, 1097–1111. [Google Scholar] [CrossRef]
- Huang, C.; Zheng, X.; Tait, A.; Dai, Y.; Yang, C.; Chen, Z.; Li, T.; Wang, Z. On using smoothing spline and residual correction to fuse rain gauge observations and remote sensing data. J. Hydrol. 2014, 508, 410–417. [Google Scholar] [CrossRef]
- Wu, H.; Yang, Q.; Liu, J.; Wang, G. A spatiotemporal deep fusion model for merging satellite and gauge precipitation in China. J. Hydrol. 2020, 584, 124664. [Google Scholar] [CrossRef]
- Chen, C.; He, M.; Chen, Q.; Zhang, J.; Li, Z.; Wang, Z.; Duan, Z. Triple collocation-based error estimation and data fusion of global gridded precipitation products over the Yangtze River basin. J. Hydrol. 2022, 605, 127307. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically weighted regression. J. R. Stat. Soc. Ser. D (Stat.) 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Dahamsheh, A.; Aksoy, H. Markov chain-incorporated artificial neural network models for forecasting monthly precipitation in arid regions. Arab. J. Sci. Eng. 2014, 39, 2513–2524. [Google Scholar] [CrossRef]
- Akbari Asanjan, A.; Yang, T.; Hsu, K.; Sorooshian, S.; Lin, J.; Peng, Q. Short-term precipitation forecast based on the PERSIANN system and LSTM recurrent neural networks. J. Geophys. Res. Atmos. 2018, 123, 12543–12563. [Google Scholar] [CrossRef]
- Nishant, N.; Hobeichi, S.; Sherwood, S.; Abramowitz, G.; Shao, Y.; Bishop, C.; Pitman, A. Comparison of a novel machine learning approach with dynamical downscaling for Australian precipitation. Environ. Res. Lett. 2023, 18, 094006. [Google Scholar] [CrossRef]
- Sadeghi, M.; Asanjan, A.A.; Faridzad, M.; Nguyen, P.; Hsu, K.; Sorooshian, S.; Braithwaite, D. PERSIANN-CNN: Precipitation estimation from remotely sensed information using artificial neural networks–convolutional neural networks. J. Hydrometeorol. 2019, 20, 2273–2289. [Google Scholar] [CrossRef]
- Grazzini, F.; Craig, G.C.; Keil, C.; Antolini, G.; Pavan, V. Extreme precipitation events over northern Italy. Part I: A systematic classification with machine-learning techniques. Q. J. R. Meteorol. Soc. 2020, 146, 69–85. [Google Scholar] [CrossRef]
- Sahoo, B.; Bhaskaran, P.K. Prediction of storm surge and coastal inundation using Artificial Neural Network–A case study for 1999 Odisha Super Cyclone. Weather. Clim. Extrem. 2019, 23, 100196. [Google Scholar] [CrossRef]
- Luo, C.; Li, X.; Ye, Y. PFST-LSTM: A spatiotemporal LSTM model with pseudoflow prediction for precipitation nowcasting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 843–857. [Google Scholar] [CrossRef]
- Boroughani, M.; Soltani, S.; Ghezelseflu, N.; Pazhouhan, I. A comparative assessment between artificial neural network, neuro-fuzzy, and support vector machine models in splash erosion modelling under simulation circumstances. Folia Oecologica 2022, 49, 23–34. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Li, C.; Li, Y.; Qi, H. Landslide susceptibility evaluation based on landslide classification and ANN-NFR modelling in the Three Gorges Reservoir area, China. Ecol. Indic. 2024, 160, 111920. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Ding, M.; Shen, Z.; Huang, R.; Liu, Y.; Wu, H. Cross-Validation Methods for Multisource Precipitation Datasets over the Sparse-Gauge Region: Applicability and Uncertainty. J. Hydrometeorol. 2024, 25, 1135–1145. [Google Scholar] [CrossRef]
- Tang, G.; Behrangi, A.; Long, D.; Li, C.; Hong, Y. Accounting for spatiotemporal errors of gauges: A critical step to evaluate gridded precipitation products. J. Hydrol. 2018, 559, 294–306. [Google Scholar] [CrossRef]
- Yu, C.; Hu, D.; Liu, M.; Wang, S.; Di, Y. Spatio-temporal accuracy evaluation of three high-resolution satellite precipitation products in China area. Atmos. Res. 2020, 241, 104952. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Eylander, J.B.; Joyce, R.J.; Huffman, G.J.; Adler, R.F.; Hsu, K.; Turk, F.J.; Garcia, M.; Zeng, J. Component analysis of errors in satellite-based precipitation estimates. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Yong, B.; Chen, B.; Tian, Y.; Yu, Z.; Hong, Y. Error-component analysis of TRMM-based multi-satellite precipitation estimates over mainland China. Remote Sens. 2016, 8, 440. [Google Scholar] [CrossRef]
- Vrugt, J.A. MODELAVG: A MATLAB toolbox for postprocessing of model ensembles. Dep. Civ. Environ. Eng. Univ. Calif. Irvine 2016, 4130. [Google Scholar]

| Type | Gain Calculation Formula | Applicable Indicators |
|---|---|---|
| Positive-oriented | POD,CSI,MP,CC,KGE | |
| Negative-oriented | FAR,FP,MAE | |
| Intermediate-optimal | HB,TB,α,β |
| Model | POD | FAR | CSI | HB | MP | FP | TB | MAE | CC | KGE | α | β |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GWRXY | 0.86 | 0.39 | 0.55 | −1.5 | −14.2 | 43.1 | 18.4 | 0.77 | 0.81 | 0.74 | 1.05 | 0.86 |
| GWRXYH | 0.86 | 0.41 | 0.53 | 4.6 | −15.5 | 50.4 | 31.1 | 0.82 | 0.80 | 0.72 | 1.08 | 0.84 |
| ANNG–GWRXY | 0.76 | 0.14 | 0.68 | −0.7 | −28.1 | 16.7 | −16.9 | 0.70 | 0.82 | 0.78 | 0.97 | 0.94 |
| ANNG–GWRXYH | 0.76 | 0.14 | 0.67 | 2.7 | −30.5 | 18.3 | −15.7 | 0.73 | 0.80 | 0.77 | 0.97 | 0.92 |
| ANNM–GWRXY | 0.76 | 0.14 | 0.68 | −2.3 | −27.6 | 16.2 | −18.9 | 0.70 | 0.82 | 0.78 | 0.97 | 0.94 |
| ANNM–GWRXYH | 0.76 | 0.14 | 0.68 | 1.2 | −28.8 | 18.4 | −15.4 | 0.73 | 0.80 | 0.77 | 0.96 | 0.92 |
| Type | Index Normalization Formula | Applicable Index |
|---|---|---|
| Forward type | POD,CSI,MP,CC,KGE | |
| Antiform | FAR,FP,MAE | |
| Intermediate-optimal type | HB,TB,α,β |
| Scheme | △POD | △FAR | △CSI | △HB | △MP | △FP | △TB | △MAE | △CC | △KGE | △α | △β |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ➀ | −8.9 | 75.7 | 71.0 | −1.6 | 10.9 | 89.3 | 80.1 | 56.3 | 68.9 | 127.3 | 80.4 | 70.4 |
| ➁ | −11.9 | 66.9 | 22.5 | 4.8 | −99.0 | 63.0 | 8.1 | 9.7 | 0.3 | 5.3 | 14.1 | 51.6 |
| ➂ | −0.1 | 2.7 | 0.4 | −1.1 | 0.9 | 3.4 | 1.4 | 0.2 | 0.0 | 0.0 | 1.4 | 0.4 |
| ➃ | −9.1 | 75.6 | 70.0 | −8.5 | 6.0 | 88.6 | 77.2 | 54.7 | 66.3 | 122.9 | 77.8 | 66.5 |
| ➄ | −12.0 | 68.0 | 27.3 | 3.8 | −88.7 | 64.0 | 43.1 | 11.3 | 0.5 | 6.5 | 43.9 | 51.9 |
| ➅ | −0.1 | 2.2 | 0.4 | 0.1 | 0.9 | 3.2 | 0.2 | 0.2 | 0.1 | 0.0 | 0.2 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, L.; Li, L.; Li, Y.; Wang, Y.; Su, X.; Li, X.; Wang, L.; Yao, F. A Hybrid ANN–GWR Model for High-Accuracy Precipitation Estimation. Remote Sens. 2025, 17, 2610. https://doi.org/10.3390/rs17152610
Zhang Y, Wang L, Li L, Li Y, Wang Y, Su X, Li X, Wang L, Yao F. A Hybrid ANN–GWR Model for High-Accuracy Precipitation Estimation. Remote Sensing. 2025; 17(15):2610. https://doi.org/10.3390/rs17152610
Chicago/Turabian StyleZhang, Ye, Leizhi Wang, Lingjie Li, Yilan Li, Yintang Wang, Xin Su, Xiting Li, Lulu Wang, and Fei Yao. 2025. "A Hybrid ANN–GWR Model for High-Accuracy Precipitation Estimation" Remote Sensing 17, no. 15: 2610. https://doi.org/10.3390/rs17152610
APA StyleZhang, Y., Wang, L., Li, L., Li, Y., Wang, Y., Su, X., Li, X., Wang, L., & Yao, F. (2025). A Hybrid ANN–GWR Model for High-Accuracy Precipitation Estimation. Remote Sensing, 17(15), 2610. https://doi.org/10.3390/rs17152610







