Evaluation and Improvement of Ocean Color Algorithms for Chlorophyll-a and Diffuse Attenuation Coefficients in the Arctic Shelf
Abstract
1. Introduction
2. Materials and Methods
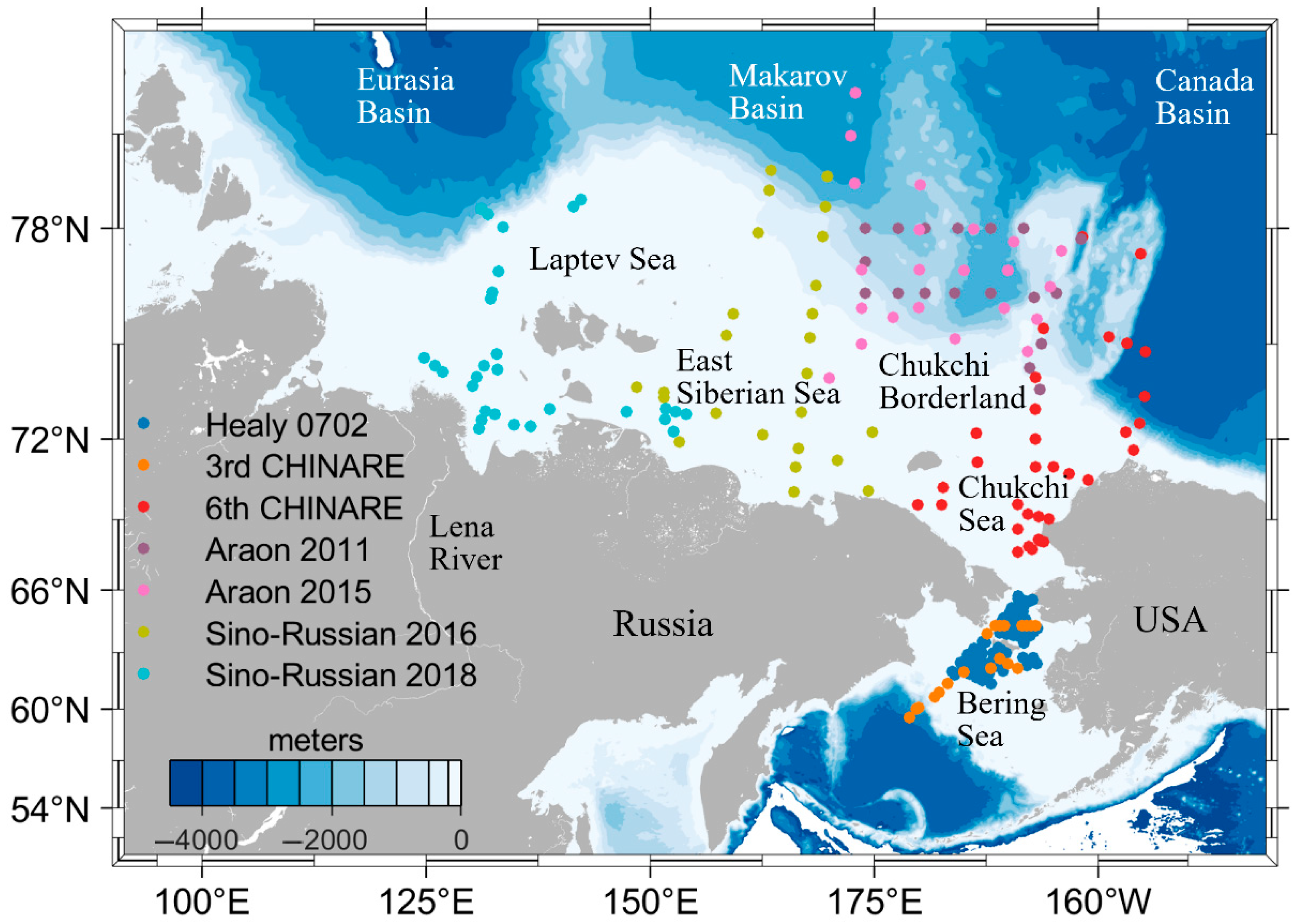
2.1. Study Area
2.2. In Situ Data
2.3. Satellite Data
2.4. Ocean Color Algorithms
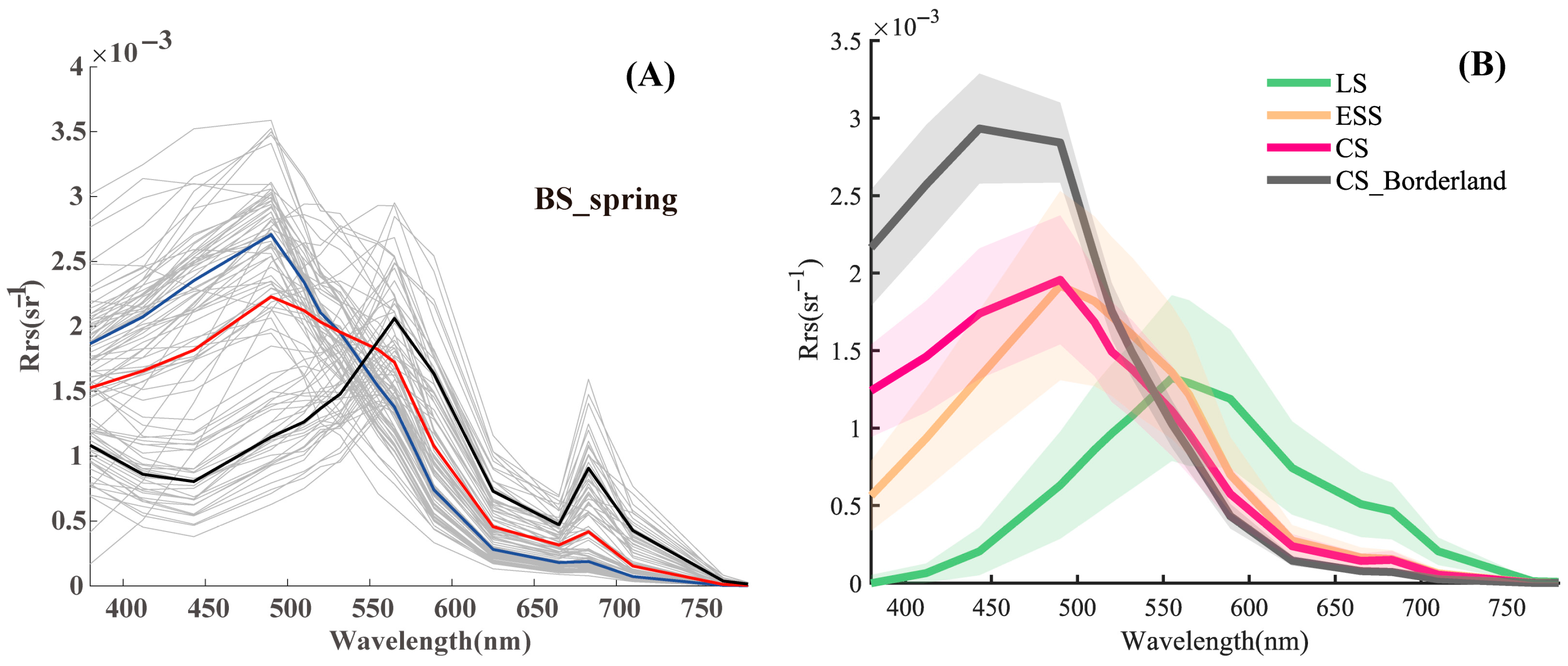
2.4.1. Remote Sensing Reflectance
2.4.2. Chl-a Algorithms
- I.
- Blue–green ratio algorithm OCx (Ocean Color X)
- II.
- Red light and NIR algorithms
2.4.3. Algorithms
- I.
- Direct Empirical Algorithms (-Direct). The empirical algorithm is the primary method currently used by satellite sensors to retrieve . The basic approach views as composed of two components: and [54]. refers to the total attenuation by biologically derived components, encompassing phytoplankton, associated microbes (e.g., viruses, bacteria), suspended particles, and CDOM:
- II.
- Indirect Empirical Algorithm (-Indirect). Morel and Maritorena [54] assumed that regional attenuation is primarily influenced by phytoplankton along with co-varying contributions from yellow substances and non-algal materials. Under this framework, a power-law function is commonly used to approximate the link between and Chl-a. Thus, a two-step empirical model relating , Chl-a, and can be constructed:
- III.
- Quasi-Analytical Algorithm (QAA). Quasi-analytical models are grounded in radiative transfer principles, linking the ocean’s apparent optical properties (AOPs) to its inherent optical properties (IOPs) and environmental boundary factors such as illumination geometry and surface conditions [58]. A crucial step in processing QAA is determining the absorption coefficient and the backscattering coefficient from . Once and along with the boundary conditions are known, can be calculated from the quasi-analytical model [23,59]. The contributions of and to attenuation are empirically quantified in the formula:
2.5. Evaluation Criteria
3. Results
3.1. Chlorophyll a
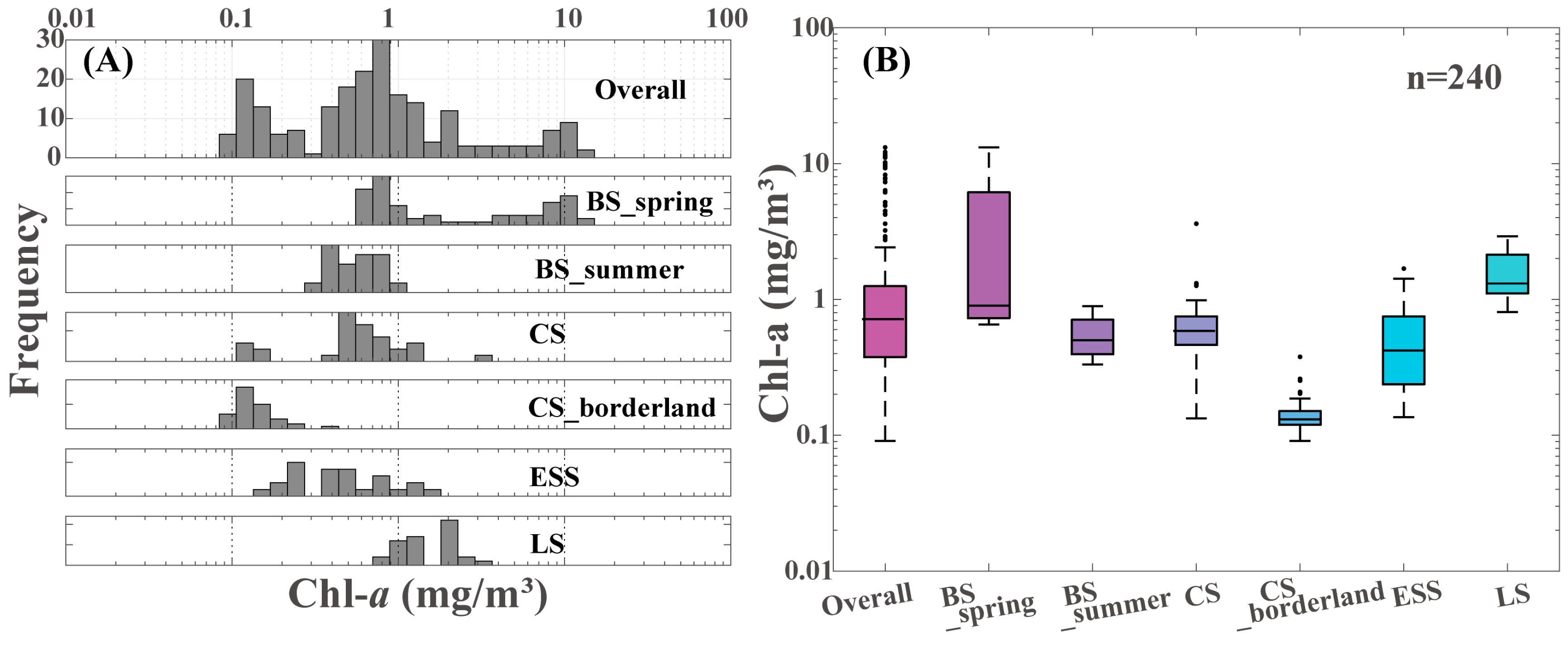
3.1.1. In Situ Observation of Chl-a Concentration
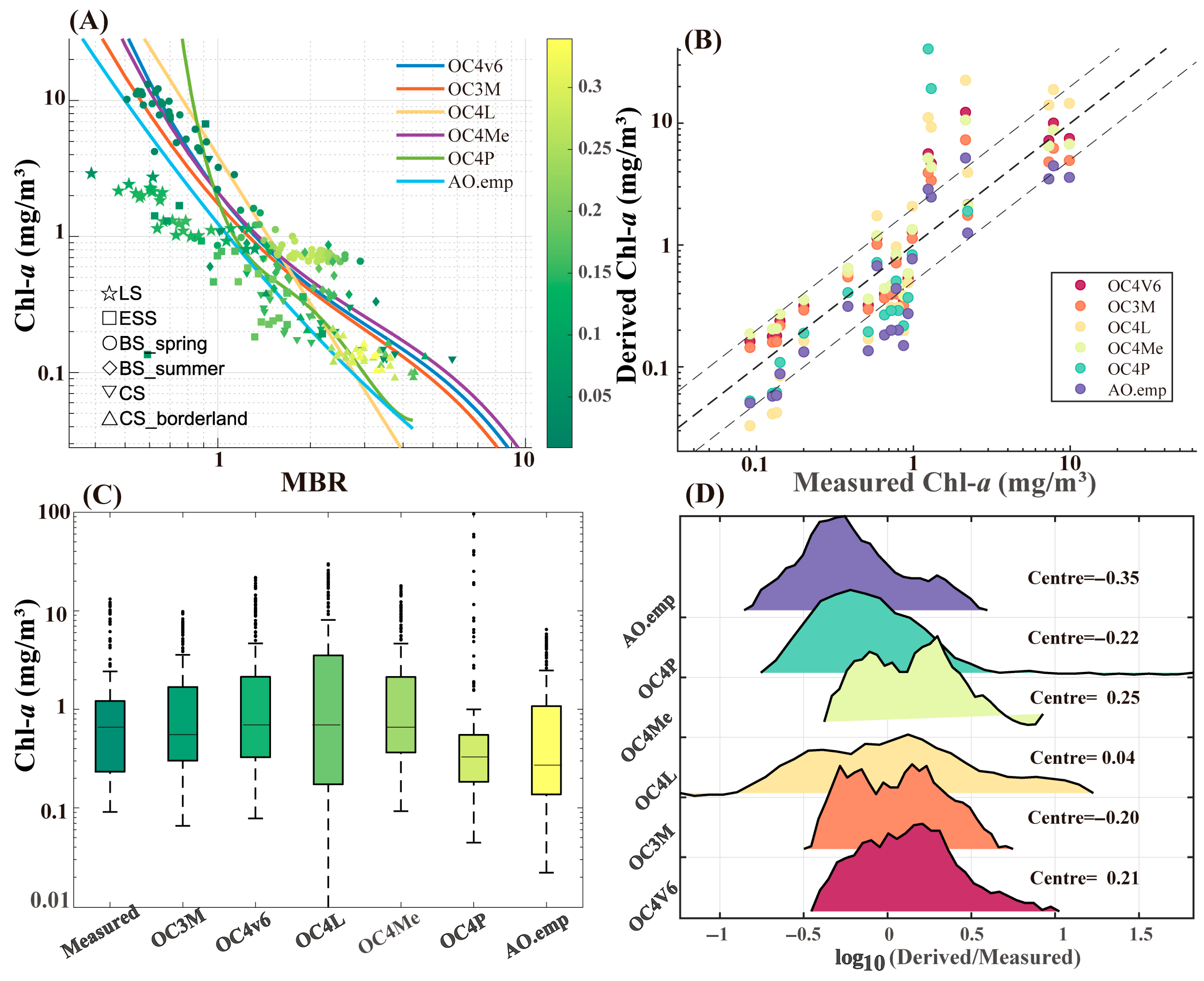
3.1.2. Evaluation of OCx Algorithms
3.1.3. Evaluation of NIR Algorithms
3.2. Diffuse Attenuation Coefficients
3.2.1. In Situ Observation of
3.2.2. Evaluation of the Empirical Algorithms for
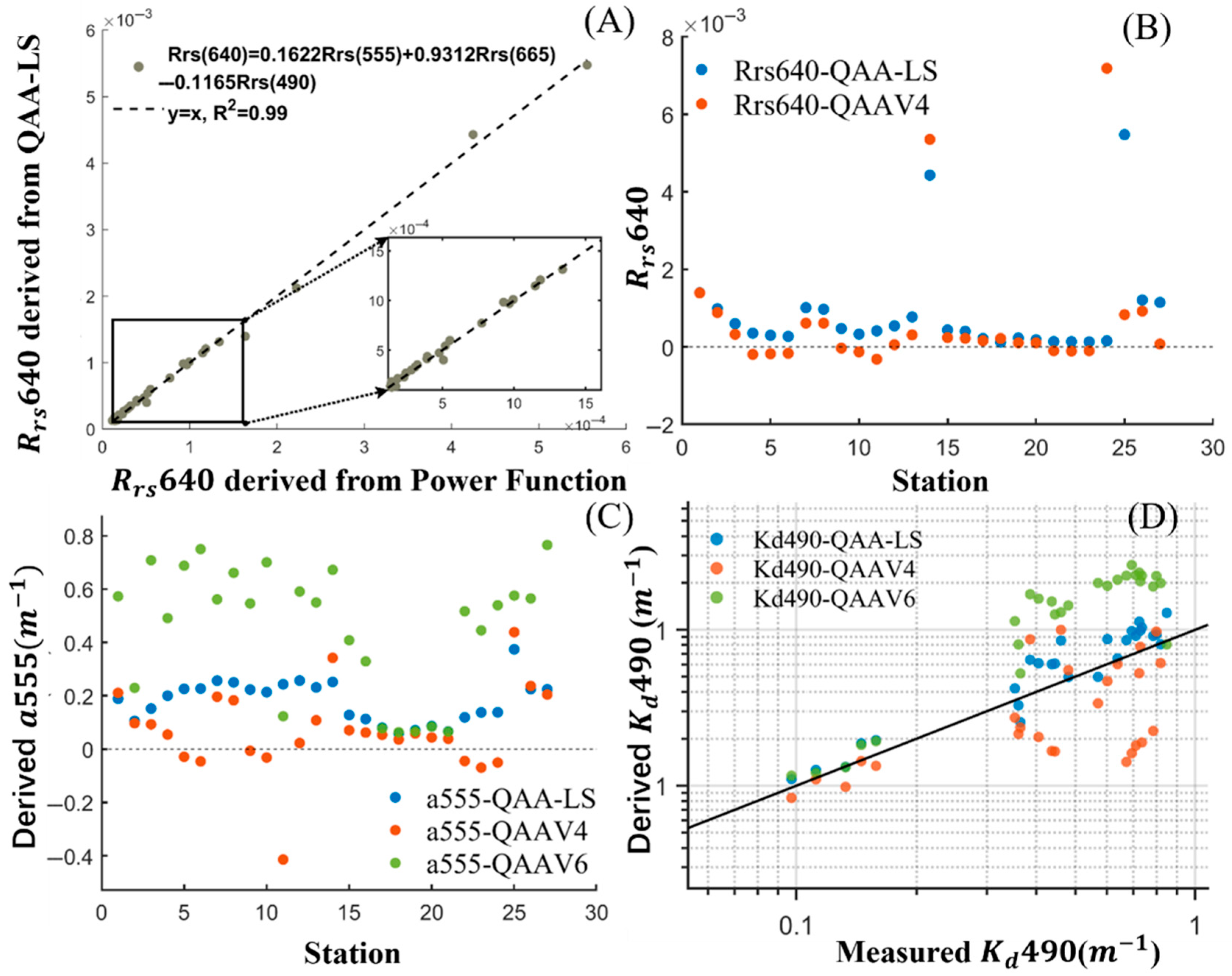
3.2.3. Evaluation of the QAA Algorithms
4. Discussion
4.1. Improvement of Algorithms
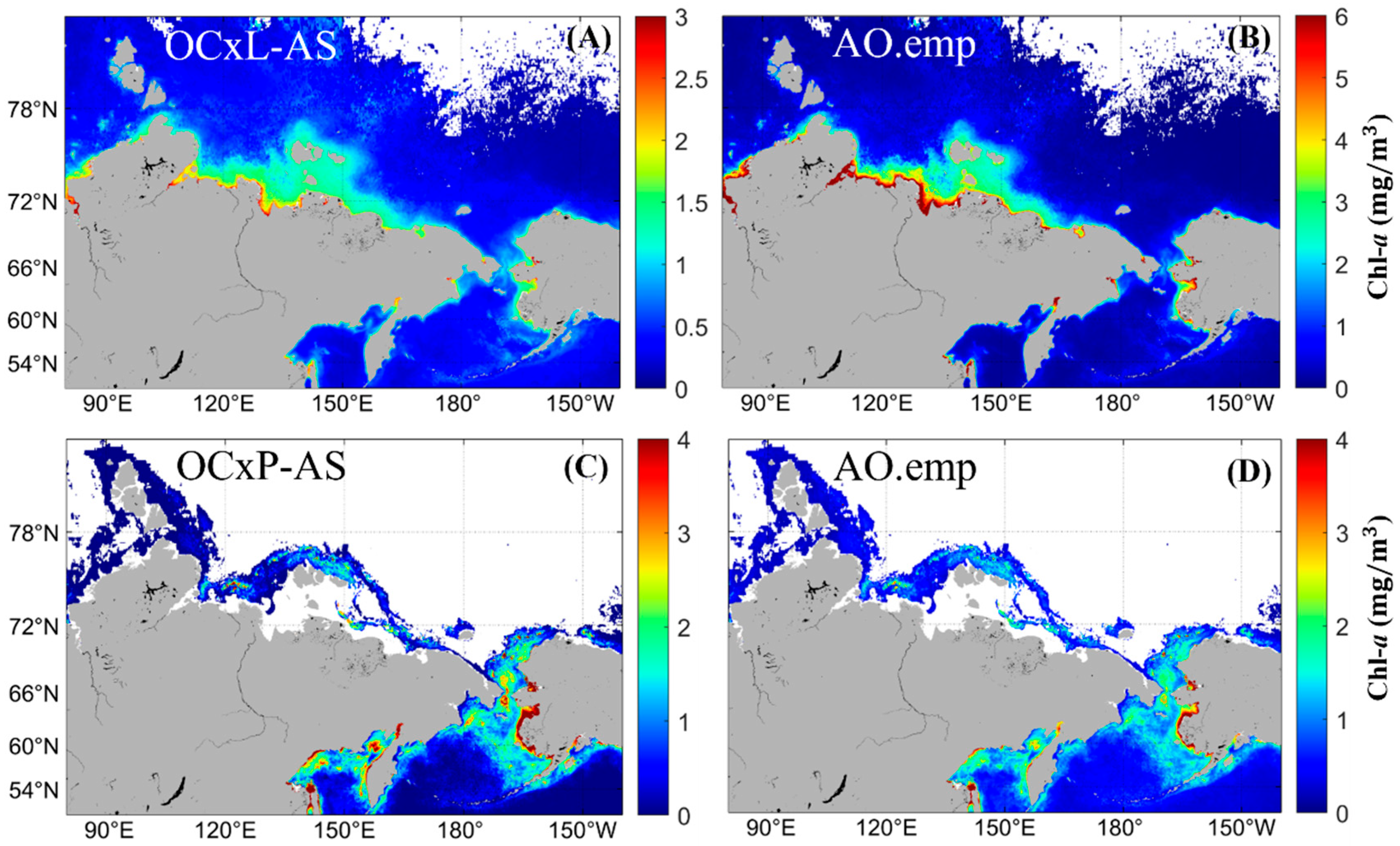
4.1.1. OCx Algorithms
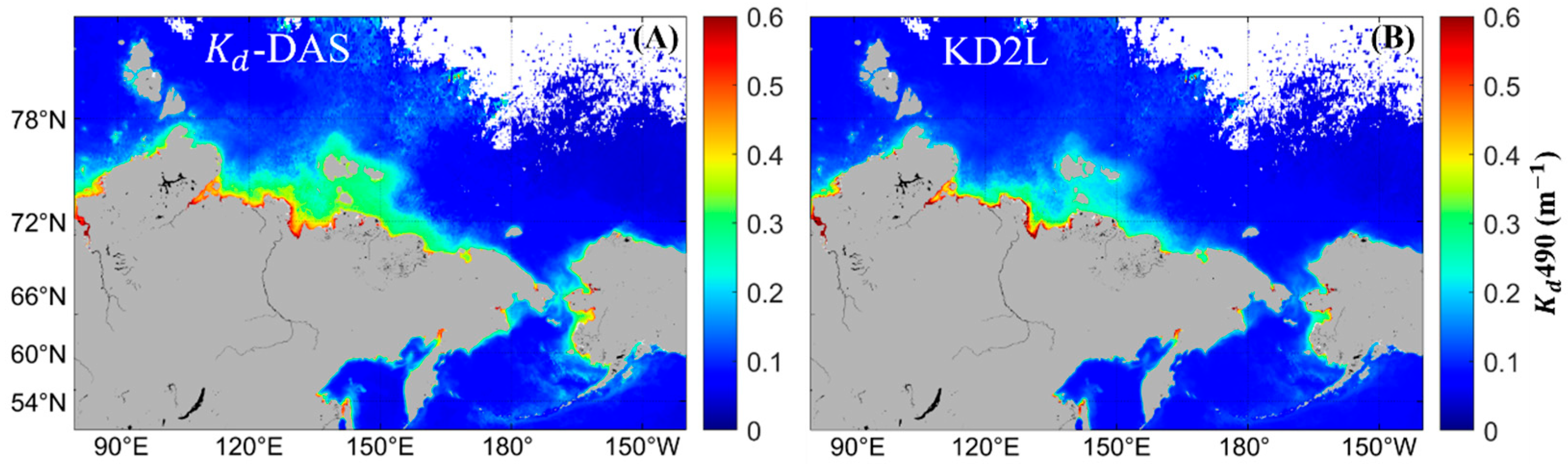
4.1.2. Empirical Algorithms for
4.1.3. QAA Algorithms for LS
4.2. Retrieval Scheme
4.2.1. Chl-a Retrieval Scheme for Arctic Shelf
4.2.2. Retrieval Scheme for Arctic Shelf
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| Absorption coefficient of the total | ||
| Absorption coefficient of colored dissolved organic matter (CDOM) and detritus | ||
| Absorption coefficient for pure water | ||
| Backscattering coefficient of the total | ||
| Backscattering coefficient of suspended particles | ||
| Backscattering coefficient of pure water | ||
| Chl-a | Concentration of chlorophyll-a | |
| Water-leaving radiance | ||
| Normalized Water-leaving radiance | ||
| Upwelling radiance | ||
| Downwelling irradiance | ||
| Downwelling irradiance just below the surface | ||
| Downwelling diffuse attenuation coefficient | ||
| Above-surface remote-sensing reflections | ||
| Below-surface remote-sensing reflections |
References
- Sledd, A.; L’Ecuyer, T.S. Emerging trends in Arctic solar absorption. Geophys. Res. Lett. 2021, 48, e2021GL095813. [Google Scholar] [CrossRef] [PubMed]
- AMAP. Impacts of Short-Lived Climate Forcers on Arctic Climate, Air Quality, and Human Health; Arctic Monitoring and Assessment Programme (AMAP): Tromsø, Norway, 2021. [Google Scholar]
- IPCC. Climate Change 2014 Synthesis Report; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2014. [Google Scholar]
- Stroeve, J.C.; Kattsov, V.; Barrett, A.; Serreze, M.; Pavlova, T.; Holland, M.; Meier, W.N. Trends in Arctic sea ice extent from CMIP5, CMIP3 and observations. Geophys. Res. Lett. 2012, 39, L16502. [Google Scholar] [CrossRef]
- Zhao, H.; Li, J.; WANG, Z.; Wang, X. CMIP6 Simulations of the Arctic Sea Ice and Their Ensemble Projection of Ice-Free Time in Boreal Summer. Adv. Mar. Sci. 2024, 42, 238–253. [Google Scholar] [CrossRef]
- Perovich, D.K.; Light, B.; Eicken, H.; Jones, K.F.; Runciman, K.; Nghiem, S.V. Increasing solar heating of the Arctic Ocean and adjacent seas, 1979–2005: Attribution and role in the ice-albedo feedback. Geophys. Res. Lett. 2007, 34, L19505. [Google Scholar] [CrossRef]
- Shimada, K.; Kamoshida, T.; Itoh, M.; Nishino, S.; Carmack, E.; McLaughlin, F.; Zimmermann, S.; Proshutinsky, A. Pacific Ocean inflow: Influence on catastrophic reduction of sea ice cover in the Arctic Ocean. Geophys. Res. Lett. 2006, 33, L08605. [Google Scholar] [CrossRef]
- Arndt, S.; Nicolaus, M. Seasonal cycle of solar energy fluxes through Arctic Sea ice. Cryosphere Discuss 2014, 8, 2923–2956. [Google Scholar] [CrossRef]
- Arrigo, K.R.; Van Dijken, G.L. Secular trends in Arctic Ocean net primary production. J. Geophys. Res. Oceans 2011, 116, C09011. [Google Scholar] [CrossRef]
- Arrigo, K.R.; Van Dijken, G.L. Continued increases in Arctic Ocean primary production. Prog. Oceanogr. 2015, 136, 60–70. [Google Scholar] [CrossRef]
- Pavlov, A.K.; Stedmon, C.A.; Semushin, A.V.; Martma, T.; Ivanov, B.V.; Kowalczuk, P.; Granskog, M.A. Linkages between the circulation and distribution of dissolved organic matter in the White Sea, Arctic Ocean. Cont. Shelf Res. 2016, 119, 1–13. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, X.; Xing, X.; Ishizaka, J.; Yu, Z. A Spectrally Selective Attenuation Mechanism-Based Kpar Algorithm for Biomass Heating Effect Simulation in the Open Ocean. J. Geophys. Res. Oceans 2017, 122, 9370–9386. [Google Scholar] [CrossRef]
- Ciavatta, S.; Brewin, R.; Skakala, J.; Sursham, D.; Ford, D. Assimilation of ocean colour to improve the simulation and understanding of the Northwest European shelf-sea ecosystem. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 23–28 April 2017; p. 18899. [Google Scholar]
- IOCCG. Ocean Colour Remote Sensing in Polar Seas; Babin, M., Arrigo, K., Bélanger, S., Forget, M.H., Eds.; International Ocean Colour Coordinating Group (IOCCG): Dartmouth, NS, Canada, 2015. [Google Scholar]
- Glukhovets, D.; Kopelevich, O.; Yushmanova, A.; Vazyulya, S.; Sheberstov, S.; Karalli, P.; Sahling, I. Evaluation of the CDOM absorption coefficient in the Arctic seas based on Sentinel-3 OLCI data. Remote Sens. 2020, 12, 3210. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; Siegel, D.A.; O Brien, M.C.; Toole, D.; Mitchell, B.G.; Kahru, M.; Chavez, F.P.; Strutton, P.; Cota, G.F. Ocean color chlorophyll a algorithm for SeaWiFS, OC2, and OC4: Version 4. SeaWiFS Postlaunch Calibration Valid. Anal. 2000, 11 Pt 3, 9–23. [Google Scholar]
- Werdell, P.J.; Bailey, S.W. An improved in-situ bio-optical data set for ocean color algorithm development and satellite data product validation. Remote Sens. Environ. 2005, 98, 122–140. [Google Scholar] [CrossRef]
- Vetrov, A.A.; Romankevich, E.A.; Belyaev, N.A. Chlorophyll, primary production, fluxes, and balance of organic carbon in the Laptev Sea. Geochem. Int. 2008, 46, 1055. [Google Scholar] [CrossRef]
- Morel, A.; Gentili, B.; Claustre, H.; Babin, M.; Bricaud, A.; Ras, J.; Tieche, F. Optical properties of the “clearest” natural waters. Limnol. Oceanogr. 2007, 52, 217–229. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W. The NIR-SWIR combined atmospheric correction approach for MODIS ocean color data processing. Opt. Express 2007, 15, 15722–15733. [Google Scholar] [CrossRef]
- Mustapha, S.B.; Belanger, S.; Larouche, P. Evaluation of ocean color algorithms in the southeastern Beaufort Sea, Canadian Arctic: New parameterization using SeaWiFS, MODIS, and MERIS spectral bands. Can. J. Remote Sens. 2012, 38, 535–556. [Google Scholar] [CrossRef]
- Cota, G.F.; Wang, J.; Comiso, J.C. Transformation of global satellite chlorophyll retrievals with a regionally tuned algorithm. Remote Sens. Environ. 2004, 90, 373–377. [Google Scholar] [CrossRef]
- Lee, Z.; Darecki, M.; Carder, K.L.; Davis, C.O.; Stramski, D.; Rhea, W.J. Diffuse attenuation coefficient of downwelling irradiance: An evaluation of remote sensing methods. J. Geophys. Res. Oceans 2005, 110, C02017. [Google Scholar] [CrossRef]
- Brunelle, C.B.; Larouche, P.; Gosselin, M. Variability of phytoplankton light absorption in Canadian Arctic seas. J. Geophys. Res. Oceans 2012, 117, C00G17. [Google Scholar] [CrossRef]
- Xing, X.; Boss, E.; Zhang, J.; Chai, F. Evaluation of ocean color remote sensing algorithms for diffuse attenuation coefficients and optical depths with data collected on BGC-Argo floats. Remote Sens. 2020, 12, 2367. [Google Scholar] [CrossRef]
- Wang, J.; Cota, G.F. Remote-sensing reflectance in the Beaufort and Chukchi seas: Observations and models. Appl. Opt. 2003, 42, 2754–2765. [Google Scholar] [CrossRef]
- Lewis, K.M.; Arrigo, K.R. Ocean color algorithms for estimating chlorophyll a, CDOM absorption, and particle backscattering in the Arctic Ocean. J. Geophys. Res. Oceans 2020, 125, e2019JC015706. [Google Scholar] [CrossRef]
- Grebmeier, J.M. Shifting patterns of life in the Pacific Arctic and sub-Arctic seas. Annu. Rev. Mar. Sci. 2012, 4, 63–78. [Google Scholar] [CrossRef]
- Woodgate, R.A.; Weingartner, T.; Lindsay, R. The 2007 Bering Strait oceanic heat flux and anomalous Arctic sea-ice retreat. Geophys. Res. Lett. 2010, 37, L01602. [Google Scholar] [CrossRef]
- Serreze, M.C.; Francis, J.A. The Arctic amplification debate. Clim. Change 2006, 76, 241–264. [Google Scholar] [CrossRef]
- Walsh, J.J.; Dieterle, D.A.; Maslowski, W.; Grebmeier, J.M.; Whitledge, T.E.; Flint, M.; Sukhanova, I.N.; Bates, N.; Cota, G.F.; Stockwell, D. A numerical model of seasonal primary production within the Chukchi/Beaufort Seas. Deep Sea Res. Part II 2005, 52, 3541–3576. [Google Scholar] [CrossRef]
- Bauch, D.; Hölemann, J.; Willmes, S.; Gröger, M.; Novikhin, A.; Nikulina, A.; Kassens, H.; Timokhov, L. Changes in distribution of brine waters on the Laptev Sea shelf in 2007. J. Geophys. Res. Oceans 2010, 115, C11008. [Google Scholar] [CrossRef]
- Coachman, L.K.; Aagaard, K.; Tripp, R.B. Bering Strait: The Regional Physical Oceanography; University of Washington Press: Seattle, WA, USA, 1995. [Google Scholar]
- Weingartner, T.J.; Danielson, S.; Sasaki, Y.; Pavlov, V.; Kulakov, M. The Siberian Coastal Current: A wind-and buoyancy-forced Arctic coastal current. J. Geophys. Res. Oceans 1999, 104, 29697–29713. [Google Scholar] [CrossRef]
- Semiletov, I.; Dudarev, O.; Luchin, V.; Charkin, A.; Shin, K.H.; Tanaka, N. The East Siberian Sea as a transition zone between Pacific-derived waters and Arctic shelf waters. Geophys. Res. Lett. 2005, 32, L10614-1. [Google Scholar] [CrossRef]
- Mueller, J.L.; Morel, A.; Frouin, R.; Davis, C.; Voss, K. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 4; Goddard Space Flight Space Centre: Greenbelt, MD, USA, 2003; Volume 3, pp. 7–19. [Google Scholar] [CrossRef]
- Morel, A.; Huot, Y.; Gentili, B.; Werdell, P.J.; Hooker, S.B.; Franz, B.A. Examining the consistency of products derived from various ocean color sensors in open ocean (Case 1) waters in the perspective of a multi-sensor approach. Remote Sens. Environ. 2007, 111, 69–88. [Google Scholar] [CrossRef]
- Ibrahim, A.; Franz, B.A.; Ahmad, Z.; Bailey, S.W. Multiband atmospheric correction algorithm for ocean color retrievals. Front. Earth Sci. 2019, 7, 116. [Google Scholar] [CrossRef]
- Bailey, S.W.; Werdell, P.J. A multi-sensor approach for the on-orbit validation of ocean color satellite data products. Remote Sens. Environ. 2006, 102, 12–23. [Google Scholar] [CrossRef]
- Volpe, G.; Colella, S.; Brando, V.E.; Forneris, V.; La Padula, F.; Di Cicco, A.; Sammartino, M.; Bracaglia, M.; Artuso, F.; Santoleri, R. Mediterranean ocean colour Level 3 operational multi-sensor processing. Ocean Sci. 2019, 15, 127–146. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. Oceans 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Werdell, P.J. Chlorophyll algorithms for ocean color sensors-OC4, OC5 & OC6. Remote Sens. Environ. 2019, 229, 32–47. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Gurlin, D.; Moses, W.J.; Barrow, T. A bio-optical algorithm for the remote estimation of the chlorophyll-a concentration in case2 waters. Environ. Res. Lett. 2009, 4, 45003. [Google Scholar] [CrossRef]
- Xu, J.P.; Li, F.; Zhang, B.; Song, K.S.; Wang, Z.M.; Liu, D.W.; Zhang, G.X. Improved conceptual three-band model for Chlorophyll-a retrieval in inland Case-II waters. In Geoinformatics 2008 and Joint Conference on GIS and Built Environment: Monitoring and Assessment of Natural Resources and Environments; SPIE: Bellingham, WA, USA, 2008; pp. 522–529. [Google Scholar]
- Gupta, R.K.; Prasad, S.; Nadham, T.; Rao, G.H. Relative sensitivity of district mean RVI and NDVI over an agrometeorological zone. Adv. Space Res. 1993, 13, 261–264. [Google Scholar] [CrossRef]
- Zhang, J.; Li, M.; Sun, Z.; Liu, H.; Sun, H.; Yang, W. Chlorophyll content detection of field maize using RGB-NIR camera. IFAC-PapersOnline 2018, 51, 700–705. [Google Scholar] [CrossRef]
- Dall Olmo, G.; Gitelson, A.A. Effect of bio-optical parameter variability on the remote estimation of chlorophyll-a concentration in turbid productive waters: Experimental results. Appl. Opt. 2005, 44, 412–422. [Google Scholar] [CrossRef]
- Song, K.; Li, L.; Tedesco, L.P.; Li, S.; Duan, H.; Liu, D.; Hall, B.E.; Du, J.; Li, Z.; Shi, K. Remote estimation of chlorophyll-a in turbid inland waters: Three-band model versus GA-PLS model. Remote Sens. Environ. 2013, 136, 342–357. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Yu, G.; Oyama, Y.; Yoshimura, K.; Fukushima, T. A hybrid algorithm for estimating the chlorophyll-a concentration across different trophic states in Asian inland waters. ISPRS-J. Photogramm. Remote Sens. 2015, 102, 28–37. [Google Scholar] [CrossRef]
- Hu, C.; Feng, L.; Lee, Z.; Franz, B.A.; Bailey, S.W.; Werdell, P.J.; Proctor, C.W. Improving satellite global chlorophyll a data products through algorithm refinement and data recovery. J. Geophys. Res. Oceans 2019, 124, 1524–1543. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Povazhnyy, V. Estimation of chlorophyll-a concentration in case II waters using MODIS and MERISdata—Successes and challenges. Environ. Res. Lett. 2009, 4, 45005. [Google Scholar] [CrossRef]
- Gilerson, A.A.; Gitelson, A.A.; Zhou, J.; Gurlin, D.; Moses, W.; Ioannou, I.; Ahmed, S.A. Algorithms for remote estimation of chlorophyll-a in coastal and inland waters using red and near infrared bands. Opt. Express 2010, 18, 24109–24125. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Gurlin, D.; Moses, W.J.; Yacobi, Y.Z. Remote Estimation of Chlorophyll-a Concentration in Inland, Estuarine, and Coastal Waters; Taylor and Francis Group: Boca Raton, FL, USA, 2001; pp. 449–478. [Google Scholar]
- Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. Oceans 2001, 106, 7163–7180. [Google Scholar] [CrossRef]
- Austin, R.W.; Petzold, T.J. Spectral dependence of the diffuse attenuation coefficient of light in ocean waters. Opt. Eng. 1986, 25, 471–479. [Google Scholar] [CrossRef]
- Mueller, J.L. SeaWiFS algorithm for the diffuse attenuation coefficient, K (490), using water-leaving radiances at 490 and 555 nm. SeaWiFS Postlaunch Calibration Valid. Anal. 2000, 3 Pt 3, 24–27. [Google Scholar]
- Yao, Y.; Li, T.; Zhu, X.; Wang, X. Characteristics of water masses and bio-optical properties of the Bering Sea shelf during 2007–2009. Acta Oceanol. Sin. 2022, 41, 140–153. [Google Scholar] [CrossRef]
- Gordon, H.R.; McCluney, W.R. Estimation of the depth of sunlight penetration in the sea for remote sensing. Appl. Opt. 1975, 14, 413–416. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Morel, A. Optical properties of pure water and pure seawater. Opt. Asp. Oceanogr. 1974, 1, 1–24. [Google Scholar]
- Twardowski, M.S.; Claustre, H.; Freeman, S.A.; Stramski, D.; Huot, Y. Optical backscattering properties of the” clearest” natural waters. Biogeosciences 2007, 4, 1041–1058. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, W.; Kang, S.; Yang, E.; Kim, T. Optical properties in waters around the Mendeleev Ridge related to the physical features of water masses. Deep Sea Res. Part II 2015, 120, 43–51. [Google Scholar] [CrossRef]
- Holmes, R.M.; McClelland, J.W.; Peterson, B.J.; Tank, S.E.; Bulygina, E.; Eglinton, T.I.; Gordeev, V.V.; Gurtovaya, T.Y.; Raymond, P.A.; Repeta, D.J. Seasonal and annual fluxes of nutrients and organic matter from large rivers to the Arctic Ocean and surrounding seas. Estuaries Coasts 2012, 35, 369–382. [Google Scholar] [CrossRef]
- Demidov, A.B.; Gagarin, V.I.; Arashkevich, E.G.; Makkaveev, P.N.; Konyukhov, I.V.; Vorobieva, O.V.; Fedorov, A.V. Spatial variability of primary production and chlorophyll in the Laptev Sea in August–September. Russ. Acad. Sci. Oceanol. 2019, 59, 678–691. [Google Scholar] [CrossRef]
- Cota, G.F.; Pomeroy, L.R.; Harrison, W.G.; Jones, E.P.; Peters, F.; Sheldon Jr, W.M.; Weingartner, T.R. Nutrients, primary production and microbial heterotrophy in the southeastern Chukchi Sea: Arctic summer nutrient depletion and heterotrophy. Mar. Ecol. Prog. Ser. 1996, 135, 247–258. [Google Scholar] [CrossRef]
- Drozdova, A.N.; Nedospasov, A.A.; Lobus, N.V.; Patsaeva, S.V.; Shchuka, S.A. CDOM optical properties and DOC content in the largest mixing zones of the Siberian shelf seas. Remote Sens. 2021, 13, 1145. [Google Scholar] [CrossRef]
- Matsuoka, A.; Larouche, P.; Poulin, M.; Vincent, W.; Hattori, H. Phytoplankton community adaptation to changing light levels in the southern Beaufort Sea, Canadian Arctic. Estuar. Coast. Shelf Sci. 2009, 82, 537–546. [Google Scholar] [CrossRef]
- Belanger, S.; Babin, M.; Larouche, P. An empirical ocean color algorithm for estimating the contribution of chromophoric dissolved organic matter to total light absorption in optically complex waters. J. Geophys. Res. Oceans 2008, 113, C04027. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Lee, Z.; Weidemann, A.; Kindle, J.; Arnone, R.; Carder, K.L.; Davis, C. Euphotic zone depth: Its derivation and implication to ocean-color remote sensing. J. Geophys. Res. Oceans 2007, 112, C03009. [Google Scholar] [CrossRef]
- Lee, Z.; Lubac, B.; Werdell, J.; Arnone, R. Update of the Quasi-Analytical Algorithm (QAA_v6). 2014. Available online: https://www.ioccg.org/groups/Software_OCA/QAA_v6_2014209.pdf (accessed on 17 March 2025).
- Wang, M.; Son, S. VIIRS-derived chlorophyll-a using the ocean color index method. Remote Sens. Environ. 2016, 182, 141–149. [Google Scholar] [CrossRef]
- Martini, K.I.; Stabeno, P.J.; Ladd, C.; Winsor, P.; Weingartner, T.J.; Mordy, C.W.; Eisner, L.B. Dependence of subsurface chlorophyll on seasonal water masses in the Chukchi Sea. J. Geophys. Res. Oceans 2016, 121, 1755–1770. [Google Scholar] [CrossRef]
- Eisner, L.B.; Gann, J.C.; Ladd, C.; Cieciel, K.D.; Mordy, C.W. Late summer/early fall phytoplankton biomass (chlorophyll a) in the eastern Bering Sea: Spatial and temporal variations and factors affecting chlorophyll a concentrations. Deep Sea Res. Part II 2016, 134, 100–114. [Google Scholar] [CrossRef]
- Welschmeyer, N.A. Fluorometric Analysis of Chlorophyll a in the Presence of Chlorophyll b and Pheopigments. Limnol. Oceanogr. 1994, 39, 1985–1992. [Google Scholar] [CrossRef]
- Zhu, X.; Li, T.; Cooper, L.W.; Yang, E.J.; Jung, J.; Cho, K.; Yao, Y.; Tang, Y. Bio-optical properties and radiant heating rates in the borderlands region of the Chukchi Sea: The roles of phytoplankton biomass and sea ice cover. Deep Sea Res. 2025, 218 Pt 1, 104458. [Google Scholar] [CrossRef]
- Wang, M.; Son, S.; Harding, L.W. Retrieval of diffuse attenuation coefficient in the Chesapeake Bay and turbid ocean regions for satellite ocean color applications. J. Geophys. Res. Oceans 2009, 114, C10011. [Google Scholar] [CrossRef]


| Algorithm | References | ||
|---|---|---|---|
| OC4v6 (SeaWiFS) | [0.327, −2.994, 2.721, −1.225, −0.568] | [16,41,42] | |
| OC3M (MODIS) | [0.242, −2.582, 1.705, −0.341, −0.881] | ||
| OC4Me (MERIS& OLCI) | [0.325, −2.767, 2.44, −1.128, −0.499] | [42] | |
| OC4L (Regional) | [0.592, −3.607] | [26] | |
| OC4P (Regional) | [0.271, −6.278, 26.29, −60.94, 45.31] | [22] | |
| AO.emp (Regional) | [0.0957, −2.7973, 0.6581] | [27] |
| Algorithm | Formula | Reference |
|---|---|---|
| RVI | [45] | |
| DVI | [46] | |
| NDVI | ||
| TBM | [48] | |
| MCI | [49] | |
| CI | [50] | |
| Meris Two-band | [51] | |
| Meris Three-band |
| Algorithm | ||
|---|---|---|
| KD2S (SeaWiFS) | [−0.8515, −1.8263, 1.8714, −2.4414, −1.0690] | / |
| KD2M (MODIS) | [−0.8813, −2.0584, 2.5878, −3.4885, −1.5061] | / |
| KD2E (MERIS) | [−0.8641, −1.6549, 2.0112, −2.5174, −1.1035] | / |
| KD2L (OLI & Landsat 8) | [−0.9054, −1.5245, 2.2392, −2.4777, −1.1099] | / |
| Region | MLD (m) | ) | ||
|---|---|---|---|---|
| Maximum | Average | Minimum | ||
| BS_spring | 7.90 ± 3.39 | 13.17 | 3.40 ± 3.88 | 0.65 |
| BS_summer | 3.84 ± 0.97 | 0.89 | 0.56 ± 0.19 | 0.33 |
| CS | 4.59 ± 2.67 | 3.61 | 0.68 ± 0.61 | 0.13 |
| CS_borderland | 10 (default) | 0.38 | 0.15 ± 0.05 | 0.09 |
| ESS | 7.06 ± 3.35 | 1.69 | 0.56 ± 0.41 | 0.14 |
| LS | 6.17 ± 2.33 | 2.91 | 1.63 ± 0.62 | 0.81 |
| Overall | \ | 13.17 | 1.66 ± 2.71 | 0.09 |
| Algorithm | Average | Std | Median | Maximum | Mean Derived/Measured |
|---|---|---|---|---|---|
| Measured | 1.66 | 2.71 | 0.30 | 13.17 | |
| OC4v6 | 2.73 | 4.64 | 0.61 | 21.76 | 2.10 |
| OC3M | 1.62 | 2.31 | 0.55 | 9.80 | 1.68 |
| OC4Me | 2.47 | 3.92 | 0.66 | 17.94 | 2.19 |
| OC4L | 3.88 | 6.91 | 0.60 | 29.90 | 2.88 |
| OC4P | 2.83 | 10.77 | 0.33 | 95.97 | 2.92 |
| AO.emp | 1.02 | 1.53 | 0.31 | 6.47 | 0.87 |
| Algorithm | RMSE | MAE | MAPE (%) |
|---|---|---|---|
| OC4v6 | 3.45 | 1.48 | 110.8 |
| OC3M | 1.76 | 0.94 | 76.4 |
| OC4Me | 2.81 | 1.29 | 108.4 |
| OC4L | 5.84 | 2.66 | 171.8 |
| OC4P | 10.56 | 2.47 | 191.5 |
| AO.emp | 1.69 | 0.89 | 59.8 |
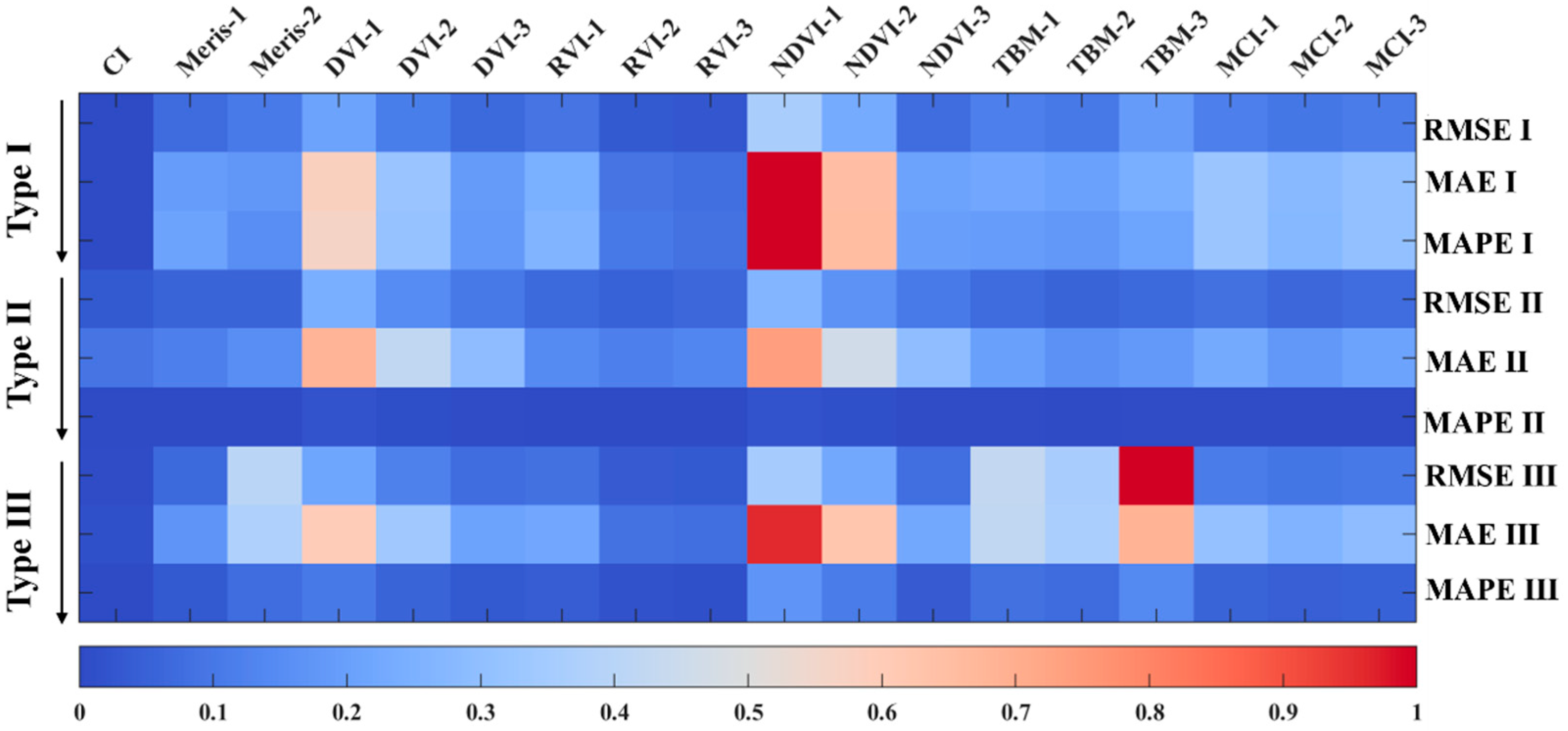
| CI | Meris | DVI | RVI | NDVI | TBM | MCI | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Two-Band | Three-Band | L | POW | POL | L | POW | POL | L | POW | POL | L | POW | POL | L | POW | POL | ||
| Type I | ||||||||||||||||||
| RMSE | 0.42 | 16.42 | 24.03 | 47.06 | 26.30 | 15.70 | 20.92 | 8.24 | 7.06 | 81.11 | 52.58 | 17.02 | 27.02 | 23.82 | 42.83 | 26.70 | 22.76 | 25.14 |
| MAE | 0.30 | 15.98 | 14.75 | 47.06 | 26.29 | 15.70 | 20.43 | 7.86 | 6.84 | 80.98 | 52.45 | 17.00 | 18.21 | 16.69 | 19.84 | 26.70 | 22.76 | 25.14 |
| MAPE (%) | 74.7 | 6586.2 | 4922.0 | 17,776.5 | 9889.9 | 5865.9 | 8386.0 | 3328.7 | 2825.7 | 31,418.5 | 20,431.0 | 6277.9 | 6132.6 | 5750.4 | 6801.8 | 10,236.0 | 8740.2 | 9644.1 |
| Type II | ||||||||||||||||||
| RMSE | 8.16 | 12.81 | 12.94 | 55.09 | 34.36 | 23.81 | 15.40 | 12.56 | 14.43 | 59.83 | 37.90 | 24.31 | 16.84 | 13.41 | 15.58 | 18.93 | 15.02 | 17.38 |
| MAE | 7.76 | 10.03 | 12.67 | 55.03 | 34.27 | 23.68 | 12.07 | 9.93 | 11.31 | 59.56 | 37.70 | 24.24 | 16.61 | 13.25 | 15.40 | 18.76 | 14.81 | 17.20 |
| MAPE (%) | 90.5 | 113.8 | 166.4 | 711.4 | 438.6 | 299.4 | 136.6 | 111.5 | 125.7 | 796.1 | 502.5 | 310.6 | 217.6 | 176.7 | 203.4 | 258.0 | 206.1 | 237.5 |
| Type III | ||||||||||||||||||
| RMSE | 1.93 | 15.46 | 91.13 | 48.46 | 27.70 | 17.12 | 19.40 | 8.64 | 7.71 | 78.21 | 50.67 | 18.58 | 95.67 | 80.71 | 223.94 | 25.35 | 21.42 | 23.79 |
| MAE | 1.41 | 14.25 | 30.44 | 48.45 | 27.68 | 17.07 | 17.97 | 7.50 | 6.81 | 77.68 | 50.17 | 18.50 | 34.59 | 29.63 | 55.19 | 25.32 | 21.38 | 23.76 |
| MAPE (%) | 71.5 | 1074.7 | 2402.7 | 3364.2 | 1908.1 | 1164.6 | 1356.0 | 564.9 | 506.8 | 5526.7 | 3574.0 | 1258.7 | 2706.9 | 2329.5 | 4541.8 | 1807.3 | 1531.4 | 1698.1 |
| Wavelength/nm | ||||||
|---|---|---|---|---|---|---|
| BS_Spring | BS_Summer | CS | CS_Borderland | ESS | LS | |
| 313 | 0.58 ± 0.27 | 0.50 ± 0.26 | 0.57 ± 0.19 | 0.49 ± 0.10 | 0.52 ± 0.24 | 0.11 ± 0.09 |
| 380 | 0.33 ± 0.23 | 0.21 ± 0.15 | 0.24 ± 0.12 | 0.14 ± 0.04 | 0.41 ± 0.17 | 0.46 ± 0.18 |
| 412 | 0.29 ± 0.23 | 0.15 ± 0.10 | 0.17 ± 0.09 | 0.09 ± 0.03 | 0.29 ± 0.14 | 1.00 ± 0.55 |
| 443 | 0.26 ± 0.23 | 0.12 ± 0.08 | 0.13 ± 0.07 | 0.07 ± 0.02 | 0.22 ± 0.12 | 0.75 ± 0.33 |
| 490 | 0.20 ± 0.19 | 0.08 ± 0.05 | 0.09 ± 0.05 | 0.05 ± 0.02 | 0.15 ± 0.10 | 0.51 ± 0.24 |
| 510 | 0.19 ± 0.17 | 0.09 ± 0.05 | 0.10 ± 0.05 | 0.07 ± 0.02 | 0.15 ± 0.09 | 0.43 ± 0.19 |
| 520 | 0.19 ± 0.16 | 0.09 ± 0.05 | 0.10 ± 0.04 | 0.07 ± 0.01 | 0.15 ± 0.08 | 0.40 ± 0.18 |
| 532 | 0.18 ± 0.15 | 0.10 ± 0.04 | 0.10 ± 0.04 | 0.08 ± 0.01 | 0.15 ± 0.08 | 0.37 ± 0.15 |
| 555 | 0.17 ± 0.12 | 0.11 ± 0.04 | 0.12 ± 0.04 | 0.10 ± 0.01 | 0.16 ± 0.07 | 0.33 ± 0.13 |
| 565 | 0.17 ± 0.10 | 0.11 ± 0.04 | 0.12 ± 0.03 | 0.11 ± 0.01 | 0.16 ± 0.07 | 0.31 ± 0.12 |
| 589 | 0.23 ± 0.09 | 0.18 ± 0.04 | 0.19 ± 0.03 | 0.17 ± 0.01 | 0.22 ± 0.07 | 0.34 ± 0.10 |
| 625 | 0.41 ± 0.09 | 0.36 ± 0.05 | 0.37 ± 0.04 | 0.36 ± 0.02 | 0.40 ± 0.07 | 0.47 ± 0.08 |
| 665 | 0.55 ± 0.12 | 0.46 ± 0.06 | 0.50 ± 0.05 | 0.49 ± 0.03 | 0.52 ± 0.07 | 0.58 ± 0.08 |
| 683 | 0.57 ± 0.11 | 0.47 ± 0.10 | 0.54 ± 0.06 | 0.54 ± 0.03 | 0.55 ± 0.09 | 0.62 ± 0.09 |
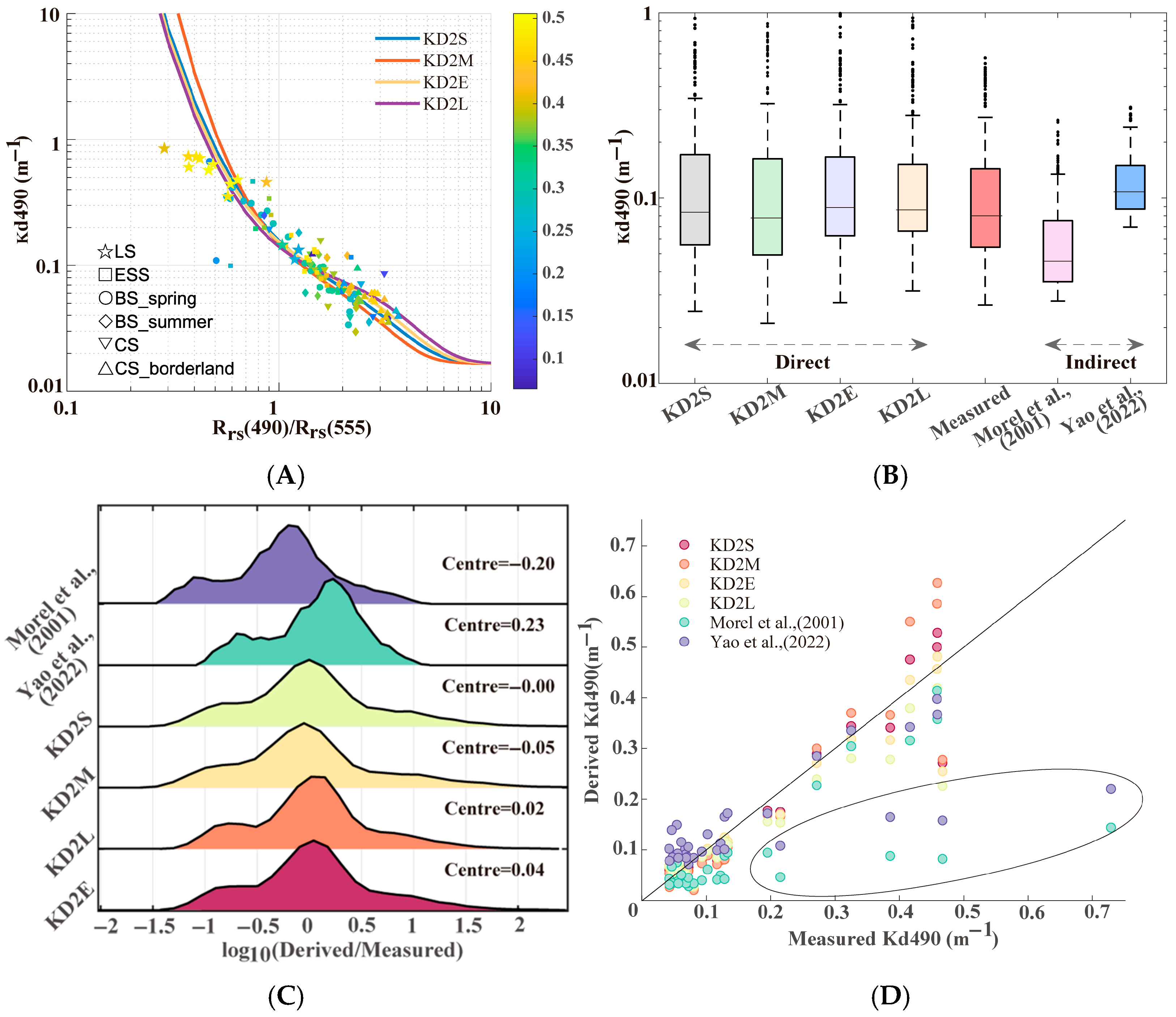
| Algorithm | Average | Std | Median | Maximum | Mean Derived/Measured |
|---|---|---|---|---|---|
| Measured | 0.18 | 0.20 | 0.09 | 0.85 | - |
| -Direct | |||||
| KD2S | 0.21 | 0.32 | 0.08 | 1.85 | 1.18 |
| KD2M | 0.25 | 0.49 | 0.07 | 3.07 | 1.36 |
| KD2E | 0.19 | 0.28 | 0.09 | 1.65 | 1.20 |
| KD2L | 0.18 | 0.24 | 0.09 | 1.43 | 1.16 |
| -Indirect | |||||
| Morel et al. [54] | 0.09 | 0.09 | 0.05 | 0.41 | 0.60 |
| Yao et al. [57] | 0.15 | 0.08 | 0.11 | 0.40 | 1.26 |
| Algorithm | RMSE | MAE | MAPE (%) |
|---|---|---|---|
| KD2S | 0.18 | 0.07 | 31.1 |
| KD2M | 0.36 | 0.12 | 42.5 |
| KD2E | 0.15 | 0.06 | 30.1 |
| KD2L | 0.12 | 0.05 | 30.6 |
| Morel et al. [54] | 0.17 | 0.09 | 43.7 |
| Yao et al. [57] | 0.15 | 0.08 | 57.1 |
| Region | RMSE | MAE | MAPE (%) | Mean Derived/Measured | |
|---|---|---|---|---|---|
| BS, CS, ESS | 0.11 | 0.05 | 39.7 | 0.16 ± 0.18 | 1.25 |
| LS | 3.81 | 2.33 | 373.5 | 2.86 ± 3.23 | 4.71 |
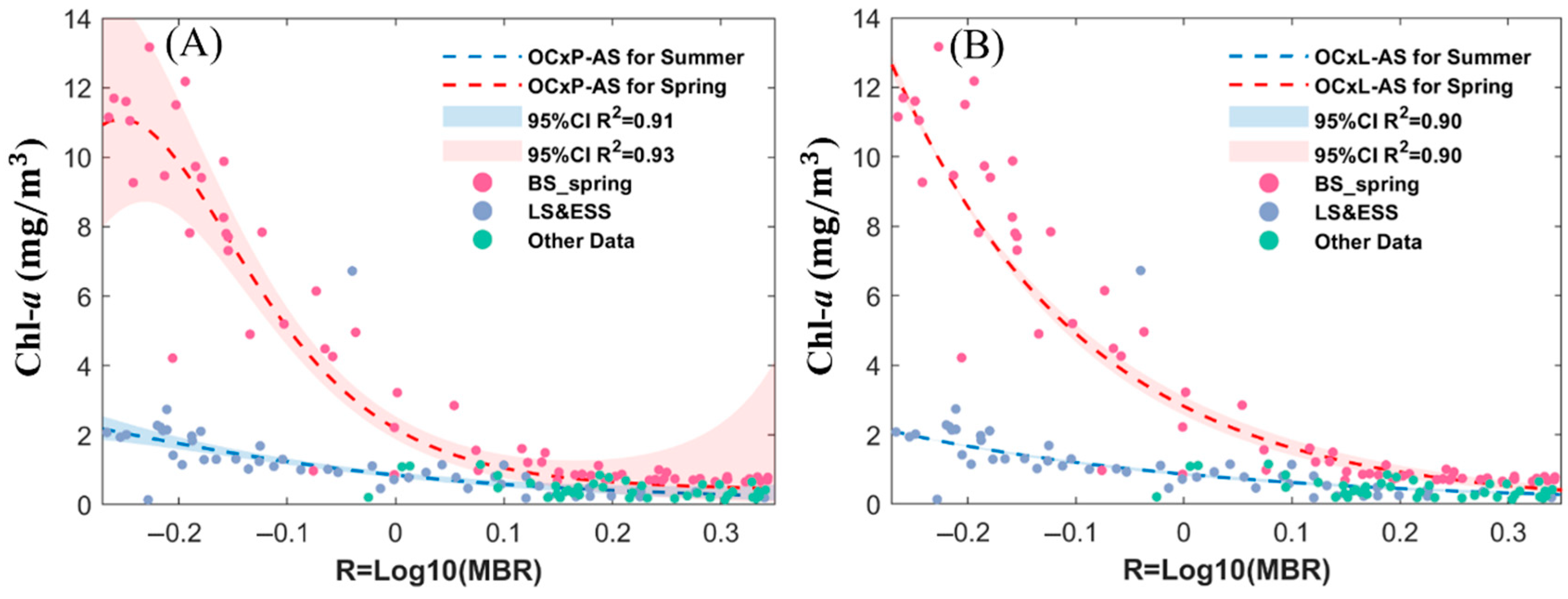
| Season | Algorithm | RMSE | ||
|---|---|---|---|---|
| Spring | OCxP-AS | [0.3393, −3.5910, 2.7730, 15.9700, −29.62] | 0.93 | 0.81 |
| OCxL-AS | [0.4491, −2.4180] | 0.90 | 0.90 | |
| Summer | OCxP-AS | [−0.0713, −1.6430, 0.0947, 1.5900, −1.931] | 0.91 | 0.21 |
| OCxL-AS | [−0.0672, −1.4410] | 0.90 | 0.22 |
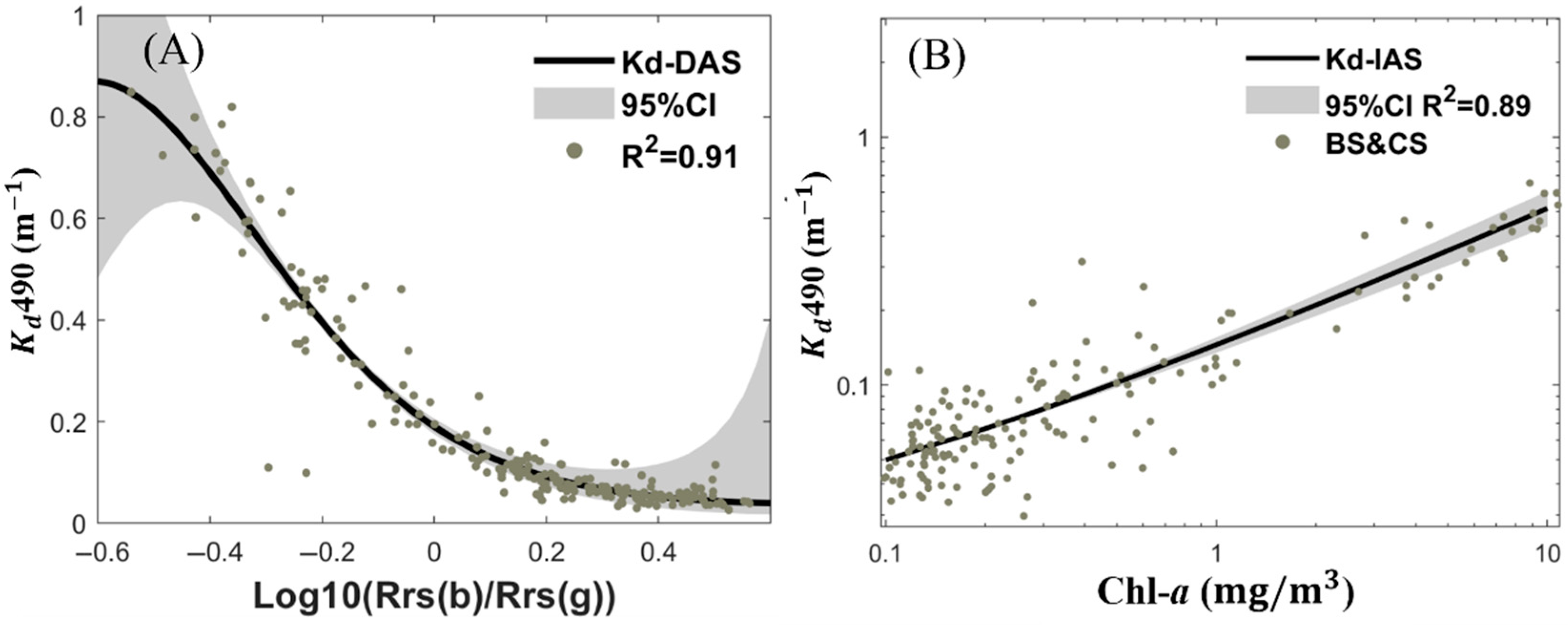
| Algorithm | Region | RMSE | ||
|---|---|---|---|---|
| -DAS | Total | 0.91 | 0.06 | |
| [−0.7602, −1.8130, −0.3174, 1.3960, 0.1500] | ||||
| -IAS | BS, CS | 0.89 | 0.05 | |
| [0.1290, 0.5875] |
| RMSE | MAE | MAPE (%) | Mean Derived/Measured | ||
|---|---|---|---|---|---|
| Measured | 0.51 ± 0.24 | ||||
| QAAV4 | 0.30 | 0.23 | 42.8 | 0.36 ± 0.28 | 0.79 |
| QAAV6 | 1.10 | 0.92 | 162.7 | 1.43 ± 0.80 | 2.62 |
| QAA-LS | 0.19 | 0.15 | 29.2 | 0.62 ± 0.33 | 1.24 |
| Step | Equation |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |
| Perturbation | +5% | −5% | +5% | −5% | +5% | −5% |
| 0.61 ± 0.32 | 0.68 ± 0.36 | 0.64 ± 0.34 | 0.64 ± 0.34 | 0.67 ± 0.36 | 0.62 ± 0.32 | |
| (%) | −1.05 | −1.16 | 0.19 | 0.18 | 0.73 | 0.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Li, T.; Xu, Q.; Xing, X.; Zhu, X.; Qiu, Y. Evaluation and Improvement of Ocean Color Algorithms for Chlorophyll-a and Diffuse Attenuation Coefficients in the Arctic Shelf. Remote Sens. 2025, 17, 2606. https://doi.org/10.3390/rs17152606
Yao Y, Li T, Xu Q, Xing X, Zhu X, Qiu Y. Evaluation and Improvement of Ocean Color Algorithms for Chlorophyll-a and Diffuse Attenuation Coefficients in the Arctic Shelf. Remote Sensing. 2025; 17(15):2606. https://doi.org/10.3390/rs17152606
Chicago/Turabian StyleYao, Yubin, Tao Li, Qing Xu, Xiaogang Xing, Xingyuan Zhu, and Yubao Qiu. 2025. "Evaluation and Improvement of Ocean Color Algorithms for Chlorophyll-a and Diffuse Attenuation Coefficients in the Arctic Shelf" Remote Sensing 17, no. 15: 2606. https://doi.org/10.3390/rs17152606
APA StyleYao, Y., Li, T., Xu, Q., Xing, X., Zhu, X., & Qiu, Y. (2025). Evaluation and Improvement of Ocean Color Algorithms for Chlorophyll-a and Diffuse Attenuation Coefficients in the Arctic Shelf. Remote Sensing, 17(15), 2606. https://doi.org/10.3390/rs17152606









