Deep Learning and Transformer Models for Groundwater Level Prediction in the Marvdasht Plain: Protecting UNESCO Heritage Sites—Persepolis and Naqsh-e Rustam
Abstract
1. Introduction
2. Study Area Description
Geological and Hydrogeological Information
3. Materials and Methods
3.1. Data Acquisition
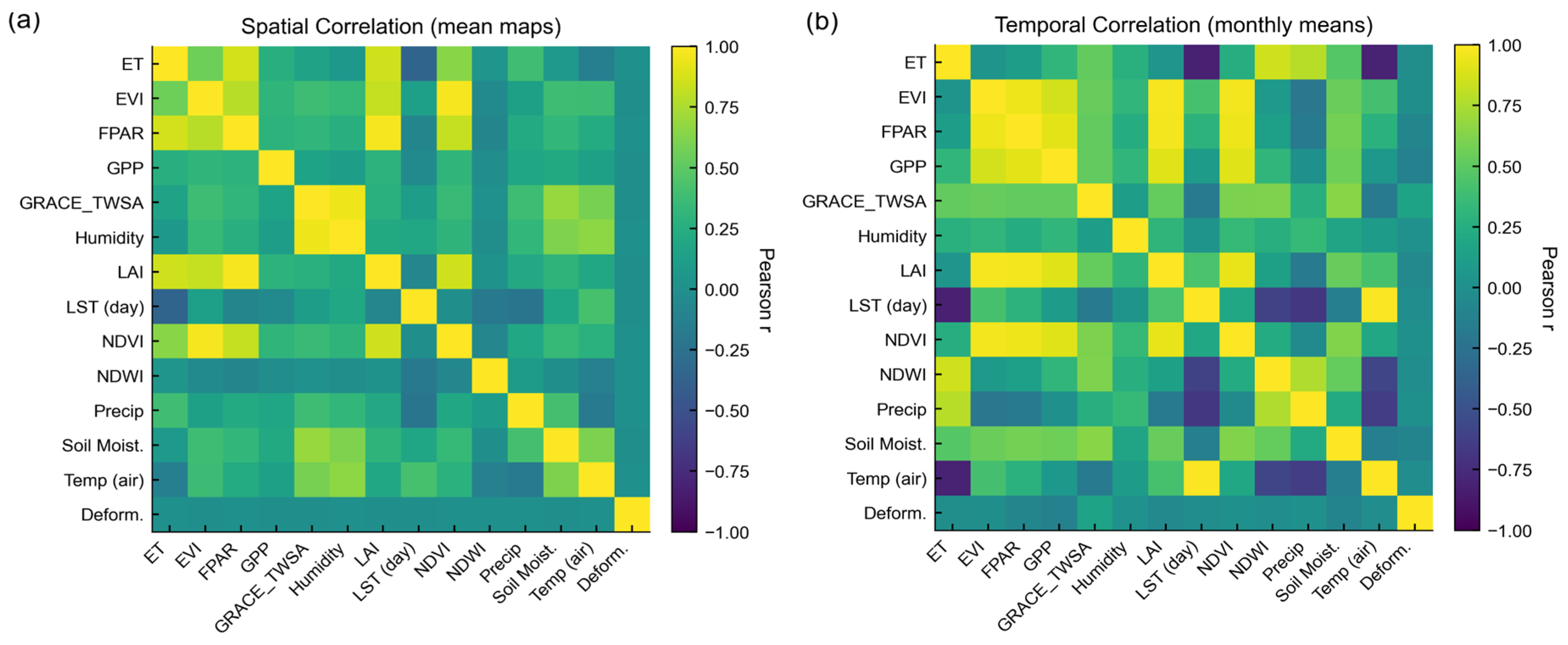
Dataset Spatial and Temporal Correlation
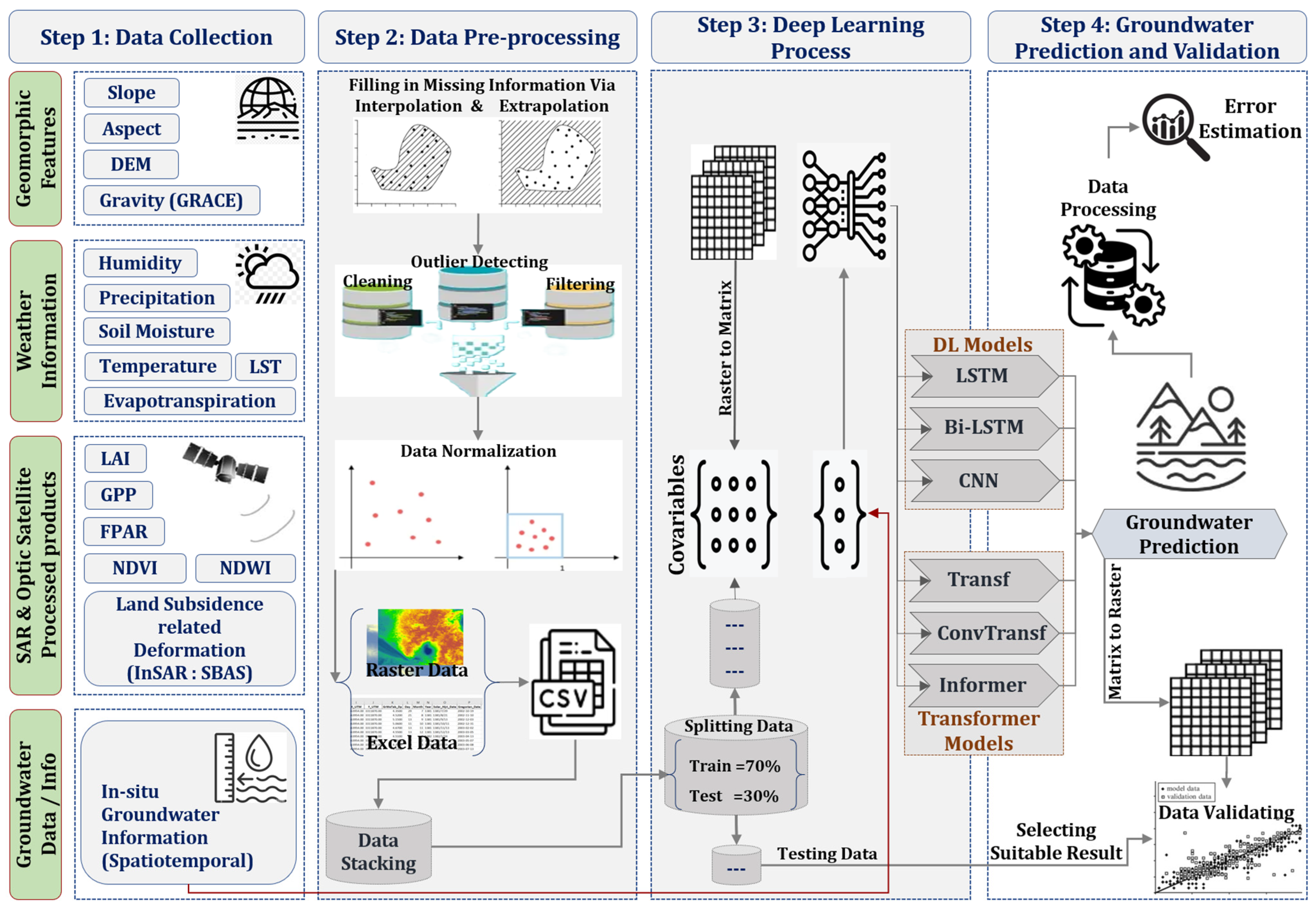
3.2. Methodology Framework
3.2.1. Data Processing
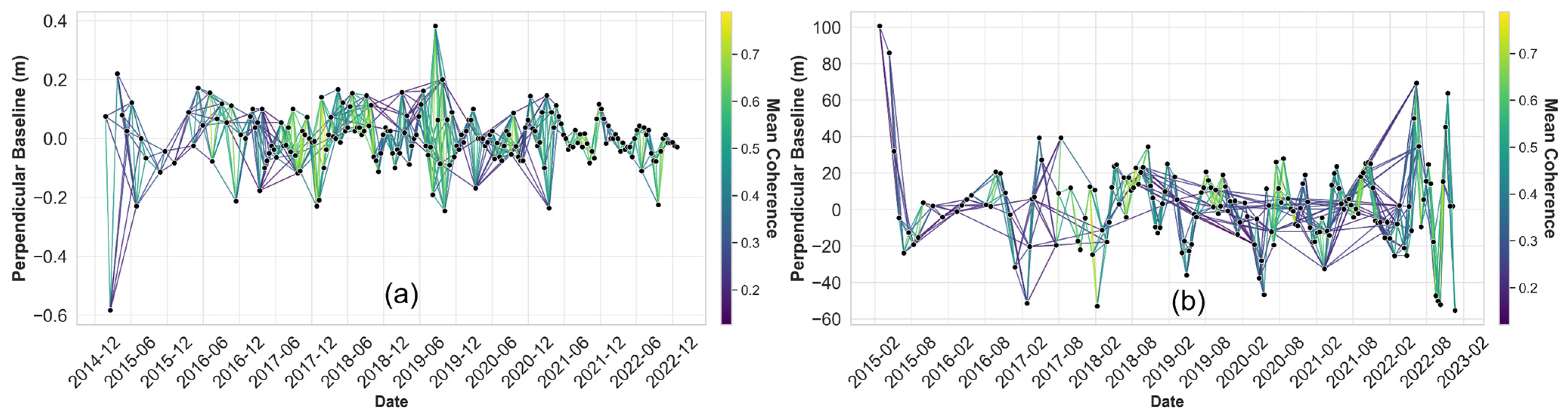
SAR Data Processing
3.2.2. Models’ Architecture
3.2.3. Training Pre-Processing
3.2.4. Prediction Process
3.2.5. Error Evaluation
4. Results and Discussion
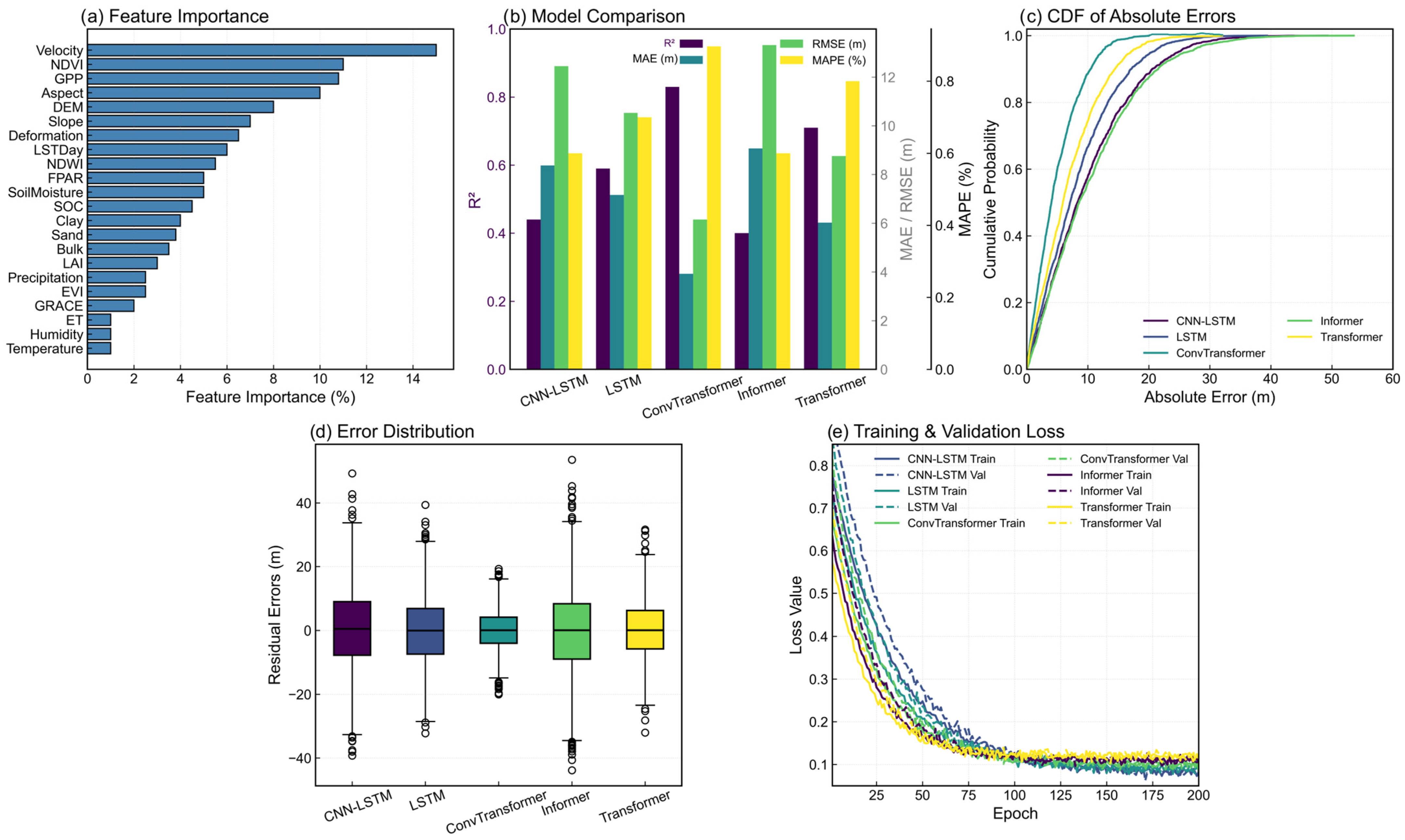
4.1. Model’s Performance
4.2. Hyperparameter Calibration
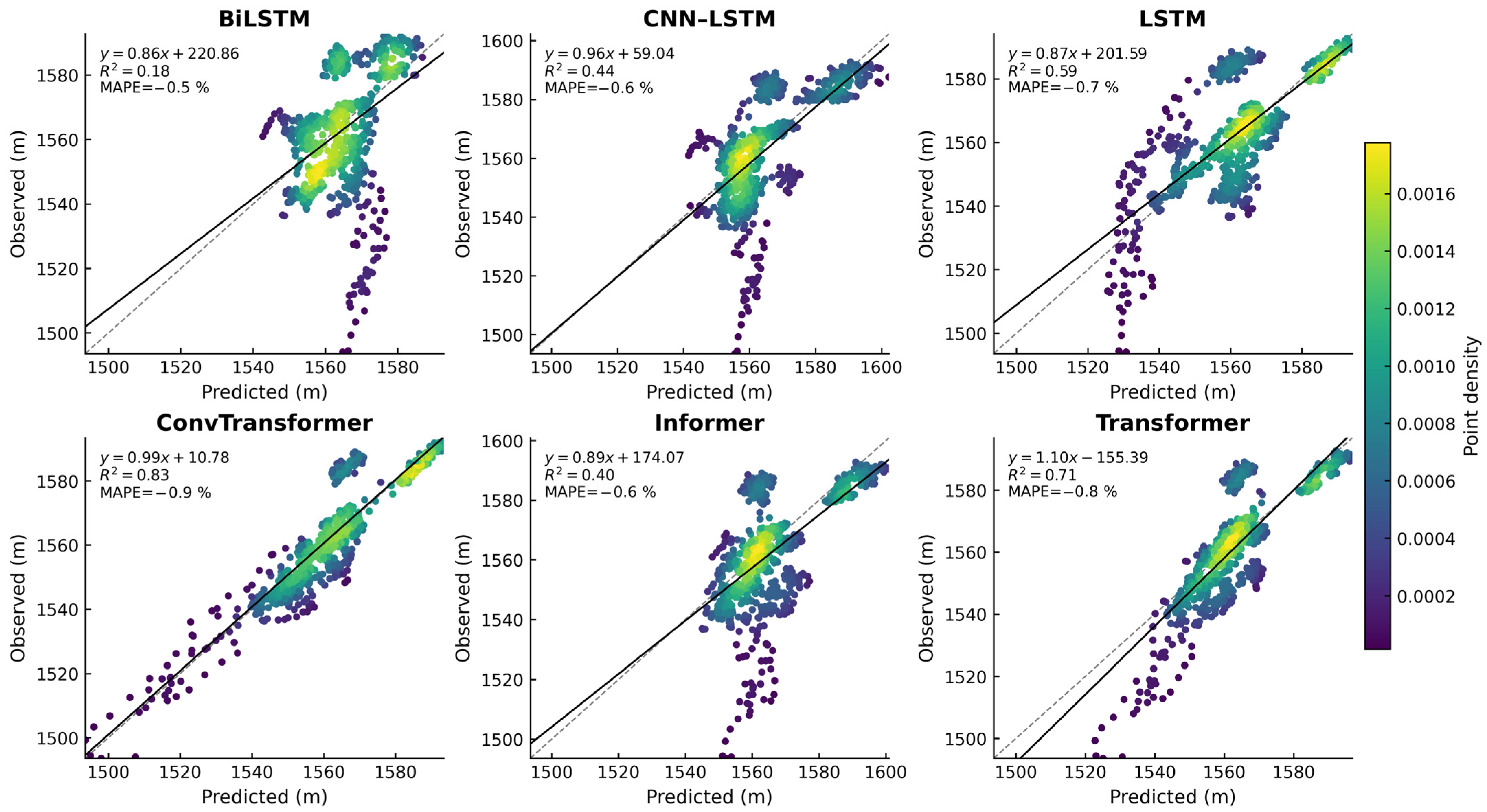
4.3. Validation
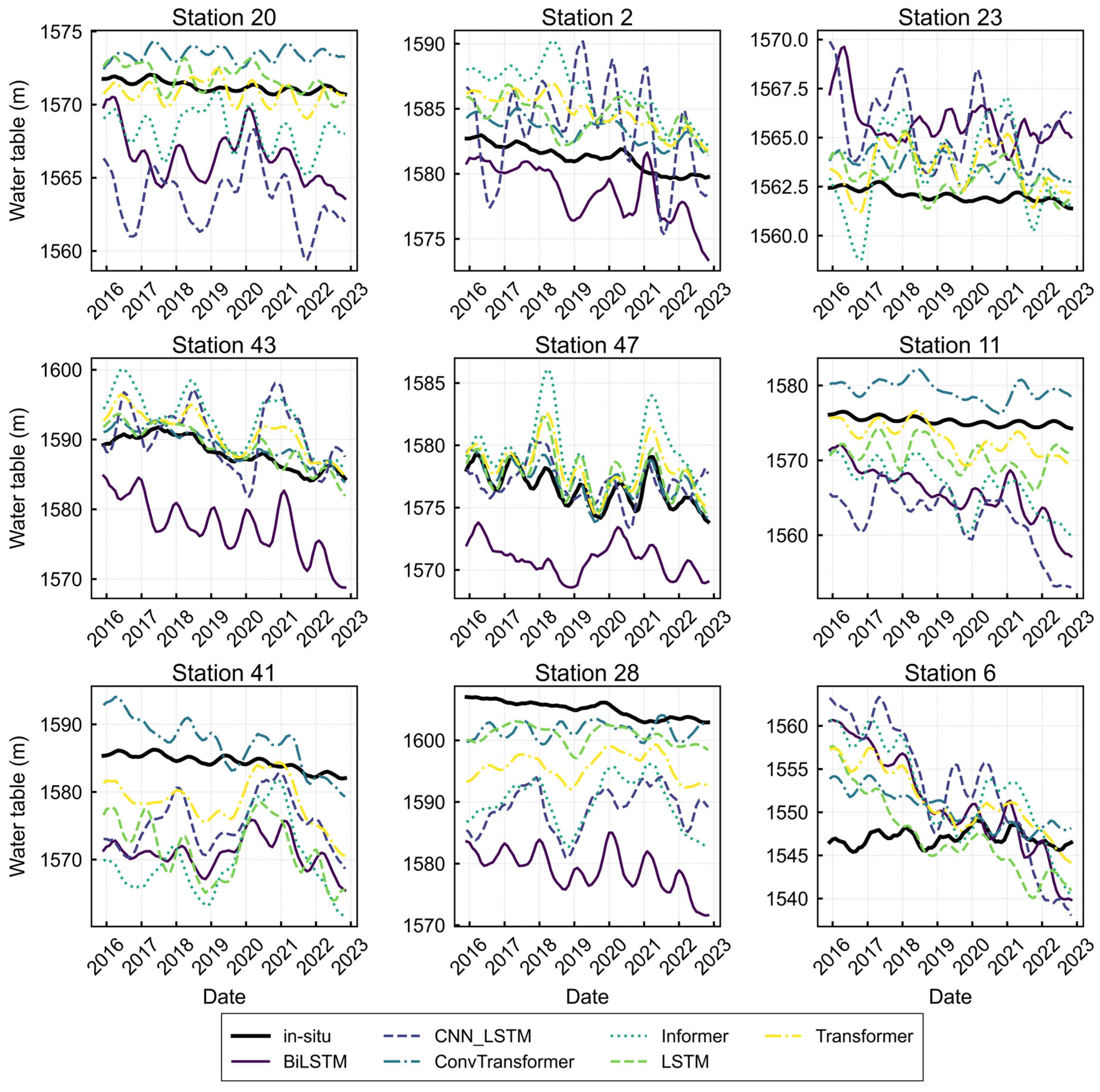
4.4. Temporal and Spatial Groundwater Level Analysis
4.5. Comparative Analysis and Implications
5. Conclusions
- (i)
- Embed Bayesian uncertainty layers to quantify forecast confidence.
- (ii)
- Assimilate forthcoming Sentinel-1C acquisitions for near-real-time updates.
- (iii)
- Couple transformer outputs with hydro-economic optimization to directly inform adaptive groundwater extraction limits.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Su, G.; Xiong, C.; Zhang, G.; Wang, Y.; Shen, Q.; Chen, X.; An, H.; Qin, L. Coupled processes of groundwater dynamics and land subsidence in the context of active human intervention, a case in Tianjin, China. Sci. Total Environ. 2023, 903, 166803. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Chang, L.C.; Chang, F.J. Deep dive into predictive excellence: Transformer’s impact on prediction. J. Hydrol. 2024, 636, 131250. [Google Scholar] [CrossRef]
- Negahdary, M. Shrinking aquifers and land subsidence in Iran. Science 2022, 376, 1279. [Google Scholar] [CrossRef] [PubMed]
- Castellazzi, P.; Longuevergne, L.; Martel, R.; Rivera, A.; Brouard, C.; Chaussard, E. Quantitative mapping of groundwater depletion at the water management scale using a combined GRACE/InSAR approach. Remote Sens. Environ. 2018, 205, 408–418. [Google Scholar] [CrossRef]
- Motagh, M.; Shamshiri, R.; Haghshenas Haghighi, M.; Wetzel, H.U.; Akbari, B.; Nahavandchi, H.; Roessner, S.; Arabi, S. Quantifying groundwater exploitation induced subsidence in the Rafsanjan plain, southeastern Iran, using InSAR time series and in situ measurements. Eng. Geol. 2017, 218, 134–151. [Google Scholar] [CrossRef]
- Lenczuk, A.; Klos, A.; Bogusz, J. Studying spatio-temporal patterns of vertical displacements caused by groundwater mass changes observed with GPS. Remote Sens. Environ. 2023, 292, 113597. [Google Scholar] [CrossRef]
- Herrera-García, G.; Ezquerro, P.; Tomás, R.; Béjar-Pizarro, M.; López-Vinielles, J.; Rossi, M.; Mateos, R.M.; Carreón-Freyre, D.; Lambert, J.; Teatini, P.; et al. Mapping the global threat of land subsidence. Science 2021, 371, 34–36. [Google Scholar] [CrossRef] [PubMed]
- Teatini, P.; Tosi, L.; Strozzi, T.; Carbognin, L.; Wegmuller, U.; Rizetto, F. Mapping regional land displacements in the Venice coastland by an integrated monitoring system. Remote Sens. Environ. 2005, 98, 403–413. [Google Scholar] [CrossRef]
- Teatini, P.; Tosi, L.; Strozzi, T.; Carbognin, L.; Cecconi, G.; Rosselli, R.; Libardo, S. Resolving land subsidence within the Venice Lagoon by persistent scatterer SAR interferometry. Phys. Chem. Earth Parts A/B/C 2012, 40, 72–79. [Google Scholar] [CrossRef]
- Tosi, L.; Carbognin, L.; Teatini, P.; Strozzi, T.; Wegmüller, U. Evidence of the present relative land stability of Venice, Italy, from land, sea, and space observations. Geophys. Res. Lett. 2002, 29, 3-1–3-4. [Google Scholar] [CrossRef]
- Castagnetti, C.; Cosentini, R.M.; Lancellotta, R.; Capra, A. Geodetic monitoring and geotechnical analyses of subsidence induced settlements of historic structures. Struct. Control Health Monit. 2017, 24, e2030. [Google Scholar] [CrossRef]
- Chen, H.Y.; Vojinovic, Z.; Lo, W.; Lee, J.W. Groundwater Level Prediction with Deep Learning Methods. Water 2023, 15, 3118. [Google Scholar] [CrossRef]
- Guo, L.; Gong, H.; Ke, Y.; Zhu, L.; Li, X.; Lyu, M.; Zhang, K. Mechanism of Land Subsidence Mutation in Beijing Plain under the Background of Urban Expansion. Remote Sens. 2021, 13, 3086. [Google Scholar] [CrossRef]
- Hung, W.C.; Hwang, C.; Tosi, L.; Lin, S.H.; Tsai, P.C.; Chen, Y.A.; Wang, W.J.; Li, E.C.; Ge, S. Toward sustainable inland aquaculture: Coastal subsidence monitoring in Taiwan. Remote Sens. Appl. 2023, 30, 100930. [Google Scholar] [CrossRef]
- Fu, G.; Schmid, W.; Castellazzi, P. Understanding the Spatial Variability of the Relationship between InSAR-Derived Deformation and Using Machine Learning. Geosciences 2023, 13, 133. [Google Scholar] [CrossRef]
- Castellazzi, P.; Martel, R.; Galloway, D.L.; Longuevergne, L.; Rivera, A. Assessing Groundwater Depletion and Dynamics Using “GRACE” and “InSAR”: Potential and Limitations. Groundwater 2016, 54, 768–780. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.Y.; Lee, S.I. Predicting Changes in Spatiotemporal Groundwater Storage Through the Integration of Multi-Satellite Data and Deep Learning Models. IEEE Access 2021, 9, 157571–157583. [Google Scholar] [CrossRef]
- Lopez, F.P.A.; Zhou, G.; Vargas, L.P.; Jing, G.; Marca, M.E.O.; Quispe, M.V.; Ticona, E.A.; Tonconi, N.M.M.; Apaza, E.O. Lithium quantification based on random forest with multi-source geoinformation in Coipasa salt flats, Bolivia. Int. J. Appl. Earth Obs. Geoinf. 2023, 117, 103184. [Google Scholar]
- An, Y.; Yang, F.; Ren, C.; Xu, J.; Hu, J.; Luo, G. Surface deformation analysis and prediction of groundwater changes from joint sar-grace satellite data. IEEE Access 2024, 12, 33671–33686. [Google Scholar] [CrossRef]
- Ali, A.; Zhou, G.; Lopez, F.P.A.; Xu, C.; Jing, G.; Tan, Y. Deep learning for water quality multivariate assessment in inland water across China. Int. J. Appl. Earth Obs. Geoinf. 2024, 133, 104078. [Google Scholar] [CrossRef]
- Kamali, M.E.; Naghibi, S.A.; Hashemi, H.; Berndtsson, R. Application of Advanced Machine Learning Algorithms to Assess Groundwater Potential Using Remote Sensing-Derived Data. Remote Sens. 2020, 12, 2742. [Google Scholar] [CrossRef]
- Afan, H.A.; Ibrahem, A.O.A.; Essam, Y.; Ahmed, A.N.; Huang, Y.F.; Kisi, O.; Sherif, M.; Sefelnasr, A.; Chau, K.W.; El-Shafie, A. Modeling the fluctuations of by employing ensemble deep learning techniques. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1420–1439. [Google Scholar]
- Na, K.; Lee, J.H.; Kim, E. LF-Transformer: Latent Factorizer Transformer for Tabular Learning. IEEE Access 2024, 12, 10690–10698. [Google Scholar] [CrossRef]
- Yin, H.; Guo, Z.; Zhang, X.; Chen, J.; Zhang, Y. RR-Former: Rainfall-runoff modeling based on Transformer. J. Hydrol. 2022, 609, 127781. [Google Scholar] [CrossRef]
- Tepetidis, N.; Koutsoyiannis, D.; Iliopoulou, T.; Dimitriadis, P. Investigating the Performance of the Informer Model for Streamflow Forecasting. Water 2024, 16, 2882. [Google Scholar] [CrossRef]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Liao, X.; Wong, M.S.; Zhu, R. Dual-gate Temporal Fusion Transformer for estimating large-scale land surface solar irradiation. Renew. Sustain. Energy Rev. 2025, 214, 115510. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Wancai, Z. Informer: Beyond Efficient Transformer for Long Sequence Time Series Forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Mostafa, N.; Ezzatolah, R.; Mohammad Hassan, T. Effect of Extreme Floods on the Archaeological Sites of Persepolis and Naghsh-e-Rustam, Iran. J. Perform. Constr. Facil. 2013, 28, 502–510. [Google Scholar]
- Tracey, R.; Warwick, B.; David, T. The Penguin Dictionary of Archaeology (Book Review). Anc. Hist. Resour. Teach. 1992, 22, 83. [Google Scholar]
- Alireza, A.C.; Pierfrancesco, C. Persepolis West (Fars, Iran): Report on the Field Work Carried Out by the Iranian-Italian Joint Archaeological Mission in 2008–2009; BAR Publishing: Oxford, UK, 2017; pp. 1–293. [Google Scholar]
- Jaleh, B.; Eslamipanah, M. Restore Iran’s declining groundwater. Science 2023, 379, 148. [Google Scholar] [CrossRef] [PubMed]
- Haghshenas, H.M.; Motagh, M. Uncovering the impacts of depleting aquifers: A remote sensing analysis of land subsidence in Iran. Sci. Adv. 2024, 10, eadk3039. [Google Scholar] [CrossRef] [PubMed]
- Safdari, Z.; Nahavandchi, H.; Joodaki, G. Estimation of Groundwater Depletion in Iran’s Catchments Using Well Data. Water 2022, 14, 131. [Google Scholar] [CrossRef]
- Alavi, M. Regional stratigraphy of the Zagros fold-thrust belt of Iran and its proforeland evolution. Am. J. Sci. 2004, 304, 1–20. [Google Scholar] [CrossRef]
- Ginés, J.; Edwards, R.; Lohr, T.; Larkin, H.; Holley, R. Remote sensing applications in the Fars Region of the Zagros Mountains of Iran. Geol. Soc. Lond. Spec. Publ. 2020, 490, 417–444. [Google Scholar] [CrossRef]
- Zarei, E.; Faghih, A.; Soleimani, M.; Zarei, S. Assessment of relative tectonic activity in the Lar region, Zagros Fold-Thrust Belt, SW Iran: Insights from geomorphometric analysis. Earth Surf. Process. Landf. 2024, 49, 1199–1213. [Google Scholar] [CrossRef]
- Karimnejad, L.H.R.; Hajialibeigi, H.; Sherkati, S.; Adabi, M.H. Tectonic evolution of the Zagros foreland basin since Early Cretaceous, SW Iran: Regional tectonic implications from subsidence analysis. J. Asian Earth Sci. 2020, 204, 104550. [Google Scholar] [CrossRef]
- Shakeri, N.; Shirzad, T.; Ashkpour, M.S.; Norouzi, S. Shallow Crustal Structure in the DehDasht Region (SW Iran) from Ambient Seismic Noise Tomography. In EGU General Assembly Conference Abstracts; EGU: Munich, Germany, 2021. [Google Scholar]
- Mohammadi, Z.; Mahdavikia, H.; Raeisi, E.; Ford, D.C. Hydrogeological characterization of Dasht-e-Arjan Lake (Zagros Mountains, Iran): Clarifying a long-time question. Environ. Earth Sci. 2019, 78, 360. [Google Scholar] [CrossRef]
- Salehi, M.F.; Hafezi, M.N.; Lashkaripour, G.R.; Dehghani, M. Geological parameters affected land subsidence in Mashhad plain, north-east of Iran. Environ. Earth Sci. 2019, 78, 405. [Google Scholar] [CrossRef]
- Azam, H.; Iraj, J. Modeling the subsidence development of Marvdasht plain in relation to groundwater abstraction. J. Nat. Environ. Hazards 2022, 11, 17–34. [Google Scholar]
- Farahzadi, E.; Alavi, S.A.; Sherkati, S.; Ghassemi, M.R. Variation of subsidence in the Dezful Embayment, SW Iran: Influence of reactivated basement structures. Arab. J. Geosci. 2019, 12, 616. [Google Scholar] [CrossRef]
- Mirzadeh, S.M.J.; Jin, S.; Parizi, E.; Chaussard, E.; Bürgmann, R.; Delgado Blasco, J.M.; Amani, M.; Bao, H.; Mirzadeh, S.H. Characterization of Irreversible Land Subsidence in the Yazd-Ardakan Plain, Iran from 2003 to 2020 InSAR Time Series. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022258. [Google Scholar] [CrossRef]
- Shang, Q.; Liu, X.; Deng, X.; Zhang, B. Downscaling of GRACE datasets based on relevance vector machine using InSAR time series to generate maps of groundwater storage changes at local scale. J. Appl. Remote Sens. 2019, 13, 048503. [Google Scholar] [CrossRef]
- Amazirh, A.; Ouassanouan, Y.; Bouimouass, H.; Baba, M.W.; Bouras, E.H.; Rafik, A.; Benkirane, M.; Hajhouji, Y.; Ablila, Y.; Chehbouni, A. Remote Sensing-Based Multiscale Analysis of Total and Groundwater Storage Dynamics over Semi-Arid North African Basins. Remote Sens. 2024, 16, 3698. [Google Scholar] [CrossRef]
- Khorrami, B.; Gunduz, O. Evaluation of the temporal variations of groundwater storage and its interactions with climatic variables using “GRACE” data and hydrological models: A study from Turkey. Hydrol. Process 2021, 35, e14076. [Google Scholar] [CrossRef]
- Kulkarni, T.; Gassmann, M.; Vajedian, S. On the difficulties in estimating water balance components from remote sensing in an anthropogenically modified catchment in southern India. In EGU General Assembly Conference Abstracts; EGU: Munich, Germany, 2020; p. 2197. [Google Scholar]
- Sahour, H.; Sultan, M.; Vazifedan, M.; Abdelmohsen, K.; Karki, S.; Yellich, J.A.; Gebremichael, E.; Alshehri, F.; Elbayoumi, T.M. Statistical Applications to Downscale GRACE-Derived Terrestrial Water Storage Data and to Fill Temporal Gaps. Remote Sens. 2020, 12, 533. [Google Scholar] [CrossRef]
- Wang, Q.; Zheng, W.; Yin, W.; Kang, G.; Huang, Q.; Shen, Y. Improving the Resolution of GRACE/InSAR Groundwater Storage Estimations Using a New Subsidence Feature Weighted Combination Scheme. Water 2023, 15, 1017. [Google Scholar] [CrossRef]
- Rateb, A.; Scanlon, B.R.; Pool, D.R.; Sun, A.; Zhang, Z.; Chen, J.; Clark, B.; Faunt, C.C.; Haugh, C.J.; Hill, M.; et al. Comparison of Groundwater Storage Changes from GRACE Satellites with Monitoring and Modeling of Major U.S. Aquifers. Water Resour. Res. 2020, 56, e2020WR027556. [Google Scholar] [CrossRef]
- O’Neil, G.L.; Goodall, J.L.; Behl, M.; Saby, L. Deep learning Using Physically-Informed Input Data for Wetland Identification. Environ. Model. Softw. 2020, 126, 104665. [Google Scholar] [CrossRef]
- Zhu, L.; Shuai, X.Y.; Lin, Z.J.; Sun, Y.J.; Zhou, Z.C.; Meng, L.X.; Zhu, Y.G.; Chen, H. Landscape of genes in hospital wastewater breaking through the defense line of last-resort antibiotics. Water Res. 2022, 209, 117907. [Google Scholar] [CrossRef] [PubMed]
- Lopes, C.L.; Mendes, R.; Caçador, I.; Dias, J.M. Assessing salt marsh extent and condition changes with 35 years of Landsat imagery: Tagus Estuary case study. Remote Sens. Environ. 2020, 247, 111939. [Google Scholar] [CrossRef]
- Zhang, H.; Chang, J.; Zhang, L.; Wang, Y.; Li, Y.; Wang, X. NDVI dynamic changes and their relationship with meteorological factors and soil moisture. Environ. Earth Sci. 2018, 77, 582. [Google Scholar] [CrossRef]
- Sharma, M.; Bangotra, P.; Gautam, A.S.; Gautam, S. Sensitivity of normalized difference vegetation index (NDVI) to land surface temperature, soil moisture and precipitation over district Gautam Buddh Nagar, UP, India. Stoch. Environ. Res. Risk Assess. 2022, 36, 1779–1789. [Google Scholar] [CrossRef] [PubMed]
- Naga Rajesh, A.; Abinaya, S.; Purna Durga, G.; Lakshmi Kumar, T.V. Long-term relationships of MODIS NDVI with rainfall, land surface temperature, surface soil moisture and groundwater storage over monsoon core region of India. Arid. Land Res. Manag. 2023, 37, 51–70. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, G.; Ma, B.; Wu, T.; Wang, X.; Wu, Q. Revealing climatic and groundwater impacts on the spatiotemporal variations in vegetation coverage in marine sedimentary basins of the North China Plain, China. Sci. Rep. 2024, 14, 10085. [Google Scholar] [CrossRef] [PubMed]
- Riedel, T.; Weber, T.; Bergmann, A. Groundwater recharge, vegetation and climate change. In EGU General Assembly Conference Abstracts; EGU: Munich, Germany, 2024; p. 5747. [Google Scholar]
- Artiemjew, P.; Chojka, A.; Rapiński, J. Deep learning for RFI artifact recognition in Sentinel-1 data. Remote Sens. 2020, 13, 7. [Google Scholar] [CrossRef]
- Morishita, Y.; Lazecky, M.; Wright, T.J.; Weiss, J.R.; Elliott, J.R.; Hooper, A. LiCSBAS: An open-source InSAR time series analysis package integrated with the LiCSAR automated Sentinel-1 InSAR processor. Remote Sens. 2020, 12, 424. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. Solid Earth 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Zebker, H.A.; Goldstein, R.M. Topographic mapping from interferometric synthetic aperture radar observations. J. Geophys. Res. Solid Earth 1986, 91, 4993–4999. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin, Germany, 2001; Volume 2. [Google Scholar]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Chidepudi, S.K.R.; Massei, N.; Jardani, A.; Dieppois, B.; Henriot, A.; Fournier, M. Training deep learning models with a multi-station approach and static aquifer attributes for simulation: What’s the best way to leverage regionalised information? Hydrol. Earth Syst. Sci. 2025, 29, 841–861. [Google Scholar] [CrossRef]
- Othman, M.M. Modeling of daily using deep learning neural networks. Turk. J. Eng. 2023, 7, 331–337. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, G.; Wu, Q.; Cui, F.; Yan, B.; Yin, S.; Soltanian, M.R.; Thanh, H.V.; Dai, Z. Transfer Learning with Transformer-Based Models for Mine Water Inrush Prediction: A Multivariate Analysis Using Sparse and Imbalanced Monitoring Data. Mine Water Environ. 2024, 43, 707–726. [Google Scholar] [CrossRef]
- Nourani, V.; Khodkar, K.; Gebremichael, M. Uncertainty assessment of LSTM based groundwater level predictions. Hydrol. Sci. J. 2022, 67, 773–790. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Rateb, A.; Anyamba, A.; Kebede, S.; MacDonald, A.M.; Shamsudduha, M.; Small, J.; Sun, A.; Taylor, R.G.; Xie, H. Linkages between GRACE water storage, hydrologic extremes, and climate teleconnections in major African aquifers. Environ. Res. Lett. 2022, 17, 014046. [Google Scholar] [CrossRef]
- Rateb, A.; Sun, A.; Scanlon, B.R.; Save, H.; Hasan, E. Reconstruction of GRACE mass change time series using a Bayesian framework. Earth Space Sci. 2022, 9, e2021EA002162. [Google Scholar] [CrossRef] [PubMed]
- Riedel, T.; Ridavits, T. Managed aquifer recharge to ensure sustainable groundwater abstraction under extreme drought conditions. In EGU General Assembly Conference Abstracts; EGU: Munich, Germany, 2024; p. 18093. [Google Scholar]




| Parameters | Specifications |
|---|---|
| Resolution | 5 × 20 m |
| Band type | C-band |
| Orbit height | 693 km |
| Orbit inclination | 98.18° |
| Temporal coverage | 12 days (12/2014 to 12/2022)/6 days (12/2014 to 12/2022) |
| Spectral range | 3.75–7.5 cm |
| Mode | Interferometric Wide (IW) |
| Variable Name | Source (Webpage, Accessed Date) | Units | Spatial Resolution |
|---|---|---|---|
| Terrain Aspect | https://zenodo.org/records/15689805, accessed on 20 November 2024 | Degrees (0–360°) | 30 m |
| Digital Elevation Model (DEM) | https://www.earthdata.nasa.gov/, accessed on 20 November 2024 | Meters (m) | 30 m |
| Slope | https://www.earthdata.nasa.gov/, accessed on 20 November 2024 | Degrees (°) | 30 m |
| Ground Deformation Time Series | https://dataspace.copernicus.eu/, accessed on 20 November 2024 | Millimeters yr−1 | 10 m |
| Potential Evapotranspiration (PET) | https://www.earthdata.nasa.gov/data/, accessed on 20 November 2024 | mm day−1 | 500 m |
| Precipitation (CHIRPS) | https://www.chc.ucsb.edu/data/chirps, accessed on 20 November 2024 | Millimeters (mm) | ~5 km |
| Terrestrial Water Storage Anomaly (GRACE) | http://grace.jpl.nasa.gov/, accessed on 20 November 2024 | cm water-eq. | 55 km |
| Soil Moisture | https://nsidc.org/data/smap, accessed on 20 November 2024 | m3 m−3 | 9 km |
| Surface Air Temperature | https://cds.climate.copernicus.eu/, accessed on 20 November 2024 | Kelvin (K) | 31 km |
| Land Surface Temperature (LST) | https://www.earthdata.nasa.gov/data, accessed on 20 November 2024 | Kelvin (K) | 1 km |
| Atmospheric Humidity | https://cds.climate.copernicus.eu/, accessed on 20 November 2024 | Percent (%) | 31 km |
| Enhanced Vegetation Index (EVI) | https://www.earthdata.nasa.gov/data/, accessed on 20 November 2024 | Dimensionless (–1–+1) | 500 m |
| Normalized Difference Vegetation Index (NDVI) | https://www.earthdata.nasa.gov/data/, accessed on 20 November 2024 | Dimensionless (–1–+1) | 500 m |
| Fraction of Photosynthetically Active Radiation (FPAR) | https://www.earthdata.nasa.gov/data/, accessed on 20 November 2024 | Fraction (0–1) | 500 m |
| Leaf Area Index (LAI) | https://www.earthdata.nasa.gov/data/, accessed on 20 November 2024 | m2 m−2 | 500 m |
| Normalized Difference Water Index (NDWI) | https://www.earthdata.nasa.gov/data/, accessed on 20 November 2024 | Dimensionless (–1–+1) | 500 m |
| Gross Primary Productivity (GPP) | https://www.earthdata.nasa.gov/data/, accessed on 20 November 2024 | g C m−2 day−1 | 500 m |
| Sand Fraction | https://stac.openlandmap.org/, accessed on 20 November 2024 | Percent (%) | 250 m |
| Clay Fraction | https://stac.openlandmap.org/, accessed on 20 November 2024 | Percent (%) | 250 m |
| Bulk Soil Organic Carbon (SOC) | https://stac.openlandmap.org/, accessed on 20 November 2024 | kg C m−2 | 250 m |
| Model | Architecture | Key Hyperparameters |
|---|---|---|
| LSTM | 1. Input: L × d sequence | • u1, u2 ∈ {32, 64, 128} |
| 2. LSTM (units = u1, return_sequences = True) | • dr ∈ {0.1, 0.2, 0.3} | |
| 3. Dropout (rate = dr) | • Learning rate ∈ {1 × 10−4, 5 × 10−4, 1 × 10−3} | |
| 4. LSTM (units = u2) | ||
| 5. Dense (1) | ||
| BiLSTM | 1. Input: L × d sequence | • u ∈ {32, 64, 128} |
| 2. Bidirectional LSTM (units = u) | • dr ∈ {0.1, 0.2, 0.3} | |
| 3. Dropout (rate = dr) | • Learning rate ∈ {1 × 10−4, 5 × 10−4, 1 × 10−3} | |
| 4. Dense (1) | ||
| CNN–LSTM | 1. Input: L × d sequence | • f, u ∈ {32, 64, 128} |
| 2. Conv1D (filters = f, kernel_size = 3, padding = “causal”, activation = ReLU) | • dr ∈ {0.1, 0.2, 0.3} | |
| 3. Dropout (rate = drd) | • Learning rate ∈ {1 × 10−4, 5 × 10−4, 1 × 10−3} | |
| 4. LSTM (units = u) | ||
| 5. Dense (1) | ||
| Transformer | 1. Input: L × d sequence | • d ∈ {32, 64, 128} |
| 2. Dense to model-dim d + Add pos-enc | • heads ∈ {2, 4} | |
| 3. Repeat n×: | • n ∈ {1, 2} | |
| 3.1. MultiHeadAttention (heads = h, key_dim = d/h) → Add and LayerNorm | • dr ∈ {0.1, 0.2, 0.3} | |
| 3.2. FFN: Dense(4d)→ReLU→Dense(d) → Add and LayerNorm | • Learning rate ∈ {1 × 10−4, 5 × 10−4, 1 × 10−3} | |
| 4. GlobalAveragePooling1D | ||
| 5. Dense (1) | ||
| ConvTransformer | 1. Input: L × d sequence | • f, d ∈ {32, 64, 128} |
| 2. Conv1D (filters = f, kernel_size = 3, padding = “same”, activation = ReLU) | • heads ∈ {2, 4} | |
| 3. Dense to model-dim d + Add pos-enc | • n∈ {1, 2} | |
| 4. Repeat n×: same TX stack as Transformer | • dr ∈ {0.1, 0.2, 0.3} | |
| 5. GlobalAveragePooling1D | • Learning rate ∈ {1 × 10−4, 5 × 10−4, 1 × 10−3} | |
| 6. Dense (1) | ||
| Informer | 1. Input: L × d sequence | • d ∈ {32, 64, 128} |
| 2. Dense to model-dim d + Add pos-enc | • heads ∈ {2, 4} | |
| 3. Repeat n×: same TX stack as Transformer (ProbSparse self-attention) | • n ∈ {1, 2} | |
| 4. GlobalAveragePooling1D | • dr ∈ {0.1, 0.2, 0.3} | |
| 5. Dense (1) | • Learning rate ∈ {1 × 10−4, 5 × 10−4, 1 × 10−3} |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heidarian, P.; Antezana Lopez, F.P.; Tan, Y.; Fathtabar Firozjaee, S.; Yousefi, T.; Salehi, H.; Osman Pour, A.; Elena Oscori Marca, M.; Zhou, G.; Azhdari, A.; et al. Deep Learning and Transformer Models for Groundwater Level Prediction in the Marvdasht Plain: Protecting UNESCO Heritage Sites—Persepolis and Naqsh-e Rustam. Remote Sens. 2025, 17, 2532. https://doi.org/10.3390/rs17142532
Heidarian P, Antezana Lopez FP, Tan Y, Fathtabar Firozjaee S, Yousefi T, Salehi H, Osman Pour A, Elena Oscori Marca M, Zhou G, Azhdari A, et al. Deep Learning and Transformer Models for Groundwater Level Prediction in the Marvdasht Plain: Protecting UNESCO Heritage Sites—Persepolis and Naqsh-e Rustam. Remote Sensing. 2025; 17(14):2532. https://doi.org/10.3390/rs17142532
Chicago/Turabian StyleHeidarian, Peyman, Franz Pablo Antezana Lopez, Yumin Tan, Somayeh Fathtabar Firozjaee, Tahmouras Yousefi, Habib Salehi, Ava Osman Pour, Maria Elena Oscori Marca, Guanhua Zhou, Ali Azhdari, and et al. 2025. "Deep Learning and Transformer Models for Groundwater Level Prediction in the Marvdasht Plain: Protecting UNESCO Heritage Sites—Persepolis and Naqsh-e Rustam" Remote Sensing 17, no. 14: 2532. https://doi.org/10.3390/rs17142532
APA StyleHeidarian, P., Antezana Lopez, F. P., Tan, Y., Fathtabar Firozjaee, S., Yousefi, T., Salehi, H., Osman Pour, A., Elena Oscori Marca, M., Zhou, G., Azhdari, A., & Shahbazi, R. (2025). Deep Learning and Transformer Models for Groundwater Level Prediction in the Marvdasht Plain: Protecting UNESCO Heritage Sites—Persepolis and Naqsh-e Rustam. Remote Sensing, 17(14), 2532. https://doi.org/10.3390/rs17142532









