A Comprehensive Review of Mathematical Error Characterization and Mitigation Strategies in Terrestrial Laser Scanning
Abstract
1. Introduction
- Manufacturers focus mostly on the subset of known systematic errors such as zero constant error or vertical index errors. However, more systematic errors have been identified that are worth investigating;
- Instrument misalignments are generally determined under controlled laboratory circumstances by the manufacturers, away from normal measurement environments [2];
- The need to return an instrument to the manufacturer for any form of calibration is an inefficient and often costly process for users of the technology [3];
- The methodologies and parameters used by each manufacturer vary from instrument to instrument (from manufacturer to manufacturer) due to the differences in scanner construction [4];
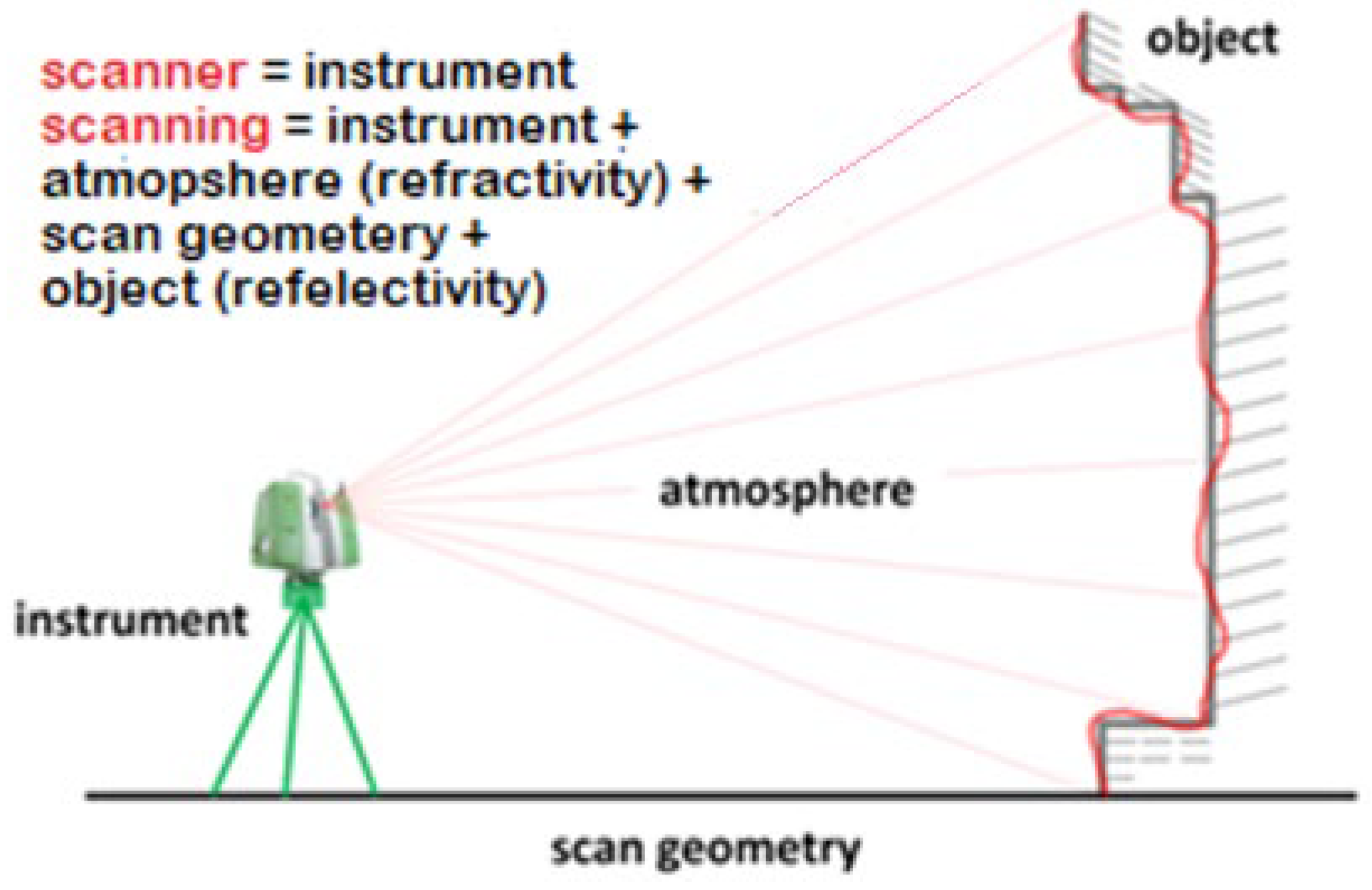
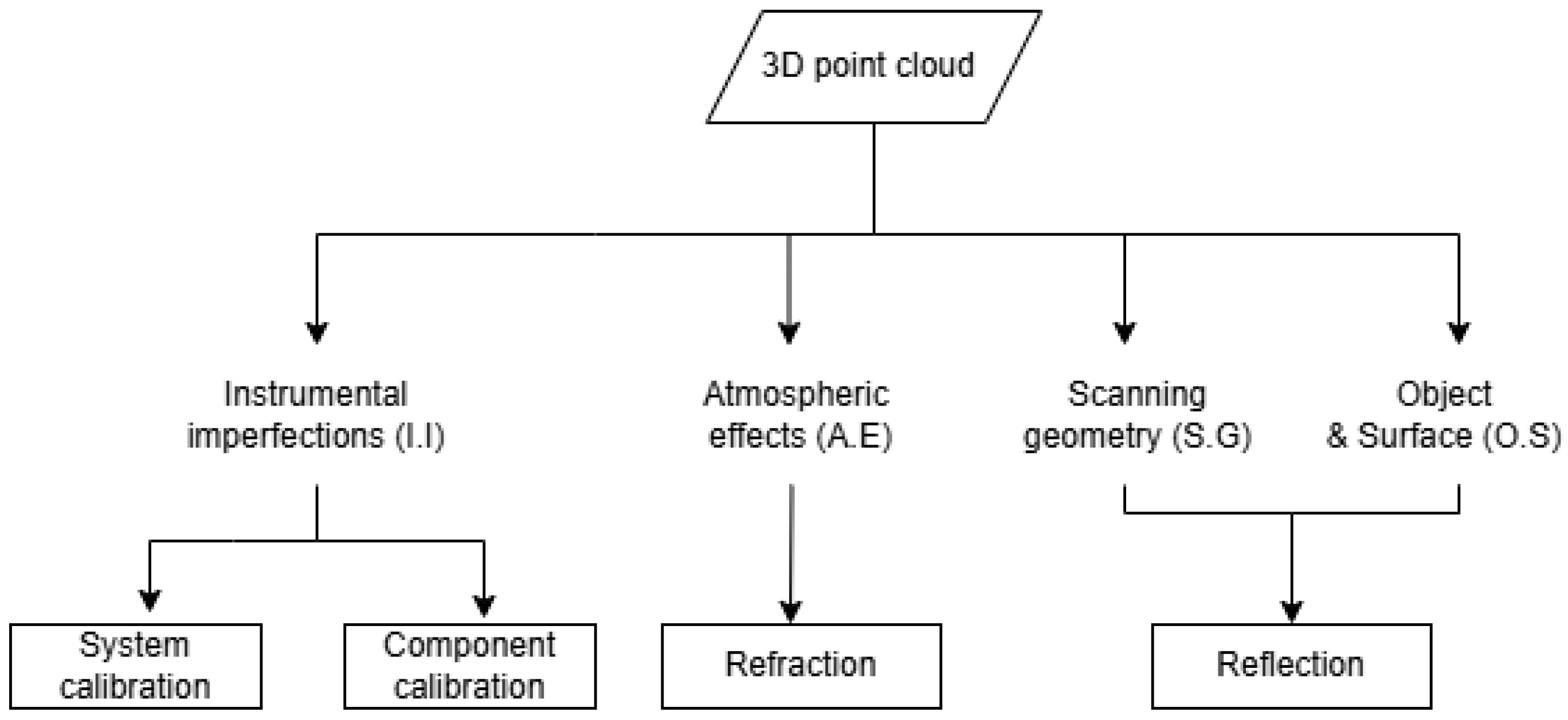
2. Principle of TLS and Error Sources
- Instrumental imperfections (I.I), which include the misalignments and abnormalities of the instrument during the design and construction;
- Atmospheric effects (A.E), which include the effects of the geometry of the line of sight in three different directions that are generated from the variations in atmospheric conditions;
- Scanning geometry and measurement configuration (S.G), which is systematically related to the geometry of scanning and its relevant configuration;
- Object- and surface-related issues (O.S), which are recognized by the reflected signals from any surface and are highly correlated to the properties and geometry of the scene.
3. Instrumental Imperfections (I.I)
3.1. System Calibration
- They require the proper knowledge of geodetic network design (rational surveying study);
- They can be finalized without a detailed study of each component and their interactions;
- They do not necessarily require special facilities and equipment to validate observations (e.g., self-calibration is one of the techniques).
3.1.1. Zero-Order Design (ZOD)
- The high cost and effort of employing the test field for setting more control points. The process needs more accurate instruments and facilities to validate the observations;
- The risk of having imprecise control points in the entire datum leads to the imprecise estimation of the TLS calibration parameters due to the higher number of points;
- Existing high precision of the control points imposes additional strains (constraints) in the geometry of network configuration;
- The stability of the points cannot be guaranteed over time.
3.1.2. First-Order Design (FOD)
3.1.3. Second-Order Design (SOD)
3.2. Component Calibration
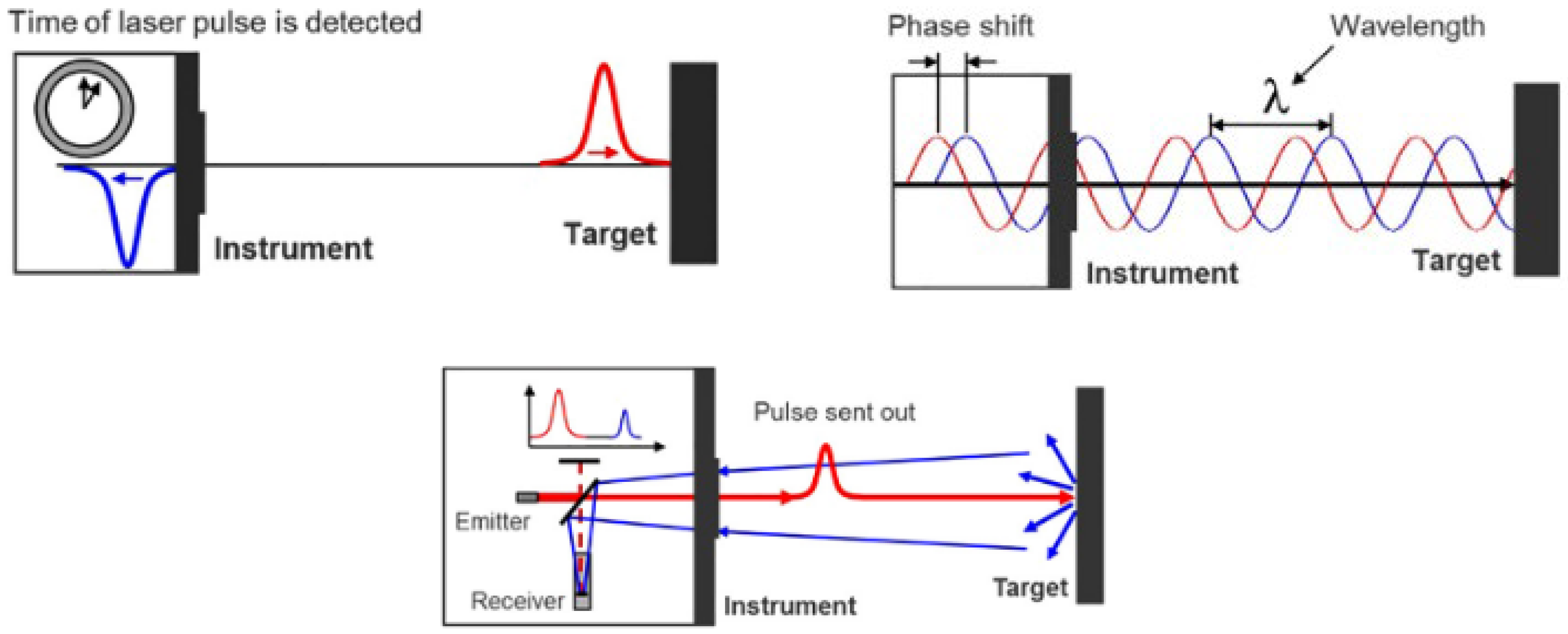
4. Atmospheric Effects (A.E)
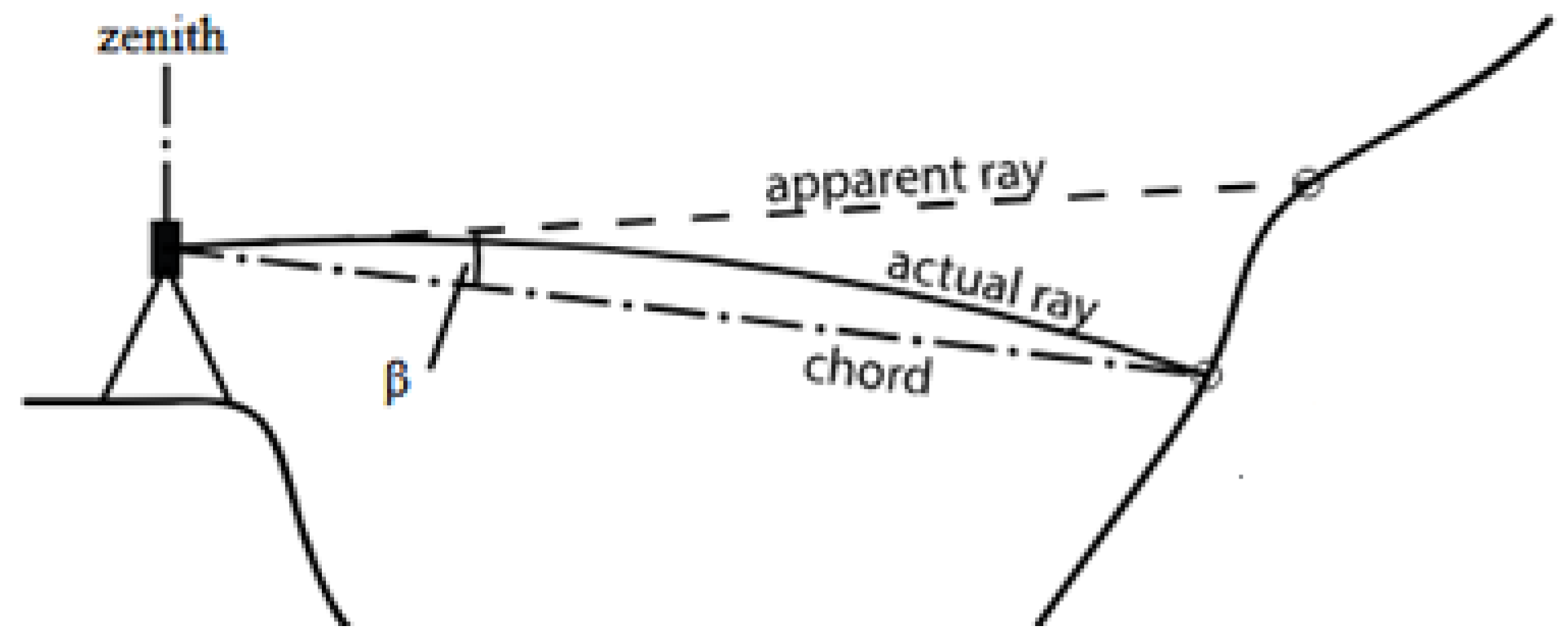
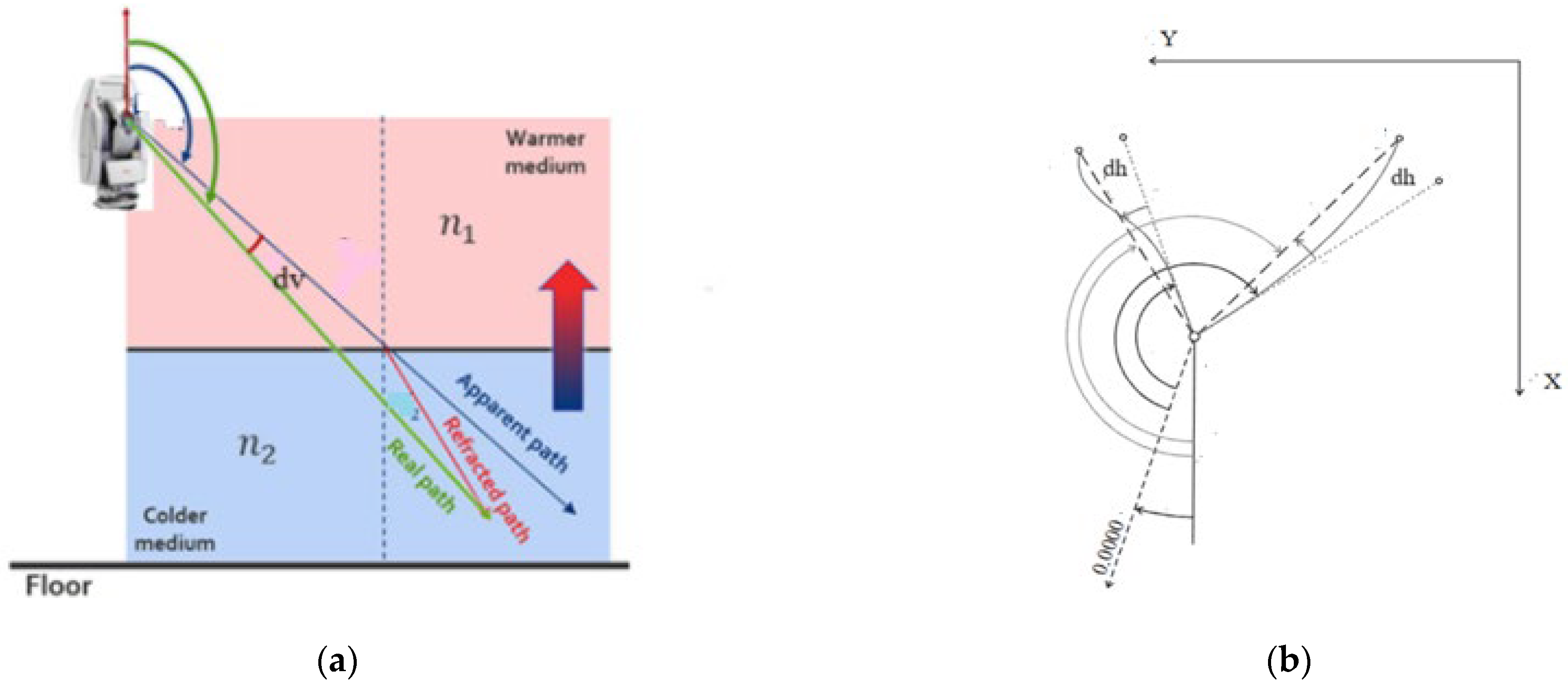
4.1. Range Refraction
4.2. Angle Refraction
5. Scanning Geometry (S.G)
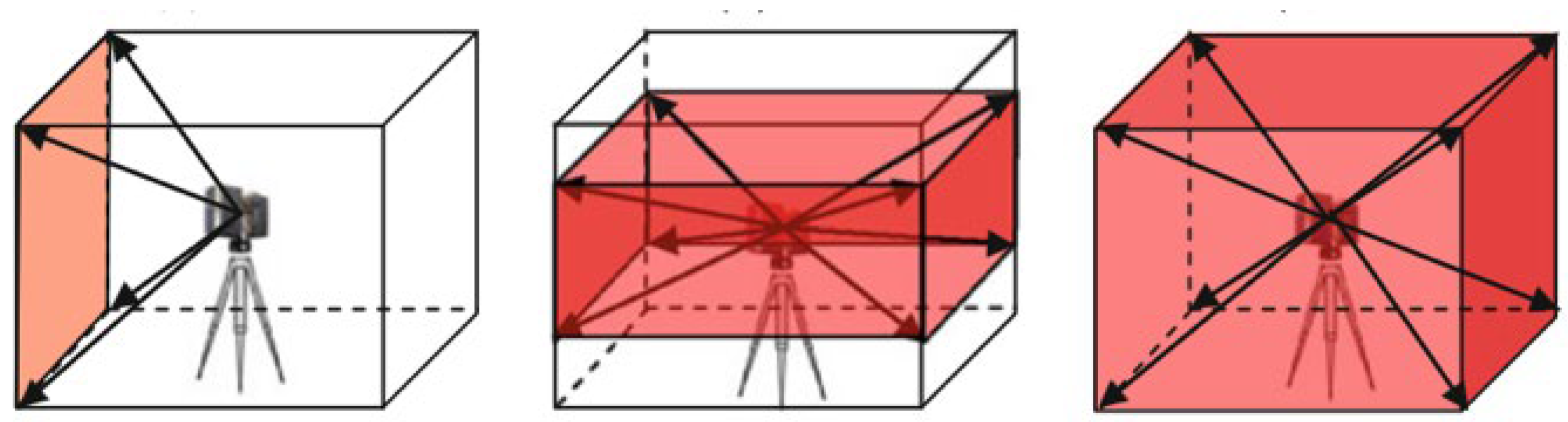
- TLS placements (i.e., the optimal condition of the scanner locations to have full coverage of the scene);
- Geometric resolution (i.e., the concern refers to the geometric point spacing between two consecutive points);
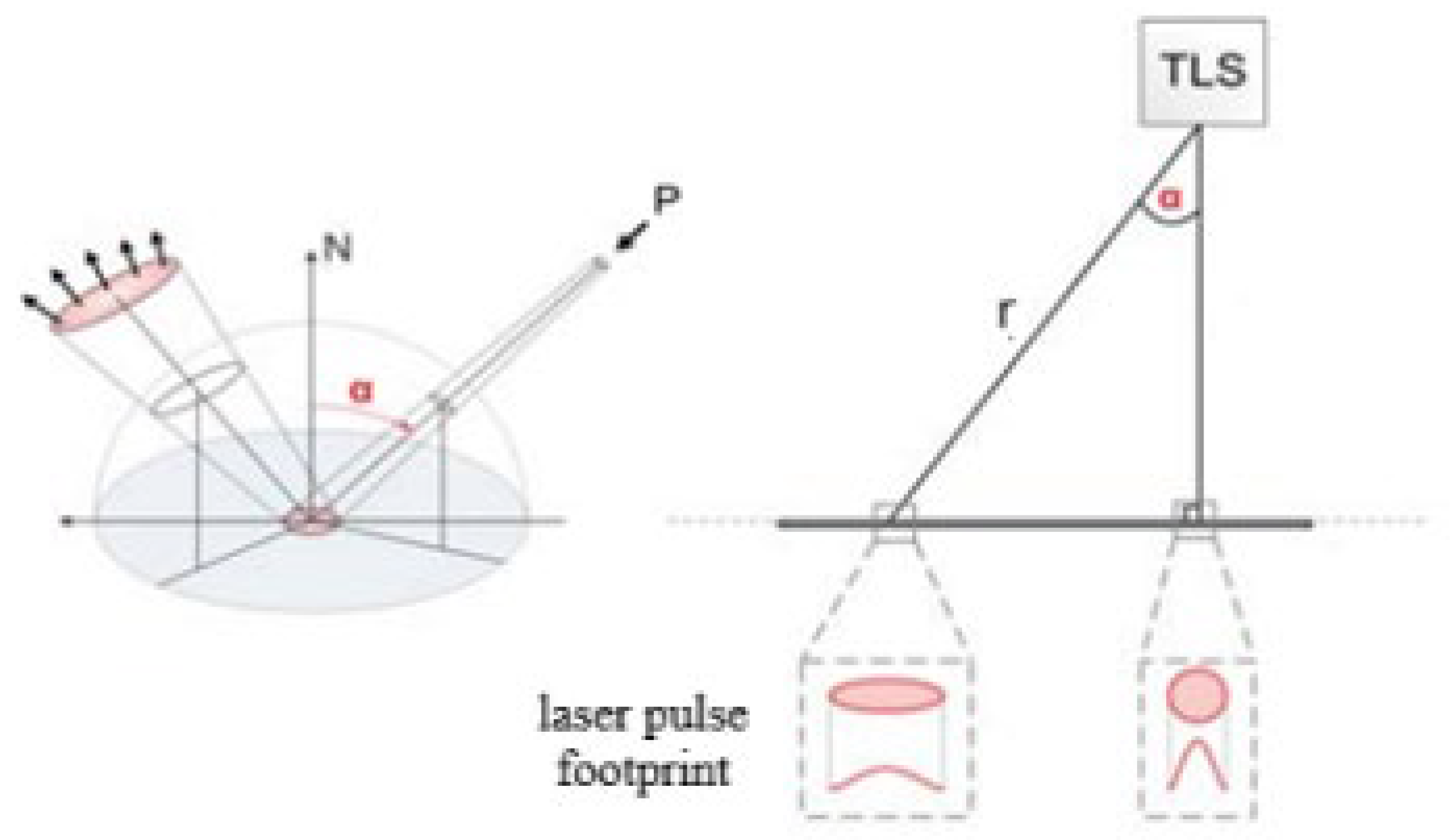
- Incidence angle (i.e., the incidence angle here regards the angle of incidence ray when it strikes the target).
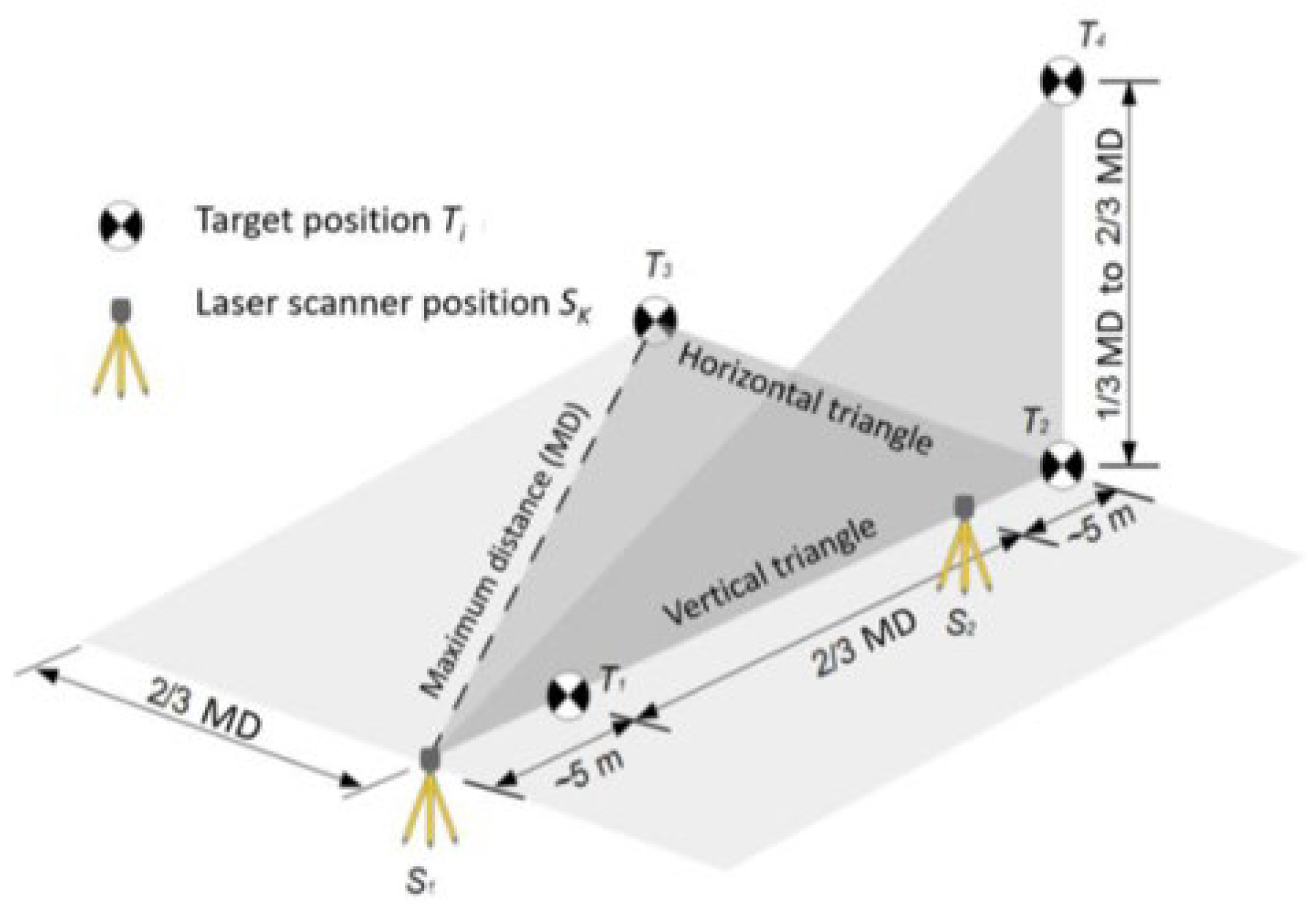
5.1. TLS Placements
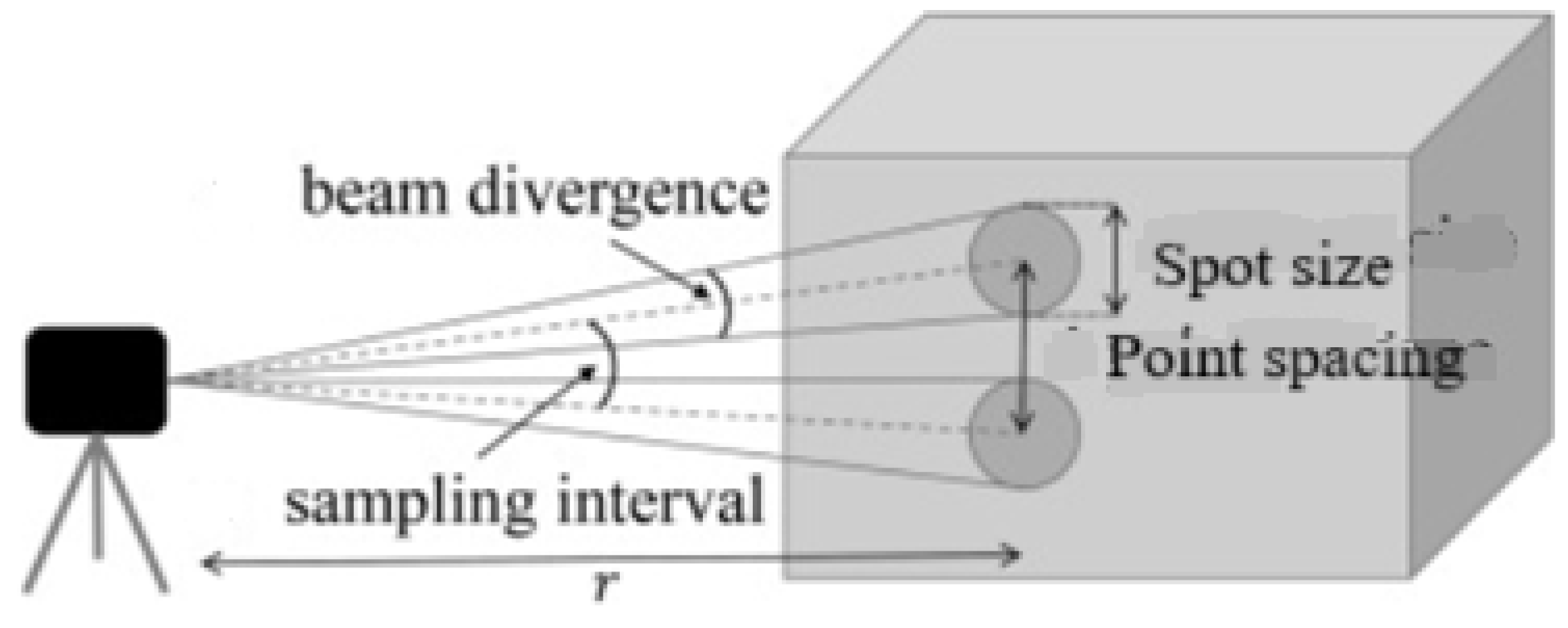
5.2. Resolution
5.3. Incidence Angle
6. Object- and Surface-Related Issues (O.S)
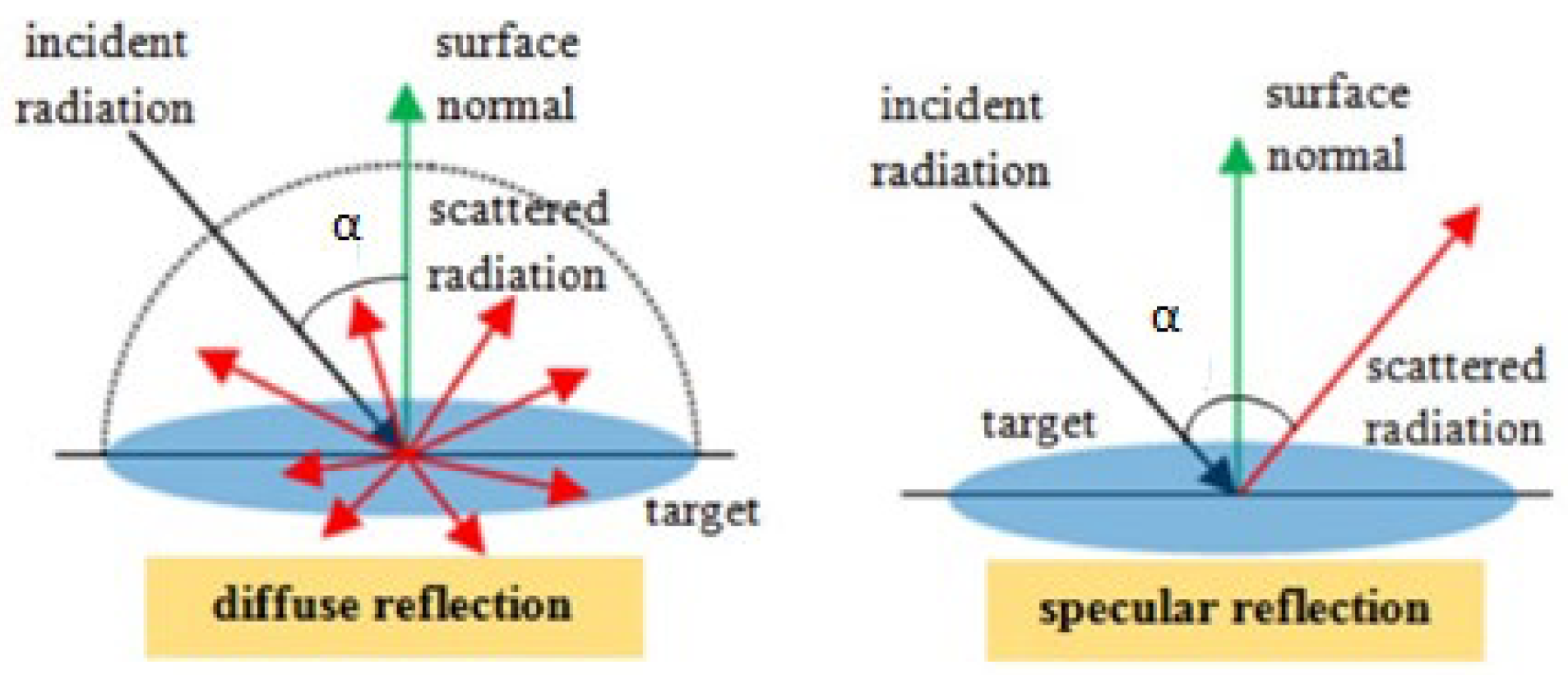
6.1. Material
6.2. Roughness
6.3. Color
6.4. Albedo
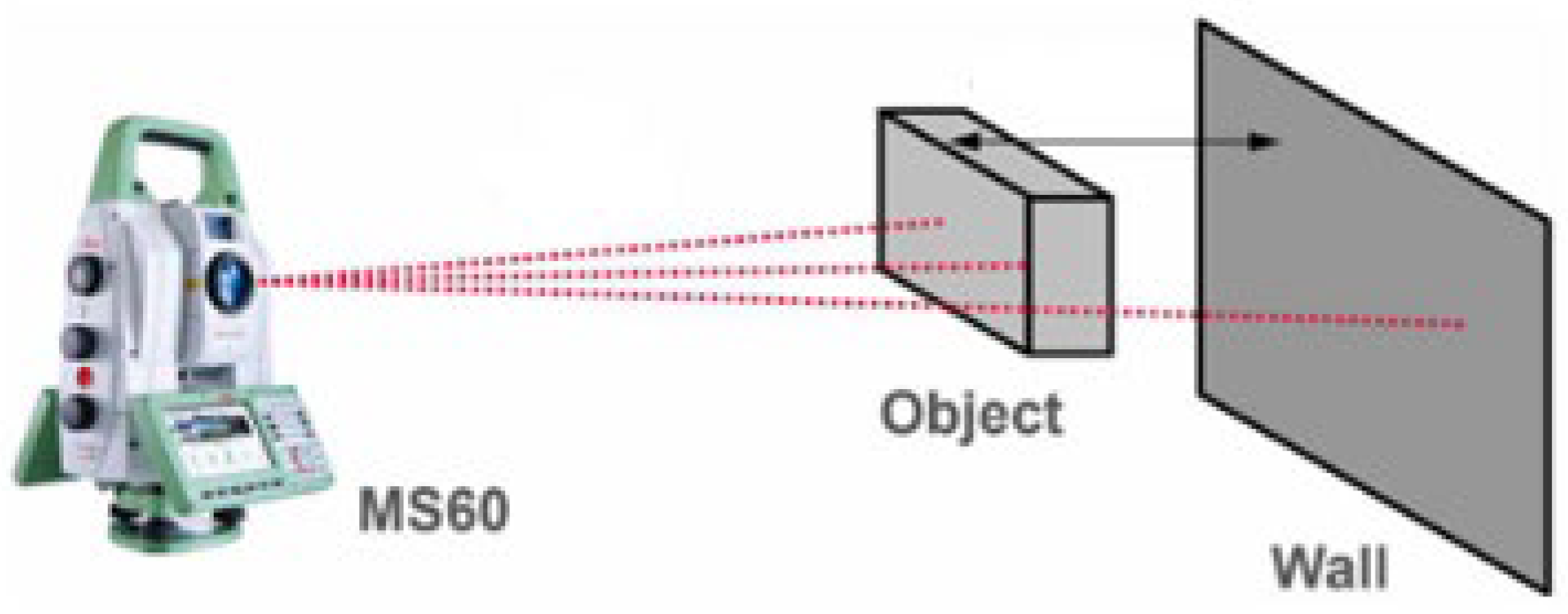
6.5. Tilted and Edged Surface
7. Current Challenges and Paths Forward
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Medic, T.; Holst, C.; Kuhlmann, H. Improving the results of terrestrial laser scanner calibration by an optimized calibration process. In Proceedings of the Oldenburger 3D-Tage 2019, Oldenburg, Germany, 6–7 February 2019. [Google Scholar]
- Shi, S.; Muralikrishnan, B.; Sawyer, D. Terrestrial laser scanner calibration and performance evaluation using the network method. Opt. Lasers Eng. 2020, 134, 106298. [Google Scholar] [CrossRef] [PubMed]
- Walsh, G. Leica ScanStation White Paper: Leica ScanStation P-Series—Details That Matter; Leica Geosystems AG: Heerbrugg, Switzerland, 2015. [Google Scholar]
- Abbas, M.A.; Setan, H.; Majid, Z.; Chong, A.K.; Luh, L.C.; Idris, K.M.; Ariff, M.F.M. Investigation of systematic errors for the hybrid and panoramic scanners. J. Teknol. 2014, 71, 65–70. [Google Scholar] [CrossRef]
- Garcia-San-Miguel, D.; Lerma, J.L. Geometric calibration of a terrestrial laser scanner with local additional parameters: An automatic strategy. ISPRS J. Photogramm. Remote Sens. 2013, 79, 122–136. [Google Scholar] [CrossRef]
- Holst, C.; Artz, T.; Kuhlmann, H. Biased and unbiased estimates based on laser scans of surface with unknown deformations. J. Appl. Geod. 2014, 8, 169–183. [Google Scholar] [CrossRef]
- Yen, J.; Leber, D.; Pibida, L. Comparing Instruments. NIST Technical Note 2016. Available online: https://nvlpubs.nist.gov/nistpubs/TechnicalNotes/NIST.TN.2106.pdf (accessed on 20 May 2025).
- Muralikrishnan, B. Performance evaluation of terrestrial laser scanners—A review. Meas. Sci. Technol. 2021, 32, 072001. [Google Scholar] [CrossRef] [PubMed]
- Al-Manasir, K.; Lichti, D.D. Self-calibration of a Leica HDS7000 Scanner. In Proceedings of the FIG Working Week 2015, Wisdom of the Ages to the Challenges of the Modern World, Sofia, Bulgaria, 17–21 May 2015; Available online: https://www.fig.net/resources/proceedings/fig_proceedings/fig2015/papers/ts07e/TS07E_al-manasir_lichti_7889.pdf (accessed on 20 May 2025).
- Medić, T.; Kuhlmann, H.; Holst, C. Designing and Evaluating a User-Oriented Calibration Field for the Target-Based Self-Calibration of Panoramic Terrestrial Laser Scanners. Remote Sens. 2020, 12, 15. [Google Scholar] [CrossRef]
- Lichti, D.D. Error modelling, calibration and analysis of an AM-CW terrestrial laser scanner system. ISPRS J. Photogramm. Remote Sens. 2007, 61, 307–324. [Google Scholar] [CrossRef]
- Legal Traceability of Length for Electronic Distance Measurement Equipment: Procedure Manual; Department of Natural Resources and Mines, Queensland Government: Brisbane, Australia, 2012.
- Zakaria, F.A.; Yatim, M.H.M.; Ariff, M.F.M.; Razali, A.F.; Choon, T.L.; Hamid, H.A. Utilizing Terrestrial Laser Scanning Dataset for Cadastral Surveying. J. Adv. Geospat. Sci. Technol. 2024, 4, 205–230. [Google Scholar] [CrossRef]
- Jia, D.; Zhang, W.; Liu, Y. Systematic Approach for Tunnel Deformation Monitoring with Terrestrial Laser Scanning. Remote Sens. 2020, 13, 3519. [Google Scholar] [CrossRef]
- Algadhi, A.; Psimoulis, P.; Grizi, A.; Neves, L. Assessment of the Accuracy of Terrestrial Laser Scanners in Detecting Local Surface Anomaly. Remote Sens. 2024, 16, 4647. [Google Scholar] [CrossRef]
- Hosseini, K.; Reindl, L.; Raffl, L.; Wiedemann, W.; Holst, C. 3D Landslide Monitoring in High Spatial Resolution by Feature Tracking and Histogram Analyses Using Laser Scanners. Remote Sens. 2024, 16, 138. [Google Scholar] [CrossRef]
- Xhou, Y.; Zhu, J.; Zhau, L.; Hu, G.; Xin, J.; Zhang, H.; Yang, J. High-Precision Monitoring Method for Bridge Deformation Measurement and Error Analysis Based on Terrestrial Laser Scanning. Remote Sens. 2024, 16, 2263. [Google Scholar] [CrossRef]
- Zhao, L.; Ma, X.; Xiang, Z.; Zhang, S.; Hu, C.; Zhou, Y.; Chen, G. Landslide Deformation Extraction from Terrestrial Laser Scanning Data with Weighted Least Squares Regularization Iteration Solution. Remote Sens. 2022, 14, 2897. [Google Scholar] [CrossRef]
- Yang, Y.; Balagne, L.; Gericke, O.; Scheer, D.; Zhang, L.; Sobek, W.; Schweiger, V. Monitoring of the Production Process of Graded Concrete Component Using Terrestrial Laser Scanning. Remote Sens. 2021, 13, 1622. [Google Scholar] [CrossRef]
- Holst, C.; Medić, T.; Kuhlmann, H. Dealing with systematic laser scanner errors due to misalignment at area-based deformation analyses. J. Appl. Geodesy 2018, 12, 169–185. [Google Scholar] [CrossRef]
- Holst, C.; Kuhlmann, H. Challenge and present fields of action at laser scanner-based deformation on analysis. J. Appl. Geod. 2016, 10, 17–25. [Google Scholar] [CrossRef]
- Boehler, W.; Vincent, M.B.; Marbs, A. Investigating laser Scanner Accuracy. IAPRS, XXXIV (5/C15). 2003, pp. 696–701. Available online: https://www.researchgate.net/publication/246536800_Investigating_laser_scanner_accuracy (accessed on 20 May 2025).
- Wunderlich, T.; Wasmeier, P.; Ohlmann-Lauber, J.; Schaefer, T.; Reidi, F. Objective Specification of TLS—A Contribution of the Geodetic Laboratory at the TUM; Blue Series Book at the Chair of Geodesy; Technical University of Munich: Munich, Germany, 2013; Volume 21, Available online: https://mediatum.ub.tum.de/doc/1188549/document.pdf (accessed on 20 May 2025).
- Jaafar, H.A.; Meng, X.; Sowter, A. Terrestrial laser scanner error quantification for the purpose of monitoring. Surv. Rev. 2018, 50, 232–248. [Google Scholar] [CrossRef]
- Liu, W.; Sun, S.; Li, Z.; Ge, S.; Sotelo, M.A.; Li, W. Compensation of Geometric Parameter Errors for Terrestrial Laser Scanner by Integrating Intensity Correction. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7483–7495. [Google Scholar] [CrossRef]
- Kermarrec, G.; Loesler, M. How to account for temporal correlations with a diagonal correlation model in a nonlinear functional model: A plane fitting with simulated and real TLS measurements. J. Geod. 2021, 95, 5. [Google Scholar] [CrossRef]
- Lichti, D.D.; Pexman, K.; Tredoux, X. New method for first-order network design applied to TLS self-calibration networks. ISPRS J. Photogramm. Remote Sens. 2021, 177, 306–318. [Google Scholar] [CrossRef]
- Maar, H.; Zogg, H.M. WFD—Wave Form Digitizer Technology White Paper; Leica Geosystem: Heerbrugg, Switzerland, 2021. [Google Scholar]
- Lichti, D.D. The impact of angle parameterization on terrestrial laser scanner self-calibration. In Laser Scanning 2009; Bretar, F., Pierrot-Deseilligny, M., Vosselman, G., Eds.; IAPRS: Paris, France, 2009. [Google Scholar]
- Abbas, M.A.; Setan, H.; Majid, Z.; Idris, K.M.; Ariff, M.F.M.; Lichti, D.D. The effect of datum constraints for terrestrial laser scanner self-calibration. In Proceedings of the FIG Congress 2014, Kuala Lumpur, Malaysia, 16–21 June 2014. [Google Scholar]
- Jurek, T.; Kuhlmann, H.; Holst, C. Impact of spatial correlations on the surface estimation based on TLS. J. Appl. Geod. 2017, 11, 143–155. [Google Scholar] [CrossRef]
- Sabzali, M.; Jazirian, I. Improvemnt of modelling of atmospheric effects for electronic distance measurements (EDM): Analysis of air temperature, atmospheric pressure and relative humidity of the air. Geod. Cartogr. 2022, 48, 20–30. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Jaakkola, A.; Kaasalainen, M.; Krooks, A.; Kukko, A. Analysis of Incidence Angle and Distance Effects on Terrestrial Laser Scanner Intensity: Search for Correction Methods. Remote Sens. 2011, 3, 2207–2221. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Ferrucci, M.; Sawyer, D.; Gerner, G.; Lee, V.; Blackburn, C.; Phillips, S.; Petrov, P.; Yakovlev, Y.; Astrelin, A.; et al. Volumetric performance evaluation of a laser scanner based on geometric error model. Precis. Eng. 2015, 40, 139–150. [Google Scholar] [CrossRef]
- Lerma, J.L.; Garcia-San-Miguel, D. Self-Calibration of Terrestrial Laser Scanners: Selection on the best Geometric Additional Parameters. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 219–226. [Google Scholar] [CrossRef]
- Neitzel, F. Investigation of Axes Errors of Terrestrial Laser Scanners. In Proceedings of the Fifth International Symposium Turkish-German Joint Geodetic Days, Berlin, Germany, 29–31 March 2006. [Google Scholar]
- Lichti, D.D. A review of geometric models and self-calibration methods for terrestrial laser scanner. Bol. Ciências Geodésicas 2010, 10, 3–19. [Google Scholar]
- Pareja, T.F.; Pablos, A.G.; Oliva, J.D.V. Terrestrial Laser Scanner (TLS) Equipment Calibration. Procedia Eng. 2013, 63, 278–286. [Google Scholar] [CrossRef]
- Holst, C.; Kuhlmann, H. Aiming at self-calibration of terrestrial laser scanners only one single object and one single scan. Appl. Geodesy 2014, 8, 295–310. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Xie, X.; Xu, L. Terrestrial laser scanner autonomous self-calibration with no prior knowledge of point-clouds. IEEE Sens. J. 2018, 18, 9277–9285. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Xie, X.; Xu, L. Lab-built terrestrial laser scanner self-calibration using mounting angle error correction. Opt. Express 2018, 26, 14444–14460. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Cheng, X.; Shan, R. A Self-Calibration Method for Terrestrial Laser Scanner. In Proceedings of the Asian Conference on Remote Sensing, Daejeon, Republic of Korea, 14–18 October 2019. [Google Scholar]
- Stark, E.; Mikhail, E. Least Squares & Non-Linear Functions. Photogramm. Eng. 1973, 39, 405–412. [Google Scholar]
- Reshetyuk, Y. Self-Calibration and Direct Georeferencing in Terrestrial Laser Scanning. Ph.D. Thesis, KTH University, Stockholm, Sweden, 2009. [Google Scholar]
- Reshetyuk, Y. A unified approach to self-calibration of terrestrial laser scanners. ISPRS J. Photogramm. Remote Sens. 2010, 65, 445–456. [Google Scholar] [CrossRef]
- Hughes, B.; Ferrucci, M.; Forbes, A. Preliminary Investigation into the Use of a Network-Based Technique for Calibration of 3D Laser Scanners; National Physical Library: Middlesex, UK, 2015. [Google Scholar]
- Zhou, Y.; Shen, S.; Hu, Z. Detail preserved surface reconstruction from point cloud. Sensors 2019, 19, 1278. [Google Scholar] [CrossRef] [PubMed]
- Chow, J.C.K.; Lichti, D.D.; Glennie, C. Point-based versus plane-based self-calibration of static terrestrial laser scanning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, 121–126. [Google Scholar] [CrossRef]
- Chan, T.O.; Lichti, D.D. Cylinder-based self-calibration of a panoramic terrestrial laser scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 169–174. [Google Scholar] [CrossRef]
- Chan, T.O.; Lichti, D.D.; Belton, D. Temporal analysis and automatic calibration of the Velodyne HDL-32E Lidar Systems. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 2, 61–66. [Google Scholar] [CrossRef]
- Chow, J.; Ebeling, A.; Teskey, B. Low cost artificial planar target measurement techniques for terrestrial laser scanning. In Proceedings of the FIG Congress 2010, Sydney, Australia, 11–16 April 2010. [Google Scholar]
- Lichti, D.D.; Chow, J.C.K. Inner constraints for planar features. Photogramm. Rec. 2013, 28, 74–85. [Google Scholar] [CrossRef]
- Glennie, C.; Lichti, D.D. Static Calibration and Analysis of the Velodyne HDL-64E32 for High Accuracy Mobile Scanning. Remote Sens. 2010, 2, 1610–1624. [Google Scholar] [CrossRef]
- Abbas, M.A.; Lichti, D.D.; Chong, A.K.; Setan, H.; Majid, Z. An on-site approach for the self-calibration of terrestrial laser scanners. Measurement 2014, 52, 111–123. [Google Scholar] [CrossRef]
- Qiao, J.; Butt, J.A. Self-calibration of terrestrial laser scanner using a M3C2-based planar patch algorithm. ISPRS J. Photogramm. Remote Sens. 2023, 197, 335–345. [Google Scholar] [CrossRef]
- Alkan, R.M.; Karsidag, G. Analysis of the Accuracy of Terrestrial Laser Scanning measurements. In Proceedings of the FIG Working Week 2012, Rome, Italy, 6–10 May 2012. [Google Scholar]
- Bae, K.H.; Lichti, D.D. On-site self-calibration planar features for Terrestrial laser scanners. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2007, 36, 14–19. [Google Scholar]
- Chow, J.C.K.; Lichti, D.D.; Teskey, W.F. Accuracy assessment of the Faro Focus and Leica HDS6100 panoramic-type terrestrial laser scanners through point-based and plane-based user self-calibration. In Proceedings of the FIG Working Week, Rome, Italy, 6–10 May 2012. [Google Scholar]
- Medić, T.; Kuhlmann, H.; Holst, C. Empirical Evaluation of Terrestrial Laser Scanner Calibration Strategies: Manufacturer-Based, Target-Based and Keypoint-Based. In Contributions to International Conferences on Engineering Surveying; Kopáčik, A., Kyrinovič, P., Erdélyi, J., Paar, R., Marendić, A., Eds.; Springer Proceedings in Earth and Environmental Sciences; Springer: Cham, Switzerland, 2021; pp. 41–56. [Google Scholar] [CrossRef]
- Grafarend, E.W. Optimization of Geodetic Network. Can. Surv. 1974, 28, 716–723. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R. Analytical Methods in Optimization and Design of Geodetic Networks. Master’s Thesis, University of Khaje Nasir Toosi (KNTU), Tehran, Iran, 1998. [Google Scholar]
- Alizadeh-Khameneh, M.A. On Optimization and Design of Geodetic Networks. Ph.D. Thesis, KTH University, Stockholm, Sweden, 2015. [Google Scholar]
- Amiri-Simkooei, A.R.; Asgari, J.; Zanganeh-Nejad, F.; Zaminpardaz, S. Basic Concepts of Optimization and Design of Geodetic Networks. J. Surv. Eng. 2012, 138, 172–183. [Google Scholar] [CrossRef]
- Lichti, D.D. Terrestrial Laser Scanner Self-Calibration: Correlation Sources and their Mitigation. ISPRS J. Photogramm. Remote Sens. 2010, 65, 93–102. [Google Scholar] [CrossRef]
- Sossan, B. Criteria for choosing test objects type for terrestrial laser scanners calibration. Geod. Cartogr. Arial Photogr. 2022, 95, 31–38. [Google Scholar]
- Gruen, A.; Huang, S.T. Calibration and Orientation of Cameras in Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mikhail, E.M.; Bethel, J.S.; McGlone, J.C. Introduction to Modern Photogrammetry; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Rodriguez, F.C.; Medeiros, L.; Klein, I.; Veiga, L.A.K. Free Network Adjustment: Minimum Inner Constraints and Pseudo-Inverse Approaches. Revista ud y La Geomatica. 2020. Available online: https://www.researchgate.net/publication/344211053_Free_network_adjustment_Minimum_inner_constraints_and_Pseudo-inverse_approaches (accessed on 20 May 2025).
- Ogundare, J.O. Understanding Least Squares Estimation and Geomatics Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Parian, J.A.; Gruen, A. Self-Calibrating Network Analysis for Panoramic Camera by Heuristic Simulation; ETH Library: Zurich, Switzerland, 2006; Available online: https://www.isprs.org/PROCEEDINGS/XXXVI/part5/paper/PARI_655.pdf (accessed on 20 May 2025).
- Parian, J.A. Sensor modeling, self-calibration and accuracy testing of panoramic cameras and laser scanners. ISPRS J. Photogramm. Remote Sens. 2010, 65, 60–76. [Google Scholar] [CrossRef]
- Parian, J.A.; Gruen, A. Integrated laser scanner and intensity Image calibration and accuracy assessment. In Proceedings of the ISPRS III/3, III/4, V/3 Workshop “Laser Scanning 2005”, Eschede, The Netherlands, 12–14 September 2005. [Google Scholar]
- Remondino, F.; Fraser, C. Digital camera calibration methods: Considerations and comparisons. ISPRS Comm. V Symp. Image Eng. Vis. Metrol. 2005, 36, 266–272. Available online: https://www.isprs.org/proceedings/xxxvi/part5/paper/remo_616.pdf (accessed on 20 May 2025).
- Sabzali, M.; Pilgrim, L. Investigation of Correlation Between Self-Calibration Parameters of Terrestrial Laser Scanner (TLS). Asian J. Geoinf. 2024. Available online: https://aars-ajg.org/article/24/AJG-2311016.pdf (accessed on 20 May 2025).
- Sabzali, M.; Pilgrim, L. New Parametrization of Bundle Block Adjustment for Self-calibration of Terrestrial Laser Scanner (TLS). Photogramm. Rec. 2025, 40, 190. [Google Scholar] [CrossRef]
- Lichti, D.D. The impact of distribution of observations on TLS self-calibration quality. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 315–322. [Google Scholar] [CrossRef]
- Lichti, D.D.; Chan, T.O.; Belton, D. Linear regression with an observation distribution model. Geodesy 2021, 95, 1–14. [Google Scholar] [CrossRef]
- Chen, Y.C. A tutorial on Kernel Density Estimation and Recent Advances. Biostat. Epidemiology 2017, 1, 161–187. [Google Scholar] [CrossRef]
- Medic, T.; Kuhlmann, H.; Holst, C. Sensitivity Analysis and minimal measurement geometry for the target-based calibration high end panoramic TLS. Remote Sens. 2019, 11, 1519. [Google Scholar] [CrossRef]
- Zhou, T.; Cheng, X.; Lin, P.; Wu, Z.; Liu, E. A General Point-Based Method for Self-Calibration of Terrestrial Laser Scanners Considering Stochastic Information. Remote Sens. 2020, 12, 2923. [Google Scholar] [CrossRef]
- Kerekes, G.; Schwieger, V. Elementary Error Model Applied to Terrestrial Laser Scanning Measurements: Study Case Arch Dam Kops. Mathematics 2020, 8, 593. [Google Scholar] [CrossRef]
- Kerekes, G.; Schwieger, V. Determining Variance-Covariance Matrices for Terrestrial Laser scans: A Case Study of the Arch Dam Kops. In Proceedings of the Contributions to International Conferences on Engineering Surveying; 2021. Available online: https://link.springer.com/chapter/10.1007/978-3-030-51953-7_5 (accessed on 20 May 2025).
- Raschhofer, J.; Kerekes, G.; Harmening, C.; Neuner, H.; Schwieger, V. Estimating Control Points for B-Spline Surfaces Using Fully Populated Synthetic Variance–Covariance Matrices for TLS Point Clouds. Remote Sens. 2021, 13, 3124. [Google Scholar] [CrossRef]
- Kresten, T.P.; Lindstaedt, M. Geometric Accuracy Investigations of Terrestrial Laser Scanner Systems in the Laboratory and in the Field. Appl. Geomat. 2022, 14, 421–434. [Google Scholar] [CrossRef]
- Wang, L.; Muralikrishnan, B.; Rachakonda, P.; Sawyer, D. Determining geometric error model parameters of a terrestrial laser scanner through Two-face, Length-consistency, and Network methods. Meas. Sci. Technol. 2017, 28, 065016. [Google Scholar] [CrossRef] [PubMed]
- Muralikrishnan, B.; Wang, L.; Rachakonda, P.; Sawyer, D. Terrestrial laser scanner geometric error model parameter correlations in the Two-face, Length-consistency, and Network methods of self-calibration. Precis. Eng. 2018, 52, 15–29. [Google Scholar] [CrossRef]
- Tsakiri, M.; Pagounis, V.; Arabatzi, O. Evaluation of a pulsed terrestrial laser scanner based on ISO standards. Surf. Topogr. Metrol. Prop. 2015, 3, 015006. [Google Scholar] [CrossRef]
- Lichti, D.D. Ray-Tracing Method for Deriving Terrestrial Laser Scanner Systematic Errors. J. Surv. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Medić, T.; Kuhlmann, H.; Holst, C. Automatic in-situ self-calibration of a panoramic TLS from a single station using 2D key points. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4, 413–420. [Google Scholar] [CrossRef]
- Neitzel, F.; Gordon, B.; Wujanz, D. Verfahren zur Standardisierten Überprüfung von Terrestrischen Laserscannern (TLS); DVW. EV Society for Geodesy, Geoinformation and land management: Berlin, Germany, 2014. [Google Scholar]
- Holst, C.; Neuner, H.; Wieser, A.; Wunderlich, T. Calibration of Terrestrial Laser Scanner. Allgem. Verm. Nachr. 2016, 123, 147–157. [Google Scholar]
- Friedli, E.; Presl, R.; Wieser, A. Influence of atmospheric refraction on terrestrial laser scanning at long range. In Proceedings of the 4th Joint International Symposium on Deformation Monitoring (JISDM), Athens, Greece, 15–17 May 2019. [Google Scholar]
- Barrell, H.; Sears, J.E. The refraction and dispersion of air for the visible spectrum. J. Philos. Trans. R. Soc. Lond. 1939, 238, 1–64. [Google Scholar]
- Edlen, B. The dispersion of standard air. J. Opt. Soc. Am. 1956, 43, 339–344. [Google Scholar] [CrossRef]
- Edlen, B. The refractive index of air. J. Meterologia 1966, 2, 71–80. [Google Scholar] [CrossRef]
- Owens, J.C. Optical refractive index of air: Dependence on pressure, temperature, and composition. Appl. Opt. 1967, 6, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Peck, E.R.; Reeder, K. Dispersion of Air. J. Opt. Soc. Am. 1972, 62, 958–962. [Google Scholar] [CrossRef]
- Jones, C.E. The air density equation and the transfer of the mass unit. J. Res. Natl. Bur. Stand. 1978, 83, 419–428. [Google Scholar] [CrossRef] [PubMed]
- Jones, C.E. The refractivity of air. J. Res. National Bur. Standards 1981, 86, 27–32. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, H. The refractive index of moist air in the 3-µ region. Metrologia 1982, 18, 49–52. [Google Scholar] [CrossRef]
- Birch, K.; Downs, M. The results of a comparison between calculated and measured values of the refractive index of air. J. Phys. E Sci. Instruments 1988, 21, 694–695. [Google Scholar] [CrossRef]
- Birch, K.; Downs, M. An updated Edlen equation for the refractive index of air. Metrologia 1993, 30, 155–162. [Google Scholar] [CrossRef]
- Ciddor, P.E. Refractive Index of Air: New Equation for Visible and Near Infrared. Appl. Opt. 1996, 35, 1566–1573. [Google Scholar] [CrossRef] [PubMed]
- Ciddor, P.E.; Hill, R.J. Refractive index of air. 2. Group Index. J. Appl. Opt. 1999, 59, 1663–1667. [Google Scholar] [CrossRef] [PubMed]
- Bonsch, G.; Potulski, E. Measurement of the refractive index of air and comparison with modified Edlen’s formulae. J. Meteologia 1998, 28, 133–139. [Google Scholar]
- IAG Resolutions. International Association of Geodesy [IAG]. In Proceedings of the IAG Resolutions at the XXIIth General Assembly, Birmingham, UK, 18–30 July 1999. [Google Scholar]
- Mathar, R.J. Refractive index of humid air in the infrared: Model fits. J. Opt. A Pure Appl. Opt. 2007, 9, 470–476. [Google Scholar] [CrossRef]
- Pollinger, F. Refractive index of air. 2. Group index: Comment. Appl. Opt. 2020, 59, 9771–9772. [Google Scholar] [CrossRef] [PubMed]
- Sabzali, M.; Pilgrim, L. Updated Atmospheric Modelling of Refracted Zenith Angle Using Vertical Temperature Gradient for Refraction Coefficient. J. Geosci. Geomatics 2023, 11, 11–20. [Google Scholar] [CrossRef]
- Sabzali, M.; Pilgrim, L. Improved Model of Refracted Horizontal Angle: Dependency on Zenith Angle. Am. J. Civ. Eng. Arch. 2023, 11, 38–44. [Google Scholar] [CrossRef]
- Bomford, B.G. Geodesy; Clarendon Press: Oxford, UK, 1962. [Google Scholar]
- Reuger, J.M. Electronic Distance Measurements, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Dvoracek, F. Interpretation and Evaluation of Procedures for Calculating the Group refractive Index of Air by Ciddor and Hill. Section Geodesy and Mine Surveying. 2018. Available online: https://www.sgem.org/index.php/elibrary-research-areas?view=publication&task=show&id=707 (accessed on 20 May 2025).
- Dodson, A.H.; Zaher, M. Refraction Effects on Vertical Angle Measurements. Surv. Rev. 1985, 28, 169–183. [Google Scholar] [CrossRef]
- Torge, W. Geodesy, 3rd ed.; Walter de Gruyter: Berlin, Germany; New York, NY, USA, 2001. [Google Scholar]
- Johnston, A. Lateral Refraction in Tunnels. Surv. Rev. 1991, 31, 201–220. [Google Scholar] [CrossRef]
- Nikolitsas, K.; Lambrou, E. A Methodology for Correcting Refraction in Vertical Angles for Precise Monitoring in Tunnels. In Proceedings of the 4th Joint International Symposium on Deformation Monitoring, Athens, Greece, 15–17 May 2019. [Google Scholar]
- Brys, H.; Justniyak, N. Mathematical-physical model of horizontal refraction in measuring alignment of elongated engineering objects. Geomat. Landmanag. Landsc. 2016, 25–32. [Google Scholar] [CrossRef]
- Bajtala, M.; Sokol, S.; Cernota, P. Estimation of a Horizontal Refraction in a Geodetic Network. J. Pol. Miner. Eng. Soc. 2016, 17, 201–212. [Google Scholar]
- Soudarissanane, S.; Lindenbergh, R.; Menenti, M.; Teunissen, P. Scanning geometry: Influencing factor on the quality of terrestrial laser scanning points. ISPRS J. Photogramm. Remote Sens. 2011, 66, 389–399. [Google Scholar] [CrossRef]
- Karaszewski, M.; Adamczyk, M.; Sitnik, R. Assessment of next-best-view algorithms performance with various 3D scanners and amnipulator. ISPRS J. Photogramm. Remote Sens. 2016, 119, 320–333. [Google Scholar] [CrossRef]
- Lichti, D.D.; Gordon, S.J.; Tipdecho, T. Error Models and Propagation in Directly Georeferenced Terrestrial Laser Scanner Networks. J. Surv. Eng. 2005, 131, 135–142. [Google Scholar] [CrossRef]
- Soudarissanane, S.; Lindenbergh, R.C. Optimizing terrestrial laser scanning measurement set-ups. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 38, 127–132. [Google Scholar] [CrossRef]
- Cabrera-Revuelta, E.; Tavolare, R.; Buldo, M.; Verdoscia, C. Planning for terrestrial laser scanning: Methods for optimal sets of locations in architectural sites. J. Build. Eng. 2024, 85. [Google Scholar] [CrossRef]
- Giorgini, M.; Marini, S.; Monica, R.; Aleotti, J. Sensor-Based Optimization of Terrestrial Laser Scanning Measurement Setup on GPU. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1452–1456. [Google Scholar] [CrossRef]
- Zeng, Y.; Liu, J.; Cao, Q.; Wu, Z.; Chen, B.; Li, D.; Cheng, G. Optimal planning of indoor laser scans based on continuous optimization. Autom. Constr. 2022, 143, 104552. [Google Scholar] [CrossRef]
- Kriegel, S.; Bodenmuller, T.; Suppa, M.; Hirzinger, G. A surface-based Next-Best-View Approach for Automated 3D Model Completion of Unkown Objects. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar] [CrossRef]
- Chen, S.Y.; Li, Y.F. Vision sensor planning for 3D model acquisition. IEEE Trans. Geosci. Remote Sens. 2005, 35, 894–904. Available online: https://personal.cityu.edu.hk/meyfli/Publication/file/CSY_SMC05.pdf (accessed on 20 May 2025).
- Collander, C.; Beksi, W.J.; Huber, M. Learning the Next Best View for 3D Point Clouds via Topological Features. arXiv 2021, arXiv:2103.02789. [Google Scholar] [CrossRef]
- Soudarissanane, S.; Lindenbergh, R.; Gorte, B. Reducing the errors in terrestrial laser scanning by optimizing the measurement set-up. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, China, 3–11 July 2008. [Google Scholar]
- Soudarissanane, S.; Ree, J.V.; Bucksch, A.; Lindenbergh, R. Error Budget of Terrestrial Laser Scanning: Influence of the Incidence Angle on the Scan Quality; Delft University: Delft, The Netherlands, 2006. [Google Scholar]
- Ling, Z.; Yuqing, M.; Ruoming, S. Study on the resolution of laser scanning point cloud. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, IGARSS 2008, Boston, MA, USA, 8–11 July 2008. [Google Scholar]
- Chen, M.; Pan, J.; Xu, J. Classification of Terrestrial Laser Scanning Data with Density-Adaptive Geometric Features. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1795–1799. [Google Scholar] [CrossRef]
- Schmitz, B.; Kuhlmann, H.; Holst, C. Investigating the resolution capability of terrestrial laser scanners and their impact on the effective number of measurements. ISPRS J. Photogramm. Remote Sens. 2020, 159, 41–52. [Google Scholar] [CrossRef]
- Lichti, D.D. A Resolution Measure for Terrestrial Laser Scanners. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. 2005. Available online: https://www.isprs.org/proceedings/xxxv/congress/comm5/papers/552.pdf (accessed on 20 May 2025).
- Lichti, D.D.; Jamtsho, S. Angular resolution of Terrestrial laser scanners. Photogrammtric Rec. 2006, 21, 141–160. [Google Scholar] [CrossRef]
- Yang, R.; Hua, X.; Liu, J.; Wu, H. Research on the three angular resolutions of terrestrial laser scanning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 187–192. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning–an introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Jelalian, A. Laser Radar Systems; Artech House: London, UK, 1992. [Google Scholar]
- Jenn, D. Laser Cross Section (LCS); Naval Postgraduate School: Monterey, CA, USA, 2010. [Google Scholar]
- Tan, K.; Zhang, W.; Shen, F.; Cheng, X. Investigation of TLS Intensity Data and Distance Measurement Errors from Target Specular Reflections. Remote Sens. 2018, 10, 1077. [Google Scholar] [CrossRef]
- Kamermann, G.W. Active Electro-Optical Systems; Optical Engineering Press: Bellingham, WA, USA, 1993; Chapter 1. [Google Scholar]
- McManamon, P.F.; Kamerman, G.; Huffaker, M. A history of Laser Radar in the United States. Int. Soc. Opt. Eng. 2010. [Google Scholar] [CrossRef]
- McManamon, P. Review of LADAR: A historic, yet emerging, sensor technology with rich phenomenology. Opt. Eng. 2012, 51, 060901. [Google Scholar] [CrossRef]
- Soudarissananae, S.; Lindenbergh, R.; Menenti, M.; Teunissen, P. Incidence Angle Influence on the Quality of Terrestrial Laser Scanning Points. In Laser Scanning, Proceedings of the ISPRS Workshop Laserscanning, Paris, France, 1–2 September 2009; Bretar, F., Pierrot-Deseillignay, M., Vosselman, G., Eds.; TU Delft: Delft, The Netherlands, 2011; Available online: https://resolver.tudelft.nl/uuid:b739bd05-c5bc-4ffa-aedb-318726f15e34 (accessed on 20 May 2025).
- Laser Radar: Progress and Opportunities in Active Electro-Optical Sensing; National Research Council (NRC): Washington, DC, USA; The National Academies Press: Washington, DC, USA, 2014.
- Lichti, D.D.; Harvey, B.R. The effects of reflecting surface material properties on time-of-flight laser scanner measurements. In Proceedings of the Symposium on Geospatial theory, Processing and Applications, Ottawa, ON, Canada, 8–12 July 2002; Available online: https://www.isprs.org/proceedings/xxxiv/part4/pdfpapers/180.pdf (accessed on 20 May 2025).
- Bolkas, D.; Martinez, A. Effect of target color and scanning geometry on terrestrial LiDAR point-cloud noise and plane fitting. J. Appl. Geod. 2017, 12, 109–127. [Google Scholar] [CrossRef]
- Tonietto, L.; Gonzaga, L.J.; Veronez, M.R.; Kazmierczak, C.D.S.; Arnold, D.C.C.; Costa, C.A.D. New Method for Evaluating Surface Roughness Parameters Acquired by Laser Scanning. Sci. Rep. 2019, 9, 15038. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.; Tagliasacchi, A.; Severesky, L.; Alliez, P.; Guennebaud, G.; Levine, J.; Sharf, A.; Silva, C. A survey of surface reconstruction from point clouds. In Computer Graphics Forum; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Santos, P.M.; Julio, E.N. A state-of-the-art review on roughness quantification methods for concrete surfaces. Constr. Build. Mater. 2013, 38, 912–923. [Google Scholar] [CrossRef]
- Moreau, N.; Roudet, C.; Gentil, C. Study and Comparison of Surface Roughness Measurements. 2014. Available online: https://www.researchgate.net/publication/281353260_Study_and_Comparison_of_Surface_Roughness_Measurements (accessed on 20 May 2025).
- Mah, J.; Samson, C.; McKinnon, S.D.; Tibodeau, D. 3D laser imaging for surface roughness analysis. Int. J. Rock Mech. Min. Sci. 2013, 58, 111–117. [Google Scholar] [CrossRef]
- Voisin, S.; Foufou, S.; Truchetet, F.; Paage, D.; Abidi, M. Study of ambient light influence for three-dimensional scanners based on structured light. Opt. Eng. 2007, 46, 030502. [Google Scholar] [CrossRef]
- Clark, J.; Robson, S. Accuracy of measurements made with a Cyrax 2500 Laser Scanner against surfaces of known color. Surv. Rev. 2004, 37, 626–638. [Google Scholar] [CrossRef]
- Pfeifer, N.; Dorininger, P.; Haring, A.; Fan, H. Investigating Terrestrial Laser Intensity Data Quality and Functional Relations. 2007. Available online: https://www.researchgate.net/publication/242037767_Investigating_terrestrial_laser_scanning_intensity_data_quality_and_functional_relations (accessed on 20 May 2025).
- Yaman, A.; Yilmaz, H.M. The effects of object surface colors on terrestrial laser scanners. Int. J. Eng. Geosci. 2017, 2, 68–74. [Google Scholar] [CrossRef]
- Wujanz, D. Intensity calibration method for 3D laser scanner. J. N. Z. Inst. Surv. 2009. Available online: https://espace.curtin.edu.au/handle/20.500.11937/9457 (accessed on 20 May 2025).
- Silva, B.B.D.; Braga, A.C.; Braga, C.C.; Olivera, L.M.M.D.; Montenegro, S.M.G.L.; Junior, B.B. Procedure for calculation of the albedo with OLI-Lnadsat 8 images: Application to Brazilian semi-arid. Rev. Bras. Eng. Agric. Ambient. 2016, 20, 3–8. [Google Scholar] [CrossRef]
- Fraser, C.S. Photogrammetric Camera Component Calibration: A Review of Analytical Techniques. In Calibration and Orientation of Cameras in Computer Vision; Gruen, A., Huang, T.S., Eds.; Springer Series in Information Sciences; Springer: Berlin/Heidelberg, Germany, 2001; Volume 34. [Google Scholar] [CrossRef]
- Alsadik, B.; Abdulateef, N.A. Epi-polar geometry between photogrammetry and Computer vision—A computational guide. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 5, 25–32. [Google Scholar] [CrossRef]
- El-Ashmawy, K.L.A. A comparison study between collinearity condition, coplanarity condition, and direct linear transformation (DLT) method for camera exterior orientation parameters determination. Geod. Cartogr. 2015, 41, 66–73. [Google Scholar] [CrossRef]
- El-Ashmawy, K.L.A. Coplanarity Condition for Photogrammetric simultaneous and self-calibration block adjustments. Int. J. Adv. Sci. Res. Eng. (IJASRE) 2021, 7, 1–14. [Google Scholar] [CrossRef]
- ISO/IEC Guide 98-3:2008; Uncertainty of Measurement. ISO: Geneva, Switzerland, 2008.
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- McManamon, P.F. LiDAR Technologies and Systems; SPIE Press Book: Bellingham, WA, USA, 2019. [Google Scholar]
- McManamon, P.F. Field Guide to Lidar; SPIE Library: Bellingham, WA, USA, 2015. [Google Scholar]
- Hartmann, J.; Alkhatib, H. Uncertainty Modelling of Laser Scanning Point Clouds Using Machine-Learning Methods. Remote Sens. 2023, 15, 2349. [Google Scholar] [CrossRef]
- Hartmann, J.; Ernst, D.; Neumann, I.; Alkhatib, H. PointNet-based modeling of systematic distance deviations for improved TLS accuracy. J. Appl. Geod. 2024, 18, 613–628. [Google Scholar] [CrossRef]



| Calibration Parameters (CPs) | Range | Angle | |
|---|---|---|---|
| Vertical | Horizontal | ||
| Beam offset along horizontal and vertical plane (a1z, a1n) | ✓ | ✓ | |
| Transit offset (a2) | ✓ | ✓ | |
| Mirror offset (a3) | ✓ | ||
| Vertical angle index offset error (a4) | ✓ | ||
| Beam tilt angle along horizontal and vertical plane (a5z, a5n) | ✓ | ✓ | |
| Mirror tilt angle (a6) | ✓ | ||
| Transit tilt angle (a7) | ✓ | ||
| Horizontal angle encoder eccentricity along x and y planes (a8x, a8y) | ✓ | ||
| Vertical angle encoder eccentricity along x and y planes (a9x, a9y) | ✓ | ||
| Constant zero error (i.e., zero offset or bird-bath error) (a10) | ✓ | ||
| Second-order scale error in horizontal angle encoder in horizontal and vertical planes (a11a, a11b) | ✓ | ✓ | |
| Second-order scale error in vertical angle encoder in horizontal and vertical planes (a12a, a12b) | ✓ | ✓ | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabzali, M.; Pilgrim, L. A Comprehensive Review of Mathematical Error Characterization and Mitigation Strategies in Terrestrial Laser Scanning. Remote Sens. 2025, 17, 2528. https://doi.org/10.3390/rs17142528
Sabzali M, Pilgrim L. A Comprehensive Review of Mathematical Error Characterization and Mitigation Strategies in Terrestrial Laser Scanning. Remote Sensing. 2025; 17(14):2528. https://doi.org/10.3390/rs17142528
Chicago/Turabian StyleSabzali, Mansoor, and Lloyd Pilgrim. 2025. "A Comprehensive Review of Mathematical Error Characterization and Mitigation Strategies in Terrestrial Laser Scanning" Remote Sensing 17, no. 14: 2528. https://doi.org/10.3390/rs17142528
APA StyleSabzali, M., & Pilgrim, L. (2025). A Comprehensive Review of Mathematical Error Characterization and Mitigation Strategies in Terrestrial Laser Scanning. Remote Sensing, 17(14), 2528. https://doi.org/10.3390/rs17142528