Classification of Precipitation Types and Investigation of Their Physical Characteristics Using Three-Dimensional S-Band Dual-Polarization Radar Data
Abstract
1. Introduction
2. Data
3. Methodology
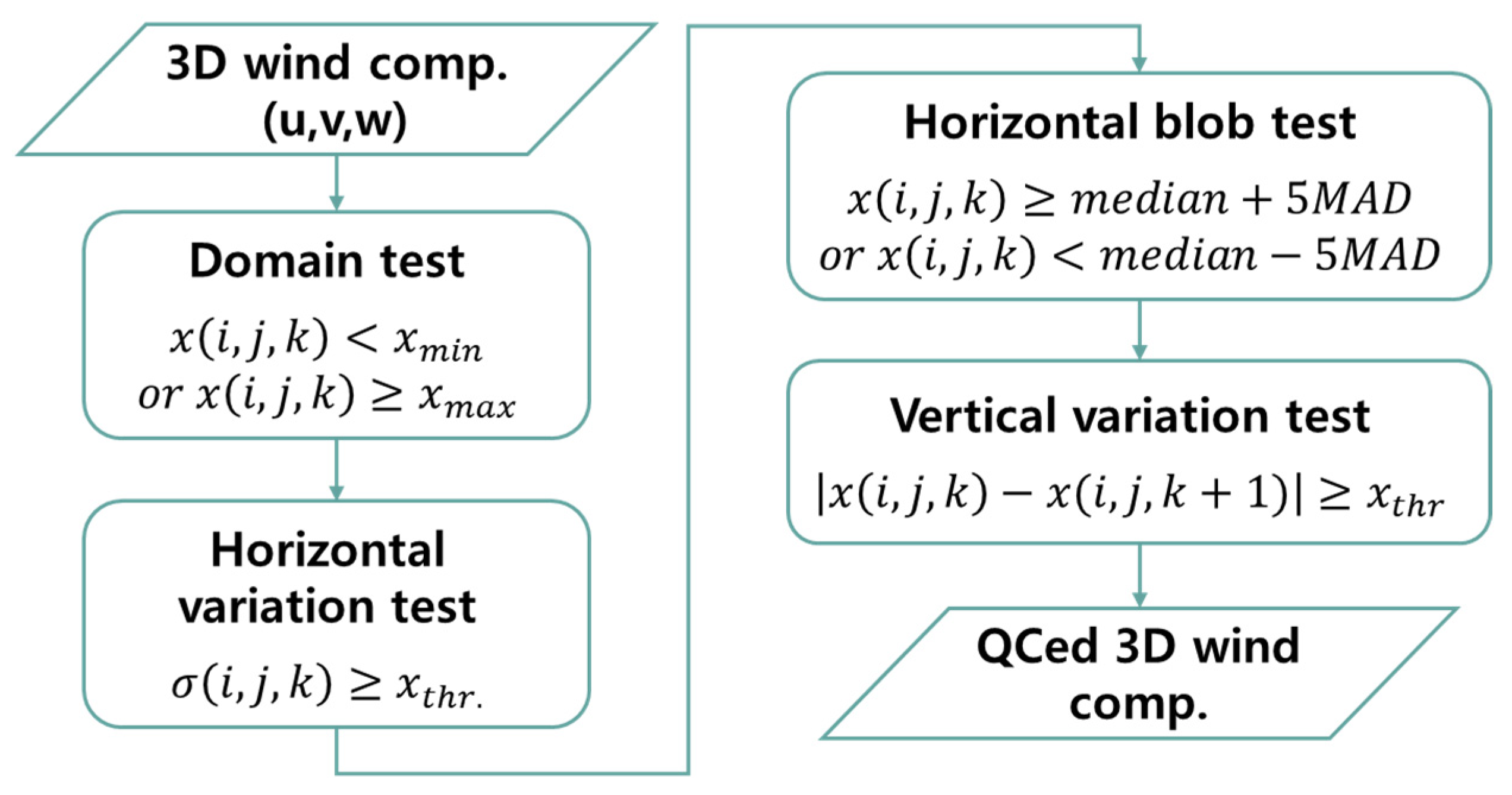
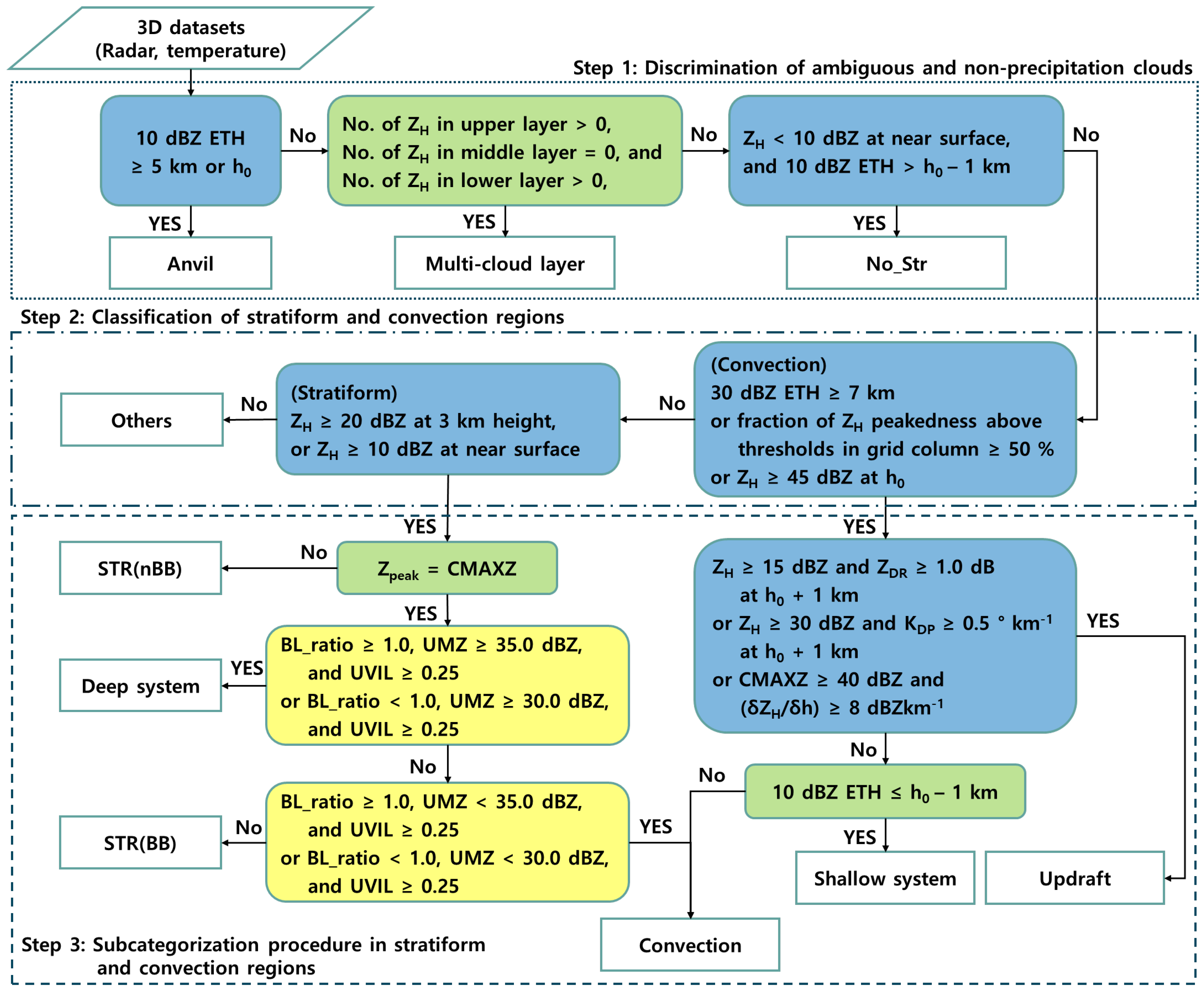
3.1. Description of Classification Algorithm for Precipitation Types (CP)
3.2. Analysis Methods of Physical Characteristics for Precipitation Types
4. Results
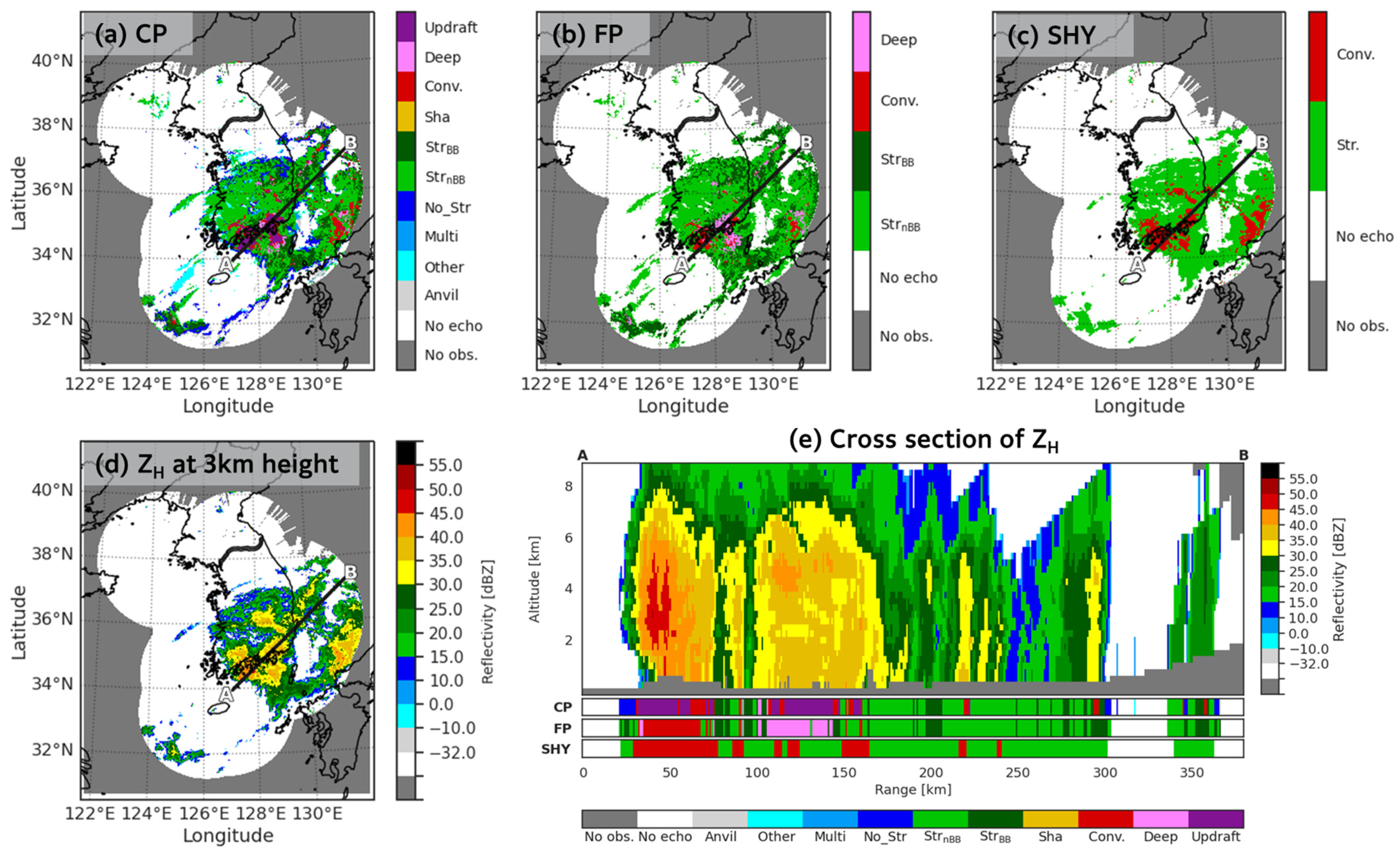
4.1. Evaluating Precipitation Type Classification: A Comparison of CP and Traditional Algorithms
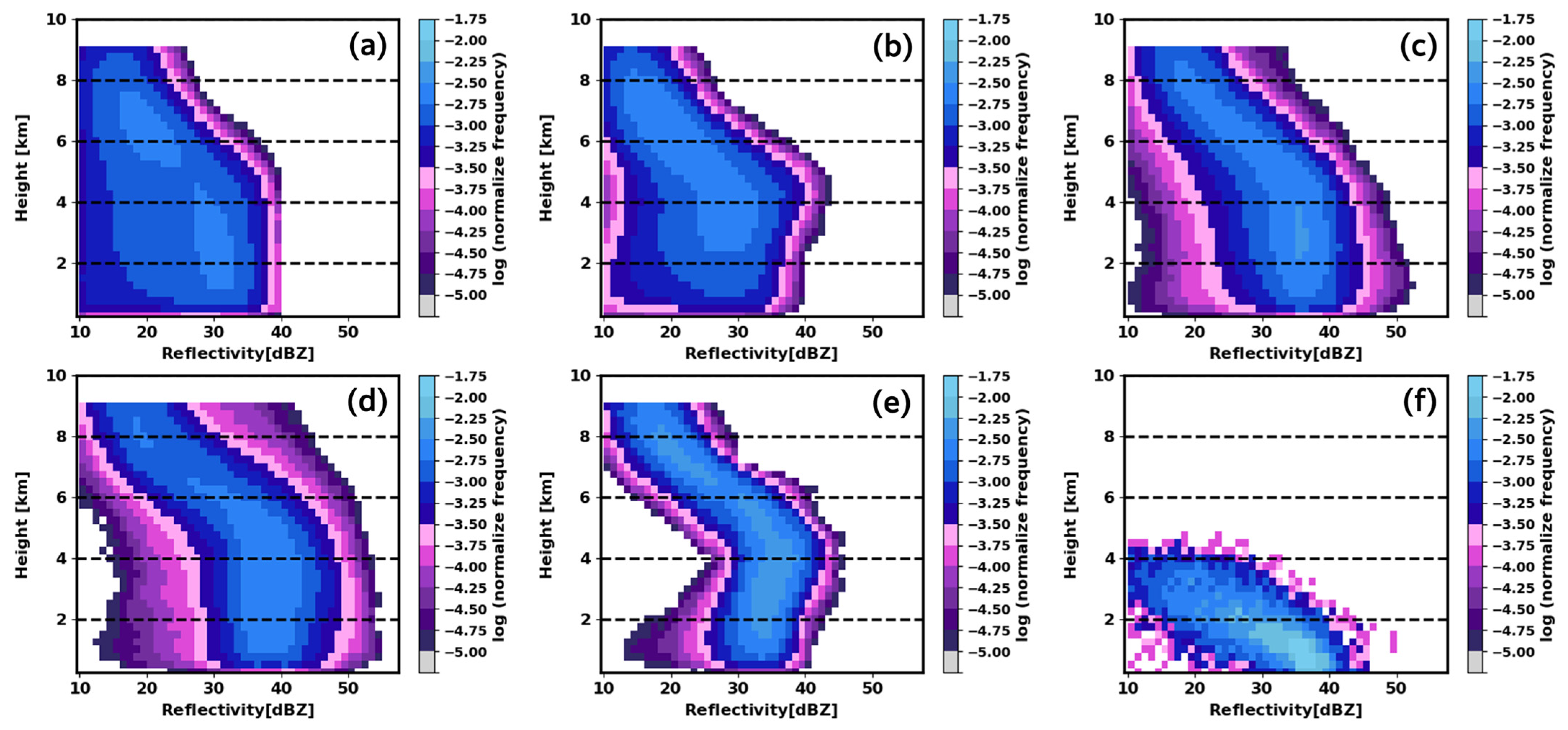
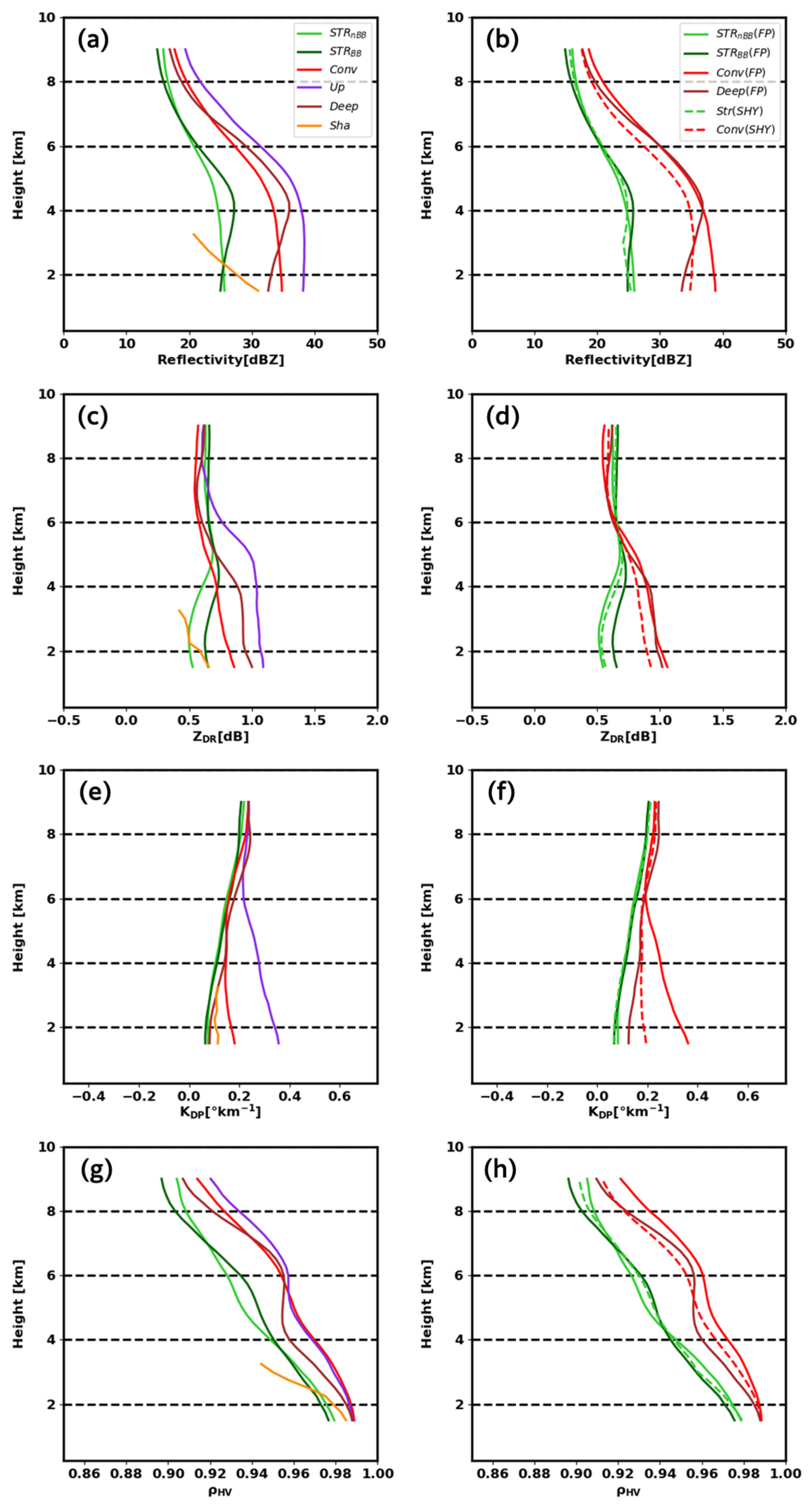
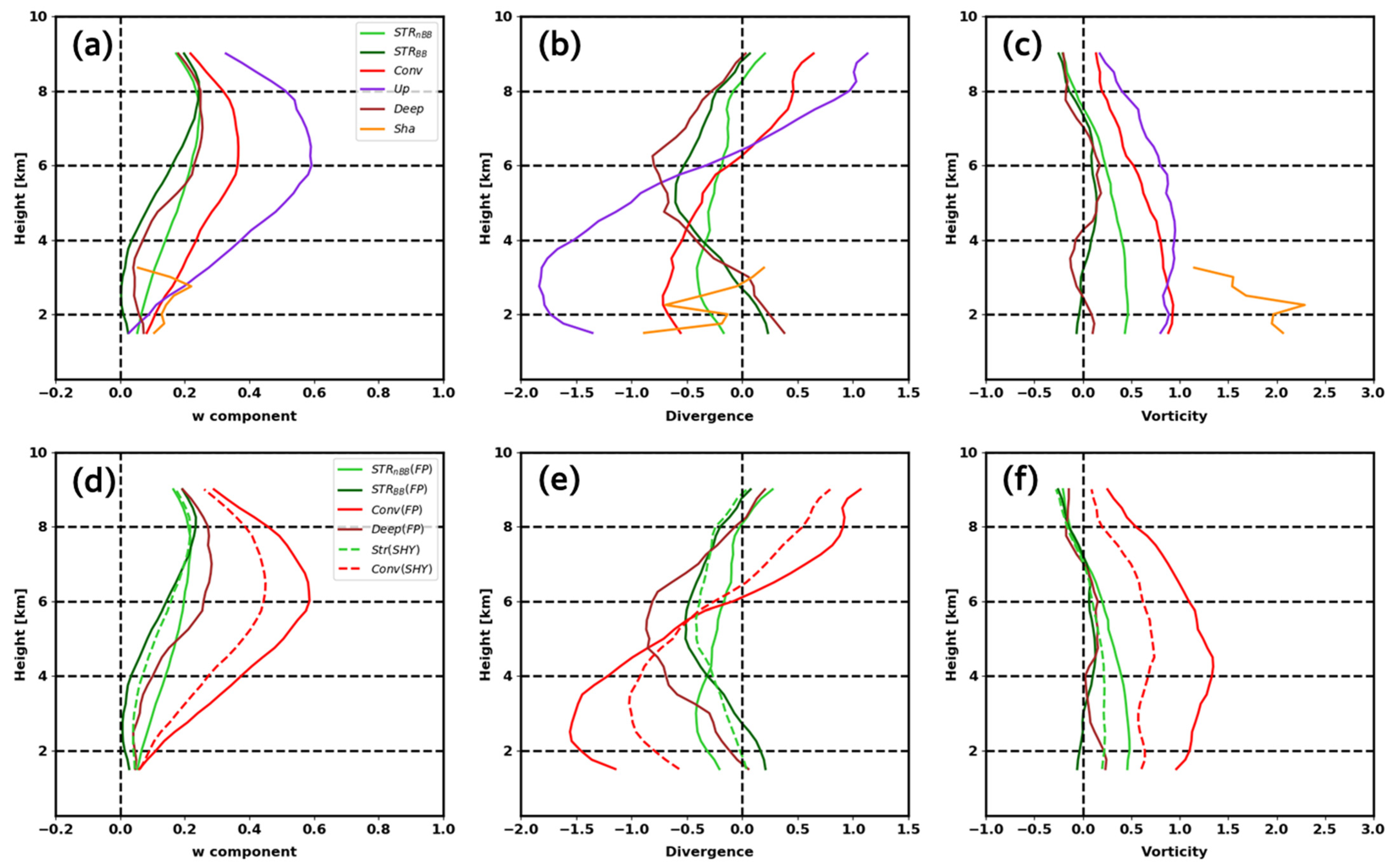
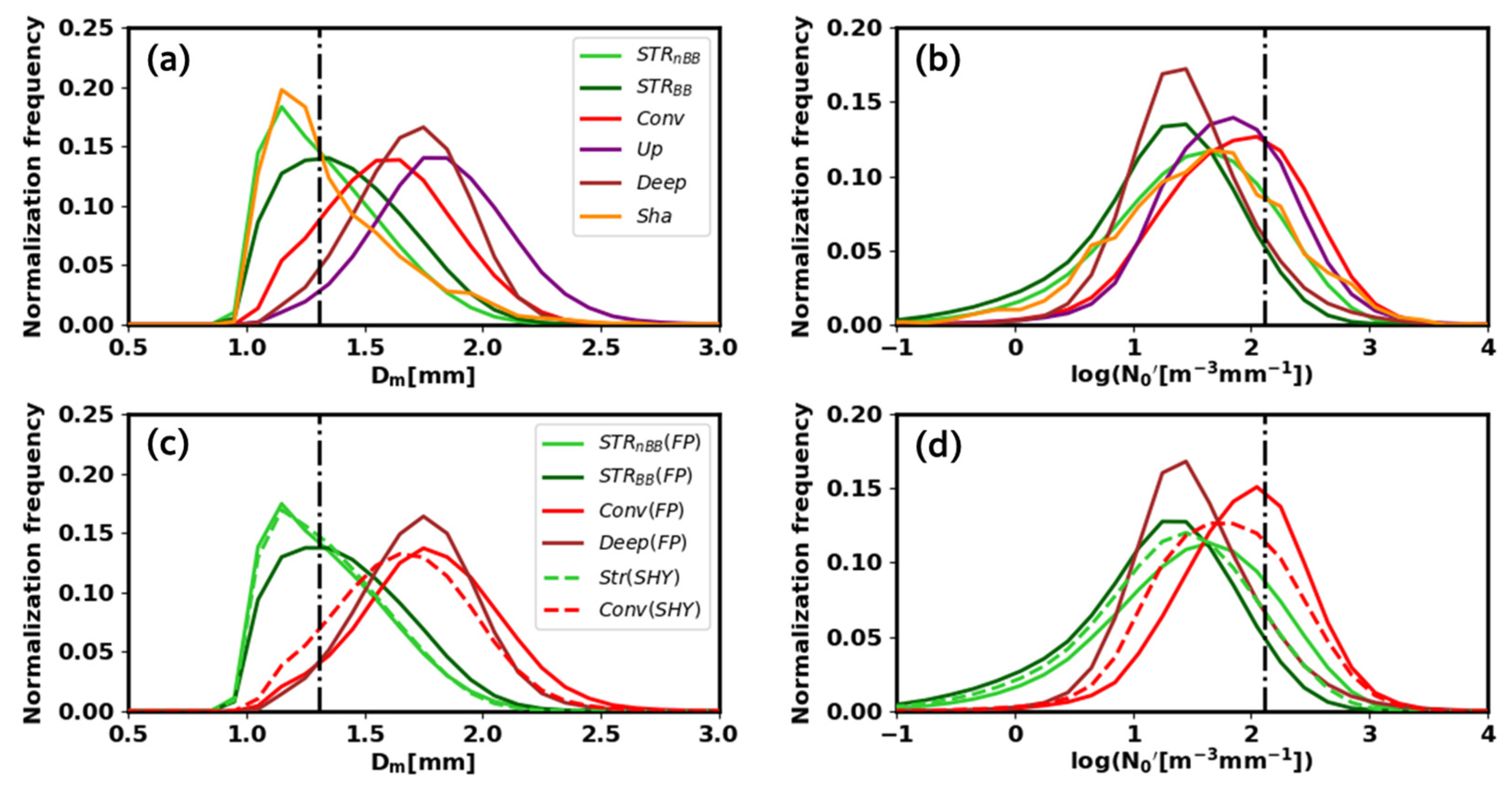
4.2. Physical Properties of Precipitation Types Identified by CP and Traditional Classification Methods
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Starzec, M.; Homeyer, C.R.; Mullendore, G.L. Storm labeling in three dimensions (SL3D): A volumetric radar echo and dual-polarization updraft classification algorithm. Mon. Weather. Rev. 2017, 145, 1127–1145. [Google Scholar] [CrossRef]
- Lee, T.Y.; Kim, Y. Heavy Precipitation systems over the Korean peninsula and their classification. J. Korean Meteorol. Soc. 2007, 43, 367–396. [Google Scholar]
- Fabry, F.; Zawadzki, I. Long-termradaroperationsofthemeltinglayerofprecipitationandtheirinterpretation. J. Atmos. Sci. 1995, 52, 838–851. [Google Scholar] [CrossRef]
- Steiner, M.; Houze, R.A., Jr.; Yuter, S.E. Climatological characterization of three-dimensional storm structure from operational radar and rain gauge data. J. Appl. Meteorol. 1995, 34, 1978–2007. [Google Scholar] [CrossRef]
- Biggerstaff, M.I.; Listemaa, S.A. An improved scheme for convective/stratiform echo classification using radar reflectivity. J. Appl. Meteorol. 2000, 39, 2129–2150. [Google Scholar] [CrossRef]
- Penide, G.; Protat, A.; Kumar, V.V.; May, P.T. Comparison of two convective/stratiform precipitation classification techniques: Radar reflectivity texture versus drop size distribution–based approach. J. Atmos. Ocean. Technol. 2013, 30, 2788–2797. [Google Scholar] [CrossRef]
- Powell, S.W.; Houze, R.A., Jr.; Brodzik, S.R. Rainfall type categorization of radar echoes using polar coordinate reflectivity data. J. Atmos. Ocean. Technol. 2016, 33, 523–538. [Google Scholar] [CrossRef]
- Schumacher, C.; Houze, R.A., Jr. Stratiform precipitation production over sub-Saharan Africa and the tropical East Atlantic as observed by TRMM. Quart. J. Roy. Meteor. Soc. 2006, 132, 2235–2255. [Google Scholar] [CrossRef]
- Deierling, W.; Petersen, W.A.; Latham, J.; Ellis, S.; Christian, H.J. The relationship between lightning activity and ice fluxes in thunderstorms. J. Geophys. Res. 2008, 113, D15210. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Kirsch, B.; Clemens, M.; Ament, F. Stratiform and convective radar reflectivity–rain rate relationships and their potential to improve radar rainfall estimates. J. Appl. Meteorol. Climatol. 2019, 58, 2259–2271. [Google Scholar] [CrossRef]
- Loh, J.L.; Lee, D.I.; Kang, M.Y.; You, C.H. Classification of rainfall types using parsivel disdrometer and S-band polarimetric radar in central Korea. Remote Sens. 2020, 12, 642. [Google Scholar] [CrossRef]
- Feng, Z.; Dong, X.Q.; Xi, B.K.; Schumacher, C.; Minnis, P.; Khaiyer, M. Top-of-atmosphere radiation budget of convective core/stratiform rain and anvil clouds from deep convective systems. J. Geophys. Res. 2011, 116, D23202. [Google Scholar] [CrossRef]
- Dixon, M.; Romatschke, U. Three-dimensional convective–stratiform echo-type classification and convectivity retrieval from radar reflectivity. J. Atmos. Ocean. Technol. 2022, 39, 1685–1704. [Google Scholar] [CrossRef]
- Lee, J.E.; Jung, S.H.; Kwon, S. Characteristics of the bright band based on quasi-vertical profiles of polarimetric observations from an S-band weather radar Network. Remote Sens. 2020, 12, 4061. [Google Scholar] [CrossRef]
- Liou, Y.-C.; Chang, Y.-J. A variational multiple–Doppler radar three-dimensional wind synthesis method and its impacts on thermodynamic retrieval. Mon. Wea. Rev. 2009, 137, 3992–4010. [Google Scholar] [CrossRef]
- Tsai, C.L.; Kim, K.; Liou, Y.C.; Lee, G.; Yu, C.K. Impacts of Topography on Airflow and Precipitation in the Pyeongchang Area Seen from Multiple-Doppler Radar Observations. Mon. Wea. Rev. 2018, 146, 3401–3424. [Google Scholar] [CrossRef]
- Jorgensen, D.P.; LeMone, M.A. Vertical velocity characteristics of oceanic convection. J. Atmos. Sci. 1989, 46, 621–640. [Google Scholar] [CrossRef]
- WMO. Guidelines on Surface Station Data Quality Control and Quality Assurance for Climate Applications (WMO-No.1269). 2021. Available online: https://library.wmo.int/idurl/4/57727 (accessed on 17 July 2025).
- Bang, W.; Lee, G.; Ryzhkov, A.; Schuur, T.; Lim, K.-S.S. Comparison of Microphysical Characteristics between the Southern Korean Peninsula and Oklahoma Using Two-Dimensional Video Disdrometer Data. J. Hydrometeorol. 2020, 21, 2675–2690. [Google Scholar] [CrossRef]
- Kruger, A.; Krajewski, W.F. Two-dimensional video disdrometer: A description. J. Atmos. Ocean. Technol. 2002, 19, 602–617. [Google Scholar] [CrossRef]
- Atlas, D.; Srivastava, R.C.; Sckhon, R.S. Doppler radar characteristics of precipitation at vertical incidence. Rev. Geophys. Sp. Phys. 1973, 11, 1–35. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural variations in the analytical form of the raindrop size distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Auf der Maur, A.N. Statistical tools for drop size distribution: Moments and generalized gamma. J. Atmos. Sci. 2001, 58, 407–418. [Google Scholar] [CrossRef]
- Carletta, N.D.; Mullendore, G.L.; Starzec, M.; Xi, B.; Feng, Z.; Dong, X. Determining the best method for estimating the observed level of maximum detrainment based on radar reflectivity. Mon. Wea. Rev. 2016, 144, 2915–2926. [Google Scholar] [CrossRef]
- Short, E.; Lane, T.P.; Vincent, C.L. Objectively diagnosing characteristics of mesoscale organization from radar reflectivity and ambient winds. Mon. Wea. Rev. 2023, 151, 643–662. [Google Scholar] [CrossRef]
- DeMott, C.A.; Rutledge, S.A. The vertical structure of Toga Coare convection. Part I: Radar echo distributions. J. Atmos. Sci. 1998, 55, 2730–2747. [Google Scholar] [CrossRef]
- Zipser, E.J. Deep cumulonimbus cloud systems in the tropics with and without lightning. Mon. Wea. Rev. 1994, 122, 1837–1851. [Google Scholar] [CrossRef]
- Petersen, W.A.; Rutledge, S.A.; Orville, R.E. Cloud-to-ground lightning observations to Toga Coare, selected results and lightning location algorithm. Mon. Wea. Rev. 1996, 124, 602–620. [Google Scholar] [CrossRef]
- Straka, J.M.; Zrnić, D.S.; Ryzhkov, A.V. Bulk hydrometeor classification and quantification using polarimetric radar data: Synthesis of relations. J. Appl. Meteorol. 2000, 39, 1341–1372. [Google Scholar] [CrossRef]
- Snyder, J.C.; Ryzhkov, A.V.; Kumjian, M.R.; Khain, A.P.; Picca, J. A ZDR Column Detection Algorithm to Examine Convective Storm Updrafts. Weather Forecast. 2015, 30, 1819–1844. [Google Scholar] [CrossRef]
- Loney, M.L.; Zrnić, D.S.; Straka, J.M.; Ryzhkov, A.V. Enhanced Polarimetric Radar Signatures above the Melting Level in a Supercell Storm. J. Appl. Meteorol. 2002, 41, 1179–1194. [Google Scholar] [CrossRef]
- Van Lier-Walqui, M.; Fridlind, A.M.; Ackerman, A.S.; Collis, S.; Helmus, J.; MacGorman, D.R.; North, K.; Kollias, P.; Posselt, D.J. On Polarimetric Radar Signatures of Deep Convection for Model Evaluation: Columns of Specific Differential Phase Observed during MC3E. Mon. Wea. Rev. 2016, 144, 737–758. [Google Scholar] [CrossRef] [PubMed]
- Musil, D.J.; Heymsfield, A.J.; Smith, P.L. Microphysical characteristics of a well-developed weak echo region in a high plains su-percell thunderstorm. J. Appl. Meteorol. Climatol. 1986, 25, 1037–1051. [Google Scholar] [CrossRef]
- Calhoun, K.M.; MacGorman, D.R.; Ziegler, C.L.; Biggerstaff, M.I. Evolution of Lightning Activity and Storm Charge Relative to Dual-Doppler Analysis of a High-Precipitation Supercell Storm. Mon. Wea. Rev. 2013, 141, 2199–2223. [Google Scholar] [CrossRef]
- Awaka, J.; Iguchi, T.; Okamoto, K. TRMM PR Standard Algorithm and its Performance on Bright Band Detection. J. Meteorol. Soc. Jpn. 2009, 87, 31–52. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ryzhkov, A.V.; Trömel, S.; Diederich, M.; Mühlbauer, K.; Simmer, C. Retrievals of Warm-Rain Microphysics Using X-Band Polarimetric Radar Data. Extended Abstracts. In Proceedings of the 92nd Annual Meeting of the American Meteorological Society, New Orleans, LA, USA, 26 January 2012; p. 406. [Google Scholar]
- Tabary, P.; Henaff, A.; Vulpiani, G.; Parent-du-Chatelet, J.; Gourley, J.J. Melting Layer Characterization and Identification with a C-Band Dual-Polarization Radar: A Long-Term Analysis. In Proceedings of the Fourth European Conference on Radar in Meteorology and Hydrology (ERAD 2006), Barcelona, Spain, 18–22 September 2006; Servei Meteorològic de Catalunya: Barcelona, Spain, 2006; pp. 17–20. [Google Scholar]
- Shusse, Y.; Takahashi, N.; Nakagawa, K.; Satoh, S.; Iguchi, T. Polarimetric radar observation of the melting layer in a convective rainfall system during the rainy season over the East China sea. J. Appl. Meteorol. Climatol. 2011, 50, 354–367. [Google Scholar] [CrossRef]
- Williams, C.R.; Ecklund, W.L.; Gage, K.S. Classification of Precipitating Clouds in the Tropics Using 915-MHz Wind Profilers. J. Atmos. Ocean. Technol. 1995, 12, 996–1012. [Google Scholar] [CrossRef]
- Boudevillain, B.; Andrieu, H. Assessment of vertically integrated liquid (VIL) water content radar measurement. J. Atmos. Ocean. Technol. 2003, 20, 807–819. [Google Scholar] [CrossRef]
- Iguchi, T.; Seto, S.; Meneghini, R.; Yoshida, N.; Awaka, J.; Le, M.; Chandrasekar, V.; Brodzik, S.; Tanelli, S.; Kanemaru, K.; et al. GPM/DPR Level-2 Algorithm Theoretical Basis Document; NASA Technical Report. 2024. Available online: https://gpm.nasa.gov/resources/documents/gpm-dpr-level-2-algorithm-theoretical-basis-document-atbd (accessed on 17 July 2025).
- Houze, R.A. Observed structure of mesoscale convective systems and implications for large-scale heating. Q. J. R. Meteorol. Soc. 1989, 115, 425–461. [Google Scholar] [CrossRef]
- Deng, M.; Kollias, P.; Feng, Z.; Zhang, C.; Long, C.N.; Kalesse, H.; Chandra, A.; Kumar, V.V.; Protat, A. Stratiform and convective precipitation observed by multiple radars during the DYNAMO/AMIE experiment. J. Appl. Meteorol. Climatol. 2014, 53, 2503–2523. [Google Scholar] [CrossRef]
- Carr, N.; Kirstetter, P.E.; Gourley, J.J.; Hong, Y. Polarimetric Signatures of Midlatitude Warm-Rain Precipitation Events. J. Appl. Meteor. Climatol. 2017, 56, 697–711. [Google Scholar] [CrossRef]
- Handler, S.L.; Homeyer, C.R. Radar-observed bulk microphysics of midlatitude leading line trailing stratiform mesoscale convective systems. J. Appl. Meteor. Climatol. 2018, 57, 2231–2248. [Google Scholar] [CrossRef]
- Huang, H.; Chen, F. Precipitation Microphysics of Tropical Cyclones Over the Western North Pacific Based on GPM DPR Observations: A Preliminary Analysis. J. Geophys. Res. Atmos. 2019, 124, 3124–3142. [Google Scholar] [CrossRef]
- Rinehart, R.E. Radar for Meteorologists, 4th ed.; Rinehart Publications: Columbia, MO, USA, 2004; 482p, ISBN 0-9658002-1-0. [Google Scholar]
- Kumjian, M.R.; Prat, O.P.; Reimel, K.J.; van Lier-Walqui, M.; Morrison, H.C. Dual-Polarization Radar Fingerprints of Precipitation Physics: A Review. Remote Sens. 2022, 14, 3706. [Google Scholar] [CrossRef]
- Schumacher, C.; Stevenson, S.N.; Williams, C.R. Vertical Motions of the Tropical Convective Cloud Spectrum over Darwin, Australia: Vertical Motions of the Tropical Convective Cloud Spectrum. Q. J. R. Meteorol. Soc. 2015, 141, 2277–2288. [Google Scholar] [CrossRef]
- Homeyer, C.; Schumacher, C.; Hopper, L.J., Jr. Assessing the applicability of the tropical convective-stratiform paradigm in the extratropics using radar divergence profiles. J. Clim. 2014, 27, 6673–6686. [Google Scholar] [CrossRef]
- Bosart, L.F. Kinematic vertical motion and relative vorticity profiles in a long-lived midlatitude convective system. J. Atmos. Sci. 1986, 43, 1297–1300. [Google Scholar] [CrossRef]
- Hopper, L.J., Jr.; Schumacher, C. Modeled and observed variations in storm divergence and stratiform rain production in southeastern Texas. J. Atmos. Sci. 2012, 69, 1159–1181. [Google Scholar] [CrossRef]
- Lee, G.; Zawadzki, I.; Szyrmer, W.; Sempere-Torres, D.; Uijlenhoet, R. A General Approach to Double-Moment Normalization of Drop Size Distributions. J. Appl. Meteorol. 2004, 43, 264–281. [Google Scholar] [CrossRef]
- Lee, G.; Bringi, V.; Thurai, M. The retrieval of drop size distribution parameters using a Dual-polarimetric radar. Remote Sens. 2023, 15, 1063. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Mackowski, D.W. T-matrix computations of light scattering by nonspherical particles: A review. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 535–575. [Google Scholar] [CrossRef]
- Thurai, M.; Huang, G.J.; Bringi, V.N.; Randeu, W.L.; Schönhuber, M. Drop shapes, model comparisons, and calculations of polarimetric radar parameters in rain. J. Atmos. Ocean. Technol. 2007, 24, 1019–1032. [Google Scholar] [CrossRef]
- Brandes, E.A.; Zhang, G.; Vivekanandan, J. Drop size distribution retrieval with polarimetric radar: Model and application. J. Appl. Meteorol. 2004, 43, 461–475. [Google Scholar] [CrossRef]
- Cao, Q.; Zhang, G.; Brandes, E. Analysis of video disdrometer and polarimetric radar data to characterize rain microphysics in Oklahoma. J. Appl. Meteorol. Climatol. 2008, 47, 2238–2255. [Google Scholar] [CrossRef]
- Kwon, S.; Jung, S.-H.; Lee, G. A case study on microphysical characteristics of mesoscale convective system using generalized DSD parameters retrieved from dual-polarimetric radar observations. Remote Sens. 2020, 12, 1812. [Google Scholar] [CrossRef]
- Houze, R.A., Jr. Mesoscale convective systems. Rev. Geophys. 2004, 42, RG4003. [Google Scholar] [CrossRef]
- Lee, Y.; Kummerow, C.D.; Zupanski, M. Latent heating profiles from GOES-16 and its impacts on precipitation forecasts. Atmos. Meas. Tech. 2022, 15, 7119–7136. [Google Scholar] [CrossRef]



| No. | Selected Time [UTC] | Precipitation Types | Duration [hours] |
|---|---|---|---|
| 1 | 17 May 2019. 20:00 | Mid-latitude cyclone | 22 |
| 2 | 26 May 2019. 23:30 | Mid-latitude cyclone | 34 |
| 3 | 6 June 2019. 11:30 | Mid-latitude cyclone | 29 |
| 4 | 26 June 2019.03:00 | Mid-latitude cyclone | 37 |
| 5 | 29 June 2019. 08:30 | Changma front | 20 |
| 6 | 10 July 2019. 06:00 | Mid-latitude cyclone | 27 |
| 7 | 21 August 2019. 23:30 | Parallel squall line | 24 |
| 8 | 26 August 2019. 23:00 | Mid-latitude cyclone | 20 |
| 9 | 2 September 2019. 00:00 | Parallel squall line | 12 |
| 10 | 2 September 2019. 21:30 | Parallel squall line | 13 |
| 11 | 18 May 2020. 08:00 | Diagonal squall line related in cold front | 23 |
| 12 | 24 June 2020. 01:30 | Mid-latitude cyclone | 30 |
| 13 | 29 June 2020. 13:00 | Mid-latitude cyclone | 47 |
| 14 | 10 July 2020. 01:00 | Mid-latitude cyclone | 30 |
| 15 | 12 July 2020. 21:30 | Mid-latitude cyclone | 42 |
| 16 | 13 July 2020. 14:30 | Mid-latitude cyclone | 14 |
| 17 | 28 July 2020. 23:30 | Parallel squall line | 11 |
| 18 | 2 August 2020. 06:30 | Diagonal squall line | 11 |
| 19 | 2 August 2020. 17:00 | Parallel squall line | 11 |
| 20 | 5 August 2020. 17:00 | Mid-latitude cyclone | 16 |
| Proxy x | [m s−1] | [m s−1] | [m s−1] | |
|---|---|---|---|---|
| Test Types | ||||
| Domain test | (minimum) −100 (maximum) 100 | (minimum) −100 (maximum) 100 | (minimum) −14 (maximum) 14 | |
| Horizontal variation test | 100 | 100 | 3 | |
| Vertical variation test | 30 | 30 | 14 | |
| Parameters | hB [km] | hT [km] |
|---|---|---|
| UVIL | hpeak + 1.5 | htop (=9 km) |
| UMZ | hpeak + 0.5 | hpeak + 1.5 |
| BMZ | hpeak − 0.5 | hpeak + 0.5 |
| LMZ | hpeak − 1.5 | hpeak − 0.5 |
| BL_ratio | = BMZ/LMZ | |
| Control Condition | Value |
|---|---|
| Radar frequency | 2.725 GHz |
| Radar elevation angle | 0° |
| Shape model of a raindrop | Thurai et al. [58] |
| Canting angle of raindrops | Gaussian distribution with μ = 0° and σ = 10° |
| Environmental temperature | 23 °C |
| Coefficient | Values |
|---|---|
| a1 | 43.05283949 |
| a2 | −81.79643382 |
| a3 | 49.01626955 |
| a4 | −9.91111241 |
| b1 | −8.99017448 |
| b2 | 18.15460729 |
| b3 | −10.62552174 |
| b4 | 2.2037548 |
| b5 | 0.027 |
| w Comp. Threshold [m s−1] | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | |
|---|---|---|---|---|---|---|---|
| POD | CP | 0.569 | 0.567 | 0.567 | 0.571 | 0.572 | 0.569 |
| FP | 0.455 | 0.457 | 0.461 | 0.466 | 0.47 | 0.47 | |
| SHY | 0.349 | 0.352 | 0.357 | 0.36 | 0.364 | 0.364 | |
| FAR | CP | 0.784 | 0.82 | 0.853 | 0.881 | 0.907 | 0.928 |
| FP | 0.792 | 0.823 | 0.853 | 0.881 | 0.906 | 0.926 | |
| SHY | 0.413 | 0.43 | 0.446 | 0.46 | 0.473 | 0.484 | |
| CSI | CP | 0.186 | 0.158 | 0.133 | 0.109 | 0.087 | 0.068 |
| FP | 0.167 | 0.146 | 0.125 | 0.104 | 0.085 | 0.068 | |
| SHY | 0.16 | 0.137 | 0.115 | 0.094 | 0.075 | 0.06 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-L.; Bang, W.; Tsai, C.-L.; Lee, G. Classification of Precipitation Types and Investigation of Their Physical Characteristics Using Three-Dimensional S-Band Dual-Polarization Radar Data. Remote Sens. 2025, 17, 2506. https://doi.org/10.3390/rs17142506
Lee C-L, Bang W, Tsai C-L, Lee G. Classification of Precipitation Types and Investigation of Their Physical Characteristics Using Three-Dimensional S-Band Dual-Polarization Radar Data. Remote Sensing. 2025; 17(14):2506. https://doi.org/10.3390/rs17142506
Chicago/Turabian StyleLee, Choeng-Lyong, Wonbae Bang, Chia-Lun Tsai, and GyuWon Lee. 2025. "Classification of Precipitation Types and Investigation of Their Physical Characteristics Using Three-Dimensional S-Band Dual-Polarization Radar Data" Remote Sensing 17, no. 14: 2506. https://doi.org/10.3390/rs17142506
APA StyleLee, C.-L., Bang, W., Tsai, C.-L., & Lee, G. (2025). Classification of Precipitation Types and Investigation of Their Physical Characteristics Using Three-Dimensional S-Band Dual-Polarization Radar Data. Remote Sensing, 17(14), 2506. https://doi.org/10.3390/rs17142506






