A Cloud Vertical Structure Optimization Algorithm Combining FY-4A and DSCOVR Satellite Data
Abstract
1. Introduction
2. Data
2.1. FY-4A Products
2.2. DSCOVR Products
2.3. CloudSat/CALIPSO Products
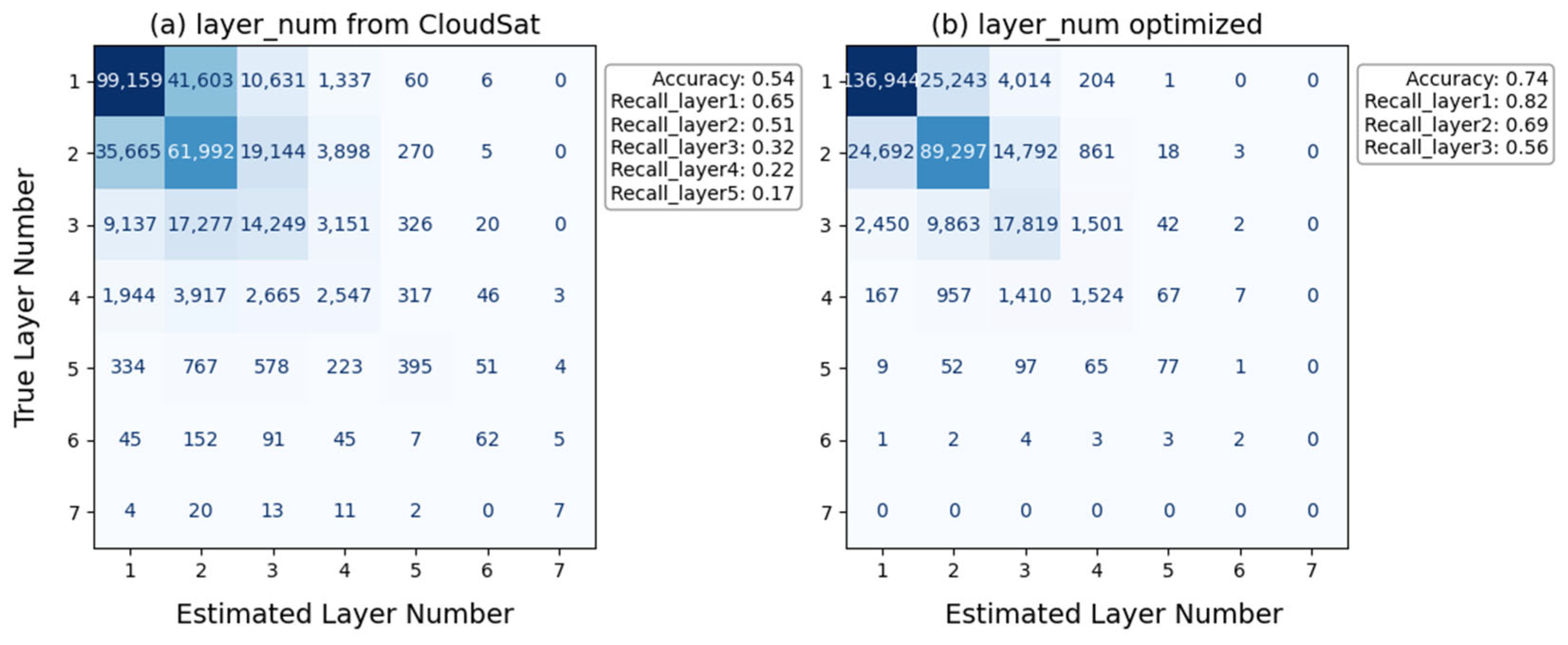
Adjustment of Cloud Layer Number
2.4. Problems in Passive Remote Sensing
2.4.1. FY-4A CTH Systematic Error
2.4.2. DSCOVR CEH Discrepancy
3. Methodology
3.1. Spatiotemporal Collocation
3.1.1. Matching for Model Training
- 1.
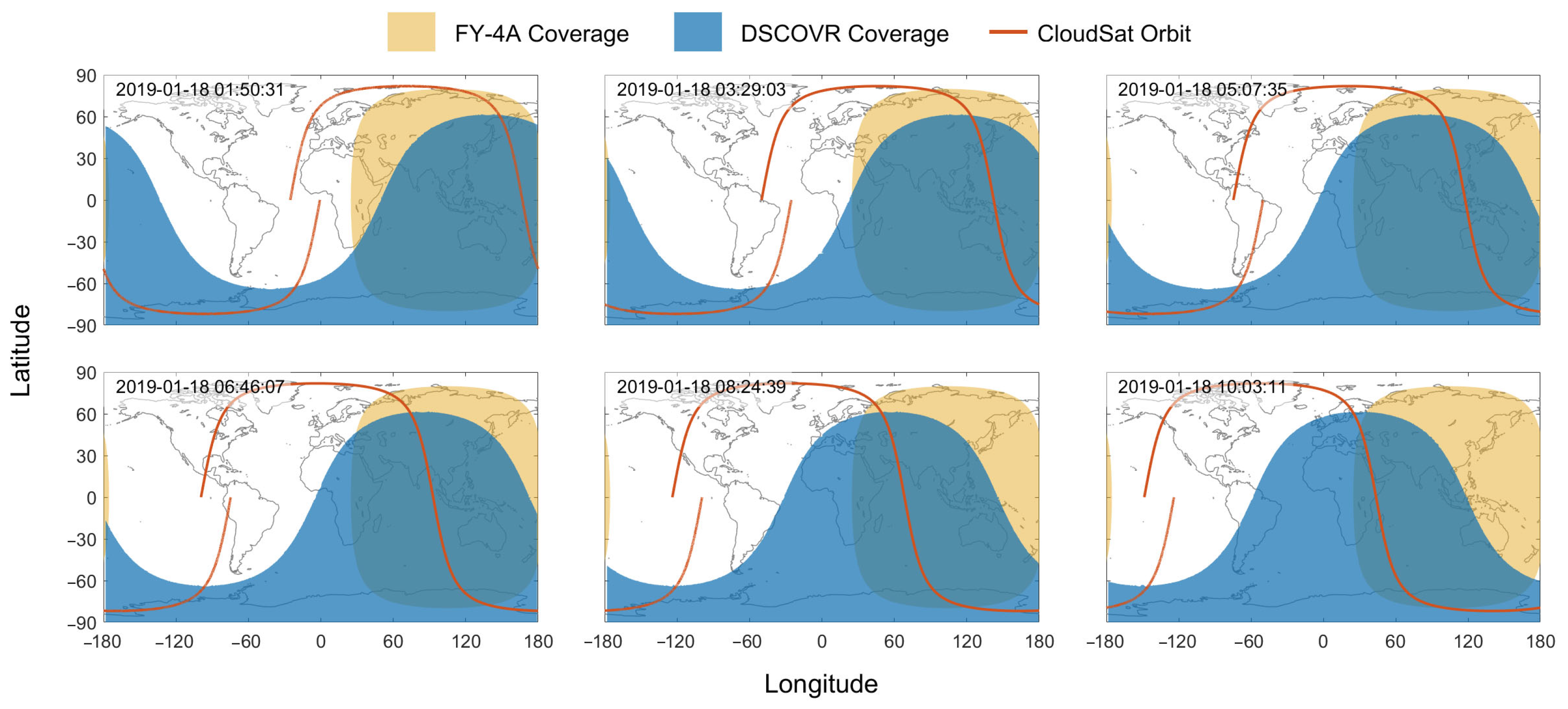
- Temporal Pre-Screening: FY-4A and DSCOVR images are selected based on their imaging times and CloudSat/CALIPSO’s flight plan. One CloudSat/CALIPSO orbit may correspond to multiple FY-4A images. This is because, when CloudSat/CALIPSO passes through the sunlit side of the Earth, FY-4A captures images many times with a much higher frequency than that of CloudSat/CALIPSO.
- 2.
- Spatial Matching: Given the large number of pixels in the images, global brute-force matching is time-consuming. Therefore, we employ a two-step method to improve the matching efficiency. First, for each CloudSat/CALIPSO sounding, we define a 3° × 3° bounding box (approximately 1.5° in each direction) and discard all FY-4A and DSCOVR pixels falling outside this area. Second, we calculate the geodesic distance from each of these candidate pixels in the box to the sounding using the Haversine formula [27]. The closest pixel is then identified, and to ensure high spatial consistency, the geodesic distance from the matched FY-4A and DSCOVR pixels to the sounding should be less than 5 km.
- 3.
- Temporal Matching: A temporal matching is carried out at the pixel level. If the time difference between the matched FY-4A and DSCOVR pixels and the CloudSat/CALIPSO sounding is less than 15 min, they are considered to have been captured within the adjacent time frame. The 15 min threshold is chosen as a compromise between dataset size and physical consistency. A stricter window (< 5 min) was found to discard over 80% of potential matches. Conversely, a longer window is physically questionable, as the cloud properties from a fixed-point perspective significantly decorrelate on a timescale of about 15.5 min [28]. Furthermore, the 15 min window is designed to accommodate occasional 30 min gaps in the FY-4A data stream, ensuring better data matching.
3.1.2. Matching for Model Application
3.2. CTH/CVE Optimization
3.2.1. Dataset Splitting
3.2.2. CLN Estimation Model
3.2.3. CTH/CVE Optimization Model
- 1.
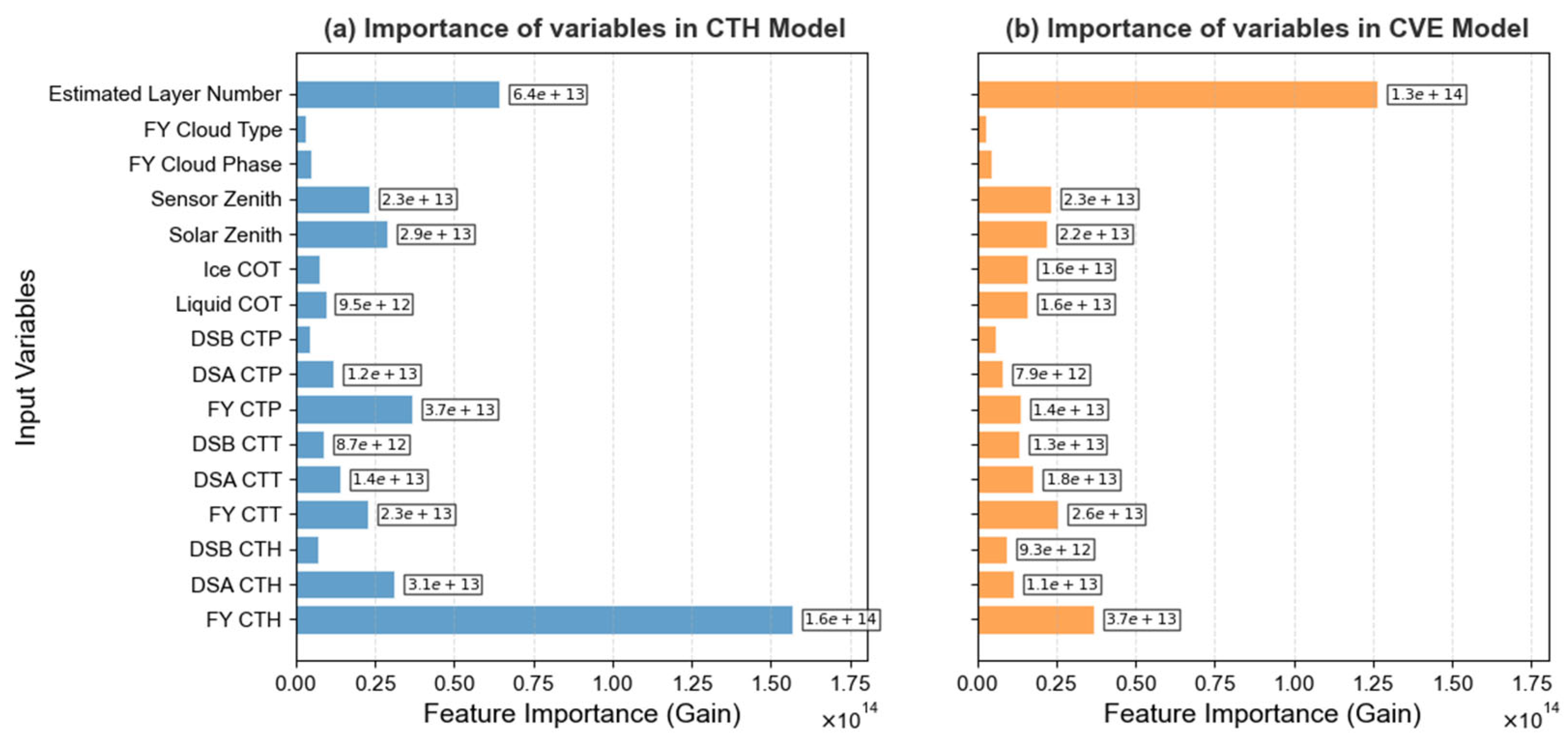
- Cloud Parameters: These include the cloud top height (), temperature (), and pressure () from the AGRI/FY-4A products, along with those retrieved from the oxygen A/B absorption bands of EPIC/DSCOVR (, , , , , ). Additionally, the cloud layer phase () and type () from FY-4A, as well as the liquid and ice cloud optical thickness (, ) from DSCOVR are selected as input variables.
- 2.
- View Geometry: Changes in the solar zenith angle () can affect the depth of photon penetration into the cloud layers and the length of the transmission path [3,29]. This geometric effect directly leads to systematic biases in the retrieval of CTH based on the O2-A/B absorption bands (as discussed in Section 2.4.2). Additionally, an increase in the sensor zenith angle () can alter the cloud top radiation characteristics [13]. The model incorporates both angle parameters as key radiation transfer constraint variables.
- 3.
- Cloud Layer Number: The number of cloud layers distinguishes between single- and multi-layer clouds. We include the estimation of cloud layer number, as discussed in Section 3.2.2, as an input variable.
3.2.4. Model Training
3.3. Evaluation Methods
4. Results
4.1. CLN Model Performance
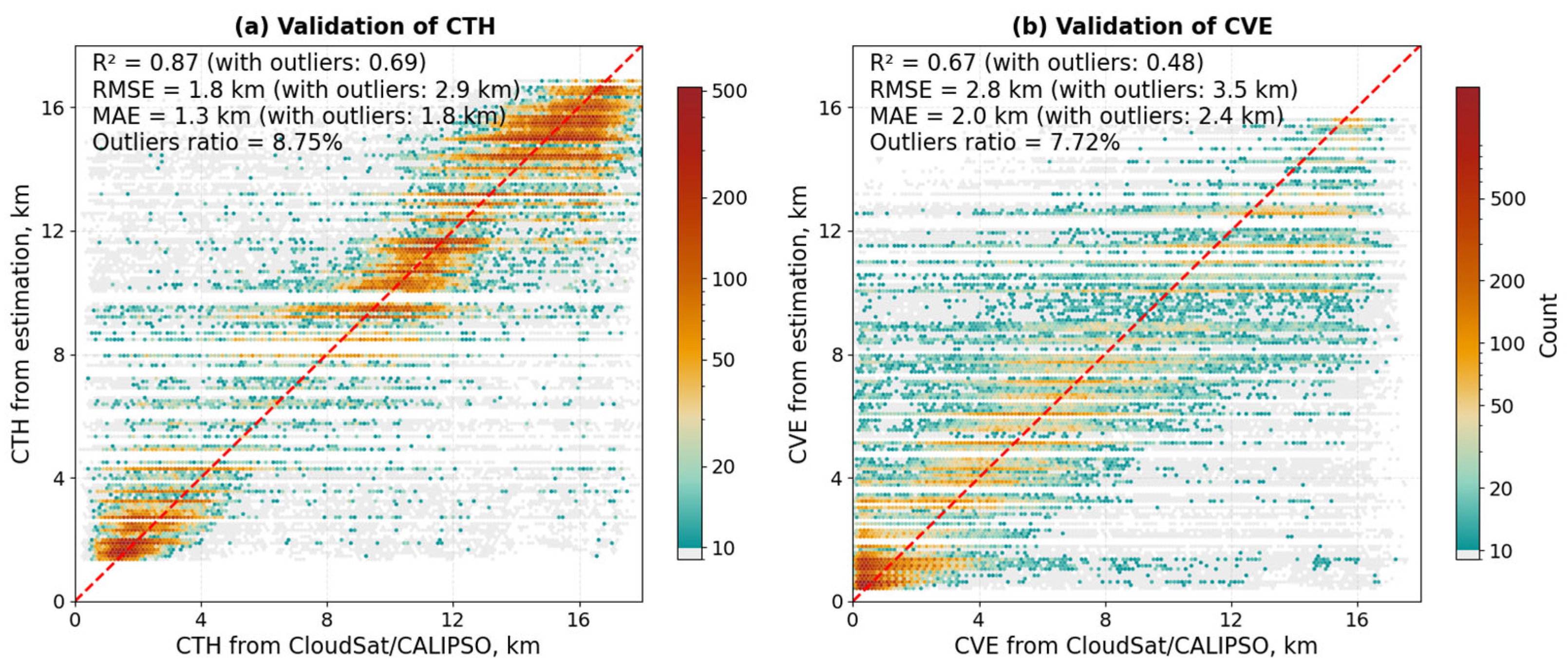
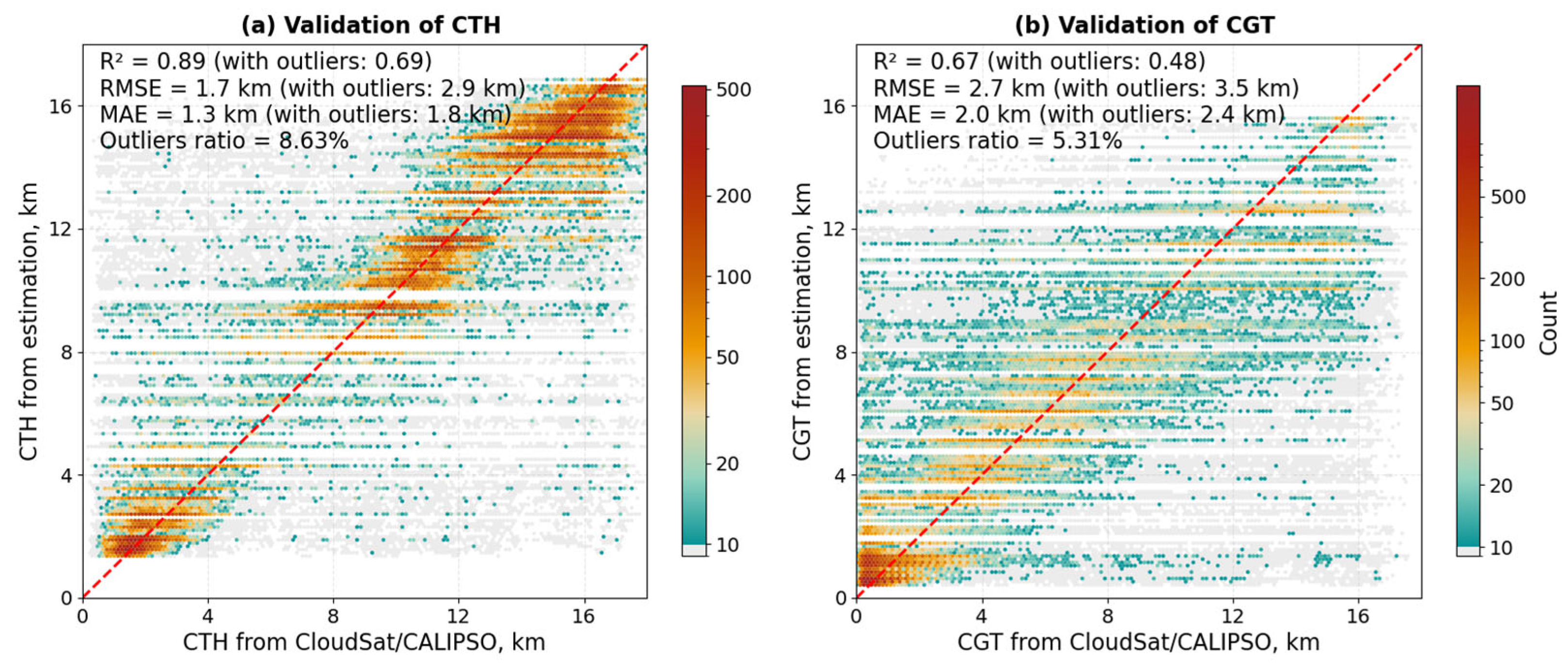
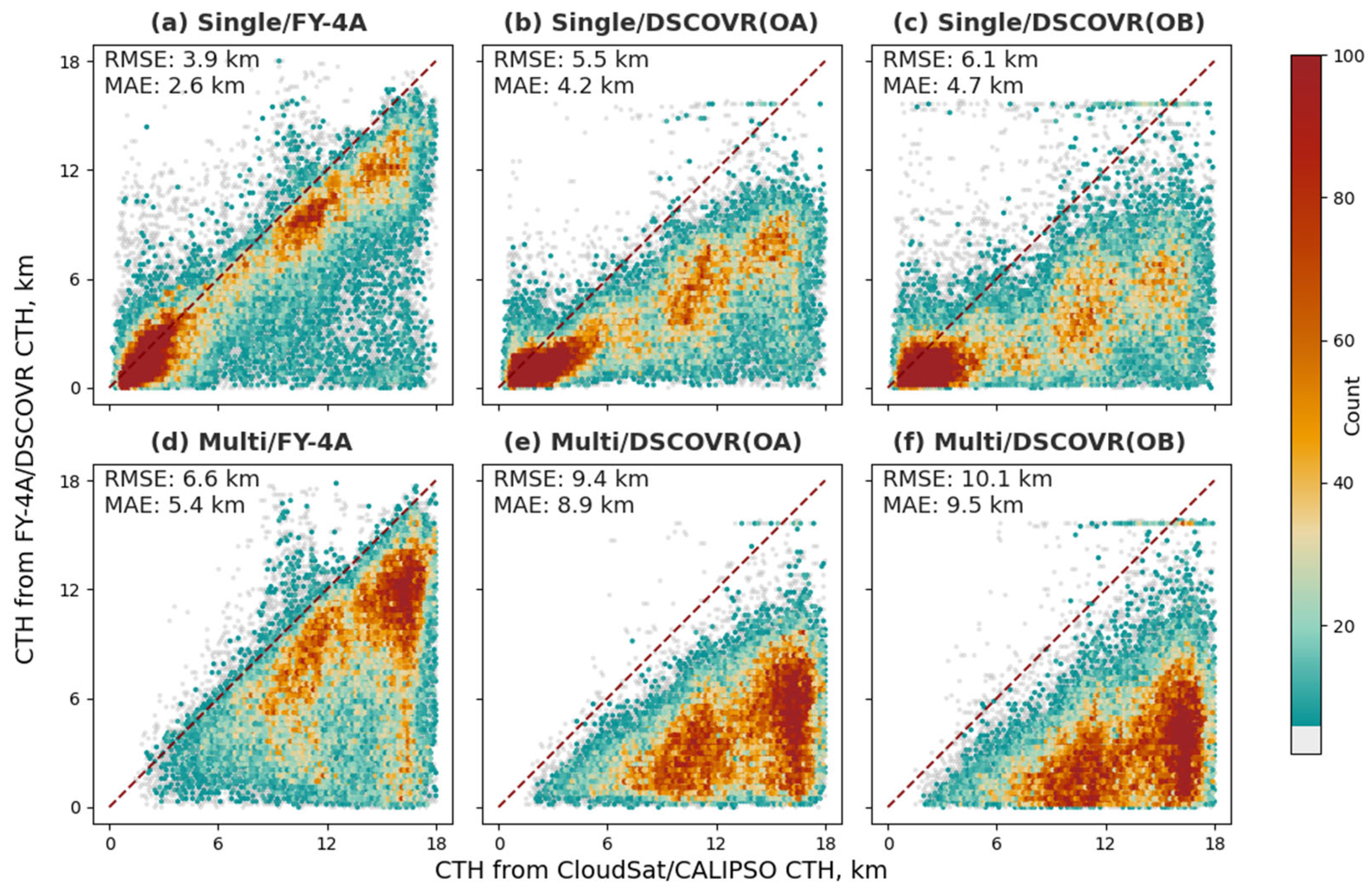
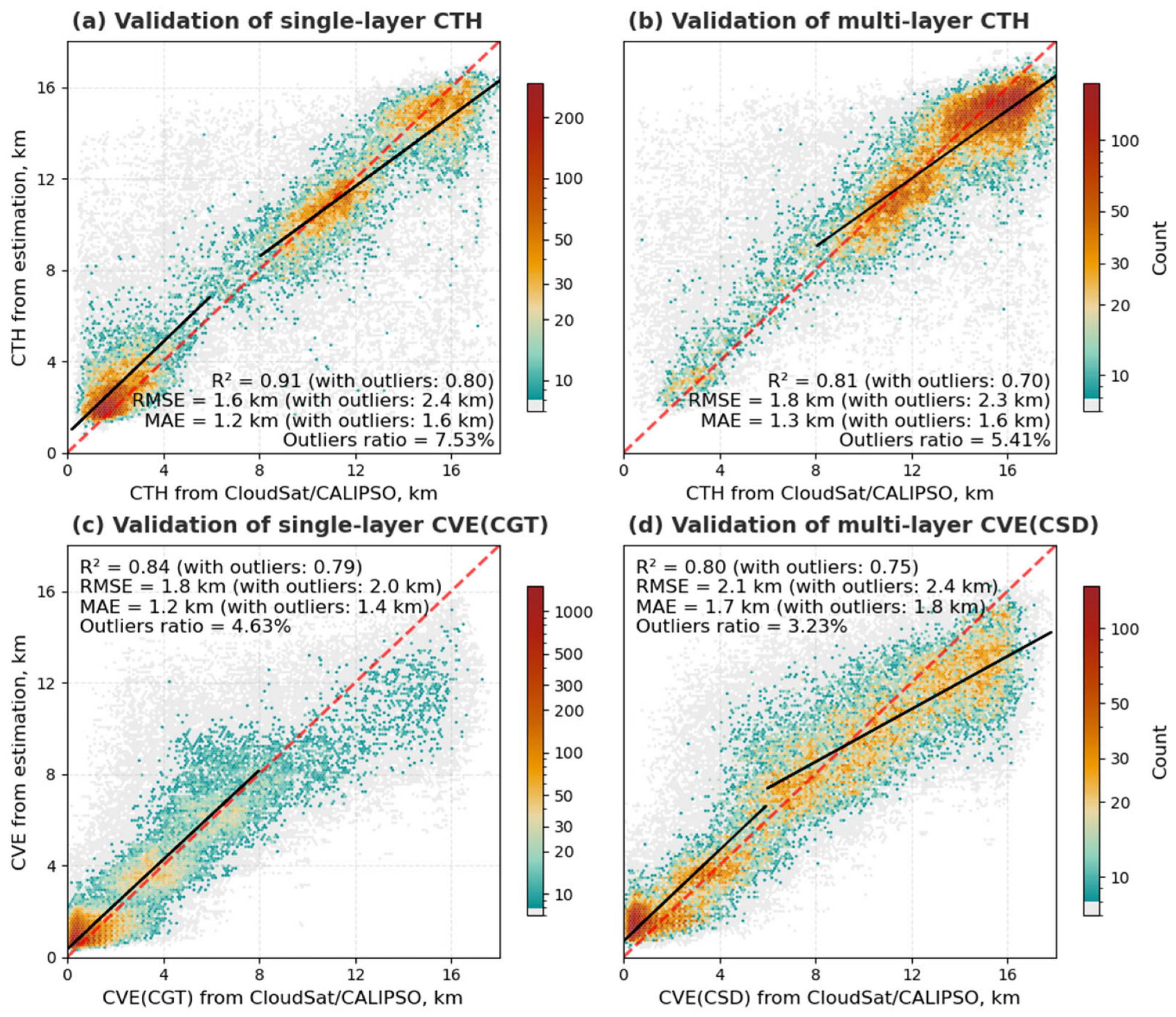
4.2. CTH/CVE Model Performance
- (A)
- Performance in Single-Layer Clouds
- (B)
- Performance in Multi-Layer Clouds
5. Discussion
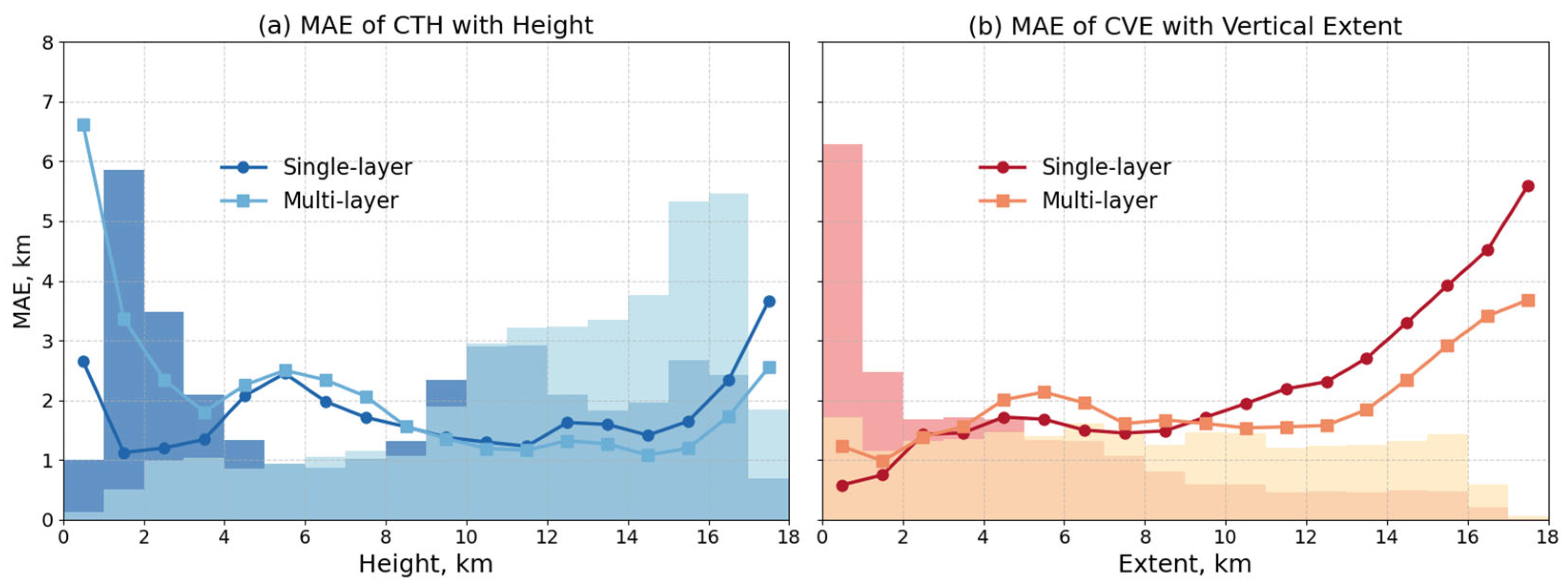
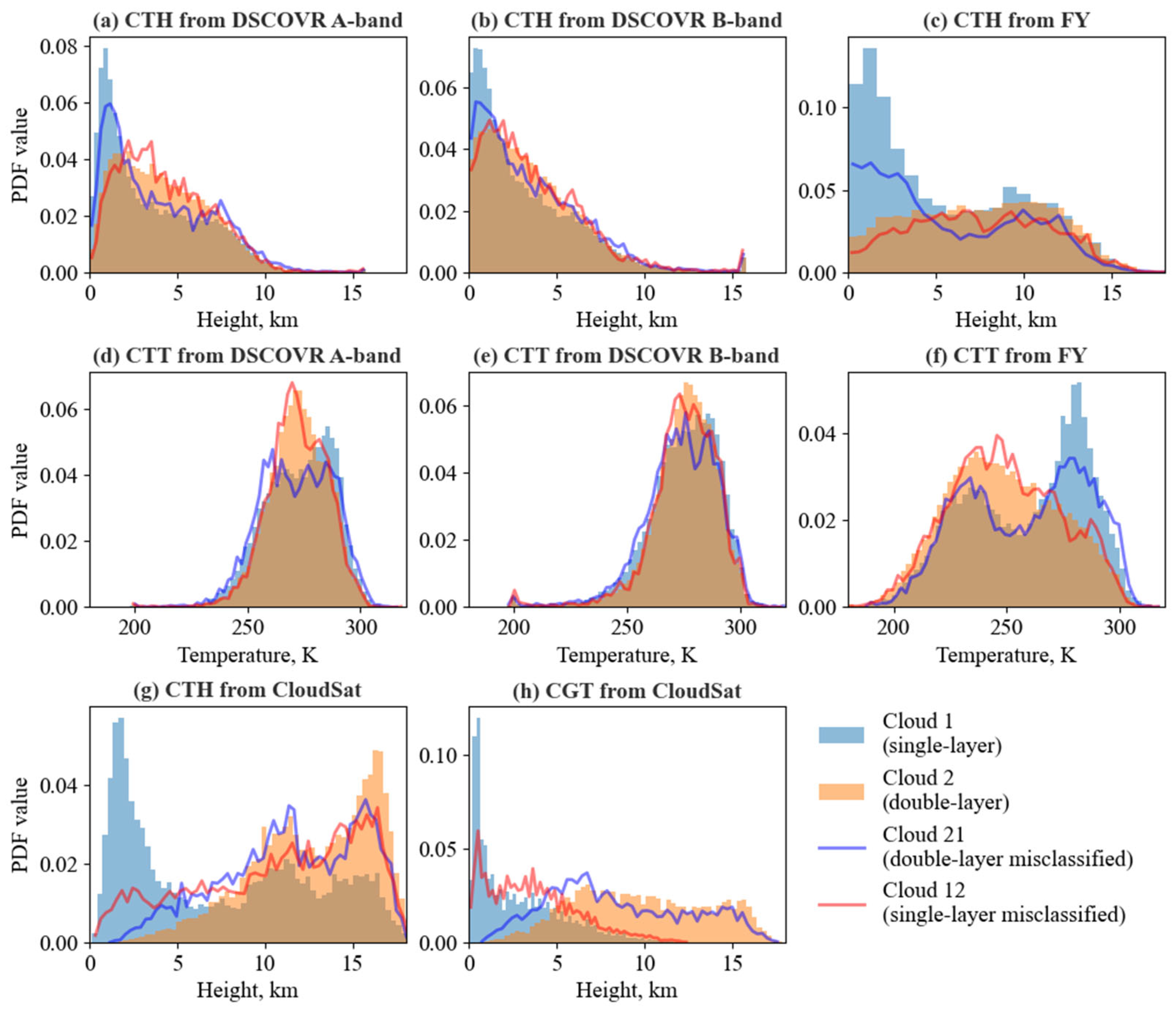
5.1. Error Source Analysis
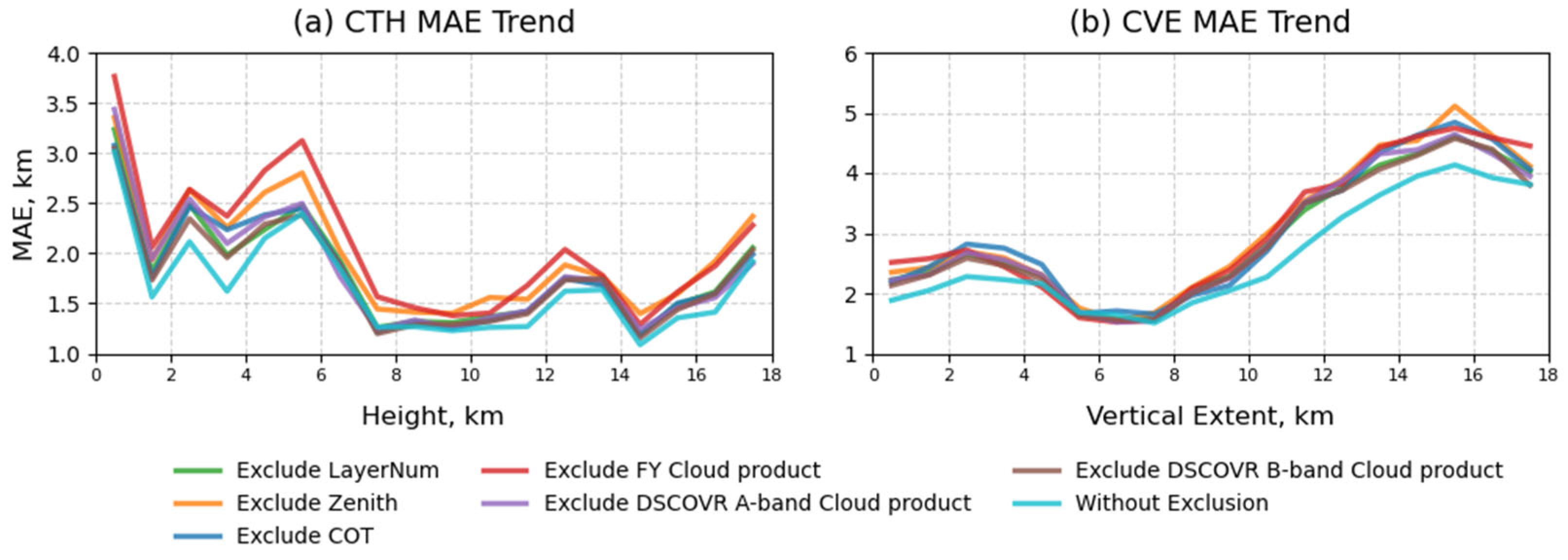
5.2. Importance of Input Variables
- 1.
- Other ablation groups removed multiple variables, whose combined effects amplified performance drops, making them comparable to the cloud layer number removal case;
- 2.
- The cloud layer number provides classification information only and lacks direct height or vertical extent information, requiring interaction with other variables for a full effect.
5.3. Underlying Principles of the ML-Based Method
5.4. Post-Processing Bias Correction
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Justification for Excluding Mixed-Phase Top-Layer Samples


Appendix B. Post-Processing Bias-Correction Experiment
Appendix B.1. Piecewise Linear Regression Correction
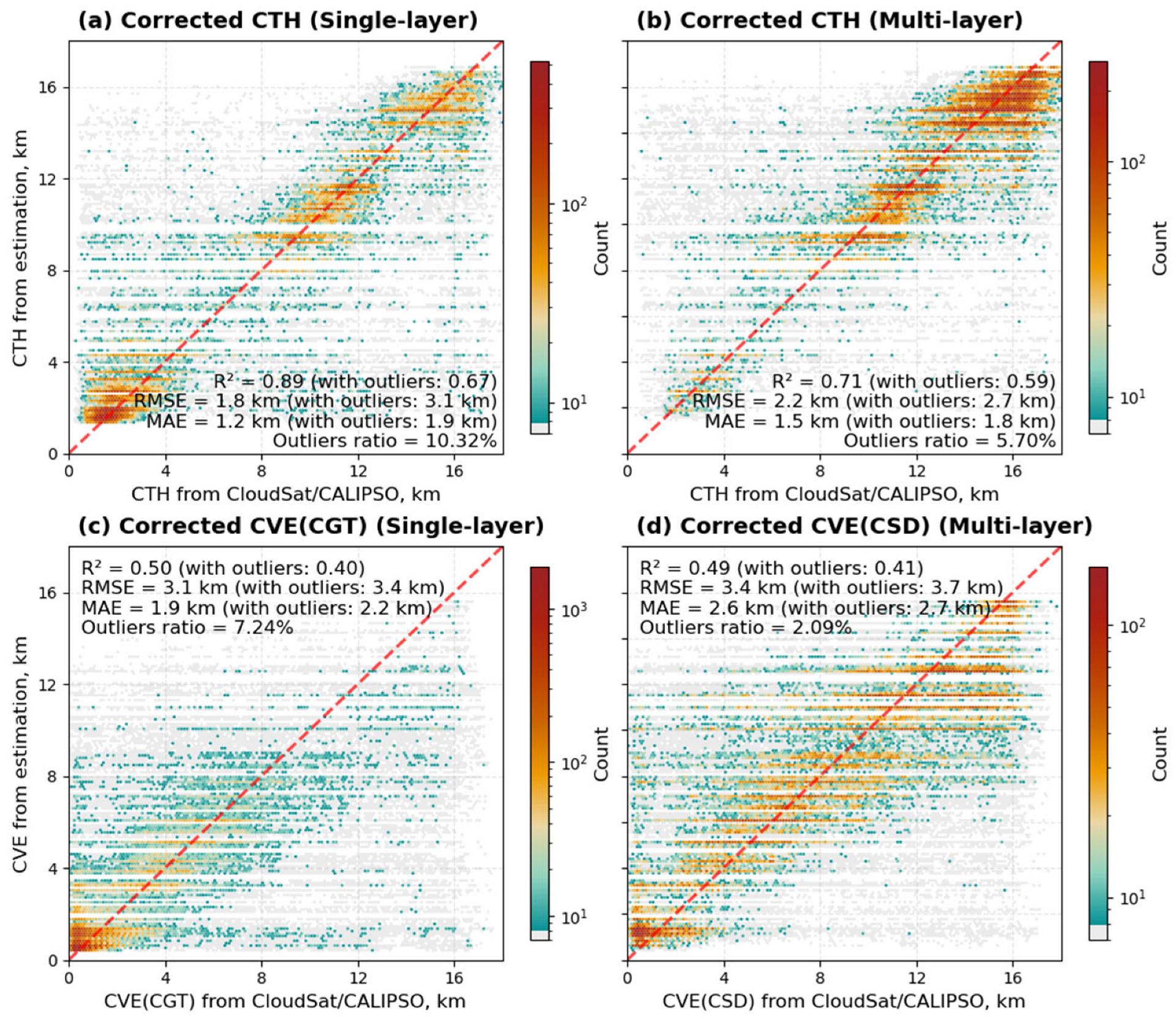
| CTH | Initial Model | Linear Regression Correction | LightGBM Correction | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (km) | MAE (km) | R2 | RMSE (km) | MAE (km) | R2 | RMSE (km) | MAE (km) | |
| Overall | 0.70 | 2.8 | 1.9 | 0.69 | 2.9 | 1.8 | 0.69 | 2.9 | 1.8 |
| Single-layer | 0.69 | 3.0 | 2.0 | 0.67 | 3.1 | 1.9 | 0.67 | 3.1 | 1.9 |
| Multi-layer | 0.60 | 2.7 | 1.8 | 0.59 | 2.7 | 1.8 | 0.59 | 2.7 | 1.8 |
| CVE | Initial Model | Linear Regression Correction | LightGBM Correction | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (km) | MAE (km) | R2 | RMSE (km) | MAE (km) | R2 | RMSE (km) | MAE (km) | |
| Overall | 0.50 | 3.5 | 2.6 | 0.48 | 3.5 | 2.4 | 0.48 | 3.5 | 2.4 |
| Single-layer | 0.43 | 3.3 | 2.3 | 0.40 | 3.4 | 2.2 | 0.40 | 3.4 | 2.2 |
| Multi-layer | 0.43 | 3.6 | 2.8 | 0.41 | 3.7 | 2.7 | 0.41 | 3.7 | 2.7 |
Appendix B.2. Data-Driven LightGBM Correction
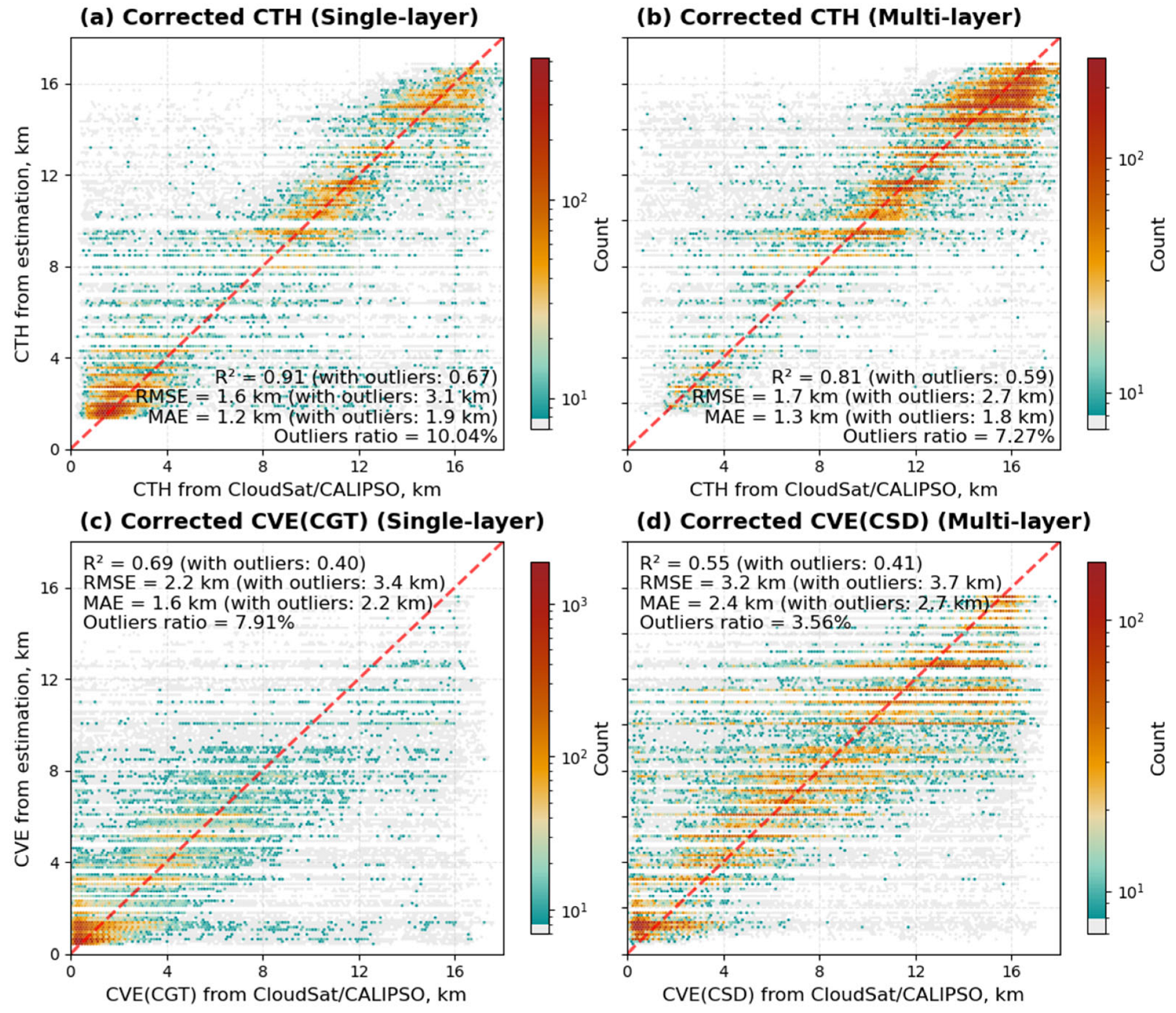
Appendix B.3. Analysis of the Correction Measurements
References
- L’Ecuyer, T.S.; Hang, Y.; Matus, A.V.; Wang, Z. Reassessing the Effect of Cloud Type on Earth’s Energy Balance in the Age of Active Spaceborne Observations. Part I: Top of Atmosphere and Surface. J. Clim. 2019, 32, 6197–6217. [Google Scholar] [CrossRef]
- Stephens, G.L.; Vane, D.G.; Boain, R.J.; Mace, G.G.; Sassen, K.; Wang, Z.; Illingworth, A.J.; O’connor, E.J.; Rossow, W.B.; Durden, S.L.; et al. THE CLOUDSAT MISSION AND THE A-TRAIN: A New Dimension of Space-Based Observations of Clouds and Precipitation. Bull. Amer. Meteor. Soc. 2002, 83, 1771–1790. [Google Scholar] [CrossRef]
- Biondi, R.; Ho, S.; Randel, W.; Syndergaard, S.; Neubert, T. Tropical Cyclone Cloud-top Height and Vertical Temperature Structure Detection Using GPS Radio Occultation Measurements. JGR Atmos. 2013, 118, 5247–5259. [Google Scholar] [CrossRef]
- Lismalini; Marzuki; Shafii, M.A.; Yusnaini, H. Relationship between Cloud Vertical Structures Inferred from Radiosonde Humidity Profiles and Precipitation over Indonesia. J. Phys. Conf. Ser. 2021, 1876, 012011. [Google Scholar] [CrossRef]
- Hamada, A.; Nishi, N. Development of a Cloud-Top Height Estimation Method by Geostationary Satellite Split-Window Measurements Trained with CloudSat Data. J. Appl. Meteorol. Climatol. 2010, 49, 2035–2049. [Google Scholar] [CrossRef]
- Xu, W.; Lyu, D. Evaluation of Cloud Mask and Cloud Top Height from Fengyun-4A with MODIS Cloud Retrievals over the Tibetan Plateau. Remote Sens. 2021, 13, 1418. [Google Scholar] [CrossRef]
- Yang, Y.; Marshak, A.; Mao, J.; Lyapustin, A.; Herman, J. A Method of Retrieving Cloud Top Height and Cloud Geometrical Thickness with Oxygen A and B Bands for the Deep Space Climate Observatory (DSCOVR) Mission: Radiative Transfer Simulations. J. Quant. Spectrosc. Radiat. Transf. 2013, 122, 141–149. [Google Scholar] [CrossRef]
- Håkansson, N.; Adok, C.; Thoss, A.; Scheirer, R.; Hörnquist, S. Neural Network Cloud Top Pressure and Height for MODIS. Atmos. Meas. Tech. 2018, 11, 3177–3196. [Google Scholar] [CrossRef]
- Min, M.; Li, J.; Wang, F.; Liu, Z.; Menzel, W.P. Retrieval of Cloud Top Properties from Advanced Geostationary Satellite Imager Measurements Based on Machine Learning Algorithms. Remote Sens. Environ. 2020, 239, 111616. [Google Scholar] [CrossRef]
- Tan, Z.; Liu, C.; Ma, S.; Wang, X.; Shang, J.; Wang, J.; Ai, W.; Yan, W. Detecting Multilayer Clouds from the Geostationary Advanced Himawari Imager Using Machine Learning Techniques. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4103112. [Google Scholar] [CrossRef]
- Tao, M.; Chen, J.; Xu, X.; Man, W.; Xu, L.; Wang, L.; Wang, Y.; Wang, J.; Fan, M.; Shahzad, M.I.; et al. A Robust and Flexible Satellite Aerosol Retrieval Algorithm for Multi-Angle Polarimetric Measurements with Physics-Informed Deep Learning Method. Remote Sens. Environ. 2023, 297, 113763. [Google Scholar] [CrossRef]
- Viggiano, M.; Cimini, D.; De Natale, M.P.; Di Paola, F.; Gallucci, D.; Larosa, S.; Marro, D.; Nilo, S.T.; Romano, F. Combining Passive Infrared and Microwave Satellite Observations to Investigate Cloud Microphysical Properties: A Review. Remote Sens. 2025, 17, 337. [Google Scholar] [CrossRef]
- Tan, Z.; Ma, S.; Zhao, X.; Yan, W.; Lu, W. Evaluation of Cloud Top Height Retrievals from China’s Next-Generation Geostationary Meteorological Satellite FY-4A. J. Meteorol. Res. 2019, 33, 553–562. [Google Scholar] [CrossRef]
- Heidinger, A.K.; Pavolonis, M.J.; Holz, R.E.; Baum, B.A.; Berthier, S. Using CALIPSO to Explore the Sensitivity to Cirrus Height in the Infrared Observations from NPOESS/VIIRS and GOES-R/ABI. J. Geophys. Res. 2010, 115, 2009JD012152. [Google Scholar] [CrossRef]
- Marshak, A.; Herman, J.; Adam, S.; Karin, B.; Carn, S.; Cede, A.; Geogdzhayev, I.; Huang, D.; Huang, L.-K.; Knyazikhin, Y.; et al. Earth Observations from DSCOVR EPIC Instrument. Bull. Am. Meteorol. Soc. 2018, 99, 1829–1850. [Google Scholar] [CrossRef] [PubMed]
- Ahn, C.; Torres, O.; Jethva, H.; Tiruchirapalli, R.; Huang, L. Evaluation of Aerosol Properties Observed by DSCOVR/EPIC Instrument From the Earth-Sun Lagrange 1 Orbit. JGR Atmos. 2021, 126, e2020JD033651. [Google Scholar] [CrossRef]
- Davis, A.B.; Merlin, G.; Cornet, C.; Labonnote, L.C.; Riédi, J.; Ferlay, N.; Dubuisson, P.; Min, Q.; Yang, Y.; Marshak, A. Cloud Information Content in EPIC/DSCOVR’s Oxygen A- and B-Band Channels: An Optimal Estimation Approach. J. Quant. Spectrosc. Radiat. Transf. 2018, 216, 6–16. [Google Scholar] [CrossRef]
- Davis, A.B.; Ferlay, N.; Libois, Q.; Marshak, A.; Yang, Y.; Min, Q. Cloud Information Content in EPIC/DSCOVR’s Oxygen A- and B-Band Channels: A Physics-Based Approach. J. Quant. Spectrosc. Radiat. Transf. 2018, 220, 84–96. [Google Scholar] [CrossRef]
- Kuze, A.; Chance, K.V. Analysis of Cloud Top Height and Cloud Coverage from Satellites Using the O2 A and B Bands. J. Geophys. Res. 1994, 99, 14481–14491. [Google Scholar] [CrossRef]
- Daniel, J.S.; Solomon, S.; Miller, H.L.; Langford, A.O.; Portmann, R.W.; Eubank, C.S. Retrieving Cloud Information from Passive Measurements of Solar Radiation Absorbed by Molecular Oxygen and O2-O2. J. Geophys. Res. 2003, 108, 2002JD002994. [Google Scholar] [CrossRef]
- Weisz, E.; Li, J.; Menzel, W.P.; Heidinger, A.K.; Kahn, B.H.; Liu, C. Comparison of AIRS, MODIS, CloudSat and CALIPSO Cloud Top Height Retrievals. Geophys. Res. Lett. 2007, 34, 2007GL030676. [Google Scholar] [CrossRef]
- Wang, W.; Sheng, L.; Dong, X.; Qu, W.; Sun, J.; Jin, H.; Logan, T. Dust Aerosol Impact on the Retrieval of Cloud Top Height from Satellite Observations of CALIPSO, CloudSat and MODIS. J. Quant. Spectrosc. Radiat. Transf. 2017, 188, 132–141. [Google Scholar] [CrossRef]
- Sassen, K.; Wang, Z. Classifying Clouds around the Globe with the CloudSat Radar: 1-year of Results. Geophys. Res. Lett. 2008, 35, 2007GL032591. [Google Scholar] [CrossRef]
- Wang, D.; Yang, C.A.; Diao, M. Validation of Satellite-Based Cloud Phase Distributions Using Global-Scale In Situ Airborne Observations. Earth Space Sci. 2024, 11, e2023EA003355. [Google Scholar] [CrossRef]
- Watts, P.D.; Bennartz, R.; Fell, F. Retrieval of Two-Layer Cloud Properties from Multispectral Observations Using Optimal Estimation. J. Geophys. Res. 2011, 116, D16203. [Google Scholar] [CrossRef]
- Yang, Y.; Meyer, K.; Wind, G.; Zhou, Y.; Marshak, A.; Platnick, S.; Min, Q.; Davis, A.B.; Joiner, J.; Vasilkov, A.; et al. Cloud Products from the Earth Polychromatic Imaging Camera (EPIC): Algorithms and Initial Evaluation. Atmos. Meas. Tech. 2019, 12, 2019–2031. [Google Scholar] [CrossRef] [PubMed]
- Upadhyay, A. Haversine Formula-Calculate Geographic Distance on Earth. 2015. Available online: Https://Www.Igismap.Com/Haversine-Formula-Calculate-Geographic-Distance-Earth/ (accessed on 18 May 2025).
- Bley, S.; Deneke, H.; Senf, F. Meteosat-Based Characterization of the Spatiotemporal Evolution of Warm Convective Cloud Fields over Central Europe. J. Appl. Meteorol. Climatol. 2016, 55, 2181–2195. [Google Scholar] [CrossRef]
- Grosvenor, D.P.; Wood, R. The Effect of Solar Zenith Angle on MODIS Cloud Optical and Microphysical Retrievals within Marine Liquid Water Clouds. Atmos. Chem. Phys. 2014, 14, 7291–7321. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, NY, USA, 4–9 December 2017. [Google Scholar]
- Xuan, L.; Lin, Z.; Liang, J.; Huang, X.; Li, Z.; Zhang, X.; Zou, X.; Shi, J. Prediction of Resilience and Cohesion of Deep-Fried Tofu by Ultrasonic Detection and LightGBM Regression. Food Control 2023, 154, 110009. [Google Scholar] [CrossRef]
- Alshboul, O.; Almasabha, G.; Shehadeh, A.; Al-Shboul, K. A Comparative Study of LightGBM, XGBoost, and GEP Models in Shear Strength Management of SFRC-SBWS. Structures 2024, 61, 106009. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hodge, V.; Austin, J. A Survey of Outlier Detection Methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Hajihosseinlou, M.; Maghsoudi, A.; Ghezelbash, R. A Novel Scheme for Mapping of MVT-Type Pb–Zn Prospectivity: LightGBM, a Highly Efficient Gradient Boosting Decision Tree Machine Learning Algorithm. Nat. Resour. Res. 2023, 32, 2417–2438. [Google Scholar] [CrossRef]



| Model | Input | Label |
|---|---|---|
| ) | | |
| CTH/CVE | |
| Hyperparameter | CLN Model | CTH/CVE Model | Description |
|---|---|---|---|
| boosting_type | gbdt | gbdt | Gradient Boosting Decision Tree |
| n_estimators | 10,000 | 10,000 | Number of boosting iterations |
| learning_rate | 0.005 | 0.005 | Step size shrinkage |
| max_depth | 10 | 10 | Maximum tree depth |
| num_leaves | 380 | 300 | Maximum number of leaves per tree |
| bagging_fraction | 0.75 | 0.75 | Fraction of data to be used for each iteration |
| feature_fraction | 0.75 | 0.75 | Fraction of features to be used for each iteration |
| objective | multiclass | regression | Specifies the learning task and objective |
| All Clouds | Single-Layer Clouds | Multi-Layer Clouds | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (km) | MAE (km) | R2 | RMSE (km) | MAE (km) | R2 | RMSE (km) | MAE (km) | |
| FY-4A | −0.09 | 5.5 | 4.0 | 0.45 | 3.9 | 2.6 | −2.85 | 6.6 | 5.4 |
| DSCOVR A-band | −1.15 | 7.7 | 6.5 | −0.06 | 5.5 | 4.2 | −6.75 | 9.4 | 8.9 |
| DSCOVR B-band | −1.52 | 8.3 | 7.1 | −0.30 | 6.1 | 4.7 | −7.90 | 10.1 | 9.5 |
| New Model | 0.70 | 2.8 | 1.9 | 0.69 | 3.0 | 2.0 | 0.60 | 2.7 | 1.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Yang, J.; Lv, T.; Yi, Y.; Lin, Z.; Dong, J.; Li, S. A Cloud Vertical Structure Optimization Algorithm Combining FY-4A and DSCOVR Satellite Data. Remote Sens. 2025, 17, 2484. https://doi.org/10.3390/rs17142484
Zheng Z, Yang J, Lv T, Yi Y, Lin Z, Dong J, Li S. A Cloud Vertical Structure Optimization Algorithm Combining FY-4A and DSCOVR Satellite Data. Remote Sensing. 2025; 17(14):2484. https://doi.org/10.3390/rs17142484
Chicago/Turabian StyleZheng, Zhuowen, Jie Yang, Taotao Lv, Yulu Yi, Zhiyong Lin, Jiaxin Dong, and Siwei Li. 2025. "A Cloud Vertical Structure Optimization Algorithm Combining FY-4A and DSCOVR Satellite Data" Remote Sensing 17, no. 14: 2484. https://doi.org/10.3390/rs17142484
APA StyleZheng, Z., Yang, J., Lv, T., Yi, Y., Lin, Z., Dong, J., & Li, S. (2025). A Cloud Vertical Structure Optimization Algorithm Combining FY-4A and DSCOVR Satellite Data. Remote Sensing, 17(14), 2484. https://doi.org/10.3390/rs17142484









