Abstract
Agriculture accounts for 29% of the Gross Domestic Product of the Nusa Tenggara Islands (NTIs). However, recurring agricultural droughts pose a major threat to the sustainability of agriculture in this region. The interplay between precipitation, solar radiation, and surface temperature as meteorological factors plays a key role in affecting vegetation (Soil-Adjusted Vegetation Index) and agricultural drought (Temperature Vegetation Dryness Index) in the NTIs. Based on the analyses of interplay with temporal lag, this study investigates the effect of each factor on agricultural drought and attempts to provide early warnings regarding drought in the NTIs. We collected surface information data from Moderate-Resolution Imaging Spectroradiometer (MODIS). Meanwhile, rainfall was estimated from Himawari-8 based on the INSAT Multi-Spectral Rainfall Algorithm (IMSRA). The results showed reliable performance for 8-day and monthly scales against gauges. The drought analysis results reveal that the NTIs suffer from mild-to-moderate droughts, where cropland is the most vulnerable, causing shifts in the rice cropping season. The driving factors could also explain >60% of the vegetation and surface-dryness conditions. Furthermore, our monthly and 8-day TVDI estimation models could capture spatial drought patterns consistent with MODIS, with coefficient of determination (R2) values of more than 0.64. The low error rates and the ability to capture the spatial distribution of droughts, especially in open-land vegetation, highlight the potential of these models to provide an estimation of agricultural drought.
1. Introduction
Agricultural drought, as a widespread natural phenomenon, typically results from global warming and the influence of climate change and is caused by reduced precipitation and increased evapotranspiration due to high temperatures [1,2]. These conditions limit vegetation growth, disrupt large-scale agricultural production, and threaten ecosystem health [3,4,5]. Understanding how agricultural drought is affected by these environmental factors is essential for revealing the mechanisms behind drought occurrences (Figure 1) and providing drought monitoring systems and forecasting, which are key to mitigating the impacts of drought on agriculture [6]. The Nusa Tenggara Islands (NTIs) are an archipelago located in Southeastern Indonesia, where agriculture is essential, accounting for almost 29% of the province’s Gross Domestic Product (GDP) in 2023 [7]. However, at the same time, the region is also vulnerable to annual drought [8,9]. This vulnerability is attributed mainly to its location and the influence of monsoonal climate patterns, which result in pronounced dry seasons and uneven rainfall distribution [10]. In addition, the El Niño phenomenon also reduces rainfall over the NTI region and increases the potential for drought disasters.
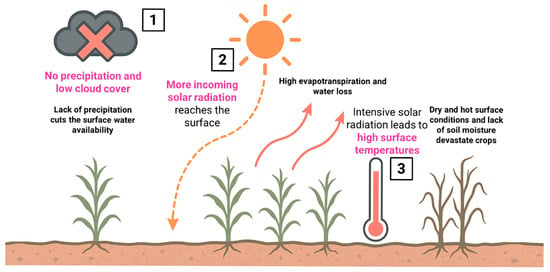
Figure 1.
Scientific hypothesis diagram. The decrease in precipitation and cloud cover reduces surface water availability, while intensified solar radiation leads to higher surface temperatures. Then, these higher surface temperatures increase evapotranspiration, leading to more significant water loss from both plants and the surface, negatively affecting vegetation growth.
Atmospheric dynamics in Indonesia, including those in the NTIs, are generally influenced by two monsoon systems, the Asian and Australian monsoons [11]. Southeasterly winds from Mainland Australia usually occur from June to August during the dry season; this is known as the Australian monsoon (marked by red arrows in Figure 2a). This wind has the characteristics of being cold and dry, and having little water vapor, because it crosses the arid desert zone in the central to near-northern part of Australia and has the impact of reducing the rainfall in areas it passes through [12,13]. Meanwhile, the Asian monsoon that occurs in the rainfall season (around December to February) is described as trade winds coming from the Asian continent or northwesterly winds (marked by blue arrows in Figure 2a). It transports warm and humid air masses from the Asian continent across the South China Sea, producing more rainfall in almost all regions of Indonesia [14,15]. However, due to their geographical location, relatively far from these moisture sources, the NTIs receive less water vapor, as the northwesterly monsoon winds have already lost much of their moisture while crossing Western and Northern Indonesia [16,17]. As a result, the NTIs tend to receive less rainfall than other regions in Indonesia. Additionally, the distance of the eastern part of the NTIs from the Pacific Ocean increases the impact of El Niño events, which are known to suppress precipitation further and have been linked to severe drought occurrences, particularly in 2019 and 2023 [18,19,20,21].

Figure 2.
(a) The scope of the study area, including Digital Elevation Model (DEM), gauge stations, and rice fields; (b) vegetation type.
A lack of previous precipitation reduces surface water availability in the NTIs [22], limiting the essential moisture needed for vegetation and soil. It has also been noted in [23] that rainfall plays a vital role in water availability and is acknowledged as the primary component controlling vegetation dynamics in over 40% of Earth’s vegetated surfaces. In parallel, under clear skies or partly cloudy conditions, more solar radiation can reach the land surface through direct or scattered radiation [24], increasing the amount of heat absorbed. This intensification of solar radiation raises surface temperatures significantly. As a result, evapotranspiration increases, accelerating water loss from the soil and plant leaves [25]. When this situation occurs for a prolonged period, it will create a dry and hot environment and lower the moisture content of the soil. This can have a devastating impact on vegetation and agriculture. Previous studies have also explained how meteorological factors affect vegetation dynamics across different climatic regions. Chen et al. [26] found that vegetation is impacted by precipitation anomalies in Northern China, especially in arid and semi-arid regions. The rainfall anomalies have a 1–2-month temporal lag response and correlate well with accumulated precipitation over 2–6 months. Additionally, Wu et al. [27] observed that solar radiation plays a significant role in influencing vegetation growth in the coastal areas of Australia. Furthermore, extensive global studies have revealed that the sensitivity of vegetation to solar radiation typically lags by about a month in many parts of the mid-latitude and high-latitude Northern Hemisphere [28,29].
These findings suggest that identifying the meteorological factors in Figure 1 (precipitation, solar radiation, and surface temperature) and understanding their lag effects on vegetation is very important, since they can influence surface dryness and play a crucial role in vegetation growth. However, the contributions of each factor to surface and vegetation dynamics in the NTIs remain insufficiently understood. Most existing studies on drought focus on monitoring the spatial distribution, intensity, and frequency of drought, often using single-index approaches such as the Standardized Precipitation Index (SPI) and Standardized Precipitation Evapotranspiration Index (SPEI) [18,30] without fully investigating the driving meteorological mechanisms behind the processes by which drought occurs. Some previous studies have also explored the relationship between vegetation and meteorological factors but have not discussed how it relates to surface dryness or agricultural drought [26,27,28,29,31,32]. Moreover, the number of surface observation stations for parameters such as rainfall, surface temperature, and solar radiation is still limited for the NTI region. Therefore, it is challenging to provide reliable monitoring and analysis.
In terms of data collection, satellite observations could provide surface information and precipitation data to overcome the lack of ground-based measurements in the study area. The Himawari-8 satellite provides high-spatiotemporal infrared observations that can continuously track cloud-top temperatures and convective developments, allowing for near-real-time precipitation estimation. This could overcome some of the limitations of microwave-based satellites, which tend to have coarse temporal and spatial resolution because of their broad wavelength and polar orbit [33]. Moreover, surface meteorological parameters such as surface reflectance, land surface temperature (LST), and Downward Surface Radiation (DSR) can be obtained from the Moderate-Resolution Imaging Spectroradiometer (MODIS). This has a high spatial resolution of 500 m to 1 km and an observation time of every 1 to 2 days, which can help to monitor land surface conditions in terms of drought observation. Validation studies also demonstrate that MODIS data have good accuracy and reliability when compared with surface observations or other satellite products across multiple regions and environmental conditions [34,35,36,37,38,39].
Understanding how meteorological factors influence agricultural drought is important for identifying drought mechanisms and providing early warnings of potential drought in the NTIs. Therefore, this study aims to monitor and predict drought through satellite data. First, we estimate precipitation using Himawari-8 satellite data and then evaluate the reliability of these estimations by comparing them with rain gauge measurements from the NTIs. This comparison is necessary to assess the accuracy of satellite-derived rainfall estimates. In addition, we characterize the spatiotemporal dynamics, frequency, and intensity of agricultural drought events and provide a view of drought in different vegetation types, especially in rice crop areas. Furthermore, we investigate three meteorological factors (precipitation, temperature, and solar radiation) and their time-lag effects on agricultural drought and vegetation. Lastly, we develop and validate an estimation model for agricultural drought prediction in the NTIs based on identified meteorological factors.
The structure of this paper is as follows. The study area, data, and methods used are described in Section 2. The results are presented in Section 3, including (1) the reliability assessment of Himawari-8 rainfall estimation (HRE); (2) the spatiotemporal analysis of agricultural drought characteristics and their impact on vegetation, especially rice crops; (3) analysis of the vegetation response and surface dryness in relation to meteorological factors; and (4) the development and validation of a multiple linear regression (MLR) agricultural drought prediction model. Section 4 and Section 5 comprise the discussion and the conclusions.
2. Materials and Methods
2.1. Study Area
The NTIs are divided into two administrative provinces, West Nusa Tenggara (NTB) and East Nusa Tenggara (NTT), and are situated in the southeastern part of Indonesia, between 7°46′ and 11°00′S and 115°46′ and 125°08′E, as shown in Figure 2a. Our study area is approximately 68,871.25 km2 [40] and has topographic differences in altitude from below mean sea level to 3600 m. This affects climatic patterns across the islands, particularly in NTT, which predominantly has dry tropical and semi-arid characteristics [41] marked by less rainfall and a long dry season spanning up to eight months per year [42]. According to historical records from the Global Precipitation Climatology Centre [41,43], the annual average rainfall in NTT is approximately 1696 mm, 36% lower than the national average rainfall. This prolonged dry season and lower rainfall mean the region is more susceptible to water scarcity and agricultural drought.
These islands have four dominant vegetation types (Figure 2b): croplands, broadleaf forests, grassland, and savanna. Savanna has the largest percentage area compared to the other categories, at around 24.3%. Broadleaf forests and croplands account for about 23.3% and 10.2% of the total area. Finally, grassland has the lowest area, with about 7%. The remaining areas not included for statistical analysis in this study are built-up areas and other small proportions of vegetation types, which together account for a total of 35.2%.
2.2. Data
Our study used rainfall estimation from the Himawari satellite and MODIS surface information to analyze the impact of meteorological factors on vegetation and agricultural drought in the NTIs. Detailed descriptions of the data types, input parameters, sources, and spatiotemporal resolutions are provided in Table 1.

Table 1.
Information about the data.
2.2.1. Himawari-8 AHI Data
Himawari-8, launched by the Japan Meteorological Agency (JMA) on 7 July 2015, is a geostationary meteorological satellite designed to monitor weather and climate phenomena across the Asia–Pacific region [44]. The data from Himawari-8 are publicly accessible via the Japan Aerospace Exploration Agency (JAXA) website (http://www.eorc.jaxa.jp/ptree/index.html, accessed on 15 September 2024). Himawari-8 has 16 observation bands, offering a spatial resolution of 0.5 to 1 km for visible and near-infrared bands and 2 km for infrared bands. It also has a high temporal resolution of every 10 min for full-disk observations and every 2.5 min for specific regions. In this study, we chose infrared bands B13 (IR1) and B15 (IR2) from 2019 to 2023, which can be used to estimate precipitation intensity based on cloud-top temperature observations.
2.2.2. Rain Gauge
Daily rainfall data from 2019 to 2023 were obtained from the Indonesian Meteorological Agency (https://dataonline.bmkg.go.id/, accessed on 15 September 2024). A total of 26 rain gauge stations were carefully selected and spatially aligned with the Himawari-8 grid boxes, where each box validation contained at least one rain gauge. The comparison between satellite and rain gauge data is based on the near point-to-pixel comparison.
2.2.3. MODIS Data
The surface meteorological information in this study comes from MODIS satellite data. We collected the land surface thermal, radiative, and vegetation conditions from 2019 to 2023. For the land surface temperature (LST) dataset analysis, we retrieved LST data from MOD11A2 Version-6.1, which provides an 8-day average at a 1 km resolution [45]. This product includes the daytime and nighttime LST, but only daytime LST from the Terra satellite was employed in our analysis. Surface reflectance data were obtained from MOD09A1 Version-6.1, which provides atmospherically corrected red (Band 1) and near-infrared (Band 2) reflectance at a 500 m resolution [46]. These reflectance data are calculated using vegetation indices such as the Normalized-Difference Vegetation Index (NDVI) and Soil-Adjusted Vegetation Index (SAVI). MODIS data also provide Surface Downward Shortwave Radiation (DSR) measurements through the MCD18A1 product, which can be monitor the incoming solar energy [38]. It has the same spatial resolution and daily temporal resolution as the LST data. Since this study aims to focus on several different vegetation types, we also use the land cover-type information from MODIS MCD12Q1 and select the International Geosphere–Biosphere Program (IGBP) Type 1 classification scheme [47]. Given the differences in spatial and temporal resolutions across datasets, we applied a maximum value composite (MVC) approach for both 8-day and monthly analyses [48]. We resampled the data to match the spatial resolution of Himawari-8. All datasets were accessed from the LPDAAC portal (https://lpdaac.usgs.gov/, accessed on 15 September 2024).
2.3. Methodology
As illustrated in the research flowchart shown in Figure 3, this study is structured to address four main objectives through a clear and systematic approach. First, precipitation levels are estimated using infrared (IR) data from the Himawari-8 satellite, and then these values are validated against ground-based rain gauge measurements. Second, the spatial and temporal characteristics of agricultural drought across the NTIs are monitored using the Temperature Vegetation Dryness Index (TVDI) derived from the SAVI and LST. Third, this study also identified the influence of meteorological variables on vegetation dynamics through partial correlation analysis and optimal time lags. Finally, a predictive model for the TVDI is developed using MLR through integrating the effect of temporal lag of meteorological factors.
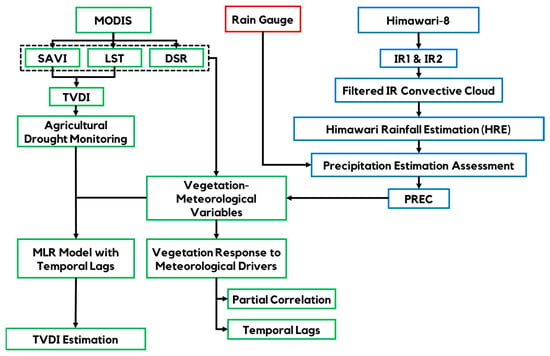
Figure 3.
Research framework.
2.3.1. Himawari Rainfall Estimation (HRE)
Rainfall over the study area is estimated through an empirical power-law relationship, derived from the Indian Satellite Multi-Spectral Rainfall Algorithm (IMSRA) as follows [49].
where R is the estimated rainfall, and IR represents the thermal infrared brightness temperature. Based on Sobajima [50], IR data are masked by excluding clear-sky pixels with cloud-top temperatures exceeding 288.15 K. Additionally, cirrus clouds are removed by filtering out areas where the brightness temperature difference between the 10.4 μm and 12.4 μm channels is less than 2 K. Excluding clear-sky pixels and cirrus clouds is a step to ensure that only convective cloud regions, which are typically associated with rainfall, are analyzed.
R = 8.613098 × exp (−(IR − 197.97)/15.7061)
2.3.2. Calculation of the NDVI and SAVI
The Soil-Adjusted Vegetation Index (SAVI) is structurally similar to the Normalized-Difference Vegetation Index (NDVI) but includes ‘L’ for soil adjustment [51]. The formula is as follows:
where NIR represents the near-infrared reflectance; R is the red reflectance; and L is the soil adjustment factor, which is determined based on the density of vegetation cover, as indicated by the NDVI value. L = 1 for sparse vegetation (NDVI ≤ 0.45), decreasing to L = 0.25 for dense vegetation (NDVI > 0.8). The purpose of including the SAVI for vegetation analysis is to avoid the limitations of the NDVI from saturation effects in high fractional vegetation cover and the impact of soil background in sparse vegetation.
NDVI = (NIR − R)/(NIR + R)
SAVI = ((NIR − R)/(NIR + R + L)) × (1 + L)
2.3.3. Vegetation Anomaly
In addition, this study also incorporates vegetation-anomaly analysis based on SAVI to better capture deviations from normal vegetation conditions. Vegetation indices often follow seasonal cycles due to plant phenology. Therefore, using anomaly values allows us to highlight abnormal vegetation stress caused by meteorological extremes such as droughts. The formula is as follows:
where SAVImean is the multi-year mean SAVI for month m, and SAVIsd is the standard deviation of SAVI values for month m. The range is from −3 to +3, where values below −2 indicate severe vegetation stress or drought.
SAVI Anomaly = (SAVIi − SAVImean)/(SAVIsd)
2.3.4. Calculation of the TVDI
The TVDI is applied to assess land surface dryness by empirically relating LST to the SAVI, a concept (Figure 4) introduced by Sandholt et al. [52].
where LST is the observed land surface temperature in a given pixel, and the minimum (LSTmin) and maximum (LSTmax) temperatures are defined from linear regressions between the LST and SAVI. These equations describe the dry and wet edges of the LST-SAVI space and are used to characterize the surface-dryness conditions. The TVDI classification will follow [53,54] and can be seen in Table 2. It should be noted that the thresholds were originally derived from dry-farming regions and may not capture the actual dryness situation in other vegetation.
TVDI = (LST − LSTmin)/(LSTmax − LSTmin)
LSTmin = a1 + b1 × SAVI
LSTmax = a2 + b2 × SAVI
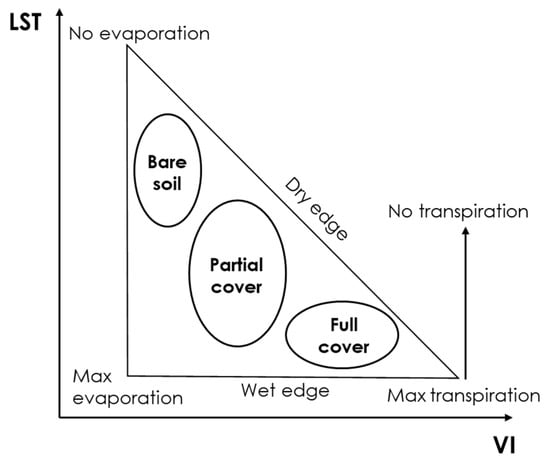
Figure 4.
Theoretical triangle in the LST-VI area.

Table 2.
Description of TVDI dryness level.
2.3.5. Standardized Precipitation Index (SPI)
The Standardized Precipitation Index (SPI) is a widely used indicator to assess precipitation anomalies over different timescales. It was first introduced by McKee et al. [55] in 1993 and is based on fitting an incomplete gamma probability density function to a long-term precipitation time series, which is then transformed into a standardized normal distribution. The detailed procedure of SPI can be referred to in the previous study [55,56]. In this study, SPI-1 and SPI-3 were calculated to assess short-to-medium-term precipitation anomalies and their influence on vegetation and surface drought conditions.
2.3.6. A Second-Order Partial Correlation
A second-order partial correlation is applied to investigate the relationship between drought and vegetation with respect to meteorological factors. It quantifies the strength and direction between two variables while controlling for the effects of two additional variables. The second-order partial correlation coefficient ranges between −1 and +1, with values close to +1 indicating a strong positive correlation, and values close to −1 representing a strong negative correlation.
The formula shown above describes the relationship between the SAVI (r1) and precipitation (r2) while controlling for the influence of both LST (r3) and DSR (r4). Specifically, represents the correlation between r1 and r2 after removing the linear effects of r3 and r4. This isolates the direct association between the vegetation conditions and precipitation, independent of surface temperature and solar radiation effects. In addition, to calculate , , and , we used the first-order partial rank correlation [57,58]. From these results, a dominant driving factor map was constructed to illustrate the primary factor influences on different vegetation types and agricultural drought.
2.3.7. Linear Regression
Previous studies have shown that vegetation responses to meteorological factors have a time lag. To determine the optimal temporal lag in this relationship, we followed the method in [59] and used linear regression analysis. In this context, three separate simple linear regression models were constructed to independently examine the influence of precipitation (PREC), land surface temperature (LST), and Downward Surface Radiation (DSR) on vegetation, represented by the SAVI. These relationships are expressed through Formulas (9)–(11):
SAVI = a × PREC + b
SAVI = a × LST + b
SAVI = a × DSR + b
Each equation uses a different meteorological variable as the independent predictor (x), and SAVI as the dependent response (y), with a and b representing the regression slope and intercept, respectively. We analyzed time lags ranging from 0 to 2 months to capture possible delayed vegetation responses. The optimal lag for each meteorological factor was identified based on the highest coefficient of determination (R2) obtained from the regression models.
2.3.8. Multiple Linear Regression (MLR)
The MLR model was developed to assess the influence of meteorological variables on vegetation dynamics and to estimate agricultural drought. The MLR model is also built by considering the temporal lag of each meteorological factor on each grid. We constructed two MLR models, one for monthly prediction and the second for 8-day prediction. The monthly model has a 1-to-2-month temporal lag, while the 8-day model captured shorter-term effects, with lags ranging from 8 days to over one month.
TVDI = a1 × PREC + a2 × LST + b
Based on the above equation, a1, a2, and a3 represent the regression coefficients, and b is the intercept.
2.3.9. Validation Metrics
We used categorical and continuous metrics (CSI, POD, FAR, R2, NRMSE, and NMBE). The CSI measures overall accuracy, the POD indicates the ability to detect rainfall events, and the FAR measures false detections. For the continuous assessment, R2 explains the proportion of variance captured by the estimation model, while the NRMSE and NMBE assess normalized error magnitude and bias, respectively. In this study, HRE was evaluated using both metric types compared against rain gauge observation, while TVDI estimation was validated using continuous metrics only compared with the TVDI calculation from MODIS. The formula of each metric is described in Table 3.

Table 3.
Description of categorical (CSI, POD, and FAR) and continuous (R2, NRMSE, and NMBE) metrics. H represents hit, M represents miss, and FA represents false alarm. The rainfall event is defined as ≥1 mm. In addition, is the observed value, is the predicted value, and is the mean of the observed values.
3. Results
3.1. Reliability Assessment of Himawari-8 Rainfall Estimation (HRE)
The spatial average daily precipitation time series across the NTIs from 2019 to 2023, derived from 26 ground-based rain gauges (red) and HRE (blue), is presented in Figure 5 for daily, 8-day, and monthly timescales. These timescale assessments are selected to provide the reliability of rainfall estimation from Himawari for further analysis in drought monitoring, especially for the 8-day and monthly scales, as they represent accumulated precipitation, which is essential for capturing and predicting agricultural drought. Rainfall dynamics in the NTIs show a monsoonal variation, as seen from the increasing precipitation from November to around March or April and the marked dry season from May or June through to October. The HRE-based rainfall estimates effectively capture this seasonal cycle, closely matching gauge-based observations across the daily, 8-day, and monthly timescales. However, HRE shows higher fluctuations when viewed on a daily scale. In contrast, the 8-day and monthly timeframes reduce this noise by averaging over extended periods, thereby capturing more consistent and reliable rainfall patterns.
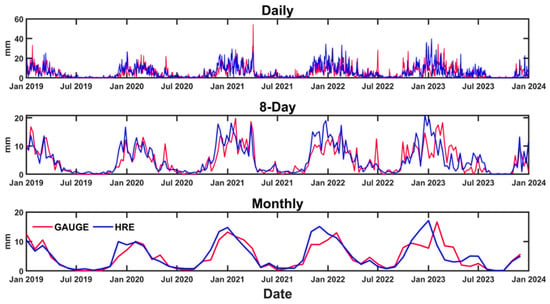
Figure 5.
Precipitation time-series analysis for daily, 8-day, and monthly variations.
The spatial plot performance of HRE against 26 rain gauge observations across the NTIs using R2 and CSI is shown in Figure 6. Overall, the performance improves at coarser temporal scales, with higher R2 and CSI values observed at the 8-day and monthly scales compared to the daily scale. This indicates that temporal aggregation helps reduce noise and better captures the rainfall variability. More detailed performance evaluations across all six metrics (R2, NRMSE, NMBE, POD, FAR, and CSI) can be found in the boxplot analysis presented in Figure 7. The daily scale shows more variability and lower R2 values in several locations between 0 and 0.5, while the NRMSE is less than 0.2. Daily POD values are consistently above 0.7, as shown in Figure 7a, confirming HRE’s capability in detecting rainfall events. The relatively high FAR values (between 0.4 and 0.7; mean 0.6) imply frequent false alarms. Consequently, the CSI scores fall between 0.2 and 0.5, with a mean value of 0.34, indicating moderate reliability for the satellite estimates at a finer temporal resolution. As the temporal scale shifts to 8 days or monthly, a general improvement is observed: there is an increase in R2 values and a decrease in NRMSE values for continuous variables, and a lower FAR and higher CSI and POD values for categorical variables.
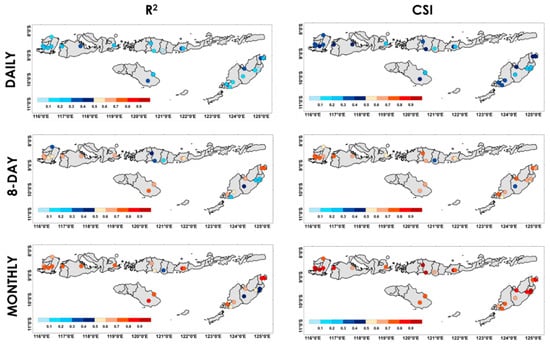
Figure 6.
Spatial distributions of metrics (R2 and CSI) for HRE relative to in situ rain gauge data across the NTIs from 2019 to 2023 (precipitation event >1 mm).

Figure 7.
Boxplots of verification metrics (R2, NRMSE, NMBE, CSI, POD, and FAR) for HRE performance across three temporal scales: (a) daily, (b) 8 days, and (c) monthly. Each boxplot color represents a different timescale: blue for daily, green for 8-day, and red for monthly.
The boxplot analyses in Figure 7b,c show that the average R2 value increases between the 8-day and monthly scales, from 0.6 to 0.7. Meanwhile, the NRMSE values are 0.24 and 0.19 for the 8-day and monthly data, respectively. The categorical scores also show a consistent upward trend as the timescale increased from 8 days to monthly: the POD increased from 0.87 to 0.96, the FAR decreased from 0.28 to 0.15, and the CSI significantly increased from 0.63 to 0.81. In addition, the NMBE values at the three timescales have variations between −0.8 and 0.9 across rain gauge stations, with an average value of about 0.16. This value indicates there is an average overestimation from all scales.
Scatter plots of the daily average HRE compared to the gauge data are shown in Figure 8. For all timescales, the distribution pattern is relatively consistent, with a gradual increase in R2 from 0.34 for the daily scale to 0.7 for the monthly scale. The relatively low R2 for the daily scale is primarily due to the high variability and intermittency of rainfall events, which are difficult to capture accurately via satellite estimations. Additionally, errors from cloud-top-temperature-based estimation can further reduce accuracy on a daily scale. The plots also show the tendency of HRE to overestimate daily rainfall under low rainfall conditions (less than ~10 mm/day) until high rainfall, reflecting the general limitation of satellite-based rainfall estimation. However, this limitation becomes less pronounced when the data are aggregated into 8-day or monthly scales, as the accumulation process smooths short-term fluctuations and random errors. Therefore, 8-day and monthly rainfall data were used to monitor and predict agricultural drought conditions based on accumulated rainfall, as cumulative rainfall is more relevant than short-term rainfall patterns, which can be subject to anomalies.
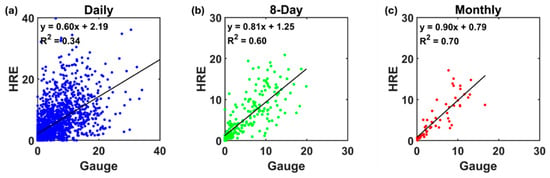
Figure 8.
Scatterplots of precipitation from HRE relative to gauge observations at three temporal scales: (a) daily, (b) 8 days, and (c) monthly. The solid line indicates the linear regression line.
3.2. Agricultural Drought and Its Impact on Vegetation
3.2.1. Spatiotemporal Patterns and Agricultural Drought Frequency in NTI
We calculated the monthly TVDI from 2019 to 2023 to monitor agricultural drought frequency in the NTI region. Figure 9a–d show the spatial frequency of the intensity of each drought, and Figure 9e is the total drought frequency over 5 years. Based on the event frequency, the region is predominantly influenced by mild-to-moderate-intensity droughts, with frequencies ranging between 5% and 40%. In contrast, the frequency of severe to extreme drought is lower, generally between 0% and 20%. The figure also highlights some areas that can experience drought conditions for up to 50% of the time, highlighting the vulnerability of the NTIs to recurring agricultural droughts. The eastern parts of the islands have become more prone to drought events, and these conditions are more frequently observed in agricultural lands, savannas, and grasslands than broadleaf forest areas.
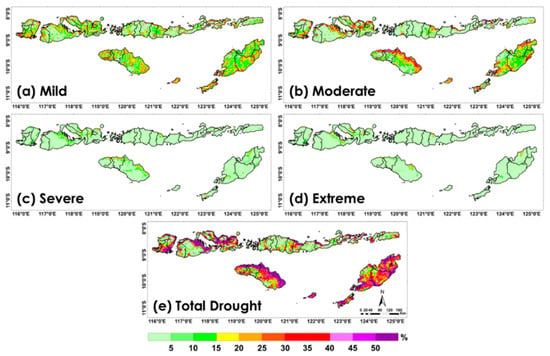
Figure 9.
Different intensities of agricultural drought frequency based on the TVDI from 2019 to 2023 in the NTIs: (a) mild drought, (b) moderate drought, (c) severe drought, (d) extreme drought, and (e) total drought frequency for the entire period.
After analyzing the frequency of drought events, we next plotted the monthly drought-area ratio across the four different intensity classes over the NTI region between 2019 and 2023 (Figure 10). We found that agricultural drought is a persistent issue in the NTIs, as drought-affected areas are present in each month, with more than 5% of the region typically experiencing drought conditions at any one time. Droughts are more common in the dry season, with moderate-intensity droughts affecting 50% to 60% of the total land area, especially in 2019 and 2023, which show the most extensive drought coverage, possibly due to significantly lower rainfall during these periods.
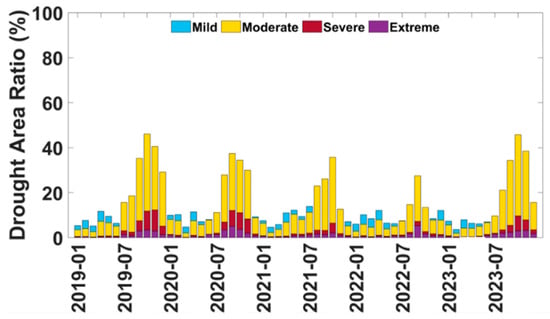
Figure 10.
The monthly distribution of the drought-area ratio in the NTI region from 2019 to 2023 is classified into four drought-intensity levels (mild, moderate, severe, and extreme).
The year 2019 has been identified as a year with a high frequency of drought in the NTIs. We would like to further investigate the temporal and spatial dynamics of agricultural drought during this period. Figure 11 presents the monthly spatial distribution of agricultural drought based on the TVDI during the dry (June to August 2019) and rainfall seasons (December 2019 to February 2020). The spatial patterns show that drought conditions first occurred in June 2019 in some parts of the NTIs and became more widespread in the following months. The total drought area peaks in December, with intensities ranging from mild to severe, and mainly affects areas dominated by agricultural vegetation, savannas, and grasslands. After December, a clear decrease in drought levels was seen in January and February, most likely due to increased rainfall during the wet season.

Figure 11.
The monthly spatial distribution of agricultural drought is based on the TVDI during the dry and rainfall seasons in the NTI region for the drought year 2019–2020.
3.2.2. TVDI Variation Across Different Vegetation Types
Boxplot analysis of the TVDI variation across four vegetation types in the NTI region from 2019 to 2023 is shown in Figure 12. The results show that cropland exhibited the highest variability in TVDI values, with a mean and standard deviation of 0.47 ± 0.21, indicating its higher susceptibility to agricultural drought. Grasslands (0.46 ± 0.21) and savannas (0.38 ± 0.18) had the second-highest variabilities.
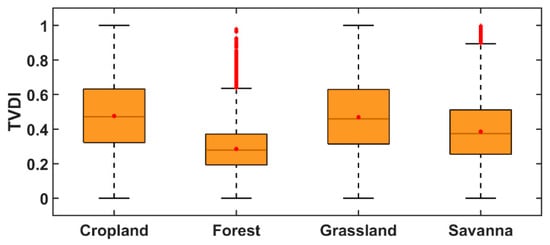
Figure 12.
Temporal variation in TVDI values represented as boxplots for four dominant vegetation types across the NTIs, illustrating surface-dryness differences among cropland, broadleaf forest, grassland, and savanna between 2019 and 2023.
This pattern highlights the greater vulnerability of agricultural land to surface drought, most likely due to shallow root systems and a reliance on surface moisture. In contrast to the other vegetation types, forests are more resistant because they have the lowest average TVDI value (0.28 ± 0.13). Forests are supported by their deep and extensive root systems that allow access to water stored in deeper soil layers, thus reducing their sensitivity to fluctuations at the surface level.
3.2.3. Impact of Agricultural Drought on Rice Crops
Figure 13 compares vegetation anomalies, TVDI, and SPI-3 during the rice-planting season at Assegaf rice field for a drought year (2019–2020) and a normal year (2021–2022). A negative relationship between SPI-3 and TVDI is observed in Figure 13a, where SPI-3 values below −2 from September to November correspond with TVDI values approaching 1, indicating severe drought conditions, which coincided with negative vegetation anomalies. In the normal year (Figure 13b), although SPI-3 reached −1.5 in September, TVDI values remained low, and vegetation anomalies were positive at the start of the season.
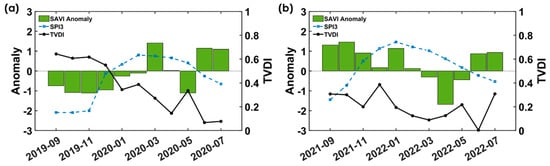
Figure 13.
Temporal monthly comparison of SAVI-vegetation anomaly, TVDI, and SPI-3 during the rice-planting season in Assegaf rice field for (a) drought year (2019–2020) and (b) normal year (2021–2022).
Figure 14 presents a time-series analysis of the 8-day TVDI, vegetation indices (NDVI/SAVI), and meteorological variables (precipitation, land surface temperature, and Downward Surface Radiation) during the rice-growing season. The TVDI values ranged from 0.4 to 0.9 during the drought year, indicating widespread mild-to-extreme agricultural drought stress from late November 2019 to July 2020. This was strongly influenced by low rainfall throughout the growing season, with an accumulated 8-day rainfall below 30 mm. Although there was a slight increase during the peak of the rainy season (January to March), the amount of rainfall again declined sharply in the 2020 dry season. In addition, we see that drought years are characterized by LST values between 30 °C and 40 °C (Figure 14c) and DSR levels close to 1000 W/m2 (Figure 14d). On the other hand, the normal year shows more favorable conditions, with higher rainfall (50–200 mm/8 day) during the growing season (Figure 14f). The lower LST and DSR values (Figure 14g,h) help keep the TVDI below 0.4 until the dry season arrives around May or July 2022.
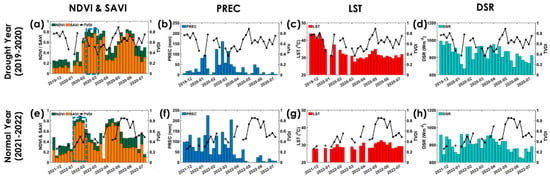
Figure 14.
Time series of 8-day TVDI (solid black line) and NDVI and SAVI for rice crops during the planting season and meteorological factors (PREC, LST, and DSR) in (a–d) drought (2019–2020) and (e–h) non-drought (2021–2022) years.
These results indicate a close association between meteorological factors and agricultural drought conditions. We can see clearly that, in drought conditions, insufficient rainfall combined with high heat and radiation stress increases surface dryness, as indicated by the larger TVDI values. In normal years, adequate rainfall and relatively milder environmental conditions contribute to lower drought stress during planting. The impact of drought on rice phenology is also evident. Figure 14e shows that the planting period in the NTIs usually starts in October to late November [60,61], as indicated by the initial decrease in the NDVI and SAVI due to waterlogging in the rice fields. However, we see a different result in the drought year, where planting was delayed until early January. This is most likely due to farmers delaying planting while waiting for sufficient rainfall. This delay shifts the rice-harvesting period from the usual January–February to March–April. This situation also leads to the negative vegetation anomaly in Figure 13a.
3.3. The Relationship Between Meteorological Factors and Both Vegetation and Agricultural Drought
3.3.1. Vegetation Response to Meteorological Factors
After we analyzed the characteristics of drought events in the NTIs, we further investigated how vegetation responds to meteorological factors, as shown in Figure 15. The partial correlation coefficients between the SAVI and three variables, PREC, LST, and DSR, are mapped in Figure 15a, Figure 15b, and Figure 15c, respectively. We found a positive correlation between both SAVI and PREC, and SAVI and DSR in most areas, indicating that higher rainfall and incoming radiation support vegetation growth. It was noticed that rainfall and DSR seem to be negatively correlated with the SAVI in some forested zones. In contrast, there is a strong negative partial correlation between the LST and SAVI in most regions of the NTIs. Our results show that higher surface temperatures are often associated with vegetation stress. Furthermore, Figure 15d presents an RGB map where red, green, and blue channels represent the strength of partial correlation between SAVI and precipitation, LST, and DSR, respectively. This visualization helps identify which factor dominates vegetation variation spatially. From the map, we can observe that LST dominates in croplands, savannas, and grasslands (seen as green or yellow areas), while rainfall (red tones) is the major influence in forest regions, where the role of temperature and radiation is limited.
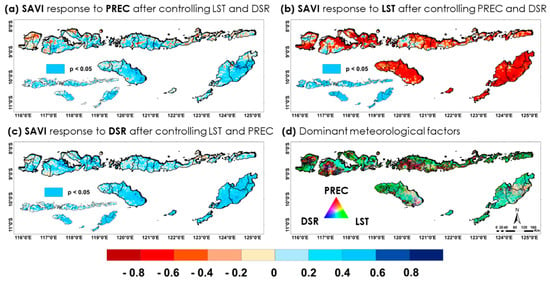
Figure 15.
Partial correlation maps showing SAVI response to individual meteorological factors over the NTIs: (a) PREC (controlling LST and DSR), (b) LST (controlling PREC and DSR), (c) DSR (controlling PREC and LST), and (d) dominant factors for vegetation. Red = precipitation, green = LST, and blue = DSR.
Table 4 presents the mean partial correlation coefficients derived from Figure 15, accompanied by 95% confidence intervals (CI) to indicate the range within which the true correlation is likely to fall with high certainty. The relationship between LST and SAVI shows a moderately strong negative correlation for open-land vegetation types, particularly in cropland (−0.71 ± 0.0108), followed by grassland (−0.67 ± 0.0114) and savanna (−0.65 ± 0.0060). In contrast, the forest area displays a much weaker negative relationship with LST, with a correlation of −0.23 ± 0.0113. Solar radiation also plays a significant role in influencing vegetation dynamics across the NTI region. A moderate positive correlation is observed in cropland, grassland, and savanna, with coefficients ranging from 0.34 to 0.38, while forest areas show a weak but still positive relationship with DSR. Precipitation shows weak positive associations with grassland (0.30 ± 0.0155) and savanna (0.23 ± 0.0080), and very weak correlations in cropland (0.14 ± 0.0136) and forest (0.04 ± 0.0099), suggesting rainfall has less direct influence in those environments.

Table 4.
Mean and 95% confidence interval of partial correlation coefficients between SAVI and meteorological factors for different vegetation types across the NTI region.
However, we observed that the weak correlation between precipitation and vegetation condition across certain land-cover types might be due to normal precipitation data. To address this, we applied a precipitation anomaly approach using SPI-1 and SPI-3 indices to assess their relationship with vegetation conditions, as shown in Table 5. The results showed an overall improvement in correlation values when using both SPI-1 and SPI-3. Among them, SPI-3 demonstrated stronger and more consistent relationships with vegetation, particularly over cropland (0.64 ± 0.0111), grassland (0.71 ± 0.0100), and savanna (0.68 ± 0.0067), while the correlation was weaker–moderate over forest areas (0.31 ± 0.0117). These findings suggest that rainfall from previous months also plays an important role in determining vegetation conditions.

Table 5.
Mean and 95% confidence interval of partial correlation coefficients between SAVI and SPI for different vegetation types across the NTI region.
Some previous studies tried to include the effect of lag time between vegetation and climate factors and obtained different results in different locations. Therefore, we also tried to find the temporal lag response of vegetation to meteorological factors across the NTI region, as illustrated in Figure 16. Figure 16a–c show the spatial distribution of the delayed response of the SAVI to PREC, LST, and DSR. The analysis shows that the responses of vegetation to PREC and DSR exhibit delayed effects, with lag periods generally ranging from 1 to 2 months. In contrast, vegetation shows a faster response to LST, suggesting this factor directly influences vegetation dynamics.
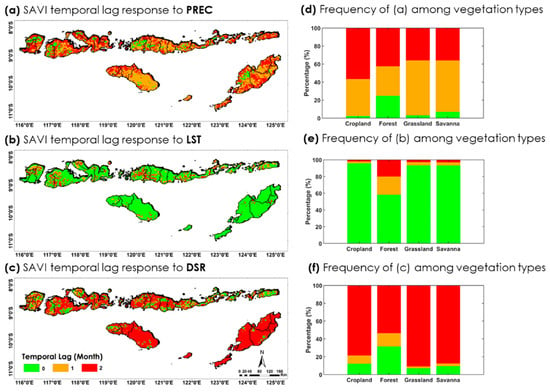
Figure 16.
Temporal lag response of meteorological factors on SAVI over the NTI region: (a) SAVI lag response to precipitation (PREC), (b) SAVI lag response to land surface temperature (LST), (c) SAVI lag response to Downward Surface Radiation (DSR), and corresponding frequency maps across vegetation types for each factor: (d) frequency map of lag response in (a), (e) frequency map of lag response in (b), and (f) frequency map of lag response in (c).
As shown in the frequency charts (Figure 16d–f), vegetation’s lagged response varies depending on the meteorological factor and vegetation type. Interestingly, all vegetation types generally exhibit similar lag responses to the same meteorological factor across the NTI region, contrasting with previous global-scale studies that reported variability among vegetation types [59]. This discrepancy may stem from the more localized focus of the current study, which allows for more homogeneous climatic and topographic conditions. However, consistent with earlier studies, different meteorological variables produce lag responses even within the same vegetation type. Precipitation-driven vegetation responses are particularly dominant, with a 1–2-month lag, accounting for over 90% of total cropland, grassland, and savanna grids. Areas that showed no lag to rainfall were mainly located in higher elevation zones. The same pattern was found for DSR but with a more prominent two-month lag for most vegetation types. In contrast, LST affects vegetation immediately in the cropland, grassland, and savanna grids, as evidenced by more than 90% of these areas responding in the same month; however, some forested areas still show a one-month delay.
We then attempted to use MLR, incorporating the effect of time lags (Figure 17a), to elucidate the relationship between meteorological factors and vegetation dynamics across the NTIs. The MLR shows that factors generally have a fairly diverse influence on some vegetation types, with values between 20 and 80%. We also present the differences in factor contributions between models with and without time-lag adjustment, as seen in Figure 17b. In addition, Figure 17c shows the average coefficient of determination for different vegetation types. When the effect of time lags is considered, the contribution of meteorological factors to vegetation growth increases by 5−30%. The model explains more than 60% of the variance in open vegetation types such as cropland, grassland, and savanna, thus indicating good model performance. However, the driving factor only explained 36% of the vegetation variability in broadleaf forest areas. This indicates that forest vegetation growth is less responsive to short-term changes in the surface meteorological conditions and is potentially influenced by underlying ecological or climatic factors. This may include factors such as deep-rooted tree systems that access groundwater. Moreover, the limited sensitivity of optical satellite indices to detect subtle variations under closed canopy cover may also contribute to the lower explanatory power in these areas.
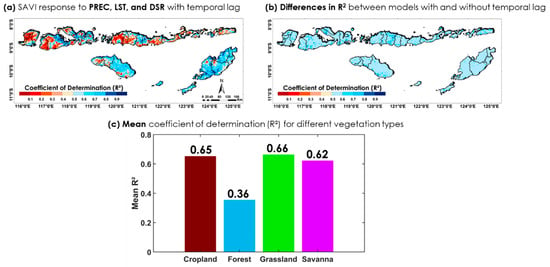
Figure 17.
(a) SAVI response to PREC, LST, and DSR based on MLR with a temporal lag. (b) The difference in model performance (R2) between models with and without temporal lag. (c) Comparison of mean R2 values across vegetation types.
3.3.2. Agricultural Drought Response to Meteorological Factors
Besides analyzing the effect of meteorological variables on vegetation, we also attempted to quantify how these variables affect surface dryness (TVDI) using the same method. Figure 18a–c present the spatial distribution of the partial correlation coefficient between the TVDI and PREC, LST, and DSR. In general, the results show a positive correlation between both the TVDI and LST, and the TVDI and DSR in most areas, indicating that higher surface temperatures and incoming radiation contribute to increased surface dryness, as captured by the TVDI. However, DSR exhibited the opposite result: there was a negative correlation between the DSR and TVDI in some regions, such as agricultural lands. In addition, in most regions of the NTIs, rainfall was negatively correlated with TVDI, indicating that increased rainfall reduces surface dryness and drought intensity. This is expected, as rainfall will help provide surface water and increase soil moisture conditions, reducing surface dryness. Figure 18d displays an RGB composite map illustrating the partial correlation between TVDI and three meteorological parameters. The color intensity reflects the relative dominance of each factor across the landscape. The widespread dominance of green hues across the NTIs indicates that LST has the strongest influence on land surface dryness (TVDI) compared to the other factors. It is important to note that the strong correlation between LST and TVDI observed in Figure 18d is expected, as LST is one of the core components in the calculation of TVDI. As such, the correlation between LST and TVDI should be interpreted with caution and not be overemphasized as evidence of meteorological control. However, we retained this information in the RGB composite to provide a complete picture of the relative contribution of all three meteorological drivers. By including PREC and DSR alongside LST in the visualization, the map allows us to identify regions where other factors have a stronger or more independent influence on surface dryness.
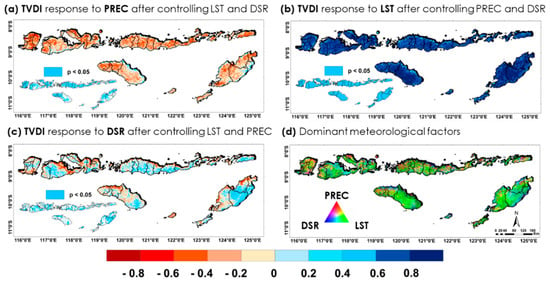
Figure 18.
Partial correlation maps showing TVDI response to individual meteorological factors over the NTIs: (a) PREC (controlling LST and DSR), (b) LST (controlling PREC and DSR), (c) DSR (controlling PREC and LST), and (d) dominant factor for surface dryness. Red = precipitation, green = LST, and blue = DSR.
Table 6 summarizes the average partial correlation values and 95% confidence intervals between TVDI and meteorological variables across vegetation types. Precipitation tends to be negatively correlated with TVDI in all vegetation types, with the strongest effect in forests (−0.29 ± 0.0065) and weakest in grasslands (−0.10 ± 0.0137). LST shows a strong positive correlation, especially in the savanna (0.78) and cropland (0.75). The correlation between solar radiation and TVDI is less consistent, particularly in forests and savannas. The effect of solar radiation varies by land-cover type, suggesting that local canopy characteristics may modulate how DSR impacts surface dryness, making it harder to identify a uniform pattern.

Table 6.
Mean and 95% confidence interval of partial correlation coefficients between TVDI and meteorological factors for different land-cover types across the NTI region.
Since TVDI incorporates LST into its calculation, using it to evaluate the role of LST in drought can lead to circular reasoning. Therefore, we used SPI as a more independent drought indicator to assess the relationships between both TVDI and LST with drought conditions across the NTIs, as shown in Table 7. Interestingly, the correlations between SPI (1 and 3) and TVDI and between SPI (1 and 3) and LST were notably similar. For instance, in cropland areas, the correlation between SPI-3 and TVDI is −0.53 ± 0.0110, while the SPI-3 and LST correlation is −0.57 ± 0.0081. A similar result can also be shown in other vegetation types. This close similarity confirms that TVDI is heavily influenced by LST. Therefore, the correlation between TVDI and LST should not be interpreted at face value. However, both LST and TVDI exhibit moderate correlations with SPI, especially SPI-3, indicating that both variables are closely linked to rainfall anomalies and meteorological drought conditions across the NTIs, making them relevant indicators for drought monitoring in the NTIs.

Table 7.
Mean and 95% confidence interval of partial correlation coefficients between SPI-1 and SPI-3 with TVDI and LST for different land-cover types across the NTI region.
3.3.3. Relationship Between Meteorological Variables
The partial correlation maps in Figure 19 illustrate the relationships between meteorological factors over the NTIs. Figure 19a,b demonstrate a negative partial correlation between PREC and LST, as well as between PREC and DSR, with correlation values ranging from −0.6 to −0.2 across most areas in the NTIs. Based on these results, the negative association suggests that fewer precipitation events will allow more solar radiation to reach the surface due to low cloud cover. The DSR intensifies heat accumulation and increases surface temperatures. In contrast, a strong positive partial correlation was observed between LST and DSR, as shown in Figure 19c, with values between 0.5 and 1. This positive relationship is expected, as higher solar radiation directly contributes to increased land surface temperatures.
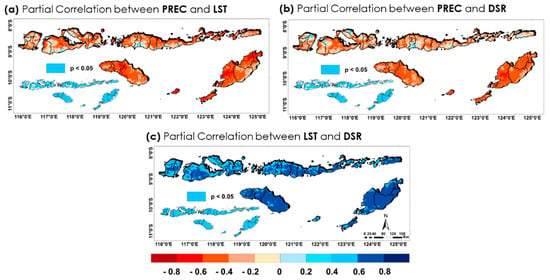
Figure 19.
Partial correlation maps showing the correlation between meteorological factors over the NTIs: (a) PREC and LST (controlling DSR), (b) PREC and DSR (controlling LST), and (c) LST and DSR (controlling PREC).
3.4. Agricultural Drought Prediction
The monthly relationship between meteorological variables and agricultural drought in the NTIs was assessed using the MLR model (Figure 20a). We used monthly data from 2019 to 2022 to construct the MLR model, while data from 2023 were used for testing. After analyzing the relationships between the factors, PREC and LST were selected as predictor variables. This selection was based on prior findings (Figure 19c), which showed a strong correlation between LST and DSR, potentially leading to multicollinearity.
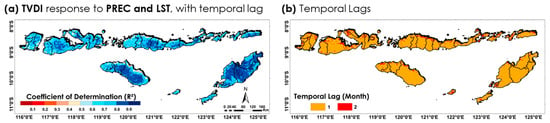
Figure 20.
(a) R2 distribution from the monthly MLR model between TVDI and meteorological factors (PREC and LST) and (b) optimal temporal lags (1–2 months prior) used in the monthly MLR analysis for TVDI estimation across the NTI region.
Multicollinearity occurs when independent variables are highly correlated, distorting coefficient interpretations and reducing model reliability. LST was prioritized for our model over DSR because the results identified LST as the dominant factor influencing surface dryness across the vegetation types in the NTI region. Furthermore, the MLR model also incorporated the time-lag effects of meteorological factors, as illustrated in Figure 20b, and will be used from one to two months before estimating the current TVDI conditions on a per-grid basis.
Figure 21 shows the performance of the MLR model in estimating the monthly TVDI for October 2023. Spatially, the MLR-based TVDI estimation (Figure 21b) effectively captures surface-dryness patterns, similar to the MODIS reference (Figure 21a), particularly across areas with TVDI values ranging from 0.5 to 0.9. However, we found that the model performs less accurately in forest regions. The scatter plot in Figure 21c indicates an R2 value of 0.66 and a regression line of 0.73x + 0.03, suggesting a tendency for the model to underestimate higher TVDI values. This underestimation is also evident from the bias error distribution (Figure 21d), where the mean bias is 0.13 ± 0.08 (TVDI MODIS subtracted by TVDI estimation). Overall, the MLR model provides reasonable estimates of the TVDI with a spatial fit to the MODIS product. However, some limitations remain in areas with dense forests or higher drought levels.
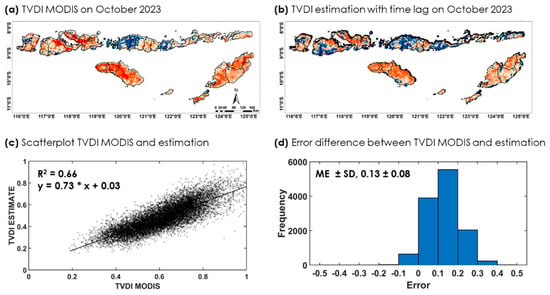
Figure 21.
Monthly TVDI estimation using MLR for October 2023. (a) Reference TVDI from MODIS. (b) Estimated TVDI based on MLR with time-lag effect. (c) Scatter plot comparing MODIS and estimated TVDI. (d) Spatial distribution of bias error between MODIS and estimated TVDI.
Following the monthly TVDI estimation model, an 8-day-scale relationship between meteorological factors and agricultural drought over the NTIs was also established using an MLR model, as shown in Figure 22a. Similar to the monthly model, PREC and LST were selected as the primary predictors. This 8-day MLR model also incorporated temporal lag effects from meteorological variables, as illustrated in Figure 22b. Generally, the model used PREC and LST data from 8 to over 32 days before the current condition for each grid, allowing for a more accurate estimation of short-term drought variability.
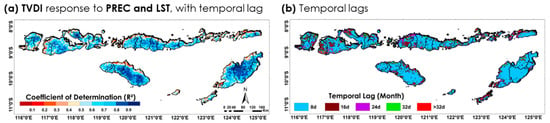
Figure 22.
(a) R2 distribution from the 8-day MLR model between TVDI and meteorological factors (PREC and LST) and (b) optimal temporal lags (8 to more than 32 days prior) used in the 8-day MLR analysis for TVDI estimation across the NTI region.
The 8-day TVDI estimation model was applied on 8, 16, and 24 October 2023, as shown in Figure 23d–f. The model successfully estimated the spatial pattern of surface drought when we compared it to MODIS reference data (Figure 23a–c) and performed well in identifying areas affected by agricultural drought, thus strengthening its applicability for short-term monitoring. Nonetheless, the model still showed underestimation in forested areas, consistent with previous findings at the monthly scale, suggesting that additional factors or a different modeling approach may be needed to improve accuracy in these areas.

Figure 23.
Comparison of reference and estimated TVDI values for three observation dates (8, 16, and 24 October 2023). (a–c) Reference TVDI derived from MODIS data. (d–f) Estimated TVDI generated using MLR model incorporating temporal lag effects.
Table 8 presents the evaluation metrics of the 8-day TVDI estimations shown in Figure 23. The model results underestimate TVDI values compared to the MODIS reference data. The model achieved R2 values for October 8, 16, and 24, 2023 of 0.69, 0.67, and 0.64, respectively, indicating a moderately strong agreement between the estimated and observed values. The normalized root mean square error (NRMSE) values for the same dates were relatively low at 0.09, 0.07, and 0.09, indicating acceptable prediction accuracy. In addition, the NMBE values (TVDI MODIS–TVDI estimation), which range from 0.03 to 0.07, confirm a slight underestimation in areas such as forests.

Table 8.
Linear regression and metrics evaluation (R2, NRMSE, and NMBE) from Figure 22.
4. Discussion
This study examined the relationship between meteorological factors that affect vegetation, such as rainfall, incoming solar radiation, and surface temperature, and agricultural drought in the NTIs. We relied on satellite data to support our observational analysis due to the large geographic coverage of the NTIs and the large-scale nature of drought events. Precipitation was estimated based on the infrared band from Himawari-8 through the IMSRA method, which has shown reliable results in previous studies across Indonesia. For instance, Meliani et al. [62] evaluated the Himawari-8 rainfall estimation in the South Sumatra region in order to construct the Indonesia Fire Danger Rating System (Ina-FDRS), and Ismanto et al. [63] achieved good results when using this method and validated it for the entire Indonesian region during the ENSO event in 2019 and 2020. They also compared the results with other Satellite Precipitation Products (SPPs), concluding that the Himawari-8 rainfall data performed quite well compared to data from other sources. However, we independently validated this method to ensure the reliability of the Himawari-8 Rainfall Estimate (HRE), as this technique was originally applied in the Indian region [49,64]. We wanted to confirm whether these estimates matched the surface rainfall conditions and are therefore reliable enough to substitute for ground-based data for our period and region of study.
The validation process in our study was carried out by comparing HREs with ground rainfall observations in three different timescales: daily, 8 days, and monthly. The daily validation results showed more variability and a tendency to overestimate rainfall during the study period. This situation also occurred in a previous study, where the finer timescale validation of SPPs often showed no advantage over coarser scales, such as the monthly scale [65,66]. This might be caused by the sensitivity of algorithms related to infrared-based retrieval to cloud-top temperature, which can lead to false detection in the presence of thin or non-rain-producing clouds [67]. Performance was improved for the 8-day and monthly scales. These timescales are particularly relevant for agricultural drought monitoring and estimation in this study, as these longer temporal aggregations are more aligned with the response times of vegetation to meteorological conditions [68,69]. In addition, the high spatial resolution (2 km) and frequent observation intervals (every 10 min) of HRE make it suitable for near-real-time rainfall observation. Other SPPs often suffer from lower spatial resolution (between 5 km and 25 km) and longer delays in final data availability (weeks to months after the actual observation) compared to HRE [70,71,72]. In contrast, HRE offers a near-real-time and detailed resolution for monitoring rainfall and analyzing the effects of rainfall parameters on vegetation and agricultural drought.
We also assessed agricultural drought characteristics and their impact on vegetation, especially rice fields in the NTIs. Our analysis using the TVDI reveals the sensitivity of our study area to agricultural drought, with varying impacts across different vegetation types. We see that the East Nusa Tenggara province experienced a higher frequency of agricultural drought in the study period, significantly impacting grassland and savanna ecosystems. Meanwhile, the West Nusa Tenggara province exhibited high drought event frequency in agricultural lands. Therefore, we also tried to analyze the factors affecting the Assegaf rice field in West Nusa Tenggara during an agricultural drought and a normal year. The limited rainfall (negative anomaly) during the drought year not only intensified drought conditions (higher TVDI) but also delayed both the planting and harvesting periods of rice crops (Figure 13 and Figure 14). In addition, the NTIs always have drought-affected areas, as shown in the monthly drought-area ratio analysis from 2019 to 2023 in Figure 10. Moreover, atmospheric dynamics such as monsoon variability are well-known drought-related factors in the NTIs. The local land characteristics in the NTIs also play an important role in generating drought; previous research [73] shows that hilly and mountainous areas are common in the NTIs. There are also shallow and rocky soils with a low organic matter content. These soil types do not have structure and porosity, which are needed to store sufficient water and nutrients, making them unsuitable for supporting surface dryness, especially during the dry season. The location of the NTIs in Southeastern Indonesia, which is close to the Pacific Ocean, makes the region highly vulnerable to drought events, especially during El Niño periods. Warm sea surface temperatures in the middle of the Pacific Ocean often cause rainfall to move to those areas, reducing the amount of rainfall in the NTIs [22]. Therefore, the combined effects of atmospheric dynamics, especially large-scale climate phenomena, and the unique geographical position of the NTIs significantly contribute to this region’s vulnerability to drought.
In view of the dominant role of meteorological factors on vegetation growth, this study confirms that the LST in the NTIs had a stronger impact on vegetation greenness than PREC and DSR. In addition, LST also shows a more rapid effect on vegetation dynamics, as it is generally associated with no time lag. This immediate response can be attributed to the fact that the LST is indicative of the thermal conditions of the soil surface itself, which reacts quickly to environmental stresses. In contrast, PREC and DSR are atmospheric processes that often take time to influence soil moisture, which results in delayed effects on vegetation. These findings are in line with those of Selvaraj et al. [74], who investigated the interaction between the NDVI and environmental factors and showed that the current LST has a stronger impact on the vegetation index compared to lagged values. In the same way, in the interaction between the TVDI and meteorological variables, LST consistently emerged as the most influential factor across all land-cover types in the NTIs. However, the high correlation between LST and TVDI might be caused by the fact that LST is one of the core components in the calculation of TVDI. Therefore, we used SPI as a more independent drought indicator to assess the relationships between both TVDI and LST with drought conditions across the NTIs. We used selected meteorological factors (PREC and LST) to predict agricultural drought through monthly and 8-day timescale models. Temporal lags were added to the model to estimate drought events. The resulting drought pattern is consistent with MODIS data, especially in most vegetated areas of the NTIs. However, underestimation is evident in forested areas, where meteorological indicators alone may not fully represent the surface conditions. These drawbacks, however, create the opportunity for future improvements, especially by incorporating non-linear modeling methods and additional variables, as the surface–atmosphere interactions in drought processes are dynamic and have non-linear behavior.
5. Conclusions
The influence of meteorological factors (PREC, LST, and DSR) on vegetation and surface dryness was investigated in this study using Himawari-8 and MODIS satellite data observations. The findings are outlined as follows:
- (1)
- A comparative analysis of Himawari-8 rainfall estimation (HRE) data and gauge observations over the NTIs shows that HRE is valuable for regional rainfall monitoring, especially for agricultural drought-related applications. Although daily scale data are affected by short-term disturbances and retrieval limitations, aggregation to 8-day and monthly scales significantly improves the reliability of rainfall estimates. The improved accuracy of continuous and categorical assessment at these timescales supports their application in drought monitoring. Therefore, this study uses HRE at 8-day and monthly intervals as a suitable satellite-based rainfall source to assess and predict agricultural drought dynamics in the NTIs.
- (2)
- Agricultural drought in the NTIs is frequent; droughts are generally categorized as being mild to moderate in intensity. In terms of vegetation type, cropland is the most vulnerable to drought, followed by grassland and savannah. In contrast, forest areas show resilience to the impacts of drought. Meteorological factors, such as insufficient rainfall, increased land surface temperature, and radiation, indicate the severity of the drought, as evidenced by the 2019–2020 drought case study. These extreme conditions not only increased the TVDI but also disrupted the cropping cycle of rice, leading to a negative vegetation anomaly due to delays in planting and harvesting.
- (3)
- Partial correlation and time-lag analyses show that LST is the dominant factor affecting the SAVI, with cropland, savanna, and grassland showing the highest sensitivity. In forested areas, however, the influence of meteorological factors was less pronounced, suggesting that other factors may play a greater role in these areas. The factors explained 36−66% of the vegetation variation. Additionally, vegetation shows a rapid response to LST and a 1–2-month time lag in terms of precipitation and DSR. Thus, incorporating the time-lag effect significantly improves the predictive relationship between meteorological factors and changes in vegetation.
- (4)
- Regarding agricultural drought estimation, applying MLR models incorporating lagged meteorological inputs proved effective in estimating the TVDI across the NTIs. By selecting PREC and LST as predictors, the monthly and 8-day estimation models could capture spatial drought patterns consistent with MODIS data, with R2 values above 0.64. The low error rates and strong spatial consistency highlight the potential of these models to be accessible tools for predicting agricultural drought.
Author Contributions
Conceptualization, T.-H.L., F.T., K.-H.T. and G.D.K.; methodology, G.D.K. and T.-H.L.; software, G.D.K. and Y.-L.C.; validation, G.D.K.; formal analysis and investigation, T.-H.L. and G.D.K.; data curation, G.D.K. and Y.-L.C.; writing—original draft preparation, G.D.K. and T.-H.L.; writing—review and editing, T.-H.L., F.T., K.-H.T. and G.D.K.; supervision, project administration, and funding acquisition, T.-H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the Taiwan National Science and Technology Council (NSTC), grants NSTC 113-2119-M-008-014 and NSTC 113-2111-M-008-029.
Data Availability Statement
The rainfall-station observation data were obtained from the Indonesian Meteorological Agency (https://dataonline.bmkg.go.id/, accessed on 15 September 2024); the data from Himawari-8 are publicly accessible via the Japan Aerospace Exploration Agency (http://www.eorc.jaxa.jp/ptree/index.html, accessed on 15 September 2024); and all of the surface information, including land-cover type based on MODIS, was obtained from the NASA LPDAAC portal (https://lpdaac.usgs.gov/, accessed on 15 September 2024).
Acknowledgments
The authors would like to thank NASA for providing the MODIS surface information and land cover-type products, the Indonesian Meteorological Agency (BMKG) for access to ground-based rainfall data, and the Japan Aerospace Exploration Agency (JAXA) for the provision of Himawari-8 AHI satellite data.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NTIs | Nusa Tenggara Islands |
| PREC | Precipitation |
| LST | Land Surface Temperature |
| DSR | Downward Shortwave Radiation |
| NDVI | Normalized-Difference Vegetation Index |
| SAVI | Soil-Adjusted Vegetation Index |
| TVDI | Temperature Vegetation Dryness Index |
| HRE | Himawari-8 rainfall estimation |
| IR | Infrared |
| MVC | Maximum value composite |
| IMSRA | Indian Satellite Multi-Spectral Rainfall Algorithm |
| MLR | Multiple linear regression |
References
- Naveendrakumar, G.; Vithanage, M.; Kwon, H.H.; Chandrasekara, S.S.K.; Iqbal, M.C.M.; Pathmarajah, S.; Fernando, W.C.D.K.; Obeysekera, J. South Asian Perspective on Temperature and Rainfall Extremes: A Review. Atmos. Res. 2019, 225, 110–120. [Google Scholar] [CrossRef]
- Rafiq, M.; Li, Y.C.; Cheng, Y.; Rahman, G.; Ullah, I.; Ali, A. Spatial and Temporal Fluctuation of Rainfall and Drought in Balochistan Province, Pakistan. Arab. J. Geosci. 2022, 15, 214. [Google Scholar] [CrossRef]
- Rahman, G.; Jung, M.K.; Kim, T.W.; Kwon, H.H. Drought Impact, Vulnerability, Risk Assessment, Management and Mitigation under Climate Change: A Comprehensive Review. KSCE J. Civ. Eng. 2025, 29, 100120. [Google Scholar] [CrossRef]
- Xu, C.; McDowell, N.G.; Fisher, R.A.; Wei, L.; Sevanto, S.; Christoffersen, B.O.; Weng, E.; Middleton, R.S. Increasing Impacts of Extreme Droughts on Vegetation Productivity under Climate Change. Nat. Clim. Change 2019, 9, 948–953. [Google Scholar] [CrossRef]
- Orimoloye, I.R. Agricultural Drought and Its Potential Impacts: Enabling Decision-Support for Food Security in Vulnerable Regions. Front. Sustain. Food Syst. 2022, 6, 838824. [Google Scholar] [CrossRef]
- Fang, Y.; Xiong, L. General Mechanisms of Drought Response and Their Application in Drought Resistance Improvement in Plants. Cell. Mol. Life Sci. 2015, 72, 673–689. [Google Scholar] [CrossRef] [PubMed]
- BPS. Statistik Pertanian Provinsi Nusa Tenggara Timur 2023 (Agricultural Statistics of East Nusa Tenggara Province 2023). Available online: https://ntt.bps.go.id/id/publication/2024/09/20/e571dcc6145f7795887626fd/statistik-pertanian-provinsi-nusa-tenggara-timur-2023.html (accessed on 5 April 2025).
- Saidah, H.; Sulistiyono, H.; Negara, I.D.G.J. Comparison of Suitable Drought Indices for Over West Nusa Tenggara. In International Conference on Rehabilitation and Maintenance in Civil Engineering; Lecture Notes in Civil Engineering; Springer: Singapore, 2023; Volume 225, pp. 587–600. [Google Scholar] [CrossRef]
- Adhyani, N.L.; June, T.; Sopaheluwakan, A. Exposure to Drought: Duration, Severity and Intensity (Java, Bali and Nusa Tenggara). IOP Conf. Ser. Earth Environ. Sci. 2017, 58, 012040. [Google Scholar] [CrossRef]
- Kuswanto, H.; Hibatullah, F.; Soedjono, E.S. Perception of Weather and Seasonal Drought Forecasts and Its Impact on Livelihood in East Nusa Tenggara, Indonesia. Heliyon 2019, 5, e02360. [Google Scholar] [CrossRef] [PubMed]
- Tjasyono, B.H.; Gernowo, R.; Sri Woro, B.H. The Character of Rainfall in the Indonesian Monsoon. In Proceedings of the International Symposium on Equatorial Monsoon System, Yogyakarta, Indonesia, 16–18 September 2008. [Google Scholar]
- Ardi, R.D.W.; Aswan; Maryunani, K.A.; Yulianto, E.; Putra, P.S.; Nugroho, S.H.; Istiana. Last Deglaciation—Holocene Australian-Indonesian Monsoon Rainfall Changes Off Southwest Sumba, Indonesia. Atmosphere 2020, 11, 932. [Google Scholar] [CrossRef]
- Wheeler, M.C.; McBride, J.L. Australian-Indonesian Monsoon. In Intraseasonal Variability in the Atmosphere-Ocean Climate System; Springer: Berlin/Heidelberg, Germany, 2005; pp. 125–173. [Google Scholar] [CrossRef]
- Giarno; Hadi, M.P.; Suprayogi, S.; Herumurti, S. Impact of Rainfall Intensity, Monsoon and MJO to Rainfall Merging in the Indonesian Maritime Continent. J. Earth Syst. Sci. 2020, 129, 164. [Google Scholar] [CrossRef]
- Matsumoto, J.; Wang, B.; Wu, G.; Li, J.; Wu, P.; Hattori, M.; Mori, S.; Yamanaka, M.D.; Ogino, S.Y.; Jun-Ichi, H.; et al. An Overview of the Asian Monsoon Years 2007–2012 (AMY) and Multi-Scale Interactions in the Extreme Rainfall Events over the Indonesian Maritime Continent. World Sci. Ser. Asia-Pac. Weather Clim. 2017, 9, 365–385. [Google Scholar] [CrossRef]
- Kirono, D.G.C. Principal Component Analysis for Identifying Period of Seasons in Indonesia. Indones. J. Geogr. 2004, 36, 109–121. [Google Scholar] [CrossRef]
- Kirono, D.G.C.; Butler, J.R.A.; McGregor, J.L.; Ripaldi, A.; Katzfey, J.; Nguyen, K. Historical and Future Seasonal Rainfall Variability in Nusa Tenggara Barat Province, Indonesia: Implications for the Agriculture and Water Sectors. Clim. Risk Manag. 2016, 12, 45–58. [Google Scholar] [CrossRef]
- Sanit, M.S.; Rachmawati, T.A.; Firdausiyah, N. Impact of Climate Change on Meteorological Drought in Insana Barat District, Timor Tengah Utara, East Nusa Tenggara. J. Syntax. Lit. 2023, 8, 417–425. [Google Scholar] [CrossRef]
- Kusmiyarti, T.B.; Adnyana, W.S.; Nuarsa, W.; Sudarma, M.; Antara, M.O.G. Drought Monitoring Using Remote Sensing Data in Nusa Tenggara Timur Province, Indonesia in Between 2018 and 2023. Ecol. Eng. Environ. Technol. 2024, 25, 134–145. [Google Scholar] [CrossRef]
- Setiawan, A.M.; Lee, W.S.; Rhee, J. Spatio-Temporal Characteristics of Indonesian Drought Related to El Niño Events and Its Predictability Using the Multi-Model Ensemble. Int. J. Climatol. 2017, 37, 4700–4719. [Google Scholar] [CrossRef]
- Rahman As-syakur, A.; Wayan Sandi Adnyana, I.; Sudiana Mahendra, M.; Wayan Arthana, I.; Nyoman Merit, I.; Wayan Kasa, I.; Wayan Ekayanti, N.; Wayan Nuarsa, I.; Nyoman Sunarta, I. Observation of Spatial Patterns on the Rainfall Response to ENSO and IOD over Indonesia Using TRMM Multisatellite Precipitation Analysis (TMPA). Int. J. Climatol. 2014, 34, 3825–3839. [Google Scholar] [CrossRef]
- Karuniasa, M.; Pambudi, P.A. The Analysis of the El Niño Phenomenon in the East Nusa Tenggara Province, Indonesia. J. Water Land. Dev. 2022, 52, 180–185. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-Driven Increases in Global Terrestrial Net Primary Production from 1982 to 1999. Science 2003, 300, 1500–1563. [Google Scholar] [CrossRef] [PubMed]
- Matuszko, D.; Library, W.O. Influence of the Extent and Genera of Cloud Cover on Solar Radiation Intensity. Int. J. Climatol. 2012, 32, 2403–2414. [Google Scholar] [CrossRef]
- Zhao, M.; A, G.; Liu, Y.; Konings, A.G. Evapotranspiration Frequently Increases during Droughts. Nat. Clim. Change 2022, 12, 1024–1030. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, W.; Fu, J. Vegetation Response to Precipitation Anomalies under Different Climatic and Biogeographical Conditions in China. Sci. Rep. 2020, 10, 830. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Zhao, X.; Zhao, W.; Tang, B.; Xu, W. Response of Vegetation to Temperature, Precipitation and Solar Radiation Time-Scales: A Case Study over Mainland Australia. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 855–858. [Google Scholar] [CrossRef]
- Ren, H.; Wen, Z.; Liu, Y.; Lin, Z.; Han, P.; Shi, H.; Wang, Z.; Su, T. Vegetation Response to Changes in Climate across Different Climate Zones in China. Ecol. Indic. 2023, 155, 110932. [Google Scholar] [CrossRef]
- Li, X.; Qu, Y. Evaluation of Vegetation Responses to Climatic Factors and Global Vegetation Trends Using GLASS LAI from 1982 to 2010. Can. J. Remote Sens. 2018, 44, 357–372. [Google Scholar] [CrossRef]
- Ma’Rufah, U.; Hidayat, R.; Prasasti, I. Analysis of Relationship between Meteorological and Agricultural Drought Using Standardized Precipitation Index and Vegetation Health Index. IOP Conf. Ser. Earth Environ. Sci. 2017, 54, 012008. [Google Scholar] [CrossRef]
- Piao, S.; Cui, M.; Chen, A.; Wang, X.; Ciais, P.; Liu, J.; Tang, Y. Altitude and Temperature Dependence of Change in the Spring Vegetation Green-up Date from 1982 to 2006 in the Qinghai-Xizang Plateau. Agric. For. Meteorol. 2011, 151, 1599–1608. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, H.; Liu, Y.; Xu, Y.; Dai, J. Phenological Response of Different Vegetation Types to Temperature and Precipitation Variations in Northern China during 1982–2012. Int. J. Remote Sens. 2017, 38, 3236–3252. [Google Scholar] [CrossRef]
- Varma, A.K. Measurement of Precipitation from Satellite Radiometers (Visible, Infrared, and Microwave): Physical Basis, Methods, and Limitations. In Remote Sensing of Aerosols, Clouds, and Precipitation; Elsevier: Amsterdam, The Netherlands, 2018; pp. 223–248. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z.L. Radiance-based Validation of the V5 MODIS Land-surface Temperature Product. Int. J. Remote Sens. 2008, 29, 5373–5395. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z. liang Validation of the Land-Surface Temperature Products Retrieved from Terra Moderate Resolution Imaging Spectroradiometer Data. Remote Sens. Environ. 2002, 83, 163–180. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S.; Zhang, Y.; Gao, X.; Brown, M.G.L.; Jia, A. A New Set of Modis Land Products (Mcd18): Downward Shortwave Radiation and Photosynthetically Active Radiation. Remote Sens. 2020, 12, 168. [Google Scholar] [CrossRef]
- Wan, Z. New Refinements and Validation of the MODIS Land-Surface Temperature/Emissivity Products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Sharma, R.C.; Hara, K.; Hirayama, H. Improvement of Countrywide Vegetation Mapping over Japan and Comparison to Existing Maps. Adv. Remote Sens. 2018, 7, 163–170. [Google Scholar] [CrossRef]
- Liang, D.; Zuo, Y.; Huang, L.; Zhao, J.; Teng, L.; Yang, F. Evaluation of the Consistency of MODIS Land Cover Product (MCD12Q1) Based on Chinese 30 m GlobeLand30 Datasets: A Case Study in Anhui Province, China. ISPRS Int. J. Geo-Inf. 2015, 4, 2519–2541. [Google Scholar] [CrossRef]
- Kumparan Kondisi Geografis Pulau Bali dan Nusa Tenggara Berdasarkan Peta|kumparan.com. Available online: https://kumparan.com/kabar-harian/kondisi-geografis-pulau-bali-dan-nusa-tenggara-berdasarkan-peta-22d0HEcXhkq (accessed on 7 April 2025).
- Silaen, M.; Yuwono, Y.; Ismail, C.; Ramadhani, A.; Takama, T. Vulnerability Assessment on Agriculture in East Nusa Tenggara. In Climate Change Management; Springer: Cham, Switzerland, 2023; Part F5; pp. 109–134. [Google Scholar] [CrossRef]
- Kuswanto, H.; Puspa, A.W.; Ahmad, I.S.; Hibatullah, F. Drought Analysis in East Nusa Tenggara (Indonesia) Using Regional Frequency Analysis. Sci. World J. 2021, 2021, 6626102. [Google Scholar] [CrossRef] [PubMed]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Ziese, M. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An Introduction to Himawari-8/9—Japan’s New-Generation Geostationary Meteorological Satellites. J. Meteorol. Soc. Jpn. 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Wan, Z. Collection-6 MODIS Land Surface Temperature Products Users’ Guide. 2013. Available online: https://lpdaac.usgs.gov/documents/118/MOD11_User_Guide_V6.pdf (accessed on 10 April 2025).
- Roger, J.C.; Ray, J.P.; Vermote, E.F. MODIS Surface Reflectance User’s Guide. 2023. Available online: https://ladsweb.modaps.eosdis.nasa.gov/archive/Document%20Archive/Science%20Data%20Product%20Documentation/MOD09_C61_UserGuide_v1.7.pdf (accessed on 10 April 2025).
- Sulla-Menashe, D.; Friedl, M.A. User Guide to Collection 6 MODIS Land Cover (MCD12Q1 and MCD12C1) Product. 2018. Available online: https://modis-land.gsfc.nasa.gov/pdf/MCD12Q1_C6_Userguide04042018.pdf (accessed on 10 April 2025).
- Holben, B.N. Characteristics of Maximum-Value Composite Images from Temporal AVHRR Data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Prakash, S.; Mishra, A.; Gairola, R.; Varma, A.; Pal, P. Combined Use of Microwave and IR Data for The Study of Indian Monsoon Rainfall-2009. In Proceedings of the ISPRS Archives XXXVIII-8/W3 Workshop Proceedings: Impact of Climate Change on Agriculture, Ahmedabad, India, 17–18 December 2009. [Google Scholar]
- Sobajima, A. Rapidly Developing Cumulus Areas Derivation Algorithm Theoretical Basis Document. 2012. Available online: https://cwg.eumetsat.int/2013/01/jmas-rapidly-developing-cumulus-areas-algorithm/ (accessed on 5 March 2025).
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A Simple Interpretation of the Surface Temperature/Vegetation Index Space for Assessment of Surface Moisture Status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- He, Y.; Chen, F.; Jia, H.; Wang, L.; Bondur, V.G. Different Drought Legacies of Rain-Fed and Irrigated Croplands in a Typical Russian Agricultural Region. Remote Sens. 2020, 12, 1700. [Google Scholar] [CrossRef]
- Li, W. Classification of Drought Grades Based on Temperature Vegetation Drought Index Using the MODIS Data. Res. Soil Water Conserv. 2017, 24, 130–135. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 17–22. [Google Scholar]
- Liu, C.; Yang, C.; Yang, Q.; Wang, J. Spatiotemporal Drought Analysis by the Standardized Precipitation Index (SPI) and Standardized Precipitation Evapotranspiration Index (SPEI) in Sichuan Province, China. Sci. Rep. 2021, 11, 1280. [Google Scholar] [CrossRef] [PubMed]
- Kendall, M.G. Partial Rank Correlation. Biometrika 1942, 32, 277–283. [Google Scholar] [CrossRef]
- Niu, Y.S.; Hao, N.; Zhang, H.H. Interaction Screening by Partial Correlation. Stat. Interface 2018, 11, 317–325. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, X.; Liang, S.; Zhou, T.; Huang, K.; Tang, B.; Zhao, W. Time-Lag Effects of Global Vegetation Responses to Climate Change. Glob. Change Biol. 2015, 21, 3520–3531. [Google Scholar] [CrossRef] [PubMed]
- Apriyana, Y.; Surmaini, E.; Estiningtyas, W.; Pramudia, A.; Ramadhani, F.; Suciantini, S.; Susanti, E.; Purnamayani, R.; Syahbuddin, H. The Integrated Cropping Calendar Information System: A Coping Mechanism to Climate Variability for Sustainable Agriculture in Indonesia. Sustainability 2021, 13, 6495. [Google Scholar] [CrossRef]
- Hayashi, K.; Bugayong, I.; Siregar, I.H.; Jonharnas; Wirajaswadi, L.; Hadiawati, L.; Agustiani, N.; Orden, M.E. Appraisal of Rainfed Rice Production and Management Practices through Case Studies in North Sumatera and West Nusa Tenggara, Indonesia. Trop. Agric. Dev. 2018, 62, 43–54. [Google Scholar] [CrossRef]
- Meliani, F.; Sulistyowati, R.; Permata, Z.D.O.; Sumargana, L.; Amaliyah, R.; Purwandani, A.; Putrantijo, N.; Ramadhan, A.R. Preliminary Study on Validation of HIMAWARI-8 Data with Ground Based Rainfall Data at South Sumatera, Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2020, 500, 012031. [Google Scholar] [CrossRef]
- Ismanto, R.D.; Prasasti, I.; Fitriana, H.L. Comparison Analysis of Himawari 8, CHIRPS and GSMaP Data to Detect Rain in Indonesia. J. Meteorol. Dan. Geofis. 2023, 24, 9–17. [Google Scholar] [CrossRef]
- Mishra, A.; Gairola, R.; Varma, A.; Agarwal, V.K. Study of Intense Rainfall Events over India Using Kalpana-IR and TRMM-Precipitation Radar Observations. Curr. Sci. 2009, 97, 689–695. Available online: https://www.jstor.org/stable/24112165 (accessed on 5 March 2025).
- Lei, H.; Li, H.; Zhao, H.; Ao, T.; Li, X. Comprehensive Evaluation of Satellite and Reanalysis Precipitation Products over the Eastern Tibetan Plateau Characterized by a High Diversity of Topographies. Atmos. Res. 2021, 259, 105661. [Google Scholar] [CrossRef]
- Bhattarai, S.; Talchabhadel, R. Comparative Analysis of Satellite-Based Precipitation Data across the CONUS and Hawaii: Identifying Optimal Satellite Performance. Remote Sens. 2024, 16, 3058. [Google Scholar] [CrossRef]
- Nasrollahi, N. Reducing False Rain in Satellite Precipitation Products Using Cloudsat Cloud Classification Maps and Modis Multi-Spectral Images. In Improving Infrared-Based Precipitation Retrieval Algorithms Using Multi-Spectral Satellite Imagery; Springer Theses; Springer: Cham, Switzerland, 2015; pp. 21–32. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Gouveia, C.; Camarero, J.J.; Beguería, S.; Trigo, R.; López-Moreno, J.I.; Azorín-Molina, C.; Pasho, E.; Lorenzo-Lacruz, J.; Revuelto, J.; et al. Response of Vegetation to Drought Time-Scales across Global Land Biomes. Proc. Natl. Acad. Sci. USA 2013, 110, 52–57. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Chen, J.; Lee, S.C.; Xiong, L.; Su, T.; Lin, Q.; Xu, C.Y. Response and Recovery Times of Vegetation Productivity under Drought Stress: Dominant Factors and Relationships. J. Hydrol. 2025, 655, 132945. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated Multi-Satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement; Advances in Global Change Research; Springer: Cham, Switzerland, 2020; Volume 67, pp. 343–353. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Suriadi, A.; Mulyani, A.; Hadiawati, L.; Suratman. Biophysical Characteristics of Dry-Climate Upland and Agriculture Development Challenges in West Nusa Tenggara and East Nusa Tenggara Provinces. IOP Conf. Ser. Earth Environ. Sci. 2021, 648, 012014. [Google Scholar] [CrossRef]
- Selvaraj, J.; Marimuthu, P.D. Modeling Vegetation Dynamics: Insights from Distributed Lag Model and Spatial Interpolation of Satellite Derived Environmental Data. In International Conference on Mathematics and Computing; Lecture Notes in Networks and Systems; Springer: Singapore, 2024; Volume 963, pp. 41–51. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).