Correction of ASCAT, ESA–CCI, and SMAP Soil Moisture Products Using the Multi-Source Long Short-Term Memory (MLSTM)
Abstract
1. Introduction
2. Datasets and Preprocessing
2.1. In-Situ Soil Moisture Measurements
2.2. Remote Sensing Datasets
2.2.1. Soil Moisture Data Products
2.2.2. Four Auxiliary Variable Datasets
2.3. DATA Preprocessing
3. Methodology
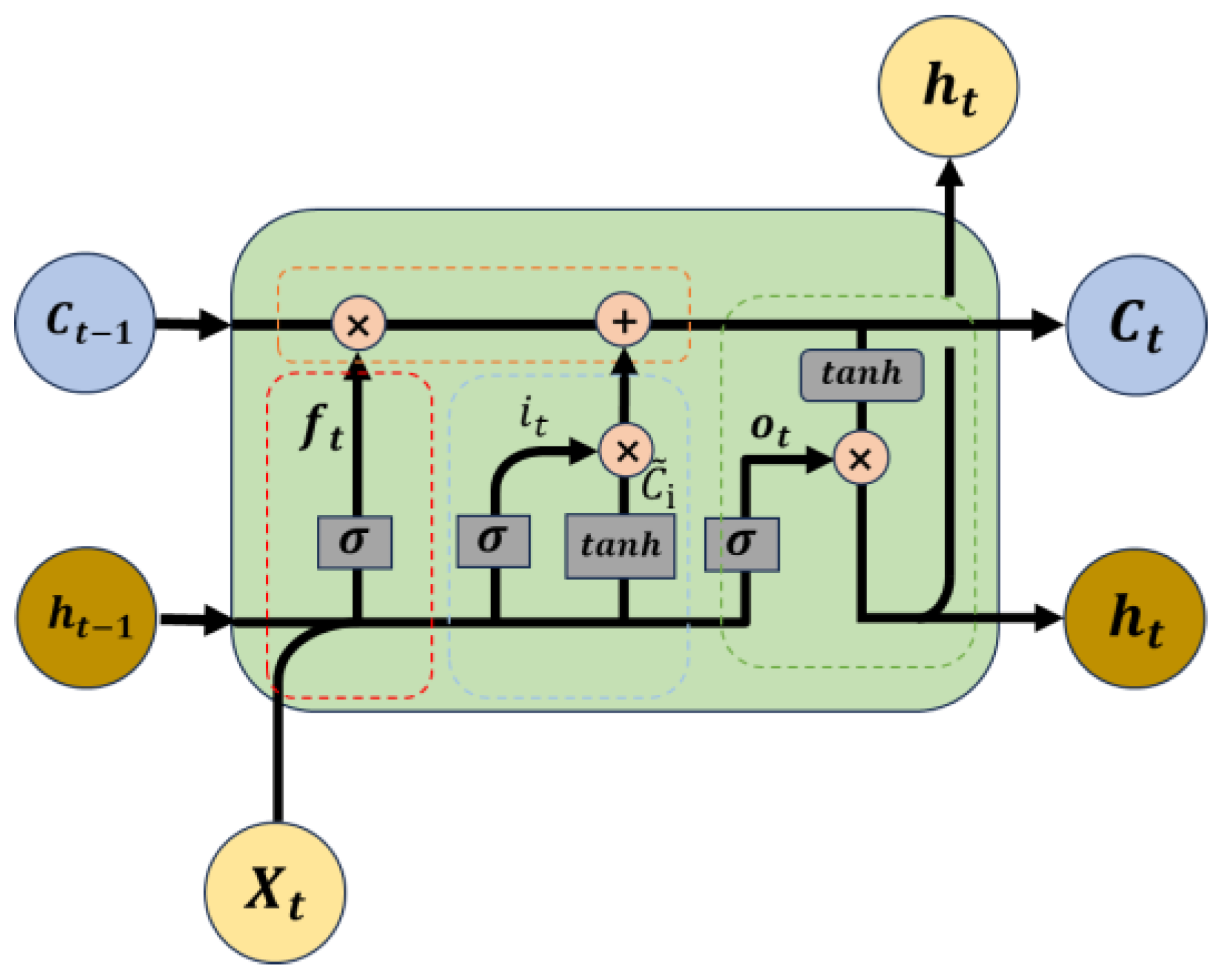
3.1. LSTM Deep Learning Method
3.2. SHAP Interpretability Method
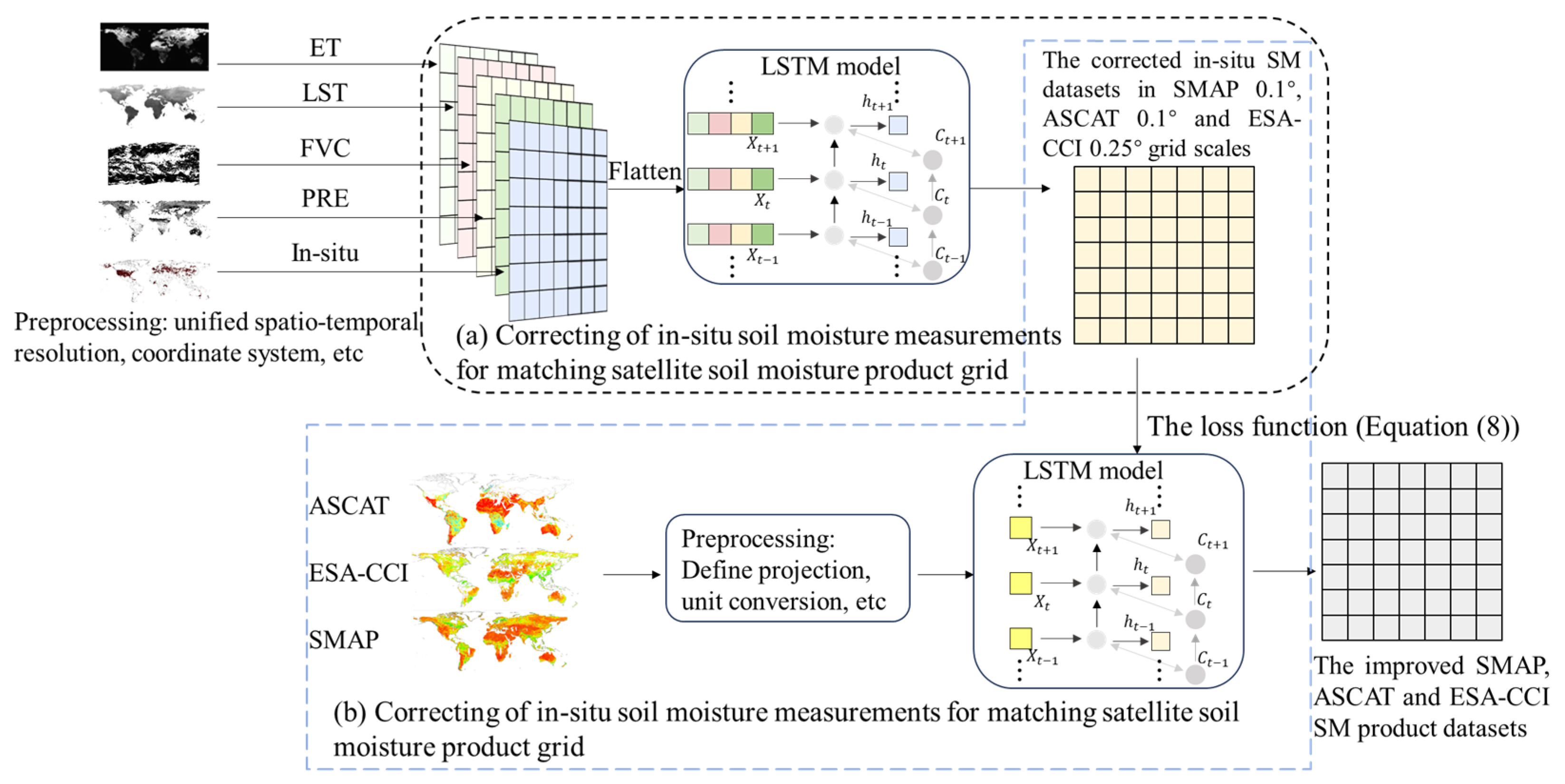
3.3. MLSTM Soil Moisture Calibration Algorithm
3.4. Evaluation Metrics
4. Results
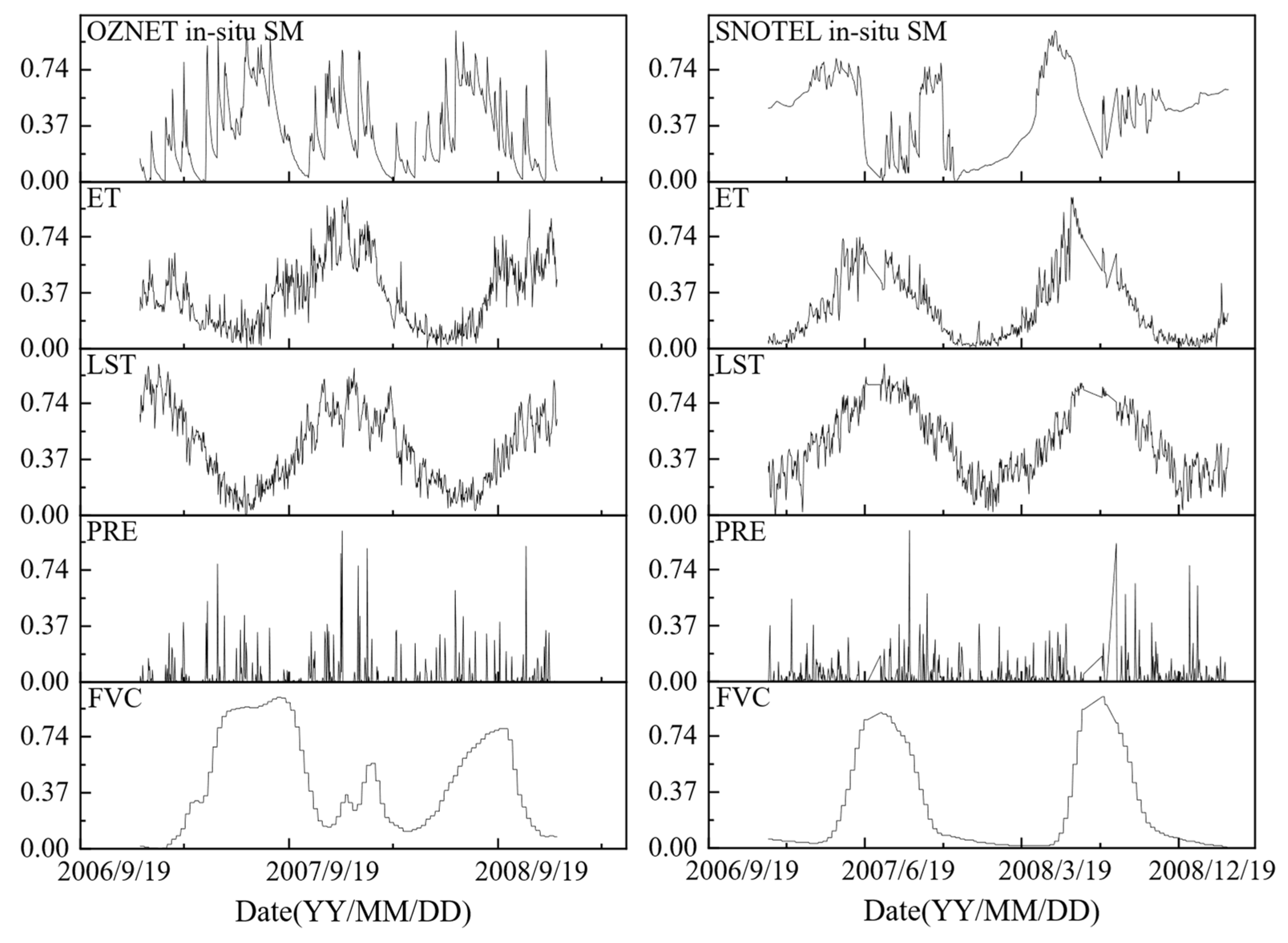
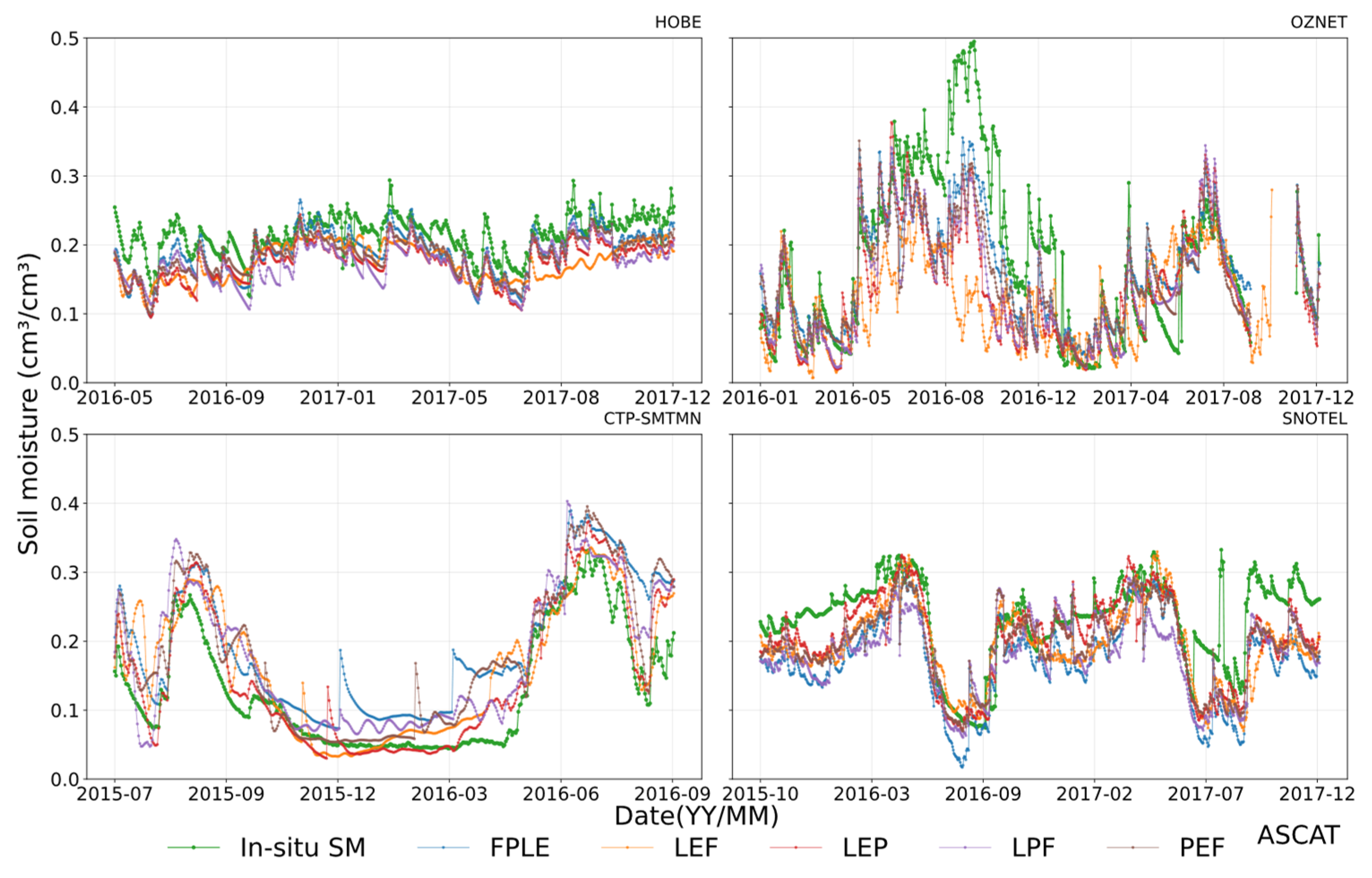
4.1. Temporal Evolutions of FVC, PRE, LST, ET, and In-Situ SM Measurements
4.2. Correction of In-Situ Soil Moisture Measurements
4.2.1. Correction of In-Situ SM Measurements for Matching Satellite SM Product Grid
4.2.2. Contribution Analysis of Auxiliary Variables to MLSTM Using the SHAP Method
4.3. The Improved ASCAT, SMAP, and ESA–CCI Products
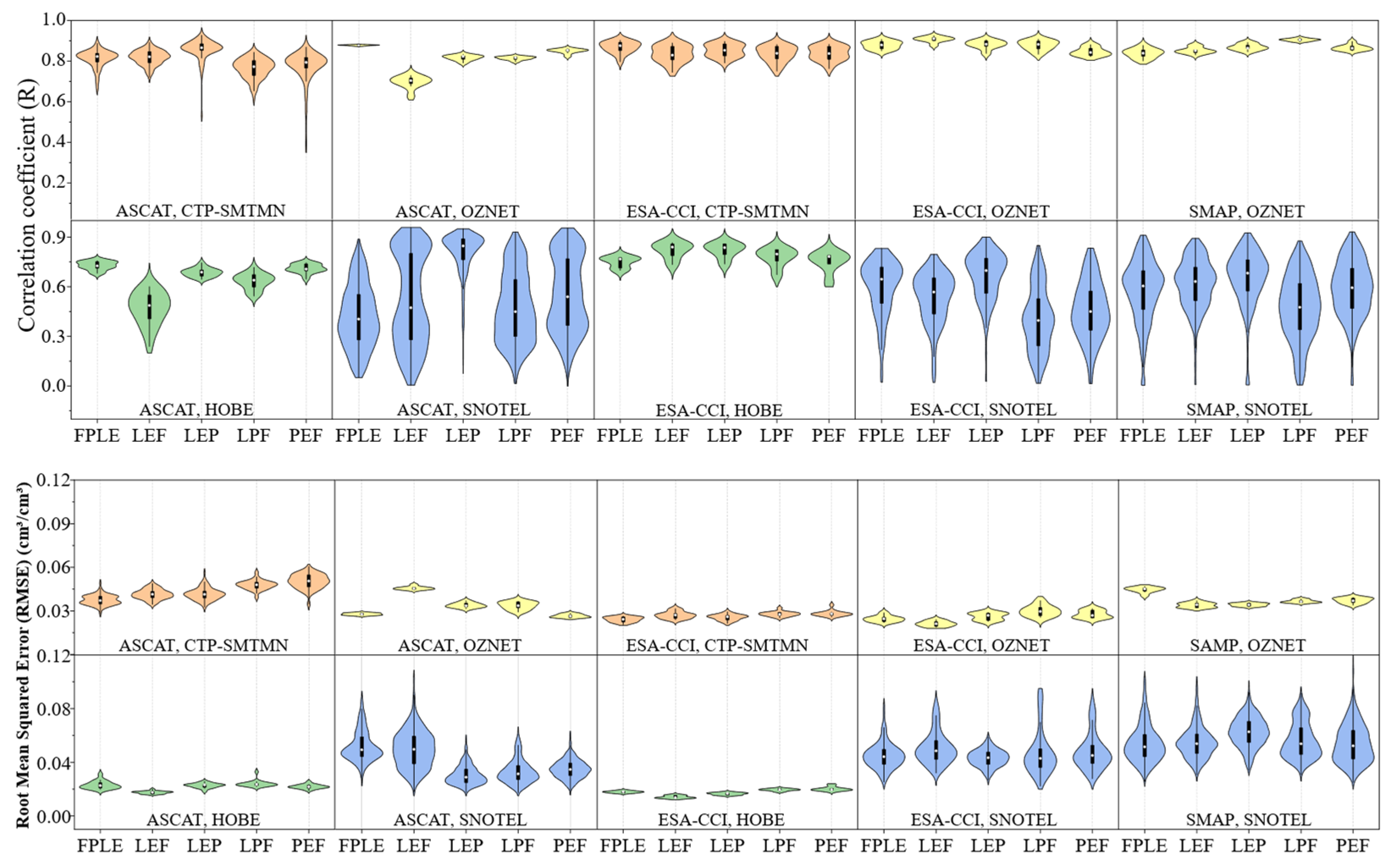
4.3.1. Violin Plots of the Improved ASCAT, SMAP, and ESA–CCI Products
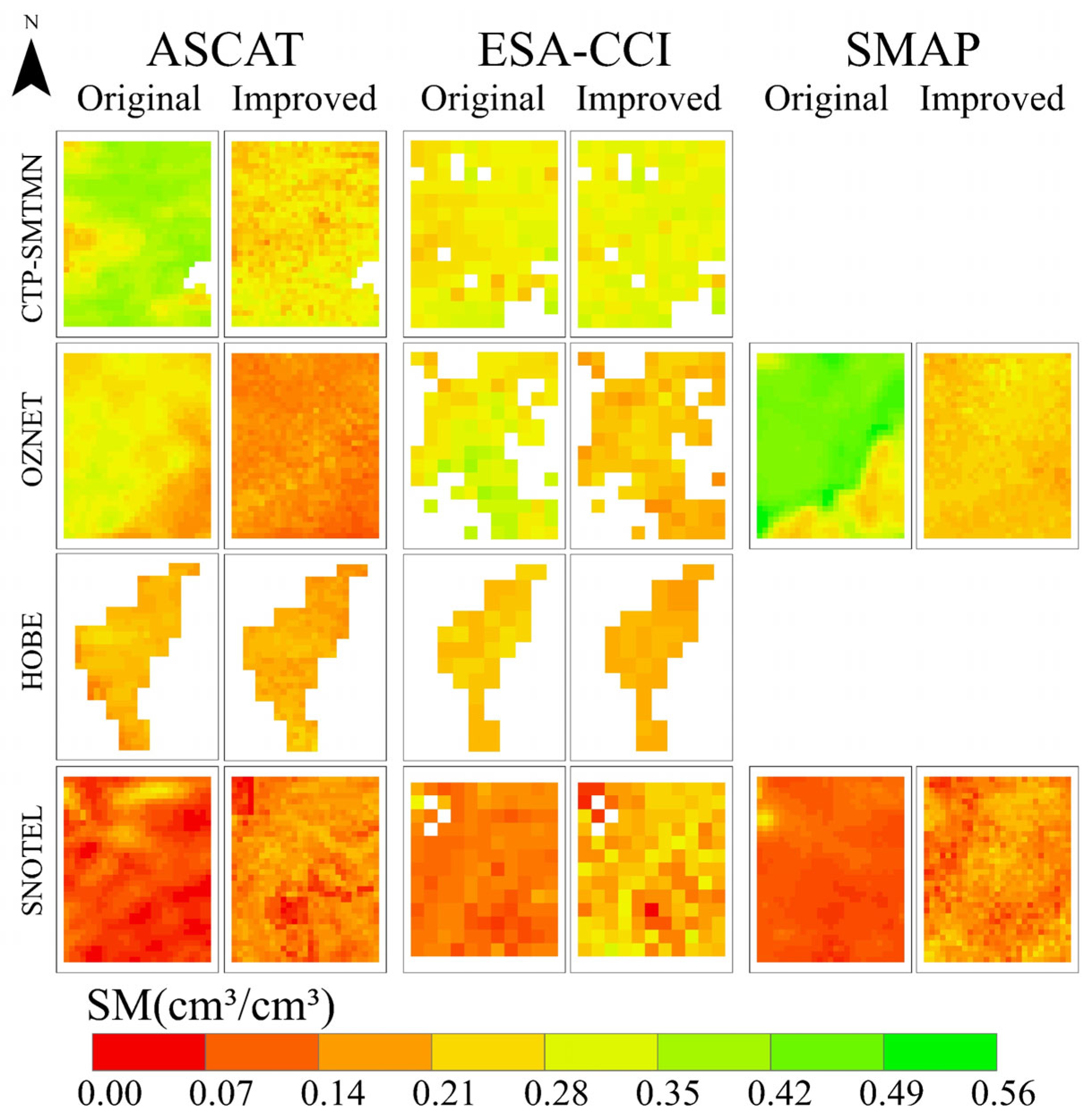
4.3.2. Spatial Distributions of the Improved ASCAT, SMAP, and ESA–CCI Products
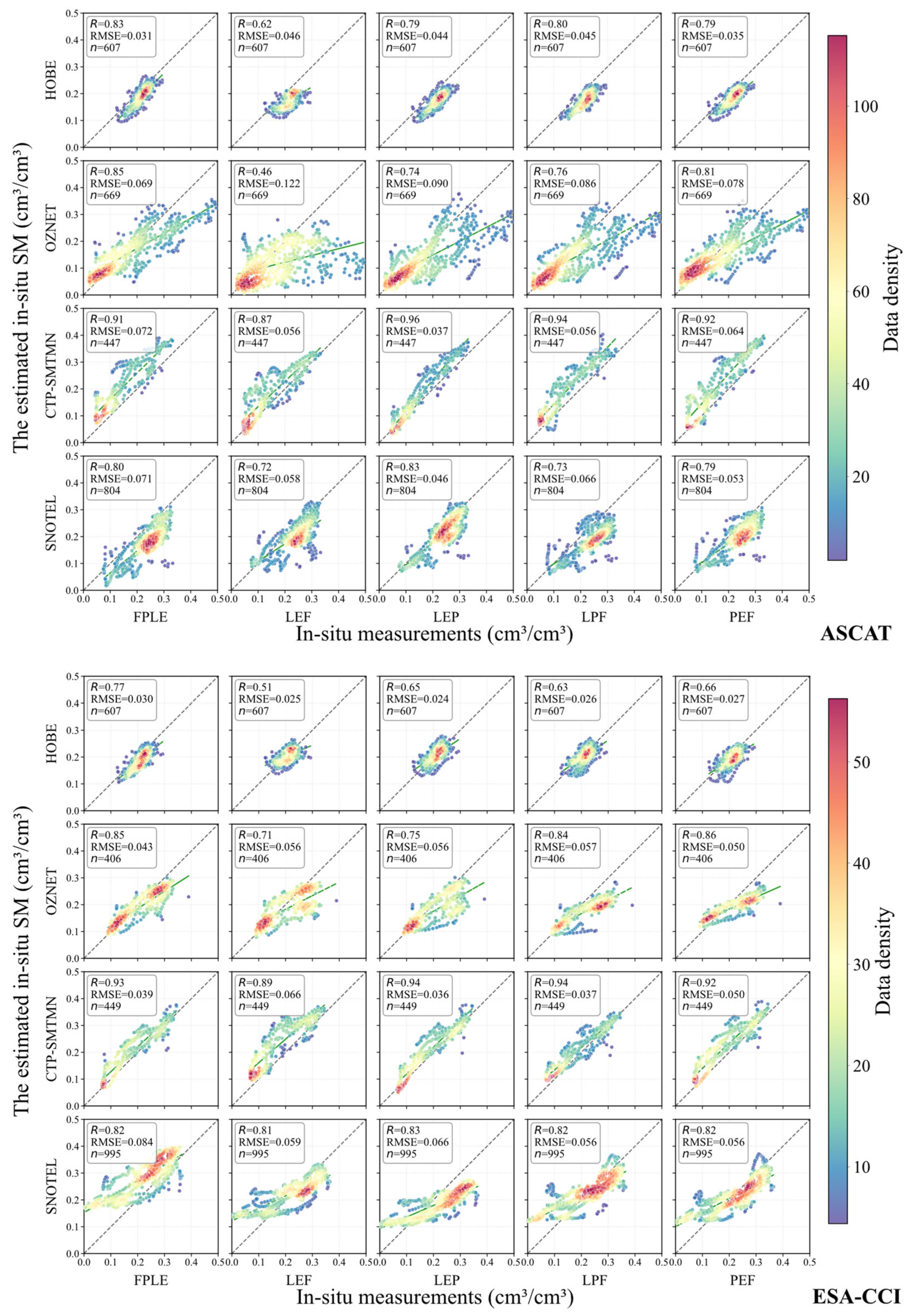
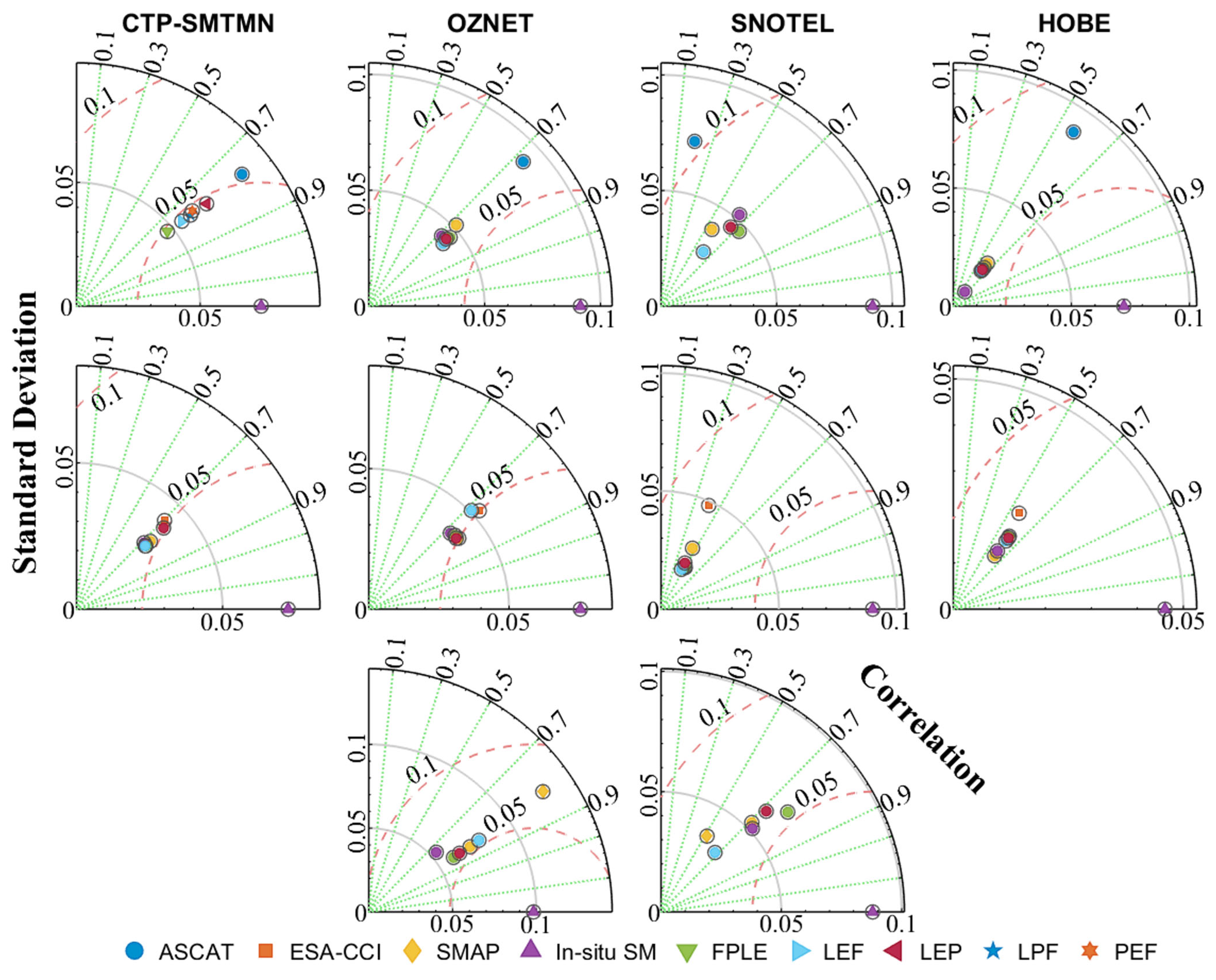
4.4. Evaluation of the Improved ASCAT, ESA–CCI, and SMAP Products
5. Discussion
6. Conclusions
- (1)
- The improved ESA–CCI had a relatively high overall accuracy and performed the best. The R-values of SMAP (OZNET: 0.80, SNOTEL: 0.68) were superior to those of ESA–CCI (OZNET: 0.78, SNOTEL: 0.46), indicating that the temporal evolution change trend of SMAP was more consistent with the in-situ SM measurements. The performance of ASCAT was poor, and its disadvantage was especially prominent with reference to the SNOTEL network. It was worth noting, however, that although the accuracy of ASCAT itself was low, the improvement effect achieved through MLSTM was the most significant among the ASCAT, ESA–CCI, and SMAP SM products.
- (2)
- The sensitivity of key auxiliary variables to input variables of MLSTM was significantly different. PRE, as a core driver of SM dynamics, showed indispensability across all networks. Notably, in the HOBE network—characterized by year-round humidity and high vegetation coverage—the FPLE variable combination achieved optimal predictive performance (R = 0.83). In contrast, for the CTP–SMTMN network with lower vegetation coverage, removing the FVC variable in the LEP combination enhanced prediction accuracy by 5.5% in ASCAT grids and 1% in ESA–CCI grids, suggesting that excessive reliance on vegetation parameters might introduce noise. These regional sensitivity differences showed the scientific value of the multivariate combination experimental framework, which not only identified dominant drivers but also quantified context-dependent optimization strategies for satellite product calibration.
- (3)
- Analysis of the SM improvement effect based on different satellite data showed that the performance of the MLSTM SM framework was affected by the network space range of the site and the combination of variables. In the violin plots of RMSE and R values for different combinations of networks and variables (Figure 9), the SNOTEL network performs poorly in key indicators of model evaluation, with the largest interquartile range between the RMSE and R values (RMSE up to 0.02 cm3/cm3 and R up to 0.5), indicating that the model’s performance is not yet very stable over a large spatial range. In the estimation at the site scale, there are significant differences in the performance of different variable combination models. The FPLE variable combination, as an estimation model with all variables input, performs the most stably and performs the best in both the OZNET and HOBE networks. In the CTP–SMTMN and SNOTEL networks, after removing the vegetation coverage variable from the FPLE variable combination, the R values of the estimation model based on the ASCAT grid increased by 0.055 and 0.025, respectively, and the R values of the estimation model based on the ESA–CCI grid increased by 0.010 and 0.011, respectively, indicating that the variable combinations adapted to different regions are different.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Q.; Fan, K.; Singh, V.P.; Song, C.; Xu, C.Y.; Sun, P. Is Himalayan-Tibetan Plateau “drying”? Historical estimations and future trends of surface soil moisture. Sci. Total Environ. 2019, 658, 374–384. [Google Scholar] [CrossRef] [PubMed]
- Bormann, H. Assessing the soil texture-specific sensitivity of simulated soil moisture to projected climate change by SVAT modelling. Geoderma 2012, 185–186, 73–83. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; de Rosnay, P.; Jann, A.; Schneider, S.; et al. The ASCAT Soil Moisture Product: A Review of its Specifications, Validation Results, and Emerging Applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef]
- Dostálová, A.; Doubková, M.; Sabel, D.; Bauer-Marschallinger, B.; Wagner, W. Seven Years of Advanced Synthetic Aperture Radar (ASAR) Global Monitoring (GM) of Surface Soil Moisture over Africa. Remote Sens. 2014, 6, 7683–7707. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Gruber, A.; De Jeu, R.A.M.; Wagner, W.; Stacke, T.; Loew, A.; Albergel, C.; Brocca, L.; Chung, D.; Parinussa, R.M.; et al. Evaluation of the ESA CCI soil moisture product using ground-based observations. Remote Sens. Environ. 2015, 162, 380–395. [Google Scholar] [CrossRef]
- Gruber, A.; Su, C.H.; Zwieback, S.; Crow, W.; Dorigo, W.; Wagner, W. Recent advances in (soil moisture) triple collocation analysis. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 200–211. [Google Scholar] [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Al-Yaari, A.; Wigneron, J.P.; Dorigo, W.; Colliander, A.; Pellarin, T.; Hahn, S.; Mialon, A.; Richaume, P.; Fernandez-Moran, R.; Fan, L.; et al. Assessment and inter-comparison of recently developed/reprocessed microwave satellite soil moisture products using ISMN ground-based measurements. Remote Sens. Environ. 2019, 224, 289–303. [Google Scholar] [CrossRef]
- Colliander, A.; Reichle, R.H.; Crow, W.T.; Cosh, M.H.; Chen, F.; Chan, S.; Das, N.N.; Bindlish, R.; Chaubell, J.; Kim, S.; et al. Validation of Soil Moisture Data Products From the NASA SMAP Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 364–392. [Google Scholar] [CrossRef]
- Zheng, J.; Zhao, T.; Lü, H.; Shi, J.; Cosh, M.H.; Ji, D.; Jiang, L.; Cui, Q.; Lu, H.; Yang, K.; et al. Assessment of 24 soil moisture datasets using a new in situ network in the Shandian River Basin of China. Remote Sens. Environ. 2022, 271, 112891. [Google Scholar] [CrossRef]
- Kim, H.; Crow, W.; Li, X.; Wagner, W.; Hahn, S.; Lakshmi, V. True global error maps for SMAP, SMOS, and ASCAT soil moisture data based on machine learning and triple collocation analysis. Remote Sens. Environ. 2023, 298, 113776. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Zhang, X.; Moradkhani, H.; Zhang, C.; Hu, C. In-situ and triple-collocation based evaluations of eight global root zone soil moisture products. Remote Sens. Environ. 2021, 254, 112248. [Google Scholar] [CrossRef]
- Zhang, J.; Becker-Reshef, I.; Justice, C. Evaluation of the ASCAT surface soil moisture product for agricultural drought monitoring in USA. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 669–672. [Google Scholar]
- Kim, H.; Parinussa, R.; Konings, A.G.; Wagner, W.; Cosh, M.H.; Lakshmi, V.; Zohaib, M.; Choi, M. Global-scale assessment and combination of SMAP with ASCAT (active) and AMSR2 (passive) soil moisture products. Remote Sens. Environ. 2018, 204, 260–275. [Google Scholar] [CrossRef]
- Ding, T.; Zhao, W.; Yang, Y. Addressing spatial gaps in ESA CCI soil moisture product: A hierarchical reconstruction approach using deep learning model. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104003. [Google Scholar] [CrossRef]
- Liu, P.W.; Judge, J.; Roo, R.D.D.; England, A.W.; Bongiovanni, T. Uncertainty in Soil Moisture Retrievals Using the SMAP Combined Active–Passive Algorithm for Growing Sweet Corn. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3326–3339. [Google Scholar] [CrossRef]
- Crow, W.T.; Berg, A.A.; Cosh, M.H.; Loew, A.; Mohanty, B.P.; Panciera, R.; de Rosnay, P.; Ryu, D.; Walker, J.P. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products. Rev. Geophys. 2012, 50, RG2002. [Google Scholar] [CrossRef]
- Meng, X.; Li, R.; Luan, L.; Lyu, S.; Zhang, T.; Ao, Y.; Han, B.; Zhao, L.; Ma, Y. Detecting hydrological consistency between soil moisture and precipitation and changes of soil moisture in summer over the Tibetan Plateau. Clim. Dyn. 2017, 51, 4157–4168. [Google Scholar] [CrossRef]
- Wang, J.; Xu, D. Artificial Neural Network-Based Microwave Satellite Soil Moisture Reconstruction over the Qinghai–Tibet Plateau, China. Remote Sens. 2021, 13, 5156. [Google Scholar] [CrossRef]
- Berg, A.; Sheffield, J.; Milly, P.C.D. Divergent surface and total soil moisture projections under global warming. Geophys. Res. Lett. 2017, 44, 236–244. [Google Scholar] [CrossRef]
- Mao, L.; Pei, X.; He, C.; Bian, P.; Song, D.; Fang, M.; Wu, W.; Zhan, H.; Zhou, W.; Tian, G. Spatiotemporal Changes in Vegetation Cover and Soil Moisture in the Lower Reaches of the Heihe River Under Climate Change. Forests 2024, 15, 1921. [Google Scholar] [CrossRef]
- Rasheed, M.W.; Tang, J.; Sarwar, A.; Shah, S.; Saddique, N.; Khan, M.U.; Imran Khan, M.; Nawaz, S.; Shamshiri, R.R.; Aziz, M.; et al. Soil Moisture Measuring Techniques and Factors Affecting the Moisture Dynamics: A Comprehensive Review. Sustainability 2022, 14, 11538. [Google Scholar] [CrossRef]
- Kwon, M.; Han, D. Assessment of remotely sensed soil moisture products and their quality improvement: A case study in South Korea. J. Hydro-Environ. Res. 2019, 24, 14–27. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, Y.; Luo, Y. Improvement of multi-layer soil moisture prediction using support vector machines and ensemble Kalman filter coupled with remote sensing soil moisture datasets over an agriculture dominant basin in China. Hydrol. Process. 2021, 35, e14154. [Google Scholar] [CrossRef]
- Cui, K.; Xing, M.; Shang, J.; Zhou, X.; Wang, J. Enhanced L-MEB Model for Soil Moisture Retrieval Over Soybean Fields During the Growing Season. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4409216. [Google Scholar] [CrossRef]
- Hagan, D.F.T.; Kim, S.; Wang, G.; Ma, X.; Hu, Y.; Liu, Y.Y.; Barth, A.; Liu, H.; Ullah, W.; Nooni, I.K.; et al. Seamless finer-resolution soil moisture from the synergistic merging of the FengYun-3 satellite series. Sci. Data 2025, 12, 983. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Xing, M.; Dong, T. An Apparent Thermal Inertia Based Trapezoid Model for Downscaling ESA CCI Soil Moisture Products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 4473–4486. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, H.; Zhang, C. Validating Data Interpolation Empirical Orthogonal Functions Interpolated Soil Moisture Data in the Contiguous United States. Agriculture 2025, 15, 1212. [Google Scholar] [CrossRef]
- Jin, M.; Zheng, X.; Jiang, T.; Li, X.; Li, X.-J.; Zhao, K. Evaluation and Improvement of SMOS and SMAP Soil Moisture Products for Soils with High Organic Matter over a Forested Area in Northeast China. Remote Sens. 2017, 9, 387. [Google Scholar] [CrossRef]
- Guo, X.; Fang, X.; Cao, Y.; Yang, L.; Ren, L.; Chen, Y.; Zhang, X. Reconstruction of ESA CCI soil moisture based on DCT-PLS and in situ soil moisture. Hydrol. Res. 2022, 53, 1221–1236. [Google Scholar] [CrossRef]
- Yin, J.; Zhan, X.; Barlage, M.; Liu, J.; Meng, H.; Ferraro, R.R. Refinement of NOAA AMSR-2 Soil Moisture Data Product—Part 2: Development With the Optimal Machine Learning Model. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4405311. [Google Scholar] [CrossRef]
- Cui, Y.; Yang, X.; Chen, X.; Fan, W.; Zeng, C.; Xiong, W.; Hong, Y. A two-step fusion framework for quality improvement of a remotely sensed soil moisture product: A case study for the ECV product over the Tibetan Plateau. J. Hydrol. 2020, 587, 124993. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Parinussa, R.M.; Dorigo, W.A.; De Jeu, R.A.M.; Wagner, W.; van Dijk, A.I.J.M.; McCabe, M.F.; Evans, J.P. Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 425–436. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Qiu, T.; Wang, T.; Zeng, C.; Zhang, B.; Shen, H. Seamless global daily soil moisture mapping using deep learning based spatiotemporal fusion. Int. J. Appl. Earth Obs. Geoinf. 2025, 139, 104517. [Google Scholar] [CrossRef]
- Nasiri Khiavi, A. Application of remote sensing indicators and deep learning algorithms to model the spatial distribution of soil moisture. Earth Sci. Inform. 2025, 18, 404. [Google Scholar] [CrossRef]
- Xu, N.; Andre, D.; Arman, A.; Derek, H.; Perez-Barquero, F.P. Soil moisture estimation with microwave remote sensing: A systematic review and meta-analysis. Int. J. Digit. Earth 2025, 18, 1–27. [Google Scholar] [CrossRef]
- Cui, Y.; Long, D.; Hong, Y.; Zeng, C.; Zhou, J.; Han, Z.; Liu, R.; Wan, W. Validation and reconstruction of FY-3B/MWRI soil moisture using an artificial neural network based on reconstructed MODIS optical products over the Tibetan Plateau. J. Hydrol. 2016, 543, 242–254. [Google Scholar] [CrossRef]
- Fang, K.; Shen, C.; Kifer, D.; Yang, X. Prolongation of SMAP to Spatiotemporally Seamless Coverage of Continental U.S. Using a Deep Learning Neural Network. Geophys. Res. Lett. 2017, 44, 11030–11039. [Google Scholar] [CrossRef]
- Fang, K.; Pan, M.; Shen, C. The Value of SMAP for Long-Term Soil Moisture Estimation With the Help of Deep Learning. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2221–2233. [Google Scholar] [CrossRef]
- Roberts, T.M.; Colwell, I.; Chew, C.; Lowe, S.; Shah, R. A Deep-Learning Approach to Soil Moisture Estimation with GNSS-R. Remote Sens. 2022, 14, 3299. [Google Scholar] [CrossRef]
- Abebe, A.K.; Zhou, X.; Lv, T.; Tao, Z.; Elnashar, A.; Kebede, A.; Wang, C.; Zhang, H. Spatial Downscaling of Soil Moisture Product to Generate High-Resolution Data: A Multi-Source Approach over Heterogeneous Landscapes in Kenya. Remote Sens. 2025, 17, 1763. [Google Scholar] [CrossRef]
- Taheri, M.; Bigdeli, M.; Imanian, H.; Mohammadian, A. An Overview of Machine-Learning Methods for Soil Moisture Estimation. Water 2025, 17, 1638. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Ren, L.; Teuling, A.J.; Zhang, X.; Jiang, S.; Yang, X.; Wei, L.; Zhong, F.; Zheng, L. Reconstruction of ESA CCI satellite-derived soil moisture using an artificial neural network technology. Sci. Total Environ. 2021, 782, 146602. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, G.; Wei, X.; Zhou, F.; Kattel, G.; Amankwah, S.O.Y.; Hagan, D.F.T.; Duan, Z. Reconstructing long-term global satellite-based soil moisture data using deep learning method. Front. Earth Sci. 2023, 11, 1130853. [Google Scholar] [CrossRef]
- Cai, G.; Xue, Y.; Hu, Y.; Wang, Y.; Guo, J.; Luo, Y.; Wu, C.; Zhong, S.; Qi, S. Soil moisture retrieval from MODIS data in Northern China Plain using thermal inertia model. Int. J. Remote Sens. 2007, 28, 3567–3581. [Google Scholar] [CrossRef]
- Yang, K.; Qin, J.; Zhao, L.; Chen, Y.; Tang, W.; Han, M.; Lazhu; Chen, Z.; Lv, N.; Ding, B.; et al. A Multiscale Soil Moisture and Freeze–Thaw Monitoring Network on the Third Pole. Bull. Am. Meteorol. Soc. 2013, 94, 1907–1916. [Google Scholar] [CrossRef]
- Jensen, K.H.; Refsgaard, J.C. HOBE: The Danish Hydrological Observatory. Vadose Zone J. 2018, 17, 1–24. [Google Scholar] [CrossRef]
- Smith, A.B.; Walker, J.P.; Western, A.W.; Young, R.I.; Ellett, K.M.; Pipunic, R.C.; Grayson, R.B.; Siriwardena, L.; Chiew, F.H.S.; Richter, H. The Murrumbidgee soil moisture monitoring network data set. Water Resour. Res. 2012, 48, W07701. [Google Scholar] [CrossRef]
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J.C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 12, 1323–1337. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Entekhabi, D.; Reichle, R.H.; Koster, R.D.; Crow, W.T. Performance Metrics for Soil Moisture Retrievals and Application Requirements. J. Hydrometeorol. 2010, 11, 832–840. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Jia, K.; Yang, L.; Liang, S.; Xiao, Z.; Zhao, X.; Yao, Y.; Zhang, X.; Jiang, B.; Liu, D. Long-Term Global Land Surface Satellite (GLASS) Fractional Vegetation Cover Product Derived From MODIS and AVHRR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 508–518. [Google Scholar] [CrossRef]
- Zhao, T.; Yu, P. Global Daily 0.05° Spatiotemporal Continuous Land Surface Temperature Dataset (2002–2020). 2021. Available online: https://cstr.cn/18406.11.Meteoro.tpdc.271663 (accessed on 21 March 2025).
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. GPM IMERG Final Precipitation L3 1 Day 0.1 Degree × 0.1 Degree V07. 2024. Available online: https://rda.ucar.edu/datasets/d734000/ (accessed on 23 March 2025).
- Jiao, L.; Guojie, W.; Tiexi, C.; Shijie, L.; Daniel, H.; Giri, K.; Jian, P.; Tong, J.; Buda, S. A Harmonized Global Land Evaporation Dataset from Model-Based Products Covering 1980–2017. 2021. Available online: https://zenodo.org/records/4595941 (accessed on 23 March 2025).
- Dorigo, W.A.; Xaver, A.; Vreugdenhil, M.; Gruber, A.; Hegyiová, A.; Sanchis-Dufau, A.D.; Zamojski, D.; Cordes, C.; Wagner, W.; Drusch, M. Global Automated Quality Control of In Situ Soil Moisture Data from the International Soil Moisture Network. Vadose Zone J. 2013, 12, 918–924. [Google Scholar] [CrossRef]
- Xie, Q.; Jia, L.; Menenti, M.; Chen, Q.; Bi, J.; Chen, Y.; Wang, C.; Yu, X. Evaluation of remote sensing soil moisture data products with a new approach to analyse footprint mismatch with in-situ measurements. Int. J. Digit. Earth 2024, 17, 2437051. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Fathololoumi, S.; Vaezi, A.R.; Firozjaei, M.K.; Biswas, A. Quantifying the effect of surface heterogeneity on soil moisture across regions and surface characteristic. J. Hydrol. 2021, 596, 126132. [Google Scholar] [CrossRef]
- Yongqiang, C.; Na, Y.; Xin, H.; Mingyuan, T. Study on Stability of Surface Soil Moisture during SMOS and SMAP Transit period. Remote Sens. Technol. Appl. 2020, 35, 58–64. [Google Scholar] [CrossRef]
- Deng, Q.; Yang, J.; Zhang, L.; Sun, Z.; Sun, G.; Chen, Q.; Dou, F. Analysis of Seasonal Driving Factors and Inversion Model Optimization of Soil Moisture in the Qinghai Tibet Plateau Based on Machine Learning. Water 2023, 15, 2859. [Google Scholar] [CrossRef]
- Rooney, E.C.; Bailey, V.L.; Patel, K.F.; Possinger, A.R.; Gallo, A.C.; Bergmann, M.; Lybrand, R. The Impact of Freeze-Thaw History on Soil Carbon Response to Experimental Freeze-Thaw Cycles. J. Geophys. Res. Biogeosci. 2022, 127, e2022JG006889. [Google Scholar] [CrossRef]
- Kumar, S.V.; Peters-Lidard, C.D.; Santanello, J.A.; Reichle, R.H.; Draper, C.S.; Koster, R.D.; Nearing, G.; Jasinski, M.F. Evaluating the utility of satellite soil moisture retrievals over irrigated areas and the ability of land data assimilation methods to correct for unmodeled processes. Hydrol. Earth Syst. Sci. 2015, 19, 4463–4478. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, Z.; Gui, H.; Chen, X.; Hu, S.; Gao, L.; Yang, H.; Qiu, J.; Xin, Q. A Meteorology-Driven Transformer Network to Predict Soil Moisture for Agriculture Drought Forecasting. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4405818. [Google Scholar] [CrossRef]






| Products | Temporal Resolution | Spatial Resolution | Temporal Coverage | Unit | Format | Main References |
|---|---|---|---|---|---|---|
| ASCAT | Daily | 0.1° × 0.1° | 2007–2017 | % | netCDF4 | Wagner et al., 1999 |
| SMAP | Daily | 9 km × 9 km | 2015–2020 | cm3/cm3 | HDF5 | Jackson 1993 |
| ESA–CCI | Daily | 0.25° × 0.25° | 2002–2017 | cm3/cm3 | NetCDF-4 | Gruber et al., 2017 |
| FVC | 8 days | 0.5 km × 0.5 km | 2002–2017 | a.u. | HDF–EOS | Jia et al., 2019 |
| LST | Daily | 0.05° × 0.05° | 2002–2017 | K | HDF5 | Tianjie and Pei 2021 |
| PRE | Daily | 0.1° × 0.1° | 2002–2017 | mm/day | netCDF | Huffman et al., 2024 |
| ET | Daily | 0.25° × 0.25° | 2002–2017 | mm | netCDF | Jiao et al., 2021 |
| Hyperparameters | CTP–SMTMN | HOBE | OZNET | SNOTEL | |
|---|---|---|---|---|---|
| 1 | Learning Rate | 0.001 | 0.001 | 0.01 | 0.001 |
| 2 | Hidden Size | 100 | 100 | 100 | 100 |
| 3 | Batch Size | 1 | 4 | 2 | 3 |
| 4 | Epochs | 100 | 100 | 110 | 130 |
| 5 | Sequence Length | 180 | 90 | 180 | 50 |
| 6 | Dropout | 0.2 | / | 0.2 | 0.2 |
| 7 | optimizer | Adam | Adam | Adam | Adam |
| 8 | activation | sigmoid | ReLU | sigmoid | sigmoid |
| Variables\Networks | CTP–SMTMN | OZNET | HOBE | SNOTEL |
|---|---|---|---|---|
| FVC | 0.720 ** | 0.501 ** | 0.089 * | −0.162 ** |
| PRE | 0.419 ** | 0.217 ** | 0.195 ** | 0.086 * |
| LST | 0.559 ** | −0.536 ** | 0.214 ** | 0.090 * |
| ET | 0.746 ** | −0.060 | 0.030 | 0.367 ** |
| Network | Variable Combination | ASCAT 0.1°Grid | ESA–CCI 0.25°Grid | SMAP 0.1° Grid | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | MAE | RMSE | ubRMSE | Bias | R | MAE | RMSE | ubRMSE | Bias | R | MAE | RMSE | ubRMSE | Bias | ||
| HOBE | FPLE | 0.831 | 0.027 | 0.031 | 0.018 | 0.025 | 0.767 | 0.025 | 0.030 | 0.019 | 0.023 | / | / | / | / | / |
| LEF | 0.618 | 0.040 | 0.046 | 0.024 | 0.039 | 0.515 | 0.020 | 0.025 | 0.025 | 0.003 | / | / | / | / | / | |
| LEP | 0.794 | 0.041 | 0.044 | 0.016 | 0.041 | 0.650 | 0.019 | 0.024 | 0.024 | 0.001 | / | / | / | / | / | |
| LPF | 0.795 | 0.041 | 0.045 | 0.019 | 0.041 | 0.630 | 0.021 | 0.026 | 0.025 | 0.008 | / | / | / | / | / | |
| PEF | 0.787 | 0.031 | 0.035 | 0.020 | 0.029 | 0.656 | 0.022 | 0.027 | 0.022 | 0.015 | / | / | / | / | / | |
| OZNET | FPLE | 0.845 | 0.053 | 0.069 | 0.067 | 0.017 | 0.854 | 0.053 | 0.043 | 0.037 | 0.052 | 0.821 | 0.055 | 0.070 | 0.040 | −0.051 |
| LEF | 0.464 | 0.084 | 0.122 | 0.106 | 0.061 | 0.711 | 0.043 | 0.056 | 0.052 | 0.021 | 0.725 | 0.035 | 0.044 | 0.043 | −0.010 | |
| LEP | 0.745 | 0.059 | 0.090 | 0.078 | 0.036 | 0.754 | 0.040 | 0.056 | 0.048 | 0.028 | 0.767 | 0.032 | 0.039 | 0.036 | −0.016 | |
| LPF | 0.764 | 0.059 | 0.086 | 0.077 | 0.038 | 0.842 | 0.045 | 0.057 | 0.043 | 0.037 | 0.843 | 0.033 | 0.040 | 0.032 | −0.024 | |
| PEF | 0.807 | 0.057 | 0.078 | 0.073 | 0.027 | 0.865 | 0.042 | 0.050 | 0.045 | 0.021 | 0.814 | 0.027 | 0.032 | 0.031 | −0.009 | |
| CTP–SMTMN | FPLE | 0.909 | 0.061 | 0.072 | 0.038 | −0.061 | 0.931 | 0.030 | 0.039 | 0.031 | −0.023 | / | / | / | / | / |
| LEF | 0.872 | 0.041 | 0.056 | 0.046 | −0.032 | 0.889 | 0.056 | 0.066 | 0.030 | −0.053 | / | / | / | / | / | |
| LEP | 0.964 | 0.028 | 0.037 | 0.030 | −0.021 | 0.941 | 0.027 | 0.036 | 0.031 | −0.019 | / | / | / | / | / | |
| LPF | 0.939 | 0.047 | 0.056 | 0.033 | −0.045 | 0.942 | 0.031 | 0.037 | 0.028 | −0.024 | / | / | / | / | / | |
| PEF | 0.916 | 0.050 | 0.064 | 0.042 | −0.048 | 0.920 | 0.040 | 0.050 | 0.035 | −0.036 | / | / | / | / | / | |
| SNOTEL | FPLE | 0.800 | 0.061 | 0.071 | 0.039 | 0.059 | 0.824 | 0.071 | 0.084 | 0.054 | −0.064 | 0.866 | 0.026 | 0.033 | 0.031 | −0.010 |
| LEF | 0.724 | 0.047 | 0.058 | 0.045 | 0.037 | 0.809 | 0.047 | 0.059 | 0.059 | −0.006 | 0.850 | 0.032 | 0.041 | 0.032 | −0.026 | |
| LEP | 0.825 | 0.035 | 0.046 | 0.037 | 0.027 | 0.835 | 0.058 | 0.066 | 0.058 | 0.031 | 0.867 | 0.027 | 0.031 | 0.030 | 0.006 | |
| LPF | 0.728 | 0.059 | 0.066 | 0.042 | 0.051 | 0.820 | 0.044 | 0.056 | 0.055 | −0.010 | 0.876 | 0.030 | 0.039 | 0.030 | −0.025 | |
| PEF | 0.786 | 0.044 | 0.053 | 0.039 | 0.036 | 0.819 | 0.044 | 0.056 | 0.056 | 0.002 | 0.777 | 0.033 | 0.044 | 0.038 | −0.022 | |
| Satellite | Network | Original | FPLE | LEF | LEP | LPF | PEF |
|---|---|---|---|---|---|---|---|
| ASCAT | HOBE | 0.0768 | 0.0606 | 0.0677 | 0.0614 | 0.0623 | 0.0619 |
| OZNET | 0.0670 | 0.0640 | 0.0671 | 0.0635 | 0.0651 | 0.0647 | |
| CTP–SMTMN | 0.0539 | 0.0485 | 0.0470 | 0.0469 | 0.0466 | 0.0475 | |
| SNOTEL | 0.1049 | 0.0770 | 0.0698 | 0.0662 | 0.0769 | 0.0702 | |
| ESA–CCI | HOBE | 0.0379 | 0.0388 | 0.0385 | 0.0373 | 0.0376 | 0.0373 |
| OZNET | 0.0502 | 0.0501 | 0.0537 | 0.0518 | 0.0523 | 0.0509 | |
| CTP–SMTMN | 0.0520 | 0.0526 | 0.0543 | 0.0533 | 0.0535 | 0.0509 | |
| SNOTEL | 0.0822 | 0.0806 | 0.0817 | 0.0814 | 0.0828 | 0.0820 | |
| SMAP | OZNET | 0.0720 | 0.0543 | 0.0681 | 0.0578 | 0.0537 | 0.0563 |
| SNOTEL | 0.0757 | 0.0625 | 0.0608 | 0.0545 | 0.0700 | 0.0609 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Q.; Chen, Y.; Chen, Q.; Wang, C.; Huang, Y. Correction of ASCAT, ESA–CCI, and SMAP Soil Moisture Products Using the Multi-Source Long Short-Term Memory (MLSTM). Remote Sens. 2025, 17, 2456. https://doi.org/10.3390/rs17142456
Xie Q, Chen Y, Chen Q, Wang C, Huang Y. Correction of ASCAT, ESA–CCI, and SMAP Soil Moisture Products Using the Multi-Source Long Short-Term Memory (MLSTM). Remote Sensing. 2025; 17(14):2456. https://doi.org/10.3390/rs17142456
Chicago/Turabian StyleXie, Qiuxia, Yonghui Chen, Qiting Chen, Chunmei Wang, and Yelin Huang. 2025. "Correction of ASCAT, ESA–CCI, and SMAP Soil Moisture Products Using the Multi-Source Long Short-Term Memory (MLSTM)" Remote Sensing 17, no. 14: 2456. https://doi.org/10.3390/rs17142456
APA StyleXie, Q., Chen, Y., Chen, Q., Wang, C., & Huang, Y. (2025). Correction of ASCAT, ESA–CCI, and SMAP Soil Moisture Products Using the Multi-Source Long Short-Term Memory (MLSTM). Remote Sensing, 17(14), 2456. https://doi.org/10.3390/rs17142456






