Precipitation Governs Terrestrial Water Storage Anomaly Decline in the Hengduan Mountains Region, China, Amid Climate Change
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Methodology and Data Sources
2.2.1. Datasets
| Categories | Indices and Aggregation | Name | Resolution | Sources |
|---|---|---|---|---|
| Water storage | Terrestrial water storage (TWSA) | HWSA | Monthly, 0.05°, covered period: 2002.04–2022.12 | [19] |
| CSR | Monthly; 1° covered period: 2002.04–2022.12 | [48] | ||
| JPL | Monthly; 0.5° covered period: 2002.04–2022.12 | [55] | ||
| GSFC | Monthly; 0.5° covered period: 2002.04–2022.12 | [47] | ||
| Vegetation | Normalized difference vegetation index (NDVI) | Monthly, 250 m | MOD13Q1 [50] | |
| Climate | Precipitation (PRE) | Monthly, 0.1° | TerraClimate [49] | |
| Potential Evapotranspiration (PET) | ||||
2.2.2. Theil–Sen Median Trend Analysis and Mann–Kendall (M–K) Test Statistics
2.2.3. Partial Correlation Coefficient
2.2.4. Attribution Analysis
2.2.5. Wavelet Coherence Analysis (WCA)
2.2.6. GRACE-Drought Severity Index (GRACE-DSI)
3. Results
3.1. Evaluation of TWSA Dataset Accuracy in the HDM Region
3.2. Spatiotemporal Changes in TWSA in the HDM Region
3.3. Spatiotemporal Variability of Driving Factors
3.4. Contribution of Each Driver to TWSAs and Dominant Factors
3.4.1. Correlation Analysis Between TWSAs and Regional Factors
3.4.2. Wavelet Coherence Between TWSAs and Global Environmental Factors
3.4.3. Relationships Between TWSAs and Regional and Global Drivers at Yearly and Seasonal Scales
3.4.4. Contribution of Driving Factors to TWSAs and Dominant Factors
3.5. Assessment of Wet–Dry Characteristics for TWSAs in the HDM Region
4. Discussion
4.1. Discrepancies and Concordance in GRACE-Derived TWSA Products in the HDM Region
4.2. Underlying Driving Mechanisms of TWSAs in the HDM Region
4.3. Uncertainties and Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef]
- Abbott, B.W.; Bishop, K.; Zarnetske, J.P.; Minaudo, C.; Chapin, F.S., III; Krause, S.; Hannah, D.M.; Conner, L.; Ellison, D.; Godsey, S.E.; et al. Human domination of the global water cycle absent from depictions and perceptions. Nat. Geosci. 2019, 12, 533–540. [Google Scholar] [CrossRef]
- Chao, N.; Jin, T.; Cai, Z.; Chen, G.; Liu, X.; Wang, Z.; Yeh, P.J. Estimation of component contributions to total terrestrial water storage change in the Yangtze river basin. J. Hydrol. 2021, 595, 125661. [Google Scholar] [CrossRef]
- Liu, M.; Pei, H.; Shen, Y. Evaluating dynamics of GRACE groundwater and its drought potential in Taihang Mountain Region, China. J. Hydrol. 2022, 612, 128156. [Google Scholar] [CrossRef]
- Wu, C.; Yeh, P.J.; Yao, T.; Gong, Z.; Niu, J.; Yuan, S. Controls of climate seasonality and vegetation dynamics on the seasonal variability of terrestrial water storage under diverse climate regimes. Water Resour. Res. 2025, 61, e2024WR038065. [Google Scholar] [CrossRef]
- Padrón, R.S.; Gudmundsson, L.; Decharme, B.; Ducharne, A.; Lawrence, D.M.; Mao, J.; Peano, D.; Krinner, G.; Kim, H.; Seneviratne, S.I. Observed changes in dry-season water availability attributed to human-induced climate change. Nat. Geosci. 2020, 13, 477–481. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Rateb, A.; Anyamba, A.; Kebede, S.; MacDonald, A.M.; Shamsudduha, M.; Small, J.; Sun, A.; Taylor, R.G.; Xie, H. Linkages between GRACE water storage, hydrologic extremes, and climate teleconnections in major African aquifers. Geophys. Res. Lett. 2022, 17, 014046. [Google Scholar] [CrossRef]
- Lu, J.; Kong, D.; Zhang, Y.; Xie, Y.; Gu, X.; Gulakhmadov, A. Hotspots of global water resource changes and their causes. Earths Future 2025, 13, e2024EF005461. [Google Scholar] [CrossRef]
- Ni, S.; Chen, J.; Wilson, C.R.; Li, J.; Hu, X.; Fu, R. Global terrestrial water storage changes and connections to ENSO events. Surv. Geophys. 2018, 39, 1–22. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Zhang, X.; Chen, Z. Spatiotemporal changes in China’s terrestrial water storage from GRACE satellites and its possible drivers. J. Geophys. Res. Atmos. 2019, 124, 11976–11993. [Google Scholar] [CrossRef]
- Liu, B.; Zou, X.; Yi, S.; Sneeuw, N.; Cai, J.; Li, J. Identifying and separating climate- and human-driven water storage anomalies using grace satellite data. Remote Sens. Environ. 2021, 263, 112559. [Google Scholar] [CrossRef]
- Swenson, S.; Yeh, P.J.F.; Wahr, J.; Famiglietti, J. A comparison of terrestrial water storage variations from GRACE with in situ measurements from Illinois. Geophys. Res. Lett. 2006, 33, L16401. [Google Scholar] [CrossRef]
- Hua, S.; Jing, H.; Qiu, G.; Kuang, X.; Andrews, C.B.; Chen, X.; Zheng, C. Long-term trends in human-induced water storage changes for China detected from GRACE data. J. Environ. Manag. 2024, 368, 122253. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Change 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.; Yang, H.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L.; Seneviratne, S.I. Assessing global water storage variability from GRACE: Trends, seasonal cycle, subseasonal anomalies and extremes. Surv. Geophys. 2016, 37, 357–395. [Google Scholar] [CrossRef]
- Ali, S.; Liu, D.; Fu, Q.; Cheema, M.J.; Pham, Q.B.; Rahaman, M.M.; Dang, D.D.; Anh, D.T. Improving the resolution of GRACE data for spatio-temporal groundwater storage assessment. Remote Sens. 2021, 13, 3513. [Google Scholar] [CrossRef]
- Nourani, V.; Paknezhad, N.J.; Ng, A.; Wen, Z.; Dabrowska, D.; Üzelaltınbulat, S. Application of the machine learning methods for GRACE data based groundwater modeling, a systematic review. Groundw. Sustain. Dev. 2024, 25, 101113. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, T.; Yin, W.; Bateni, S.M.; Jun, C.; Kim, D.; Liu, S.; Xu, Z.; Ming, W.; Wang, J. A machine learning downscaling framework based on a physically constrained sliding window technique for improving resolution of global water storage anomaly. Remote Sens. Environ. 2024, 313, 114359. [Google Scholar] [CrossRef]
- Chang, L.L.; Yuan, R.; Gupta, H.V.; Winter, L.; Niu, G. Why is the terrestrial water storage in dryland regions declining? A perspective based on gravity recovery and climate experiment satellite observations and Noah land surface model with multiparameterization schemes model simulations. Water Resour. Res. 2020, 56, e2020WR027102. [Google Scholar] [CrossRef]
- Mo, X.; Wu, J.; Wang, Q.; Zhou, H. Variations in water storage in China over recent decades from GRACE observations and GLDAS. Nat. Hazards Earth Syst. Sci. 2016, 16, 469–482. [Google Scholar] [CrossRef]
- Shi, X.; Wang, Y.; Mao, J.; Thornton, P.E.; Ricciuto, D.M.; Hoffman, F.M.; Hao, Y. Quantifying the long-term changes of terrestrial water storage and their driving factors. J. Hydrol. 2024, 635, 131096. [Google Scholar] [CrossRef]
- Trautmann, T.; Koirala, S.; Carvalhais, N.; Güntner, A.; Jung, M. The importance of vegetation in understanding terrestrial water storage variations. Hydrol. Earth Syst. Sci. 2022, 26, 1089–1109. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Save, H. Terrestrial water storage in 2024. Nat. Rev. Earth Environ. 2025, 6, 261–263. [Google Scholar] [CrossRef]
- Chen, A.; Xiong, J.; Wu, S.; Yang, Y. Changes in terrestrial water storage in the Three-North region of China over 2003–2021: Assessing the roles of climate and vegetation restoration. J. Hydrol. 2024, 637, 131303. [Google Scholar] [CrossRef]
- Meng, F.; Su, F.; Li, Y.; Tong, K. Changes in terrestrial water storage during 2003–2014 and possible causes in Tibetan Plateau. J. Geophys. Res. Atmos. 2019, 124, 2909–2931. [Google Scholar] [CrossRef]
- Xu, G.; Wu, Y.; Liu, S.; Chen, S.; Zhang, Y.; Pan, Y.; Wang, L.; Dokuchits, E.Y.; Nkwazema, O.C. How 2022 extreme drought influences the spatiotemporal variations of terrestrial water storage in the Yangtze River Catchment: Insights from GRACE-based drought severity index and in-situ measurements. J. Hydrol. 2023, 626, 130245. [Google Scholar] [CrossRef]
- Shen, X.; Niu, L.; Jia, X.; Yang, T.; Hu, W.; Chu, J.; Biswas, A.; Shao, M. Disentangling ecological restoration’s impact on terrestrial water storage. Geophys. Res. Lett. 2025, 52, e2024GL111669. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Hu, Q.; Liu, J. Responses of terrestrial water storage to climate variation in the Tibetan Plateau. J. Hydrol. 2020, 584, 124652. [Google Scholar] [CrossRef]
- Nie, N.; Zhang, W.; Chen, H.; Guo, H. A Global Hydrological Drought Index Dataset Based on Gravity Recovery and Climate Experiment (GRACE) Data. Water Resour Manag. 2018, 32, 1275–1290. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, X.; Xu, Y.; Li, C.; Zhang, X.; Wang, X. Characteristics of groundwater drought and its correlation with meteorological and agricultural drought over the North China Plain based on GRACE. Ecol. Indic. 2024, 161, 111925. [Google Scholar] [CrossRef]
- Zhao, J.; Li, G.; Zhu, Z.; Hao, Y.; Hao, H.; Yao, J.; Bao, T.; Liu, Q.; Yeh, T.J. Analysis of the spatiotemporal variation of groundwater storage in Ordos Basin based on GRACE gravity satellite data. J. Hydrol. 2024, 632, 130931. [Google Scholar] [CrossRef]
- Awange, J.L.; Forootan, E.; Kuhn, M.; Kusche, J.; Hech, B. Water storage changes and climate variability within the Nile Basin between 2002 and 2011. Adv. Water Resour. 2014, 73, 1–15. [Google Scholar] [CrossRef]
- Guo, L.; Li, T.; Chen, D.; Liu, J.; He, B.; Zhang, Y. Links between global terrestrial water storage and large-scale modes of climatic variability. J. Hydrol. 2021, 598, 126419. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Fakhreddine, S.; Rateb, A.; Graaf, I.; Famiglietti, J.; Gleeson, T.; Grafton, R.Q.; Jobbagy, E.; Kebede, S.; Kolusu, S.R.; et al. Global water resources and the role of groundwater in a resilient water future. Nat. Rev. Earth Environ. 2023, 4, 87–101. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Zhang, Y.; Li, X.; Huang, W. Drought variability at various timescales over Yunnan Province, China: 1961–2015. Theor. Appl. Climatol. 2019, 138, 743–757. [Google Scholar] [CrossRef]
- Cheng, Q.; Gao, L.; Zhong, F.; Zuo, X.; Ma, M. Spatiotemporal variations of drought in the Yunnan-Guizhou Plateau, southwest China, during 1960–2013 and their association with large-scale circulations and historical records. Ecol. Indic. 2020, 112, 106041. [Google Scholar] [CrossRef]
- Yang, W.; Jin, F.; Si, Y.; Li, Z. Runoff change controlled by combined effects of multiple environmental factors in a headwater catchment with cold and arid climate in northwest China. Sci. Total Environ. 2021, 756, 143995. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, W.; Nie, N.; Guo, Y. Long-term groundwater storage variations estimated in the Songhua River Basin by using GRACE products, land surface models, and in-situ observations. Sci. Total Environ. 2019, 649, 372–387. [Google Scholar] [CrossRef]
- Yang, S.; Zhong, Y.; Wu, Y.; Yang, K.; An, Q.; Bai, H.; Liu, S. Quantifying long-term drought in China’s exorheic basins using a novel daily GRACE reconstructed TWSA index. J. Hydrol. 2025, 655, 132919. [Google Scholar] [CrossRef]
- Thomas, B.F.; Famiglietti, J.S.; Landerer, F.W.; Wiese, D.N.; Molotch, N.P.; Argus, D.F. GRACE groundwater drought index: Evaluation of California Central Valley groundwater drought. Remote Sens. Environ. 2017, 198, 384–392. [Google Scholar] [CrossRef]
- Shi, S.; Liu, G.; Li, Z.; Ye, X. Elevation-dependent growth trends of forests as affected by climate warming in the southeastern Tibetan Plateau. For. Ecol. Manag. 2021, 498, 119551. [Google Scholar] [CrossRef]
- Zhong, X.H.; Liu, S.Z. Theoryand Practice of Mountain Environment; Science Press: Beijing, China, 2015; pp. 163–174. [Google Scholar]
- Yang, J.; Dai, J.; Yao, H.; Tao, Z.; Zhu, M. Vegetation distribution and vegetation activity changes in the Hengduan Mountains from 1992 to 2020. Acta Geogr. Sin. 2022, 77, 2787–2802. [Google Scholar]
- Lu, E.; Luo, Y.; Zhang, R.; Wu, Q.; Liu, L. Regional atmospheric anomalies responsible for the 2009–2010 severe drought in China. J. Geophys. Res. Atmos. 2011, 116, D21114. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Loomis, B.D.; Luthcke, S.B.; Sabaka, T.J. Regularization and error characterization of GRACE mascons. J. Geod. 2019, 93, 1381–1398. [Google Scholar] [CrossRef] [PubMed]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef]
- Gao, J.; Shi, Y.; Zhang, H.; Shen, W.; Xiao, T.; Zhang, Y. China Regional 250 m Normalized Difference Vegetation Index Data Set (2000–2022); National Tibetan Plateau/Third Pole Environment Data Center: Beijing, China, 2023. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, S.; Huang, Q.; Leng, G.; Wang, H.; Li, P. Watershed water-energy balance dynamics and their association with diverse influencing factors at multiple time scales. Sci. Total Environ. 2020, 711, 135189. [Google Scholar] [CrossRef]
- Li, B.; Yang, Y.; Li, Z. Combined effects of multiple factors on spatiotemporally varied soil moisture in China’s Loess Plateau. Agric. Water Manag. 2021, 258, 107180. [Google Scholar] [CrossRef]
- Zuo, J.; Ren, H.; Li, W.; Wang, L. Interdecadal Variations in the Relationship between the Winter North Atlantic Oscillation and Temperature in South-Central China. J. Clim. 2016, 29, 7477–7493. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1080. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Wang, F.; Lai, H.; Li, Y.; Feng, K.; Tian, Q.; Guo, W.; Qu, Y.; Yang, H. Spatio-temporal evolution and teleconnection factor analysis of groundwater drought based on the GRACE mascon model in the Yellow River Basin. J. Hydrol. 2023, 626, 130349. [Google Scholar] [CrossRef]
- Yang, B.; Li, Y.; Tao, C.; Cui, C.; Hu, F.; Cui, Q.; Meng, L.; Zhang, W. Variations and drivers of terrestrial water storage in ten basins of China. J. Hydrol. Reg. Stud. 2023, 45, 101286. [Google Scholar] [CrossRef]
- Gan, T.Y.; Gobena, A.K.; Wang, Q. Precipitation of southwestern Canada: Wavelet, scaling, multifractal analysis, and teleconnection to climate anomalies. J. Geophys. Res. Atmos. 2007, 112, D10110. [Google Scholar] [CrossRef]
- Zhao, M.; Geruo, A.; Velicogna, I.; Kimball, J.S. Satellite observations of regional drought severity in the continental united states using grace-based terrestrial water storage changes. J. Clim. 2017, 30, 6297–6308. [Google Scholar] [CrossRef]
- Yoshe, A.K. Water availability identification from GRACE dataset and GLDAS hydrological model over data-scarce river basins of Ethiopia. Hydrol. Sci. J. 2024, 69, 721–745. [Google Scholar] [CrossRef]
- Rzepecka, Z.; Birylo, M.; Jarsjö, J.; Cao, F.; Pietroń, J. Groundwater Storage Variations across Climate Zones from Southern Poland to Arctic Sweden: Comparing GRACE-GLDAS Models with Well Data. Remote Sens. 2024, 16, 2104. [Google Scholar] [CrossRef]
- Cho, Y. Analysis of terrestrial water storage variations in South Korea using GRACE satellite and GLDAS data in Google Earth Engine. Hydrol. Sci. J. 2024, 69, 1032–1045. [Google Scholar] [CrossRef]
- Rana, S.K.; Chamoli, A. GRACE-derived groundwater variability and its resilience in north India: Impact of climatic and socioeconomic factors. Hydrol. Sci. J. 2024, 69, 2159–2171. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W.; Zhou, W.; Huang, G. Understanding and detecting super-extreme droughts in Southwest China through an integrated approach and index. Q. J. R. Meteorol. Soc. 2015, 142, 529–535. [Google Scholar] [CrossRef]
- Deng, H.; Pepin, N.C.; Liu, Q.; Chen, Y. Understanding the spatial differences in terrestrial water storage variations in the Tibetan Plateau from 2002 to 2016. Clim. Change 2018, 151, 379–393. [Google Scholar] [CrossRef]
- Boulahia, A.K.; García-García, D.; Trottini, M.; Sayol, J.-M.; Vigo, M.I. Hydrological Cycle in the Arabian Sea Region from GRACE/GRACE-FO Missions and ERA5 Data. Remote Sens. 2024, 16, 3577. [Google Scholar] [CrossRef]
- Dash, P.; Shekhar, S.; Paul, V.; Feng, G. Influence of Land Use and Land Cover Changes and Precipitation Patterns on Groundwater Storage in the Mississippi River Watershed: Insights from GRACE Satellite Data. Remote Sens. 2024, 16, 4285. [Google Scholar] [CrossRef]
- Cook, B.I.; Smerdon, J.E.; Seager, R.; Coats, S. Global warming and 21st century drying. Clim. Dyn. 2014, 43, 2607–2627. [Google Scholar] [CrossRef]
- Chen, X.; Su, Y.; Liao, J.; Shang, J.; Dong, T.; Wang, C.; Liu, W.; Zhou, G.; Liu, L. Detecting significant decreasing trends of land surface soil moisture in eastern China during the past three decades (1979–2010). Geophys. Res. Atmos. 2016, 121, 5177–5192. [Google Scholar] [CrossRef]
- Wang, C.; Cui, A.; Ji, R.; Huang, S.; Li, P.; Chen, N.; Shao, Z. Spatiotemporal Responses of Global Vegetation Growth to Terrestrial Water Storage. Remote Sens. 2025, 17, 1701. [Google Scholar] [CrossRef]
- Wei, Z.; Wan, X. Spatial and temporal characteristics of NDVI in the Weihe River Basin and its correlation with terrestrial water storage. Remote Sens. 2022, 14, 5532. [Google Scholar] [CrossRef]
- Zeng, Z.; Piao, S.; Li, L.Z.; Wang, T.; Ciais, P.; Lian, X.; Yang, Y.; Mao, J.; Shi, X.; Myneni, R.B. Impact of earth greening on the terrestrial water cycle. J. Clim. 2018, 31, 2633–2650. [Google Scholar] [CrossRef]
- Pereira, A.; Cornero, C.; Oliveira Cancoro de Matos, A.C.; Seoane, R.; Pacino, M.C.; Blitzkow, D. Assessing water storage variations in La Plata basin and sub-basins from GRACE, global models data and connection with ENSO events. Hydrol. Sci. J. 2024, 69, 1012–1031. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]


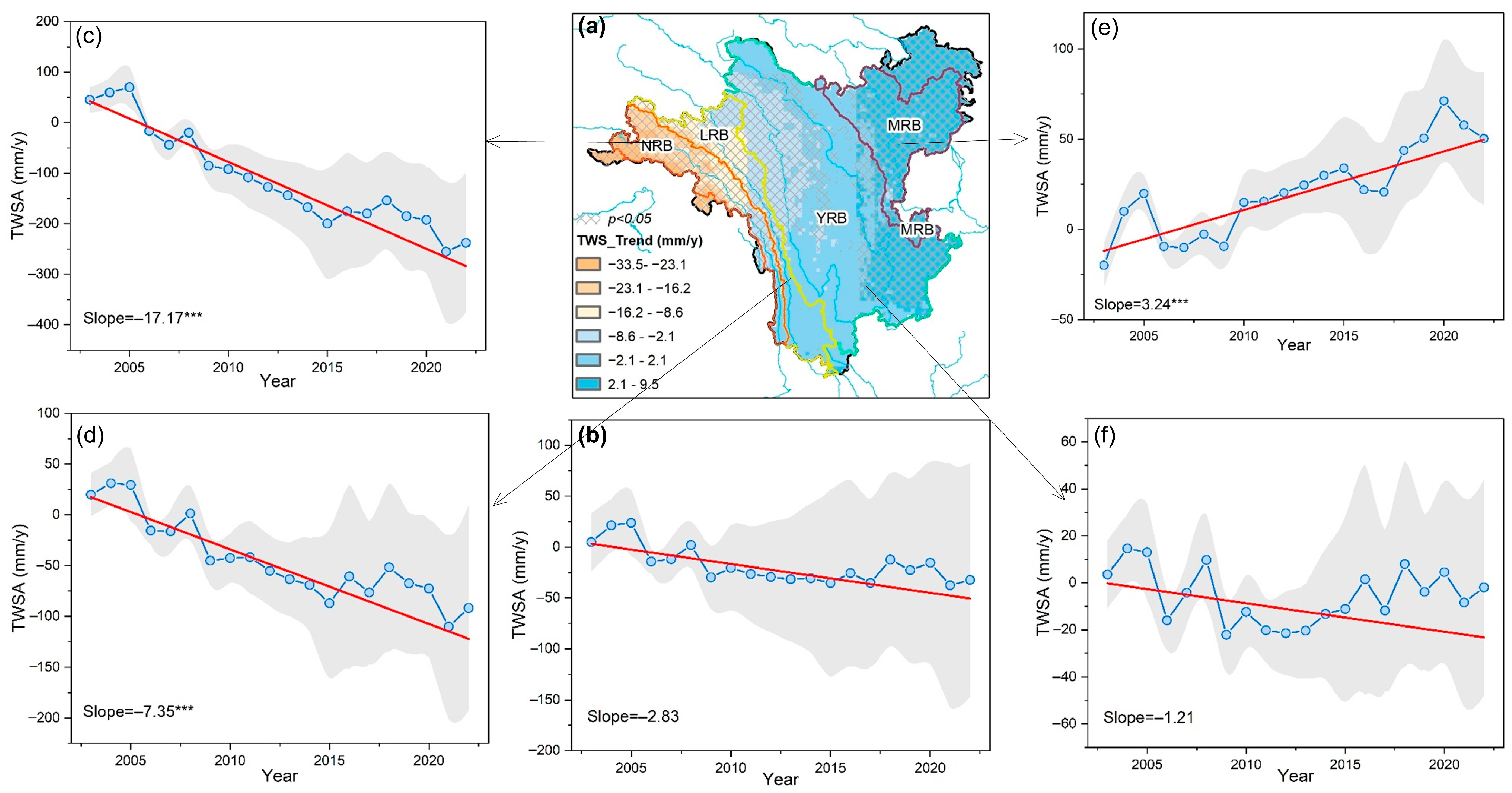



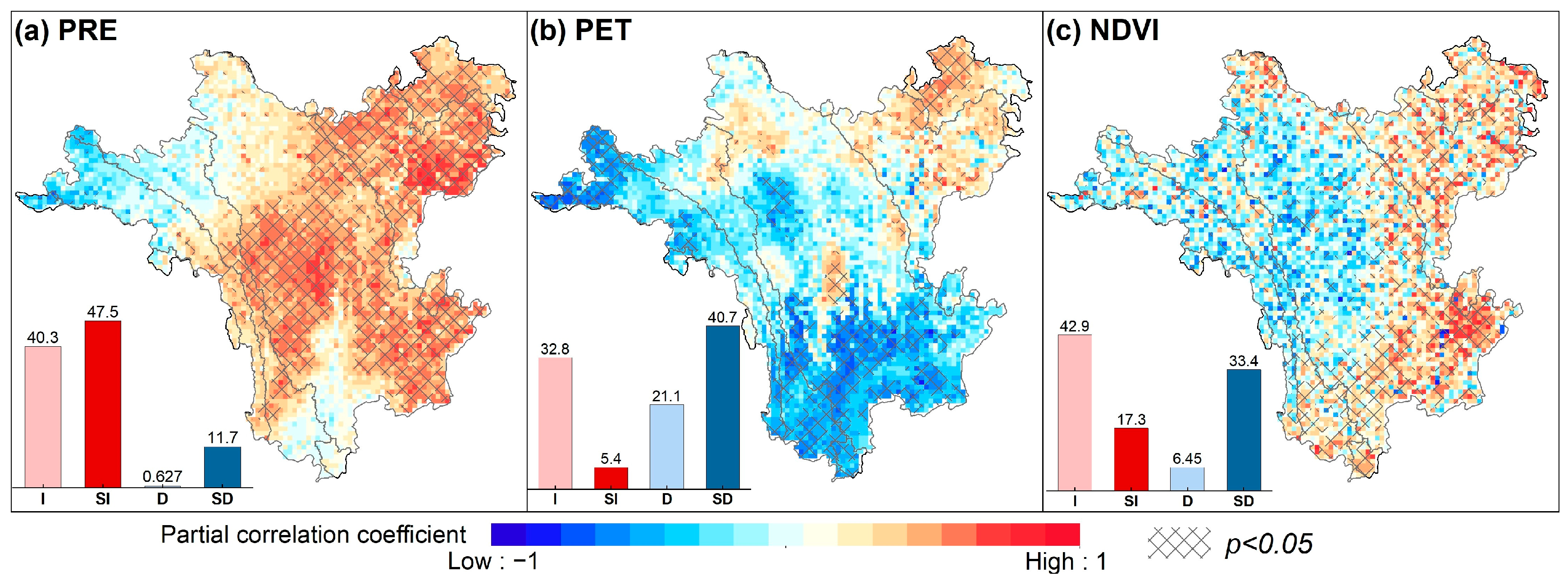


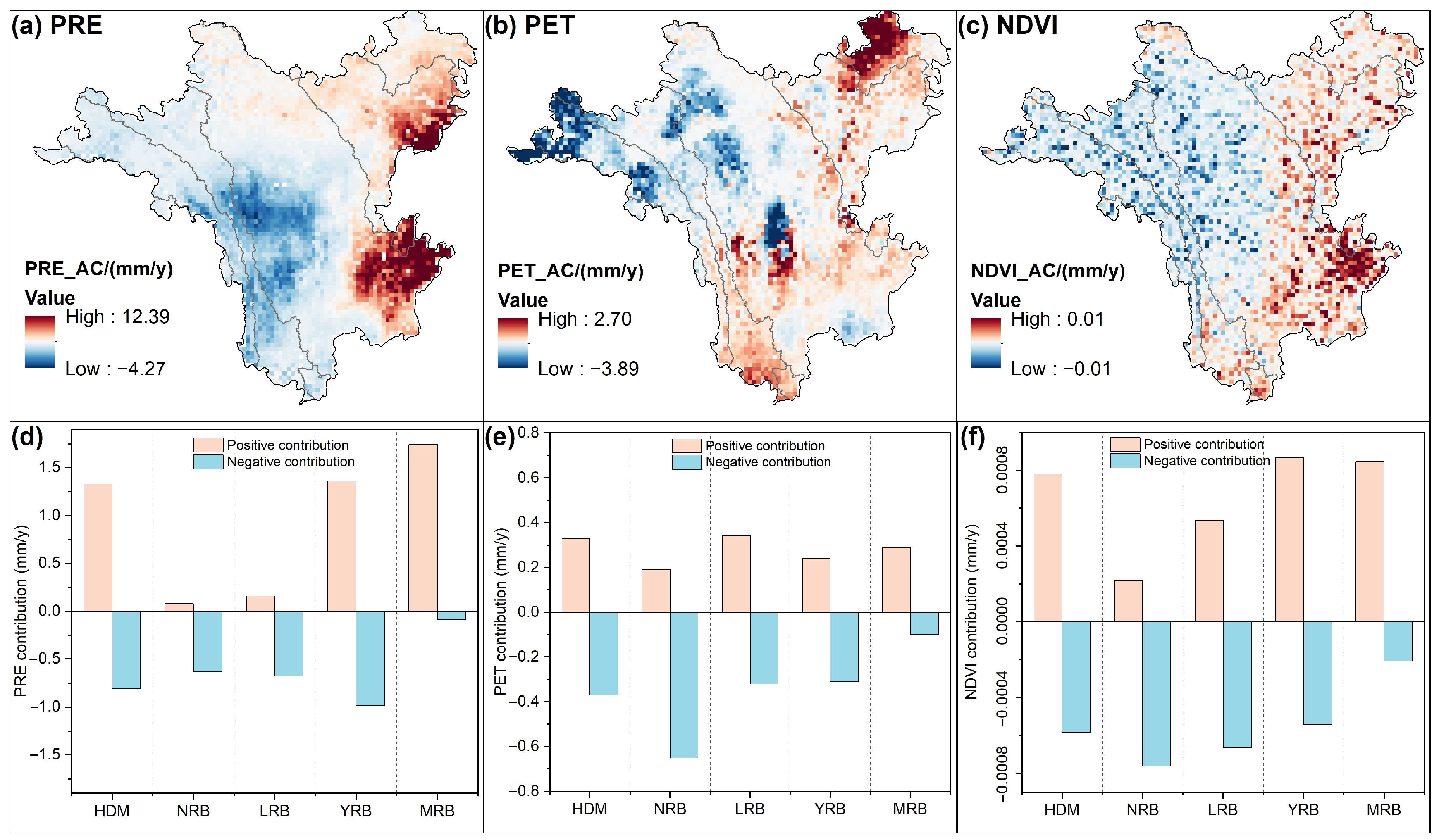
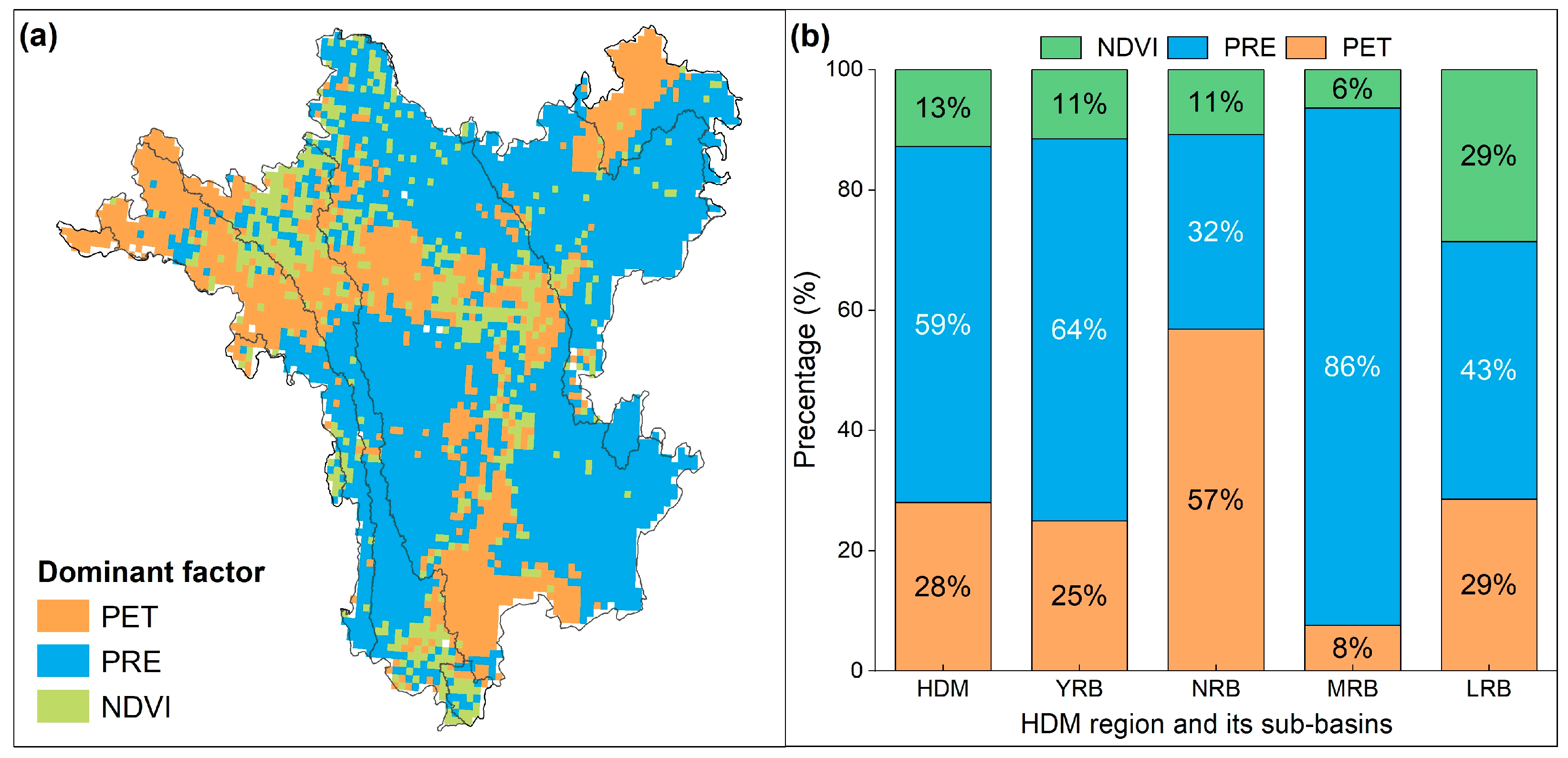
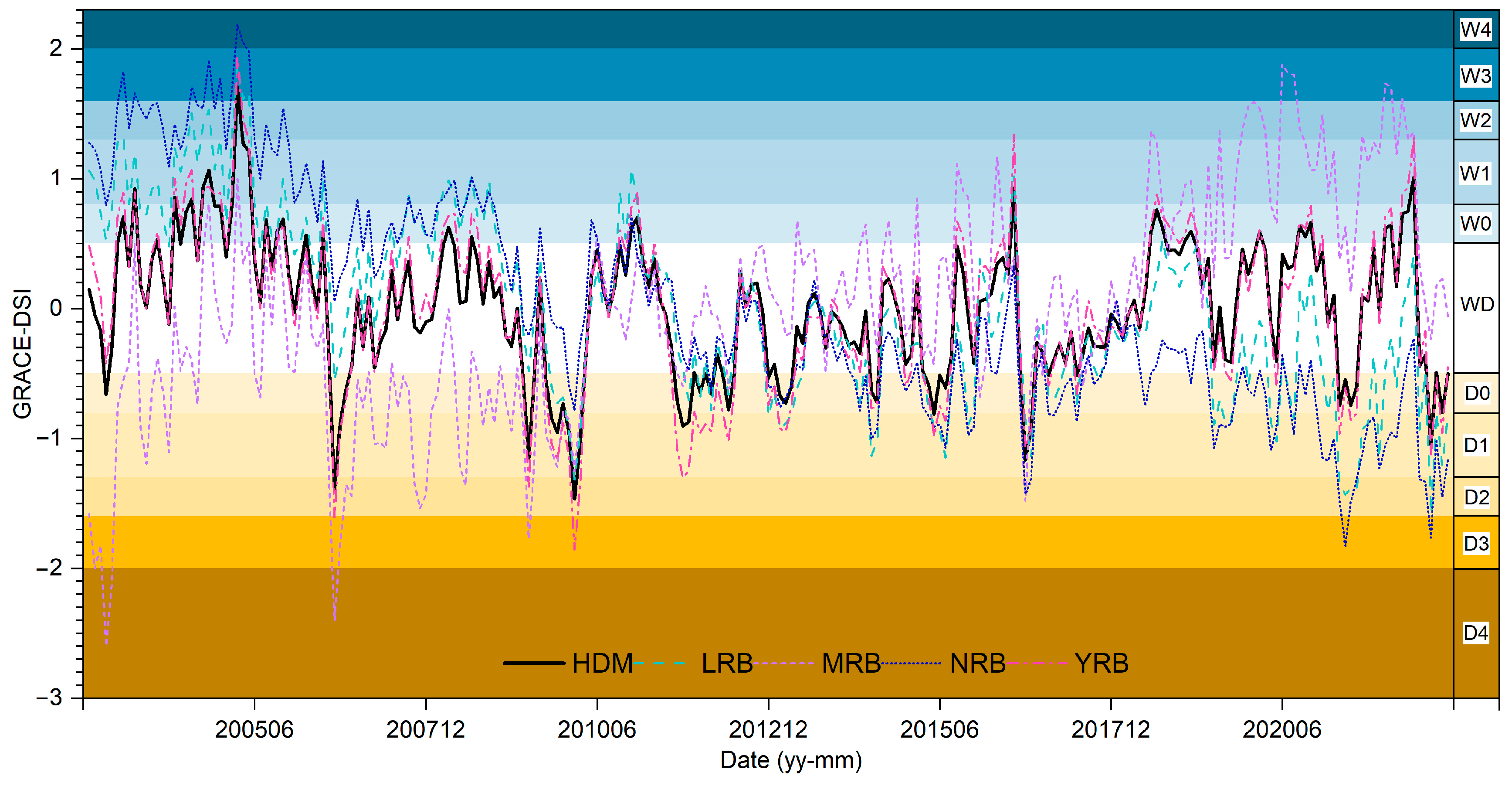
| Category | Description | GRACE-DSI | Category | Description | GRACE-DSI |
|---|---|---|---|---|---|
| W4 | Exceptionally wet | ≥2.0 | D0 | Abnormally dry | −0.50–−0.79 |
| W3 | Extremely wet | 1.60–1.99 | D1 | Moderate drought | −0.80–−1.29 |
| W2 | Very wet | 1.30–1.59 | D2 | Severe drought | −1.30–−1.59 |
| W1 | Moderately wet | 0.80–1.29 | D3 | Extreme drought | −1.60–−1.99 |
| W0 | Slightly wet | 0.50–0.79 | D4 | Exceptional drought | ≤−2.0 |
| WD | Near normal | 0.49–0.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Xue, Y.; Wu, D.; Tan, S.; Cao, X.; Zhao, W. Precipitation Governs Terrestrial Water Storage Anomaly Decline in the Hengduan Mountains Region, China, Amid Climate Change. Remote Sens. 2025, 17, 2447. https://doi.org/10.3390/rs17142447
Li X, Xue Y, Wu D, Tan S, Cao X, Zhao W. Precipitation Governs Terrestrial Water Storage Anomaly Decline in the Hengduan Mountains Region, China, Amid Climate Change. Remote Sensing. 2025; 17(14):2447. https://doi.org/10.3390/rs17142447
Chicago/Turabian StyleLi, Xuliang, Yayong Xue, Di Wu, Shaojun Tan, Xue Cao, and Wusheng Zhao. 2025. "Precipitation Governs Terrestrial Water Storage Anomaly Decline in the Hengduan Mountains Region, China, Amid Climate Change" Remote Sensing 17, no. 14: 2447. https://doi.org/10.3390/rs17142447
APA StyleLi, X., Xue, Y., Wu, D., Tan, S., Cao, X., & Zhao, W. (2025). Precipitation Governs Terrestrial Water Storage Anomaly Decline in the Hengduan Mountains Region, China, Amid Climate Change. Remote Sensing, 17(14), 2447. https://doi.org/10.3390/rs17142447







