Surface Reconstruction Planning with High-Quality Satellite Stereo Pairs Searching
Abstract
1. Introduction
- A regression method is customized to provide accurate estimation of DSM quality using real reconstructed point cloud geopositioning errors for training. Feature enhancement and selection are applied to retain key factors that contribute significantly to the quality prediction.
- Multi-objective satellite image acquisition planning is modeled to maximize the 3D reconstruction quality while balancing with task quantity and timeliness, which is NP-hard and solved efficiently with constrained optimization algorithms.
- The orbits of satellite WorldView-3 and its constellation are both simulated and aligned with the real stereo image dataset to form a comprehensive dataset for quality-driven stereo sensing task planning evaluation, which is to be released to the community.
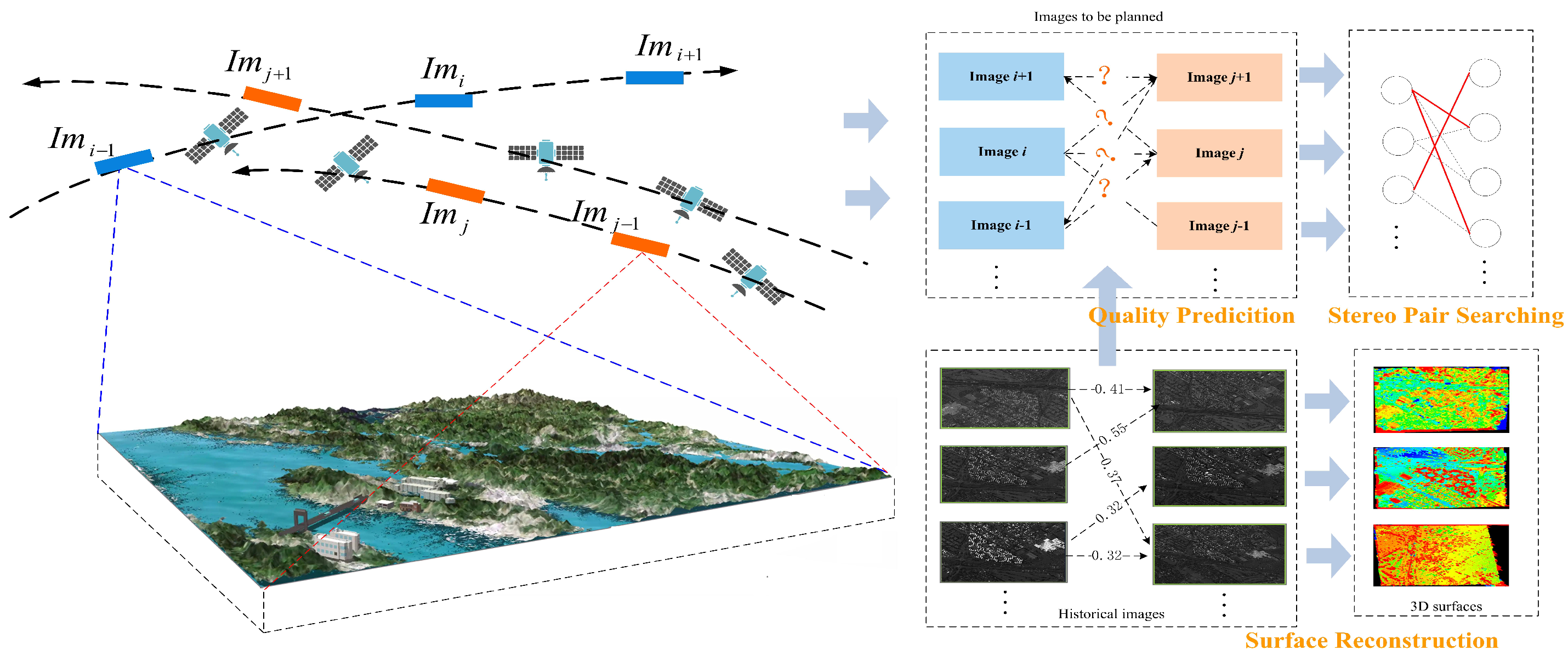
2. Motivation and Method Overview
2.1. Surface Reconstruction Planning Description
2.2. Framework of Quality-Driven Stereo Planning Algorithm
3. Quality Estimation of Earth Surface Reconstruction
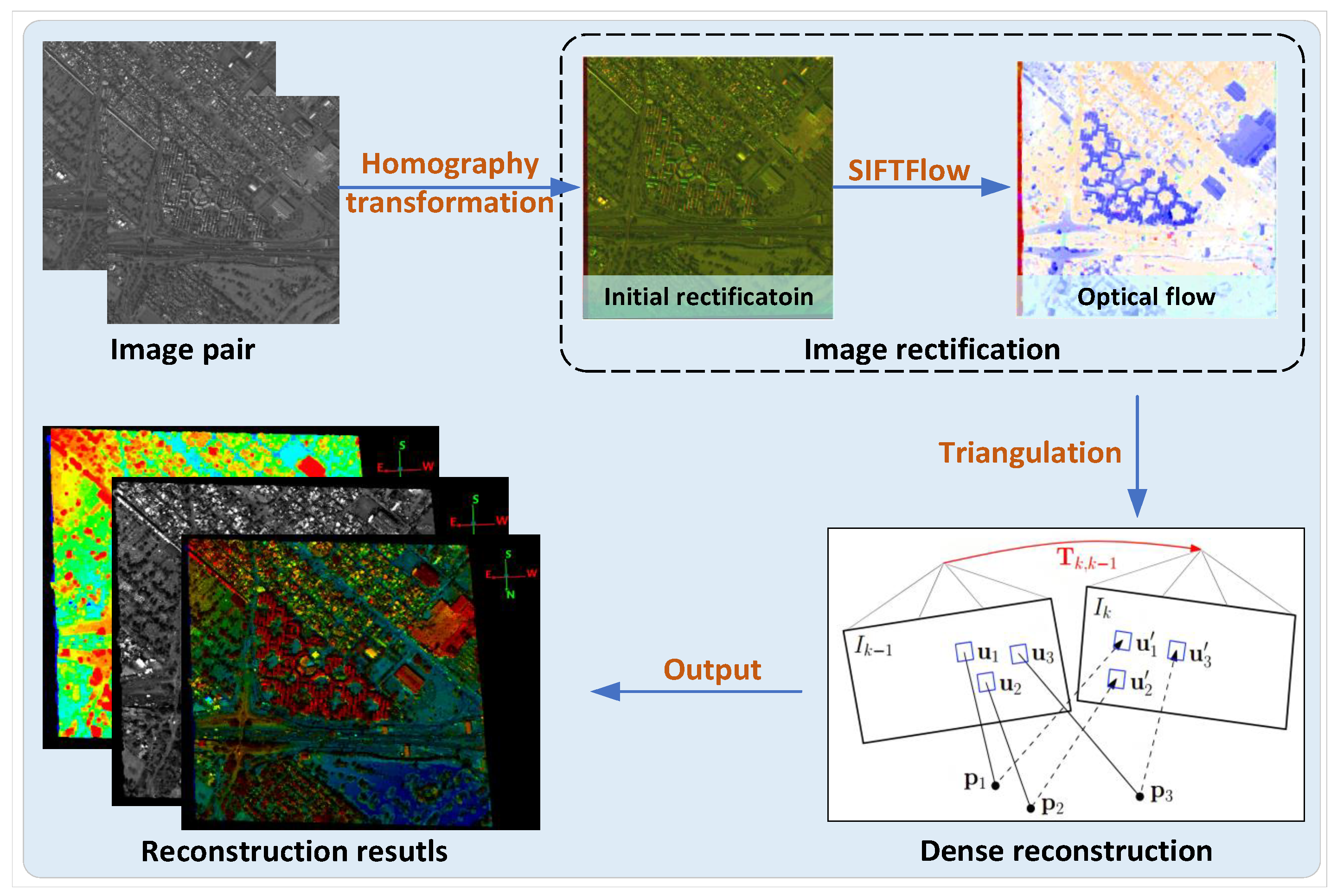
3.1. Earth Surface 3D Reconstruction
3.2. Regression Model for Quality Estimation
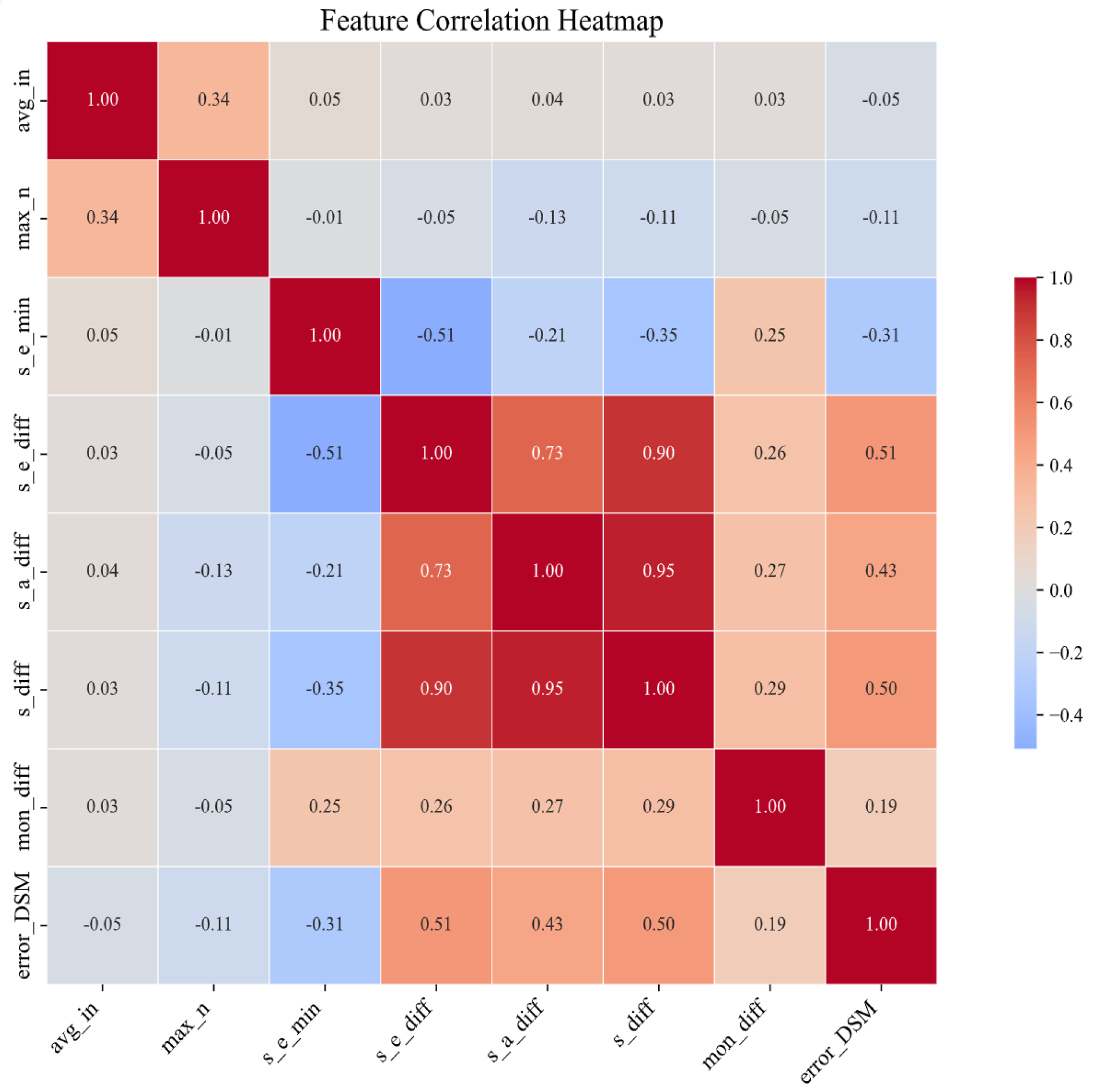
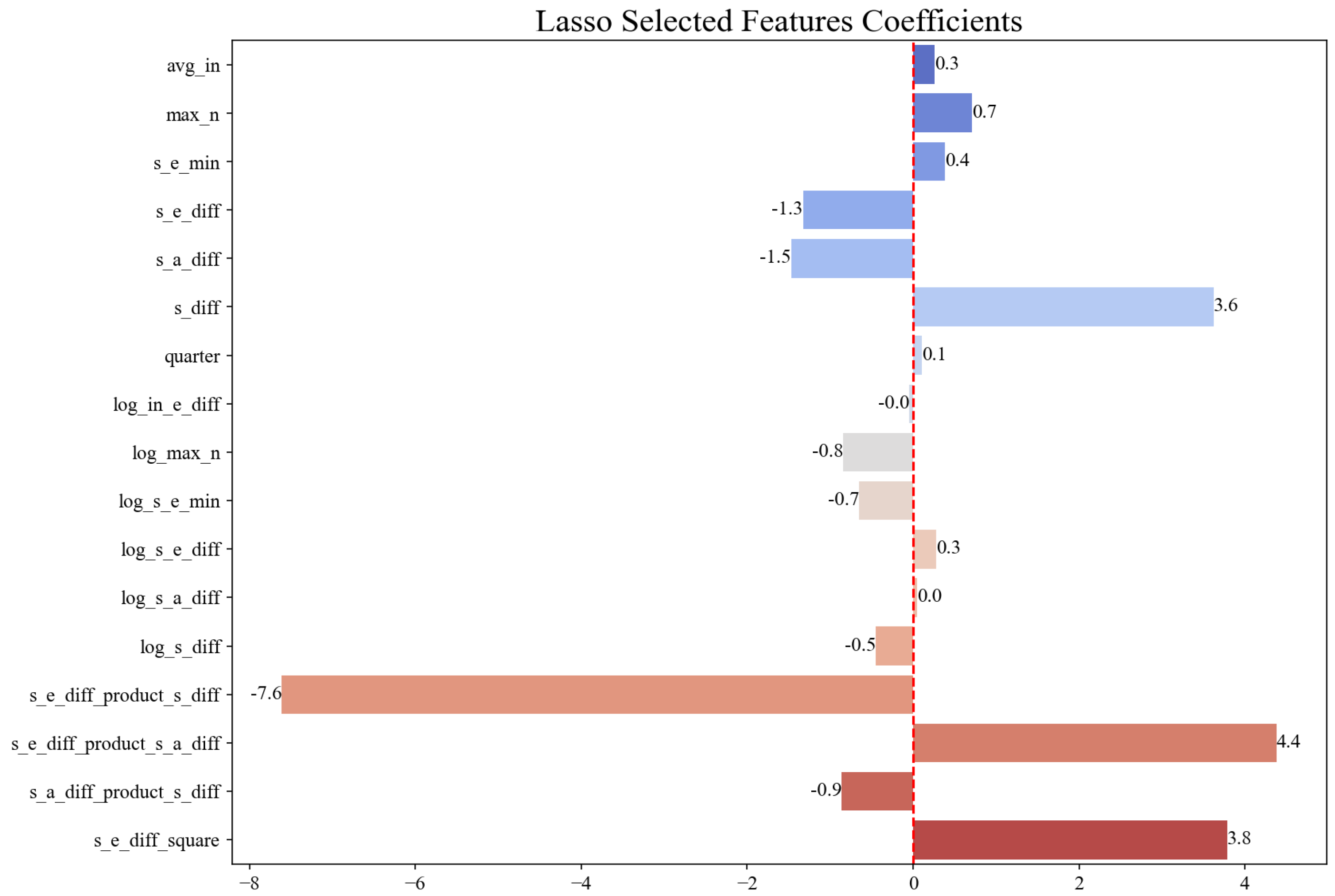
3.2.1. Selection for High-Dimensional Features
3.2.2. CatBoost Parameter Tuning
3.2.3. Evaluation Metrics
4. High-Quality DSM with Stereo Pairs Searching
4.1. Quality-Driven Planning Model of Stereo Sensing
4.2. Searching for Optimized Stereo Pairs
5. Experiments and Evaluation
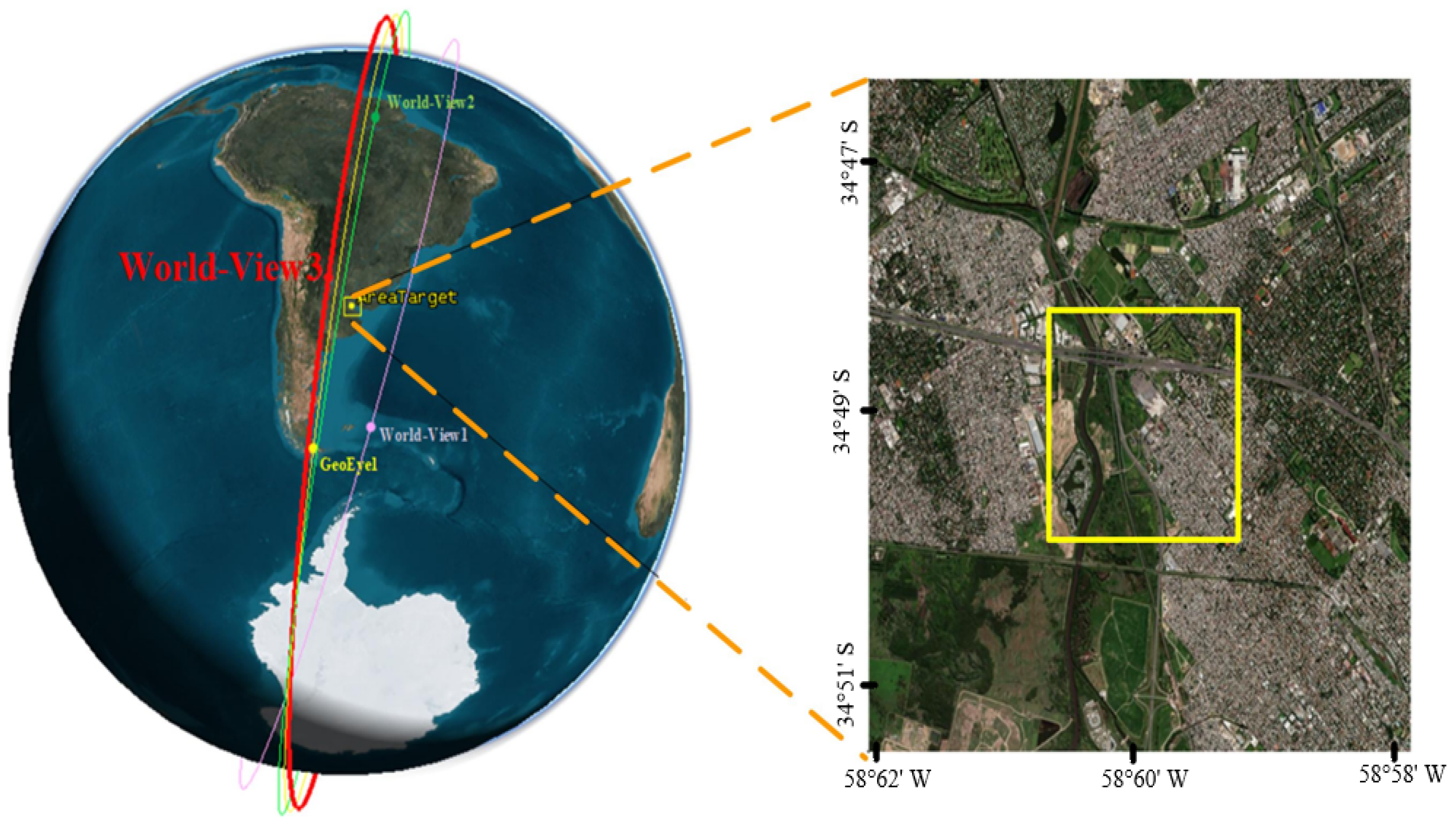
5.1. Experiment Settings
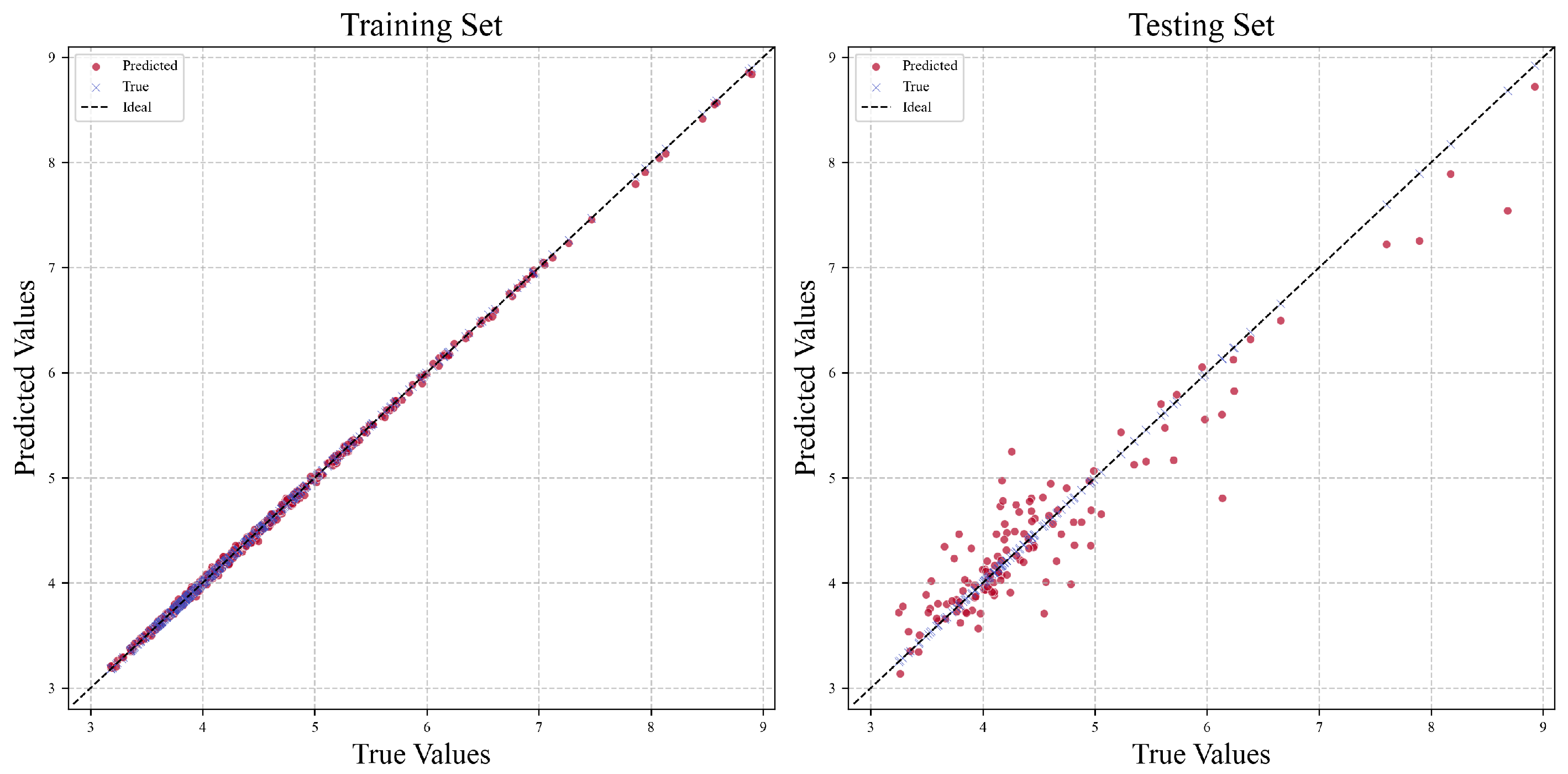
5.2. Evaluation on Surface Reconstruction Quality Estimation
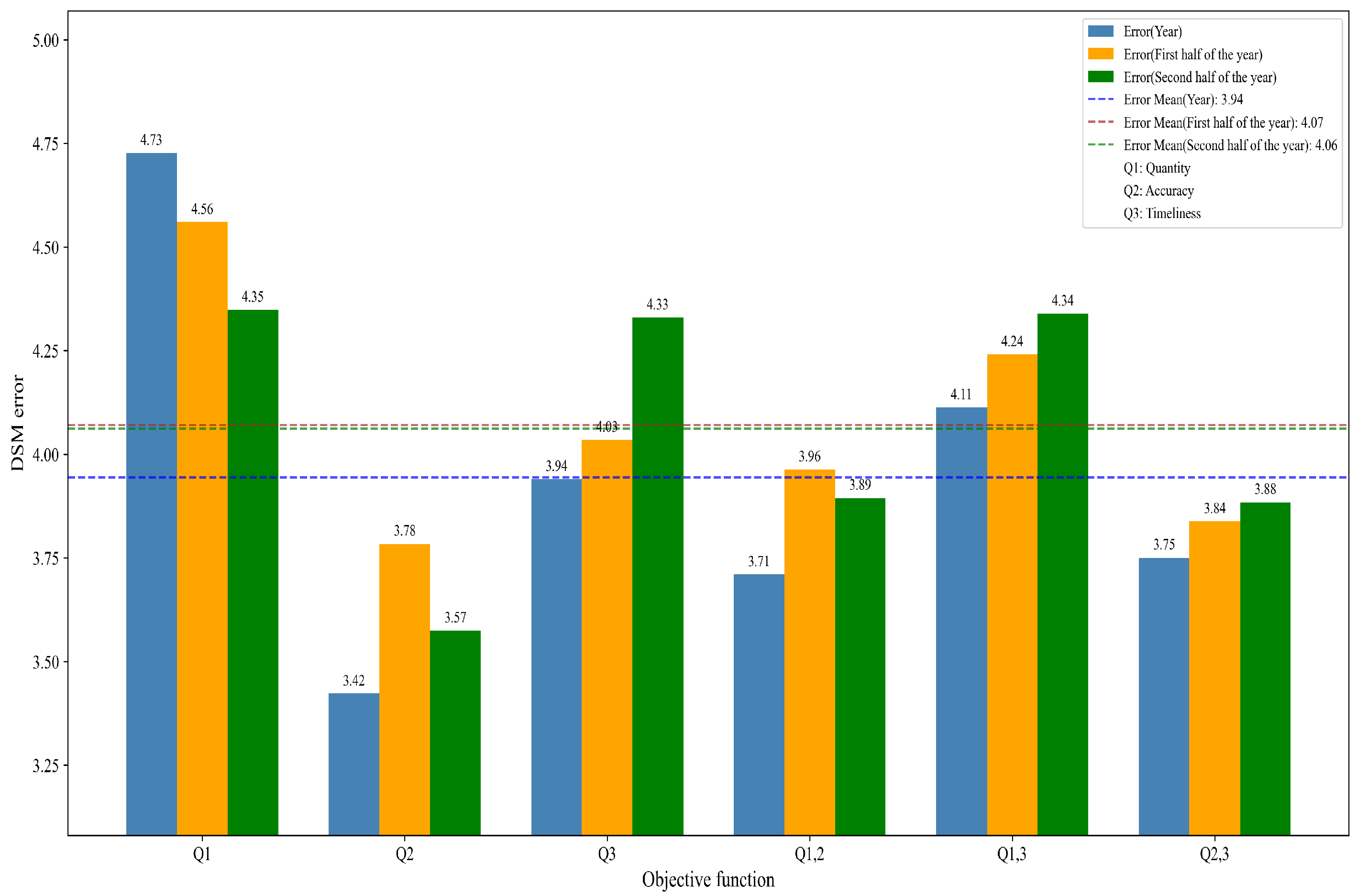
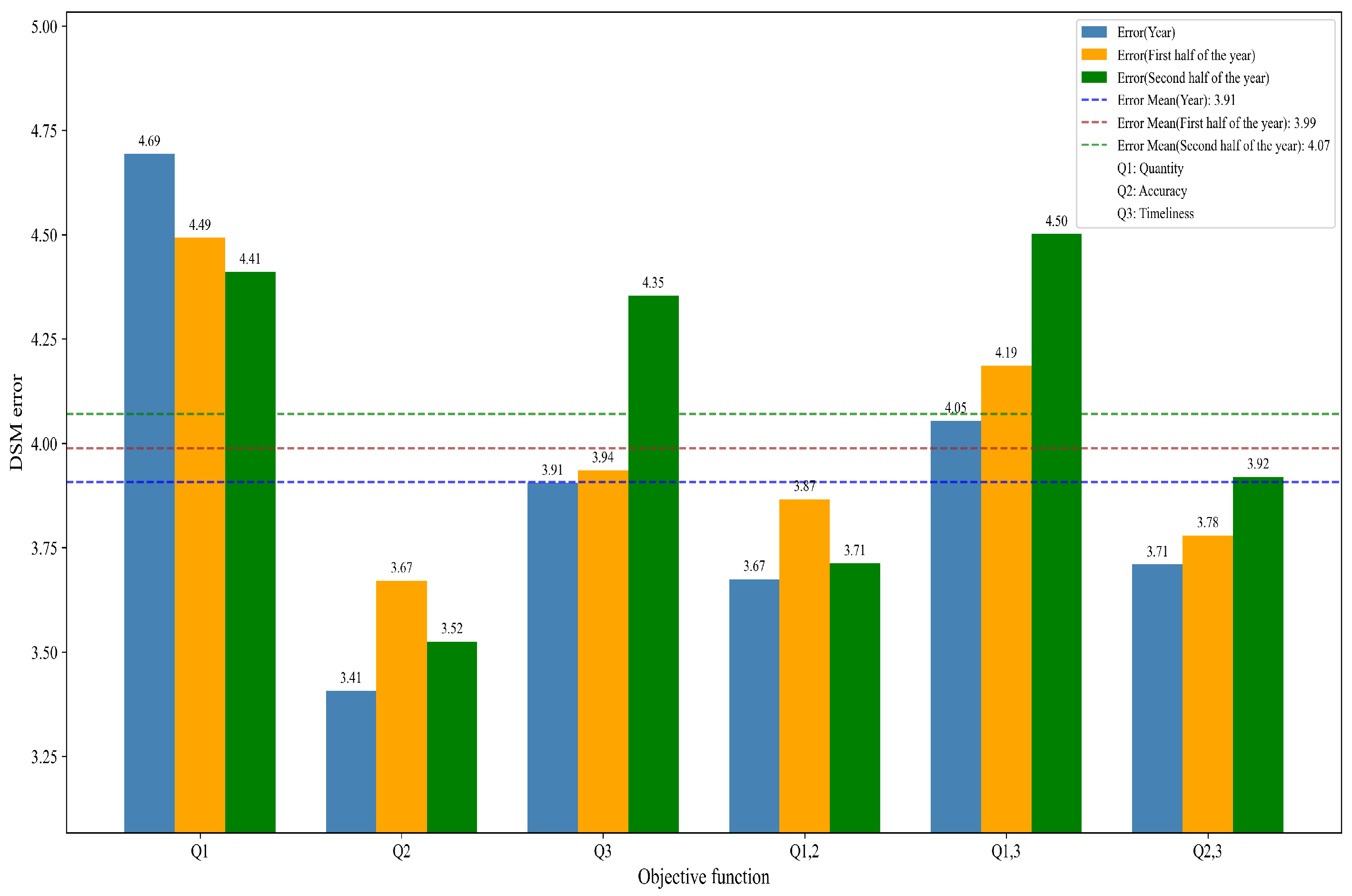
5.3. Evaluation on Planning Using Single Satellite
6. Discussion
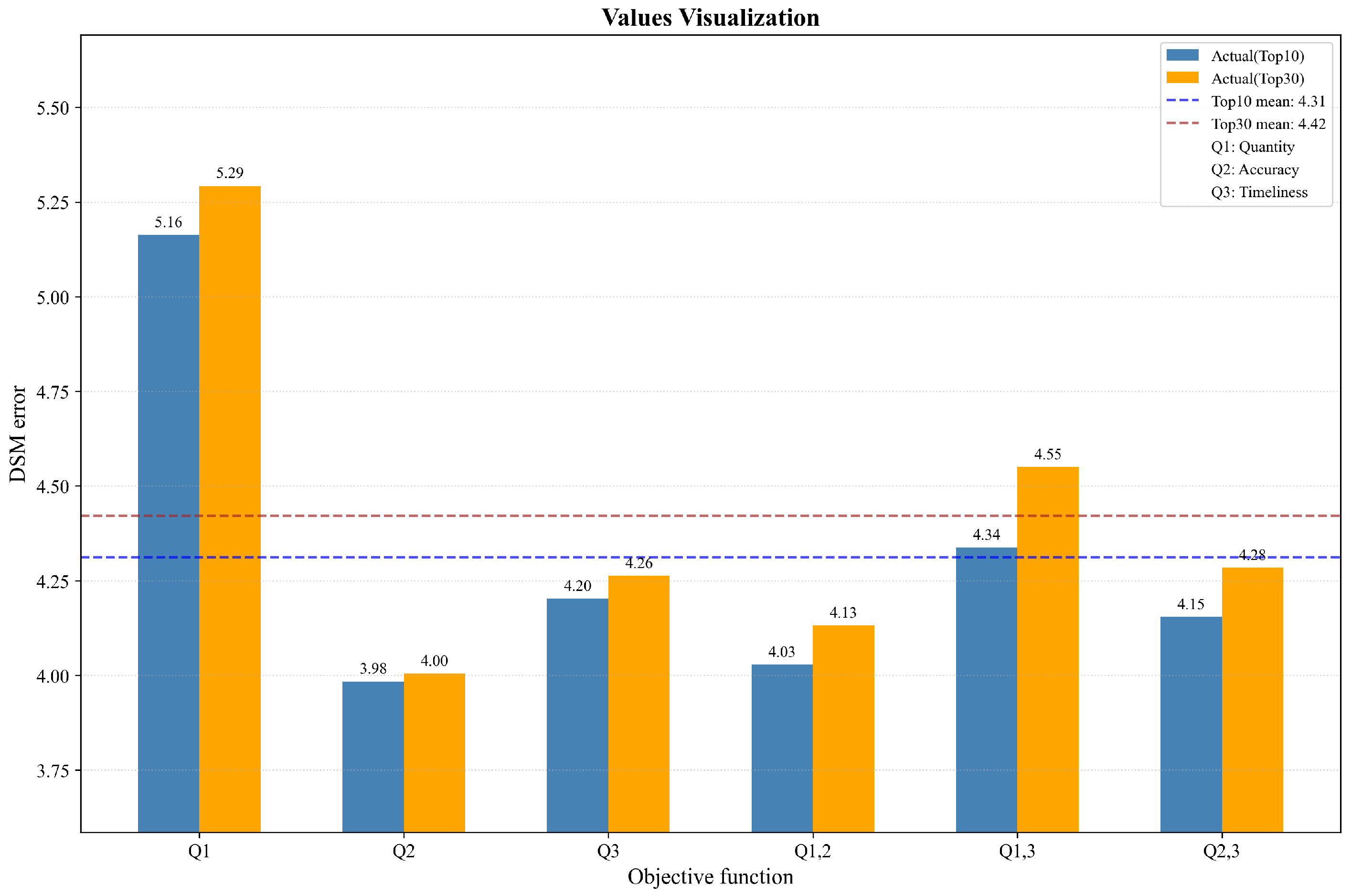
6.1. Quality Comparison Using Real Images
6.2. Further Planning Using Simulated Constellation
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, K.; Snavely, N.; Sun, J. Leveraging vision reconstruction pipelines for satellite imagery. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27–28 October 2019. [Google Scholar]
- Bosch, M.; Kurtz, Z.; Hagstrom, S.; Brown, M. A multiple view stereo benchmark for satellite imagery. In Proceedings of the 2016 IEEE Applied Imagery Pattern Recognition Workshop (AIPR), Washington, DC, USA, 18–20 October 2016; pp. 1–9. [Google Scholar]
- Beyer, R.A.; Alexandrov, O.; McMichael, S. The Ames Stereo Pipeline: NASA’s open source software for deriving and processing terrain data. Earth Space Sci. 2018, 5, 537–548. [Google Scholar] [CrossRef]
- Wang, P.; Shi, L.; Chen, B.; Hu, Z.; Qiao, J.; Dong, Q. Pursuing 3-D scene structures with optical satellite images from affine reconstruction to Euclidean reconstruction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5632214. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, Y.; Men, C.; Men, Y. Double propagation stereo matching for urban 3-d reconstruction from satellite imagery. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5601717. [Google Scholar] [CrossRef]
- Yang, S.; Chen, H.; Chen, W. Generalized Stereo Matching Method Based on Iterative Optimization of Hierarchical Graph Structure Consistency Cost for Urban 3D Reconstruction. Remote Sens. 2023, 15, 2369. [Google Scholar] [CrossRef]
- Orsingher, M.; Zani, P.; Medici, P.; Bertozzi, M. Revisiting PatchMatch multi-view stereo for urban 3D reconstruction. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 4–9 June 2022; pp. 190–196. [Google Scholar]
- Stucker, C.; Schindler, K. ResDepth: A deep residual prior for 3D reconstruction from high-resolution satellite images. ISPRS J. Photogramm. Remote Sens. 2022, 183, 560–580. [Google Scholar] [CrossRef]
- Oh, J.; Lee, W.H.; Toth, C.K.; Grejner-Brzezinska, D.A.; Lee, C. A Piecewise Approach to Epipolar Resampling of Pushbroom Satellite Images Based on RPC. Photogramm. Eng. Remote Sens. 2010, 76, 1353–1363. [Google Scholar] [CrossRef]
- Carl, S.; Bärisch, S.; Lang, F.; d’Angelo, P.; Arefi, H.; Reinartz, P. Operational Generation of High-Resolution Digital Surface Models from Commercial Tri-Stereo Satellite Data. Photogramm. Week 2013, 13, 261–269. [Google Scholar]
- D’Angelo, P.; Rossi, C.; Minet, C.; Eineder, M.; Flory, M.; Niemeyer, I. High Resolution 3D Earth Observation Data Analysis for Safeguards Activities. In Proceedings of the 12th Symposium on International Safeguards, Vienna, Austria, 20–24 0ctober 2014. [Google Scholar]
- Qin, R. A Critical Analysis of Satellite Stereo Pairs for Digital Surface Model Generation and A Matching Quality Prediction Model. ISPRS J. Photogramm. Remote Sens. 2019, 154, 139–150. [Google Scholar] [CrossRef]
- Facciolo, G.; Franchis, C.D.; Meinhardt-Llopis, E. Automatic 3D Reconstruction from Multi-date Satellite Images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Krauß, T.; d’Angelo, P.; Wendt, L. Cross-track satellite stereo for 3D modelling of urban areas. Eur. J. Remote Sens. 2018, 52, 89–98. [Google Scholar] [CrossRef]
- Pan, Y.; Hui, X.; Li, J.; Zhu, X.; Xu, F.; Wang, P. A Hybrid Method for Dense Points Enclosing and Observation Planning. In Proceedings of the 2024 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Kuching, Malaysia, 6–10 October 2024; pp. 4868–4874. [Google Scholar]
- Lu, Z.; Shen, X.; Li, D.; Cheng, S.; Wang, J.; Yao, W. Super-agile satellites imaging mission planning method considering degradation of image MTF in dynamic imaging. Int. J. Appl. Earth Obs. Geoinf. 2024, 131, 103968. [Google Scholar] [CrossRef]
- Li, L.; Chen, H.; Li, J.; Jing, N.; Emmerich, M. Preference-based Evolutionary Many-Objective Optimization for Agile Satellite Mission Planning. IEEE Access 2018, 6, 40963–40978. [Google Scholar] [CrossRef]
- Yang, W.; Chen, Y.; He, R.; Chang, Z.; Chen, Y. The Bi-objective Active-Scan Agile Earth Observation Satellite Scheduling Problem: Modeling and Solution Approach. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]
- Ren, L.; Ning, X.; Wang, Z. A competitive Markov decision process model and a recursive reinforcement-learning algorithm for fairness scheduling of agile satellites. Comput. Ind. Eng. 2022, 169, 108242. [Google Scholar] [CrossRef]
- d’Angelo, P.; Reinartz, P. DSM based orientation of large stereo satellite image blocks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 209–214. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications To Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Liu, C.; Yuen, J.; Torralba, A.; Sivic, J.; Freeman, W.T. SIFT Flow: Dense Correspondence across Different Scenes; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Dial, G.; Grodecki, J. RPC replacement camera models. In Proceedings of the American Society for Photogrammetry and Remote Sensing, Baltimore, MD, USA, 7–11 March 2005; pp. 183–191. [Google Scholar]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar] [CrossRef]
- Muthukrishnan, R.; Rohini, R. LASSO: A feature selection technique in predictive modeling for machine learning. In Proceedings of the 2016 IEEE International Conference on Advances in Computer Applications (ICACA), Coimbatore, India, 24 October 2016. [Google Scholar] [CrossRef]
- Benoit, K. Linear Regression Models with Logarithmic Transformations. Lond. Sch. Econ. Lond. 2011, 22, 23–36. [Google Scholar]
- Heaton, J. An Empirical Analysis of Feature Engineering for Predictive Modeling. In Proceedings of the SoutheastCon 2016, Norfolk, VA, USA, 30 March–3 April 2016. [Google Scholar] [CrossRef]
- Ha, T.N.; Lubo-Robles, D.; Marfurt, K.J.; Wallet, B.C. An in-depth analysis of logarithmic data transformation and per-class normalization in machine learning: Application to unsupervised classification of a turbidite system in the Canterbury Basin, New Zealand, and supervised classification of salt in the Eugene Island minibasin, Gulf of Mexico. Interpretation 2021, 9, T685–T710. [Google Scholar]
- Cui, C.; Wang, D. High dimensional data regression using Lasso model and neural networks with random weights. Inf. Sci. 2016, 372, 505–517. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of Feature Selection and CatBoost for Prediction: The First Application to the Estimation of Aboveground Biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Kartini, D.; Nugrahadi, D.T.; Farmadi, A. Hyperparameter Tuning using GridsearchCV on The Comparison of The Activation Function of The ELM Method to The Classification of Pneumonia in Toddlers. In Proceedings of the 2021 4th International Conference of Computer and Informatics Engineering (IC2IE), Depok, Indonesia, 14–15 September 2021; pp. 390–395. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, C. Application of Grey Wolf Optimization for Solving Combinatorial Problems: Job Shop and Flexible Job Shop Scheduling Cases. IEEE Access 2018, 6, 26231–26240. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Gu, K. A support vector regression (SVR)-based method for dynamic load identification using heterogeneous responses under interval uncertainties. Appl. Soft Comput. 2021, 110, 107599. [Google Scholar] [CrossRef]
- Nguyen, H.; Cao, M.T.; Tran, X.L.; Tran, T.H.; Hoang, N.D. A novel whale optimization algorithm optimized XGBoost regression for estimating bearing capacity of concrete piles. Neural Comput. Appl. 2023, 35, 3825–3852. [Google Scholar] [CrossRef]
| Notation | Description |
|---|---|
| / | Start/end time of imaging time window i |
| / | Start/end time of entire tasks |
| Maneuvering time needed for satellite k | |
| Side-swing angle of imaging time window i | |
| Maximum side-swing angle of satellites | |
| DSM error of stereo imaging pair | |
| Intersection angle of imaging pair | |
| / | Minimum/maximum intersection angle |
| Decision variable indicating whether to select stereo imaging pair . if is selected; otherwise |
| Notation | Description |
|---|---|
| avg_in | average intersection angle |
| max_n | maximum off-nadir angle |
| s_e_min | minimum sun elevation angle |
| s_e_diff | difference of sun elevation angle |
| s_a_diff | difference of sun azimuth angle |
| s_diff | root of sum of squares (s_a_diff and s_e_diff) |
| mon_diff | time interval |
| Model | RMSE | MAE | |
|---|---|---|---|
| SVR | 0.5454 | 0.7032 | 0.4654 |
| SVR-FE | 0.5503 | 0.6994 | 0.4595 |
| XGBoost | 0.7485 | 0.5230 | 0.3612 |
| XGBoost-FE | 0.7719 | 0.4981 | 0.3474 |
| CatBoost-FE | 0.8856 | 0.3527 | 0.2466 |
| CatBoost-LASSO | 0.8606 | 0.3894 | 0.2742 |
| CatBoost-FE-LASSO | 0.8920 | 0.3427 | 0.2462 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Ren, G.; Pan, Y.; Sun, J.; Wang, P.; Xu, F.; Liu, Z. Surface Reconstruction Planning with High-Quality Satellite Stereo Pairs Searching. Remote Sens. 2025, 17, 2390. https://doi.org/10.3390/rs17142390
Li J, Ren G, Pan Y, Sun J, Wang P, Xu F, Liu Z. Surface Reconstruction Planning with High-Quality Satellite Stereo Pairs Searching. Remote Sensing. 2025; 17(14):2390. https://doi.org/10.3390/rs17142390
Chicago/Turabian StyleLi, Jinwen, Guangli Ren, Youmei Pan, Jing Sun, Peng Wang, Fanjiang Xu, and Zhaohui Liu. 2025. "Surface Reconstruction Planning with High-Quality Satellite Stereo Pairs Searching" Remote Sensing 17, no. 14: 2390. https://doi.org/10.3390/rs17142390
APA StyleLi, J., Ren, G., Pan, Y., Sun, J., Wang, P., Xu, F., & Liu, Z. (2025). Surface Reconstruction Planning with High-Quality Satellite Stereo Pairs Searching. Remote Sensing, 17(14), 2390. https://doi.org/10.3390/rs17142390






