Construction and Application of Carbon Emissions Estimation Model for China Based on Gradient Boosting Algorithm

Abstract

Accurate forecasting of carbon emissions at the county level is critical to support China’s dual-carbon goals. However, most current studies are limited to national or provincial scales, employing traditional statistical methods inadequate for capturing complex nonlinear interactions and spatiotemporal dynamics at finer resolutions. To overcome these limitations, this study develops and validates a high-resolution predictive model using advanced gradient boosting algorithms—Gradient Boosting Decision Tree (GBDT), Extreme Gradient Boosting (XGBoost), and Light Gradient Boosting Machine (LightGBM)—based on socioeconomic, industrial, and environmental data from 2732 Chinese counties during 2008–2017. Key variables were selected through correlation analysis, missing values were interpolated using K-means clustering, and model parameters were systematically optimized via grid search and cross-validation. Among the algorithms tested, LightGBM achieved the best performance (R² = 0.992, RMSE = 0.297), demonstrating both robustness and efficiency. Spatial–temporal analyses revealed that while national emissions are slowing, the eastern region is approaching stabilization, whereas emissions in central and western regions are projected to continue rising through 2027. Furthermore, SHapley Additive exPlanations (SHAP) were applied to interpret the marginal and interaction effects of key variables. The results indicate that GDP, energy intensity, and nighttime lights exert the greatest influence on model predictions, while ecological indicators such as NDVI exhibit negative associations. SHAP dependence plots further reveal nonlinear relationships and regional heterogeneity among factors. The key innovation of this study lies in constructing a scalable and interpretable county-level carbon emissions model that integrates gradient boosting with SHAP-based variable attribution, overcoming limitations in spatial resolution and model transparency.

1. Introduction

Global climate change has emerged as one of the most pressing environmental and economic challenges facing humanity in the 21st century. According to the Intergovernmental Panel on Climate Change (IPCC) Sixth Assessment Report (AR6) released in 2023, the global average temperature has increased by 1.1 °C compared to pre-industrial levels, with greenhouse gas emissions from human activities identified as the dominant driver of global warming [1]. As the world’s largest carbon emitter [2], China accounted for 9.89 Gt of CO₂ emissions in 2019, representing 30.7% of the global total [3]. The effectiveness of China’s emission reduction policies plays a pivotal role in the achievement of global climate governance targets. In response to its “dual carbon” pledge, the Chinese government has implemented a range of stringent mitigation measures, including the establishment of a national carbon trading system, the promotion of green finance, the expansion of renewable energy industries, and deep adjustments to industrial structures [4]. However, the accurate implementation of these policies at the county level requires high-precision carbon emission forecasting models as critical support. Carbon emission forecasting efforts have primarily focused on national [5,6,7], provincial [8,9], and city-level scales [10,11], with comparatively limited attention given to the county level. Moreover, existing studies often analyze either temporal trends or spatial distributions in isolation, lacking an integrated spatiotemporal approach necessary to fully capture the dynamic evolution of county-level emissions. Thus, developing forecasting models that incorporate both spatial and temporal dimensions at the county scale has become a key scientific challenge in enhancing the accuracy and resolution of carbon emission simulations and in advancing China’s dual-carbon goals.

The choice of forecasting model directly influences the reliability of carbon emission predictions. Traditional regression models, especially linear regression [11], are widely used due to their simplicity and interpretability. However, these models are inherently limited in capturing nonlinear relationships, making them less suitable for complex, high-dimensional forecasting tasks and inadequate in modeling the interaction effects of multiple driving factors [12]. Gray forecasting models (GMs), while adaptable to small-sample scenarios [13], heavily rely on initial assumptions and expert knowledge during model construction [14], restricting their generalizability. In contrast, machine learning models—known for their robust nonlinear fitting capabilities—have opened new avenues for carbon emission prediction. Among them, shallow learning models such as support vector machines (SVMs) have demonstrated significant advantages in small-sample, high-dimensional contexts [15]. For instance, Agbulut successfully employed SVMs to predict CO₂ emissions in Turkey’s transportation sector [16], while Sun et al. developed a particle swarm optimization (PSO)-LSSVM model that achieved low error rates (0.663) in forecasting carbon emissions in Hebei Province [17]. These models can effectively map complex nonlinear relationships between emissions and their drivers and are particularly suited to data-constrained environments due to their global optimization and computational efficiency [18].

The advent of deep learning has further expanded the application scope of machine learning in this domain. Wen et al. employed a PSO-enhanced backpropagation neural network (BPNN) combined with random forest (RF) to accurately predict CO₂ emissions in China’s commercial sector. Similarly, Zhou et al. applied a PSO-optimized BPNN to forecast emissions from the thermal power industry in the Beijing–Tianjin–Hebei region, achieving error rates within 6%. Long short-term memory (LSTM) networks have also improved prediction accuracy through their ability to model time series data—Bismark et al., for example, successfully applied BiLSTM networks to forecast emissions in African countries such as Ghana and Nigeria [19]. In addition, convolutional neural networks (CNNs), with their automatic feature learning mechanisms, have proven effective in handling multivariable inputs, as demonstrated by Hien and Kor in their high-accuracy, high-stability CNN-based prediction model [20]. Nevertheless, the “black-box” nature of deep learning models poses challenges for interpretability [21], limiting their applicability in policy-making contexts where transparency and mechanism insight are critical.

While deep learning models offer strong capabilities in modeling complex spatiotemporal and nonlinear dependencies, their “black-box” nature and computational demands often limit their practicality for structured tabular datasets commonly used in regional carbon emission studies. This is particularly challenging in policy-making contexts, where interpretability and transparency are essential. Given these constraints, gradient boosting algorithms—such as GBDT, XGBoost, and LightGBM—have gained increasing attention as effective alternatives. These models strike a balance between predictive accuracy, computational efficiency, and interpretability, making them well-suited for carbon emission forecasting tasks that involve structured and high-dimensional socioeconomic and environmental datasets at the county scale. GBDT models, leveraging tree-based nonlinear fitting, have shown superior prediction performance compared to support vector machines (SVMs) and random forests in many scenarios [22], while maintaining computational advantages [23,24]. XGBoost improves generalization by introducing regularization, and LightGBM accelerates training through histogram-based algorithms [25,26]. These innovations have facilitated wide adoption of boosting algorithms across various domains, including air pollution forecasting [27], natural disaster prediction [28], electricity load modeling [29], and energy demand analysis [30]. In the field of carbon emission forecasting, XGBoost has achieved high accuracy in megacity-scale modeling in China, with RMSE as low as 0.036 [31]. LightGBM, when combined with the SHAP interpretability framework, has enhanced transparency and feature attribution in building-level carbon modeling [32]. Despite their proven success at larger spatial scales, systematic assessments of these algorithms at the county level remain limited. Their potential to model fine-grained carbon emissions across diverse regions and uncover underlying drivers has yet to be fully explored. To address these gaps, this study conducts a comparative analysis of GBDT, XGBoost, and LightGBM, focusing on both predictive effectiveness and interpretability in the context of county-level carbon emissions in China. Their potential to model fine-grained carbon emissions across diverse regions and uncover underlying drivers has yet to be fully explored. To address these gaps, this study conducts a comparative analysis of GBDT, XGBoost, and LightGBM, focusing on both predictive effectiveness and interpretability in the context of county-level carbon emissions in China.

Equally important is the rational selection of emission-driving variables, which plays a critical role in building accurate forecasting models [33]. Prior research has established that factors such as economic growth, energy consumption, industrial structure, population size, urbanization, and natural conditions significantly influence regional carbon emissions [34]. For example, Lukman et al. employed an ARDL cointegration model to analyze Nigeria’s data from 1981 to 2015, finding that population size, per capita GDP, urbanization level, and energy consumption all had significant long-term positive effects on carbon emissions [35]. Singh’s work also revealed a strong influence of climate change on greenhouse gas emissions [11]. Nonetheless, current studies often suffer from redundant variable inclusion, which increases model complexity and may reduce both prediction accuracy and interpretability [36]. Therefore, scientifically grounded feature selection is essential to eliminate redundant inputs, streamline model complexity, and significantly enhance both performance and explainability in carbon emission forecasting.

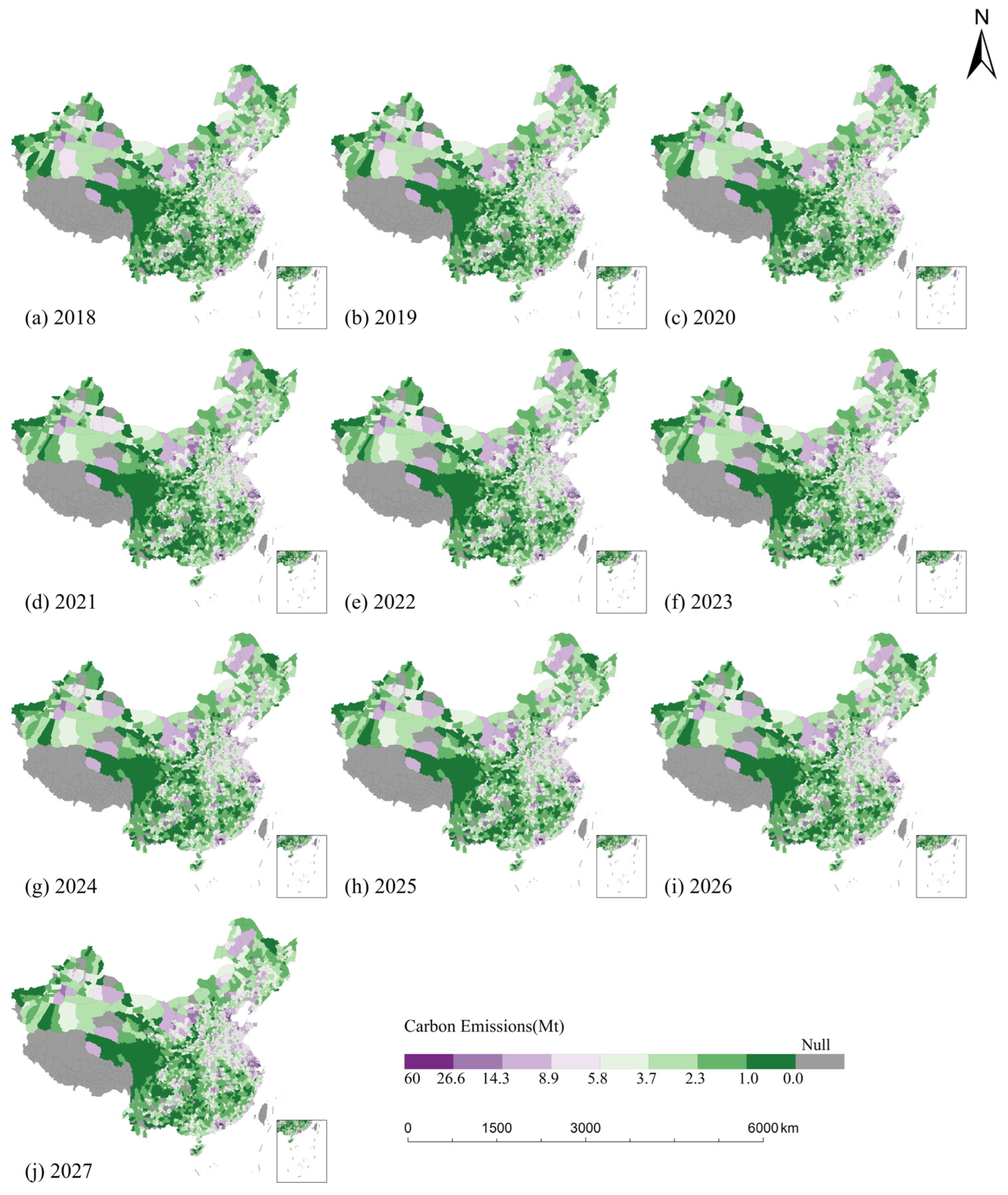
This study aims to address the following three key scientific questions: (1) How can high-precision carbon emission forecasting models be effectively constructed at the county level to accurately quantify the contributions of different driving factors? (2) How can gradient boosting algorithms (GBDT, XGBoost, LightGBM) be optimized based on the characteristics of county-level data to further improve prediction accuracy and generalizability? (3) How can the underlying driving mechanisms of county-level carbon emissions in China be revealed, and how can the spatial evolution of future emissions be reliably predicted? To tackle these issues, this study develops a county-scale carbon emission forecasting framework based on gradient boosting algorithms, aiming to explore high-precision modeling techniques suitable for fine-grained analysis. Coupled with feature importance analysis, the study identifies key driving forces behind emissions. Using data from 2008 to 2017 on county-level emissions and related factors, the research first conducts correlation analysis for initial feature screening and applies interpolation methods to address missing values, ensuring data completeness and consistency. Then, GBDT, XGBoost, and LightGBM models are constructed and optimized through grid search and cross-validation techniques to enhance predictive performance. Finally, the best-performing model is used to forecast emission trends from 2018 to 2027, thereby revealing the spatiotemporal dynamics of future county-level emissions and providing crucial support for policy formulation aimed at achieving emission reductions at the county scale in China.

2. Materials and Methods

2.1. Study Area and Data

2.1.1. Study Area

China is located in East Asia, with a total land area of approximately 9.6 million square kilometers. Its administrative structure consists of three levels: provinces, cities, and counties. The eastern region is mainly composed of plains, with subtropical or temperate monsoon climates, dense population distribution, and developed urban systems. The central region includes hills, plains, and basins, with a relatively balanced population and a combination of agricultural and industrial activities. The western region is dominated by plateaus and mountains, with arid or semi-arid climates, lower population density, and diverse natural resources. At the provincial level, there are variations in carbon emissions (Figure 1). Provinces differ in terms of industrial structure, energy usage, population size, and resource endowment, leading to different spatial characteristics of carbon emissions. Within the eastern, central, and western regions, further heterogeneity is observed.

This study was conducted at the county level in China, based on the 2010 administrative division framework. Due to data availability constraints, regions such as the Tibet Autonomous Region, Hong Kong Special Administrative Region, Macao Special Administrative Region, and Taiwan Province are excluded from the analysis. The study area encompasses 2732 counties across 30 provinces (including autonomous regions and municipalities), covering approximately 87% of China’s land area, more than 90% of its population, and over 90% of its GDP.

2.1.2. Data Sources and Preprocessing

The analysis is based on county-level carbon emissions data and associated influencing factors spanning the period from 2008 to 2017. The sources of all data used in this study are summarized in

Table 1. Data sources.

Data Type	Source	Spatial Resolution
Carbon emissions	CEADs [37]	County level
GDP	figshare dataset [38]	1 km × 1 km
Nighttime light data	Third Pole Environment Center [39]	1 km × 1 km
Population density	Oak Ridge National Laboratory [40,41,42,43,44,45,46,47,48,49]	1 km × 1 km
Value added of primary industry	China County Statistical Yearbook	County level
Value added of secondary industry	China County Statistical Yearbook	County level
Value added of tertiary industry	China County Statistical Yearbook	County level
Electricity consumption	figshare dataset [38]	1 km × 1 km
Energy intensity	figshare dataset [50]	County level
Total energy consumption
Temperature	Third Pole Environment Center [51]	1 km × 1 km
NDVI	Resource and Environmental Science Data Platform	1 km × 1 km
GPP	GOSIF-GPP, Global Ecology and Remote Sensing Lab [52]	1 km × 1 km
Proportion of green land area	Zenodo Repository [53]	1 km × 1 km
Proportion of built-up area	Zenodo Repository [53]	1 km × 1 km

.

To ensure consistency and comparability, raster datasets were overlaid with county-level administrative boundaries in ArcGIS 10.4 (Esri Inc., Redlands, CA, USA). This allowed for the extraction and aggregation of data across 2732 counties under a unified spatial framework. Missing and abnormal values were imputed using a K-means clustering-based interpolation method. The approach considered both spatial proximity and attribute similarity, minimizing the influence of data incompleteness. Land use data at 30 m resolution were resampled to 1 km to align with the study scale. A reclassification was then applied based on standardized land use categories. From this, green land and built-up area proportions were calculated for each county.

2.2. Indicator System Construction

Indicator selection followed the principles of representativeness, systematization, and observability. Based on county-level data availability, a comprehensive framework covering five dimensions was developed. Fourteen variables were categorized into economic development, population size, industrial structure, energy consumption, and natural factors (

Table 2. Construction of indicator system.

Primary Category	Secondary Indicator	Abbreviation
Economic Development	Gross Domestic Product	GDP
	Nighttime Light Intensity	NL
Population Size	Population Density	PD
Industrial Structure	Share of Primary Industry in GDP	P1
	Share of Secondary Industry in GDP	P2
	Share of Tertiary Industry in GDP	P3
Energy Consumption	Electricity Consumption	Econs
	Energy Intensity	EI
	Energy Consumption	EC
Natural Factors	Temperature	TEM
	Normalized Difference Vegetation Index	NDVI
	Gross Primary Productivity	GPP
	Proportion of Green Land Area	GA
	Proportion of Built-up Land Area	BA

). Economic growth intensifies resource use and production, making it a major driver of emissions. Population size shapes spatial patterns and emission volumes through its effects on demand and production. Industrial structure plays a decisive role—counties with higher industrial shares tend to emit more, while agriculture- and service-dominated regions show lower emissions. Energy consumption determines emission intensity and scale; efficiency significantly influences the emission profile. Natural factors regulate the carbon balance, affecting emissions through their impact on sources and sinks.

2.3. Methodological Framework

This study proposes an integrated and interpretable modeling framework for county-level carbon emission prediction, which combines gradient boosting algorithms with ARIMA-based data forecasting, correlation feature selection, and SHAP-based variable attribution. The framework encompasses the construction of a multi-dimensional indicator system using multi-source socioeconomic and environmental data, a systematic comparison of GBDT, XGBoost and LightGBM under unified input settings and evaluation criteria, and hyperparameter optimization via grid search and k-fold cross-validation to enhance model robustness. To enable future scenario prediction, the ARIMA method is used to extrapolate unavailable input variables from 2018 to 2027. By integrating predictive modeling with transparent post hoc interpretation using SHAP, this study develops a comprehensive modeling pipeline that addresses both accuracy and explainability in carbon emission.

2.3.1. Gradient Boosting Algorithms

Gradient boosting is an ensemble learning method that builds multiple weak learners in sequence. A strong learner is formed by aggregating these weak learners with weighted combinations. In each iteration, the algorithm fits a new model to the residuals of the previous iteration. This process corrects prior prediction errors, gradually improving overall accuracy.

GBDT employs decision trees as base learners and optimizes the model by minimizing a loss function. The objective is to iteratively adjust the weights of each learner to reduce prediction error. The loss function is defined as follows:

$$L\left(f\right)=\sum _{i=1}^{n}L\left(y_i,f\left(x_i\right)\right)+\lambda \sum _{j=1}^T{w}_j^2$$

(1)

where $L\left(y_i,f\left(x_i\right)\right)$ represents the loss from a single prediction. $\lambda$ is the regularization parameter, $T$ denotes the number of leaf nodes, and $w_j$ refers to the weight of the leaf.

XGBoost introduces several improvements over GBDT. It incorporates second-order derivatives to accelerate convergence and includes both L1 and L2 regularization to prevent overfitting. The objective function contains two components: the loss function capturing prediction error and the regularization term penalizing model complexity. The objective function is expressed as follows:

$$Obj=\sum _{i=1}^{n}L\left(y_i,{\widehat{y}}_i\right)+\gamma T+{\displaystyle \frac{1}{2}}\lambda \sum _{j=1}^T{w}_j^2$$

(2)

where $\lambda$ controls the penalty on the number of leaf nodes, and ${ \widehat{y}}_i$ denotes the predicted value. XGBoost improves computational efficiency through techniques such as node-splitting cache, feature parallelism, and data parallelism.

LightGBM further enhances XGBoost by introducing a histogram-based data binning method. Continuous features are discretized into fixed bins, reducing memory usage and computational complexity. The histogram algorithm narrows the candidate split space by grouping feature values. LightGBM also adopts a leaf-wise growth strategy rather than a level-wise one. This approach splits the leaf node with the largest loss reduction, accelerating convergence and improving training efficiency.

The input data are structured at the county level with annual resolution, covering the period from 2008 to 2017. All feature variables are continuous numerical data that have been standardized and compiled into the model’s input feature matrix. The target variable is the annual CO₂ emissions for each county. The modeling follows a supervised regression structure, with training and validation based on historical data (2008–2017). The trained model, combined with projected values of input features, is then applied to forecast county-level carbon emissions for 2018–2027. The output consists of predicted annual CO₂ emissions at the county scale, serving as the basis for subsequent spatiotemporal analyses.

2.3.2. ARIMA

Within the modeling framework of this study, future values of certain input variables (for the years 2018–2027) are unavailable due to a lack of observed data. However, accurate carbon emission forecasting requires a complete set of predictor variables. To address this limitation and enable future scenario predictions, the ARIMA model was employed to forecast selected time series. ARIMA is well-suited for univariate time series with relatively stable trends and offers a parsimonious structure with interpretable parameters. It is particularly appropriate for medium-term forecasting tasks. In this context, ARIMA is used to generate necessary future inputs for the emission prediction model, supporting its temporal extensibility.

The ARIMA model consists of three components—autoregression (AR), integration (I), and moving average (MA)—and its general form can be expressed as follows:

$$y_t=c+\sum _{i=1}^p{\varphi }_i{y}_{t-i}+\sum _{j=1}^q{\theta }_j{ϵ}_{t-j}+{ϵ}_t$$

(3)

where $y_t$ denotes the feature value at time, $c$ is a constant, ${\varphi }_i$ represents the autoregressive coefficients indicating the influence of past $i$ values, ${\theta }_j$ is the moving average coefficient adjusting for previous white noise terms, and ${ϵ}_t$ denotes the random error.

To ensure stationarity, differencing is applied when necessary. The differencing formula is as follows:

$$y_t^{\prime }=y_t-y_{t-1}$$

(4)

where $y_t^{\prime }$ is the differenced value. $d$ indicates the number of differencing operations.

Model development involves analyzing autocorrelation (ACF) and partial autocorrelation (PACF) plots to assess stationarity and identify the autoregressive order $p$, differencing order $d$, and moving average order $q$. The Akaike Information Criterion (AIC) is then used to evaluate candidate models and select the optimal structure for accurate time series forecasting.

2.3.3. Model Validation Methods

Model validation was conducted in two distinct phases based on the temporal scope of the data. For the historical period of 2008–2017, 10-fold cross-validation was employed to assess model fit and generalization capability. In this process, the dataset was randomly partitioned into ten subsets, each used once as the validation set while the remaining served as the training set. During model training, all gradient boosting models were optimized using the training data, and performance was evaluated on held-out test sets. Evaluation metrics included the coefficient of determination (R²), root mean squared error (RMSE), mean absolute error (MAE), and mean squared error (MSE), which together quantify prediction accuracy and error magnitude.

R² reflects the model’s explanatory power for observed variation. Values closer to 1 indicate better fit.

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^n{(y_i-\overline{y})}^2}}$$

(5)

RMSE measures average deviation between predicted and observed values. Lower values imply smaller prediction errors.

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

(6)

MAE represents the mean absolute difference between predicted and observed values.

$$MAE={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|y_i-{\widehat{y}}_i\right|$$

(7)

MSE is the average of squared errors, offering a general assessment of prediction error.

$$MSE={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2$$

(8)

For the prediction period of 2018–2027, ARIMA was first applied to extrapolate input variables beyond the observed data range. To verify the reliability of the extrapolated inputs, predicted values for the year 2018 were compared against actual observed values using the same error metrics. Once validated, ARIMA-based projections were used to generate feature inputs for the years 2018–2027, enabling the trained models to estimate carbon emissions under future scenarios. This procedure ensures both the continuity and credibility of the model outputs for the forecasting horizon.

3. Results

3.1. Model Development and Optimization

3.1.1. Feature Selection

To reduce redundancy and lower computational burden, Pearson correlation analysis was conducted on 14 carbon-related variables. GDP and Econs were found to be perfectly correlated (r = 1.0), and EC also exhibited strong correlation with both (r = 0.83). In addition, P3 and P2 were highly correlated (r = 0.81). Therefore, Econs, EC, and P3 were removed due to redundancy. Among the remaining variables, GDP showed the highest correlation with carbon emissions (r = 0.80). Features such as PD, NL, EI, P1, P2, TEM, and BA were positively correlated with emissions, while NDVI, GPP, and GA were negatively correlated (as shown in Figure 2). A total of 11 features were retained for subsequent modeling.

To further assess the impact of feature selection on model performance, Recursive Feature Elimination (RFE) was introduced alongside the correlation-based method to construct feature subsets. RFE was executed independently for GBDT, XGBoost, and LightGBM models to rank and recursively eliminate features, resulting in 11 selected variables per model. The correlation-based method also retained 11 features, though the selected sets varied. Each model was then trained using both feature subsets, and their predictive performance was evaluated. The complete results, including R², RMSE, MAE, and the corresponding selected features, are summarized in

Table 3. Comparison of model performance and selected features under different feature selection methods.

Method	Model	Selected Features	R2	RMSE	MAE
Pearson correlation	GBDT	[GDP, PD, NL, NDVI, GPP, EI, P1, P2, TEM, GA, BA]	0.9431	0.7737	0.4385
	XGBoost	[GDP, PD, NL, NDVI, GPP, EI, P1, P2, TEM, GA, BA]	0.9745	0.5180	0.2911
	LightGBM	[GDP, PD, NL, NDVI, GPP, EI, P1, P2, TEM, GA, BA]	0.9703	0.5592	0.3167
RFE	GBDT	[GDP, NL, NDVI, GPP, EI, EC, P2, P3, TEM, GA, BA]	0.9650	0.6068	0.3533
	XGBoost	[PD, NL, GPP, Econs, EI, EC, P1, P2, TEM, GA, BA]	0.9816	0.4402	0.2515
	LightGBM	[PD, NL, GPP, Econs, EI, EC, P1, P2, TEM, GA, BA]	0.9771	0.4914	0.2796

for direct comparison and analysis.

The results showed that RFE-selected features led to slightly higher predictive accuracy in all models. For example, XGBoost achieved an R² of 0.9816 with RFE features, compared to 0.9745 with correlation-based features; similar improvements were observed in LightGBM. However, Variance Inflation Factor (VIF) analysis revealed that the correlation-based feature set exhibited stronger control over multicollinearity, with all VIF values below 5. In contrast, some RFE-selected features showed moderate multicollinearity risks, such as GDP (VIF = 5.42) and EC (VIF = 5.28) in the GBDT model (see

Table 4. (a) Multicollinearity analysis (VIF) based on correlation features; (b) multicollinearity analysis (VIF) for GBDT model (RFE features); (c) multicollinearity analysis (VIF) for XGBoost model (RFE features); (d) multicollinearity analysis (VIF) for LightGBM model (RFE features).

(a)
Feature	VIF	Collinearity Risk
GDP	2.609180377	Low
PD	1.40418562	Low
NL	2.062884505	Low
NDVI	1.953570438	Low
GPP	2.635201753	Low
EI	1.219472723	Low
P1	1.469894943	Low
P2	1.416107123	Low
TEM	2.00488311	Low
GA	2.093075546	Low
BA	1.777283194	Low
(b)
Feature	VIF	Collinearity Risk
GDP	5.416579853	Medium (5–10)
NL	2.142533994	Low
NDVI	1.929793745	Low
GPP	2.622956322	Low
EI	1.565168069	Low
EC	5.275177233	Medium (5–10)
P2	3.201765717	Low
P3	3.115172182	Low
TEM	1.984728355	Low
GA	1.82486631	Low
BA	1.853681863	Low
(c)
Feature	VIF	Collinearity Risk
PD	1.422623776	Low
NL	1.993063778	Low
GPP	2.188293111	Low
Econs	4.766801685	Low
EI	1.549493766	Low
EC	5.221173996	Medium (5–10)
P1	1.450186149	Low
P2	1.474780219	Low
TEM	1.975692812	Low
GA	2.08429926	Low
BA	1.687660058	Low
(d)
Feature	VIF	Collinearity Risk
PD	1.422623776	Low
NL	1.993063778	Low
GPP	2.188293111	Low
Econs	4.766801685	Low
EI	1.549493766	Low
EC	5.221173996	Medium (5–10)
P1	1.450186149	Low
P2	1.474780219	Low
TEM	1.975692812	Low
GA	2.08429926	Low
BA	1.687660058	Low

a–d).

Although the RFE-based feature subsets demonstrated superior predictive performance, the correlation-based method provided stronger advantages in redundancy control, feature stability, and physical interpretability, while still maintaining high predictive power. Considering the potential for further improvement via hyperparameter tuning, the correlation-based feature selection was retained for model development, striking a better balance between accuracy and stability.

3.1.2. Model Training

Three gradient boosting algorithms were selected—GBDT, XGBoost, and LightGBM (Figure 3). Carbon emission forecasting models were developed using county-level feature data from 2008 to 2017 as input variables. The dataset was randomly divided into training and testing subsets, with an 80 to 20 split. Training data supported model fitting. Testing data served for performance evaluation. During model development, grid search, and cross-validation were applied on the training set to optimize parameters. The goal was to enhance both prediction accuracy and generalization.

Parameter tuning was performed in two stages—coarse and fine. The first stage focused on three key parameters: number of estimators (n_estimators), maximum tree depth (max_depth), and learning rate (learning_rate). Initial ranges were set as follows: n_estimators ranged from 400 to 900, with a step size of 100. max_depth ranged from 4 to 9, with a step size of 1. learning_rate were tested at 0.05, 0.1, and 0.2. This stage yielded the optimal learning rate for each model and narrowed the parameter search space. In the fine-tuning stage, parameter ranges were further narrowed and step sizes refined. Final tuning produced the optimal combination of key parameters for GBDT, XGBoost, and LightGBM.

After determining the optimal values for n_estimators, max_depth or num_leaves, and learning_rate, further tuning was performed on other parameters. Once core parameters were optimized for GBDT, XGBoost, and LightGBM, additional tuning targeted model-specific parameters. Each model’s final parameter combination is summarized in

Table 5. Optimal parameter values for each model.

Parameter	Description	Model	Optimal Value
learning_rate	Learning rate	GBDT	0.1
		XGBoost	0.1
		LightGBM	0.1
max_depth	Maximum tree depth	GBDT	5
		XGBoost	6
num_leaves	Number of leaf nodes	LightGBM	31
n_estimators	Number of boosting iterations	GBDT	775
		XGBoost	875
		LightGBM	950
subsample	Subsampling ratio	GBDT	0.8
		XGBoost	0.8
		LightGBM	0.8
min_samples_leaf	Minimum samples per leaf	GBDT	15
min_samples_split	Minimum samples to split	GBDT	20
gamma	Minimum loss reduction	XGBoost	0.5
colsample_bytree	Feature subsampling ratio	XGBoost	0.8
reg_alpha	L1 regularization term weight	XGBoost	0.1
reg_lambda	L2 regularization term weight	XGBoost	0.1
min_child_weight	Minimum sum of instance weight per node	XGBoost	5
min_child_samples	Minimum data in one leaf	LightGBM	10
min_split_gain	Minimum gain to perform a split	LightGBM	0
lambda_l1	L1 regularization term weight	LightGBM	0.1
lambda_l2	L2 regularization term weight	LightGBM	0

. For XGBoost and LightGBM, regularization parameters including reg_alpha and lambda_l1 for L1 and reg_lambda and lambda_l2 for L2 were also adjusted. L1 regularization applies constraints on weights, reducing the influence of less important features. L2 regularization limits weight magnitude changes, lowering the risk of overfitting.

Figure 4 presents the learning curves for GBDT, XGBoost, and LightGBM before and after regularization. Without regularization, training error scores remained near 1. Cross-validation errors were significantly higher. As the training set expanded, cross-validation error decreased slowly, with a persistent gap between training and validation curves. This indicates a clear overfitting tendency and limited generalization. After introducing regularization parameters, training error remained stable. Cross-validation error dropped markedly. The gap between training and validation narrowed. Regularization effectively reduced model complexity and alleviated overfitting.

A comparison of learning curves with and without regularization shows substantial gains in accuracy and stability on testing data. This pattern appeared consistently in both LightGBM and XGBoost, validating the importance of regularization in complex modeling tasks. Regularization controls model complexity, enhances robustness and generalizability, and mitigates overfitting. These improvements make the models more reliable and adaptive in real-world applications.

3.1.3. Model Validation

To evaluate the performance of GBDT, XGBoost, and LightGBM in county-level carbon emission forecasting, this study used scatter density plots (Figure 5) for visual comparison and adopted four quantitative metrics—R², RMSE, MAE, and MSE.

The GBDT model yielded a regression equation of Y = 0.97X + 0.08. The R² reached 0.986, indicating strong explanatory power. However, RMSE, MAE, and MSE were 0.379, 0.186, and 0.144, respectively, which are slightly higher than the other models. The scatter density plot shows strong overall correlation between predictions and observations, though deviations emerged in the high-emission range. In contrast, performance remained stable in the low-emission range, capturing trends effectively within that interval. The XGBoost model produced a regression equation of Y = 0.98X + 0.07. R² reached 0.988, indicating improved fit. RMSE, MAE, and MSE were 0.360, 0.178, and 0.130, respectively, reflecting lower error levels. The scatter plot suggests high agreement in the mid-emission range. Some underestimation appeared in the high-emission zone, suggesting room for further refinement. The LightGBM model showed the strongest performance. The regression equation was Y = 0.98X + 0.06, with an R² of 0.992. RMSE, MAE, and MSE were 0.297, 0.149, and 0.088, respectively—the lowest among all models. The scatter density plot shows close alignment between predicted and observed values across the entire range, especially in mid-emission intervals where prediction errors were minimal. This indicates strong stability and robustness.

Overall, all three gradient boosting models showed good applicability to county-level carbon forecasting. Differences emerged in prediction accuracy and generalization. GBDT remained stable in low-emission ranges but showed lower overall precision. XGBoost captured trends in mid- to high-emission ranges with stronger fit. LightGBM demonstrated the best accuracy and stability, making it the most suitable model for this task.

3.2. Spatiotemporal Patterns of County-Level Emissions: 2008–2017

3.2.1. Spatial Distribution of County-Level Carbon Emissions

As shown in Figure 6, the spatial distribution of county-level carbon emissions in 2008, 2011, 2014, and 2017 reveals distinct regional disparities. High-emission clusters concentrated along the eastern coastal economic belt. Low-emission zones remained widespread across the ecologically fragile western region. The overall pattern follows a clear east-high west-low gradient. Regionally, the Bohai Rim, Yangtze River Delta, and Pearl River Delta urban clusters show emission intensities well above the national average. The spatial distribution aligns closely with China’s economic geography. Coastal counties in the Shandong Peninsula, southern Jiangsu Plain, and Pearl River Delta form continuous high-emission belts. These areas are characterized by export-oriented industries, dense port logistics networks, and intensive urban construction. By contrast, most counties in western ecological barrier zones maintained low emission levels. Counties on the Qinghai–Tibet Plateau and Yunnan–Guizhou Plateau remained persistently low-emission due to ecological protection policies. However, certain regions such as the Shanxi–Shaanxi–Inner Mongolia energy triangle and the Chengdu–Chongqing urban cluster exhibited localized emission spikes. These high-emission anomalies reflect the spatial influence of resource-dependent development. Many of these hotspots align with major transportation corridors, indicating a spatial coupling between infrastructure networks and carbon emission intensity.

As shown in Figure 7, the spatial pattern of per capita carbon emissions in 2008, 2010, 2014, and 2017 exhibits a clear north-high south-low and east-high west-low trend. Overall, per capita emissions increased steadily during this period. The pattern correlates with regional industrial structures, energy usage habits, and development levels. Northern provinces such as Inner Mongolia, Shanxi, and Hebei recorded significantly higher per capita emissions. These areas rely heavily on resource extraction, energy production, and heavy industry. Despite low population densities, concentrations of coal, steel, and other energy-intensive sectors drive up emissions. Typical examples include Shanxi’s coal mining bases and Inner Mongolia’s petrochemical zones. In contrast, per capita emissions in southwestern provinces such as Yunnan, Guizhou, and Sichuan remained relatively low. These areas are characterized by lower economic output, limited industrialization, and reduced energy consumption. Agriculture and tourism dominate the local economy. A high share of hydropower further reduces emission pressure. Eastern coastal provinces showed relatively high per capita emissions. These results reflect advanced industrialization, strong manufacturing sectors, and dense energy consumption. Over time, from 2008 to 2017, per capita emissions rose steadily, particularly in coastal regions experiencing rapid economic and urban growth. Intensified industrial activity and shifts in energy structure, especially the expansion of energy-intensive industries, contributed to the rise in emissions in both eastern and northern regions. In summary, spatial differences in per capita emissions between 2008 and 2017 are closely linked to regional economic development, industrial patterns, and energy consumption. Northern regions tended to exhibit higher emissions. Western regions remained low-emission zones. Per capita carbon emissions increased over time, driven by industrial expansion and structural changes in energy use.

3.2.2. Temporal Evolution of County-Level Carbon Emissions

As shown in Figure 8, total carbon emissions increased from 6908.11 Mt in 2008 to 9466.27 Mt in 2017. The average annual growth rate reached 3.2 percent, though with noticeable fluctuations. Four distinct phases emerged. From 2008 to 2011, emissions entered a rapid growth phase. Total emissions rose from 6908.11 Mt to 9103.17 Mt. Annual growth climbed from 7.86 percent in 2009 to 11.64 percent in 2011. Emissions increased by 31.8 percent over three years. The sharp rise reflected fast-paced economic growth and increasing energy consumption. From 2012 to 2014, growth slowed. Total emissions continued to rise but at a reduced pace. Annual growth rates during this period were 2.05, 0.54, and 2.13 percent. Average growth dropped by about 8 percentage points compared to the previous phase. Emission increases became more moderate, and the expansion trend weakened. In 2015, emissions declined for the first time. Total emissions dropped by 5.51 percent from the previous year to 9013.65 Mt. This marked a turning point, indicating a temporary pause in the upward trend. From 2016 to 2017, emissions rebounded slightly. Annual growth was 3.11 percent in 2016 and 1.86 percent in 2017. However, compared to pre-2011 levels, growth rates fell by approximately 80 percent. Emissions returned to an upward trajectory but with much lower momentum. The overall trend moved toward stabilization.

As shown in Figure 9, emission changes varied widely across regions. Spatial heterogeneity was closely linked to differences in economic development, industrial structure, and energy use patterns. Eastern developed provinces such as Beijing, Shanghai, Jiangsu, and Zhejiang recorded lower emission growth. Some counties even showed negative growth. This trend resulted from industrial upgrading, strict environmental regulations, and increased adoption of clean energy. In Beijing, most districts experienced absolute reductions in emissions, indicating successful decoupling of economic growth from carbon output through policy support and technological innovation. In contrast, central and western regions showed higher growth. Provinces such as Inner Mongolia, Shanxi, and Shaanxi—known for having energy-intensive industries—recorded annual growth rates ranging from 5 to 25 percent. Some areas exceeded 25 percent. These patterns reflect rapid industrialization, rising energy demand, and intensified resource extraction. Coal, steel, and other heavy industries contributed heavily to the increase. Spatially, the eastern region achieved effective control over emission growth, with some areas realizing absolute reductions. The central and western regions experienced continued expansion. This pattern highlights the link between development stage and emission trends. Economically advanced areas progressed toward low-carbon transformation through structural and technological change. Industrializing regions faced mounting emission pressures during their development surge.

3.3. County-Level Carbon Emission Forecast in China (2018–2027)

3.3.1. Validation of Extrapolated Data

The ARIMA model was applied to forecast key carbon emission drivers from 2018 to 2027. Variables included GDP, PD, NL, NDVI, GPP, TEM, BA, P1, P2, and EI. To assess model performance, 2018 was selected as the validation point. Out-of-sample predictions were compared with observed values, as shown in Figure 10. The results indicate that the ARIMA model performed well for most variables. Strong linear agreement was observed for GDP, PD, NL, GPP, TEM, and GA. Predicted values aligned closely with actual data. Regression slopes approached one. NDVI showed some fluctuations but remained centered around the regression line. This confirms its suitability for time series modeling. P1, P2, and EI displayed greater dispersion. Although prediction accuracy declined, trends were generally preserved. The model successfully captured key variation patterns. Overall, the regression trends of predicted values closely matched the observed trajectories. These findings confirm the ARIMA model’s capability to fit multiple categories of time-dependent carbon-related variables. Given its strong performance across most indicators, the model was adopted for long-term dynamic forecasting from 2018 to 2027.

3.3.2. Carbon Emission Forecast and Uncertainty Analysis

Based on the optimized LightGBM model and ARIMA-extrapolated input variables, county-level carbon emissions in China were forecasted from 2018 to 2027. The national total emissions are expected to follow a steady upward trend. Compared with the 2008–2017 period, the growth rate of emissions appears to moderate, yet remains positive. The rising trend in predicted values can be attributed to the inherent growth characteristics of the input variables, including GDP, energy intensity, and population density. These indicators were extrapolated using time series models that preserve long-term structural momentum, resulting in cumulative effects on the output predictions. The emissions forecast, therefore, mirrors the historical trajectory of its primary drivers under a business-as-usual scenario.

To assess the reliability of these projections, a bootstrap resampling method was applied. Specifically, 1000 resampled datasets were generated and used to retrain the LightGBM model, producing a distribution of national-level carbon emission predictions for each year. The mean forecast, standard deviation, and 95% confidence intervals were calculated based on this ensemble. As summarized in

Table 6. Forecasted carbon emissions from 2018 to 2027 with associated uncertainty estimates based on bootstrap resampling.

Year	Mean Emissions	Std. Dev. (σ)	95% CI Lower	95% CI Upper
2018	9616.82	0.144	8880.8	10,419.64
2019	9807.06	0.151	9039.04	10,643.4
2020	9963.05	0.157	9160.08	10,838.91
2021	10,145.31	0.163	9314.94	11,051.8
2022	10,301.6	0.169	9442.89	11,239.62
2023	10,463.67	0.173	9582.07	11,427.4
2024	10,610.25	0.178	9703.25	11,605.86
2025	10,761.7	0.183	9833.3	11,783.39
2026	10,903.69	0.188	9952.94	11,950.03
2027	11,044.74	0.192	10,072.81	12,114.74

, the national carbon emissions are expected to rise from approximately 9615 Mt in 2018 to over 10,900 Mt by 2027. While the confidence intervals remain relatively narrow, indicating strong model stability, a gradual widening is observed in later years, which reflects increasing uncertainty associated with long-range forecasting and accumulated input errors. Nonetheless, the predicted values provide a reliable approximation of expected emission levels under the current developmental trajectory.

3.3.3. Spatiotemporal Patterns of Carbon Emissions: 2018–2027

As shown in Figure 11, the spatial distribution of county-level carbon emissions in China from 2018 to 2027 is expected to retain the overall “east high, west low” pattern. Compared with the situation during 2008–2017, the next decade shows clear deviations in the trend.

The eastern region will likely continue contributing a large share of total emissions, though growth will slow significantly. Over the past decade, rapid industrialization and expansion of an export-oriented economy drove sustained emission increases. With steady economic transition, wider adoption of green and low-carbon technologies, and deeper structural adjustments, the emission growth momentum in the east is expected to weaken. Some areas may even see slight declines in total emissions. The western region will remain low in absolute emissions, yet growth is expected to accelerate from 2018 to 2027. Compared with 2008–2017, policies such as the “Western Development Strategy” and the “Belt and Road Initiative” have boosted regional economic development. Industrial activity and energy use have expanded, pushing up emission growth. Despite this, the total emissions in the west are still far below those in the east, and overall growth remains within a controllable range.

Between 2018 and 2027, carbon emissions will likely follow a “steady but rising” trend. Although the growth rate is relatively moderate, total emissions continue to increase. This reflects the ongoing influence of economic momentum and energy demand during the gradual enforcement of low-carbon development policies. Compared with the rapid growth of 2008–2017, the coming decade will likely see a more stabilized increase in emissions.

4. Discussion

4.1. Model Comparison

This study conducted a systematic evaluation of three gradient boosting algorithms—GBDT, XGBoost, and LightGBM—in the context of county-level carbon emission forecasting in China. Their predictive performance was further compared with traditional statistical models (ARIMA) and other machine learning methods (SVR, RF, ANN, and LSTM) (

Table 7. Performance comparison of different models for carbon emission prediction.

Model Category	Model	R2	RMSE	MAE	MSE
Traditional Models	ARIMA [55]	0.6677	\	\	\
Machine Learning Models	SVR [56]	0.876	0.618	0.451	\
	RF [57]	0.88	0.556	0.409	\
Deep Learning Models	BPNN [58]	0.9426	0.3699	\	\
	ANN [56]	0.930	0.466	0.339	\
	LSTM [56]	0.920	0.497	0.363	\
Gradient Boosting Models	GBDT	0.986	0.379	0.186	0.144
	XGBoost	0.988	0.360	0.178	0.130
	LightGBM	0.992	0.297	0.149	0.088

). The results show that gradient boosting algorithms consistently outperformed both the traditional ARIMA model and standalone machine learning models. Among the three, LightGBM delivered the best performance, significantly surpassing XGBoost and GBDT. This finding aligns with previous studies, which confirm that gradient boosting methods are more suited to complex, multi-factor prediction tasks due to their strong nonlinear fitting capacity and robustness [54]. From a model-type perspective, ARIMA showed the weakest performance with R² = 0.68 and relatively large prediction errors. Although SVR and RF performed better than ARIMA, their accuracy still fell short of gradient boosting methods. ANN and LSTM yielded higher R² values, but their RMSE and MAE remained higher than those of gradient boosting models, indicating limitations in complex forecasting scenarios.

Further comparison among GBDT, XGBoost, and LightGBM highlights key differences in computational efficiency and generalization. GBDT, while showing solid fitting ability, lacks effective regularization and uses a level-wise tree structure. This leads to high computational complexity and weak generalization when handling large-scale or high-dimensional data. Overfitting is more likely to occur. XGBoost mitigates overfitting by introducing L1 and L2 regularization, enhancing stability and generalization. However, its complex structure increases computational cost on large datasets, which may limit practical applications. LightGBM, by contrast, uses histogram-based feature splitting and a leaf-wise tree growth strategy. These features significantly improve both computational efficiency and prediction accuracy. The results show that under the same data conditions, LightGBM achieved better performance than both GBDT and XGBoost in terms of speed and accuracy.

4.2. Driver Attribution Analysis Based on SHAP

To explore the influence mechanisms of various socioeconomic and environmental variables on county-level carbon emissions, we employed SHAP to interpret the LightGBM model. Compared to traditional feature importance rankings, SHAP is grounded in game theory and quantifies the marginal contribution of each variable to the model output. It further captures nonlinear effects and inter-feature interactions, thus enhancing the interpretability of complex machine learning models.

Figure 12 displays a SHAP summary plot ranking all features by their average absolute SHAP values, which indicate their global contributions to carbon emissions. GDP and energy intensity (EI) emerged as the two most influential predictors, exerting a stable and positive effect across most counties—especially in the higher range of values. Nighttime light intensity (NL) and temperature (TEM) follow, underscoring the role of urbanization and climate. In contrast, ecological indicators such as NDVI and GPP show lower and predominantly negative SHAP values, suggesting their mitigation role through ecosystem carbon sinks.

Figure 13 further presents SHAP dependence plots for individual features. These plots illustrate how changes in feature values affect the SHAP values and reflect interaction effects via color gradients. Most variables exhibit strong nonlinear relationships with model output. For instance, GDP shows a steadily increasing trend in SHAP values, with a sharper slope in the high-GDP range, indicating stronger marginal effects. Similarly, energy intensity (EI) displays a threshold effect, with its marginal impact rising sharply once beyond a certain point. In contrast, NDVI and GPP tend to have negative marginal effects, especially in regions with high vegetation coverage or productivity, supporting their carbon sink role. The color gradients in the dependence plots reveal inter-feature synergies—for instance, the marginal effect of NL increases significantly under high population density (PD), indicating that urban growth and demographic concentration jointly intensify carbon emissions.

4.3. Research Limitations and Future Outlook

While the county-level carbon emission estimation model developed in this study demonstrates a degree of applicability and interpretability through the use of SHAP, there remain several limitations. First, the model inputs are relatively limited, excluding potentially important factors such as transportation data and land use dynamics, which may affect the completeness of the emission mechanism analysis. Second, although SHAP effectively reveals marginal effects and interactions, its interpretation largely depends on visual analysis, and it is not designed to identify causal relationships or detailed interaction pathways in a quantitative manner.

Future research could consider the following directions: (1) incorporating higher-resolution remote sensing indicators and localized energy activity data to improve the model’s sensitivity to spatial heterogeneity; (2) applying causal inference frameworks or local interpretation models (e.g., LIME) to validate and enrich SHAP-based findings; (3) and further exploring how model outputs can be linked to specific policy instruments to support targeted evaluations.

5. Conclusions

This study developed a county-level carbon emission estimation and forecasting framework by integrating multi-source statistical and remote sensing data. It systematically evaluated the performance of gradient boosting algorithms (GBDT, XGBoost, LightGBM) in carbon modeling. The results suggest that LightGBM achieves a favorable balance between predictive accuracy and computational efficiency, making it suitable for large-scale and high-resolution emission prediction tasks. Model outputs indicate a marked increase in county-level carbon emissions across China from 2008 to 2017, with a distinct spatial pattern characterized by higher emissions in the east and lower levels in the west. Forecasts for 2018–2027 suggest continued overall growth, though at a slower pace. Some eastern regions are likely to experience a deceleration or even reduction in emissions, whereas central and western regions may sustain increasing trends driven by ongoing industrial activities. SHAP-based interpretation highlights GDP, energy intensity, and nighttime lights as major influencing variables. Several factors exhibit nonlinear marginal effects and interaction patterns, enhancing the model’s interpretability and offering insights into region-specific emission mechanisms.