LIO-GC: LiDAR Inertial Odometry with Adaptive Ground Constraints
Abstract
1. Introduction
- 1.
- A SLAM framework named LIO-GC is proposed, which integrates the Cloth Simulation Filtering (CSF) algorithm to extract the ground points to significantly reduce Z-axis drift in mapping in diverse environments.
- 2.
- Optimizations including the use of efficient data structures, parallel processing techniques, and adaptive resolution adjustments are introduced, enabling the algorithm to operate more efficiently in real-time applications.
- 3.
- A newly collected dataset featuring environments with notable terrain undulations and various ground objects is developed for the comprehensive evaluation of SLAM algorithms.
2. Related Works
2.1. Traditional SLAM Methods
2.2. Factor Graph-Based Approaches and Recent Developments
2.3. Deep Learning and Neural SLAM
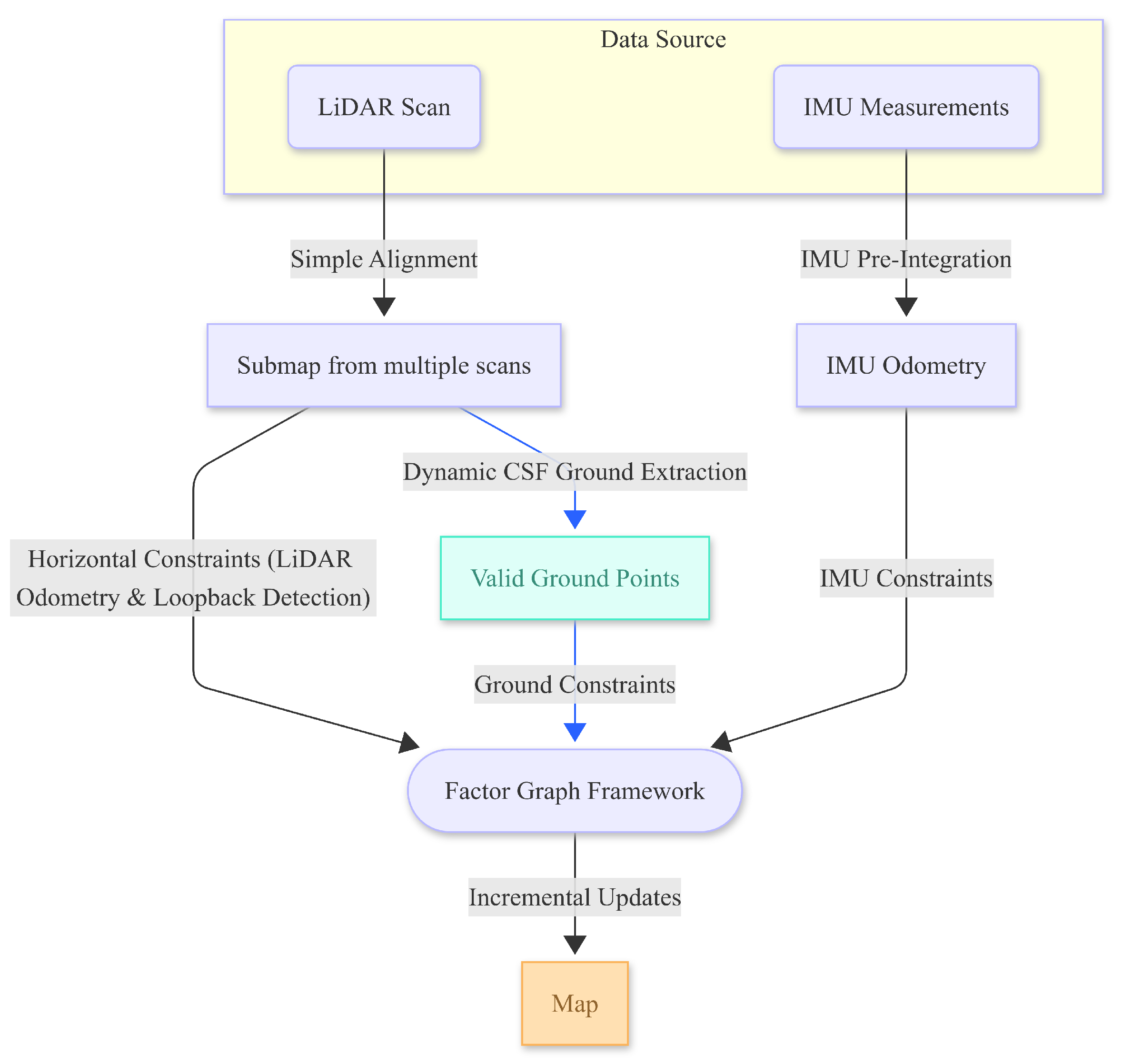
3. Method
3.1. Overview
- 1.
- LiDAR and IMU Data Preprocessing: raw LiDAR point clouds and IMU data are preprocessed to remove noise and outliers.
- 2.
- Optimized Cloth Simulation Filtering (CSF): ground points are extracted from the LiDAR point cloud using an optimized CSF algorithm.
- 3.
- Ground Constraint Factor Integration: the extracted ground points are used to create ground features, which are integrated into the LIO-SAM factor graph for ground constraints.
- 4.
- Factor Graph Optimization: the LIO-SAM framework optimizes the system’s state estimation using the factor graph, incorporating the ground constraint factor to reduce Z-axis drift between factor nodes.
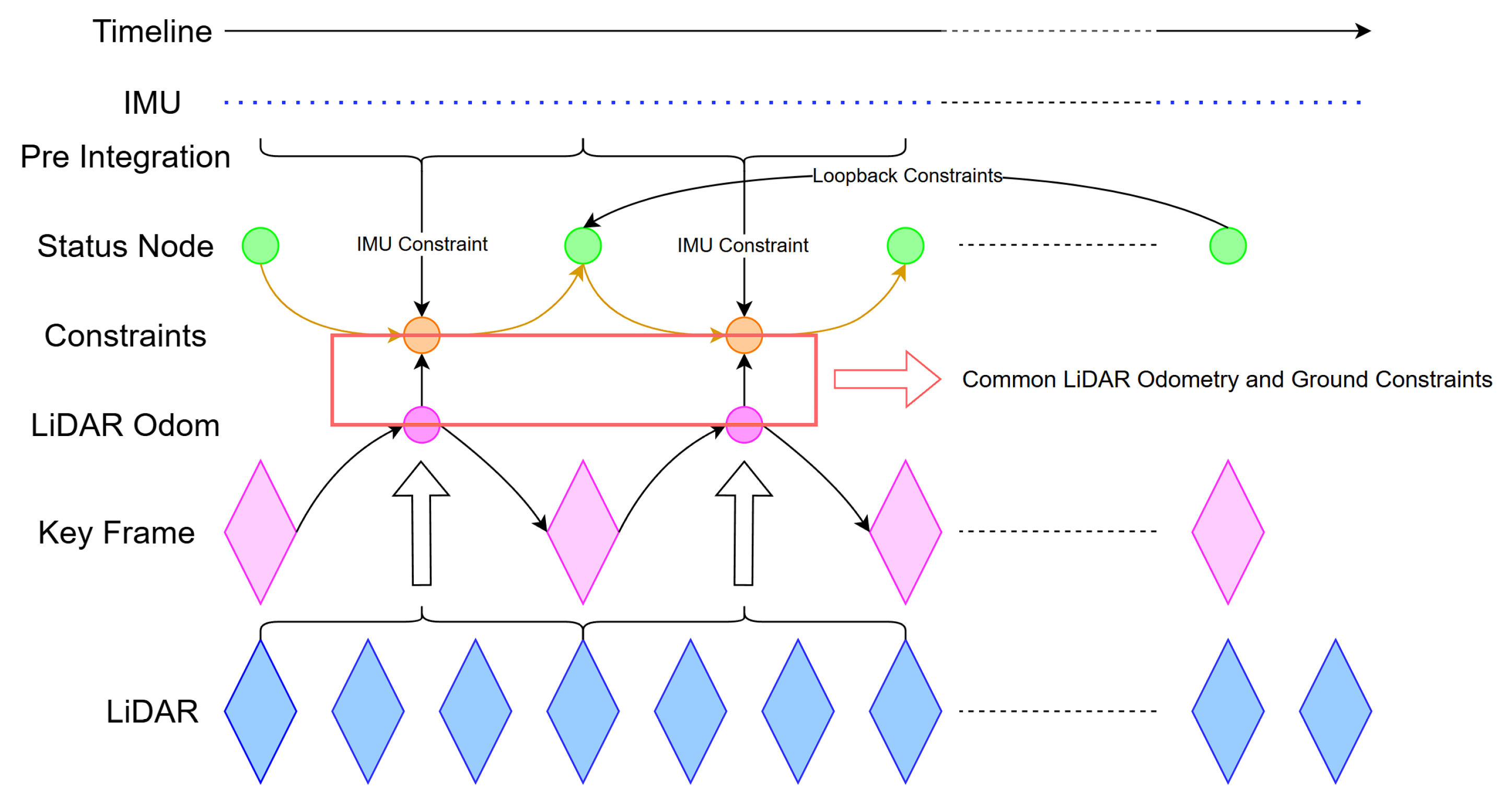
3.2. Dual Pipelines for Horizontal and Ground Constraints
3.3. Back-End Optimization with Separate Ground and Horizontal Constraints
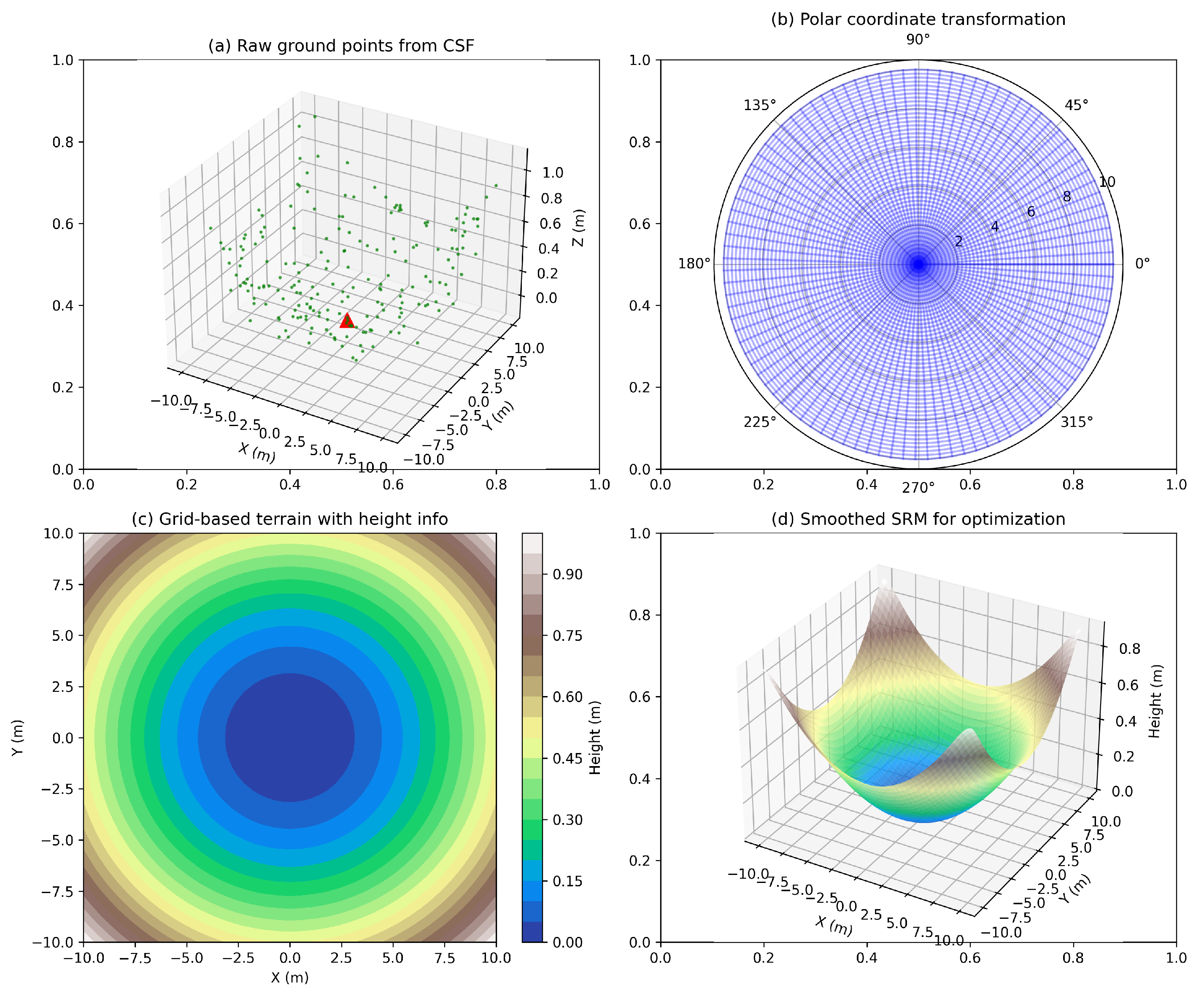
3.3.1. Slope Range Map
- 1.
- Height : the elevation of the terrain at a distance (radius) r and direction (angle) relative to the vehicle’s current position.
- 2.
- Slope : the angle of the terrain’s incline relative to the horizontal plane at the given point. The slope is defined as the change in height per unit distance in the radial direction.
- 3.
- Direction : the orientation of the slope relative to the vehicle’s current heading, which indicates the steepest descent at that particular point.
3.3.2. Factor Graph Optimization Incorporating Ground Constraints
- 1.
- Local Bundle Adjustment: For all keyframes within a certain spatial distance threshold from the new keyframe, odometry measurements are computed, and bundle adjustment is performed within the current sliding window:
- 2.
- Window Management: When the window size exceeds the predefined limit, the oldest keyframe is marginalized out, and its information is compressed into prior factors to maintain computational efficiency.
- 3.
- Loop Closure Handling: Upon loop closure detection between the current pose and a historical pose (where the historical pose may be outside the current window), the system extends the optimization scope to include both poses:Following loop closure, a global bundle adjustment is performed on all keyframes to propagate the correction throughout the entire trajectory.
4. Experiments and Results
4.1. Dataset Description
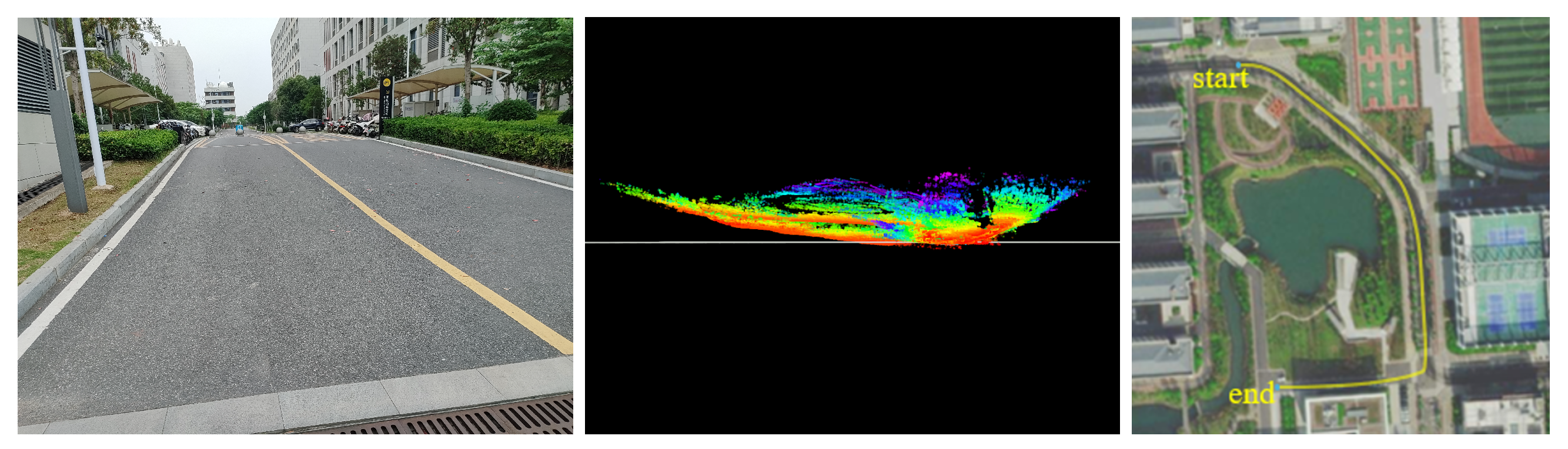
- “Path” Datasets: Our newly collected dataset, named “Path”, was compiled to capture different environmental characteristics and terrains to comprehensively evaluate the performance of SLAM algorithms including the proposed LIO-GC. As shown in Figure 5, this dataset features substantial ground undulations and includes complex environmental objects such as lakes, dirt mounds, trenches, and irregular buildings. The platform does not revisit any previous locations in a trajectory. Therefore, no loop closure should occur in SLAM algorithms.Figure 5. Features of our dataset: pictures of slopes (left), ground points generated by LIO-GC with horizontal viewport (middle), and satellite pictures (right).Figure 5. Features of our dataset: pictures of slopes (left), ground points generated by LIO-GC with horizontal viewport (middle), and satellite pictures (right).
- S3E Dataset: This is a large-scale multi-robot multimodal dataset [42] designed for collaborative SLAM research, featuring diverse environments and cooperative trajectory patterns, making it suitable for evaluating SLAM algorithms in various scenarios. This dataset was made using a fleet of unmanned ground vehicles, each equipped with a 16-line LiDAR, several high-resolution cameras, a 9-axis IMU, and a dual-antenna RTK receiver. Here, we use the “Dormitory” subset as our additional testing data because this part has complete ground truth.
4.2. Evaluation Metrics
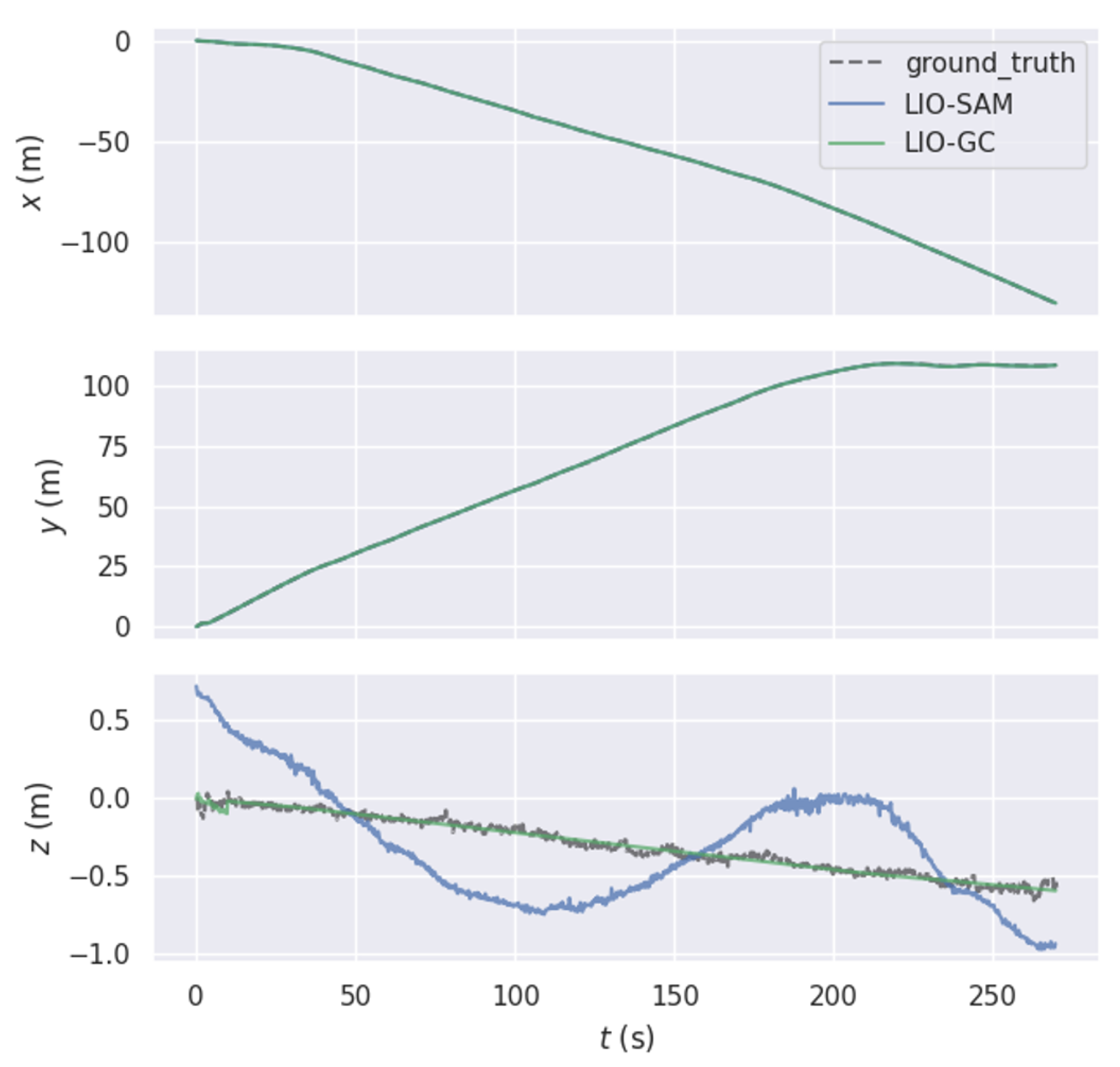
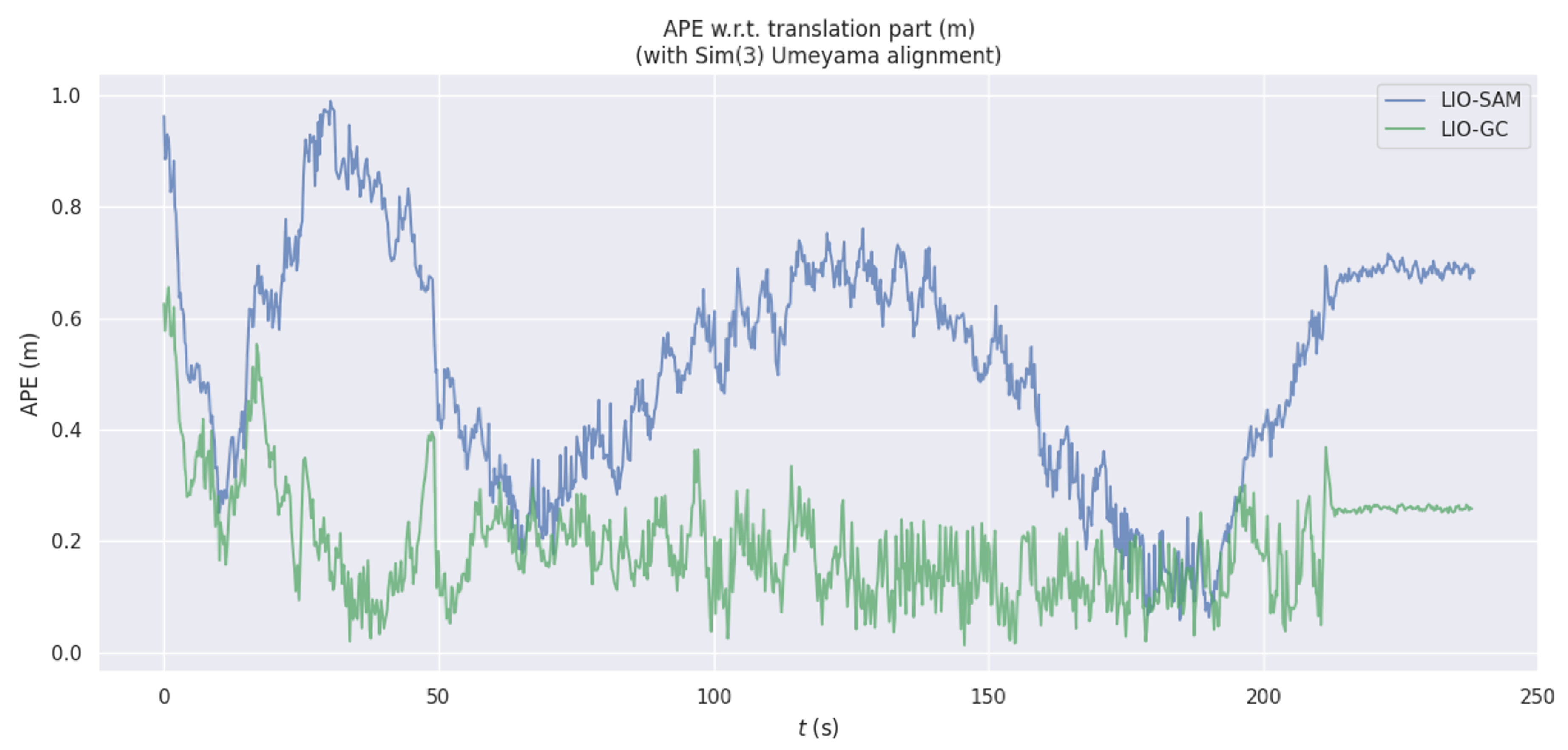
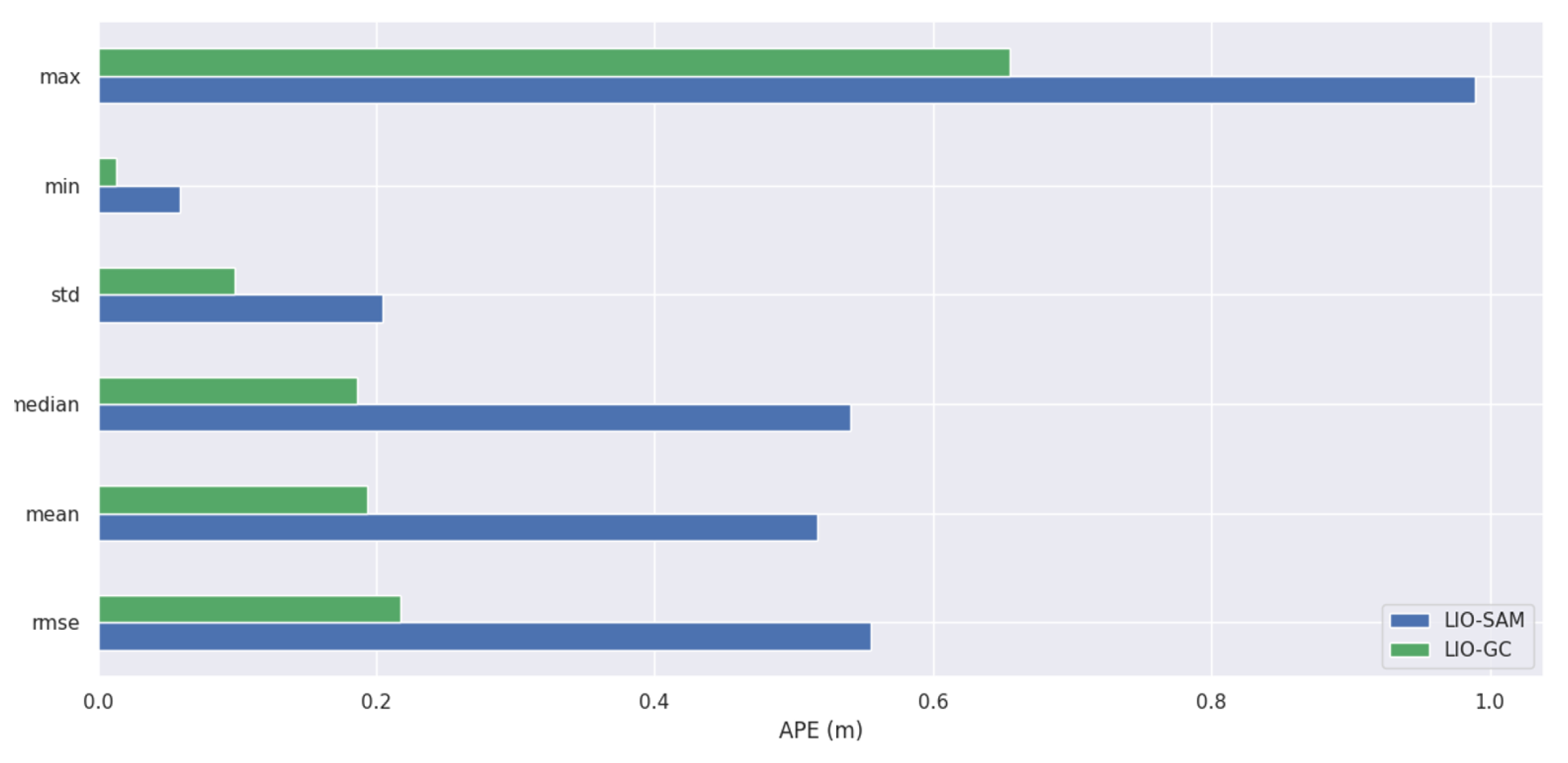
- Root Mean Square Error (RMSE): This metric measures the average magnitude of the error in the estimated trajectory. It provides a quantitative assessment of the system’s localization accuracy.
- Maximum Error (Max Error): This metric measures the maximum error during the whole experiment process. It provides an indication of the worst-case performance of the system, like running on a long path without any loopback.
- Computational Efficiency: This metric measures the computational resources required by the system, including average CPU and memory consumption. It provides an assessment of the system’s real-time performance and the possibility of integration with other systems
4.3. Overall Performance Comparison
4.4. Ablation Study
5. Discussion
5.1. Summary of Key Findings
5.2. Performance–Accuracy Trade-Off
- Voxel Filtering Granularity: The LIO-SAM algorithm has a default downsampling factor of 2, meaning that half of the points from the original point cloud are considered valid points for processing. Initially, we planned to apply the same downsampling factor when using CSF on point cloud maps generated by stitching multiple submaps. However, experimental results revealed that continuing with downsampling not only fails to yield significant improvements in computational efficiency—as downsampling itself incurs computational costs—but also leads to noticeable errors in ground extraction that cannot be ignored.
- GPU vs. CPU Trade-offs: Our algorithm quickly occupied almost all computing resources after startup and then gradually fell back to normal fluctuations. We moved some CPU load to GPU, and the iteration speed of CSF was boosted by up to eight times. However, due to the switch from CPU tasks to GPU tasks, the overall real-time performance slightly improved. Nonetheless, the average CPU load decreased from 65% to 54%, and power consumption increased to 18W. Theoretically, the CPU load should drop even more. However, when reducing the CPU’s direct calculation of point cloud data, we add to the task of handing the data to the GPU and assigning tasks.
- Parameters: The extrinsic parameter calibration between sensors has a great impact on this type of tightly coupled LIO algorithm. In our experimental setup, the initial guess of the extrinsic parameters came from the direct calculation of the mechanical structure, and the external parameters were calibrated by the automatic calibration algorithm. We also tested different parameters among the CSF algorithm and found that limiting CSF iterations to 300 (from 500) had almost no significant influence on the mapping result of our “Path” dataset.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSF | Cloth Simulation Filtering |
| LIO | LiDAR-Inertial Odometry |
| GC | Ground Constraint |
| RMSE | Root Mean Square Error |
| SSE | Sum of Squared Error |
References
- Capobianco, G.; Enea, M.R.; Ferraro, G. Geometry and analysis in Euler’s integral calculus. Arch. Hist. Exact Sci. 2017, 71, 1–38. [Google Scholar] [CrossRef]
- Yang, T.; Li, Y.; Zhao, C.; Yao, D.; Chen, G.; Sun, L.; Krajnik, T.; Yan, Z. 3D ToF LiDAR in mobile robotics: A Review. arXiv 2022, arXiv:2202.11025. [Google Scholar]
- Wang, J.; Xu, L.; Fu, H.; Meng, Z.; Xu, C.; Cao, Y.; Lyu, X.; Gao, F. Towards Efficient Trajectory Generation for Ground Robots beyond 2D Environment. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 7858–7864. [Google Scholar]
- Jardali, H.; Ali, M.; Liu, L. Autonomous Mapless Navigation on Uneven Terrains. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 13227–13233. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are We Ready for Autonomous Driving? The KITTI Vision Benchmark Suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Yin, J.; Li, A.; Li, T.; Yu, W.; Zou, D. M2DGR: A Multi-Sensor and Multi-Scenario SLAM Dataset for Ground Robots. IEEE Robot. Autom. Lett. 2022, 7, 2266–2273. [Google Scholar] [CrossRef]
- Kim, G.; Park, Y.; Cho, Y.; Jeong, J.; Kim, A. MulRan: Multimodal Range Dataset for Urban Place Recognition. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–4 June 2020; pp. 6246–6253. [Google Scholar]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Wei, W.; Shirinzadeh, B.; Ghafarian, M.; Esakkiappan, S.; Shen, T. Hector SLAM with ICP Trajectory Matching. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Toronto, ON, Canada, 8–9 July 2020. [Google Scholar]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-Time. In Proceedings of the Robotics: Science and Systems X, Berkeley, CA, USA, 13–17 July 2015. [Google Scholar]
- Deschaud, J.-E. IMLS-SLAM: Scan-to-model matching based on 3D data. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 2480–2485. [Google Scholar]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. LIO-SAM: Tightly-Coupled Lidar Inertial Odometry via Smoothing and Mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020. [Google Scholar]
- Kaess, M.; Johannsson, H.; Roberts, R.; Ila, V.; Leonard, J.J.; Dellaert, F. iSAM2: Incremental Smoothing and Mapping Using the Bayes Tree. Int. J. Robot. Res. 2012, 31, 216–235. [Google Scholar] [CrossRef]
- Dellaert, F. Factor Graphs and GTSAM: A Hands-on Introduction; Georgia Institute of Technology: Atlanta, GA, USA, 2012. [Google Scholar]
- Jiang, C.; Chen, Y.; Xu, B.; Jia, J.; Sun, H.; Chen, C.; Duan, Z.; Bo, Y.; Hyyppa, J. Vector Tracking Based on Factor Graph Optimization for GNSS NLOS Bias Estimation and Correction. IEEE Internet Things J. 2022, 9, 16209–16221. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Chen, C. Application of IMU Pre-Integration in Variable-Height Lidar Odometry. In Proceedings of the 2020 4th International Conference on Robotics and Automation Sciences (ICRAS), Chengdu, China, 14–16 June 2020; Volume 49, pp. 112–116. [Google Scholar]
- Wu, Y.; Niu, X.; Kuang, J. A Comparison of Three Measurement Models for the Wheel-Mounted MEMS IMU-Based Dead Rechoning System. IEEE Trans. Veh. Technol. 2021, 70, 11193–11203. [Google Scholar] [CrossRef]
- Shi, H.-h.; He, F.-j.; Dang, S.-w.; Wang, K.-l. Research on Slam Algorithm of Iterated Extended Kalman Filtering for Multi-Sensor Fusion. In Proceedings of the Proceedings of the 3rd International Conference on Communication and Information Processing, Tokyo, Japan, 24–26 November 2017. [Google Scholar]
- Chen, K.; Nemiroff, R.; Lopez, B. Direct LiDAR-Inertial Odometry: Lightweight LIO with Continuous-Time Motion Correction. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023. [Google Scholar]
- Liu, Z.; Zhang, F. BALM: Bundle Adjustment for Lidar Mapping. IEEE Robot. Autom. Lett. 2021, 6, 3184–3191. [Google Scholar] [CrossRef]
- Lee, S.; Lim, H.; Myung, H. Patchwork++: Fast and Robust Ground Segmentation Solving Partial Under-Segmentation Using 3D Point Cloud. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022. [Google Scholar]
- Ren, H.; Wang, M.; Li, W.; Liu, C.; Zhang, M. Adaptive Patchwork: Real-Time Ground Segmentation for 3D Point Cloud with Adaptive Partitioning and Spatial-Temporal Context. IEEE Robot. Autom. Lett. 2023, 8, 7162–7169. [Google Scholar] [CrossRef]
- Huang, K.; Zhao, J.; Zhu, Z.; Ye, C.; Feng, T. LOG-LIO: A LiDAR-Inertial Odometry with Efficient Local Geometric Information Estimation. IEEE Robot. Autom. Lett. 2024, 9, 459–466. [Google Scholar] [CrossRef]
- Oh, M.; Jung, E.; Lim, H.; Song, W.; Hu, S.; Lee, E.; Park, J.; Kim, J.; Lee, J.; Myung, H. TRAVEL: Traversable Ground and Above-Ground Object Segmentation Using Graph Representation of 3D LiDAR Scans. IEEE Robot. Autom. Lett. 2022, 7, 7255–7262. [Google Scholar] [CrossRef]
- An, Y.; Liu, W.; Cui, Y.; Wang, J.; Li, X.; Hu, H. Multilevel Ground Segmentation for 3-D Point Clouds of Outdoor Scenes Based on Shape Analysis. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, Y.; Yang, X.; Dou, Z.; Kang, L. Robust multi-task learning network for complex LiDAR point cloud data preprocessing. Expert Syst. Appl. 2024, 237, 121552. [Google Scholar] [CrossRef]
- Chen, X.; Milioto, A.; Palazzolo, E.; Giguere, P.; Behley, J.; Stachniss, C. SuMa++: Efficient LiDAR-Based Semantic SLAM. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4530–4537. [Google Scholar]
- Matsuki, H.; Murai, R.; Kelly, P.H.J.; Davison, A.J. Gaussian Splatting SLAM. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 18039–18048. [Google Scholar]
- Yan, C.; Qu, D.; Xu, D.; Zhao, B.; Wang, Z.; Wang, D.; Li, X. GS-SLAM: Dense Visual SLAM with 3D Gaussian Splatting. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 17–21 June 2024; pp. 19595–19604. [Google Scholar]
- Liso, L.; Sandström, E.; Yugay, V.; Gool, L.; Oswald, M.; Zürich, E.; Leuven, K. Loopy-SLAM: Dense Neural SLAM with Loop Closures. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 17–21 June 2024; pp. 20363–20373. [Google Scholar]
- Li, Y.; Li, C.; Wang, S.; Fang, J. A CSF-modified filtering method based on topography feature. Remote Sense Technol. Appl. 2019, 34, 1261–1268. [Google Scholar]
- Gavin, H.P. The Levenberg-Marquardt Algorithm for Nonlinear Least Squares Curve-Fitting Problems; Technical Report; Department of Civil and Environmental Engineering, Duke University: Durham, NC, USA, 2019. [Google Scholar]
- Kim, G.; Kim, A. Scan Context: Egocentric Spatial Descriptor for Place Recognition Within 3D Point Cloud Map. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Lu, F.; Milios, E. Globally Consistent Range Scan Alignment for Environment Mapping. Auton. Robot. 1997, 4, 333–349. [Google Scholar] [CrossRef]
- Singh, H.; Mishra, K.; Chattopadhyay, A. Inverse Unscented Kalman Filter. IEEE Trans. Signal Process. 2024, 72, 2692–2709. [Google Scholar] [CrossRef]
- Júnior, G.P.C.; Renzende, A.M.C.; Miranda, V.R.F.; Fernandes, R.; Azpúrua, H.; Neto, A.A.; Pessin, G.; Freitas, G.M. EKF-LOAM: An adaptive fusion of LiDAR SLAM with wheel odometry and inertial data for confined spaces with few geometric features. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1458–1471. [Google Scholar] [CrossRef]
- Pan, H.; Liu, D.; Ren, J.; Huang, T.; Yang, H. LiDAR-IMU Tightly-Coupled SLAM Method Based on IEKF and Loop Closure Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 6986–7001. [Google Scholar] [CrossRef]
- Li, S.; Li, G.; Wang, L.; Yang, X. LiDAR/IMU tightly coupled real-time localization method. Acta Autom. Sin. 2021, 47, 1377–1389. [Google Scholar]
- Jiang, T.; Wang, Y.; Liu, S.; Cong, Y.; Dai, L.; Sun, J. Local and Global Structure for Urban ALS Point Cloud Semantic Segmentation with Ground-Aware Attention. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Yang, L.; Sang, J.; Sun, W.; Liao, X.; Sun, M. Non-Stationary SBL for SAR Imagery Under Non-Zero Mean Additive Interference. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar]
- Feng, D.; Qi, Y.; Zhong, S.; Chen, Z. S3E: A Multi-Robot Multimodal Dataset for Collaborative SLAM. IEEE Robot. Autom. Lett. 2024, 9, 11401–11408. [Google Scholar] [CrossRef]
- Bai, C.; Xiao, T.; Chen, Y.; Wang, H.; Zhang, F.; Gao, X. Faster-LIO: Lightweight Tightly Coupled Lidar-Inertial Odometry Using Parallel Sparse Incremental Voxels. IEEE Robot. Autom. Lett. 2022, 7, 4861–4868. [Google Scholar] [CrossRef]
- He, D.; Xu, W.; Chen, N.; Kong, F.; Yuan, C.; Zhang, F. Point-LIO: Robust High-Bandwidth Light Detection and Ranging Inertial Odometry. Adv. Intell. Syst. 2023, 5, 2200459. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, F. R3LIVE: A Robust, Real-Time, RGB-Colored, LiDAR-Inertial-Visual Tightly-Coupled State Estimation and Mapping Package. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022. [Google Scholar]

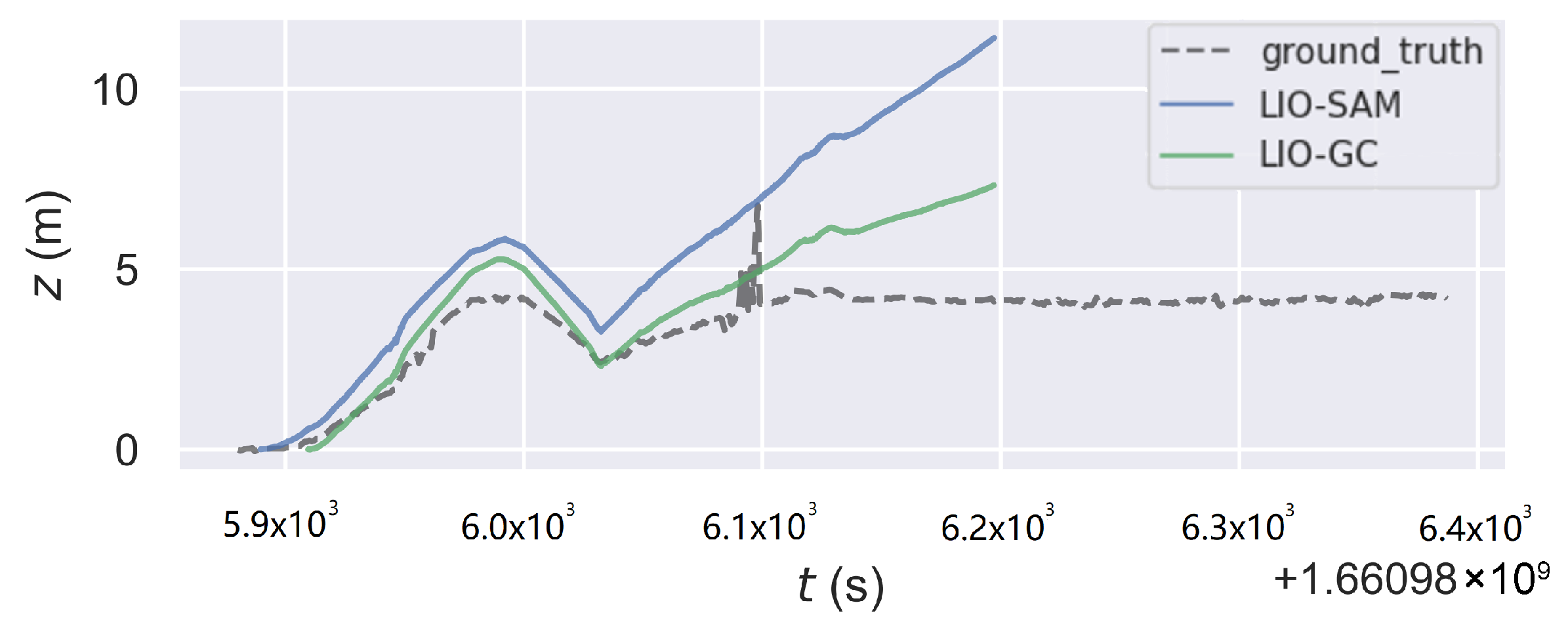
| Algorithm | RMSE (m) | Mean (m) | SSE (m2) | Max (m) |
|---|---|---|---|---|
| LIO-SAM | 0.38 | 0.34 | 176.98 | 8.77 |
| Faster-LIO [43] | 0.36 | 0.30 | 188.56 | 11.08 |
| Point-LIO [44] | 0.76 | 0.69 | 293.31 | 11.96 |
| r3live [45] | Failed | Failed | Failed | Failed |
| LIO-GC (ours) | 0.14 | 0.12 | 171.46 | 8.49 |
| Algorithm | RMSE (m) | Mean (m) | SSE (m2) | Max (m) |
|---|---|---|---|---|
| LIO-SAM | 4.43 | 3.99 | 93,588.16 | 13.92 |
| Faster-LIO | 10.24 | 7.21 | 1,856,489.33 | 25.50 |
| Point-LIO | 7.31 | 5.97 | 938,152.02 | 30.58 |
| r3live | 8.64 | 7.14 | 1,324,997.26 | 31.07 |
| LIO-GC (ours) | 4.46 | 4.12 | 72,086.44 | 10.43 |
| Algorithm | Max (%) | Average (%) |
|---|---|---|
| LIO-GC (without SRM) | 100.0 | 88.7 |
| LIO-GC (with SRM) | 99.2 | 64.4 |
| Configuration | RMSE (m) | Mean (m) | Max (m) | CPU (%) |
|---|---|---|---|---|
| LIO-SAM (baseline) | 0.38 | 0.34 | 8.77 | 45.2 |
| LIO-GC (CSF only) | 0.32 | 0.29 | 6.84 | 88.7 |
| LIO-GC (no optim.) | 0.26 | 0.24 | 6.12 | 85.3 |
| LIO-GC (complete) | 0.14 | 0.12 | 8.49 | 68.2 |
| Configuration | RMSE (m) | Mean (m) | Max (m) | CPU (%) |
|---|---|---|---|---|
| LIO-SAM (baseline) | 0.89 | 0.76 | 15.43 | 43.8 |
| LIO-GC (CSF only) | 0.54 | 0.48 | 14.67 | 86.2 |
| LIO-GC (no optim.) | 0.31 | 0.28 | 9.45 | 83.7 |
| LIO-GC (complete) | 0.29 | 0.26 | 9.82 | 62.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, W.; Wang, J.; Yang, P.; Xiao, W.; Zlatanova, S. LIO-GC: LiDAR Inertial Odometry with Adaptive Ground Constraints. Remote Sens. 2025, 17, 2376. https://doi.org/10.3390/rs17142376
Tian W, Wang J, Yang P, Xiao W, Zlatanova S. LIO-GC: LiDAR Inertial Odometry with Adaptive Ground Constraints. Remote Sensing. 2025; 17(14):2376. https://doi.org/10.3390/rs17142376
Chicago/Turabian StyleTian, Wenwen, Juefei Wang, Puwei Yang, Wen Xiao, and Sisi Zlatanova. 2025. "LIO-GC: LiDAR Inertial Odometry with Adaptive Ground Constraints" Remote Sensing 17, no. 14: 2376. https://doi.org/10.3390/rs17142376
APA StyleTian, W., Wang, J., Yang, P., Xiao, W., & Zlatanova, S. (2025). LIO-GC: LiDAR Inertial Odometry with Adaptive Ground Constraints. Remote Sensing, 17(14), 2376. https://doi.org/10.3390/rs17142376