Applying Deep Learning Methods for a Large-Scale Riparian Vegetation Classification from High-Resolution Multimodal Aerial Remote Sensing Data
Abstract
1. Introduction
- The evaluation of the performance of CNN architectures on the large-scale classification of riparian vegetation in high-resolution aerial images. The influence of different inputs (RGB, NIR, elevation models) and random seeds on the model performance is analyzed. For the combination of the optical images and elevation models, two fusion approaches are evaluated.
- The calibration of the model uncertainties.
- The evaluation of the generalization ability of the trained model. Furthermore, the influence of labelling errors in the ground truth will be investigated.
2. Materials and Methods
2.1. Study Areas
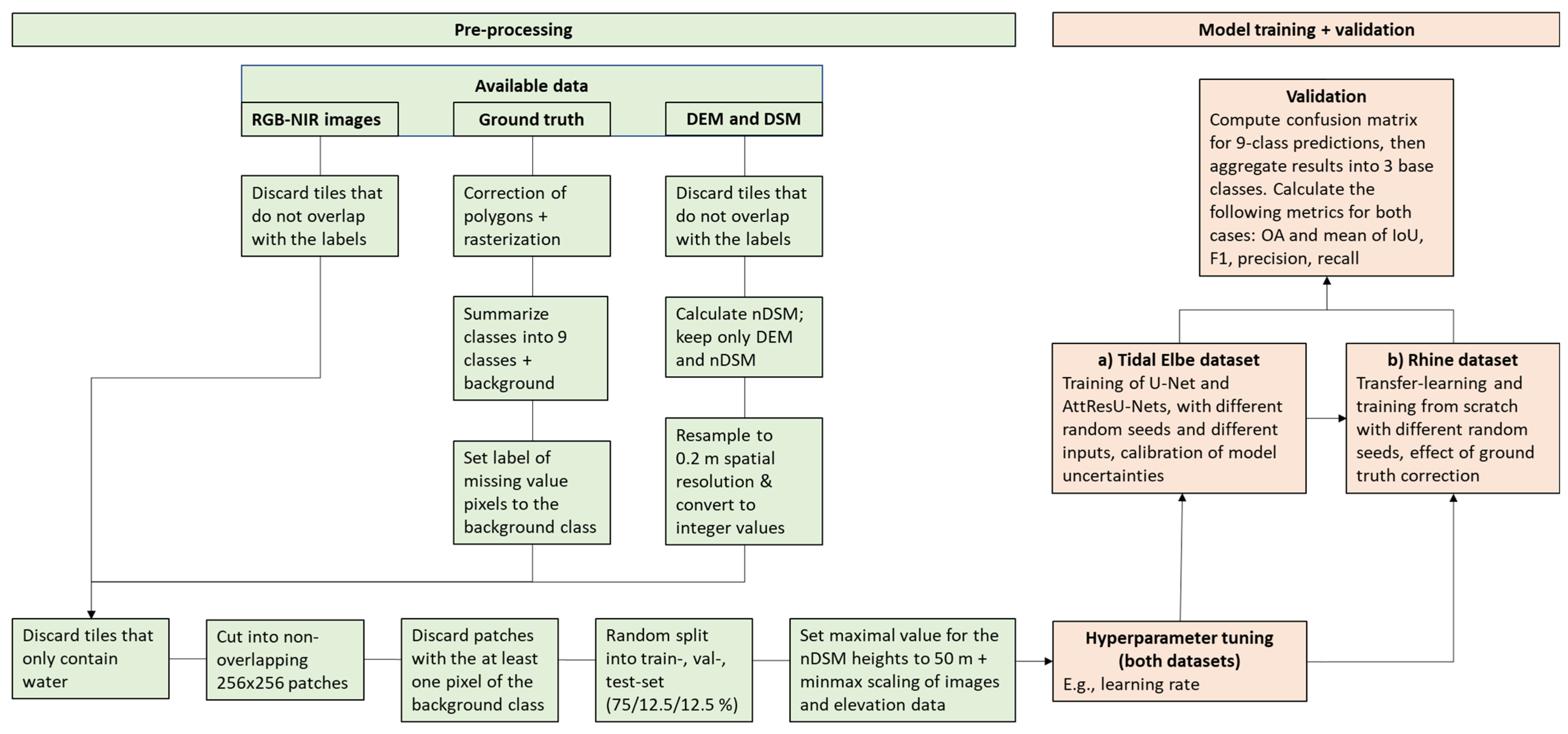
2.2. Data and Pre-Processing
2.3. Classification Algorithms
2.3.1. Basics of CNNs
2.3.2. U-Nets
2.3.3. Residual Connections
2.3.4. Attention
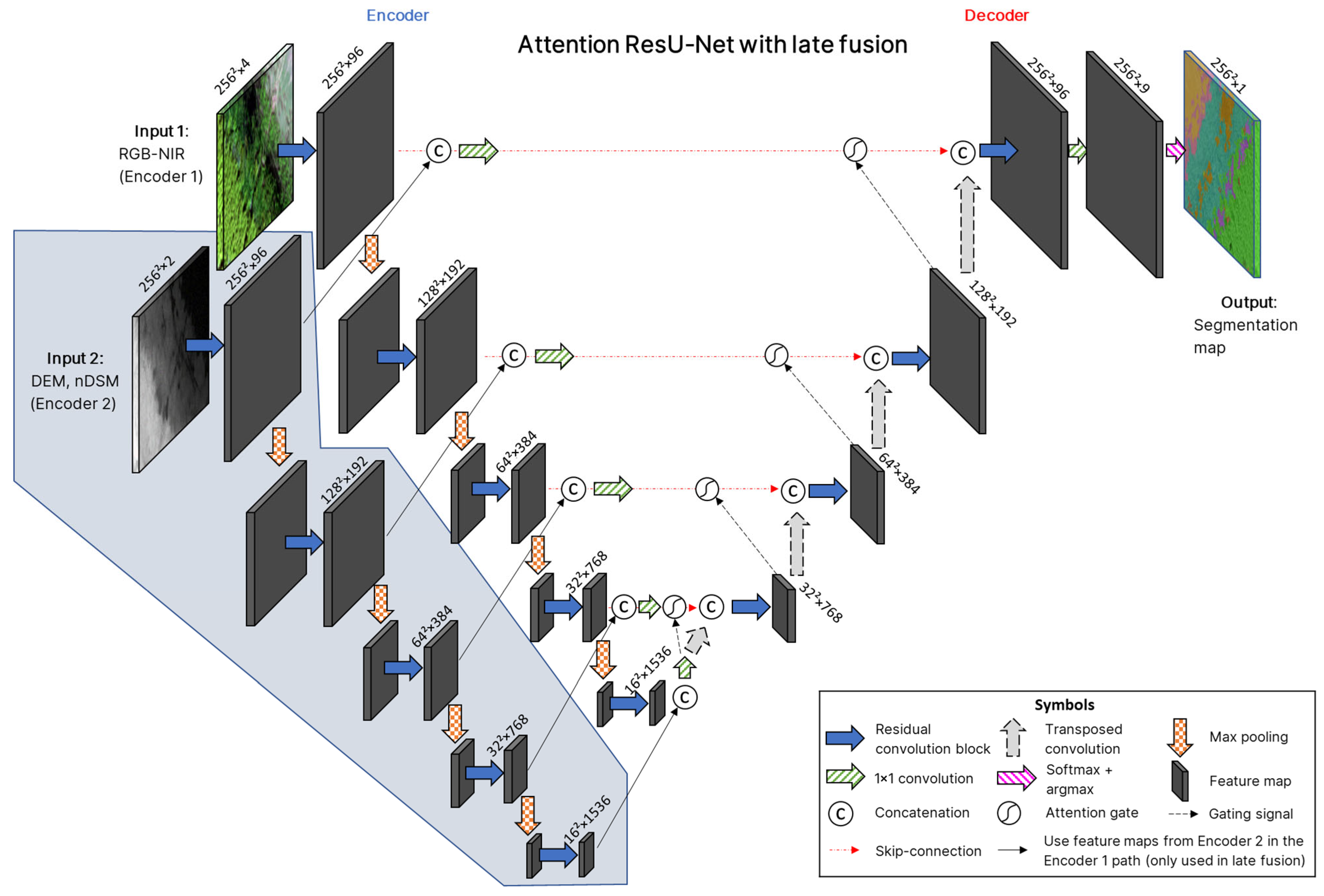
2.3.5. Model Architecture with Early and Late Fusion
2.4. Accuracy Measures
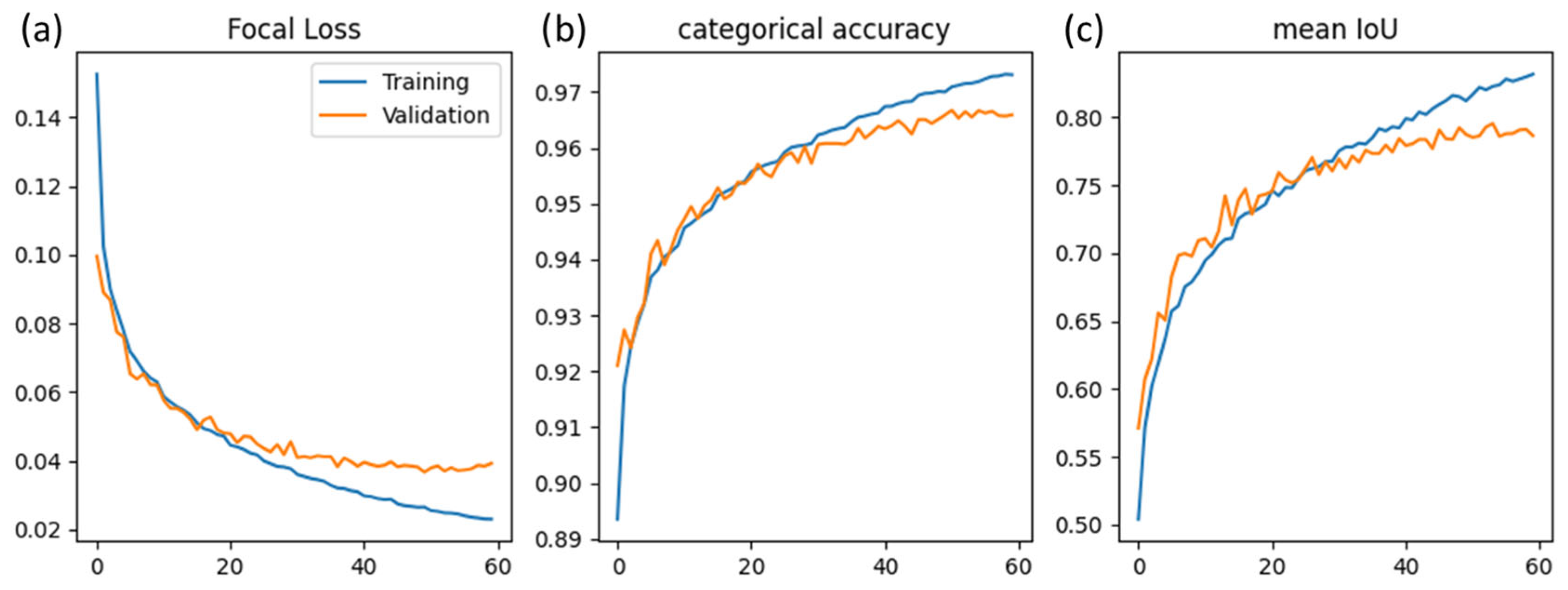
2.5. Model Training
- The loss function (used to quantify the deviation of the model predictions and the ground truth values).
- The optimization algorithm (used to adapt the model weights during training to minimize the loss).
- The initialization of the parameters in the convolutional layers.
- The upsampling method used in the decoder of the U-Net to increase the spatial size of the feature maps.
- The activation function (used to introduce non-linearity into the network).
Transfer Learning
3. Results
3.1. Hyperparameter Tuning
3.2. Performance on the Tidal Elbe Dataset
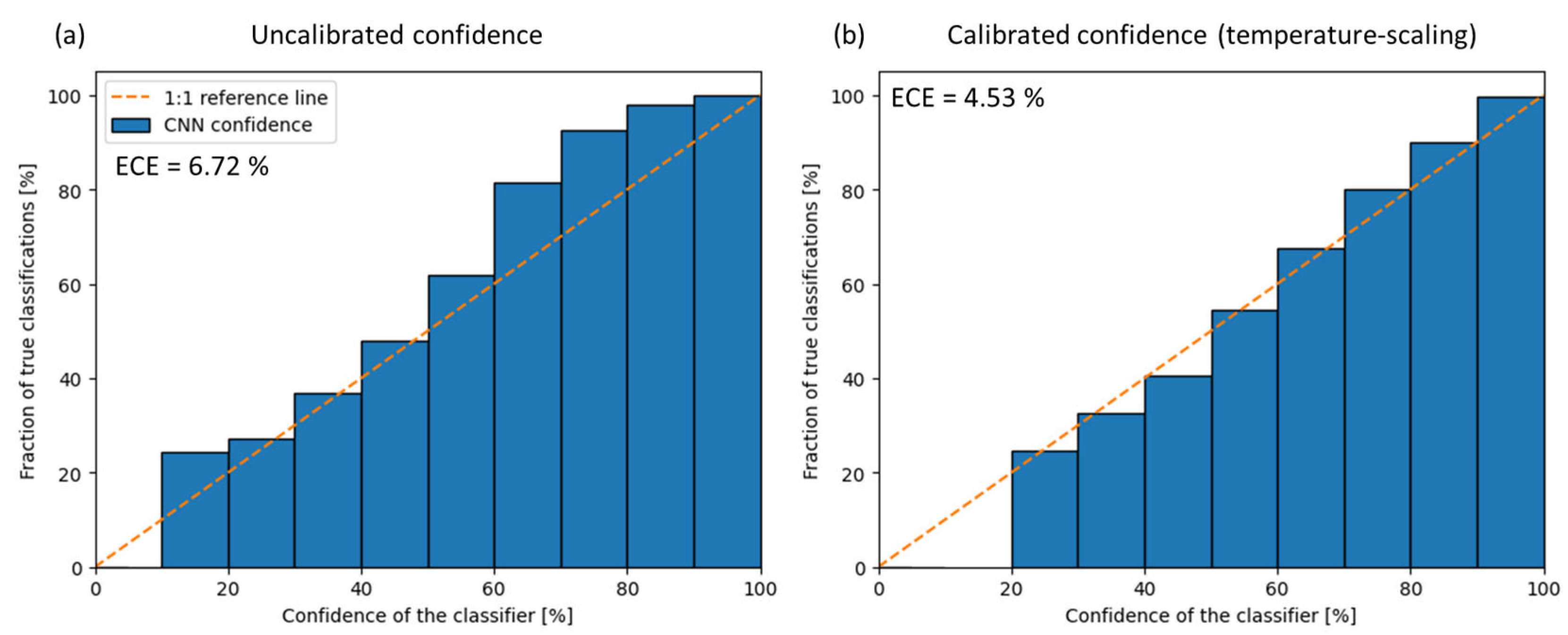
3.3. Model Calibration
3.4. Performance on the Rhine Dataset (Generalization)
4. Discussion
4.1. Random Seeds
4.2. Early vs. Late Fusion
4.3. Model Performance on the Tidal Elbe Dataset
4.4. Model Uncertainties
4.5. Generalization to the Rhine Dataset
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ward, J.V.; Tockner, K.; Schiemer, F. Biodiversity of floodplain river ecosystems: Ecotones and connectivity. Regul. Rivers Res. Manag. 1999, 15, 125–139. [Google Scholar] [CrossRef]
- Wenskus, F.; Hecht, C.; Hering, D.; Januschke, K.; Rieland, G.; Rumm, A.; Scholz, M.; Weber, A.; Horchler, P. Effects of floodplain decoupling on taxonomic and functional diversity of terrestrial floodplain organisms. Ecol. Indic. 2025, 170, 113106. [Google Scholar] [CrossRef]
- Riis, T.; Kelly-Quinn, M.; Aguiar, F.C.; Manolaki, P.; Bruno, D.; Bejarano, M.D.; Clerici, N.; Fernandes, M.R.; Franco, J.C.; Pettit, N.; et al. Global Overview of Ecosystem Services Provided by Riparian Vegetation. BioScience 2020, 70, 501–514. [Google Scholar] [CrossRef]
- Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: A review. J. Plant Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
- Cavender-Bares, J.; Schneider, F.D.; Santos, M.J.; Armstrong, A.; Carnaval, A.; Dahlin, K.M.; Fatoyinbo, L.; Hurtt, G.C.; Schimel, D.; Townsend, P.A.; et al. Integrating remote sensing with ecology and evolution to advance biodiversity conservation. Nat. Ecol. Evol. 2022, 6, 506–519. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Semantic Segmentation of Earth Observation Data Using Multimodal and Multi-scale Deep Networks. arXiv 2016, arXiv:1609.06846. [Google Scholar]
- Holloway, J.; Mengersen, K. Statistical Machine Learning Methods and Remote Sensing for Sustainable Development Goals: A Review. Remote Sens. 2018, 10, 1365. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Rommel, E.; Giese, L.; Fricke, K.; Kathöfer, F.; Heuner, M.; Mölter, T.; Deffert, P.; Asgari, M.; Näthe, P.; Dzunic, F.; et al. Very High-Resolution Imagery and Machine Learning for Detailed Mapping of Riparian Vegetation and Substrate Types. Remote Sens. 2022, 14, 954. [Google Scholar] [CrossRef]
- Fiorentini, N.; Bacco, M.; Ferrari, A.; Rovai, M.; Brunori, G. Remote Sensing and Machine Learning for Riparian Vegetation Detection and Classification. In Proceedings of the 2023 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Pisa, Italy, 6–8 November 2023; pp. 369–374. [Google Scholar]
- Ahmed, S.F.; Alam, M.S.B.; Hassan, M.; Rozbu, M.R.; Ishtiak, T.; Rafa, N.; Mofijur, M.; Shawkat Ali, A.B.M.; Gandomi, A.H. Deep learning modelling techniques: Current progress, applications, advantages, and challenges. Artif. Intell. Rev. 2023, 56, 13521–13617. [Google Scholar] [CrossRef]
- Osco, L.P.; Marcato Junior, J.; Marques Ramos, A.P.; de Castro Jorge, L.A.; Fatholahi, S.N.; de Andrade Silva, J.; Matsubara, E.T.; Pistori, H.; Gonçalves, W.N.; Li, J. A review on deep learning in UAV remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102456. [Google Scholar] [CrossRef]
- Boston, T.; Van Dijk, A.; Larraondo, P.; Thackway, R. Comparing CNNs and Random Forests for Landsat Image Segmentation Trained on a Large Proxy Land Cover Dataset. Remote Sens. 2022, 14, 3396. [Google Scholar] [CrossRef]
- Song, W.; Feng, A.; Wang, G.; Zhang, Q.; Dai, W.; Wei, X.; Hu, Y.; Amankwah, S.O.Y.; Zhou, F.; Liu, Y. Bi-Objective Crop Mapping from Sentinel-2 Images Based on Multiple Deep Learning Networks. Remote Sens. 2023, 15, 3417. [Google Scholar] [CrossRef]
- Ulku, I.; Akagunduz, E.; Ghamisi, P. Deep Semantic Segmentation of Trees Using Multispectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7589–7604. [Google Scholar] [CrossRef]
- Zhang, X.; Han, L.; Han, L.; Zhu, L. How Well Do Deep Learning-Based Methods for Land Cover Classification and Object Detection Perform on High Resolution Remote Sensing Imagery? Remote Sens. 2020, 12, 417. [Google Scholar] [CrossRef]
- Bazi, Y.; Bashmal, L.; Rahhal, M.M.A.; Dayil, R.A.; Ajlan, N.A. Vision Transformers for Remote Sensing Image Classification. Remote Sens. 2021, 13, 516. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, M.; Lei, F. Mapping Vegetation Types by Different Fully Convolutional Neural Network Structures with Inadequate Training Labels in Complex Landscape Urban Areas. Forests 2023, 14, 1788. [Google Scholar] [CrossRef]
- Correa Martins, J.A.; Marcato Junior, J.; Pätzig, M.; Sant’Ana, D.A.; Pistori, H.; Liesenberg, V.; Eltner, A. Identifying plant species in kettle holes using UAV images and deep learning techniques. Remote Sens. Ecol. Conserv. 2022, 9, 1–16. [Google Scholar] [CrossRef]
- Detka, J.; Coyle, H.; Gomez, M.; Gilbert, G.S. A Drone-Powered Deep Learning Methodology for High Precision Remote Sensing in California’s Coastal Shrubs. Drones 2023, 7, 421. [Google Scholar] [CrossRef]
- Fricker, G.A.; Ventura, J.D.; Wolf, J.A.; North, M.P.; Davis, F.W.; Franklin, J. A Convolutional Neural Network Classifier Identifies Tree Species in Mixed-Conifer Forest from Hyperspectral Imagery. Remote Sens. 2019, 11, 2326. [Google Scholar] [CrossRef]
- Kim, K.; Lee, D.; Jang, Y.; Lee, J.; Kim, C.-H.; Jou, H.-T.; Ryu, J.-H. Deep Learning of High-Resolution Unmanned Aerial Vehicle Imagery for Classifying Halophyte Species: A Comparative Study for Small Patches and Mixed Vegetation. Remote Sens. 2023, 15, 2723. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Schiefer, F.; Kattenborn, T.; Frick, A.; Frey, J.; Schall, P.; Koch, B.; Schmidtlein, S. Mapping forest tree species in high resolution UAV-based RGB-imagery by means of convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2020, 170, 205–215. [Google Scholar] [CrossRef]
- Thisanke, H.; Deshan, C.; Chamith, K.; Seneviratne, S.; Vidanaarachchi, R.; Herath, D. Semantic Segmentation using Vision Transformers: A survey. Eng. Appl. Artif. Intell. 2023, 126, 106669. [Google Scholar] [CrossRef]
- Veras, H.F.P.; Ferreira, M.P.; da Cunha Neto, E.M.; Figueiredo, E.O.; Corte, A.P.D.; Sanquetta, C.R. Fusing multi-season UAS images with convolutional neural networks to map tree species in Amazonian forests. Ecol. Inform. 2022, 71, 101815. [Google Scholar] [CrossRef]
- Wagner, F.H.; Sanchez, A.; Tarabalka, Y.; Lotte, R.G.; Ferreira, M.P.; Aidar, M.P.M.; Gloor, E.; Phillips, O.L.; Aragão, L.E.O.C.; Pettorelli, N.; et al. Using the U-net convolutional network to map forest types and disturbance in the Atlantic rainforest with very high resolution images. Remote Sens. Ecol. Conserv. 2019, 5, 360–375. [Google Scholar] [CrossRef]
- Yao, M.; Zhang, Y.; Liu, G.; Pang, D. SSNet: A Novel Transformer and CNN Hybrid Network for Remote Sensing Semantic Segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 3023–3037. [Google Scholar] [CrossRef]
- Yu, A.; Quan, Y.; Yu, R.; Guo, W.; Wang, X.; Hong, D.; Zhang, H.; Chen, J.; Hu, Q.; He, P. Deep Learning Methods for Semantic Segmentation in Remote Sensing with Small Data: A Survey. Remote Sens. 2023, 15, 4987. [Google Scholar] [CrossRef]
- Zhao, S.; Tu, K.; Ye, S.; Tang, H.; Hu, Y.; Xie, C. Land Use and Land Cover Classification Meets Deep Learning: A Review. Sensors 2023, 23, 8966. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y. Study on Vegetation Extraction from Riparian Zone Images Based on Cswin Transformer. Adv. Comput. Signals Syst. 2024, 8, 57–62. [Google Scholar] [CrossRef]
- Gröschler, K.-C.; Muhuri, A.; Roy, S.K.; Oppelt, N. Monitoring the Population Development of Indicator Plants in High Nature Value Grassland Using Machine Learning and Drone Data. Drones 2023, 7, 644. [Google Scholar] [CrossRef]
- Aleissaee, A.A.; Kumar, A.; Anwer, R.M.; Khan, S.; Cholakkal, H.; Xia, G.-S.; Khan, F.S. Transformers in Remote Sensing: A Survey. Remote Sens. 2023, 15, 1860. [Google Scholar] [CrossRef]
- Maurício, J.; Domingues, I.; Bernardino, J. Comparing Vision Transformers and Convolutional Neural Networks for Image Classification: A Literature Review. Appl. Sci. 2023, 13, 5521. [Google Scholar] [CrossRef]
- Wang, G.; Chen, H.; Chen, L.; Zhuang, Y.; Zhang, S.; Zhang, T.; Dong, H.; Gao, P. P2FEViT: Plug-and-Play CNN Feature Embedded Hybrid Vision Transformer for Remote Sensing Image Classification. Remote Sens. 2023, 15, 1773. [Google Scholar] [CrossRef]
- Huang, L.; Jiang, B.; Lv, S.; Liu, Y.; Fu, Y. Deep-Learning-Based Semantic Segmentation of Remote Sensing Images: A Survey. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 8370–8396. [Google Scholar] [CrossRef]
- Lin, X.; Cheng, Y.; Chen, G.; Chen, W.; Chen, R.; Gao, D.; Zhang, Y.; Wu, Y. Semantic Segmentation of China’s Coastal Wetlands Based on Sentinel-2 and Segformer. Remote Sens. 2023, 15, 3714. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Bester, M.S.; Ramezan, C.A. Enhancing Reproducibility and Replicability in Remote Sensing Deep Learning Research and Practice. Remote Sens. 2022, 14, 5760. [Google Scholar] [CrossRef]
- Steier, J.; Goebel, M.; Iwaszczuk, D. Is Your Training Data Really Ground Truth? A Quality Assessment of Manual Annotation for Individual Tree Crown Delineation. Remote Sens. 2024, 16, 2786. [Google Scholar] [CrossRef]
- Berg, P.; Pham, M.-T.; Courty, N. Self-Supervised Learning for Scene Classification in Remote Sensing: Current State of the Art and Perspectives. Remote Sens. 2022, 14, 3995. [Google Scholar] [CrossRef]
- Hosseiny, B.; Mahdianpari, M.; Hemati, M.; Radman, A.; Mohammadimanesh, F.; Chanussot, J. Beyond Supervised Learning in Remote Sensing: A Systematic Review of Deep Learning Approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 1035–1052. [Google Scholar] [CrossRef]
- Rußwurm, M.; Wang, S.; Kellenberger, B.; Roscher, R.; Tuia, D. Meta-learning to address diverse Earth observation problems across resolutions. Commun. Earth Environ. 2024, 5, 37. [Google Scholar] [CrossRef]
- Wang, Y.; Albrecht, C.M.; Braham, N.A.A.; Mou, L.; Zhu, X.X. Self-supervised Learning in Remote Sensing: A Review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 213–247. [Google Scholar] [CrossRef]
- Al-Najjar, H.A.H.; Kalantar, B.; Pradhan, B.; Saeidi, V.; Halin, A.A.; Ueda, N.; Mansor, S. Land Cover Classification from fused DSM and UAV Images Using Convolutional Neural Networks. Remote Sens. 2019, 11, 1461. [Google Scholar] [CrossRef]
- Qiu, K.; Budde, L.E.; Bulatov, D.; Iwaszczuk, D.; Schulz, K.; Nikolakopoulos, K.G.; Michel, U. Exploring fusion techniques in U-Net and DeepLab V3 architectures for multi-modal land cover classification. In Proceedings of the Earth Resources and Environmental Remote Sensing/GIS Applications XIII, Berlin, Germany, 5–7 September 2022. [Google Scholar]
- Maretto, R.V.; Fonseca, L.M.G.; Jacobs, N.; Korting, T.S.; Bendini, H.N.; Parente, L.L. Spatio-Temporal Deep Learning Approach to Map Deforestation in Amazon Rainforest. IEEE Geosci. Remote Sens. Lett. 2021, 18, 771–775. [Google Scholar] [CrossRef]
- Piramanayagam, S.; Saber, E.; Schwartzkopf, W.; Koehler, F. Supervised Classification of Multisensor Remotely Sensed Images Using a Deep Learning Framework. Remote Sens. 2018, 10, 1429. [Google Scholar] [CrossRef]
- Gadzicki, K.; Khamsehashari, R.; Zetzsche, C. Early vs Late Fusion in Multimodal Convolutional Neural Networks. In Proceedings of the 2020 IEEE 23rd International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 6–9 July 2020; pp. 1–6. [Google Scholar]
- Snoek, C.G.M.; Worring, M.; Smeulders, A.W.M. Early versus Late Fusion in Semantic Video Analysis. In Proceedings of the MULTIMEDIA ’05: Proceedings of the 13th Annual ACM International Conference on Multimedia, Singapore, 6–11 November 2005; pp. 339–402. [Google Scholar] [CrossRef]
- Baltrušaitis, T.; Ahuja, C.; Morency, L.-P. Multimodal Machine Learning: A Survey and Taxonomy. arXiv 2019, arXiv:1705.09406. [Google Scholar] [CrossRef]
- Damer, N.; Dimitrov, K.; Braun, A.; Kuijper, A. On Learning Joint Multi-biometric Representations by Deep Fusion. In Proceedings of the 2019 IEEE 10th International Conference on Biometrics Theory, Applications and Systems (BTAS), Tampa, FL, USA, 23–26 September 2019; pp. 1–8. [Google Scholar]
- Fivash, G.S.; Temmerman, S.; Kleinhans, M.G.; Heuner, M.; van der Heide, T.; Bouma, T.J. Early indicators of tidal ecosystem shifts in estuaries. Nat. Commun. 2023, 14, 1911. [Google Scholar] [CrossRef]
- Nature-Consult. Semiautomatisierte Erfassung der Vegetation der Tideelbe auf Grundlage Vorhandener Multisensoraler Fernerkundungsdaten 2017, Report on behalf of the Federal Institute of Hydrology, Koblenz, Germany 61 pages. Unpublished work.
- German Federal Agency for Cartography and Geodesy (BKG). Available online: https://www.bkg.bund.de/EN/Home/home.html (accessed on 18 December 2024).
- BfG; Björnsen Beratende Ingenieure GmbH. Bestandserfassung Rhein Km 49,900 bis Km 50,500 und Km 51,000 bis Km 52,200. Im Auftrag des Wasserstraßen- und Schifffahrtsamtes Bingen. Bundesanstalt für Gewässerkunde, Koblenz, BfG-1942, 2017; Unpublished work.
- Ponti, M.A.; Ribeiro, L.S.F.; Nazare, T.S.; Bui, T.; Collomosse, J. Everything You Wanted to Know about Deep Learning for Computer Vision but Were Afraid to Ask. In Proceedings of the 2017 30th SIBGRAPI Conference on Graphics, Patterns and Images Tutorials (SIBGRAPI-T), Niterói, Brazil, 17–18 October 2017; pp. 17–41. [Google Scholar]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A survey of the recent architectures of deep convolutional neural networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaria, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Lecture Notes in Computer Science. Volume 9351. [Google Scholar] [CrossRef]
- Ouyang, S.; Li, Y. Combining Deep Semantic Segmentation Network and Graph Convolutional Neural Network for Semantic Segmentation of Remote Sensing Imagery. Remote Sens. 2020, 13, 119. [Google Scholar] [CrossRef]
- Shirvani, Z.; Abdi, O.; Goodman, R.C. High-Resolution Semantic Segmentation of Woodland Fires Using Residual Attention UNet and Time Series of Sentinel-2. Remote Sens. 2023, 15, 1342. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37, pp. 448–456. [Google Scholar] [CrossRef]
- Santurkar, S.; Tsipras, D.; Ilyas, A.; Mądry, A. How Does Batch Normalization Help Optimization? In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 2488–2498. [Google Scholar]
- Szandała, T. Review and Comparison of Commonly Used Activation Functions for Deep Neural Networks. arXiv 2021, arXiv:2010.09458. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Chen, Z.; Zhao, J.; Deng, H. Global Multi-Attention UResNeXt for Semantic Segmentation of High-Resolution Remote Sensing Images. Remote Sens. 2023, 15, 1836. [Google Scholar] [CrossRef]
- Park, J.; Woo, S.; Lee, J.-Y.; Kweon, I.S. BAM: Bottleneck Attention Module. arXiv 2018, arXiv:1807.06514. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the ECCV, Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Shi, W.; Meng, Q.; Zhang, L.; Zhao, M.; Su, C.; Jancsó, T. DSANet: A Deep Supervision-Based Simple Attention Network for Efficient Semantic Segmentation in Remote Sensing Imagery. Remote Sens. 2022, 14, 5399. [Google Scholar] [CrossRef]
- Nirthika, R.; Manivannan, S.; Ramanan, A.; Wang, R. Pooling in convolutional neural networks for medical image analysis: A survey and an empirical study. Neural Comput. Appl. 2022, 34, 5321–5347. [Google Scholar] [CrossRef] [PubMed]
- O’Shea, K.; Nash, R. An Introduction to Convolutional Neural Networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Zafar, A.; Aamir, M.; Mohd Nawi, N.; Arshad, A.; Riaz, S.; Alruban, A.; Dutta, A.K.; Almotairi, S. A Comparison of Pooling Methods for Convolutional Neural Networks. Appl. Sci. 2022, 12, 8643. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Guillén, L.A. Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 2: Recommendations and Best Practices. Remote Sens. 2021, 13, 2591. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Guillén, L.A. Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 1: Literature Review. Remote Sens. 2021, 13, 2450. [Google Scholar] [CrossRef]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On Calibration of Modern Neural Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1321–1330. [Google Scholar]
- Patra, R.; Hebbalaguppe, R.; Dash, T.; Shroff, G.; Vig, L. Calibrating Deep Neural Networks using Explicit Regularisation and Dynamic Data Pruning. arXiv 2023, arXiv:2212.10005. [Google Scholar]
- Wojciuk, M.; Swiderska-Chadaj, Z.; Siwek, K.; Gertych, A. Improving classification accuracy of fine-tuned CNN models: Impact of hyperparameter optimization. Heliyon 2024, 10, e26586. [Google Scholar] [CrossRef]
- Taylor, L.; Nitschke, G. Improving Deep Learning with Generic Data Augmentation. In Proceedings of the IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization. J. Mach. Learn. Res. 2018, 18, 1–52. [Google Scholar]
- O’Malley, T.; Bursztein, E.; Long, J.; Chollet, F.; Jin, H.; Invernizzi, L. KerasTuner. Available online: https://github.com/keras-team/keras-tuner (accessed on 18 December 2024).
- Cui, B.; Chen, X.; Lu, Y. Semantic Segmentation of Remote Sensing Images Using Transfer Learning and Deep Convolutional Neural Network With Dense Connection. IEEE Access 2020, 8, 116744–116755. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Chollet, F. Keras. Available online: https://keras.io (accessed on 18 December 2024).
- Bhattiprolu, S. Available online: https://github.com/bnsreenu/python_for_microscopists/blob/master/224_225_226_models.py (accessed on 18 December 2024).
- artemmavrin. Available online: https://github.com/artemmavrin/focal-loss (accessed on 18 December 2024).
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar] [CrossRef]
- Kupidura, P.; Osińska-Skotak, K.; Lesisz, K.; Podkowa, A. The Efficacy Analysis of Determining the Wooded and Shrubbed Area Based on Archival Aerial Imagery Using Texture Analysis. ISPRS Int. J. Geo-Inf. 2019, 8, 450. [Google Scholar] [CrossRef]
- Tu, Y.-H.; Johansen, K.; Phinn, S.; Robson, A. Measuring Canopy Structure and Condition Using Multi-Spectral UAS Imagery in a Horticultural Environment. Remote Sens. 2019, 11, 269. [Google Scholar] [CrossRef]
- Akesson, J.; Toger, J.; Heiberg, E. Random effects during training: Implications for deep learning-based medical image segmentation. Comput. Biol. Med. 2024, 180, 108944. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 6105–6114. [Google Scholar]
- Tzepkenlis, A.; Marthoglou, K.; Grammalidis, N. Efficient Deep Semantic Segmentation for Land Cover Classification Using Sentinel Imagery. Remote Sens. 2023, 15, 27. [Google Scholar] [CrossRef]
- Vaze, S.; Foley, C.J.; Seddiq, M.; Unagaev, A.; Efremova, N. Optimal Use of Multi-spectral Satellite Data with Convolutional Neural Networks. arXiv 2020, arXiv:2009.07000. [Google Scholar]
- Barros, T.; Conde, P.; Gonçalves, G.; Premebida, C.; Monteiro, M.; Ferreira, C.S.S.; Nunes, U.J. Multispectral Vineyard Segmentation: A Deep Learning Comparison Study. arXiv 2022, arXiv:2108.01200. [Google Scholar] [CrossRef]
- Radke, D.; Radke, D.; Radke, J. Beyond Measurement: Extracting Vegetation Height from High Resolution Imagery with Deep Learning. Remote Sens. 2020, 12, 3797. [Google Scholar] [CrossRef]
- Jiao, L.; Huang, Z.; Lu, X.; Liu, X.; Yang, Y.; Zhao, J.; Zhang, J.; Hou, B.; Yang, S.; Liu, F.; et al. Brain-Inspired Remote Sensing Foundation Models and Open Problems: A Comprehensive Survey. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 10084–10120. [Google Scholar] [CrossRef]
- Lu, S.; Guo, J.; Zimmer-Dauphinee, J.R.; Nieusma, J.M.; Wang, X.; VanValkenburgh, P.; Wernke, S.A.; Huo, Y. Vision Foundation Models in Remote Sensing: A Survey. arXiv 2025, arXiv:2408.03464v2. [Google Scholar] [CrossRef]


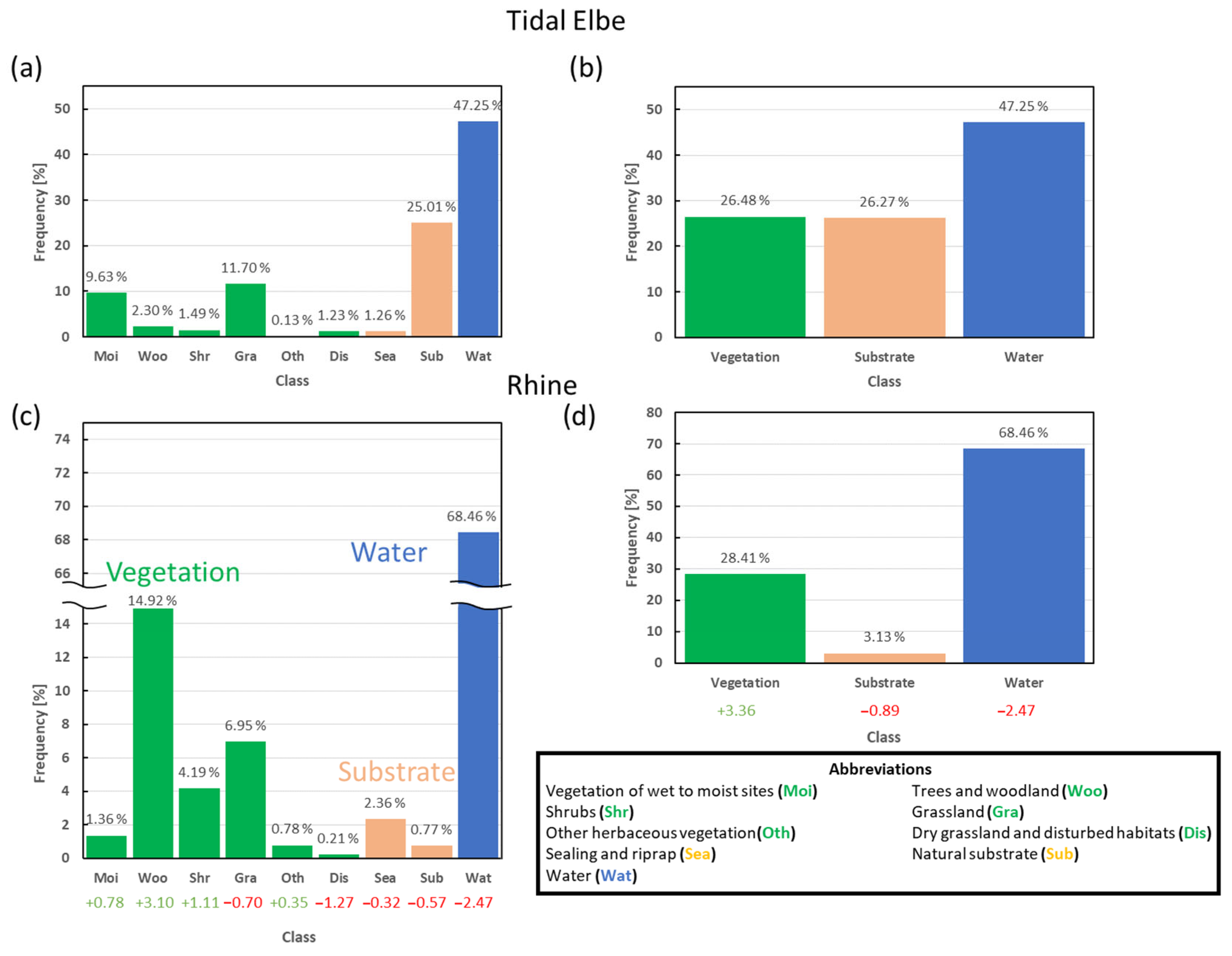


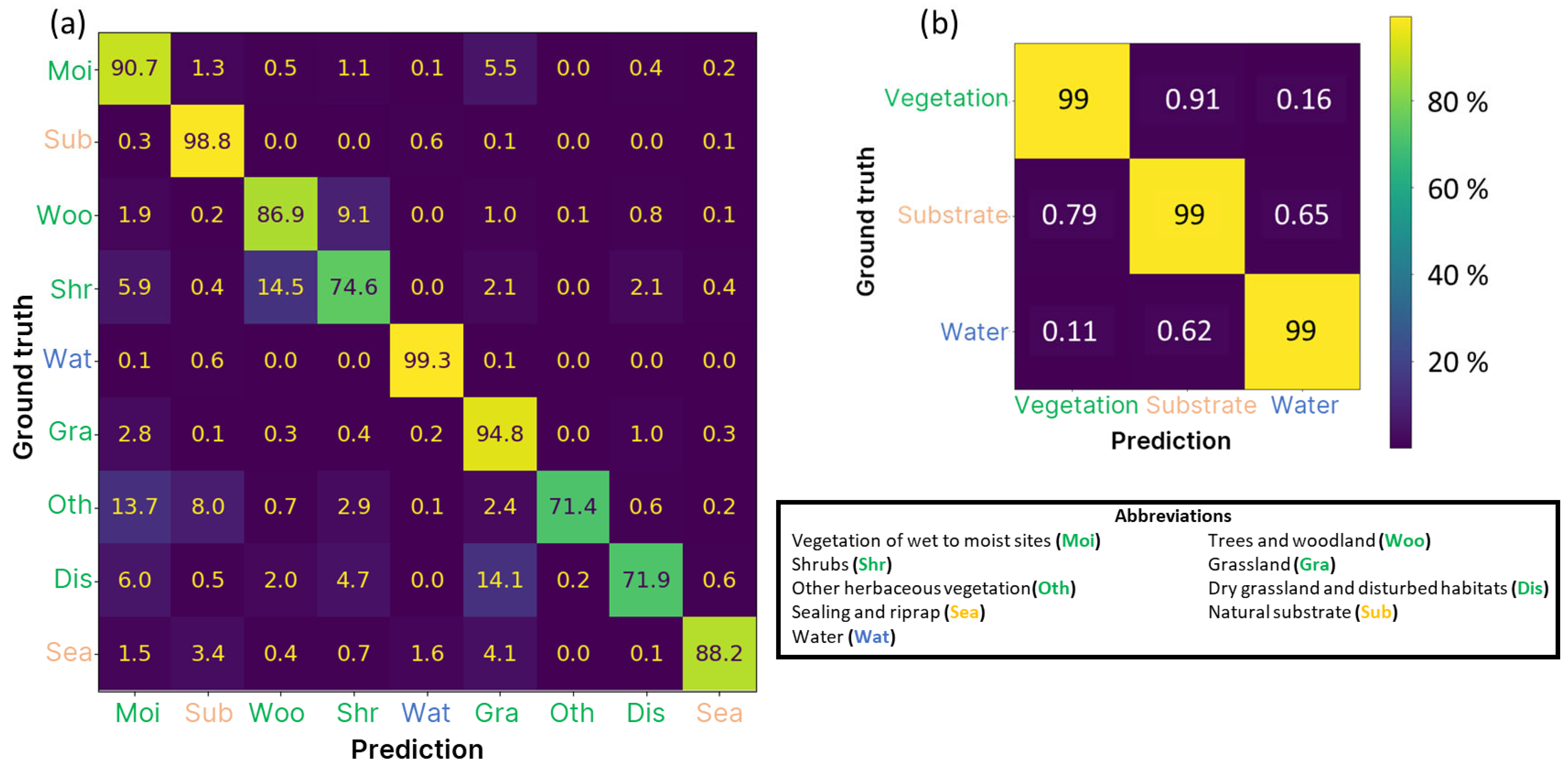




| Class | Description |
|---|---|
| Vegetation of wet to moist sites (Moi) | Vegetation in the immediate vicinity of rivers and lakes. Example units: reed, pioneers, perennials of moist locations |
| Natural substrate (Sub) | Areas without sealing or vegetation. Example units: sand, gravel, fine-grained material, tidal flats, un-sealed roads |
| Trees and Woodland (Woo) | Woody vegetation with a height of >3 m. Example units: deciduous forest, hardwood meadow. Example species: Salix spp., Populus spp. |
| Shrubs (Shr) | Woody vegetation with a height of <3 m |
| Water (Wat) | Rivers, lakes, ponds |
| Grassland (Gra) | Vegetation dominated by grasses. Example units: pasture, grassland of intensive or extensive usage |
| Other herbaceous vegetation (Oth) | Non-woody, herbaceous vegetation at nutrient-rich sites. Example species: Rubus spp., Urtica dioica |
| Dry grassland and disturbed habitats (Dis) | Example units: medium to tall forbs of dry sites. Example species: Calamagrostis epigejos, Artemisia vulgaris |
| Sealing and riprap (Sea) | Example units: rocks, buildings, roads |
| Dataset | Number of 256 × 256 Tiles | Modalities | Number of Field Survey Classes | Number of Large Images | ||
|---|---|---|---|---|---|---|
| Training Set | Validation Set | Test Set | ||||
| Tidal Elbe | 63,327 | 10,772 | 10,545 | RGB-NIR, DSM, DEM | 37 | 392 |
| Rhine | 4312 | 773 | 742 | RGB | 271 | 47 |
| Hyperparameter | Variation | Best Settings for the U-Net Models |
|---|---|---|
| Learning rate | Initial LR: 1 × 10−5, 5 × 10−5, 1 × 10−4, 5 × 10−4, 1× 10−3 Decay schemes: none, step decay (Step size: 3, 4, 5, 6, 7; decay rate: 0.7, 0.75, 0.8, 0.85, 0.9) | 1 × 10−4 with a step decay (5, 0.8) |
| Batch normalization (BN) | With/without Momentum parameter: 0.7, 0.75, 0.8, 0.85, 0.9 | With BN, momentum = 0.85 |
| Optimization Algorithm | Adam RMSprop SGD | Adam |
| Loss function | Focal loss (gamma = 2) Cross-entropy loss Dice loss | Focal loss |
| Number of stages in the U-Nets (without the bridge) | 3, 4 | 4 |
| Dropout layer | Without/with: 0.1, 0.2 | Without |
| Parameter initialization | Random He-normal | He-normal |
| Number of Epochs | Up to 100 | 60 |
| Upscaling | Transposed convolution Upsampling (nearest neighbor) | Transposed convolution |
| Activation function | ReLU Leaky ReLU (alpha = 0.1) | ReLU |
| Input Data Modality | Mean IoU | Mean F1-Score | Overall Accuracy | Mean Precision | Mean Recall | Training Duration per Epoch [s] | Number of Trainable Parameters |
|---|---|---|---|---|---|---|---|
| U-Net | |||||||
| RGB-NIR | 75.05 74.74–75.23 | 84.69 84.50–84.81 | 96.00 95.87–96.07 | 86.83 86.23–87.43 | 83.23 83.02–83.44 | ~1755 | 69,834,249 |
| AttResU-Net | |||||||
| RGB | 75.41 74.97–75.80 | 84.97 84.61–85.27 | 96.03 95.97–96.08 | 87.13 87.07–87.27 | 83.51 82.98–83.96 | ~2398 | 78,472,545 |
| RGB-NIR | 76.47 76.23–76.73 | 85.75 85.57–85.89 | 96.32 96.29–96.36 | 87.55 87.44–87.78 | 84.39 84.21–84.49 | ~2406 | 78,473,505 |
| RGB, DEM, nDSM | 77.91 77.56–78.19 | 86.82 86.57–87.02 | 96.43 96.37–96.49 | 88.20 87.59–88.51 | 85.39 85.39–85.87 | ~2567 | 78,474,465 |
| DEM, nDSM | 65.71 | 77.42 | 93.49 | 80.84 | 75.28 | ~2493 | 78,471,585 |
| RGB-NIR, DEM, nDSM (EF1) | 77.68 77.49–77.87 | 86.60 86.46–86.75 | 96.55 96.52–96.58 | 87.75 87.50–88.03 | 85.64 85.55–85.71 | ~2650 | 78,475,425 |
| RGB-NIR, DEM, nDSM (LF) | 77.81 77.53–78.12 | 86.73 86.51–86.92 | 96.49 96.44–96.54 | 88.55 88.16–88.96 | 85.40 85.04–85.83 | ~3486 | 128,741,601 |
| RGB-NIR, DEM, nDSM (EF2) | 78.33 77.96–78.66 | 87.08 86.81–87.31 | 96.61 96.58–96.64 | 88.30 87.26–88.81 | 86.13 85.51–86.43 | ~3901 | 128,805,018 |
| Input Modalities | Mean IoU | Mean F1-Score | Overall Accuracy | Mean Precision | Mean Recall |
|---|---|---|---|---|---|
| RGB | 97.19 96.90–97.33 | 98.56 98.40–98.63 | 98.71 98.57–98.76 | 98.57 98.43–98.67 | 98.58 98.43–98.67 |
| RGB-NIR | 97.58 97.53–97.60 | 98.77 98.73–98.80 | 98.90 98.89–98.91 | 98.73 98.73–98.73 | 98.79 98.77–98.80 |
| RGB, DEM, nDSM | 97.62 97.57–97.67 | 98.78 98.73–98.83 | 98.92 98.88–98.94 | 98.74 98.70–98.77 | 98.83 98.80–98.87 |
| DEM, nDSM | 94.30 | 97.07 | 97.42 | 96.93 | 97.23 |
| RGB-NIR, DEM, nDSM (EF1) | 97.74 97.70–97.77 | 98.86 98.83–98.87 | 98.98 98.97–98.99 | 98.85 98.83–98.87 | 98.88 98.87–98.90 |
| RGB-NIR, DEM, nDSM (LF) | 97.68 97.63–97.70 | 98.83 98.80–98.87 | 98.95 98.94–98.97 | 98.77 98.73–98.80 | 98.88 98.87–98.90 |
| RGB-NIR, DEM, nDSM (EF2) | 97.75 97.70–97.79 | 98.87 98.87–98.87 | 98.99 98.97–99.00 | 98.84 98.83–98.87 | 98.89 98.87–98.93 |
| Classes | Mean IoU [%] | Mean F1-Score [%] | Overall Accuracy [%] | Mean Precision [%] | Mean Recall [%] |
|---|---|---|---|---|---|
| Direct application of the AttResU-Net with corrected ground truth data (without fine-tuning) | |||||
| 9 | 21.85 18.53–24.77 | 30.32 27.33–33.27 | 54.66 40.42–69.13 | 33.48 31.67–36.68 | 37.65 35.87–39.55 |
| 3 | 46.96 36.50–57.17 | 63.01 53.50–71.60 | 67.03 54.16–80.28 | 65.36 59.83–70.13 | 71.80 66.40–76.90 |
| Fine-tuning with uncorrected ground truth data | |||||
| 9 | 38.53 38.42–38.57 | 49.30 49.04–49.51 | 88.47 88.29–88.61 | 56.49 55.51–57.02 | 52.30 51.96–52.60 |
| 3 | 70.25 70.03–70.50 | 79.22 79.07–79.43 | 94.14 94.07–94.26 | 79.22 79.10–79.47 | 79.87 79.63–80.13 |
| Fine-tuning with corrected ground truth data | |||||
| 9 | 59.95 58.83–60.59 | 72.34 70.98–73.10 | 93.87 93.82–93.91 | 77.83 76.54–79.07 | 69.72 68.20–70.78 |
| 3 | 85.71 85.50–85.93 | 91.55 91.40–91.69 | 98.04 97.98–98.06 | 91.66 91.13–91.83 | 91.47 91.23–91.67 |
| Training from scratch with corrected ground truth data (randomly initialized weights) | |||||
| 9 | 58.15 57.72–58.68 | 70.46 69.92–71.08 | 93.45 93.07–93.65 | 76.73 74.12–77.99 | 67.70 66.76–68.21 |
| 3 | 85.17 84.89–85.37 | 91.13 90.93–91.27 | 98.01 97.95–98.05 | 91.59 91.37–91.83 | 90.68 90.49–90.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reinhardt, M.; Rommel, E.; Heuner, M.; Baschek, B. Applying Deep Learning Methods for a Large-Scale Riparian Vegetation Classification from High-Resolution Multimodal Aerial Remote Sensing Data. Remote Sens. 2025, 17, 2373. https://doi.org/10.3390/rs17142373
Reinhardt M, Rommel E, Heuner M, Baschek B. Applying Deep Learning Methods for a Large-Scale Riparian Vegetation Classification from High-Resolution Multimodal Aerial Remote Sensing Data. Remote Sensing. 2025; 17(14):2373. https://doi.org/10.3390/rs17142373
Chicago/Turabian StyleReinhardt, Marcel, Edvinas Rommel, Maike Heuner, and Björn Baschek. 2025. "Applying Deep Learning Methods for a Large-Scale Riparian Vegetation Classification from High-Resolution Multimodal Aerial Remote Sensing Data" Remote Sensing 17, no. 14: 2373. https://doi.org/10.3390/rs17142373
APA StyleReinhardt, M., Rommel, E., Heuner, M., & Baschek, B. (2025). Applying Deep Learning Methods for a Large-Scale Riparian Vegetation Classification from High-Resolution Multimodal Aerial Remote Sensing Data. Remote Sensing, 17(14), 2373. https://doi.org/10.3390/rs17142373









